Ch2例题与证明四-1
- 格式:doc
- 大小:216.00 KB
- 文档页数:12

§9.3 简单级数反应的动力学规律凡是反应速率只与反应物浓度有关,而且反应级数,无论是、、…或n都只是零或正整数的反应,统称为“简单级数反应”。
简单反应都是简单级数反应,但简单级数反应不一定就是简单反应,前已述及的HI气相合成反应就是一例。
具有相同级数的简单级数反应的速率遵循某些简单规律,本节将分析这类反应速率公式的微分形式、积分形式及其特征。
(1)一级反应反应速率与反应物浓度的一次方成正比的反应称为一级反应。
其速率公式可表示为(9.7)式中c为t时刻的反应物浓度。
将上式改写成的形式,积分可得(9.8)B为积分常数,其值可由t = 0时反应物起始浓度c0确定:B = ln c0。
故一级反应速率公式积分形式可表示为(9.9)或(9.10)或(9.11)使用这些公式可求算速率常数k1的数值,只要知道了k1和c0的值,即可求算任意t时刻反应物的浓度。
从(9.8)式可看出,以lnc对t作图应得一直线,其斜率即为k1。
如图9.2所示。
反应物浓度由c0消耗到c=c0/2所需的反应时间,称为反应的半衰期,以t1/2表示。
由(9.9)式可知,一级反应的t1/2表示式为(9.12)可以看出,一级反应的半衰期与反应物起始浓度c0无关。
许多分子的重排反应和热分解反应属一级反应。
还有些反应例如蔗糖水解实际上是二级反应,但由于水溶液中反应物之一H2O大大过量,其浓度在整个反应过程中可视为常数,故表观上表现为一级反应,这类反应称为“准一级反应”。
例题1 30℃时N2O5在CCl4中的分解反应为一级反应,由于N2O4和NO2均溶于CCl4中,只有O2能逸出,用量气管测定不同时刻逸出O2的体积有下列数据:t / s 0 2400 4800 7200 9600 12000 14400 16800 19200V(O2) / cm3 0 15.65 27.65 37.70 45.85 52.67 58.30 63.00 66.8584.85求算此反应的速率常数k1和半衰期t1/2。

专题1.4 正方形的性质与判定-重难点题型【北师大版】【题型1 正方形的性质(求角的度数)】【例1】(2021春•海珠区校级期中)如图,以正方形ABCD的一边AD为边向外作等边△ADE,则∠ABE 的度数是.【分析】由正方形的性质和等边三角形的性质可得AB=AD=AE,∠BAE=150°,进而可求得∠ABE=15°.【解答】解:∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∵△ADE是等边三角形,∴AD=AE,∠DAE=60°,∴∠BAE=∠BAD+DAE=150°,AB=AE,∴∠ABE=∠AEB,∴∠ABE=12(180°﹣∠BAE)=15°,故答案为:15°.【点评】本题考查了正方形的性质,等边三角形的性质,等腰三角形的性质,灵活运用这些性质进行推理是本题的关键.【变式1-1】(2021春•黄浦区期末)如图,E为正方形ABCD外一点,AE=AD,BE交AD于点F,∠ADE =75°,则∠AFB=°.【分析】根据等腰三角形的性质得∠AED=∠ADE=75°,由三角形内角和求出顶角∠DAE的度数,根据正方形的性质得△ABE为等腰三角形,再由直角三角形的两锐角互余得答案.【解答】解:∵AE=AD,∴∠AED=∠ADE=75°,∴∠DAE=180°﹣75°﹣75°=30°,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴AB=AE,∴∠ABE=∠AEB,∵∠BAE=90°+30°=120°,∴∠ABE=180°−120°2=30°,∴∠AFB=90°﹣30°=60°.故答案为:60.【点评】此题考查了正方形的性质,正方形的四个角都是直角,且各边都相等;在几何证明中常运用等边对等角和等角对等边来证明边相等或角相等;在三角形中,要熟练掌握三角形的内角和定理和直角三角形的两个锐角互余.【变式1-2】(2021春•海淀区校级月考)如图,在正方形ABCD内,以AB为边作等边△ABE,则∠BEG =°.【分析】本题通过正方形的性质得到AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°,在由等边三角形的性质得到AB=AE=BE,∠EAB=∠ABE=∠AEB=60°.进而得到∠ADE=∠AED=75°,从而得到答案即可.【解答】解:∵四边形ABCD是正方形,∴AB=BC=CD=DA,∠ABC=∠BCD=∠CDA=∠DAB=90°.又∵三角形ABE是等边三角形,∴AB=AE=BE,∠EAB=∠ABE=∠AEB=60°.∴∠DAE=∠DAB﹣∠EAB=90°﹣60°=30°,∴AE=AD,∴∠ADE=∠AED=75°,∴∠BEG=180°﹣∠DAE﹣∠AEB=180°﹣75°﹣60°=45°.故答案为:45.【点评】本题考查了正方形的性质,等边三角形的性质,熟练掌握基础知识是解题的关键.【变式1-3】(2021春•大兴区期中)在正方形ABCD外侧作直线AP,点B关于直线AP的对称点为E连接BE,DE,其中DE交直线AP于点F.连接AE,若∠P AB=20°,求∠ADF的度数.【分析】由对称的性质可得AE=AB,∠EAB=40°,即可求得∠EAD的度数,根据正方形的性质可得∠ADF=∠AED,进而可求解.【解答】解:∵点B关于直线AP的对称点为E,∴AP是对称轴,∴∠P AB=∠P AE=20°,∴∠EAB=2∠BAP=40°,AE=AB,∵四边形ABCD是正方形,∴∠BAD=90°,AB=AD,∴∠EAD=130°,∴AE=AD,∴∠ADF=∠AED,∴∠ADF=180°−130°2=25°.【点评】本题主要考查正方形的性质,对称的性质,等腰三角形的性质,证得AE=AD是解题的关键.【题型2 正方形的性质(求线段的长度)】【例2】(2021春•崇川区校级月考)如图,正方形ABCD的边长为1,点E在对角线BD上,且∠BAE=22.5°,则BE的长为.【分析】先由勾股定理求出BD,再求出AD=ED,根据题意列方程即可得到结论.【解答】解:过E作EF⊥AB于F,设EF=x,∵四边形ABCD是正方形,∴AB=AD,∠BAD=90°,∠ABD=∠ADB=45°,∴BD=√2AB=√2,EF=BF=x,∴BE=√2x,∵∠BAE=22.5°,∴∠DAE=90°﹣22.5°=67.5°,∴∠AED=180°﹣45°﹣67.5°=67.5°,∴∠AED=∠DAE,∴AD=ED,∴BD=BE+ED=√2x+1=√2,∴x=1−√2 2,∴BE=√2−1,故答案为:√2−1.【点评】本题考查了正方形的性质、勾股定理、等腰直角三角形的性质、等腰三角形的判定;证明三角形是等腰三角形,列出方程是解决问题的关键.【变式2-1】(2021春•余杭区月考)边长为4的正方形ABCD中,点E、F分别是AB、BC的中点,连结EC、FD,点G,H分别是EC、DF的中点,连结GH,则GH的长为.【分析】连接CH并延长交AD于P,连接PE,根据正方形的性质得到/A=90°,AD∥BC,AB=AD=BC=4,根据全等三角形的性质得到PD=CF=2√2,根据勾股定理和三角形的中位线定理即可得到结论.【解答】解:连接CH并延长交AD于P,连接PE,∵四边形ABCD 是正方形,∴∠A =90°,AD ∥BC ,AB =AD =BC =4,∵E ,F 分别是边AB ,BC 的中点,∴AE =CF =12×4=2,∵AD ∥BC ,∴∠DPH =∠FCH ,在△PDH 和△CFH 中,{∠DPH =∠FCH ∠DHP =∠FHC DH =FH,∴△PDH ≌△CFH (AAS ),∴PD =CF =2,∴AP =AD ﹣PD =2,∴PE =√AP 2+AE 2=√22+22=2√2,∵点G ,H 分别是EC ,FD 的中点,∴GH =12EP =√2.【点评】本题考查了正方形的性质,全等三角形的判定和性质,解题的关键是掌握正方形的性质,全等三角形的判定和性质.【变式2-2】(2021春•南开区期中)如图,正方形ABCD 和正方形CEFG ,点G 在CD 上,AB =5,CE =2,T 为AF 的中点,求CT 的长.【分析】连接AC ,CF ,如图,根据正方形的性质得到AC =√2,AB =5√2,CF =√2CE =2√2,∠ACD =45°,∠GCF =45°,则利用勾股定理得到AF =√58,然后根据直角三角形斜边上的中线性质得到CT 的长.【解答】解:连接AC 、CF ,如图,∵四边形ABCD 和四边形CEFG 都是正方形,∴AC =√2AB =5√2,CF =√2CE =2√2,∠ACD =45°,∠GCF =45°,∴∠ACF =45°+45°=90°,在Rt △ACF 中,AF =√(5√2)2+(2√2)2=√58,∵T 为AF 的中点,∴CT =12AF =√582,∴CT 的长为√582. 【点评】本题考查了正方形的性质:正方形的四条边都相等,四个角都是直角;正方形的两条对角线相等,互相垂直平分,并且每条对角线平分一组对角;正方形具有四边形、平行四边形、矩形、菱形的一切性质,也考查了直角三角形斜边上的中线性质.【变式2-3】(2021春•綦江区校级月考)正方形ABCD 的边长为3,E 、F 分别是AB 、BC 边上的点,且∠EDF =45°.(1)求证:EF =AE +CF ;(2)当AE =1时,求EF 的长.【分析】(1)延长BC 至H ,使CH =AE ,连接DH ,可得△DAE ≌△DCH ,则DE =DH ,∠ADE =∠CDH ;由于∠ADE +∠FDC =45°,所以∠FDC +∠HCD =45°,可得∠EDF =∠HDF ,这样△EDF ≌△HDF ,可得EF =FH ,结论得证;(2)设EF =x ,由(1)的结论可知CF =x ﹣1,BF =4﹣x ,在Rt △BEF 中,由勾股定理列出方程,解方程即可求解.【解答】解:(1)证明:延长BC 至H ,使CH =AE ,连接DH ,如图,∵四边形ABCD 是正方形,∴AD =CD ,∠A =∠DCE =90°.∴△DAE ≌△DCH (SAS ).∴DE =DH ,∠ADE =∠CDH .∵∠ADC =90°,∠EDF =45°,∴∠ADE +∠FDC =45°.∴∠FDC +∠CDH =45°.即∠FDH =45°.∴∠EDF =∠FDH =45°.在△EDF 和△HDF 中,{DE =DH ∠EDF =∠HDF DF =DF.∴△EDF ≌△HDF (SAS ).∴EF =FH .∵FH =FC +CH =FC +AE ,∴EF =AE +FC .(2)设EF =x ,则FH =x .∵正方形ABCD 的边长为3,∴AB =BC =3.∵AE =1,∴BE=2,CH=1.∴FC=x﹣1.∴BF=BC﹣CF=3﹣(x﹣1)=4﹣x.在Rt△BEF中,∵BE2+BF2=EF2,∴22+(4﹣x)2=x2.解得:x=5 2.∴EF=5 2.【点评】本题主要考查了正方形的性质,三角形的全等的判定与性质,勾股定理.证明一条线段等于两条线段的和的题目一般采用补短法或截长法,通过构造三角形的全等来解决.【题型3 正方形的性质(求面积、周长)】【例3】(2020春•仪征市期末)正方形ABCD中,AB=4,点E、F分别在BC、CD上,且BE=CF,线段BF、AE相交于点O,若图中阴影部分的面积为14,则△ABO的周长为.【分析】由“SAS”可证△ABE≌△BCF,可得S△ABE=S△BCF,∠BAE=∠CBF,可求S△ABO=12×(4×4﹣14)=1,可得2AO•BO=4,由勾股定理可求AO+BO的值,即可求解.【解答】解:∵四边形ABCD是正方形,∴AB=BC,∠ABC=∠BCD=90°,又∵BE=CF,∴△ABE≌△BCF(SAS),∴S△ABE=S△BCF,∠BAE=∠CBF,∴S△ABO=S四边形ECFO,∠BAE+∠AEB=90°=∠CBF+∠AEB=∠AOB,∵图中阴影部分的面积为14,∴S△ABO=12×(4×4﹣14)=1,∴12×AO ×BO =1, ∴2AO •BO =4,∵AB 2=AO 2+BO 2=16,∴(AO +BO )2=20,∴AO +BO =2√5,∴△ABO 的周长=AB +AO +BO =2√5+4,故答案为:2√5+4.【点评】本题考查了正方形的性质,全等三角形的判定和性质,勾股定理,求出AO +BO 的值是本题的关键.【变式3-1】(2021春•仓山区期中)如图,在正方形ABCD 中,AB =4,点E ,F 分别在CD ,AD 上,CE =DF ,BE ,CF 相交于点H .若图中阴影部分的面积与正方形ABCD 的面积之比为3:4,则△BCH 的周长为( )A .2√5−4B .2√5C .2√5+4D .2√6+4【分析】先计算出正方形的面积,再由比例求出空白部分的面积,通过证明△BCE ≌△CDF 可求解S △BCH ,∠BHC =90°,再由勾股定理及完全平方公式可求解BH +CH 的长,即可求出△BCG 的周长﹒【解答】解:∵四边形ABCD 为正方形,BC =CD =AB =4,∠BCE =∠CDF =90°,∴S 正方形ABCD =16,∵S 阴影:S 正方形ABCD =3:4,∴S 阴影=34×16=12, ∴S 空白=16﹣12=4,在△BCE 和△CDF 中,{BC =CD ∠BCE =∠D =90°CE =DF,∴△BCE ≌△CDF (SAS ),∴S△BCH=S四边形EDFH=2,∠HBC=∠DCF,∵∠DCF+∠HCB=90°,∴∠HBC+∠HCB=90°,∴∠BHC=90°,∴BH2+CH2=BC2=16,BH•CH=4,∴(BH+CH)2=BH2+CH2+2BH•CH=16+2×4=24,∴BH+CH=2√6,∴△BCH的周长为BH+CH+BC=2√6+4,故选:D.【点评】本题考查了正方形的性质,全等三角形的判定与性质及面积的和差相关知识,关键是证明全等两个三角形面积全等,得到△BCH面积.【变式3-2】(2021春•海淀区校级期中)如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=6,F为DE的中点.若OF的长为1,则△CEF的周长为()A.14B.16C.18D.12【分析】由正方形的性质及三角形的中位线可求得BE=2,由直角三角形斜边上的中线可求得△CEF的周长为ED+EC,利用勾股定理可求解ED的长,进而可求解.【解答】解:在正方形ABCD中,BO=DO,BC=CD,∠BCD=90°,∵F为DE的中点,∴OF为△DBE的中位线,ED=2CF=2EF,∴△CEF的周长为EF+EC+FC=ED+EC,∵OF=1,∴BE=2OF=2,∵CE=6,∴BC=BE+CE=2+6=8,∴CD=BC=8,在Rt△CED中,∠ECD=90°,CD=8,CE=6,∴ED=√CD2+CE2=√82+62=10,∴△CEF的周长为EF+EC+FC=ED+EC=10+6=16,故选:B.【点评】本题主要考查勾股定理,正方形的性质,三角形的中位线,求解ED的长是解题的关键.【变式3-3】(2021春•河西区期中)将5个边长为2cm的正方形按如图所示摆放,点A1,A2,A3,A4是正方形的中心,则这个正方形重叠部分的面积和为()A.2cm2B.1cm2C.4cm2D.6cm2【分析】在正方形ABCD中,作A1E⊥AD,A1F⊥DC,即可证得:△A1EN≌△A1MF,则四边形A1MA2N的面积=四边形EA1F A2的面积=14正方形ABCD的面积,据此即可求解.【解答】解:如图,在正方形ABCD中,作A1E⊥AD,A1F⊥DC,两边相交于M和N,∠A1EN=∠A1MF=90°,∠EA1N+∠ENA1=90°,∠EA1N+∠F A1M=90°,∴∠ENA1=∠F A1M,A1E=A1F,∴△A 1EN ≌△A 1MF (ASA ),∴四边形A 1MA 2N 的面积=四边形EA 1F A 2的面积=14正方形ABCD 的面积,同理可证,另外三个阴影四边形的面积都等于14正方形ABCD 的面积, ∴图中重叠部分(阴影部分)的面积和=正方形ABCD 的面积=4cm 2,故选:C .【点评】本题主要考查了正方形的性质,正确作出辅助线,证得:四边形A 1MA 2N 的面积=四边形EA 1F A 2的面积=14正方形ABCD 的面积是解题的关键.【题型4 正方形的性质(探究数量关系)】【例4】(2020秋•和平区期末)如图,若在正方形ABCD 中,点E 为CD 边上一点,点F 为AD 延长线上一点,且DE =DF ,则AE 与CF 之间有怎样的数量关系和位置关系?请说明理由.【分析】延长AE 交CF 于点G ,根据四边形ABCD 是正方形,证明△ADE ≌△CDF ,进而可得AE =CF ,AE ⊥CF .【解答】解:AE =CF ,AE ⊥CF ,理由如下:如图,延长AE 交CF 于点G ,∵四边形ABCD 是正方形,∴AD =CD ,∠ADC =∠CDE =90°,在△ADE 和△CDF 中,{AD =CD ∠ADE =∠CDF DE =DF,∴△ADE ≌△CDF (SAS ),∴AE =CF ,∠DAE =∠DCF ,∵∠DCF +∠F =90°,∴∠DAE +∠F =90°,∴AG ⊥CF ,即AE ⊥CF .∴AE =CF ,AE ⊥CF .【点评】本题考查了正方形的性质、全等三角形的判定与性质,解决本题的关键是掌握正方形的性质.【变式4-1】(2020春•西山区期末)如图(1),正方形ABCD 的对角线AC ,BD 相交于点O ,E 是AC 上一点,连接DE ,过点A 作AM ⊥DE ,垂足为M ,AM 与BD 相交于点F .(1)直接写出OE 与OF 的数量关系: ;(2)如图(2)若点E 在AC 的延长线上,AM ⊥DE 于点M ,AM 交BD 的延长线于点F ,其他条件不变.试探究OE 与OF 的数量关系,并说明理由.【分析】(1)根据正方形的性质对角线垂直且平分,得到OB =OA ,又因为AM ⊥BE ,所以∠MEA +∠MAE =90°=∠AFO +∠MAE ,从而求证出△AOF ≌△BOE ,得到OE =OF .(2)由“ASA ”可证△AOF ≌△BOE ,得到OE =OF .【解答】解:(1)∵正方形ABCD 的对角线AC 、BD 相交于点O ,AM ⊥DE ,∴∠AOD =∠DOE =∠AME =90°,OA =OD ,∴∠MEA +∠MAE =90°=∠AFO +∠MAE ,∴∠AFO =∠MEA ,在△AOF 和△DOE 中,{∠AFO =∠MEA AO =DO ∠AOF =∠DOE =90°,∴△AOF ≌△BOE (ASA ),∴OE =OF ,故答案为:OE =OF ;(2)OE =OF ,理由如下:∵正方形ABCD 的对角线AC 、BD 相交于点O ,AM ⊥DE ,∴∠AOD =∠DOE =∠AME =90°,OA =OD ,∴∠MEA +∠MAE =90°=∠AFO +∠MAE ,∴∠AFO =∠MEA ,在△AOF 和△DOE 中,{∠AFO =∠MEA AO =DO ∠AOF =∠DOE =90°,∴△AOF ≌△BOE (ASA ),∴OE =OF .【点评】本题考查了正方形的性质,全等三角形的判定和性质,掌握全等三角形的判定定理是本题的关键.【变式4-2】(2020春•安阳县期末)四边形ABCD 是正方形,G 是直线BC 上任意一点,BE ⊥AG 于点E ,DF ⊥AG 于点F ,当点G 在BC 边上时(如图1),易证DF ﹣BE =EF .(1)当点G 在BC 延长线上时,在图2中补全图形,写出DF 、BE 、EF 的数量关系,并证明.(2)当点G 在CB 延长线上时,在图3中补全图形,写出DF 、BE 、EF 的数量关系,不用证明.【分析】由ABCD 是正方形,得到AB =DA 、AB ⊥AD ,由BE ⊥AG 、DF ⊥AG ,结合题干得到∠ABE =∠DAF ,于是得出△ABE ≌△DAF ,即可AF =BE .(1)同理证明△ABE ≌△DAF ,得AF =BE ,DF =AE ,根据图2可得结论;(2)同理证明△ABE ≌△DAF ,得AF =BE ,DF =AE ,根据图3可得结论.【解答】证明:如图1,∵ABCD 是正方形,∴AB =DA 、AB ⊥AD .∵BE ⊥AG 、DF ⊥AG ,∴∠AEB =∠AFD =90°,又∵∠BAE +∠DAF =90°,∠BAE +∠ABE =90°,∴∠ABE =∠DAF ,在△ABE 和△DAF 中,{∠AEB =∠AFD ∠ABE =∠DAF AB =AD,∴△ABE ≌△DAF (AAS ),∴AF =BE ,DF =AE ,∴DF ﹣BE =AE ﹣AF =EF .(1)如图2,DF 、BE 、EF 的数量关系是:BE =DF +EF ,理由是:∵ABCD 是正方形,∴AB =DA 、AB ⊥AD .∵BE ⊥AG 、DF ⊥AG ,∴∠AEB =∠AFD =90°,又∵∠BAE +∠DAF =90°,∠BAE +∠ABE =90°,∴∠ABE =∠DAF ,在△ABE 和△DAF 中,{∠AEB =∠AFD ∠ABE =∠DAF AB =AD,∴△ABE ≌△DAF (AAS ),∴AF =BE ,DF =AE ,∴BE =AF =AE +EF =DF +EF ;(2)如图3,DF 、BE 、EF 的数量关系是:EF =DF +BE ;理由是:∵ABCD 是正方形,∴AB =DA ,AB ⊥AD .∵BE ⊥AG ,DF ⊥AG ,∴∠AEB =∠AFD =90°,又∵∠BAE +∠DAF =90°,∠BAE +∠ABE =90°,∴∠ABE =∠DAF ,在△ABE 和△DAF 中,{∠AEB =∠AFD ∠ABE =∠DAF AB =AD,∴△ABE ≌△DAF (AAS ),∴AF =BE ,DF =AE ,∴EF =AE +AF =DF +BE .【点评】本题主要考查正方形的性质,解答本题的关键是熟练掌握全等三角形的判定与性质定理,此题难度适中.【变式4-3】(2021春•天河区校级期中)如图,已知四边形ABCD 是正方形,对角线AC 、BD 相交于O .(1)如图1,设E 、F 分别是AD 、AB 上的点,且∠EOF =90°,线段AF 、BF 和EF 之间存在一定的数量关系.请你用等式直接写出这个数量关系;(2)如图2,设E 、F 分别是AB 上不同的两个点,且∠EOF =45°,请你用等式表示线段AE 、BF 和EF 之间的数量关系,并证明.【分析】(1)首先证明△EOA ≌△FOB ,推出AE =BF ,从而得出结论;(2)在BC 上取一点H ,使得BH =AE .由△OAE ≌△OBH ,推出AE =BH ,∠AOE =∠BOH ,OE =OH ,由△FOE ≌△FOH ,推出EF =FH ,由∠FBH =90°,推出FH 2=BF 2+BH 2,由此即可解答.【解答】解:(1)EF 2=AF 2+BF 2.理由:如图1,∵四边形ABCD 是正方形,∴OA =OB ,∠OAE =∠OBF =45°,AC ⊥BD ,∴∠EOF =∠AOB =90°,∴∠EOA =∠FOB ,在△EOA 和△FOB 中,{∠EOA =∠FOB OA =OB ∠OAE =∠OBF,∴△EOA ≌△FOB (ASA ),∴AE =BF ,在Rt △EAF 中,EF 2=AE 2+AF 2=AF 2+BF 2;(2)在BC 上取一点H ,使得BH =AE .∵四边形ABCD 是正方形,∴OA =OB ,∠OAE =∠OBH ,∠AOB =90°,在△OAE 和△OBH 中,{OA =OB ∠OAE =∠OBH AE =BH∴△OAE ≌△OBH (SAS ),∴AE =BH ,∠AOE =∠BOH ,OE =OH ,∵∠EOF =45°,∴∠AOE +∠BOF =45°,∴∠BOF +∠BOH =45°,∴∠FOE =∠FOH =45°,在△FOE 和△FOH 中•,{OF =OF ∠FOE =∠FOH OE =OH,∴△FOE ≌△FOH (SAS ),∴EF =FH ,∵∠FBH =90°,∴FH 2=BF 2+BH 2,∴EF 2=BF 2+AE 2,【点评】本题考查正方形的性质、全等三角形的判定和性质,解题的关键是学会添加常用辅助线,构造全等三角形解决问题.【题型5 正方形的性质综合应用】【例5】(2020秋•周村区期末)(1)如图1的正方形ABCD 中,点E ,F 分别在边BC ,CD 上,∠EAF =45°,延长CD 到点G ,使DG =BE ,连接EF ,AG .求证:EF =FG ;(2)如图2,等腰Rt △ABC 中,∠BAC =90°,AB =AC ,点M ,N 在边BC 上,且∠MAN =45°.若BM =1,CN =3,求MN 的长.【分析】(1)证△ADG ≌△ABE ,△F AE ≌△F AG ,根据全等三角形的性质求出即可;(2)过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .通过证明△ABM ≌△ACE (SAS )推知全等三角形的对应边AM =AE 、对应角∠BAM =∠CAE ;然后由等腰直角三角形的性质和∠MAN =45°得到∠MAN =∠EAN =45°,所以△MAN ≌△EAN (SAS ),故全等三角形的对应边MN =EN ;最后由勾股定理得到EN 2=EC 2+NC 2即MN 2=BM 2+NC 2.【解答】(1)证明:在正方形ABCD 中,∠ABE =∠ADG ,AD =AB ,在△ABE 和△ADG 中,{AD =AB ∠ABE =∠ADG DG =BE,∴△ABE ≌△ADG (SAS ),∴∠BAE =∠DAG ,AE =AG ,∴∠EAG =90°,在△F AE 和△GAF 中,{AE =AG∠EAF =∠FAG =45°AF =AF,∴△F AE ≌△GAF (SAS ),∴EF =FG ;(2)解:如图,过点C 作CE ⊥BC ,垂足为点C ,截取CE ,使CE =BM .连接AE 、EN .∵AB =AC ,∠BAC =90°,∴∠B =∠ACB =45°.∵CE ⊥BC ,∴∠ACE =∠B =45°.在△ABM 和△ACE 中,{AB =AC ∠B =∠ACE BM =CE ,∴△ABM ≌△ACE (SAS ).∴AM =AE ,∠BAM =∠CAE .∵∠BAC =90°,∠MAN =45°,∴∠BAM +∠CAN =45°.于是,由∠BAM =∠CAE ,得∠MAN =∠EAN =45°.在△MAN 和△EAN 中,{AM =AE ∠MAN =∠EAN AN =AN,∴△MAN ≌△EAN (SAS ).∴MN =EN .在Rt △ENC 中,由勾股定理,得EN 2=EC 2+NC 2.∴MN 2=BM 2+NC 2.∵BM =1,CN =3,∴MN 2=12+32,∴MN =√10.【点评】本题主要考查正方形的性质,全等三角形的判定和性质、等腰直角三角形的性质以及勾股定理的综合应用,解题的关键是学会添加常用辅助线,构造全等三角形解决问题;【变式5-1】(2021春•余杭区月考)已知正方形ABCD 如图所示,连接其对角线AC ,∠BCA 的平分线CF 交AB 于点F ,过点B 作BM ⊥CF 于点N ,交AC 于点M ,过点C 作CP ⊥CF ,交AD 延长线于点P .(1)求证:BF =DP ;(2)若正方形ABCD 的边长为4,求△ACP 的面积;(3)求证:CP =BM +2FN .【分析】(1)由“ASA ”可证△CDP ≌△CBF ,可得BF =DP ;(2)根据等角对等边易证AP =AC ,根据勾股定理求得AC 的长,然后根据三角形的面积公式即可求解;(3)由全等三角形的性质可得CP =CF ,在CN 上截取NH =FN ,连接BH ,则可以证明△AMB ≌BHC ,得到CH=BM,即可证得.【解答】证明:(1)∵四边形ABCD是正方形,∴AB=BC=CD=AD,∠CAD=∠ACD=45°,∵CP⊥CF,∴∠FCP=90°=∠BCD,∴∠BCF=∠DCP,∵CD=CB,∠CBF=∠CDP=90°,∴△CDP≌△CBF(ASA)∴BF=DP;(2)∵CF平分∠ACB,∴∠ACF=∠BCF=22.5°,∴∠BFC=67.5°,∵△CDP≌△CBF,∴∠P=∠BFC=67.5°,且∠CAP=45°,∴∠ACP=∠P=67.5°,∴AC=AP,∵AC=√2AB=4√2,∴S△ACP=12AP×CD=8√2;(3)在CN上截取NH=FN,连接BH,∵△CDP≌△CBF,∴CP=CF,∵FN=NH,且BN⊥FH,∴BH=BF,∴∠BFH=∠BHF=67.5°,∴∠FBN=∠HBN=∠BCH=22.5°,∴∠HBC=∠BAM=45°,∵AB=BC,∠ABM=∠BCH,∴△AMB≌△BHC(ASA),∴CH=BM,∴CF=BM+2FN,∴CP=BM+2FN.【点评】本题是正方形的性质,全等三角形的判定与性质,等腰三角形的性质等知识,正确作出辅助线是关键.【变式5-2】(2021春•莆田期末)如图1,在正方形ABCD中,∠AEF=90°,且EF交正方形外角的平分线CF于点F.(1)若点E是BC边上的中点,求证:AE=EF;(2)如图2,若点E是BC的延长线上(除C点外)的任意一点,其他条件不变,那么结论“AE=EF”是否仍然成立,若成立,请写出证明过程;若不成立,请说明理由;(3)如图3,若点E是BC边上的任意点一,在AB边上是否存在点M,使得四边形DMEF是平行四边形?若存在,请给予证明;若不存在,请说明理由.【分析】(1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;(2)成立,延长BA到M,使AM=CE,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;(3)存在,作DM⊥AE于AB交于点M,则有:DM∥EF,连接ME、DF,证明△ADM≌△BAE(ASA),得到DM=AE,由(1)AE=EF,所以DM=EF,所以四边形DMEF为平行四边形.【解答】(1)证明:取AB的中点H,连接EH;如图1所示∵四边形ABCD 是正方形,AE ⊥EF ;∴∠1+∠AEB =90°,∠2+∠AEB =90°∴∠1=∠2,∵BH =BE ,∠BHE =45°,且∠FCG =45°,∴∠AHE =∠ECF =135°,AH =CE ,在△AHE 和△ECF 中,{∠1=∠2AH =CE ∠AHE =∠ECF ,∴△AHE ≌△ECF (ASA ),∴AE =EF ;(2)解:AE =EF 成立,理由如下:如图2,延长BA 到M ,使AM =CE ,∵∠AEF =90°,∴∠FEG +∠AEB =90°.∵∠BAE +∠AEB =90°,∴∠BAE =∠FEG ,∴∠MAE =∠CEF .∵AB =BC ,∴AB +AM =BC +CE ,即BM =BE .∴∠M =45°,∴∠M =∠FCE .在△AME 与△ECF 中,{∠MAE =∠CEF AM =CE ∠M =∠FCE,∴△AME ≌△ECF (ASA ),∴AE =EF .(3)存在,理由如下:点E 是BC 边上的中点,如图3,作DM ⊥AE 于AB 交于点M ,则有:DM ∥EF ,连接ME 、DF ,在△ADM 与△BAE 中,{∠ADM =∠BAE AD =AB ∠DAM =∠ABE ,∴△ADM ≌△BAE (ASA ),∴DM =AE ,由(1)AE =EF ,∴DM =EF ,∴四边形DMEF 为平行四边形.【点评】此题考查学生对正方形的性质及全等三角形判定的理解及运用,解决本题的关键是作出辅助线.【变式5-3】(2021春•江津区期中)在正方形ABCD 中,对角线AC 、BD 相交于点O ,点E 在线段OC 上,点F 在线段AB 上,连接BE ,连接EF 交BD 于点M ,已知∠AEB =∠OME .(1)如图1,求证:EB =EF ;(2)如图2,点N 在线段EF 上,AN =EN ,AN 延长线交DB 于H ,连接DF ,求证:DF =√2AH .【分析】(1)依据四边形ABCD是正方形,即可得出AC⊥BD,∠1=∠2=45°,进而得到∠5=∠FBE,即可得到EF=EB;(2)连接DE,先判定△AOH≌△BOE,即可得出AH=BE,再判定△DCE≌△BCE,即可得到DE=BE =AH=EF,再根据△DEF是等腰直角三角形,即可得出结论.【解答】证明:(1)如图所示:∵四边形ABCD是正方形,∴AC⊥BD,∠1=∠2=45°,∴在Rt△OME和Rt△OEB中,∠3+∠OME=∠4+∠OEB=90°,∵∠OME=∠OEB,∴∠3=∠4,∴∠5=∠1+∠3=∠2+∠4=∠FBE,∴EF=EB;(2)连接DE,∵AN =EN ,∴∠3=∠5,∵∠3=∠4,∴∠4=∠5,∵四边形ABCD 是正方形,∴OA =OB ,AC ⊥BD ,∴∠7=∠8=90°,在△AOH 和△BOE 中,{∠5=∠4OA =OB ∠7=∠8,∴△AOH ≌△BOE (ASA ),AH =BE ,∵四边形ABCD 是正方形,∴DC =BC ,∠1=∠2=45°,在△DCE 和△BCE 中,{DC =BC ∠1=∠2CE =CE,∴△DCE ≌△BCE (SAS ),∴DE =BE =AH =EF ,∵AC ⊥BD ,∴∠6=∠AEB ,∵∠3=∠4,∠4+∠AEB =90°,∴∠3+∠6=90°,即∠DEF =90°,∴△DEF 是等腰直角三角形,∴DF =√DE 2+EF 2=√2EF =√2AH .【点评】本题主要考查了正方形的性质,全等三角形的判定与性质,关键是对全等三角形的判断.③还可以先判定四边形是平行四边形,再用1或2进行判定.【题型6 判定正方形成立的条件】【例6】(2020春•上蔡县期末)下列说法正确的个数是()①对角线互相垂直或有一组邻边相等的矩形是正方形;②对角线相等或有一个角是直角的菱形是正方形;③对角线互相垂直且相等的平行四边形是正方形;④对角线互相垂直平分且相等的四边形是正方形.A.1个B.2个C.3个D.4个【分析】根据正方形的判定、线段垂直平分线的性质、平行四边形的性质和矩形的性质即可求解.【解答】解:①对角线互相垂直或有一组邻边相等的矩形是正方形,故①正确;②对角线相等或有一个角是直角的菱形是正方形,故②正确;③对角线互相垂直且相等的平行四边形是正方形,故③正确;④对角线互相垂直平分且相等的四边形是正方形,故④正确;综上所述,正确的个数为4个,故选:D.【点评】本题考查了正方形的判定、线段垂直平分线的性质、平行四边形的性质和矩形的性质,解题关键是逐个判断即可得出答案.【变式6-1】(2020春•建湖县期中)如图,在△ABC中,∠ACB=90°,BC的垂直平分线EF交BC于点D,交AB于点E,且BE=BF,添加一个条件,仍不能证明四边形BECF为正方形的是()A.BC=AC B.BD=DF C.AC=BF D.CF⊥BF【分析】根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC进而得出四边形BECF是菱形;由菱形的性质知,以及菱形与正方形的关系,进而分别分析得出即可.【解答】解:∵EF垂直平分BC,∴BE=EC,BF=CF,∵BF=BE,∴BE=EC=CF=BF,∴四边形BECF是菱形;当BC=AC时,∵∠ACB=90°,则∠A=45°时,菱形BECF是正方形.∵∠A=45°,∠ACB=90°,∴∠EBC=45°,∴∠EBF=2∠EBC=2×45°=90°,∴菱形BECF是正方形.故选项A正确,但不符合题意;当BD=DF时,利用正方形的判定得出,菱形BECF是正方形,故选项B正确,但不符合题意;当AC=BF时,无法得出菱形BECF是正方形,故选项C错误,符合题意;当CF⊥BF时,利用正方形的判定得出,菱形BECF是正方形,故选项D正确,但不符合题意.故选:C.【点评】本题考查了菱形的判定和性质及中垂线的性质、直角三角形的性质、正方形的判定等知识,熟练掌握正方形的相关定理是解题关键.【变式6-2】(2020春•开原市校级月考)已知四边形ABCD是平行四边形,再从四个条件中,选两个作为补充条件后,使得四边形ABCD是正方形,现有下列四种选法,其中错误的是()①AB=BC,②∠ABC=90˚,③AC=BD,④AC⊥BDA.选①②B.选①③C.选②③D.选②④【分析】根据要判定四边形是正方形,则需能判定它既是菱形又是矩形进而分别分析得出即可.【解答】解:A、由①得有一组邻边相等的平行四边形是菱形,由②得有一个角是直角的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;B、由①得有一组邻边相等的平行四边形是菱形,由③得对角线相等的平行四边形是矩形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;C、由②得有一个角是直角的平行四边形是矩形,由③得对角线相等的平行四边形是矩形,所以不能得出平行四边形ABCD是正方形,错误,故本选项符合题意.D、由②得有一个角是直角的平行四边形是矩形,由④得对角线互相垂直的平行四边形是菱形,所以平行四边形ABCD是正方形,正确,故本选项不符合题意;故选:C.【点评】本题考查了正方形的判定方法:①先判定四边形是矩形,再判定这个矩形有一组邻边相等;②先判定四边形是菱形,再判定这个矩形有一个角为直角.③还可以先判定四边形是平行四边形,再用1或2进行判定.【变式6-3】(2020秋•陕西期中)如图,E、F、G、H分别是AB、BC、CD、DA的中点.要使四边形EFGH 是正方形,BD、AC应满足的条件是.【分析】依据条件先判定四边形EFGH为菱形,再根据∠FEH=90°,即可得到菱形EFGH是正方形.【解答】解:满足的条件应为:AC=BD且AC⊥BD.理由:∵E,F,G,H分别是边AB、BC、CD、DA的中点,∴在△ADC中,HG为△ADC的中位线,∴HG∥AC且HG=12AC;同理EF∥AC且EF=12AC,同理可得EH=12BD,则HG∥EF且HG=EF,∴四边形EFGH为平行四边形,又∵AC=BD,∴EF=EH,∴四边形EFGH为菱形,∵AC⊥BD,EF∥AC,∴EF⊥BD,∵EH∥BD,∴EF⊥EH,∴∠FEH=90°,∴菱形EFGH是正方形.故答案为:AC=BD且AC⊥BD.【点评】此题考查了中点四边形的性质、三角形中位线定理以及正方形的判定.解题时注意:三角形的中位线平行于第三边,并且等于第三边的一半.【题型7 正方形判定的证明】【例7】(2020秋•富平县期末)如图,已知四边形ABCD是矩形,点E在对角线AC上,点F在边CD上(点F与点C、D不重合),BE⊥EF,且∠ABE+∠CEF=45°.求证:四边形ABCD是正方形.【分析】作EM⊥BC于点M,可证EM∥AB,可得∠ABE=∠BEM,∠BAC=∠CEM,由角的数量关系可得∠CEM=45°=∠BAC,可证AB=BC,可得结论.【解答】证明:如图,作EM⊥BC于点M,∵四边形ABCD是矩形,∴AB⊥BC,∴EM∥AB,∴∠ABE=∠BEM,∠BAC=∠CEM,∵∠ABE+∠CEF=45°,∴∠BEM+∠CEF=45°,∵BE⊥EF,∴∠CEM=45°=∠BAC,∴∠BAC=∠ACB=45°,∴AB=BC,∴矩形ABCD是正方形.【点评】本题考查了正方形的判定,矩形的性质,灵活运用这些性质进行推理是本题的关键.【变式7-1】(2021春•娄星区校级期中)已知,如图,在Rt△ABC中,∠ACB=90°,E是两锐角平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.【分析】过E作EM⊥AB,根据角平分线的性质可得EF=ED=EM.再证明四边形EFDC是矩形,可根据邻边相等的矩形是正方形得到四边形CDEF是正方形.【解答】证明:过E作EM⊥AB,∵AE平分∠CAB,∴EF=EM,∵EB平分∠CBA,∴EM=ED,∴EF=ED,∵ED⊥BC,EF⊥AC,△ABC是直角三角形,∴∠CFE=∠CDE=∠C=90°,∴四边形EFDC是矩形,∵EF=ED,∴四边形CDEF是正方形.【点评】此题主要考查了正方形的判定,关键是掌握邻边相等的矩形是正方形.【变式7-2】(2020春•新乡期末)如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P 作PM ⊥AD ,PN ⊥CD ,垂足分别为M 、N .(1)求证:∠ADB =∠CDB ;(2)若∠ADC = °时,四边形MPND 是正方形,并说明理由.【分析】(1)根据角平分线的性质和全等三角形的判定方法证明△ABD ≌△CBD ,由全等三角形的性质即可得到:∠ADB =∠CDB ;(2)由三个角是直角的四边形是矩形,可证四边形MPND 是矩形,再根据邻边相等的矩形是正方形即可证明四边形MPND 是正方形.【解答】证明:(1)∵对角线BD 平分∠ABC ,∴∠ABD =∠CBD ,在△ABD 和△CBD 中,{AB =BC ∠ABD =∠CBD BD =BD,∴△ABD ≌△CBD (SAS ),∴∠ADB =∠CDB ;(2)当∠ADC =90°时,四边形MPND 是正方形,理由如下:∵PM ⊥AD ,PN ⊥CD ,∴∠PMD =∠PND =90°,∵∠ADC =90°,∴四边形MPND 是矩形,∵∠ADB =∠CDB ,∴∠ADB =45°,∵∠PMD =90°,∴∠MPD =∠PDM =45°,∴PM=MD,∴矩形MPND是正方形,故答案为:90.【点评】本题考查了正方形的判定,全等三角形的判定和性质,角平分线的性质,矩形的判定和性质,解题的关键是熟记各种几何图形的性质和判定.【变式7-3】(2020秋•渠县期末)如图,在△ABC中,AB=AC,D是BC中点、F是AC中点,AN是△ABC的外角∠MAC的平分线,延长DF交AN于点E,连接CE.(1)求证:四边形ADCE是矩形;(2)若AB=BC=4,则四边形ADCE的面积为多少?(3)直接回答:当△ABC满足时,四边形ADCE是正方形.【分析】(1)根据AN是△ABC外角∠CAM的平分线,推得∠MAE=12(∠B+∠ACB),再由∠B=∠ACB,得∠MAE=∠B,则AN∥BC,根据三角形中位线的性质得FD∥AB,可得四边形ABDE为平行四边形,则AE=BD=CD,得出四边形ADCE为平行四边形,再证出AD⊥AE即可得出四边形ADCE为矩形.(2)由(1)知四边形ADCE是矩形,由条件可证明△ABC为等边三角形,求出CD和AD长,则四边形ADCE的面积可求出;(3)由(1)知四边形ADCE是矩形,增加条件能使AD=DC即可【解答】(1)证明:∵AN是△ABC外角∠CAM的平分线,∴∠MAE=12∠MAC,∵∠MAC=∠B+∠ACB,∵AB=AC,∴∠B=∠ACB,。

物理化学练习(一)一、选择题1. 对于理想气体的内能有下述四种理解:(1) 状态一定,内能也一定(2) 对应于某一状态的内能是可以直接测定的(3) 对应于某一状态,内能只有一个数值,不可能有两个或两个以上的数值(4) 状态改变时,内能一定跟着改变其中正确的是:( )(A) (1),(2) (B) (3),(4)(C) (2),(4) (D) (1),(3)2. 下面陈述中,正确的是:( )(A) 虽然Q和W是过程量,但由于Q V =ΔU,Q p=ΔH,而U和H是状态函数,所以Q V和Q p是状态函数(B) 热量是由于温度差而传递的能量,它总是倾向于从含热量较多的高温物体流向含热量较少的低温物体(C) 封闭体系与环境之间交换能量的形式非功即热(D) 两物体之间只有存在温差,才可传递能量,反过来体系与环境间发生热量传递后, 必然要引起体系温度变化3. 在 SI单位中,压力的单位是:( )(A) atm (B) kg×m-2(C) Pa (D) mmHg6. (1) 体系的同一状态能否具有不同的体积?(2) 体系的不同状态能否具有相同的体积?(3) 体系的状态改变了,是否其所有的状态函数都要发生变化?(4) 体系的某一状态函数改变了,是否其状态必定发生变化?*8. 压力为106 Pa的2 m3范德华气体进行绝热自由膨胀,直至体系压力达到5×105 Pa时为止。
此变化中,该气体做功为多少? ( )(A) 2×106 J (B) 106 J(C) 105 J (D) 0 J12. 下述说法哪一个错误? ( )(A) 封闭体系的状态与其状态图上的点一一对应(B) 封闭体系的状态即是其平衡态(C) 封闭体系的任一变化与其状态图上的实线一一对应(D) 封闭体系的任一可逆变化途径都可在其状态图上表示为实线14. 体系的压力p(体系)与环境的压力p(环境)有何关系? ( )(A) 相等(B) 无关系(C) p(体系)>p(环境) (D) 可逆变化途径中p(体系)=p(环境)15. 封闭体系中,有一个状态函数保持恒定的变化途径是什么途径? ( )(A) 一定是可逆途径(B) 一定是不可逆途径(C) 不一定是可逆途径(D) 体系没有产生变化17. “封闭体系等压过程中体系吸收的热量Q p等于其焓的增量ΔH”,这种说法:( )(A) 正确(B) 需增加无非体积功的条件(C) 需加可逆过程的条件(D) 需加可逆过程与无非体积功的条件18. 理想气体从相同始态分别经绝热可逆膨胀和绝热不可逆膨胀到达相同的压力,则其终态的温度、体积和体系的焓变必定是:( )(A) T可逆 > T不可逆,V可逆 > V不可逆,ΔH可逆 > ΔH不可逆(B) T可逆 < T不可逆,V可逆 < V不可逆,ΔH可逆 < ΔH不可逆(C) T可逆 < T不可逆,V可逆 > V不可逆,ΔH可逆 < ΔH不可逆(D) T可逆 < T不可逆,V可逆 < V不可逆,ΔH可逆 > ΔH不可逆19. 在非等压过程中加热某体系, 使其温度从T1升至T2, 吸热Q, 则此过程的焓增量ΔH为:( )(A) ΔH=Q(B) ΔH=0(C) ΔH=ΔU+Δ(pV) (D) ΔH等于别的值20. 恒压下,无相变的单组分封闭体系的焓值随温度的升高而: ( )(A) 增加(B) 减少(C) 不变(D) 不一定21. 当体系传热给环境之后,其焓值: ( )(A) 必定减少(B) 必定增加(C) 必定不变(D) 都不一定22. 非理想气体进行绝热自由膨胀时,下述答案中哪一个错误? ( )(A) Q=0 (B) W=0(C) ∆U=0 (D) ∆H=023. 下述哪一种说法正确? ( )因为∆H p = Q p,所以:(A) 等压过程中,焓不再是状态函数(B) 等压过程中,体系与环境无功的交换(C) 等压过程中,焓变不能量度体系对外所做的功(D) 等压过程中, ∆U不一定为零24. 下述哪一种说法错误? ( )(A) 焓是定义的一种具有能量量纲的热力学量(B) 只有在某些特定条件下,焓变∆H才与体系吸热相等(C) 焓是状态函数(D) 焓是体系能与环境能进行热交换的能量25. 当体系将热量传递给环境之后,体系的焓:( )(A) 必定减少(B) 必定增加(C) 必定不变(D) 不一定改变26. 将某理想气体从温度T1加热到T2。



第四节基本营养物质第1课时糖类【课程标准要求】1.知道糖类的组成、重要性质和主要用途。
2.认识葡萄糖的分子结构,掌握葡萄糖、蔗糖和淀粉的特征反应。
3.能够设计实验确认淀粉水解产物及水解程度。
一、营养物质1.食物中的营养物质主要包括:糖类、蛋白质、油脂、维生素、无机盐和水。
2.人体必需的基本营养物质糖类、蛋白质、油脂。
二、糖类的组成及分类1.糖类的组成:糖类是绿色植物光合作用的产物,也是人类最重要的能量来源。
糖类是由碳、氢、氧三种元素组成的一类有机化合物,其组成大多数可用通式C n(H2O)m表示,因此糖类也被称为碳水化合物。
2.常见的糖类物质提醒(1)淀粉和纤维素的通式都为(C6H10O5)n,但n取值不同,且结构单元结构也不同,故两者不是同分异构体。
(2)符合通式C n(H2O)m的有机物并不都属于糖类,如乙酸C2H4O2满足通式,但乙酸为羧酸类。
不符合C n(H2O)m通式的有机物也可能是糖类,如鼠李糖(C6H12O5)。
(3)糖类不一定有甜味,如多糖纤维素等。
(4)蔗糖水解产生1分子果糖和1分子葡萄糖,麦芽糖水解产生2分子葡萄糖。
【微自测】1.下列有关糖类的说法正确的是()A.糖类都符合通式C n(H2O)mB.符合通式C n(H2O)m的都是糖类C.糖类物质都有甜味D.糖类是人类维持生命的六大类营养素之一答案D解析糖类俗称碳水化合物,但它不是水与碳直接化合的产物。
糖类大都可用C n(H2O)m来表示,但符合这一通式的不一定都是糖,如乙酸CH3COOH、甲酸甲酯HCOOCH3[C2(H2O)2]等;而不符合C n(H2O)m这一通式的物质也可能是属于糖类的,如脱氧核糖C5H10O4、鼠李糖C6H12O5。
糖不一定有甜味,如淀粉、纤维素等。
三、葡萄糖的结构及性质1.葡萄糖的物理性质葡萄糖是一种有甜味的无色晶体,能溶于水。
2.葡萄糖的结构或)3.葡萄糖的主要化学性质及应用 (1)与新制的氢氧化铜反应:葡萄糖与新制的氢氧化铜反应,生成砖红色的氧化亚铜沉淀。

第七章 有机化合物第二节 乙烯与高分子材料第1课时 乙烯1.认识乙烯的结构及其主要性质与应用。
2.知道氧化、加成、聚合反应等有机反应类型。
3.知道有机化合物之间在一定条件下是可以相互转化的。
一.乙烯的组成与结构分子式 C 2H 4 电子式 结构式结构简式 CH 2=CH 2 空间构型 平面形分子球棍模型 比例模型二.乙烯的物理性质颜色 状态 气味 密度 水溶性 无色气体稍有气味略小于空气难溶于水三.乙烯的化学性质 1.乙烯的氧化反应实验 现象及反应点燃乙烯 火焰明亮,伴有黑烟,同时放出大量热,化学方程式为 __C 2H 4+3O 2——→点燃2CO 2+2H 2O__通入酸性高锰酸钾溶液__酸性高锰酸钾溶液褪色__点拨:高锰酸钾将乙烯最终氧化为CO 2,所以除去烷烃中的乙烯时不能用酸性高锰酸钾溶液。
2.加成反应(1)乙烯使溴的四氯化碳溶液(或溴水)__褪色__,反应的化学方程式为: CH 2==CH 2+Br 2―→CH 2Br —CH 2Br 1,2-二溴乙烷(2)乙烯与H 2加成,反应的化学方程式为__CH 2==CH 2+H 2——→催化剂△CH 3CH 3__。
(3)乙烯与H 2O 加成,反应的化学方程式为__CH 2==CH 2+H 2O ——→催化剂加热、加压CH 3CH 2OH__。
(4)加成反应概念:有机物分子中的不饱和碳原子与其他__原子或原子团__直接结合生成新的化合物的反应。
【思考】加成反应与取代反应有什么区别?加成反应只上不下,取代反应有上有下。
3.聚合反应(1)乙烯之间相互加成可得到聚乙烯,化学方程式为__n CH 2==CH 2——→催化剂-[-CH 2—CH 2-]-n __。
(2)认识加成聚合反应①由相对分子质量小的化合物分子相互结合成相对分子质量大的聚合物的反应叫做聚合反应。
乙烯的聚合反应同时也是__加成反应__,称为加成聚合反应,简称加聚反应。
②能合成高分子的小分子物质称为单体;高分子化合物中化学组成相同、可重复的最小单位称为__链节__;含有链节的数目称为__聚合度__,通常用n 表示。

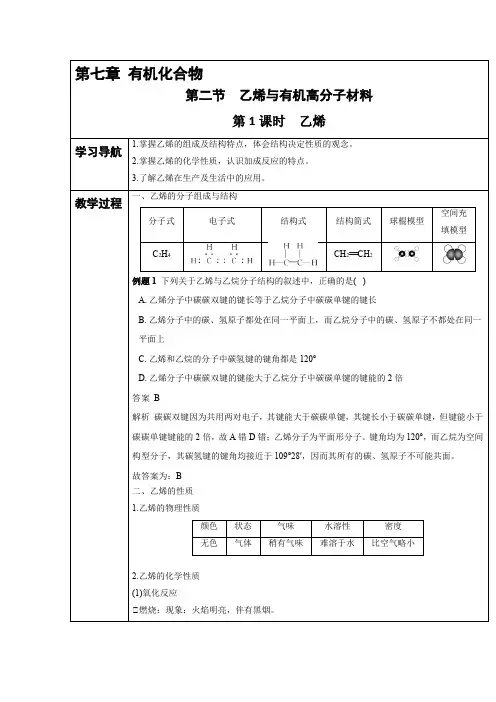
化学方程式:C 2H 4+3O 2――→点燃2CO 2+2H 2O 。
①和酸性KMnO 4溶液反应 现象:酸性KMnO 4溶液褪色。
结论:乙烯能被酸性KMnO 4溶液氧化。
(2)加成反应①将乙烯通入溴的四氯化碳溶液中 现象:溴的四氯化碳溶液褪色。
化学方程式:。
①加成反应定义:有机物分子中的不饱和碳原子与其他原子或原子团直接结合生成新的化合物的反应。
书写下列加成反应的化学方程式:(3)聚合反应①定义:由相对分子质量小的化合物分子互相结合成相对分子质量大的聚合物的反应。
①乙烯自身加成生成聚乙烯的方程式:该反应是聚合反应,同时也是加成反应,这样的反应又被称为加成聚合反应,简称加聚反应。
其中,—CH 2—CH 2—称为链节,n 称为聚合度,小分子乙烯称为聚乙烯的单体。
例题2 实验室制乙烯并验证其性质,请回答下列问题: (1)写出以乙醇为原料制取乙烯的化学方程式________。
(2)某同学欲使用如图1所示装置制取乙烯,请改正其中的错误:________。
(3)实验过程中发现烧瓶中出现黑色固体,这会导致生成的乙烯中含有杂质气体。
用如图2所示装置验证乙烯的化学性质(尾气处理装置已略去),请将虚线框中的装置补充完整并标出所盛试剂。
(4)有些同学提出以溴乙烷为原料制取乙烯,该反应的化学方程式为________。
若以溴乙烷为原料,图2中虚线框内的装置________(填“能”或“不能”)省略,请说明理由________。
答案 (1)CH 3CH 2OH →△浓硫酸CH 2=CH 2+H 2O(2)未加温度计(3)(4)CH 3CH 2Br→NaOH 的醇溶液,加热CH 2=CH 2+HBr ;不能;生成的乙烯会带走醇溶液的醇,故检验乙烯前要除去醇解析(1)CH 3CH 2OH →△浓硫酸CH 2=CH 2+H 2O(2)未加温度计,乙醇的消去反应要控制温度在170摄氏度,否则会发生副反应 (3)装置的作用是除去乙烯当中的乙醇的,故试剂为水,接导管为长进短出 (4)CH 3CH 2Br→NaOH 的醇溶液,加热CH 2=CH 2+HBr ;不能省略,生成的乙烯会带走醇溶液的醇,故检验乙烯前要除去醇 三、乙烯的用途1.乙烯是重要的化工原料,在一定条件下用来制聚乙烯塑料、聚乙烯纤维、乙醇等。
有机化学复习题(第一章—第八章)一、用系统命名法命名或写出结构式1.CH 3 CH 3CH 2 CHCH 2 CHCHCH32. 反 二异丙基环已烷的优势构象3 2 2CH 2CH 33. 1-氯丙烷的优势构象(纽曼式)4. ( R 、 S ) -三羟基丁醛5. 10. 1, 3-二甲基环己烯6.CH 3CH CHCH 2CH CH CC CH 37.8. COOHSO 3HCOOC 4H 9ClClNO 29.Cl10. CH 3CH 2CH 2CCH 2CH 3ClCCH 3CH 2CHCH 3Cl11.12. (E)-3-甲基 -2- 戊烯13. 3-氯环已醇的优势构象14.CH 3 CHCH 3 NO 215.COOH H OH H OHCOOH16. 3-苯基 -2-烯丙醇17.HOCOOHCH 3C 2H 518. 4- 甲基 -6- 硝基 -1-萘酚H HH3CCH319.H C(CH3)320、 1,7-二甲基双环 [3.2.2]壬烷MeMe21.C=C22. 5- 甲基螺 [] 庚烷n-Bu EtCH 323、24. 5-硝基 -1-萘酚HBr二、综合判断题(将结果写在括号内)3)1.以下物质与 AgNO /EtOH 反响的快慢序次为(Ⅰ. 1-溴 -3-甲基丁烷Ⅱ . 2-溴 -2-甲基丁烷Ⅲ. 3-溴 -2-甲基丁烷Ⅳ . 1-溴-2-甲基丁烷A. Ⅱ >Ⅲ>Ⅳ>ⅠB. Ⅲ>Ⅰ >Ⅳ >ⅡC.Ⅳ >Ⅱ >Ⅲ>ⅠD. Ⅳ >Ⅰ >Ⅲ>Ⅱ2.拥有对映异构现象的烷烃,其最少碳原子数是()A. 6B. 7C. 8D. 93.光照下Br 2是经过哪一种中间体进行的()BrA.正碳离子B.游离基C.负碳离子D.共同反响,无中间体4.甲基环戊烷在光照下一元溴化的主产物是()A.CH BrB.BrC.CH 3D.CH3CH 32BrBr 5.以下碳正离子的稳固性次序是()Ⅰ.CH 2 =CHCH 2+Ⅱ .CH2=CH C + H CH=CH 2Ⅲ.(CH 3)2CH +Ⅳ .CH 2CH 2+Ⅱ>Ⅲ >Ⅳ >Ⅰ A.Ⅱ >Ⅰ >Ⅲ>Ⅳ B. Ⅱ >Ⅳ >Ⅲ>Ⅰ C.Ⅱ>Ⅳ >Ⅰ >Ⅲ D. Ⅰ>Ⅱ >Ⅲ >Ⅳ6.某烯烃经臭氧化和水解后生成等物质的量的丙酮和乙醛,则该化合物是()A. (CH3)2C=C(CH3)2B.CH 3 CH=CHCH3C. (CH3)2C=CHCH3D.(CH 3 ) 2 C=C=CH27. CH2=CHCHCH2C≡ CH+Br2(1mol) →产物是().A. CH2=CHCH2 CBr=CHBrB. CH2 BrCHBrCH2CH2C≡ CHC. CH2=CHCHBrCH2C≡ CHD. BrCH2CH2CH2CH2CH=CHBr8. 丙炔与 H2O 在 HgSO4催化下生成()A. CH CH CHOB.CH COCH3233C.CH 3CHCH 2 OHD.CH 3CHCHOOH OH9. 以下哪一种化合物能与CuCl(NH3)作用产物红色积淀()=CHCH32C≡ CH=CH2=CH-CH=CH210.以下化合物中不可以作为双烯体发生狄尔斯-阿德尔反响的化合物是()A. B. C.ArD.OArArAr11. 傅 -克反响烷基易发生重排,为了获得正烷基苯,最靠谱的方法是()A. 使用 AlCl3作催化剂。
第1章 绪论思考题1–1 典型有机物和典型无机物性质上有何不同?举例说明。
有机物易燃烧,不易溶于水,熔点和沸点都比较低。
如:有机物的熔点一般低于300℃,通常在40~300℃之间,而食盐的熔点为808℃。
思考题1–2 解释为何C=C 的键能比C –C 的键能的2倍要小。
σ键的键能比π键的键能大得多。
如C –C 键能为348 kJ·mol -1,而C=C 键能为610 kJ·mol -1,这表明π键的键能只有264 kJ·mol -1。
表1–1是一些常见共价键的键能。
思考题1–3 用δ+和δ-分别表示下列化合物的正负极(1)CH 3-NH 2 (2)CH 3-OHδ+ δ-δ+δ-思考题1–4 下列化合物哪些是极性化合物,哪些是非极性化合物? 极性化合物:CH 3Cl ,CH 3OH 非极性化合物:CCH 4, CCl 4, CH 3COCH 3思考题1–5 酸碱的质子理论中,下列化合物中哪些为酸?哪些为碱?哪些既为酸,又能为碱?酸:NH 4+, HI 碱:CN –既为酸,又能为碱:HS – ,H 2O思考题1–6 按酸碱的电子理论下列反应中,哪个反应物为酸,哪个反应物为碱? AlCl 3为酸,COCl 2为碱思考题1–7 下列化合物沸点由高到低的顺序为:CH 3(CH 2)4OHCH 3(CH 2)3CH 3(CH 3)4C abcd(CH 3)2CHCH 2CH 3c>a>d>b思考题1–8 矿物油(相对分子质量较大的烃的混合物)能溶于己烷,但不溶于乙醇和水,说明原因。
根据“相似相溶”原理,矿物油是非极性分子,而水和乙醇是极性分子,故不宜互溶。
习 题1.下列化合物各属于有机化合物还是无机化合物,分别属于哪一类别? 有机化合物:(1)(3)(4)(5)(6)(7)(8)(9)(10) 无机化合物:(2)2.写出甲烷CH 4分子的一个C –H 键均裂产生的自由基结构。
第二章 群 论 §1 群的定义群论是代数学中内容最丰富的分支之一,它是近世代数的基础。
在所有只含一个代数运算的代数系统中,最重要的一个研究对象就是群。
本节只是依照教材作一些一般性地介绍,为扩大知识面,这里引入 “半群”和“幺半群”基本概念。
说明:群的代数运算“ ”习惯上称为乘法(群也称为乘法群),b a 简记成ab 。
一 单位元与逆元定义1 设},{ A 是一个代数系统,如果A 中存在一个特殊的元素e ,具有性质:A a ∈∀都有a ae ea ==,那么称e 为A 的关于“ ”的单位元(幺元)。
结论1若},{ A 中有单位元,那么单位元一定是唯一的。
证明 设21,e e 都是A 的单位元,2211e e e e ==⇒。
定义2设},{ A 是一个代数系统,如果A 中存在一个特殊的元素L e ,具有性质:A a ∈∀都有a a e L =,那么称L e 为A 的关于“ ”的左单位元(左幺元)。
如果A 中存在一个特殊的元素R e ,具有性质:A a ∈∀都有a ae R =,那么称R e 为A 的关于“ ”的右单位元(右幺元)。
结论2若},{ A 中有左单位元L e 和右单位元R e ,则R L e e =,且就是},{ A 的单位元。
证明 R R L L e e e e ==。
例1 },{},{},,{+++R ,Z N 的单位元是0,},{},{},,{⋅⋅⋅R ,Z N 的单位元是1。
例2 )(R M n 是n 阶实矩阵的全体,“+”和“.”是矩阵加法与乘法,})({+,R M n 的单位元是n 阶零矩阵n O ,})({⋅,R M n 的单位元是n 阶单位阵n I 。
例3 A 是一个非空集合,)(A P 是A 的幂集,即A 的所有子集的集合。
}),({ A P 的单位元是Φ,}),({ A P 的单位元是A 。
例4 }{-Z ,,}{-R ,中无单位元,但有右单位元0。
连续熵的性质1.连续熵可为负值2.可加性连续信源也有与离散信源类似的可加性。
即)/()()(X Y H X H XY H c c c += (1) )/()()(Y X H Y H XY H c c c += (2) 下面我们证明式(1)。
⎰⎰-=2)(log )()(2Rc dxdyxy p xy p XY H⎰⎰⎰⎰--=22)/(log )()(log )(22RRdxdyx y p xy p dxdy x p xy p⎰⎰+-=RRc X Y H dx dy xy p x p )/(])()[(log 2)/()(X Y H X H c c +=其中,⎰=Rx p dy xy p )()(同理,可证明式(2)。
连续信源熵的可加性可以推广到N 个变量的情况。
即)/()/()/()()(12121312121-++++=N N N c X X X X H X X X H X X H X H X X X H3. 平均互信息的非负性定义连续信源的无条件熵和条件熵之差为连续信源的平均互信息。
记为);(Y X I c ,即有)/()();(Y X H X H Y X I c c c -= )/()();(X Y H Y H X Y I c c c -=连续信源的平均互信息仍保留了非负性。
即0);();(≥=X Y I Y X I C C证明条件熵小于等于无条件熵。
即)()/(X H Y X H c c ≤ (3) )()/(Y H X Y H c c ≤ (4)现在我们证明式(3):dxx p x p dxdy y x p xy p X H Y X H R Rc c )(log )()/(log )()()/(222⎰⎰⎰+-=-由⎰=Rx p dy xy p )()(可得dxdyx p xy p dxdy y x p xy p X H Y X H R c c R )(log )()/(log )()()/(2222⎰⎰⎰+-=-⎰⎰⎰⎰=-=22)/()(log )()()/(log )(22R R dxdy y x p x p xy p dxdy x p y x p xy p根据对数变换关系z e z ln log log 22=和著名不等式1ln -≤z z 0>z并注意到0)/(,0)(≥≥y x p x p 故有 0)/()(≥y x p x p 令)/()(y x p x p z =,只要)(x p 不恒为0,则0>z⎰⎰⎥⎦⎤⎢⎣⎡-≤-21)/()()()()/(R c c dxdy y x p x p xy p X H Y X H⎰⎰⎥⎦⎤⎢⎣⎡-=21)/()()/()(R dxdy y x p x p y x p y p⎰⎰⎰⎰-=2)()()(R RRdxdy xy p dy y p dx x p=1-1=0即 )()/(X H Y X H c c ≤ 其中 ⎰⎰⎰⎰===21)(,1)(,1)(R RRdxdyxy p dy y p dx x p由式(3)得0);(≥Y X I C (5) 同理可得0);(≥X Y I C (6)4. 平均互信息的对称性容易证明,连续信源的平均互信息也满足对称性。
即(;)(;)()()()C C c c c I X Y I Y X H X H Y H XY ==+-(7)5. 满足数据处理定理另外,连续信源还满足数据处理定理。
换句话说,把连续随机变量Y 处理成另一随机变量Z 时,一般也会丢失信息。
即(;)(;)C C I X Z I X Y ≤ (8)最大连续熵定理(1)限峰值功率的最大熵定理若代表信源的N 维随机变量的取值被限制在一定的范围之内,则在有限的定义域内,均匀分布的连续信源具有最大熵。
设N 维随机变量 1(,)Niii X a b =∈∏ i ia b>其均匀分布的概率密度函数为1111()()()0()Ni i N i i i i N i i i x b a b a p x x b a ===⎧∈-⎪⎪-⎪=⎨⎪⎪∉-⎪⎩∏∏∏除均匀分布以外的其他任意概率密度函数记为()q x ,并用(),c H p x X ⎡⎤⎣⎦和(),c H q x X ⎡⎤⎣⎦分别表示均匀分布和任意非均匀分布连续信源的熵。
在 11111212()()1NNNNb b b b N N a a a a p x dx dx dx q x dx dxdx ==⎰⎰⎰⎰的条件下有1121(),()log()NN b b c Na a H q x X q x q x dx dx ⎡⎤=-⎣⎦⎰⎰1111112121211()()log ()()()log()()()log ()NN NN NNb b Na ab b N a a b b Na a p x q x dx dx q x p x q x p x dx dx p x q x dx dx q x ⎡⎤=⋅⎢⎥⎣⎦=-+⎰⎰⎰⎰⎰⎰令(),0()p x z z q x =≥有运用著名不等式 1ln -≤z z 0>z 则11112111211[(),]()log()()()1()log ()11[(),]NN NNb bc N Na a iii b b Na a N i i c i H q x X q x dx dxb a p x q x dx dx q x b a H p x X ==≤-+-⎡⎤-⎢⎥⎣⎦=-+-=⎰⎰∏⎰⎰∏至此已证明了在定义域有限的条件下,以均匀分布的熵为最大。
在实际问题中,随机变量i X 的取值限制在i b ±之间,峰值为||i b 。
如果把取值看作是输出信号的幅度,则相应的峰值功率就是2i b 。
所以上述定理被称为峰值功率受限条件下的最大连续熵定理。
此时最大熵值为:∏∏===--=Ni Ni ii i c b b b X x p H 11222log )]([log ]),([(2)限平均功率的最大熵定理若信源输出信号的平均功率P 和均值m 被限定,则其输出信号幅度的概率密度函数为高斯分布时,信源具有最大熵值。
单变量连续信源X 呈高斯分布时,PDF 222)(221)(σπσm x ex p --=当X 是高斯分布以外的其它任意分布时 ,PDF 记为)(x q ,由约束条件已知22()()1()()()()p x dx q x xp x dx xq x m x p x dx x q x P ∞∞-∞-∞∞∞-∞-∞∞∞-∞-∞⎧==⎪⎪==⎨⎪⎪==⎩⎰⎰⎰⎰⎰⎰ 由于随机变量的方差222222][])[(σ=-=-=-m P m X E m X E当均值m 为0时,平均功率就等于方差P =2σ,可见对平均功率和均值的限制就等于对方差的限制。
用[]X x p H c ),(和[]X x q H c ),(分别表示高斯分布和任意非高斯分布连续信源的熵由前面的讨论已知)2(log 21]),([22σπe X x p H c =222222222[(),]()log ()1()()log ()()()()log ()()log ()1()log (2)()1log 2()1log (2)11[(),]2c c H q x X q x q x dxp x q x q x p x p x q x p x dx q x dx q x p x e q x e dxq x e H p x X πσπσ∞-∞∞-∞∞∞-∞-∞∞-∞=-⎡⎤=⋅⎢⎥⎣⎦⎡⎤=-+⎢⎥⎣⎦⎡⎤≤+-⋅⎢⎥⎣⎦=+-=⎰⎰⎰⎰⎰其中222()222()22222222222()log ()()[log ]()[log log ]()log log ()21log log 21log 22x m x m q x p x dx q x dxq x edxx m e q x dx ee σσσπσ--∞∞-∞-∞--∞-∞∞-∞-=-=-+-=⋅==⎰⎰⎰⎰(3)均值受限条件下的最大连续熵定理若连续信源X 输出非负信号的均值受限,则其输出信号幅度呈指数分布时,连续信源X 具有最大熵值。
连续信源X 为指数分布时PDF 为)0(1)(≥=-x emx p mx用[]X x p H c ),(和[]X x q H c ),(分别表示指数分布和任意非指数分布连续信源的熵。
记限制条件为:mx xq dx x xp x q dx x p ====⎰⎰⎰⎰∞∞∞∞0)()(1)()( me X x p H c 2log ]),([=,任意其它分布的信源熵为20202222020[(),]()log ()1()()log ()()()()log ()()log ()1()()log log ()1()log ()l c xm H q x X q x q x dxp x q x q x p x p x q x p x dx q x dx q x p x q x e dx e q x d xm q x m q x dx ∞∞∞∞-∞-∞-∞∞-∞-∞=∞=-⎡⎤=⋅⎢⎥⎣⎦⎡⎤=-+⎢⎥⎣⎦⎡⎤⎡⎤≤-+⋅-⎢⎥⎢⎥⎣⎦⎣⎦=⋅+⎰⎰⎰⎰⎰⎰⎰202og ()log [(),]c xe q x dx mme H p x X ∞==⎰总结:连续信源与离散信源不同,它不存在绝对的最大熵。
其最大熵与信源的限制条件有关,在不同的限制条件下,有不同的最大连续熵值。
熵功率设连续信源X 在PDF 为)(x p 时达到最大熵值]),([X x p H c ,除此之外的其它任何PDF )(x q 达到的熵值为]),([X x q H c ,两熵之差即表示信源的剩余,记为q p I ,,也叫信息变差(或信源的冗余)。
即信源从一种PDF )(x p 转到另一种PDF )(x q 时,信源所含信息量发生的变化。
]),([]),([,X x q H X x p H I c c q p -=从信息变差的概念出发,连续信源的熵可理解为最大熵与信息变差之间的差值。
q p c c I X x p H X x q H ,]),([]),([-= 讨论均值为零、平均功率限定为P 的连续信源的冗余问题。
当PDF 为高斯分布时达到最大熵eP X x p H c π2log 21]),([2=仅随限定功率P 的变化而变化。
假定限定的功率为P ,相应的熵为]),([p c X x p H ,若P P ≤,则有]),([]),([X x p H X x p H c p c ≤当PDF 为其它任何分布)(x q 时,也有 ]),([]),([X x p H X x q H c c ≤ 总能找到某一个P P ≤,使P e X x p H X x q H p c c π2log 21]),([]),([2== 此即P 的大小决定了实际信源的熵值。