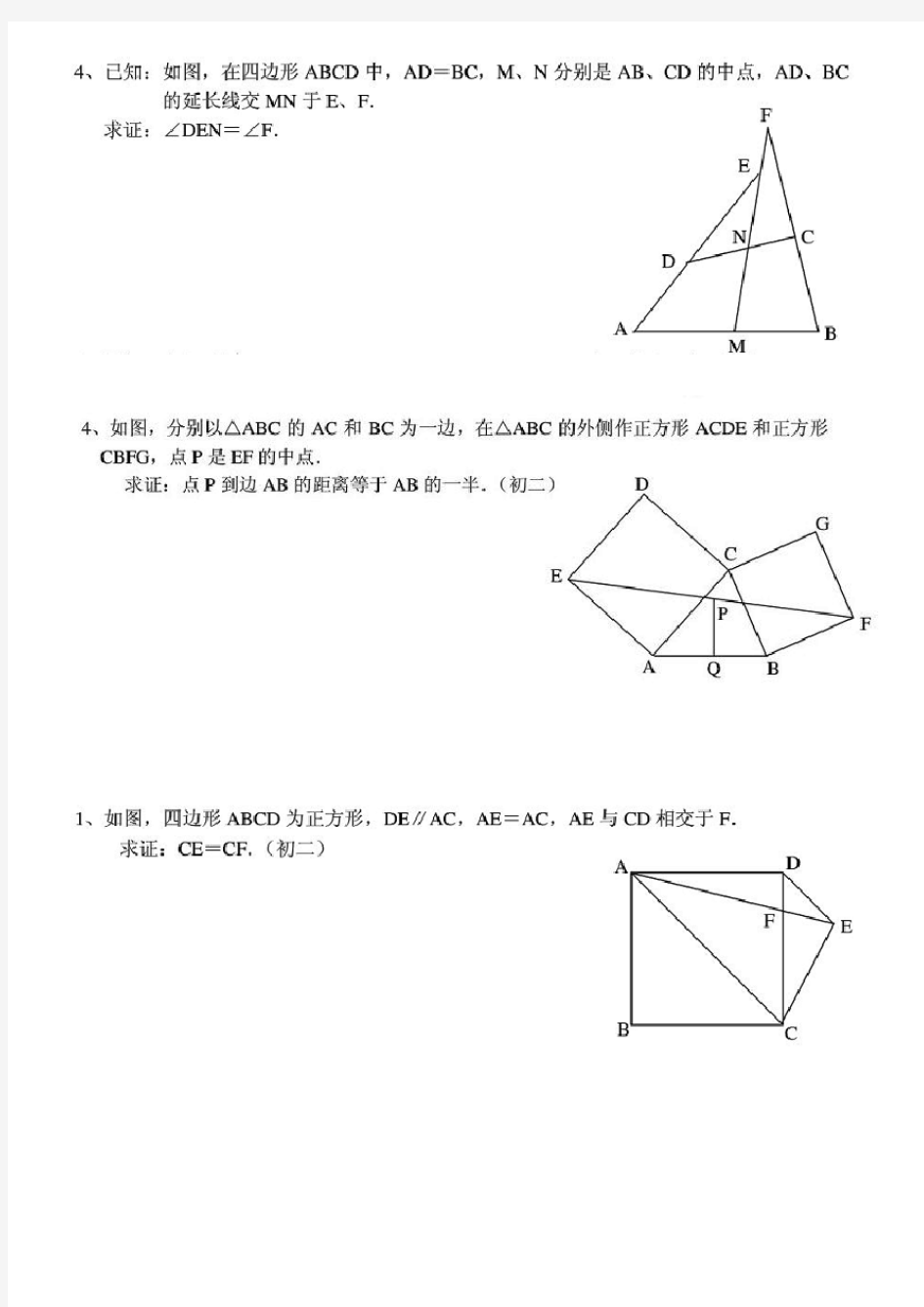
1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第4 题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F . B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO .(初二) 第1题图 第2题图 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q .求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 第3题图 第4题图 F
初中三年级中考复习平面几何证明题一题多解 如图:已知青AB=AC ,E 是AC 延长线上一点,且有BF=CE ,连接FE 交BC 于D 。求证:FD=DE 。 分析:本题有好多种证明方法,由于新课标主 要用对称、旋转方法证明,但平行四边形的性质、平行线性质等都是证题的好方法,我在这里向初中三年级同学面对中考需对平面几何证明题的证明方法有一个系统的复习和提高。 下边我将自己证明这道题的方法给各位爱好者作以介绍,希望各位有所收获,仔细体会每 中方法的异同和要点,从中能得到提高。我是一位数学业余爱好者,不是学生,也不是老师,如有错误,请批评指证。信箱: wangsj629@https://www.doczj.com/doc/c68853502.html, . 证法一 ∧≌∠⊥∥△□° 证明:过E 点作EM ∥AB 交DC 延长线于M 点,则∠M=∠B ,又因为∠ACB=∠B ∠ACB=∠ECM=∠M ,所以CE=EM , 又EC=BF 从而EM=BF ,∠BFD=∠DEM 则△DBF ≌△DME ,故 FD=DE ; 证法二 证明:过F 点作FM ∥AE ,交BD 于点M , 则∠1=∠2 = ∠B 所以BF=FM , 又 ∠4=∠3 ∠5=∠E 所以△DMF ≌△DCE ,故 FD=DE 。 证法三 以BC 为对称轴作△BDF 的对称△BDN ,连接NE ,则△DBF ≌△DBN ,DF=DN ,BN=BF , NF ⊥BD ,∠FBD=∠NBD ,又因为∠C=∠FBD 所以∠NBD=∠C 。 BN ∥CE ,CE=BF=BN ,所以四边形BNCE 为平行四边形。故NF ∥BC , 所以NF ⊥NE ,因FN 衩BD 垂直平分,故D 是FE 的中点,所以FD=DE 。(也可证明D 是直角△NEF 斜边的中点)。 证法四: F C A E N E
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第 4题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延 B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A P C D B A F G C E B O D
长线交MN于E、F.求证:∠DEN=∠F. 经典难题(二) 1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于M. (1)求证:AH=2OM; (2)若∠BAC=600,求证:AH=AO.(初二) 第1题图第2题图 2、设MN是圆O外一直线,过O作OA⊥MN于A,自A引圆的两条直线,交圆于B、C及 D、E,直线EB及CD分别交MN于P、Q.求证:AP=AQ.(初二) 3、如果上题把直线MN由圆外平移至圆内,则由此可得以下命题: 设MN是圆O的弦,过MN的中点A任作两弦BC、DE,设CD、EB分别交MN于P、Q.求证:AP=AQ.(初二)
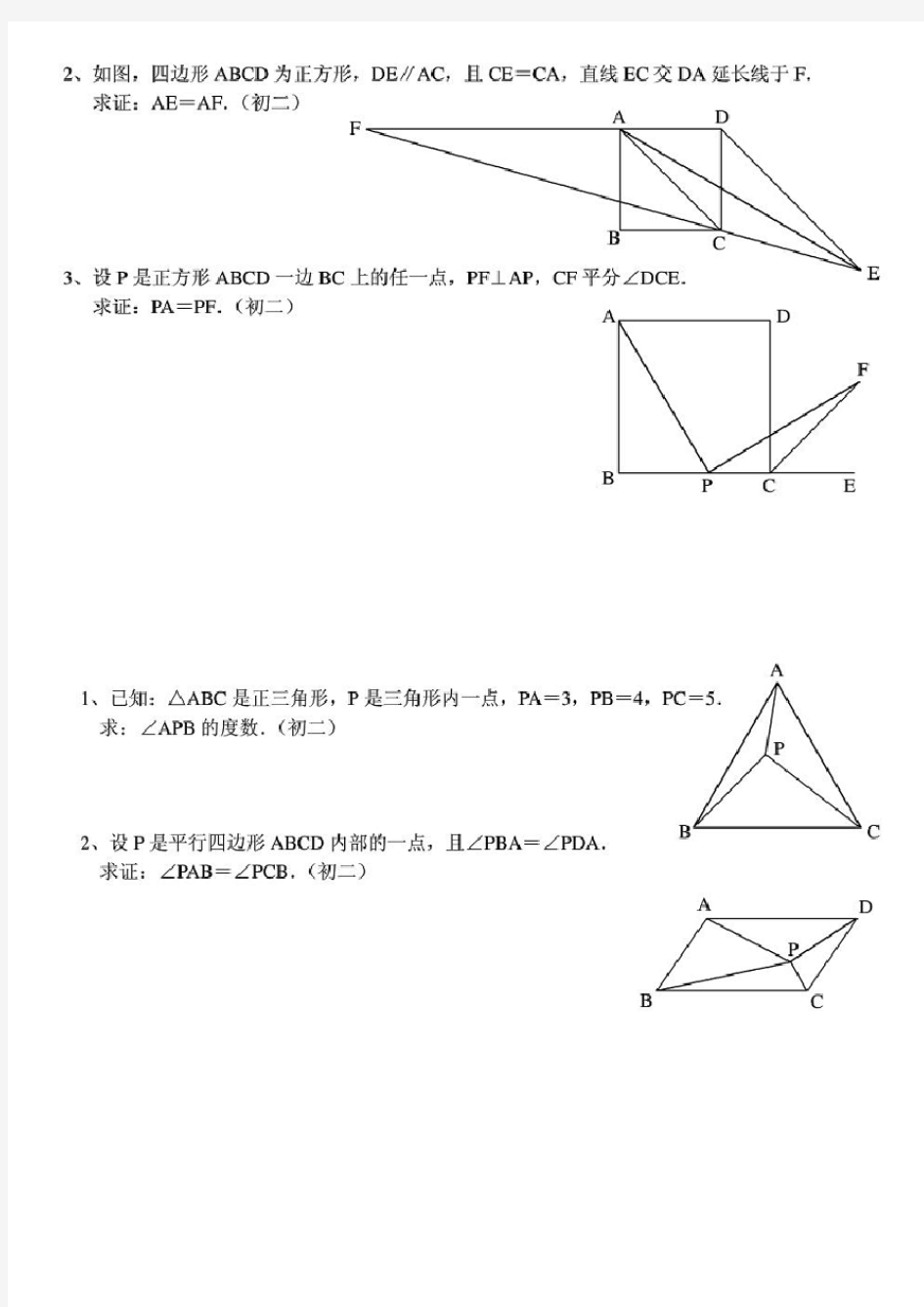
第3题图 第4题图 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二) 经典难题(三) 1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二) 第1题图 第2题图 2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F . 求证:AE =AF .(初二)
初中平面几何训练题(较难) 中考平面几何训练题较难 1.在锐角三角形ABC中,AB上的高CE与AC上的高BD相交于点H,以DE为直径的圆分别交AB、AC于F、G两点,FG与AH相交于点K,已知BC,25,BD=20,BE,7,求AK的长。 B。所作割线交圆于C、D两点,2过圆外一点P作圆的两条切线和一条割线,切点为A、 C在PD之间,要统CD上取一点Q,使?DAQ=?PBC,求证:?DBQ=?PAC( 3.如图,在,ABC中,,A,60:,AB,AC,点O是外心。两条高BE、CF交于H 点,点M、 MH,NH N分别在线段BH、HF上,且满足BM,CN,求的值。OH
4.如图,,ABC中,O为外心,三条高AD、BE、 CF交于点H,直线ED和AB交于点M, FD和AC交于点N。求证:(1)OB,DF,OC,DE;(2)OH,MN; 5.如图,在锐角,ABC的BC边上有两点E、F,满足,BAE,,CAF,作 FM,AB,FN,AC (M、N是垂足),延长AE交,ABC的外接圆于D点,证明四边形AMDN 与,ABC的面积相等; 6.如图,在四边形ABCD中,对角线AC平分,BAD,在CD上取一点E,BE与AC 相交于F,延长DF交BC于G,求证:,GAC,,EAC
如图,已知两个半径不相等的圆O和圆O相交于M、N两点,且圆O、圆O分别 与圆O7.1212 内切于S、T两点,求证:OM,MN的充分必要条件是S、N、T三点共线; 参考答案
1. 2.
证:如图:连结AB,在,ADQ与,ABC中,,ADQ,,ABC,,DAQ,,PBC,,CAB ?,ADQ,,ABC BCDQ 从而有,,BC,AD,AB,DQABAD 又由切割线关系可知:,PCA,,PAD PCAC?,PAAD PCBC同理:由,PCB,,PBD得:,PBBD 又?PA,PB ACBC?,,AC,BD,BC,AD,AB,DQADBD 又?关于圆内接四边形ABCD的托勒密定理有:AC,BD,BC,AD,AB,CD 1于是:AB,CD,2AB,DQ,DQ,CD,CQ,DQ 2 ADDQCQ在,CBQ与,ABD中:,,,,BCQ,,BADABBCBC?,CBQ,,ABD ?,CBQ,,ABD ?,DBQ,,ABC,,PAC 3. 解:如图在BE上取BK,CH,连结OB、OC、OK由三角形的外心的性质可知:,BOC,2,,A,120:由三角形的垂心的性质可知:,BHC,180:,,A,120:
ABC ABC V :V 2017中考平面几何题目 (北京)28.在等腰直角ABC ?中,090ACB ∠=,P 是线段BC 上一动点 (与点B C 、不重合),连接AP ,延长BC 至点Q ,使得CQ CP =,过点Q 作QH AP ⊥于点H ,交AB 于点M . (1)若PAC α∠=,求AMQ ∠的大小(用含α的式子表示). (2)用等式表示线段MB 与PQ 之间的数量关系,并证明.( CP =) (成都)20. 如图,在ABC ?中,AB AC =,以AB 为直径作圆O ,分别交BC 于点D ,交CA 的延长线于点E ,过点D 作DH AC ⊥于点H ,连接DE 交线段OA 于点F . (1)求证:DH 是圆O 的切线; (2)若A 为EH 的中点,求EF FD 的值; 23 EF FD = (3)若1EA EF ==,求圆O 的半 径.( 1,,EA EF OD OF r BD BE BF ====== )1,,1,1EA FD r BF r AF r ===+=- 111EA AF r BF FD r r -=?=+ ,r = (安徽)23.已知正方形ABCD ,点M 为边AB 的中点. (1)如图1,点G 为线段CM 上的一点,且90AGB ∠=?,延长AG ,BG 分别与边BC ,CD 交于点E ,F . ② 证:BE CF =; ②求证:2BE BC CE =?.(,CEG CGB CG FC BE ==V :V ) (2)如图2,在边BC 上取一点E ,满足2BE BC CE =?,连接AE 交CM 于点G ,
连接BG延长交CD于点F,求tan CBF ∠的值. ( 51 tan 2 CBF - ∠=) H (CH=BE,CH/AM=CG/GM=FC/MB,FC=CH=BE,设BC=1,BE=x,得 51 x 2 -=,) (福州)24.(12分)如图,矩形ABCD中,AD=8,AB=6,P,Q分为线段AC、BC上一点,且四边形PDRQ是矩形, (1)若PDC V为等腰三角形,求AP;(三种情况,PD=DC时,取PC的中垂线较好。) (2)若AP=2,求线段RC的长。(△PND∽△QMP→△PQR∽△ABC∽△PMC,→PRCQ共圆,∠PCR=90°,△KRC∽△PMC,三边符合3:4:5,算 出RC=3 2 4 ) N K M (白银)27.如图,AN是M e的直径,// NB x轴,AB交M e于点C. (1)若点()()0 0,6,0,2,30 A N ABN ∠=,求点B的坐标;(3,2) (2)若D为线段NB的中点,求证:直线CD是M e的切线. (天水) (BC=62) (广东)25.如题25图,在平面直角坐标系中,O为原点,四边形ABCD是矩
初三数学总复习辅导学习资料(6)——几何经典难题 1.已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO .求证:CD =GF . 2.已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 .求证:△PBC 是正三角形. 3.如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、 C 2、 D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2 C 2 D 2是正方形. 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . 5.已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M .(1)求证:AH =2OM ;(2)若∠BAC =600 ,求证:AH =AO . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1
F 6.设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及 CD 分别交MN 于P 、Q .求证:AP =AQ . 7.如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作 两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q .求证:AP =AQ . 8.如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半. 9.如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于 10.如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF . E
平面几何证明题的一般思路及方法简述 【摘要】惠特霍斯曾说过,“一般地,解题之所以成功,在很大程度上依赖于选择一种最适宜的方法。”灵活、恰当地选择解题方法是求解平面几何问题的良好途径。解决任何一道平面几何证明题,都要应用这样或那样的方法,而选择哪一种方法,就取决于我们用什么样的解题思路。本文试对平面几何证明题中常用的几种解题思路及方法进行分析。 【关键词】平面几何证明题思路方法 平面几何难学,是很多初中生在学习中的共识,这里面包含了很多主观和客观因素,而学习不得法,没有适当的解题思路则是其中的一个重要原因。波利亚曾说过,“解题的成功要靠正确思路的选择,要靠从可以接近它的方向去攻击堡垒。为了辨别哪一条思路正确,哪一个方向可接近它,就要试探各种方向和思路。”由此可见,掌握证明题的一般思路、探索证题过程中的数学思维、总结证题的基本规律是求解几何证明题的关键。常见的证题思路有直接式思路和间接式思路。 一、直接式思路 证题时,首先应仔细审查题意,细心观察题目,分清条件和结论,并尽量挖掘题目中隐含的一些解题信息,以在缜密审题的基础上,根据定义、公式、定理进行一系列正面的逻辑推理,最后得出命题的证明,这种证题的思路被称为直接式思路。由于思维方式的逆顺,在证题时运用的方法主要有“分析法”和“综合法”。 1.分析法。分析法是从命题的结论入手,先承认它是正确的,执果索因,寻求结论正确的条件,这样一步一步逆而推之,直到与题设会合,于是就得出了由题设通往结论的思维过程。在由结论向已知条件的寻求追溯过程中,则由于题设条件的不同,或已知条件之间关系的隐含程度不同等,寻求追溯的形式会有一定差异,因而常把分析法分为以下四种类型。 (1)选择型分析法。选择型分析法解题,首先要从题目要求解的结论A出发,逐步把问题转化为分析要得出结论A需要哪些充分条件。假设有条件B,就有结论A,那么B就成为选择找到的使A成立的充分条件,然后再分析在什么条件下能选择得到B……最终追溯到命题中的某一题设条件。 (2)可逆型分析法。如果再从结论向已知条件追溯的过程中,每一步都是推求的充分必要条件,那么这种分析法又叫可逆型分析法,因而,可逆型分析法是选择型分析法的特殊情形。用可逆型分析法证明的命题用选择型分析法一定能证明,反之用选择型分析法证明的命题,用可逆型分析不一定能证明。 (3)构造型分析法。如果在从结论向已知条件追溯的过程中,在寻找新的充分条件的转化“三岔口”处,需采取相应的构造型措施:如构造一些条件,作某些辅助图等,进行探讨、推导,才能追溯到原命题的已知条件的分析法叫做构造型分析法。 (4)设想型分析法。在向已知条件追溯的过程中,借助于有根据的设想、假定,形成“言之成理”的新构思,再进行“持之有据”的验证,逐步地找出正确途径的分析法称为设想型分析法。 2.综合法。综合法则是由命题的题设条件入手,由因导果,通过一系列的正确推理,逐步靠近目标,最终获得结论。再从已知条件着手,根据已知的定义、公式、定理,逐步推导出结论。在这一过程中,由于思考角度不同,立足点不同,综合法常分为四种类型: (1)分析型综合法。我们把分析法解题的叙述倒过来,稍加整理而得到的解法称为分析型综合法。 (2)奠基型综合法。当由已知条件着手较难,或没有熟悉的模式可供归纳推导,就可转而寻找简单的模式,然后再将一般情形化归到这个简单的模式中来,这样的综合法称为奠基型综合法。 (3)媒介型综合法。当问题给出的已知条件较少,且看不出与所求结论的直接联系时,或条
九年级数学练习题 1.如图,分别以△ABC 的边AB 、AC 为边,向外作正方形ABFG 和ACDE ,连接EG 求证:ABC AEG S S △△ 2.如图,分别以△ABC 的边AB 、AC 为边,向外作正方形ABFG 和ACDE ,连接EG 。若O 为EG 的中点 求证:EG=2AO 3. 如图,分别以△ABC 的边AB 、AC 为边,向外作正方形ABFG 和ACDE ,连接EG ,若O 为EG 的中点,OA 的延长线交BC 于点H 求证:OH ⊥BC
4. 如图,分别以△ABC的边AB、AC为边,向外作正方形ABFG和ACDE,连接EG,若AH⊥BC,HA的延长线交EG于点O 求证:O为EG的中点 5. 如图,分别以△ABC的边AB、AC为边,向外作正方形ABFG和ACDE,连接CE,BG、GE M、N、P、Q分别是EG、GB、BC、CE的中点 求证:四边形MNPQ是正方形 答案: 1.作CM⊥AB于点M,EN⊥GA,交GA的一次性于点N ∵∠MAN=∠CAE=90° ∴∠CAM=∠EAN ∵∠ANE=∠CMA=90°,AC=AE ∴△ACM≌△AEN ∴CM=EN ∵S△ABC=1/2*AB *CM,S△AGE=1/2*AG*EN 又∵AG=AB,CM=EN ∴S△ABC=S△AEG 2.证明: 延长AO到点M,使OM=OA,连接MG、ME 则四边形AEMG是平行四边形 ∴GM=AE=AC,MG‖AE
∴∠MGA+∠GAE=180° ∵∠BAG+∠CAE=180° ∴∠BAC+∠GAE=180° ∴∠BAC=∠AGM ∵AC=AB ∴△AGM≌△BAC ∴BC=AM=2AO 3. OA与OH共线,所以向量AO与向量BC的数量积为0即可证出AH⊥BC 我用AB表示向量AB,即此时字母AB都有方向性,下边的都是如此, 2AO=AG+GE 过A作直线BC的平行线交FG于M,交DE于N, 2AO*BC =(AG+AE)*BC =AG*BC+AE*BC =-|AG||BC|cos∠GAM+|AE||BC|cos∠EAN =|BC|*(-|AB|*sin∠MAB+|AC|*sin∠NAC) =|BC|*(-|AB|sin∠ABC+|AC|sin∠ACB) 设BC上的高长为h, 上式=|BC|(-h+h)=0 所以AO与BC垂直,即AH⊥BC 5.连结BE、CG, ∵PQ是△BEC的中位线, ∴PQ//BE,且PQ=BE/2, 同理MN//BC,MN=BE/2, ∴MN=PQ,且MN//PQ, ∴四边形PQMN是平行四边形, 同理MQ=PN=CG/2, 在△BAE和△GAC中, BA=GA, AC=AE, ∵〈BAG=〈CAE=90°, 〈BAG+〈BAC=〈CAE+〈BAC, ∴〈BAE=〈GAC, ∴△BAE≌△GAC,(SAS), ∴BE=CG, ∴BE/2=CG/2,
初中平面几何经典练习题 1如图,在⊙O 中,弦CD 垂直于直径AB ,M 是OC 的中点,AM 的延长线交⊙O 于点E ,DE 与BC 交于点N.求证:BN=CN. 2.如图,直角梯形OABC 中,AB ∥OC ,O 为坐标原点,点A 在y 轴正半轴上,点C 在x 轴正半轴 上,点B 坐标为(2,2 3),∠BCO = 60°,BC OH ⊥于点H .动点P 从点H 出发,沿线段HO 向点O 运动,动点Q 从点O 出发,沿线段OA 向点A 运动,两点同时出发,速度都为每秒1个单位长度. 设点P 运动的时间为t 秒. (1) 求OH 的长; (2) 若OPQ ?的面积为S (平方单位). 求S 与t 之间的函数关系式.并求t 为何值时,OPQ ?的面积最大,最大值是多少? (3) 设PQ 与OB 交于点M .①当△OPM 为等腰三角形时,求(2)中S 的值. ②探究线段OM 长度的最大值是多少?(直接写出答案).
3.已知实数x 、y 、z 满足4=+y x 及42+=z xy ,求z y x 32++的值。6 4. 已知半径为R 的⊙O ′经过半径为r 的⊙O 的圆心,⊙O 与⊙O?′交于E 、F 两点. (1)如图甲,连结OO ′交于⊙O 于点C ,并延长交⊙O ′于点D ,过点C 作⊙O?的切线交⊙O ′于A 、B 两点,求OA ·OB 的值; (2)若点C 为⊙O 上一动点.. , ①当点C 运动到⊙O ′内时,如图乙,过点C 作⊙O ′的切线交⊙O 于A 、B 两点,则OA ·OB 的值与(1)中的结论相比较有无变化?请说明理由. ②当点C 运动到⊙O ′外时,过点C 作⊙O 的切线,若能交⊙O ′于A 、B 两点,如图丙,则OA ·OB 的值与(1)中的结论相比较有无变化?请说明理由. 5.(1)在正方形ABCD 中,∠MAN=45°,∠MAN 绕点A 顺时针旋转,它的两边分别交CB 、DC(或它们的延长线)于点M 、N .如果∠MAN 在如图1所示的位置时,有BM+DN=MN 成立(不必证明).请问当∠MAN 绕点A 旋转到如图2所示的位置时,线段BM 、DN 和MN 之间又有怎样的数量关系?请说明理由.
初中数学经典几何难题及答案
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内一点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) A P C D B A F G C E B O D
3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正 方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC , M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . 求证:∠DEN =∠F . D 2 C 2 B 2 A 2 D 1 C 1 B 1 C D A A 1 A N F E C D M B
经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初 二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) · A D H E M C B O · G A O D B E C Q P N M
C G D E 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边, 在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点. · O Q P B D E C N M · A
平面几何选讲练习题 1.如图所示,已知⊙O 1与⊙O 2相交于A ,B 两点,过点A 作⊙O 1的切线交⊙O 2于点C , 过点B 作两圆的割线,分别交⊙O 1,⊙O 2于点D ,E ,DE 与AC 相交于点P. (1)求证:AD ∥EC; (2)若AD 是⊙O 2的切线,且PA=6,PC=2,BD=9,求AD 的长; 2.如图:已知AD 为⊙O 的直径,直线BA 与⊙O 相切于点A ,直线OB 与弦AC 垂直并 相 交于点G ,连接DC . 求证:BA ·DC =GC ·AD . 3. 已知:如图,△ABC 中,AB=AC ,∠BAC=90°,AE= 31AC ,BD=3 1 AB ,点F 在BC 上,且CF= 3 1 BC 。求证: (1)EF ⊥BC ; (2)∠ADE=∠EBC 。 B E D O 1 O 2 A P C
F E D A B C 4.如图,在△ABC 中,D 是AC 的中点,E 是BD 的中点,AE 的延长线交BC 于F . (1)求FC BF 的值; (2)若△BEF 的面积为1S ,四边形CDEF 的面 积为2S ,求21:S S 的值. 5.已知C 点在圆O 直径BE 的延长线上,CA 切圆O 于A 点,DC 是ACB ∠的平分线 交AE 于点F ,交AB 于D 点. (1)求ADF ∠的度数; (2)若AB=AC ,求AC:BC . 6.自圆O 外一点P 引切线与圆切于点A ,M 为PA 中点,过M 引割线交圆于B,C 两点. 求证:∠MCP=∠MPB . O A B D E F
7.如图,AD是⊙O的直径,AB是⊙O于点M、N,直线BMN交AD的延长线于点C,NC MN BM= =,2 = AB,求BC的长和⊙O的半径. 8.如图,AB是⊙O的直径,C,F为⊙O上的点,CA是∠BAF的角平分线,过点C作CD⊥AF交AF的延长线于D点,CM⊥AB,垂足为点M. (1)求证:DC是⊙O的切线; (2)求证:AM·MB=DF·DA. 9.如图,已知AP是⊙O的切线,P为切点,AC是⊙O的割线,与⊙O交于B、C两点,圆心O在PAC ∠的部,点M是BC的中点. (Ⅰ)证明A,P,O,M四点共圆; (Ⅱ)求∠OAM+∠APM的大小. B M C O P
初二数学几何经典难题 初二数学几何经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 F
G D 求证:∠DEN =∠F . 经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形 CBFG ,点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.(初二) · A D H E M C B O · G A O D B E C Q P N M · O Q P B D E C N M · A
B M N D A C O 图5 C E D B A O 平面几何证明习题 1. 如图5所示,圆O 的直径6AB =,C 为圆周上一点,3BC = , 过C 作圆的切线l ,过A 作l 的垂线AD ,垂足为D , 则DAC ∠= ,线段AE 的长为 线段CD 的长为 ,线段AD 的长为 2. 已知PA 是圆O 的切线,切点为A ,2PA =.AC 是圆O 的直径,PC 与圆O 交于点B ,1PB , 则圆O 的半径R = . 3. 如图4,点,,A B C 是圆O 上的点, 且0 4,45AB ACB =∠=,则圆O 的面积等于 . 4. 如图3, 半径为5的圆O 的两条弦AD 和BC 相交于点P , ,OD BC P ⊥为AD 的中点, 6BC =, 则弦AD 的长度为 . 5. 如图5, AB 为⊙O 的直径, AC 切⊙O 于点A ,且cm AC 22=,过C 的割线 CMN 交AB 的延长线于点D ,CM=MN=ND.AD 的长等于_______cm . 6. 如图,AB 是圆O 的直径,直线CE 和圆O 相切于点于C , AD CE ⊥于D ,若AD =1,30ABC ∠=?,则圆O 的面积是 7. 如图,O 是半圆的圆心,直径62=AB ,PB 是圆的一条切线,割线PA 与半圆交于点C ,4=AC ,则=PB . 8. 如图,点,,A B C 是圆O 上的点,且2,6,120AB BC CAB == ∠=o , 则AOB ∠对应的劣弧长为 . 9. 如图,圆O 的割线PAB 交圆O 于,A B 两点,割线PCD 经过圆心O , 已知6PA =,22 3 AB =,12PO =,则圆O 的半径是__ . 10. 如图,已知P 是圆O 外一点,PD 为圆O 的切线,D 为切点, 割线PEF 经过圆心O ,若12,3PF PD ==则圆O 的半径长为 , EFD ∠的度数为 . 11. 如图4,已知PA 是⊙O 的切线,A 是切点,直线PO 交⊙O 于B 、C 两点,D 是OC 的中点,连结AD 并延长交⊙O 于点E . 若32=PA ,30APB ∠=?,则AE = . 12. 如图,在ABC ?中,DE //BC ,EF //CD ,若 3,2,1BC DE DF ===,则BD 的长为 , AB 的长为___________. l 图5 E D C O B P C O A B O B A P A B O C D E ? 4 图
(完整word 版)初中数学经典几何难题及答案 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 第1题图 第2题图 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150 . 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、 CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二) 第3题图 第4题图 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN 于E 、F .求证:∠DEN =∠F . 经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600 ,求证:AH =AO .(初二) A F G C E B O D A P C D B D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1 A N F E C D M B 亲爱的读者: 本文内容由我和我的同事精心收集整理后编辑发布到文库,发布之前我们对文中内容进行详细的校对,但难免会 有错误的地方,如果有错误的地方请您评论区留言,我们 予以纠正,如果本文档对您有帮助,请您下载收藏以便随 时调用。下面是本文详细内容。 最后最您生活愉快 ~O(∩_∩)O ~
在△ABC中,AB=AC,P是△ABC内部的一点,且∠APB﹥∠APC。求证:PB<PC 由于AB=AC,可将△ABP旋转至AP'C。 ∵AP‘=AP,∴∠APP'=∠AP'P ∵∠AP’C = ∠APB > ∠APC ∴∠PP'C > ∠P'PC ∴ BP=CP' < PC
在△ABC中,∠C=90°,M在BC上,且BM=AC,N在AC上,且AN=MC,AM与BN相交于点P,求证:∠BPM=45° 在直角三角形ABC中,∠C=90°,M在BC上,N在AC上,且BM=AC,AN=MC,求证∠BPM=45°。 证明设AC=b,BC=a, 则CM=AM=a-b,CN=2b-a。 过N点作NH∥AM,过M点作MH∥AC,交于H.连BH. 则四边形ANHM是平行四边形, 所以 MH=AN=CM=a-b,AM=NH. 由勾股定理得: BN^2=BC^2+CN^2=a^2+(2b-a)^2=2(a^2-2ab+2b^2); AM^2=AC^2+CM^2=b^2+(a-b)^2= a^2-2ab+2b^2; BH^2=BM^2+MH^2=b^2+(a-b)^2= a^2-2ab+2b^2. 所以得 AM=BH,AM^2+BH^2=BN^2。 故三角形BHN是等腰直角三角形。 因此∠BPM=∠BNH=45°。
这里的O 点相当于你们作业上的G 点 将边长为1+n/2(n=1,2,3,……)的正方形纸片从左到右顺次摆放,其对应的正方形的中心依次为A1A2A3,…… 2011-2-19 10:16 提问者: 兔兔漂亮吗 | 浏览次数:1369次 (1)若摆放前6个正方形纸片,则被遮盖的线段长度和为( ),(2)若摆放前n (n 为大于1的正整数)个正方形纸片,则被遮盖的线段长度之和为( ) 答案为:10 1/4*(n+2)(n-1) ①过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D ,根据正方形的性质推出∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D ,求出∠AA 1B=∠DA A C ,证△BAA 1≌△CDA 1,得到AB=DC ,求出虚线部分的线段之和是1,依次求出其它虚线之和,相加即可; ②根据①的结论求出 1 2 ×(2+3+4+…+n )即可. ①解:过A 1作A 1A ⊥EF 于A ,A 1D ⊥FG 于D , ∵正方形EFGH , ∴∠A 1AB=∠A 1DC=∠EFG=90°,A 1A=A 1D , ∴∠AA 1D=∠BA 1C=90°, ∴∠AA 1B=∠DA A C , ∴△BAA 1≌△CDA 1, ∴AB=DC , ∴BF+FC=FA+FD= 1+1 2 =1, 同理第2个虚线之和是 1+2 2 = 3 , 同理第3个虚线之和是2, 同理第4个虚线之和是 5
经典难题(一) 1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二) 2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二) 3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、 DD 1的中点. 求证:四边形A 2B 2C 2D 2是正方形.(初二) 4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延 长线交MN 于E 、F . 求证:∠DEN =∠F . A P C D B A F G C E B O D D 2 C 2 B 2 A 2 D 1 C 1 B 1 C B D A A 1
经典难题(二) 1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且 (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二) 2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A D 、E ,直线EB 及 CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二) 3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题: 设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、 Q . 求证:AP =AQ .(初二) 4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG , 点P 是EF 的中点. 求证:点P 到边AB 的距离等于AB 的一半.
初二几何经典训练题 1、如图,在直角梯形ABCD中,AB∥DC,∠ABC=90°,AB=2DC,对角线AC⊥BD,垂足为F,过点F作EF∥AB,交AD于点E,CF=4cm. ⑴求证:四边形ABFE是等腰梯形; ⑵求AE的长. 2、如图,矩形ABCD的对角线AC、BD相交于点O,E、F分别是OA、OB的中点. (1)求证:△ADE≌△BCF; (2)若AD=4cm,AB=8cm,求CF和OF的长。 3、如图,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=12cm,BC=8cm,DC=13cm,动点P沿A→D→C线路以2cm/秒的速度向C运动,动点Q沿B→C线路以1cm/秒的速度向C运动.P、Q两点分别从A、B同时出发,当其中一点到达C点时,另一点也随之停止.设运动时间为t秒,△PQB的面积为ycm2.(1)求A D的长及t的取值范围;(2)当≤t≤t0(t0为(1)中t的最大值)时,求y关于t的函数关系式;(3)请具体描述:在动点P、Q的运动过程中,△PQB的面积随着t的变化而变化的规律。 4、如图,AB与CD相交于E,AE=EB,CE=ED,D为线段FB的中点,GF与AB相交于点G,若CF=15cm,求GF之长。
5、如图所示,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连接AE,F为AE上的一点,且∠BFE =∠C。(1)求证:△ABF∽△EAD;(2)若AB=4,∠BAE=30°,求AE的长;(3)在(1)、(2)的条件下,若AD=3,求BF的长(计算结果可含根号)。 6、如图是一个常见铁夹的侧面示意图,OA,OB表示铁夹的两个面,C是轴,CD⊥OA于点D,已知DA=15mm,DO=24mm,DC=10mm, 我们知道铁夹的侧面是轴对称图形,请求出A、B两点间的距离。 7、如图,用三个全等的菱形ABGH、BCFG、CDEF拼成平行四边形ADEH,连接AE与BG、CF分别交于P、Q,(1)若AB=6,求线段BP的长; (2)观察图形,是否有三角形与△ACQ全等并证明你的结论. 8、如图已知点E、F在△ABC的边AB所在的直线上,且AE=BF,FH∥FG∥AC,FH、EG分别交边BC所在的直线于点H、G。 (1)如图1,如果点E、F在边AB上,那么EG+FH=AC; (2)如图2,如果点E在边AB上,点F在AB的延长线上,那么线段EG、FH、AC的长度关系是_________ ;(3)如图3,如果点E在AB的反向延长线上,点F在AB的延长线上,那么线段EG、FH、AC的长度关系是_____________。
初中平面几何145个知识点 几何要想取得好成绩,几何公式一定要烂熟于胸。几何公式是做好几何题的根基,因此同学们一定要在几何公式上多下功夫。 线 1 过两点有且只有一条直线 2 两点之间线段最短 3 同角或等角的补角相等 4 同角或等角的余角相等 5 过一点有且只有一条直线和已知直线垂直 6 直线外一点与直线上各点连接的所有线段中,垂线段最短 7 平行公理经过直线外一点,有且只有一条直线与这条直线平行 8 如果两条直线都和第三条直线平行,这两条直线也互相平行初中几何公式: 角 9 同位角相等,两直线平行 10 内错角相等,两直线平行 11 同旁内角互补,两直线平行 12 两直线平行,同位角相等 13 两直线平行,内错角相等 14 两直线平行,同旁内角互补 初中几何公式:三角形 15 定理三角形两边的和大于第三边 16 推论三角形两边的差小于第三边 17 三角形内角和定理三角形三个内角的和等于180° 18 推论1 直角三角形的两个锐角互余 19 推论2 三角形的一个外角等于和它不相邻的两个内角的和 20 推论3 三角形的一个外角大于任何一个和它不相邻的内角 21 全等三角形的对应边、对应角相等 22 边角边公理有两边和它们的夹角对应相等的两个三角形全等 23 角边角公理有两角和它们的夹边对应相等的两个三角形全等 24 推论有两角和其中一角的对边对应相等的两个三角形全等 25 边边边公理有三边对应相等的两个三角形全等 26 斜边、直角边公理有斜边和一条直角边对应相等的两个直角三角形全等 27 定理1 在角的平分线上的点到这个角的两边的距离相等 28 定理2 到一个角的两边的距离相同的点,在这个角的平分线上 29 角的平分线是到角的两边距离相等的所有点的集合 初中几何公式:等腰三角形 30 等腰三角形的性质定理等腰三角形的两个底角相等 31 推论1 等腰三角形顶角的平分线平分底边并且垂直于底边
标准 经典难题(一).⊥AB,EGCO⊥是半圆的圆心,C、E是圆上的两点,CDAB,EF ⊥、已知:如图,1O (初二)CD=GF.求证:C E G A B O D F P2、已知:如图,是形ABCD点,∠15=.PDAPAD=∠0D A (初二)PBC 求证:△是正三角形.P C B
文案. 标准 、CC、BB、DA、B、C、分别是AAB3、如图,已知四边形ABCD、ACD都是形,12221111112A D DA DD的中点.2 2 1A1 D1 是形.(初二)D求证:四边形ABC2222B1 C1 BC2 2 C B BC、分别是AB、CD的中点,MAD4、已知:如图,在四边形ABCD中,=BC,、NAD F
E、.FMN的延长线交于E .DEN求证:∠=∠F C N D A B M 经典难题(二) 文案. 标准 1、已知:△ABC中,H为垂心(各边高线的交点),O为外心,且OM⊥BC于 M. A ;AH=2OM (1)求证:AO.(初二),求证:)若∠BAC=60AH=(20O ·H E B C D M
CB、于A,自A引圆的两条直线,交圆于OAO2、设MN是圆外一直线,过O作⊥MN G E .QMNEBD及、E,直线及CD分别交于P、O ·(初二)AQAP求证:=.C B D N M Q P A
MN3、如果上题把直线由圆外平移至圆,则由此可得以下命题:文案. 标准 MNEB分别交DE,设CD、O的弦,过MN的中点A任作两弦BC、设MN是圆 E C Q.于P、A Q M ·N P (初二)=AQ.求证:AP·O B D PCBFG,点ABC的外侧作形ACDE和形为一边,在△4、如图,分别以△ABC的AC和BC