人工智能作业—迷宫问题

4127：迷宫问题（bfs）总时间限制:1000ms内存限制:65536kB描述定义⼀个⼆维数组：int maze[5][5] = {0, 1, 0, 0, 0,0, 1, 0, 1, 0,0, 0, 0, 0, 0,0, 1, 1, 1, 0,0, 0, 0, 1, 0,};它表⽰⼀个迷宫，其中的1表⽰墙壁，0表⽰可以⾛的路，只能横着⾛或竖着⾛，不能斜着⾛，要求编程序找出从左上⾓到右下⾓的最短路线。

输⼊⼀个5 × 5的⼆维数组，表⽰⼀个迷宫。

数据保证有唯⼀解。

输出左上⾓到右下⾓的最短路径，格式如样例所⽰。

样例输⼊0 1 0 0 00 1 0 1 00 0 0 0 00 1 1 1 00 0 0 1 0样例输出(0, 0)(1, 0)(2, 0)(2, 1)(2, 2)(2, 3)(2, 4)(3, 4)(4, 4)指针被我⽤着⽤着迷糊了。

不过还是ac了1 #include <bits/stdc++.h>2using namespace std;3int a[6][6],visit[6][6];4struct Node {5int r,c;6 Node *pre;7 Node(int rr,int cc,Node *a):r(rr),c(cc),pre(a){}8 };9int dr[4]={1,-1,0,0};10int dc[4]={0,0,1,-1};11 queue <Node*> q;1213void fun(Node *s){14if(s->r==0&&s->c==0){15 printf("(%d, %d)\n",s->r,s->c);16return;17 }19 fun(s->pre);20 printf("(%d, %d)\n",s->r,s->c);21 }22 }2324int main() {25 memset(visit,0,sizeof(visit));26for(int i=0; i<5; i++) {27for(int j=0; j<5; j++) {28 cin>>a[i][j];29 }30 }31while(!q.empty())q.pop();32 visit[0][0]=1;33 q.push(new Node(0,0,NULL));34while(!q.empty()){35 Node *p=q.front();36 q.pop();37if(p->r==4&&p->c==4){38 fun(p);39return0;40 }41else{42for(int i=0;i<4;i++){43int rr=p->r+dr[i];44int cc=p->c+dc[i];45if(!visit[rr][cc]&&a[rr][cc]==0&&rr>=0&&rr<=4&&cc>=0&&cc<=4){46 visit[rr][cc]=1;47 q.push(new Node(rr,cc,p));48 }49 }5051 }52 }5354return0;55 }下⾯的代码忘记转⾃哪⾥了，好理解点；1 #include <stdio.h>2 #include <iostream>3 #include <algorithm>4 #include <queue>56using namespace std;7struct node8 {9int x,y;10 }vis[6][6];11//⽤于存放路径 - ⼆维数组第⼀维存放当前路径的x、⼆维存放y12//.x存放上⼀个路径的x、.y存放上⼀个路径的y13int a[6][6],book[6][6]; //book⽤来标记14int oper[4][2] = {15 {0,1},16 {1,0},17 {0,-1},18 {-1,0}19 };20void bfs()21 {22 queue<node> q;23 node now;24 now.x = now.y = 0;25 book[0][0] = 1;26 q.push(now);27while(!q.empty())28 {29 now = q.front();30 q.pop();31for(int i = 0;i < 4;i++)32 {33 node next;34 next.x = now.x + oper[i][0];35 next.y = now.y + oper[i][1];36if(next.x>=0 && next.x<5 && next.y>=0 && next.y<5 && !book[next.x][next.y] && a[next.x][next.y]!=1)37 {38 book[next.x][next.y] = 1;39 vis[next.x][next.y] = now; //记录上⼀个路径信息40 q.push(next);42if(next.x == 4 && next.y == 4) 43return;44 }45 }46 }47//使⽤递归输出路径48void print(int x, int y)49 {50if(x == 0 && y == 0)51 printf("(0, 0)\n");52else53 {54 print(vis[x][y].x, vis[x][y].y);55 printf("(%d, %d)\n",x,y);56 }57 }5859int main()60 {61int i,j;62for(i = 0;i < 5;i++)63for(j = 0;j < 5;j++)64 scanf("%d",&a[i][j]);65 bfs();66 print(4, 4);67return0;68 }。

广 度 优 先 搜 索 （ ＢＦＳ） ： 从 入 口 出 发 ， 离 开 入 口 后 依 次 访 问 与当前位置邻接的单元格（ 上下左右方向） ， 然后分别从这些相 邻 单 元 格 出 发 依 次 访 问 它 们 的 邻 接 格 ， 并 使 “先 被 访 问 的 单 元 格 的 邻 接 格 ‘先 于 ’后 被 访 问 的 单 元 格 的 邻 接 格 ”被 访 问 ， 直 至 访问到迷宫出口， 则找到了迷宫问题的最优解， 即迷宫最短路 径。该算法的显著特点是“层层推进”， 探索点会随着探索的深 入急剧增加， 相应地， 需要大量的空间用来保存探索过程的记 录， 空间复杂度大。
与此同时， 上述两种算法都比较抽象复杂， 编程实现容易 出现问题， 调试比较困难， 因此在本篇论文中提出了一种新的 容易理解和调试的算法， 该算法复杂度较低， 求解较大规模的 迷宫问题也有不俗的表现。
２ 经典算法
求解迷宫问题， 经典算法有深度优先搜索和广度优先搜索 两种。
３ 本文算法 ３．１ 本文算法基本思想描述
图 １ 迷宫 而迷宫最短路径问题就是找出从迷宫入口到出口所经过 单元格个数最少的路径。
深 度 优 先 搜 索 （ ＤＦＳ） ： 从 入 口 出 发 ， 顺 着 某 一 方 向 向 前 探 索， 若能走通， 则继续往前走； 否则沿原路退回（ 回溯） ， 换一个 方向再继续探索， 直至所有可能的通路都探索到为止。如果恰 好某一步探索到出口， 则就找到了从入口到出口的路径。为了 保证在任何位置上都能沿原路退回， 防止死循环， 需要使用堆 栈来保存大量记录。而要求解迷宫最短路径， 则必须用深度优 先搜索出所有到达出口的路径， 通过比较得到最短距离的路 径， 这样也必然要求增加数据空间来保存搜索过程中当前最短 路径， 增加了空间复杂度。

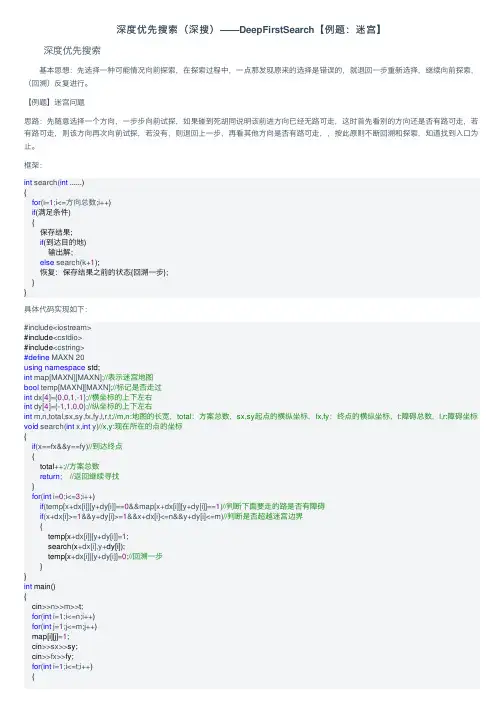
深度优先搜索（深搜）——DeepFirstSearch【例题：迷宫】深度优先搜索 基本思想：先选择⼀种可能情况向前探索，在探索过程中，⼀点那发现原来的选择是错误的，就退回⼀步重新选择，继续向前探索，（回溯）反复进⾏。

【例题】迷宫问题思路：先随意选择⼀个⽅向，⼀步步向前试探，如果碰到死胡同说明该前进⽅向已经⽆路可⾛，这时⾸先看别的⽅向还是否有路可⾛，若有路可⾛，则该⽅向再次向前试探，若没有，则退回上⼀步，再看其他⽅向是否有路可⾛，，按此原则不断回溯和探索，知道找到⼊⼝为⽌。

框架：int search(int ......){for(i=1;i<=⽅向总数;i++)if(满⾜条件){保存结果;if(到达⽬的地)输出解;else search(k+1);恢复：保存结果之前的状态{回溯⼀步};}}具体代码实现如下：#include<iostream>#include<cstdio>#include<cstring>#define MAXN 20using namespace std;int map[MAXN][MAXN];//表⽰迷宫地图bool temp[MAXN][MAXN];//标记是否⾛过int dx[4]={0,0,1,-1};//横坐标的上下左右int dy[4]={-1,1,0,0};//纵坐标的上下左右int m,n,total,sx,sy,fx,fy,l,r,t;//m,n:地图的长宽，total：⽅案总数，sx,sy起点的横纵坐标，fx,fy：终点的横纵坐标，t:障碍总数，l,r:障碍坐标void search(int x,int y)//x,y:现在所在的点的坐标{if(x==fx&&y==fy)//到达终点{total++;//⽅案总数return; //返回继续寻找}for(int i=0;i<=3;i++)if(temp[x+dx[i]][y+dy[i]]==0&&map[x+dx[i]][y+dy[i]]==1)//判断下⾯要⾛的路是否有障碍if(x+dx[i]>=1&&y+dy[i]>=1&&x+dx[i]<=n&&y+dy[i]<=m)//判断是否超越迷宫边界{temp[x+dx[i]][y+dy[i]]=1;search(x+dx[i],y+dy[i]);temp[x+dx[i]][y+dy[i]]=0;//回溯⼀步}}int main(){cin>>n>>m>>t;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)map[i][j]=1;cin>>sx>>sy;cin>>fx>>fy;for(int i=1;i<=t;i++){cin>>l>>r;map[l][r]=0;}map[sx][sy]=0; search(sx,sy); printf("%d",total); return0;}。

迷宫问题求解是一个经典的NP完全问题，求解难度较大，需要高效的算法和策略。同时，迷宫问题的规模和复 杂度随着迷宫的增大而急剧增加，对计算资源和算法性能提出了更高的要求。
机遇
随着人工智能和机器学习技术的不断发展，越来越多的算法和模型被应用于迷宫问题求解，如深度学习、强化学 习等。这些算法和模型在处理大规模、复杂迷宫问题方面展现出了强大的潜力和优势，为迷宫问题求解带来了新 的机遇和突破。
并行化搜索适用于具 有良好并行性的迷宫 问题，可以显著提高 求解效率。
通过使用并行计算资 源，可以同时搜索多 个路径，加快求解速 度。
04
迷宫求解的实践案例
简单的迷宫求解
使用深度优先搜索（DFS）
01
从起点开始，探索所有可能的路径，直到找到终点或无路可走。
使用广度优先搜索（BFS）
02
按照从起点到终点的路径长度，逐层搜索，直到找到终点或无
未来研究方向
算法优化
智能化求解
应用拓展
理论分析
针对迷宫问题求解，进一步优 化现有算法和模型，提高求解 效率和质量。研究新的算法和 模型，以更好地处理大规模、 复杂迷宫问题。
结合人工智能和机器学习技术 ，研究智能化求解方法，如基 于深度学习的路径规划、强化 学习算法等。通过智能化技术 提高迷宫问题求解的自动化和 智能化水平。
路可走。
使用回溯法
03
从起点开始，尝试所有可能的路径，如果遇到死胡同或无法到
达终点，则回溯到上一个节点，继续尝试其他路径。优先搜索，在迷宫中寻找 最短路径。
使用遗传算法
模拟生物进化过程，通过交叉、变异等操作，寻 找最优解。
使用模拟退火算法
模拟物理退火过程，通过随机扰动和接受概率， 寻找最优解。

《数据结构与算法设计》迷宫问题实验报告——实验二专业：物联网工程班级：物联网1班学号：********姓名：***一、实验目的本程序是利用非递归的方法求出一条走出迷宫的路径，并将路径输出。

首先由用户输入一组二维数组来组成迷宫，确认后程序自动运行，当迷宫有完整路径可以通过时，以0和1所组成的迷宫形式输出，标记所走过的路径结束程序；当迷宫无路径时，提示输入错误结束程序。

二、实验内容用一个m*m长方阵表示迷宫，0和1分别表示迷宫中的通路和障碍。

设计一个程序对于任意设定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

三、程序设计1、概要设计（1）设定栈的抽象数据类型定义ADT Stack{数据对象：D={ai|ai属于CharSet，i=1、2…n，n>=0}数据关系：R={<ai-1,ai>|ai-1,ai属于D，i=2,3,…n}基本操作：InitStack(&S)操作结果：构造一个空栈Push（&S，e）初始条件：栈已经存在操作结果：将e所指向的数据加入到栈s中Pop（&S,&e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元素，并删除栈顶元素Getpop（&S，&e）初始条件：栈已经存在操作结果：若栈不为空，用e返回栈顶元StackEmpty(&S)初始条件：栈已经存在操作结果：判断栈是否为空。

若栈为空，返回1，否则返回0Destroy(&S)初始条件：栈已经存在操作结果：销毁栈s}ADT Stack（2）设定迷宫的抽象数据类型定义ADT yanshu{数据对象：D={ai,j|ai,j属于{‘’、‘*’、‘@’、‘#’},0<=i<=M,0<=j<=N}数据关系：R={ROW,COL}ROW={<ai-1,j,ai,j>|ai-1,j,ai,j属于D，i=1,2,…M,j=0,1,…N}COL={<ai,j-1,ai,j>|ai,j-1,ai,j属于D,i=0,1,…M，j=1,2,…N}基本操作：InitMaze(MazeType &maze, int a[][COL], int row, int col){初始条件：二维数组int a[][COL],已经存在，其中第1至第m-1行，每行自第1到第n-1列的元素已经值，并以值0表示障碍，值1表示通路。

基础教育与人工智能的案例一、智能辅导系统助力学习困难的小明。

1. 案例情况。

小明是个四年级的学生，数学一直是他的老大难。

每次做数学作业，他就像进入了一个迷宫，完全摸不着头脑。

尤其是乘法和除法的混合运算，对他来说就像是外星密码。

他的父母给他报了一个线上的智能辅导系统。

这个系统就像是一个超级耐心的数学小助手。

2. 辅导过程。

当小明登录系统，输入他的作业题目，比如“36÷(4×3)”时，系统首先会用非常形象的动画来解释运算顺序。

动画里有一群小动物分果子，先分小堆（括号里的乘法），再把小堆合并起来分（除法）。

然后，系统会逐步给出解题步骤，并且在每一步旁边都有语音讲解。

如果小明还是不明白，他可以点击“我还不懂”按钮，系统就会换一种更简单的方式重新讲解，可能会用实物的图片来代替小动物，像把苹果分成堆那样演示计算过程。

经过一段时间的使用，小明对数学运算的理解能力大大提高，在最近的一次数学小测验中，他的成绩从原来的不及格提高到了七十分呢。

二、人工智能辅助小学英语教学。

1. 案例情况。

在一所小学里，英语老师张老师发现班上的同学对英语单词的发音总是不准确。

她自己一个人纠正不过来，而且传统的教学方法效果不明显。

于是，学校引进了一套人工智能英语教学软件。

2. 教学过程。

这个软件有一个很有趣的功能，叫做“语音模仿秀”。

当张老师教完新单词，比如“elephant”，同学们就可以打开软件对着手机或者电脑读这个单词。

软件会立刻对同学们的发音进行分析，它能准确地指出是哪个音发错了，比如有的同学把“e”的音发成了“a”的音。

然后，软件会播放标准发音和同学们的发音对比，并且给出纠正的小提示，像“舌尖要抵住下齿，嘴巴向两边咧开一点”之类的。

而且软件里还有一些英语小短剧，同学们可以选择自己喜欢的角色，然后跟着剧里的角色一起说英语。

这样既提高了同学们的发音准确性，又增加了他们学习英语的兴趣。

期末考试的时候，班级的英语平均成绩提高了十分左右呢。

第一章1.3 什么是人工智能？它的研究目标是什么？人工智能（Artificial Intelligence），英文缩写为AI。

它是研究、开发用于模拟、延伸和扩展人的智能的理论、方法、技术及应用系统的一门新的技术科学。

研究目标：人工智能是计算机科学的一个分支，它企图了解智能的实质，并生产出一种新的能以人类智能相似的方式做出反应的智能机器，该领域的研究包括机器人、语言识别、图像识别、自然语言处理和专家系统等。

1.7 人工智能有哪几个主要学派？各自的特点是什么？主要学派：符号主义，联结主义和行为主义。

1.符号主义：认为人类智能的基本单元是符号，认识过程就是符号表示下的符号计算，从而思维就是符号计算；2.联结主义：认为人类智能的基本单元是神经元，认识过程是由神经元构成的网络的信息传递，这种传递是并行分布进行的。

3.行为主义：认为，人工智能起源于控制论，提出智能取决于感知和行动，取决于对外界复杂环境的适应，它不需要只是，不需要表示，不需要推理。

1.8 人工智能有哪些主要研究和应用领域？其中有哪些是新的研究热点？1.研究领域：问题求解，逻辑推理与定理证明，自然语言理解，自动程序设计，专家系统，机器学习，神经网络，机器人学，数据挖掘与知识发现，人工生命，系统与语言工具。

2.研究热点：专家系统，机器学习，神经网络，分布式人工智能与Agent，数据挖掘与知识发现。

第二章2.8 用谓词逻辑知识表示方法表示如下知识：(1)有人喜欢梅花，有人喜欢菊花，有人既喜欢梅花又喜欢菊花。

三步走：定义谓词，定义个体域，谓词表示定义谓词P(x)：x是人L(x,y)：x喜欢yy的个体域：{梅花，菊花}。

将知识用谓词表示为：(∃x)(P(x)→L(x, 梅花)∨L(x, 菊花)∨L(x, 梅花)∧L(x, 菊花))(2) 不是每个计算机系的学生都喜欢在计算机上编程序。

定义谓词S(x)：x是计算机系学生L(x, pragramming)：x喜欢编程序U(x,computer)：x使用计算机将知识用谓词表示为：¬ (∀x) (S(x)→L(x, pragramming)∧U(x,computer))2.18 请用语义网络表示如下知识：高老师从3月到7月给计算机系的学生讲“计算机网络”课。

人工智能原理练习题-1从习题中选择自己感兴趣的题目进行思考和解答，任何尝试都是有益的。

必要时，仔细阅读教科书当中的某些章节。

对于加星号的习题，应该编写程序来完成。

第1章人工智能概述1 用自己的语言定义：（a）智能，（b）人工智能，（c）智能体。

2 用你自己的话定义下列术语：智能体、智能体函数、智能体程序、理性、自主、反射型智能体、基于模型的智能体、基于目标的智能体、基于效用的智能体、学习智能体。

3 对于下列智能体，分别给出任务环境PEAS描述：a. 机器人足球运动员；b. 因特网购书智能体；c. 自主的火星漫游者；d. 数学家的定理证明助手。

4 检查AI的文献，去发现下列任务现在计算机是否能够解决：a.打正规的乒乓球比赛。

b.在开罗市中心开车。

c.在市场购买可用一周的杂货。

d.在万维网上购买可用一周的杂货。

e.参加正规的桥牌竞技比赛。

f.发现并证明新的数学定理。

g.写一则有内涵的有趣故事。

h.在特定的法律领域提供令人满意的法律建议。

i.从英语到西班牙语的口语实时翻译。

j.完成复杂的外科手术。

对于现在不可实现的任务，试着找出困难所在，并预测如果可能的话它们什么时候能被克服。

5 Loebner奖每年颁发给最接近天通过某个版本图灵测试的程序。

查找和汇报Loebner奖最近的得主。

它使用了什么技术？它对AI目前的发展水平有什么推动？6 这道习题要探讨的是智能体函数与智能体程序的区别：a. 是否有不止一个智能体程序可以实现给定的智能体函数？请举例，或者说明为什么不可能。

b. 有没有无法用任何智能体程序实现的智能体函数。

c．给定一个机器体系结构，能使每个智能体程序刚好实现一个智能体函数吗？d. 给定一个存储量为n 比特的体系结构，可以有多少种可能的不同智能体程序？7 有一些类众所周知的难题对计算机而言是难以解决的困难，其它类问题是不能判定的。

这是否意味着AI是不可能的？8 内省-----汇报自己的内心想法-----是如何不精确的？我会搞错我怎么想的吗？请讨论。

作者： 刘超[1]
作者机构： [1]江苏省扬州中学,江苏扬州225009
出版物刊名： 实验教学与仪器
页码： 66-68页
年卷期： 2021年 第9期
主题词： 人工智能教与学;深度优先搜索;经典迷宫问题

摘要：人工智能搜索是指从海量的信息源中通过约束条件和额外信息运用算法找到问题所对
应的答案,其中,深度优先搜索和宽度优先搜索又是众多智能算法的基石,而经典迷宫问题常常作为
搜索算法教与学的重要载体.以经典迷宫问题为例,归纳出深度优先搜索算法的教学流程为:问题抽
象—数学建模—问题解决—算法优化.同时,绘出可视化思维模型.

人工智能交大题目及答案本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March《人工智能导论》全真试题一、判断题（在单选框内选择）1、只有在单位耗散值的情况下，当问题有解时，宽度优先算法才能保证找到最优解。

2、在A*算法结束之前，OPEN表中任何满足f(n)<f*(s)的节点n，一定被扩展。

3、设有机器人走迷宫问题，其入口坐标为(x0, y0)，出口坐标为(x t, y t)，当前机器人位置为(x, y)，若定义，当从入口到出口存在通路时，用A算法求解该问题，定能找到从入口到出口的最佳路径。

4、在A算法中，满足单调条件的h必然满足A*算法的条件。

5、比起极小 -- 极大法来，α-β剪枝法增大了找不到最佳走步的危险性，但其效率较高。

二、填空题（在横线上作答）1、基于规则的正向演绎系统使用的条件是（1）事实表达式是（2）规则形式为，其中（3）目标公式为2、基于规则的逆向演绎系统使用的条件是（1）事实表达式是（2）规则形式为，其中（3）目标公式为3、归结法中，可以通过的方法得到问题的解答。

三、问答题（在每题下面的空白框上作答）1、某问题状态图如右图所示。

假定k连接符的耗散值为k。

各节点的h值假定为：h(A)=3, h(B)=2, h(C)=6, h(D)=3,h(E)=4, h(F)=2, h(G)=3, h(H)=h(I)=0 (目标节点)用AO*算法求解该问题，给出每次循环后的搜索图，并给出求得的解图。

3、有四人过河，只有一条船，最多可乘坐两人。

若单个过，各需1，1，5，9分钟，若两人一起过，则需要的时间以多的为准（如需要5分和9分的两人同时乘坐，则需要9分）。

问最少需要多少分钟。

(1)、用产生式系统描述该问题，要求给出综合数据库的定义，规则集，初始状态和结束状态。

(2)、定义一个h函数，并说明是否满足A*条件。

人工智能哎，说人工智能这事儿吧，真是让人又爱又恨。

咱就拿我前几天的事儿说吧，简直绝了！我那天去超市买菜，本来想买点儿西红柿炒鸡蛋的菜，结果就…就迷路了！可不是夸张，那超市大的啊，就跟个迷宫似的。

绕来绕去，最后走到了一堆进口零食中间，好家伙，全是些我从来没见过的玩意儿。

我当时就琢磨，要是能有个AI帮我导航一下就好了，直接告诉我西红柿在哪儿。

可是吧，这AI要是真这么干，是不是得先分析我的购物习惯，然后根据我的年龄、性别、购买历史等等，再结合超市的布局图，最后才能给我指路？想想就觉得复杂！你说这算法训练数据得多麻烦？得先建立个庞大的数据库，记录每个人的购物习惯，还得不断更新，因为咱口味这东西，三天两头就变！比如我以前爱吃辣条，现在都改吃水果了，AI要是数据没更新，给我推荐辣条，那不是坑我嘛！哈哈，想想就觉得好笑。

而且这AI还得学习各种语言模式，才能把导航指令说出来，要是说“尊敬的顾客，您欲购买的西红柿位于西侧货架第三排，请沿箭头方向前进”这种官方话，我听着都烦！我就想听个简单的，“哎，西红柿在那边儿呢，赶紧去吧！” 多方便！所以啊，与其搞那些复杂的算法和数据，不如直接点——超市里弄个清晰明了的指示牌，或者弄个电子地图，简单明了，多好！就说我那天的事儿，最后还是靠着问一个热心的阿姨才找到西红柿的，那阿姨人可好了，还跟我推荐了一个她家包的饺子，说是特别好吃，买完西红柿我顺手还真买了一袋，晚饭就吃上了。

这感觉，比AI导航靠谱多了！你看，这AI的事儿吧，其实没那么玄乎。

有时候，简单的办法才是最好的办法。

与其搞一堆高科技让人摸不着头脑，还不如先把基础工作做好，你说是不是？与其让AI去分析我的购物习惯，不如给我个靠谱的超市地图，我还能自己选择买什么，多自由！嗯，说到底，还是那句话，简单点，简单点，生活会更美好呀！。

第五章搜索策略习题参考解答5.1 练习题5.1 什么是搜索？有哪两大类不同的搜索方法？两者的区别是什么？5.2 用状态空间法表示问题时，什么是问题的解？求解过程的本质是什么？什么是最优解？最优解唯一吗？5.3 请写出状态空间图的一般搜索过程。

在搜索过程中OPEN表和CLOSE表的作用分别是什么？有何区别？5.4 什么是盲目搜索？主要有几种盲目搜索策略？5.5 宽度优先搜索与深度优先搜索有何不同？在何种情况下，宽度优先搜索优于深度优先搜索？在何种情况下，深度优先搜索优于宽度优先搜索？5.6 用深度优先搜索和宽度优先搜索分别求图5.10所示的迷宫出路。

图5.10 习题5.6的图5.7 修道士和野人问题。

设有3个修道士和3个野人来到河边，打算用一条船从河的左岸渡到河的右岸去。

但该船每次只能装载两个人，在任何岸边野人的数目都不得超过修道士的人数，否则修道士就会被野人吃掉。

假设野人服从任何一种过河安排，请使用状态空间搜索法，规划一使全部6人安全过河的方案。

（提示：应用状态空间表示和搜索方法时，可用(N m,N c)来表示状态描述，其中N m和N c分别为传教士和野人的人数。

初始状态为(3,3)，而可能的中间状态为(0,1),(0,2),(0,3), (1,1),(2,1),(2,2),(3,0),(3,1),(3,2)等。

）5.8 用状态空间搜索法求解农夫、狐狸、鸡、小米问题。

农夫、狐狸、鸡、小米都在一条河的左岸，现在要把它们全部送到右岸去。

农夫有一条船，过河时，除农夫外，船上至多能载狐狸、鸡和小米中的一样。

狐狸要吃鸡，鸡要吃小米，除非农夫在那里。

试规划出一个确保全部安全的过河计划。

（提示：a.用四元组(农夫，狐狸，鸡，米)表示状态，其中每个元素都可为0或1，0表示在左岸，1表示在右岸；b.把每次过河的一种安排作为一个算符，每次过河都必须有农夫，因为只有他可以划船。

）5.9 设有三个大小不等的圆盘A 、B 、C 套在一根轴上，每个圆盘上都标有数字1、2、3、4，并且每个圆盘都可以独立地绕轴做逆时针转动，每次转动90°，初始状态S 0和目标状态S g 如图5.11所示，用宽度优先搜索法和深度优先搜索法求从S 0到S g 的路径。

利用DQN实现迷宫寻路迷宫寻路是一种经典的问题，它指的是在一个由墙壁和路径构成的迷宫中，找到从起点到终点的最短路径。

为了解决这个问题，我们可以利用深度强化学习中的DQN算法。

首先，我们需要定义迷宫的状态和动作空间。

迷宫的状态空间可以表示为一个二维的格子，每个格子可以有三种状态：墙壁、路径、终点。

动作空间包括上、下、左、右四个方向。

我们还需要定义迷宫的奖励机制，比如到达终点奖励1，碰到墙壁奖励-1，其他情况奖励0。

接下来，我们可以使用DQN算法来训练一个迷宫寻路的智能体。

DQN算法由两个部分组成：一个Q网络和一个目标网络。

Q网络用于估计每个状态动作对的Q值，目标网络用于计算目标Q值。

通过不断地更新Q网络和目标网络，智能体可以学会最优策略。

具体的训练过程如下：1.初始化Q网络和目标网络，并设定超参数，如学习率、折扣因子、探索率等。

2.初始化一个空的经验回放缓冲区，用于存储智能体的经验。

3.进入迭代训练的循环，每次循环包括以下步骤：a. 根据当前状态和探索率选择一个动作，可以使用ε-greedy策略。

b.执行选择的动作，观察新的状态和奖励，并存储经验到经验回放缓冲区。

c.从经验回放缓冲区中随机采样一批经验，用于更新Q网络。

d.使用目标网络计算目标Q值，并更新Q网络的参数。

e.更新目标网络的参数。

f.逐渐减小探索率，使智能体更加倾向于选择Q值最大的动作。

g.如果达到终点，结束训练。

通过不断迭代上述步骤，智能体可以逐渐学会最优的行动策略，从起点到终点的路径也会逐渐优化。

可以使用Python中的深度学习框架，如TensorFlow或PyTorch，来实现DQN算法。

这些框架提供了各种神经网络的操作和优化方法，方便我们构建和训练Q网络和目标网络。

最后，我们可以使用训练好的智能体来解决新的迷宫问题。

智能体根据当前状态选择最优的动作，直到达到终点。

总结起来，利用DQN实现迷宫寻路的步骤包括定义迷宫的状态和动作空间，构建Q网络和目标网络，通过经验回放和目标Q值更新Q网络的参数，最后使用训练好的智能体找到最短路径。

迷宫问题的设计与实现1.问题描述以一个m×n的长方阵表示迷宫，0和1分别表示迷宫中的通路和障碍。

本程序主要是对任意给定的迷宫，求出一条从入口到出口的通路，或得出没有通路的结论。

2.需求分析1.迷宫的建立：迷宫中存在通路和障碍，为了方便迷宫的创建，可用0表示通路，用1表示障碍，这样迷宫就可以用0、1矩阵来描述。

2.迷宫的存储：迷宫是一个矩形区域，可以使用二维数组表示迷宫，这样迷宫的每一个位置都可以用其行列号来唯一指定，但是二维数组不能动态定义其大小，我们可以考虑先定义一个较大的二维数组maze[M+2][N+2],然后用它的前m行n列来存放元素，即可得到一个m×n的二维数组，这样(0,0)表示迷宫入口位置，(m-1,n-1)表示迷宫出口位置。

注：其中M，N分别表示迷宫最大行、列数，本程序M、N的缺省值为39、39，当然，用户也可根据需要，调整其大小。

3.迷宫路径的搜索：首先从迷宫的入口开始，如果该位置就是迷宫出口，则已经找到了一条路径，搜索工作结束。

否则搜索其上、下、左、右位置是否是障碍，若不是障碍，就移动到该位置，然后再从该位置开始搜索通往出口的路径；若是障碍就选择另一个相邻的位置，并从它开始搜索路径。

为防止搜索重复出现，则将已搜索过的位置标记为2，同时保留搜索痕迹，在考虑进入下一个位置搜索之前，将当前位置保存在一个队列中，如果所有相邻的非障碍位置均被搜索过，且未找到通往出口的路径，则表明不存在从入口到出口的路径。

这实现的是广度优先遍历的算法，如果找到路径，则为最短路径。

3.概要设计因为迷宫可行路径之间存在线性关系，并且需要在端点处进行增删操作，因此采用队列结构类型存储迷宫可行路径的信息。

下面给出队列结构的ADT的定义。

3.1 队列结构的ADT的定义ADT Queue{数据对象：D={a i|a i∈ElemSet,t=1,2……,n, n>=0}数据关系：R1={<a i-1,a i>|a i-1,a i∈D,i=2,……,n}基本操作：InitQueue（&Q）操作结果：创建一个空队列QDestroy Queue (&Q)初始条件：队列Q已存在操作结果：队列Q被销毁ClearQueue(&Q)初始条件：队列Q已存在操作结果：队列Q清为空栈QueueEmpty(Q)初始条件：队列Q已存在操作结果：若队列Q为空栈，则返回TRUE，否则FALSEQueueLength(Q)初始条件：队列Q已存在操作结果：返回Q的元素个数，即队列的长度GetHead(Q,&e)初始条件：队列Q已存在且非空操作结果：用e返回Q的队头元素EnQueue(&Q,e)初始条件：队列Q已存在操作结果：插入元素e为新的队尾元素DeQueue(&Q,&e)初始条件：队列Q已存在且非空操作结果：删除Q的队头元素，并用e返回其值QueueTraverse(Q,visit() )初始条件：队列Q已存在且非空操作结果：从队头到队尾依次对Q的每个数据元素调用函数visit()。