数学建模 机器人避障问题

机器人避障优化模型摘要“机器人避障问题”是在一个规定的区域范围内，有12个位置各异、形状不同的障碍物分布，求机器人从出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的避障最短路径及其最短时间，其中必须考虑如圆与切线的关系等问题。

基于优化模型，对于题目实际情况进行研究和分析，对两个问题都用合适的数学思想做出了相应的解答和处理，以此建立符合题意的数学模型。

问题一，要求建立机器人从原点出发到达以区域中另一点为终点的最短路径模型。

机器人的避障路径规划主要包括环境建模、路径搜索、路径平滑等环节，针对本题的具体情况，首先对图形进行分析，并用AutoCAD 软件进行环境建模，使其在障碍物外围延伸10个单位，然后考虑了障碍物对路径安全的影响再通过蚁群算法来求它的的最短路径，由于此时最短路径中存在转弯路径，需要用人工势场法进行路径平滑处理，从而使它的最短路径在蚁群算法算出的结果情况下，可以进一步缩短其路径，从而存在机器人以区域中一点到达另一点使其避障的路径达到最短，在最终求解时，通过matlab 软件求其最优解。

问题二，仿照问题一机器人避障路径规划的基本环节所建立的一般模型，再根据题二所提出的具体问题，建立机器人从O （0，0）出发，使达到A 的最短时间路径模型。

其中已知最大速度为50=v 个单位/秒，机器人转弯时，最大转弯速度为21.0100e 1)(ρρ-+==v v v ，其中ρ是转弯半径，并有ν为增函数。

且有0νν<恒成立，则可知行走路径应尽量减少走圆弧，且可时间由走两段直线加圆弧的时间之和。

关键词： 最短路径 蚁群算法 人工势场法 机器人避障一 、问题重述图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

√ （ ７ ３ ＋ ０ ７ ｐ ） ＋
） ７ ｐ ＇ — （ ７ — ３ ＋０ — ２ ２ ７ ）＋ — （ １ ８ 一 ８ ｐ－６ ０ ）
： 、 ６ ２ ９ ２ ９ ｐ （ ９ １ ２ ６ ２ ＋３ ５ ４ ｐ ） （ Ｉ １ ０ ２ ５ ８ ｐ（ ７ ０ ８ ｐ ５ １ ４ ７ ６ ¨
使 之更 好 地 服务 油 田开 发项 目 ， 重 点关 心油 井 挤注 防 垢。油 田 进 入 中后 期 开发 后 ， 含 水 率 不断 升 高 ， 各种 结垢 问题 也将 日益 严重 ， 井 下挤 注 防垢 技术 的应 用 势在 必 行 ， 科 学合 理地 应用 油
井 挤注 防垢 技术 ， 做 好应 尽 的准 备 工作 ， 将 会 大 大提 高我 国油
所以： 最短 时 间路径为
ｍ ｉ ｎ ＝ 喜 厶，
用此模 型就 可 以对起 点到 目标 点之 间的路 径进行 优化 求解 。

４ ３ 给定场 景下 最短 路径模 型求 解
应 用 “拉 线 原 理 ” ， 计 算 各 个 路 线 的 最 短 路 径 相 互 比 较 可 得 最 优 行 走 路 线 以 及 最 短 路 径 。 知 ｏ （ ｏ ， ０ ） Ａ （ ３ ０ ０ ， ３ ０ ０ ）的 最 优 行 走 路 线 为 Ｏ Ａ Ａ ，最
ｏ （ ｏ ， ０ ） － － － ） Ａ （ ３ ０ ０ ， ３ ０ ０ ） Ｂ ００ ０ ， ７ ０ ０ ） Ｃ（ ７ ０ ０ ， ６ ４ ０ ） 的最优 行走 路
线为 Ｄ一 ５ 一 一 ７ 一 Ｄ８ 一 一 一 ９ 一 ９一 Ａ１ ０ 一Ｂ ｔ ０ 一Ｃ 一０ ， 最 短路径 Ｌ＝３ ０ ４ ２ ． ８ ０ ２ ２。
验 及应 用 。
模型缺陷 ： 在 障碍 物 较 多 时 ， 且形 状 不规 则 时 ， 模型 需 要 ０ 一 Ａ的最短路 径 ｏ （ ｏ ， ０ ） Ｃ （ ７ ０ ０ ， ６ ４ ０ ） 的 最 ０一 Ｂ的最 短路 径 优 行 走 路 线 为 参 考 文献 ［ １ ］ 机 器人 行走 问题． ｈ ｔ ｔ ｐ ： ／ ／ ｗ ｅ ｎ ｋ ｕ ． ｂ ａ ｉ ｄ ｕ ． ｃ ｏ ｍ ／

D題：机器人避障问題本文就机器人避强冋題，建立了相应的优化模里。

模1-：关干Hl器人从区域中一点到达另一贞的遐障最短路径的问题。

首先，题恿，师出HI器人行走的可行区域与危险区域；其次，在证明了具有園形限定区域的最皱路径间题为根据的前提下，可以得岀最短路径一定是由直线和闊弘组成，并依此建立了线岡结沟，将路径则分为若干个逆种线圆结构来求辭最短路径通用模型；最后，根弼最姬路径通用模型，采用穷举法把可能路径的最短路径列举出来，通il比较最终得出各种最短路径的坐标及总路程8UT：(1 ) 0-A的最矯路程为：471.04个单位(2) O T B的最短路程为:853.71个单位(3 ) 0->C的最短路程1088.20个单位(4 ) O T A—B T C T O的最短路径为：2730.01个单E模塑二：关于机器人UEM中一点到这另一点的避障最類时间路径的间题。

首先，根锯題意,找出公共切点，得出转弯时最大圆和最小圆的圆心坐标,确定冏心的变化X 围；其次，依擴圆心的变ItX围，得出转弯半径的变化X围；然后，利用MATLAB^件编程来求解最姬时间路径通用模型；最后，根据最短时间路径通用模里，得出所有结果，通过比较最终得岀机最后,我『1对模型进行了改进、检验、评价与推广。

关键词：优化模型最短路程线圆结构最短时间穷举法1问題重述1.1背景资料图1是一个800x800的平面场景图,在原点0(0,0)点处有一个机器人，它只能在该平面场景X围内活动。

图中有12f不同形状的区域是机器人不能与之发生磁撞的障碍物，障1.2 息(1)在图1的平面场景中，障碍物外荷定一点为机器人要到这的目标点。

现定机器人的行走路径由直筑段和冏弧组成，其中冏弧是机器人转弯路径。

(2)机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弘组成，也可以由两个或多个相切的凰聲路径组成，但毎个圆聲的半径最小为10个单也。

(3)HI器人直线行走的最大速度为v0 = 5个单位/秒。

精心整理机器人避障问题摘要本文研究了在一个800800⨯平面场景里，机器人通过直线和圆弧转弯，绕过障碍物，到达目标点的问题，解决了到达目标点路径最短，以及到达A 点时间最短的问题。

文章将路径划分为若干个这种线圆结构来求解。

对于途中经过节点的再到达目标点的状况，我们采用了在拐点和节点最小转弯半径的形式.O A →O →B O →C O →A →B 10个单位为50=v对场景图中4(1)(2)1.出发，分别做圆的切线，直到终点。

对于经过路径中的目标点的问题，我们采用最小转弯模式，建立优化模型，最终求的最短路径。

2．问题二要求从起始点到达A 点所用的时间最短，从题意以及生活经验可得，拐弯半径越大，所用时间越短，拐弯半径越小，所用时间越大。

半径最小不低于10，取最大值时机器人应刚好未碰到4、6三角形，可通过几何解法计算出来，并对时间进行优化处理。

三、模型假设假设机器人可以抽象成点来处理假设机器人的能源充足，且在整个行走过程中无故障发生四,符号说明】5（为起点，，OA圆弧的切点，角度1OO A ∠=,11OO M ∠=,11AO N ∠=，111M O N θ∠=.设这段路程机器人的总路程为L. 解法如下：如上图可得有以下关系：1 AOO ∆在中：在11Rt OO M ∆：222arccos(2b c a bcα+-=在11Rt AO N 中：所以：从而可得：结果如下：机器人行走路线1OM =1N A 弧11M N =224.7221；b=237.6973c=O 同理了解比较可得，O 从上面绕到到目标点A 的距离最短，最短路径为471.0372。

→2.O B→有多条路径，可以从O到正方形5的右下角直接到8的右上角，再绕到B。

1）O B2）可以从O到正方形5的右下角直接到8的右下角，再绕到8的左下角，绕到B。

3）可以从O到正方形5的左下角到左上角绕过6的右下角再8的右上角绕到B。

4）可以从O到正方形5的左下角到左上角绕过6的右下角再8的右下角，再绕到8的左下角，绕到B。

Ａ ｐ ｒ ． ２ ０ １ ３
ａ ＝ 、 厂 ６ ＝ 、 厂
， ，
Ｅ
ｃ ＝ 、 ／ ｒ
如图 ５ ． １ ， 设Ａ 。 ， Ｙ 。 ） 为起点， Ｂ 。 ， ｙ ２ ） 为 目标
点， 延长直线 Ｏ到． Ｃ Ｄ中点交圆弧 Ｃ Ｄ于 日 ， 过 圆心 作Ｏ Ｈ 的垂线分别 交 Ａ Ｃ 、 Ｃ Ｄ于 Ｆ 、 ，圆心 ０ 舢 ｃ ， ， 和Ｄ ， 为机器人经过拐点分别于 脱离危 险线 拐角 小 圆弧 的切 点 ，圆的半径 为 ｒ ，
其 中Ｐ是转弯 半径． 若超过该速度 ， 则机器人无法 完成行走 ： （ ３ ） 机器人变速和转身瞬间完成． ３模型假设 （ １ ） 机器人能够抽象成点来处理： ｃ ２ ） 机器人的性能足够好， 能准确地沿圆弧转弯； （ ３ ） 机器人行走过程 中不会意外停止； （ ４ ） 机器人行走不小于最小转弯半径和最小安 全距 离 ； （ ５ ） 机器人不会进 入 两个相接触的障碍物的死角． ４ 定义 与符 号说 明 ｒ ， Ｐ ： 转弯半径 ． ， 啦 ： 直线倾角或夹角． ｔ ： 时间． Ｌ ： 最 短路 径 总长 ． ５模 型 的建 立 查 阅相 关文 献 知 ，具有 圆形 限定 区域 的最短 路 径是由两部分组成的， 一部分是平面上的 自 然最短 路径 （ ａ Ｐ 直线段） ，另一部分是限定区域的部分边 界， 这两部分是相切 的， 这两条直线段是 由圆弧连 接的． 对于 问题 １ ， 我们经过深入分析知， 起 点到 目标 点无论中间障碍物有 多少 ， 最短路径都应该是若干 个线 圆结构所组成．在本题 中存在障碍物的状况 ， 且障碍物在拐点处 的危 险区域 是一个半径为 ｒ的 圆弧， 而求两点之间的最短路径 中的转弯半径我们 应该按照最小的转弯半径来算才能达到最优． ５ ． １基本线 圆结构的数学模型

２ 模 型假 设
１ ） 假设绕过障碍物我们均走最小半径的圆弧 ； ２ ） 假设 机 器人 能够 抽象 成点 来处理 ；
３ ） 假 设不 考虑 弧度 计算 ；
圆相 切 ， 切点 分别 为 Ｅ和 Ｆ， 当 Ｙ趋 近 于 Ｙ 时 ， 显 然 Ａ Ｃ Ｂ是这 种折 线 路 径 中最 短 的。 因 为 当 ： ０＜ Ｏ ｔ ＜
１ ８
数
字
通
信
第４ ０卷
与障碍 物 问的最 近距离 为 １ ０个单 位 ， 否则将 发 生碰 撞， 若碰 撞 发生 ， 机 器 人则无 法完 成行 走 。 建立 机器人 从 区域 中一点 到达 另一 点 的避 障最 短路径 和 最短 时问路 径 的数 学模 型 。场 景 图 中有 ４ 个 目标 点 ０（ ０ ， ０） ， ４（ ３ ０ ０ ， ３ ０ ０ ） ， Ｂ（ １ ０ ０ ，７ ０ ０ ） ， Ｃ （ ７ ０ ０ ， ６ ４ ０ ） 。具 体分 别计算 ：机 器人 从 ０（ ０ ， ０ ） 点
出发 ， Ｄ 一４， Ｄ —Ｂ， Ｄ — Ｃ和 Ｄ —Ａ —Ｂ —Ｃ — Ｄ 的最 短路 径及 长度 。
问题 ： 证 明绳 子拉 紧时 的情况 ， 则 为 ２个 点 之 间
的最 短路 径 。 假设 在平 面 中有 Ａ（ ａ ， ０ ） 和 曰（一ａ ， ０ ） ２点 ， 中
间有 １ 个半圆形的障碍物 ， 证 明从 到 Ｂ的最路径
分析 中的绳子拉到最紧时的情况 。
Ｔ Ａ Ｅ Ｆ Ｂ是 满足 条件 Ａ到 的最短 路径 。
第 ６期
侯学 慧 ： 机器人避 障问题模型研究
ｌ ９
３ ． ２ 模型 准 备 １
所 以，
＝２ 一Ｏ ｔ 一卢 一

机器人避障问题模型的几何画板解法探析作者：刘晓可孙志杰来源：《科技探索》2012年第10期摘要：本文对2012年全国大学生数学建模竞赛D题“机器人行走避障问题”，给出了利用“几何画板”这一数学软件进行求解的方法，并对该方法的优缺点进行了分析。

关键词：数学模型机器人避障几何画板2012年全国大学生数学建模竞赛D题“机器人行走避障问题”如下：在一个800×800的平面场景图中，原点O（0， 0）点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的圆弧组成，每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位。

计算机器人从O（0，0）出发，O→A、O→B、O→C和O→A→B→C→O的最短路径。

这个题目是平面区域的最短路径问题，难度在于路线的具体长度和拐点的坐标不容易计算，但可以利用几何画板的度量与标记坐标的功能实现求解，具体做法为：1. 在几何画板中画出平面区域的相关障碍物。

2. 先目测可能的最短路线并画出。

3. 计算几条路线的总长并进行比较。

4. 选取出最短的路线，并标记拐点的坐标。

下面是针对O→C的具体做法：如图，首先选取两条可能的最短路线，再利用几何画板的度量功能，分别计算出总长度。

经计算，S1=1087.37，S2=1102.32。

因为，S1问题中到其他点的路径可以用类似方法求得，在这里不一一表述。

该方法的优点是简单易操作、直观性强，缺点是计算结果没有用matlab等数学软件求解的精确，但现有的精确度已经足够，因此其不失为一个简单高效的方法。

参考文献：[1]赵静，数学建模与数学实验，北京：高等教育出版社，2008。

，机器人从圆弧 i 切点到圆 k 1,2 ，如 ( xi1 , yi1 ) 表示为圆弧 i 的第一个切点坐标（ xi1 xi 2 ）
弧 j 切点的直线距离 sij 为
sij ( xi 2 x j 2 )2 ( yi 2 y j1 )2
机器人在圆弧 i 两切点间圆弧距离 sij
三、模型假设
1.模型中由于已将将机器人与障碍物距离考虑，故可将机器人视为质点运动； 2.不考虑机器人的加速运动过程，即加速过程时间不考虑； 3.路径不考虑走场地的边界； 4.所有障碍物形状规则。
四、符号说明
L ：避障最短路径； ：圆弧的半径； sij ：圆弧 i 切点到圆弧 j 切点的直线距离，即机器人从圆弧 i 切点到圆弧 j 切点的直线路
kx2 b y2 1 k 2
Байду номын сангаас
r，
y y1 k ( x x1 ) b 1 y y2 ( x x2 ) k
进而求出切点 Q1 坐标。 （2） 圆与圆相切
Q2 B
(4)
Q1
A
图 5 两圆外切
圆心 A( x1 , y1 ) ，B( x2 , y2 ) ， 且两圆的半径分别为 r1 、r2 。两外公切线线切点分别为 Q1 、 y y 1 Q2 则直线 Q1Q2 斜率为 k 2 1 ，直线 AQ1 、 BQ2 的斜率为 ，联立 k x2 x1
机器人避障问题
摘 要
在科学探索和紧急抢险中经常会遇到对与一些危险或人类不能直接到达的地域的 探测，这些就需要用机器人来完成.而机器人在复杂地形中行进时自动避障是一项必不 可少也是最基本的功能。 本文建立了机器人从目标区域内一点到达另一点的最短路径、最短时间的非线性 0-1 整数规划模型。 具体来说是在一个区域中存在 12 个障碍物， 由出发点到达目标点以 及由出发点经过途中的若干目标点回到出发点的两种情况针对机器人避障问题， 并且要 满足机器只能走直线和弧线的行走特点。 针对问题一，建立区域内一点到达另外一点的最短路径模型。首先证明了机器人在 最短路径前提下的转弯位置必在绕过障碍物的顶角， 此时圆弧中心点坐标为障碍物顶点 坐标，并且此时圆弧的半径为10个单位。然后，最短路径的问题转化成图论里最短路径 优选问题，选用Floyd算法求解，其中问题的0-1规划选择与否问题涉及到基本的线段相 交、线圆相切、圆圆相切、点圆相切等几何关系的判断。最后，利用数学工具Matlab编 程实现模型算法，得到的O→A、O→B、O→C和O→A→B→C→O的最短路径如下 O→A的最短路径为(0,0)→(70.5063,213.1405) →(76.4888,219.3633)→ （300,300)，对应圆弧的圆心坐标为(80,210) O→B的最短路径经过的圆弧的圆心坐标：(60,300)，(150,435)， （220、470） ， (220,530)，(150,600) O→C经过的圆心：(410,100)，(230,60)，(720,520)， （720,600） ，(500,200) O→A→B→C→O经过的圆心：(410,100)，(230,60)，(80,210)，(220,530)， (150,600)，(270,680)，(370,680)，(430,680)，(670,730)，(540,730)，(720,520)， (720,600)，(500,200) 针对问题二，首先根据理论分析得到转弯圆心的大致范围；然后建立最短时间与转 弯圆弧对应圆心的横纵坐标、转弯半径的一般表达式，并给出的符合问题要求的约束条 件；最后在合理范围内，选择合适的步长，转弯半径的每增加一步，在理论转弯范围内 产生大量随机圆心坐标，得到最优的结果。最后求的在最短时间下，O→A 所经过的路径 为(0, 0) →(69.9614,212.2697)→(77.3879 ， ,219.8984)→(300, 300), 求得最短时 间路径下转弯半径为，同时最短时间路径时间长为个单位。相应圆弧的圆心坐标为 （81.5014,208.4663） ， 两切点坐标分别为(69.9614,212.2697)、 (77.3879， ,219.8984)， 经历最短时间是 94.6933s。

机器人避障问题摘 要本文讨论的是机器人避障问题，运用改良的橡皮筋算法思想，对最优路径逐步探索，并进行了大胆猜想．通过分析，利用几何关系证明了猜想的正确性，以此得到判断最短路径的三个原则：一、所走路线应尽可能接近两目标点与目的地连线；二、目标点转弯半径越小越好；三、找不到两圆间的公切线时，机器人应尽可能沿障碍物边界运动． 对于问题一，依据路径最优原则，确定转弯半径为10个单位，建立了机器人从区域中一点到达另一点的避障最短路径的优化模型．利用MATLAB 求解得到结果如下：A O →:总时间为：96.00826秒，总路程为471.0372个单位；B O →:总时间为179.09982秒，总长度为853.7113单位；C O →:总时间为239.72602秒，总路程为1100.19单位；O C B A O →→→→：总路程：2794.512单位 ，最终总时间为598.5477秒．对于问题二，要使机器人行走时间最短，需在尽可能保证最短路径的基础上适当增加转弯半径．利用几何知识推导出机器人行走时间与转弯半径的关系，时间对半径求导，并令导数为零，得出最短时间所对应的半径5055.11=r ，进而建立最短时间路径的优化模型．利用MATLAB 软件求解得，当机器人从)0,0(O 出发到达A 时，所用最短时间为2130.94秒，总距离为470.8301个单位．关键词：导数；橡皮筋算法；优化模型一、问题的重述图1是一个800⨯800的平面场景图，在原点)0,0(O 点处有一个机器人，它只能在该平面场景范围活动．图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物单位数学描述如下表：表1．12个不同形状区域的特性障碍物的距离至少超过10个单位）．规定机器人的行走路线有直线段和圆弧组成，其中圆弧是机器人的转弯路径．机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位．为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若发生碰撞，则机器人无法完成行走．机器人直线行走的最大速度为50=v 个单位/秒．机器人转弯时，最大转弯速度为21.01001)(ρρ-+==e v v v ，其中ρ是转弯半径．如果超过该速度，机器人将发生侧翻，无法完成行走．请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型．对场景图中4个点)0,0(O ，)300,300(A ，)700,100(B ，)640,700(C ，具体计算：（1）机器人从)0,0(O 出发，A O →、B O →、C O →和O C B A O →→→→的最短路径．（2）机器人从)0,0(O 出发，到达A 的最短时间路径．注：要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间 ．图1 800⨯800平面场景图二、问题分析对题目条件进行分析：要求目标点与障碍物的距离至少超过10个单位，又知O 点坐标为（0,0），即边界不视为障碍物，但目标点不能超出界限．规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径，转弯路径只能由一段圆弧组成也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位，因为半径趋于0的时候，圆弧长度趋于0，圆弧趋于折线．机器人行走路径与障碍物之间的最近距离为10个单位，否则发生碰撞，即可将障碍物区域向外扩充10个单位，余下部分为目标点可行走范围，对条件中所给最大转弯速度21.01001)(ρρ-+==e v v v 进行分析，当半径∞→ρ时，即可视为直线运动，50==v v 个单位/秒；当半径10→ρ时，最小速度5.220min ==v v 个单位/秒；半径ρ越大，机器人转弯速度越大． 对问题一分析：机器人从)0,0(O 出发，A O →、B O →、C O →和O C B A O →→→→的最短路径问题．首先分析A O →，在没有障碍物的情况下，A O →两点间线段最短，但在两点之间有正方形障碍物5阻碍，必须绕开障碍物5到达A ，要使A O →路径最短，则实际路径越逼近OA 线段越短．根据目标点的位置，可以猜想出机器人的几种避障路径．同理分析B O →、C O →路段．当分析O C B A O →→→→路径时，采用分段处理的方法，将其分为A O →、B A →、C B →、O C →；使各分段路径最短，最后将分段路径综合起来也是最短．对问题二分析：机器人从)0,0(O 出发，到达A 的最短时间路径．在前文条件分析中，半径ρ越大，机器人转弯速度越大，速度v 越大．在问题一最短路径基础上，在转弯路段进行优化处理，适当增大转弯半径ρ，速度增大，与此同时转弯路段圆弧长度必然增加，综合使得到达目的地总时间最短．最后将给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间 ．三、模型假设1．假设机器人在行进过程中为质点；2．假设机器人直线路段以速度50=v 个单位/秒行进；3．假设机器人在各转弯路段匀速行进；4．假设机器人从直线段至圆弧段，速度由直线行进速度瞬间降至转弯速度，速度不存在过度阶段；5．假设平面范围边界不是障碍物，不要求目标点与边界的距离至少超过十个单位，机器人目标点不出界即可．四、符号说明i l 表示机器人每段路径，2,1=i ；r 表示转弯半径；i t 表示机器人所用时间，2,1=i ；i ω表示 第i 段圆弧对应的圆心角；⎩⎨⎧=,0,1其它个切点与目标点相连个障碍物第第j i m ij ； ),(ij ij ωτ表示切点坐标．五、模型的建立与求解问题一模型的建立模型准备：根据对问题的分析及两点之间直线最短的原理，为使机器人能以最短的路径避过障碍达到目标点，应使所走的路线尽可能的接近两目标点的连线，对此，可以猜想出几种机器人行走的路径并对其进行探索．首先对机器人所能行走的区域进行分析，根据题意，需要将区域向外扩展10个单位，区域边界角也应扩展10个单位，即机器人能运动范围是由4/1圆弧和相应的线段围成的，具体结果如下图1所示：200400600800Y图1：机器人行走范围图假设机器人可以看成是一个支点，则机器人可以在边界线上运动而不会发生碰撞．为使得机器人能以最短路径避过障碍物，首先进行局部分析，考虑A O →段路径，由图可知：（1）若无障碍物，A O →最短路径为OA 线段；（2）A O →路段被障碍物5阻隔最短路径探索．探索最短路径原则：实际路径越逼近OA 线段越优．①先不考虑弧长问题，探索大致路径.图3（a ）.路径一 图3（b ）路径二路径一是机器人在保证尽量沿边界线运动的情况下得到的．要从O 点到达A 点，机器人必须绕过边界角，根据两点之间直线最短的原理，可以得到图3（b ）的路径二．通过比较，可以得出：在尽可能沿OA 路径行走的前提下，不需要转弯就能到达的路径尽量选用直线路径，减少圆弧路径阶段，使路径得到优化．②转弯圆弧半径相等时，目标点在不同地点转弯，探索较优路径．2B如图所示，三段弧33B A 、22B A 、11B A 对应圆半径相等且依次远离障碍物,离AB 线段的距离越来越远．以A 为圆心，3AA 为半径画弧，分别交1A 、2A ;同理以B 为圆心，3BB 为半径画弧； 即3AA =2AA =1AA ，3BB =2BB =1BB ；显然11B A →的距离最大，22B A →距离次之，33B A →距离最小；所以由B A →最段路径选择B B A A →→→33．由此可得出结论：在确定转弯圆弧半径的情况下，机器人转弯越靠近障碍物，行走路线越接近两目标点之间的连线，总路程越小．③在距障碍物最近的前提下，考虑圆弧半径的影响，确定最短路径．自定义：边界圆弧中点称为节点．通过②中结论可知：在确定转弯圆弧长度的情况下，机器人转弯越靠近障碍物，行走路线越接近两目标点之间的连线，总路程越小．由机器人所能行走的区域范围及转弯半径至少为10的约束可知，画出的4/1圆弧边界是机器人行走最短路径的边界，若需增大转弯半径，只能在节点处进行变化，否则将超出机器人行走范围．节点是边界圆弧的中点．现判断在节点处，转弯半径对最优路径选择的影响．各图形顶角所对应的外围10个单位区域为边界圆弧，该圆弧为转弯最小圆弧．过最小圆弧节点做与节点相切的半径大于10个单位的圆及相应的路径，如下图3（c ）中的2号路径．图3．（c ）路径三可做如下猜想：圆弧的半径越小，机器人从第一个目标点到达目的地总路程越小．下面对猜想进行证明：A图4：证明猜想示意图如图4所示，以O 为圆心，半径为r 画圆，BD 与圆O 相切，切点为D ，AC 与与圆O 相切，切点为C ；角ωγβα,,,位置如图所示．设A 点坐标为),(11b a ,B 点坐标为),(22b a ,圆心O 点坐标为),(y x ．AC =1l ，CD 弧长=2l ，BD =3l ,由几何知识可得： 2121)()(a x b y a -+-=，2222)()(a x b y b -+-=，212212)()(b b a a c -+-=，在C Rt AO ∆和BOD Rt ∆中，可得：a r=αcos ，b r=γcos ，由余弦定理得： ab c b a 2cos 222-+=β，B A →总路程为=L 1l ＋2l ＋3l ，221r a AC l -==,223r b BD l -==，=L 22r a -+22r b -+r ⋅ω，γβαπω---=2，∴总长度L 与转弯半径r 的关系式为：=L 22r a -+22r b -+r ⋅---)2(γβαπ，为寻求总长度L 与转弯半径r 的具体关系，将L 对半径r 求导，即:)arccos arccos 2(2222b r a r rb r r a r dr dL ---+--+--=βπ )1111(2222b r b a rar -+-+ 化简得：br a r dr dL arccos arccos 2---=βπ， πβ<，当且仅当O B A ,,三点共线时，πβ=，此种情况下不存在两个切点． 角γα,均在直角三角形内，非直角，∴πγα<+． 综上所述：0arccos arccos 2>---=br a r dr dL βπ． 即：总路程L 关于半径r 的函数单调递增，机器人从一个目标点到另一个目的点行走的总路程随着转弯圆弧半径增大而增加．故，猜想：圆弧的半径越小，机器人从第一个目标点到达目的地总路程越小，是正确的．由于机器人转弯半径至少为10个单位，要使行走路径最短，转弯半径10=R .经过上述对机器人避障路线的探究，可得为使机器人行走最短路径，需遵循以下几个原则：1.所走路线应尽可能接近两目标点的连线；2.转弯半径越小越好；3．找不到两圆间的公切线时，机器人应尽可能的沿障碍物边界运动．模型的建立：根据以上原则，可以建立机器人从一个目标点到达另一个目标点的最短路径优化模型．设切点坐标为),(ij ij ωτ，表示第i 个障碍物第j 个切点．通过对路径的探索，可知机器人的路径是由直线和一条或多条圆弧组成的．在此模型中，假设机器人的路径是分阶段的，每一阶段的路径由一条线段和一段圆弧组成，包括了一条线段和多条圆弧的情况．如第１段路径中，线段和圆弧相连，在第２段路径中，线段与第１段路径中的圆弧相连，当此线段长度为０时，机器人从第１段起点到第２段末点的路径就是由一条线段和两段圆弧组成的．线段的长度1l 可由两点间的距离公式解得：2122121)()(y y x x l -+-=．圆弧的角度为ω，半径为r ，则圆弧弧长2l ：ω⋅=R l 2．已知切点时，圆弧角度ω为：R y y x x 2)()(arcsin 2212212-+-⨯=ω．机器人从第一个目标点（11,n m ）到第二个目标点（22,n m ）过程中，⎩⎨⎧= ,0,1其它个切点与目标点相连个障碍物第第j i m ij ， 此时要避过i 个障碍点，设从第一个目标点出发到达另一处时，0=i ，则线段部分长度 :22)2)(2(22)2)(1()1()1(2)1()1(2010221102210121011)()()()()()()()(n m n m l j i j i j i j i j i j i -+-+-+-+-+-+-+-=++++++++ωτττωωττωωωτ,同理，此时对应的圆弧长度：∑=-+-⋅⨯=12122122122)()(arcsin2i i i i i R R l ωωττ.为使机器人行走路径最短，即：21min l l +.综上，可以建立最优规划模型：21min l l +∑∑==-+-⋅=2112221)()(j i k ij k ij ij n m m l ωτ ∑∑==++++-+-+120212)1()1(2)1()1()()(i j j i j i j i j i ττωω 2,1=k∑=-+-⋅=12022122122)()(arcsin2i i i i i R R l ωωττ.10=R问题二的模型建立要使机器人从一个目标点到达另一个目标点所用的时间最短，需考虑行走总路程与速度的影响．对条件中所给最大转弯速度21.01001)(ρρ-+==ev v v 进行分析可知，当半径∞→ρ时，即可视为直线运动，此时50==v v 个单位/秒；当半径10→ρ时， 最小速度5.22min ==v v 个单位/秒，即机器人的速度范围为2.5到5.且半径ρ越大，机器人转弯速度越大．所以为追求最小时间，应在模型一的基础上适当增大转弯半径．同样要保证总路程尽可能的短，机器人转弯时要接近障碍物，即所走路线应尽可能接近两目标点的连线．故可以在最小圆弧基础上增大转弯半径，以下讨论速度与半径之间的关系．如上述图4所示，总路程由线段长度和圆弧长度组成．a r =αcos ，b r =γcos ，abc b a 2cos 222-+=β，221r a AC l -==,223r b BD l -==，=L 22r a -+22r b -+r ⋅ω，γβαπω---=2，=L 22r a -+22r b -+r ⋅---)2(γβαπ，则总时间 21t t t +=，22221v r b r a t -+-=， v r t ⋅=ω2即总时间t 为：2222v r b r a v rt -+-+⋅=ω21.01001)(r ev r v v -+==t 对半径r 求导:)arccos arccos 2((122220b ra r rb r r a r v dr dt ---+--+--⨯=βπ ))2.0()arccos arccos 2(21.010r e b r r r a r r r r -⋅⋅⋅-⋅-⋅-+⋅-βπ)1())1111(21.0102222r e br b a r a r ⋅-+⨯-+-+化简得：)2.01()arccos arccos 2(221.0101.010r r e e br a r dr dt ⋅-⋅-⨯-+⋅---=βπ， 令导数 0=drdt, 由模型一可知：bra r arccos arccos 2---βπ0>,解得当5055.11=r 时，0=drdt．且函数在 )5055.11,10(∈x 区间内是单调递减的，在5055.11>x 时是逐渐增大的，故要使时间最短，满足5055.11=r ．模型的建立：模型二是在模型一的基础上增大转弯半径得到的，是追求最短时间和最短路径的双目标规划问题．建立模型如下：21 t min t +21min l l +..t s ∑=-+-⋅=1222122122)()(arcsin2i i i i i RR l ωωττ∑∑==-+-⋅=2112221)()(j i k ij k ij ij n m m l ωτ∑∑==++++-+-+120212)1()1(2)1()1()()(i j j i j i j i j i ττωω，2,1=k11v l t =， v l t 22=，.5055.11=r问题一、问题二模型的求解：根据建立的模型可利用橡皮筋算法]1[探索最短路径．机器人行走时，如果不知道确定路线时，可以先假设机器人会朝着目的地的方向走，如图3(a)中的A O →；如果中途碰到障碍物，就试图绕过障碍物，再重新朝向目的地的方向行走，如图所示A c b a O →→→→，其中绿色的圆点S 表示出发点，红圆点T 表示目的地．实际上，如果视觉上没有障碍，运动者会选择较近的直切障碍物边沿的行走路线，如图3(b)所示A c b O →→→．这种形状，就像在出发点和目的地之间拉了根橡皮筋，由于障碍物的存在，橡皮筋不能横穿过去，所以沿障碍物边沿拉伸，而正是因为橡皮筋具有的弹性，使得路径趋于最短．根据这种思路，提出了自动漫游路径生成的橡皮筋算法．根据制定的三条原则：1.所走路线应尽可能接近两目标点的连线；2.转弯半径越小越好；3．找不到两圆间的公切线时，机器人应尽可能的沿障碍物边界运动．可以得到机器人从)300,300()0,0(A O →的几条最优路线，如图5所示：200400600200400图5：A O →最短路径示意图从图中可以看出，从)300,300()0,0(A O →有两条路线需要比较计算，利用MATLAB 软件求解得到结果如下（长度单位为单位）：A O →最优路径为：A b a O →→→00．总路程分为2条线段和1段圆弧．其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是： 线段OC ：O （0，0）→C (70.4825，213.0686) 长度224.4237弧CD ： C (70.4825，213.0686) →D （76.4914,219.3643）圆心（80,210）长度9.0041 线段DA ： D （76.4914,219.3643）→A （300,300） 长度237.6094 总时间：96.00826秒 总路程471.0372单位同理可以根据原则得到从O 到B 的几条路线，如图6所示：可编辑200400600800200400600800XY图6：B O →最短路径示意图利用MATLAB 软件求解得到结果如下： 从)700,100()0,0(B O →的最优路径为：B L K J I h f e d c b O →→→→→→→→→→→其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：线段: Oa )6396.301,1353.50()0,0(a O → , 长度：305.7777 弧ac : ）圆心（300,60, )5474.305()6396.301,1353.50(c a →， 弧长：4.3214 线段cd : )40.5474141.6798,4( )5474.305(d c → 长度：162.1731 弧de ： )435,150, )44.7901147.9621,4()40.5474141.6798,4(圆心（e d → 弧长：7.7751线段ef ： )60.2099222.0379,4()44.7901147.9621,4(f e → 长度： 75.6637 弧fh ： )470,220 (230,470),)60.2099222.0379,4(圆心（h f → 弧长：13.6556 线段hI ： )530,230((230,470)I h → 长度：60 弧IJ ：)530,220 , )3534.538,4967.225()530,230(圆心（J I → 弧长： 9.8883 线段JK ： ,6462915 503314435345384967225). ,.K() .,.J(→ 长度：96.9537 弧KL ： )600,150 ,)96.3458140.6916,5()91.6462144.5033,5(圆心（L K → 弧长：6.1474线段LB ：,)700,100()96.3458140.6916,5(B L → 长度：111.3553 总路程为853.7113 个单位 总时间： 811.9235秒同理可以根据原则得到从O 到C 的几条路线，如图7所示200400600800Y图7：C O →最短路径示意图机器人C O →段路径有4条，利用MATLAB 求解得出结果如下：最优路径为：C k J I H f e d c b a O →→→→→→→→→→→1111111111其中，各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：线段1Oa ：)0.2262232.1149,5()0,0(1a O → 长度： 237.4868 弧11b a ：）圆心（60,230 , )5.2128238.7797,5()0.2262232.1149,5(11b a → 弧长：8.5850线段11c b ：)34.7872391.2203,3(c )5.2128238.7797,5(11→b 长度：318.4336 弧11c d ： )330,400( , )39.8254398.1397,3()34.7872391.2203,3(c 11圆心d → 弧长：8.8448线段11e d ：371.3965)(564.8828,)39.8254398.1397,3(11e d → 长度：169.7056 弧11f e ： )450,550( 400.4069),(612.7736,f 371.3965)(564.8828,11圆心→e 弧长：57.2031线段11h f ：510.0731)(718.7935,h 400.4069)(612.7736,f 11→ 长度：152.5349 弧11I h ： )520,720( (730,520),I 510.0731)(718.7935,h 11圆心→ 弧长：16.9174 线段11J I ：(730,600)J (730,520)I 11→ 长度：80弧11k J ： )600,720(, 606.3589)(727.7178,k (730,600)J 11圆心→ 弧长6.8916 线段C k 1： C(700,640) 606.3589)(727.7178,k 1→ 长度：43.5890 总路程：1001.7499+98.4401=1100.19单位 总时间：200.34998+39.37604=239.72602秒同理，找出O C B A O →→→→的最优路径，如图8所示：200400600800Y图8：O C B A O →→→→最短路径示意图利用MATLAB 求解得出各起终点坐标、圆弧圆心坐标及相应的弧长、线段长度分别是：弧22d c ：2c (292.7141, 280.3754) →2d (299.3452, 293.5596)圆心（300,300） 长度：16.5989线段22e d ：d2(299.3452, 293.5596) →2e （229.7932，532.02307）长度 248.3995 弧22f e ：2e （229.7932，532.02307）→2f （225.4967，538.3538）圆心：（220,530）长度7.8147线段22i f ：2f （225.4967，538.3538）→2i （140.4000,597.200） 长度103.4617 弧22i h ： 2h （144.5033,591.6462）→2i （140.4000,597.200）圆心（150,600） 长度7.0503线段22j i :2i （140.4000,597.200）→2j (92.000，694.000) 长度108.2257 弧22k j ： 2j (92.000，694.000) →2k （102.3208,709.7270） 圆心（100,700） 长度24.4852线段22l k ：2k （102.3208,709.7270）→2l （270,690） 长度168.8356 弧22m l ：2l （270,690）→2m （272，689.7980）圆心（180,770）， 长度2.0136线段22n m ： 2m （272，689.7980）→2n （368,670.2020） 长度97.9796 弧22o n ：2n （368,670.2020）→2o （370,670）圆心（370，680） 长度2.0136 线段22p o ： 2o （370,670）→2p （430,670） 长度60 弧22q p ： 2p （430,670）→2q （435.5878,671.7068）圆心（430,680）长度5.9291 线段22r q : 2q （435.5878,671.7068）→2r (534.4122,738.2932) 长度119.1638 弧22s r ： 2r (534.4122,738.2932) →2s （540,740）圆心（670,600） 长度5.9291 线段22t s ：2s （540,740）→2t （670,740） 长度130 弧22u t ： 2t （670,740）→2u （679.7725,732.1211）圆心（670,730）长度13.5707 线段22v u ： 2u （679.7725,732.1211）→2v （700.2275,637.8789） 长度96.4365 弧22w v ：2v （700.2275,637.8789）→2w （702.6928,633.1732）圆心（700,640） 长度5.3769最终总路程：2794.512 单位； 最终总时间：598.5477秒 问题二的求解问题二是在建立最短时间优化模型的基础上求解出从O 到A 的最短时间．根据建立的模型，可知当转弯半径5055.11=r 时，时间有最小值．因为 21.01001r ev v ⨯-+=，此时转弯时机器人的速度： 81115.4=v ． 利用问题一的方法解得各起终点的坐标、圆弧圆心坐标如下： 线段Oa ：)210,70(00a O →），（； 弧ab ：)3992.219,0916.78()210,70(b a →， 圆心为（81.5055,210）)300,300()3992.219,0916.78(A b →；总时间2130.94=t 秒， 总距离470.8301单位．模型检验对于问题一的模型检验，由于软件CAD 在处理图形、获取坐标方面较方便快捷，利用CAD 可以自动读取坐标、线段长度、弧长的优点，粗略的估计从A O →、B O →、C O →和O C B A O →→→→的可能较短路线，由CAD 软件可求得得粗略解．将在Autocad 中得到的结果与计算值相比较得表如下：短路线中的最短路径，因此本模型在解决机器人避开障碍物探索最短路径是相对较客观合理的．模型的评价与推广优点：（1）：本模型借鉴“橡皮筋算法”的精华的思想基础，并改良其不足，利用改良后的“橡皮筋算法”使解决机器人机器人避开障碍物探索最短路径的问题变得生动形象，化抽象为具体，使本模型在其它类似问题方面的迁移性较强．（2）：本模型充分体现数形结合思想，在处理机器人行走路线由直线到曲线、由曲线到直线等问题时，巧妙利用解析几何中，圆的切线、两圆公切线处理，同时，采用CAD 软件进行图像上的检验，使本模型在几何关系、数学关系上得出的结果都是客观合理的．缺点：由于行走路线的限制，且路线的连续性以及机器人只能利用圆弧拐弯，因此求出的拐点（直路线线和圆弧切的点）基本上是小数，而且本模型中只精确到0.0001，可能会给具体的机器人实践行走时带来误差．模型的推广：本模型可用于推广解决机器人快速灭火，迷宫路径探索等相似路径的探索问题，也可推广至交警疏通堵车问题中路径规划问题．参考文献[1] 陈勇，王栋，陈戈，一种三维虚拟场景自动漫游的快速路径规划算法，系统仿真学报，第19卷，第11期：2508-2510页，2007.[2] 杨文茂，李全英，空间解析几何，武汉大学出版社，2006.[3] 胡良剑，孙晓君，MATLAB数学实验，高等教育出版社，2006.附录附录1：%两圆公切线，两圆大小相等．求切点%保存为函数wfunction wa1=80+1.5055;b1=210;a2=720;b2=600;%两圆圆心坐标[x,f,h]=fsolve(@li,[a1,b1])endfunction f=li(x)a1=80+1.5055;b1=210;a2=720;b2=600;%zx=(a1+a2)/2;zy=(b1+b2)/2;%两圆相切zx=300;zy=300;%zx=0;zy=0;%直线与圆相切时f(1)=(x(1)-a1)^2+(x(2)-b1)^2-10^2;%在某圆上f(2)=(x(1)-zx)^2+(x(2)-zy)^2+10^2-((zx-a1)^2+(zy-b1)^2);%与两圆圆心连线的中点构成勾股定理end附录2：%求弧长公式要每个点迭代clear;clc;R=11.5055;x1=78.0916;y1=219.3992;%第一点坐标x2=70;y2=210;%第二点坐标f=R*2*asin(sqrt((x2-x1)^2+(y2-y1)^2)/2/R) %弧长附录3：%两圆公切线，两圆大小不等function oformat short[x,f,h]=fsolve(@laz,[580 450])endfunction f=laz(x)f(1)=sqrt((550-x(1))^2+(450-x(2))^2)/(sqrt((720-x(1))^2+(520-x(2))^2))-8;f(2)=7/17*x(1)+3800/17-x(2);end附录4：%算线段长度，要迭代clear;clc;R=10;x1=0;y1=0;%第一点坐标x2=50.1353;y2=301.6396;%第二点坐标f=sqrt((x2-x1)^2+(y2-y1)^2) %线段长度.。

机器人避障问题1. 简介机器人避障（obstacle avoidance）是指机器人通过使用各种传感器和算法来识别和避免障碍物的能力。

在自动驾驶、无人机和工业自动化等领域，机器人避障问题是一个非常重要的研究热点。

2. 避障传感器为了实现机器人的避障功能，需要配备各种传感器来获取环境信息。

常用的避障传感器包括：2.1 超声波传感器超声波传感器利用超声波的回波时间来测量机器人与障碍物之间的距离。

通过安装多个超声波传感器，可以实现对机器人周围环境的全方位感知。

2.2 激光雷达激光雷达是一种高精度的避障传感器，通过发射激光束并测量其回波时间来获取周围环境的三维信息。

激光雷达可以提供非常精确的障碍物位置和距离数据，因此被广泛应用于无人驾驶和导航系统中。

2.3 摄像头摄像头可以通过图像处理算法来识别和检测障碍物。

常用的算法包括边缘检测、目标跟踪和物体识别等。

利用摄像头可以获取丰富的视觉信息，对于机器人的避障任务具有重要意义。

3. 避障算法为了使机器人能够根据传感器获取的数据进行避障决策，需要设计和实现相应的避障算法。

常用的避障算法包括：3.1 基于障碍物距离的避障基于障碍物距离的避障算法利用传感器测量的障碍物距离信息来进行避障决策。

例如，当障碍物靠近时，机器人可以选择停下或改变方向来避免碰撞。

3.2 基于虚拟势场的避障基于虚拟势场的避障算法利用虚拟势场模型来描述机器人周围的环境。

机器人被视为一个负电荷，障碍物被视为正电荷，通过计算势能梯度来确定机器人应该前进的方向。

3.3 机器学习算法机器学习算法可以通过训练数据来学习和优化避障策略。

常用的机器学习算法包括神经网络、决策树和支持向量机等。

这些算法可以根据输入的传感器数据预测机器人的动作，从而实现避障功能。

4. 实际应用机器人避障技术已经被广泛应用于各个领域，包括但不限于以下几个方面：•自动驾驶车辆：通过避障技术，自动驾驶车辆能够在复杂的交通环境中安全地行驶。

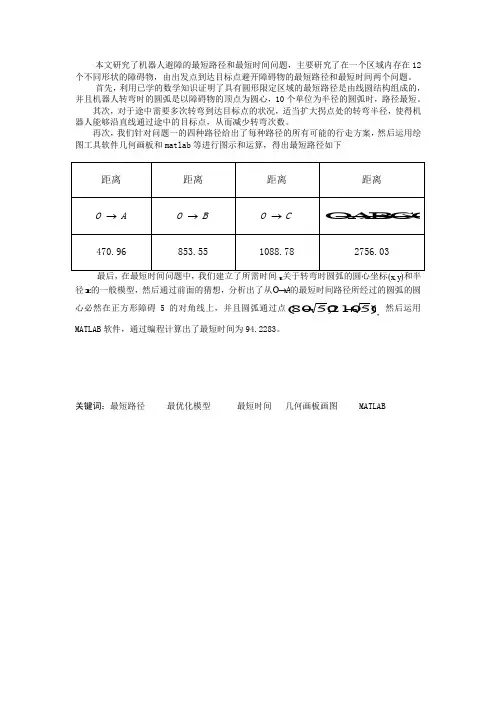
本文研究了机器人避障的最短路径和最短时间问题，主要研究了在一个区域内存在12个不同形状的障碍物，由出发点到达目标点避开障碍物的最短路径和最短时间两个问题。

首先，利用已学的数学知识证明了具有圆形限定区域的最短路径是由线圆结构组成的，并且机器人转弯时的圆弧是以障碍物的顶点为圆心，10个单位为半径的圆弧时，路径最短。

其次，对于途中需要多次转弯到达目标点的状况，适当扩大拐点处的转弯半径，使得机器人能够沿直线通过途中的目标点，从而减少转弯次数。

再次，我们针对问题一的四种路径给出了每种路径的所有可能的行走方案，然后运用绘图工具软件几何画板和matlab 等进行图示和运算，得出最短路径如下距离距离距离距离A O →B O →C O →OC B A O →→→→ 470.96853.551088.782756.03最后，在最短时间问题中，我们建立了所需时间t 关于转弯时圆弧的圆心坐标()y x ,和半径r 的一般模型，然后通过前面的猜想，分析出了从A O →的最短时间路径所经过的圆弧的圆心必然在正方形障碍5的对角线上，并且圆弧通过点)50210,5080(+-，然后运用MATLAB 软件，通过编程计算出了最短时间为94.2283。

关键词：最短路径 最优化模型 最短时间 几何画板画图 MATLAB一、问题重述1.1 背景材料：在一个800×800的平面场景，在原点（0，0）点处有一个机器人，他只能在该平面场景内活动，图中12个不同形状的区域是机器人不能碰撞的障碍物，障碍物描述如下：编号障碍物名称左下顶点坐标其它特性描述1 正方形(300, 400) 边长2002 圆形圆心坐标(550, 450)，半径703 平行四边形(360, 240) 底边长140，左上顶点坐标(400, 330)4 三角形(280, 100) 上顶点坐标(345, 210)，右下顶点坐标(410, 100)5 正方形(80, 60) 边长1506 三角形(60, 300) 上顶点坐标(150, 435)，右下顶点坐标(235, 300)7 长方形(0, 470) 长220，宽608 平行四边形(150, 600) 底边长90，左上顶点坐标(180, 680)9 长方形(370, 680) 长60，宽12010 正方形(540, 600) 边长13011 正方形(640, 520) 边长8012 长方形(500, 140) 长300，宽60图一800*800平面场景图1.2 问题提出：问题一：建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。

模型的建立与求解
一、对问题一模型的建立与求解
该问题要求路径最短，即不要求速度与时间，同时由直线圆弧相切连接最优可得： 本论文问题一求路径最短可采用 10 单位过弯半径， 即以半径为 10 个单位的圆弧过弯可 满足两点避障过弯最短问题。 1、机器人从 O(0, 0)出发，O→A 的最短路径 已知机器人所走路线为直线或圆弧，通过规划可得实际得如下（图四）四种避障行进方 案：
圆弧的圆心坐标为(80,210)。路线一（Da11 、Da12）和路线三 Da31、Da32）的切点坐标： 点号 坐标 Da11 70.5060 213.1406 Da12 76.6064 219.4066
表1
Da31 232.1149 50.2262
Da32 239.7043 57.5862
x y
模型假设
1、假设机器人为一可运动的质点，即质点机器人不考虑其外形尺寸； 2、假设半径不变时，机器人在行进、转弯过程中能一直保持最大速度； 3、假设机器人可准确执行运动轨道，无任何偏差； 4、假设机器人的行进速度可瞬时加减变化，不受条件限制。
符号说明
符号 说明
Dhij
Lhij Dij Dhj T R
111.36
总长 878.05
所以可以得到 O→B 的最短路径长为：853.7。 圆弧的圆心坐标为：(60,300),(150,435),(150,600),(220,470),(220,530) 路径坐标： (0,0)→(50.1354,301.6396)→(51.6795,305.547)→(141.6795,440.547)→ (147.9621,444.79)→(222.038,460.2096)→(230,470)→(230,530)→(229.9563,530.9242) →(229.5746,532.8954)→(229.2564,533.7791)→(229.1263,534.0782)→ (225.4971,538.3544)→(144.5036,591.6465)→(140.6922,596.346)→(100,700) 3、机器人从 O(0, 0)出发，O→C 的最短路径 如图八所示， 机器人从 O 到 C 点有五条可能最短路线， 在路径途中经过多次转弯到达目 标点。先通过对简化模型即对直线段的直接求和筛选出较短的路径，如图九。

机器人避障问题摘要我们了解到我们需要解决的是机器人从O→A、O→B、O→C和O→A→B→C→O的最短路径以及O→A的最短时间问题，但与传统的问题相比因为有了障碍物的制约使得部分区域无法通过，而且物体的运动轨迹也会对其速度造成制约，联系现实生活我们知道对于无法以最短直线路径通过时如果两点间有一根足够长的绳子，在绕开障碍物及其所影响的范围后绳子绷紧状态下所形成的轨迹即为最短路径，在最短的路径和最快的速度间找制约点可获得最短时间，该题时间制约因素为。

受此启发，在分析问题后我们建立了数学模型来合理解决如何使机器人避障的优化问题。

针对问题一；问题一中O→A可简化为两点避开单个障碍物的问题、O→B、O→C为两点避开多个障碍物的问题、对于O→A→B→C→O是一个回路的多点避开多个障碍物的问题，运用几何的求解方式证明。

针对问题二；问题二是时间最优的问题，我假设存在个半径为最优时间半径，然后我们找到个最优圆弧圆心的位置，圆心在两点连线为X轴的最高障碍点作X轴的该条垂线上。

关键词最短路径最优化模型几何求解最短时间一、问题重述1.1、基本情况:在给定的平面场景中，要求机器人绕开障碍物到达指定的目标点（要求目标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

1.2、相关信息：(1) 机器人直线行走的最大速度为50=v 个单位/秒。

(2) 机器人转弯时，最大转弯速度为21.0100e1)(ρρ-+==v v v ，其中ρ是转弯半径。

如果超过该速度，机器人将发生侧翻，无法完成行走。

1.3、需要解决的问题：(1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。

1 机器人避障优化模型 摘要 “机器人避障问题”是在一个规定的区域范围内，有12个位置各异、形状不同的障碍物分布，求机器人从出发点到达目标点以及由出发点经过途中的若干目标点到达最终目标点的避障最短路径及其最短时间，其中必须考虑如圆与切线的关系等问题。基于优化模型，对于题目实际情况进行研究和分析，对两个问题都用合适的数学思想做出了相应的解答和处理，以此建立符合题意的数学模型。 问题一，要求建立机器人从原点出发到达以区域中另一点为终点的最短路径模型。机器人的避障路径规划主要包括环境建模、路径搜索、路径平滑等环节，针对本题的具体情况，首先对图形进行分析，并用AutoCAD软件进行环境建模，使其在障碍物外围延伸10个单位，然后考虑了障碍物对路径安全的影响再通过蚁群算法来求它的的最短路径，由于此时最短路径中存在转弯路径，需要用人工势场法进行路径平滑处理，从而使它的最短路径在蚁群算法算出的结果情况下，可以进一步缩短其路径，从而存在机器人以区域中一点到达另一点使其避障的路径达到最短，在最终求解时，通过matlab软件求其最优解。 问题二，仿照问题一机器人避障路径规划的基本环节所建立的一般模型，再根据题二所提出的具体问题，建立机器人从O（0，0）出发，使达到A的最短时间路径模型。

其中已知最大速度为50v个单位/秒，机器人转弯时，最大转弯速度为

21.0100e1)(

vvv，其中是转弯半径，并有为增函数。且有0恒成立，则可

知行走路径应尽量减少走圆弧，且可时间由走两段直线加圆弧的时间之和。

关键词： 最短路径 蚁群算法 人工势场法 机器人避障 2

一 、问题重述 图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍物，障碍物的数学描述如下表： 编号 障碍物名称 左下顶点坐标 其它特性描述

机器人路径规划中的避障算法在机器人的路径规划中，避障算法扮演着重要的角色。

机器人需要能够准确地感知环境中的障碍物，并且通过合适的算法来规划避开这些障碍物的路径。

本文将讨论机器人路径规划中常用的几种避障算法，包括代价地图法、局部感知法和深度学习法，以及它们的优缺点和应用领域。

1. 代价地图法代价地图法是一种基于环境建模的避障算法。

它通过在机器人周围建立一个代表环境障碍物信息的地图，来引导机器人规划路径。

代价地图通常由栅格地图或者连续场景地图构成，其中每个栅格或者像素都有一个代表障碍物的代价值。

机器人规划器会根据这些代价值来选择通行的路径，避开高代价区域。

代价地图法的优点是可以精确地规划路径，同时能够考虑到环境中的障碍物分布情况。

然而，它需要对环境进行建模和传感器信息处理，对算法的实现和计算资源要求较高。

2. 局部感知法局部感知法是一种基于即时感知的避障算法。

它通过机器人的传感器实时感知到周围的障碍物，并且根据这些信息进行路径规划。

局部感知法通常采用传统的避障策略，比如沿着障碍物边缘行进、避开障碍物的凹陷区域等。

局部感知法的优点是简单易于实现，对硬件资源的要求较低。

然而，它只关注机器人周围的局部环境，可能无法全局优化路径。

在复杂的环境下，可能会导致路径不够优化和高频率的避障操作。

3. 深度学习法深度学习法近年来在机器人路径规划领域取得了显著的进展。

它利用深度神经网络来学习环境中的表示和对应的路径规划策略。

深度学习法可以通过大量的数据来训练，能够有效地处理复杂的环境和障碍物分布情况。

深度学习法的优点是可以自动从数据中学习环境的隐藏规律，具有很强的泛化能力。

然而，深度学习法需要大量的训练数据和计算资源，并且对网络结构和参数的选择也是一项挑战。

综上所述，机器人路径规划中的避障算法有代价地图法、局部感知法和深度学习法等。

不同的算法适用于不同的应用场景，可以根据具体需求来选择合适的算法。

未来的研究需要进一步提高算法的效率和实时性，以满足日益复杂和动态的环境要求。

2012高教社杯全国大学生数学建模竞赛题目
（请先阅读“全国大学生数学建模竞赛论文格式规范”）
D 题 机器人避障问题
图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该平面场景范围内活动。

图中有12个不同形状的区域是机器人不能与之发生碰
标点与障碍物的距离至少超过10个单位）。

规定机器人的行走路径由直线段和圆弧组成，其中圆弧是机器人转弯路径。

机器人不能折线转弯，转弯路径由与直线路径相切的一段圆弧组成，也可以由两个或多个相切的圆弧路径组成，但每个圆弧的半径最小为10个单位。

为了不与障碍物发生碰撞，同时要求机器人行走线路与障碍物间的最近距离为10个单位，否则将发生碰撞，若碰撞发生，则机器人无法完成行走。

机器人直线行走的最大速度为50=v 个单位/秒。

机器人转弯时，最大转弯速度为21.0100e
1)(ρρ-+==v v v ，其中ρ是转弯半径。

如果超过该速度，机器人将发生侧 翻，无法完成行走。

请建立机器人从区域中一点到达另一点的避障最短路径和最短时间路径的数学模型。

对场景图中4个点O(0, 0)，A(300, 300)，B(100, 700)，C(700, 640)，具体计算：
(1) 机器人从O(0, 0)出发，O→A 、O→B 、O→C 和O→A→B→C→O 的最短路径。

(2) 机器人从O (0, 0)出发，到达A 的最短时间路径。

注：要给出路径中每段直线段或圆弧的起点和终点坐标、圆弧的圆心坐标以及机器人行走的总距离和总时间。

图1 800×800平面场景图。

关键词：基本线圆组合 拉绳子法 穷举法 非线性规划 中间目标点转弯圆心
1
1 问题重述
附图1是一个800×800的平面场景图，在原点O(0, 0)点处有一个机器人，它只能在该 平面场景范围内活动。图中有12个不同形状的区域是机器人不能与之发生碰撞的障碍 物，障碍物的数学描述如下表：
编号 1 2 3 4 5 6 7 8 9 10 11 12
3 模型假设
为了简化计算，给出如下模型合理性的假设： 【1】假设所有障碍物是固定不动的； 【2】机器人性能足够好，能准确地沿圆弧转弯； 【3】假设机器人在初始时的速度为5个单位每秒； 【4】假设机器人在直线切入弧线时的速度是瞬间变化完成的； 【5】机器人行走过程中不会意外停止； 【6】忽略影响机器人行走非最小转弯半径以及最小安全距离因素。
机器人避障问题
【摘要】
本文主要是对机器人在一个平面区域内的通过不同障碍物到指定目标点进行研 究，首先通过机器人与障碍物的最小安全距离对不同障碍物的禁区进行了划分见图 1， 把障碍物划分为有顶点和无顶点两大类。然后证明了机器人在障碍物顶点处转弯路径最 优，转弯半径最小路径最优，转弯圆心在障碍物顶点处（圆行障碍物在圆心）路径最优。
针对多目标点问题，由于机器人不能直线转向，所以在经过目标点时，应该提前转 向，且中间目标点应该在转弯弧上。因此先建立优化模型（模型三）对进行中间目标点 处转弯圆弧圆心搜索求解。求出中间目标点转弯圆心后，用把中间目标点的圆心看做“障 碍物”的办法把问题转化为单目标点问题。然后利用模型二和模型一进行求解，解得 O-A-B-C-O 的最短路径长为 2812.52 个单位，所用时间为 585.6712 秒，具体见附表 1。
L1 + S + L2 < L1¢ + S ¢ + L2¢ 因为两圆圆心不同在过点 D 所引的垂线上，且两圆交于点 D，因此它们只能有两