
一、傅立叶变换的由来
关于傅立叶变换,无论是书本还是在网上可以很容易找到关于傅立叶变换的描述,但是大都是些故弄玄虚的文章,太过抽象,尽是一些让人看了就望而生畏的公式的罗列,让人很难能够从感性上得到理解,最近,我偶尔从网上看到一个关于数字信号处理的电子书籍,是一个叫Steven W. Smith, Ph.D.外国人写的,写得非常浅显,里面有七章由浅入深地专门讲述关于离散信号的傅立叶变换,虽然是英文文档,我还是硬着头皮看完了有关傅立叶变换的有关内容,看了有茅塞顿开的感觉,在此把我从中得到的理解拿出来跟大家分享,希望很多被傅立叶变换迷惑的朋友能够得到一点启发,这电子书籍是免费的,有兴趣的朋友也可以从网上下载下来看一下,URL地址是:
https://www.doczj.com/doc/c315538717.html,/pdfbook.htm
要理解傅立叶变换,确实需要一定的耐心,别一下子想着傅立叶变换是怎么变换的,当然,也需要一定的高等数学基础,最基本的是级数变换,其中傅立叶级数变换是傅立叶变换的基础公式。
二、傅立叶变换的提出
让我们先看看为什么会有傅立叶变换?傅立叶是一位法国数学家和物理学家的
名字,英语原名是Jean Baptiste Joseph Fourier(1768-1830), Fourier对热传递
很感兴趣,于1807年在法国科学学会上发表了一篇论文,运用正弦曲线来描述温度分布,论文里有个在当时具有争议性的决断:任何连续周期信号可以由一组适当的正弦曲线组合而成。当时审查这个论文的人,其中有两位是历史上著名的数学家拉格朗日(Joseph Louis Lagrange, 1736-1813)和拉普拉斯(Pierre Simon de Laplace, 1749-1827),当拉普拉斯和其它审查者投票通过并要发表这个论文时,拉格朗日坚决反对,在近50年的时间里,拉格朗日坚持认为傅立叶的方法无法表示带有棱角的信号,如在方波中出现非连续变化斜率。法国科学学会屈服于拉格朗日的威望,拒绝了傅立叶的工作,幸运的是,傅立叶还有其它事情可忙,他参加了政治运动,随拿破仑远征埃及,法国大革命后因会被推上断头台而一直在逃避。直到拉格朗日死后15年这个论文才被发表出来。
谁是对的呢?拉格朗日是对的:正弦曲线无法组合成一个带有棱角的信号。但是,我们可以用正弦曲线来非常逼近地表示它,逼近到两种表示方法不存在能量差别,基于此,傅立叶是对的。
为什么我们要用正弦曲线来代替原来的曲线呢?如我们也还可以用方波或三角
波来代替呀,分解信号的方法是无穷的,但分解信号的目的是为了更加简单地处理原来的信号。用正余弦来表示原信号会更加简单,因为正余弦拥有原信号所不具有的性质:正弦曲线保真度。一个正弦曲线信号输入后,输出的仍是正弦曲线,只有幅度和相位可能发生变化,但是频率和波的形状仍是一样的。且只有正弦曲线才拥有这样的性质,正因如此我们才不用方波或三角波来表示。
三、傅立叶变换分类
根据原信号的不同类型,我们可以把傅立叶变换分为四种类别:
1非周期性连续信
傅立叶变换(Fourier Transform)
号
2
周期性连续信号 傅立叶级数(Fourier Series) 3 非周期性离散信号 离散时域傅立叶变换(Discrete Time Fourier
Transform )
4
周期性离散信号 离散傅立叶变换(Discrete Fourier Transform)
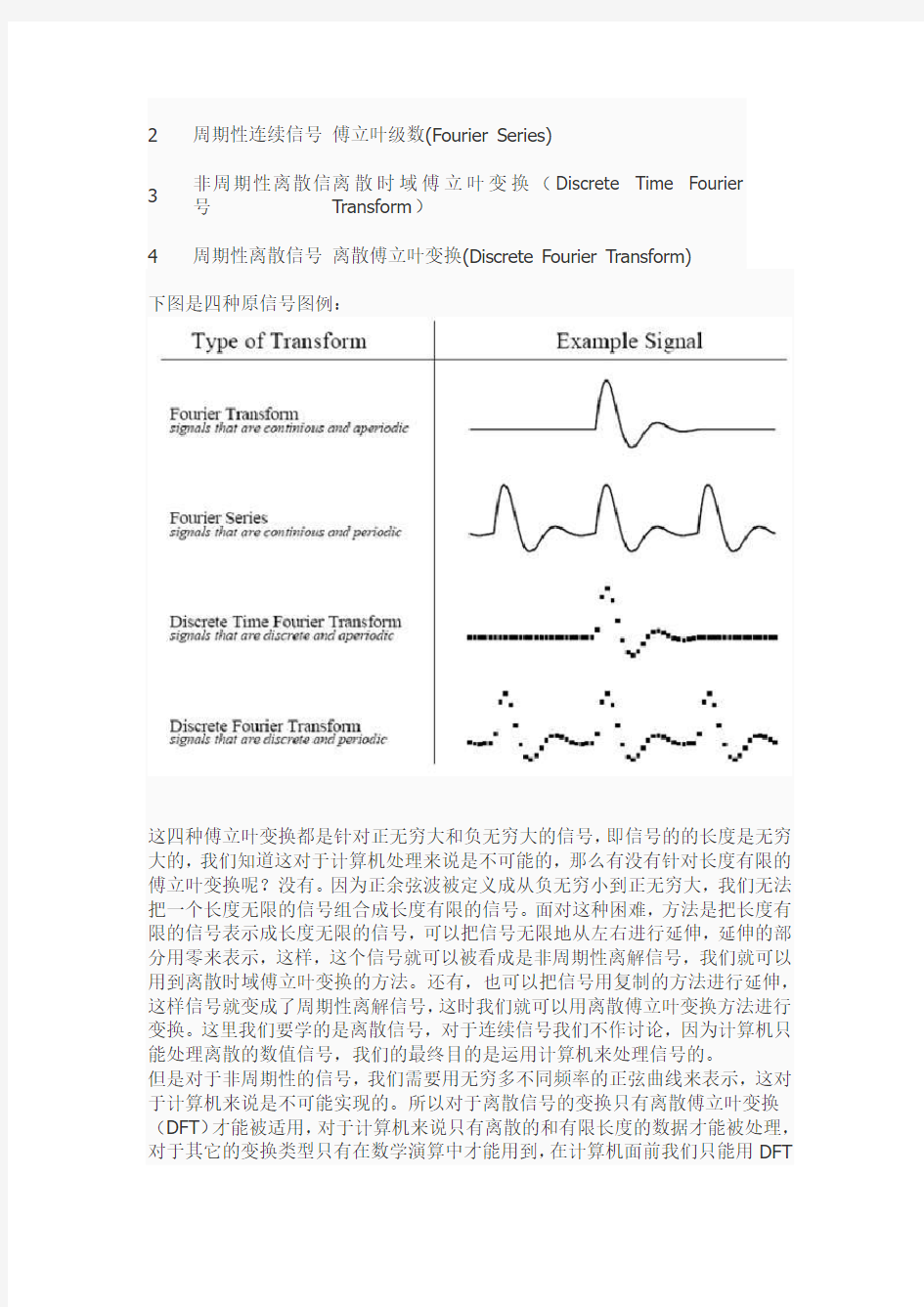
下图是四种原信号图例:
这四种傅立叶变换都是针对正无穷大和负无穷大的信号,即信号的的长度是无穷大的,我们知道这对于计算机处理来说是不可能的,那么有没有针对长度有限的傅立叶变换呢?没有。因为正余弦波被定义成从负无穷小到正无穷大,我们无法把一个长度无限的信号组合成长度有限的信号。面对这种困难,方法是把长度有限的信号表示成长度无限的信号,可以把信号无限地从左右进行延伸,延伸的部分用零来表示,这样,这个信号就可以被看成是非周期性离解信号,我们就可以用到离散时域傅立叶变换的方法。还有,也可以把信号用复制的方法进行延伸,这样信号就变成了周期性离解信号,这时我们就可以用离散傅立叶变换方法进行变换。这里我们要学的是离散信号,对于连续信号我们不作讨论,因为计算机只能处理离散的数值信号,我们的最终目的是运用计算机来处理信号的。
但是对于非周期性的信号,我们需要用无穷多不同频率的正弦曲线来表示,这对于计算机来说是不可能实现的。所以对于离散信号的变换只有离散傅立叶变换(DFT )才能被适用,对于计算机来说只有离散的和有限长度的数据才能被处理,对于其它的变换类型只有在数学演算中才能用到,在计算机面前我们只能用DFT
方法,后面我们要理解的也正是DFT方法。这里要理解的是我们使用周期性的信号目的是为了能够用数学方法来解决问题,至于考虑周期性信号是从哪里得到或怎样得到是无意义的。
每种傅立叶变换都分成实数和复数两种方法,对于实数方法是最好理解的,但是复数方法就相对复杂许多了,需要懂得有关复数的理论知识,不过,如果理解了实数离散傅立叶变换(real DFT),再去理解复数傅立叶就更容易了,所以我们先把复数的傅立叶放到一边去,先来理解实数傅立叶变换,在后面我们会先讲讲关于复数的基本理论,然后在理解了实数傅立叶变换的基础上再来理解复数傅立叶变换。
还有,这里我们所要说的变换(transform)虽然是数学意义上的变换,但跟函数变换是不同的,函数变换是符合一一映射准则的,对于离散数字信号处理(DSP),有许多的变换:傅立叶变换、拉普拉斯变换、Z变换、希尔伯特变换、离散余弦变换等,这些都扩展了函数变换的定义,允许输入和输出有多种的值,简单地说变换就是把一堆的数据变成另一堆的数据的方法。
四、傅立叶变换的物理意义
傅立叶变换是数字信号处理领域一种很重要的算法。要知道傅立叶变换算法的意义,首先要了解傅立叶原理的意义。傅立叶原理表明:任何连续测量的时序或信号,都可以表示为不同频率的正弦波信号的无限叠加。而根据该原理创立的傅立叶变换算法利用直接测量到的原始信号,以累加方式来计算该信号中不同正弦波信号的频率、振幅和相位。
和傅立叶变换算法对应的是反傅立叶变换算法。该反变换从本质上说也是一种累加处理,这样就可以将单独改变的正弦波信号转换成一个信号。因此,可以说,傅立叶变换将原来难以处理的时域信号转换成了易于分析的频域信号(信号的频谱),可以利用一些工具对这些频域信号进行处理、加工。最后还可以利用傅立叶反变换将这些频域信号转换成时域信号。
从现代数学的眼光来看,傅里叶变换是一种特殊的积分变换。它能将满足一定条件的某个函数表示成正弦基函数的线性组合或者积分。在不同的研究领域,傅里叶变换具有多种不同的变体形式,如连续傅里叶变换和离散傅里叶变换。
在数学领域,尽管最初傅立叶分析是作为热过程的解析分析的工具,但是其思想方法仍然具有典型的还原论和分析主义的特征。"任意"的函数通过一定的分解,都能够表示为正弦函数的线性组合的形式,而正弦函数在物理上是被充分研究而相对简单的函数类:1. 傅立叶变换是线性算子,若赋予适当的范数,它还是酉算子;2. 傅立叶变换的逆变换容易求出,而且形式与正变换非常类似;3. 正弦基函
数是微分运算的本征函数,从而使得线性微分方程的求解可以转化为常系数的代数方程的求解.在线性时不变杂的卷积运算为简单的乘积运算,从而提供了计算卷积的一种简单手段;4. 离散形式的傅立叶的物理系统内,频率是个不变的性质,从而系统对于复杂激励的响应可以通过组合其对不同频率正弦信号的响应来获取;5. 著名的卷积定理指出:傅立叶变换可以化复变换可以利用数字计算机快速的算出(其算法称为快速傅立叶变换算法(FFT))。
正是由于上述的良好性质,傅里叶变换在物理学、数论、组合数学、信号处理、
概率、统计、密码学、声学、光学等领域都有着广泛的应用。
五、图像傅立叶变换的物理意义
图像的频率是表征图像中灰度变化剧烈程度的指标,是灰度在平面空间上的梯度。如:大面积的沙漠在图像中是一片灰度变化缓慢的区域,对应的频率值很低;而对于地表属性变换剧烈的边缘区域在图像中是一片灰度变化剧烈的区域,对应的频率值较高。傅立叶变换在实际中有非常明显的物理意义,设f是一个能量有限的模拟信号,则其傅立叶变换就表示f的谱。从纯粹的数学意义上看,傅立叶变换是将一个函数转换为一系列周期函数来处理的。从物理效果看,傅立叶变换是将图像从空间域转换到频率域,其逆变换是将图像从频率域转换到空间域。换句话说,傅立叶变换的物理意义是将图像的灰度分布函数变换为图像的频率分布函数,傅立叶逆变换是将图像的频率分布函数变换为灰度分布函数。
傅立叶变换以前,图像(未压缩的位图)是由对在连续空间(现实空间)上的采样得到一系列点的集合,我们习惯用一个二维矩阵表示空间上各点,则图像可由z=f(x,y)来表示。由于空间是三维的,图像是二维的,因此空间中物体在另一个维度上的关系就由梯度来表示,这样我们可以通过观察图像得知物体在三维空间中的对应关系。为什么要提梯度?因为实际上对图像进行二维傅立叶变换得到频谱图,就是图像梯度的分布图,当然频谱图上的各点与图像上各点并不存在一一对应的关系,即使在不移频的情况下也是没有。傅立叶频谱图上我们看到的明暗不一的亮点,实际上图像上某一点与邻域点差异的强弱,即梯度的大小,也即该点的频率的大小(可以这么理解,图像中的低频部分指低梯度的点,高频部分相反)。一般来讲,梯度大则该点的亮度强,否则该点亮度弱。这样通过观察傅立叶变换后的频谱图,也叫功率图,我们首先就可以看出,图像的能量分布,如果频谱图中暗的点数更多,那么实际图像是比较柔和的(因为各点与邻域差异都不大,梯度相对较小),反之,如果频谱图中亮的点数多,那么实际图像一定是尖锐的,边界分明且边界两边像素差异较大的。对频谱移频到原点以后,可以看出图像的频率分布是以原点为圆心,对称分布的。将频谱移频到圆心除了可以清晰地看出图像频率分布以外,还有一个好处,它可以分离出有周期性规律的干扰信号,比如正弦干扰,一副带有正弦干扰,移频到原点的频谱图上可以看出除
了中心以外还存在以某一点为中心,对称分布的亮点集合,这个集合就是干扰噪音产生的,这时可以很直观的通过在该位置放置带阻滤波器消除干扰。
另外我还想说明以下几点:
1、图像经过二维傅立叶变换后,其变换系数矩阵表明:
若变换矩阵Fn原点设在中心,其频谱能量集中分布在变换系数短阵的中心附近(图中阴影区)。若所用的二维傅立叶变换矩阵Fn的原点设在左上角,那么图像
信号能量将集中在系数矩阵的四个角上。这是由二维傅立叶变换本身性质决定的。同时也表明一股图像能量集中低频区域。
2 、变换之后的图像在原点平移之前四角是低频,最亮,平移之后中间部分是低频,最亮,亮度大说明低频的能量大(幅角比较大)。
六、一个关于实数离散傅立叶变换(Real DFT)的例子
先来看一个变换实例,一个原始信号的长度是16,于是可以把这个信号分
解9个余弦波和9个正弦波(一个长度为N的信号可以分解成N/2+1个正余弦信号,这是为什么呢?结合下面的18个正余弦图,我想从计算机处理精度上就不难理解,一个长度为N的信号,最多只能有N/2+1个不同频率,再多的频率就超过了计算机所能所处理的精度范围),如下图:
9个正弦信号:
9个余弦信号:
把以上所有信号相加即可得到原始信号,至于是怎么分别变换出9种不同频率信号的,我们先不急,先看看对于以上的变换结果,在程序中又是该怎么表示的,我们可以看看下面这个示例图:
上图中左边表示时域中的信号,右边是频域信号表示方法,从左向右表示正向转换(Forward DFT),从右向左表示逆向转换(Inverse DFT),用小写x[]表示信号在每个时间点上的幅度值数组, 用大写X[]表示每种频率的副度值数组, 因为有N/2+1种频率,所以该数组长度为N/2+1,X[]数组又分两种,一种是表示余弦波的不同频率幅度值:Re X[],另一种是表示正弦波的不同频率幅度值:Im X[],Re是实数(Real)的意思,Im是虚数(Imagine)的意思,采用复数的表示方法把正余弦波组合起来进行表示,但这里我们不考虑复数的其它作用,只记住是一种组合方法而已,目的是为了便于表达(在后面我们会知道,复数形式的傅立叶变换长度是N,而不是N/2+1)。
七、用Matlab实现快速傅立叶变换
FFT是离散傅立叶变换的快速算法,可以将一个信号变换到频域。有些信号在时域上是很难看出什么特征的,但是如果变换到频域之后,就很容易看出特征了。这就是很多信号分析采用FFT变换的原因。另外,FFT可以将一个信号的频谱提取出来,这在频谱分析方面也是经常用的。
虽然很多人都知道FFT是什么,可以用来做什么,怎么去做,但是却不知道FFT 之后的结果是什意思、如何决定要使用多少点来做FFT。
现在就根据实际经验来说说FFT结果的具体物理意义。一个模拟信号,经过ADC 采样之后,就变成了数字信号。采样定理告诉我们,采样频率要大于信号频率的两倍,这些我就不在此啰嗦了。
采样得到的数字信号,就可以做FFT变换了。N个采样点,经过FFT之后,就
可以得到N个点的FFT结果。为了方便进行FFT运算,通常N取2的整数次方。假设采样频率为Fs,信号频率F,采样点数为N。那么FFT之后结果就是一个为N点的复数。每一个点就对应着一个频率点。这个点的模值,就是该频率值下的幅度特性。具体跟原始信号的幅度有什么关系呢?假设原始信号的峰值为A,那么FFT的结果的每个点(除了第一个点直流分量之外)的模值就是A的N/2倍。而第一个点就是直流分量,它的模值就是直流分量的N倍。而每个点的相位呢,就是在该频率下的信号的相位。第一个点表示直流分量(即0Hz),而最后一个点N的再下一个点(实际上这个点是不存在的,这里是假设的第N+1个点,也可以看做是将第一个点分做两半分,另一半移到最后)则表示采样频率Fs,这
中间被N-1个点平均分成N等份,每个点的频率依次增加。例如某点n所表示
的频率为:Fn=(n-1)*Fs/N。由上面的公式可以看出,Fn所能分辨到频率为为
Fs/N,如果采样频率Fs为1024Hz,采样点数为1024点,则可以分辨到1Hz。1024Hz的采样率采样1024点,刚好是1秒,也就是说,采样1秒时间的信号
并做FFT,则结果可以分析到1Hz,如果采样2秒时间的信号并做FFT,则结果可以分析到0.5Hz。如果要提高频率分辨力,则必须增加采样点数,也即采样时间。频率分辨率和采样时间是倒数关系。
假设FFT之后某点n用复数a+bi表示,那么这个复数的模就是An=根号a*a+b*b,相位就是Pn=atan2(b,a)。根据以上的结果,就可以计算出n点(n≠1,且n<=N/2)对应的信号的表达式为:An/(N/2)*cos(2*pi*Fn*t+Pn),即
2*An/N*cos(2*pi*Fn*t+Pn)。对于n=1点的信号,是直流分量,幅度即为A1/N。由于FFT结果的对称性,通常我们只使用前半部分的结果,即小于采样频率一
半的结果。
下面以一个实际的信号来做说明。假设我们有一个信号,它含有2V的直流分量,频率为50Hz、相位为-30度、幅度为3V的交流信号,以及一个频率为75Hz、
相位为90度、幅度为1.5V的交流信号。用数学表达式就是如下:
S=2+3*cos(2*pi*50*t-pi*30/180)+1.5*cos(2*pi*75*t+pi*90/180)。式中cos
参数为弧度,所以-30度和90度要分别换算成弧度。我们以256Hz的采样率对
这个信号进行采样,总共采样256点。按照我们上面的分析,Fn=(n-1)*Fs/N,我们可以知道,每两个点之间的间距就是1Hz,第n个点的频率就是n-1。我们的信号有3个频率:0Hz、50Hz、75Hz,应该分别在第1个点、第51个点、第76个点上出现峰值,其它各点应该接近0。实际情况如何呢?我们来看看FFT 的结果的模值如图所示。
从图中我们可以看到,在第1点、第51点、和第76点附近有比较大的值。我们分别将这三个点附近的数据拿上来细看:
1点:512+0i
2点:-2.6195E-14 - 1.4162E-13i
3点:-2.8586E-14 - 1.1898E-13i
50点:-6.2076E-13 - 2.1713E-12i
51点:332.55 - 192i
52点:-1.6707E-12 - 1.5241E-12i
75点:-2.2199E-13 -1.0076E-12i
76点:3.4315E-12 + 192i
77点:-3.0263E-14 +7.5609E-13i
很明显,1点、51点、76点的值都比较大,它附近的点值都很小,可以认为是0,即在那些频率点上的信号幅度为0。接着,我们来计算各点的幅度值。分别计算这三个点的模值,结果如下:
1点:512
51点:384
76点:192
按照公式,可以计算出直流分量为:512/N=512/256=2;50Hz信号的幅度为:384/(N/2)=384/(256/2)=3;75Hz信号的幅度为192/(N/2)=192/(256/2)=1.5。可见,从频谱分析出来的幅度是正确的。
然后再来计算相位信息。直流信号没有相位可言,不用管它。先计算50Hz信号的相位,atan2(-192, 332.55)=-0.5236,结果是弧度,换算为角度就是
180*(-0.5236)/pi=-30.0001。再计算75Hz信号的相位,atan2(192,
3.4315E-12)=1.5708弧度,换算成角度就是180*1.5708/pi=90.0002。可见,相位也是对的。根据FFT结果以及上面的分析计算,我们就可以写出信号的表达式了,它就是我们开始提供的信号。
总结:假设采样频率为Fs,采样点数为N,做FFT之后,某一点n(n从1开始)表示的频率为:Fn=(n-1)*Fs/N;该点的模值除以N/2就是对应该频率下
的信号的幅度(对于直流信号是除以N);该点的相位即是对应该频率下的信号的相位。相位的计算可用函数atan2(b,a)计算。atan2(b,a)是求坐标为(a,b)点的角度值,范围从-pi到pi。要精确到xHz,则需要采样长度为1/x秒的信号,并
做FFT。要提高频率分辨率,就需要增加采样点数,这在一些实际的应用中是不现实的,需要在较短的时间内完成分析。解决这个问题的方法有频率细分法,比较简单的方法是采样比较短时间的信号,然后在后面补充一定数量的0,使其长度达到需要的点数,再做FFT,这在一定程度上能够提高频率分辨力。具体的频率细分法可参考相关文献。
八、让傅立叶变换从理性蜕变到感性,从抽象升华到具体(应不少网友反应说以上7部分还是不够浅显而另加的一部分,希望对大家有所启发)
1、我们都知道,LTI系统对谐波函数的响应也是相同频率的谐波函数,只是幅
度和相位可能不同罢了,因此我们用谐波函数来表示信号正是为了导出频域的概念。那你就会问为什么我们要在频域来分析信号,它比时域分析究竟好在哪里呢?这个问题非常好,我来回答你,第一,在频域观察和分析信号有助于揭示系统的本质属性,更重要的是对于某些系统可以极大地简化其设计和分析过程。这一点想必大家都知道,我不再啰嗦!第二,从数学上来看,系统从时域到频域的转换就意味着系统的微分或差分方程将转变为代数方程,而系统的分析也将采用描述系统的复系数代数方程而不是微分或差分方程。既然如此,那么请问?童鞋,你是喜欢跟微分差分方程玩儿呢还是喜欢跟代数方程玩儿呢?假若你说你更喜欢
跟微分差分方程玩儿。那我也无话可说啦!
可能你还是觉得以上所述只是一个很理性的认识,那么接下来,满足你的感性需求。其实,在生活中,我们无时无刻不在进行着傅立叶变换。(什么?我没有听错吧?!)对的,请相信你的耳朵,你完全没有听错。我们来看人类听觉系统的处理过程:当我们听到一个声音,大脑的实际反应是什么?事实上耳朵感觉到一个时变的空气压力,这种变化也许是一个类似于口哨声的单音。当我们听到一个口哨声时,我们所关心的并不是气压随时间的振动(它非常非常快!),而是声音的三个特征:基音、声强以及音长。基音可以理解为频率的同义词,声强不是别的,它就是幅度。我们的耳朵—大脑系统能有效地将信号表示成三个简单的特征参数:基音、声强以及音长,并不理会气压的快速变化过程(一个重复的变化过程)。这样耳朵—大脑系统就提取了信号的本质信息。傅立叶变换的分析过程与此类似,只不过我们从数学意义把它更加精确化和专业话罢了。
2、不要把傅立叶变换想得那么高深莫测,其实它就是对傅立叶级数的一种拓展。我们知道,傅立叶级数能描述无限时间的周期信号。那么,傅立叶级数能不能描述某些特殊的无限时间的非周期信号呢?答案是,不能。但我们经常要分析处理这样的信号啊!于是傅立叶变换这个家伙现身啦!傅立叶变换就是为了使傅立叶级数能够描述所有(没错!就是所有!)周期和非周期的无限时间信号而导出的,因而傅立叶变换是对傅立叶级数的一种拓展。
可能你还是觉得以上所述只是一个很抽象的认识,那么接下来,满足你的具体需
求。我们先不管是怎么进行拓展的。我们先关注另外两个概念:周期信号和非周期信号。他们的显著区别就在于:周期信号每隔一个有限的时间即基波周期To 重复一次。它自始至终都将以这个基波周期To重复。而非周期信号则没有一个确定的或固定的周期,可能在一段时间内他将重复某一段波形很多次,但不会在整个无限长时间范围都如此。我们找到一个周期信号的傅立叶级数,然后让这个信号的基波周期趋于无限,就完成了从傅立叶级数到傅立叶变换的演变过程。因为当周期信号的基波周期趋于无限时,它的波形在有限长时间内都不会重复,这时它就不具有周期性啦!也就是说,说一个信号具有无限长的周期和说它是一个非周期信号实际上是一回事!
XXXX大学 2012届学士学位论文 离散傅里叶变换的分析与研究 学院、专业物理与电子信息学院 电子信息工程 研究方向数字信号处理 学生姓名XX 学号 XXXXXXXXXXX 指导教师姓名XXX 指导教师职称讲师 2012年4月26日
离散傅里叶变换的分析与研究 XX 淮北师范大学物理与电子信息学院 235000 摘要离散傅里叶变换是连续傅里叶变换在时域和频域上都离散的形式,是对连续时间信号频谱分析的逼近。离散傅里叶变换不仅在理论上有重要意义,而且在各种信号的处理中亦起着核心作用。 本文首先介绍了离散傅里叶变换的定义及性质,然后介绍了离散傅里叶变换的应用,主要包括对线性卷积的计算和对连续信号的谱分析。在理解理论的基础上,在matlab环境下实现了线性卷积和对连续信号频谱分析的仿真。仿真结果表明:当循环卷积长度大于或等于线性卷积长度时,可利用循环卷积计算线性卷积;利用DFT对连续信号进行频谱分析必然是近似的,其近似的结果与信号带宽,采样频率和截取长度都有关。 关键词离散傅里叶变换;线性卷积;谱分析
The Analysis and Research of Discrete Fourier Transform XX School of Physics and Electronic Information, Huai Bei Normal University, Anhui Huaibei, 235000 Abstract The discrete Fourier transform is the form that the continuous Fourier transform are discrete both in the time domain and frequency domain,it is a approach to the analysis of continuous time signal spectrum . The discrete Fourier transform not only has important significance in theory, but also plays a central role in all kinds of signal processing . This paper introduced the definition and properties of the discrete Fourier transform first of all.Then introduced the application of the discrete Fourier transform, which mainly including the calculation of linear convolution and analysis of continuous signal the spectral. On the basement of understanding theory, we realized the linear convolution and analysis of continuous signal spectrum on the Matlab environment . The simulation results show that when the length of the cyclic convolution is equal to or greater than linear convolution,we can use cyclic convolution to calculate linear convolution;It is approximately use continuous DFT spectrum to analyze the frequency domain of continuous time signal, the approximation of the results is related to the signal bandwidth, sampling frequency and intercept length. Keywords The discrete Fourier transform; Linear convolution; Spectrum analysis
傅里叶级数通俗解析-CAL-FENGHAI.-(YICAI)-Company One1
傅里叶级数 本文意在阐述傅里叶级数是什么,如何通过数学推导得出,以及傅里叶级数代表的物理含义。 1.完备正交函数集 要讨论傅里叶级数首先得讨论正交函数集。如果n个函数 ,…构成一个函数集,若这些函数在区间上满足 如果是复数集,那么正交条件是 为函数的共轭复函数。 有这个定义,我们可以证明出一些函数集是完备正交函数集。比如三角函数集和复指数函数集在一个周期内是完备正交函数集。 先证明三角函数集: 设,,把代入(1)得 当n时 = = =0 (n,m=1,2,3,…,n) 当n=m时 = = 再证两个都是正弦的情况 设,,把代入(1)得
当n时 = = =0 (n,m=1,2,3,…,n) 当n=m时 = = 最后证明两个是不同名的三角函数的情况 设,,把代入(1)得 = = =0 (n,m为任意整数) 因为两个三角函数相乘只有以上三种情况:两个皆为余弦函数相乘;两个皆为正弦函数相乘;一个为正弦函数,另一个为余弦函数相乘;三种情况皆满足正交函数集的定义,所以三角函数集为正交函数集。至于三角函数集的完备性可以从n,m的取值为任意整数可以得出,三角函数集是完备正交函数集。证毕。 由于三角函数集是完备正交函数集,而根据欧拉公式,我们容易联想到复指数函数集是否也是完备正交函数集呢。 接着是复指数函数集的证明 设,,则把代入(2)得 当n时,根据欧拉公式
= =0 (n,m=1,2,3,…,n) 当n=m时, =1 (n,m=1,2,3,…,n) 所以,复指数函数集也是正交函数集。因为n,m的取值范围是所有整数,所以复指数函数集是完备的正交函数集。 明明是讨论傅里叶级数,为什么第一部分在阐述完备正交函数集呢。因为,在自然界中,没有规则的信号,比如说找一个正弦信号,是完全不可能找到的。有的是一堆杂乱的信号,无规律的波形。我们要研究它,基本的思想是把它拆分,分解成一个一个有规律的可研究的波形,这些波形能用数学表达式准确表达出来。 把一个复杂的信号分解的过程,可以理解成用已知的可以准确表达的函数表示他,比如一个复杂的信号把它分解,就是 其中,…是我们所熟悉的函数, 比如二次函数,一次函数,三角函数,指数函数等等。我们的任务就是求出所分解出来的函数,以及前方的系数n,然后对其研究。那么怎么求呢。完备正交函数集给了我们提供了一种方法。完备正交函数集就像是空间直角坐标系,集合里面的每一个元素相当于坐标系的一条轴,我们知道空间直角坐标系只有3条轴,3条轴,足够表示空间上所有点的位置,不需要再多一条,但是如果只有两条轴,又不能准确地表达立体空间上所有的点,所以3条就是完备的。对于一个函数集的完备性也可以这么理解,表达任意一个周期信号只需要用不多于函数集里面元素的函数就可以表达清楚。再说其正交性,所谓正交,就是函数集里两个不同函数之乘积的积分为0,正交性可以理解成函数集内任意两函数不相关。 既然三角函数集和复指数函数集是完备的正交函数集,那么用其中的一种函数集都可以表达周期信号。 用复指数函数集来表示一个复杂信号: = 其中,(n=1,2,3,…,n)。 用三角函数集表示一个复杂信号:
傅里叶分析之掐死教程(完整版)更新于2014.06.06 Heinrich · 6 个月前 作者:韩昊知乎:Heinrich 微博:@花生油工人知乎专栏:与时间无关的故事 谨以此文献给大连海事大学的吴楠老师,柳晓鸣老师,王新年老师以及张晶泊老师。 转载的同学请保留上面这句话,谢谢。如果还能保留文章来源就更感激不尽了。 我保证这篇文章和你以前看过的所有文章都不同,这是12年还在果壳的时候写的,但是当时没有来得及写完就出国了……于是拖了两年,嗯,我是拖延症患者…… 这篇文章的核心思想就是: 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生
上来就懵圈并从此对它深恶痛绝。老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。(您把教材写得好玩一点会死吗?会死吗?)所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。 ——————————————以上是定场诗—————————————— 下面进入正题: 抱歉,还是要啰嗦一句:其实学习本来就不是易事,我写这篇文章的初衷也是希望大家学习起来更加轻松,充满乐趣。但是千万!千万不要把这篇文章收藏起来,或是存下地址,心里想着:以后有时间再看。这样的例子太多了,也许几年后你都没有再打开这个页面。无论如何,耐下心,读下去。这篇文章要比读课本要轻松、开心得多…… p.s.本文无论是cos还是sin,都统一用“正弦波”(Sine Wave)一词来代表简谐波。 一、什么是频域 从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。 先举一个公式上并非很恰当,但意义上再贴切不过的例子: 在你的理解中,一段音乐是什么呢?
深入浅出的讲解傅里叶变换 我保证这篇文章和你以前看过的所有文章都不同,这是12年还在果壳的时候写的,但是当时没有来得及写完就出国了……于是拖了两年,嗯,我是拖延症患者…… 这篇文章的核心思想就是: 要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。但不幸的是,傅里叶分析的公式看起来太复杂了,所以很多大一新生上来就懵圈并从此对它深恶痛绝。老实说,这么有意思的东西居然成了大学里的杀手课程,不得不归咎于编教材的人实在是太严肃了。(您把教材写得好玩一点会死吗?会死吗?)所以我一直想写一个有意思的文章来解释傅里叶分析,有可能的话高中生都能看懂的那种。所以,不管读到这里的您从事何种工作,我保证您都能看懂,并且一定将体会到通过傅里叶分析看到世界另一个样子时的快感。至于对于已经有一定基础的朋友,也希望不要看到会的地方就急忙往后翻,仔细读一定会有新的发现。 ————以上是定场诗———— 下面进入正题: 抱歉,还是要啰嗦一句:其实学习本来就不是易事,我写这篇文章的初衷也是希望大家学习起来更加轻松,充满乐趣。但是千万!千万不要把这篇文章收藏起来,或是存下地址,心里想着:以后有时间再看。这样的例子太多了,也许几年后你都没有再打开这个页面。无论如何,耐下心,读下去。这篇文章要比读课本要轻松、开心得多…… 一、嘛叫频域 从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。 先举一个公式上并非很恰当,但意义上再贴切不过的例子: 在你的理解中,一段音乐是什么呢?
傅里叶级数及变换的本质解释和形象阐述 ——老师不会这么讲,书上也不会讲很多人学信号与系统、数字信号处理学了几年,关于傅里叶级数和傅里叶变换可能还是一知半解,只能套用公式,根本不理解为什么要这么算,也就是有什么实际含义——可以说,几乎所有信号与系统里面的数学公式都是有实实在在的物理含义的!那么,什么是傅里叶变换,它是怎样一种变换,具体有怎么变换,有没有确切一点或者形象一点的物理解释呢?下面笔者将尝试将自己的理解比较本质和形象地讲出来,形式是思考探讨渐进的模式,也就是我自己的思考过程,希望对大家有所帮助。 首先,要知道傅里叶变换是一种变换,准确点说是投影。傅里叶变换的投影问题,一直想不明白那一系列的正交函数集,到底是什么样一个函数集合,或者说是怎么样的一个空间。所谓三角傅里叶级数当成谐波分析的时候很好理解——同一个时间轴,也就是说同一个维度的分解和叠加,肯定没错,也很实用。但是要是从投影(或者说变换)的角度来说,怎么解释呢?这一系列正弦余弦的函数,在一个区间内,是一个完备的正交函数集,每一个函数所带的系数(或者叫权重),就是原函数在这个函数的方向上的一个投影(说方向不准确,但找不到其他的词)。那么,原函数到底是一个什么样的函数,和各正交基函数又是怎样的一种关系呢?这个投影又是怎么投的呢?三维或者二维空间,一个矢量在各正交基的投影很好理解,那么,傅里
叶变换的正交基函数,也是这样一种相互垂直的关系么???投影也是取余弦值么? 这可以很容易地想清,我们只用余弦或者只用正弦就可以,如cos(2pi*nf0)系列,显然每两个函数图像之间不可能是垂直关系,相反可以看出这是在同一个维度里面的!所以上面两个答案是否定的。 那么,到底是怎么正交、怎么投影的呢。出现这个问题,是因为开始看书的时候我看得太粗心太浅显,没有认真透彻地理解函数正交的含义,没想到那才是最重要最根本的,从那里面再深刻理解一下,问题就迎刃而解。 函数正交和矢量正交完全不一样,是两个概念。函数正交是两个函数,一个不变另一个取共轭值然后逐点相乘再求积分的结果,积分就涉及到一个区间,这也很重要。如果满足:当这两个函数不同时,积分值为0;当两函数相同,积分值不为0。那么这两个函数在这个区间上正交。现在再回过头去看正弦或者余弦函数序列,在各个周期内,都满足上述条件,在正弦和余弦函数之间同样满足,所以这些函数是正交的。至于完备,很明显看出,不去证明了。 第一个问题解决了,现在看怎么去投影了。为更易于理解,我们取指数傅里叶变换为例。众所周知exp(jwt)表示的是一个圆周,我们用来作傅里叶变换的因子,正是这个形式(exp(-jwt)),这里我们还要理解一下傅里叶变换和傅里叶级数的区别,前者求的是复指数傅里叶级数的系数,即每个正交函数的系数(权重),复指数傅里叶级数的正交函数集正是exp(jwt),所以求系数刚好乘以一个共轭
实验报告 课程名称: 信号分析与处理 指导老师: 成绩:__________________ 实验名称:离散傅里叶变换和快速傅里叶变换 实验类型: 基础实验 同组学生姓名: 第二次实验 离散傅里叶变换和快速傅里叶变换 一、实验目的 1.1掌握离散傅里叶变换(DFT )的原理和实现; 1.2掌握快速傅里叶变换(FFT )的原理和实现,掌握用FFT 对连续信号和离散信号进行谱分析的方法。 1.3 会用Matlab 软件进行以上练习。 二、实验原理 2.1关于DFT 的相关知识 序列x (n )的离散事件傅里叶变换(DTFT )表示为 n j n j e n x e X Ω-∞ -∞ =Ω ∑= )()(, 如果x (n )为因果有限长序列,n =0,1,...,N-1,则x (n )的DTFT 表示为 n j N n j e n x e X Ω--=Ω ∑=1 )()(, x (n )的离散傅里叶变换(DFT )表达式为 )1,...,1,0()()(21 -==--=∑N k e n x k X nk N j N n π, 序列的N 点DFT 是序列DTFT 在频率区间[0,2π]上的N 点灯间隔采样,采样间隔为2π/N 。通过DFT ,可以完成由一组有限个信号采样值x (n )直接计算得到一组有限个频谱采样值X (k )。X (k )的幅度谱为 )()()(22k X k X k X I R += ,其中下标R 和I 分别表示取实部、虚部的运算。X (k )的相位谱为 ) () (arctan )(k X k X k R I =?。 离散傅里叶反变换(IDFT )定义为 )1,...,1,0()(1)(21 -==∑-=N n e k X N n x nk N j N n π 。 2.2关于FFT 的相关知识 快速傅里叶变换(FFT )是DFT 的快速算法,并不是一个新的映射。FFT 利用了n N j e π2-函数的周期性 和对称性以及一些特殊值来减少DFT 的运算量,可使DFT 的运算量下降几个数量级,从而使数字信号处 装 订 线
傅里叶变换的本质 傅里叶变换的公式为 dt e t f F t j ?+∞ ∞ --= ωω)()( 可以把傅里叶变换也成另外一种形式: φπt j e t f F ωπ ω),(21 )(= 可以看出,傅里叶变换的本质是内积,三角函数是完备的正交函数集,不同频率的三角函数的之间的内积为0,只有频率相等的三角函数做内积时,才不为0。 )(2,21)(2121Ω-Ω==?Ω-ΩΩΩπδdt e e e t j t j t j φπ 下面从公式解释下傅里叶变换的意义 因为傅里叶变换的本质是内积,所以f(t)和t j e ω求内积的时候,只有f(t)中频率为ω的分量 才会有内积的结果,其余分量的内积为0。可以理解为f(t)在t j e ω上的投影,积分值是时间从负 无穷到正无穷的积分,就是把信号每个时间在ω的分量叠加起来,可以理解为f(t)在t j e ω上的投 影的叠加,叠加的结果就是频率为ω的分量,也就形成了频谱。 傅里叶逆变换的公式为 ωωπ ωd e F t f t j ? +∞ ∞ -= )(21 )( 下面从公式分析下傅里叶逆变换的意义 傅里叶逆变换就是傅里叶变换的逆过程,在)(ωF 和t j e ω-求内积的时候,)(ωF 只有t 时 刻的分量内积才会有结果,其余时间分量内积结果为0,同样积分值是频率从负无穷到正无穷的积分,就是把信号在每个频率在t 时刻上的分量叠加起来,叠加的结果就是f(t)在t 时刻的值,这就回到了我们观察信号最初的时域。 对一个信号做傅里叶变换,然后直接做逆变换,这样做是没有意义的,在傅里叶变换和傅里叶逆变换之间有一个滤波的过程。将不要的频率分量给滤除掉,然后再做逆变换,就得到了想要的信号。比如信号中掺杂着噪声信号,可以通过滤波器将噪声信号的频率给去除,再做傅里叶逆变换,就得到了没有噪声的信号。 优点:频率的定位很好,通过对信号的频率分辨率很好,可以清晰的得到信号所包含的频率成分,也就是频谱。 缺点:因为频谱是时间从负无穷到正无穷的叠加,所以,知道某一频率,不能判断,该频率的时间定位。不能判断某一时间段的频率成分。 例子: 平稳信号:x(t)=cos(2*pi*5*t)+cos(2*pi*10*t)+cos(2*pi*20*t)+cos(2*pi*50*t)
第一章 信号与系统的基本概念 1.信号、信息与消息的差别? 信号:随时间变化的物理量; 消息:待传送的一种以收发双方事先约定的方式组成的符号,如语言、文字、图像、数据等 信息:所接收到的未知内容的消息,即传输的信号是带有信息的。 2.什么是奇异信号? 函数本身有不连续点或其导数或积分有不连续点的这类函数统称为奇异信号或奇异函数。例如: 单边指数信号 (在t =0点时,不连续), 单边正弦信号 (在t =0时的一阶导函数不连续)。 较为重要的两种奇异信号是单位冲激信号δ(t )和单位阶跃信号u(t )。 3.单位冲激信号的物理意义及其取样性质? 冲激信号:它是一种奇异函数,可以由一些常规函数的广义极限而得到。 它表达的是一类幅度很强,但作用时间很短的物理现象。其重要特性是筛选性,即: ()()()(0)(0)t x t dt t x dt x δδ∞ ∞ -∞ -∞ ==? ? 4.什么是单位阶跃信号? 单位阶跃信号也是一类奇异信号,定义为: 10()00t u t t >?=?
12()()()x t ax t bx t =+,其中a 和b 是任意常数时, 输出信号()y t 是1()y t 和2()y t 的线性叠加,即:12()()()y t ay t by t =+; 且当输入信号()x t 出现延时,即输入信号是0()x t t -时, 输出信号也产生同样的延时,即输出信号是0()y t t -。 其中,如果当12()()()x t x t x t =+时,12()()()y t y t y t =+,则称系统具有叠加性; 如果当1()()x t ax t =时,1()()y t ay t =则称系统具有均匀性。 线性时不变系统是最基本的一类系统,是研究复杂系统,如非线性、时变系统的基础。 6.线性时不变系统的意义与应用? 线性时不变系统是我们本课程分析和研究的主要对象,对线性时不变性进行推广,可以得到线性时不变系统具有微分与积分性质,假设系统的输入与输出信号分别为()x t 和()y t ,则 当输入信号为 ()dx t dt 时,输出信号则为() dy t dt ; 或者当输入信号为()t x d ττ-∞ ?时,输出信号则为()t y d ττ-∞ ?。 另外,线性时不变系统对信号的处理作用可以用冲激响应(或单位脉冲响应)、系统函数或频率响应进行描述。而且多个系统可以以不同的方式进行连接,基本的连接方式为:级联和并联。 假设两个线性时不变系统的冲激响应分别为:1()h t 和2()h t , 当两个系统级联后,整个系统的冲激响应为:12()()*()h t h t h t =; 当两个系统并联后,整个系统的冲激响应为:12()()()h t h t h t =+; 当0t <时,若()0h t =, 则此系统为因果系统; 若|()|h t dt ∞ -∞<∞?, 则此系统为稳定系统。 第二章 连续时间系统的时域分析 1.如何获得系统的数学模型? 数学模型是实际系统分析的一种重要手段,广泛应用于各种类型系统的分析和控制之中。 不同的系统,其数学模型可能具有不同的形式和特点。对于线性时不变系统,其数学模型
傅里叶级数 本文意在阐述傅里叶级数是什么,如何通过数学推导得出,以及傅里叶级数代表的物理含义。 1.完备正交函数集 要讨论傅里叶级数首先得讨论正交函数集。如果n个函数 φ1t,φ2t,…,φn t构成一个函数集,若这些函数在区间t1,t2上满足 φi tφj t t2 t1dt= 0 ,i≠j K i ,i=j(1) 如果是复数集,那么正交条件是 φi tφj?t t2 t1dt= 0 ,i≠j K i ,i=j(2) φj?t为函数φj t的共轭复函数。 有这个定义,我们可以证明出一些函数集是完备正交函数集。比如三角函数集和复指数函数集在一个周期内是完备正交函数集。 先证明三角函数集: 设φn t=cos nωt,φm t=cos mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt cos mωt dt t0+T t0 当n≠m时 =1 2 cos n+mωt+cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω +sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 再证两个都是正弦的情况 设φn t=sin nωt,φm t=sin mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=sin nωt sin mωt dt t0+T t0 当n≠m时
=1 2 cos n+mωt?cos n?mωt t0+T t0 dt =1 2sin n+mωt (n+m)ω ?sin n?mωt (n?m)ωt t0+T =0 (n,m=1,2,3,…,n≠m) 当n=m时 =1 2 cos2nωt t0+T t0 dt =T 2 最后证明两个是不同名的三角函数的情况 设φn t=cos nωt,φm t=sin mωt,把φn t,φm t代入(1)得 φi tφj t t0+T t0dt=cos nωt sin mωt dt t0+T t0 =1 2 sin n+mωt?sin n?mωt t0+T t0 dt =1 2 ?cos n+mωt (n+m)ω +cos n?mωt (n?m)ωt t0+T =0 (n,m为任意整数) 因为两个三角函数相乘只有以上三种情况:两个皆为余弦函数相乘;两个皆为正弦函数相乘;一个为正弦函数,另一个为余弦函数相乘;三种情况皆满足正交函数集的定义,所以三角函数集为正交函数集。至于三角函数集的完备性可以从n,m的取值为任意整数可以得出,三角函数集是完备正交函数集。证毕。 由于三角函数集是完备正交函数集,而根据欧拉公式,我们容易联想到复指数函数集是否也是完备正交函数集呢。 接着是复指数函数集的证明 设φn t=?jnωt,φm t=?jmωt,则φj?t=??jmωt把φn t,φj?t代入(2)得 φi tφj?t t0+T t0dt=?jnωt t0+T t0 ??jmωt dt =?j(n?m)ωt t0+T t0 dt 当n≠m时,根据欧拉公式 =cos n?mωt+j sin?(n?m)ωt t0+T t0 dt =sin n?mωt n?mω?j cos?(n?m)ωt n?mωt t0+T =0 (n,m=1,2,3,…,n≠m)
傅里叶级数的推导
————————————————————————————————作者:————————————————————————————————日期:
傅里叶级数的推导 2016年12月14日09:27:47 傅里叶级数的数学推导 首先,隆重推出傅里叶级数的公式,不过这个东西属于“文物”级别的,诞生于19世纪初,因为傅里叶他老人家生于1768年,死于1830年。 但傅里叶级数在数论、组合数学、信号处理、概率论、统计学、密码学、声学、光学等领域都有着广泛的应用,这不由得让人肃然起敬。一打开《信号与系统》、《锁相环原理》等书籍,动不动就跳出一个“傅里叶级数”或“傅里叶变换”,弄一长串公式,让人云山雾罩。 如下就是傅里叶级数的公式: 不客气地说,这个公式可以说是像“臭婆娘的裹脚布——又臭又长”,而且来历相当蹊跷,不知那个傅里叶什么时候灵光乍现,把一个周期函数f(t)硬生生地写成这么一大堆东西。单看那个①式,就是把周期函数f(t)描述成一个常数系数a0、及1倍ω的sin和cos函数、2倍ω的sin和cos函数等、到n 倍ω的sin和cos函数等一系列式子的和,且每项都有不同的系数,即An和Bn,至于这些系数,需要用积分来解得,即②③④式,不过为了积分方便,积分区间一般设为[-π, π],也相当一个周期T的宽度。 能否从数学的角度推导出此公式,以使傅里叶级数来得明白些,让我等能了解它的前世今生呢?下面来详细解释一下此公式的得出过程: 1、把一个周期函数表示成三角级数:
首先,周期函数是客观世界中周期运动的数学表述,如物体挂在弹簧上作简谐振动、单摆振动、无线电电子振荡器的电子振荡等,大多可以表述为: f(x)=A sin(ωt+ψ) 这里t表示时间,A表示振幅,ω为角频率,ψ为初相(与考察时设置原点位置有关)。 然而,世界上许多周期信号并非正弦函数那么简单,如方波、三角波等。傅叶里就想,能否用一系列的三角函数An sin(nωt+ψ)之和来表示那个较复杂的周期函数f(t)呢?因为正弦函数sin可以说是最简单的周期函数了。于是,傅里叶写出下式:(关于傅里叶推导纯属猜想) 这里,t是变量,其他都是常数。与上面最简单的正弦周期函数相比,5式中多了一个n,且n从1到无穷大。这里f(t)是已知函数,也就是需要分解的原周期函数。从公式5来看,傅里叶是想把一个周期函数表示成许多正弦函数的线性叠加,这许许多多的正弦函数有着不同的幅度分量(即式中An)、有不同的周期或说是频率(是原周期函数的整数倍,即n)、有不同的初相角(即ψ),当然还有一项常数项(即A0)。要命的是,这个n是从1到无穷大,也就是是一个无穷级数。 应该说,傅里叶是一个天才,想得那么复杂。一般人不太会把一个简单的周期函数弄成这么一个复杂的表示式。但傅里叶认为,式子右边一大堆的函数,其实都是最简单的正弦函数,有利于后续的分析和计算。当然,这个式能否成立,关键是级数中的每一项都有一个未知系数,如A0、An等,如果能把这些系数求出来,那么5式就可以成立。当然在5式中,唯一已知的就是原周期函数f(t),那么只需用已知函数f(t)来表达出各项系数,上式就可以成立,也能计算了。 于是乎,傅里叶首先对式5作如下变形: 这样,公式5就可以写成如下公式6的形式: 这个公式6就是通常形式的三角级数,接下来的任务就是要把各项系数an和bn及a0用已知函数f(t)来表达出来。 2、三角函数的正交性:
第三讲 Part3 DFT 的理论难点 1、抽样定理 连接离散信号与连续信号的桥梁。 ()(){ ()()j t a a j j n s n X j x t e dt X e x nT e ω ω∞ -Ω-∞ ∞ -=-∞ Ω== ?∑ 根据频域卷积定理推导 () ()()() {1()()()()()2j j j j j y n x n h n Y e X e H e X e H e d πωωωθωθπ θ π--==*=? 得到:1 ()()j a s k s X e X j jk T ω ∞ =-∞ = Ω-Ω∑ 2、FT 中的待研究的理论难点与关键之处 2.1 DFT 与DTFT 的关系 两种论述方法: 方法1:书P119-P120的论述;请同学看书后,上黑板叙述推演相关的过程。 方法2:书P121,连续频谱的抽样也必然使原来的时域信号变成周期的。 2.2 DFT 的()X k 是“()x n 的傅里叶变换”的某种程度上的近似。 用DFT 对连续信号和离散信号进行谱分析的基本原理和方法 2.2.1 怎样理解DFT 对FT 的近似? 由于用DFT 对连续信号做频谱分析的过程中隐含了频域和时域的两个周期延拓,又由于信号时宽和带宽的制约关系,因此,做DFT 得到的()N X k ,及由()N X k 做IDFT 得到的 ()N x n 都是对原()a X j Ω及()a x t 的某种近似。 如果s T 选得足够小,则式1 ()|()s j a T a s l s X e X j jl T ω ω∞ =Ω=-∞ = Ω-Ω∑ 中将避免或大大减轻 频域的混叠。 如果N 选得足够大,一方面可以减轻式()()*()j j j a X e X e D e ω ω ω =的窗口效应,另一方面也会减轻式()(),0,1, (1) l x n x n lN n N ∞ =-∞ = +=-∑的时域混叠。 结论:在这两个条件均满足的情况下,上述的近似误差将减小到可接受的程度,从而
脉搏、语音及图像信号的傅里叶分析 一、实验简介 任何波形的周期信号均可用傅里叶级数来表示。傅里叶级数的各项代表了不同频率的正弦或余弦信号,即任何波形的周期信号都可以看作是这些信号(谐波)的叠加。利用不同的方法,可以从周期信号中分解出它的各次谐波的幅值和相位。也可依据信号的傅里叶级数表达式,将各次谐波按表达式的要求叠加得到所期望的信号。 二、实验目的 1、了解常用周期信号的傅里叶级数表示。 2、了解周期脉搏信号、语音信号及图像信号的傅里叶分析过程 3、理解体会傅里叶分析的理论及现实意义 三、实验仪器 脉搏语音实验仪器,数字信号发生器,示波器 四、实验原理 1、周期信号傅里叶分析的数学基础 任意一个周期为T 的函数f(t)都可以表示为傅里叶级数: 00010000 1 ()(cos sin ) 21()() 1 ()cos()()1 ()sin()()n n n n n f t a a n t b n t a f t d t a f t n t d t b f t n t d t π π π ππ πωωωωπ ωωωπ ωωωπ ∞ =-- - =++=== ∑??? 其中0ω为角频率,称为基频,0a 为常数,n a 和n b 称为第n 次谐波的幅值。任何
周期性非简谐交变信号均可用上述傅里叶级数进行展开,即分解为一系列不同次谐波的叠加。 对于如图1所示的方波,一个周期内的函数表达式为: (0t<)2() (-t 0) 2 h f t h ππ? ≤??=? ?-≤
kn N W N N 第四章 快速傅里叶变换 有限长序列可以通过离散傅里叶变换(DFT)将其频域也离散化成有限长 序列.但其计算量太大,很难实时地处理问题,因此引出了快速傅里叶变换 (FFT). 1965 年,Cooley 和 Tukey 提出了计算离散傅里叶变换(DFT )的快 速算法,将 DFT 的运算量减少了几个数量级。从此,对快速傅里叶变换(FFT ) 算法的研究便不断深入,数字信号处理这门新兴学科也随 FFT 的出现和发 展而迅速发展。根据对序列分解与选取方法的不同而产生了 FFT 的多种算 法,基本算法是基2DIT 和基2DIF 。FFT 在离散傅里叶反变换、线性卷积 和线性相关等方面也有重要应用。 快速傅里叶变换(FFT )是计算离散傅里叶变换(DFT )的快速算法。 DFT 的定义式为 N ?1 X (k ) = ∑ x (n )W N R N (k ) n =0 在所有复指数值 W kn 的值全部已算好的情况下,要计算一个 X (k ) 需要 N 次复数乘法和 N -1 次复数加法。算出全部 N 点 X (k ) 共需 N 2 次复数乘法 和 N ( N ? 1) 次复数加法。即计算量是与 N 2 成正比的。 FFT 的基本思想:将大点数的 DFT 分解为若干个小点数 DFT 的组合, 从而减少运算量。 W N 因子具有以下两个特性,可使 DFT 运算量尽量分解为小点数的 DFT 运算: (1) 周期性: ( k + N ) n N = W kn = W ( n + N ) k (2) 对称性:W ( k + N / 2 ) = ?W k N N 利用这两个性质,可以使 DFT 运算中有些项合并,以减少乘法次数。例子: 求当 N =4 时,X(2)的值
第15章 傅里叶级数 § 傅里叶级数 一 基本内容 一、傅里叶级数 在幂级数讨论中 1 ()n n n f x a x ∞ ==∑,可视为()f x 经函数系 21, , , , , n x x x 线性表出而得.不妨称 2 {1,,,,,}n x x x 为基,则不同的基就有不同的级数.今用三角函数 系作为基,就得到傅里叶级数. 1 三角函数系 函数列{}1, cos , sin , cos 2, sin 2, , cos , sin , x x x x nx nx 称为三角函数系.其有下 面两个重要性质. (1) 周期性 每一个函数都是以2π为周期的周期函数; (2) 正交性 任意两个不同函数的积在[,]ππ-上的积分等于 零,任意一个函数的平方在上的积分不等于零. 对于一个在[,]ππ-可积的函数系{}() [, ], 1,2, n u x x a b n ∈=:,定义两个函数的内积 为 (),()()()d b n m n m a u x u x u x u x x =??, 如果 0 (),() 0 n m l m n u x u x m n ≠=?=? ≠?,则称函数系{}() [, ], 1,2, n u x x a b n ∈=:为正交系. 由于 1, sin 1sin d 1cos d 0 nx nx x nx x ππ π π --=?=?=??; sin , sin sin sin d 0 m n mx nx mx nx x m n ππ π-=?=?=? ≠??; cos , cos cos cos d 0 m n mx nx mx nx x m n ππ π-=?=?=? ≠??; sin , cos sin cos d 0 mx nx mx nx x ππ -=?=? ; 2 1, 11d 2x ππ π -==?, 所以三角函数系在[],ππ-上具有正交性,故称为正交系. 利用三角函数系构成的级数 ()01 cos sin 2n n n a a nx b nx ∞ =++∑ 称为三角级数,其中011,,, ,,,n n a a b a b 为常数 2 以2π为周期的傅里叶级数
实验二 用快速傅里叶变换对信号进行频谱分析 一、实验目的 1.理解离散傅里叶变换的意义; 2.掌握时域采样率的确定方法; 3.掌握频域采样点数的确定方法; 4.掌握离散频率与模拟频率之间的关系; 5.掌握离散傅里叶变换进行频谱分析时,各参数的影响。 二、实验原理 序列的傅里叶变换结果为序列的频率响应,但是序列的傅里叶变换是频率的连续函数,而且在采用计算机计算时,序列的长度不能无限长,为了便于计算机处理,作如下要求:序列x (n )为有限长,n 从0~N -1,再对频率ω在0~2π范围内等间隔采样,采样点数为N ,采样间隔为2π/N 。第k 个采样点对应的频率值为2πk /N 。可得离散傅里叶变换及其逆变换的定义为 ∑-=-=1 02)()(N n n N k j e n x k X π (1) ∑-==1 02)(1)(N k k N n j e k X N n x π (2) 如果把一个有限长序列看作是周期序列的一个周期,则离散傅里叶变换就是傅里叶级数。离散傅里叶变换也是周期的,周期为N 。 数字频率与模拟频率之间的关系为 s f f /2πω=,即s s T f f πωπω22== (3) 则第k 个频率点对应的模拟频率为 N kf NT k T N k f s s s k ==?=ππ212 (4) 在用快速傅里叶变换进行频谱分析时,要确定两个重要参数:采样率和频域采样点数,采样率可按奈奎斯特采样定理来确定,采样点数可根据序列长度或频率分辨率△f 来确定 f N f s ?≤,则f f N s ?≥ (5) 用快速傅里叶变换分析连续信号的频谱其步骤可总结如下: (1)根据信号的最高频率,按照采样定理的要求确定合适的采样频率f s ; (2)根据频谱分辨率的要求确定频域采样点数N ,如没有明确要求频率分辨率,则根据实际需要确定频率分辨率; (3)进行N 点的快速傅里叶变换,最好将纵坐标根据帕塞瓦尔关系式用功率来表示,
第四章 离散系统分析和离散傅里叶变换 4-1概述 在上一章中我们已经介绍了连续时间信号(周期的或非周期的)的傅里叶变换。在第一、二章中介绍了离散信号和离散系统的概念,在这一章中主要讨论离散信号的傅里叶变换。 4-2离散信号的傅里叶变换 时域抽样定理告诉我们,连续时间信号可以由它的样本值恢复出来,即 ]2 ) ([ )()(∑ ∞ -∞ =-Ω= n s nT t Sa nT f t f 当抽样频率s Ω给定时,抽样函数]2 ) ([ nT t Sa s -Ω就确定了,唯一与信号相关的是信号的样本值)(nT f ,换句话说传载)(t f 中信息的是样本值)(nT f 。因此研究连续时间信号)(t f 中的信息,就转 变为研究样本值)(nT f 中的信息。当抽样频率s Ω给定时,T 也就一定了,样本值)(nT f 就可以抽象为序列)(n f ,也就是说离散信号的数学抽象是序列。以后我们就用序列)(n f 表示离散信号(样本值)。 由于序列的变量是整数变量,与连续信号的变量不同,因此对序列的处理方法与连续时间变量的处理方法也必定不同。先来看看序列的傅里叶变换,连续非周期时间信号)(t f 的傅里叶变换为 ? ∞ ∞ -Ω-= =Ωdt e t f t f F t j )(])([)(F ? ∞ ∞ -ΩΩΩ= Ω=d e F F t f t j -)(21 )]([)(1 π F 假定)(n f 是非周期的,仿照连续时间信号的傅里叶变换形式可以定义序列的傅里叶变换: ∑∞ -∞ =-= n jn j e n f e F ω ω )()( (4-1) ?- = π πωω ωπ d e e F n f jn j )(21 )( (4-2) 式中ω为数字角频率。(4-1)式和(4-2)式构成了序列的傅里叶变换对,前者称为序列的傅里叶正变换,后者称为序列的傅里叶逆变换。注意到序列傅里叶正变换公式是个和式,这是因为序列)(n f 的变量是离散的整数,序列的傅里叶逆变换公式是个积分式,由此也说明序列的傅里叶变换是ω的连续函数,也就是说,离散信号的傅里叶变换是频域中连续的函数。此外因
这篇文章的核心思想就是:要让读者在不看任何数学公式的情况下理解傅里叶分析。 傅里叶分析不仅仅是一个数学工具,更是一种可以彻底颠覆一个人以前世界观的思维模式。 一、嘛叫频域 关键词:从侧面看 从我们出生,我们看到的世界都以时间贯穿,股票的走势、人的身高、汽车的轨迹都会随着时间发生改变。这种以时间作为参照来观察动态世界的方法我们称其为时域分析。而我们也想当然的认为,世间万物都在随着时间不停的改变,并且永远不会静止下来。但如果我告诉你,用另一种方法来观察世界的话,你会发现世界是永恒不变的,你会不会觉得我疯了?我没有疯,这个静止的世界就叫做频域。 先举一个公式上并非很恰当,但意义上再贴切不过的例子:在你的理解中,一段音乐是什么呢? 这是我们对音乐最普遍的理解,一个随着时间变化的震动。但我相信对于乐器小能手们来说,音乐更直观的理解是这样的: 上图是音乐在时域的样子,而下图则是音乐在频域的样子。所以频域这一概念对大家都从不陌生,只是从来没意识到而已。 现在我们可以回过头来重新看看一开始那句痴人说梦般的话:世界是永恒的。 将以上两图简化: 时域: 频域: 在时域,我们观察到钢琴的琴弦一会上一会下的摆动,就如同一支股票的走势;而在频域,只有那一个永恒的音符。 你眼中看似落叶纷飞变化无常的世界,实际只是躺在上帝怀中一份早已谱好的乐章。
傅里叶同学告诉我们,任何周期函数,都可以看作是不同振幅,不同相位正/余弦波的叠加。在第一个例子里我们可以理解为,利用对不同琴键不同力度,不同时间点的敲击,可以组合出任何一首乐曲。 而贯穿时域与频域的方法之一,就是传中说的傅里叶分析。傅里叶分析可分为傅里叶级数(Fourier Serie)和傅里叶变换(Fourier Transformation),我们从简单的开始谈起。 二、傅里叶级数(Fourier Series) 如果说能用余弦曲线波叠加出一个带90度角的矩形波来,你会相信吗?但是看看下图: 第一幅图是一个郁闷的余弦波cos(x) 第二幅图是2个卖萌的余弦波的叠加cos(x)+a cos(3x) 第三幅图是4个发春的余弦波的叠加 第四幅图是10个便秘的余弦波的叠加 随着余弦波数量逐渐的增长,他们最终会叠加成一个标准的矩形,大家从中体会到了什么道理? 随着叠加的递增,所有余弦波中上升的部分逐渐让原本缓慢增加的曲线不断变陡,而所有正弦波中下降的部分又抵消了上升到最高处时继续上升的部分使其变为水平线。一个矩形就这么叠加而成了。但是要多少个余弦波叠加起来才能形成一个标准90度角的矩形波呢?不幸的告诉大家,答案是无穷多个。 不仅仅是矩形,你能想到的任何波形都是可以如此方法用正/余弦波叠加起来的。 这是没有接触过傅里叶分析的人在直觉上的第一个难点,但是一旦接受了这样的设定,游戏就开始有意思起来了。 还是上图的余弦波累加成矩形波,我们换一个角度来看看: