【真题】17年北京市海淀区高三(上)数学期中试卷含答案(文科)

高三数学 期中测试卷（文)试卷满分共计150分 考试时间:120分钟一、选择题：本大题共8小题，每小题5分，共40分 1．若集合{1,2,3}A =,{0,1,2}B =,则AB =A ．{0,1,2,3}B ．{0,1,2}C ．{1,2}D ．{1,2,3}2．设3log 2a =,21log 8b =,2c =,则A ．a b c >> B ．c b a >> C ．a c b >> D ．c a b >>3．“数列{}na 既是等差数列又是等比数列”是“数列{}na 是常数列"的A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．若实数,x y 满足010x y x y x -≤⎧⎪+≤⎨⎪≥⎩，则2z x y =+的最大值为A ．0B ．1C ．32D ．25．从,,,,A B C D E 5名学生中随机选出2人，A 被选中的概率为A ．15B ．25C ．825D ．9256。

下列函数中,其定义域和值域分别与函数lg 10xy =的定义域和值域相同的是A ．y x =B ．lg y x =C ．2xy = D ．1y x=7．执行如图所示的程序框图,输出的k 的值为A ．3B ．4C ．5D ．68．函数()2sin()(0,)22f x x ππωϕωϕ=+>-<<的部分图象如图所示,则,ωϕ的值分别是（ ）A ．2,3π-B ．2,6π-C ．4,6π-D ．4,3π二、填空题：本大题共6小题，每小题5分，共30分 9．设命题p ：∃n ∈N ，2n >2n，则p ⌝为______ 。

10．若i 为虚数单位，则21i=+______ 。

11．数列}{na 中,若11=a,211+=-n n a a (2≥n ），则数列}{n a 的前9项和等于______ .12．曲线ln y x x =+在点()1,1处的切线方程为______ .13．ABC ∆中，角,,A B C 所对的边分别为,,a b c . 若3a =,2b =，1cos()3A B +=，则边c =______ 。

海淀区高三年级第一学期期中练习数 学（理科）本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上 作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 已知集合{2}A x x =>，{(1)(3)0}B x x x =--<，则AB =A. {1}x x >B. {23}x x <<C. {13}x x <<D. {2x x >或1}x < 2. 已知向量(1,2),(2,4)=-=-a b ，则与b A. 垂直 B. 不垂直也不平行 C. 平行且同向 D. 平行且反向3. 函数222x xy =+的最小值为 A. 1B. 2C. D. 44. 已知命题:p 0c ∃>，方程20x x c -+= 有解，则p ⌝为 A. 0c ∀>，方程20x x c -+=无解 B. c ∀≤0，方程20x x c -+=有解 C. 0c ∃>，方程20x x c -+=无解 D. c ∃≤0，方程20x x c -+=有解5. 已知函数,,log xbc y a y x y x ===的图象如图所示，则A. a b c >>B. a c b >>C. c a b >>D. c b a >> 6. 设,a b 是两个向量，则“+>-a b a b ”是“0⋅>a b ”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 已知函数42()cos sin f x x x =+，下列结论中错误．．的是A. ()f x 是偶函数B. 函数()f x 最小值为34C. π2是函数()f x 的一个周期 D. 函数()f x 在π0,2（）内是减函数8．如图所示，A 是函数()2x f x =的图象上的动点，过点A 作直线平行于x 轴，交函数2()2x g x +=的图象于点B ，若函数()2x f x =的图象上存在点C 使得ABC ∆为等边三角形，则称A 为函数()2xf x =上的好位置点. 函数()2xf x =上的好位置点的个数为A. 0B. 1C. 2D. 大于2第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

2017海淀区高三（上）期中数学（文）一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．（5分）已知集合A={x|x＞2}，B={x|（x﹣1）（x﹣3）＜0}，则A∩B=（）A．{x|x＞1} B．{x|2＜x＜3} C．{x|1＜x＜3} D．{x|x＞2或x＜1}2．（5分）已知向量=（﹣1，x），=（﹣2，4）．若∥，则x的值为（）A．﹣2 B．C．D．23．（5分）已知命题p：∀x＞0，x+≥2命题q：若a＞b，则ac＞bc．下列命题为真命题的是（）A．q B．￢p C．p∨q D．p∧q4．（5分）若角θ的终边过点P（3，﹣4），则tan（θ+π）=（）A．B．C．D．5．（5分）已知函数y=x a，y=log b x的图象如图所示，则（）A．b＞1＞a B．b＞a＞1 C．a＞1＞b D．a＞b＞16．（5分）设，是两个向量，则“|+|＞|﹣|”是“•＞0”的（）A．充分而不必要条件 B．必要而不充分条件C．充分必要条件 D．既不充分也不必要条件7．（5分）给定条件：①∃x0∈R，f（﹣x0）=﹣f（x0）；②∀x∈R，f（1﹣x）=f（1+x）的函数个数是下列三个函数：y=x3，y=|x﹣1|，y=cosπx中，同时满足条件①②的函数个数是（）A．0 B．1 C．2 D．38．（5分）已知定义在R上的函数f（x）=，若方程f（x）=有两个不相等的实数根，则a的取值范围是（）A．﹣≤a＜B．C．0≤a＜1 D．二、填空题共6小题，每小题5分，共30分．9．（5分）计算lg2﹣lg+3lg5= ．10．（5分）已知sinα=，则cos2α= ．11．（5分）已知函数y=f（x）的导函数有且仅有两个零点，其图象如图所示，则函数y=f（x）在x= 处取得极值．12．（5分）在正方形ABCD中，E是线段CD的中点，若=λ+μ，则λ﹣μ= ．13．（5分）在△ABC中，cosA=，7a=3b，则B= ．14．（5分）去年某地的月平均气温y（℃）与月份x（月）近似地满足函数y=a+bsin（x+φ）（a，b为常数，0＜φ＜）．其中三个月份的月平均气温如表所示：x 5 8 11y 13 31 13则该地2月份的月平均气温约为℃，φ= ．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．（13分）已知函数f（x）=cos（2x﹣）﹣cos2x．（Ⅰ）求f（0）的值；（Ⅱ）求函数f（x）的最小正周期和单调递增区间．16．（13分）已知数列{a n}是等差数列，且a2=﹣1，数列{b n}满足b n﹣b n﹣1=a n（n=2，3，4，…），且b1=b3=1．（Ⅰ）求a1的值；（Ⅱ）求数列{b n}的通项公式．17．（13分）如图，△ABC是等边三角形，点D在边BC的延长线上，且BC=2CD，AD=．（Ⅰ）求的值；（Ⅱ）求CD的长．18．（14分）已知函数f（x）=．（Ⅰ）当a=1时，求函数f（x）的单调区间；（Ⅱ）当a＜0时，求函数f（x）在区间[0，1]上的最小值．19．（13分）已知{a n}是等比数列，a2=2且公比q＞0，﹣2，a1，a3成等差数列．（Ⅰ）求q的值；（Ⅱ）已知b n=a n a n+2﹣λna n+1（n=1，2，3，…），设S n是数列{b n}的前n项和．若S1＞S2，且S k＜S k+1（k=2，3，4，…），求实数λ的取值范围．20．（14分）已知函数f（x）=x3﹣9x，g（x）=3x2+a．（Ⅰ）若曲线y=f（x）与曲线y=g（x）在它们的交点处具有公共切线，求a的值；（Ⅱ）若存在实数b使不等式f（x）＜g（x）的解集为（﹣∞，b），求实数a的取值范围；（Ⅲ）若方程f（x）=g（x）有三个不同的解x1，x2，x3，且它们可以构成等差数列，写出实数a的值．（只需写出结果）数学试题答案一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．【解答】由B中不等式解得：1＜x＜3，即B={x|1＜x＜3}，∵A={x|x＞2}，∴A∩B={x|2＜x＜3}，故选：B．2．【解答】向量=（﹣1，x），=（﹣2，4）．若∥，可得﹣2x=﹣4，解得x=2．故选：D．3．【解答】∵x＞0时，，当且仅当x=1时取“=”；∴命题p为真命题，则￢p假；若a＞b＞0，c＜0，则ac＞bc不成立；∴命题q为假命题；∴p∨q为真命题．故选C．4．【解答】∵角θ的终边过点P（3，﹣4），则tan（θ+π）=﹣tanθ=﹣=﹣=，故选：C．5．【解答】由图象可知，0＜a＜1，b＞1，故选：A．6．【解答】若|+|＞|﹣|，则等价为|+|2＞|﹣|2，即||2+||2+2•＞||2+||2﹣2•，即4•＞0，则•＞0成立，反之，也成立，即“|+|＞|﹣|”是“•＞0”的充要条件，故选：C．7．【解答】条件②说明函数的对称轴是x=1，函数y=x3是奇函数，满足条件．①，但不满足条件②，y=|x﹣1|的对称轴是x=1，满足条件．②，不满足条件①，y=cosπx中，当x=1时，y=cos（﹣π）=﹣1，此时函数关于x=1对称，满足条件②，当x=时，f（﹣）=cos（﹣π）=0，f（）=cos（π）=0，即此时满足f（﹣）=﹣f（），满足条件．①，故同时满足条件①②的函数是y=cosπx，故选：B．8．【解答】当x≤0时，a＜f（x）≤1+a，若a≥0，当x＞0时，f（x）=ln（x+a）≥lna，若方程f（x）=有两个不相等的实数根，则，即，得≤a＜，∵a≥0，∴0≤a＜，若a＜0，当x＞0时，f（x）=ln（x+a）∈R，即此时函数f（x）=有一个解，则当x≤0时，f（x）=有一个解即可，此时满足1+a≥＞a，即可，则﹣≤a＜0，综上﹣≤a＜，故选：A．二、填空题共6小题，每小题5分，共30分．9．【解答】lg2﹣lg+3lg5=3lg2+3lg5=3lg10=3．故答案为：3．10．【解答】∵sinα=，∴cos2α=1﹣2sin2α=1﹣2×=．故答案为：．11．【解答】函数y=f（x）的导函数有且仅有两个零点，其图象如图所示，x＜﹣1时，f′（x）＜0，x＞﹣1时，f′（x）≥0，所以函数只有在x=﹣1时取得极值．故答案为：﹣1．12．【解答】如图在正方形ABCD中，E是线段CD的中点，若=λ+μ===，所以，；故答案为：．13．【解答】∵在△ABC中，cosA=，∴sinA==，∵7a=3b，∴sinB==×=，∵B∈（0，π），∴B=或．故答案为：或．14．【解答】∵函数y=a+bsin（x+φ）（a，b为常数），∴当x==8时，sin（x+φ）取得最大或最小值，∴×8+φ=+kπ，k∈Z，解得φ=kπ﹣，k∈Z，又0＜φ＜，∴φ=；∴a﹣b=31，且a+bsinπ=13，解得a=13，b=﹣18；∴y=13﹣18sin（x+），当x=2时，y=13﹣18sin（×2+）=﹣5（°C）．故答案为：﹣5，．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程．15．【解答】（Ⅰ）∵函数f（x）=cos（2x﹣）﹣cos2x=（cos2x+sin2x）﹣cos2x=sin2x﹣cos2x=sin （2x﹣），∴f（0）=sin（0﹣）=﹣．（Ⅱ）由于函数f（x）=sin（2x﹣），故它的最小正周期为=π，令2kπ﹣≤2x﹣≤2kπ+，求得kπ﹣≤x≤kπ+，可得函数的单调递增区间为[kπ﹣，kπ+]，k∈Z．16．【解答】（Ⅰ）由数列{b n}满足b n﹣b n﹣1=a n，（n≥2，n∈N*），∴b2﹣b1=a2=﹣1，b1=b3=1，∴b2=0，a3=b3﹣b2=1，∵数列{a n}是等差数列，∴d=a3﹣a2=1﹣（﹣1）=2，∴a1=a2﹣d=﹣1﹣2=﹣3，a1的值﹣3；（Ⅱ）由（Ⅰ）可知数列{a n}是以﹣3为首项，以2为公差的等差数列，a n=﹣3+2（n﹣1）=2n﹣5，∴当n≥2时，b n﹣b n﹣1=2n﹣5，b n﹣1﹣b n﹣2=2（n﹣2）﹣5，…b2﹣b1=﹣1，将上述等式相加整理得：b n﹣b1=•（n﹣1）=n2﹣4n+3，∴b n=n2﹣4n+4，（n≥2），当n=1时，b1=1也满足，∴b n=n2﹣4n+4（n∈N*）．17．【解答】（Ⅰ）∵△ABC是等边三角形，∴AC=BC，又∵BC=2CD，∴AC=2CD，∴在△ACD 中，由正弦定理可得：，∴==．（Ⅱ）设CD=x，则BC=2x，∴BD=3x，∵△ABD中，AD=，AB=2x，∠B=，∴由余弦定理可得：AD2=AB2+BD2﹣2AB•BD•cos∠B，即：7=4x2+9x2﹣2x×3x，解得：x=1，∴CD=1．18．【解答】（Ⅰ）a=1时，f（x）=，x∈R，∴f′（x）=，令f′（x）＞0，解得：x＜2，令f′（x）＜0，解得：x＞2，∴f（x）在（﹣∞，2）递增，在（2，+∞）递减；（Ⅱ）由f（x）=得：f′（x）=，x∈[0，1]，令f′（x）=0，∵a＜0，解得：x=1+＜1，①1+≤0时，即﹣1≤a＜0时，f′（x）≥0对x∈[0，1]恒成立，∴f（x）在[0，1]递增，f（x）min=f（0）=﹣1；②当0＜1+＜1时，即a＜﹣1时，x，f′（x），f（x）在[0，1]上的情况如下：x 0 （0，1+）1+（1+，1）1f′（x）﹣0 + f（x）递减极小值递增∴f（x）min=f（1+）=；综上，﹣1≤a＜0时，f（x）min=﹣1，a＜﹣1时，f（x）min=．19．【解答】（Ⅰ）由﹣2，a1，a3成等差数列，∴2a1=﹣2+a3，∵{a n}是等比数列，a2=2，q＞0，∴a3=2q，a1==，代入整理得：q2﹣q﹣2=0，解得：q=2，q=﹣1（舍去），∴q=2，（Ⅱ）由（Ⅰ）a n=2n﹣1，b n=a n a n+2﹣λna n+1=4n﹣λn2n，由S1＞S2，∴S2﹣S1＜0，即b2＜0，∴42﹣2λ•22＜0，解得：λ＞2，S k＜S k+1（k=2，3，4，…）恒成立，b n=a n a n+2﹣λna n+1，即λ＜，设c k=（k≥2，k∈N*），只需要λ＜（c k）min（k≥2，k∈N*）即可，∵=×=＞1，∴数列{c n}在k≥2且k∈N*上单调递增，∴（c k）min=c2==，∴λ＜，∵λ＞2，∴λ∈（2，）．20．【解答】（Ⅰ）设f（x）与g（x）的交点坐标为（x0，y0），由，解得x0=﹣1或x0=3，解得a的值为：5或﹣27．（Ⅱ）令h（x）=x3﹣3x2﹣9x，则y=h（x）的图象在直线y=a下方的部分对应点的横坐标x∈（﹣∞，b），由h′（x）=3x2﹣6x﹣9=0，解得x的值．h′（x），h（x）的情况如下：x （﹣∞，﹣1）﹣1 （﹣1，3） 3 （3，+∞） h（x）+ 0 ﹣0 + h′（x）增极大值减极小值增因为h（a2+5）=（a2+5）（a4+7a2+1）＞a2+5≥2|a|≤a，即h（a2+5）＞a；h（﹣a2﹣2）=﹣（a2+2）（a4+7a2+1）＜﹣（a2+2）≤﹣2|a|≤a，即h（﹣a2﹣2）＜a，（或者：因为当x→+∞时，h（x）→+∞，当x→﹣∞时，h（x）→﹣∞），又因为：h（x）max=h（﹣1）=5，h（x）min=h（3）=﹣27．所以当a＞5或a≤﹣27满足条件．（Ⅲ）由（Ⅱ）h（x）=x3﹣3x2﹣9x，h′（x）=3x2﹣6x﹣9，则h′′（x）=6x﹣6，令6x﹣6=0，可知x=1，此时y=﹣11，函数h（x）的对称中心为：（1，﹣11），方程f（x）=g（x）有三个不同的解x1，x2，x3，且它们可以构成等差数列，实数a的值：﹣11．11 / 11。

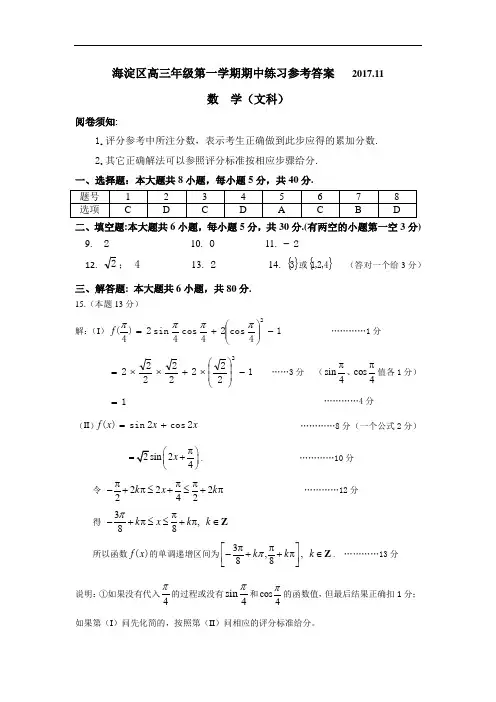
海淀区高三年级第一学期期中练习参考答案 2017.11数 学（文科）阅卷须知:1.评分参考中所注分数，表示考生正确做到此步应得的累加分数.2.其它正确解法可以参照评分标准按相应步骤给分. 一、选择题：本大题共8小题，每小题5分，共40分.二、填空题:本大题共6小题，每小题5分，共30分.(有两空的小题第一空3分) 9. 2 10. 0 11. 2- 12.2； 4 13. 2 14. {}3或{}4,2,1 （答对一个给3分）三、解答题: 本大题共6小题，共80分.15.（本题13分）解：（I ）14cos 24cos 4sin 2)4(2-⎪⎪⎭⎫⎝⎛+=ππππf …………1分1222222222-⎪⎪⎭⎫⎝⎛⨯+⨯⨯= ……3分 （sin 4π、cos 4π值各1分） 1= …………4分（II ）x x x f 2cos 2sin )(+= …………8分 （一个公式2分）24x π⎛⎫=+ ⎪⎝⎭. …………10分令 222242k x k πππ-+π≤+≤+π …………12分 得 3, 88k x k k ππ-+π≤≤+π∈Z 所以函数)(x f 的单调递增区间为3,, 88k k k πππ⎡⎤-++π∈⎢⎥⎣⎦Z . …………13分说明：①如果没有代入4π的过程或没有sin 4π和cos 4π的函数值，但最后结果正确扣1分；如果第（I ）问先化简的，按照第（II ）问相应的评分标准给分。

② （II)4x π-，参照上面步骤给分。

③求单调区间时，3, 88k x k k ππ-+π≤≤+π∈Z 正确，但没有写成区间形式、无k ∈Z ，只要居其一扣一分，不累扣。

16．（本题13分）解：（Ⅰ）设等比数列{}n a 的公比为q . 因为8321=a a a ，且2132a a a =所以832=a ，得22=a ， …………2分又因为35216a a q ==，所以38q = ，得2=q ，11=a . …………4分所以12-=n n a （∈n N +）， …………5分所以1(1)1n n a q S q-=- …………6分1212n-=-21n =- …………7分 （Ⅱ）因为nn a 21=+，所以n a b n n ==+12log ， …………9分 所以111)1(111+-=+=+n n n n b b n n . …………11分所以数列⎭⎬⎫⎩⎨⎧+11n n b b 的前n 项和 =n T ⎪⎪⎭⎫ ⎝⎛+-++⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫ ⎝⎛-1113121211n n …………12分 111+-=n 1+=n n. …………13分17．（本题13分）解：（Ⅰ）因为△ABD 为正三角形，//AC DB ，所以在△ABC 中，3BAC π∠=，所以()3ACB ABC π∠=π-+∠.所以sin sin()3ACB ABC π∠=+∠ …………1分 = sincos cos sin )33ABC ABC ππ∠+∠ …………3分 （一个公式2分） 因为在△ABC中，cos ABC ∠=，(0,)ABC ∠∈π …………4分所以sin ABC ∠=…………5分 所以sin ACB ∠=12=. …………6分 （Ⅱ）方法1：在△ABC 中，4AC =，由正弦定理得：sin sin AB ACACB ABC=∠∠， ……8分所以4sin 5sin AC ACBAB ABC∠===∠ …………9分 又在正△ABD 中，AB AD =， 3DAB π∠=， 所以在△ADC 中，3DAC 2π∠=， …………10分 由余弦定理得：DAC AD AC AD AC CD ∠⋅-+=cos 2222 …………12分1625245cos6132π=+-⨯⨯= 所以CD 的长为61. …………13分方法2：在△ABC 中，由正弦定理得：sin sin sin AB AC BCACB ABC BAC==∠∠∠， …………8分所以4sin 5sin AC ACBAB ABC∠===∠ , …………9分4sin sin 7AC BAC BC ABC ∠===∠ …………10分 所以12727=⨯-14=-. …………11分 在△DBC 中，由余弦定理得2222cos CD DB BC DB BC DBC =+-⨯⨯∠ …………12分252125()14=+-⨯-61=.所以CD 的长为61. …………13分18. （本题13分）解：（Ⅰ）由3()f x x x =-，得13)(2-='x x f , …………1分所以(1)2f '=，又(1)0f = …………3分所以曲线()y f x =在点(1,(1))f 处的切线方程为：()120-=-x y ，即：022=--y x . …………4分cos cos()DBC DBA ABC ∠=∠+∠cos cos sin sin DBA ABC DBA ABC =∠∠-∠∠（Ⅱ）令()0='x f ，得33±=x . …………5分 ()f x 与()f x '在区间[0,2]的情况如下：…………7分因为()00,f =()26,f = …………8分 所以函数)(x f 在区间[]2，0上的最大值为6. …………9分 （Ⅲ）证明：设()()()x g x f x h -==333+-x x ，则()()1132+-=-='x x x x h 33)(， …………10分 令()0h x '=，得1x =±.()h x 与()h x ' 随x 的变化情况如下：则()x h 的增区间为()1,-∞-，()+∞,1，减区间为()1,1-. …………11分又()110h =>，()()011>>h h -，所以函数)(x h 在()+∞,1-没有零点， ……12分 又()03<=-15-h ，所以函数)(x h 在()1,-∞-上有唯一零点0x . …………13分 综上，在()+∞∞-,上存在唯一的0x ，使得)()(00x g x f =.19.（本题14分）解：（Ⅰ） 341,3a a =-=5,365=-=a a ； …………2分（Ⅱ）设n n a b 2=，*N n ∈则2)1(222221=-=-=-++nn n n n a a b b ， …………4分所以{}n b 是以1为首项，2为公差的等差数列， …………5分 所以1(1)221n b n n =+-=- . …………6分（Ⅲ）解法1：2)1(2121212-=-=---+n n n a a ，*n ∈N ，所以{}12-n a 是以1为首项，2-为公差d 的等差数列， …………7分 所以数列{}n a 的前n 个奇数项之和为2122)1(n n d n n na -=-+ …………8分 由（Ⅱ）可知，122-=n a n ， 所以数列{}n a 的前n 个偶数项之和为()2222n na an =+ …………10分所以n S n 22=， …………11分 所以182182-=-n S n .因为22218(18)2n n S S ----=，且21816S -=-所以数列{}182-n S 是以16-为首项，2为公差的等差数列. …………12分 由0182182≤-=-n S n 可得9≤n ， …………13分 所以当8=n 或9=n 时，数列{}182-n S 的前n 项和n T 的最小值为72291698-=⨯-==T T . …………14分 解法二：由*22(1)()nn n a a n +=+-∈N 得22*2222(1)(,2)n n n a a n n --=+-∈≥N ①， …………7分 23*21232(1)(,2)n n n a a n n ---=+-∈≥N ②， …………8分把①②两个等式相加可得，2232212---+=+n n n n a a a a *(,2)n n ∈≥N，所以2212232212=+==+=+---a a a a a a n n n n . …………10分 所以数列{}n a 的前n 2项和n S n 22=， …………11分 （或：由*22(1)()nn n a a n +=+-∈N 得211(1)3(3)5......(23)(21)n S n n =++-++-+++-++- …………7分(11)[(1)3][(3)5]......[(23n n =++-++-+++-++- …………10分2n = …………11分） 所以182182-=-n S n .因为22218(18)2n n S S ----=，且21816S -=-所以数列{}182-n S 是以16-为首项，2为公差的等差数列. …………12分 由0182182≤-=-n S n 可得9≤n ， …………13分 所以当8=n 或9=n 时，数列{}182-n S 的前n 项和n T 的最小值为72291698-=⨯-==T T . …………14分20．（本题14分）（Ⅰ）证明：证法1：x x x x f ln )()(2-=的定义域为(0,)+∞ ……………1分 由x x x x f ln )()(2-= 得21'()(21)ln ()(21)ln 1f x x x x x x x x x=-+-=-+-， ……………2分 '(1)0f ∴=. ………………3分当1x >时，(21)ln 0,10x x x ->->，'()0f x ∴>，故()f x 在(1,)+∞上单调递增； ………………4分 当112x <<时，(21)ln 0,10x x x -<-<，'()0f x ∴<，故()f x 在1(,1)2上单调递减； ……………5分(此处为推理说明，若用列表说明则扣1分)所以1是函数()f x 的极值点. ………………6分证法2：（根据极值的定义直接证明）x x x x f ln )()(2-=的定义域为(0,)+∞ ……………1分()(1)ln f x x x x =- ， (1)0f ∴= ……………3分当1x >时，(1)0,ln 0,()0x x x f x ->>∴>，即()(1)f x f >； ………………4分 当01x <<时，(1)0,ln 0,()0x x x f x -<<∴>，即()(1)f x f >； ……………5分 根据极值的定义， 1是()f x 的极值点. ………………6分 （Ⅱ）由题意可知，1ln )12()(-+-=x x x x g 证法1：1'()2ln 3,(0,)g x x x x=-+∈+∞， 令1()2ln 3,(0,)h x x x x=-+∈+∞， 222121'()0x h x x x x+∴=+=>，故()h x 在(0,)+∞上单调递增. ………………7分 又1(1)20,()1ln 4ln 024eh h =>=-=<，又()h x 在(0,)+∞上连续，01(,1)2x ∴∃∈使得0()0h x =，即0'()0g x =， ………………8分∴0012ln 30x x -+=.（*） ………………9分 '(),()g x g x 随x 的变化情况如下：………………10分∴min 0000()()(21)ln 1g x g x x x x ==-+-. ………………11分由（*）式得0013ln 22x x =-，代入上式得 min 0000001313()()(21)()122222g x g x x x x x x ==--+-=--+. ………………12分 令131()2,(,1)222t x x x x =--+∈， 221(12)(12)'()2022x x t x x x +-=-=<，故()t x 在1(,1)2上单调递减. ………………13分()(1)t x t ∴>，又(1)1t =-，()1t x ∴>-.即0()1g x >- ()1g x ∴>-. ………………14分 证法2：()(21)ln 12ln ln 1,(0,)g x x x x x x x x x =-+-=-+-∈+∞，令()2ln ,()ln 1,(0,)h x x x t x x x x ==-+-∈+∞， ………………7分'()2(ln 1)h x x =+，令'()0h x =得1x e=. ………………8分'(),()h x h x 随x 的变化情况如下：min 12()()h x h e e ∴==-，即22ln x x e ≥-，当且仅当1x e =时取到等号.………………10分1'()x t x x-=，令'()0t x =得1x =. ………………11分 '(),()t x t x 随x 的变化情况如下：………………12分min ()(1)0t x t ∴==，即1ln 0x x --≥，当且仅当1x =时取到等号. ………………13分 22ln (ln 1)1x x x x e∴+-+->->-. 即()1g x >-. ………………14分。

海淀区高三年级第一学期期中练习数 学（理科）本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上 作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 已知集合{2}A x x =>，{(1)(3)0}B x x x =--<，则AB =A. {1}x x >B. {23}x x <<C. {13}x x <<D. {2x x >或1}x < 2. 已知向量(1,2),(2,4)=-=-a b ，则与b A. 垂直 B. 不垂直也不平行 C. 平行且同向 D. 平行且反向3. 函数222x xy =+的最小值为 A. 1B. 2C. D. 44. 已知命题:p 0c ∃>，方程20x x c -+= 有解，则p ⌝为 A. 0c ∀>，方程20x x c -+=无解 B. c ∀≤0，方程20x x c -+=有解 C. 0c ∃>，方程20x x c -+=无解 D. c ∃≤0，方程20x x c -+=有解5. 已知函数,,log xbc y a y x y x ===的图象如图所示，则A. a b c >>B. a c b >>C. c a b >>D. c b a >> 6. 设,a b 是两个向量，则“+>-a b a b ”是“0⋅>a b ”的A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 已知函数42()cos sin f x x x =+，下列结论中错误．．的是A. ()f x 是偶函数B. 函数()f x 最小值为34C. π2是函数()f x 的一个周期 D. 函数()f x 在π0,2（）内是减函数8．如图所示，A 是函数()2x f x =的图象上的动点，过点A 作直线平行于x 轴，交函数2()2x g x +=的图象于点B ，若函数()2x f x =的图象上存在点C 使得ABC ∆为等边三角形，则称A 为函数()2xf x =上的好位置点. 函数()2xf x =上的好位置点的个数为A. 0B. 1C. 2D. 大于2第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

2016-2017学年北京四中高三（上）期中数学试卷（文科）一、选择题：本大题共8小题，每小题5分，共40分1．若集合A={1，2，3}，B={0，1，2}，则A∩B=（）A．{0，1，2，3}B．{0，1，2}C．{1，2}D．{1，2，3}2．设a=log32，b=log2，c=，则（）A．a＞b＞c B．c＞b＞a C．a＞c＞b D．c＞a＞b3．“数列{a n}既是等差数列又是等比数列”是“数列{a n}是常数列”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件4．若x，y满足，则z=x+2y的最大值为（）A．0 B．1 C．D．25．从A，B，C，D，E5名学生中随机选出2人，A被选中的概率为（）A．B．C．D．6．下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（）A．y=x B．y=lgx C．y=2x D．y=7．执行如图所示的程序框图，输出的k值为（）A．3 B．4 C．5 D．68．函数f（x）=2sin（ωx+φ）（ω＞0，﹣＜φ＜）的部分图象如图所示，则ω，φ的值分别是（）A．B．C．D．二、填空题：本大题共6小题，每小题5分，共30分9．设命题p：∃n∈N，n2＞2n，则￢p为．10．i是虚数单位，则=．11．已知数列{a n}中，a1=1，a n=a n+（n≥2），则数列{a n}的前9项和等于．﹣112．函数y=x+lnx在点（1，1）处的切线方程为．13．△ABC中，角A，B，C所对的边分别为a，b，c．若a=3，b=2，cos（A+B）=，则边c=．14．设函数f（x）=，①若a=1，则f（x）的最小值为；②若f（x）恰有2个零点，则实数a的取值范围是．三、解答题：本大题共6小题，共80分.解答应写出文字说明，验算步骤或证明过程.15．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知asin2B=bsinA．（1）求B；（2）已知cosA=，求sinC的值．16．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．（1）估计顾客同时购买乙和丙的概率；（2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；（3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？17．已知：函数f（x）=2x+sin2x．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）的单调递增区间；（Ⅲ）把函数y=f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移个单位，得到函数y=g（x）的图象，求的值．18．已知函数f（x）=（ax2+bx+c）e x（a＞0）的导函数y=f′（x）的两个零点为﹣3和0．（Ⅰ）求f（x）的单调区间；（Ⅱ）若f（x）的极小值为﹣1，求f（x）的极大值．19．已知：f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若a，b∈[﹣1，1]，且a+b≠0时，有＞0恒成立．（Ⅰ）用定义证明函数f（x）在[﹣1，1]上是增函数；（Ⅱ）解不等式：＜f（1﹣x）；（Ⅲ）若f（x）≤m2﹣2m+1对所有x∈[﹣1，1]恒成立，求：实数m的取值范围．20．对于无穷数列{a n}与{b n}，记A={x|x=a n，n∈N*}，B={x|x=b n，n∈N*}，若同时满足条件：①{a n}，{b n}均单调递增；②A∩B=∅且A∪B=N*，则称{a n}与{b n}是无穷互补数列．（1）若a n=2n﹣1，b n=4n﹣2，判断{a n}与{b n}是否为无穷互补数列，并说明理由；（2）若a n=2n且{a n}与{b n}是无穷互补数列，求数量{b n}的前16项的和；（3）若{a n}与{b n}是无穷互补数列，{a n}为等差数列且a16=36，求{a n}与{b n}的通项公式．2016-2017学年北京四中高三（上）期中数学试卷（文科）参考答案与试题解+析一、选择题：本大题共8小题，每小题5分，共40分1．若集合A={1，2，3}，B={0，1，2}，则A∩B=（）A．{0，1，2，3}B．{0，1，2}C．{1，2}D．{1，2，3}【考点】交集及其运算．【分析】利用交集定义求解．【解答】解：∵集合A={1，2，3}，B={0，1，2}，∴A∩B={1，2}．故选：C．2．设a=log32，b=log2，c=，则（）A．a＞b＞c B．c＞b＞a C．a＞c＞b D．c＞a＞b【考点】对数值大小的比较．【分析】利用对数函数的单调性即可得出．【解答】解：∵a=log32∈（0，1），b=log2＜0，c=＞1，则c＞a＞b，故选：D．3．“数列{a n}既是等差数列又是等比数列”是“数列{a n}是常数列”的（）A．充分不必要条件 B．必要不充分条件C．充要条件D．既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断．【分析】根据等比数列和等差数列的性质结合充分条件和必要条件的定义进行判断即可．【解答】解：若数列{a n}既是等差数列又是等比数列，则数列{a n}为常数列，且a n ≠0，则反之当a n=0时，满足数列{a n}为常数列，但数列{a n}不是等比数列，即“数列{a n}既是等差数列又是等比数列”是“数列{a n}是常数列”的充分不必要条件，故选：A4．若x，y满足，则z=x+2y的最大值为（）A．0 B．1 C．D．2【考点】简单线性规划．【分析】作出题中不等式组表示的平面区域，再将目标函数z=x+2y对应的直线进行平移，即可求出z取得最大值．【解答】解：作出不等式组表示的平面区域，当l经过点B时，目标函数z达到最大值2×1=2．∴z最大值=0+故选：D．5．从A，B，C，D，E5名学生中随机选出2人，A被选中的概率为（）A．B．C．D．【考点】列举法计算基本事件数及事件发生的概率．【分析】先求出基本事件总数n=，再求出A被选中包含的基本事件个数m==4，由此能求出A被选中的概率．【解答】解：从A，B，C，D，E5名学生中随机选出2人，基本事件总数n=，A被选中包含的基本事件个数m==4，∴A被选中的概率为p=．故选：B．6．下列函数中，其定义域和值域分别与函数y=10lgx的定义域和值域相同的是（）A．y=x B．y=lgx C．y=2x D．y=【考点】对数函数的定义域；对数函数的值域与最值．【分析】分别求出各个函数的定义域和值域，比较后可得答案．【解答】解：函数y=10lgx的定义域和值域均为（0，+∞），函数y=x的定义域和值域均为R，不满足要求；函数y=lgx的定义域为（0，+∞），值域为R，不满足要求；函数y=2x的定义域为R，值域为R（0，+∞），不满足要求；函数y=的定义域和值域均为（0，+∞），满足要求；故选：D7．执行如图所示的程序框图，输出的k值为（）A．3 B．4 C．5 D．6【考点】程序框图．【分析】模拟执行程序框图，依次写出每次循环得到的a，k的值，当a=时满足条件a＜，退出循环，输出k的值为4．【解答】解：模拟执行程序框图，可得k=0，a=3，q=a=，k=1不满足条件a＜，a=，k=2不满足条件a＜，a=，k=3不满足条件a＜，a=，k=4满足条件a＜，退出循环，输出k的值为4．故选：B．8．函数f（x）=2sin（ωx+φ）（ω＞0，﹣＜φ＜）的部分图象如图所示，则ω，φ的值分别是（）A．B．C．D．【考点】y=Asin（ωx+φ）中参数的物理意义．【分析】根据函数在同一周期内的最大值、最小值对应的x值，求出函数的周期T==π，解得ω=2．由函数当x=时取得最大值2，得到+φ=+kπ（k∈Z），取k=0得到φ=﹣．由此即可得到本题的答案．【解答】解：∵在同一周期内，函数在x=时取得最大值，x=时取得最小值，∴函数的周期T满足=﹣=，由此可得T==π，解得ω=2，得函数表达式为f（x）=2sin（2x+φ）又∵当x=时取得最大值2，∴2sin（2•+φ）=2，可得+φ=+2kπ（k∈Z）∵，∴取k=0，得φ=﹣故选：A．二、填空题：本大题共6小题，每小题5分，共30分9．设命题p：∃n∈N，n2＞2n，则￢p为∀n∈N，n2≤2n．【考点】命题的否定．【分析】根据特称命题的否定是全称命题进行求解即可．【解答】解：命题是特称命题，则命题的否定是“∀n∈N，n2≤2n”，故答案为：“∀n∈N，n2≤2n”10．i是虚数单位，则=1﹣i．【考点】虚数单位i及其性质．【分析】先进行复数的除法运算，分子和分母同乘以分母的共轭复数，分子和分母再进行复数的除法运算，整理成最简形式．【解答】解：∵===1﹣i，∴=1﹣i，故答案为：1﹣i11．已知数列{a n}中，a1=1，a n=a n+（n≥2），则数列{a n}的前9项和等于27．﹣1【考点】数列递推式．【分析】通过a n=a n﹣1+（n≥2）可得公差，进而由求和公式即得结论．【解答】解：∵a n=a n﹣1+（n≥2），=（n≥2），∴a n﹣a n﹣1∴数列{a n}的公差d=，又a1=1，∴a n=1+（n﹣1）=，∴S9=9a1+•d=9+36×=27，故答案为：27．12．函数y=x+lnx在点（1，1）处的切线方程为2x﹣y﹣1=0．【考点】利用导数研究曲线上某点切线方程．【分析】由y=x+1nx，知，由此能求出函数y=x+1nx在点（1，1）处的切线方程．【解答】解：∵y=x+1nx，∴，∴k=y′|x=1=1+1=2，∴函数y=x+1nx在点（1，1）处的切线方程为y﹣1=2（x﹣1），整理，得2x﹣y﹣1=0．故答案为：2x﹣y﹣1=0．13．△ABC中，角A，B，C所对的边分别为a，b，c．若a=3，b=2，cos（A+B）=，则边c=．【考点】正弦定理．【分析】由已知利用三角形内角和定理，诱导公式可求cosC，进而利用余弦定理即可计算得解．【解答】解：∵cos（A+B）=cos（π﹣C）=，可得：cosC=﹣，又∵a=3，b=2，∴由余弦定理可得：c===．故答案为：．14．设函数f（x）=，①若a=1，则f（x）的最小值为﹣1；②若f（x）恰有2个零点，则实数a的取值范围是≤a＜1或a≥2．【考点】函数的零点；分段函数的应用．【分析】①分别求出分段的函数的最小值，即可得到函数的最小值；②分别设h（x）=2x﹣a，g（x）=4（x﹣a）（x﹣2a），分两种情况讨论，即可求出a的范围．【解答】解：①当a=1时，f（x）=，当x＜1时，f（x）=2x﹣1为增函数，f（x）＞﹣1，当x＞1时，f（x）=4（x﹣1）（x﹣2）=4（x2﹣3x+2）=4（x﹣）2﹣1，当1＜x＜时，函数单调递减，当x＞时，函数单调递增，故当x=时，f（x）min=f（）=﹣1，②设h（x）=2x﹣a，g（x）=4（x﹣a）（x﹣2a）若在x＜1时，h（x）=与x轴有一个交点，所以a＞0，并且当x=1时，h（1）=2﹣a＞0，所以0＜a＜2，而函数g（x）=4（x﹣a）（x﹣2a）有一个交点，所以2a≥1，且a＜1，所以≤a＜1，若函数h（x）=2x﹣a在x＜1时，与x轴没有交点，则函数g（x）=4（x﹣a）（x﹣2a）有两个交点，当a≤0时，h（x）与x轴无交点，g（x）无交点，所以不满足题意（舍去），当h（1）=2﹣a≤0时，即a≥2时，g（x）的两个交点满足x1=a，x2=2a，都是满足题意的，综上所述a的取值范围是≤a＜1，或a≥2．三、解答题：本大题共6小题，共80分.解答应写出文字说明，验算步骤或证明过程.15．在△ABC中，内角A，B，C所对的边分别为a，b，c，已知asin2B=bsinA．（1）求B；（2）已知cosA=，求sinC的值．【考点】解三角形．【分析】（1）利用正弦定理将边化角即可得出cosB；（2）求出sinA，利用两角和的正弦函数公式计算．【解答】解：（1）∵asin2B=bsinA，∴2sinAsinBcosB=sinBsinA，∴cosB=，∴B=．（2）∵cosA=，∴sinA=，∴sinC=sin（A+B）=sinAcosB+cosAsinB==．16．某超市随机选取1000位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．（1）估计顾客同时购买乙和丙的概率；（2）估计顾客在甲、乙、丙、丁中同时购买3种商品的概率；（3）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中哪种商品的可能性最大？【考点】相互独立事件的概率乘法公式．【分析】（1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，从而求得顾客同时购买乙和丙的概率．（2）根据在甲、乙、丙、丁中同时购买3种商品的有300人，求得顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率．（3）在这1000名顾客中，求出同时购买甲和乙的概率、同时购买甲和丙的概率、同时购买甲和丁的概率，从而得出结论．【解答】解：（1）从统计表可得，在这1000名顾客中，同时购买乙和丙的有200人，故顾客同时购买乙和丙的概率为=0.2．（2）在这1000名顾客中，在甲、乙、丙、丁中同时购买3种商品的有100+200=300（人），故顾客顾客在甲、乙、丙、丁中同时购买3种商品的概率为=0.3．（3）在这1000名顾客中，同时购买甲和乙的概率为=0.2，同时购买甲和丙的概率为=0.6，同时购买甲和丁的概率为=0.1，故同时购买甲和丙的概率最大．17．已知：函数f（x）=2x+sin2x．（Ⅰ）求f（x）的最小正周期；（Ⅱ）求f（x）的单调递增区间；（Ⅲ）把函数y=f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），再把得到的图象向左平移个单位，得到函数y=g（x）的图象，求的值．【考点】函数y=Asin（ωx+φ）的图象变换；三角函数中的恒等变换应用；正弦函数的图象．【分析】（Ⅰ）利用三角函数恒等变换的应用化简函数解+析式为f（x）=，进而利用周期公式即可计算得解．（Ⅱ）由（k∈Z），即可解得f（x）的单调递增区间．（Ⅲ）利用函数y=Asin（ωx+φ）的图象变换的规律可求，进而利用特殊角的三角函数值即可计算得解．【解答】（本题满分为13分）解：===，…（Ⅰ）；…（Ⅱ）由（k∈Z），得（k ∈Z），则f（x）的单调递增区间是（k∈Z）；…（Ⅲ）函数y=f（x）的图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到函数的图象，再把得到的图象向左平移个单位得到函数的图象，即，则．…18．已知函数f（x）=（ax2+bx+c）e x（a＞0）的导函数y=f′（x）的两个零点为﹣3和0．（Ⅰ）求f（x）的单调区间；（Ⅱ）若f（x）的极小值为﹣1，求f（x）的极大值．【考点】利用导数研究函数的极值；导数的运算；利用导数研究函数的单调性．【分析】（Ⅰ）f'（x）=[ax2+（2a+b）x+b+c]e x．令g（x）=ax2+（2a+b）x+b+c，简化运算；（Ⅱ）由f（x）的极小值为﹣1确定参数值，通过导数求极大值．【解答】解：（Ⅰ）f'（x）=（2ax+b）e x+（ax2+bx+c）e x=[ax2+（2a+b）x+b+c]e x．令g（x）=ax2+（2a+b）x+b+c，∵e x＞0，∴y=f'（x）的零点就是g（x）=ax2+（2a+b）x+b+c的零点，且f'（x）与g（x）符号相同．又∵a＞0，∴当x＜﹣3，或x＞0时，g（x）＞0，即f'（x）＞0，当﹣3＜x＜0时，g（x）＜0，即f'（x）＜0，∴f（x）的单调增区间是（﹣∞，﹣3），（0，+∞），单调减区间是（﹣3，0）．（Ⅱ）由（Ⅰ）知，x=0是f（x）的极小值点，所以有解得a=1，b=1，c=﹣1．所以函数的解+析式为f（x）=（x2+x﹣1）e x．又由（Ⅰ）知，f（x）的单调增区间是（﹣∞，﹣3），（0，+∞），单调减区间是（﹣3，0）．所以，函数f（x）的极大值为．19．已知：f（x）是定义在[﹣1，1]上的奇函数，且f（1）=1，若a，b∈[﹣1，1]，且a+b≠0时，有＞0恒成立．（Ⅰ）用定义证明函数f（x）在[﹣1，1]上是增函数；（Ⅱ）解不等式：＜f（1﹣x）；（Ⅲ）若f（x）≤m2﹣2m+1对所有x∈[﹣1，1]恒成立，求：实数m的取值范围．【考点】奇偶性与单调性的综合；函数恒成立问题．【分析】（Ⅰ）设任意x1，x2∈[﹣1，1]，且x1＜x2，由奇函数的性质化简f（x2）﹣f（x1），由得，判断出符号后，由函数单调性的定义证明结论成立；（Ⅱ）根据函数的单调性和定义域列出不等式，求出不等式的解集；（Ⅲ）由函数的单调性求出f（x）的最大值，由恒成立列出不等式，求出实数m 的取值范围．【解答】证明：（Ⅰ）设任意x1，x2∈[﹣1，1]，且x1＜x2，∵f（x）是定义在[﹣1，1]上的奇函数，∴f（x2）﹣f（x1）=f（x2）+f（﹣x1）∵x1＜x2，∴x2+（﹣x1）≠0，由题意知，，则，∵x2+（﹣x1）=x2﹣x1＞0，∴f（x2）+f（﹣x1）＞0，即f（x2）＞f（x1），∴函数f（x）在[﹣1，1]上是增函数．…解：（Ⅱ）由（Ⅰ）和不等式得，，解得，∴不等式的解集是[0，）…（Ⅲ）由（Ⅰ）得，f（x）最大值为f（1）=1，所以要使f（x）≤m2﹣2m+1对所有x∈[﹣1，1]，只需1≤m2﹣2m+1恒成立，解得m≤0或m≥2，得实数m的取值范围为m≤0或m≥2．…20．对于无穷数列{a n}与{b n}，记A={x|x=a n，n∈N*}，B={x|x=b n，n∈N*}，若同时满足条件：①{a n}，{b n}均单调递增；②A∩B=∅且A∪B=N*，则称{a n}与{b n}是无穷互补数列．（1）若a n=2n﹣1，b n=4n﹣2，判断{a n}与{b n}是否为无穷互补数列，并说明理由；（2）若a n=2n且{a n}与{b n}是无穷互补数列，求数量{b n}的前16项的和；（3）若{a n}与{b n}是无穷互补数列，{a n}为等差数列且a16=36，求{a n}与{b n}的通项公式．【考点】数列的应用；数列的求和．【分析】（1）{a n}与{b n}不是无穷互补数列．由4∉A，4∉B，4∉A∪B=N*，即可判断；（2）由a n=2n，可得a4=16，a5=32，再由新定义可得b16=16+4=20，运用等差数列的求和公式，计算即可得到所求和；（3）运用等差数列的通项公式，结合首项大于等于1，可得d=1或2，讨论d=1，2求得通项公式，结合新定义，即可得到所求数列的通项公式．【解答】解：（1）{a n}与{b n}不是无穷互补数列．理由：由a n=2n﹣1，b n=4n﹣2，可得4∉A，4∉B，即有4∉A∪B=N*，即有{a n}与{b n}不是无穷互补数列；（2）由a n=2n，可得a4=16，a5=32，由{a n}与{b n}是无穷互补数列，可得b16=16+4=20，即有数列{b n}的前16项的和为（1+2+3+…+20）﹣（2+4+8+16）=×20﹣30=180；（3）设{a n}为公差为d（d为正整数）的等差数列且a16=36，则a1+15d=36，由a1=36﹣15d≥1，可得d=1或2，若d=1，则a1=21，a n=n+20，b n=n（1≤n≤20），与{a n}与{b n}是无穷互补数列矛盾，舍去；若d=2，则a1=6，a n=2n+4，b n=．综上可得，a n=2n+4，b n=．2017年2月13日。

海淀区高三年级第一学期期末练习数学（文科） 2017.1本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 复数i(2i)-在复平面内对应的点的坐标为 A.(2,1)- B.(2,1)- C.(1,2) D.(1,2)-2. 抛物线22y x =的焦点到准线的距离为 A.12B.1C.2D.33. 下列函数中，既是偶函数又在区间(0+)∞，上单调递增的是 A.1()2x y = B.2y x =- C.2log y x = D.||1y x =+ 4. 已知向量a,b 满足2-0a b =，()2-⋅=a b b ，则=|b | A. 12B. 1C. D.2 5. 右侧程序框图所示的算法来自于《九章算术》.若输入a 的值为16，b 的值为24，则执行该程序框图输出的结果为 A. 6 B. 7 C. 8 D. 96. 在ABC ∆中，“30A <︒”是“1sin 2A <”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 7.C.28. 如图，已知正方体1111ABCD A B C D -的棱长为1，,E F 分别是棱11,AD B C 上的动点，设1,A E x B F y ==.若棱．1DD 与平面BEF 有公共点，则x y +的取值范围是 A.[0,1] B.13[,]22C.[1,2]D. 3[,2]2二、填空题共6小题，每小题5分，共30分。

9. 已知双曲线C :2214y x -=，则双曲线C 的一条渐近线的方程为___.10.已知数列{}n a 满足12,,n n a a n +-=∈*N 且33a =，则1a =____，其前n 项和n S =___. 11.已知圆C :2220x y x +-=，则圆心C 的坐标为___，圆C 截直线y x =的弦长为___. 12.已知,x y 满足04,03,28,x y x y ≤≤⎧⎪≤≤⎨⎪+≤⎩则目标函数2z x y =+的最大值为____.13如图所示，点D 在线段AB 上，30CAD ∠= ，50CDB ∠= . 给出下列三组条件（给出线段的长度）:①,AD DB ；②,AC DB ；③,CD DB .其中，能使ABC ∆唯一确定的条件的序号为____.（写出所有所和要求的条件的序号） 14.已知A 、B 两所大学的专业设置都相同（专业数均不小于2），数据显示，A 大学的各专业的男女生比例均高于B 大学的相应专业的男女生比例（男女生比例是指男生人数与女生人数的比）.据此，甲同学说：“A 大学的男女生比例一定高于B 大学的男女生比例”；乙同学说：“A 大学的男女生比例不一定高于B 大学的男女生比例”；丙同学说：“两所大学的全体学生的男女生比例一定高于B 大学的男女生比例”.其中，说法正确的同学是____.三、解答题共6小题，共80分。

海淀区高三年级第一学期期中练习数 学（理科）本试卷共4页，150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上 作答无效。

考试结束后，将本试卷和答题卡一并交回。

第一部分（选择题 共40分）一、选择题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

1. 已知集合{2}A x x =>，{(1)(3)0}B x x x =--<，则AB =A. {1}x x >B. {23}x x <<C. {13}x x <<D. {2x x >或1}x < 2. 已知向量(1,2),(2,4)=-=-a b ，则与b A. 垂直 B. 不垂直也不平行 C. 平行且同向 D. 平行且反向3. 函数222x xy =+的最小值为 A. 1B. 2C. D. 44. 已知命题:p 0c ∃>，方程20x x c -+= 有解，则p ⌝为 A. 0c ∀>，方程20x x c -+=无解 B. c ∀≤0，方程20x x c -+=有解 C. 0c ∃>，方程20x x c -+=无解 D. c ∃≤0，方程20x x c -+=有解5. 已知函数,,log xbc y a y x y x ===的图象如图所示，则A. a b c >>B. a c b >>C. c a b >>D. c b a >> 6. 设,a b 是两个向量，则“+>-a b a b ”是“0⋅>a bA. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件7. 已知函数42()cos sin f x x x =+，下列结论中错误．．的是A. ()f x 是偶函数B. 函数()f x 最小值为34C. π2是函数()f x 的一个周期 D. 函数()f x 在π0,2（）内是减函数8．如图所示，A 是函数()2x f x =的图象上的动点，过点A 作直线平行于x 轴，交函数2()2x g x +=的图象于点B ，若函数()2x f x =的图象上存在点C 使得ABC ∆为等边三角形，则称A 为函数()2xf x =上的好位置点. 函数()2x f x =上的好位置点的个数为 A. 0 B. 1 C. 2 D. 大于2第二部分（非选择题 共110分）二、填空题共6小题，每小题5分，共30分。

海淀区高三年级第一学期期末练习数学（文科） 2017.1本试卷共4页，150分．考试时长120分钟．考生务必将答案答在答题卡上，在试卷上 作答无效．考试结束后，将本试卷和答题卡一并交回．一、选择题共8小题，每小题5分，共40分．在每小题列出的四个选项中，选出符合题目要求的一项．1．复数i(2i)-在复平面内对应的点的坐标为A ．(2,1)-B ．(2,1)-C ．(1,2)D ．(1,2)-2．抛物线22y x =的焦点到准线的距离为A ．12B ．1C ．2D ．33．下列函数中，既是偶函数又在区间(0+)∞，上单调递增的是 A ．1()2x y =B ．2y x =-C ．2log y x =D ．||1y x =+4．已知向量a,b 满足2-0a b =，()2-⋅=a b b ，则=|b |A ．12B ．1CD ．25．右侧程序框图所示的算法来自于《九章算术》.若输入a 的值为16，b 的值为24，则执行该程序框图输出的结果为A ．6B ．7C ．8D ．96．在ABC ∆中，“30A <︒”是“1sin 2A <”的 A ．充分而不必要条件B ．必要而不充分条件C ．充分必要条件D ．既不充分也不必要条件7．已知某四棱锥的三视图如右图所示，则该几何体的体积为ABC ．2D8．如图，已知正方体1111ABCD A B C D -的棱长为1，,E F 分别是棱11,AD B C 上的动点，设1,AE x B F y ==． 若棱．1DD 与平面BEF 有公共点，则x y +的取值范围是 A ．[0,1] B ．13[,]22 C ．[1,2]D ．3[,2]2二、填空题共6小题，每小题5分，共30分．9．已知双曲线C :2214y x -=，则双曲线C 的一条渐近线的方程为________．10．已知数列{}n a 满足12,,n n a a n +-=∈*N 且33a =，则1a =____，其前n 项和n S =____． 11．已知圆C :2220x y x +-=，则圆心C 的坐标为_____，圆C 截直线y x =的弦长为____． 12．已知,x y 满足04,03,28,x y x y ≤≤⎧⎪≤≤⎨⎪+≤⎩则目标函数2z x y =+的最大值为________．13．如图所示，点D 在线段AB 上，30CAD ∠=，50CDB ∠=．给出下列三组条件（给出线段的长度）： ①,AD DB ； ②,AC DB ； ③,CD DB ．其中，能使ABC ∆唯一确定的条件的序号为____．（写出所有所和AD BCABCD1D 1A 1B 1C E F主视图俯视图要求的条件的序号）14．已知A 、B 两所大学的专业设置都相同（专业数均不小于2），数据显示，A 大学的各专业的男女生比例均高于B 大学的相应专业的男女生比例（男女生比例是指男生人数与女生人数的比）． 据此，甲同学说：“A 大学的男女生比例一定高于B 大学的男女生比例”； 乙同学说：“A 大学的男女生比例不一定高于B 大学的男女生比例”；丙同学说：“两所大学的全体学生的男女生比例一定高于B 大学的男女生比例”． 其中，说法正确的同学是________．三、解答题共6小题，共80分．解答应写出文字说明、演算步骤或证明过程． 15．（本小题满分13分）已知数列{}n a 是各项均为正数的等比数列，且21a =，346a a +=． （Ⅰ）求数列{}n a 的通项公式；（Ⅱ）设数列{}n a n -的前n 项和为n S ，比较4S 和5S 的大小，并说明理由．16．（本小题满分13分）已知函数2sin 22cos ()cos x xf x x+=．（Ⅰ）求()f x 的定义域及π()4f 的值；（Ⅱ）求()f x 在π(0,)2上的单调递增区间．17．（本小题满分13分）诚信是立身之本，道德之基．某校学生会创设了“诚信水站”，既便于学生用水，又推进诚信教育，并用“周实际回收水费周投入成本”表示每周“水站诚信度”．为了便于数据分析，以四周为一个周期，下表为该水站连续八周（共两个周期）的诚信度数据统计，如表1：表1第一周 第二周 第三周 第四周 第一个周95%98%92%88%期第二个周期94% 94% 83% 80%（Ⅰ）计算表1中八周水站诚信度的平均数x；（Ⅱ）从表1诚信度超过91%的数据中，随机抽取2个，求至少有1个数据出现在第二个周期的概率；（Ⅲ）学生会认为水站诚信度在第二个周期中的后两周出现了滑落，为此学生会举行了“以诚信为本”主题教育活动，并得到活动之后一个周期的水站诚信度数据，如表2：表2第一周第二周第三周第四周第三个周期85% 92% 95% 96% 请根据提供的数据，判断该主题教育活动是否有效，并根据已有数据说明理由．18．（本小题满分14分）如图，在四棱锥P ABCD中，PD⊥底面ABCD，AB//DC, CD=2AB, AD⊥CD，E为棱PD的中点．（Ⅰ）求证：CD⊥AE；（Ⅱ）求证：平面PAB⊥平面PAD；（Ⅲ）试判断PB与平面AEC是否平行？并说明理由．19．（本小题满分13分）PA BC DE已知椭圆2222:1(0)x y G a b a b+=>>直线l 过椭圆G 的右顶点(2,0)A ，且交椭圆G于另一点C ．（Ⅰ）求椭圆G 的标准方程；（Ⅱ）若以AC 为直径的圆经过椭圆G 的上顶点B ，求直线l 的方程．20．（本小题满分14分）已知函数ln 1()x f x x+=． （Ⅰ）求曲线()y f x =在函数()f x 零点处的切线方程； （Ⅱ）求函数()y f x =的单调区间；（Ⅲ）若关于x 的方程()f x a =恰有两个不同的实根12,x x ，且12x x <，求证：2111x x a->-．海淀区高三年级第一学期期末练习数学（文科）答案及评分标准2017.1一、选择题共8小题，每小题5分，共40分。