
密克定理是几何学中关于相交圆的定理。1838年,奥古斯特·密克叙述并证明了数条相关定理。许多有用的定理可由其推出。
1. 定理陈述
三圆定理:设三个圆21,C C ,3C 交于一点O ,而P N M ,,,
分别是1C 和2C ,2C 和3C , 3C 和1C 的另一交点。设A 为1C 的点,直线MA 交2C 于B ,直线PA 交3C 于C 。那么B, N,C 这三点共线。
逆定理:如果△ABC 是三角形,M, N,P 三点分别在边AB, BC,CA 上,那么三角形△APM, △BMN, △CNP 的外接圆交于一点O 。
完全四线形定理:如果ABCDEF 是完全四线形,那么三角形△EAD, △EBC,△FAB △FDC 的外接圆交于一点O ,称为密克点。
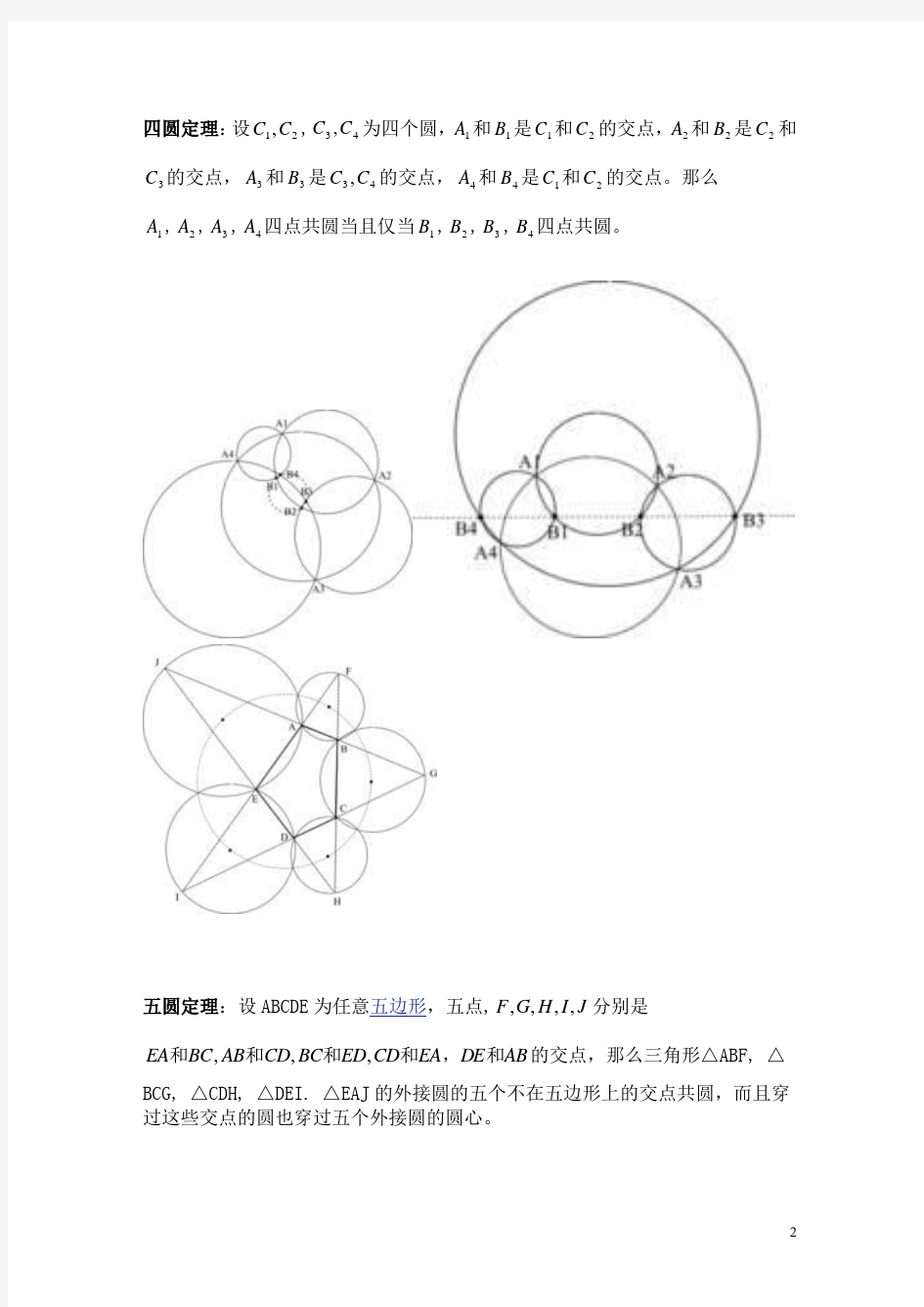
四圆定理:设21,C C ,43,C C 为四个圆,1A 和1B 是1C 和2C 的交点,2A 和2B 是2C 和3C 的交点,3A 和3B 是43,C C 的交点,4A 和4B 是1C 和2C 的交点。那么1A ,2A ,3A ,4A 四点共圆当且仅当1B ,2B ,3B ,4B 四点共圆。
五圆定理:设ABCDE 为任意五边形,五点,J I H G F ,,,,分别是
AB DE EA CD ED BC CD AB BC EA 和,和和和和,,,的交点,那么三角形△ABF, △BCG, △CDH, △DEI. △EAJ 的外接圆的五个不在五边形上的交点共圆,而且穿过这些交点的圆也穿过五个外接圆的圆心。
逆定理:设21,C C ,43,C C 5C 五个圆的圆心都在圆上C ,相邻的圆交于C 上,那么把它们不在C 上的交点与比邻同样的点连起来,所成的五条直线相交于这五个圆上。
葛尔刚点:△ABC 的内切圆分别切边AB 、BC 、CA 于F 、D 、E ,则AD 、BE 、CF 三线共点,此点即为葛尔刚点
牛顿定理1
R,L,Q共线
QL/LR=EA/AB M,R,P共线RM/MP=CD/DE N,P,Q共线PN/NQ=BF/FC 三式相乘得: QL/LR*RM/MP*PN/NQ=EA/AB*CD/DE*BF/FC
由梅涅劳斯定理QL/LR*RM/MP*PN/NQ=1
由梅涅劳斯定理的逆定理知:L,M,N三点共证毕故牛顿定理1成立
牛顿定理2圆外切四边形的两条对角线的中点,及该圆的圆心,三点共线。
证明:设四边形ABCD是⊙I的外切四边形,E和F分别是它的对角线AC和BD的中点,连接EI只需证它过点F,即只需证△BEI与△DEI面积相等。
牛顿定理2图
显然,S△BEI=-S△BIC+S△CEI+S△BCE,而S△DEI=-S△ADE+S△AIE+S△AID。
注意两个式子,由ABCD外切于⊙I,AB+CD=AD+BC,S△BIC+S△AID=1/2*S 四边形ABCD,S△ADE+S△BCE=1/2*S△ACD+1/2*S△ABC=1/2*S四边形ABCD 即S△BIC+S△AID=S△ADE+S△BCE,移项得S△BIC-S△BCE=S△ADE-S△AID,由E是AC中点,S△CEI=S△AEI,故S△BIC-S△CEI-S△BCE=S△ADE-S△AIE-S△AID,即S△BEI=△DEI,而F是BD中点,由共边比例定理EI过点F即EF 过点I,故结论成立。证毕。
牛顿定理 3 圆的外切四边形的对角线的交点和以切点为顶点的四边形对角线交点重合。
证明:设四边形ABCD的边AB,BC,CD,DA与内切圆分别切于点E,F,G,H. 首先证明,直线AC,EG,FH交于一点.设EG,FH分别交AC于点I,I'. 显然∠AHI‘=∠BFI ’ 因此易知AI'*HI'/FI'*CI'=S(AI'H)/S(CI'F)=AH*HI'/CF*FI'
故AI'/CI'=AH/CF.
同样可证:AI/CI=AE/CG
又AE=AH,CF=CG.
故AI/CI=AH/CF=AI'/CI'.
从而I,I'重合.即直线AC,EG,FH交于一点.
同理可证:直线BD,EG,FH交于一点. 因此直线AC,BD,EG,FH交于一点. 证毕。
等角共轭点:描述一:三角形内一点P,过A 做直线L1与AP 关于角A 的角平分线对称,同样过B,C 分别做L2,L3.这三条直线交于P1,则P1是P 的等角共轭点;
描述二:设P 、Q 是三角形ABC 内两点,∠PAB=∠QAC,∠PBC=∠QBA,∠PCB=∠QCA,满足题设条件的两点P 、Q 称为△ABC 的等角共轭点。
圆内接四边形与外切四边形
当四边形与其它的知识点综合在一起时,其内容丰富多彩。在本节,我们主要介绍圆内接四边形与外切四边形的内容。
对于圆内接四边形与外切四边形,显然有以下的性质:
1.圆内接凸四边形的对角互补;圆内接接凹四边形的对角相等。
2.圆内接凸四边形的一个外角等于其不相邻的内对角。
3.圆外切四边形的对边之和相等。
命题1 如图,证明 ),(),(CD AB O CD AB O '=。
证明:根据交比的定义和圆的性质,得 ),(s i n s i n s i n s i n s i n s i n s i n s i n ),(CD AB O C O B D O A D O B C O A BOC
AOD BOD AOC CD AB O '='∠?'∠'∠?'∠=∠?∠∠?∠=
4.托勒密定理:圆内接四边形的对边之积的和等于对角线之积。
证明一 在BD 上选一点E ,使得∠BAC=∠EAD 。
在ΔABC 和ΔAED 中,
∵ ∠BAC=∠EAD ,∠BCA=∠EDA ∴ ΔABC ∽ΔAED , ∴ AD AC ED BC =,即 AC
BC AD ED ?=。 (1) 在ΔABE 和ΔACD 中,
∵ ∠BAE=∠CAD ,∠ABE=∠ACD
∴ ΔABE ∽ΔACD , ∴ CD BE AC AB =,即 AC
CD AB BE ?=。 (2) (1)+(2)得 BD ED BE AC
CD AB AC BC AD =+=?+?, 即 BD AC BC AD CD AB ?=?+?。
证明二 如图,因为 X(BC, AD) + X(BA, CD)=1,即
1sin sin sin sin sin sin sin sin =∠?∠∠?∠+∠?∠∠?∠AXC
BXD AXD BXC CXA BXD CXD BXA 由正弦定理得
D
1=??+??AC
BD AD BC CA BD CD BA 即 BD AC BC AD CD AB ?=?+?。
5.圆内接凸四边形的密克点在一条对边交点的连线上。
证明:如图,设M 是密克点,连CM 、EM 、FM ,那么
∠CME =∠CBA =∠BCA =∠CDF = 1800 – ∠CMF
所以E 、M 、F 共线。
例 圆内接四边形对边交点连线的平方等于由此二点向圆所作切线的平方和。
证明:如图,作四边形ABCD 的密克点,即ΔBCE 和ΔCDF 的外接圆的交点M ,则M 在EF 上。从而有
222FH EG FB FC ED EC FM
EF EM EF EF +=?+?=?+?=
例1 如图, (CD ,PQ )= – 1。
证明:根据命题1知 A(A B ,C D) = B(A B ,C D),
即 (PQ ,CD )=(QP ,CD )。
所以 (PQ ,CD )= – 1。
本结论可叙述为:过圆外一点P 任作割线PCD ,则C 、D 、P 的第四调和点在一条定直线上。
命题2 如图,PC ,PD 是切线,OP 是圆的直径,过Q 任作一弦AB ,求证:PO 平分∠APB 。
证明:因为PC ,PD 是切线,所以 2PQ QO PC AQ QB ?==?,
所以O 、A 、P 、B 四点共圆,所以
∠APO=∠ABO=∠BAO=∠BPO ,
即PO 平分∠APB 。
例2 过圆内一点P 任作直线交圆于A 、B 两点,则A 、B 、P 的第四调和点Q 在一条定直线上。
证明:如图,过H 作HQ 垂直于OP 交AB 于Q ,那么根据
命题2知HO 平分∠AHB ,但HQ ⊥HP ,从而HQ 也是∠AHB 的平分线。根据角平分线的性质知,
(AB ,PQ )= – 1。
所以A 、B 、P 的第四调和点在一条定直线上。
本结论可叙述为:过圆内一点P 任作割线PCD ,则C 、D 、P 的第四调和点在一条定直线上。
定义 过一点P 作直线交圆于A 、B ,则A 、B 、P 的第四调和点称为P (关于圆)的共轭点。
根据例1和例2知,我们有
定理 点P 的共轭点的轨迹l p 是一条直线。
注:我们称l p 是P 的极线,而P 称为l p 的极点。当点P 在圆上时,规定P 的极线为过P 的切线,而切线的极点就是切点。当点P 在圆外时,P 的极线就是P 的切点弦所在的直线。
例3 设⊙O 与直线l 相离,过l 上的点P 作⊙O 的切线PA 、PB ,则切点A 、B 的连线过定点。
证明:连AB ,过O 作OH ⊥l 于H ,且交AB 于K 。 ∵ O 、A 、P 、H 共圆, ∴ ∠OBK=∠OPA=∠OPB=∠OHB ,
∴ ΔOHB ∽ΔOBK ∴ OB 2=OK ?OH ,即R 2= OK ?OH (其中R 是⊙O 的半径), 从而K 是一个定点,即AB 过一个定点。
问题探索:(1)本命题可叙述为:共线点的极线共点。
(2)当l 与圆相切时,结论是否仍成立?
(3)当l 与相交时结论是否成立? (分析:过O 作l 的垂线,垂足为H ,则O 、H 、B 、
P 、A 共圆。如图,∠BHK=∠BPO=∠APO=∠ABO , 故∠OHB=∠OBK ,从而ΔOHB ∽ΔOBK 。
所以OK OB OB OH ,即OK 为常数。所以P
(4)在(3)中,当P 进入圆的内部时,情形会起什么变化?
例4 过圆外一点H 任作一条割线交圆于两点A 、B ,求证:A 、B 处的切线的交点P 在一条定直线上。
证明:任作一条割线HAB
,交⊙O 于A 、B ,过H 作切线C 是切点,作CK ⊥OH 于K ,那么
HK ?OH=HC 2= HA ?HB ∴ O 、K 、B 、A 共圆,
∵ O 、A 、P 、B 共圆,
∴ O 、K 、B 、A 、P 共圆,
∴ OH ⊥KP 。
由此即得P 在过K 且垂直于OH 的直线(即H 的切点弦)上,所以所有的P 共线。
问题探索 (1)本命题可叙述为:共点线的极点共线。
(2)当H 点在圆上时,结论是否成立?
(3)当H 在圆内时,结论是否成立?
(分析:如图,过H 作OH 的垂线交圆于C ,作C 处的切线
交OH 的延长线于K ,则
BH AH HC HO KH ?==?2,
所以O 、A 、K 、B 、P 共圆,故PK 垂直于OH 。但K 是固定点,所以P 在一条定直线上。)
(4)当HAB 与圆相离时,情形会起什么变化?
定理 共线点的极线共点,共点线的极点共线。
定理 过圆的内接四边形一组对边的交点作圆的切线,则两个切点,另一组对边的交点,及对角线的交点,四点共线。
证明:如图,根据完全四边形的调和性可知P 的极线就是QR ,另一方面,P 的极线就是P 的切点弦XY 。所以Q 、R 、X 、Y 共线。
定理 圆内接四边形一组对边的端点处切线的交点,对角线交点及另一组对边的交点,四点共线,且它们互相调和分割。
证明:如图,因为Q 的极线是PR ,故Q 与R 是一对共轭点,同理P 与R 也是一对共轭点,故R 的极线是PQ ,即PQ 的极点是R 。因为PAB 的极点为T ,PDC 的极点为S ,PR 的极点为Q ,PQ 的极点为R ,而共点线的极点共线,所以Q 、T 、R 、S 共线。同理有P 、U 、R 、V 共线。
设AD 与PR 的交点为X ,则(AD ,QX )= –1,从而在中心U 的投影下有
(TS ,QR )=(AD ,QX )= –1。
由此定理还可得,
麦克劳林定理 圆外切四边形的对角线,对边切点的连线,四线共点,且对角线调和分割对边切点的连线。
例
练 习 A (切点弦专题)
1. 设⊙O 与直线l 相离,过l 上的点P作⊙O 的切线PA、PB,则切点A、B的连线过定点。
2. 设⊙O 外有n 个共线点P i (i=1, 2, ……,n),过P i 作⊙O 的切线,切点为Ai ,B i ,则直线Ai B i 共点。
3. 过圆外一点任作一条割线交圆于两点,则这两点处的切线的交点在一条定直线上。
4. 过圆外一点P 作圆的切线PA 、PB ,切点为A 、B ,连AB 、OP 交于K 。过K 任作一弦CD ,则OH 平分∠CHD 。
5. 设P 为圆外一点,任作圆的直径Ai B i ,则ΔP Ai B i 的垂心在一条定直线上。
6.设H为锐角ΔABC的垂心,由A向以BC为直径的圆作切线AP、AQ,切点为P、Q,求证:P、H、Q三点共线。(1996年,CMO)
7.直线m(不过圆心)与⊙O相交,过m在圆外的点作圆的两条切线,切点为A、B,则AB与OK交于定点(其中OK⊥m于K)。
8.过⊙O内任一点K作弦Ai B i(直径除外),再过A i、B i分别作圆的切线交于P i,则所有P i共线。
9.设K是⊙O直径MN上异于O的一点,过K任作一弦Ai B i,连Ai M、B i N交于P i,则所有P i共线。
10.设K是圆内异于圆心的任一点,过K作两条不等的弦Ai B i,C i D i,连A i C i、B i D i 交于P i,则所有P i共线。
11.设AB是圆O的直径,直线m过K且与AB垂直,Q i为m上任一点,连AQ i、BQ i 分别交圆于D i、C i,则C i D i共点。
12.设P是圆外定点,过P任作两条不相等的割线PD i A i、PC i B i。设Ai B i、C i D i交于
Q i,则所有Q i共线。
13.四边形ABCD内接于圆,其边AB和CD的延长线交于点P,AD与BC的延长线交于点Q,由Q作圆的两条切线QE、QF,切点为E、F,求证P、E、F三点共线。
14.设n为过圆心的一条直线。过圆内异于圆心的任一点K,在直线n的同侧作直线AK、BK分别交圆O于A、B,使它们与直线n成等角,则AB与n交于定点H。
15.过圆外一点H作割线HBA(直径除外),试问OH上是否存在一点K,使∠BKH= ∠AKO。
16.如图,已知A为平面上两半径不等的⊙O1和⊙O2的一个交点,两外公切线P1P2,Q1Q2分别切两圆于P1、P2、Q1、Q2;M1、M2分别为P1Q1、P2Q2的中点,求证:∠O1AO2=∠M1AM2。
17.设A、B、C、D是一条直线上依次排列的四个不同点,分别以AC、BD为直径的两圆相交于X和Y,直线XY交BC于Z。若P为直线XY上异于Z的一点,直线CP与以AC为直径的圆相交于C及M,直线BP与以BD为直径的圆相交于B及N。证明:AM、DN、XY三线共点。
18.如图,设PA、PB是⊙O的切线,A、B是切点,
割线PEC交AB于D,若PE=2,CD=1,求DE的长。
19.直线AB与圆相切于B,弦CD经过AB的中点M,
直线AC交圆于E,AD交圆于F,证明:EF//AB。
20.在直角ΔABC中AB为斜边,CH为斜边上的高,以AC为半径作⊙A。过B作⊙A 的任一割线交⊙A于D、E,交CH于F(D在B、F之间),又作∠ABG=∠ABD,G在⊙A 上,G与D在AB异侧,求证:E、H、G共线。
练习 B
1.四边形的每双对边的中点连线及对角线中点连线互相平分。
2.若四边形的两对角线互相垂直,则一双对边的平方和等于另一双对边的和。
3.四边形对边中点连线的平方和,等于两对角线平方和的一半。
4.顺次连接简单四边形各边中点所成四边形的面积等于原四边形面积的一半。
5.在凸四边形ABCD中,设E、F、G、H各是四边AB、BC、CD、DA的中点,I、J 分别是对角线AC、BD的中点。作直线IO//BD,JO//AC,求证:S OHAE=S OEBF=S OFCG=S OGDH。
6.凸多边形的内角不能有多于三个的锐角。
7.凸四边形中,若一双对边的平分线或平行或重合,则他双对角相等;反之,若一双
对角相等,则另一双对角的平分线平行或重合。
8.设四边形ABCD 有内切圆,则ΔABC 与ΔCDA 的内切圆相切,ΔBCD 与ΔDAB 的内切圆也相切。
9.在圆内接四边形ABCD 中,若AC 平分CD ,则AB 2+BC 2+CD 2+DA 2=2AC 2 。
10.设四边形ABCD 有内切圆或旁切圆⊙O ,则⊙AOB 与⊙COD 、⊙AOD 与⊙BOC 分别相切。
11.设四边形有一双对边相等,则它双对边的中点连线与该双对边所在直线的交角相等。
12.设一直线与圆内接四边形一双对边所在直线交成相等的同侧内角,则变与他双对边所在直线交成相等的同侧内角。
13.四点两两连成四个三角形,求证它们的内切圆中任两圆的公切线等于它两圆的公切线,但这些公切线以落在各连线上面的为限。
14.既有内切圆又有外接圆的四边形其对边切点的连线必互相垂直。
15.设四边形无外接圆,两双对边的中垂线垂直相交,则这两交点的连线垂直于两对角线中点的连线。
16.以一简单四边形的每边向外作正方形,求证对边上二形的中心连线垂直并且相等。
17.高逡一圆内接四边形每双对边所在直线的交角的平分线,则所作四线交成一个矩形。
18.圆上四点两两连成四个三角形,它们的内心是一个矩形的顶点。
19.在四边形ABCD 中,设AD ≠BC ,内外分AB 边于E 、F ,又内外分CD 边于G 、H ,使
BC
AD HC HD GC GD FB FA EB EA ====, 求证:EG ⊥FH 。
20.设四边形ABCD 内接于一圆,作弦AE 及BF ,若AE//BD 且BF//AC ,则EF//CD 。
21.ABCD 是圆内接四边形,过A 、B 任作一圆交直线AD 、BC 、AC 、BD 于E 、F 、G 、H ,则CD//EF//GH 。
22.ABCD 是圆内接四边形,过A 、B 任作一圆交直线AD 、BC 、AC 、BD 于E 、F 、G 、H ,设BE 与AC ,AF 与BD ,BG 与AD ,AH 与BC 交于E ′、F ′、G ′、H ′,则CD//E ′F ′//G ′H ′。
23.设四边形有一角是直角且对角线相等,则对边的中垂线交点与该直角的顶点共线。
24.在圆内接四边形中,设每边两端所引邻接边的长线相交,则所得四交点与四边形的对角线交点及外接圆心共线。
24.;圆上四点两两连成四个三角形,它们的内心、旁心合计十六点分配在八条直线上,每线上四点,而这八线是两组互相垂直的平行线,每组含四线。
25.设四边形ABCD 内接于圆O ,且AC ⊥BD ,则ΔOAB 、ΔOBC 、ΔOCD 、ΔODA 的垂心共线。
26.圆内接四边形的一双对边(所在直线)交角的平分线,与他双对边(所在直线)交角的平分线分别垂直,两垂足与两对角线的中点组成调和点列。
27.设自四边形的对角线的交点引直线平行于每边而与对边(所在直线)相交,则四交点共线。
28.在四边形ABCD 中,A ′、C ′是AC 上的两点,B ′、D ′是BD 上的两点。若A ′B ′//AB ,B ′C ′//BC ,C ′D ′//CD ,则D ′A ′//DA ,且A ′B ′与CD ,B ′C ′与DA ,C ′D ′与AB ,D ′A ′与BC 的交点共线。
29.在四边形ABCD 中,O 是AC 与BD 的交点,一直线交AB 、BC 、CD 、DA 于E 、F 、G 、H ,连EO 、FO 、GO 、HO ,设依次各交CD 、DA 、AB 、BC 于E ′、F ′、G ′、H ′,求证这四交点共线。
30.在四边形ABCD 中,A ′、C ′是AC 上的两点,B ′、D ′是BD 上的两点。若A ′B ′与AB 、B ′C ′与BC 、C ′D ′与CD 的交点共线,则D ′A ′与DA 的交点也在此线上,且A ′B ′与CD ,B ′C ′与DA ,C ′D ′与AB ,D ′A ′与BC 的交点共线。
31.在一个四边形中,若有一双对角的平分线与另一对角线共点,则它双对角的平分线也与另一对角线共点。
32.在二对角互相垂直的四边形中,过对角线交点向每边作长线,得四垂足,并设所作垂线又与对边相交,得四交点,则所得八点共圆。
33.若一个四边形有等角共轭点,那么这双等角共轭点在各边(所在直线)上的射影必共圆。
34.凸四边形各外角的平分线顺次相交,则所得四交点共圆。
35.P 是四边形ABCD 的对角线交点,设⊙PAB 与⊙PCD 交于Q ,⊙PAD 与⊙PBC 交于R ,则P 、Q 、R 三点与AC 、BD 的中点,五点共圆。
36.圆内接四边形两对角线的中点,在四边中点所连成的平行四边形各边(所在直线)上的射影八点共圆。
37.设圆内接四边形的两对角线互相垂直,则其交点在四边上的射影与四边的中点,八点共圆。
38.在四边形ABCD 中,AC ⊥BD ,A ′、C ′是AC 上的两点,B ′、D ′是BD 上的两点。若A ′B ′⊥AB 、B ′C ′⊥BC 、C ′D ′⊥CD ,则D ′A ′⊥DA ,且四垂足及A ′B ′与CD ,B ′C ′与DA ,C ′D ′与AB ,D ′A ′与BC 的交点,八点共圆。
39.平面上无三点共线的四点两两相连所的四个三角形,它们的九点圆共点。
40.一个完全四边形中包含三个四边形(凸的、凹的、折的各一个),每个四边形的对边都叫作完全四边形的对节。
通过完全四边形每双对节的中点及它们所在边的交点作圆,证明所得六圆共点。
41.设P 、P ′是四边形ABCD 的等角共轭点,求证:
(1)四圆⊙PAB 、⊙PBC 、⊙PCD 、⊙P ′DA 会于一点Q ;
(2)四圆⊙P ′AB 、⊙P ′BC 、⊙P ′CD 、⊙PDA 会于一点Q ′;
(3)Q 与Q ′也是四边形的等角共轭点。
42.设四边形ABCD 内接于⊙O ,P 是AC 与BD 的交点,求证:
(1)四圆⊙OAB 、⊙PBC 、⊙OCD 、⊙PDA 共点;
(2)四圆⊙PAB 、⊙OBC 、⊙PCD 、⊙ODA 共点。
43.在一完全四角形中,依次除掉一双对边,然后通过余四边所成的完全四边形的密克点及所除两边之一的两端作圆,证明所得六圆共点。
44.在一完全四角形中,求证下列八圆共点:
(1)通过共顶点三边的中点所作的圆,共四圆;
(2)通过每双对边的中点及在这两边上的对角点所作的圆,共三圆;
(3)通过每双对边的中垂线交点所作的圆。
45.在圆内接四边形ABCD 中,设每双对边的和各m 和n ,两对角线的和为l ,ΔBCD 、ΔCDA 、ΔDAB 、ΔABC 的内切圆直径分别为d 1、d 2、d 3、d 4。求证:(l-m)(l-n)=d 1d 3+d 2d 4。
46.设ABCD 是圆内接四边形,则DA
CD BC AB CD BC AB DA BD AC ?+??+?=。 47.已知圆内接四边形的四边长为a 、b 、c 、d ,试求两对角线的长。
48.设凸四边形ABCD 内接于⊙O (R ),而AE 是⊙O 中平行于BD 的弦,则该四边形的面积为R CE BD AC S 4??=
。
49.同时有外接圆和内切圆的四边形的面积告示于四边连乘积的平方根。
50.若凸四边形的对边乘积之和等于对角线之积,则此四边形必有外接圆。
51.完全四边形各边所成的四个三角形的垂心同在一条平行于西摩松线的直线(此直线称为完全四边形的垂心线)上。
52.完全四边形的牛顿线垂直于西摩松线及垂心线。
53.完全四边形的密克点至每双对顶点的距离之积彼此相等。
学生做题前请先回答以下问题 问题1:圆中相关的定理以及推论: 垂径定理:____________________________________________________; 推论:________________________________________________________; 总结:知二推三①___________________________________, ②_______________________,③______________________, ④_______________________,⑤______________________. 问题2:四组量关系定理:在_____________________中,如果_______________、______________、_______________、_______________中有一组量相等,那么它们所对应的其余各组量都分别相等. 问题3:圆周角定理:_______________________________________; 推论1:______________________________________; 推论2:____________________________;________________________________. 推论3:______________________________________. 问题4:三点定圆定理:_____________________________________. 问题5:圆中处理问题的思路: ①_______________________________________; ②_______________________________________; ③_______________________________________; ④_______________________________________. 圆中的基本概念及定理(一) 一、单选题(共10道,每道10分) 1.如图,CD是⊙O直径,弦AB⊥CD,垂足为点F,连接BC,BD,则下列结论不一定正确的是( ) A. B.AF=BF C.OF=CF D.∠DBC=90°
1、勾股定理(毕达哥拉斯定理) 2、射影定理(欧几里得定理) 3、三角形的三条中线交于一点,并且,各中线被这个点分成2:1的两部分 4、四边形两边中心的连线的两条对角线中心的连线交于一点 5、间隔的连接六边形的边的中心所作出的两个三角形的重心是重合的。 6、三角形各边的垂直一平分线交于一点。 7、三角形的三条高线交于一点 8、设三角形ABC的外心为O,垂心为H,从O向BC边引垂线,设垂足为L,则AH=2OL 9、三角形的外心,垂心,重心在同一条直线(欧拉线)上。 10、(九点圆或欧拉圆或费尔巴赫圆)三角形中,三边中心、从各顶点向其对边所引垂线的垂足,以及垂心与各顶点连线的中点,这九个点在同一个圆上, 11、欧拉定理:三角形的外心、重心、九点圆圆心、垂心依次位于同一直线(欧拉线)上 12、库立奇*大上定理:(圆内接四边形的九点圆) 圆周上有四点,过其中任三点作三角形,这四个三角形的九点圆圆心都在同一圆周上,我们把过这四个九点圆圆心的圆叫做圆内接四边形的九点圆。 13、(内心)三角形的三条内角平分线交于一点,内切圆的半径公式:r=(s-a)(s-b)(s-c)s,s为三角形周长的一半 14、(旁心)三角形的一个内角平分线和另外两个顶点处的外角平分线交于一点 15、中线定理:(巴布斯定理)设三角形ABC的边BC的中点为P,则有AB2+AC2=2(AP2+BP2) 16、斯图尔特定理:P将三角形ABC的边BC内分成m:n,则有n×AB2+m×AC2=(m+n)AP2+mnm+nBC2 17、波罗摩及多定理:圆内接四边形ABCD的对角线互相垂直时,连接AB中点M和对角线交点E的直线垂直于CD 18、阿波罗尼斯定理:到两定点A、B的距离之比为定比m:n(值不为1)的点P,位于将线段AB分成m:n的内分点C和外分点D为直径两端点的定圆周上 19、托勒密定理:设四边形ABCD内接于圆,则有AB×CD+AD×BC=AC×BD 20、以任意三角形ABC的边BC、CA、AB为底边,分别向外作底角都是30度的等腰△BDC、△CEA、△AFB,则△DEF是正三角形,
圆中的基本概念及定理(讲义) ?课前预习 在小学的时候,我们知道“一中同长”表示的是圆,中心称为,固定的线段长称为,还知道半径为r 的圆的周长为,面积为. 在七年级我们学习了圆的另外一种说法:平面上,一条线段绕着它固定的一个端点旋转一周,另一个端点形成的图形叫做圆.固定的端点O 称为圆心,线段OA 称为半径. 一条弧AB 和经过这条弧的两条半径OA,OB 所组成的图形叫做扇形. 顶点在圆心的角叫做圆心角.
1
?知识点睛 1.在一个平面内,线段OA 绕它固定的一个端点O 旋转一周, 另一个端点A 所形成的图形叫做.其固定的端点O 叫做,线段OA 叫做.以点O 为圆心的圆,记作,读作“圆O”. 2.圆中概念: 弧:,弧包括和; 弦:; 圆周角:; 圆心角:; 弦心距:; 等圆:; 等弧:. 3.圆的对称性: 圆是轴对称图形,其对称轴是; 圆是中心对称图形,其对称中心为.4.圆中基本定理: *(1)垂径定理: .推论: .(2)四组量关系定理:在中,如果 、、、 中有一组量相等,那么它们所对应的其余各组量都分别相等. (3)圆周角定理: .推论1:. 推论2:, .推论3: .注:如果一个多边形的所有顶点都在同一个圆上,那么这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.圆中处理问题的思路: ①找圆心,连半径,转移边; ②遇弦,作垂线,垂径定理配合勾股定理建等式; ③遇直径,找直角,由直角,找直径; ④由弧找角,由角看弧.
2
? 精讲精练 1. 如图,AB 是⊙O 的直径,弦 CD ⊥AB ,垂足为 M ,下列结论不一定成立的是( ) ︵ ︵ A .CM =DM B . CB = B D C .∠AC D =∠ADC D .OM =MB 第 1 题图 第 2 题图 2. 如图,⊙O 的弦 AB 垂直平分半径 OC ,若 AB = 的半径为 . ,则⊙O 3. 工程上常用钢珠来测量零件上小圆孔的宽口,假设钢珠的直径是 10 mm ,测得钢珠顶端离零件表面的距离为 8 mm ,如图所示,则这个小圆孔的宽口 AB 的长度为 mm . 第 3 题图 第 4 题图 4. 如图,圆拱桥桥拱的跨度 AB =12 m ,桥拱高 CD =4 m ,则拱桥的直径为 . 5. 如图,在⊙O 中,直径 CD 垂直于弦 AB ,垂足为 E ,连接 OB , CB .已知⊙O 的半径为 2,AB = 2 ,则∠BCD = . 6 3
高中平面几何常用定理 总结 -CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN
1 (高中)平面几何基础知识(基本定理、基本性质) 1. 勾股定理(毕达哥拉斯定理)(广义勾股定理)(1)锐角对边的平方,等于其他两边之平方和,减去这两边中的一边和另一边在这边上的射影乘积的两倍. (2)钝角对边的平方等于其他两边的平方和,加上这两边中的一边与另一边在这边上的射影乘积的两倍. 2. 射影定理(欧几里得定理) 3. 中线定理(巴布斯定理)设△ABC 的边BC 的中点为P ,则有)(22222BP AP AC AB +=+; 中线长:222222a c b m a -+=. 4. 垂线定理:2222BD BC AD AC CD AB -=-?⊥. 高线长:C b B c A a bc c p b p a p p a h a sin sin sin ))()((2===---=. 5. 角平分线定理:三角形一个角的平分线分对边所成的两条线段与这个角的两边对应成比例. 6. 如△ABC 中,AD 平分∠BAC ,则AC AB DC BD =;(外角平分线定理). 角平分线长:2cos 2)(2A c b bc a p bcp c b t a +=-+= (其中p 为周长一半). 7. 正弦定理:R C c B b A a 2sin sin sin ===,(其中R 为三角形外接圆半径). 8. 余弦定理:C ab b a c cos 2222-+=. 9. 张角定理:AB DAC AC BAD AD BAC ∠+∠=∠sin sin sin . 10. 斯特瓦尔特(Stewart )定理:设已知△ABC 及其底边上B 、C 两点间的一点D ,则有AB 2·DC +AC 2·BD -AD 2·BC =BC ·DC ·BD .
14 初三秋季·第2讲·尖子班·学生版 围田地 漫画释义 满分晋级阶梯 圆7级 期末复习之圆中的 重要结论及应用 圆6级 期末复习之圆的综合 圆5级 圆中三大切线定理 2 圆中三大切线定理
中考内容与要求 中考考点分析 圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考 15
16 初三秋季·第2讲·尖子班·学生版 查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新的题型。 要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解决圆中的动态问题。 年份 2011年 2012年 2013年 题号 20,25 8,20,25 8,20,25 分值 13分 17分 17分 考点 圆的有关证明,计算(圆周角定理、切线、等腰三角形、相似、解直角三角形);直线与圆的位置关系 圆的基本性质,圆的切线证明,圆同相似和三角函数的结合;直线与圆的位置关系 圆中的动点函数图像,圆的基本性质(垂径定理、圆周角定理),圆同相似和三角函数的结合;直线与圆的位置关系 知识互联网 题型一:切线的性质定理
17 题目中已知圆的切线,可以“连半径,标直角”,然后在直角三角形中利用勾股、相似或锐角三角函数解决问题。 【例1】 如图,在△ABC 中,BC AB =,以AC 为直径的⊙0与BC 边 交于点D ,过点D 作⊙O 的切线DE ,交AB 于点E ,若 DE ⊥AB .求证:BE AE 3=. 判定切线共有三种方法:定义法、距离法和定理法,其中常用的是距离法和定理法,可以总结为六字口诀,定理法是“连半径,证垂直”,距离法是“作垂直,证半径”,定理法的使用频率最高,必须熟练掌握。 【例2】 如图,C 是以AB 为直径的⊙O 上一点,过O 作OE ⊥AC 于点E ,过点A 作⊙O 的切线 交OE 的延长线于点F , 典题精练 思路导航 典题精练 思路导航 题型二:切线的判定定理 E O D C B A
专题平面几何的四个重 要定理 SANY标准化小组 #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
竞赛专题讲座06 -平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、 Q、R共线的充要条件是。 塞瓦(Ceva)定理(塞瓦点) △ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点 的充要条件是。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该 四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是 该点落在三角形的外接圆上。 例题: 1.设AD是△ABC的边BC上的中线,直线CF交AD于F。求 证:。
【分析】CEF截△ABD→(梅氏定理) 【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。 2.过△ABC的重心G的直线分别交AB、AC于E、F, 交CB于D。 求证:。 【分析】连结并延长AG交BC于M,则M为BC的 中点。 DEG截△ABM→(梅氏定理) DGF截△ACM→(梅氏定理) ∴===1 【评注】梅氏定理 3. D、E、F分别在△ABC的BC、CA、AB边上, ,AD、BE、CF交成△LMN。 求S△LMN。 【分析】 【评注】梅氏定理 4.以△ABC各边为底边向外作相似的 等腰△BCE、△CAF、△ABG。求证:AE、 BF、CG相交于一点。
【分析】 【评注】塞瓦定理 5.已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。 【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。则 CD=DA=AB,AC=BD。 由托勒密定理, AC·BD=AD·BC+CD·AB。 【评注】托勒密定理 6.已知正七边形A 1A2A3A4A5A6A7。 求证:。(第21届全苏数学竞赛) 【分析】 【评注】托勒密定理 7.△ABC的BC边上的高AD的延长线交 外接圆于P,作PE⊥AB于E,延长ED交 AC延长线于F。 求证:BC·EF=BF·CE+BE·CF。 【分析】 【评注】西姆松定理(西姆松线) 8.正六边形ABCDEF的对角线AC、CE分别被内分点M、N分成的 比为AM:AC=CN:CE=k,且B、M、N共 线。求k。(23-IMO-5) 【分析】 【评注】面积法 9. O为△ABC内一点,分别以d a、d b、d c表示O到BC、CA、AB的距离,以R a、 R b、R c表示O到A、B、C的距离。
1.圆的周长C=2πr=πd 2.圆的面积S=πr2 3.扇形弧长l=nπr/180 4.扇形面积S=nπr2/360=rl/2 5.圆锥侧面积S=πrl 〖圆的定义〗 几何说:平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径。 轨迹说:平面上一动点以一定点为中心,一定长为距离运动一周的轨迹称为圆周,简称圆。 集合说:到定点的距离等于定长的点的集合叫做圆。 〖圆的相关量〗 圆周率:圆周长度与圆的直径长度的比叫做圆周率, 值是 3.141592653589793238462643383279502884197169399375105820974944 5923078164062862089986280348253421170679..., 通常用π表示,计算中常取3.14为它的近似值(但奥数常取3或3.1416)。 圆弧和弦:圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。 圆心角和圆周角:顶点在圆心上的角叫做圆心角。顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。 内心和外心:过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。 扇形:在圆上,由两条半径和一段弧围成的图形叫做扇形。圆锥侧面展开图是一个扇形。这个扇形的半径成为圆锥的母线。 〖圆和圆的相关量字母表示方法〗 圆—⊙半径—r 弧—⌒直径—d 扇形弧长/圆锥母线—l 周长—C 面积—S 〖圆和其他图形的位置关系〗 圆和点的位置关系:以点P与圆O的为例(设P是一点,则PO是点到圆心的距离),P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r。
第十九讲平面几何中的几个著名定理 几何学起源于土地测量,几千年来,人们对几何学进行了深入的研究,现已发展成为一门具有严密的逻辑体系的数学分支.人们从少量的公理出发,经过演绎推理得到不少结论,这些结论一般就称为定理.平面几何中有不少定理,除了教科书中所阐述的一些定理外,还有许多著名的定理,以这些定理为基础,可以推出不少几何事实,得到完美的结论,以至巧妙而简捷地解决不少问题.而这些定理的证明本身,给我们许多有价值的数学思想方法,对开阔眼界、活跃思维都颇为有益.有些定理的证明方法及其引伸出的结论体现了数学的美,使人们感到对这些定理的理解也可以看作是一种享受.下面我们来介绍一些著名的定理. 1.梅内劳斯定理 亚历山大里亚的梅内劳斯(Menelaus,约公元100年,他和斯巴达的Menelaus是两个人)曾著《球面论》,着重讨论球面三角形的几何性质.以他的名子命名的“梅内劳斯定理”现载在初等几何和射影几何的书中,是证明点共线的重要定理. 定理一直线与△ABC的三边AB,BC,CA或延长线分别相交于X,Y,Z,则 证过A,B,C分别作直线XZY的垂线,设垂足分别为Q,P,S,见图3-98.由△AXQ∽△BXP得
同理 将这三式相乘,得 说明(1)如果直线与△ABC的边都不相交,而相交在延长线上,同样可证得上述结论,但一定要有交点,且交点不在顶点上,否则定理的结论中的分母出现零,分子也出现零,这时定理的结论应改为 AX×BY×CZ=XB×YC×ZA, 仍然成立. (2)梅内劳斯定理的逆定理也成立,即“在△ABC 的边AB和AC上分别取点X,Z,在BC的延长线上取点Y,如果 那么X,Y,Z共线”.梅内劳斯定理的逆定理常被用来证明三点共线. 例1 已知△ABC的内角∠B和∠C的平分线分别为BE和CF,∠A的外角平分线与BC的延长线相交于D,求证:D,E,F共线. 证如图3-99有 相乘后得
- - - 平面几何四个重要定理 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R , 则P 、Q 、R 共线的充要条件是 1RB AR QA CQ PC BP =??。 塞瓦(Ceva)定理(塞瓦点) △ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是 1RB AR QA CQ PC BP =??。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 该点落在三角形的外接圆上。 例题: 1. 设AD 是△ABC 的边BC 上的中线,直线CF 交AD 于F 。 求证: FB AF 2ED AE = 。 【分析】CEF 截△ABD → 1FA BF CB DC ED AE =??(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B 、D 之一作CF 的平行 线。
DEG 截△ABM →1DB MD GM AG EA BE =??(梅氏定理) DGF 截△ACM →1DC MD GM AG FA CF =??(梅氏定理) ∴FA CF EA BE +=MD AG )DC DB (GM ?+?=MD GM 2MD 2GM ??=1 【评注】梅氏定理 3. D 、E 、F 分别在△ABC 的BC 、CA 、AB 边上, λ===EA CE FB AF DC BD ,AD 、BE 、CF 交成△LMN 。 求S △LMN 。 【分析】 【评注】梅氏定理 4. 以△ABC 各边为底边向外作相似的等腰△BCE 、△CAF 、 △ABG 。求证:AE 、BF 、CG 相交于一点。 【分析】 B
费尔巴赫定理 费尔巴赫定理三角形的九点圆与内切圆内切,而与旁切圆外切。 此定理由德国数学家费尔巴赫(K·W·Feuerbach,1800—1834)于1822年提出。 费尔巴赫定理的证明 在不等边△ABC中,设O,H,I,Q,Ia分别表示△ABC的外心,垂心,内心,九点圆心和∠A所对的旁切圆圆心.s,R,r,ra分别表示△ABC的半周长,外接圆半径,内切圆半径和∠A 所对的旁切圆半径,BC=a,CA=b,AB=c. 易得∠HAO=|B-C|,∠HAI=∠OAI=|B-C|/2; AH=2R*cosA,AO=R,AI=√[(s-a)bc/s],AIa=√[sbc/(s-a)] 在△AHI中,由余弦定理可求得: HI^2=4R^2+4Rr+3r^2-s^2; 在△AHO中,由余弦定理可求得: HO^2=9R^2+8Rr+2r^2-2s^2; 在△AIO中,由余弦定理可求得: OI^2=R(R-2r). ∵九点圆心在线段HO的中点, ∴在△HIO中,由中线公式可求得. 4IQ^2=2(4R^2+4Rr+3r^2-s^2)+ 2(R^2-2Rr)-(9R^2+8Rr+2r^2-2s^2) =(R-2r)^2 故IQ=(R-2r)/2. 又△ABC的九点圆半径为R/2, 所以九点圆与内切圆的圆心距为 d=R/2-r=(R-2r)/2=IQ. 因此三角形的九点圆与内切圆内切。 在△AHIa中,由余弦定理可求得: IaH^2=4R^2+4Rr+r^2-s^2+2(ra)^2; 在△AOIa中,由余弦定理可求得: IaO^2=R(R+2ra). 在△HIaO中,由中线公式可求得. 4IaQ^2=2(4R^2+4Rr+r^2-s^2+2ra^2)+2(R^2+2Rra)-(9R^2+8Rr+2r^2-2s^2)=(R+2ra) ^2 故IaQ=(R+2ra)/2.
1、数学竞赛考纲 二试 1、平面几何 基本要求:掌握高中数学竞赛大纲所确定的所有内容。 补充要求:面积和面积方法。 几个重要定理:梅涅劳斯定理、、、。 几个重要的极值:到三角形三顶点距离之和最小的点--。到三角形三顶点距离的平方和最小的点--。三角形内到三边距离之积最大的点--重心。 几何不等式。 简单的。了解下述定理: 在周长一定的n边形的集合中,正n边形的面积最大。 在周长一定的的集合中,圆的面积最大。 在面积一定的n边形的集合中,正n边形的周长最小。 在面积一定的简单闭曲线的集合中,圆的周长最小。 几何中的运动:反射、平移、旋转。 方法、方法。 平面、及应用。 2、代数 在一试大纲的基础上另外要求的内容: 周期函数与周期,带的函数的图像。 ,三角形的一些简单的恒等式,三角不等式。 。 ,一阶、二阶递归,法。 函数,求n次迭代,简单的函数方程。 n个变元的平均不等式,,及应用。 复数的指数形式,欧拉公式,,单位根,单位根的应用。 圆排列,有重复的排列与组合,简单的组合恒等式。 一元n次方程(多项式)根的个数,根与系数的关系,实系数方程虚根成对定理。 简单的初等数论问题,除初中大纲中所包括的内容外,还应包括,,欧几里得除法,非负最小完全剩余类,,,,,格点及其性质。 3、立体几何 多面角,多面角的性质。三面角、直三面角的基本性质。 正多面体,欧拉定理。 体积证法。 截面,会作截面、表面展开图。 4、平面解析几何 直线的式,直线的,直线束及其应用。 二元一次不等式表示的区域。 三角形的。 圆锥曲线的切线和法线。 圆的幂和根轴。 5、其它。。。集合的划分。覆盖。西姆松线的存在性及性质()。及其逆定理。
中考内容 中考要求 A B C 圆的有关概念理解圆及其有关概念会过不在同一直线上的三点作圆;能利用圆的有关概念解决简单问题 圆的性质知道圆的对称性,了解弧、弦、 圆心角的关系 能用弧、弦、圆心角的关 系解决简单问题 能运用圆 的性质解 决有关问 题 圆周角了解圆周角与圆心角的关系; 知道直径所对的圆周角是直角 会求圆周角的度数,能用 圆周角的知识解决与角有 关的简单问题 能综合运 用几何知 识解决与 圆周角有 关的问题 垂径定理会在相应的图形中确定垂径定 理的条件和结论 能用垂径定理解决有关问 题 点与圆的位置关系了解点与圆的位置关系 直线与圆的位置关系了解直线与圆的位置关系;了 解切线的概念,理解切线与过 切点的半径之间的关系;会过 圆上一点画圆的切线;了解切 线长的概念 能判定直线和圆的位置关 系;会根据切线长的知识 解决简单的问题;能利用 直线和圆的位置关系解决 简单问题 能解决与 切线有关 的问题 圆与圆的位置关系了解圆与圆的位置关系能利用圆与圆的位置关系解决简单问题 弧长会计算弧长能利用弧长解决有关问题 扇形会计算扇形面积能利用扇形面积解决有关问题 圆锥的侧面积和全面积会求圆锥的侧面积和全面积 能解决与圆锥有关的简单 实际问题 中考内容与要求 圆中三大基本定理
圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新题型。 要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解 年份2011年2012年2013年 题号20,25 8,20,25 8,20,25 分值13分17分17分 考点 圆的有关证明,计 算(圆周角定理、 切线、等腰三角形、 相似、解直角三角 形);直线与圆的 位置关系 圆的基本性质,圆 的切线证明,圆同 相似和三角函数的 结合;直线与圆的 位置关系 圆中的动点函数图 像,圆的基本性质 (垂径定理、圆周角 定理),圆同相似和 三角函数的结合; 直线与圆的位置关 系 中考考点分析 知识互联网 题型一:垂径定理
平面几何四大定理 平面几何四个重要定理 四个重要定理: 梅涅劳斯(Me nelau s)定理(梅氏线) △ABC 的三边BC 、CA 、AB 或其延长线上有点P 、Q 、R,则P、Q 、R共线的充要条件是 1RB AR QA CQ PC BP =??。 塞瓦(Ceva)定理(塞瓦点) △ABC 的三边BC 、CA 、AB 上有点P 、Q 、R ,则AP 、BQ 、CR 共点的充要条件是 1RB AR QA CQ PC BP =??。 托勒密(Pto lemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(S imso n)定理(西姆松线) 该点落在三角形的外接圆上。 例题: 1. 设AD 是△A BC的边BC 上的中线,直线CF 交AD 于F 。求 证:FB AF 2ED AE = 。 【分析】CEF 截△ABD → 1FA BF CB DC ED AE =??(梅氏定理) 【评注】也可以添加辅助线证明:过A 、B、D 之一作CF 的平行 线。 2. 过△ABC 的重心G 的直线分别交AB 、AC 于E 、F,交CB 于
平面几何四大定理 D 。 求证: 1FA CF EA BE =+。 【分析】连结并延长AG 交BC 于M,则M为BC 的中点。 DEG 截△AB M→1DB MD GM AG EA BE =??(梅氏定理) D GF 截△AC M→1DC MD GM AG FA CF =??(梅氏定理) ∴FA CF EA BE + =MD AG )DC DB (GM ?+?=MD GM 2MD 2GM ??=1 【评注】梅氏定理 3. D 、E 、F 分别在△ABC 的BC 、C A、AB 边上, λ===EA CE FB AF DC BD ,A D、BE 、CF 交成△LMN 。 求S △LMN 。 【分析】 【评注】梅氏定理 4. 以△ABC 各边为底边向外作相似的等腰△B CE 、△CAF 、 △ABG 。求证:AE 、BF 、CG 相交于一点。 【分析】 【评注】塞瓦定理 5. 已知△ABC 中,∠B=2∠C。求证:AC 2=AB 2+AB ·B C。
学生做题前请先回答以下问题 问题1:圆中处理问题的思路: ①找圆心,连半径,转移边; ②遇弦,_________,垂径定理配合__________建等式; ③遇直径,__________,由直角,__________; ④由弧找______,由_____看______. 圆中的基本概念及定理(二)(人教版) 一、单选题(共10道,每道10分) 1.下列说法正确的是( ) A.长度相等的弧叫等弧 B.平分弦的直径一定垂直于该弦 C.三角形的外心是三条角平分线的交点 D.不在同一直线上的三个点确定一个圆 答案:D 解题思路: 试题难度:三颗星知识点:三角形的外接圆与外心 2.如图,CD是⊙O的直径,已知∠1=30°,则∠2=( ) A.30° B.45° C.60° D.70°
答案:C 解题思路: 试题难度:三颗星知识点:圆心角、弧、弦的关系 3.一个圆形人工湖如图所示,弦AB是湖上的一座桥,已知桥AB长100m,测得圆周角∠ACB=45°,则这个人工湖的直径AD的长为( ) A. B. C. D. 答案:B 解题思路:
试题难度:三颗星知识点:圆周角定理 4.CD是⊙O的一条弦,作直径AB,使AB⊥CD,垂足为E,若AB=10,CD=8,则BE的长是( ) A.8 B.7 C.2或8 D.3或7 答案:C 解题思路:
试题难度:三颗星知识点:垂径定理 5.如图,⊙O的半径为4,△ABC是⊙O的内接三角形,连接OB,OC,若∠BAC与∠BOC互补,则弦BC的长为( ) A. B. C. D. 答案:B 解题思路:
试题难度:三颗星知识点:垂径定理、圆周角定理、解直角三角形 6.如图所示,一圆弧过方格的格点A,B,C,试在方格中建立平面直角坐标系,使点A的坐标为(-2,4),则该圆弧所在圆的圆心坐标是( ) A.(-1,2) B.(1,-1) C.(-1,1) D.(2,1) 答案:C 解题思路:
平面几何的几个重要的定理 一、梅涅劳斯定理: 1=??=??B A A C C B C B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度,则:到直线 、、分别是、、证:设 注:此定理常运用求证三角形相似的过程中的 线段成比例的条件; 。 的交点,证明:与是的中点,是上,在点 的平分线,是是斜边上的高,中,:若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠?11PC BP R Q P AB CA BC ABC ABC l 1=??RB AR QA CQ ,则 、、的延长线分别交于或它们、、的三边的顶点,并且与不经过:若直线定理??CE //BF CKE FKB KE BK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FC KF EK AE DA CD F E D ACK EP CK EP BC EBC CE BH 90HCB ACE HCB HBC ACE HBC ACK EBC BH B EBC ∴?∴= ====??=∴⊥?=∠+∠=∠+∠∠=∠∠=∠∠?????= 依分比定理有:=即:=于是依梅涅劳斯定理有:、、和三点对于,则:上的高作为等腰三角形 即:则:的平分线中,作在证:Θ
1 11 111111111D B D A : C B C A B D AD :BC AC D C B A D C B A K 1=,试证:、、、和、、、线分别交这四条直线于引四条直线,另两条直】从点【练习 注:此定理常用于证明三点共线的问题,且常需要多次使用 再相乘; 共线; 、、证明点引的垂线的垂足, 、、向是从点、、的外接圆上;位于点例111111C B A AB CA BC P C B A ABC P .2? 三点共线; 、、综上可得:也重合与的延长线上时,同在与类似地可证得当矛盾=这与于是可得即这时设必定重合,不然的话,与线段上,则同在与若的延长线上; 线段上,或者同在或者同在与因此,或边上的点的个数也为三点中,位于、、由于在同一直线上的= ,则:又得: ,于是由定理交于与直线证:设直线R Q P R R AB R R BR AR BR AR BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RB AR B R AR 1RB AR QA CQ 1B R AR QA CQ 1R AB PQ ''' ' ' ' ' ' ''''''''' '> <-<->=??=???PC BP PC BP Θ三点共线; 、、求证:, ,这时若或边上的点的个数为三点中,位于、、三点,并且 上或它们的延长线上的、、的三边分别是、、:设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RB AR QA CQ =???? C B A 1 A 1 B 1 C 三点共线; 、、依梅涅劳斯定理可知,=可得 且将上面三条式子相乘, 证:易得:1111 1 1111111111C B A 1BC AC AB CB CA BA 180PBA PCA ,PCB PAB ,PBC PAC PBA cos PB PAB cos AP BC AC PAC cos AP PCA cos CP AB CB , PCB cos CP PBC cos BP CA BA ???=∠+∠∠=∠∠=∠∠?∠?-=∠?∠?-=∠?∠?-=Θ
圆的性质及定理 圆的初步认识 一、圆及圆的相关量的定义(28个)?1.平面上到定点的距离等于定长的所有点组成的图形叫做圆。定点称为圆心,定长称为半径。 2.圆上任意两点间的部分叫做圆弧,简称弧。大于半圆的弧称为优弧,小于半圆的弧称为劣弧。连接圆上任意两点的线段叫做弦。经过圆心的弦叫做直径。? 3.顶点在圆心上的角叫做圆心角。顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角。 4.过三角形的三个顶点的圆叫做三角形的外接圆,其圆心叫做三角形的外心。和三角形三边都相切的圆叫做这个三角形的内切圆,其圆心称为内心。?5.直线与圆有3种位置关系:无公共点为相离;有2个公共点为相交;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点。?6.两圆之间有5种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有2个公共点的叫相交。两圆圆心之间的距离叫做圆心距。?7.在圆上,由2条半径和一段弧围成的图形叫做扇形。圆锥侧面展开图是一个扇形。这个扇形的半径成为圆锥的母线。?二、有关圆的字母表示方法(7个) 圆--⊙半径—r 弧--⌒直径—d?扇形弧长/圆锥母线—l 周长—C 面积—S 三、有关圆的基本性质与定理(27个) 1.点P与圆O的位置关系(设P是一点,则PO是点到圆心的距离): P在⊙O外,PO>r;P在⊙O上,PO=r;P在⊙O内,PO<r。?2.圆是轴对称图形,其对称轴是任意一条过圆心的直线。圆也是中心对称图形,其对称中心是圆心。?3.垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的弧。逆定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的弧。? 4.在同圆或等圆中,如果2个圆心角,2个圆周角,2条弧,2条弦中有一组量相等,那么他们所对应的其余各组量都分别相等。 5.一条弧所对的圆周角等于它所对的圆心角的一半。 6.直径所对的圆周角是直角。90度的圆周角所对的弦是直径。?7.不在同一直线上的3个点确定一个圆。?8.一个三角形有唯一确定的外接圆和内切圆。外接圆圆心是三角形各边垂直平分线的交点,到三角形3个顶点距离相等;内切圆的圆心是三角形各内角平分线的交点,到三角形3边距离相等。 9.直线AB与圆O的位置关系(设OP⊥AB于P,则PO是AB到圆心的距离): AB与⊙O相离,PO>r;AB与⊙O相切,PO=r;AB与⊙O相交,PO<r。 10.圆的切线垂直于过切点的直径;经过直径的一端,并且垂直于这条直径的直线,是这个圆的切线。 11.圆与圆的位置关系(设两圆的半径分别为R和r,且R≥r,圆心距为P):?外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P 竞赛专题讲座-平面几何四个重要定理 重庆市育才中学瞿明强 四个重要定理: 梅涅劳斯(Menelaus)定理(梅氏线) △ABC的三边BC、CA、AB或其延长线上有点P、Q、R,则P、Q、R共线的充要条件是四个重要定理: 。 塞瓦(Ceva)定理(塞瓦点) △ABC的三边BC、CA、AB上有点P、Q、R,则AP、BQ、CR共点的充要条件是 。 托勒密(Ptolemy)定理 四边形的两对边乘积之和等于其对角线乘积的充要条件是该四边形内接于一圆。 西姆松(Simson)定理(西姆松线) 从一点向三角形的三边所引垂线的垂足共线的充要条件是该点落在三角形的外接圆上。 例题: 1.设AD是△ABC的边BC上的中线,直线CF交AD于F。求证:。 【分析】CEF截△ABD→(梅氏定理) 【评注】也可以添加辅助线证明:过A、B、D之一作CF的平行线。 2.过△ABC的重心G的直线分别交AB、AC于E、F,交CB于D。 求证:。 【分析】连结并延长AG交BC于M,则M为BC的中点。DEG截△ABM→(梅氏定理) DGF截△ACM→(梅氏定理) ∴===1 【评注】梅氏定理 3.D、E、F分别在△ABC的BC、CA、AB边上, ,AD、BE、CF交成△LMN。 求S△LMN。 【分析】 【评注】梅氏定理 4.以△ABC各边为底边向外作相似的等腰△BCE、△CAF、△ABG。求证:AE、BF、CG相交于一点。 【分析】 【评注】塞瓦定理 5.已知△ABC中,∠B=2∠C。求证:AC2=AB2+AB·BC。 【分析】过A作BC的平行线交△ABC的外接圆于D,连结BD。则CD=DA=AB,AC=BD。由托勒密定理,AC·BD=AD·BC+CD·AB。 【评注】托勒密定理 1 初三秋季·第1讲·尖子班·教师版 π是什么? 满分晋级阶梯 漫画释义 圆5级 圆中三大切线定理 圆4级 圆中三大基本定理 圆3级 正多边形 和圆与圆中的计算 1 圆中三大基本定理 2 初三秋季·第1讲·尖子班·教师版 圆是北京中考的必考内容,主要考查圆的有关性质与圆的有关计算,每年的第20题都会考中考考点分析 中考内容与要求 3 初三秋季·第1讲·尖子班·教师版 查,第1小题一般是切线的证明,第2小题运用圆与三角形相似、解直角三角形等知识求线段长度问题,有时也以阅读理解、条件开放、结论开放探索题作为新题型。 要求同学们重点掌握圆的有关性质,掌握求线段、角的方法,理解概念之间的相互联系和知识之间的相互转化,理解直线和圆的三种位置关系,掌握切线的性质和判定方法,会根据条件解 年份 2011年 2012年 2013年 题号 20,25 8,20,25 8,20,25 分值 13分 17分 17分 考点 圆的有关证明,计算(圆周角定理、切线、等腰三角形、相似、解直角三角形);直线与圆的位置关系 圆的基本性质,圆的切线证明,圆同相似和三角函数的结合;直线与圆的位置关系 圆中的动点函数图像,圆的基本性质(垂径定理、圆周角定理),圆同相似和三角函数的结合;直线与圆的位置关系 垂径定理反映的是经过圆心的直线和圆中弦的关系,“要求弦长,先求弦长的一半”,注意对由半径、半弦长和弦心距构成的直角三角形模型的理解和应用. 暑期知识点回顾: 知识互联网 思路导航 题型一:垂径定理 4 初三秋季·第1讲·尖子班·教师版 【例1】 ⑴ 如图,BD 是⊙O 的弦,点C 在BD 上,以BC 为边作等边三角形 △ABC ,点A 在圆内,且AC 恰好经过点O ,其中BC =12,OA =8, 则BD 的长为( ) A .20 B .19 C .18 D .16 (2012通州一模) ⑵ 如图,在Rt △ABC 中,∠ACB =90°,AC =3,BC =4,以点C 为 圆心,CA 为半径的圆与AB 交于点D ,则AD 的长为 . (2013黄石) 【解析】 ⑴A; ⑵ 5 18 . 【例2】 ⑴ 如图,AB 是O 直径,弦CD 交AB 于E ,45AEC ∠=?, 2AB =.设A E x =,22CE DE y +=.下列图象中,能表示y 与x 的函数关系的是( ) A B C D (2012海淀期中) ⑵ 如图,圆心在y 轴的负半轴上,半径为5的⊙B 与y 轴的正半轴交于点()1 0, A ,过点()7 0-,P 的直线l 与 ⊙ B 相交于 C 、 D 两点.则弦CD 长的所有可能的整 数值有( ) 典题精练 B A C D B A 平面几何的几个重要的定理 一、梅涅劳斯定理: 1=??=??B A A C C B C B A h h h h h h RB AR QA CQ PC BP l C B A h h h 的垂线的长度,则:到直线 、、分别是、、证:设 注:此定理常运用求证三角形相似的过程中的 线段成比例的条件; 。 的交点,证明:与是的中点,是上,在点 的平分线,是是斜边上的高,中,:若直角例CE //BF CK DE F AC D AK E ACK CE CK ABC ∠?11PC BP R Q P AB CA BC ABC ABC l 1=??RB AR QA CQ ,则 、、的延长线分别交于或它们 、、的三边的顶点,并且与不经过:若直线定理?? 1 11 111111111D B D A : C B C A B D AD :BC AC D C B A D C B A K 1=,试证:、、、和、、、线分别交这四条直线于引四条直线,另两条直】从点【练习于是可得即这时设必定重合,不然的话,与线段上,则同在与若的延长线上; 线段上,或者同在或者同在与因此,或边上的点的个数也为三点中,位于、、由于在同一直线上的= ,则:又得: ,于是由定理交于与直线证:设直线BR AR BR AR ,BR BR ,AR AB AR AB ,AR AR R R AB R R AB AB R R 20ABC R Q P RB AR B R AR 1RB AR QA CQ 1B R AR QA CQ 1R AB PQ ' ' ' ' ' ''''''''' '> <-<->=??=???PC BP PC BP ΘCE //BF CKE FKB KE BK KC KF BE BK FC KF BE BK BC BP AC EP AC CK AE EK FC KF 1FC KF EK AE DA CD F E D ACK EP CK EP BC EBC CE BH 90HCB ACE HCB HBC ACE HBC ACK EBC BH B EBC ∴?∴= ====??=∴⊥? =∠+∠=∠+∠∠=∠∠=∠∠?????=依分比定理有:= 即:=于是依梅涅劳斯定理有:、、和三点对于,则:上的高作为等腰三角形 即:则:的平分线中,作在证:Θ三点共线; 、、求证:, ,这时若或边上的点的个数为三点中,位于、、三点,并且 上或它们的延长线上的、、的三边分别是、、:设定理R Q P PC BP 20ABC R Q P AB CA BC ABC R Q P 21RB AR QA CQ =????平面几何四个重要定理
第1讲.圆中三大基本定理.尖子班.教师版
平面几何的几个重要的定理~~梅涅劳斯定理