
专题六几何探究题的解题思路
一、方法简述
随着中考的改革,几何的综合题不再是定格在”条件----演绎----结论”这样封闭的模式中,而是必须利用题设大胆猜想、分析、比较、归纳、推理,或由条件去探索不明确的结论,或由结论去探索未给予的条件,或讨论存在的各种可能性;探索图形的运动、变换规律更是中考的热点题型.解决此类问题,数学思想的合理应用起着关键性的作用,一个题目往往需要几个思想方法交织应用.
二、思想方法
1.分类讨论思想
分类讨论思想是数学中的重要思想方法之一,数学中的许多问题由于题设交代笼统,需要进行讨论,另外由于题意复杂,包含情况多也需要讨论。分类是按照数学对象的相同点或差异点,将数学对象分为不同种类的方法,其目的是复杂问题简单化。正确的分类必须周全,不重不漏;分类的原则是:(1)分类中的每一部分必须是独立的;(2)一次分类必须是一个标准;(3)分类讨论应逐级进行。
2.数形结合思想
数型结合就是将数和有关的图形结合起来,通过对图形的研究探索数量之间的关系,从而达到解决问题的方法。利用数型结合思想,可以将复杂的形化为具体的数,由形索数,由数导形,将数形有机地结合起来,加强数形思想的训练,对巩固数学知识,提高问题的解决能力,至关重要。
3.函数与方程思想
函数关系是指某个变化过程中两个变量之间的对应关系,方程是由已知量和未知量构成的矛盾的统一体,它是由已知探知未知的桥梁,从分析问题的数量关系入手,抓住问题的函数关系或等量关系,用数学语言将函数或等量关系转化为函数关系式或方程式,在通过函数的性质或方程的理论使问题获得解决的思想方法,就称为函数与方程思想。
4.转化与化归思想
转化与化归思想,也是初中数学常用的思想方法之一,是将不熟悉的问题转化、归结成熟悉问题的思想方法,就是将待解决的问题,通过分析、联想、类比等过程,选择恰当的方法进行变换,转化到已解决或比较容易解决的问题上,最终达到解决问题的目的,解决问题的过程实际上就是转化的过程。转化与化归原则主要有:熟悉化原则、简单化原则、直观性原则、正
图 2
P
D
C
B
A
图 1
D
C
B
A 难则反原则。
三、典例分析
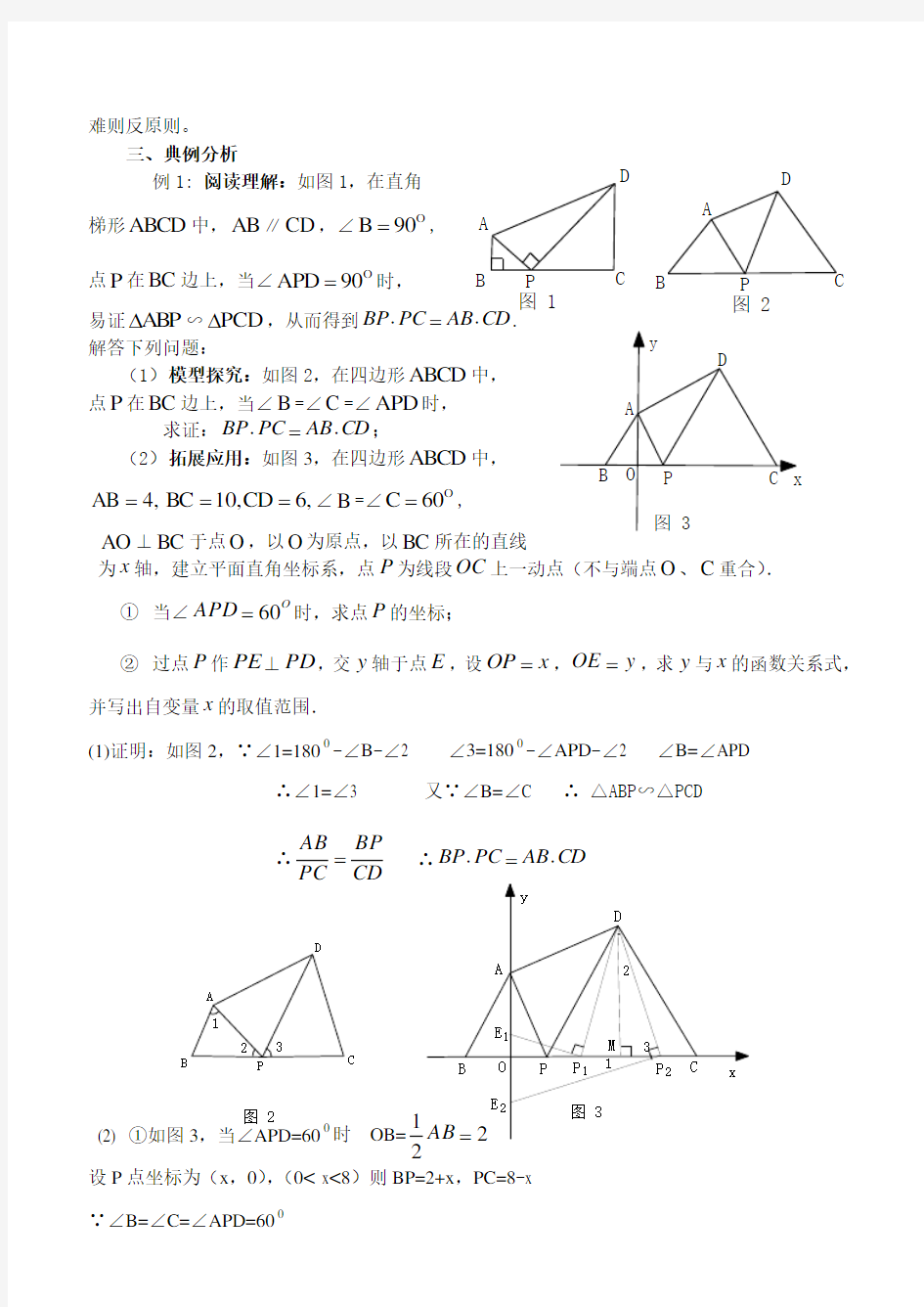
例1: 阅读理解:如图1,在直角 梯形ABCD 中,AB ∥CD ,∠O
90B =, 点P 在BC 边上,当∠O
90APD =时,
易证A B P ?∽PCD ?,从而得到CD AB PC BP ?=?. 解答下列问题:
(1) 模型探究:如图2,在四边形ABCD 中, 点P 在BC 边上,当∠B =∠C =∠APD 时,
求证:CD AB PC BP ?=?; (2) 拓展应用:如图3,在四边形ABCD 中,
4,AB =6,CD 10,BC ==∠B =∠O
60C =,
AO ⊥BC 于点O ,以O 为原点,以BC 所在的直线
为x 轴,建立平面直角坐标系,点P 为线段OC 上一动点(不与端点O 、C 重合).
① 当∠O
APD 60=时,求点P 的坐标;
② 过点P 作PE ⊥PD ,交y 轴于点E ,设x OP =,y OE =,求y 与x 的函数关系式,并写出自变量x 的取值范围.
(1)证明:如图2,∵∠1=1800
-∠B -∠2 ∠3=1800
-∠APD -∠2 ∠B=∠APD ∴∠1=∠3 又∵∠B=∠C ∴ △ABP ∽△PCD
∴
CD
BP
PC AB =
∴CD AB PC BP ?=?
(2) ①如图3,当∠APD=600时
设P 点坐标为(x ,0),(0< x <8)则BP=2+x ,PC=8-x
∵∠B=∠C=∠APD=600
图 2
3
2
1
P D
C
B
A
∴CD AB PC BP ?=? 即(2+x )(8-x)=64? 解得:x 1=2, 2x =4 ∴点P 的坐标为P (2,0)或P (4,0)
②解法一:如图3,过点D 作DM ⊥x 轴于点M 则CM=
32
1
=CD ,DM=33 ∴OM=5 (Ⅰ)当点P 在线段OM 上设为P 1,P 1M=x-5 (0 ∴OP 1?P 1M=OE ?1?DM 即x x -5()=33?y ∴x x y 9 35932+-= (0 ∵∠1+∠3=900 ∠2+∠3=900 ∴∠1=∠2 ∴Rt △E 2OP 2∽Rt △P 2MD ∴DM OP M P OE 222= ∴DM OE M P OP ?=?222 即x(x-5)= 33?y ∴x x y 9 3 5932-= (5 则CM=32 1 =CD ,DM=33 ∴OM=5 ∴D(5,33) (Ⅰ)当点P 在线段OM 上设为P 1,P 1M=5-x (0 ∵2121211D E D P P E =+ 即 x 5(22++y -x)2+ (33)2=(33-y)2+52 ∴x x y 9 3 5932+- = (0 ∵2222222D E D P P E =+ 即x x y (2 2++-5)2+ (33)2=(33+y)2+52 ∴x x y 9 35932-= (5 图 3 图 2 图 1 F E O D C B A 入手,到“一般”(图2为非直角情形);再从“一般”(问题(2)①)上升到新背景中的“特殊”(问题(2)②),使学生经历了“特殊—一般—特殊”由浅入深、归纳与演绎交替变化的思维过程.试题在第一环节中提供了 “易证, A B P ?∽PCD ?”的启示,学生在解破“易证”中的具有广泛意义的思考或研究方法(即所谓“一般性方法”)后,就能类比解决后续的各个问题.考查学生利用类比方法进行自主探究学习的能力.本题的价值不仅在于环环相扣、层层推进的精彩设置,更在于其本身突出地展示着“一般性方法”的深刻含义和普遍适用性,能掌握并善于运用一般性方法,就显示出较高的数学学习能力. 例2. 已知菱形ABCD 的边长为1,0 60ADC ∠=,等边AEF ?两边分别交边DC 、CB 于点E 、F . (1)特殊发现:如图1,若点E 、F 分别是边DC 、CB 的中点, 求证:菱形ABCD 对角线AC 、BD 的交点O 即为等边AEF ?的外心; (2)若点E 、F 始终在分别在边DC 、CB 上移动,记等边AEF ?的外心为点P . ①猜想验证:如图2,猜想AEF ?的外心P 落在哪一直线上,并加以证明; ②拓展运用:如图3,当AEF ?面积最小时,过点P 任作一直线分别交边DA 于点N , 交边DC 的延长线于点M ,试判断11 DM DN + 是否为定值,若是,请求出该定值;若不是,请说明理由 解:(1)证明:如图1,分别连接OE 、OF ∵四边形ABCD 是菱形 ∴AC ⊥BD ,BD 平分ADC ∠,BC DC AD == ∴O AOD COB COD 90=∠=∠=∠ O O ADC ADO 30602 1 21=?=∠= ∠ 又∵E 、F 分别为DC 、CB 中点 ∴CD OE 21=、BC OF 21=、AD AO 2 1 = ∴OA OF OE == ∴点O 即为AEF ?的外心 (2)①猜想:外心P 一定落在直线DB 上 图1 证明:如图2,分别连接PE 、PA ,过点P 分别作PI CD ⊥于I ,PJ AD ⊥于J . 则O PJD PIE 90=∠=∠ ∵O ADC 60=∠ ∴JDI PJD PIE IPJ O ∠-∠-∠-=∠360 ∴O O O O O IPJ 120609090360=---=∠ ∵点P 是等边AEF ?的外心, ∴O EPA 120=∠,PA PE = ∴EPA IPJ ∠=∠ ∴JPA IPJ ∠=∠ ∴PIE ?≌PJA ? ∴PJ PI =∠ ∴点P 在ADC ∠的平分线上,即点P 落在直线DB 上 分析:证点P 落在ADC ∠的平分线上,也就证明点P 到直线AD 、AC 的距离相等,如此便可构造两个直角三角形证明全等。若考虑对角互补,便可联想到四点共圆, 从而利用圆的性质便有下面两种解法。 另解法一:分别连接PA 、PC 、PD ∵四边形ABCD 是菱形,O ADC 60=∠ ∴O BCD 120=∠,CD AD = ∵点P 是等边AEF ?的外心, ∴O EAF 60=∠, ∴O BCE EAF 180=∠+∠ ∴A 、F 、C 、E 四点共圆,∴PC PA = ∵DC DA = ∴CDP ?≌ADP ? ∴ADP CDP ∠=∠ ∴P 落在ADC ∠的平分线上.即点P 落在直线DB 上. 另解法二::分别连接PA 、PE 、PD ∵点P 是等边AEF ?的外心 ∴O EPA 120=∠,PA PE = ∴O PEA 30=∠ ∵O EPA ADC 180=∠+∠ ∴A 、P 、E 、 D 四点共圆. ∵O PEA PDA 30=∠=∠ ∴P 落在ADC ∠的平分线上.即点P 落在直线DB ② 11DM DN +为定值2 当AE DC ⊥时,AEF ?面积最小, 图2 J 图3 图4 此时点E 、F 分别为DC 、CB 中点 连接BD 、AC 交于点P ,由(1) 可得点P 即为AEF ?的外心 解法一:如图,设MN 交BC 于点G 设,(0,0)DM x DN y x y ==≠≠,则1CN y =- ∵BC ∥DA ,且DA BC =,P 是BD 的中点 ∴GBP ?≌MDP ? ∴x DM BG == ∴x CG -=1 ∵BC ∥DA ∴NCG ?∽NDM ? ∴ DM CG DN CN = ∴x x y y -=-11 ∴xy y x 2=+ ∴211=+y x 即21 1=+DN DM 分析:观察图形,得到结论CG AM =,把1用AD 或CD 代替,把要计算的线段或相关 线段集中到两个相似的三角形NCG ?,NDM ?中,并把长度用字母表示,化简含字母的代数式从而得到结论。依据此策略,可得到解法二、三、四。 解法二:如图,连接PE ∵点P 、E 分别为AC 、DC ∴2 1 21== DA PE ,PE ∥DA ∴NEP ?∽NDM ∴DM EP ND NE = 设,DM x DN y == ,则2 1- =y NE ∴x y y 2121=- ∴y x xy 2 1 21=- ∴211211=+=+DN DM y x ,则 解法三:过点G 作直线GH ∥CD 交AD 于点H , ∵GH ∥CD ∴HMG ?∽DMN ? ∴ DM HM DN HG = ∴DM DM DM DM AM DM DN )1(1--= -= ∴211=+DN DM 解法四:过点C 作直线CK ∥MN 交BD 于点K ,过点A 作AH ∥MN 交BD 于H . ∵CK ∥MN ,AH ∥MN ∴DCK ?∽DNP ?,DMP ?∽DAH ? 图6 M H 图7 D ∴ DP DK DN DC =,DP DH DM DA = ∴DP DK DN =1,DP DH DM = 1 ∴DP DH DK DN DM +=+11 由CKP ?≌AHP ?得:HP KP = ∴DP DH DK 2=+ ∴21 1=+DN DM 解法五:如图,过点P 作PI DC ⊥于I ,PJ DA ⊥于J ,则4 PI PJ == ∵DMN DMP DNP S S S ???=+ ∴o DN DM PJ DM PI DN 60sin 212121??=?+? ∴2 3 2143214321??=?+?DN DM DM DN ∴DN DM DN DM ?=+2 ∴ 21 1=+DN DM 分析:因为11DM DN DM DN DM DN ++= ?,而DM DN ?正与DMN ?的面积有关,其中DM ,DN 也可以看成是将DMN ?分为DNP ?和DMP ?后,计算面积过程中涉及的底边。这种对 所求的结论作等份变形,找寻解题思路的方法是我们分析问题时常采用的一种重要方法。 解法六:如图4,以点D 为坐标原点,DA 所在直线为x 轴,建立平面直角坐标系 设直线MN 的解析式为y kx b =+ 可求得点P 的坐标为3(4 ∴34k b += ∴k b 4 3 43-= ∴直线MN 的解析式为k kx y 4 343-+ = 求得直线DN 的解析式为y = 图9 图10 令344kx k + -= ,∴3k x - = ∴3 232360cos --==k k x DN o 令3044kx k + -= ,∴344k x k = ∴k k DM 4343-= ∴ 2)33(21332 3233434311=--=- -+-=+k k k k k k DN DM 评析:本题是一道集阅读理解、实验操作、猜想证明、应用探究于一体的综合题型。试题 以菱形中的一个等边三角形旋转作为载体,综合考查了等边三角形、菱形两个基本图形的性质,同时考查了等边三角形的外心(中心)、三角形的中位线、相似、全等等初中数学几何主干知识;试题源于教材,立足数学通性、通法,具有公平性、原创性,既紧扣双基,又突出能力要求。本题就改变了传统几何证明题的模式(已知,求证,证明),将合情推理与演绎推理有机融合在一起,试题引导学生学会一种解决问题的策略——试验、发现、联想、推广。其新意主要体现在让学生在操作、实验等尝试性活动中表现出对基础知识的理解水平,对图形的分解与组合的能力,考查了学生的分析、观察、猜测、验证、计算与推理能力。本题结论开放、方法开放、思路开放,能有效地反映高层次思维,融会了特殊与一般、转化思想、数学建模思想、函数思想、数形结合思想。 其中第一道小题在静态图形中考查了特殊点下等边三角形外心(中心)的的判定,属于基础题;第二问为先猜想,因有第一步作铺垫不难猜测点P 落在直线DB 上,证点P 落在∠ADC 的平分线上,也就证明点P 到直线AD 、AC 的距离相等(结论转换),如此便可构造两个直角三角形证明相等,思路自然,知识基本,方法核心,属于能力考查范围;第﹙2﹚小题第②以探究性问题让学生先判断、后推理,重思维,轻计算,对学生的思维能力要求较高。 四、强化训练 1. 如图,在矩形ABCD 中,9AB = ,AD =P 是边BC 上的动点(点P 不与点B 、点C 重合),过点P 作直线PQ BD ∥,交CD 边于Q 点,再把PQC △沿着动直线PQ 对折,点C 的对应点是R 点,设CP 的长度为x ,PQR △与矩形ABCD 重叠部分的面积为y . (1)求CQP ∠的度数; (2)当x 取何值时,点R 落在矩形ABCD 的AB 边上? (3)求y 与x 之间的函数关系式; D Q C B P R A B A D C B A D C 备用图 图 2 图 1 F E C B A F E D C B A 2.如图1,在ABC Rt ?中,0 90=∠C ,6==BC AC ,D 是AB 边上一点,E 是在AC 边上的一个动点(与点A 、C 不重合),DE DF ⊥,DF 与射线CB 相交于点F 。 (1)如图1,如果点D 是边AB 的中点,求证:DF DE =; (2)如图2,如果m DB AD =,求DF DE 的值; (3)如果2 1 =DB AD ,设x AE =,y BF =,求y 关于x 的函数关系式,并写出x 的取值范围; A 3.四边形ABCD 是矩形,2=AB ,3=AD ,点M 是射线DC 上的一个动点(点M 不与点D 重合),N 是点M 关于AD 的对称点,射线AM 交射线BC 于E ,设m DM =, n CE =,ANE ?的面积为S . (1)如图1,当点M 在DC 边上..运动时,试用m 的代数式表示n ,并写出m 的取值范围; (2)当点M 在射线..DC 上运动时,判断ANE ?的面积S 是否为定值,若是定值,请求出该定值;若不是,请用m 的代数式表示S ,并写出m 的取值范围. 图 2 图` 1 H H G F E D C B A G F E D C B A 4. 已知:在矩形ABCD 中,10=AB ,12=BC ,四边形EFGH 的三个顶点E 、F 、H 分别在矩形ABCD 边AB 、BC 、DA 上,2=AE . (1)如图1,当四边形EFGH 为正方形时,求GFC ?的面积; (2)如图2,当四边形EFGH 为菱形,且a BF =时,求GFC ?的面积(用含a 的代数式表示); (3)在(2)的条件下,GFC ?的面积能否等于2?请说明理由. 5.已知,ABC ?是等腰直角三角形,0 90=∠BAC ,2=BC ,D 是线段BC 上一点,以 AD 为边,在AD 的右侧作正方形ADEF .直线AE 与直线BC 交于点G ,连接CF . (1)如图1,当1 (2)如图2,当1>BD 时,请在图中作出相应的图形,猜测线段CF 与线段BD 的关系,并 说明理由; (3)连接GF ,判断线段BD 为何值时,GFC ?是等腰三角形. A B C F D E G 图1 A B C D 图2 θ θ 图 3 图 2 图 1 P H G F E D C B A G F E D C B A G F E D C B A 6.有公共顶点大小不等的正方形ABCD 与正方形AEFG ,两个正方形分别绕着点A 旋转至下列图形的位置,其中θ=∠BAE ()1800(0 <<θ. (1) 如图1,连接BG 、DE ,判断线段BG 与DE 的数量及位置之间的关系,并说明理由; (2)连接BE 、DG ,过点A 的直线垂直DG 于H 交BE 于P . ①如图2,求证ABE ?与ADG ?的面积相等; ②如图3,试判断DG AP 是否为定值,如果是定值,求出该定值;如果不是,请说明理由. 图 2 图 1 M E D C B M E D C B A 7. (1)如图1,在ABC ?中,22==BC AC ,O ACB 90=∠,点E 在AC 边上(不 与点C A 、重合),过E 作AB DE ⊥于D ,连接BE CD 、,M 为BE 的中点,连接 DM CM 、. ①求证:CDM ?是等腰直角三角形; ②若x AD =,CDM ?的面积为S ,求S 与x 的函数关系式,并写出自变量x 的取值范围; (2)如果把图1中的ADE ?绕着点A 逆时针旋转至图2的位置,其它的条件不变,那么 CDM ?是否还是等腰直角三角形?请说明理由. 8.如图1,在菱形ABCD 中,AB =4,∠O BAD 120=,M 是BC 边上的点, ∠α=BAM (O 0<α 60),点N 在CD 边上,∠O MAN 60=,AM 、AN 分别与BD 相交于P 、Q 两点,当∠MAN 绕着点A 旋转时,点M 、N 、P 、Q 也随之运动.请解答下列问题; (1)求证:AMN ?是等边三角形; (2)在∠MAN 旋转的过程中,当α为何值时,四边形AMCN 的周长最小?求四边形AMCN 周长的最小值; (3)如图2,当DQ BP 2=时,判断PQ 与DQ 之间的数量关系,并说明理由. 图 1 图 2