重庆一中高2020级高三下5月月考试题

2017年重庆一中高2017级高三下期第一次月考数学试卷(理科)一选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且 只有一项符合题目要求.1. 若复数乙满足2z + Z = 3-2i ，其中i 为虚数单位，贝收=A. 1 + 2/B. 1-2/C. -1 + 2/D. -1-2/2. 已知U = R,M={xl_l<x<2},N = {xlx<3},贝i](QM)A^ =A. {xlx<-1或2vx<3}B. {xl2vx5 3}C. {xlx<-l^c2<x<3}D. {x12<x<3} 3. 下列说法正确的是A. a e 心丄v 1”是”d > 1”的必要不充分条件B. “ p W 为真命题是“ pyq 为真命题”的必要不充分条件C. 命题”3xeR,使得X 2+2X + 3<0"的否定是"VxwR,x2 + 2x + 3>0"D. 命题 p: e R 、sin x + cos x < ，则-y?是真命题个单位后得到函数g (x) = cos 的图象，则函数于(x)的图象5•如图是一个空间几何体的三视图，则该几何体的表而三角形中为直角三角形的个数为 :A. 2B. 3C.4D.5； 6. 在如图所示的程序框图中，若输出的值是3,则输入的x 取值范囤是t I A. (2,4] B. (2,g) C.(4JO] D. (4,g) ； ■7. 《算数书》竹简于上世纪八十年代在湖北省江陵县张家山出土，这是 ； 我国现存最早的有系统的数学典籍，其中记载有求“盖”的术：置如其'周，令相承也•又以高乘之，三十六成一•该术相当于给出了有圆锥的底而周长L 与高，计算4•已知函数/(x) = sin (Q¥ + 0)co>0.\(p\的最小正周期为兀，且其图象向左平移扌 A.关于直线2醫对称B.关于直线“菩对称c.关珂討对称D.关于点 对称其体积V的近似公式它实际上是将圆锥体积公式中的圆周率兀近似取为4,48那么近似公式Eh相当于将圆锥体积公式中兀的近似取为■ 25 厂25 厂25 小25A. —B. —C. —D.—6 8 3 48.等比数列｛%｝中,坷=1,畋=4,函数/(x)=x(x-tz1)(x-a2)(x-o3)---(x-6!n),若y = f(x)的导函数为y =广(兀)・则广(0)=A. IB. 2°C. 212D.2159•甲、乙.丙、丁.戊五位同学站成一排照相留念，则在甲乙相邻的情况下，甲丙也相邻的概率为1211A.—B. —C. 一D.-1033410.已知椭圆^- + p- = l(«>Z?>0)的左、右焦点分别为片迅，焦距为2近,若直线y = —J5(x +J㊁)与椭圆交于点M,满足丄ZMF｝F2 = ，则离心率是2A.返B.苗—1C.耳D.迺2 2 211 •点M为棱长是2血的正方体ABCD-A X B X C X D｛的内切球O球而上的动点，点N为的中点.若满足QM丄BN,则动点M的轨迹的长度为A.R),若关于X的方程f2(A-)-丄mf(x) +丄m — 1 = 0恰好有2 24个不相等的实根，则加的取值范国是二填空题：本大题共4小题，每小题5分，共20分・13.("X + J7)'的展开式中疋项的系数为20,则实数14.已知awR ,则函数/(x) = l-sin2(x+a)+cos(x+a)sin(x+a)的最大值为____________ :15.一般吧数字岀现的规律满足如图的模型称为蛇形模型：数字1 出现在第1行，数字2,3出现在第2行：数字6.5,4 (从左到右)出现在第3行：数字7,8.930出现在第4行，以此类推，第21行从左到右的第4个数字应是___B.12•已知函数/(%) =16•如图，正三棱柱ABC-A^Q的各棱长均相等，D为人人的中点，M,N分别是线段和线段CC；上的动点（含端点），且满足BM = C{N ,当M,N运动时，下列结论中正确的序号为____________①△DMN可能是直角三角形；②三棱锥A、一 DMN的体积为左值：③平而QMN丄平而BCCb ；④平而DA/N与平而ABC所成的锐二而角范用为三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.17.（本题满分12分）在AABC中，a,b,c分别是A.B.C的对边，且汇£ = ?匸^a+c = 2.cosB b（1）求角B;（2）求边长b的最小值.18.（本题满分12分）某校高三（5）班的一次数学小测试成绩的茎叶图和频率分布直方图都受到不同程度的破坏, 但可见部分如下，据此解答如下问题：（1）求全班人数，并讣算频率分布直方图中［80,90］间的矩形的髙：（2）若要从分数在［80,100］之间的试卷中任选三份来分析学生失分情况，其中"表示分数在［80,90］之间被选上的人数，u表示分数在之［90,100］间被选上的人数，记变量4= H-V.求§的分布列和期望.19.（本题满分12分）如图，正方形AMDE的边长为2, 分别为AM.MD的中点，在五棱锥P-ABCDE中，F为棱PE■的中点，平而4BF与棱PD、PC分别交于G,H两点.（1）求证：ABHFG；' G（2）若P4丄平而ABCDE,且= 求平面PCD与平面 E "ABF所成角（锐角）的余弦值，并求线段PH的长.20.（本题满分12分）A B M2 2已知椭圆C:* +计=1（°＞方＞0）的左焦点F（-l,0）,过点F作与x轴垂直的宜线与椭圆交于M,N两点，且\MN\ = 3.（1）求椭圆C的方程；（2）过点F（-l,0）的直线交椭圆于A.B两点，线段AB的中为GAB的中垂线与x轴和y轴分别交于ZXE两点，记的而积为5, 取值范围.21.（本题满分12 分）已知f（x） = 2c\nx-x2（ceR）.（1）讨论函数.f（x）的单调区间；⑵若c = l,设函数g（x） = f（x）-mx的图象与x轴交于A（^,0）,B（E，0）两点，且0 ＜册v勺，又y = g\x）是y = g（X）的导函数，若正常数匕〃满足a + b = ^b＞a，证明：g'@[ +bx2）＜0请考生在第22、23两题中任选一题作答，如果多做，则按照所做的第一题计分.22.（本题满分10分）选修4-4：极坐标与参数方程已知曲线C]的极坐标方程为Q（J?COS&-sin8）= “ ,曲线C2的参数方程为x = sin& + cos&门（0为参数），且G与c,有两个不同的交点.y = l+sin2&（1）写岀曲线q的直角坐标方程和曲线C?的普通方程：（2）求实数。

一．方法综述三视图几乎是每年的必考内容，一般以选择题、填空题的形式出现，一是考查相关的识图，由直观图判断三视图或由三视图想象直观图，二是以三视图为载体，考查面积、体积的计算等，均属低中档题.还原几何体的基本要素是“长对齐，高平直，宽相等”.要切实弄清常见几何体(圆柱、圆锥、圆台、棱柱、棱锥、棱台、球)的三视图的特征，熟练掌握三视图的投影方向及正视图原理，才能迅速破解三视图问题，由三视图画出其直观图．对于简单几何体的组合体的三视图，首先要确定正视、侧视、俯视的方向，其次要注意组合体由哪些几何体组成，弄清它们的组成方式，特别应注意它们的交线的位置．解题时一定耐心加细心，观察准确线与线的位置关系，区分好实线和虚线的不同. 根据几何体的三视图确定直观图的方法： （1）三视图为三个三角形，对应三棱锥；（2）三视图为两个三角形，一个四边形，对应四棱锥； （3）三视图为两个三角形，一个带圆心的圆，对应圆锥； （4）三视图为一个三角形，两个四边形，对应三棱锥； （5）三视图为两个四边形，一个圆，对应圆柱.对于几何体的三视图是多边形的，可构造长方体（正方体），在长方体（正方体）中去截得几何体.二．解题策略类型一 构造正方体（长方体）求解【例1】某几何体的三视图如图所示，关于该几何体有下述四个结论：①体积可能是56；②体积可能是23；③AB 和CD 在直观图中所对应的棱所成的角为3；④在该几何体的面中，互相平行的面可能有四对；其中所有正确结论的编号是（ ）A ．①③B ．②④C ．①②③D ．①②③④【来源】河南省开封市2021届高三三模文科数学试题专题4.1 复杂的三视图问题【答案】D【举一反三】1．（2020·江西高三）某几何体的三视图如图所示，其中网格纸上小正方形的边长为1，则该几何体的体积为（）A．9B．92C．6D．32、某三棱锥的三视图如图所示，则该三棱锥的体积为（）A.16B.13C.12D.13．若一个几何体的三视图如图所示，则该几何体的体积为（）A ．4B ．8C ．12D ．14类型二 旋转体与多面体组合体的三视图【例2】（2020·内蒙古高三）如图所示，是某几何体的正视图（主视图），侧视图（左视图）和俯视图，其中俯视图为等腰直角三角形,则该几何体体积为（ ）A ．620π+B ．916π+C ．918π+D ．2063π+【举一反三】一个四棱柱被截去一个半圆柱后剩余部分的三视图如图，则截去部分与剩余几何体的体积比为（ ）A ．18ππ- B ．318ππ-C ．12ππ-D ．312ππ-类型三 与三视图相关的外接与内切问题【例3】（2020·辽宁鞍山一中高三月考）已知四棱锥P ABCD -的三视图如图所示，则四棱锥P ABCD -外接球的表面积是（ ）A．20πB．1015πC．25πD．22π【举一反三】1．（2020·四川成都七中高考模拟）某多面体的三视图如图所示，则该几何体的体积与其外接球的体积之比为（）A．618πB．69πC．63πD．13π2.如图，网格纸上小正方形的边长为2，粗实线及粗虚线画出的是某几何体的三视图，则该几何体的外接球的表面积为A ．30B ．41C ．30D ．64【来源】甘肃省兰州市第一中学2020届高三冲刺模拟考试（一）数学（文）试题 3．（2020·山西高三）某棱锥的三视图如图所示，则该棱锥的外接球的表面积为（ ）A ．11πB ．12πC ．13πD ．14π类型四 与三视图相关的最值问题【例4】（2020·武邑宏达学校高考模拟（理））已知在直三棱柱111ABC A B C -中，120BAC ∠=︒，12AB AC AA ===，若棱1AA 在正视图的投影面α内，且AB 与投影面α所成角为(3060)θθ︒≤≤︒.设正视图的面积为m ，侧视图的面积为n ，当θ变化时，mn 的最大值是__________．【举一反三】1.某几何体的一条棱长为7，在该几何体的正视图中，这条棱的投影是长为6的线段，在该几何体的侧视图与俯视图中，这条棱的投影分别是长为a 和b 的线段，则a+b 的最大值为 （A ）22 （B ）23 （C ）4 （D ）252、某三棱锥的三视图如图所示，且三个三角形均为直角三角形，则xy 的最大值为（ ）A.32 732.B C.64 764.D3．（2020·西安市长安区第五中学高三（理））如图是一个几何体的三视图，在该几何体的各个面中，面积最小的面的面积为（）A．8 B．4C．42D．43三．强化训练1．（2020·福建高三）中国古代数学名著《九章算术》中记载了公元前344年商鞅监制的一种标准量器——商鞅铜方升，某商鞅铜方升模型的三视图，如图所示(单位：寸)，若 取3，则该模型的体积（单位：立方寸）为（）A．11.9 B．12.6 C．13.8 D．16.22．（2020·北京人大附中高三）已知某多面体的三视图如图所示，则在该多面体的距离最大的两个面中，两个顶点距离的最大值为（）A．2 B5C6D．23．（2020·北京市十一学校高三）某四棱锥的三视图如图所示，网格纸上小正方形的边长为1，则该四棱锥的体积为A．43B．4C．423D．424．（2020·湖南雅礼中学高三月考（理））一个多面体的三视图如图所示，其中正视图是正方形，侧视图是等腰三角形，则该几何体的表面积为（）A．168 B．98 C．108 D．885．（2020·重庆一中高三月考（理））如图的虚线网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图.在该几何体的直观图中，直线AB与CD所成角的余弦值为（）A．15B．25C5D256．（2020·江西高三）半正多面体(semiregular solid) 亦称“阿基米德多面体”，是由边数不全相同的正多边形为面的多面体，体现了数学的对称美．二十四等边体就是一种半正多面体，是由正方体切截而成的，它由八个正三角形和六个正方形为面的半正多面体.如图所示，图中网格是边长为1的正方形，粗线部分是某二十四等边体的三视图，则该几何体的体积为（）A．83B．4C．163D．2037.（2020·江西高三期末（理））如图，网格纸上小正方形的边长为1，粗实线画出的是一个三棱锥的三视图，则该三棱锥的外接球的表面积是（）A．B．C．D．8.（2020合肥市高三）我国古代《九章算术》将上、下两面为平行矩形的六面体称为刍童.右图是一个刍童的三视图，其中正视图及侧视图均为等腰梯形，两底的长分别为2和4，高为2，则该刍童的表面积为A． B．40 C． D．9．一个几何体的三视图如图所示，则这个几何体的体积为A． B． C． D．10．榫卯（sǔnmǎo）是两个木构件上所采用的一种凹凸结合的连接方式.凸出部分叫榫，凹进去的部分叫卯，榫和卯咬合，起到连接作用.代表建筑有北京的紫禁城、天坛祈年殿，山西悬空寺等，如图是一种榫卯构件中榫的三视图，则该榫的表面积和体积为（）A． B． C． D．11．如图是某几何体的三视图，其中网格纸上小正方形的边长为1，则该几何体的表面积为（）A ．3682+B ．3282+C ．3242+D ．3642+【来源】云南师范大学附属中学2021届高三高考适应性月考卷（六）理科数学试题12．（2020·安徽高三月考）一副三角板由一块有一个内角为60︒的直角三角形和一块等腰直角三角形组成，如图所示，1AB =，60A ∠=︒，90B F ∠=∠=︒，BC DE =.现将两块三角板拼接在一起，使得二面角F BC A --为直二面角，则三棱锥F ABC -的外接球表面积为（ ）A ．4πB ．3πC ．2πD ．π13．已知正方体1111ABCD A B C D -（如图1），点P 在侧面11CDD C 内（包括边界）.若三棱锥1B ABP -的俯视图为等腰直角三角形（如图2），则此三棱锥的左视图不可能是（ ）A．B．C．D．【来源】北京市海淀区2021届高三二模数学试题14．如图，网格纸上小正方形的边长为1，粗线是某几何体的三视图，则该几何体的各个面中最大面积为（）A．6 B22C．32D13【来源】贵州省普通高等学校招生2021届高三适应性测试（3月）数学（文）试题15．已知一个三棱锥的三视图如图所示，其中俯视图是等腰直角三角形，则该三棱锥的外接球表面积（）A．3πB．23πC．43πD．12π【来源】四川省泸州市泸县第五中学2021届高三高考数学（文）一诊试题16．已知某几何体的三视图如图所示，则该几何体的体积为（）A．12B．32C．1D．3317．某几何体的三视图如图所示（单位：cm），则该几何体内切球的表面积（单位：2cm）是（）A ．9π16B ．9π4C ．1π4D ．9π2【来源】安徽省江淮十校2021届高三下学期4月第三次质量检测理科数学试题18．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，该三棱锥所有表面中，最大的面积为（ ）A ．2B ．22C ．23D ．42【来源】安徽省五校联盟2021届高三下学期第二次联考理科数学试题19．如图，正四棱锥P ABCD -的高为12，62AB =，E ，F 分别为PA ，PC 的中点，过点B ，E ，F 的截面交PD 于点M ，截面EBFM 将四棱锥分成上下两个部分，规定BD 为主视图方向，则几何体CDAB FME -的俯视图为（ ）A．B．C．D．【来源】江西省南昌市2021届高三二模数学（理）试题20．三棱柱被一平面截去一部分后，剩余部分的三视图如图所示，则该几何体的体积为（）A．203B．6 C．52D162【来源】景德镇市2021届高三第三次质检数学（理）试题21．某几何体的三视图如图所示，则该几何体的体积为（）A ．246π-B ．86π-C ．246π+D ．86π+【来源】河南省六市2021届高三第二次联考（二模）数学（文科）试题22．某几何体的三视图如图所示，则该几何体的体积为（ ）A ．2B ．4C ．163D ．22323．正三棱锥（底面为正三角形，顶点在底面的射影为底面中心的棱锥）的三视图如图所示，俯视图是正三角形，O是其中心，则正视图（等腰三角形）的腰长等于（）A．5B．2 C．3D．224．某几何体的三规图如图所示. 则其外接球的表面积为（）A．803πB．1369πC．5449πD．483π【来源】百师联盟2020-2021学年高三下学期开年摸底联考考理科数学试卷（全国Ⅰ卷）25．已知一个三棱锥的三视图如图所示，则该三棱锥的外接球的体积为（）A．32πB．823πC．833πD．8π26．（2020·湖北高三期末（理））中国的计量单位可以追溯到4000多年前的氏族社会末期，公元前221年，秦王统一中国后，颁布同一度量衡的诏书并制发了成套的权衡和容量标准器.下图是古代的一种度量工具“斗”（无盖，不计量厚度）的三视图（其正视图和侧视图为等腰梯形），则此“斗”的体积为（单位：立方厘米）27．（2020·陕西高三（理））某几何体的三视图如图所示，若该几何体的体积为103，则棱长为a的正方体的外接球的表面积为28．（2020·深圳市高级中学高三（理））某几何体的三视图如图所示，主视图是直角三角形，侧视图是等腰三角形，俯视图是边长为3的等边三角形，若该几何体的外接球的体积为36 ，则该几何体的体积为__________．29．（2020·福建高三期末（理））农历五月初五是端午节，民间有吃粽子的习惯，粽子又称粽籺，俗称“粽子”，古称“角黍”，是端午节大家都会品尝的食品，传说这是为了纪念战国时期楚国大臣、爱国主义诗人屈原.如图，平行四边形形状的纸片是由六个边长为1的正三角形构成的，将它沿虚线折起来，可以得到如图所示粽子形状的六面体，则该六面体的体积为____；若该六面体内有一球，则该球体积的最大值为____．30．某三棱锥的正视图和俯视图如图所示，已知该三棱锥的各顶点都在球O的球面上，过该三棱锥最短的棱的中点作球O的截面，截面面积最小为______．【来源】内蒙古锡林郭勒盟全盟2021届高三第二次模拟考试数学（理科）试题31．一个直三棱柱的三视图如图所示，则该直三棱柱的体积为_______，它的外接球的表面积为________．。

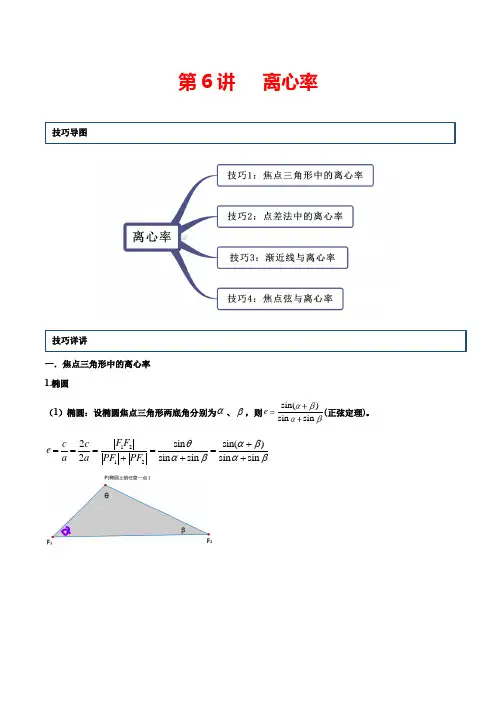
第6讲离心率一．焦点三角形中的离心率1.椭圆（1）椭圆：设椭圆焦点三角形两底角分别为α、β，则sin()sin sine(正弦定理)。

12122sin sin()2sin sin sin sinF Fc cea a PF PFθαβαβαβ+=====+++222121212212121221212221212212212(2)2cos =()22cos =()2(1cos ) ()2()(1cos )21=()[1(1cos )]21=()(F F PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF θθθθθ=+-+--+-++≥+-++-++12222222cos )==2111144(cos )cos (12sin )sin 222222sin2PF PF P c c a a e θθθθθθ-∴≥-≥-=--=∴≥（当且仅当取，即在短轴端点处）即2.双曲线：利用焦点三角形两底角,αβ来表示:sin()sin sine。

12122sin sin()2sin sin sin sin +=====---F F c c e a a PF PF θαβαβαβ二．双曲线的渐进线与离心率关系 直线与双曲线相交时，两个交点的位置（1）两个交点在双曲线的两支：b k e a >⇔=（2）两个交点在双曲线的同一支:b k e a <⇔=（3）两个交点在双曲线的左支:12120x x 0x x 0>⎧⎪⎪+<⎨⎪>⎪⎩（4）两个交点在双曲线的右支:12120x x 0x x 0>⎧⎪⎪+>⎨⎪>⎪⎩三．焦点弦与离心率关系λ=，则有11cos +-=λλθe (θ为直线与焦点所在轴的夹角)。

技巧1 焦点三角形中的离心率【例1】(1)．已知1F ，2F 是双曲线E ：22221x y a b-=的左、右焦点，点M 在E 上，1MF 与x 轴垂直，12tan FMF ∠=E 的离心率为（ ） A ．B ．2CD （2）（2020·安徽省高三三模）已知椭圆E ：()222210x y a b a b+=>>的左右焦点分别为1F ，2F ，若在椭圆E 上存在点P ，使得12PF PF ⊥，则椭圆E 的离心率的取值范围为（ ）A ．,12⎫⎪⎪⎣⎭ B ．0,2⎛⎫⎪ ⎪⎝⎭ C ．,12⎫⎪⎪⎣⎭D ．1,12⎛⎫⎪⎝⎭【答案】（1）C （2）A【解析】（1）不妨设(,),0M c y y ->代入双曲线方程得22,(,)b b y M c a a =∴-21212222,tan 0,c F F c F MF ac ba=∠==-= 2220ac e --=--=，()10,e e -+=∴=故答案选：C（2）12PF PF ⊥，2221212PF PF F F ∴+=()()()()222212122212121212222PF PF PF PF PF PF PF PF PF PF PF PF +++=+-⋅≥+-=（当且仅当12PF PF =时取等号），()2122122PF PF F F +∴≥，由椭圆定义知：122PF PF a +=，又122F F c =，2242c a ∴≥，212e ∴≥，2e ∴≥，又1e <，∴离心率e的取值范围为,12⎫⎪⎪⎣⎭.故选：A . 【举一反三】1．（2020·沙坪坝区·重庆一中高三月考）已知点P 在以12,F F 为左，右焦点的椭圆()2222:102x y C b b b+=>上，在12PF F △中，若12PF F α∠=，21PF F β∠=，则()sin sin sin αβαβ+=+（ ）A ．12BC．2D【答案】B【解析】12PF F △中，()()12121212||||||||||||sin sin sin sin sin sin PF PF F F PF PF F F αβαβαβαβ+==∴=+++ 所以()1212sin ||2sin sin ||||22F F c c PF PF a a αβαβ+=====++故选：B 2．（2020·全国高三专题练习）已知点P 是以1F 、2F 为焦点的椭圆()222210x y a b a b +=>>上一点，若12PF PF ⊥，21tan 2PF F ∠=，则椭圆的离心率e =（ ）AB ．13C ．23D ．12【答案】A【解析】点P 是以1F 、2F 为焦点的椭圆()222210x y a b a b+=>>上一点，12PF PF ⊥，1212tan 2PF PF F PF ∠==，122PF PF ∴=， 122PF PF a +=，可得143a PF =，223a PF =， 由勾股定理可得2221212PF PF F F +=，即222049a c =，2259ca ∴=，因此，该椭圆的离心率为3e =. 故选：A.3．（2019·辽宁沈阳市·沈阳二中高三月考（理））椭圆22221(0)x y a b a b+=>>，1F 、2F是椭圆的两个焦点，P 是圆上一动点，则12cos F PF ∠的最小值是（ ） A ．13- B ． C ．1-D ．0【答案】A【解析】椭圆22221(0)x y a b a b +=>>，即2223c a =.122PF PF a +=≥212PF PF a ⋅≤，当12PF PF a ==时等号成立.根据余弦定理：()222221211212121212122cos 22PF PF PF PF F F PF PF F F F PF PF PF PF PF +-⋅-+-∠==⋅⋅22222124444111223a c a c PF PF a --=-≥-=-⋅.故选：A .技巧2 点差法中的离心率【例2】（1）（2020·四川外国语大学附属外国语学校）过点()1,2M 作直线16y x m =-+与椭圆()222210x y a b a b+=>>相交于,A B 两点，若M 是线段AB 的中点，则该椭圆的离心率是（ ） A ．23B．3C ．1112D．6（2）（2020·安徽省潜山第二中学）已知A ，B 是椭圆E ：22221(0)x y a b a b+=>>的左、右顶点，M 是E 上不同于A ，B 的任意一点，若直线AM ，BM 的斜率之积为49-，则E 的离心率为() A．3BC ．23D【答案】（1）B （2）D【解析】（1）设()11,A x y ，()22,B x y ， 由直线AB 的斜率为16-可得121216y y x x ， 由线段AB 的中点为()1,2M 可得1212x x +=，1222y y+=， 由点,A B 在椭圆上可得22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，作差得22221212220x x y y a b --+=， 所以()()()()12121212220x x x x y y y y a b +-+-+=，即()()121222240x x y y a b --+=，所以()212212213y y b a x x -=-=-，所以该椭圆的离心率c e a ===故选：B.（2）由题意方程可知，(,0),(,0)A a B a -，设00(,)M x y ,0000,,AM BM y y k k x a x a∴==+- 则000049y y x a x a ⋅=-+- ,，整理得：2022049y x a =--，① 又2200221x y a b+=，得2222002()b y a x a =-，即2202220y b x a a =--，② 联立①②，得2249b a -=-，即22249a c a -=，解得e =． 故选D ． 【举一反三】1．已知双曲线C ：()222210,0x y a b a b-=>>，斜率为2的直线与双曲线C 相交于点A 、B ，且弦AB 中点坐标为()1,1，则双曲线C 的离心率为（ ） A ．2 BCD ．3【答案】B【解析】设11(,)A x y 、22(,)B x y ，则2211221x y a b -=，2222221x y a b-=， 所以2222121222x x y y a b --=，所以2121221212y y x x b x x a y x -+=⨯-+， 又弦AB 中点坐标为()1,1，所以122x x +=，122y y +=，又12122y y x x --=，所以22222b a =⨯，即222b a=，所以双曲线的离心率c e a ======. 故选：B.2．（2020·全国高三专题）已知1F 、2F 是椭圆的两个焦点，满足120MF MF ⋅=的点M 总在椭圆内部，则椭圆离心率的取值范围是（ ）.A ．1(0)2， B ．(02， C ．1(22， D ．1)2【答案】B【解析】∵120MF MF ⋅=，∴12MF MF ⊥，∴点M 在以12F F 为直径的圆上，又点M 在椭圆内部，∴c b <，∴2222<=-c b a c ，即222c a <，∴2212c a <，即c a <0e >，∴02e <<，故选：B.3．（2020·全国高三专题练习）若1F ，2F 是椭圆的两个焦点，P 是椭圆上一点，当12PF PF ⊥，且1230PF F ∠=︒，则椭圆的离心率为（ ）A 1B ．3C 1D ．2【答案】C【解析】依题意可知1290F PF ∠=︒，12||2F F c =，1230PF F ∠=︒，112PF F F ∴==，21212PF F F c ==，由椭圆定义可知1221)PF PF a c +==，1ce a∴==.故选：C. 技巧3 渐近线与离心率【例3】已知圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>有两个交点，则双曲线C 的离心率的取值范围是（ ）A ．B ．(1,2)C ．)+∞D ．(2,)+∞【答案】D【解析】由题意，圆心到直线的距离2d ==，解得k =圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>有两个交点，所以b a >22214b e a=+>，所以2e >.故选：D.【举一反三】1．若双曲线22221x y a b-=（0a >，0b >）与直线y x =无公共点，则离心率e 的取值范围是（ ）A ．(B ．(C ．(]1,2D ．()1,2【答案】A 【解析】若双曲线22221(0,0)x y a b a b-=>>与直线y x =无公共点，∴等价为双曲线的渐近线b y x a =的斜率1ba，即b a ，即22b a ，即222c a a -，即222c a ， 则2ca ，则2e ，1e >，∴离心率满足12e<，即双曲线离心率的取值范围是(，故选：A ．2．已知双曲线22221x y a b-= (a>0，b>0)的右焦点为F ，若过点F 且倾斜角为60°的直线l 与双曲线的右支有且只有一个交点，则此双曲线的离心率e 的取值范围是（ ） A ．[2,)+∞ B ．(1,2),C ．(2,)+∞D ．(1,2]【答案】A【解析】已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为3π的直线与双曲线的右支有且只有一个交点，则该直线的斜率的绝对值小于等于渐近线的斜率b a， ∴3b a，离心率22224a b e a +=，2e ∴，故选A ．3．（2020·河南新乡市·高三）已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ，过原点O的直线交C 的右支于点A ，若1223F AF π∠=，则双曲线的离心率为（ ） AB1CD【答案】D【解析】题可知123FOA π∠=，121AFO F AF ∠=∠，112FOA F AF ∠=∠，112FOA F AF ∴△△， 所以11112FO F A F AF F =，可得1F A =.在12F AF 中，由余弦定理可得22212121222cos3F F AF AF AF AF π=+-⋅，即222220AF AF c ⋅-=，解得22AF c=.双曲线的离心率为1212F FeAF AF===-.故选：D.技巧4 焦点弦与离心率【例4】（2020·石嘴山市第三中学高三三模）已知椭圆22221x ya b+=的左右焦点分别为12,F F，过1F作倾斜角为45的直线与椭圆交于,A B两点，且112F B AF=，则椭圆的离心率=（）A．3B．2C．2D．3【答案】D【解析】椭圆22221x ya b+=的左右焦点分别为12F F、，过1F c-（，）且斜率为1k=的直线为y x c=+联立直线与椭圆方程22221x ya by x c⎧+=⎪⎨⎪=+⎩消x后，化简可得2222222220a b y cb y c b a b+++-=（）因为直线交椭圆于A，B，设1122A x yB x y（，），（，）由韦达定理可得22222121222222y y,y ycb c b a ba b a b-+=-=++且112F B AF=，可得212y y=-，代入韦达定理表达式可得2222221122222,2cb c b a by ya b a b--=--=++即222222222222cb c b a ba b a b⎛⎫--=⎪++⎝⎭化简可得229c2a=所以cea==故选：D．【举一反三】1．（2020·河南省高三月考）倾斜角为4π的直线经过椭圆22221(0)x y a b a b+=>>右焦点F ，与椭圆交于A 、B 两点，且2AF FB =，则该椭圆的离心率为（ ）A ．2B ．3C ．2D ．3【答案】B【解析】设B 到右准线距离为d ，则BF ed =，因为2AF FB =，则2AF ed =，所以 A 到右准线距离为2d ，从而3AB ed= 倾斜角为4π，cos 433d e ed π∴=∴=，选B. 2．（2020·全国高三专题练习）已知1F 、2F 是双曲线22221x y a b-=(0a >，0b >)的左、右焦点，过2F 作双曲线一条渐近线的垂线，垂足为点A ，交另一条渐近线于点B ，且2213AF F B =，则该双曲线的离心率为（ ） A ．3或33B ．6或3C 或D 【答案】B【解析】（1）当2213AF F B =时，设2F OA α∠=，则2AOB α∠=，设1a =，由题意可知1OA a ==，2OF c e ==，2AF b =，23BF b =，则4AB b =，tan b b a α==，4tan 24b b a α==， 代入得222tan 2tan 241tan 1bb b ααα===--，即2244b =-，解得b =2e c ====，（2）当2213F A F B =时，设2F OA α∠=，AOB β∠=，设1a =，则2F OB αβ∠=+，1()FOB παβ∠=-+， 由题意可知1OA a ==，2OF c e ==，2AF b =，23BF b =， 则2AB b =，tan b b a α==，2tan 2b b aβ==， 则1tan tan[()]tan()tan FOB παβαβα∠=-+=-+=， 则tan tan tan()tan 1tan tan αβαβααβ++==--⋅，代入得212b bb b b+=--⋅，即2321b =-，解得b =则e c === 故选：B .3．（2019·浙江高三其他模拟）已知过双曲线()222210,0x y a b a b-=>>的右焦点F ，且与双曲线的渐近线平行的直线l 交双曲线于点A ，交双曲线的另一条渐近线于点B （A ，B 在同一象限内），满足2FB FA =，则该双曲线的离心率为（ ）A ．43BC D ．2【答案】B【解析】双曲线的渐近线方程为by x a=±，如图，不妨设,A B 在第一象限，直线l 的方程为()b y x c a =--，与22221x y a b-=联立，得32A b y ac =；直线l 与by x a =联立，得2B bc y a=． 由||2||FB FA =，得2B A y y =，即3222bc b a ac=⨯， 得222c b =，即222c a =，则e =B ．1．已知倾斜角为π4的直线与双曲线C ：22221x y a b-=（0a >，0b >）相交于A ，B 两点，(4,2)M 是弦AB的中点，则双曲线的离心率为（ ） A BC ．32D 【答案】D【解析】因为倾斜角为π4的直线与双曲线C ：22221x y a b-=（0a >，0b >）相交于A ，B 两点，所以直线的斜率tan14πk ==， 设()()1122,,,A x y B x y ，则2211221x y a b -=①2222221x y a b-=②由①-②得()()()()1212121222x x x x y y y y a b -+-+=则2121221212y y b x x k x x a y y -+==⋅-+因为(4,2)M 是弦AB 的中点，12128,4x x y y ∴+=+=因为直线的斜率为122814b a ∴=⋅即222211,22b b a a==所以2222112c a b a ⎛⎫=+=+ ⎪⎝⎭232e ∴=，则2e =，故选：D2．设F 是双曲线22221(0,0)x y a b a b-=>>的右焦点.过点F 作斜率为-3的直线l 与双曲线左、右支均相交.则双曲线离心率的取值范围为（ ）A ．B ．C ．)+∞D ．)+∞【答案】C【解析】因为双曲线22221(0,0)x y a b a b -=>>的两条渐近线方程为b y x a=±，当过点F 且斜率为-3的直线l 与渐近线by x a=-平行时. 直线l 只与双曲线右支有一个交点，数形结合可知， 当渐近线by x a =-的斜率满足3b a -<-，即3b a>时， 直线l 与双曲线左、右支均相交，所以22223910b a b a c a e >⇒>⇒>⇒>故选:C.3．（2019·黑龙江佳木斯市·佳木斯一中高三月考）已知1F ，2F 分别是椭圆22142x y +=的左、右焦点，P 是此椭圆上一点，若为12F PF △直角三角形，则这样的点P 有（ ）.A ．2个B ．4个C ．6个D ．8个【答案】C【解析】由题意2,a b ==，则c =P 为椭圆短轴顶点时，122PF PF ==，12F F =2221212PF PF F F +=，即12PF PF ⊥，短轴顶点有2 个，过1F 或2F 作x 轴垂直与椭圆相交的点P 在4个，12PF F ∆都是直角三角形，因此共有6个． 故选：C.4．（2020·广东广州市）已知1F ,2F 分别是椭圆C ()2222:10x y a b a b+=>>的左, 右焦点, 椭圆C 上存在点P 使12F PF ∠为钝角, 则椭圆C 的离心率的取值范围是A．2⎛⎫⎪ ⎪⎝⎭B ．1,12⎛⎫⎪⎝⎭C．2⎛⎫ ⎪⎝⎭D ．10,2⎛⎫⎪⎝⎭【答案】A【解析】设椭圆的上顶点为0A b （，），则∵椭圆上存在点P ，使12F PF ∠为钝角, 121212904511bF AF AF F tan AF F c∠>︒∴∠<︒∴∠<∴≤2220112a c e e e ∴∴∴<＜＜＜故答案为A 5．（2020·河北石家庄市）已知椭圆22221(0)x y a b a b+=>> ，点M,N 为长轴的两个端点，若在椭圆上存在点H ，使1(,0)2MH NH k k ∈- ,则离心率e 的取值范围为 A ．2 B ．2C ．D ． 【答案】A【解析】由题意00M a N a -（，），（，）． 设00H x y （，） ，则222202 ()b y a x a．=- 2222202000222220000()1,02MH NHb a x y y y b a k k x a x a x a x a a -⎛⎫∴=⋅===-∈- ⎪+---⎝⎭可得：22221 1(0)1)22c a e e a -=-∈-∴∈，， 故选A ．6．（2020·全国高三专题练习）椭圆C ：()222210x y a b a b+=>>的左焦点为F ，若F ＋y ＝0的对称点A 是椭圆C 上的点，则椭圆C 的离心率为（ ）A ．12B．12CD1【答案】D【解析】设F （－c ,0＋y ＝0的对称点为A （m ，n ），则(1022nm c m c n ⎧⋅=-⎪⎪+-+=，解得m ＝2c ，n =，代入椭圆方程可得22223441c c a b +=化简可得 e 4－8e 2＋4＝0， 又0＜e ＜1，解得e1. 故选：D .7．（2020·全国高三专题练习）已知椭圆（a>b>0）的左右焦点分别为F 1，F 2．P 是椭圆上一点．PF 1F 2为以F 2P 为底边的等腰三角形，当60°<PF 1F 2<120°，则该椭圆的离心率的取值范围是（ ）A ．（）B ．（）C ．（）D ．（0）【答案】B 【解析】由题意可得，即，所以，又，则，所以，则，即．故答案选B ．8．（2020·广东肇庆市）已知椭圆2222:1(0)x y C a b a b+=>>的左右顶点分别为,A B ，P 是椭圆上异于,A B的一点，若直线PA 的斜率PA k 与直线PB 的斜率PB k 乘积14PA PB k k =-，则椭圆C 的离心率为（ ）A ．14B ．12C ．34D．2【答案】D【解析】依题意可知()(),0,,0A a B a -.设()00,P x y ，代入椭圆方程得2222002b y x b a=-+.代入1·4PA PBk k =-得000014y y x a x a ⋅=-+-，即22200144a y x =-+，与2222002b y x b a =-+对比后可得2214b a =，所以椭圆离心率为2c e a ====.故选D. 9．（2020·全国高三专题练习）已知双曲线：22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ，2F ，焦距为2c，直线)y x c =+与双曲线的一个交点M 满足12212MF F MF F ∠=∠，则双曲线的离心率为（ ）ABC ．2D1【答案】D【解析】由题意，直线)y x c =+过左焦点1F 且倾斜角为60°，12212MF F MF F ∠=∠∴1260MF F ∠=︒，2130MF F ∠=︒，∴1290F MF ∠=︒，即12F M F M ⊥ ∴11212MF F F c ==，∴212sin 60MF F F ︒==，双曲线定义有212MF MF c a -=-=，∴离心率e 1ca==. 11．（2020·全国）若A 、B 为椭圆C ：22221x y a b+=(0a b >>)长轴的两个端点，垂直于x 轴的直线与椭圆交于点M 、N ，且14AM BN k k ⋅=，则椭圆C 的离心率为______【解析】设()M x y ，、()N x y -，，因为(),0A a -，(,0)B a ， 所以2222222222214AM BNb x b y y y b a k k x a x a x a x a a ---⋅=⋅====+---， 所以22222222314c a b b e a a a -===-=，所以e =故答案为：212．（2020·全国高三专题练习）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12，过右焦点F 作倾斜角60°的直线l 交C 于A ，B 两点（A 在第一象限），则AF BF=________.【答案】35【解析】 因为离心率为12，所以2,a c b ==, 设直线AB的方程)y x c =-代入椭圆方程：2222143x y c c+=得：2580x cx -=，又∵点A 在第一象限，故8c 50A B x x ⎧=⎪⎨⎪=⎩，所以8|||3.||5c c AF BF -==13．（2020·全国高三专题练习）设双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ，若在双曲线的右支上存在一点P ，使得122PF PF =，则双曲线C 的离心率e 的取值范围是____.【答案】(]1,3【解析】由双曲线的定义可得1222222PF PF PF PF PF a -=-==， 又22PF a c a =≥-，则3c a ≤，1e >，所以，13e <≤.因此，双曲线C 的离心率e 的取值范围是(]1,3. 故答案为：(]1,3.14．（2020·台州市书生中学高三其他）已知椭圆22221(0)x y a b a b+=>>，1F ，2F 分别是椭圆的左、右焦点，A 是椭圆的下顶点，直线2AF 交椭圆于另一点P ，若1PF PA =，则椭圆的离心率为【答案】3【解析】如图，点P 在椭圆上，所以12+2PF PF a =，由1222,PF PA PF AF AF a ==+=，代入上式得，123,22a aPF PF == 在1APF △，222222111133122cos 32322a a a AF AP PF PAF a AF APa ⎛⎫⎛⎫+- ⎪ ⎪+-⎝⎭⎝⎭∠===⨯，又2111cos 12sin 3PAF OAF ∠=-∠=，所以1sin 3OAF ∠=，即1sin 3c OAF e a ∠===， 15．（2020·开鲁县第一中学）已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，P 是椭圆上一点，12PF F ∆是以1PF 为底边的等腰三角形，若12(0,)3PF F π∠∈，则该椭圆的离心率的取值范围是【答案】11(,)32【解析】由题意可得 PF 2=F 1F 2=2c ，再由椭圆的定义可得 PF 1 =2a-PF 2=2a-2c ．设∠PF 2F 1 =θ，则1,1cos 32πθπθ<<∴-<<，△PF 1F 2中，由余弦定理可得 cos θ=22222ac c a c+- 由-1＜cos θ 可得 3e 2+2e-1＞0，e ＞13，由cos θ＜12，可得 2ac ＜a 2，e= 12c a <，综上1132e << 16．（2020·四川省绵阳南山中学高三）设1F ，2F 分别是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点，过2F 的直线交椭圆于A ，B 两点，且120AF AF ⋅=，222AF F B =，则椭圆E 的离心率为【答案】3【解析】222AF F B =设2BF x =，则22AF x =由椭圆的定义，可以得到1122,2AF a x BF a x =-=-120AF AF ⋅=,12AF AF ∴⊥在1Rt AF B 中，有()()()2222232a x x a x -+=-，解得3a x = 2124,33a a AF AF ∴== 在12Rt AF F △中，有()22242233a a c ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭整理得225=9c a ，c e a ∴==17．（2020·河北省高三）已知椭圆()222210x y a b a b+=>>，()0,2P ，()0,2Q -，过点P 的直线1l 与椭圆交于A ，B ，过点Q 的直线2l 与椭圆交于C ，D ，且满足12//l l ，设AB 和CD 的中点分别为M ，N ，若四边形PMQN 为矩形，且面积为，则该椭圆的离心率为【解析】如图，不妨设1l ，2l 两条直线的斜率大于零时，连结OM ，由题意知2216PM MQ PM MQ ⎧⋅=⎪⎨+=⎪⎩， 解得2PM =，MQ =PM =2MQ =（舍）2PM =，MQ =在PMQ 中，因为2OM PM PO ===，所以60BPO POM ∠=∠=︒，故此时tan 30AB k =︒=tan150OM k =︒=． 设()11,A x y ，()22,B x y ，则22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩， 两式相减得()()()()12121212220x x x x y y y y a b -+-++=， 即2121221212y y y y b x x x x a -+⋅=--+，即2213AB OM b k k a⋅=-=-， 因此离心率22222213c b e a a ==-=，所以e ． 18．（2020·广东省高三月考）已知F 是椭圆E ：()222210x y a b a b+=>>的左焦点，经过原点O 的直线l 与椭圆E 交于P ，Q 两点，若3PF QF =，且120PFQ ∠=︒，则椭圆E 的离心率为【解析】设椭圆的右焦点F '，连接PF '，QF '，根据椭圆对称性可知四边形PFF Q '为平行四边形，则QF PF '=，且由120PFQ ∠=︒，可得60FPF '∠=︒， 所以42PF PF PF a ''+==，则12PF a '=，32PF a = 由余弦定理可得 ()()222222cos603c PF PF PF PF PF PF PF PF ''''=+-︒=+-， 即2222974444c a a a =-=，∴椭圆的离心率e ===。

绝密★启用前 【考试时间： 】重庆一中高2020级高三下学期期中考试理 科 数 学 试 题 卷第I 卷（选择题)一、选择题：（本大题 12个小题，每小题5分，共60分,每小题有且只有一个选项是正确的）.1.已知集合{}0123A =，，，，2{|230},B x x x =--≥则()R A B U ð=（ ） A. (-1,3) B. (-1,3] C. (0,3) D. (0,3]2．已知复数z 满足i z z a i ⋅=+⋅（i 为虚数单位），且2z =a 的值为（ ） A.2 B.1 2 D.123.已知某超市2019年中的12个月的收入与支出数据的折线图如图所示,则下列说法中，错误的是（ ）. 注：收益=收入-支出A.该超市在2019年的12个月中，7月份的收益最高；B.该超市在2019年的12个月中，4月份的收益最低；C.该超市在2019年7月至12月的总收益比2109年1月至6月的总收益增长了90万元；D.该超市在2019年1月至6月的总收益低于2109年7月至12月的总收益.(3题图)4.冰雹猜想也称奇偶归一猜想：对给定的正整数进行一系列变换，则正整数会被螺旋式吸入黑洞(4,2,1)，最终都会归入“4－2－1”的模式.该结论至今既没被证明，也没被证伪. 右边程序 （4题图）框图示意了冰雹猜想的变换规则，则输出的i =（ ）A.4B.5C.6D.75.在正方体1111ABCD A B C D -中，,E F 分别是11,AD C D 的中点，O 为正方形ABCD 的中心，则（ ）A.直线1,EF OD 是异面直线，且1EF OD =B.直线11,OD B B 是异面直线且11OD B B ≠C.直线1,EF OD 是相交直线，且1EF OD =D.直线11,OD B B 是相交直线且11OD B B =6.等比数列{a n }的前n 项和为S n ，已知2533a a a =，且4a 与79a 的等差中项为2，则5S =（ ） A.1123 B.112 C.12127D.121 7.空间直角坐标系中的点(,,)P x y z 满足,,x y z {2,4,6}∈，则恰有两个坐标相同的点P 有（ ）A.18个B.12个C.9 个D.6个8.“3a ≥”是“1x =为函数321()(3)12f x x a x ax =-++--的极小值点”的（ ） A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件9.函数22()41x x x f x ⋅=-的图像大致为（ ）A B C D10. 函数()2sin(),(0,)f x x ωϕωϕπ=+><的部分图像如右图所示,且()f x 的图像过(,1),(,1)2A B ππ-两点,为了得到()2sin g x x ω=的图像，只需将()f x 的图像（ ） A.向右平移56π B.向左平移56π C.向左平移512π D.向右平移512π 11．已知,O F 分别是双曲线)0,0(1:2222>>=-b a by a x C 的中心和右焦点，以OF 为直径的圆与双曲线的两条渐近线分别交于B A ,两点（B A ,异于原点O ），若3AB b =，则双曲线C 的离心率e 为（ ）A.2B.3C.23D.2 12.已知四棱锥P ABCD -的棱长都是12，,,E F M 为,,PA PC AB 的中点，则经过,,E F M 的平面截四棱锥P ABCD -所得截面的面积为（ ）A.542B.452C.72D.96第II 卷（非选择题)二、填空题：（本大题4个小题，每小题5分，共20分）.13.若(,2),(1,1)a x b x ==-r r ，若()()a b a b +⊥-r r r r ，则x = ． 14.在第35届全国中学生数学冬令营中，某市甲、乙两所学校数学冬令营成绩的茎叶图05≤≤≤≤∈()，89，,x y x y N 如下图：已知甲校成绩的中位数、平均分都比乙校成绩的中位数、平均分少1分，则x y +=_____________.15.设数列{}n a 满足*112(1),,2n n a a n n N a +=++∈=，则数列{}(1)n n a -⋅的前40项和是_____________.16.已知抛物线22(0)y px p =>的焦点F ，过其准线与x 轴的交点E 作直线l ，(1)若直线l 与抛物线相切于点M ，则EMF ∠=_____________.(2)设6p =，若直线l 与抛物线交于点,A B ，且AB BF ⊥，则AF BF -=_____________.三.解答题：（本大题6个小题，共70分.各题解答必须在答题卷上作答，在相应题目指定的方框内必须写出必要的文字说明、演算步骤或推理过程）.17.（本小题满分12分）设函数2()sin(2)2cos 6f x x x π=+-.(1)求()f x 的单调增区间；(2)在ABC ∆中，若5()264A f π-=-，且102,10,cos CD DA BD ABD ==∠=u u u r u u u r ，求BC 的值. 18.（本小题满分12分）某次数学测验共有12道选择题，每道题共有四个选项，且其中只有一个选项是正确的，评分标准规定：每选对1道题得5分，不选或选错得0分. 在这次数学测验中，考生甲每道选择题都按照规则作答，并能确定其中有9道题能选对；其余3道题无法确定正确选项，在这3道题中，恰有2道能排除两个错误选项，另1题只能排除一个错误选项. 若考生甲做这3道题时，每道题都从不能排除的选项中随机挑选一个选项作答，且各题作答互不影响．在本次测验中，考生甲选择题所得的分数记为x(1)求55x =的概率；(2)求x 的分布列和数学期望．19.（本小题满分12分）如图，在由三棱锥E ADF -和四棱锥F ABCD -拼接成的多面体ABCDEF 中，AE ⊥平面ABCD ,平面BCF ⊥平面ABCD ，且ABCD 是边长为23的正方形，BCF ∆是正三角形.(1)求证：AE P 平面BCF ；(2)若多面体ABCDEF 的体积为16，求BF 与平面DEF 所成角的正弦值.20.（本小题满分12分）已知椭圆C ：2221(0)3x y b b+=>的右焦点为F ，过F 作两条直线分别与圆O ：222(0)x y r r +=>相切于,A B ，且ABF ∆为直角三角形. 又知椭圆C 上的点与圆O 31.(1)求椭圆C 及圆O 的方程；(2)若不经过点F 的直线l ：y kx m =+（其中0,0k m <>）与圆O 相切，且直线l 与椭圆C 交于,P Q ，求FPQ ∆的周长.21.（本小题满分12分） 已知函数121()(1),02x f x x a e x ax x -=---+> (1)若()f x 为单调增函数，求实数a 的值;(2)若函数()f x 无最小值，求整数a 的最小值与最大值之和.请考生在22、23两题中任选一题作答，如果都做，则按所做的第一题记分.22.（本小题满分10分）选修4 - 4 坐标系与参数方程在平面直角坐标系xoy 中，直线1l 的参数方程为4x t y kt=-⎧⎨=⎩，(t 为参数)，直线2l 的普通方程为1y x k =，设1l 与2l 的交点为P ，当k 变化时，记点P 的轨迹为曲线1C . 在以原点O 为极点，x 轴正半轴为极轴的极坐标系中，直线3l 的方程为:sin()24πρθ-=(1)求曲线1C 的普通方程；(2)设点A 在3l 上，点B 在1C 上，若直线AB 与3l 的夹角为4π，求AB 的最大值. 23.（本小题满分10分）选修4 - 5 不等式选讲已知0a >，0b >，23a b +=．(1)求 22a b +的取值范围；(2)求证：3381416a b ab +≤． 命题：李红林 审题：王中苏 王明。

秘密★启用前 【考试时间： 】2020年重庆一中高2020级高三下期期中考试数学（文科）试题卷（含标准答案）注意事项：1. 答卷前，考生务必将自己的姓名、准考证号码填写在答卷上。

2. 作答时，务必将答案写在答题卡上，写在本试卷及草稿纸上无效。

3. 考试结束后，将答题卡交回。

第 Ⅰ 卷（选择题，共60分）一、选择题（本题共12小题，每小题5分，共60分. 每小题给出的四个选项中，只有一项符合题目要求） 1. 设集合{}22P x x x =+≥，{}3Q x Nx =∈≤，则P Q =I ( )A ．[1,2]-B ．[0,2]C ．{}0,1,2D ．{}1,0,1,2-2. 已知向量(1,2)a =r ，(1,)b x =-r ，若a b r r∥ ，则b =r ( )A. 3B. C. 5D.3. 复数12z i =+，若复数1z 与2z 在复平面内的对应点关于虚轴对称，则12z z =g ( ) A.B.C.D.4. 一场考试之后，甲乙丙三位同学被问及语文、数学、英语三个科目是否达到优秀时，甲说：有一个科目我们三个人都达到了优秀；乙说：我的英语没有达到优秀；丙说：乙达到优秀的科目比我多.则可以完全确定的是( )A ．甲同学三个科目都达到优秀B ．乙同学只有一个科目达到优秀C ．丙同学只有一个科目达到优秀D ．三位同学都达到优秀的科目是数学5. 2020年，新型冠状病毒引发的疫情牵动着亿万人的心，八方驰援战疫情，众志成城克时难，社会各界支援湖北共抗新型冠状病毒肺炎，重庆某医院派出3名医生，2名护士支援湖北，现从这5人中任选2人定点支援湖北某医院，则恰有1名医生和1名护士被选中的概率为( )A ．0.7B ．0.4C ．0.6D ．0.36. 已知一组数据12345,,,,x x x x x 的平均数是m ，方差是n ，将这组数据的每个数都乘以(0) a a >得到一组新数据，则下列说法正确的是( )A ．这组新数据的平均数是mB ．这组新数据的平均数是a m +C ．这组新数据的方差是an D．这组新数据的标准差是7. 已知107700,0x y x y x y -+≥⎧⎪--≤⎨⎪≥≥⎩表示的平面区域为D ，若对(,)x y D ∀∈都有2x y a +≤，则实数a 的取值范围是( ) A ．[)5,+∞B ．[)2,+∞C ．[)1,+∞D ．[)0,+∞5-534i -+34i -8. 将表面积为36π的圆锥沿母线将其侧面展开，得到一个圆心角为23π的扇形，则该圆锥的轴截面的面积为( )A． B． C． D． 9. 若函数ln )() (f x a x a R =∈与函数()g x =a 的值为( )A ．4B ．12 C ．2eD ．e10. 已知12,F F 是双曲线2222:1(0,0)x y E a b a b-=>>的左、右焦点，P 是双曲线E 右支上一点，M 是线段1F P的中点，O 是坐标原点，若1OF M ∆的周长为3c a +（c 为双曲线的半焦距）且13F MO π∠=，则双曲线E 的渐近线方程为( ) A．y x = B．y = C ．12y x =±D ． 2y x =± 11. 已知函数()2sin()(0,)2x f x πωϕωϕ+><=的图象过点(0,1)A -，且在(,)183ππ上单调，同时将()f x 的图象向左平移π个单位后与原图象重合，当12172,(,)123x x ππ∈--且12x x ≠时12()()f x f x =，则12()f x x +=( )A． B ．1- C ．1 D12. 已知函数()f x 是定义在(,0)(0,)-∞+∞U 上的偶函数，当(0,)x ∈+∞时，2(1),02()1(2),22x x f x f x x ⎧-<≤⎪=⎨->⎪⎩，则函数2()8()6()1g x f x f x =-+的零点个数为( ) A. 20B. 18C. 16D. 14第Ⅰ卷（非选择题，共90分）二、填空题（本题共4小题，每小题5分，共20分） 13. 已知等比数列{}n a 的前n 项和为n S ，且132455,24a a a a +=+=，则33S a =_________.14. 已知抛物线212y x =的焦点为F ，过点(2,1)P 的直线l 与该抛物线交于,A B 两点，且点P 恰好为线段AB 的中点，则AF BF +=_________.15. 设n S 为数列{}n a 的前n 项和，若0n a >，11a =，且2()n n n S a a t =+（, t R n N *∈∈），则100S = _________.16. 在三棱锥P ABC -中，2,1,90 PA PC BA BC ABC ︒====∠=，若PA 与底面ABC 所成的角 为60︒，则点P 到底面ABC 的距离是_________；三棱锥P ABC -的外接球的表面积是_________. （本小题第一空2分，第二空3分）三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生 都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分.17.（12分）如图，ABC ∆是等边三角形，D 是BC 边上的动点（不含端点）记BAD ∠=α,ADC β∠=. （1）求2cos cos αβ-的最大值； （2）若11,cos 7BD β==，求ABD ∆的面积.18.（12分）如图，在直三棱柱111ABC A B C -中，1111A B AC ⊥，D 是11B C 的中点，1112A A A B ==.（1）求证：11AB A CD ∥平面；（2）若异面直线1AB 和BC 所成角为60︒，求四棱锥11A CDB B -的体积.19.（12甲公司前期的经营状况，对该公司2019月（5—10据绘制了相应的折线图，如右图所示.（1利润y （单位：百万元）与月份代码x 求y 关于x （2）甲公司新研制了一款产品，需要采购一批新型材料，现有,A B 两种型号的新型材料可供选择，按规定每种新型材料最多可使用4个月，但新材料的不稳定性会导致材料损坏的年限不同，现对,A B 两种型1号的新型材料对应的产品各100件进行科学模拟测试，得到两种新型材料使用寿命的频数统计表（表1）. 若从产品使用寿命的角度考虑，甲公司的负责人选择采购哪款新型材料更好？ 参考数据：6196i i y ==∑ ；61371i i i x y ==∑.参考公式：回归直线方程ˆˆˆybx a =+，其中()()()1122211ˆ=n niii ii i nniii i x x y y x y nx yb x x xnx====---⋅=--∑∑∑∑，ˆ.ˆˆay x b =- 20.（12分）已知椭圆2222: 1 (0)x y C a b a b+=>>的长轴长为4，且经过点2P . （1）求椭圆C 的方程； （2）直线l 的斜率为12，且与椭圆交于,A B 两点（异于点P ），过点P 作APB ∠的角平分线交椭圆于另一点Q . 证明：直线PQ 与坐标轴平行.21.（12分）已知函数()()2ln 1,.f x x ax x a R =++-∈（1）当14a =时，求函数()y f x =的极值； （2）若对于任意实数(1,2)b ∈，当(1,]x b ∈-时，函数()f x 的最大值为()f b ，求实数a 的取值范围.（二）选考题：共10分.请考生在第22、23题中任选一题作答，如果多做，则按第一题计分. 22. [选修4—4：坐标系与参数方程] （10分） 在直角坐标系xOy 中，曲线1C 的参数方程为22cos 2sin x y ϕϕ=+⎧⎨=⎩ (ϕ为参数). 以原点O 为极点，以x 轴的非负半轴为极轴建立极坐标系，曲线2C 的极坐标方程为4sin ρθ=． （1）求曲线1C 的极坐标方程；（2）设点M 的极坐标为(4,0)，射线(0)4πθαα=<<分别交1C 、2C 于点,A B （,A B 异于极点），当4AMB π∠=时，求tan α的值.23. [选修4—5：不等式选讲] （10分） 已知0a >，0b >，22143a b ab+=+. （1）求证：1ab ≤； （2）若b a >，求证：3311113a b a b ⎛⎫->- ⎪⎝⎭. 命题人：张 露审题人：张志华 付红12020年重庆一中高2020级高三下期期中考试数学（文科）试题卷（参考答案）二、填空题13. 7 14. 10 15. 505016. 5 π三、解答题17.解：（1）,(0,)33ππβαα=+∈Q ，∴2cos α－cos β=2cos α－cos +3πα⎛⎫ ⎪⎝⎭+3πα⎛⎫ ⎪⎝⎭，又2(0,)(,)3333ππππαα∈∴+∈Q ，，故当32ππα+=·································· 6分 （2）由cos β＝17 ，得sin β＝7，故sin α＝sin 3πβ⎛⎫- ⎪⎝⎭＝sin βcos 3π－cos βsin 3π＝14，在ABD ∆中，由正弦定理sin sin AB BD ADB BAD =∠∠，得AB ＝sin sin βαBD ＝83， 故S △ABD ＝12AB·BD·sin B ＝18123⨯⨯=. ·····································································12分18.（1）证明：如图，连1AC 交1A C 于点E ，连DE .因为直三棱柱111ABC A B C -中，四边形11AAC C 是矩形，故点E 是1AC 中点，又D 是11B C 的中点，故1DE AB ∥，又111,, AB ACD DE ACD ⊄⊂平面平面故11AB A CD ∥平面. ·····································（2）解：由（1）知1DE AB ∥，又1C D BC ∥，故1C DE ∠或其补角为异面直线1AB 和BC 所成角. 设2AC m =，则11C E C D DE ===1C DE ∆为等腰三角形，故160C DE ︒∠=，故1C DE ∆=1m =.故111A B C ∆为等腰直角三角形，故111A D C B ⊥，又11111111B B A B C A D A B C ⊥⊂平面，平面， 故11A D B B ⊥，又1111B B C B B =I ，故11A D CDB B ⊥平面，又梯形1CDB B的面积11122CDB B S A D =⨯⨯==， 则四棱锥11A CDB B -的体积1111233CDB B V S A D ==⨯=g . ·············································· 12分19. 解：（1）由折线图可知统计数据(),x y 共有6组，即(1,11)，(2,13)，(3,16)，(4,15)，(5,20)，(6,21)，计算可得1234563.56x +++++==，y =6111961666i i y ==⨯=∑， 所以616221ˆ=i ii i i x y nx ybx nx==-⋅=-∑∑37163.516217.5-⋅⋅=，162 3.59a y b x =-=-⨯=))).所以月度利润y 与月份代码x 之间的线性回归方程为29y x =+. ··················································· 6分 由题意推得2020年5月份对应的年份代码为13，故当13x =时，213935y =⨯+=)（百万元），故预计甲公司2020年5月份的利润为35百万元. ······················································································ 8分 （2）A 型新材料对应产品的使用寿命的平均数为12013523531042.35100x ⨯+⨯+⨯+⨯==（个月），B 型新材料对应的产品的使用寿命的平均数为21013024032042.7100x ⨯+⨯+⨯+⨯==（个月）， 12x x <Q ，∴采购B 型新材料更好. ······················································································ 12分 注：若采用其他数字特征（如中位数、众数等）进行合理表述，也可酌情给分。

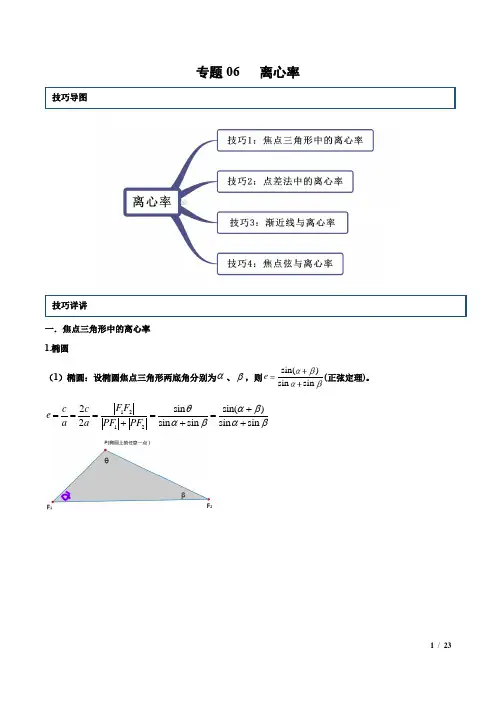
专题06 离心率一．焦点三角形中的离心率1.椭圆（1）椭圆：设椭圆焦点三角形两底角分别为α、β，则sin()sin sine(正弦定理)。

12122sin sin()2sin sin sin sinF Fc cea a PF PFθαβαβαβ+=====+++222121212212121221212221212212212(2)2cos =()22cos =()2(1cos ) ()2()(1cos )21=()[1(1cos )]21=()(F F PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF PF θθθθθ=+-+--+-++≥+-++-++12222222cos )==2111144(cos )cos (12sin )sin 222222sin2PF PF P c c a a e θθθθθθ-∴≥-≥-=--=∴≥（当且仅当取，即在短轴端点处）即2.双曲线：利用焦点三角形两底角,αβ来表示:sin()sin sine。

12122sin sin()2sin sin sin sin +=====---F F c c e a a PF PF θαβαβαβ二．双曲线的渐进线与离心率关系 直线与双曲线相交时，两个交点的位置（1）两个交点在双曲线的两支：b k e a >⇔=（2）两个交点在双曲线的同一支:b k e a <⇔=（3）两个交点在双曲线的左支:12120x x 0x x 0>⎧⎪⎪+<⎨⎪>⎪⎩（4）两个交点在双曲线的右支:12120x x 0x x 0>⎧⎪⎪+>⎨⎪>⎪⎩三．焦点弦与离心率关系BF AF λ=，则有11cos +-=λλθe (θ为直线与焦点所在轴的夹角)。

技巧1 焦点三角形中的离心率【例1】(1)．已知1F ，2F 是双曲线E ：22221x y a b-=的左、右焦点，点M 在E 上，1MF 与x 轴垂直，12tan FMF ∠=E 的离心率为（ ） A ．B ．2CD （2）（2020·安徽省高三三模）已知椭圆E ：()222210x y a b a b+=>>的左右焦点分别为1F ，2F ，若在椭圆E 上存在点P ，使得12PF PF ⊥，则椭圆E 的离心率的取值范围为（ ）A ．,12⎫⎪⎪⎣⎭ B ．0,2⎛⎫⎪ ⎪⎝⎭ C ．,12⎫⎪⎪⎣⎭D ．1,12⎛⎫⎪⎝⎭【答案】（1）C （2）A【解析】（1）不妨设(,),0M c y y ->代入双曲线方程得22,(,)b b y M c a a =∴-21212222,tan 0,c F F c F MF ac ba=∠==-= 2220ac e --=--=，()10,e e -+=∴=故答案选：C（2）12PF PF ⊥，2221212PF PF F F ∴+=()()()()222212122212121212222PF PF PF PF PF PF PF PF PF PF PF PF +++=+-⋅≥+-=（当且仅当12PF PF =时取等号），()2122122PF PF F F +∴≥，由椭圆定义知：122PF PF a +=，又122F F c =，2242c a ∴≥，212e ∴≥，2e ∴≥，又1e <，∴离心率e的取值范围为,12⎫⎪⎪⎣⎭.故选：A . 【举一反三】1．（2020·沙坪坝区·重庆一中高三月考）已知点P 在以12,F F 为左，右焦点的椭圆()2222:102x y C b b b+=>上，在12PF F △中，若12PF F α∠=，21PF F β∠=，则()sin sin sin αβαβ+=+（ ）A ．12BC．2D【答案】B【解析】12PF F △中，()()12121212||||||||||||sin sin sin sin sin sin PF PF F F PF PF F F αβαβαβαβ+==∴=+++ 所以()1212sin ||2sin sin ||||22F F c c PF PF a a αβαβ+=====++故选：B 2．（2020·全国高三专题练习）已知点P 是以1F 、2F 为焦点的椭圆()222210x y a b a b +=>>上一点，若12PF PF ⊥，21tan 2PF F ∠=，则椭圆的离心率e =（ ）AB ．13C ．23D ．12【答案】A【解析】点P 是以1F 、2F 为焦点的椭圆()222210x y a b a b+=>>上一点，12PF PF ⊥，1212tan 2PF PF F PF ∠==，122PF PF ∴=， 122PF PF a +=，可得143a PF =，223a PF =， 由勾股定理可得2221212PF PF F F +=，即222049a c =，2259ca ∴=，因此，该椭圆的离心率为3e =. 故选：A.3．（2019·辽宁沈阳市·沈阳二中高三月考（理））椭圆22221(0)x y a b a b+=>>，1F 、2F是椭圆的两个焦点，P 是圆上一动点，则12cos F PF ∠的最小值是（ ） A ．13- B ． C ．1-D ．0【答案】A【解析】椭圆22221(0)x y a b a b +=>>，即2223c a =.122PF PF a +=≥212PF PF a ⋅≤，当12PF PF a ==时等号成立.根据余弦定理：()222221211212121212122cos 22PF PF PF PF F F PF PF F F F PF PF PF PF PF +-⋅-+-∠==⋅⋅22222124444111223a c a c PF PF a --=-≥-=-⋅.故选：A .技巧2 点差法中的离心率【例2】（1）（2020·四川外国语大学附属外国语学校）过点()1,2M 作直线16y x m =-+与椭圆()222210x y a b a b+=>>相交于,A B 两点，若M 是线段AB 的中点，则该椭圆的离心率是（ ） A ．23B．3C ．1112D．6（2）（2020·安徽省潜山第二中学）已知A ，B 是椭圆E ：22221(0)x y a b a b+=>>的左、右顶点，M 是E 上不同于A ，B 的任意一点，若直线AM ，BM 的斜率之积为49-，则E 的离心率为() A．3BC ．23D【答案】（1）B （2）D【解析】（1）设()11,A x y ，()22,B x y ， 由直线AB 的斜率为16-可得121216y y x x ， 由线段AB 的中点为()1,2M 可得1212x x +=，1222y y+=， 由点,A B 在椭圆上可得22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩，作差得22221212220x x y y a b --+=， 所以()()()()12121212220x x x x y y y y a b +-+-+=，即()()121222240x x y y a b --+=，所以()212212213y y b a x x -=-=-，所以该椭圆的离心率c e a ===故选：B.（2）由题意方程可知，(,0),(,0)A a B a -，设00(,)M x y ,0000,,AM BM y y k k x a x a∴==+- 则000049y y x a x a ⋅=-+- ,，整理得：2022049y x a =--，① 又2200221x y a b+=，得2222002()b y a x a =-，即2202220y b x a a =--，② 联立①②，得2249b a -=-，即22249a c a -=，解得e =． 故选D ． 【举一反三】1．已知双曲线C ：()222210,0x y a b a b-=>>，斜率为2的直线与双曲线C 相交于点A 、B ，且弦AB 中点坐标为()1,1，则双曲线C 的离心率为（ ） A ．2 BCD ．3【答案】B【解析】设11(,)A x y 、22(,)B x y ，则2211221x y a b -=，2222221x y a b-=， 所以2222121222x x y y a b --=，所以2121221212y y x x b x x a y x -+=⨯-+， 又弦AB 中点坐标为()1,1，所以122x x +=，122y y +=，又12122y y x x --=，所以22222b a =⨯，即222b a=，所以双曲线的离心率c e a ======. 故选：B.2．（2020·全国高三专题）已知1F 、2F 是椭圆的两个焦点，满足120MF MF ⋅=的点M 总在椭圆内部，则椭圆离心率的取值范围是（ ）.A ．1(0)2， B ．(02， C ．1(22， D ．1)2【答案】B【解析】∵120MF MF ⋅=，∴12MF MF ⊥，∴点M 在以12F F 为直径的圆上，又点M 在椭圆内部，∴c b <，∴2222<=-c b a c ，即222c a <，∴2212c a <，即c a <0e >，∴02e <<，故选：B.3．（2020·全国高三专题练习）若1F ，2F 是椭圆的两个焦点，P 是椭圆上一点，当12PF PF ⊥，且1230PF F ∠=︒，则椭圆的离心率为（ ）A 1B ．3C 1D ．2【答案】C【解析】依题意可知1290F PF ∠=︒，12||2F F c =，1230PF F ∠=︒，112PF F F ∴==，21212PF F F c ==，由椭圆定义可知1221)PF PF a c +==，1ce a∴==.故选：C. 技巧3 渐近线与离心率【例3】已知圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>有两个交点，则双曲线C 的离心率的取值范围是（ ）A ．B ．(1,2)C ．)+∞D ．(2,)+∞【答案】D【解析】由题意，圆心到直线的距离2d ==，解得k =圆223(1)4x y -+=的一条切线y kx =与双曲线2222:1(0,0)x y C a b a b -=>>有两个交点，所以b a >22214b e a=+>，所以2e >.故选：D.【举一反三】1．若双曲线22221x y a b-=（0a >，0b >）与直线y x =无公共点，则离心率e 的取值范围是（ ）A ．(B ．(C ．(]1,2D ．()1,2【答案】A 【解析】若双曲线22221(0,0)x y a b a b-=>>与直线y x =无公共点，∴等价为双曲线的渐近线b y x a =的斜率1ba，即b a ，即22b a ，即222c a a -，即222c a ， 则2ca ，则2e ，1e >，∴离心率满足12e<，即双曲线离心率的取值范围是(，故选：A ．2．已知双曲线22221x y a b-= (a>0，b>0)的右焦点为F ，若过点F 且倾斜角为60°的直线l 与双曲线的右支有且只有一个交点，则此双曲线的离心率e 的取值范围是（ ） A ．[2,)+∞ B ．(1,2),C ．(2,)+∞D ．(1,2]【答案】A【解析】已知双曲线22221(0,0)x y a b a b-=>>的右焦点为F ，若过点F 且倾斜角为3π的直线与双曲线的右支有且只有一个交点，则该直线的斜率的绝对值小于等于渐近线的斜率b a， ∴3b a，离心率22224a b e a +=，2e ∴，故选A ．3．（2020·河南新乡市·高三）已知双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ，过原点O的直线交C 的右支于点A ，若1223F AF π∠=，则双曲线的离心率为（ ） AB1CD【答案】D【解析】题可知123FOA π∠=，121AFO F AF ∠=∠，112FOA F AF ∠=∠，112FOA F AF ∴△△， 所以11112FO F A F AF F =，可得1F A =.在12F AF 中，由余弦定理可得22212121222cos3F F AF AF AF AF π=+-⋅，即222220AF AF c ⋅-=，解得22AF c=.双曲线的离心率为1212F FeAF AF===-.故选：D.技巧4 焦点弦与离心率【例4】（2020·石嘴山市第三中学高三三模）已知椭圆22221x ya b+=的左右焦点分别为12,F F，过1F作倾斜角为45的直线与椭圆交于,A B两点，且112F B AF=，则椭圆的离心率=（）A．3B．2C．2D．3【答案】D【解析】椭圆22221x ya b+=的左右焦点分别为12F F、，过1F c-（，）且斜率为1k=的直线为y x c=+联立直线与椭圆方程22221x ya by x c⎧+=⎪⎨⎪=+⎩消x后，化简可得2222222220a b y cb y c b a b+++-=（）因为直线交椭圆于A，B，设1122A x yB x y（，），（，）由韦达定理可得22222121222222y y,y ycb c b a ba b a b-+=-=++且112F B AF=，可得212y y=-，代入韦达定理表达式可得2222221122222,2cb c b a by ya b a b--=--=++即222222222222cb c b a ba b a b⎛⎫--=⎪++⎝⎭化简可得229c2a=所以cea==故选：D．【举一反三】1．（2020·河南省高三月考）倾斜角为4π的直线经过椭圆22221(0)x y a b a b+=>>右焦点F ，与椭圆交于A 、B 两点，且2AF FB =，则该椭圆的离心率为（ ）A ．2B ．3C ．2D ．3【答案】B【解析】设B 到右准线距离为d ，则BF ed =，因为2AF FB =，则2AF ed =，所以 A 到右准线距离为2d ，从而3AB ed= 倾斜角为4π，cos 433d e ed π∴=∴=，选B. 2．（2020·全国高三专题练习）已知1F 、2F 是双曲线22221x y a b-=(0a >，0b >)的左、右焦点，过2F 作双曲线一条渐近线的垂线，垂足为点A ，交另一条渐近线于点B ，且2213AF F B =，则该双曲线的离心率为（ ） A ．3或332B ．62或3C 或D 【答案】B【解析】（1）当2213AF F B =时，设2F OA α∠=，则2AOB α∠=，设1a =，由题意可知1OA a ==，2OF c e ==，2AF b =，23BF b =，则4AB b =，tan b b a α==，4tan 24b b a α==， 代入得222tan 2tan 241tan 1bb b ααα===--，即2244b =-，解得b =2e c ====，（2）当2213F A F B =时，设2F OA α∠=，AOB β∠=，设1a =，则2F OB αβ∠=+，1()FOB παβ∠=-+， 由题意可知1OA a ==，2OF c e ==，2AF b =，23BF b =， 则2AB b =，tan b b a α==，2tan 2b b aβ==， 则1tan tan[()]tan()tan FOB παβαβα∠=-+=-+=， 则tan tan tan()tan 1tan tan αβαβααβ++==--⋅，代入得212b bb b b+=--⋅，即2321b =-，解得b =则e c === 故选：B .3．（2019·浙江高三其他模拟）已知过双曲线()222210,0x y a b a b-=>>的右焦点F ，且与双曲线的渐近线平行的直线l 交双曲线于点A ，交双曲线的另一条渐近线于点B （A ，B 在同一象限内），满足2FB FA =，则该双曲线的离心率为（ ）A ．43BC D ．2【答案】B【解析】双曲线的渐近线方程为by x a=±，如图，不妨设,A B 在第一象限，直线l 的方程为()b y x c a =--，与22221x y a b-=联立，得32A b y ac =；直线l 与by x a =联立，得2B bc y a=． 由||2||FB FA =，得2B A y y =，即3222bc b a ac=⨯， 得222c b =，即222c a =，则e =B ．1．已知倾斜角为π4的直线与双曲线C ：22221x y a b-=（0a >，0b >）相交于A ，B 两点，(4,2)M 是弦AB的中点，则双曲线的离心率为（ ） A BC ．32D 【答案】D【解析】因为倾斜角为π4的直线与双曲线C ：22221x y a b-=（0a >，0b >）相交于A ，B 两点，所以直线的斜率tan14πk ==， 设()()1122,,,A x y B x y ，则2211221x y a b -=①2222221x y a b-=②由①-②得()()()()1212121222x x x x y y y y a b -+-+=则2121221212y y b x x k x x a y y -+==⋅-+因为(4,2)M 是弦AB 的中点，12128,4x x y y ∴+=+=因为直线的斜率为122814b a ∴=⋅即222211,22b b a a==所以2222112c a b a ⎛⎫=+=+ ⎪⎝⎭232e ∴=，则2e =，故选：D2．设F 是双曲线22221(0,0)x y a b a b-=>>的右焦点.过点F 作斜率为-3的直线l 与双曲线左、右支均相交.则双曲线离心率的取值范围为（ ）A ．B ．C ．)+∞D ．)+∞【答案】C【解析】因为双曲线22221(0,0)x y a b a b -=>>的两条渐近线方程为b y x a=±，当过点F 且斜率为-3的直线l 与渐近线by x a=-平行时. 直线l 只与双曲线右支有一个交点，数形结合可知， 当渐近线by x a =-的斜率满足3b a -<-，即3b a>时， 直线l 与双曲线左、右支均相交，所以22223910b a b a c a e >⇒>⇒>⇒>故选:C.3．（2019·黑龙江佳木斯市·佳木斯一中高三月考）已知1F ，2F 分别是椭圆22142x y +=的左、右焦点，P 是此椭圆上一点，若为12F PF △直角三角形，则这样的点P 有（ ）.A ．2个B ．4个C ．6个D ．8个【答案】C【解析】由题意2,a b ==，则c =P 为椭圆短轴顶点时，122PF PF ==，12F F =2221212PF PF F F +=，即12PF PF ⊥，短轴顶点有2 个，过1F 或2F 作x 轴垂直与椭圆相交的点P 在4个，12PF F ∆都是直角三角形，因此共有6个． 故选：C.4．（2020·广东广州市）已知1F ,2F 分别是椭圆C ()2222:10x y a b a b+=>>的左, 右焦点, 椭圆C 上存在点P 使12F PF ∠为钝角, 则椭圆C 的离心率的取值范围是A．2⎛⎫⎪ ⎪⎝⎭B ．1,12⎛⎫⎪⎝⎭C．2⎛⎫ ⎪⎝⎭D ．10,2⎛⎫⎪⎝⎭【答案】A【解析】设椭圆的上顶点为0A b （，），则∵椭圆上存在点P ，使12F PF ∠为钝角, 121212904511bF AF AF F tan AF F c∠>︒∴∠<︒∴∠<∴≤2220112a c e e e ∴∴∴<＜＜＜故答案为A 5．（2020·河北石家庄市）已知椭圆22221(0)x y a b a b+=>> ，点M,N 为长轴的两个端点，若在椭圆上存在点H ，使1(,0)2MH NH k k ∈- ,则离心率e 的取值范围为 A ．2 B ．2C ．D ． 【答案】A【解析】由题意00M a N a -（，），（，）． 设00H x y （，） ，则222202 ()b y a x a．=- 2222202000222220000()1,02MH NHb a x y y y b a k k x a x a x a x a a -⎛⎫∴=⋅===-∈- ⎪+---⎝⎭可得：22221 1(0)1)22c a e e a -=-∈-∴∈，， 故选A ．6．（2020·全国高三专题练习）椭圆C ：()222210x y a b a b+=>>的左焦点为F ，若F ＋y ＝0的对称点A 是椭圆C 上的点，则椭圆C 的离心率为（ ）A ．12B．12CD1【答案】D【解析】设F （－c ,0＋y ＝0的对称点为A （m ，n ），则(1022nm c m c n ⎧⋅=-⎪⎪+-+=，解得m ＝2c ，n =，代入椭圆方程可得22223441c c a b +=化简可得 e 4－8e 2＋4＝0， 又0＜e ＜1，解得e1. 故选：D .7．（2020·全国高三专题练习）已知椭圆（a>b>0）的左右焦点分别为F 1，F 2．P 是椭圆上一点．PF 1F 2为以F 2P 为底边的等腰三角形，当60°<PF 1F 2<120°，则该椭圆的离心率的取值范围是（ ）A ．（）B ．（）C ．（）D ．（0）【答案】B 【解析】由题意可得，即，所以，又，则，所以，则，即．故答案选B ．8．（2020·广东肇庆市）已知椭圆2222:1(0)x y C a b a b+=>>的左右顶点分别为,A B ，P 是椭圆上异于,A B的一点，若直线PA 的斜率PA k 与直线PB 的斜率PB k 乘积14PA PB k k =-，则椭圆C 的离心率为（ ）A ．14B ．12C ．34D．2【答案】D【解析】依题意可知()(),0,,0A a B a -.设()00,P x y ，代入椭圆方程得2222002b y x b a=-+.代入1·4PA PBk k =-得000014y y x a x a ⋅=-+-，即22200144a y x =-+，与2222002b y x b a =-+对比后可得2214b a =，所以椭圆离心率为2c e a ====.故选D. 9．（2020·全国高三专题练习）已知双曲线：22221(0,0)x y a b a b-=>>的左、右焦点分别为1F ，2F ，焦距为2c，直线)y x c =+与双曲线的一个交点M 满足12212MF F MF F ∠=∠，则双曲线的离心率为（ ）ABC ．2D1【答案】D【解析】由题意，直线)y x c =+过左焦点1F 且倾斜角为60°，12212MF F MF F ∠=∠∴1260MF F ∠=︒，2130MF F ∠=︒，∴1290F MF ∠=︒，即12F M F M ⊥ ∴11212MF F F c ==，∴212sin 60MF F F ︒==，双曲线定义有212MF MF c a -=-=，∴离心率e 1ca==. 11．（2020·全国）若A 、B 为椭圆C ：22221x y a b+=(0a b >>)长轴的两个端点，垂直于x 轴的直线与椭圆交于点M 、N ，且14AM BN k k ⋅=，则椭圆C 的离心率为______【解析】设()M x y ，、()N x y -，，因为(),0A a -，(,0)B a ， 所以2222222222214AM BNb x b y y y b a k k x a x a x a x a a ---⋅=⋅====+---， 所以22222222314c a b b e a a a -===-=，所以e =故答案为：212．（2020·全国高三专题练习）已知椭圆2222:1(0)x y C a b a b+=>>的离心率为12，过右焦点F 作倾斜角60°的直线l 交C 于A ，B 两点（A 在第一象限），则AF BF=________.【答案】35【解析】 因为离心率为12，所以2,a c b ==, 设直线AB的方程)y x c =-代入椭圆方程：2222143x y c c+=得：2580x cx -=，又∵点A 在第一象限，故8c 50A B x x ⎧=⎪⎨⎪=⎩，所以8|||3.||5c c AF BF -==13．（2020·全国高三专题练习）设双曲线()2222:10,0x y C a b a b-=>>的左、右焦点分别为1F 、2F ，若在双曲线的右支上存在一点P ，使得122PF PF =，则双曲线C 的离心率e 的取值范围是____.【答案】(]1,3【解析】由双曲线的定义可得1222222PF PF PF PF PF a -=-==， 又22PF a c a =≥-，则3c a ≤，1e >，所以，13e <≤.因此，双曲线C 的离心率e 的取值范围是(]1,3. 故答案为：(]1,3.14．（2020·台州市书生中学高三其他）已知椭圆22221(0)x y a b a b+=>>，1F ，2F 分别是椭圆的左、右焦点，A 是椭圆的下顶点，直线2AF 交椭圆于另一点P ，若1PF PA =，则椭圆的离心率为【答案】3【解析】如图，点P 在椭圆上，所以12+2PF PF a =，由1222,PF PA PF AF AF a ==+=，代入上式得，123,22a aPF PF == 在1APF △，222222111133122cos 32322a a a AF AP PF PAF a AF APa ⎛⎫⎛⎫+- ⎪ ⎪+-⎝⎭⎝⎭∠===⨯，又2111cos 12sin 3PAF OAF ∠=-∠=，所以1sin 3OAF ∠=，即1sin 3c OAF e a ∠===， 15．（2020·开鲁县第一中学）已知椭圆22221(0)x y a b a b+=>>的左、右焦点分别为1F ，2F ，P 是椭圆上一点，12PF F ∆是以1PF 为底边的等腰三角形，若12(0,)3PF F π∠∈，则该椭圆的离心率的取值范围是【答案】11(,)32【解析】由题意可得 PF 2=F 1F 2=2c ，再由椭圆的定义可得 PF 1 =2a-PF 2=2a-2c ．设∠PF 2F 1 =θ，则1,1cos 32πθπθ<<∴-<<，△PF 1F 2中，由余弦定理可得 cos θ=22222ac c a c+- 由-1＜cos θ 可得 3e 2+2e-1＞0，e ＞13，由cos θ＜12，可得 2ac ＜a 2，e= 12c a <，综上1132e << 16．（2020·四川省绵阳南山中学高三）设1F ，2F 分别是椭圆2222:1(0)x y E a b a b +=>>的左、右焦点，过2F 的直线交椭圆于A ，B 两点，且120AF AF ⋅=，222AF F B =，则椭圆E 的离心率为【答案】3【解析】222AF F B =设2BF x =，则22AF x =由椭圆的定义，可以得到1122,2AF a x BF a x =-=-120AF AF ⋅=,12AF AF ∴⊥在1Rt AF B 中，有()()()2222232a x x a x -+=-，解得3a x = 2124,33a a AF AF ∴== 在12Rt AF F △中，有()22242233a a c ⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭整理得225=9c a ，c e a ∴==17．（2020·河北省高三）已知椭圆()222210x y a b a b+=>>，()0,2P ，()0,2Q -，过点P 的直线1l 与椭圆交于A ，B ，过点Q 的直线2l 与椭圆交于C ，D ，且满足12//l l ，设AB 和CD 的中点分别为M ，N ，若四边形PMQN 为矩形，且面积为，则该椭圆的离心率为【解析】如图，不妨设1l ，2l 两条直线的斜率大于零时，连结OM ，由题意知2216PM MQ PM MQ ⎧⋅=⎪⎨+=⎪⎩， 解得2PM =，MQ =PM =2MQ =（舍）2PM =，MQ =在PMQ 中，因为2OM PM PO ===，所以60BPO POM ∠=∠=︒，故此时tan 30AB k =︒=tan150OM k =︒=． 设()11,A x y ，()22,B x y ，则22112222222211x y a b x y a b ⎧+=⎪⎪⎨⎪+=⎪⎩， 两式相减得()()()()12121212220x x x x y y y y a b -+-++=， 即2121221212y y y y b x x x x a -+⋅=--+，即2213AB OM b k k a⋅=-=-， 因此离心率22222213c b e a a ==-=，所以e ． 18．（2020·广东省高三月考）已知F 是椭圆E ：()222210x y a b a b+=>>的左焦点，经过原点O 的直线l 与椭圆E 交于P ，Q 两点，若3PF QF =，且120PFQ ∠=︒，则椭圆E 的离心率为【解析】设椭圆的右焦点F '，连接PF '，QF '，根据椭圆对称性可知四边形PFF Q '为平行四边形，则QF PF '=，且由120PFQ ∠=︒，可得60FPF '∠=︒， 所以42PF PF PF a ''+==，则12PF a '=，32PF a =由余弦定理可得()()222222cos603c PF PF PF PF PF PF PF PF ''''=+-︒=+-， 即2222974444c a a a =-=，∴椭圆的离心率e ===。

西南大学附属中学校高2020级第五次月考数学试题（文）一、选择题：本大题共12小题，每题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}1A x x =>-，*2{N |60}B x x x =∈--<，则A B ⋂=（ ）A. {}13x x -<< B. {}0,1,2 C. {}1,0,1,2- D. {}1,2【答案】D 【解析】 【分析】解一元二次不等式求得集合B ，由此求得两个集合的交集.【详解】由()()26320x x x x --=-+<，解得23x -<<，所以{}1,2B =，所以A B =I {}1,2.故选：D【点睛】本小题主要考查集合交集的概念和运算，考查一元二次不等式的解法，属于基础题. 2.已知复数z 满足()3425(i z i i -=为虚数单位)，则z 的虚部为（ ） A. 3 B. 4C. 4iD. -4【答案】B 【解析】 【分析】设出z ，根据复数相等条件列式求得z 的虚部.【详解】设z a bi =+，所以()()3425i a bi i -+=，即34(34)25a b b a i ++-=，所以3425340a b b a +=⎧⎨-=⎩，解得4b =，所以z 的虚部为4. 故选：B【点睛】本小题主要考查复数乘法、模的运算，考查复数相等的条件，考查复数的虚部的求法，属于基础题.3.设0k <，由不等式组00240x y y kx y x ≤⎧⎪≥⎪⎨-≤⎪⎪--≤⎩确定的平面区域Ω的面积为7，则k 的值为（ ） A. -1 B. -3C. -4D. -5【答案】A 【解析】 【分析】画出图像，利用平面区域Ω的面积为7列方程，解方程求得k 的值.【详解】画出平面区域Ω的图像如下图所示四边形ABCD .由24y kx y x =+⎧⎨=+⎩，解得21D x k =-.所以ABCD BCE ADE S S S ∆∆=-1124427221k =⨯⨯-⨯⨯=-，解得1k =-（正根舍去）. 故选：A【点睛】本小题主要考查根据线性规划中可行域的面积求参数，考查数形结合的数学思想方法，属于中档题. 4.倾斜角为4π的直线l 经过抛物线24y x =的焦点F ，与抛物线相交于,A B 两点，则弦AB 的长为（ ） A. 2 B. 4C. 6D. 8【答案】D 【解析】试题分析：设1122()()A x y B x y A B ，，，，，到准线的距离分别为A B d d ，，由抛物线的定义可知1211A B AF d x BF d x ==+==+，，于是122AB AF BF x x =+=++；由已知得抛物线的焦点为(10)F ，，斜率tan 451k =︒=，所以直线AB 方程为1y x =-，将1y x =-代入方程24y x =，得()214x x -=，化简得2610x x -+=，由求根公式得126x x +=，于是1228AB AF BF x x =+=++=；考点：双曲线的简单性质．【思路点睛】本题主要考查了抛物线的应用以及直线与圆锥曲线的综合问题和方程的思想，解答本题时，首先根据题意写出直线的方程，再将直线的方程与抛物线24y x =的方程组成方程组，消去y 得到关于x 的二次方程，最后利用根与系数的关系结合抛物线的定义即可求线段AB 的长． 5.已知()()2sin (0,0)2f x x πωϕωϕ=+><<的图象关于直线6x π=对称，若存在12,x x R ∈，使得对于任意的x 都有()()()12f x f x f x ≤≤，且12x x -的最小值为2π，则ϕ等于（ ） A.12πB.6π C. 4π D. 3π【答案】B 【解析】 【分析】根据()f x 的最大值和最小值对应的横坐标的距离，求得()f x 的半周期，由此求得ω的值，结合根据()f x 的对称轴列方程，求得ϕ的值.【详解】依题意存在12,x x R ∈，使得对于任意的x 都有()()()12f x f x f x ≤≤，所以()()12,f x f x 分别是()f x 的最小值和最大值，而12x x -的最小值为2π，所以π,π22T T ==，由()2ππ0T ωω==>解得2ω=，所以()()2sin 2f x x ϕ=+.由于()f x 的图象关于直线6x π=对称，所以ππ2sin 63f ϕ⎛⎫⎛⎫=+⎪ ⎪⎝⎭⎝⎭的值为2或2-，即πsin 3ϕ⎛⎫+ ⎪⎝⎭的值为1或1-，由于ππ50,2336ππϕϕ<<<+<，所以πππ,326ϕϕ+==.故选：B【点睛】本小题主要考查三角函数的周期性和对称性，考查化归与转化的数学思想方法，属于基础题. 6.为了弘扬我国优秀传统文化，某中学广播站从中国5个传统节日(春节、元宵节、清明节、端午节、中秋节)中随机选取3个节日来讲解其文化内涵，那么春节和中秋节都被选中的概率是（ ） A.310B.25C.35D.710【解析】 【分析】利用列举法列举出所有的可能选取方法，根据古典概型概率计算公式计算出所求概率.【详解】首先编号：春节为1，中秋节为2，元宵节为3，清明节为4，端午节为5.从中任选3个节目的选法有：{}{}{}{}{}{}1,2,3,1,2,4,1,2,5,1,3,4,1,3,5,1,4,5,{}{}{}{}2,3,4,2,3,5,2,4,5,3,4,5共10种选法.其中春节和中秋节都被选中的选法有{}{}{}1,2,3,1,2,4,1,2,5共3种选法，根据古典概型概率计算公式可知，春节和中秋节都被选中的概率是310. 故选：A【点睛】本小题主要考查列举法计算古典概型概率，属于基础题.7.已知,,A B C 在圆221x y +=上运动，且.AB BC ⊥若点P 的坐标为()2,0，则PA PB PC ++u u u r u u u r u u u r的最大值为（ ） A. 7 B. 8C. 9D. 10【答案】A 【解析】 【分析】根据AB BC ⊥得出AC 是圆的直径，由此将PA PB PC ++u u u r u u u r u u u r 转化为3OB OP -u u u r u u u r，结合向量减法的几何意义，求得3OB OP -u u u r u u u r的最大值.【详解】由于AB BC ⊥，所以AC 是单位圆221x y +=的直径.故0OA OC +=u u u r u u u r r,所以PA PB PC++u u u r u u u r u u u r PO OA PO OB PO OC =+++++u u u r u u u r u u u r u u u r u u u r u u u r 3OB OP =-u u u r u u u r .3OB OP -u u u r u u u r表示圆上的点到点()()32,06,0=的距离.根据圆的几何性质可知，当()1,0B -时，3OB OP -u u u r u u u r取得最大值为617+=.故选：A【点睛】本小题主要考查平面向量加法和减法的运算，考查平面向量减法的几何意义，属于基础题. 8.《九章算术》中对一些特殊的几何体有特定的称谓，例如：将底面为直角三角形的直三棱柱称为堑堵，将一堑堵沿其一顶点与相对的棱刨开，得到一个阳马(底面是长方形，且有一条侧棱与底面垂直的四棱锥)和一个鳖臑(四个面均为直角三角形的四面体).在如图所示的堑堵111ABC A B C -中，已知3,4,5AB BC AC ===，若阳马111C ABB A -的外接球的表面积等于50π，则鳖臑1C ABC -的所有棱中，最长的棱的棱长为（ ）A. 5B.C. D. 8【答案】C 【解析】 【分析】根据堑堵、阳马和、鳖臑的几何特征判断出堑堵的外接球的直径为1AC ，根据阳马111C ABB A -的外接球的表面积求得1AC ，由此求得1CC 、1BC ，从而判断出鳖臑1C ABC -的所有棱中，最长的棱的棱长. 【详解】根据堑堵、阳马和、鳖臑的几何特征可知，111111,,,AC A AC B AC B AC C ∆∆∆∆都是以1AC 为斜边的直角三角形，所以堑堵111ABC A B C -的外接球的直径为1AC ，所以214π50π2AC ⎛⎫⋅= ⎪⎝⎭，所以1AC =，所以15CC ==,1BC ==，而3,4,5AB BC AC ===.所以鳖臑1C ABC -的所有棱中，最长的棱的棱长为1AC =故选：C【点睛】本小题主要考查几何体外接球有关计算，考查中国古代数学文化，属于基础题.9.在ABC ∆中，角、、A B C 的对边分别为a b c 、、，已知ABC ∆，且2cos 22A A π⎛⎫-+= ⎪⎝⎭ABC ∆的周长为（ ）A. 3+B. 3+C.32+D.32+【答案】A 【解析】 【分析】利用降次公式、诱导公式、同角三角函数的基本关系式化简2cos 22A A π⎛⎫-+= ⎪⎝⎭，由此求得A ，利用正弦定理求得a ，利用余弦定理和三角形面积公式求得b c +，由此求得三角形ABC 的周长. 【详解】由2cos 22A A π⎛⎫-+= ⎪⎝⎭得)1cos sin A A -+=，sin A A =，所以tan A =0πA <<，所以π3A =.由正弦定理得2sin a r A=（r 为三角形ABC 外接球的半径），即2sin 23a r A =⋅==.由三角形面积公式和余弦定理得2221sin 22cos bc A a b c bc A⎧⋅⋅=⎪⎨⎪=+-⎩，即22413bc b c =⎧⎨+=⎩，即()()22213,13221b c bc b c bc +-=+=+=，所以b c +=，所以三角形ABC 的周长为3a b c ++=故选：A【点睛】本小题主要考查正弦定理和余弦定理解三角形，考查三角形的面积公式，考查三角形周长的求法，考查降次公式和同角三角函数的基本关系式，属于中档题.10.设函数()()22lg 21f x x x =+-+，已知40.30.31000.3,log ,47a b c ===，则（ ） A. ()()()f a f b f c << B. ()()()f a f c f b << C. ()()()f c f b f a << D. ()()()f b f a f c <<【答案】B 【解析】 【分析】首先判断出函数()f x 的奇偶性和单调性，结合,,a b c 的大小判断出()()(),,f a f b f c 的大小关系.【详解】函数()f x 的定义域为R ，()()f x f x -=，所以()f x 为偶函数.当0x ≥时，()2lg 2x +和21x-+都是单调递增，所以()f x 在[)0,+∞上是增函数.0.30.3100log log 107<=，20.310103310010010log log log 2773b ⎛⎫=-=>= ⎪⎝⎭，4000.30.31<<=，00.30.54442<<=.所以012a c b <<<<<.所以()()()()()f a f c f b f b f b <<=-=.故选：B【点睛】本小题主要考查利用函数的奇偶性和单调性比较大小，考查指数式和对数式比较大，考查化归与转化的数学思想方法，属于中档题.11.已知正项数列{}n a 的前n 项和为n S ，且21122n n n S a a =+，若数列()2112n n nn b S +=-，数列{}n b 的前2020项和为（ ） A.20192020B. 20192020-C.20202021D. 20202021-【答案】D 【解析】【分析】 利用11,1,2n n n S n a S S n -=⎧=⎨-≥⎩求得数列{}n a 的通项公式，由此求得n S ，从而求得n b 的表达式，利用裂项求和法求得{}n b 的前2020项和. 【详解】由21122n n n S a a =+①，当1n =时21111122a a a =+，解得()110n a a =>.当2n ≥时，21111122n n n S a a ---=+②， ①-②得221111112222n n n n n a a a a a --=-+-，整理得()()1110n n n n a a a a --+--=，由于0n S >，所以1110,1n n n n a a a a ----=-=，所以数列{}n a 是首项为11a =，公差为1的等差数列，所以n a n =，()1122nn n n a a S n ++=⋅=.所以()()()21211121n n n nn n b S n n ⋅⋅++=-=-+()1111n n n ⎛⎫=-⋅+ ⎪+⎝⎭.所以数列{}n b 的前2020项和为：111111112233420202021--++--+++L 12020120212021=-+=-. 故选：D【点睛】本小题主要考查已知n S 求n a ，考查由递推关系证明等差数列，考查等差数列前n 项和，考查裂项求和法，考查运算求解能力，属于中档题.12.在ABC ∆中，()1,10,sin ,cos 328A B BC C A B >==-=，若点P 是ABC ∆所在平面内任意一点，则PA PC -u u u r u u u r的取值范围是（ ）A. []5,5-B. []6,6-C. []7,7-D. []8,8-【答案】D 【解析】 【分析】利用正弦定理和余弦定理解三角形，求得AC ，由此求得PA PC -u u u r u u u r的取值范围.【详解】由于A B >，设D 是BC 上一点，且BD AD =，所以B DAB =∠，CAB B CAD ∠-=∠.由()1cos 8A B -=，得1cos 8CAD ∠=，sin CAD ∠==设BD x =，在三角形ADC中，,10,sin AD x CD x CAD C ==-∠==.由正弦定理得sin sin AD CD C CAD =∠，即328=，解得2x =，所以2,8AD CD ==.在三角形ADC 中，由余弦定理得24641cos 48AC CAD AC +-∠==⋅，化简得221200AC AC ⋅--=，解得8AC =.PA PC -u u u r u u u r 表示平面内的点P 到,A C 两点的距离之差，所以8PA PC CA ≤=-u u u r u u u r u u u r ，所以88PA PC -≤-≤u u u r u u u r.故选：D【点睛】本小题主要考查正弦定理、余弦定理解三角形，考查同角三角函数的基本关系式，考查向量模的减法运算的几何意义，考查数形结合的数学思想方法，属于中档题.二、填空题：本大题共4小题，每题5分，共20分.13.某三棱锥的三视图如图所示，该三棱锥的四个面的面积中最大的值是______.【解析】根据三视图得到原图是三棱锥，一条侧棱垂直于底面．根据各个侧面的图形特点，高最大和底最大，三角形面积为：12s==14.已知函数()21,02log,0xxf xx x⎧≤⎪=⎨⎪>⎩，若()()()24g x f x f x m=-+有4个零点，则m的取值范围是_________.【答案】[)3,4【解析】【分析】画出()f x图像，令()t f x=，将“()()()24g x f x f x m=-+有4个零点”的问题转化为240t t m-+=在[)1,+∞上有两个不同实数根来列不等式组，解不等式求得m的取值范围.【详解】画出()f x图像如下图所示，由于可知，当()1f x≥时，每个函数值y都有两个不同自变量x与其对应.令()t f x=，则“()()()24g x f x f x m=-+有4个零点”的问题转化为240t t m-+=在[)1,+∞上有两个不同实数根.令()()2401h t t t m t=-+=≥，依题意()h t在[)1,+∞上有两个不同实数根，由于其对称轴2x=，所以()216401140mh m∆=->⎧⎨=-+≥⎩，解得34m≤<.所以实数m的取值范围是[)3,4.故答案为：[) 3,4的【点睛】本小题主要考查分段函数的图像与性质，考查根据函数零点的个数求参数的取值范围，考查数形结合的数学思想方法，属于中档题.15.已知双曲线()222210,0x y a b a b-=>>的左、右焦点分别为12,F F ，点P 在双曲线的右支上，且126PF PF =，则此双曲线的离心率e 的最大值为_________.【答案】75【解析】 【分析】利用余弦定理求得2c 关于2PF 的表达式，将2a 也表示成2PF 的形式，由此求得离心率e 的表达式，进而求得离心率的最大值. 【详解】由于126PF PF =，在三角形12F F P 中，由余弦定理得222121212122cos F F PF PF PF PF F PF =+-⋅⋅∠，即2c =根据双曲线的定义有12225PF PF PF a -==.所以双曲线的离心率22c e a===当P 位于双曲线右顶点时，12πF PF ∠=，75=，也即双曲线的离心率的最大值为75.故答案：75【点睛】本小题主要考查双曲线离心率的最大值的求法，考查双曲线的定义，考查余弦定理解三角形，考查化归与转化的数学思想方法，属于中档题.16.已知函数()2xf x e x =-，下列说法正确的是__________.()f x ①的值域是[)1,+∞；②当1a =时，方程()10f x ax --= 有两个不等实根；③若函数()1y f x ax =--有三个零点时，则()2,1a e ∈-；④经过()0,1有三条直线与()y f x =相切. 【答案】①②③ 【解析】 【分析】①：结合导数，用函数的单调性和奇偶性，求得()f x 的值域；②利用导数，证得方程()10f x x --= 有两个不等实根；③根据()f x 为偶函数，故可先考虑0x ≥的情况，再由对称性得到0x ≤的情况.当0x ≥时，首先确定0x =是函数()1y f x ax =--的零点，令()10y f x ax =--=，分离常数a ，利用导数求得a 的取值范围.再根据对称性，求得a 的取值范围.④利用导数，求得过()0,1的切线的条数.【详解】①函数()f x 的定义域为R ，且()()f x f x -=，所以()f x 为偶函数，图像关于y 轴对称.当0x ≥时，()2xf x e x =-，()'2x fx e x =-，()''2x f x e =-.令()''0f x =解得ln 2x =，所以()'f x 在[)0,ln 2上递减，在()ln 2,+∞上递增，()()'ln2ln 22ln 222ln 221ln 20fe =-=-=->，所以()()''ln 20f x f ≥>，所以()f x 在[)0,+∞上单调递增，从而()()01f x f =≥.由于()f x 为偶函数，所以()f x 在(],0-∞上单调递减，且()()01f x f =≥.所以()f x 的值域是[)1,+∞.故①正确.②显然，0x =是方程()10f x ax --=的根.方程()10f x ax --=可化为()1f x ax =+.当1a =时，即()1f x x =+.根据①的分析，结合图像可知，当0x <时()f x 与1y x =+的图像没有公共点.故只需考虑0x ≥的情况.由()1f x x =+得21x e x x -=+，即210x e x x ---=.构造函数()()210x g x e x x x =---≥，()00g =，()()'''21,2x x g x e x g x e =--=-，令()''20x g x e =-=，解得ln 2x =.所以()'21xg x e x =--在[)0,ln 2上递减，在()ln 2,+∞上递增，且()()()''ln2'200,ln 22ln 2112ln 20,250g g e g e ==--=-<=->，所以存在()0ln 2,2x ∈，使得()'00g x =.故()g x 在[)00,x 上递减，在()0,x +∞上递增.()()()200,130,270g g e g e ==-<=->，所以存在()11,2x ∈，使()10g x =.综上所述，当1a =时，方程()10f x ax --= 有两个不等实根成立，故②正确.③()f x 为偶函数，故可先考虑0x ≥的情况.当0x ≥时，函数()1y f x ax =--为()210x y e x ax x =---≥，故方程()2100x e x ax x ---=≥有三个不相等的实数根.首先0x =是方程()2100x e x ax x ---=≥的根.先证1a <：令()()210xm x e x ax x =---≥，()'2xm x e x a =--，()''2xm x e =-，令()''20x m x e =-=解得ln 2x =.所以()'2x m x e x a =--在[)0,ln 2上递减，在()ln 2,+∞上递增.()'01m a =-，当x →+∞，()'m x →+∞.若()'010m a =-≤，即1a ≥，则()m x 在区间[)0,+∞上先减后增，在区间[)0,+∞上至多只有两个零点，不符合题意.故1a <.故下证2a e >-：当0x >时，由210xe x ax ---=得21x e x a x--=有两个不同的实数根.构造函数()()210x e x n x x x --=>，()()()'211x x e x n x x ---=.令()()10x h x e x x =--≥，()00h =，()'10x h x e =-≥,所以()h x 在[)0,+∞上单调递增，所以当0x >时，()0h x >.所以由()()()'211x x e x n x x ---=可知()n x 在()0,1上递减，在()1,+∞上递增，所以()n x 在1x =处取得极小值也即是最小值()12n e =-，所以2a e >-.综上所述，a 的取值范围是()2,1e -.由于()f x 为偶函数，根据函数图像的对称性可知a 的取值范围是()2,1e -.故③正确.④当0x ≥时，设经过点()0,1的切线的切点为()0200,xx e x -，()'2x fx e x =-，()0'002xf x e x =-，故切线方程为()()()002002x xy e x e x x x --=--，将()0,1代入上式得()()()00200012x x ex e x x --=--，化简得()()000110xx e x ---=.令()()10x h x e x x =--≥，()00h =，()'10xh x e =-≥,所以()h x 在[)0,+∞上单调递增.所以方程()()00110xx e x ---=解得00x =或01x =.所以当0x ≥时，()f x 有两条切线.根据()f x 为偶函数，所以当0x ≤时，()f x 也有两条切线方程. 所以经过()0,1有四条直线与()y f x =相切，④错误.特别的，当0x ≥时，()2xf x e x =-，()()''2,01x fx e x f =-=，即当0x ≥时，()f x 在0x =处的切线的斜率为1.当0x ≤时，()()()2'',2,01xx f x e x f x e x f --=-=--=-，即当0x ≤时，()f x 在0x =处的切线的斜率为1-. 故答案为：①②③【点睛】本小题主要考查利用导数研究函数的单调性、极值和最值，考查利用导数研究函数零点问题，考查利用导数研究函数图象的切线，考查化归与转化的数学思想方法，考查运算求解能力，考查分析、思考与解决问题的能力，属于难题.三、解答题：共70分.解答应写出文字说明、证明过程或演算步骤.第17～21题为必考题，每个试题考生都必须作答.第22、23题为选考题，考生根据要求作答. （一）必考题：共60分.17.党的十九大报告指出，在全面建成小康社会的决胜阶段，让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中，精准扶贫助推社会公平显得尤其重要.若某地区有100户贫困户，经过一年扶贫后，为了考查该地区的“精准扶贫”的成效(该地区脱贫标准为“每户人均年收入不少于4000元”)，现从该地区随机抽取A、B两个村庄，再从这两个村庄的贫困户中随机抽取20户，调查每户的现人均年收入，绘制如图所示的茎叶图(单位：百元).（1）观察茎叶图中的数据，判断哪个村庄扶贫成效较好？并说明理由；（2）计划对没有脱贫的贫困户进一步实行“精准扶贫”，下一年的资金投入方案如下：对人均年收入不高于2000元的贫困户，每户每年增加扶贫资金5000元；对人均年收入高于2000元但不高于3000元的贫困户，每户每年增加扶贫资金3000元；对人均年收入高于3000元但不高于4000元的贫困户，每户每年增加扶贫资金1000元；对已经脱贫的贫困户不再增加扶贫资金投入.依据此方案，试估计下一年该地区共需要增加扶贫资金多少元？【答案】（1）B，理由见解析；（2）115000元.【解析】【分析】（1）通过茎叶图，根据脱贫标准，判断两个村庄中数据集中的区间，由此判断扶贫较好的村庄.或计算出两个村庄贫困户人均年收入的平均值，由此判断出扶贫较好的村庄.（2）根据分组的区间，计算出每组的频率，乘以对应的扶贫资金，然后相加，求得下一年该地区共需要增加扶贫资金.【详解】（1）B村庄扶贫效果较好.理由一：由茎叶图中的样本数据可以看出，经过一年的扶贫之后，A村庄中的贫困户人均年收入都集中在3000到5000之间，B村庄中的贫困户人均年收入都集中在4000到6000之间，所以B村庄扶贫效果较好.理由二：由茎叶图中的样本数据可以看出，经过一年的扶贫之后，A村庄中的贫困户人均年收入的平均值估计为3160元，B村庄中的贫困户人均年收入的平均值估计为4870元，所以B村庄中扶贫效果较好.(答出其中一种理由即可)(2)该地区人均年收入不高于2000元的贫困户的频率估计为220，高于2000元但不高于3000元的贫困户的频率估计为320，高于3000元但不高于4000元的贫困户的频率估计为420，所以该地区共需要增加的扶贫资金估计为234500030001000100115000202020⎛⎫⨯+⨯+⨯⨯=⎪⎝⎭元.【点睛】本小题主要考查茎叶图在实际生活中的应用，考查用数学方法解决实际问题，属于基础题. 18.已知等比数列{}n a 的前n 项和为n S ，且当*n N ∈时，n S 是12n +与2m 的等差中项(m 为实数). （1）求m 的值及数列{}n a 的通项公式；（2）令()*21log n n b a n N =+∈，是否存在正整数k ，使得1111210n n n kb b b n ++⋅⋅⋅+>+++对任意正整数n 均成立？若存在，求出k 的最大值；若不存在，说明理由.【答案】（1）1-，12n n a -=；（2）存在，4.【解析】 【分析】（1）根据等差中项的性质列方程，求得n S 的表达式.利用11,1,2n n n S n a S S n -=⎧=⎨-≥⎩，结合{}n a 是等比数列，求得m 的值及数列{}n a 的通项公式. （2）由（1）求得n b 的表达式，将不等式1111210n n n kb b b n ++⋅⋅⋅+>+++左边看成()f n ，利用差比较法判断出()f n 的单调性，由此求得()f n 的最小值，进而求得k 的最大值.【详解】(1)Q n S 是12n +与2m 的等差中项， ∴ 1222n n S m +=+，即 2nn S m =+，当1n =时， 112S a m ==+，当2n ≥时， 112n n n n a S S --=-=，Q {}n a 是等比数列，∴ 11a =，则 21m +=，∴ 1m =-，且数列{}n a 的通项公式为12n n a -=.(2)存在正整数k ，使不等式恒成立，k 的最大值为4.21log n n b a n =+= ()*.n N ∈()11111112122n n n f n b b b n n n n=++=++++++++L L ， ()()1111110212212122f n f n n n n n n +-=+-=->+++++Q ∴ ()()1.f n f n +>∴数列(){}f n 单调递增，()()min 112f n f ∴==， 由不等式恒成立得：1102k <，∴ 5k <. 故存在正整数k ，使不等式恒成立，k 的最大值为4.【点睛】本小题主要考查等差中项的性质，考查等比数列通项公式，考查数列单调性的证明，考查不等式恒成立问题的求解，属于中档题.19.如图1所示，在等腰梯形ABCD 中，//BC AD ，CE AD ⊥，垂足为E ，33AD BC ==， 1.EC =将DEC∆沿EC 折起到1D EC ∆的位置，如图2所示，使平面1D EC ⊥平面ABCE .（1）连结BE ，证明：AB ⊥平面1D BE ；（2）在棱1AD 上是否存在点G ，使得//BG 平面1D EC ，若存在，直接指出点G 的位置(不必说明理由)，并求出此时三棱锥1G D EC -的体积；若不存在，请说明理由. 【答案】（1）证明见解析；（2）存在，点G 为1AD 的中点，16. 【解析】 【分析】（1）通过面面垂线的性质定理，证得1D E ⊥平面ABCE ，由此证得1D E AB ⊥.利用勾股定理计算证明BE AB ⊥，从而证得AB ⊥平面1D EB .（2）通过线面平行的判定定理，判断出点G 为1AD 的中点.利用换顶点的方法，通过11G D EC C D EG V V --=，来计算出三棱锥1G D EC -的体积.【详解】(1)因为平面1D EC ⊥平面ABCE ，平面1D EC I 平面ABCE EC =，11,D E EC D E ⊥⊂平面1D EC ，所以 1D E ⊥平面ABCE ，又因为 AB Ì平面ABCE ，所以 1D E AB ⊥ ，又2AB BE AE ==，满足222AE AB BE =+，所以 BE AB ⊥，又 1BE D E E =I ，所以 AB ⊥平面1D EB .(2)在棱1AD 上存在点G ，使得//BG 平面1D EC ，此时点G 为1AD 的中点.11G D EC C D EG V V --=， 由(1)知，1D E ⊥平面ABCE ，所以 1CE D E ⊥， 又CE AE ⊥，所以 CE ⊥平面1AED ，所以CE 为三棱锥1C D EG -的高，且1CE =， 在1Rt D EA V 中，11,2D E AE ==，G 为斜边1AD 的中点， 所以 111111212222D EG D EA S S ==⨯⨯⨯=， 所以 111111113326G D ECC D EG D EG V V S CE --==⋅=⨯⨯=.故，在棱1AD 上存在点G ，使得//BG 平面1D EC ， 此时三棱锥1G D EC -的体积为16. 【点睛】本小题主要考查线面垂线的证明，考查面面垂直的性质定理的运用，考查三棱锥体积的计算，考查空间想象能力和逻辑推理能力，属于中档题.20.已知函数()()()11ln x x f x x++=，()()ln g x x mx m R =-∈ .（1）求函数()g x 的单调区间；（2）当0m >时，对任意的[]11,2x ∈，存在[]21,2x ∈，使得()()123f x m g x ->成立，试确定实数m 的取值范围.【答案】（1）当0m ≤时，()g x 的单调递增区间是()0,+∞，无递减区间；当0m >时，()g x 的单调递增区间是10,m ⎛⎫ ⎪⎝⎭，递减区间是1,m ⎛⎫+∞ ⎪⎝⎭；（2）()0,2ln2-. 【解析】 【分析】（1）求得()g x 的导函数，对m 分成0m ≤和0m >两种情况，讨论函数()g x 的单调区间. （2）将问题转化为()()min min 3f x m g x ->，利用导数求得()f x 的最小值，结合（1）对m 分成111,1,022m m m ≥<<<≤三种情况进行分类讨论，求得()g x 的最小值.从而确定m 的取值范围.【详解】（1）由()()ln 0g x x mx x =->，得()'1g x m x=-.当0m ≤时，()'0g x >，所以()g x 的单调递增区间是()0,∞+，没有减区间.当0m >时，由()'0g x >，解得10x m <<；由()'0g x <，解得1x m >，所以()g x 的单调递增区间是10,m ⎛⎫ ⎪⎝⎭，递减区间是1,m ⎛⎫+∞ ⎪⎝⎭.综上所述，当0m ≤时，()g x 的单调递增区间是()0,∞+，无递减区间；当0m >时，()g x 的单调递增区间是10,m ⎛⎫ ⎪⎝⎭，递减区间是1,m ⎛⎫+∞ ⎪⎝⎭. （2）当0m >时，对任意[]11,2x ∈，存在[]21,2x ∈，使得()()123f x m g x ->成立，只需()()min min 3f x m g x ->成立.由()()()11ln ln 1ln 1x x x f x x xxx++==+++，得()'2221ln 11ln x x x f x x x x x --=+-=.令()()ln 0h x x x x =->，则()'1x h x x-=.所以当()0,1x ∈时，()'0h x <，当()1,x ∈+∞时，()'0h x >.所以()h x 在()0,1上递减，在()1,+∞上递增，且()11h =，所以()()()min 110h x h x h ≥==>.所以()'0f x >，即()f x 在()0,∞+上递增，所以()f x 在[]1,2上递增，所以()()min 12f x f ==.由（1）知，当0m >时，()g x 在10,m ⎛⎫ ⎪⎝⎭上递增，在1,m ⎛⎫+∞ ⎪⎝⎭上递减， ①当101m<≤即m 1≥时，()g x 在[]1,2上递减，()()min 2ln22g x g m ==-； ②当112m <<即112m <<时，()g x 在11,m ⎡⎫⎪⎢⎣⎭上递增，在1,2m ⎛⎤ ⎥⎝⎦上递减，()()(){}min min 1,2g x g g =，由()()()21ln22ln2g g m m m -=---=-， 当1ln22m <≤时，()()21g g ≥，此时()()min 1g x g m ==-， 当ln21m <<时，()()21g g <，此时()()min 2ln22g x g m ==-， ③当12m ≥即102m <≤时，()g x 在[]1,2上递增，()()min 1g x g m ==-， 所以当0ln2m <≤时，()()min 1g x g m ==-，由0ln223m m m<≤⎧⎨->-⎩，得0ln2.m <≤当ln2m >时，()()min 2ln22g x g m ==-，由ln223ln22m m m>⎧⎨->-⎩，得 ln22ln2m <<-．∴ 02ln2m <<-．综上，所求实数m 的取值范围是()0,2ln2-．【点睛】本小题主要考查利用导数研究函数的单调区间，考查利用导数研究不等式恒成立、存在性综合问题，考查化归与转化的数学思想方法，考查分类讨论的数学思想方法，属于难题.21.已知椭圆C ：22221(0)x y a b a b+=>>的左、右焦点分别是()()121,0,1,0F F -，点()0,A b ，若12AF F ∆的内切圆的半径与外接圆的半径的比是1:2. （1）求椭圆C 的方程；（2）点M 是椭圆C 的左顶点，P 、Q 是椭圆上异于左、右顶点的两点，设直线MP 、MQ 的斜率分别为1k 、2k ，若1214k k ⋅=-，试问直线PQ 是否过定点？若过定点，求该定点坐标；若不过定点，请说明理由.【答案】（1）22143x y +=；（2）是，() 1,0. 【解析】 【分析】（1）设内切圆和外接圆的半径分别是,r R ，则2R r =.利用三角形的面积公式求得r 与,a b 的关系式，利用正弦定理求得R 与,a b 的关系式，由此求得,a b 两者直线的关系式，进而求得,a b 的值，以及椭圆C 的方程.（2）当直线PQ 的斜率不存在时，设出,P Q 的坐标，利用1214k k ⋅=-列方程，结合,P Q 在椭圆上，求得,P Q 的坐标，由此求得直线PQ 的方程.当直线PQ 斜率存在时，设出直线PQ 的方程y kx m =+，代入椭圆方程，化简后写出韦达定理和判别式，利用1214k k ⋅=-列方程，求得,k m 的关系式，由此判断出直线PQ 所过定点坐标.【详解】（1）由已知()0,A b 是椭圆C 的顶点，又()()121,0,1,0F F -分别是椭圆的左右焦点，则有221a b -=，且1212,2AF AF a F F ===.设12AF F ∆的内切圆半径与外接圆的半径分别是r 和R ，则2R r =.由()121212121122AF F S AF AF F F r F F OA ∆=++⋅=⋅⋅，得()112222a a r b ++⋅=⋅⋅，得1br a =+. 设12AF F α∠=，在1Rt AOF ∆中，sin ba α=，在12AF F ∆中，由正弦定理得22sin AF R α=，即22sin a a a R b b aα===，所以22a R b =.所以2221a b b a =+，即()2241b a a =+，即()()22411a a a -=+，化简得()()2120a a +-=，解得2a =（1a =-舍去），所以b =所以所求椭圆C 的方程是22143x y +=.（2）由已知()2,0M -，设()()1122,,,P x y Q x y ，①若直线PQ 的斜率不存在，不妨设()()1111,,,P x y Q x y -n n n n ， 由1214k k ⋅=-得11111224y y x x -⋅=-++，即()221142y x =+，又2211143x y +=，即221143120y x +-=，得21120x x +-=，解得12(x =-舍)或11x =，331,,1,22P Q ⎛⎫⎛⎫∴- ⎪ ⎪⎝⎭⎝⎭或331,,1,22P Q ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭，此时直线PQ 的方程为1x =，②若直线PQ 的斜率存在，设直线PQ 的方程为y kx m =+，由22143y kx mx y =+⎧⎪⎨+=⎪⎩，得()2223484120k xkmx m +++-=，21212228412,3434km m x x x x k k-∴+=-=++n n n n ， 由()()()2222226443441248430k m kmk m ∆=-+-=-+>，得2243k m +>，又1214k k ⋅=-n n ，即12121224y y x x ⋅=-++n n n n ，即()()12124220y y x x +++=n n n n ，即()()()()12124220kx m kx m x x +++++=n n n n ， 整理得()()()2212124142440k x x km x x m ++++++=n n n n ，()()22222412841424403434m km k km m k k -⎛⎫∴+⋅++-++= ⎪++⎝⎭， 整理得2220m km k --=，解得2m k =，或m k =-，当2m k =时，直线PQ ：()22y kx k k x =+=+，即过定点()2,0-，不符合题意， 当m k =-时，直线PQ ：()1y kx k k x =-=-，即过定点()1,0． 综上，直线PQ 过定点()1,0．【点睛】本小题主要考查椭圆的标准方程的求法，考查三角形内切圆、外接圆半径的有关计算，考查椭圆的几何性质，考查直线和椭圆的位置关系，考查椭圆中的定点问题，考查运算求解能力，属于难题.（二）选考题：共10分.请考生在第22、23题中任选一题作答.如果多做则按所做的第一题计分.选修4—4坐标系与参数方程22.已知平面直角坐标系中，直线l 的参数方程为1(82x t t y t=+⎧⎨=-⎩为参数)，以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为223695sin ρθ=-. （1）求直线l 的普通方程以及曲线C 的参数方程；（2）过曲线C 上任意一点E 作与直线l 的夹角为75o 的直线，交l 于点F ，求EF 的最小值.【答案】（1）2100x y +-=，2cos 3sin x y ϕϕ=⎧⎨=⎩；（2【解析】 【分析】（1）利用加减消元法消去直线l 的参数方程中的参数t ，求得直线l 的普通方程.先将曲线C 的极坐标方程转化为直角坐标方程，再转化为参数方程.（2）根据（1）写出E 点的坐标，求得E 到直线l 的距离d ，将EF 转化为sin 75do，通过d 的最小值来求得EF 的最小值.【详解】（1）由182x t y t =+⎧⎨=-⎩得22282x t y t=+⎧⎨=-⎩，两式相加并化简得2100x y +-=.将222,sin x y y ρρθ=+=n n 代入曲线C 的极坐标方程，可得曲线C 的直角坐标方程为229436x y +=，即22194y x +=，故曲线C 的参数方程为2cos 3sin x y ϕϕ=⎧⎨=⎩（ϕ为参数）（2）由（1）得()2cos ,3sin E ϕϕn n ，则E 到l 距离105sind ϕγ-+==中4tan 3γ=.()sin 75sin 4530sin 45cos30cos 45sin 30=+=+=o o o o o o o如图，过点E 作EG l ⊥，交l 于G ，则d EG =，在Rt EFG ∆中，sin754dEF==o，当()sin 1ϕγ+=，d EF=【点睛】本小题主要考查参数方程化为普通方程，考查极坐标方程化为直角坐标方程，考查直角坐标方程化为参数方程，考查点到直线的距离公式，考查三角函数最值的求法，考查数形结合的数学思想方法，考查化归与转化的数学思想方法，属于中档题.选修4—5不等式选讲23.已知实数a 、b 、c R +∈（1）若24ab ac bc a +++=-，求2a b c ++的最小值； （2）若3a b c ++=，求证：3331118a b c ⎛⎫⎛⎫⎛⎫---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭. 【答案】（1）)21 ；（2）证明见解析.【解析】 【分析】（1）将方程24ab ac bc a +++=-转化为()())21a c a b ++=，然后将所求表达式2a b c ++转化为()()a b a c +++，然后利用基本不等式求得2a b c ++的最小值.（2）利用综合法证明不等式：先利用基本不等式证得31a a -≥、31b b -≥、31c c-≥，然后三者相乘，证得不等式成立.【详解】（1）24ab ac bc a +++=-Q ，()()22ab ac bc a a ab ac bc ∴+++=+++ ()()()())241a a b c a b a c a b =+++=++=-=，.()())221a b c a b a c ∴++=+++≥=，当且仅当a b a c +=+时，等号成立.（2）331a b c a a a a -+-==≥Q，①（当且仅当b c =时取等号）.331b a c b b b b-+-==≥，②（当且仅当a c =时取等号）.331c a b ccc-+-==≥，③（当且仅当a b =时取等号）. 又因为实数a 、b 、c +∈R ， 由⨯⨯①②③得：3331118.(a b c ⎛⎫⎛⎫⎛⎫---≥⎪⎪⎪⎝⎭⎝⎭⎝⎭当且仅当a b c ==时取等号) 3331118.a b c ⎛⎫⎛⎫⎛⎫∴---≥ ⎪⎪⎪⎝⎭⎝⎭⎝⎭【点睛】本小题主要考查利用基本不等式求最小值，考查综合法证明不等式，考查化归与转化的数学思想方法，属于中档题.。