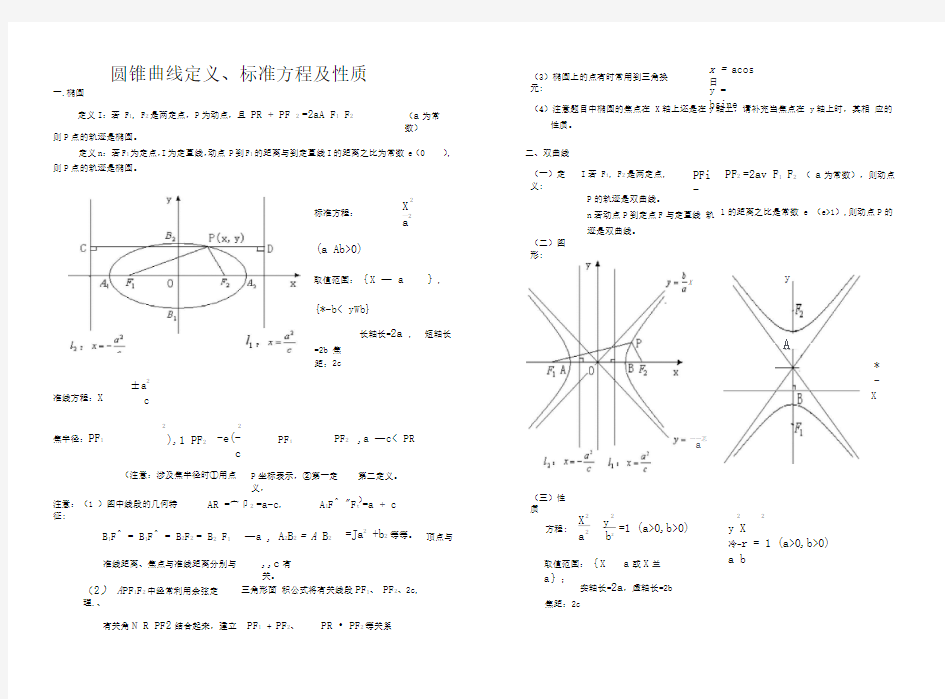

一.椭圆圆锥曲线定义、标准方程及性质(3)椭圆上的点有时常用到三角换
元:
x = acos
日
y =
bsine
定义I:若 F1, F2是两定点,P为动点,且PR + PF 2 =2aA F1 F2(a为常
数)(4)注意题目中椭圆的焦点在 X轴上还是在y轴上,请补充当焦点在 y轴上时,其相应的性质。
则P点的轨迹是椭圆。
定义n:若F1为定点,I为定直线,动点P到F1的距离与到定直线I的距离之比为常数e (0 (一)定 义: I若 F i, F2是两定点, PFi - PF2 =2av F1F2(a为常数),则动点 标准方程:(a Ab>0) 准线方程:X ±a2 c 焦半径:PF1 2 ),1 PF2 2 -e(- c PF i (注意:涉及焦半径时①用点 注意:(1 )图中线段的几何特征: 2 X —2 a P的轨迹是双曲线。 n若动点P到定点F与定直线轨 迹是双曲线。 l的距离之比是常数 e (e>1),则动点P的 取值范围:{X — a {*-b< yWb} 长轴长=2a , 短轴长 =2b 焦 距:2c PF2 ,a —c< PR P坐标表示,②第一定 义, 第二定义。 ) (二)图 形: X y A * - X AR =宀卩2 =a-c, A1F^ "F t =a + c (三)性 质 B1F^ = B1F^ = B2F2 = B2 F1 准线距离、焦点与准线距离分别与(2)A PF1F2中经常利用余弦定理.、 有关角N R PF2结合起来,建立 —a , A2B2 = A B2 =J a2+b2 等等。顶点与方程: 2 X 2 a 2 y b2 =1 (a>0,b>0) ,,c有 关。 取值范围:{X a或X兰 a}; 三角形面积公式将有关线段PF1、PF2、2c, 实轴长=2a,虚轴长=2b 焦距:2c PF1+ PF2、PR ? PF2等关系 一一忑 a 2 2 y X 冷-r = 1 (a>0,b>0) a b 准线方程: 2 a x = ±—— c 焦半径:PF2 2 e(—-x) I , c PF1 - PF2 =2a; 注意:(1) 图中线段的几何特 征: 顶点到准线的距离: AF i a2 BF2 =c-a, AF2 = BF-i a2 或a + —;焦点到准线的距 离: c =a +c 2 2 a十丄a c-——或c +— — c 两准线间的距离=2a- (2)若双曲线方程 为 2 y b2 =1二渐近线方程: 2 x ~2 a 2 y b2 b =±— x a 若渐近线方程为y =±-x = a 2 x ~2 a x2 若双曲线与— a 2 爲=1有公共渐近线,可设为 b2 2 x ~2 a (z >0,焦点在x轴上,A <0,焦点在y轴上) (3)特别地当a = b时二离心率e =」2= 两渐近线互相垂直,分别为y= ± X, 此时双曲线为等轴双曲线,可设为X2 - y2 = A ; (4)注意△ PF1F2中结合定义PF i - PF2 =2a与余弦定理coMF i PF2,将有关线段PF1、PF2、F1F2和角结合起来。 (5)完成当焦点在y轴上时,标准方程及相应性质。 三、抛物线 (一)定义:到定点 F与定直线I的距离相等的点的轨迹是抛物线。 即:至庞点F的距离与到定直线l的距离之比是常数 e( e=1)。 (二)图形:(三)性质:方 程: y2=2 px,(pA 0), p-—焦参 数; 焦点:(学),通径A B=2 P ; 1 准线: X—卫- x 2 ; 焦半 径: CF =X Q+卫,过焦点弦长CD =捲+ 卫+x2+-p = x 1 + X2+ P 焦点到准线的距离=P ;通径长=2p -卫. = , 2 顶点是焦点向准线所作垂线段中点。 注意:(1)几何特征:焦点到顶点的距离 (2 )抛物线y2=2 px上的 2 动点可设为P筍⑷或 P(2pt2,2pt)或P(X G, w)其中yl = 2pxG 考点一求圆锥曲线方程 求指定的圆锥曲线的方程是高考命题的重点,主要考查学生识图、画图、数形结合、等 价转化、分类讨论、逻辑推理、合理运算及创新思维能力,解决好这类问题,除要求同学们 熟练掌握好圆锥曲线的定义、性质外,命题人还常常将它与对称问题、弦长问题、最值问题 等综合在一起命制难度较大的题,解决这类问题常用定义法和待定系数法 . ?典例探究 [例1]某电厂冷却塔的外形是如图所示的双曲线的一部分,绕其中轴 (即双曲线的虚轴) 旋转所成的曲面,其中 A 、A '是双曲线的顶点,C 、C '是冷却塔上口直径的两个端点, B'是下底直径 的两个端点,已知 AA ‘ =14 m, CC ‘ =18 m,BB' =22 m,塔高20 m. 命题意图:本题利用对称问题来考查用待定系数法求曲线方程的方法,设计新颖,基础 性强. 知识依托:待定系数法求曲线方程,如何处理直线与圆锥曲线问题, 错解分析:不能恰当地利用离心率设出方程是学生容易犯的错误 是解决好本题的关键. 技巧与方法:本题是典型的求圆锥曲线方程的问题,解法一,将曲线方程,两式相减得关于直线 AB 斜率的等式.解法二,用韦达定理. 1 于A 、B 两点,直线y=」x 过线段AB 的中点,同时椭圆 C 上存在一点与右焦点关于直线 I 对 2 称,试求直线I 与椭圆C 的方程. 建立坐标系并写出该双曲线方程 . 命题意图:本题考查选择适当的坐标系建立曲线方程和解方程组的基础知识,考查应用 所学积分知识、思想和方法解决实际问题的能力 . 知识依托:待定系数法求曲线方程;点在曲线上,点的坐标适合方程。 错解分析:建立恰当的坐标系是解决本题的关键。 技巧与方法:本题第一问是待定系数法求曲线方程。 解:如图,建立直角坐标系 xOy,使AA’在x 轴上,AA '的中点 为坐标原点0, CC '与 BB '平行于x 轴. 解法一:由十;2 ,得冷bl ;,从而a2=2b2,c =b . 设椭圆方程为 x 2+2y 2=2b 2 A(X 1,y 1),B(x 2,y 2)在椭圆上. Q o o o o o o o o o 则 x i +2y i =2b ,X 2 +2y 2 =2b ,两式相减得,(x i — X 2 )+2 (y i — y 2 )=0, y 1— y 2 X 1— X 2 2(yi+ y 2) 2 设双曲线方程为 x 2 a -y 2=1(a>0,b>0),则 a=2AA ’ =7 b 2 2 又设B(11,y i ),C(9,X 2)因为点B 、C 在双曲线上,所以有 x 1 设AB 中点为(X 0,y 0),则k AB =——-,又(X 0,y 0)在直线y=— x 上, 2y 0 2 X 0 2y 0 y o=_ x o ,于是一 2 X 0 2y 0 72 b 2 72 b 2 —1,k AB =— 1,设 I 的方程为 y= — X+1. 右焦点 (b,0)关于I 的对称点设为(X' ,y'), 则H 二1 .2 2 解得吃「-b 由题意,知y 2 — y 1=20,由以上三式得:y 1 = — 12,y 2=8,b=7 J 2 由点(1,1 — b)在椭圆上,得 1+2(1 — b)2 =2b 2 ,b 2^9 a^- 16’ 8 2 2 故双曲线方程为 ——^― =1. 49 98 ???所求椭圆C 的方程为¥+刖2 =1,l 的方程为y= — X+1. [例2]过点(1, 0)的直线I 与中心在原点,焦点在 X 轴上且离心率为 —的椭圆C 相交 2 解法二:由e= C a 1 2 2 2 ,从而 a =2b ,C =b . 对称冋题 . .恰当地利用好对称问A 、B 两点坐标代入圆锥 设椭圆C 的方程为 2 2 2 x+2y=2b,l 的方程为 y=k(x — 1), 将I 的方程代入 C 的方程,得(1+2k 2)x 2— 4k 2x+2k 2— 2b 2 =0,则 4k 2 X 1+X 2= ----- 2 ,y 1+y 2=k(X 1 — 1 +2k 2 设双曲线方程为 2 2 X y =1(a> 0,b > 0) a b 1)+ k(x 2 — 1)=k(x 1+x 2) — 2k= 1 +2k 2 由 e 2 = C 2 a 直线 l: y=1x 过 AB 的中点(x 1 +X 2 y1+y 2 2 ),则亠T=;1 2 1+2k 2 2 2 k 2 '行,解得k =0,或k = ???两渐近线0P 1、0P 2方程分别为 y=-x 和 2 3 y= --- x 2 —1. 若k=0,则I 的方程为y=0,焦点F(c,O)关于直线I 的对称点就是 所以k=0舍去,从而k= — 1,直线l 的方程为y=— (x — 1),即y= — x+1,以下同解法一. [例3]如图,已知△ P 1OP 2的面积为 一,P 为线段P 1P 2的一个三等分点,求以直线 4 OP 1、OP 2为渐近线且过点 P 的离心率为 用 2 F 点本身,不能在椭圆C 上, 3 3 --- 设点 P1(X1 , -X1), P2(X2,- 尹胁>0,X2>0), 则由点P 分 P 1P 2 所成的比入=点=2 ,得P 点坐标 P i P 为(42,心2),又点P 在双曲线与_丝=1上,所以 空25^_0^=1, 3 2 a 2 9a 2 * * 9a 2 9a 2 的双曲线方程. Q 即(X 1+2X 2)— (X 1 — 2x 2) =9a ,整理得 8x 1X 2=9a ¥X 1,|OP|=J X 22+"4X 22 2x 3 2 4 又 |0P1| =Jxj+# 宀 2tan pOx SinP 10P 「+ tan 2p 10x 亍 2 命题意图: 问题的能力. 知识依托: 程. 错解分析: 本题考查待定系数法求双曲线的方程以及综合运用所学知识分析问题、解决 定比分点坐标公式;三角形的面积公式;以及点在曲线上, 利用离心率恰当地找出双曲线的渐近线方程是本题的关键, 点的坐标适合方 正确地表示出 △ P 1OP 2的面积是学生感到困难的. 技巧与方法:利用点 P 在曲线上和△ P 1OP 2的面积建立关于参数 求出a 、b 的值. 解:以0为原点,/ P 1OP 2的角平分线为x 轴建立如图所示的直角坐标系 a 、b 的两个方程,从而 1 1 S 朋0P 2 =2 |OP 1 | HOP ? | sinROP ? =? 即 X 1X 2=— 2 由①、②得a 2 =4,b 2 =9 2 2 故双曲线方程为一-L=1. 4 9 13 12 ■— X1X2 ”一 4 13 27 4 ?思路方法 一般求已知曲线类型的曲线方程问题,可采用“先定形,后定式,再定量”的步骤 . 定形一一指的是二次曲线的焦点位置与对称轴的位置 . 定式一一根据“形”设方程的形式,注意曲线系方程的应用,如当椭圆的焦点不确定在 哪个坐标轴上时,可设方程为 mx 2 + ny 2 =1(m> 0, n> 0). 定量一一由题设中的条件找到“式”中特定系数的等量关系,通过解方程得到量的大小 . ?考点一训练 一、选择题 . 2 2 1已知直线x+2y — 3=0与圆x+y+x — 6y+m=0相交于P 、Q 两点,0为坐标原点,若 OP 丄OQ ,则m 等于( ) A.3 B. — 3 C.1 D. — 1 2中心在原点,焦点在坐标为(0, ± 5 J2)的椭圆被直线3x— y — 2=0截得的弦的中点的横?典例探究 [例1]如图所示,抛物线 y2=4x的顶点为0,点A的坐标为(5, 坐标为1,则椭圆方程为( ) 2 2x22y2 A.——+丄=1 25 75 2 2 C.x+y =1 25 75 二、填空题 2x2 B.— — 75 D.x2 75 2y2 ?+丄=1 25 25 3.直线l的方程为y=x+3,在I上任取一点P,若过点P且以双曲线12x2— 4y2=3的焦点作椭圆的焦点,那么具有最短长轴的椭圆方程为_________________ . 4.已知圆过点P(4,— 2)、Q( — 1,3)两点,且在y轴上截得的线段长为4寸3,则该圆的方程为__________ . 三、解答题 5已知椭圆的中心在坐标原点,焦点在IMF I的最大值和最小值的几何平均数为 2,|M1M2|=^^^,试求椭圆的方程. 6.某抛物线形拱桥跨度是 20米,拱高最长的支柱的长. x轴上,它的一个焦点为F ,M是椭圆上的任意点,椭圆上存在着以 y=x为轴的对称点 M i和M2,且 4米,在建桥时每隔 4米需用一支柱支撑,求其中 7.已知圆C1的方程为(x — 2)2+(y— 1)2=-20,椭圆C2的方程为 3 2 2 ■x2+'y^=1(a>b>0), C2的离心率为-—,如果C1与C2相交于a b 2 A 、 B两点,且线段AB恰为圆C i的直径,求直线 AB的方程和椭圆C2的方程. 考点二直线与圆锥曲线 直线与圆锥曲线联系在一起的综合题在高考中多以高档题、压轴题出现,主要涉及位置 关系的判定,弦长问题、最值问题、对称问题、轨迹问题等.突出考查了数形结合、分类讨 论、 函数与方程、等价转化等数学思想方法,要求考生分析问题和解决问题的能力、计算能力较高,起到了拉开考生“档次”,有利于选拔的功能. 0),倾斜角为一的直线I与线段OA相交(不经过点O或点A)且交抛物 4 线于M、N两点,求△ AMN面积最大时直线I的方程,并求△ AMN的最大面积. 命题意图:直线与圆锥曲线相交,一个重要的问题就是有关弦长的问题.本题考查处理直线与圆锥曲线相交问题的第一种方法一一“韦达定理法” 知识依托:弦长公式、三角形的面积公式、不等式法求最值、函数与方程的思想. 错解分析:将直线方程代入抛物线方程后,没有确定m的取值范围.不等式法求最值忽略了适用的条件. 技巧与方法:涉及弦长问题,应熟练地利用韦达定理设而不求计算弦长,涉及垂直关系往往也是利用韦达定理,设而不求简化运算. 解:由题意,可设I的方程为y=x+m, — 5 < mv 0. [y = X + m 2 2 由万程组J 2,消去y,得x2+(2m— 4)x+m2=0 l y =4x ???直线I与抛物线有两个不同交点 M、N, ???方程①的判别式△ =(2m— 4)2— 4m2=16(1 — m) > 0, 解得mv 1,又一5< mv 0,A m的范围为(一5,0) 设 M(X1,y1),N(X2,y2)则 X1+x2=4 — 2m,x』X2=m , ??? |MN 1=4J2(1 - m). 点A到直线I的距离为d=^^m. 42 S A=2(5+ m) J1 - m ,从而S A2=4(1 — m)(5+ m)2 =2(2 — 2m)2 (5+m)(5+m)< 2( ^ 2^ m )3=128. ???S A W8丘,当且仅当2 — 2m=5+m,即m= — 1时取等号 故直线l的方程为y=x— 1, △ AMN的最大面积为8 J2 . [例2]已知双曲线C: (1)求过P (1,2)点的直 线 交占 (2)若Q(1,1),试判断以 2 2 / \. 2x — y =2 与点 P (1,2) I的斜率取值范围,使I与C分别有一个交点,两个交点,没有 Q为中点的弦是否存在. 命题意图:第一问考查直线与双曲线交点个数问题,归结为方程组解的问题 处理直线与圆锥曲线问题的第二种方法一一“差分法”. .第二问考 查 知识依托:二次方程根的个数的判定、两点连线的斜率公式、中点坐标公式. 错解分析:第一问,求二次方程根的个数,忽略了二次项系数的讨论.第二问,算得以 Q 为中点弦的斜率为 2,就认为所求直线存在了. 技巧与方法:涉及弦长的中点问题,常用“差分法”设而不求,将弦所在直线的斜率,弦的中点坐标联系起来,相互转化. 解:(1)当直线l的斜率不存在时,I的方程为x=1,与曲线C有一个交点.当I的斜率存在时,设 直线l的方程为y— 2=k(x— 1),代入C的方程,并整理得 2 2 2 2 (2 — k )x +2(k — 2k)x— k +4k— 6=0 (i )当2 — k2=0,即k= 士J2时,方程()有一个根, (ii )当 2 — k2M O,即 k M±时 △ = : 2(k2— 2k):2— 4(2 — k2)( — k2+4k — 6)=16(3 — 2k) ①当△ =O,即3 — 2k=O,k=e时,方程(*)有一个实根,I与C有一个交点. 2 ②当△ > O,即k< -,又 k工± ,故当k<—或—< k<血或< k< -时,方 2 程(*)有两不等实根,I与C有两个交点. 3 * ③当△ < O,即k> 一时,方程()无解,I与C无交点. 2 综上知:当k= ± J2,或k=-,或k不存在时,I与C只有一个交点; 2 当近< k< —,或一< k< V2,或kv—J2时,I与C有两个交点; 2 当k> 3时,I与C没有交点. 2 2 (2)假设以 Q为中点的弦存在,设为 AB,且A(x i,y i),B(X2,y2),则2x i 两式相减得:2(X I— X2)(x i+X2)=(y i — y2)(y i+y2) 又X i+x2=2,y i+y2=2 2(x i — X2)=y i — y i 即 k AB= —y^ =2 X i -X2 但渐近线斜率为± J2,结合图形知直线 AB与C无交点,所以假设不正确,即以Q为中点的 弦不存在. [例3]如图,已知某椭圆的焦点是 F i(— 4, 0)、F2(4, 0),过点F2并垂直于x轴的直线与椭圆的一个交点为 B,且|F I B|+|F2B|=10,椭圆上不同的两点 A(x i,y i),C(X2,y2)满足条件:|F2A|、IF2BI、IF2CI成等差数列. (1)求该弦椭圆的方程; (2)求弦AC中点的横坐标; (3)设弦AC的垂直平分线的方程为 y=kx+m,求m的取值范围. 命题意图:本题考查直线、椭圆、等差数列等基本知识,一、二问较简单,第三问巧妙 地借助中垂线来求参数的范围,设计新颖,综合性,灵活性强. 知识依托:椭圆的定义、等差数列的定义,处理直线与圆锥曲线的方法. 错解分析:第三问在表达出“k=^5y o”时,忽略了“ k=0”时的情况,理不清题目中变 36 量间的关系. 技巧与方法:第一问利用椭圆的第一定义写方程;第二问利用椭圆的第二定义(即焦半径公式)求解,第三问利用 m表示出弦AC的中点P的纵坐标y o,利用y o的范围求m的范围. 解:⑴由椭圆定义及条件知,2a=|F i B|+|F2B|=10,得a=5,又c=4,所以b=J a2—『=3. 2 2 故椭圆方程为X + y=1. 25 9 9 25 4 (2)由点B(4,y B)在椭圆上,得|F2B|=|y B|=—.因为椭圆右准线方程为x=,离心率为一,根 5 4 5 425 4 25 据椭圆定义,有|F2A|=-(空—X I),|F2C|=上(竺—X2), 5 4 5 4 由|F2A|、|F2B|、|F2C|成等差数列,得 425 4 25 9 -( —x i)+— ( — X2)=23 —,由此得出:x i+x2=8. 5 4 5 4 5 设弦AC的中点为P(X o,y o),则 x o=2X^ =4. 2 (3)解法一:由 A(x i,y i),C(x2,y2)在椭圆上. 得J9x i2+25y i2=9沢25 得> 2 2 9X22 +25y22=9X25 ①一②得 9(X1? — x^)+25(y^ — y^)=0, 即 93(4)+ 25(4mg)=O(x i -X2) 2 2 X i — X2 () I与C有一个交点 2 - - —y i =2,2X2— y2 =2 X i X i +X 2 将宁f =4,屮=y 0,嵌 T (k 主 0) 代入上式,得 93 4 畑 0(- 存0 (心0) 25 即k=一 y 0(当k=0时也成立). 36 5 5 3.已知两点M(1, - )、N(— 4,—上),给出下列曲线方程:① 4x+2y — 1=0, 4 4 X 2 x 2 ②x 2 +y 2 =3,③ —+y 2 =1,④三 —y 2 =1,在曲线上存在点 P 满足|MP|=|N P|的所有曲线方程是 由点 由点 P (4,y 。)在弦 AC 的垂直平分线上,得 y 0=4k+m,所以 m=y 0— 4k =y 0- ^5 y 0= — 16 y 0. 9 9 9 < y 0< rn,所以一16 < 5 5 5 P(4, y o )在线段BB’(B '与B 关于X 轴对称)的内部,得一 1 6 m< . 5 解法二:因为弦 AC 的中点为P(4,y 0),所以直线AC 的方程为 1 y — y 0= --- (X — 4)(kM 0) k 2 2 将③代入椭圆方程—亠=1,得 25 9 (9k 2 +25)x 2 — 50(ky 0+4)x+25(ky 0+4)2 — 253 9k 2 =0 所以X 什X 2= _ =8,解得k= 25 y 0.(当k=0 时也成立) 9k 2 +25 36 (以下同解法一). ?思路方法 1. 直线与圆锥曲线有无公共点或有几个公共点的问题, 实际上是研究它们的方程组成的方 程是否有实数解成实数解的个数问题,此时要注意用好分类讨论和数形结合的思想方法 . 2. 当直线与圆锥曲线相交时:涉及弦长问题,常用“韦达定理法”设而不求计算弦长 应用 弦长公式);涉及弦长的中点问题,常用“差分法”设而不求,将弦所在直线的斜率、弦 的中点坐标联系起来,相互转化 活转化,往往就能事半功倍. ?考点二训练 一、选择题 ?同时还应充分挖掘题目的隐含条件,寻找量与量间的关系灵 1.斜率为 1的直线 I 与椭圆 2 X 2 —— +y=i 相交于A 、B 两点,贝y AB |的最大值为( ) 4 A.2 4^5 B.—— 5 (即 4(10 8/10 C. ----- D. ----- 5 5 y=ax 2 与直线y=kX+b(kM 0)交于A 、B 两点,且此两点的横坐标分别为 X i ,x 2,直线 ) 2抛物线 与X 轴交点的横坐标是X 3,则恒有( A . X 3=X 1 + X 2 C.X I +X 2+X 3=0 二、填空题 B.X 1X 2=X 1X 3+X 2X 3 D.X l X 2+X 2X 3+X 3X l =0 2 4. __________ 正方形ABCD 的边AB 在直线y=X+4上,C 、D 两点在抛物线 y =x 上,则正方形 ABCD 的面积为 _____ . 5. ________________________________________________________________________ 在抛物线y 2 =16x 内,通过点(2, 1)且在此点被平分的弦所在直线的方程是 _________________ . 三、解答题 2 6. 已知抛物线y=2px(p> 0),过动点M(a,0)且斜率为1的直线I 与该抛物线交于不同的两点 A 、 B ,且 |AB|W 2p. (1)求a 的取值范围. P (6, 6). (1) 求双曲线方程. (2) 动直线I 经过△ A I PA 2的重心G ,与双曲线交于不同的两点 M 、N ,问:是否存在直线 I,使G 平分线段MN ,证明你的结论. 8.已知双曲线C 的两条渐近线都过原点, 且都以点A(5/2 , 0)为圆心,1为半径的圆相切, 双曲线的一个顶点 A 1与A 点关于直线y=X 对称. (1) 求双曲线C 的方程. (2) 设直线I 过点A ,斜率为k,当0< k< 1时,双曲线C 的上支上有且仅有一点 B 到直线I 的距离为J 2,试求k 的值及此时B 点的坐标. 考点三圆锥曲线综合题 圆锥曲线的综合问题包括:解析法的应用,与圆锥曲线有关的定值问题、最值问题、参 数问题、应用题和探索性问题,圆锥曲线知识的纵向联系,圆锥曲线知识和三角、复数等代 数知识的横向联系,解答这部分试题,需要较强的代数运算能力和图形认识能力,要能准确 地进行数与形的语言转换和运算,推理转换,并在运算过程中注意思维的严密性,以保证结 果的完整. ?典例探究 微专题71 求曲线(或直线)的方程 一、基础知识: 1、求曲线(或直线)方程的思考方向大体有两种,一个方向是题目中含几何意义的条件较多(例如斜率,焦距,半轴长,半径等),那么可以考虑利用几何意义求出曲线方程中的要素的值,从而按定义确定方程;另一个方向是若题目中没有明显的几何条件,主要依靠代数运算,那么就考虑先用待定系数法设出方程(未知的部分用字母代替),从而该方程便可参与题目中的运算,再利用题目条件求出参数的值,即可确定方程。可以说两个方向各有侧重,一个倾向于几何意义,另一个倾向于代数运算,下面将对两个方向涉及到的知识进行详细梳理 2、所学方程中字母的几何意义 (1)直线::斜率;()00,x y :直线所过的定点 (2)圆:(),a b :圆心的坐标; :r 圆的半径 (3)椭圆:2a :长轴长,焦半径的和;2:b 短轴长;2c :焦距 (4)双曲线:2a :实轴长,焦半径差的绝对值;2:b 虚轴长;2c :焦距 注:在椭圆和双曲线中,很多几何性质也围绕着,,a b c 展开,通过这些条件也可以求出,,a b c 的值,从而确定曲线方程。例如(椭圆与双曲线共有的): 离心率:c e a =;通径(焦点弦长的最小值):22b a 等 (5)抛物线::p 焦准距 3、待定系数法中方程的形式: (1)直线与曲线方程通式: ① 直线:y kx m =+,x my t =+ ② 圆:2 2 0x y Dx Ey F ++++= ③ 椭圆: 标准方程:()222210x y a b a b +=>>(或()22 2210y x a b a b +=>>,视焦点所在轴来决定) 椭圆方程通式:()2 2 10,0mx ny m n +=>> ④ 双曲线: 椭圆的定义、性质及标准方程 1. 椭圆的定义: ⑴第一定义:平面内与两个定点12F F 、的距离之和等于常数(大于12F F )的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫做椭圆的焦距。 ⑵第二定义:动点M 到定点F 的距离和它到定直线l 的距离之比等于常数)10(< 圆锥曲线标准方程求法 一、椭圆标准方程求法 1、定义法 【例1】已知ABC ?的周长是18,)0,4(),0,4(B A -,求点C 的轨迹方程。 【变式】:在周长为定值的△ABC 中,已知|AB|=6,且当顶点C 位于定点P 时,cosC 有最小值为25 7.建立适当的坐标系,求顶点C 的轨迹方程. 【例2】已知椭圆C 以坐标轴为对称轴,以坐标原点为对称中心,椭圆的一个焦点为()0,1,点??? ? ??26,23M 在椭圆上,求椭圆C 的方程; 【例3】已知圆221:(1)16F x y ++=,定点2(1,0)F .动圆M 过点F 2,且与圆F 1相内切.求点M 的轨迹C 的方程. 【例4】设R y x ,,,∈为直角坐标系内y x ,轴正方向的单位向量, ,)2(j y i x a ++=j y i x b )2(-+=,且8||||=+.求点),(y x M 的轨迹C 的方程; 2、待定系数法 1.已知椭圆G 的中心在坐标原点,长轴在x 轴上,离心率为 2 ,且G 上一点到G 的两个焦点的距离之和为12,椭圆G 的方程. 2.已知椭圆1C :22 221(0)y x a b a b +=>>的右顶点为(1,0)A ,过1C 的焦点且垂直长轴的弦长为1.求椭圆1C 的方程. 3.已知椭圆C 的中心为直角坐标系xOy 的原点,焦点在x 轴上,它的一个顶点到两个焦点的距离分别是7和1.求椭圆C 的方程. 4.设椭圆:E 22 221x y a b +=(,0a b >>)过2)M ,(6,1)N 两点,O 为坐标原点,求椭圆E 的方程。 3、转化已知条件 【例1】已知点,A B 的坐标分别是(0,1)-,(0,1),直线,AM BM 相交于点M ,且它们的斜率之积为12- .求点M 轨迹C 的方程; 【例2】设Q 、G 分别为ABC ?的外心和重心,已知)0,1(-A ,)0,1(B ,AB QG //?求点C 的轨迹E 【例3】已知动点P 到直线33 4- =x 的距离是到定点(0,3-)的距离的332倍.求动点P 的轨迹方程; 高中数学复习:圆锥曲线的方程与性质 1.已知A 为抛物线C :y 2 =2px (p >0)上一点,点A 到C 的焦点的距离为12,到y 轴的距离为9,则p =( ) A.2 B.3 C.6 D.9 解析 设A (x ,y ),由抛物线的定义知,点A 到准线的距离为12,即x +p 2=12. 又因为点A 到y 轴的距离为9,即x =9, 所以9+p 2=12,解得p =6.故选C. 答案 C 2.设O 为坐标原点,直线x =2与抛物线C :y 2 =2px (p >0)交于D ,E 两点,若OD ⊥OE ,则C 的焦点坐标为( ) A.? ????14,0 B.? ?? ??12,0 C.(1,0) D.(2,0) 解析 将x =2与抛物线方程y 2 =2px 联立, 可得y =±2p , 不妨设D (2,2p ),E (2,-2p ), 由OD ⊥OE ,可得OD →·OE → =4-4p =0,解得p =1, 所以抛物线C 的方程为y 2 =2x .其焦点坐标为? ?? ??12,0.故选B. 答案 B 3.设F 1,F 2是双曲线C :x 2 -y 2 3 =1的两个焦点,O 为坐标原点,点P 在C 上且|OP |=2,则△ PF 1F 2的面积为( ) A.72 B.3 C.52 D.2 解析 法一 由题知a =1,b =3,c =2,F 1(-2,0),F 2(2,0), 如图,因为|OF 1|=|OF 2|=|OP |=2,所以点P 在以F 1F 2为直径的圆上,故PF 1⊥PF 2,则|PF 1|2 +|PF 2|2 =(2c )2 =16. 由双曲线的定义知||PF 1|-|PF 2||=2a =2,所以|PF 1|2 +|PF 2|2 -2|PF 1||PF 2|=4,所以|PF 1||PF 2|=6, 所以△PF 1F 2的面积为1 2 |PF 1||PF 2|=3.故选B. 法二 由双曲线的方程可知,双曲线的焦点F 1,F 2在x 轴上,且|F 1F 2|=21+3=4.设点P 的坐标为(x 0,y 0),则?????x 20-y 2 03=1,x 20+y 20 =2,解得|y 0|=32. 所以△PF 1F 2的面积为12|F 1F 2|·|y 0|=12×4×3 2=3.故选B. 答案 B 4.已知椭圆C 1:x 2a 2+y 2 b 2=1(a >b >0)的右焦点F 与抛物线C 2的焦点重合,C 1的中心与C 2的顶点 重合.过F 且与x 轴垂直的直线交C 1于A ,B 两点,交C 2于C ,D 两点,且|CD |=4 3|AB |. (1)求C 1的离心率; (2)设M 是C 1与C 2的公共点.若|MF |=5,求C 1与C 2的标准方程. 解 (1)由已知可设C 2的方程为y 2 =4cx ,其中c =a 2 -b 2 . 不妨设A ,C 在第一象限,由题设得A ,B 的纵坐标分别为b 2a ,-b 2 a ;C ,D 的纵坐标分别为2c , -2c ,故|AB |=2b 2 a ,|CD |=4c . 由|CD |=43|AB |得4c =8b 2 3a ,即3×c a =2-2? ?? ??c a 2 . 解得c a =-2(舍去)或c a =1 2 . 所以C 1的离心率为12 . (2)由(1)知a =2c ,b =3c ,故C 1:x 24c 2+y 2 3c 2=1. 设M (x 0,y 0),则x 204c 2+y 203c 2=1,y 2 0=4cx 0, 故x 20 4c 2+4x 03c =1.① 微专题19 1.答案:x 2=2y . 解析:假设抛物线标准方程x 2=2py (p >0),因为准线方程y =-12=-p 2 ,所以p =1,抛物线标准方程为x 2=2y . 2.答案:x 28-y 28 =1. 解析:因为e =c a =2,又b a =4c ,所以b =22,a =22,所以双曲线的E 的标准方程为x 28-y 28 =1. 3.答案:x 24+y 22 =1. 解析:由c a =22,2a 2c =42解得a =2,c =2,所以b = 2.所以椭圆的方程为x 24+y 2 2=1. 4.答案:y =±2x . 解析:因为m +4m =3,得出m =2,所以渐近线方程为x 22-y 2 4 =0,所以y =±2x . 5.答案:x 216+y 2 8 =1. 解析:由???c a =22,c +a 2 c =62,解得???a =4,c =22 则b =22,所以椭圆C 的标准方程为x 216+y 28=1. 6.答案:x 2-y 2 3 =1. 解析:因为c a =2,不妨设焦点为(c ,0),渐近线为y =b a x ,即bx -ay =0,所以bc b 2+a 2=b =3,c 2=4a 2=a 2+b 2,所以 a 2=1,双曲线C 的标准方程为x 2-y 23 =1. 7.答案:x 24+y 2 4 3 =1. 解析:因为a =2,由|OC →-OB →|= 2|BC →-BA →|,得|BC →|=2|AC →|,所以|OC →|=|AC →|,又由AC →·BC →=0,所以|OC →|=|AC →|=2,则点C (1,-1)代入椭圆E ,得b 2=43,所以椭圆E :x 24+y 2 4 3=1. 椭圆的标准方程与性质 教学目标: 1了解椭圆的实际背景,了解椭圆在刻画现实世界和解决实际问题中的作用; 2 掌握椭圆的定义、几何图形、标准方程及简单几何性质. 高考相关点: 在高考中所占分数:13分 考查出题方式:解答题的形式,而且考查方式很固定,涉及到的知识点有:求曲线方程,弦长,面积,对称关系,范围问题,存在性问题。 涉及到的基础知识 1.引入椭圆的定义 在平面内与两定点F1,F2的距离的和等于常数(大于|F1F2|=2c)的点的轨迹叫做椭圆.这两定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.集合P={M||MF1|+|MF2|=2a},|F1F2|=2c,其中a>0,c>0,且a,c为常数: 有以下3种情况 (1)若a>c,则集合P为椭圆; (2)若a=c,则集合P为线段; (3)若a 标准方程x2 a2 +\f(y2,b2)=1 (a>b>0) \f(y2,a2)+错误!=1 (a>b>0) 图形 性质范围 -a≤x≤a -b≤y≤b -b≤x≤b -a≤y≤a 对称性对称轴:坐标轴;对称中心:原点 顶点 A1(-a,0),A2(a,0) B1(0,-b),B2(0,b) A1(0,-a),A2(0,a) B1(-b,0),B2(b,0)轴长轴A1A2的长为2a;短轴B1B2的长为2b 焦距|F1F2|=2c 离心率e=错误!∈(0,1) a,b,c的关系c2=a2-b2题型总结 类型一椭圆的定义及其应用 例1:如图所示,一圆形纸片的圆心为O,F是圆内一定点,M是圆周上一动点,把纸片折叠使M与F重合,然后抹平纸片,折痕为CD,设CD与OM交于点P,则点P的轨迹是( ) A.椭圆? B.双曲线 C.抛物线 D.圆 【解析】根据CD是线段MF的垂直平分线.可推断出,进而可以知道 结果为定值,进而根据椭圆的定义推断出点P的轨迹【答案】根据题意知,CD是线段MF的垂直平分线.,(定值),又显然,根 据椭圆的定义可推断出点P轨迹是以F、O两点为焦点的椭圆.所以A选项是正确的 练习1:已知F1,F2是椭圆C: 22 22 1 x y a b +=(a>b>0)的两个焦点,P为椭圆C 上的一点,且 错误! 1⊥2 PF,若△PF1F2的面积为9,则b=________. 【解析】由题意的面积∴故答案为: 【答案】3 练习2:已知F1,F2是椭圆错误!+错误!=1的两焦点,过点F2的直线交椭圆于A,B两点,在△AF1B中,若有两边之和是10,则第三边的长度为() A.6?B.5 C.4 D.3 椭圆及其标准方程练习题 【基础知识】 一.椭圆的基本概念 1.椭圆的定义:我们把平面内与两个定点的距离的和等于常数 ( )的点 的轨迹叫做椭圆,用符号表示为这两个定点叫椭圆的 ,两个焦点之间的距离叫做椭圆的 。 椭圆方程的总形式为 [经典例题]: 例1. 根据定义推导椭圆标准方程. 已知B ,C 是两个定点,|BC |=6,且ABC ?的周长等于16,求顶点A 的轨迹方程 已知F 1, F 2是定点,| F 1 F 2|=8, 动点M 满足|M F 1|+|M F 2|=8,则点M 的轨迹是 (A )椭圆 (B )直线 (C )圆 (D )线段 例2.写出适合下列条件的椭圆的标准方程: ⑴两个焦点坐标分别是(-4,0)、(4,0),椭圆上一点P 到两焦点的距离之和等于10; ⑵两个焦点坐标分别是(0,-2)和(0,2)且过(23-,2 5) 例3 求适合下列条件的椭圆的标准方程: (1)两个焦点坐标分别是(-3,0),(3,0),椭圆经过点(5,0). (2)两个焦点坐标分别是(0,5),(0,-5),椭圆上一点P 到两焦点的距离和为26. 例4 已知椭圆经过两点()5,3()2 5 ,23与-,求椭圆的标准方程 例5 1.椭圆短轴长是2,长轴是短轴的2倍,则椭圆离心率是 ; 2.如果椭圆的焦距、短轴长、长轴长成等差数列,则其离心率为 ; 3.若椭圆的两个焦点F 1、F 2与短轴的一个端点B 构成一个正三角形,则椭圆的离心率为 ; [典型练习]: 椭圆 19 252 2=+y x 上一点P 到一个焦点的距离为5,则P 到另一个焦点的距离为( ) A.5 B.6 C.4 D.10 2.椭圆 1169 252 2=+y x 的焦点坐标是( ) A.(±5,0) B.(0,±5) C.(0,±12) D.(±12,0) 3.已知椭圆的方程为 182 2 2=+m y x ,焦点在x 轴上,则其焦距为( ) A.228m - B.2m -22 C.282-m D.222-m 4.1,6==c a ,焦点在y 轴上的椭圆的标准方程是 圆锥曲线定义、标准方程及性质 一.椭圆 定义Ⅰ:若F 1,F 2是两定点,P 为动点,且21212F F a PF PF >=+ (a 为常数)则P 点的轨迹是椭圆。 定义Ⅱ:若F 1为定点,l 为定直线,动点P 到F 1的距离与到定直线l 的距离之比为常数e (0 双曲线的定义及标准方程 题型一、圆锥曲线的标准方程 例1、讨论 19252 2 =-+ -k y k x 表示何种圆锥曲线,它们有何共同特征. 分析:由于9≠k ,25≠k ,则k 的取值范围为9 4.2解析几何--圆锥曲线的概念及性质 一、选择题 1.(2010·安徽双曲线方程为x2-2y2=1,则它的右焦点坐标为 ( A. B. C. D.(,0 解析:∵原方程可化为-=1,a2=1, b2=,c2=a2+b2=, ∴右焦点为. 答案:C 2.(2010·天津已知双曲线-=1(a>0,b>0的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为 ( A.-=1 B.-=1 C.-=1 D.-=1 解析:∵渐近线方程是y=x,∴=.① ∵双曲线的一个焦点在y2=24x的准线上, ∴c=6.② 又c2=a2+b2,③ 由①②③知,a2=9,b2=27, 此双曲线方程为-=1. 答案:B 4.(2010·辽宁设抛物线y2=8x的焦点为F,准线为l,P为抛物线上一点,PA⊥l,A为垂足.如果直线AF的斜率为-,那么|PF|= ( A.4 B.8 C.8 D.16 解析:解法一:AF直线方程为: y=-(x-2, 当x=-2时,y=4,4A(-2,4. 当y=4时代入y2=8x中,x=6, 4P(6,4, 4|PF|=|PA|=6-(-2=8.故选B. 解法二:5PA∞l,4PA%x轴. 又5 AFO=60°,4 FAP=60°, 又由抛物线定义知PA=PF, 4≥PAF为等边三角形. 又在Rt≥AFF′中,FF′=4, 4FA=8,4PA=8.故选B. 答案:B 5.高8 m和4 m的两根旗杆笔直竖在水平地面上,且相距10 m,则地面上观察两旗杆顶端仰角相等的点的轨迹为 ( A.圆 B.椭圆 C.双曲线 D.抛物线 解析:如图1,假设AB、CD分别为高4 m、8 m的旗杆,P点为地面上观察两旗杆顶端仰角相等的点,由于∠BPA=∠DPC,则Rt△ABP∽Rt△CDP,=,从而 PC=2PA.在平面APC上,以AC为x轴,AC的中垂线为y轴建立平面直角坐标系(图2,则A(-5,0,C(5,0,设P(x,y,得=2 化简得x2+y2+x+25=0,显然,P点的轨迹为圆. 答案:A 二、填空题 解析:由题知,垂足的轨迹为以焦距为直径的圆,则c 椭圆标准方程的求法举例 一、定义法 例1.已知圆22:(1)8C x y ++=,点(10)A ,是圆内一点,AM 的垂直平分线l 交CM 于点N ,当点M 在圆C 上运动时,求点N 的轨迹方程。 解:连结AN ,由NM NA = ,得NC NA NC NM CM +=+==, 而2CA =,因此,点N 的轨迹是以点C A ,为焦点的椭圆, 设为22 221(0)x y a b a b +=>> ,2a =,22c =, 所以a =1c = ,21b =。因此,所求轨迹方程为2 212x y +=。 评注:用定义法求椭圆的方程,首先要清楚椭圆的中心是否在原点、对称轴是否为坐标轴;其次,要紧紧的抓住定义,由定义产生椭圆的基本量a 、b 、c . 二、待定系数法 例2 .已知椭圆的焦距离为 ,求焦点在x 轴上时,它的标准方程. 解析:焦点在x 轴上,设所求方程为22 221x y a b +=(0)a b >>, 由题意得2222321a b a b ?+=???-? ,,解之得2293.a b ?=??=??,因此,所求方程为22193x y +=. 评注:用待定系数法求椭圆方程的基本步骤是:首先设出含待定系数的椭圆方程;然后根据题目条件再逐步求出待定的系数,从而得到方程. 三、轨迹法 例3.点()P x y ,到定点(01)A -,的距离与定直线14y =- ,求动点P 的轨迹方程. 解析:设d 为动点()P x y ,到定直线14y =-的距离,根据题意动点P 的轨迹就是集合 ()PA M P x y d ??==????? ,| =. 将上式两边平方,并化简得2214131413x y +=?,即22 11314 x y +=为所求. 评注:用轨迹法求椭圆方程,首先要写出适合条件的点集,然后用坐标代入,再对含x y ,的式子进行化简,最后产生所求方程,这是必须的基本步骤. 四、奇思妙解法 例4 .已知椭圆的中心在原点,以坐标轴为对称轴,且经过两点1 (02)2A B ? ?,, 求 第2讲 圆锥曲线的方程与性质 一、 单项选择题 1. (2020·重庆调研)已知双曲线C :x 2a 2-y 2 b 2=1(a >0,b >0)的一条渐近线方程为y =52x ,且与椭圆x 212+y 2 3=1有公共焦点,那么双曲线C 的方程为( ) A. x 28-y 2 10=1 B. x 24-y 2 5=1 C. x 25-y 2 4=1 D. x 24-y 2 3=1 2. (2020·惠州调研)已知F 是抛物线C :y =2x 2的焦点,N 是x 轴上一点,线段FN 与抛物线C 交于点M ,若2FM →=MN →,则|FN →|等于( ) A. 58 B. 12 C. 38 D. 1 3. (2020·三明一模)已知双曲线x 2a 2-y 2 b 2=1(a >0,b >0)的离心率为2,过右焦点且垂直于x 轴的直线与双曲线交于A ,B 两点.若A ,B 到双曲线的同一条渐近线的距离分别为d 1和d 2,且d 1+d 2=6,则双曲线的方程为( ) A. x 24-y 2 12=1 B. x 212-y 2 4=1 C. x 23-y 2 9=1 D. x 29-y 2 3=1 4. (2020·淮北二模)已知椭圆C :x 2a 2+y 2 b 2=1(a >b >0)的左焦点为F ,椭圆C 与 过原点的直线相交于A ,B 两点,连接AF ,BF .若AB =10,BF =8,cos ∠ABF =4 5,则椭圆C 的离心率为( ) A. 35 B. 57 C. 45 D. 67 二、 多项选择题 5. 若F 为拋物线C :y 2=3x 的焦点,过点F 且倾斜角为30°的直线交抛物线C 于A ,B 两点,O 为坐标原点,下列说法中正确的是( ) A. 抛物线的焦点到准线的距离为3 B. A ,B 两点之间的距离为12 C. 原点O 到直线AB 的距离为38 D. △OAB 的面积为9 4 6. 已知圆M :x 2 +y 2 +2mx -3=0(m <0)的半径为2,椭圆C :x 2a 2+y 2 3=1(a >0) 的左焦点为F (-c,0),若垂直于x 轴且经过点F 的直线l 与圆M 相切,则( ) A. m =-1 B. m =13 C. c =-1 D. a =2 7. 已知椭圆C :x 24+y 2 =1的左、右焦点分别为F 1,F 2,O 为坐标原点,那么以下说法中正确的是( ) A. 若过点F 2的直线与椭圆C 交于A ,B 两点,则△ABF 1的周长为8 B. 椭圆C 上存在一点P ,使得PF 1→·PF 2→ =0 C. 椭圆C 的离心率为12 D. 若P 为椭圆x 24+y 2 =1上的一点,Q 为圆x 2+y 2=1上的一点,则点P ,Q 的最大距离为3 三、 填空题 8. 在平面直角坐标系xOy 中,若中心在原点,焦点在y 轴上的双曲线的一条渐近线经过点(-3,1),则该双曲线的离心率为________. 9. (2020·广州质检)若抛物线x 2=4y 的焦点为F ,过点F 作斜率为3 3的直线l 与抛物线在y 轴右侧的部分相交于另一点A ,过点A 作抛物线准线的垂线,垂足为H ,则△AHF 的面积是________. 10. 已知点P (0,1),椭圆x 24+y 2=m (m >1)上两点A ,B 满足AP →=2PB →,那么当 高考数学知识点之圆锥曲线方程 考试内容: 椭圆及其标准方程.椭圆的简单几何性质.椭圆的参数方程. 双曲线及其标准方程.双曲线的简单几何性质. 抛物线及其标准方程.抛物线的简单几何性质. 考试要求: (1)掌握椭圆的定义、标准方程和椭圆的简单几何性质,了解椭圆的参数方程. (2)掌握双曲线的定义、标准方程和双曲线的简单几何性质. (3)掌握抛物线的定义、标准方程和抛物线的简单几何性质. (4)了解圆锥曲线的初步应用. §08. 圆锥曲线方程 知识要点 一、椭圆方程. 1. 椭圆方程的第一定义: 为端点的线段 以无轨迹方程为椭圆21212 1 21212121,2, 2,2F F F F a PF PF F F a PF PF F F a PF PF ==+=+=+ ⑴①椭圆的标准方程: i. 中心在原点,焦点在x 轴上: ) 0(12 22 2 b a b y a x =+ . ii. 中心在原点,焦点在 y 轴上: )0(12 22 2 b a b x a y =+ . ②一般方程: ) 0,0(12 2 B A By Ax =+.③椭圆的标准参数方程: 1 2 22 2=+ b y a x 的参数方程为 ?? ?==θ θs in cos b y a x (一象限θ应是属于2 0π θ ). ⑵①顶点:),0)(0,(b a ±±或)0,)(,0(b a ±±.②轴:对称轴:x 轴,y 轴;长轴长a 2,短轴长b 2.③焦点:)0,)(0,(c c -或),0)(,0(c c -.④焦距:2 2 21,2b a c c F F -==.⑤准线:c a x 2 ± =或 c a y 2 ± =.⑥ 离心率:)10( e a c e = .⑦ 焦点半径: i. 设),(00y x P 为椭圆 )0(12 22 2 b a b y a x =+ 上的一点,2 1,F F 为左、右焦点,则 由椭圆方程的第二定义可以推出. ii.设),(00y x P 为椭圆 ) 0(12 22 2 b a a y b x =+ 上的一点,21,F F 为上、下焦点,则 由椭圆方程的第二定义可以推出. 由椭圆第二定义可知: )0()( ),0()(0002 2 002 01 x a ex x c a e pF x ex a c a x e pF -=-=+=+ =归结起来为 “左加右减”. 注意:椭圆参数方程的推导:得→)sin ,cos (θθb a N 方程的轨迹为椭圆. ⑧通径:垂直于x 轴且过焦点的弦叫做通经.坐标:) , (22 2 2a b c a b d -=和) , (2 a b c ? -=+=02 01,ex a PF ex a PF ? -=+=02 01,ey a PF ey a PF 圆锥曲线基本题型总结:提纲: 一、定义的应用: 1、定义法求标准方程: 2、涉及到曲线上的点到焦点距离的问题: 3、焦点三角形问题: 二、圆锥曲线的标准方程: 1、对方程的理解 2、求圆锥曲线方程(已经性质求方程) 3、各种圆锥曲线系的应用: 三、圆锥曲线的性质: 1、已知方程求性质: 2、求离心率的取值或取值范围 3、涉及性质的问题: 四、直线与圆锥曲线的关系: 1、位置关系的判定: 2、弦长公式的应用: 3、弦的中点问题: 4、韦达定理的应用: 一、定义的应用: 1. 定义法求标准方程: (1)由题目条件判断是什么形状,再由该形状的特征求方程:(注意细节的处 理) 1.设F1, F2 为定点,|F1F2| =6,动点M满足|MF1| + |MF2| = 6,则动点M的轨 迹是() A.椭圆 B.直线 C.圆 D.线段【注:2a>|F1 F2| 是椭圆,2a=|F1 F2|是线段】 2. 设 B - 4,0) , C4,0),且厶ABC的周长等于18,则动点A的轨迹方程为) x2 y2 y2 x2 A.25+ -9 = i y z0) B.25^9 = 1 徉0) x2 y2 y2 x2 C.^+16= 1 y z 0) D£+_9 = 1 y z 0) 【注:检验去点】 3. 已知A0, - 5)、B0,5) ,|PA| - |PB| = 2a,当a= 3 或 5 时,P点的轨迹为) A. 双曲线或一条直线 B. 双曲线或两条直线 C. 双曲线一支或一条直线 D. 双曲线一支或一条射线【注:2av|F1 F2|是双曲线,2a=|F1 F2|是射线,注意一支与两支的判断】 专题训练五——圆锥曲线的标准方程与几何性质 类型一、椭圆的标准方程与几何性质 例1.(1) 椭圆的中心在原点,焦点在x 轴上,长轴长是短轴长的2倍,焦距为4,则椭圆的标准方程为________________. (2)已知焦点在x 轴上,中心在的椭圆上一点到两焦点的距离之和为6,若该椭圆的离心率为13 ,则椭圆的方程是( ) A. 2 214 x y += B. 22198x y += C. 22143x y += D. 22189x y += 练习:1、求满足下列各条件的椭圆的标准方程: (1)长轴是短轴的3倍且经过点()3,0A ; (2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为3; 例2、(1)P 为椭圆19 252 2=+y x 上一点,21,F F 为左右焦点,若 6021=∠PF F ,则21PF F ?的面积为 . (2)已知F 1、F 2是椭圆C :x 2a 2+y 2 b 2=1(a >b >0)的两个焦点,P 为椭圆C 上的一点,且PF 1→⊥PF 2→.若△PF 1F 2的面积为9,则b =________. 例3、(1)错误!未找到引用源。在椭圆C :x 2a 2+y 2 b 2=1(a >b >0)上,是椭圆的两个焦点,,且的三条边,,成等差数列,则此椭圆的离心率是( ) A. B. C. D. (2)已知椭圆C :x 2a 2+y 2 b 2=1(a >b >0)的一条弦所在的直线方程是 ,弦的中点坐标是,则 椭圆的离心率是( ) A. B. C. D. (3)如图,椭圆的中心在坐标原点,焦点在x 轴上, 1212,,,A A B B 为椭圆的 顶点, 2F 为右焦点,延长12B F 与12A B 交于点P ,若12B PB ∠为钝角,则 该椭圆的离心率的取值范围是( ) A. ????? B. ? ?? C. ? ?? D. ????? 类型二、双曲线的标准方程与几何性质 例1.(1)已知双曲线两个焦点分别为F 1(-5,0),F 2(5,0),双曲线上一点P 到F 1,F 2的距离的差的绝对值等于6,则双曲线的标准方程为__________________. (2)双曲线的渐近线方程为y =±3x ,虚轴长为23,则双曲线的方程为________________________. (3)已知双曲线C :﹣=1的焦距为10,点P (2,1)在C 的渐近线上,则C 的方程为_______. (4)已知F 1,F 2为双曲线x 25-y 24 =1的左、右焦点,P (3,1)为双曲线内一点,点A 在双曲线上,则|AP |+|AF 2|的最小值为_______. §8.圆锥曲线方程 知识要点 一、椭圆方程. 1. 椭圆方程的第一定义:为端点的线段 以无轨迹方程为椭圆21212121212121,2, 2, 2F F F F a PF PF F F a PF PF F F a PF PF ==+=+=+ ⑴①椭圆的标准方程:i. 中心在原点,焦点在x 轴上:)0(12 222 b a b y a x =+ . ii. 中心在原点,焦点在y 轴上:)0(12 22 2 b a b x a y =+ . ②一般方程:)0,0(122 B A By Ax =+. ③椭圆的标准方程:122 2 2=+ b y a x 的参数方程为?? ?==θ θsin cos b y a x (一象限θ应是属于20π θ ). ⑵①顶点:),0)(0,(b a ±±或)0,)(,0(b a ±±. > ②轴:对称轴:x 轴,y 轴;长轴长a 2,短轴长b 2. ③焦点:)0,)(0,(c c -或),0)(,0(c c -. ④焦距:2221,2b a c c F F -==. ⑤准线:c a x 2±=或c a y 2 ±=. ⑥离心率:)10( e a c e =. ⑦焦点半径: i. 设),(00y x P 为椭圆 )0(12222 b a b y a x =+ 上的一点,21,F F 为左、右焦点,则 》 ii.设),(00y x P 为椭圆)0(12 22 2 b a a y b x =+ 上的一点,21,F F 为上、下焦点,则 由椭圆第二定义可知:)0()(),0()(0002 200201 x a ex x c a e pF x ex a c a x e pF -=-=+=+=归结起来为“左加右减”. 注意:椭圆参数方程的推导:得→)sin ,cos (θθb a N 方程的轨迹为椭圆. ⑧通径:垂直于x 轴且过焦点的弦叫做通经.坐标:),(222 2a b c a b d -=和),(2a b c ⑶共离心率的椭圆系的方程:椭圆 )0(12 22 2 b a b y a x =+的离心率是)(22b a c a c e -== ,方程t t b y a x (2 22 2=+是大于0的参数,)0 b a 的离心率也是a c e = 我们称此方程为共离心率的椭圆系方程. ⑸若P 是椭圆: 12 22 2=+b y a x 上的点.21,F F 为焦点,若θ=∠21PF F ,则21F PF ?的面积为2 tan 2θ b (用 ? -=+=0201,ex a PF ex a PF ? -=+=0201,ey a PF ey a PF 圆锥曲线的标准方程与几何性质 1、 椭圆的标准方程与几何性质: 1、椭圆第一定义: 平面内与两个定点12F F ,的距离的和等于常数(大于12F F )的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫椭圆焦距. 2、椭圆第二定义: 平面内到一个定点的距离和它到一条定直线l 的距离之比是常数(01)e e <<的点的轨迹叫做椭圆.定点是椭圆的焦点,定直线l 叫做椭圆的准线,常数e 叫椭圆的离心率. 另外:(1)椭圆的通径就是过焦点垂直于长轴的直线与椭圆相交所得的线段长度 椭圆的通径长:2 2b a . (2)焦点三角形的面积为:2 12tan ,2 S b F MF θ θ==∠. 2. 双曲线 ② 一、 第一定义:平面内与两个定点 12,F F 的距离之差的绝对值是常数(小于12F F )的点的轨迹叫双 曲线。 第二定义:到定点F 的距离与到定直线l 的距离之比为常数) 0(>>a c a c 的点的轨迹是双曲线. 共轭双曲线的四个焦点共圆. 一:抛物线的定义 定义:平面内与一个定点和一条定直线(不经过点 )的距离相等的点的轨迹叫做抛物线, 定点 叫做抛物线的焦点,定直线叫做抛物线的准线. 二:抛物线的标准方程 抛物线标准方程的四种形式:,, ,。 三、抛物线的几何性质: 1.通径:过抛物线的焦点且垂直于对称轴的弦称为通径,通径长为2p 因为通过抛物线y2=2px(p>0)的焦点而垂直于x轴的直线与抛物线两交点的坐标分别为,,所以抛物线的通径长为2p 2.已知过抛物线的焦点F的直线交抛物线于A、B两点。 设A(x1,y1),B(x2,y2),则: ①焦点弦长 ② ③,其中|AF|叫做焦半径, ④焦点弦长最小值为2p。根据时,即AB垂直于x轴时,弦AB的长最短,最短值为2p 测试题 一、填空题 专题-圆锥曲线与方程 抓住3个高考重点 重点1 椭圆及其性质 1.椭圆的定义:椭圆的第一定义:对椭圆上任意一点M 都有1212||||2||2MF MF a F F c +=>= 椭圆的第二定义:对椭圆上任意一点M 都有 || ,(01)MF e e d =<< 2.求椭圆的标准方程的方法 (1)定义法:根据椭圆定义,确定2 2 ,a b 的值,再结合焦点位置,直接写出椭圆的标准方程. (2)待定系数法:根据椭圆焦点是在x 轴还是在y 轴上,设出相应形式的标准方程,然后根据条件确定关于,,a b c 的方程组,解出2 2 ,a b ,从而写出椭圆的标准方程. 3.求椭圆的标准方程需要注意以下几点? (1)如果椭圆的焦点位置不能确定,可设方程为2 2 1(0,0,)Ax By A B A B +=>>≠或22 221x y m n += (2)与椭圆2222 221()x y m n m n +=≠共焦点的椭圆方程可设为22222 21(,)x y k m k n m k n k +=>->-++ (3)与椭圆22221(0)x y a b a b +=>>有相同离心率的椭圆方程可设为22 122x y k a b +=(10k >,焦点在x 轴上)或 22 222 y x k a b +=(20k >,焦点在y 轴上) 4.椭圆的几何性质的应用策略 (1)与几何性质有关的问题要结合图形进行分析,即使不画出图形,思考时也要联想到图形:若涉及顶点、焦点、长轴、短轴等椭圆的基本量,则要理清它们之间的关系,挖掘出它们之间的联系,求解自然就不难了. (2)椭圆的离心率2 21c b e a a ==-当e 越接近于1时,椭圆越扁,当e 越接近于0时, 椭圆越接近于圆, 求椭圆的标准方程需要两个条件,而求椭圆的离心率只需要根据一个条件得到关于,,a b c 的齐次方程,再结合2 2 2 a b c =+即可求出椭圆的离心率 [高考常考角度] 角度1若椭圆12222=+b y a x 的焦点在x 轴上,过点)2 1,1(作圆12 2=+y x 的切线,切点分别为A ,B ,直线AB 恰好 经过椭圆的右焦点和上顶点,则椭圆方程是 14 52 2=+y x . 解析:方法一:设过点)21,1(的直线方程为:当斜率存在时,1 (1)2 y k x =-+,即22120kx y k -+-= 求椭圆的标准方程 1、求适合下列条件的椭圆的标准方程: (1)两个焦点的坐标分别为(-4,0)和(4,0),且椭圆经过点(5,0); (2)焦点在y 轴上,且经过两个点(0,2)和(1,0); . (3)经过点A (3,-2)和点B (-23,1). . 2、求适合下列条件的椭圆的标准方程. (1)焦点在x 轴上,且a =4,c =2; (2)经过点A (0,2)和B ? ?? ??12,3. 3、已知一椭圆的标准方程中b =3,c =4,求此椭圆的标准方程. 4、已知椭圆过点P ? ????35,-4和点Q ? ?? ??-45,3,则此椭圆的标准方程是( A ) +x 2=1 +y 2=1或x 2+y 2 25=1 +y 2=1 D .以上都不对 5、求适合下列条件的椭圆的标准方程. (1)椭圆过(3,0),离心率e =63 ; (2)在x 轴上的一个焦点与短轴两个端点的连线互相垂直,且焦距为8. 6、中心在原点,焦点在坐标轴上的椭圆上有M ? ????1,432,N ? ?? ??-322,2两点. 求椭圆的标准方程; 7、求满足下列各条件的椭圆的标准方程. (1)长轴是短轴的3倍且经过点A (3,0),焦点在x 轴上; (2)短轴一个端点与两焦点组成一个正三角形,且焦点到同侧顶点的距离为 3. 答案: 1、(1)x2 25 + y2 9 =1(2) y2 4 +x2=1(3) x2 15 + y2 5 =1 2、(1)x2 16 + y2 12 =1(2)x2+ y2 4 =1 3、当焦点在x轴上时,椭圆的标准方程为x2 25 + y2 9 =1. 当焦点在y轴上时,椭圆的标准方程为x2 9 + y2 25 =1. 4、A 5、(1)若焦点在x轴上,椭圆的方程为x2 9 + y2 3 =1. 若焦点在y轴上,椭圆的方程为y2 27 + x2 9 =1. (2)x2 32 + y2 16 =1. 6、x2 9 + y2 4 =1 7、x2 9 +y2=1 8、x2 12 + y2 9 =1或 x2 9 + y2 12 =1求圆锥曲线方程
圆锥曲线的定义方程和性质知识点总结
圆锥曲线标准方程求法(学生版)
高中数学复习:圆锥曲线的方程与性质
微专题19圆锥曲线的标准方程的求法答案
椭圆的标准方程与性质
椭圆及其标准方程练习题
圆锥曲线定义、标准方程及性质(精)
双曲线的定义及标准方程 (1)
解析几何-- 圆锥曲线的概念及性质
椭圆标准方程的求法举例
第2讲 圆锥曲线的方程与性质
高考数学知识点之圆锥曲线方程
圆锥曲线基本题型总结
圆锥曲线的方程与性质
圆锥曲线方程知识点总结
圆锥曲线标准方程与几何性质
专题-圆锥曲线与方程(教师)
求椭圆的标准方程(含答案)