随机信号分析实验百度
- 格式：docx
- 大小：124.11 KB
- 文档页数：15
下载文档原格式
合集下载
通信原理第2章-随机信号分析
1 1 2
f ( x)dx f ( x)dx
a
2
在点 a 处取极大值: 1
2
■ a f x 左右平移
f x宽窄
a
x
37
二、正态分布函数
积分无法用闭合形式计算，要设法把这个积分式和可以在数学 手册上查出积分值的特殊函数联系起来，常引入误差函数和互 补误差函数表示正态分布函数。
38
三、误差函数和互补误差函数
39
40
四、为了方便以后分析，给出误差函数和互补误差 函数的主要性质：
41
42
2.5.4 高斯白噪声
43
这种噪声称为白噪声，是一种理想的宽带随机过程。 式子是一个常数，单位是瓦/赫兹。白噪声的自相关 函数：
说明，白噪声只有在 ＝0 时才相关，而在任意
两个时刻上的随机变量都是不相关的。白噪声的功 率谱和自相关函数如图。
F1 x1 ,
x1
t1
f1 x1 ,
t1
则称 f1 x1 , t1 为 (t的) 一维概率密度函数。
显然，随机过程的一维分布函数或一维概率密度函数 仅仅描述了随机过程在各个孤立时刻的统计特性，没 有说明随机过程在不同时刻取值之间的内在联系，因 此需要在足够多的时间上考虑随机过程的多维分布函 数
60
用示波器观 察一个实现 的波形，如 图所示，是 一个频率近 似为fc，包 络和相位随 机缓变的正 弦波。
Df －fc
s(t)
S( f )
O (a) 缓慢变化的包络[a(t)]
O
频率近似为 fc (b)
窄带过程的频谱和波形示意
61
Df
fc
f
t
因此，窄带随机过程ξ(t)可表示成:
西安电子科技大学 电院 《随机信号分析》大作业
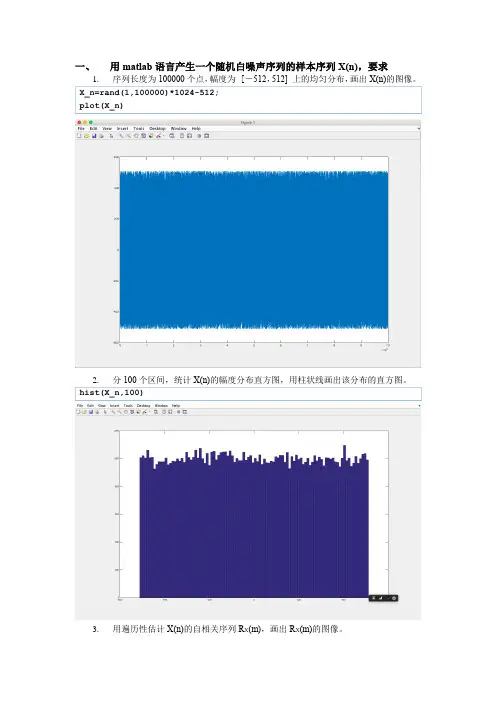
一、用matlab语言产生一个随机白噪声序列的样本序列X(n)，要求
3.用遍历性估计X(n)的自相关序列R X(m)，画出R X(m)的图像。
二、将一中产生的序列通过一个线性系统，其单位脉冲响应为h(n)=0.9n，n=0，
1，…，100
三、比较X(n)与Y(n)的幅度分布直方图，发生了什么变化。
分析其变化的原
因。
随机信号经过线性系统后，不会增加新的频率分量，但是输出的幅度和相位会发生变化。
白噪声X(n)的幅度基本相同，而Y(n)的幅度基本呈正态分布。
因为均匀白噪声是一种宽带非正态过程，所以通过一有限带宽线性系统后，输出Y(n)近似呈正态分布。
——via 1402011 赵春昊。
随机信号分析与处理
一、基本概念1、随机过程随机信号是非确定性信号，不能用确定的数学关系式来描述，不能预测它未来任何瞬时的精确值，任一次观测值只代表在其变动范围内可能产生的结果之一，但其值的变动服从统计规律。
随机信号的描述必须采用概率和统计学的方法。
对随机信号按时间历程所作的各次长时间观测记录称为样本函数，记作x(t)。
在有限时间区间上的样本函数称为样本记录。
在同一试验条件下，全部样本函数的集合(总体)就是随机过程，以{x(t)}表示，即2、随机信号类型3、平稳随机过程平稳随机过程就是统计特征参数不随时间变化而改变的随机过程。
例如，对某一随机过程的全部样本函数的集合选取不同的时间t进行计算，得出的统计参数都相同，则称这样的随机过程为平稳随机过程，否则就是非平稳随机过程。
如采样记录的均值不随时间变化4、各态历经随机过程若从平稳随机过程中任取一样本函数，如果该单一样本在长时间内的平均统计参数(时间平均)和所有样本函数在某一时刻的平均统计参数(集合平均)是一致的，则称这样的平稳随机过程为各态历经随机过程。
显然，各态历经随机过程必定是平稳随机过程，但是平稳随机过程不一定是各态历经的。
各态历经随机过程是随机过程中比较重要的一种，因为根据单个样本函数的时间平均可以描述整个随机过程的统计特性，从而简化了信号的分析和处理。
但是要判断随机过程是否各态历经的随机过程是相当困难的。
一般的做法是，先假定平稳随机过程是各态历经的，然后再根据测定的特性返回到实际中分析和检验原假定是否合理。
由大量事实证明，一般工程上遇到的平稳随机过程大多数是各态历经随机过程。
虽然有的不一定是严格的各态历经过程，但在精度许可的范围内，也可以当作各态历经随机过程来处理。
事实上，一般的随机过程需要足够多的样本(理论上应为无限多)才能描述它，而要进行大量的观测来获取足够多的样本函数是非常困难或做不到的。
在测试工作中常以一个或几个有限长度的样本记录来推断整个随机过程，以其时间平均来估计集合平均。
随机信号分析课件1(常建平)
随机信号是通信、信号与信息处理、自动控制等学科领域必 须研究的信号形式。比如我们电子信息类专业的后修课程中需要 对随机信号进行处理的课程有：通信原理、雷达原理、数字信号 处理、信息论、图像信号处理、语音信号处理、线性控制系统等 等课程。
－课程的特点与研究方法－
❖ 学会用统计的观点来看研究对象－随机信号 ❖ 由于随机信号是随机变化和不确定的，只有它的统计规律才是
设事件A表示这批产品通过检查，即抽样检查的10个产品都是 合格品。则
P( A B0 ) 1，
P( A
B3 )
C10 97
C10 100
0.73
P( A
B1 )
C10 99
C10 100
=0.90，
P( A
B4
)
C10 96
C10 100
0.65
P( A
B2
)
C10 98
C10 100
0.81，
由全概率公式求出 4 P( A) P(Bi )P( A Bi ) 0.815 i0
An1)P( A1 An2 )P( A1
An 1 ) An2 )
P( A1A2 A3 ) P( A3 A1A2 )P( A1A2 ) P( A1A2 ) P( A2 A1)P( A1)
P( A1 A2 A n ) P( An A1 An1) P( A3 A1A2 )P( A2 A1)P( A1)
在概率论的发展史上，人们曾针对不同问题，从不同角度
给出了概率的三种定义和计算方法。这三种定义和计算方法都 具有各自的适用范围，存在一定的局限性，但在三种定义下概 率的性质却是完全相同的。因此，人们从概率的性质出发，给 概率赋予一个新的数学定义，即概率的公理化定义。这个定义 只指明概率应具有的基本性质，不具体规定概率的计算方法。
－课程的特点与研究方法－
❖ 学会用统计的观点来看研究对象－随机信号 ❖ 由于随机信号是随机变化和不确定的，只有它的统计规律才是
设事件A表示这批产品通过检查，即抽样检查的10个产品都是 合格品。则
P( A B0 ) 1，
P( A
B3 )
C10 97
C10 100
0.73
P( A
B1 )
C10 99
C10 100
=0.90，
P( A
B4
)
C10 96
C10 100
0.65
P( A
B2
)
C10 98
C10 100
0.81，
由全概率公式求出 4 P( A) P(Bi )P( A Bi ) 0.815 i0
An1)P( A1 An2 )P( A1
An 1 ) An2 )
P( A1A2 A3 ) P( A3 A1A2 )P( A1A2 ) P( A1A2 ) P( A2 A1)P( A1)
P( A1 A2 A n ) P( An A1 An1) P( A3 A1A2 )P( A2 A1)P( A1)
在概率论的发展史上，人们曾针对不同问题，从不同角度
给出了概率的三种定义和计算方法。这三种定义和计算方法都 具有各自的适用范围，存在一定的局限性，但在三种定义下概 率的性质却是完全相同的。因此，人们从概率的性质出发，给 概率赋予一个新的数学定义，即概率的公理化定义。这个定义 只指明概率应具有的基本性质，不具体规定概率的计算方法。
噪声匹配
四、实验结果（含程序、数据记录及分析和实验总结等，可附页）：
程序：
%%%%%%%%%%%%%噪声平滑与匹配滤波%%%%%%%%%
clc;
closeall;
%%%噪声平滑%%%
h=fir1(20,0.1,hanning(21));
N=500;f=1/150;
u=rand(1,N);
s=sin(2*pi*f*[0:N-1]);
x=u(1:N)+s;
y=fftfilt(h,x);
figure(1);subplot(311);plot(x);
figure(1);subplot(312);plot(y);
%%%匹配滤波%%%
N=200;
y1=[3*ones(1,100),zeros(1,100)];
y2=y1+randn(1,N);
噪声平滑如图所示：
原信号为正弦波信号，加上白噪声后如上图加噪信号所示，波形上出现波动，设计时我利用fftfilt设计低通滤波器，该函数是利用效率高的基于FFT算法实现对数据的滤波，而FIR滤波器设计的方法中我采用的是窗函数法，这里用的是汉宁窗，最后波形如上图平滑后信号所示波动大大减小。
匹配滤波如图所示：
y3=ifft(conj(fft(y2)));
y4=conv(y3,y2);
figure(2);subplot(311);plot(y1);axis([0 200 0 5]);
figure(2);subplot(312);plot(y2);axis([0 200 0 5]);
figure(2);subplot(313);plot(y4);axis([0 400 0 1000]);
MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。MATLAB的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似，故用MATLAB来解算问题要比用C，FORTRAN等语言完成相同的事情简捷得多，并且MATLAB也吸收了像Maple等软件的优点，使MATLAB成为一个强大的数学软件。在新的版本中也加入了对C，FORTRAN，C++，JAVA的支持。
程序：
%%%%%%%%%%%%%噪声平滑与匹配滤波%%%%%%%%%
clc;
closeall;
%%%噪声平滑%%%
h=fir1(20,0.1,hanning(21));
N=500;f=1/150;
u=rand(1,N);
s=sin(2*pi*f*[0:N-1]);
x=u(1:N)+s;
y=fftfilt(h,x);
figure(1);subplot(311);plot(x);
figure(1);subplot(312);plot(y);
%%%匹配滤波%%%
N=200;
y1=[3*ones(1,100),zeros(1,100)];
y2=y1+randn(1,N);
噪声平滑如图所示：
原信号为正弦波信号，加上白噪声后如上图加噪信号所示，波形上出现波动，设计时我利用fftfilt设计低通滤波器，该函数是利用效率高的基于FFT算法实现对数据的滤波，而FIR滤波器设计的方法中我采用的是窗函数法，这里用的是汉宁窗，最后波形如上图平滑后信号所示波动大大减小。
匹配滤波如图所示：
y3=ifft(conj(fft(y2)));
y4=conv(y3,y2);
figure(2);subplot(311);plot(y1);axis([0 200 0 5]);
figure(2);subplot(312);plot(y2);axis([0 200 0 5]);
figure(2);subplot(313);plot(y4);axis([0 400 0 1000]);
MATLAB和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等，主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。MATLAB的基本数据单位是矩阵，它的指令表达式与数学、工程中常用的形式十分相似，故用MATLAB来解算问题要比用C，FORTRAN等语言完成相同的事情简捷得多，并且MATLAB也吸收了像Maple等软件的优点，使MATLAB成为一个强大的数学软件。在新的版本中也加入了对C，FORTRAN，C++，JAVA的支持。
随机信号分析PPT课件
RY ( )
N0 (bebu)(beb(u))du 20
N0b2 eb e2budu N 0b e b
2
0
4
相关函数为偶函数，τ<0时
R Y ( )
输出自相关函数为
N 0b e b 4
RY()
N0beb 4
a
25
输出的平均功率为
E[Y 2 (t)] RY (0)
N 0b 4
b为时间常数的倒数
a
2
4.1 线性系统的基本理论 4.1.1 线性时不变系统
x(t)
y(t)
L[ ·]
y(t)L[x(t)]
连续时间系统 双侧系统
离散时间系统
单侧系统
a
双侧信号 单侧信号
3
线性系统
L [ a 1 ( t ) x b 2 ( t ) x a ][ x 1 ( t L ) b ][ x 2 ( L t )]
RXY()0 h(u)RX(u)du
输出自相关R 函YX数(为)0 h(u)RX(u)du
RY()h(u)h(v)RX(uv)dudv
0
R Y()0 h(u)RXY(u)du
R Y()0 h(u)R Y aX(u)du
18
输出的均方值（总平均功率）
E[Y2(t)]h(u)h(v)RX(uv)dudv
(
)
N 0b 4
eb
与白噪声输入时 情况相同
a
31
例4.3中的相关函数可以进一步表示为
R Y()4 N 0e b 1 b 1 2/ 2 1be ( b)
二、双侧随机信号
K X(t)
Y(t) h(t)
Y(t)0h(u)X (tu)U (tu)du
随机信号分析11
T 2 T T 2
1 1 2 x ( t ) dt ] E [lim X ( ) d ] T T 2 T 2T SX ( ) 1 1 2 E[lim X T ( ) ]d 随机过程的平均功率 P 2 T 2T 1 E[lim T 2T
二、随机过程的功率谱密度函数
随机信号的样本函数能量是无限的, 但功率往往是有限的.
截取函数：
x(t )
x(t ) xT (t ) 0
t T t T
xT (t )
T
t
0
T
2T
X T ( ) xT (t )e
jt
dt x(t )e jt dt
T
随机信号分析
第11讲
叶方
哈尔滨工程大学信息与通信工程学院
本章学习内容
3.1 随机过程的谱分析
一、预备知识：确定信号的谱分析
包含： 振幅谱 相位谱
3.1 随机过程的谱分析
一、预备知识：确定信号的谱分析
（ 1）
（ 2）
能量谱
能量型信号：能量有限的信号 功率型信号：平均功率有限、能量无限的信号
3.1 随机过程的谱分析
3.2 功率谱密度与自相关函数的关系
3.2 功率谱密度与自相关函数的关系
一、维纳—辛钦定理
平稳随机过程X(t) 的自相关函数与其功率谱密度构成 一对傅里叶变换
利用自相关函数和功率谱密度皆为偶函数的性质
3.2 功率谱密度与自相关函数的关系
二、推论
对于一般的随机过程X(t)，有：
说明：一般的随机过程X(t) 的自相关函数的时间均值 与过程的功率谱密度函数互为傅里叶变换
T
3.1 随机过程的谱分析
1 1 2 x ( t ) dt ] E [lim X ( ) d ] T T 2 T 2T SX ( ) 1 1 2 E[lim X T ( ) ]d 随机过程的平均功率 P 2 T 2T 1 E[lim T 2T
二、随机过程的功率谱密度函数
随机信号的样本函数能量是无限的, 但功率往往是有限的.
截取函数：
x(t )
x(t ) xT (t ) 0
t T t T
xT (t )
T
t
0
T
2T
X T ( ) xT (t )e
jt
dt x(t )e jt dt
T
随机信号分析
第11讲
叶方
哈尔滨工程大学信息与通信工程学院
本章学习内容
3.1 随机过程的谱分析
一、预备知识：确定信号的谱分析
包含： 振幅谱 相位谱
3.1 随机过程的谱分析
一、预备知识：确定信号的谱分析
（ 1）
（ 2）
能量谱
能量型信号：能量有限的信号 功率型信号：平均功率有限、能量无限的信号
3.1 随机过程的谱分析
3.2 功率谱密度与自相关函数的关系
3.2 功率谱密度与自相关函数的关系
一、维纳—辛钦定理
平稳随机过程X(t) 的自相关函数与其功率谱密度构成 一对傅里叶变换
利用自相关函数和功率谱密度皆为偶函数的性质
3.2 功率谱密度与自相关函数的关系
二、推论
对于一般的随机过程X(t)，有：
说明：一般的随机过程X(t) 的自相关函数的时间均值 与过程的功率谱密度函数互为傅里叶变换
T
3.1 随机过程的谱分析
随机信号分析李晓峰
随机信号分析李晓峰引言随机信号分析是一门研究信号及其性质的学科，其在现代通信、图像处理、生物医学工程等领域中具有重要的应用价值。
本文将介绍随机信号分析的基本概念、常见的分析方法以及李晓峰教授在随机信号分析领域的研究成果。
随机信号的定义随机信号是指在某个时间段内具有随机性质的信号。
其特点是信号的取值在时间和幅度上都是不确定的，只能通过概率统计的方法来描述。
一个随机信号可以用一个概率密度函数来描述其取值的分布情况。
随机信号有两种基本的分类方式：离散随机信号和连续随机信号。
离散随机信号是在离散的时间点上进行取样的信号，连续随机信号则是在连续的时间上变化的信号。
随机信号分析方法统计特性分析统计特性分析是随机信号分析的基本方法之一，它通过对信号进行统计分析，从而得到信号的数学特性。
常见的统计特性包括均值、方差、自相关函数和谱密度等。
均值是衡量随机信号集中程度的一个指标，它表示信号的中心位置。
方差则用来衡量信号的离散程度，方差越大表示信号的波动性越大。
自相关函数描述了信号在不同时间点之间的相关性，而谱密度则表示信号在不同频率上的能量分布情况。
概率密度函数分析随机信号的概率密度函数描述了信号取值的概率分布情况。
常见的概率密度函数包括高斯分布、均匀分布和指数分布等。
高斯分布是最常用的概率密度函数之一，其形状呈钟型曲线，具有对称性。
均匀分布则表示信号的取值在一个区间上是均匀分布的，而指数分布则表示信号的取值在一个时间段内的分布服从指数规律。
谱分析谱分析是通过对随机信号进行频域分析来研究其频率成分的分析方法。
常见的谱分析方法有功率谱密度分析和相关函数分析。
功率谱密度分析可以用来分析信号在不同频率上的能量分布情况，通过功率谱密度分析可以得到信号的频谱图。
相关函数分析则是通过对信号进行自相关操作，得到信号的相关函数，从而分析信号在不同频率上的相关性。
李晓峰教授的研究成果李晓峰教授是我国著名的随机信号分析专家，他在随机信号分析领域做出了许多重要的研究成果。
《随机信号分析》课件
连续随机信号
连续时间和连续幅度的随机信号，如噪声信号。
高斯随机信号
服从高斯分布的随机信号，常用于描述自然界 的随机现象。
非高斯随机信号
不服从高斯分布的随机信号，如脉冲信号和干 扰信号。
常见的随机信号分析方法
自相关分析
用于分析信号的自身相关性和 平稳性。
频谱分析
通过对信号进行频域分析，得 到信号的频谱特性。
统计特性分析
对信号的均值、方差等统计特 性进行分析。
使用MATLAB进行随机信号分析的步骤
1
准备据
收集并整理所需信号的数据。
2
数据预处理
对数据进行去噪、归一化等预处理操作。
3
信号分析
运用MATLAB提供的工具进行信号分析和特征提取。
随机信号分析的应用领域
通信系统
用于优化信道传输和抗干扰能力的研究。
金融市场
用于分析股票价格、汇率等随机变动的特性。
生物医学
用于分析心电图、脑电图等生物信号。
气象预报
用于分析天气数据，提高气象预报的准确性。
总结
通过本课件，您了解了随机信号的定义、特性、分类以及分析方法，以及其在不同领域的应用。
《随机信号分析》PPT课 件
本课件将介绍随机信号分析的基本概念和方法，包括随机信号的定义、特性、 分类以及常见的分析方法。
分析随机信号的定义
1 随机信号
随机信号是不确定的信号，具有随机性和不可预测性。
2 随机过程
随机信号可以看作是随时间变化的随机过程。
3 概率论基础
随机信号的定义和性质可以通过概率论进行分析和描述。
随机信号的特性
1 均值和方差
随机信号的均值和方差是 表征其平均值和离散程度 的重要特性。
2. 随机信号分析_随机信号的时域分析
X (t ) X (t1 ) 0 t1 X (t 2 ) t2 X (ti ) ti X (t n ) tn t
随机过程X(t)在任意n个时刻t1,t2,…,tn状态X(t1) ,X(t2) ,…,X(tn)构 成n维随机变量[ X(t1),X(t2),…,X(tn) ]，当t0,n ∞时的 n维随 机变量近似随机过程。因此，可以借用对n维随机变量的分析研 究来“替代”或“近似”对随机过程的分析研究。 一、随机过程的一维分布
E[ X (t )] x 2 f X ( x, t )dx
2
将t视为变量时，即为过程X (t)的均方值。 同理，过程X(t)的方差：
D[ X (t )] E{[ X (t ) mX (t )] } [ x mX (t )]2 f X ( x, t )dx X 2 (t )
t
确定信号——幅度、相位均随时间做 有规律的、已知的变化。可以用确定 的时间函数来描述。可以准确的与测 其未来的变化。 随机信号——幅度、相位均随时间做 无规律的、未知的、随机的变化。无 法用确定的时间函数来描述。无法准 确的与测其未来的变化。 t 但，随机信号的统计规律则是确定的。
因此，人们用统计学方法建立了随机信号的数学模型→随机过程。
整个时间段T上，任意两个时刻的状态的联合概率分布情况。
所以定义随机过程X(t) 二维分布函数：
FX ( x1 , x2 ; t1 , t 2 ) P{X (t1 ) x1 ; X (t 2 ) x2 }......... .........1 , t 2 T t
随机过程X(t) 二维概率密度：
§2.1
随机过程的基本概念
下面由一个试验实例来建立随机过程的概念。 举例： 在相同条件下，对同一雷达接收机的内部噪声电压（或电 流）经过大量的重复测试后，设观测 到的所有的可能结果有n种， 记录下n个不相同的波形。
随机过程X(t)在任意n个时刻t1,t2,…,tn状态X(t1) ,X(t2) ,…,X(tn)构 成n维随机变量[ X(t1),X(t2),…,X(tn) ]，当t0,n ∞时的 n维随 机变量近似随机过程。因此，可以借用对n维随机变量的分析研 究来“替代”或“近似”对随机过程的分析研究。 一、随机过程的一维分布
E[ X (t )] x 2 f X ( x, t )dx
2
将t视为变量时，即为过程X (t)的均方值。 同理，过程X(t)的方差：
D[ X (t )] E{[ X (t ) mX (t )] } [ x mX (t )]2 f X ( x, t )dx X 2 (t )
t
确定信号——幅度、相位均随时间做 有规律的、已知的变化。可以用确定 的时间函数来描述。可以准确的与测 其未来的变化。 随机信号——幅度、相位均随时间做 无规律的、未知的、随机的变化。无 法用确定的时间函数来描述。无法准 确的与测其未来的变化。 t 但，随机信号的统计规律则是确定的。
因此，人们用统计学方法建立了随机信号的数学模型→随机过程。
整个时间段T上，任意两个时刻的状态的联合概率分布情况。
所以定义随机过程X(t) 二维分布函数：
FX ( x1 , x2 ; t1 , t 2 ) P{X (t1 ) x1 ; X (t 2 ) x2 }......... .........1 , t 2 T t
随机过程X(t) 二维概率密度：
§2.1
随机过程的基本概念
下面由一个试验实例来建立随机过程的概念。 举例： 在相同条件下，对同一雷达接收机的内部噪声电压（或电 流）经过大量的重复测试后，设观测 到的所有的可能结果有n种， 记录下n个不相同的波形。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
《随机信号分析》试验报告班级班学号_______________姓名_________________实验一1、熟悉并练习使用下列 Matlab 的函数，给出各个函数的功能说明和内部参数 的意义，并给出至少一个使用例子和运行结果：1)randn()产生随机数数组或矩阵，其元素服从均值为 0，方差为 1 的正态分布1) Y = randn产生一个伪随机数 2) Y = randn(n) 产生 n x n 的矩阵， 的正态分布其元素服从均值为0，方差为 13)Y = randn(m,n)产生 m x n 的矩阵， 的正态分布其元素服从均值为0，方差为 14) Y= randn([m n]) 产生 m x n 的矩阵， 的正态分布其元素服从均值为0，方差为 1选择( 2)作为例子，运行结果如下： >> Y = randn(3)1.3005 0.0342 0.97920.2691 0.9913 -0.8863 -0.1551 -1.3618 -0.3562生成n 々随机矩阵，其元素在(0, 1)内 生成mxn 随机矩阵 生成m x n 随机矩阵生成mxn 和x …随机矩阵或数组 生成m x n 和x …随机矩阵或数组 生成与矩阵 A 相同大小的随机矩阵 选择( 3)作为例子，运行结果如下：>> Y = rand([3 4])Y =0.05790.0099 0.1987 0.19883)normrnd()产生服从均值为mu 标准差为sigma 的随机数, mu 和sigma 可以为向量、矩阵、或多维数组。
（2）R = normrnd （mu,sigma,v ） 产生服从均值为 mu 标准差为 sigma 的随机数，v 是一个行向量。
如果v 是一个1 X 2的向量， 则R 为一个1行2列的矩阵。
如果v 是1X n 的, 那么R 是一个n 维数组（3）R = normrnd （mu,sigma,m,n ） 产生服从均值为 mu 标准差为 sigma 的随机数,2)rand()(1)Y = rand(n) (2)Y = rand(m,n) (3)Y = rand([m n])(4) Y = rand(m,n,p,…) (5) Y = rand([m n p …]) (6) Y = rand(size(A)) 0.3529 0.81320.1389 0.2028 0.6038 0.2722 0.0153 0.7468产生服从正态分布的随机数(1)R= normrnd(mu,sigma)标量m和n是R的行数和列数。
选择（3）作为例子,运行结果如下：>> R = normrnd（1,1,3,4）R =1.41172.1139 1.9044 0.66384.1832 3.0668 1.1677 2.71431.86362.0593 2.29443.62364)mean()(1)M = mean(A) 如果A是一个向量，则返回A的均值。
如果A是一个矩阵，则把A的每一列看成一个矩阵，返回一个均值（每一列的均值）行矩阵(2)M= mean(A,dim) 返回由标量dim标定的那个维度的平均值。
如（A，2）是一个列向量，包含着A中每一行的均值。
选择（2）作为例子,运行结果如下：>>A =3 4 5 6 745) var()r、、 . 、$.求方差(1)V = var(X)(2)V = var(X,w) 返回X的每一列的方差，即返回一个行向量。
计算方差时加上权重w选择（2）作为例子,运行结果如下：>> X=[1:1:5;1:2:10];V=var（X,1）V =0 0.2500 1.0000 2.2500 4.00006)xcorr()计算互相关(1) c=xcorr(x,y)(2)c=xcorr(x) 计算x,y 的互相关计算x 的自相关选择（2）作为例子,运行结果如下：R=normrnd（1,2,3）c=xcorr（R）c =-2.0953 0.8081 5.4014 -1.6986 0.6551 4.37871.6072 -0.6198 -4.1432-1.2036-0.8064 -4.4636 -3.2012 0.2046 2.1184 1.4050 0.4327 2.18189.1743 1.7032 -8.7548 1.7032 2.2426 -0.3519 -8.7548 -0.3519 12.8829-1.2036-3.2012 1.4050 -0.8064 0.2046 0.4327 -4.4636 2.1184 2.1818-2.0953-1.6986 1.6072 0.8081 0.6551 -0.6198 5.4014 4.3787 -4.14327) periodogram()计算功率谱密度[Pxx,w]=periodogram(x) 计算x的功率谱密度运行结果如下：X=[-20:4:20];Y=periodogram(X);plot(Y)8) fft()离散傅里叶变换(1)Y = fft(X)返回向量X用快速傅里叶算法得到的离散傅里叶变换，如果X是一个矩阵，则返回矩阵每一列的傅里叶变换(2)Y = fft(X,n) 返回n点的离散傅里叶变换，如果X的长度小于n，X的末尾填零。
如果X的长度大于n，则X被截断。
当X是一个矩阵时，列的长度也服从同样的操作。
选择(1)作为例子，运行结果如下:X=0:0.1:1;Y=fft(X)Y =Columns 1 through 55.5000 -0.5500 + 1.8731i -0.5500 + 0.8558i -0.5500 + 0.4766i-0.5500 + 0.2512iColumns 6 through 10-0.5500 + 0.0791i -0.5500 - 0.0791i -0.5500 - 0.2512i -0.5500 - 0.4766i -0.5500 - 0.8558iColum n 11-0.5500 - 1.8731i9) n ormpdf()求正态分布概率密度函数值Y = normpdf(X,mu,sigma)对每一个X 中的值返回参数为 mu,sigma 的正 态分布概率密度函数值运行结果如下：>> x=-5:0.1:5;y=normpdf(x,1,2);plot(x,y)10) normcdf()求正态分布概率分布函数值P = normcdf(X,mu,sigma)对每一个X 中的值返回参数为 mu,sigma 的 累计分布函数值运行结果如下：>> p = no rmcdf(1:4,0,1) p =0.8413 0.9772 0.9987 1.000011) u nifpdf()求连续均匀分布的概率密度函数值 Y = un ifpdf(X,A,B) 运行结果如下：对每一个X 中的值返回参数为A,B 的均匀分布函数值>> x = 1:0.1:3; y = un ifpdf(x,1,2) y =□n.12O.D60 D2Colum ns 1 through 101 1 1 1 1 1 1 1 1 1Colum ns 11 through 201 0 0 0 0 0 0 0 0 0Colum n 2112) un ifcdf()求连续均匀分布的概率分布函数值P = un ifcdf(X,A,B) 对每一个X中的值返回参数为A,B的均匀分布累计分布函数值运行结果如下：>> y=u nifcdf(0.5,-1,1) y =0.750013) raylpdf()求瑞利概率密度分布函数值Y = raylpdf(X,B) 对每一个X中的值返回参数为B的瑞利概率分布函数值运行结果如下：x = 0:024;p = raylpdf(x,1);14) raylcdf()求瑞利分布的概率分布函数值P = raylcdf(X,B) 对每一个X中的值返回参数为B的瑞利分布的累计分布函数值运行结果如下: x = 0:025; p = raylcdf(x,1);Plot(x,p)15) exppdf()求指数分布的概率密度函数值Y = exppdf(X,mu) 对每一个X中的值返回参数为mu的瑞利分布的概率密度函数值运行结果如下：>> y = exppdf(3,2:6)y =0.1116 0.1226 0.1181 0.1098 0.101116) expcdf()求指数分布的概率分布函数值P = expcdf(X,mu) 对每一个X中的值返回参数为mu的瑞利分布的概率分布函数值运行结果如下：>> x = 0:0.2:5;p = expcdf(x,2);plot(x,p)17) chol()对称正定矩阵的Cholesky 分解 (1) R=chol(X) 产生一个上三角阵R,使R'R=%若X 为非对称正定，则输出一个出错信息(2) [R,p]=chol(X) 不输出出错信息。
当X 为对称正定的，则p=0, R 与上述格式得到的结果相同；否则 p 为一个正整数。
如果 X 为满秩矩阵，则R 为一个阶数为q=p-1的上三角阵， 且满足R'R=X(1:q,1:q)。
选择(2)作为例子，运行结果如下>> n =4;X = pascal( n);R = chol(X) R =1 1 1 1 0 123 0 0 1 3 0 00 118) ksde nsity()计算概率密度估计R = n ormrnd(2,1);[f, xi] = ksde nsity(R);plot(xi,f)(1) [f,xi] = ksdensity(x)(2)f = ksdensity(x,xi)选择(1)作为例子，运行结果如下:计算向量x 样本的一个概率密度估计，返 回向量f 是在xi 各个点估计出的密度值 计算在确定点xi 处的估计值19)hist()画直方图 (1)n = hist(Y) (2) n = hist(Y,x) (3) n = hist(Y,nbins) 运行结果如下：将向量丫中的元素分成10个等长的区间，再返 回每区间中元素个数，是个行向量 画以x 元素为中心的柱状图 画以n bi ns 为宽度的柱状图20) int()对符号表达式s 中确定的符号变量计算计算不定积分 对符号表达式s 中指定的符号变量V 计算不定积分• 符号表达式s 的定积分，a,b 分别为积分的上、下限 符号表达式s 关于变量v 的定积分，a,b 为积分的上下限1/2*x A 22、产生高斯随机变量 （1） 产生数学期望为0，方差为1的高斯随机变量； （2） 产生数学期望为2，方差为5的高斯随机变量；（3） 利用计算机求上述随机变量的100个样本的数学期望和方差，并与理论 值比较；解：（1） randn （3,4）ans =0.9572 0.1419 0.7922 0.0357 0.4854 0.4218 0.9595 0.8491 0.8003 0.9157 0.6557 0.9340 (2) normrnd(2,5A0.5,3,4) ans =0.4658 3.80366.5414 3.81546.0902 2.3977 -1.4405 -2.8379 1.3752 1.9891 -1.3931 3.8373(3) 若 x=randn(1,100) y=mea n(x)z=var(x,1) 经matlab 运行后得到：-0.0102 z =Y=ra nd(80,2);hist(Y,8)计算积分 (1) int(s) (2) int(s,v) (3) int(s,a,b) (4) int(s,v,a,b) 运行结果如下： >> syms x;int(x) ans =1.0122 计算结果中均值与方差均为随机变量，经多次运算，均值与方差均变化较大，但他们的值均可近似认为是0和1。