三角、反三角函数图像(实用)
- 格式:doc
- 大小:138.00 KB
- 文档页数:3
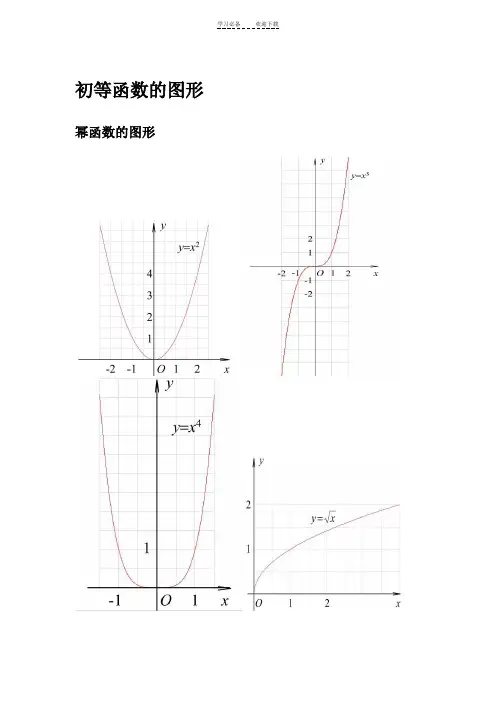
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质 函数y=sinxy=cosxy=tanxy=cotx 定义域 R R{x |x ∈R 且x≠kπ+2π,k ∈Z }{x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1 x=2kπ-2π 时y min =-1[-1,1] x=2kπ时y max =1x=2kπ+π时y min =-1 R无最大值 无最小值R无最大值 无最小值周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数 单调性在[2kπ-2π,2kπ+2π ]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k ∈Z) 在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z) 在(kπ-2π,kπ+2π)内都是增函数(k ∈Z)在(kπ,kπ+π)内都是减函数(k ∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π]且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于(-2π,2π),且正切值等于x 的角arccotx 表示属于(0,π)且余切值等于x 的角 性质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域[-2π,2π] [0,π](-2π,2π) (0,π) 单调性 在〔-1,1〕上是增函数在[-1,1]上是减函数 在(-∞,+∞)上是增数在(-∞,+∞)上是减函数 奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosx arctan(-x)=-arcta nx arccot(-x)=π-a rccotx 周期性 都不是同期函数恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π])cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π])tan(arctanx)=x(x ∈R)arctan(tanx)=x(x ∈(-2π,2π))cot(arccotx)=x (x ∈R)arccot(cotx)=x (x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosαcos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2asin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
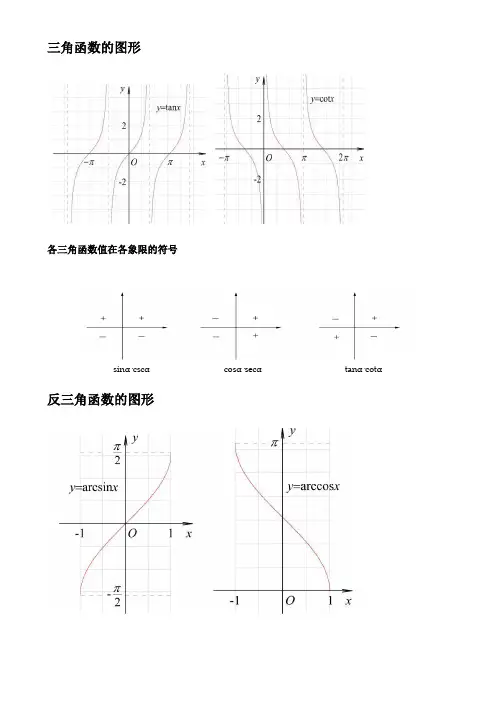

反三角函数的图像和性质yx,arccos yx,arctanyx,arcsin,1,1,1,1,,,,R 定义域,,,,,,,, ,,,,值域 [0,π] ,,,,2222,,,,在上单调递增在上单调递减 ,1,1,1,1,,,,在R上单调递增单调性无减区间无减区间无增区间3奇偶性奇函数非奇非偶函数奇函数32,32,,21212,-1图象 -22468-224682O11-1,-1-,2-2 -22468-1 -1O2-2 -1arcsin()arcsin,,,xxarccos()arccos,,,xx,arctan()arctan,,,xx 运算公x,,[1,1]x,,[1,1] xR,式1运算公,,,, arccos(cos),[0,]xxx,,,arctan(tan),(,)xxx,,,arcsin(sin),[,]xxx,,,2222式2运算公sin(arcsin),[1,1]xxx,,,cos(arccos),[1,1]xxx,,,tan(arctan),xxxR,, 式3 , arctancotxarcx,,运算公,2 arcsinarccos,[1,1]xxx,,,,2式4 xR, 三角函数的图像和性质4 yx,cosy,tanx yx,sin kZ,34332221一个周11(((113,,2,,,期的图-22468,-22468(-4-2246823,,O,2,O2O--12-12-1-1-1 22像 -2-2-2-3,,,x|x,k,,k,Z ,定义域 R R ,,2,,[1,1],[1,1], 值域 R 奇偶性奇函数偶函数奇函数, 2,2,周期对,直线xk,kZ, ,,,称直线,无 xk,,kZ,2轴对称对性称k,,(,0)k,,kZ, 点,kZ, 点(,0)k,(,0)点,kZ, ,22中心,,,,,在上 [2,2]kk,,[2,22]kk,,,,,,,,,上在,上在(,)kk,,,,2222单调性 ,,3,在上,,[2,2]kk,,,,,[2,2]kk,,在上无减区间 22。
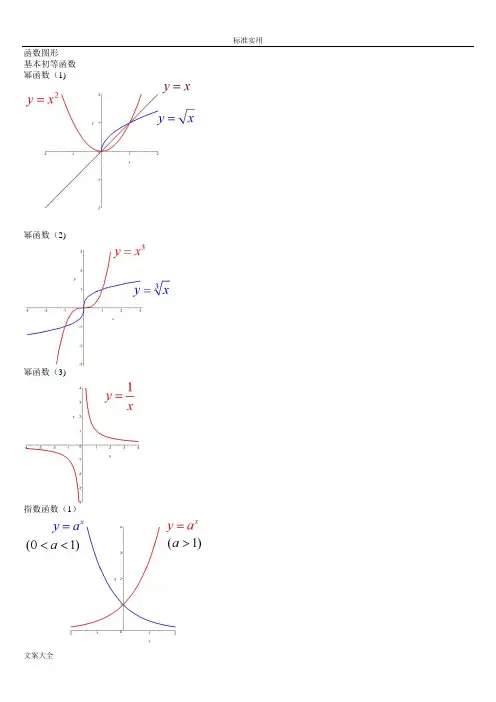
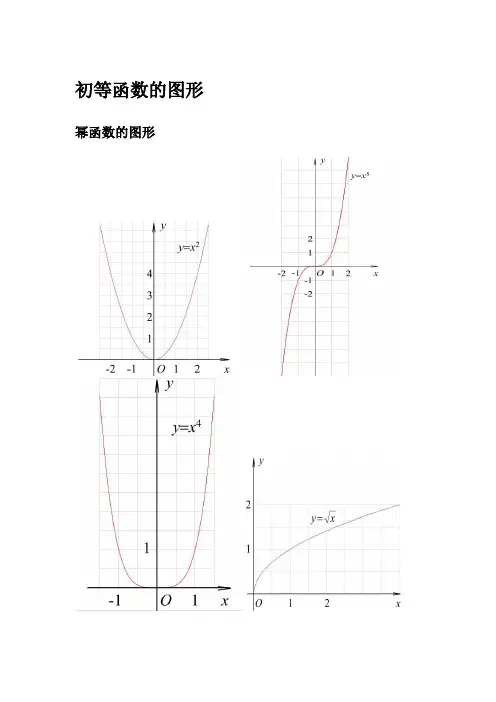
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(4)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1) y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4) y = [1/x](1) y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1)极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性)极限的性质(3) (不等式性质)极限的性质(4) (局部有界性)极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3)e的值(1)e的值(2)等价无穷小(x->0)sinx等价于xarcsinx等价于xtanx等价于xarctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2) 数列的夹逼性(1) 数列的夹逼性(2)。

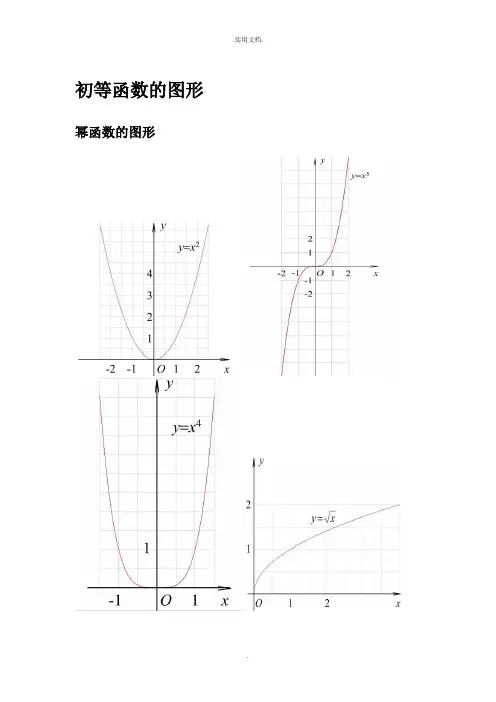
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=a b ] a•sin(a)-b•cos(a) =)b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin 2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa + tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin 〔2kπ+α〕= sinαcos 〔2kπ+α〕= cosαtan 〔2kπ+α〕= tanαcot 〔2kπ+α〕= cotα设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin〔π+α〕= -sinαcos〔π+α〕= -cosαtan〔π+α〕= tanαcot〔π+α〕= cotα公式三任意角α与-α的三角函数值之间的关系:sin〔-α〕= -sinαcos〔-α〕= cosαtan〔-α〕= -tanαcot〔-α〕= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin〔π-α〕= sinαcos〔π-α〕= -cosαtan〔π-α〕= -tanαcot〔π-α〕= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin〔2π-α〕= -sinαcos〔2π-α〕= cosαtan〔2π-α〕= -tanαcot〔2π-α〕= -cotα2π±α及23π±α与α的三角函数值之间的关系: sin 〔2π+α〕= cosα cos 〔2π+α〕= -sinα tan 〔2π+α〕= -cotα cot 〔2π+α〕= -tanα sin 〔2π-α〕= cosα cos 〔2π-α〕= sinα tan 〔2π-α〕= cotα cot 〔2π-α〕= tanα sin 〔23π+α〕= -cosα cos 〔23π+α〕= sinα tan 〔23π+α〕= -cotα cot 〔23π+α〕= -tanα sin 〔23π-α〕= -cosα cos 〔23π-α〕= -sinα tan 〔23π-α〕= cotα cot 〔23π-α〕= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明〔全部〕公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/6 13+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:〔a,b〕是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的外表积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。

初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质 函数y=sinxy=cosxy=tanxy=cotx 定义域 R R{x |x ∈R 且x≠kπ+2π,k ∈Z }{x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1 x=2kπ-2π 时y min =-1[-1,1] x=2kπ时y max =1x=2kπ+π时y min =-1 R无最大值 无最小值R无最大值 无最小值周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数 单调性在[2kπ-2π,2kπ+2π ]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k ∈Z) 在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z) 在(kπ-2π,kπ+2π)内都是增函数(k ∈Z)在(kπ,kπ+π)内都是减函数(k ∈Z)反三角函数的图形反三角函数的性质名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π]且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于(-2π,2π),且正切值等于x 的角arccotx 表示属于(0,π)且余切值等于x 的角 性质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域[-2π,2π] [0,π](-2π,2π) (0,π) 单调性 在〔-1,1〕上是增函数在[-1,1]上是减函数 在(-∞,+∞)上是增数在(-∞,+∞)上是减函数 奇偶性arcsin(-x)=-arcsinxarccos(-x)=π-arccosx arctan(-x)=-arcta nx arccot(-x)=π-a rccotx 周期性 都不是同期函数恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π])cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(x ∈[0,π])tan(arctanx)=x(x ∈R)arctan(tanx)=x(x ∈(-2π,2π))cot(arccotx)=x (x ∈R)arccot(cotx)=x (x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinBsin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2- Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosAtan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A )=2cos 1A - cos(2A )=2cos 1A + tan(2A )=A A cos 1cos 1+- cot(2A )=AA cos 1cos 1-+ tan(2A )=A A sin cos 1-=AA cos 1sin + 和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosacos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosatgA=tanA =aacos sin万能公式sina=2)2(tan 12tan2aa + cosa=22)2(tan 1)2(tan 1aa+- tana=2)2(tan 12tan2aa -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=ba ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a)2其他非重点三角函数csc(a) =a sin 1 sec(a) =acos 1双曲函数sinh(a)=2e -e -aacosh(a)=2e e -aa +tg h(a)=)cosh()sinh(a a公式一设α为任意角,终边相同的角的同一三角函数的值相等: sin (2kπ+α)= sinα cos (2kπ+α)= cosα tan (2kπ+α)= tanα cot (2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinαcos (π+α)= -cosαtan (π+α)= tanαcot (π+α)= cotα公式三任意角α与 -α的三角函数值之间的关系:sin (-α)= -sinαcos (-α)= cosαtan (-α)= -tanαcot (-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系: sin (π-α)= sinαcos (π-α)= -cosαtan (π-α)= -tanαcot (π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin (2π-α)= -sinαcos (2π-α)= cosαtan (2π-α)= -tanαcot (2π-α)= -cotα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosαcos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanα sin (23π-α)= -cosα cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα (以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2)三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b≤a≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA) 倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2asin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA))ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA))和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2 cosA+cosB=2cos((A+B)/2)sin((A-B)/2) tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3正弦定理a/sinA=b/sinB=c/sinC=2R注:其中R 表示三角形的外接圆半径b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]} 圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积,L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h。
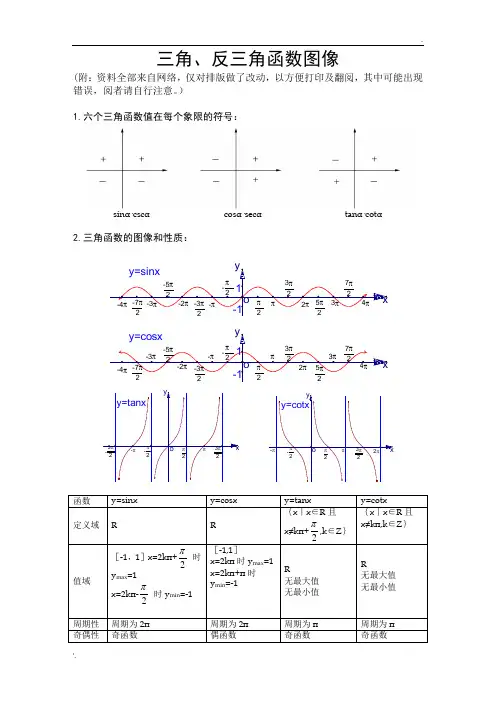
三角、反三角函数图像(附:资料全部来自网络,仅对排版做了改动,以方便打印及翻阅,其中可能出现错误,阅者请自行注意。
)1.六个三角函数值在每个象限的符号:sinα·cscα cosα·secα tanα·cotα2.三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanxy=cotx定义域RR{x |x ∈R 且x≠kπ+2π,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max =1 x=2kπ+π时y min =-1R 无最大值 无最小值R无最大值 无最小值 周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性奇函数偶函数奇函数奇函数单调性在[2kπ-2π,2kπ+2π]上都是增函数;在[2kπ+2π,2kπ+32π]上都是减函数(k∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k∈Z)在(kπ-2π,kπ+2π)内都是增函数(k∈Z)在(kπ,kπ+π)内都是减函数(k∈Z)3.反三角函数的图像和性质:arcsinx arccosxarctanx arccotx名称反正弦函数反余弦函数反正切函数反余切函数定义y=sinx(x∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsinyy=cosx(x∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosyy=tanx(x∈(-2π,2π)的反函数,叫做反正切函数,记作x=arctanyy=cotx(x∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx表示属于[-2π,2π]且正弦值等于x的角arccosx表示属于[0,π],且余弦值等于x的角arctanx表示属于(-2π,2π),且正切值等于x的角arccotx表示属于(0,π)且余切值等于x的角性质定义域[-1,1][-1,1](-∞,+∞)(-∞,+∞)值域[-2π,2π][0,π](-2π,2π) (0,π)单调性在〔-1,1〕上是增函数在[-1,1]上是减函数在(-∞,+∞)上是增数在(-∞,+∞)上是减函数奇偶性arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是周期函数arcsin(-x)=-arcsinx arccos(-x)=π-arccosxarctan(-x)=-arctanx arccot(-x)=π-arccotxarcsinx+arccosx=arctanx+arccotx=π/2sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x当 x∈[-π/2, π/2] arcsin(sinx)=xx∈[0,π] arccos(cosx)=xx∈(-π/2, π/2) arctan(tanx)=xx∈(0, π) arccot(cotx)=x三角公式总表1.正弦定理:A a sin =B b sin =Cc sin = 2R (R 为三角形外接圆半径)2.余弦定理:a 2=b 2+c 2-2bc A cos b 2=a 2+c 2-2ac B cos c 2=a 2+b 2-2ab C cosbca cb A 2cos 222-+=3.S ⊿=21a a h ⋅=21ab C sin =21bc A sin =21ac B sin =R abc 4=2R 2A sinB sinC sin=A C B a sin 2sin sin 2=B C A b sin 2sin sin 2=CB A c sin 2sin sin 2=pr=))()((c p b p a p p ---(其中)(21c b a p ++=, r 为三角形内切圆半径)4.同角关系:⑴商的关系:①θtg =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅==ctg ③θθθtg ⋅=cos sin ④θθθθcsc cos 1sec ⋅==tg ⑤θθθctg ⋅=sin cos ⑥θθθθsec sin 1csc ⋅==ctg⑵倒数关系:1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg⑶平方关系:1csc sec cos sin 222222=-=-=+θθθθθθctg tg⑷)sin(cos sin 22ϕθθθ++=+b a b a (其中辅助角ϕ与点(a,b )在同一象限,且abtg =ϕ)5.和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos(=± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++Ctg B tg C tg A tg B tg A tg6.二倍角公式:(含万能公式)①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -=④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=7.半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sin θθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±= ④2cos 12cos 2θθ+= ⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin 2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg8.积化和差公式:①[])sin()sin(21cos sin βαβαβα-++=②[])sin()sin(21sin cos βαβαβα--+=③[])cos()cos(21cos cos βαβαβα-++= ④()[]βαβαβα--+-=cos )cos(21sin sin9.和差化积公式:①2cos2sin2sin sin βαβαβα-+=+②2sin 2cos 2sin sin βαβαβα-+=- ③2cos 2cos 2cos cos βαβαβα-+=+ ④2sin2sin 2cos cos βαβαβα-+-=-。

三角函数与反三角函数的图像与性质一、三角函数的图像和性质
R R
-1,1-1,1
x = + 2 k 时, y= 1,k Z x = -+ 2k时, y最小= -1,k Z x = 2k 时, y= 1,k Z x = + 2 k 时, y = - 1,k Z
在每个[-+2k,+2k]上递增在每个[+ 2k, 3+ 2k]上递减k Z 在每个[-+ 2k, 2k]上递增在每个[2k, + 2k]上递减
k Z
是周期函数,2为最小正周期是周期函数,2为最小正周期
对称中心(k, 0) ,对称轴:x = +k,(k Z)对称中心(+ k, 0) ,对称轴: x = k,(k Z)
{x| x R且x +k,k Z}{x| x R且x+k,k Z} R R
在每个(-+k,+k)上递增
k Z 在每个(k,+ k)上递减
k Z
是周期函数,为最小正周期是周期函数,为最小正周期对称中心(k2,0)对称中心(k2,0)
二、反三角函数的图像与性质
反正弦函数y= arcsin x
是y=sin x,x-2,2的反函数反余弦函数y= arccos x 是y = cos x,x0,的反函数
-1,1-1,1
0,
对称中心(0,)
2. 反正切与反余切函数的图像与性质
反正切函数y= arctan x
是y = tan x,x(-,) 的反函数
22反余切函数y= arccot x
是y = cot x,x(0,)的反函数
(-,+,)(-,+,)
(0,)
在(-,+,)上递增在(-,+,)上递减
对称中心(0,)。
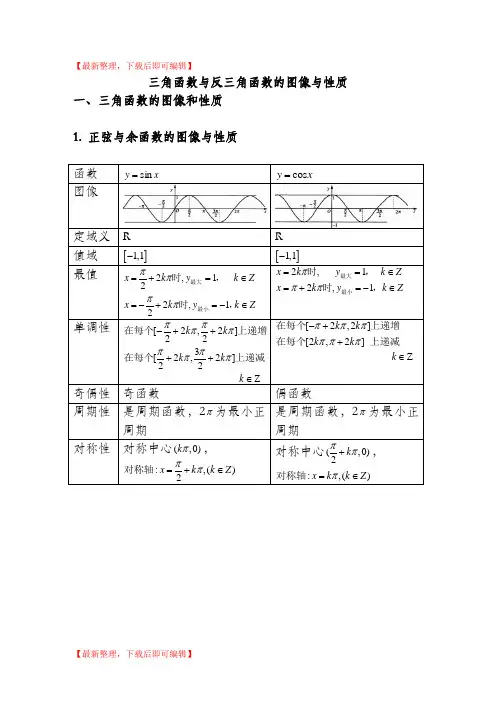
【最新整理,下载后即可编辑】三角函数与反三角函数的图像与性质一、三角函数的图像和性质1. 正弦与余函数的图像与性质 函数 x y sin = x y cos = 图像定域义 R R值域 []1,1-[]1,1-最值 2,1 22,1 2x k yk Zx k y k Zππππ=+=∈=-+=-∈最大最小时,时,2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时,时, 单调性 [2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2] Zk k k k k ππππππ-++∈在每个上递增在每个上递减 奇偶性 奇函数偶函数周期性 是周期函数,2π为最小正周期是周期函数,2π为最小正周期 对称性 对称中心(,0)k π,:,()2x k k Z ππ=+∈对称轴对称中心(,0)2k ππ+,:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质 函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且{|,}x x R x k k Z ππ∈≠+∈且值域 R R单调性 (,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数,π为最小正周期是周期函数,π为最小正周期 对称性 对称中心(,0)2k π对称中心(,0)2k π二、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质 函数 反正弦函数arcsin y x = 是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦,的反函数反余弦函数arccos y x =是[]cos 0,y x x π=∈,的反函数图像定域义 []1,1-[]1,1-值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性 [1,1]-+在上递增 [1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心(0,0)对称中心(0,)2π2. 反正切与反余切函数的图像与性质函数 反正切函数arctan y x = 是tan (,)22y x x ππ=∈-,的反函数反余切函数arccot y x =是()cot 0,y x x π=∈,的反函数图像定域(,,)-∞+∞(,,)-∞+∞。
三角函数与反三角函数的图像与性质一、三角函数的图像和性质1. 正弦与余函数的图像与性质 函数 x y sin =x y cos =图像定域义 RR值域 []1,1-[]1,1-最值2,1 22,1 2x k y k Zx k y k Zππππ=+=∈=-+=-∈最大最小时,时,2, 1 2,1x k y k Zx k y k Z πππ==∈=+=-∈最大最小时,时, 单调性[2,2]223[2,2]22Zk k k k k ππππππππ-++++∈在每个上递增在每个上递减[2,2][2,2] Zk k k k k ππππππ-++∈在每个上递增在每个上递减奇偶性 奇函数偶函数周期性 是周期函数,2π为最小正周期 是周期函数,2π为最小正周期 对称性对称中心(,0)k π,:,()2x k k Z ππ=+∈对称轴 对称中心(,0)2k ππ+,:,()x k k Z π=∈对称轴2. 正切与余切函数的图像与性质函数 x y tan = x y cot =图像定域义 {|,}2x x R x k k Z ππ∈≠+∈且 {|,}x x R x k k Z ππ∈≠+∈且值域RR单调性(,)22Zk k k ππππ-++∈在每个上递增(,) Zk k k πππ+∈在每个上递减奇偶性 奇函数奇函数周期性 是周期函数,π为最小正周期 是周期函数,π为最小正周期 对称性对称中心(,0)2k π 对称中心(,0)2k π 二、反三角函数的图像与性质1. 反正弦与反余函数的图像与性质 函数反正弦函数arcsin y x =是sin ,22y x x ππ⎡⎤=∈-⎢⎥⎣⎦,的反函数 反余弦函数arccos y x =是[]cos 0,y x x π=∈,的反函数图像定域义 []1,1-[]1,1-值域 ,22ππ⎡⎤-⎢⎥⎣⎦[]0,π单调性 [1,1]-+在上递增[1,1]-+在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性对称中心(0,0)对称中心(0,)2π函数反正切函数arctan y x = 是tan (,)22y x x ππ=∈-,的反函数 反余切函数arccot y x = 是()cot 0,y x x π=∈,的反函数图像定域义 (,,)-∞+∞(,,)-∞+∞值域 ,22ππ⎛⎫- ⎪⎝⎭()0,π单调性 (,,)-∞+∞在上递增(,,)-∞+∞在上递减奇偶性 奇函数 非奇非偶 周期性 无无对称性 对称中心(0,0)对称中心(0,)2π。
经典三角函数公式及其图像大全三角函数是中学课程里,非常重要的一部分,应将其作为学习的一个重点。
⒌同角关系:⑴商的关系:①θtg =xy =θθcos sin =θθsec sin ⋅ ②θθθθθcsc cos sin cos ⋅===y x ctg ③θθθtg ry⋅==cos sin ④θθθθcsc cos 1sec ⋅===tg x r ⑤θθθctg r x ⋅==sin cos ⑥θθθθsec sin 1csc ⋅===ctg y r ⑵倒数关系:1sec cos csc sin =⋅=⋅=⋅θθθθθθctg tg ⑶平方关系:1csc sec cos sin 222222=-=-=+θθθθθθctg tg ⑷)sin(cos sin 22ϕθθθ++=+b a b a(其中辅助角ϕ与点(a,b )在同一象限,且ab tg =ϕ)⒍函数y=++⋅)sin(ϕωx A k 的图象及性质:(0,0>>A ω) 振幅A ,周期T =ωπ2, 频率f =T1, 相位ϕω+⋅x ,初相ϕ⒎五点作图法:令ϕω+x 依次为ππππ2,23,,20 求出x 与y ,依点()y x ,作图 ⒏诱导公试三角函数值等于α的同名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名不变,符号看象限 三角函数值等于α的异名三角函数值,前面加上一个把α看作锐角时,原三角函数值的符号;即:函数名改变,符号看象限⒐和差角公式①βαβαβαsin cos cos sin )sin(±=± ②βαβαβαsin sin cos cos )cos( =± ③βαβαβαtg tg tg tg tg ⋅±=± 1)( ④)1)((βαβαβαtg tg tg tg tg ⋅±=±⑤γβγαβαγβαγβαγβαtg tg tg tg tg tg tg tg tg tg tg tg tg ⋅-⋅-⋅-⋅⋅-++=++1)( 其中当A+B+C=π时,有:i).tgC tgB tgA tgC tgB tgA ⋅⋅=++ ii).1222222=++Ctg B tg C tg A tg B tg A tg ⒑二倍角公式:(含万能公式)sin cos tg ctg-α-αsin +αcos -αtg -αctg π-α +αsin -αcos -αtg -αctg π+α-αsin -αcos +αtg +αctg 2π-α-αsin +αcos -αtg -αctg 2k π+α +αsin +αcos +αtg +αctgsin con tg ctgαπ-2 +αcos +αsin +αctg +αtg απ+2+αcos -αsin -αctg -αtgαπ-23 -αcos -αsin +αctg +αtg απ+23 -αcos +αsin -αctg -αtg①θθθθθ212cos sin 22sin tg tg +== ②θθθθθθθ22222211sin 211cos 2sin cos 2cos tg tg +-=-=-=-= ③θθθ2122tg tg tg -= ④22cos 11sin 222θθθθ-=+=tg tg ⑤22cos 1cos 2θθ+=⒒三倍角公式:①)60sin()60sin(sin 4sin 4sin 33sin 3θθθθθθ+︒-︒=-= ②)60cos()60cos(cos 4cos 4cos 33cos 3θθθθθθ+︒-︒=+-=③)60()60(313323θθθθθθθ+⋅-⋅=--=tg tg tg tg tg tg tg ⒓半角公式:(符号的选择由2θ所在的象限确定) ①2cos 12sin θθ-±= ②2cos 12sin 2θθ-= ③2cos 12cos θθ+±=④2cos 12cos 2θθ+=⑤2sin 2cos 12θθ=- ⑥2cos 2cos 12θθ=+ ⑦2sin2cos )2sin 2(cos sin 12θθθθθ±=±=±⑧θθθθθθθsin cos 1cos 1sin cos 1cos 12-=+=+-±=tg⒔积化和差公式:[])sin()sin(21cos sin βαβαβα-++=[])sin()sin(21sin cos βαβαβα--+=[])cos()cos(21cos cos βαβαβα-++= ()[]βαβαβα--+-=cos )cos(21sin sin⒕和差化积公式:①2cos2sin2sin sin βαβαβα-+=+ ②2sin2cos2sin sin βαβαβα-+=-③2cos 2cos 2cos cos βαβαβα-+=+ ④2sin 2sin 2cos cos βαβαβα-+-=- ⒖反三角函数: ⒗最简单的三角方程方程方程的解集a x =sin1=a{}Z k a k x x ∈+=,arcsin 2|π1<a (){}Z k a k x x k∈-+=,arcsin 1|πa x =cos1=a {}Z k a k x x ∈+=,arccos 2|π1<a{}Z k a k x x ∈±=,arccos 2|π a tgx ={}Z k arctga k x x ∈+=,|πa ctgx ={}Z k arcctga k x x ∈+=,|π三角、反三角函数图像六个三角函数值在每个象限的符号:名称函数式定义域值域性质反正弦函数 x y arcsin = []1,1-增 ⎥⎦⎤⎢⎣⎡-2,2ππ -arcsinx arcsin(-x)= 奇 反余弦函数 xy arccos =[]1,1-减 []π,0x x arccos )arccos(-=-π反正切函数 arctgxy = R 增⎪⎭⎫ ⎝⎛-2,2ππ arctgx - arctg(-x)= 奇 反余切函数arcctgxy =R 减()π,0arcctgx x arcctg -=-π)(sinα·cscα cosα·secα tanα·cotα三角函数的图像和性质:1-1y=sinx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoy x1-1y=cosx-3π2-5π2-7π27π25π23π2π2-π2-4π-3π-2π4π3π2ππ-πoyxy=tanx3π2ππ2-3π2-π-π2oyxy=cotx3π2ππ22π-π-π2oyx函数 y=sinx y=cosx y=tanx y=cotx定义域RR{x |x ∈R 且x≠kπ+2π,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }值域[-1,1]x=2kπ+2π 时y max =1 x=2kπ-2π时y min =-1[-1,1] x=2kπ时y max =1 x=2kπ+π时y min =-1R 无最大值 无最小值R 无最大值 无最小值 周期性周期为2π 周期为2π周期为π周期为π奇偶性 奇函数偶函数 奇函数 奇函数单调性在[2kπ-2π,2kπ+2π ]上都是增函数;在[2kπ+2π ,2kπ+32π]上都是减函数(k ∈Z)在[2kπ-π,2kπ]上都是增函数;在[2kπ,2kπ+π]上都是减函数(k ∈Z) 在(kπ-2π,kπ+2π)内都是增函数(k ∈Z) 在(kπ,kπ+π)内都是减函数(k ∈Z).反三角函数:arcsinx arccosxarctanx arccotx名称反正弦函数 反余弦函数 反正切函数 反余切函数定义y=sinx(x ∈〔-2π,2π〕的反函数,叫做反正弦函数,记作x=arsiny y=cosx(x ∈〔0,π〕)的反函数,叫做反余弦函数,记作x=arccosy y=tanx(x ∈(-2π , 2π)的反函数,叫做反正切函数,记作x=arctany y=cotx(x ∈(0,π))的反函数,叫做反余切函数,记作x=arccoty理解arcsinx 表示属于[-2π,2π] 且正弦值等于x 的角arccosx 表示属于[0,π],且余弦值等于x 的角arctanx 表示属于(-2π,2π),且正切值等于x 的角arccotx 表示属于(0,π)且余切值等于x 的角性质定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域 [-2π,2π] [0,π](-2π,2π) (0,π)单调性 在〔-1,1〕上是增函数 在[-1,1]上是减函数在(-∞,+∞)上是增数 在(-∞,+∞)上是减函数奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-arccosx arctan(-x)=-arctanx arccot(-x)=π-arccotx 周期性都不是同期函数 恒等式sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2π]) cos(arccosx)=x(x ∈[-1,1])arccos(cosx)=x(x ∈[0,π])tan(arctanx)=x(x ∈R)arctan(tanx)=x (x ∈(-2π,2π)) cot(arccotx)=x(x ∈R)arccot(cotx)=x(x ∈(0,π))互余恒等式 arcsinx+arccosx=2π(x ∈[-1,1]) arctanx+arccotx=2π(X ∈R)。
初等函数的图形幂函数的图形指数函数的图形各三角函数值在各象限的符号sinα·cscα cosα·secα tanα·cotα三角函数的性质反三角函数的图形反三角函数的性质三角函数公式两角和公式sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinBtan(A+B) =tanAtanB -1tanBtanA +tan(A-B) =tanAtanB 1tanBtanA +-cot(A+B) =cotA cotB 1-cotAcotB +cot(A-B) =cotAcotB 1cotAcotB -+倍角公式tan2A =Atan 12tanA2-Sin2A=2SinA•CosACos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A三倍角公式sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3π-a)半角公式sin(2A)=2cos 1A -cos(2A)=2cos 1A +tan(2A)=A A cos 1cos 1+-cot(2A )=A A cos 1cos 1-+tan(2A )=A A sin cos 1-=A A cos 1sin +和差化积sina+sinb=2sin2b a +cos 2ba - sina-sinb=2cos 2b a +sin 2ba -cosa+cosb = 2cos 2b a +cos 2ba -cosa-cosb = -2sin 2b a +sin 2ba -tana+tanb=ba b a cos cos )sin(+积化和差sinasinb = -21[cos(a+b)-cos(a-b)] cosacosb = 21[cos(a+b)+cos(a-b)]sinacosb = 21[sin(a+b)+sin(a-b)]cosasinb = 21[sin(a+b)-sin(a-b)]诱导公式sin(-a) = -sina cos(-a) = cosasin(2π-a) = cosa cos(2π-a) = sinasin(2π+a) = cosacos(2π+a) = -sinasin(π-a) = sina cos(π-a) = -cosasin(π+a) = -sinacos(π+a) = -cosa tgA=tanA =aa cos sin 万能公式 sina=2)2(tan 12tan2a a+ cosa=22)2(tan 1)2(tan 1a a +- tana=2)2(tan 12tan 2a a -其它公式a•sina+b•cosa=)b (a 22+×sin(a+c) [其中tanc=ab ] a•sin(a)-b•cos(a) = )b (a 22+×cos(a-c) [其中tan(c)=b a ] 1+sin(a) =(sin2a +cos 2a )2 1-sin(a) = (sin 2a -cos 2a )2其他非重点三角函数 csc(a) =asin 1 sec(a) =a cos 1 双曲函数 sinh(a)=2e -e -aa cosh(a)=2e e -aa tg h(a)=)cosh()sinh(a a 公式一设α为任意角,终边相同的角的同一三角函数的值相等:sin (2kπ+α)= sinαcos (2kπ+α)= cosαtan (2kπ+α)= tanαcot (2kπ+α)= cotα公式二设α为任意角,π+α的三角函数值与α的三角函数值之间的关系: sin (π+α)= -sinαtan(π+α)= tanαcot(π+α)= cotα公式三任意角α与 -α的三角函数值之间的关系:sin(-α)= -sinαcos(-α)= cosαtan(-α)= -tanαcot(-α)= -cotα公式四利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)= sinαcos(π-α)= -cosαtan(π-α)= -tanαcot(π-α)= -cotα公式五利用公式-和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)= -sinαcos(2π-α)= cosαtan(2π-α)= -tanα公式六2π±α及23π±α与α的三角函数值之间的关系: sin (2π+α)= cosα cos (2π+α)= -sinα tan (2π+α)= -cotα cot (2π+α)= -tanα sin (2π-α)= cosα cos (2π-α)= sinα tan (2π-α)= cotα cot (2π-α)= tanα sin (23π+α)= -cosα cos (23π+α)= sinα tan (23π+α)= -cotα cot (23π+α)= -tanαsin (23π-α)= -cos α cos (23π-α)= -sinα tan (23π-α)= cotα cot (23π-α)= tanα(以上k ∈Z)这个物理常用公式我费了半天的劲才输进来,希望对大家有用 A•sin(ωt+θ)+ B•sin(ωt+φ) =)cos(222ϕθ⋅++AB B A ×sin )cos(2)Bsin in arcsin[(As t 22ϕθϕθω⋅++++AB B A三角函数公式证明(全部)公式表达式乘法与因式分解a2-b2=(a+b)(a-b) a3+b3=(a+b)(a2-ab+b2) a3-b3=(a-b)(a2+ab+b2) 三角不等式|a+b|≤|a|+|b||a-b|≤|a|+|b||a|≤b<=>-b ≤a ≤b|a-b|≥|a|-|b|-|a|≤a≤|a|一元二次方程的解-b+√(b2-4ac)/2a -b-b+√(b2-4ac)/2a根与系数的关系X1+X2=-b/aX1*X2=c/a注:韦达定理判别式 b2-4a=0 注:方程有相等的两实根b2-4ac>0 注:方程有一个实根b2-4ac<0 注:方程有共轭复数根三角函数公式两角和公式sin(A+B)=sinAcosB+cosAsinB sin(A-B)=sinAcosB-sinBcosAcos(A+B)=cosAcosB-sinAsinB cos(A-B)=cosAcosB+sinAsinBtan(A+B)=(tanA+tanB)/(1-tanAtanB) tan(A-B)=(tanA-tanB)/(1+tanAtanB) ctg(A+B)=(ctgActgB-1)/(ctgB+ctgA) ctg(A-B)=(ctgActgB+1)/(ctgB-ctgA)倍角公式tan2A=2tanA/(1-tan2A) ctg2A=(ctg2A-1)/2ctgacos2a=cos2a-sin2a=2cos2a-1=1-2sin2a半角公式sin(A/2)=√((1-cosA)/2) sin(A/2)=-√((1-cosA)/2)cos(A/2)=√((1+cosA)/2) cos(A/2)=-√((1+cosA)/2)tan(A/2)=√((1-cosA)/((1+cosA)) tan(A/2)=-√((1-cosA)/((1+cosA)) ctg(A/2)=√((1+cosA)/((1-cosA)) ctg(A/2)=-√((1+cosA)/((1-cosA)) 和差化积2sinAcosB=sin(A+B)+sin(A-B) 2cosAsinB=sin(A+B)-sin(A-B)2cosAcosB=cos(A+B)-sin(A-B) -2sinAsinB=cos(A+B)-cos(A-B)sinA+sinB=2sin((A+B)/2)cos((A-B)/2cosA+cosB=2cos((A+B)/2)sin((A-B)/2)tanA+tanB=sin(A+B)/cosAcosB tanA-tanB=sin(A-B)/cosAcosBctgA+ctgBsin(A+B)/sinAsinB -ctgA+ctgBsin(A+B)/sinAsinB某些数列前n项和1+2+3+4+5+6+7+8+9+…+n=n(n+1)/21+3+5+7+9+11+13+15+…+(2n-1)=n22+4+6+8+10+12+14+…+(2n)=n(n+1)12+22+32+42+52+62+72+82+…+n2=n(n+1)(2n+1)/613+23+33+43+53+63+…n3=n2(n+1)2/41*2+2*3+3*4+4*5+5*6+6*7+…+n(n+1)=n(n+1)(n+2)/3 正弦定理a/sinA=b/sinB=c/sinC=2R注:其中 R 表示三角形的外接圆半径余弦定理b2=a2+c2-2accosB注:角B是边a和边c的夹角正切定理[(a+b)/(a-b)]={[Tan(a+b)/2]/[Tan(a-b)/2]}圆的标准方程(x-a)2+(y-b)2=r2 注:(a,b)是圆心坐标圆的一般方程x2+y2+Dx+Ey+F=0 注:D2+E2-4F>0抛物线标准方程y2=2px y2=-2px x2=2py x2=-2py直棱柱侧面积S=c*h斜棱柱侧面积S=c'*h正棱锥侧面积S=1/2c*h'正棱台侧面积S=1/2(c+c')h'圆台侧面积S=1/2(c+c')l=pi(R+r)l 球的表面积S=4pi*r2圆柱侧面积S=c*h=2pi*h圆锥侧面积S=1/2*c*l=pi*r*l弧长公式l=a*ra是圆心角的弧度数r >0 扇形面积公式s=1/2*l*r锥体体积公式V=1/3*S*H圆锥体体积公式V=1/3*pi*r2h斜棱柱体积V=S'L注:其中,S'是直截面面积, L是侧棱长柱体体积公式V=s*h圆柱体V=pi*r2h--------------------------------------------------------------------------------------------三角函数积化和差和差化积公式记不住就自己推,用两角和差的正余弦:cos(A+B)=cosAcosB-sinAsinBcos(A-B)=cosAcosB+sinAsinB这两式相加或相减,可以得到2组积化和差:相加:cosAcosB=[cos(A+B)+cos(A-B)]/2相减:sinAsinB=-[cos(A+B)-cos(A-B)]/2sin(A+B)=sinAcosB+sinBcosAsin(A-B)=sinAcosB-sinBcosA这两式相加或相减,可以得到2组积化和差:相加:sinAcosB=[sin(A+B)+sin(A-B)]/2相减:sinBcosA=[sin(A+B)-sin(A-B)]/2这样一共4组积化和差,然后倒过来就是和差化积了不知道这样你可以记住伐,实在记不住考试的时候也可以临时推导一下正加正正在前正减正余在前余加余都是余余减余没有余还负正余正加余正正减余余余加正正余减还负.3.三角形中的一些结论:(不要求记忆)(1)anA+tanB+tanC=tanA·tanB·tanC(2)sinA+tsinB+sinC=4cos(A/2)cos(B/2)cos(C/2)(3)cosA+cosB+cosC=4sin(A/2)·sin(B/2)·sin(C/2)+1(4)sin2A+sin2B+sin2C=4sinA·sinB·sinC(5)cos2A+cos2B+cos2C=-4cosAcosBcosC-1 ...........................已知sinα=m sin(α+2β), |m|<1,求证tan(α+β)=(1+m)/(1-m)tanβ解:sinα=m sin(α+2β)sin(a+β-β)=msin(a+β+β)sin(a+β)cosβ-cos(a+β)sinβ=msin(a+β)cosβ+mcos(a+β)sinβ sin(a+β)cosβ(1-m)=cos(a+β)sinβ(m+1)tan(α+β)=(1+m)/(1-m)tanβ。
.反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心):,该点切线斜率为拐点(同曲线对称中心): 11该点切线斜率为-,反正切曲线图像与特征反余切曲线图像与特征拐点:,该点切线斜率:(同曲线对称中心)拐点 1为,该点切线斜率为-1渐近线:渐近线:反正割曲线反余割曲线名称1 / 4.方程图顶点渐近线反三角函数的定义域与主值范围主值范定义函主值记反正弦,则若反余弦若,则反正切,则若反余切,则若反正割若,则反余割若,则为式中一般反三角函数与主值的关系为n任意数百科名片是个多值是一种数学术语。
反,并不能狭义的理解为三角函数的反函数三角函数rccot xrctan x正切rccos x反余弦rcsin x反正弦函数。
它是a,a,反a,反a余切x这些函数的统称,各自表示其正弦、余弦、正切、余切为的角。
数学术语2 / 4.作为将y限在-π/2≤y≤π/2,为限制反三角函数为单值函数,将反正弦函数的值y的主值限y=arcsin x;相应地,反余弦函数y=arccos x,记为反正弦函数的主值y=arccot xπ/2<y<π/2;反余切函数在0≤y≤π;反正切函数y=arctan x的主值限在-实际上并不能叫做函数,因为它并不满足反三角函数的主值限在0<y<π。
对称。
对应一个函数值的要求,图与其原函数关于函数y=一自变函数名】的形式表示反三角函数概念首先欧提出,并且首先使用了arc+反正弦π/2,π/2]上的反函数,叫做⑴正弦函数y=sin x在[-而不是f-1(x)。
【图,π/2]区间内。
xarcsin x表示一个正弦值为的角,该角的范围在[-π/2函数。
arccos π]上的反函数,叫做反余弦函数。
⑵余弦函数y=cos x在[0,中红线】⑶x的角,该角的范围在[0,π]区间内。
【图中蓝线】x表示一个余弦值为表示一π/2)上的反函数,叫做反正切函数。
arctan x正切函数y=tan x在(-π/2,注释:π/2,π/2)区间内。
三角、反三角函数图像
六个三角函数值在每个象限的符号:
sinα·cscα cosα·secα tanα·cotα
三角函数的图像和性质:
1-1y=sinx
-3π2
-5π2
-7π2
7π2
5π
2
3π2
π2
-π2
-4π-3π
-2π4π
3π
2ππ
-π
o
y x
1-1y=cosx
-3π
2
-5π2
-7π
2
7π2
5π2
3π2
π2
-π2
-4π-3π-2π4π
3π
2π
π
-π
o
y
x
y=tanx
3π2
π
π2
-
3π2
-π
-
π2
o
y
x
y=cotx
3π2
π
π2
2π
-π
-
π2
o
y
x
函数 y=sinx y=cosx y=tanx
y=cotx
定义域
R
R
{x |x ∈R 且x≠kπ+
2
π
,k ∈Z } {x |x ∈R 且x≠kπ,k ∈Z }
值域
[-1,1]x=2kπ+
2π
时y max =1
x=2kπ-2
π
时y min =-1
[-1,1] x=2kπ时y max =1
x=2kπ+π时
y min =-1
R 无最大值 无最小值
R
无最大值 无最小值
周期性 周期为2π 周期为2π 周期为π 周期为π 奇偶性
奇函数
偶函数
奇函数 奇函数
单调性
在[2kπ-2π,2kπ+2
π
]上都是增函数;在
[2kπ+2π ,2kπ+3
2
π]上都是减函数(k ∈Z)
在[2kπ-π,2kπ]上都是增函数;
在[2kπ,2kπ+π]上都是减函数(k ∈Z)
在(kπ-2
π,kπ+
2
π
)内都是增函数(k ∈Z)
在(kπ,kπ+π)内都是减函数(k ∈Z)
.反三角函数:
arcsinx arccosx
arctanx arccotx
名称
反正弦函数 反余弦函数 反正切函数 反余切函数 定义
y=sinx(x ∈〔-2π,2π 〕的反函数,叫做反正弦函数,记作x=arsiny y=cosx(x ∈〔0,π〕)的反函数,叫做反余弦
函数,记作x=arccosy y=tanx(x ∈(-2π
, 2
π
)的反函数,叫做反正切函数,记作
x=arctany
y=cotx(x ∈(0,π))的反函数,叫做反余切函数,记作x=arccoty
理解
arcsinx 表示属于[-2π,2π] 且正弦值等于x 的角
arccosx 表示属于[0,π],且余弦值等于x 的角 arctanx 表示属于
(-2π,2π
),且正切值等于x 的角 arccotx 表示属于(0,π)且余切值等于x 的角
性
质 定义域 [-1,1] [-1,1] (-∞,+∞) (-∞,+∞) 值域 [-2π,2π] [0,π]
(-
2π,2
π) (0,π)
单调性
在〔-1,1〕上是增函数 在[-1,1]上是减函数
在(-∞,+∞)上是增数 在(-∞,+∞)上是减函数
奇偶性 arcsin(-x)=-arcsinx arccos(-x)=π-ar
ccosx
arctan(-x)=-arctanx arccot(-x)=π-arc
cotx 周期性
都不是同期函数
恒等式
sin(arcsinx)=x(x ∈[-1,1])arcsin(sinx)=x(x ∈[-2π,2
π
])
cos(arccosx)=x(x ∈[-1,1]) arccos(cosx)=x(
x ∈[0,π]) tan(arctanx)=x(x ∈R)arctan(tanx)=x (x ∈(-2π,2
π)) cot(arccotx)=x(x ∈R)
arccot(cotx)=x(x ∈(0,π))
互余恒等式 arcsinx+arccosx=
2
π
(x ∈[-1,1]) arctanx+arccotx=
2
π
(X ∈R)
反三角函数其他公式
arcsin(-x)=-arcsinx ;
arccos(-x)=π-arccosx ;
arctan(-x)=-arctanx ;
arccot(-x)=π-arccotx ;
arcsinx+arccosx=π/2=arctanx+arccotx;
sin(arcsinx)=cos(arccosx)=tan(arctanx)=cot(arccotx)=x ;
当x∈[-π/2, π/2] 有arcsin(sinx)=x ;
x∈[0,π], arccos(cosx)=x ;
x∈(-π/2, π/2), arctan(tanx)=x ;
x∈(0, π), arc cot(cotx)=x ;。