
拆分函数解析式结构,巧解问题
——-———----————函数()ax b f x cx d
+=
+值域(最值)问题的解法 在高中,初学函数之时,我们接触的具体函数并不多。前面我们已经给出了一元二次函数值域(最值)的求法步骤。除此,还有一类()(0)ax b f x c cx d
+=≠+函数也很常见,它也是今后解决其他复杂函数值域(最值)问题的基础.此类函数看似生疏,而实际这类函数的图像,就是我们初中学过的反比例函数图像。
此类问题有三种类型,一种是函数式子决定定义域,不额外附加函数定义域;另一种是附加定义域。还有一种是可转化为()(0)ax b f x c cx d +=
≠+型的函数,此类随着学习的深入,再行和大家见面。
下面我们以具体实例,说明如何依据函数解析式的结构特征,选择适当的方法步骤解决问题。
【例题1】:求函数21()3
x f x x +=-的值域; 【思路切入】:从函数结构可以得出,函数定义域由分式决定,为{|3}x x R x ∈≠且,此时,将函数解析式的结构进行拆分变换,不难得出反比例函数结构,如此,得到解法程序:
1、将函数分解为反比例的结构;
2、根据反比例结构特性,或者利用图像,或者利用数式属性得到函数值域。
【解析】:原函数可化为212677()2333
x x f x x x x +-+===+---, 7303
x x ≠≠-且
,2y ∴≠,函数()f x 值域为{|2}y y R y ∈≠且; 【例题2】:求函数21(),(2,4]1x f x x x -=∈-的值域; 【思路切入】:由例1的结构拆分法,我们不难得到函数的反比例结构。但由于函数有附加定义域(2,4],所以在例1方法的基础上,结合一元二次函数值域的解法步骤,我们改进此类问题解法程序步骤为:
(一)数形结合法:
1、将函数分解为反比例的结构;
2、根据反比例结构特性,画出函数图像示意;
3、观察定义域内的曲线形状,找到最高点和最低点,得到函数值域.
(二)代数法:
1、利用变换,将x 用y 表示;
2、利用给定的函数定义域(x 的取值范围)建立关于y 的不等式;
3、解关于y 的不等式,得到函数值域.
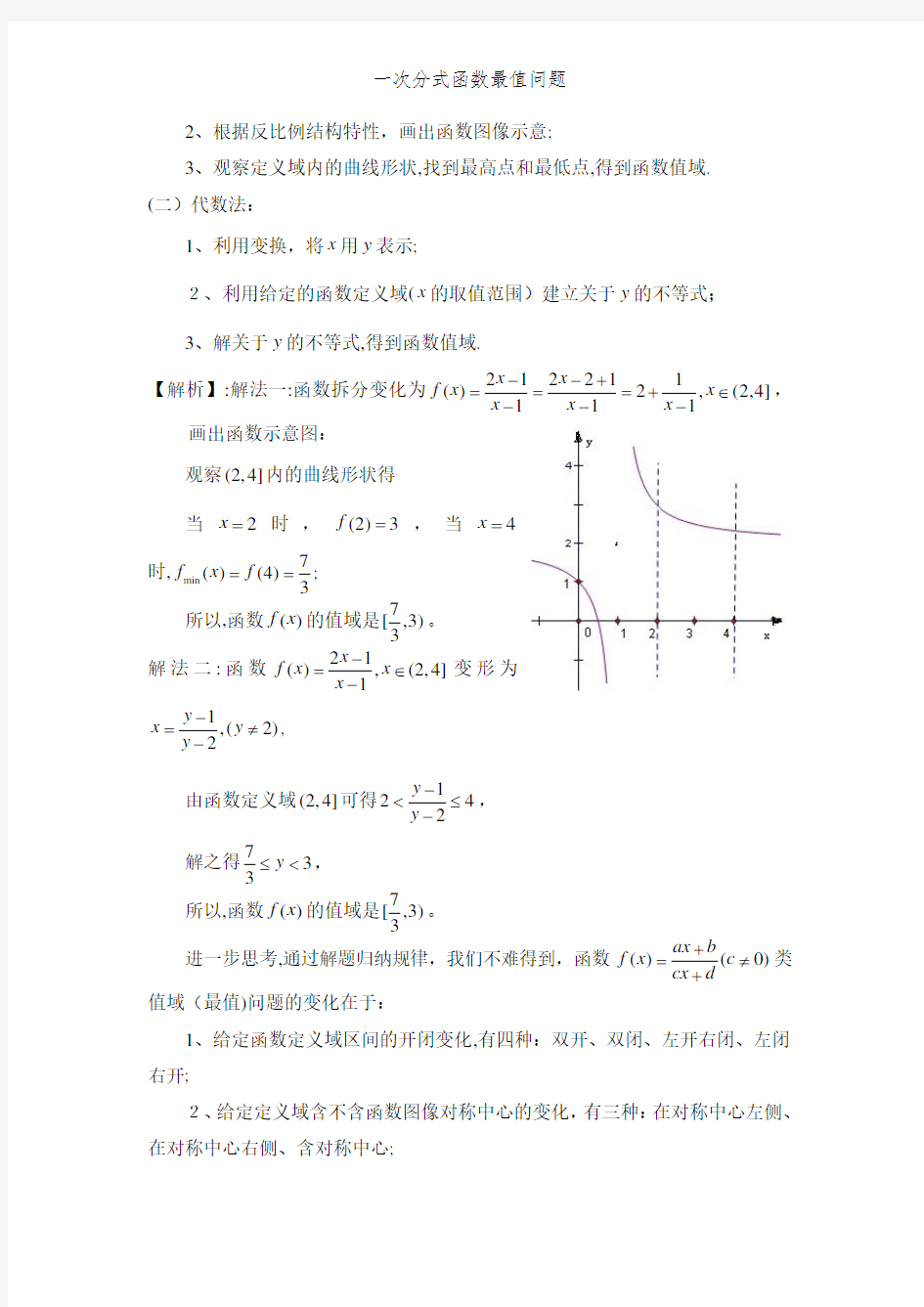
【解析】:解法一:函数拆分变化为212211()2,(2,4]111x x f x x x x x --+=
==+∈---,画出函数示意图:
观察(2,4]内的曲线形状得
当2x =时,(2)3f =,当4
x =时,min 7()(4)3
f x f ==; 所以,函数()f x 的值域是7[,3)3
。 解法二:函数21(),(2,4]1
x f x x x -=∈-变形为1,(2)2
y x y y -=≠-, 由函数定义域(2,4]可得1242y y -<
≤-, 解之得733
y ≤<, 所以,函数()f x 的值域是7[,3)3
。 进一步思考,通过解题归纳规律,我们不难得到,函数()(0)ax b f x c cx d
+=
≠+类值域(最值)问题的变化在于:
1、给定函数定义域区间的开闭变化,有四种:双开、双闭、左开右闭、左闭右开;
2、给定定义域含不含函数图像对称中心的变化,有三种:在对称中心左侧、在对称中心右侧、含对称中心;
3、反比例函数结构的变化,有两种:,0a y a x
=>图像在一、三象限,,0a y a x
=<图像在二、四象限。 如此,此类函数的值域(最值)问题就全在你的掌控之中了。任题目千变万化,但解题方法步骤不变,我们完全可以“以不变应万变"。
【文化提升】:某个事物所具备的结构特征,决定了这个事物的转变方向。有时,我们可以把复杂事物,通过结构拆分,转化为我们所熟知的基本事物,然后,透过有条理的线索,逐步解决问题.单就数学来说,解决任何数学问题,透过数学结构,其解决方法的适当选取是培养数学思维素质的好途径。
【落实提高】:
1、求函数21(),(0,4)1
x f x x x -=∈-的值域; 答案:7(,1)(,)3
-∞+∞ 2、求函数21(),[4,2)1
x f x x x -=∈--+的值域; 答案:[3,5)
3、求函数3(),(0)21
x f x x x -=≥+的值域; 答案:1(,3]2
- 4、函数21()(),(0,4)()11()
f x
g x x f x x f x -=∈=-+且,求函数()g x 的值域; 答案:7(,)8
-+∞