matlab编程平面梁问题有限元分析
- 格式:docx
- 大小:156.12 KB
- 文档页数:5

基于Matlab平面梁四单元的分析摘要:Matlb平面梁单元分析目标:通过对两单元的分析,掌握梁单元分析的一般方法和步骤,了解两单元的应变状态。
模型:如图一方形截面的悬臂梁,截面每边长为5cm,长度为10m,在左端约束固定,在右端施以一个沿y轴负方向的集中力w=100N,求其绕度与转角。
图一内容:解:将这个两分成4个平面梁单元,求出每个单元的刚度矩阵,然后将4个单元刚度矩阵组集成总体刚度矩阵。
引入边界条件后,再求解出各节点的挠度和转角。
Matlab程序如下:>>clearx1=0;x2=sym('L');x=sym('x');j=0:3;v=x.^jm=...[1 x1 x1^2 x1^30 1 2*x1 3*x1^21 x2 x2^2 x2^30 1 2*x2 3*x2^2]mm=inv(m);N=v*mm%N=[1 x x^2 x^3]*(inv(mm))B=diff(N,2)k=transpose(B)*B;Ke=int(k,0,'L')%Element 1: E=4.0e11, I=bh^3/12=5.2e-7EI=4.0e11*5.2e-7Ke1=EI*subs(Ke,'L',2.5)Ke2=Ke1Ke3=Ke1Ke4=Ke1T=eye(4,4)Ke1=T*Ke1*T';Ke2=T*Ke2*T';Ke3=T*Ke3*T';Ke4=T*Ke4*T';% system analysis F=[K]uG1=...[1 0 0 0 0 0 0 0 0 00 1 0 0 0 0 0 0 0 00 0 1 0 0 0 0 0 0 00 0 0 1 0 0 0 0 0 0];G2=...[0 0 1 0 0 0 0 0 0 00 0 0 1 0 0 0 0 0 00 0 0 0 1 0 0 0 0 00 0 0 0 0 1 0 0 0 0];G3=...[0 0 0 0 1 0 0 0 0 00 0 0 0 0 1 0 0 0 00 0 0 0 0 0 1 0 0 00 0 0 0 0 0 0 1 0 0];G4=...[0 0 0 0 0 0 1 0 0 00 0 0 0 0 0 0 1 0 00 0 0 0 0 0 0 0 1 00 0 0 0 0 0 0 0 0 1];K1=G1'*Ke1*G1K2=G2'*Ke2*G2K3=G3'*Ke3*G3K4=G4'*Ke4*G4K=K1+K2+K3+K4F=[0,0,0,0,0,0,0,0,-100,0]'%u=F*inv(K) u=[v1,xta1,v2,xta2,v3,xta3,v4,xta4,v5,xta5]', v1=xta1=0 %K(1,:)=0;K(:,1)=0;K(2,:)=0;K(:,2)=0;KX=K(3:10, 3:10)F(1,1)=0;F(2,1)=0;FX=F(3: 10, 1);u=inv(KX)*FX%求得悬臂梁节点2、3、4、5处得挠度和转角为:u =-0.0138-0.0105-0.0501-0.0180-0.1014-0.0225-0.1603-0.0240结果分析:(1)上述实验结果可知,悬臂梁在端点处的挠度和转角最大,这和材料力学得出的结论是一致的。

Matlab 对梁元的分析与应用勾都2010021212摘要:随着现代科技的快速发展,人们在工程领域的研究也越来越深入,对科学的研究要求快速化,简单化,精确化,实用化。
所以市场上出现了一大批针对工程分析与运用的软件,matlab就以实用,简单,精确而为广大用户推重。
ATLAB 的名称源自 Matrix Laboratory ,它是一种科学计算软件,专门以矩阵的形式处理数据。
MATLAB 将高性能的数值计算和可视化集成在一起,并提供了大量的内置函数,从而被广泛地应用于科学计算、控制系统、信息处理等领域的分析、仿真和设计工作。
目前 MATLAB 产品族可以用来进行:数值分析数值和符号计算工程与科学绘图数字图像处理数字信号处理通讯系统设计与仿真财务与金融工程。
本文是基于MATLAB的对工程分析,主要介绍了用MATLAB对梁元的分析与计算,和相关图的绘制。
关键词:工程分析梁元图的绘制引言:1有限元法的步骤(1)离散化域(2)写出单元刚度矩阵(3)集成整体刚度矩阵(4)引入边界条件(5)解方程(6)后处理由上步骤可看出,结决问题的过程结合使用了matlab和某些有限的手动操作(步骤1、4、5)。
可以看出,所有冗长、反复的计算都可由matla b完成。
2用于有限元分析的函数1 BeamElementStiffness(E,I,L)——该函数用于计算弹性模量E 、转动惯量I 、长度L 的梁的单元刚度矩阵。
返回4x4的单元刚度矩阵k 。
2 BeamAssemble (K,k,i,j )——该函数连接节点i 和节点j 的梁元的单元刚度矩阵k 集成到整体刚度矩阵K 。
每集成一个单元,该函数都返回2nX2n 的整体刚度矩阵K.3 BeamElementForces(k,u)——该函数用单元刚度矩阵k 和单元节点位移矢量u 计算单元节点矢量。
返回4x1的单元节点力矢量f 。
4 BeamElementShearDiagram(f,L)——该函数绘制节点力矢量为f 和长度为L 的单元剪力图。
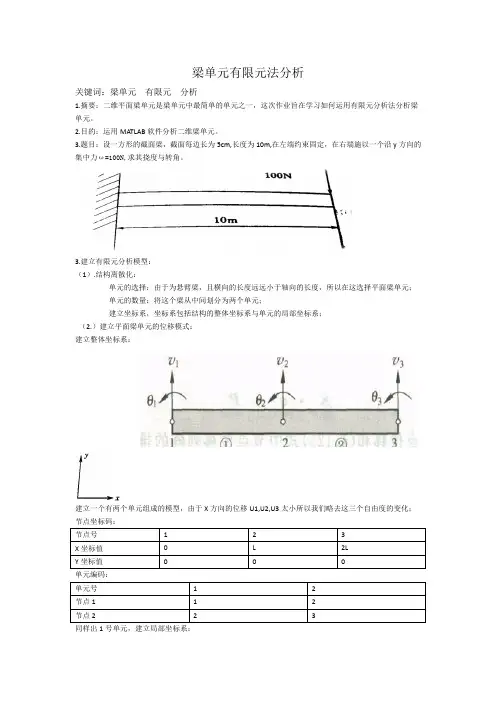
梁单元有限元法分析关键词:梁单元有限元分析1.摘要:二维平面梁单元是梁单元中最简单的单元之一,这次作业旨在学习如何运用有限元分析法分析梁单元。
2.目的:运用MATLAB软件分析二维梁单元。
3.题目:设一方形的截面梁,截面每边长为5cm,长度为10m,在左端约束固定,在右端施以一个沿y方向的集中力ω=100N,求其挠度与转角。
3.建立有限元分析模型:(1).结构离散化:单元的选择:由于为悬臂梁,且横向的长度远远小于轴向的长度,所以在这选择平面梁单元;单元的数量:将这个梁从中间划分为两个单元;建立坐标系,坐标系包括结构的整体坐标系与单元的局部坐标系;(2.)建立平面梁单元的位移模式:建立整体坐标系:建立一个有两个单元组成的模型,由于X方向的位移U1,U2,U3太小所以我们略去这三个自由度的变化;节点坐标码:单元编码:同样出1号单元,建立局部坐标系:4.具体的MATLAB求解过程与结果:>> clearx1=0;x2=sym('L');x=sym('x');j=0:3;v=x.^jv =[ 1, x, x^2, x^3]>> %计算形函数矩阵m=...[1 x1 x1^2 x1^30 1 2*x1 3*x1^21 x2 x2^2 x2^30 1 2*x2 3*x2^2]m =[ 1, 0, 0, 0][ 0, 1, 0, 0][ 1, L, L^2, L^3][ 0, 1, 2*L, 3*L^2]>> mm=inv(m)mm =[ 1, 0, 0, 0] [ 0, 1, 0, 0] [ -3/L^2, -2/L, 3/L^2, -1/L][ 2/L^3, 1/L^2, -2/L^3, 1/L^2]>> mm=inv(m);N =[ (2*x^3)/L^3 - (3*x^2)/L^2 + 1, x - (2*x^2)/L + x^3/L^2, (3*x^2)/L^2 - (2*x^3)/L^3, x^3/L^2 - x^2/L]>> %N=[1 x x^2 x^3]*(inv(m))%由最小势能原理导出刚度矩阵keB=diff(N,2) %梁单元的单元应变矩阵是形函数矩阵的2介导数(由梁的应变能得出)B =[ (12*x)/L^3 - 6/L^2, (6*x)/L^2 - 4/L, 6/L^2 - (12*x)/L^3, (6*x)/L^2 - 2/L]>> k=transpose(B)*(B);ke=int(k,0,'L') %从0到L上积分k矩阵ke =[ 12/L^3, 6/L^2, -12/L^3, 6/L^2][ 6/L^2, 4/L, -6/L^2, 2/L][ -12/L^3, -6/L^2, 12/L^3, -6/L^2][ 6/L^2, 2/L, -6/L^2, 4/L]>> %Element1:E=4.0e11,I=bh^3/12=5.2e-7EI=4.0e11*5.2e-7EI =208000>> ke1=EI*subs(ke,'L',5)ke1 =19968 49920 -19968 4992049920 166400 -49920 83200-19968 -49920 19968 -4992049920 83200 -49920 166400>> %由上市我们就计算出了1号单元刚度矩阵ke,由于分成两个单元,所以L=10/2=5>> %同理,我们运用上述办法得到2号单元的刚度矩阵ke2>> clearx2=5;x=sym('x');j=0:3;v=x.^jv =[ 1, x, x^2, x^3]>> m=...[1 x2 x2^2 x2^30 1 2*x2 3*x2^21 x3 x3^2 x3^30 1 2*x3 3*x3^2]m =[ 1, 5, 25, 125][ 0, 1, 10, 75][ 1, L, L^2, L^3][ 0, 1, 2*L, 3*L^2]>> mm=inv(m);N=v*mmN =[ (2*x^3)/(L - 5)^3 + (30*L*x)/(L - 5)^3 - (x^2*(3*L + 15))/(L - 5)^3 + (L^2*(L - 15))/(L - 5)^3, x^3/(L - 5)^2 -(5*L^2)/(L - 5)^2 - (x^2*(2*L + 5))/(L - 5)^2 + (L*x*(L + 10))/(L - 5)^2, (75*L - 125)/(L - 5)^3 - (2*x^3)/(L - 5)^3 - (30*L*x)/(L - 5)^3 + (x^2*(3*L + 15))/(L - 5)^3, x^3/(L - 5)^2 - (25*L)/(L - 5)^2 + (x*(10*L + 25))/(L - 5)^2 - (x^2*(L + 10))/(L - 5)^2]>> B=diff(N,2)B =[ (12*x)/(L - 5)^3 - (2*(3*L + 15))/(L - 5)^3, (6*x)/(L - 5)^2 - (2*(2*L + 5))/(L - 5)^2, (2*(3*L + 15))/(L - 5)^3 -(12*x)/(L - 5)^3, (6*x)/(L - 5)^2 - (2*(L + 10))/(L - 5)^2]>> k=transpose(B)*(B);ke =[ 12/(L - 5)^3, 6/(L - 5)^2, -12/(L - 5)^3, 6/(L - 5)^2][ 6/(L - 5)^2, 4/(L - 5), -6/(L - 5)^2, 2/(L - 5)][ -12/(L - 5)^3, -6/(L - 5)^2, 12/(L - 5)^3, -6/(L - 5)^2][ 6/(L - 5)^2, 2/(L - 5), -6/(L - 5)^2, 4/(L - 5)]>> %Element1:E=4.0e11,I=bh^3/12=5.2e-7EI=4.0e11*5.2e-7EI =208000>> ke2=EI*subs(ke,'L',10)ke2 =19968 49920 -19968 4992049920 166400 -49920 83200-19968 -49920 19968 -4992049920 83200 -49920 166400>> %由此我们也得到了2号单元的刚度矩阵ke2>> %由于ke1,ke2都是在各自的局部坐标下得到的,所以我们必须把他们向整体坐标系做变换>> %局部坐标系想整体坐标系的转换>> T=eye(4,4) %定义坐标变换矩阵T =1 0 0 00 1 0 00 0 1 00 0 0 1>> %由于局部坐标系与整体坐标系的的夹角为零度,所以得到的T矩阵是一个4行4列的单位阵>> ke1=ke2ke1 =19968 49920 -19968 4992049920 166400 -49920 83200-19968 -49920 19968 -4992049920 83200 -49920 166400>> %由于运算问题,这里必须再次,定义ke1,而我们得到的ke2恰好等于之前的ke1 >> ke1=T*ke1*T';>> ke2=T*ke2*T';>> %系统分析F=[K]u>> %首先我们要在这里对整体刚度矩阵组集:直接法>> G1=...[1 0 0 0 0 00 1 0 0 0 00 0 1 0 0 00 0 0 1 0 0];>> G2=...[0 0 1 0 0 00 0 0 1 0 00 0 0 0 1 00 0 0 0 0 1];>> K1=G1'*ke1*G1K1 =19968 49920 -19968 49920 0 049920 166400 -49920 83200 0 0-19968 -49920 19968 -49920 0 049920 83200 -49920 166400 0 00 0 0 0 0 00 0 0 0 0 0 >> K2=G2'*ke2*G2K2 =0 0 0 0 0 00 0 0 0 0 00 0 19968 49920 -19968 499200 0 49920 166400 -49920 832000 0 -19968 -49920 19968 -499200 0 49920 83200 -49920 166400 >> K=K1+K2K =19968 49920 -19968 49920 0 049920 166400 -49920 83200 0 0 -19968 -49920 39936 0 -19968 4992049920 83200 0 332800 -49920 832000 0 -19968 -49920 19968 -499200 0 49920 83200 -49920 166400>> %引入约束条件>> %v1=0,xta1=0相当于>> K(1,:)=0;K(:,1)=0;>> KK =0 0 0 0 0 00 0 0 0 0 00 0 39936 0 -19968 499200 0 0 332800 -49920 832000 0 -19968 -49920 19968 -499200 0 49920 83200 -49920 166400 >>F=[0 0 0 0 -100 0]' %节点外载荷F =-100>>%求解系统方程,得到所有节点的位移>>%排除V1,与Xta1的影响>> KX=K(3:6,3:6)KX =39936 0 -19968 499200 332800 -49920 83200-19968 -49920 19968 -4992049920 83200 -49920 166400>> FX=F(3:6,1)FX =-100>> u=inv(KX)*FXu =-0.0501-0.0180-0.1603-0.0240>>%上述得到了2,3节点的挠曲与转角其中中间点(2)的挠曲与转角位:-0.1603 -0.0240右端点(3)的挠曲与转角位:-0.0501 -0.01805.参考文献:1.弹性力学与及有限元法基础教程韩清凯孙伟编著东北大学出版社2009.062.百度文库魏磊学号:200818932011.04~05。

计算力学(有限元方法部分) 程序设计程序说明书程序1:平面问题的有限元分析文件名:h01.m算例文本:h01.txt输出文本:result1.txt使用前请先将h01.txt放入默认的文本读取路径(我的要求与m文件在同一文件夹内)!文本输入顺序:材料信息(编号、弹性模量、泊松比)注意:材料编号须按1、2、3、4……的顺序排列节点信息(编号、x坐标、y坐标)注意:节点编号须按1、2、3、4……的顺序排列约束信息(约束节点号、x方向有无约束、y方向有无约束、x方向位移、y 方向位移)有约束处填一正数,无约束处填0。
无约束处请勿输入位移。
单元信息(厚度、材料编号、节点编号,若为3节点单元,则第四个编号填0)注意:单元编号须按1、2、3、4……的顺序排列集中力(作用节点号、x方向力、y方向力)线荷载(作用边上的两个节点号、x方向分布力、y方向分布力)面荷载(作用单元号、x方向分布力、y方向分布力)程序可调部分:4-6行中可以指定输出哪些图像(按顺序依次为节点、单元图像,x、y方向位移图像,xx、yy、xy方向应力图像),第7行中可以指定输入的.txt文本名称。
文本输出内容:结点位移信息(节点号、x方向位移、y方向位移)单元形心处的应变信息(单元号、x方向正应变、y方向正应变、xy方向工程切应变)单元形心处的应力信息(单元号、x方向正应力、y方向正应力、xy方向切应力)本程序附有三角形单元自动加密前处理部分h01auto.m,其算例文本:h01coarse.txt,输出文本:h01new.txt。
它可以适用于本题的要求,在已给定本题所需全部信息的情况下将已有的单元加密为三角形单元。
其输出文本可直接作为上面程序的输入文本。
h01.m h01.txt h01auto.m h01coarse.txt欢迎交流与提问!附上邮箱:***************。
祝力学学习顺利!。
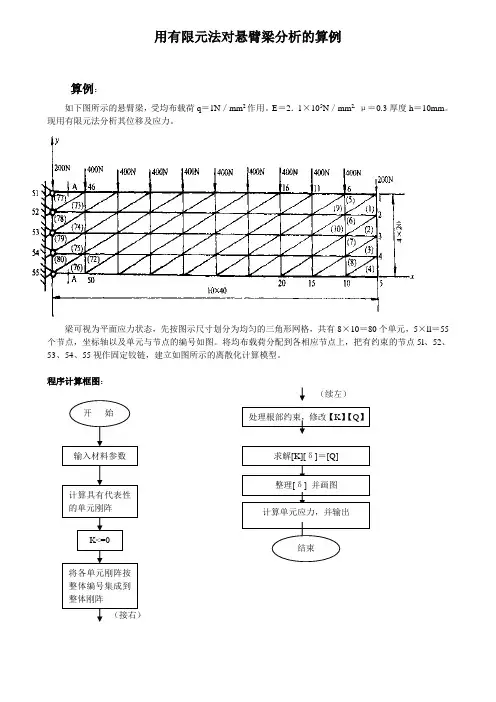
用有限元法对悬臂梁分析的算例算例:如下图所示的悬臂梁,受均布载荷q =1N /mm 2作用。
E =2.1×105N /mm 2, μ=0.3厚度h =10mm 。
现用有限元法分析其位移及应力。
梁可视为平面应力状态,先按图示尺寸划分为均匀的三角形网格,共有8×10=80个单元,5×ll =55个节点,坐标轴以及单元与节点的编号如图。
将均布载荷分配到各相应节点上,把有约束的节点5l 、52、53、54、55视作固定铰链,建立如图所示的离散化计算模型。
程序计算框图:(续左)(接右)开 始 输入材料参数 计算具有代表性的单元刚阵 K<=0 将各单元刚阵按整体编号集成到整体刚阵 处理根部约束,修改【K 】【Q 】 求解[K][δ]=[Q] 整理[δ] 并画图计算单元应力,并输出结束程序中的函数功能介绍及源代码1. LinearTriangleElementStiffness(E,NU,t,xi,yi,xj,yj,xm,ym)――该函数用于计算平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)、第二个节点坐标为(xj,yj)、第三个节点坐标为(xm,ym)时的线性三角形元的单元刚度矩阵.该函数返回6×6的单位刚度矩阵k.2. LinearTriangleAssemble(K,k,i,j,m)――该函数将连接节点i,j,m的线性三角形元的单元刚度矩阵k集成到整体刚度矩阵K。
每集成一个单元,该函数都将返回2N×2N的整体刚度矩阵K.3. LinearTriangleElementStresses(E,NU,t,xi,yi,xj,yj,xm,ym,u)-- 该函数计算在平面应力情况下弹性模量为E、泊松比为NU、厚度为t、第一个节点坐标为(xi,yi)第二个节点坐标为(xj,yj)、第三个节点坐标为(xm,ym)以及单元位移矢量为u时的单元应力。

平面梁单元MATLAB有限元程序function []=beam2n()clear allclose allclearclose%------------------------ BEAM2 ---------------------------disp('========================================'); disp(' PROGRAM BEAM2 '); disp(' Beam Bending Analysis '); disp(' T.R.Chandrupatla and A.D.Belegundu '); disp('========================================');InputData;Bandwidth;Stiffness;ModifyForBC;BandSolver;ReactionCalc;Output;%------------------------ function InputData ---------------------------function [] = InputData();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal TITLE FILE1 FILE2global LINP LOUTglobal NQdisp(blanks(1));FILE1 = input('Input Data File Name ','s'); LINP = fopen(FILE1,'r');FILE2 = input('Output Data File Name ','s'); LOUT = fopen(FILE2,'w');DUMMY = fgets(LINP);TITLE = fgets(LINP);DUMMY = fgets(LINP);TMP = str2num(fgets(LINP));[NN, NE, NM, NDIM, NEN, NDN] =deal(TMP(1),TMP(2),TMP(3),TMP(4),TMP(5),TMP(6));NQ = NDN * NN;DUMMY = fgets(LINP);TMP = str2num(fgets(LINP));[ND, NL, NMPC]= deal(TMP(1),TMP(2),TMP(3));NPR=1; % E%----- Coordinates -----DUMMY = fgets(LINP);for I=1:NNTMP = str2num(fgets(LINP));[N, X(N,:)]=deal(TMP(1),TMP(2:1+NDIM)); end%----- Connectivity -----DUMMY = fgets(LINP);for I=1:NETMP = str2num(fgets(LINP));[N,NOC(N,:), MAT(N), SMI(N)] = ...deal(TMP(1),TMP(2:1+NEN), TMP(2+NEN), TMP(3+NEN));end%----- Specified Displacements ----- DUMMY = fgets(LINP); for I=1:NDTMP = str2num(fgets(LINP));[NU(I,:),U(I,:)] = deal(TMP(1), TMP(2)); end%----- Component Loads -----DUMMY = fgets(LINP);F = zeros(NQ,1);for I=1:NLTMP = str2num(fgets(LINP));[N,F(N)]=deal(TMP(1),TMP(2)); end%----- Material Properties ----- DUMMY = fgets(LINP);for I=1:NMTMP = str2num(fgets(LINP));[N, PM(N,:)] = deal(TMP(1), TMP(2:NPR+1));end%----- Multi-point Constraints B1*Qi+B2*Qj=B0if NMPC > 0DUMMY = fgets(LINP);for I=1:NMPCTMP = str2num(fgets(LINP));[BT(I,1), MPC(I,1), BT(I,2), MPC(I,2), BT(I,3)] = ...deal(TMP(1),TMP(2),TMP(3),TMP(4),TMP(5));endendfclose(LINP);%------------------------ function Bandwidth ---------------------------function []=Bandwidth();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBW global X NOC F AREA MAT SMI S global PM NU U MPC BT STRESS REACT global CNSTglobal TITLE FILE1 FILE2global LINP LOUT%----- Bandwidth Evaluation ----- NBW = 0;for N=1:NENABS = NDN*(abs(NOC(N, 1) - NOC(N, 2)) + 1);if (NBW < NABS)NBW = NABS;endendfor I=1:NMPCNABS = abs(MPC(I, 1) - MPC(I, 2)) + 1;if (NBW < NABS)NBW = NABS;endenddisp(sprintf('Bandwidth = %d', NBW));%------------------------ function Stiffness ---------------------------function []=Stiffness();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBW global X NOC F AREA MAT SMI S global PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Global Stiffness Matrix S = zeros(NQ,NBW);for N = 1:NEdisp(sprintf('Forming Stiffness Matrix of Element %d', N));%-------- Element Stiffness and Temperature Load -----N1 = NOC(N, 1);N2 = NOC(N, 2);M = MAT(N);EL = abs(X(N1) - X(N2));EIL = PM(M, 1) * SMI(N) / EL^3;SE(1, 1) = 12 * EIL;SE(1, 2) = EIL * 6 * EL;SE(1, 3) = -12 * EIL;SE(1, 4) = EIL * 6 * EL;SE(2, 1) = SE(1, 2);SE(2, 2) = EIL * 4 * EL * EL;SE(2, 3) = -EIL * 6 * EL;SE(2, 4) = EIL * 2 * EL * EL;SE(3, 1) = SE(1, 3);SE(3, 2) = SE(2, 3);SE(3, 3) = EIL * 12;SE(3, 4) = -EIL * 6 * EL;SE(4, 1) = SE(1, 4);SE(4, 2) = SE(2, 4);SE(4, 3) = SE(3, 4);SE(4, 4) = EIL * 4 * EL * EL;disp('.... Placing in Global Locations'); for II = 1:NENNRT = NDN * (NOC(N, II) - 1);for IT = 1:NDNNR = NRT + IT;I = NDN * (II - 1) + IT;for JJ = 1:NENNCT = NDN * (NOC(N, JJ) - 1);for JT = 1:NDNJ = NDN * (JJ - 1) + JT;NC = NCT + JT - NR + 1;if (NC > 0)S(NR, NC) = S(NR, NC) + SE(I, J);endendendendendend%------------------------ function ModifyForBC ---------------------------function []=ModifyForBC();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Decide Penalty Parameter CNST ----- CNST = 0;for I = 1:NQif CNST < S(I, 1); CNST = S(I, 1); end endCNST = CNST * 10000;%----- Modify for Boundary Conditions ----- % --- Displacement BC ---for I = 1:NDN = NU(I);S(N, 1) = S(N, 1) + CNST;F(N) = F(N) + CNST * U(I);end%--- Multi-point Constraints ---for I = 1:NMPCI1 = MPC(I, 1);I2 = MPC(I, 2);S(I1, 1) = S(I1, 1) + CNST * BT(I, 1) * BT(I, 1);S(I2, 1) = S(I2, 1) + CNST * BT(I, 2) * BT(I, 2);IR = I1;if IR > I2; IR = I2; endIC = abs(I2 - I1) + 1;S(IR, IC) = S(IR, IC) + CNST * BT(I, 1) * BT(I, 2);F(I1) = F(I1) + CNST * BT(I, 1) * BT(I, 3);F(I2) = F(I2) + CNST * BT(I, 2) * BT(I, 3); end%------------------------ function BandSolver ---------------------------function []=BandSolver();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal NQ%----- Equation Solving using Band Solver ----- disp('Solving using Band Solver(bansol.m)');[F] = bansol(NQ,NBW,S,F);%------------------------ function ReactionCalc ---------------------------function []=ReactionCalc();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTfor I = 1:NDN = NU(I);REACT(I) = CNST * (U(I) - F(N));end%------------------------ function Output ---------------------------function []=Output();global NN NE NM NDIM NEN NDNglobal ND NL NCH NPR NMPC NBWglobal X NOC F AREA MAT SMI Sglobal PM NU U MPC BT REACTglobal CNSTglobal TITLE FILE1 FILE2global LINP LOUTdisp(sprintf('Output for Input Data from file %s\n',FILE1)); fprintf(LOUT,'Output for Input Data from file %s\n',FILE1);disp(TITLE);fprintf(LOUT,'%s\n',TITLE);disp(' Node# X-Displ Rotation');fprintf(LOUT,' Node# X-Displ Rotation\n'); I=[1:NN]';% print a matrixdisp(sprintf(' %4d %15.4E %15.4E\n',[I,F(2*I-1),F(2*I)]')); fprintf(LOUT,' %4d %15.4E %15.4E\n',[I,F(2*I-1),F(2*I)]');%----- Reaction Calculation -----disp(sprintf(' DOF# Reaction'));fprintf(LOUT,' DOF# Reaction\n');for I = 1:NDN = NU(I);R = CNST * (U(I) - F(N));disp(sprintf(' %4d %15.4E',N,REACT(I)));fprintf(LOUT,' %4d %15.4E\n',N,REACT(I)); endfclose(LOUT);disp(sprintf('The Results are available in the text file %s', FILE2));。

有限元大作业——钢架结构分析选题人:日期:2016年6月2日目录:第一章:问题重述 (1)一、题目内容: (1)二、题目要求: (1)第二章:有限元法手工求解 (2)一、平面两单元离散化 (2)二、单元分析 (2)三、单元组装 (5)四、边界条件引入及组装总体方程 (5)五、求解整体刚度方程;计算节点2的位移和转角 (6)六、求节点1、3支撑反力 (6)七、设定数据;求解结果 (7)八、绘制轴力图、弯矩图、剪力图 (8)第三章、matlab编程求解: (9)一、总体流程图绘制: (9)二、输入数据: (9)三、计算单元刚度矩阵: (10)四、建立总体刚度矩阵: (10)五、计算未约束点位移: (10)六、计算支反力: (10)七、输出数据: (10)八、编程: (10)第四章有限元求解 (10)一、预处理 (11)二、模型建立: (12)二、分析计算 (14)三、求解结果 (15)四、绘制图像 (16)第五章结果比较 (19)第六章心得体会 (19)一、王小灿: ...................................................................................................................... 错误!未定义书签。
二、孙明哲: ...................................................................................................................... 错误!未定义书签。
三、张国威 .......................................................................................................................... 错误!未定义书签。
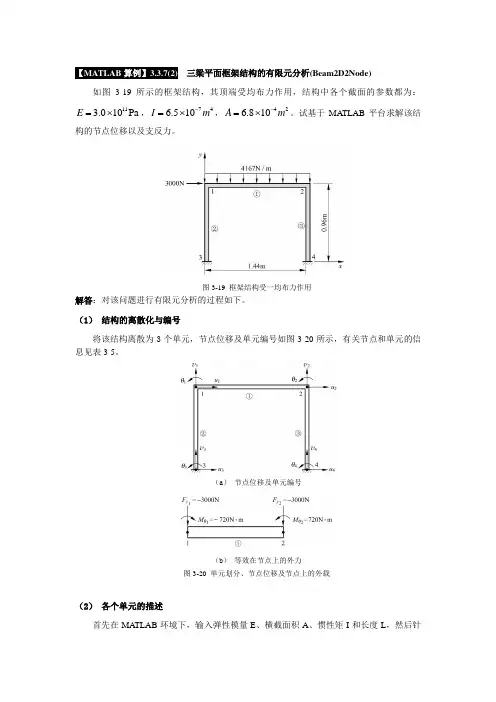
【MATLAB 算例】3.3.7(2) 三梁平面框架结构的有限元分析(Beam2D2Node)如图3-19所示的框架结构,其顶端受均布力作用,结构中各个截面的参数都为:113.010Pa E =⨯,746.510I m -=⨯,426.810A m -=⨯。
试基于MA TLAB 平台求解该结构的节点位移以及支反力。
图3-19 框架结构受一均布力作用解答:对该问题进行有限元分析的过程如下。
(1) 结构的离散化与编号将该结构离散为3个单元,节点位移及单元编号如图3-20所示,有关节点和单元的信息见表3-5。
(a ) 节点位移及单元编号(b ) 等效在节点上的外力图3-20 单元划分、节点位移及节点上的外载(2) 各个单元的描述首先在MA TLAB 环境下,输入弹性模量E 、横截面积A 、惯性矩I 和长度L ,然后针对单元1,单元2和单元3,分别二次调用函数Beam2D2Node_ElementStiffness ,就可以得到单元的刚度矩阵k1(6×6)和k2(6×6),且单元2和单元3的刚度矩阵相同。
>> E=3E11;>> I=6.5E-7;>> A=6.8E-4;>> L1=1.44;>> L2=0.96;>> k1=Beam2D2Node_Stiffness(E,I,A,L1);>> k2=Beam2D2Node_Stiffness(E,I,A,L2);(3) 建立整体刚度方程将单元2和单元3的刚度矩阵转换成整体坐标下的形式。
由于该结构共有4个节点,则总共的自由度数为12,因此,结构总的刚度矩阵为KK(12×12),对KK 清零,然后两次调用函数Beam2D2Node_Assemble 进行刚度矩阵的组装。
>> T=[0,1,0,0,0,0;-1,0,0,0,0,0;0,0,1,0,0,0;0,0,0,0,1,0;0,0,0,-1,0,0;0,0,0,0,0,1];>> k3=T'*k2*T;>> KK=zeros(12,12);>> KK=Beam2D2Node_Assemble(KK,k1,1,2);>> KK=Beam2D2Node_Assemble(KK,k3,3,1);>> KK=Beam2D2Node_Assemble(KK,k3,4,2)KK = 1.0e+008 *1.4431 0 0.0127 -1.4167 0 0 -0.0264 0 0.0127 0 0 0 02.1328 0.0056 0 -0.0078 0.0056 0 -2.1250 0 0 0 0 0.0127 0.0056 0.0135 0 -0.0056 0.0027 -0.0127 0 0.0041 0 0 0 -1.4167 0 0 1.4431 0 0.0127 0 0 0 -0.0264 0 0.0127 0 -0.0078 -0.0056 0 2.1328 -0.0056 0 0 0 0 -2.1250 0 0 0.0056 0.0027 0.0127 -0.0056 0.0135 0 0 0 -0.0127 0 0.0041 -0.0264 0 -0.0127 0 0 0 0.0264 0 -0.0127 0 0 0 0 -2.1250 0 0 0 0 0 2.1250 0 0 0 0 0.0127 0 0.0041 0 0 0 -0.0127 0 0.0081 0 0 0 0 0 0 -0.0264 0 -0.0127 0 0 0 0.0264 0 -0.0127 0 0 0 0 -2.1250 0 0 0 0 0 2.1250 0 0 0 0 0.0127 0 0.0041 0 0 0 -0.0127 0 0.0081(4) 边界条件的处理及刚度方程求解该问题的位移边界条件为0444333======θθv u v u 。

基于MATLAB的有限元结构分析王剑(重庆交通大学土木建筑学院,重庆400074)摘要: MATLAB 是当今国际科学界最具影响力和活力的软件。
文章介绍了MATLAB 语言的特点,详细介绍了用MATLAB语言编写结构内力的有限元方法,并通过实例对平面钢架结构进行了内力分析。
关键词:MATLAB 有限元结构0引言MATLAB是Mathworks公司推出的,集算法开发、数值运算、符号运算以及图形处理等强大功能于一体的高级技术计算语言和交互式环境。
MATLAB意为矩阵实验室,它将数值分析、矩阵计算、科学数据可视化以及非线性动态系统的建模和仿真等诸多强大功能集成在一个易于使用的视窗环境中,为科学研究、工程设计以及必须进行有效数值计算的众多科学领域提供了一种全面的解决方案,并在很大程度上摆脱了传统非交互式程序设计语言的编辑模式,代表了当今国际科学计算软件的先进水平。
有限元法的基本思想是将物体(即连续求解域)离散成有限个且按一定方式相互连接在一起的单元组合,来模拟和逼近原来的物体,从而将一个连续的无限自由度问题简化为离散的有限自由度问题求解的数值分析法。
有限元法还有一个特点是,它的理论采用矩阵形式表达。
这并不利于一般的计算机语言编制计算机程序,因为传统的计算机语言处理的对象是标量,使用矩阵形式的有限元理论时,必须把矩阵形式的公式转换成标量表示的公式。
而如果采用MATLAB,这个特点就变成了有限元法的优点,运算更便捷。
1运用MATLAB编写有限元程序的操作步骤1.1建立有限元模型建立有限元模型就是为求解有限元模型做铺垫。
需要对节点、单元以及材料的定义。
同时对约束条件、集中力、分布力进行定义。
然后在M函数文件中以矩阵或向量的形式输入单元号、节点数、材料的性质、约束条件、集中力、分布力。
1.2求解有限元模型用MATLAB写出每个单元的单元刚度矩阵。
按照刚度集成法,把各个单元的刚度矩阵分别放到整体刚度矩阵中的相应位置上,然后根据边界条件进行修正得到整体刚度矩阵。

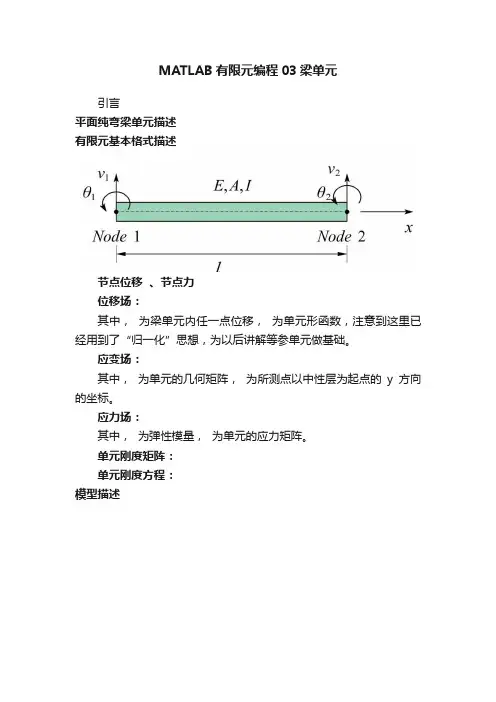
MATLAB有限元编程03梁单元引言平面纯弯梁单元描述有限元基本格式描述节点位移、节点力位移场:其中,为梁单元内任一点位移,为单元形函数,注意到这里已经用到了“归一化”思想,为以后讲解等参单元做基础。
应变场:其中,为单元的几何矩阵,为所测点以中性层为起点的y方向的坐标。
应力场:其中,为弹性模量,为单元的应力矩阵。
单元刚度矩阵:单元刚度方程:模型描述Matlab编程:% 公众号:易木木响叮当,回复梁单元,即可自动获取。
function k =Beam1D2Node_Stiffness(E,I,L)% 直接组装梁单元刚度k = E*I/(L*L*L)*[12 6*L -12 6*L6*L 4*L*L -6*L 2*L*L-12 -6*L 12 -6*L6*L 2*L*L -6*L 4*L*L];function z = Beam1D2Node_Assembly(KK,k,i,j)% 该函数进行整体刚度矩阵的组装% 输入单元刚度矩阵k,单元的节点编号i、j% 输出整体刚度矩阵KKDOF(1)=2*i-1;DOF(2)=2*i;DOF(3)=2*j-1;DOF(4)=2*j;for n1=1:4for n2=1:4KK(DOF(n1),DOF(n2))= KK(DOF(n1),DOF(n2))+k(n1,n2); endendz=KK;function v = Beam1D2Node_Deflection(x,L,u)% 该函数计算单元内某点的挠度% 输入所测点距梁单元左节点的水平距离x% 输入梁单元的长度L,节点位移列阵ue=x/L;N1=1-3*e*e+2*e*e*e;N2=L(e-2*e*e+e*e*e);N3=3*e*e-2*e*e*e;N4=L(e*e*e-e*e);N=[N1,N2,N3,N4];v=N*u% -----------主程序----------------format compactE = 200*10^9;I = 118.6*10^-6;L1 = 5;L2 = 2.5;% cal element stiffnessk1 = Beam1D2Node_Stiffness(E,I,L1);k2 = Beam1D2Node_Stiffness(E,I,L2);% stiffness assemblyKK = zeros(6,6);KK = Beam1D2Node_Assembly(KK,k1,1,2);KK = Beam1D2Node_Assembly(KK,k2,2,3)% cal displacementk = KK(4:6,4:6);p = [39062;-31250;13021];u = k\p% cal node forceU = [0;0;0;u];P = KK*U% cal RFF = [-62500;-52083;-93750;39062;-31250;13021];RF = P-F最终计算得到的支反力、节点位移值与书中解析解一致,可自行验证。
matlab编译平面有限元计算编译平面有限元计算是一种常用的数值计算方法,可以用于求解各种复杂的工程问题。
在本文中,我们将介绍如何使用MATLAB编写平面有限元计算程序,并通过一个实例来说明其应用。
让我们了解一下有限元方法的基本原理。
有限元方法是一种将连续体划分为有限个单元,根据物理方程和边界条件,在每个单元上建立离散方程组,最终求解得到整个连续体的近似解的方法。
在平面问题中,连续体被划分为三角形或四边形单元。
MATLAB是一种功能强大的数值计算软件,它提供了丰富的工具箱和函数,可以方便地进行有限元计算。
下面我们将以求解平面弹性力学问题为例,介绍如何使用MATLAB编写平面有限元计算程序。
我们需要定义问题的几何信息、边界条件和材料参数。
在MATLAB中,可以通过定义节点坐标、单元连接关系、边界条件和材料参数来描述问题。
节点坐标可以用一个矩阵表示,其中每一行代表一个节点的坐标。
单元连接关系可以用一个矩阵表示,其中每一行代表一个单元的节点编号。
边界条件可以用一个向量表示,其中每个元素代表一个节点的边界条件。
材料参数可以用一个矩阵表示,其中每一行代表一个单元的材料参数。
接下来,我们需要建立有限元离散方程组。
在平面弹性力学问题中,离散方程组可以通过组装单元刚度矩阵和外力向量得到。
单元刚度矩阵可以通过单元的几何信息和材料参数计算得到。
外力向量可以根据边界条件和载荷信息计算得到。
最终,我们可以通过求解离散方程组得到节点的位移解。
我们可以根据节点的位移解计算出单元的应力和应变。
在平面弹性力学问题中,应力可以通过单元的几何信息和位移解计算得到。
应变可以通过应力和材料参数计算得到。
通过计算应力和应变,我们可以评估结构的稳定性和性能。
MATLAB编译平面有限元计算程序是一种强大的工具,可以用于求解各种复杂的工程问题。
通过定义几何信息、边界条件和材料参数,建立有限元离散方程组,求解得到节点的位移解,最终计算出单元的应力和应变。
一维梁的M A T L A B有限元法分析问题如下:梁A B在A和B两端固定,中间点表示为C,在中间区域承受均匀分布的载荷q,如图所示。
梁A B的抗弯刚度为E I。
1,使用R i t z法确定点C处的位移和弯矩,并讨论随着包含更多基本函数的准确性。
提示:根据偏转曲线的形状,可以选择基函数的形式,其中系数,并且应该由点A或B处的边界条件确定。
2,采用一维有限元法解决问题,并讨论网格越细时的准确性。
提示:使用1-D梁单元。
1R i t z法一维欧拉-伯努利梁的势能如下:设选择基函数,容易看出基函数满足边界条件设,代入势能表达式得到由于三角函数是正交函数系,所以得到令q=10N/m m,E=200000M P a,I=10000,L=200m m在M A T L A B中计算A k前十项得到A=-0.008400754770396-0.000320811945459-0.000049922673823 -0.000020050746591-0.000009258470170-0.000003960641302 -0.000001943426801-0.000001253171662-0.000000837688763 -0.000000513299113计算C点位移,使用1-10个试函数结果如下:0.0084007547703960.0084007547703960.0085006001180410.0085006001180410.0085191170583800.0085191170583800.0085230039119830.0085230039119830.0085246792895100.008524679289510计算C点弯矩,,使用1-10个试函数结果如下:0.8291212625436840.7024697829907620.746814316705690 0.7151514468174600.7379958063005830.723923419683592 0.7333220380018130.7254063205297550.732103122461494 0.727037063279377可以看到,位移收敛是很快的,弯矩收敛速度慢于位移。
matlab 有限元法
Matlab中的有限元法(Finite Element Method,FEM)是一种常用的数值分析方法,用于模拟和解决包括结构力学、热传导、流体力学等问题。
它将连续介质划分为离散的有限单元,通过建立数学模型和使用近似解法来求解。
下面是一般步骤来使用Matlab进行有限元分析:
1. 剖分网格:将要模拟的连续介质划分为离散的有限单元(如三角形或四边形元素)。
2. 建立数学模型:根据具体问题的物理方程或导引方程,建立线性或非线性的方程模型。
3. 施加边界条件:确定并施加边界条件,如位移、载荷或约束等。
4. 组装刚度矩阵和载荷向量(Assembly):通过元素刚度矩阵的组装,得到总系统的刚度矩阵和载荷向量。
5. 求解方程:通过求解总系统的线性方程组,得到未知位移或其他需要的结果。
6. 后处理结果:对求解结果进行可视化或分析,如绘制应力分布、位移云图、应变曲线等。
Matlab提供了丰富的工具箱和函数,用于各种结构和物理问题的有限元分析,例如Partial Differential Equation Toolbox(部分微分方程工具箱)和Structural Analysis T oolbox(结构分析工具箱),其中包含了常用的有限元分析函数和设置界面。
另外,Matlab还支持用户自定义编程,允许使用脚本或函
数来实现特定的有限元算法。
总之,通过Matlab的有限元分析工具和编程能力,可以方便地进行各种结构和物理问题的数值分析和模拟。
前处理程序
clear;clc
XY = [1, 0, 0
2, 2, 0
3, 2, -2]; %XY为N行3列,N为节点总数
ELB = [1, 1, 2, 1
2, 2, 3, 1]; %ELB为MB行4列,MB为单元总数
b = 4.5e-2;
h = 2e-1; %截面宽b和高h
A1 = b*h;
IZ1 = 3e-5; %惯性矩
EAIZ = [200e9, A1, IZ1]; %弹性模量与截面积和惯性矩
ELPQ = [1, 1, -2e4, 2
2, 1, -1e4, 2]; %ELPQ第一列为受载荷单元号,第二列为长度C(见下表),三列为载荷大小,四列为载荷类型
SU = [1,0
2, 0
3,0]; %SU第一列为已知节点位移对应的方程号,第2列为节点位移数值,约束即等于0
子程序1
function [PO, ii, jj] = dxjd(ELB, XY, ELPQ1)
PO = zeros(6,1);
k = ELPQ1(1);
jj = ELB(k, 3);
dxy = [XY(ii, 2), XY(ii, 3)
XY(jj, 2), XY(jj, 3)];
DY = dxy(2,2) - dxy(1,2);
DX = dxy(2,1) - dxy(1,1);
L = sqrt(DX^2 + DY^2);
C = ELPQ1(2);
Q = ELPQ1(3);
type = ELPQ1(4);
switch type
case 1
PO(2) = PO(2) + 0.5*Q*C*(2-2*C^2/L^2 + C^3/L^3);
PO(3) = PO(3) + Q*C^2*(6-8*C/L+3*C^2/L^2)/12;
PO(5) = PO(5)+Q*C-PO(2);
PO(6) = PO(6) - Q*C^3*(4-3*C/L)/12/L;
case 2
D = L - C;
PO(2) = PO(2) + Q*(L+2*C)*D^2/L^3;
PO(3) = PO(3) + Q*C*D^2/L^2;
PO(5) = PO(5) + Q-PO(2);
PO(6) = PO(6) + Q*D*C^2/L^2;
case 3
D = L - C;
PO(1) = PO(1) + Q*D/L;
PO(4) = PO(4) + Q*C/L;
case 4
PO(2) = PO(2) + 7*Q*L/20;
PO(3) = PO(3) + Q*L^2/20;
PO(5) = PO(5) + 3*Q*L/20;
PO(6) = PO(6) + Q*L^2/30;
end
子程序2
function [KE, T] = ketb(dxy, E, A, IZ)
DY = dxy(2,2) - dxy(1,2);
DX = dxy(2,1) - dxy(1,1);
L = sqrt(DX^2 + DY^2);
S = DY/L;
C = DX/L;
a1 = IZ/L;
a2 = a1/L;
a3 = E/L;
KE = a3*[A, 0, 0, -A, 0, 0 0, 12*a2, 6*a1, 0, -12*a2, 6*a1
0, 6*a1, 4*IZ, 0, -6*a1, 2*IZ
-A, 0, 0, A, 0, 0
0, -12*a2, -6*a1, 0, 12*a2, -6*a1
0, 6*a1, 2*IZ, 0, -6*a1, 4*IZ]; t = [C, S, 0; -S, C, 0; 0, 0, 1];
t1 = zeros(3,3);
T = [t, t1; t1, t];
end
子程序
function KZ = kztb(XY, ELB, EAIZ)
[N,M] = size(XY);
KZ =zeros(9, 9);
[MB, m] = size(ELB);
for k = 1 :2
ii = ELB(k, 2);
jj = ELB(k, 3);
LTB = ELB(k, 4);
dxy = [XY(ii,2), XY(ii,3)
XY(jj,2), XY(jj,3)];
E = EAIZ(LTB, 1);
A = EAIZ(LTB, 2);
IZ = EAIZ(LTB, 3);
[KE, T] = ketb(dxy, E, A, IZ);
CN = [3*ii-2, 3*ii-1, 3*ii, 3*jj-2, 3*jj-1, 3*jj];
KE = (T')*KE*T;
for i = 1:6
for j = 1:6
KZ(CN(i), CN(j)) = KZ(CN(i), CN(j)) + KE(i, j);
end
end
end
子程序
function U = weiyi(KZ, P, SU)
[LR, m] = size(SU);
for k =1:LR
i = SU(k, 1);
P(i) = 1e10*SU(k, 2);
KZ(i,i) = 1e10*KZ(i, i);
end
U = KZ\P;
end
子程序
function P = ydx(XY, ELB, EAIZ, ELPQ)
[N, m] = size(XY)
P = zeros(3*N, 1)
[LPQ, m] = size(ELPQ)
for j = 1:LPQ
ELPQ1 = ELPQ(j, :)
k = ELPQ(j, 1)
[PO, ii, jj] = dxjd(ELB, XY, ELPQ1)
LTB = ELB(k, 4);
dxy = [XY(ii,2), XY(ii,3)
XY(jj,2), XY(jj, 3)];
E = EAIZ(LTB, 1);
A = EAIZ(LTB, 2);
IZ = EAIZ(LTB, 3);
[KE, T] = ketb(dxy, E, A, IZ );
PO = (T')*PO;
CN = [3*ii-2, 3*ii-1, 3*ii, 3*jj-2, 3*jj-1, 3*jj]
for i = 1:6
P(CN(i)) = P(CN(i)) + PO(i);
end
end
后处理程序
clc;
[N, M] = size(XY);
DU = zeros(N,4);
for i = 1:N
DU(i,1) = i;
DU(i,2) = U(3*i-2);
DU(i,3) = U(3*i-1);
DU(i,4) = U(3*i);
end
[MB, M] = size(ELB);
for i = 1:MB
P1(i, 1) = i;
end
'节点号水平位移竖直位移转角'
DU
主程序
>>GJINPUT;
>>KZ = kztb(XY, ELB,EAIZ);
>>P = ydx(XY, ELB, EAIZ, ELPQ);
>>U = weiyi(KZ, P, SU);
>>GJOUTPUT;
运行结果:
ans =
'节点号水平位移竖直位移转角' DU =
1.0000 -0.0000 -0.0000 -0.0000
2.0000 -0.0000 -0.0111 -0.0100
3.0000 -0.0231 -0.0111 -0.0125。