基于MATLAB的温度模糊控制系统的设计

例 阀控制 器调节 热交 换器 进水 口阀门开度 的过 程 中 ， 以增 加进 水 的 阻力 来 减少 流 体 （ 冻水 ） 是 冷 在
热交换 器 中的流 动 速 度 ， 样 就 以浪 费 一 大 部分 这
冷冻水 的动能来 达 到 调 温 ， 而 浪 费 的这 一 部分 然
动能恰 恰是 中央空 调 的 冷冻 泵 所 给 予 ， 冷 冻泵 而
中 图 分 类 号 ： Ｐ ７ Ｔ ２２ 文献标识码 ： Ａ
Ｄｅ ｉ ｎ ｏ ｎｔ ｏ ｙ ｔ ｍ ｏ ｍ ｐｅ ａ ｕ ｅ ｏ ｎｔａ ｉ‘ ｏ ｄ ｔｏ ｎ ｓｇ ｆＣｏ ｒ ｌＳ ｓｅ ｆ ｒＴｅ ｒ ｔ ｒ ｆＣｅ ｒ ｌＡ ｒｃ ｎ ｉｉ ｎｉ ｇ Ｂａ ｅ ｎ ＶＣ＋＋ ａ ｄＭ ａｌｂ ｓｄ ｏ ｎ ｔ ａ
Ｅ Ｅ Ｔ Ｉ Ｒ ＶＥ ２ ０ Ｖ １３ Ｎ ． ２ Ｌ Ｃ ＲＣＤ Ｉ ０８ ｏ． ８ ｏ １
电 气 传 动 ２ ０ ０ ８年 第 ３ ８卷 第 １ 期 ２
基 于 ＶＣ＋ 和 Ｍａｌｂ的 中央 空 调 温度 ＋ ｔ ａ 控 电 气工程 学院 ， 北京 １ ０ ４ ） ０ ０ ４
电机是 要 消耗 电能 的 ， 就 是 说采 用 比例 阀 调温 也
浪费 了一部 分 的 电 能 。其 次 ， 管风 机 是 以电机 盘 来 驱动 的， 电机是 长期 以满 速 运行 的， 以工频 而 即
Ｋｅ ｒ ｓ ｃ ｎｒ ｌ ｉ－ｏ ｄｔ ｎｎ ｆｚ ｙｃ ｎ ｒ ｌｔｍｐ ｒ ｔｒ ； ｙｗｏｄ ：ｅ ｔａ ｒｃ ｎ ｉｉ ｉｇ；ｕ ｚ ｏ ｔｏ ；ｅ ｅ ａｕ ｅ ＶＣ＋＋ ＆ Ｍ ａｌｂ ｅ ｅ ｇ ａ ｉｇ ａ ｏ ｔａ ； ｎ ｒ ｙ ｓｖｎ
近 年来 ， 随着 高 层 建筑 的兴 起 和人 们 生 活 水

｛ 鳓
｛ｔ｛ 蟪 《 ＃《
一
优点 ． 而且算 法简单 。但是 。 由于房间 温
度 变 化 缓 慢 ． 能 出 现 长 时 间 偏 差 较 大 可 的 情 况 。 导 致 积 分 饱 和 ： 外 ． 缩 机 会 另 压 的正 常运行 转 速也 是有 一 定 的范 围 的 ．
删
一
５
、
处 于待 机 状 态 ， 房 间 的温 升 Ｔ（ 与 则 ｏ Ｃ） 压缩 机运转 频率 ｎ Ｈ ） 的传 递 函数 的 （ ｚ间
形 式 见 式 （ ） 示 。其 中 ’ 延 迟 时 间 １所 Ｔ为 （）Ｔ 为 时 间 常 数 （ ）Ｉ 为 放 大 系 数 。 Ｓ ；ｏ ｓ；０ ＜ Ｇ （） ０ｓ＝ ＝ ｅ （） １
在 Ｍａｌ 下 建 立 Ｓｍｕｉｋ仿 真 框 ｔｂ ａ ｉ ｌ ｎ
图 （ 图 １ 见 ）
１０ ． ８ ｓ 将延 迟 时 间改 为 １０ ｓ 则 压缩 机 ２０ ． 的工 作频 率 波动 较大 ． 温度 响应 也 有轻
应用 最 为广 泛 的一 种 控制 方法 ． 不仅 使 用方 便 ． 对受 控 对象 特性 的轻微 变化 也 不敏 感 ． 其调 控 品质 能够 满 足大 多数 的 应用要 求 空调控 制系统 中常用 的有 双 位调 节器 、 节 器 、 Ｉ Ｐ调 Ｐ 调节 器 等 ， 般 一
取 ＂ １０ ，ｏ １０ ｓＫ ＝ ． Ｃ Ｈｚ ｒ ２ ｓＴ ＝ ８０ ， ｏ ０３ ／ ， ＝ ￣
图 ２ Ｐ 控 制 系统 仿 真 结 果 Ｉ
则 传递 函数 为 ：
Ｇ （） ｏｓ＝ ｅ （） ２
另外 ． 在仿 真过程 中 ． 分别 修改房 间 模 型的 时 间常数 和延 迟 时 间 ． 控制 性能

论教学和科研的典型对象 ， 主要通过软件仿真或在精密倒立摆上实现各种控制算法 ， 而对于倒立摆硬 件系统开发的相关报道甚少。 目前 ， 国内各高校基本上都采用香港 固高公 司和加拿大 Ｑ ａｓ 公司 ｕｎｅ ｒ 生产的系统 ， 由于采用高精度的零部件 ， 硬件成本较高 ； 而其软件大多采用 ｖ ｃ等可视化编程软件来 开 发 ， 发周 期 长 ， 且 不提 供 源代 码 ， 乏可 读性 和再 利用 性 。 研 并 缺 本文介绍一种倒立摆的软硬件系统的开发 ， 其硬件系统具有低成本、 高可靠性和稳定性等优点 ； 其 软件 系统 在 Ｍａａ ｔ ｂ环境 下 进行 编 程 和实 时 控 制 ， 代码 完 全开 放 ， ｌ 源 而且 可 调 用 丰 富 的 Ｍａｌ ｔｂ工 具 ａ
维普资讯
第２ ７卷 第 ３期
湖北 师范学院学报 （ 自然科学版 ）
Ｊｕ ａ ｏ ｂｉ ｏｍ ｌＵ ｉｅ ｉ （ ａ ｒ ｃ ｎｅ ｏ ｒｌ ｆ ｎ Ｈｕ ｅ Ｎ ｒ ａ ｎ ｒ ｔ Ｎ ｔ ａ Ｓ ｉ ｃ） ｖ ｓｙ ｕｌ ｅ
Ｖ０． ７ １２
中图分类号 ：Ｐ ７ Ｔ ２３
文献标 识码 ： Ａ
文章编号 ：０９２ １ （０ ７ ０ ． ０ ９ ０ １０ －７ ４ ２ ０ ）３ ０ ７ ． ５
０ 引 言
倒 立摆 系统 是 一种 是 非最 小 相位 系统 ， 它具 有非 线 性 、 多变 量 和不 稳 定 的特 点 ， 而成 为 控制 理 因
・
７ ・ ９
维普资讯
表 １ 一级 水平倒立摆硬件 系统主 块与摆杆
力矩电机
说 明
自制 北京 勇光高特微 电机有 限公司 自制 自制
ＮＩ ＥＣ ＮＥＭＩ ０Ｎ Ｃ０ Ｄ Ｃ ＲＰ．

收稿 日期 ： ０ ５ ０ ２ ２ ０ ７ ２ 基金项 目：上海工程技术大学青年基金资助项 目（０ ２ ０ ） ２ ０ Ｑ ２
制器设计模糊 控制器 Ｉ
温度模糊控制器采用以房间温度变化和温度 变化率为输入变量 ， 以压缩机转速为输 出变量的双 输入单输 出结构。其设计 内容主要包括 ：１ （ ）确定
维普资讯
第２ ０卷第 １ 期 ２０ ０ ６年 ３月
上
海
Ｔ ｌ
程
技
术
大
学
学
报
Ｖｏ． ０ Ｎｏ １２ １ Ｍ ａ ．２ ０６ ｒ ０
Ｊ ＯＵＲＮ ， Ｆ Ｓ ＡＮ ＩＵＮＩ Ｒ Ｉ Ｙ （ ＧＩ Ｅ Ｎ ｓ ｌ ｃ ＡｌＯ Ｈ （ＨＡ ＶＥ Ｓ Ｔ ） ＥＮ ＮＥ ＲＩ Ｇ Ｃ Ｅ Ｆ
ｅ ｓｌ ａ ｒ ｄｏ ｔ ａｉ ｃ ｒｉ ｕ ． ｙ ｅ Ｋ ｙｗｏ ｄ ：ｆ ｚｙ ｃ ｎ ｒ ｌ ｅ ｒ ｓ ｕ ｚ ｏ ｔｏ ；ＦＩ Ｓ；Ｓｍｕｉｋ ｉ ｌ ｎ
模糊控制是一种基 于语言规则和模糊推理的 控制方法， 采用人类 的语言语句表述 ， 较为直观 ， 也 易于理解 ， 可以对非线性 、 大惯性 、 大滞后对象以及
下半部 的右侧 白框内输入“ 压缩机转速 ”为输出语 （ 言变量 ｏ ｔｕ 重新 命 名 ） ｕｐ ｔ 。在 下半 部 左 侧 为 “ ” 与 、 “ 、蕴涵”模糊规则的合成运算 以及解模糊选 或”“ 、
图 １ 模糊推理 系统 图形 编辑器
Ｆ ｇ １ Ｆ Ｓ Ｅｄ ｔ ｒ ｉ ． Ｉ ｉ ｏ
难以建立数学模型 的对 象取得较好 控制效果… 。 １
但 由于模糊控制器 ｝计过程 中存在诸多主观因素， 殳
如隶属度确定 、 控制规则构造等， 使得 控制 系统需 要反复调试才能达到较好的鲁棒性和适应性。因 此， 利用计算机预先对模糊控制器进行仿真研究显

用 Matlab 的 Fuzzy 工具箱实现模糊控制Matlab, Fuzzy, 模糊控制, 工具箱用Matlab 中的Fuzzy 工具箱做一个简单的模糊控制，流程如下：1、创建一个FIS (Fuzzy Inference System ) 对象，a = newfis(fisName,fisType,andMethod,orMethod,impMethod, aggMethod,defuzzMethod)一般只用提供第一个参数即可，后面均用默认值。

2、增加模糊语言变量a = addvar(a,'varType','varName',varBounds)模糊变量有两类：input 和output。

在每增加模糊变量，都会按顺序分配一个index，后面要通过该index 来使用该变量。

3、增加模糊语言名称，即模糊集合。

a = addmf(a,'varType',varIndex,'mfName','mfType',mfParams)每个模糊语言名称从属于一个模糊语言。

Fuzzy 工具箱中没有找到离散模糊集合的隶属度表示方法，暂且用插值后的连续函数代替。

参数mfType 即隶属度函数(Membership Functions)，它可以是Gaussmf、trimf、trapmf等，也可以是自定义的函数。

每一个语言名称也会有一个index，按加入的先后顺序得到，从 1 开始。

4、增加控制规则，即模糊推理的规则。

a = addrule(a,ruleList)其中ruleList 是一个矩阵，每一行为一条规则，他们之间是ALSO 的关系。

假定该FIS 有N 个输入和M 个输出，则每行有N+M+2 个元素，前N 个数分别表示N 个输入变量的某一个语言名称的index，没有的话用0 表示，后面的M 个数也类似，最后两个分别表示该条规则的权重和个条件的关系，1 表示AND，2 表示OR。

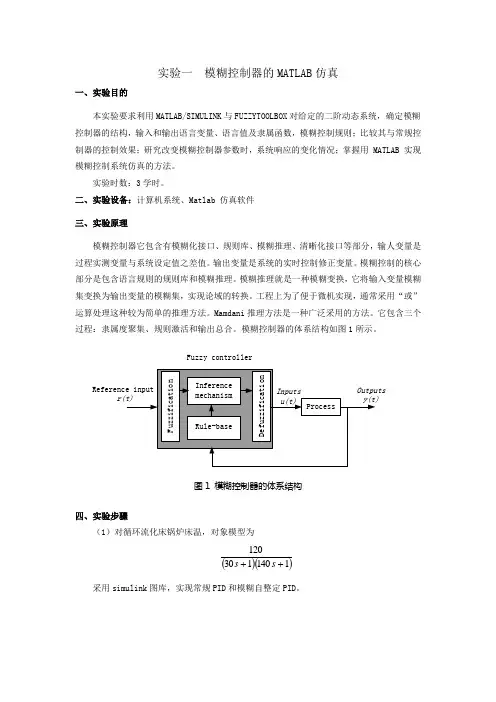
实验一 模糊控制器的MATLAB 仿真一、实验目的本实验要求利用MATLAB/SIMULINK 与FUZZYTOOLBOX 对给定的二阶动态系统，确定模糊控制器的结构，输入和输出语言变量、语言值及隶属函数，模糊控制规则；比较其与常规控制器的控制效果；研究改变模糊控制器参数时，系统响应的变化情况；掌握用 MATLAB 实现模糊控制系统仿真的方法。

实验时数：3学时。

二、实验设备：计算机系统、Matlab 仿真软件 三、实验原理模糊控制器它包含有模糊化接口、规则库、模糊推理、清晰化接口等部分，输人变量是过程实测变量与系统设定值之差值。

输出变量是系统的实时控制修正变量。

模糊控制的核心部分是包含语言规则的规则库和模糊推理。

模糊推理就是一种模糊变换，它将输入变量模糊集变换为输出变量的模糊集，实现论域的转换。

工程上为了便于微机实现，通常采用“或”运算处理这种较为简单的推理方法。

Mamdani 推理方法是一种广泛采用的方法。

它包含三个过程：隶属度聚集、规则激活和输出总合。

模糊控制器的体系结构如图1所示。

图1 模糊控制器的体系结构四、实验步骤（1）对循环流化床锅炉床温，对象模型为()()1140130120++s s采用simulink 图库，实现常规PID 和模糊自整定PID 。

（2）确定模糊语言变量及其论域：模糊自整定PID 为2输入3输出的模糊控制器。

该模糊控制器是以|e|和|ec|为输入语言变量，Kp 、Ki 、Kd 为输出语言变量，其各语言变量的论域如下：误差绝对值：e={0，3，6，10}；误差变化率绝对值：ec={0，2，4，6}；输出Kp：Up={0，0.5，1.0，1.5}；输出Ki：Ui={0，0.002，0.004，0.006}；输出Kd：Ud={0，3，6，9}。

（3）语言变量值域的选取：输入语言变量|e|和|ec|的值域取值“大”(B)、“中”(M)、“小”(s)和“零”(Z) 4种；输出语言变量Kp、Ki、Kd的值域取值为“很大”(VB)、“大”(B)、“中”(M)、“小”(s) 4种。

虽 然是 清 晰值 ，但 其 取 值 范 围 是 由模 糊 推 理得 到 的所 有 模 糊 子 集 确定 的 ， 盖 这些 模 糊 子 集 的数 值 范 围称 为 模 糊 论域 。 个 模 覆 这
糊 论域 和后 面 的执 行 机 构 需 求 的 数值 范 围也 就 是 物 理 论 域 未 必
一
本 文 以 石 灰 窑 的 温 度 控 制 为对 象 ， 用 ＭＡ Ｌ Ｂ设 计 石 灰 运 ＴＡ 窑 温 度控 制 系统 的模 糊 ＰＤ控 制 器 。 过语 言变 量 的模 糊 化 ， Ｉ 通 并 有 机 地 将 ＭＡ Ｌ Ｂ与 Ｓｍｕｉ ＴＡ ｉ ｌｋ结 合 起 来 ， 细 介绍 了模 糊 ＰＤ ｎ 详 ｌ 控 制 器 的设 计 过 程 ， 对 其 控 制 性 能进 行 了仿 真 。 并
《 工业 控制 计 算 机 ｝ ０ ２年 第 ２ ２１ ５卷第 ３期
基于 ＭＡ Ｌ Ｂ的石灰窑模糊控制器设计 ＴＡ
Ｆ ｚ ｙ — ｏ ｔ ｌ ｒ Ｄｅ ｉ ｏ ｉ ｋｌ－ ｓ ｄ ｏ ｕ ｚ — ｎ ｒ ｌ ｓｇｎ ｆ ｒ Ｌｍｅ ｉ Ｂａ ｅ ｎ ＭＡＴ ＡＢ ｃ ｏｅ ｎ Ｌ
在模 糊 控 制 中 ， 入 量 一 般 是计 算 机 采 样 得 到 的 确定 值 。 输 由 于模 糊逻 辑 控 制 对 数 据 进行 处理 是基 于模 糊 集 合 的方 法 ， 因此 必 须 对输 入 量 进 行 模 糊 化 。 化 因子 是 模 糊 控制 器 的输 入 接 口 ， 量 是对 输入 清 晰 量 进 行 的 放 大 或缩 小 变 换 。 为 了使 这 些 清 晰 值 能 与 语 言 表述 的模 糊 规 则 相适 配 ， 行 近 似 推 理 ， 须 把 它 们 变 换 进 必 成模 糊量 ， 即模 糊 子 集 。 这 些 输 人 的 清晰 值 映 射 成模 糊 子 集 及 把 其 隶 属度 函数 的变 换 过 程称 为模 糊 化 …。 １１ 量 化 因子 和 比 例 因子 ．

1.模糊控制的相关理论和概念1.1 模糊控制的发展模糊控制理论是在美国加州伯克利大学的L. A.Zadeh教授于1965年建立的模糊集合论的数学基础上发展起来的。

之后的几年间Zadeh又提出了模糊算法、模糊决策、模糊排序、语言变量和模糊IF-THEN规则等理论，为模糊理论的发展奠定了基础。

1975年, Mamdan和Assilian创立了模糊控制器的基本框架，并用于控制蒸汽机。

1978年，Holmblad和Ostergaard为整个工业过程开发出了第一个模糊控制器——模糊水泥窑控制器。

20世纪80年代，模糊控制开始在工业中得到比较广泛的应用，日本仙台地铁模糊控制系统的成功应用引起了模糊领域的一场巨变。

到20世纪90年代初，市场上已经出现了大量的模糊消费产品。

近30 年来, 因其不依赖于控制对象的数学模型、鲁棒性好、简单实用等优点, 模糊控制已广泛地应用到图像识别、语言处理、自动控制、故障诊断、信息检索、地震研究、环境预测、楼宇自动化等学科和领域, 并且渗透到社会科学和自然科学许多分支中去, 在理论和实际运用上都取得了引人注目的成果。

1.2 模糊控制的一些相关概念用隶属度法来定义论域U中的集合A，引入了集合A的0-1隶属度函数，用A(x) 表示，它满足：A(x)用0-1之间的数来表示x属于集合A的程度，集合A等价与它的隶属度函数A(x)模糊系统是一种基于知识或基于规则的系统。

它的核心就是由所谓的IF-THEN规则所组成的知识库。

一个模糊的IF-THEN规则就是一个用连续隶属度函数对所描述的某些句子所做的IF-THEN形式的陈述。

例如：如果一辆汽车的速度快，则施加给油门的力较小。

这里的“快”和“较小”分别用隶属度函数加以描述。

模糊系统就是通过组合IF-THEN规则构成的。

构造一个模糊系统的出发点就是要得到一组来自于专家或基于该领域知识的模糊IF-THEN规则，然后将这些规则组合到单一系统中。

不同的模糊系统可采用不用的组合原则。

将模糊控制理论和 PID 控制系统结合起来，能够提
高 控 制 系 统 的 性 能 ，来 适 应 各 种 工 业 环 境 。 为 此 ，
设 计 了 一 种 模 糊 PID 控 制 系 统 ，以 炉 温 控ห้องสมุดไป่ตู้制 为 例 ，
应 用 模 糊 推 理 的 方 法 实 现 了 PID 参 数 的 自 适 应 调
（1）
Ts + 1
其中，K 为被控对象的静态增益；T 为系统的时
基金项目：河南省教育厅项目（17A413009）
作者简介：宋 璐（1984—），女，陕西咸阳人，硕士，讲师。研究方向：大学物理和电子教学以及实验。
- 51 -
《电子设计工程》2020 年第 21 期
K p = K p′ +{e,e c}K p = K p′ + ΔK p
systems of traditional PID and fuzzy PID are established based on Simulink respectively. The simulation
results show that compared with traditional PID， Fuzzy PID has obvious advantages in control
以炉温控制为例进行对象模型的建立，为适应不
以 适 应 不 同 的 场 合 [1-5] 。 而 模 糊 控 制 具 有 智 能 化 的
同的工作环境，炉温需要进行动态的调整并进行精确
特 点 ，能 够 根 据 被 控 对 象 特 性 的 变 化 来 调 整 参 数 ，
地控制。根据实验结果或文献可知，由于温度传感
糊 PID 在控制性能上具有明显的优越性，具有无静差无超调，抗干扰能力强和鲁棒性好等特点。

一
工 程 应 用 体 现 了 其在 控 制 方 面 的 “ 智能 ” 的核 心 ，是根 据输 入模 糊量 ，由模 糊规 则 由 性 。模 糊Ｐ Ｉ Ｄ 控 制就 是 利 用 当前 的 控 制偏 差 模 糊 规 则 完 成 模 糊 推 理 来 求 解 模 糊 关 系方 和 偏差 的变 化 率 ，结合 被控 过程 动态 特性 的 程 ， 并 获 得 模 糊 控 制 量 的部 分 。常 用 的成 绩 。本 文 介 绍 的 难 以建 立准 确模 型 的复 杂对 象更有 优 势 ，而 是基 于 传 统 的Ｐ Ｉ Ｄ 控 制和 现 代 控 制理 论 中 的 且 大 多数复 杂 的工 业控 制都 可 以用 经 验模 型 智 能 模 糊 控 制 相 结 合 的一 种 控 制 方 法 ， 用 来 进行 仿真 ，因此 控制 对象 选择 实 际控 制 中 Ｍ Ａ Ｔ Ｌ Ａ Ｂ ＆ Ｓ ｉ ｍ ｕ ｌ ｉ ｎ ｋ 软 件 和 模糊 逻 辑工 具 箱 设 常见 的非线 性经 验 模型 。 ２ ） 基 本 论 域 划 分 ： 在 进 行 输 入 模 糊 化 计控 制 系统结 构模 型 ，并 通过 仿真 结 果证 明
图１ Ｐ Ｉ Ｄ 模糊控制 结构 图
ａ ｍ ｄ ａ ｎ ｉ 法 、Ｌ ａ ｅ ｓ ｅ ｎ 法和Ｔ ｓ ｕ ｋ ａ ｍ ｏ ｔ ｏ 法。 ： 变 化 ，根 据 控 制 要 求 或 目标 函 数 ，建 立 用 Ｍ ｉ ｆ —ｔ ｈ ｅ ｎ 产 生 式 语 句 规 则 所 表 达 的调 整 模 ５ ） 解 模 糊 ： 模 糊 推 理 的 结 果 是 模 糊 型 ，对 Ｐ Ｉ Ｄ 控制 器 的三 个参 数进 行调 整 。 量 ，而 实 际用于 控制 的 是清 晰量 ，解模 糊就
Ｐ Ｉ Ｄ 模 糊 控 制 是 一个 两输 入 三 输 出 的结 是将 模 糊推 理 的结果 转化 成精 确 的控制 量 。 构 ，如 图ｉ 所示 。 常用 的解 模 糊方 法有 最大 隶属度 法 、 中位数 ３ ． 利 用Ｍ Ａ Ｔ Ｌ Ａ Ｂ ＆ Ｓ ｉ ｍ ｕ ｌ ｉ ｎ ｋ 软件 进 行控 制 法和 重 心法 。

基于MATLAB控制系统的仿真与应用毕业设计论文目录一、内容概括 (2)1. 研究背景和意义 (3)2. 国内外研究现状 (4)3. 研究目的和内容 (5)二、MATLAB控制系统仿真基础 (7)三、控制系统建模 (8)1. 控制系统模型概述 (10)2. MATLAB建模方法 (11)3. 系统模型的验证与校正 (12)四、控制系统性能分析 (14)1. 稳定性分析 (14)2. 响应性能分析 (16)3. 误差性能分析 (17)五、基于MATLAB控制系统的设计与应用实例分析 (19)1. 控制系统设计要求与方案选择 (20)2. 基于MATLAB的控制系统设计流程 (22)3. 实例一 (23)4. 实例二 (25)六、优化算法在控制系统中的应用及MATLAB实现 (26)1. 优化算法概述及其在控制系统中的应用价值 (28)2. 优化算法介绍及MATLAB实现方法 (29)3. 基于MATLAB的优化算法在控制系统中的实践应用案例及分析对比研究31一、内容概括本论文旨在探讨基于MATLAB控制系统的仿真与应用，通过对控制系统进行深入的理论分析和实际应用研究，提出一种有效的控制系统设计方案，并通过实验验证其正确性和有效性。

本文对控制系统的基本理论进行了详细的阐述，包括控制系统的定义、分类、性能指标以及设计方法。

我们以一个具体的控制系统为例，对其进行分析和设计。

在这个过程中，我们运用MATLAB软件作为主要的仿真工具，对控制系统的稳定性、动态响应、鲁棒性等方面进行了全面的仿真分析。

在完成理论分析和实际设计之后，我们进一步研究了基于MATLAB 的控制系统仿真方法。

通过对仿真模型的建立、仿真参数的选择以及仿真结果的分析，我们提出了一种高效的仿真策略。

我们将所设计的控制系统应用于实际场景中，通过实验数据验证了所提出方案的有效性和可行性。

本论文通过理论与实践相结合的方法，深入探讨了基于MATLAB 控制系统的仿真与应用。

基于MATLAB控制系统的仿真与应用毕业设计论文目录1. 内容概述 (2)1.1 研究背景与意义 (2)1.2 国内外研究现状 (4)1.3 研究内容与目标 (5)1.4 论文结构安排 (6)2. 控制系统基本原理 (7)2.1 控制系统概述 (8)2.2 线性控制理论 (10)2.3 线性离散控制系统 (11)2.4 系统仿真方法 (12)3. MATLAB控制系统仿真模块设计 (13)3.1 MATLAB环境介绍 (15)3.2 控制系统基本模块设计 (17)3.3 控制策略实现 (18)3.4 仿真界面设计 (20)4. 控制系统仿真案例分析 (21)4.1 单输入单输出系统仿真 (22)4.2 多输入多输出系统仿真 (23)4.3 非线性控制系统仿真 (25)4.4 实际工程应用案例 (27)5. 控制系统性能分析与优化 (28)5.1 控制系统性能指标 (30)5.2 系统性能仿真分析 (32)5.3 性能优化方法研究 (33)5.4 优化效果验证 (34)6. 系统实现及验证 (36)6.1 系统设计实现 (37)6.2 仿真实验与结果分析 (39)6.3 系统测试与验证 (41)6.4 误差分析及解决方案 (42)1. 内容概述本文介绍了控制系统建模的基本理论和MATLAB建模方法，通过实例演示了如何利用MATLAB进行系统建模与仿真，包括线性系统、非线性系统以及多变量系统的建模与仿真。

论文详细阐述了基于MATLAB的控制器设计方法，包括PID控制器、模糊控制器、神经网络控制器等，通过实例分析了不同控制器的设计过程与应用效果。

本文对控制系统稳定性分析进行了深入研究，包括奈奎斯特准则、Bode图、Nyquist图等分析方法，并通过MATLAB工具箱实现了稳定性分析的自动化。

论文探讨了MATLAB在实时仿真与测试方面的应用，介绍了Simulink仿真平台，并通过实际案例演示了MATLAB在嵌入式系统仿真、硬件在环仿真等场景中的应用。

图 ｌ
模 糊 ＰＩ 控 制 系 统 框 图 Ｄ
整定规则如下 ：
ａ 当 ｌ 大 时 ， ． Ｊ ｅ较 为使 系 统 具 有 较 好 的 跟 踪 性 能 ， 取 应 较 大 的 Ｋ 与 较 小 的 Ｋ ， 时 为 避 免 系 统 响 应 出 现 较 大 同
１ 模 糊 Ｐ Ｄ控 制 器 的 设 计 Ｉ
纯 滞 后 、 糊 控 制 鲁 棒 性 较 强 以 及 Ｐ Ｄ 控 制 稳 态 精 度 高 这 三 者 的优 点 ， 出 了一 种 模 糊 Ｐ 【 Ｓ ｔ 模 Ｉ 提 Ｉ ＿ ｍｉ ） ｈ控 制 器 的 设 计 方 法 ， 将 其 应 用 于 电机 网络 控 制 系统 中 。ＭＡ Ａ 并 ＴＬ Ｂ仿 真 结 果 表 明 ， 的 控 制 方 案 与 传 统 的 Ｓ ｔ 新 ｍｉ ｈ控 制 器 、 ｕ ｚ－ Ｉ Ｆ ｚｙ Ｐ Ｄ
Ｐ Ｄ控 制 是 一 种 典 型 的 传 统 反 馈 控 制 器 ， 有 结 构 简 Ｉ 具 单 、 棒 性 好 和 易 于 实 现 等 优 点 ， 广 泛 地 应 用 于 工 业 过 鲁 被
程 控 制 。在 网 络 化 控 制 系 统 中 ， 统 Ｐ Ｄ 控 制 器 的 参 数 传 Ｉ
的 调 整 对 被 控 对 象 的 数 学 模 型 依 赖 较 大 ， 且 控 制 过 程 中 并
Ｌ —— 吉 ． 疆两泵 ． ． ． ！ ．
．
结合 传 统 的 Ｓ ｔ 制 对 时 滞 过 程 控 制 的 有 效 性 ， 出 了 ｍｉ ｈ控 提
模 糊 Ｐ Ｄ－ｍｉ Ｉ Ｓ ｔ ｈ控 制方 案 ， 对 直 流 伺 服 电 机 控 制 系 统 进 并 行 实 例仿 真 分 析 ， 明 了 该 方 案 的有 效 性 。 证
３桂 林 理 工大 学 信 息科 学与 工程 学 院 ， 西 桂 林 ５ １０ ） ． 广 ４ ０ ４

统 的性 能。 关薯调 ： Ｉ ＬＩ Ｋ； ＳＭＵ Ｎ 模糊逻辑 ； 计算机仿 真 中围分冀号 ： Ｐ ７ Ｔ ２３ 文献标识 码 ： Ａ
ＭＡ Ｌ Ｂ是一种 以复数矩 阵为基本编程单元的 ＴＡ 程 序语 言， 面 向 科学 与 工程 计 算 的 高级 语 言。 是 ＭＡ Ｌ Ｂ和其它高级语言之 间的关 系， ＴＡ 如同高级语 言和汇编语言的关 系。因为高级语言的执行效率要 低于汇编语言， ＭＡ Ｌ Ｂ的编程效率 与可读性和 而 Ｔ Ａ 可移植 ｝要远远高于其它高级语言， 生 所以在计算机辅 助设计与仿真中， 适合从 ＭＡ Ｌ Ｂ专用高级语言开 ＴＡ 始， 不但可以提高编程效率， 而且可以提高编程的可 靠性与质量。ＭＡ Ｌ Ｂ有很 强的开放性 ， ＴＡ 针对不同 的应用学 科， ＭＡ Ｌ Ｂ上 可 以推 出不 同的工具 在 ＴＡ 箱， 这样就扩展 了 ＭＡ Ｌ Ｂ的运用范围【 。 ＴＡ ， 模糊控制 由于不依赖对 象的数学模型而受到广
供了很 大方 便。本 文在 ＭＡ Ｉ ５ ３版 本 的基 础 Ｔ ＡＢ ． 上， 将模糊 工具 箱与 动 态仿真 软件 ＳＭＵＬ Ｎ Ｉ Ｉ Ｋ结 合，介 绍 了 如 何 利 用 Ｆ ｚ ｏｉ Ｔ ｏ ｏ 和 ｕｚ Ｌ ｇ ｏｌ ｘ ｙ ｃ ｂ ＳＭＵ Ｋ对模糊控制系统进行计 算机仿真的建模 Ｉ ＩＮ Ｉ 方法、 基本步骤和应注意的问题， 并举例说明。
Ａ 州 ：ＭＡ Ａ （ Ｉ ＴＬ Ｂ Ｓ ＭＵＬ ＮＫ）ｌ ｔ ａ ｅ ｔ ｚｙ ｌ ｉ ｌ １ ａ ｇ ｇ ，ｉ ｆ ｚ ｇｃ ｒｕ ｓｕ ｏ ａ
Ｃｏ ｐ ｔｒ ｍ ｕ ｅ
ｔ ｏｂ ｘ ａ ｄ ｔ ｅ ｒ ｃｅ ｂｎ ｔ ａ ｅ ｐ ｅ ｅ ｔｄ ｏ ｌｏ ｎ ｈ ｉ ｃｎ ｉ ａ ｉ ｎ ｏ ｒ ｒｓｎ ｅ

控制系统中的模糊控制算法设计与实现现代控制系统在实际应用中，往往面临着多变、复杂、非线性的控制问题。

传统的多变量控制方法往往无法有效应对这些问题，因此，模糊控制算法作为一种强大的控制手段逐渐受到广泛关注和应用。

本文将从控制系统中的模糊控制算法的设计和实现两个方面进行介绍，以帮助读者更好地了解和掌握这一领域的知识。

一、模糊控制算法的设计1. 模糊控制系统的基本原理模糊控制系统是一种基于模糊逻辑的控制系统，其基本思想是通过将输入和输出变量模糊化，利用一系列模糊规则来实现对系统的控制。

模糊控制系统主要由模糊化、规则库、模糊推理和解模糊四个基本部分组成，其中规则库是模糊控制系统的核心部分，包含了一系列的模糊规则，用于描述输入和输出变量之间的关系。

2. 模糊控制算法的设计步骤（1）确定输入和输出变量：首先需要明确系统中的输入和输出变量，例如温度、压力等。

（2）模糊化：将确定的输入和输出变量进行模糊化，即将其转换为模糊集合。

（3）建立模糊规则库：根据实际问题和经验知识，建立一系列模糊规则。

模糊规则关联了输入和输出变量的模糊集合之间的关系。

（4）模糊推理：根据当前的输入变量和模糊规则库，利用模糊推理方法求解输出变量的模糊集合。

（5）解模糊：将求解得到的模糊集合转换为实际的输出值，常用的方法包括最大值法、加权平均法等。

3. 模糊控制算法的设计技巧（1）合理选择输入和输出变量的模糊集合：根据系统的实际需求和属性，选择合适的隶属函数，以便更好地描述系统的特性。

（2）精心设计模糊规则库：模糊规则库的设计是模糊控制算法的关键，应根据实际问题与经验知识进行合理的规则构建。

可以利用专家经验、试验数据或者模拟仿真等方法进行规则的获取和优化。

（3）选用合适的解模糊方法：解模糊是模糊控制算法中的一项重要步骤，选择合适的解模糊方法可以提高控制系统的性能。

常用的解模糊方法有最大值法、加权平均法、中心平均法等，应根据系统的需求进行选择。

Matlab模糊控制器系统参数调优方法概述在控制系统中，模糊控制器是一种常用的控制策略，它模拟人类的思维方式来实现对系统的控制。

模糊控制器的性能取决于其参数的选择，如何调优模糊控制器的参数成为一个重要的问题。

本文将介绍一些常用的Matlab模糊控制器系统参数调优方法。

1. 反向传播算法反向传播算法是一种机器学习算法，可以用于调优模糊控制器的参数。

该算法通过不断调整参数的值，使得模糊控制器的输出与期望输出之间的误差最小化。

具体步骤如下：（1）初始化模糊控制器的参数；（2）将系统输入传递给模糊控制器，并计算输出；（3）计算模糊控制器输出与期望输出之间的误差；（4）基于误差调整模糊控制器的参数；（5）重复步骤2-4，直到误差小于某个阈值或达到最大迭代次数。

2. 遗传算法遗传算法是一种模拟生物进化过程的优化算法，可以用于参数调优。

在遗传算法中，通过选择、交叉和变异等操作，逐渐优化参数的值，以达到控制器性能的最优化。

具体步骤如下：（1）初始化种群，随机生成一组控制器参数；（2）根据适应度函数，计算每个个体的适应度值；（3）根据适应度值选择个体，进行交叉和变异操作，生成新的个体；（4）重复步骤2-3，直到达到终止条件，如适应度值收敛或达到最大迭代次数。

3. 粒子群优化算法粒子群优化算法是一种模拟鸟群觅食行为的优化算法，可以用于模糊控制器参数的调优。

在粒子群优化算法中，控制器的参数被看作是粒子的位置，通过粒子的移动来寻找最优解。

具体步骤如下：（1）初始化粒子群，随机生成一组控制器参数；（2）根据适应度函数，计算每个粒子的适应度值；（3）更新每个粒子的速度和位置；（4）重复步骤2-3，直到达到终止条件，如适应度值收敛或达到最大迭代次数。

4. 改进的粒子群优化算法针对传统粒子群优化算法的缺点，研究者们提出了一些改进的粒子群优化算法，如自适应粒子群优化算法、混沌粒子群优化算法等。

这些改进算法通过引入自适应机制或混沌序列，增强了算法的收敛性和全局搜索能力，提高了参数调优的效果。

均不 满 足 牧草 烘 干温 度 控制 系 统 的要 求 … 。
量 。为 了研究问题方便 ， 在此建立风速和滚筒转速恒 定下 燃 油 机 的 数 学 模 型 。试 验 条 件 ： 筒 转 速 １ｒ 滚 ０／
ｍ ｎ 出 口风速 ２ ． ｍ ｓ ｉ； １７ ／ 。
热风 炉 的 数 学 模 型 可 用 一 阶 惯 性 滞 后 环 节 来 描
ｘ１０ ３ ＠ １６ ｃｒ。 ｊ５ ０ ０ ２ ．ｏ ｎ
通讯 作者 ：周 修 理 （ ９ ６一） 男 ， １６ ， 山东 文登 人 ， 教 授 ， Ｅ—ｍ ｉ 副 （ ａ） ｌ
ｘ ｚ ｏ ０ ５１ ｇ ｉ． ｏ ｌ ｈ ｕ ４ ＠ ｍａｌ ｃ ｍ。
２１ ０ １年 ７月
农 机 化 研 究
１ 上 ＿
数； 下为纯 滞后 时 间。 采用 阶跃 飞 升 曲线 法 来 对 热 风 炉 进 行 动 态 试
ＰＤ算法对牧草烘 干机 温度控制器进行 了仿真研究 ， Ｉ
分 析 Ｆ ｚｙ—ＰＤ算 法 用 于 牧 草 烘 干 温 度 控 制 系统 的 ｕｚ Ｉ
可 行 性
验建模。系统的动态特性测定方法如下 ： １ 断开控制器使热风炉的工作状态 为手动状态 ， ） 当系统在 给定值处平衡后 ， 突然增加 １ 以燃 油量为 个
２ ．ｍ ／ １５ ｈ的 阶跃 扰 动 信 号 ， 出 的 入 口温 度 相 对 应 输 也 有 一个 变 化部 分 。 此后 ， 隔 １ ｓ 录下 热 风 炉被 每 ０记
１ 建 模 试 验
１ １ 试 验设 备 ．
试 验 平 台采 用 东 北 农 业 大 学 研 制 的 四 重 滚 筒 式 牧 草 干燥 机 ， 要 由滚 筒 干 燥 机 主 体 和燃 油机 两 部 分 主 组 成 。滚 筒转 速 可 由变 频 器 调 整 ； 源部 分 由燃 油 热 热 风炉 提 供 ； 风 风量 通过 出 口风机来 进 行 调节 ］ 热 。