下载文档原格式
有用的统计学Statistics第7讲分类方法中央财经大学统计与数学学院7.3判别分析和Logistic回归的R语言操作head(iris) #本例使用iris数据，展示iris数据的5个变量和前几行样本观测值summary(iris$Species) # 输出三个类的样本量by(iris[, 1:4], iris[,5], colMeans) #比较三类鸢尾花在4个变量上的均值library(MASS) #加载MASS包z <-lda(Species ~ ., iris, prior = c(1,1,1)/3) #Fisher 判别，设定三个类别的先验概率均为1/3z # 输出估计结果iris.lda.values<-predict(z) # 对现有样本做出预测ldahist(data = iris.lda.values$x[,1], g=iris$Species) #输出在第一个方向上、三个类别投影的直方图ldahist(data = iris.lda.values$x[,2],g=iris$Species) #输出在第二个方向上、三个类别投影的直方图图1在第一个方向上、三个类别投影的直方图图2在第二个方向上、三个类别投影的直方图Logistic回归library(ElemStatLearn)#加载ElemStatLearn包head(SAheart) #本例使用SAheart数据，这是关于冠状动脉心脏病的数据，展示SAheart数据的变量和前几行样本观测值summary(factor(SAheart$chd))#查看两个类的样本量glm.SA<-glm(chd~. , family=binomial(link="logit"), data= SAheart) #建立全模型summary(glm.SA) # 输出全模型结果glm.SA.step<-step(glm.SA, direction = "both") #逐步回归summary(glm.SA.step)# 输出逐步回归结果predict(glm.SA.step, SAheart, type = "response") # 预测样本的患病概率。
#第十章多元统计分析介绍#10.1 主成分分析与因子分析#10.1.1 主成分的简要定义与计算#10.1.2 主成分R 通用程序student<-data.frame(X1=c(148, 139, 160, 149, 159, 142, 153, 150, 151, 139, 140, 161, 158, 140, 137, 152, 149, 145, 160, 156,151, 147, 157, 147, 157, 151, 144, 141, 139, 148),X2=c(41, 34, 49, 36, 45, 31, 43, 43, 42, 31,29, 47, 49, 33, 31, 35, 47, 35, 47, 44,42, 38, 39, 30, 48, 36, 36, 30, 32, 38),X3=c(72, 71, 77, 67, 80, 66, 76, 77, 77, 68,64, 78, 78, 67, 66, 73, 82, 70, 74, 78,73, 73, 68, 65, 80, 74, 68, 67, 68, 70),X4=c(78, 76, 86, 79, 86, 76, 83, 79, 80, 74,74, 84, 83, 77, 73, 79, 79, 77, 87, 85,82, 78, 80, 75, 88, 80, 76, 76, 73, 78))student.pr<-princomp(student, cor=TRUE)summary(student.pr,loadings=TRUE)#10.1.3 因子分析的简要定义与计算#10.1.4 因子分析R 通用程序student<-read.table("e:/data/student.txt")names(student)=c("math", "phi", "chem", "lit", "his", "eng") fa<-factanal(student, factors=2)fa#10.2 判别分析#10.2.1 距离判别#10.2.2 Fisher 判别法#10.2.3 R 通用程序library(MASS)data(iris)attach(iris)names(iris)library(MASS)iris.lda <- lda(Species ~ Sepal.Length + Sepal.Width+ Petal.Length + Petal.Width)【原创】定制代写开发r/python/spss/matlab/WEKA/sas/sql/C++/stata/eviews数据挖掘和统计分析可视化调研报告程序等服务（附代码数据）,咨询：3025393450@有问题到淘宝找“大数据部落”就可以了iris.ldairis.pred=predict(iris.lda) $ classtable(iris.pred, Species)detach(iris)w <- read.table("e:/data/disc.txt")names(w)=c("group", "x1", "x2", "x3", "x4")library(MASS)z <- lda(group~x1+x2+x3+x4, data=w, prior=c(1, 1)/2) newdata<-rbind(c(8.85, 3.38, 5.17, 26.10), c(28.60, 2.40, 1.20, 127.0),c(20.70, 6.70, 7.60, 30.20), c(7.90, 2.40, 4.30, 33.20),c(3.19, 3.20, 1.43, 9.90), c(12.40, 5.10, 4.43, 24.60),c(16.80, 3.40, 2.31, 31.30), c(15.00, 2.70, 5.02, 64.00)) dimnames(newdata)<-list(NULL, c("x1", "x2", "x3", "x4")) newdata<-data.frame(newdata)predict(z, newdata=newdata)#10.3 聚类分析#10.3.1 基本思想#10.3.2 R通用程序x<-c(1, 2, 4.5, 6, 8)dim(x)<-c(5, 1)d<-dist(x)hc1<-hclust(d, "single")hc2<-hclust(d, "complete")hc3<-hclust(d, "median")hc4<-hclust(d, "ward")opar<-par(mfrow=c(2, 2))plot(hc1, hang=-1);plot(hc2, hang=-1)plot(hc3, hang=-1);plot(hc4, hang=-1)par(opar)data(iris);attach(iris)iris.hc<-hclust(dist(iris[,1:4]))plot(iris.hc, hang = -1)plclust(iris.hc,labels = FALSE, hang=-1)re<-rect.hclust(iris.hc,k=3)iris.id <- cutree(iris.hc,3)table(iris.id,Species)#10.4 典型相关分析#10.4.1 基本思想#10.4.2 R通用程序invest=read.table("e:/data/invest.txt")names(invest)=c("x1", "x2", "x3", "x4", "x5", "x6", "y1", "y2", "y3", "y4", "y5")ca<-cancor(invest[, 1:6], invest[, 7:11])ca#x10.5 对应分析#10.5.1 基本思想#10.5.2 R通用程序x.df=data.frame(HighlyFor=c(2, 6, 41, 72, 24), For =c(17, 65, 220, 224, 61),Against=c(17, 79, 327, 503, 300), HighlyAgainst=c(5, 6, 48, 47, 41))rownames(x.df)<-c("BelowPrimary", "Primary", "Secondary", "HighSchool","College")library(MASS)biplot(corresp(x.df, nf=2))。
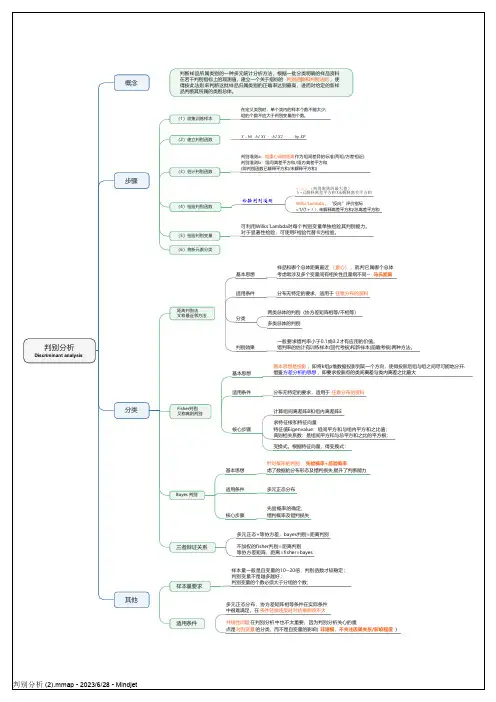
判别分析Discriminant analysis 概念判断样品所属类别的一种多元统计分析方法，根据一批分类明确的样品资料在若干判别指标上的观测值，建立一个关于指标的判别函数和判别法则，使得按此法则来判断这批样品归属类别的正确率达到最高，进而对给定的新样品判断其所属的类别总体。
步骤（1）收集训练样本在定义类别时，单个类内的样本个数不能太少;组的个数不应大于判别变量的个数。
（2）建立判别函数Y b0b1 X1b2 X2bp XP（3）估计判别函数判别准则a：组重心间的距离作为组间差异的标准(两组/方差相近）判别准则b：组间离差平方和/组内离差平方和(即判别函数已解释平方和/未解释平方和)（4）检验判别函数检验判别准则（判别准则的最大值）λ=已解释离差平方和/未解释离差平方和Wilks'Lambda，“反向”评价指标=1/(1+λ),未解释离差平方和/总离差平方和（5）检验判别变量可利用Wilks'Lambda对每个判别变量单独检验其判别能力。
对于显著性检验，可使用F检验代替卡方检验。
（6）将新元素分类分类距离判别法又称最近邻方法基本思想样品和哪个总体距离最近（重心），就判它属哪个总体考虑常涉及多个变量间有相关性且量纲不同--马氏距离适用条件分布无特定的要求，适用于任意分布的资料分类两类总体的判别（协方差矩阵相等/不相等）多类总体的判别判别效果一般要求错判率小于0.1或0.2才有应用的价值。
错判率的估计有训练样本(回代考核)和新样本(前瞻考核)两种方法。
Fisher判别又称典则判别基本思想基本思想是投影，即将k组p维数据投影到某一个方向，使得投影后组与组之间尽可能地分开.借鉴方差分析的思想，即要求投影点的类间离差与类内离差之比最大适用条件分布无特定的要求，适用于任意分布的资料核心步骤计算组间离差阵B和组内离差阵E求特征根和特征向量特征值Eigenvalue：组间平方和与组内平方和之比值；典则相关系数：是组间平方和与总平方和之比的平方根；变换式。
R语⾔中Fisher判别的使⽤⽅法最近编写了Fisher判别的相关代码时，需要与已有软件⽐照结果以确定⾃⼰代码的正确性，于是找到了安装⽅便且免费的R。
这⾥把R中进⾏Fisher判别的⽅法记录下来。
1. 判别分析与Fisher判别不严谨但是通俗的说法，判别分析（Discriminant Analysis）是⼀种多元（多个变量）统计分析⽅法，它根据样本的多个已知变量的值对样本进⾏分类的⽅法。
⼀般来说，判别分析由两个阶段构成——学习（训练）和判别。
在学习阶段，给定⼀批已经被分类好的样本，根据它们的分类情况和样本的多个变量的值来学习（训练）得到⼀种判别⽅法；在判别阶段⽤前⼀阶段得到的判别⽅法对其他样本进⾏判别。
Fisher判别（Fisher Discrimination Method）⼜被称为线性判别（LDA，Linear Discriminative Analysis），是判别分析的⼀种，历史可以追溯到1936年。
它的核⼼思想是将多维数据（多个变量）投影（使⽤线性运算）到⼀维（单⼀变量）上，然后通过给定阈值将样本根据投影后的单⼀变量进⾏分类。
Fisher判别的学习（训练）阶段，就是找到合适的投影⽅式，使得对于已经被分类好的样本，同⼀类的样本被投影后尽量扎堆。
学习阶段的结果是找到⼀系列的系数（Coeffcient），构成形如y=a1 * x1 + a2 * x2 + a3 * x3 + ... + an * xn其中：a1，a2，... an是系数，x1，x2，... ，xn是变量值。
的判别式和阈值。
⽽判别阶段可以根据这个判别式计算出y，并根据阈值将样本进⾏分类。
2. 在R中使⽤Fisher判别R中使⽤Fisher判别说起来很简单，但是我当初也放狗搜索了不短的时间才搞明⽩如何使⽤。
⾸先，它在R⾥不叫Fisher，⽤Fisher搜索多半误⼊歧途。
在R中，它叫LDA（Linear Discriminative Analysis）。
利用R语言如何判别和分类楼主在学习数据挖掘期间，老师讲了很多的判别和分类方法，只是没有平时时间整理，这次利用周末的时间特地整理自己以前的知识点，这篇文章会引用大量网上的图片和文字，若有侵权，及时告知，本人会马上修改。
这篇文章中的案例统一使用著名的鸢尾花数据。
若有错误，也请及时指出，大家相互学习，共同进步判别分析（discriminant analysis）是一种分类技术。
它通过一个已知类别的“训练样本”来建立判别准则，并通过预测变量来为未知类别的数据进行分类。
判别分析根据所采用的数据模型，可分为线性判别分析和非线性判别分析。
根据判别准则可分为Fisher判别、Bayes判别和距离判别。
其中最基本的Fisher判别方法也被称为线性判别方法。
该方法的主要思想是将多维数据投影到某个方向上，投影的原则是将总体与总体尽可能的分开，然后再选择合适的判别规则将新的样本分类判别。
Fisher判别会投影降维，使多维问题简化为一维问题来处理。
选择一个适当的投影轴,使所有的样品点都投影到这个轴上得到一个投影值。
对这个投影轴的方向的要求是：使每一组内的投影值所形成的组内离差尽可能小，而不同组间的投影值所形成的类间离差尽可能大。
Bayes 判别思想是根据先验概率求出后验概率，并依据后验概率分布作出统计推断。
距离判别思想是根据已知分类的数据计算各类别的重心，对未知分类的数据，计算它与各类重心的距离，与某个重心距离最近则归于该类。
1.线性判别当不同类样本的协方差矩阵相同时，我们可以在R中使用MASS 包的lda函数实现线性判别。
值得注意的是当分类只有两种且总体服从多元正态分布条件下，Bayes判别与Fisher判别、距离判别是等价的。
利用table函数建立混淆矩阵，比对真实类别和预测类别。
> library(MASS)> data(iris)> iris.lda=lda(Species~.,data=iris)> table(Species,predict(iris.lda,iris)$class)Species setosa versicolor virginicasetosa 50 0 0versicolor 0 48 2virginica 0 1 49> table<-table(Species,predict(iris.lda,iris)$class)> sum(diag(prop.table(table)))###判对率[1] 0.982.二次判别当不同类样本的协方差矩阵不同时，则应该使用二次判别。
多元统计分析公式主成分分析判别分析多元统计分析是一种通过收集和分析多个变量之间相互作用关系来帮助我们理解、解释和预测数据的方法。
其中，主成分分析和判别分析是常用的多元统计分析方法。
本文将对这两种方法的公式和应用进行介绍。
一、主成分分析主成分分析（Principal Component Analysis，简称PCA）是一种通过线性变换将一组可能存在相关性的变量转化为一组线性无关的新变量的方法。
它的基本思想是通过将原始变量进行线性组合来构建主成分，这些主成分能够解释原始数据中大部分的方差。
主成分分析的公式如下：X = A * T其中，X是原始数据矩阵，A是变量相关系数矩阵，T是主成分得分矩阵。
主成分分析的步骤如下：1. 标准化数据：将原始数据标准化，确保各个变量具有相同的尺度。
2. 计算相关系数矩阵：计算标准化后的数据的相关系数矩阵A。
3. 计算特征值和特征向量：对相关系数矩阵进行特征值分解，得到特征值和对应的特征向量。
4. 选择主成分：根据特征值的大小选择前n个主成分。
5. 计算主成分得分：将原始数据投影到所选的主成分上，得到主成分得分矩阵T。
主成分分析的应用十分广泛，常用于降维、数据可视化、变量选择等领域。
例如，在社会科学研究中，可以将大量的社会经济指标通过主成分分析进行降维，从而更好地理解社会现象。
二、判别分析判别分析（Discriminant Analysis）是一种帮助我们根据已知类别数据预测未知类别数据的方法。
判别分析通过寻找最佳投影方向，将不同类别的样本在投影后最大程度地分离开来，从而提高分类的准确性。
判别分析的公式如下：D = W * X其中，D是判别得分，W是权重系数，X是原始数据。
判别分析的步骤如下：1. 计算类内散度矩阵和类间散度矩阵：分别计算各个类别的散度矩阵。
2. 计算广义特征值和广义特征向量：对类内散度矩阵和类间散度矩阵进行广义特征值分解，得到广义特征值和对应的广义特征向量。
.\ 前言 判别分析（discriminant analysis）是多元统计分析中较为成熟的一种分类方法，它的核心思想是“分类与判断”，即根据已知类别的样本所提供的信息，总结出分类的规律性，并建立好判别公式和判别准则，在此基础上，新的样本点将按照此准则判断其所属类型。例如，根据一年甚至更长时间的每天的湿度差及压差，我们可以建立一个用于判别是否会下雨的模型，当我们获取到某一天（建立模型以外的数据）的湿度差及压差后，使用已建立好的模型，就可以得出这一天是否会下雨的判断。
根据判别的组数来区分，判别分析可以分为两组判别和多组判别。接下来，我们将学习三种常见的判别分析方法，分别是：
• 距离判别 • Bayes判别 • Fisher判别
一、距离判别基本理论 假设存在两个总体和，另有为一个维的样本值，计算得到该样本到两个总体的距离和,如果大于，则认为样本属于总体，反之样本则属于总体；若等于，则该样本待判。这就是距离判别法的基本思想。 .\ 在距离判别法中，最核心的问题在于距离的计算，一般情况下我们最常用的是欧式距离，但由于该方法在计算多个总体之间的距离时并不考虑方差的影响，而马氏距离不受指标量纲及指标间相关性的影响，弥补了欧式距离在这方面的缺点，其计算公式如下：
，为总体之间的协方差矩阵
二、距离判别的R实现（训练样本） 首先我们导入数据 # 读取SAS数据 > library(sas7bdat) > data1 <- read.sas7bdat('disl01.sas7bdat') # 截取所需列数据，用于计算马氏距离 > testdata <- data1[2:5] > head(testdata,3) X1 X2 X3 X4 1 -0.45 -0.41 1.09 0.45 2 -0.56 -0.31 1.51 0.16 3 0.06 0.02 1.01 0.40 # 计算列均值 > colM <- colMeans(testdata) > colM .\ X1 X2 X3 X4 0.096304348 -0.006956522 2.033478261 0.431739130 # 计算矩阵的协方差 > cov_test <- cov(testdata) > cov_test X1 X2 X3 X4 X1 0.068183816 0.027767053 0.14996870 -0.002566763 X2 0.027767053 0.015363865 0.05878251 0.001252367 X3 0.149968696 0.058782512 1.01309874 0.028607150 X4 -0.002566763 0.001252367 0.02860715 0.033912464 # 样本的马氏距离计算 > distance <- mahalanobis(testdata,colM,cov_test) > head(distance,5) [1] 12.726465 11.224681 1.692702 1.347885 2.369820
这样，我们得到了距离判别中最关键的马氏距离值，在此基础上就可以进行进一步的判别分析了。不过我们介绍一个R的第三方包WMDB，该包的wmd()函数可以简化我们的距离判别过程，函数将输出样本的分类判别结果、错判的样本信息以及判别分析的准确度。 > library(WMDB) > head(data1,3) A X1 X2 X3 X4 1 1 -0.45 -0.41 1.09 0.45 2 1 -0.56 -0.31 1.51 0.16 3 1 0.06 0.02 1.01 0.40 .\ # 提取原始数据集的A列生成样品的已知类别 > testdata_group <- data1$A # 转换为因子变量，用于wmd()函数中 > testdata_group <- as.factor(testdata_group) > wmd(testdata,testdata_group) 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27
blong 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 2 1 1 1 1 2 2 2
28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 blong 2 2 2 2 2 2 1 2 2 2 1 1 1 1 1 2 1 2 2 [1] "num of wrong judgement" [1] 15 16 20 22 23 24 34 38 39 40 41 42 44 [1] "samples divided to" [1] 2 2 2 1 1 1 1 1 1 1 1 1 1 [1] "samples actually belongs to" [1] 1 1 1 2 2 2 2 2 2 2 2 2 2 Levels: 1 2 [1] "percent of right judgement" [1] 0.7173913
由分析结果可知，根据已知分类的训练样品建立的判别规则，重新应用于训练样品后，出现了13个错判样品，拥有71.7%的准确度。
三、距离判别的R实现（测试样本） .\ 接着，当我们获取到未分类的新样本数据时，使用wmd()函数，在训练样本的基础上进行这些数据的距离判别 # 导入数据，一共10个样本 > data2 <- read.sas7bdat('disldp01.sas7bdat') # 截取所需列数据 > newtestdata <- data2[1:4] # 进行判别分析 > wmd(testdata,testdata_group,TstX = newtestdata) 1 2 3 4 5 6 7 8 9 10 blong 1 1 1 1 1 1 2 2 2 1
根据马氏距离判别分析得到的结果，10个待判样品中，第一类7个，第二类3个。
距离判别方法简单实用，它只要求知道总体的数字特征，而不涉及总体的分布，当总体均值和协方差未知时，就用样本的均值和协方差矩阵来估计，因此距离判别没有考虑到每个总体出现的机会大小，即先验概率，没有考虑到错判的损失。因此，我们进一步学习贝叶斯判别法。
一、贝叶斯判别基本理论 贝叶斯判别法的前提是假定我们已经对所要分析的数据有所了解（比如数据服从什么分别，各个类别的先验概率等），根据各个类别的先验概率求得新样本属于某类的后验概率。该算法应用到经典的贝叶斯公式，该公式为： .\ 假设有两个总体和，分别具有概率密度函数和，并且根据以往的统计分析，两个总体各自出现的先验概率为和，当一个样本发生时，求该样本属于某一类的概率，计算公式为：
这样，我们得到了该样本属于两类总体的概率，分别为和，属于哪一类总体的概率值大，我们则将样本划分到该类中。
二、贝叶斯判别的R实现 在R中，我们使用klaR包中的NaiveBayes()函数实现贝叶斯判别分析，函数调用公式如下： > NaiveBayes(formula, data, ..., subset, na.action = na.pass) # formula指定参与模型计算的变量，以公式形式给出，类似于y=x1+x2+x3 # na.action指定缺失值的处理方法，默认情况下不将缺失值纳入模型计算，也不会发生报错信息，当设为“na.omit”时则会删除含有缺失值的样本
# 数据准备，使用R内置数据集iris # 通过抽样建立训练样本(70%)和测试样本(30%) > index <- sample(2,size = nrow(iris),replace = TRUE,prob = c(0.7,0.3)) > train_data <- iris[index == 1,] > test_data <- iris[index == 2,] .\ # 载入所用包 > library(klaR) # 构建贝叶斯模型 > Bayes_model <- NaiveBayes(Species ~ ., data = train_data) # 进行预测 > Bayes_model_pre <- predict(Bayes_model, newdata = test_data[,1:4]) # 生成实际与预判交叉表 > table(test_data$Species,Bayes_model_pre$class)
setosa versicolor virginica setosa 20 0 0 versicolor 0 17 0 virginica 0 3 7
从上表生成的交叉表中，我们可以看到在该模型中错判了3个。 # 生成预判精度 > sum(diag(table(test_data$Species,Bayes_model_pre$class))) + / sum(table(test_data$Species,Bayes_model_pre$class)) [1] 0.9361702
三、Fisher判别基本理论 Fisher判别法的基本思想是“投影”，将组维的数据向低维空间投影，使其投影的组与组之间的方差尽可能的大，组内的方差尽可能的小。因
