Comsol案例解析03:PDE之-E-H方程
- 格式:pdf
- 大小:755.13 KB
- 文档页数:11


COMSOL Multiphysics弱形式入门物理问题的描述方式有三种:1、偏微分方程2、能量最小化形式3、弱形式本文希望通过比较浅显的方式来讲解弱形式,使用户更有信心通过COMSOL Multiphysics的弱形式用户界面来求解更多更复杂的问题。
COMSOL Multiphysics是唯一的直接使用弱形式来求解问题的软件,通过理解弱形式也能更进一步的理解有限元方法(FEM)以及了解COMSOL Multiphysics的实现方法。
本文假定读者没有太多的时间去研究数学细节,但是却想将弱形式快速的应用到实际工程中去。
另外,本文也会帮助理解COMSOL Multiphysics文档中常用的到一些术语和标注方法,相关理论可以参考Zienkiewicz[1],Hughes[2],以及Johnson [3]等。
为什么必须要理解PDE方程的弱形式?一般情况下,PDE方程都已经内置在COMSOL Multiphysics的各个模块当中,这种情况下,没有必要去了解PDE方程和及其相关的弱形式。
有时候可能问题是没有办法用COMSOL Multiphysics内置模块来求解的,这个时候可以使用经典PDE模版。
但是,有时候可能经典PDE模版也不包括要求解的问题,这个时候就只能使用弱形式了(虽然这种情况是极少数的)。
掌握弱形式可以使你的水平超过一般的COMSOL Multiphysics用户,让你更容易去理解模型库中利用弱形式做的算例。
另一个原因就是弱形式有时候描述问题比PDE方程紧凑的多。
还有,如果你是一个教授去教有限元分析方法,可以帮助学生们直接利用弱形式来更深入的了解有限元。
最后,你对有限元方法了解的越多,对于COMSOL Multiphysics中的一些求解器的高级设置就懂得更多。
一个重要的事实是:在所有的应用模式和PDE模式求解的时候,COMSOL Multiphysics 都是先将方程式系统转为了弱形式,然后进行求解。


第二章发展方程的有限元分析W. B. J. ZIMMERMAN,B. N. HEWAKANDAMBYDepartment of Chemical and Process Engineering, University of Sheffield,Newcastle Street, Sheffield S1 3JD United KingdomE-mail:科学研究和工程应用中的偏微分方程(PDE)多源自复杂的平衡方程。
常见的偏微分方程主要来自质量守恒、动量守恒、组分守恒和能量守恒定律。
由于这些守恒定律是整个域上的积分方程,所以在连续性假设下,偏微分方程很容易用有限元方法近似描述。
本章介绍了COMSOL Multiphysics中典型的三种不同类型“时间-空间”系统偏微分方程——椭圆方程,抛物线方程和双曲线方程。
本章还对有限元方法进行了总体介绍,结合应用实例讲解有限元方法精确计算的特性,更深层次的内容将在后续章节中引出。
1. 简介在科学研究和工程应用中常会遇到满足守恒定律约束的偏微分方程,通常以积分形式出现。
所有由质量守恒、动量守恒、组分守恒和能量守恒控制的传递现象都会产生连续逼近的偏微分方程。
相信化工人员对传热、传质和动量传递现象不会感到陌生。
与前一章COMSOL Multiphysics化工实例中介绍的零维、一维空间系统相比,化工课程中通常不会出现超过二维或三维的偏微分方程计算。
从文献[1]中找到一个非常珍贵的例子。
实际上,很多常见的化工模型和公式都是由实际过程中更高维数的动力学过程简化而来的。
流体动力学中的阻力系数,传热传质系数,多相催化的Thiele模型,精馏塔设计中的McCabe-Thiele图等许多描述高维数系统传递现象或非稳态动力学过程的技术,都是半经验性的方法,也许可以用偏微分方程来描述这些过程,但是由于基本物理、化学现象的复杂性,这些方程通常很难求解。
所以对于初步的设计计算,这些快速计算的简化方法很受欢迎,但是对于细节设计、设计翻新、过程分析和优化过程,只有简化方法是不够的。


课程名称:大学物理实验(二)实验名称:卡门涡街的Comsol仿真图3.1卡门涡街仿真图四、实验内容及步骤:4.1建模本实验的的建模与仿真可分为八步:1.模型向导2.参数定义3.几何建模4.材料设置5.层流设置6.划分网格7.研究求解8.结果分析操作步骤:1.模型向导1)打开COMSOL软件,在新建窗口中单击模型向导;2)在模型向导窗口中,单击二维;3)在选择物理场树中双击流体流动单相流层流;4)单击添加,然后单击下方的研究;5)在选择研究中选择一般研究瞬态;6)单击底部的完成;2.参数定义1)在左侧模型开发器窗口的全局定义节点下,单击参数1;2)在参数的设置窗口中,定位到参数栏;3)在表中输入以下设置:图4.1 设置示范图4)在左侧主屏幕工具栏中单击f(x)函数,选择全局阶跃;5)在阶跃的设置窗口中,定位到参数栏;6)在位置文本框中输入0.1;3.几何建模1)在上方的几何工具栏中单击矩形;图4.2 建模完成后图材料设置在模型开发器窗口的组件(comp1)节点下,右键单击材料并选择空材料;在材料的设置窗口中,定位到材料属性明细栏;图4.3 设置示范图图层流设置在模型开发器窗口的组件1(comp1)节点下,右键单击层流(spf)并选择入口;在入口的设置窗口中,边界选择栏里选择边界1(单击右侧图形窗口里矩形的左边界即可)在入口的设置窗口中,定位到速度栏,在U0文本框中输入图4.4 划分网格后的图形在模型开发器窗口的研究节点下,单击步骤1: 瞬态;图6.3升力系数随时间的变化由图5.1可知,升力系数的大小在前0.5s几乎为0,0.5s到3.5s升力系数大幅不断变大然后减小,同时升力系数的峰值和谷值的绝对值都在变大,而且峰值和谷值的绝对值近似相等,3.5s到5.0s力系数的峰值和谷值的绝对值缓慢增大,直到5.0s时都取到最大约0.89,此后5.0s到7.0s升力系数在峰值和谷值的绝对值的最大值之间波动。
作出曳力系数随时间变化图图6.4 曳力系数随时间的变化由图5.2可知,曳力系数在0.5s前就从0急剧变大至约3.1,随后在0.5s到3.5s缓慢且小幅减小再增大至约3.17,在3.5s到7.0s时,曳力系数仅在3.17之间微小波动。
Comsol经典实例011: 铜柱的感应加热铜柱中的感应电流会使铜柱的温度升高, 而温度的变化会导致铜的电导率发生变化。
该模型涉及电磁场与热场之间的相互耦合, 要准确描述次物理过程, 需要同时求解传热过程和电磁场传播。
由感应电流引起的加热称为感应加热。
由电流引起的加热称为电阻加热或欧姆加热。
感应电流加热中要解决的难题是需要对感应线圈中的大电流进行主动冷却。
采用空心的线圈导体并在其中灌入水可以实现这一目的。
也就是使流速相当低, 冷却水会形成高度发展的湍流, 在导体和流体之间进行高效传热。
本案例阐明了基于湍流和实时混合假设的水冷却简化的建模方法。
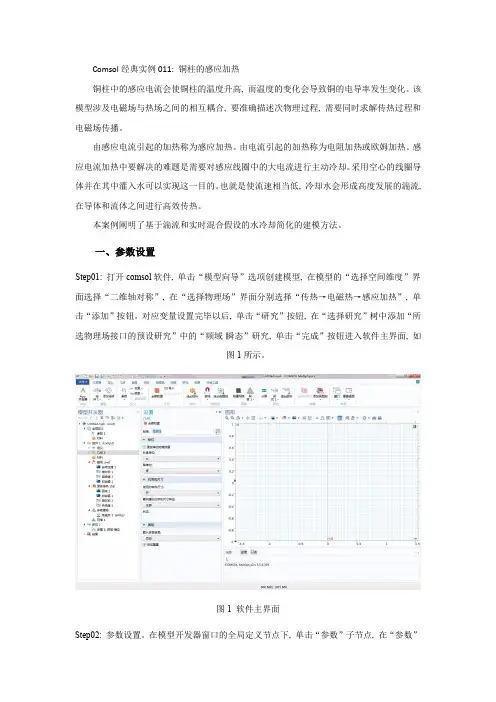
一、参数设置Step01: 打开comsol软件, 单击“模型向导”选项创建模型, 在模型的“选择空间维度”界面选择“二维轴对称”, 在“选择物理场”界面分别选择“传热→电磁热→感应加热”, 单击“添加”按钮。
对应变量设置完毕以后, 单击“研究”按钮, 在“选择研究”树中添加“所选物理场接口的预设研究”中的“频域-瞬态”研究, 单击“完成”按钮进入软件主界面, 如图1所示。
图1 软件主界面Step02: 参数设置。
在模型开发器窗口的全局定义节点下, 单击“参数”子节点, 在“参数”设置窗口中, 定位到“参数”栏, 输入如图2所示的参数。
图2 设置全局参数二、几何模型1.矩形绘制Step03: 添加第一个矩形。
右键单击“几何1”节点, 在弹出的下拉菜单中选择“矩形”, 定位到“大小和半径”栏, 在“宽度”文本输入框中输0.3, 在“高度”文本输入框中输0.4;定位到“位置”栏, 在“z”的文本输入框中输入-0.2。
单击“构建选定对象”, 如图3所示。
Step04:添加第二个矩形。
右键单击“几何1”节点, 在弹出的下拉菜单中选择“矩形”, 定位到“大小和半径”栏, 在“宽度”文本输入框中输0.02, 在“高度”文本输入框中输0.15;定位到“位置”栏, 在“z”的文本输入框中输入-0.075。




磁场和电场(mef):功率电感的电感量简单描述:∇⋅A=0n×A=0n ⋅J=0 )1Im(1111Y L ω= (一)设定物理场物理场:3维“AC/DC>磁场和电场(mef)”研究:“预设研究>频域”保存名为“功率电感的电感量”(二)建立几何模型导入CAD 中的模型主屏幕>导入,浏览找到“功率电感的电感量(模型).mphbin”,然后单击导入创建空气域几何>长方体,打开设置框尺寸和形状>宽度=0.2;深度=0.15;高度=0.12位置>x=-0.1;y=-0.08;z=-0.04(三)设置材料属性材料>添加材料>内置材料>Copper ,域:3材料>添加材料>内置材料>Air ,电导率:1S/m ,域:1材料>空材料>重命名为Core ,相对磁导率:1000,电导率:10S/m ,相对介电常数:1,域:2(四)设置边界条件物理场>域>磁标势场度规修复,域:1,2,3组件1>磁场和电场(mef )>磁绝缘1右击>接地,边界:63组件1>磁场和电场(mef )>磁绝缘1右击>终端,边界:17,终端类型:电压(五)网格划分组件1>网格1右击>自由剖分四面体网格组件1>网格1>尺寸,预定义:粗化单击全部构建(六)求解组件1>研究1>步骤1:频域,频率设置:1kHz研究>显示默认求解器组件1>研究1>求解器设置>解1(sol )>稳态求解器1,相对容差:1e-6组件1>研究1,取消生成默认绘图研究>计算(七)后处理1. 切面:磁通密度模(T )主屏幕>添加绘图组>三维绘图组模型开发器>结果>右击三维绘图组1>切面,设置:替换方程式:mef.normB-磁通密度模平面:zx-平面面数:1单击绘制2.体箭头:磁通密度模型开发器>结果>右击三维绘图组>体箭头,设置:替换方程式:mef.Bx,mef.By,mef.Bz-磁通密度箭头位置:x格点数:20,y格点数:10,z格点数:15 单击绘制3.切面:电势(V)主屏幕>添加绘图组>三维绘图组模型开发器>结果>右击三维绘图组2>曲面结果>选择,几何实体选择>边界:3,5-79返回三维绘图组2,显示曲面:电势分布图4.导纳计算结果>全局计算,mef.Y11,替换方程式:mef.Y11-导纳单击计算,结果显示为0.58836-1.3871i5.电感计算表达式:imag(1/mef.Y11)/(2*pi*freq)单击计算,结果显示为9.7242E-5H。
COMSOL Multiphysics仿真步骤1算例介绍一电磁铁模型截面及几何尺寸如图1所示,铁芯为软铁,磁化曲线(B-H)曲线如图2所示,励磁电流密度J=250 A/cm2。
现需分析磁铁内的磁场分布。
图1电磁铁模型截面图(单位cm)图2铁芯磁化曲线2 COMSOL Multiphysics仿真步骤根据磁场计算原理,结合算例特点,在COMSOL Multiphysics中实现仿真。
(1) 设定物理场COMSOL Multiphysics 4.0以上的版本中,在AC/DC模块下自定义有8种应用模式,分别为:静电场(es)、电流(es)、电流-壳(ecs)、磁场(mf)、磁场和电场(mef)、带电粒子追踪(cpt)、电路(cir)、磁场-无电流(mfnc)。
其中,“磁场(mef)”是以磁矢势A作为因变量,可应用于:①已知电流分布的DC线圈;②电流趋于表面的高频AC线圈;③任意时变电流下的电场和磁场分布;根据所要解决的问题的特点——分析磁铁在线圈通电情况下的电磁场分布,选择2维“磁场(mf)”应用模式,稳态求解类型。
(2) 建立几何模型根据图1,在COMSOL Multiphysics中建立等比例的几何模型,如图3所示。
图3几何模型有限元仿真是针对封闭区域,因此在磁铁外添加空气域,包围磁铁。
由于磁铁的磁导率,因此空气域的外轮廓线可以理想地认为与磁场线迹线重合,并设为磁位的参考点,即(21)式中,L为空气外边界。
(3) 设置分析条件①材料属性本算例中涉及到的材料有空气和磁铁,在软件自带的材料库中选取Air和Soft Iron。
对于磁铁的B-H曲线,在该节点下将已定义的离散B-H曲线表单导入其中即可。
②边界条件由于磁铁的磁导率,因此空气域的外轮廓线可以理想地认为与磁场线迹线重合,并设为磁位的参考点,即(21)式中,L为空气外边界。
为引入磁铁的B-H曲线,除在材料属性节点下导入B-H表单之外,还需在“磁场(mef)”节点下选择“安培定律”,域为“2”,即磁铁区域,在“磁场> 本构关系”处将本构关系选择为“H-B曲线”。
第一章COMSOL MULTIPHYSICS及数值分析基础W. B. J. ZIMMERMAN,B. N. HEWAKANDAMBYDepartment of Chemical and Process Engineering, University of Sheffield,Newcastle Street, Sheffield S1 3JD United KingdomE-mail: w.本章主要介绍COMSOL Multiphysics 在零维和一维模型数值分析方面的几个关键内容。
这些内容包括求根、步进式数值积分、常微分方程数值积分和线性系统分析。
这几乎是所有的化工过程数学分析方法。
下面通过COMSOL Multiphysics中的一些常见化工过程使用实例来介绍这些方法,包括:闪蒸、管式反应器设计、扩散反应系统和固体中热传导。
1.简介本章内容很多,可以分为几个不同的目标。
首先介绍了COMSOL Multiphysics的主要工作特性;其次介绍了如何使用这些特性来分析一些简单的,位于零维空间、一维空间或“空间-时间”系统中的化工问题。
本章还希望通过展示COMSOL Multiphysics和MATLAB工具在化工过程分析中的强大功能,激发读者对使用COMSOL Multiphysics进行建模和仿真的兴趣。
由于COMSOL Multiphysics不是一个通用的问题求解工具,所以一些目标需要迂回实现。
作者在使用FORTRAN、Mathematica和MATLAB解决化工问题方面有着丰富的教学经验,并用这些工具实现过这里所有的例子。
而且,扩展化工问题的数值分析也已经在POL YMATH[1]中实现,这似乎只在化工委员会的CACHE项目中使用过。
本书前一版已经介绍过在零维空间中求解非线性代数方程和和时间有关的常微分方程的内容。
从概念上讲,零维域就是一个简单的有限元。
通过研究某一特定有限元中的变化对理解有限元方法非常有用。
COMSOL自定义PDE仿真入门专题COMSOL自定义方程方法主要内容自定义PDE系数型边界约束通式型边界失效弱解型弱解型弱边界弱边界ODEs和DAEs系数型方程注意时刻记住什么是边界条件什么是初始条件1.线性系数只是空间或时间的函数或常量2.非线性系数是因变量的函数方程中各项含义质量阻尼质量扩散对流源对流吸收源fauuuuctudtueaa22守恒通量质量阻尼质量弹性力初始/热应力惯性力重力aaedccu22aaedcafttuuuuuu系数形式——波动方程密度阻尼系数应力刚性―弹簧常数‖fauuuuc tudtueaa22堆积/储存扩散对流源对流吸收源系数形式——输送扩散方程扩散Helmholtz项源222cukufakkHelmholtz 方程波数波长系数形式——频率响应波动方程fauuuuctudtueaa22案例1——Telegraph方程式??电报线按照Telegraph方程传递电压脉冲。
αβ0.5时结果αβ0.5时波形传播稳态问题——系数c0022tutu稳态各项异性时的c系数α和γ系数β和af三个量都是矢量瞬态问题——系数ea和da系数的时间微分设为γ??项设为f??项有空间分布的时间微分可以利用γf??项添加特征值问题1.对比瞬态求解将时间微分项替换为lambd2.处理线性特征值求解非线性特征值要结合ODE约束处理边界条件1通量/源边界零通量少了一项约束狄氏边界周期边界边界条件2边界吸收边界源项约束力项边界书写规范边界的时间微分设为g??项边界上的时间微分可以利用源项g项添加通式型守恒通量源狄氏边界纽曼边界系数型和通式型比较约束的失效x1x0uv0方程狄氏边界纽曼边界x1u01x1uvxxxxuv因为Lagrange乘子μ1μ2可以任意取值所以纽曼边界ux0失效方程和约束??以二维通式形方程为例稳态下方程和约束如下方程狄氏边界修正的纽曼边界约束情形一??无约束只剩下纽曼边界约束约束情形二??添加狄氏边界条件因为Lagrange乘子μ1μ2可以任意取值所以纽曼边界失效约束情形三??如下添加约束因为Lagrange乘子μ1??可以任意取值所以第一个纽曼边界失效约束情形四??仅改变情形3中方程的排序第二个纽曼边界失效可见方程排序对边界有时也有影响约束情形五??如下添加约束因为这两个纽曼边界不可忽略因为两个边界可以联立得到如下关系双向约束Vs单项约束??多个物理场之间变量调用时发生??区别——Lagrange乘子的提供方式前者是为保证对称与所有约束变量对称相关后者只由物理场的该边界上的因变量有关约束双向约束单向约束弱形式书写方式1audFtaudvdAvdAvFdAtaudvdAvdsvdAvFdAtn0auvvFdvdAvdstn对于Poisson方程‐ux‐uy??F1??Ru??u??约束为01在―弱‖编辑框中输入上面的求解域积分-testuxux-testuyuy testuF –datestuut2在边界上设置约束u通式形式的弱形式弱形式书写方式2系数形式的弱形式域内方程书写方式边界方程书写方式再次看到两个对流项的不同弱贡献常用于边界或边或点上添加源项圆形求解域求解方法弱解形式弱贡献约束在中心处有点源1此处有弱贡献项p1ds应当输入testu1弱约束??弱约束是积分约束与之相对的是逐点约束除开弱约束有优势的边界推荐使用逐点约束??优点1添加非线性约束2添加非对称约束——最好选择单向约束??缺点1由于添加了Lagrange乘子增加了求解规模2会造成雅克比行列式主对角元为0而迭代法对于线性系统的刚度矩阵特征值分布很敏感不易求解。
Comsol案例解析03:PDE之-E-H方程
本期导读
使用广义型PDE模块
注意在comsol中推导柱坐标系下的扩散项
使用积分耦合算子
从材料属性中提取函数单独使用
计算背景
Elenbaas与Heller最早研究电弧采用一维的壁稳弧,即可近似无限长的通道电弧,利用一维扩散方程研究径向上温度的分布。
其著名的Elenbaas-Heller方程如下(包括边界条件等)
建模流程
维度:一维轴对称
参数:
几何:线段,长R0
材料:在材料库中选择-平衡放电-选择空气
从材料中提取函数:从方程可以看出,我们只需要材料的电导率和热导率。
展开空气下面的基础属性,选择【热导率k的插值函数】,右击它选择【复制】,然后鼠标右击【定义】,弹出下拉菜单选择【粘贴插值函数】,提取函数完毕。
电导率同样方法。
调用函数注意格式:f_name(parameters)
积分:定义-组件耦合-选择积分(注意计算回转几何)
设置变量:
源项(将上述方程的扩散项展开,发现除了温度的二阶导数项,还包括一项,这一项我们归类到源项中,需要注意的是,在comsol的散度计算中,无论原方程变量使用的是哪种坐标系,▽算符计算散度都只有一种,即都与直角坐标系下相同,因此用户自己需要注意柱坐标系和球坐标系下对应的散度计算,将多余项统统归类为源项即可,其他复杂的方程都可以这样处理。
)
其他变量
这里需要注意的是,电流变量I的计算表达式与给出的不同,这是因为积分已经选择了计算回转几何。
物理场设置:
模块主节点:设置单位,特别是对于有强迫症的同学,否则会出现各种黄色单位警告(虽然单位错误不影响最终计算结果)
添加源项:因为方程是稳态的,所以关于时间导数项系数均为0;另外设置源项时注意它在等号的左边还是右边,因为需要考虑变号;
边界条件:第一类边条
网格:
参数化扫描:
计算电流-全局计算
计算壁面热流密度-点计算
温度径向分布。