八年级练习

八年级上册数学练习题八年级上册数学练习题在平时的学习、工作中，我们会经常接触并使用试题，试题是命题者按照一定的考核目的编写出来的。

什么样的试题才能有效帮助到我们呢？下面是店铺收集整理的八年级上册数学练习题，仅供参考，大家一起来看看吧。

八年级上册数学练习题篇1一、选择题1.下列形中，是正多边形的是( )A.直角三角形B.等腰三角形C.长方形D.正方形2.九边形的对角线有( )A. 25条B.31条C.27条D.30条3. 下面四边形的表示方法：①四边形ABCD;②四边形ACBD;③四边形ABDC;④四边形ADCB.其中正确的有( )A.1种B.2种C.3种D.4种4. 四边形没有稳定性，当四边形形状改变时，发生变化的是( )A.四边形的边长B.四边形的周长C.四边形的某些角的大小D.四边形的内角和5.下列中不是凸多边形的是( )6.把一张形状是多边形的纸片剪去其中某一个角，剩下的'部分是一个四边形，则这张纸片原来的形状不可能是( )A. 六边形B. 五边形C. 四边形D. 三角形7.木工师傅从边长为90cm的正三角形木板上锯出一正六边形木块，那么正六边形木板的边长为( )A. 34cmB. 32cmC. 30cmD. 28cm8.下列形中具有稳定性的有( )A.正方形B.长方形C.梯形D.直角三角形二、填空题9.以线段a=7，b=8，c=9，d=11为边作四边形，可作_________个.10.把一张形状是多边形的纸片剪去其中某一个角，剩下的部分是一个四边形，则这张纸片原来的形状不可能是_________边形.11.在平面内，由一些线段________________相接组成的_____________叫做多边形。

12.多边形_________组成的角叫做多边形的内角。

13.多边形的边与它的的邻边的__________组成的角叫做多边形的外角。

14.连接多边形_________的两个顶点的线段叫做多边形的对角线。

八年级上册语文练习册答案人教版八年级上册语文练习册答案人教版二、语言积累1、xiè;sāng;jí;sù;赋;颓;琐;躇2、(1)指不幸的事接二连三地发生(2)看到(家庭败落的情况)心里感到悲伤(3)蹒跚(4)簌簌三、问题思考1、(1)到徐州见着父亲，看见满院狼藉的东西，又想起祖母，不禁簌簌地流下眼泪。

(2)这时我看见他的背影，我的泪很快地流下来了。

(3)等他的背影混入来来往往的人里，再找不着了，我便进来坐下，我的眼泪又来了。

(4)在晶莹的泪光中，又看见那肥胖的、青布棉袍黑布马褂的背影。

思想的变化：一次次地流泪，反映了在父亲的关爱中，自己内心一次次受到触动，对父亲的爱体会得也越来越深。

2、描写的背影分别是：开篇难忘背影、过铁道买橘子时的背影、父子惜剐时背影、读信时再现背影。

详细描写了父亲过铁道买橘子的背影，因为这个背影是故事情节的重点，也最能体现父亲的爱心，所以详写。

课文研读四、整体感知1、紫毛大衣;对比手法;突出了父亲对自己的吝啬，对孩子的舍得、大方和爱护。

2、结构上：“背影”是连接情节的线索;内容上：“背影”是父亲的父爱的载体，我通过对父亲“背影”的描写来感受父爱，怀念、感激父亲。

3、慈爱，关爱孩子，面对困难表现出刚强。

五、片段探究1、动作和语言描写。

父亲过铁道买橘子的情境。

通过父亲攀爬铁道的艰辛表现出父爱的伟大，父亲对“我”的关心体贴。

2、(1)想让儿子休息，自己去为儿子买点路上吃的水果。

(2)关心儿子是否能顺利到达北京。

(3)担心儿子行李的安全。

3、父亲终于为儿子买回了橘子，感到尽了照顾儿子的责任。

4、父亲在车站为“我”买橘子的场景。

5、主要表现父亲的心细和体贴。

具体表现在不放心茶房，坚持自己来送“我”;给“我”挑选火车上的座位，并且嘱咐“我”很多事情。

6、悔恨自己当时未能体会父亲的深情。

7、原句是反问句，加强语气，更能体现出“我”当时对父亲做法的不满。

课外延伸六、拓展阅读1、三个故事：“我”用鸡蛋换糖吃被母亲发现;“我”因砍公家的`树做冰排溜冰被母亲打;唐山大地震中母亲用身体保护“我”。

人教版八年级上册语文练习册答案一、阅读理解1. B2. C3. A4. C5. B二、单词拼写1. 导弹2. 出事故的；不幸3. 标记；标志4. 相反5. 展示；出示三、单项选择1. D2. B3. A4. C5. A四、完形填空1. C2. B3. D4. A5. C五、阅读填空1. 表2.发展3.工具4.文章5.出版6.现代7.微电影8.创9.网络 10.影响六、句子翻译1. 科学技术在过去的几十年里取得了巨大的进步。

2. 一个好的阅读习惯对我们的学习很有帮助。

3. 良好的沟通技巧能够帮助我们在人际交往中更加顺利。

4. 音乐会非常精彩，我决定再去听一次。

5. 他为了让大家理解更加清楚，用简单的语言解释了这个问题。

七、任务型阅读1. Manners2. apologize3. respect4. environment5. behaviors6. guests7. polite8. yourself9.appropriate 10. harmony八、书面表达根据现实社会的需求和学生的实际情况，人教版八年级上册语文练习册的答案也显得尤为重要。

语文练习册提供了丰富的习题和练习内容，帮助学生巩固知识、提高能力。

下面是人教版八年级上册语文练习册的答案，供同学们参考:一、阅读理解1. B解析：根据短文第一段的"The most important holiday in the USA is Thanksgiving. "可知，美国最重要的节日是感恩节。

2. C解析：根据短文第二段的"One president even made Thanksgiving a national holiday."可知，一位总统将感恩节定为国定假日。

3. A解析：根据短文第三段的"Thanksgiving traditions are different in different parts of the USA."可知，感恩节的传统在美国的不同地区有所不同。

八年级英语语法练习题40题含答案解析1.Tom plays _____ basketball after school.A.aB.anC.theD./答案解析：D。

play basketball 是固定用法，球类运动前不加冠词。

选项A“a”用于辅音音素开头的可数名词单数前；选项B“an”用于元音音素开头的可数名词单数前；选项C“the”是定冠词，表特指等特定用法。

2.There is _____ art room in our school.A.aB.anC.theD./答案解析：B。

“art”是以元音音素开头的单词，所以用“an”。

选项A“a”用于辅音音素开头的可数名词单数前；选项C“the”是定冠词，表特指等特定用法；选项D 不用于可数名词单数前。

3.My hobby is reading _____ books.A.aB.anC.the答案解析：D。

“books”是复数形式，前面不用加冠词。

选项A“a”用于辅音音素开头的可数名词单数前；选项B“an”用于元音音素开头的可数名词单数前；选项C“the”是定冠词，表特指等特定用法。

4.We have _____ English class every day.A.aB.anC.theD./答案解析：B。

“English”是以元音音素开头的单词，所以用“an”。

选项A“a”用于辅音音素开头的可数名词单数前；选项C“the”是定冠词，表特指等特定用法；选项D 不用于可数名词单数前。

5.There is _____ beautiful flower on the teacher's desk.A.aB.anC.theD./答案解析：A。

“beautiful”是以辅音音素开头的单词，所以用“a”。

选项B“an”用于元音音素开头的可数名词单数前；选项C“the”是定冠词，表特指等特定用法；选项D 不用于可数名词单数前。

6.I want to buy _____ new pencil.A.aC.theD./答案解析：A。

人教版八年级英语练习题(必备6篇）人教版八年级英语练习题（1）He is going to go to a cooking (对划线部分提问)is he going to ?father wants to be a (写出一般疑问句)your father to be a pilot?’s a good time to make resolutions at the beginning of the (写出同义句)The of the year is a good time foryou make a model plane for her? (写出同义句)you to make a model plane for her?enjoys Peter enjoys swimming,(合并句)John Peter人教版八年级英语练习题（2）can’t stand (listen) to the noisy(be) some exciting news in today’syou mind (open) the window?you watch (sport) show on TV yesterday?do you plan (go) this Sunday?you want (watch) the news?thinks soap operas are (educational) thanhope (watch) the action movie oneMing is a (success) player inthink Xi Yangyang is as (famous) as Mikey人教版八年级英语练习题（3）He is going to go to a cooking (对划线部分提问)is he going to ?father wants to be a (写出一般疑问句)your father to be a pilot?’s a good time to make resolutions at the beginning of the (写出同义句)The of the year is a good time foryou make a model plane for her? (写出同义句)you to make a model plane for her?enjoys Peter enjoys swimming,(合并句)John Peter人教版八年级英语练习题（4）is (funny) than the other students in hisyou have fun (learn) something?practiced (dance) a lot more thanmother often makes him (clean) his room onpracticed a lot more and wanted (win).’s necessary for us (learn) Englishis (different) from his They have some (different).’m (good) at physics than my人教版八年级英语练习题（5）Mike goes to see his grandparents _________(one) aHe spends more than an hour __________(exercise) every He didn’t go to He could ________(hard) read orIt’s a good habit to brush your (tooth) everykeep healthy，I decide _______ (exercise) half an hour every ! Your pet dog is (die).is (health) for the mind and theYour sweater is I want _________(buy) one，How about (go) shopping on Sundays?He usually study English by (read) it in the人教版八年级英语练习题（6）decided (go) to the beach near ourreally enjoy (walk) around thewanted (walk) up to thefamily (go) to the beach everyyou have a great time (talk) in groups?Lucy usually ______to school But today she ________to school (go) ---Where did you______ (study) last night? ---No, I__________(help) my mother_______(clean) theyou feel like (drink) some orange?teacher often keeps us (read) English in theIt’s very interesting ( feed) theHe is ____(bad) at learning He is much _____(bad) at Chinese an d he is the ____ (bad) atAnnie says Sally is the ______ (kind) person in theHe is one of the_________(friendly) people in the class, IA dictionary is much _________ (expensive) than aAn orange ia a little ______ (big) than an apple,but much _______ _ (small) than aThe Changjiang River is the _______ (long) river in。

八年级数学经典练习题附答案( 因式分解 )因式分解练习题一、填空题：2．(a－ 3)(3－2a)=_______(3－a)(3－2a)；12．若 m2－ 3m＋ 2=(m＋ a)(m＋b)，则 a=______，b=______；15．当 m=______时， x2＋2(m－ 3)x＋ 25 是完好平方式．二、选择题：1．以下各式的因式分解结果中，正确的选项是()A． a2b＋ 7ab－b＝b(a2＋ 7a)B．3x2y－ 3xy－6y=3y(x－2)(x＋ 1)C．8xyz－6x2y2＝2xyz(4－3xy)D．－ 2a2＋4ab－ 6ac＝－ 2a(a＋ 2b－3c)2．多项式 m(n－2)－ m2(2－n)分解因式等于 ()A． (n－2)(m＋ m2)B． (n－2)(m－m2)C．m(n－2)(m＋1)D．m(n－2)(m－ 1) 3．在以低等式中，属于因式分解的是()A． a(x－y)＋ b(m＋n)＝ ax＋bm－ay＋bn C．－ 4a2＋9b2＝(－2a＋3b)(2a＋3b)B．a2－2ab＋b2＋1=(a－b)2＋1 D． x2－7x－8=x(x－ 7)－84．以下各式中，能用平方差公式分解因式的是()A． a2＋b2B．－ a2＋b2C．－ a2－b2D．－ (－a2)＋b25．若9x2＋mxy＋ 16y2是一个完好平方式，那么m 的值是 ()A．－ 12B．± 24C．12D．± 126．把多项式 a n+4－ a n+1分解得 ()A． a n(a4－ a) B．a n-1(a3－1) C．a n+1(a－1)(a2－a＋ 1)D．a n+1(a－1)(a2＋a＋ 1) 7．若 a2＋ a＝－ 1，则 a4＋2a3－3a2－4a＋ 3 的值为 ()A． 8B．7C．10D． 128．已知 x2＋ y2＋2x－ 6y＋10=0，那么 x，y 的值分别为 ()A． x=1， y=3B．x=1，y=－ 3C．x=－ 1， y=3D．x=1，y=－ 3 9．把 (m2＋3m)4－8(m2＋3m)2＋16 分解因式得 ( )A． (m＋1)4(m＋ 2)2B．(m－1)2(m－ 2)2(m2＋ 3m－ 2)C．(m＋4)2(m－ 1)2D． (m＋1)2(m＋ 2)2(m2＋ 3m－ 2)210．把 x2－7x－ 60 分解因式，得 ()A． (x－ 10)(x＋ 6)B．(x＋5)(x－ 12)C． (x＋3)(x－20)D．(x－ 5)(x＋12) 11．把 3x － 2xy－8y分解因式，得 ()22A． (3x＋4)(x－ 2)B．(3x－ 4)(x＋2) C．(3x＋4y)(x－2y)D．(3x－4y)(x＋2y)12．把 a ＋8ab－33b2分解因式，得 ()2A． (a＋11)(a－3) B．(a－ 11b)(a－3b) C．(a＋ 11b)(a－3b)D．(a－ 11b)(a＋3b)13．把x4－3x2＋2 分解因式，得()A． (x2－2)(x2－1)B． (x2－2)(x＋ 1)(x－1)C．(x2＋2)(x2＋1)D． (x2＋ 2)(x＋1)(x－ 1)14．多项式x2－ ax－bx＋ab 可分解因式为()A．－ (x＋a)(x＋b)B．(x－a)(x＋b)C． (x－ a)(x－b)D． (x＋a)(x＋b)15．一个关于 x 的二次三项式，其x2项的系数是 1，常数项是－ 12，且能分解因式，这样的二次三项式是()A． x2－11x－12 或 x2＋11x－12B．x2－ x－12或x2＋x－12C．x2－4x－12 或x2＋4x－ 12D．以上都能够16．以下各式 x3－x2－ x＋ 1，x2＋ y－ xy－x，x2－2x－y2＋1，(x2＋3x)2－ (2x＋ 1)2中，不含有 (x －1)因式的有 ( )A． 1 个B．2 个C．3 个D．4 个17．把9－ x2＋12xy－36y2分解因式为()A． (x－ 6y＋3)(x－ 6x－3)B．－ (x－ 6y＋3)(x－ 6y－3)C．－ (x－6y＋ 3)(x＋6y－3)D．－ (x－ 6y＋3)(x－ 6y＋3)18．以下因式分解错误的选项是()A． a2－bc＋ ac－ab=(a－b)(a＋ c)B． ab－5a＋3b－ 15=(b－5)(a＋3)C．x2＋3xy－2x－ 6y=(x＋ 3y)(x－ 2)D．x2－6xy－1＋9y2=(x＋3y＋ 1)(x＋3y－ 1)19．已知 a2x2± 2x＋b2是完好平方式，且a， b 都不为零，则 a 与 b 的关系为 ()A．互为倒数或互为负倒数B．互为相反数C．相等的数D．任意有理数20．对 x4＋4 进行因式分解，所得的正确结论是 ( )A．不能够分解因式B．有因式 x2＋2x＋2C． (xy＋2)(xy－ 8) D．(xy－2)(xy－8)21．把 a ＋2a b2＋ b －a b 分解因式为 ()42422A． (a2＋b2＋ab)2B． (a2＋ b2＋ab)(a2＋b2－ab) C．(a2－b2＋ab)(a2－ b2－ab)D．(a2＋b2－ab)222．－ (3x－1)(x＋ 2y)是以下哪个多项式的分解结果()A． 3x ＋ 6xy－ x－ 2y B．3x －6xy＋ x－2y 22C．x＋2y＋3x2＋6xy D．x＋2y－ 3x2－6xy 23．64a8－b2因式分解为 ()A． (64a4－ b)(a4＋ b)B． (16a2－ b)(4a2＋b)C．(8a4－b)(8a4＋ b)D． (8a2－b)(8a4＋ b) 24．9(x－y) ＋12(x －y)＋4(x＋y) 因式分解为 ()2222A． (5x－y)2 B． (5x＋ y)2C．(3x－2y)(3x＋2y) D． (5x－ 2y)2 25．(2y－3x)2－ 2(3x－2y)＋1 因式分解为 ()A． (3x－2y－1)2B．(3x＋2y＋ 1)2C．(3x－2y＋1)2D．(2y－3x－ 1)226．把 (a＋ b) － 4(a －b )＋4(a－b) 分解因式为 ()2222A． (3a－ b)2B．(3b＋a)2C．(3b－a)2D． (3a＋ b)227．把 a (b＋c) －2ab(a－c)(b＋ c)＋b (a－ c) 分解因式为 ( )2222A． c(a＋b)2B． c(a－ b)2C．c2(a＋b)2D．c2(a－ b)28．若 4xy－4x2－y2－k 有一个因式为 (1－ 2x＋y)，则 k 的值为 ()A． 0B． 1C．－ 1D． 429．分解因式 3a2x－4b2y－3b2x＋4a2y，正确的选项是 ()A．－ (a2＋ b2)(3x＋4y)B． (a－b)(a＋b)(3x＋4y) C．(a2＋b2)(3x－4y)D．(a－b)(a＋b)(3x－4y) 30．分解因式 2a2＋ 4ab＋2b2－8c2，正确的选项是 ()A． 2(a＋ b－2c)B．2(a＋b＋c)(a＋b－c) C．(2a＋b＋4c)(2a＋b－4c)D．2(a＋b＋2c)(a＋b－2c)三、因式分解：1．m2(p－q)－ p＋q；2．a(ab＋bc＋ac)－abc；3．x4－2y4－2x3y＋ xy3；4．abc(a2＋b2＋ c2)－a3bc＋2ab2c2；5．a2(b－c)＋b2(c－ a)＋c2(a－ b)；6． (x2－ 2x)2＋2x(x－ 2)＋1；7．(x－ y)2＋12(y－x)z＋36z2；8．x2－ 4ax＋ 8ab－4b2；9．(ax＋by)2＋(ay－ bx)2＋2(ax＋by)(ay－bx)；10．(1－a2)(1－b2)－(a2－1)2(b2－ 1)2；11．(x＋1)2－9(x－1)2；12．4a2b2－(a2＋ b2－c2)2；13．ab2－ac2＋4ac－4a；14．x3n＋y3n；15．(x＋y)3＋125；16．(3m－ 2n)3＋(3m＋ 2n)3；17．x6(x2－y2)＋y6(y2－x2)；18．8(x＋y)3＋1；19．(a＋b＋c)3－a3－ b3－c3；20．x2＋ 4xy＋3y2；21．x2＋ 18x－ 144；22．x4＋2x2－8；23．－ m4＋18m2－ 17；24．x5－ 2x3－ 8x；25．x＋ 19x －216x ；26．(x －7x) ＋10(x －7x)－24；85222227．5＋7(a＋1)－6(a＋1)2；28．(x2＋x)(x2＋x－ 1)－2；29．x2＋ y2－x2y2－ 4xy－ 1；30．(x－ 1)(x－2)(x－3)(x－ 4)－48；四、证明 (求值 )：1．已知 a＋b=0，求 a3－ 2b3＋a2b－2ab2的值．2．求证：四个连续自然数的积再加上1，必然是一个完好平方数．3．证明： (ac－bd)2＋(bc＋ ad)2=(a2＋ b2)(c2＋d2)．4．已知 a=k＋ 3， b=2k＋2，c=3k－1，求 a2＋b2＋ c2＋2ab－ 2bc－ 2ac 的值．5．若 x2＋mx＋n=(x－3)(x＋4)，求 (m＋ n)2的值．6．当 a 为何值时，多项式x2＋7xy＋ay2－5x＋43y－24 能够分解为两个一次因式的乘积．7．若 x，y 为任意有理数，比较6xy 与 x2＋9y2的大小．8．两个连续偶数的平方差是 4 的倍数．参照答案 :一、填空题：7．9，(3a－1)10．x－5y，x－5y，x－5y，2a－b11．＋ 5，－ 212．－ 1，－ 2(或－ 2，－ 1)14．bc＋ ac，a＋b，a－c15．8 或－ 2二、选择题：1．B2．C 3．C 4．B 5．B6．D7．A8．C 9．D10．B11．C12．C 13．B14．C 15．D16．B 17．B18．D19．A 20．B 21．B 22．D 23．C 24．A25．A 26．C27． C 28．C29．D30． D三、因式分解：1．(p－ q)(m－ 1)(m＋1)．8．(x－ 2b)(x－ 4a＋2b)．11．4(2x－ 1)(2－x)．20．(x＋3y)(x＋y)．21．(x－6)(x＋ 24)．27．(3＋2a)(2－ 3a)．四、证明 (求值 )：2．提示：设四个连续自然数为n，n＋1，n＋2，n＋3八年级数学经典练习题附答案6．提示： a=－18．∴a=－18．11 / 11。

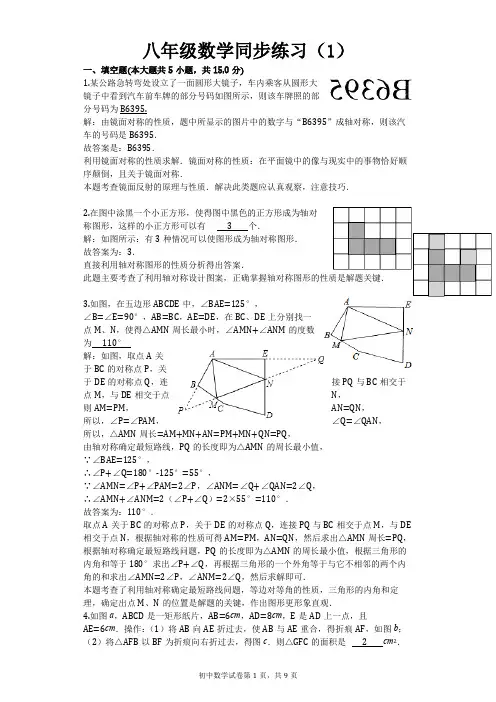
八年级数学同步练习（1）一、填空题(本大题共5小题，共15.0分)1.某公路急转弯处设立了一面圆形大镜子，车内乘客从圆形大镜子中看到汽车前车牌的部分号码如图所示，则该车牌照的部分号码为B6395.解：由镜面对称的性质，题中所显示的图片中的数字与“B6395”成轴对称，则该汽车的号码是B6395．故答案是：B6395．利用镜面对称的性质求解．镜面对称的性质：在平面镜中的像与现实中的事物恰好顺序颠倒，且关于镜面对称．本题考查镜面反射的原理与性质．解决此类题应认真观察，注意技巧．2.在图中涂黑一个小正方形，使得图中黑色的正方形成为轴对称图形，这样的小正方形可以有3个．解：如图所示：有3种情况可以使图形成为轴对称图形．故答案为：3．直接利用轴对称图形的性质分析得出答案．此题主要考查了利用轴对称设计图案，正确掌握轴对称图形的性质是解题关键．3.如图，在五边形ABCDE中，∠BAE=125°，∠B=∠E=90°，AB=BC，AE=DE，在BC、DE上分别找一点M、N，使得△AMN周长最小时，∠AMN+∠ANM的度数为110°解：如图，取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC相交于点M，与DE相交于点N，则AM=PM，AN=QN，所以，∠P=∠PAM，∠Q=∠QAN，所以，△AMN周长=AM+MN+AN=PM+MN+QN=PQ，由轴对称确定最短路线，PQ的长度即为△AMN的周长最小值，∵∠BAE=125°，∴∠P+∠Q=180°-125°=55°，∵∠AMN=∠P+∠PAM=2∠P，∠ANM=∠Q+∠QAN=2∠Q，∴∠AMN+∠ANM=2（∠P+∠Q）=2×55°=110°．故答案为：110°．取点A关于BC的对称点P，关于DE的对称点Q，连接PQ与BC相交于点M，与DE 相交于点N，根据轴对称的性质可得AM=PM，AN=QN，然后求出△AMN周长=PQ，根据轴对称确定最短路线问题，PQ的长度即为△AMN的周长最小值，根据三角形的内角和等于180°求出∠P+∠Q，再根据三角形的一个外角等于与它不相邻的两个内角的和求出∠AMN=2∠P，∠ANM=2∠Q，然后求解即可．本题考查了利用轴对称确定最短路线问题，等边对等角的性质，三角形的内角和定理，确定出点M、N的位置是解题的关键，作出图形更形象直观．4.如图a，ABCD是一矩形纸片，AB=6cm，AD=8cm，E是AD上一点，且AE=6cm．操作：（1）将AB向AE折过去，使AB与AE重合，得折痕AF，如图b；（2）将△AFB 以BF为折痕向右折过去，得图c．则△GFC的面积是 2 cm2．解：∵将AB向AE折过去，使AB与AE重合，∴∠BAF=∠EAB=45°，在图b中，∠BAF=45°，BD=AD-AB=8-6=2cm，∴FC=2cm，在图c中，∵∠BAC=45°，∴∠AFC=45°，∴△GFC为等腰直角三角形，∴CG=CF=2cm，∴△GFC的面积=12CF•CG=12×2×2=2（cm2）．根据折叠的性质得到图a中，四边形ABFE为正方形，得到∠BAF=∠EAB=45°；在图b中，∠BAF=45°，可求出BD=AD-AB，从而得到FC；在图c中，根据折叠的性质得到，∠BAC=45°，易得到△GFC为等腰直角三角形，然后利用三角形的面积公式计算即可．本题考查了折叠的性质：折叠前后两图形全等，即对应角相等，对应边相等．也考查了矩形的性质以及等腰直角三角形的性质．5.如图，∠MON内有一点P，P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，GH分别交OM、ON于A、B点．若GH的长为14，则△PAB的周长为14.解：∵P点关于OM的轴对称点是G，P点关于ON的轴对称点是H，∴PA=AG，PB=BH，∴△PAB的周长=AP+PB+AB=AG+AB+BH=GH=14．故答案为：14．先根据轴对称的性质得出PA=AG，PB=BH，由此可得出结论．本题考查的是轴对称的性质，熟知如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线是解答此题的关键．二、选择题(本大题共7小题，共21.0分)6.图中序号（1）（2）（3）（4）对应的四个三角形，都是△ABC这个图形进行了一次变换之后得到的，其中是通过轴对称得到的是（A）A.（1）B.（2）C.（3）D.（4）解：∵轴对称是沿着某条直线翻转得到新图形，∴通过轴对称得到的是（1）．故选：A．轴对称是沿着某条直线翻转得到新图形，据此判断出通过轴对称得到的是哪个图形即可．此题主要考查了轴对称图形的性质和应用，要熟练掌握，解答此题的关键是要明确：轴对称是沿着某条直线翻转得到新图形，观察时要紧扣图形变换特点，进行分析判断．7.如果一个等腰三角形的两边分别是3和6，则它的周长是（B）A.12B.15C.12或15D.无法确定解：∵等腰三角形的两边分别是3和6，∴应分为两种情况：①3为底，6为腰，6+6+3=15；②6为底，3为腰，则3+3=6，则应舍去；∴它的周长是15．故选B．本题应分为两种情况：①3为底，6为腰，②6为底，3为腰．注意还要考虑三角形的三边关系．本题考查了等腰三角形的性质和三角形的三边关系；求三角形的周长，不能盲目地将三边长相加起来，而应养成检验三边长能否组成三角形的好习惯，把不符合题意的舍去．8.如图，△ABC中，AB=AC=15，AD平分∠BAC，点E为AC的中点，连接DE，若△CDE的周长为21，则BC的长为（C）A.16B.14C.12D.6解：∵AB=AC，AD平分∠BAC，∴AD⊥BC，∴∠ADC=90°，∵点E为AC的中点，∴DE=CE=12AC=152．∵△CDE的周长为21，∴CD=6，∴BC=2CD=12．故选C．根据等腰三角形的性质可得AD⊥BC，再根据在直角三角形中，斜边上的中线等于斜边的一半可得答案．此题主要考查了等腰三角形的性质，以及直角三角形的性质，关键是掌握在直角三角形中，斜边上的中线等于斜边的一半．9.如图，已知等腰三角形ABC，AB=AC，若以点B为圆心，BC长为半径画弧，交腰AC于点E，则下列结论一定正确的是（C）A.AE=ECB.AE=BEC.∠EBC=∠BACD.∠EBC=∠ABE解：∵AB=AC，∴∠ABC=∠ACB，∵以点B为圆心，BC长为半径画弧，交腰AC于点E，∴BE=BC，∴∠ACB=∠BEC，∴∠BEC=∠ABC=∠ACB，∴∠A=∠EBC，故选C．利用等腰三角形的性质分别判断后即可确定正确的选项．本题考查了等腰三角形的性质，当等腰三角形的底角对应相等时其顶角也相等，难度不大．10.若等腰三角形中有一个角等于40°，则这个等腰三角形顶角的度数为（C）A.40°B.100°C.40°或100°D.40°或70°解：∵等腰三角形中有一个角等于40°，∴①若40°为顶角，则这个等腰三角形的顶角的度数为40°；②若40°为底角，则这个等腰三角形的顶角的度数为：180°-40°×2=100°．∴这个等腰三角形的顶角的度数为：40°或100°．故选：C．由等腰三角形中有一个角等于40°，可分别从①若40°为顶角与②若40°为底角去分析求解即可求得答案．此题考查了等腰三角形的性质．此题比较简单，解题的关键是掌握等边对等角的知识，掌握分类讨论思想的应用．11.如图，三角形ABC中，AB=AC，D，E分别为边AB，AC上的点，DM平分∠BDE，EN平分∠DEC，若∠DMN=110°，则∠DEA=（A）A.40°B.50°C.60°D.70°解：∵AB=AC，∴∠B=∠C，∵DM平分∠BDE，EN平分∠DEC，∴∠BDN=∠MDE，∠DEN=∠CEN，∵∠B=∠DMN-∠BDM=∠DMN-∠MDE，∠C=∠MNE-∠NEC=∠MNE-∠NED，∴∠DMN-∠MDE=∠MNE-∠NED，即∠DMN+∠NED=∠ME+∠MDE，∵∠DMN+∠NED=∠MNE+∠MDE，∵∠DMN+∠NED=∠MNE+∠MDE=180°，∴∠NED=70°，∴∠DEA=180°-2∠NED=40°．故选A．根据等腰三角形的性质得到∠B=∠C，由角平分线的定义得到∠BDN=∠MDE，∠DEN=∠CEN，根据外角的性质得到∠B=∠DMN-∠BDM=∠DMN-∠MDE，∠C=∠MNE-∠NEC=∠MNE-∠NED，于是推出∠DMN-∠MDE=∠MNE-∠NED，即∠DMN+∠NED=∠ME+∠MDE，由于∠DMN+∠NED=∠MNE+∠MDE，∠DMN+∠NED=∠MNE+∠MDE=180°，得到∠NED=70°于是得到结论．本题考查了等腰三角形的性质，角平分线的定义，外角的性质，熟练掌握等腰三角形的性质是解题的关键．12.把一张长方形纸片按如图①，图②的方式从右向左连续对折两次后得到图③，再在图③中挖去一个如图所示的三角形小孔，则重新展开后得到的图形是（C）A. B.C. D.解：重新展开后得到的图形是C，故选C．解答该类剪纸问题，通过自己动手操作即可得出答案．本题主要考查了剪纸问题，培养学生的动手能力及空间想象能力．对于此类问题，学生只要亲自动手操作，答案就会很直观地呈现．三、解答题(本大题共4小题，共32.0分)13.在如图所示的正方形网格中，已知△ABC的三个顶点分别是格点A、B、C．（1）请在正方形网格中作△A1B1C1，使它与△ABC关于直线m轴成轴对称，其中点A1、B1、C1分别是A、B、C的对称点．（2）若网格中小正方形的边长为1，求四边形BCC1B1的面积．解：（1）如图所示；（2）S四边形BCC1B1=12（2+6）×1=4．【解析】（1）根据轴对称的性质画出△A1B1C1即可；（2）根据梯形的面积公式即可得出结论．本题考查的是作图-轴对称变换，熟知图形轴对称的性质是解答此题的关键．14.如图，用三角尺画出△ABC关于直线m对称的三角形．解：如图所示：△A′BC′即为所求．【解析】直接利用关于直线对称图形的性质得出对应点位置进而得出答案．此题主要考查了轴对称变换，正确得出对应点位置是解题关键．15.如图所示，△ABC为等边三角形，BD为中线，延长BC至E，使DE=BD．求证：（1）CE=12BC．（2）把（1）中的BD为中线换成其它什么条件也能得到同样的结论．证明：（1）∵△ABC为等边三角形，BD为中线，∴AD=CD=12AC=12BC，∠DBC=12∠ABC=12×60°=30°．∵DE=BD，∴∠DBC=∠DEC=30°．又∵∠ACB=60°，是△DCE的一个外角，∴∠EDC=∠ACB-∠DEC=60°-30°=30°．∴CE=12BC．（2）根据等腰三角形三线合一的性质：把（1）中的BD为中线换成BD是高或是∠ABC 的角平分线也能得到同样的结论．【解析】（1）根据已知条件，△ABC为等边三角形，BD为中线，可知∠DBE=30°，∠DCE=120°，∠CDE=30°，求得CD=CE即可解答．（2）根据等腰三角形三线合一的性质解答即可．本题考查了等边三角形的性质及全等三角形的判定与性质；巧妙利用三角形外角与内角的关系是解答本题的关键．16.如图在△ABC中，点D、E分别是AB、AC边上的定点，请你在BC边上确定一点P，使△PDE的周长最小（在图中作出点P，保留作图痕迹，不写作法）解：如图所示：【解析】由题意可知DE的长度固定，故此△PDE的周长最小即PD+PE有最小值，先作出点D关于BC的对称点D′，连接D′E交BC于点P，点P即为所求．本题主要考查的是轴对称-最短路线问题，明确当点D′、P、E在一条直线上时，三角形PDE的周长最小是解题的关键．17.在△ABC中，∠C=90°，AC=BC=2，将一块三角板的直角顶点放在斜边AB的中点P处，将此三角板绕点P旋转，三角板的两直角边分别交射线AC、CB与点D、点E，图①，②，③是旋转得到的三种图形．（1）观察线段PD和PE之间的有怎样的大小关系，并以图②为例，加以说明；（2）△PBE是否构成等腰三角形？若能，指出所有的情况（即求出△PBE为等腰三角形时CE的长）；若不能请说明理由．解：（1）PD=PE．以图②为例，如图，连接PC∵△ABC是等腰直角三角形，P为斜边AB的中点，∴PC=PB，CP⊥AB，∠DCP=∠B=45°，又∵∠DPC+∠CPE=90°，∠CPE+∠EPB=90°∴∠DPC=∠EPB∴△DPC≌△EPB（ASA）∴PD=PE；BC=1．（2）能，①当EP=EB时，CE=12②当EP=PB时，点E在BC上，则点E和C重合，CE=0．③当BE=BP时，若点E在BC上，则CE=2-2．若点E在CB的延长线上，则CE=2+2．【解析】（1）连接PC，通过证明△DPC≌△EPB，得出PD=PE．（2）分EP=EB、EP=PB时、BE=BP三种情况进行解答．本题考查了等腰三角形的性质与判定；此题是分类讨论题，应分情况进行论证，不能漏解．辅助线的作出是解答本题的关键．18.如图，已知：△ABC中，AB=AC，BD和CE分别是∠ABC和∠ACB的角平分线，且相交于O点．（1）试说明△OBC是等腰三角形；（2）试判断∠BOC与∠A的关系，（并加以说明）．解：（1）∵在△ABC中，AB=AC，∴∠ABC=∠BCA；∵BD、CE分别平分∠ABC、∠BCA，∴∠OBC=∠BCO；∴OB=OC，∴△OBC为等腰三角形．（2）∠BOC=90°+12∠A．在△ABC中，AB=AC，∴∠ABC=∠BCA，∴∠ABC=12（180°-∠A），∵BD、CE分别平分∠ABC、∠BCA，∴∠OBC=∠BCO；∴∠BOC=180°-2×12∠ABC=180°-12（180°-∠A），∴∠BOC=90°+12∠A．【解析】（1）根据对边对等角得到∠ABC=∠ACB，再结合角平分线的定义得到∠OBC=∠OCB，从而证明OB=OC；（2）根据三角形的内角和即可得到结论．此题考查了等腰三角形的性质，综合利用了全等三角形的判定和角平分线的定义，对各知识点要能够熟练运用．19.如图，△ABC是等边三角形，BD是中线，延长BC至E，CE=CD，（1）求证：DB=DE．（2）在图中过D作DF⊥BE交BE于F，若CF=4，求△ABC的周长．（1）证明：∵△ABC是等边三角形，BD是中线，∴∠ABC=∠ACB=60°．∠DBC=30°（等腰三角形三线合一）．又∵CE=CD，∴∠CDE=∠CED．又∵∠BCD=∠CDE+∠CED，∴∠CDE=∠CED=12∠BCD=30°．∴∠DBC=∠DEC．∴DB=DE（等角对等边）；（2）解：∵∠CDE=∠CED=12∠BCD=30°，∴∠CDF=30°，∵CF=4，∴DC=8，∵AD=CD，∴AC=16，∴△ABC的周长=3AC=48．【解析】（1）根据等边三角形的性质得到∠ABC=∠ACB=60°，∠DBC=30°，再根据角之间的关系求得∠DBC=∠CED，根据等角对等边即可得到DB=DE．（2）由DF的长可求出CD，进而可求出AC的长，则△ABC的周长即可求出．此题主要考查学生对等边三角形的性质及三角形外角的性质的理解及运用；利用三角形外角的性质得到∠CDE=30°是正确解答本题的关键．20.如图a，△ABC和△CEF是两个大小不等的等边三角形，且有一个公共顶点C，连接AF和BE．(1)线段AF和BE有怎样的大小关系？请证明你的结论；(2)将图a中的△CEF绕点C旋转一定的角度，得到图b，这时(1)中的结论还成立吗？作出判断并说明理由；(3)若将图a中的△ABC绕点C旋转一定的角度，请你画出一个变换后的图形(草图即可)，(1)中的结论还成立吗？作出判断不必说明理由；(4)根据以上证明、说理、画图，归纳你的发现．解：(1)AF=BE．证明：在△AFC和△BEC中，∵△ABC和△CEF是等边三角形，∴AC=BC，CF=CE，∠ACF=∠BCE=60°，∴△AFC≌△BEC．∴AF=BE．(2)成立．理由：在△AFC和△BEC中，∵△ABC和△CEF是等边三角形，∴AC=BC，CF=CE，∠ACB=∠FCE=60°，∴∠ACB-∠FCB=∠FCE-∠FCB，即∠ACF=∠BCE．∴△AFC≌△BEC，∴AF=BE．(3)此处图形不惟一，仅举几例．如图，(1)中的结论仍成立．(4)根据以上证明、说明、画图，归纳如下：如图a，大小不等的等边三角形ABC和等边三角形CEF有且仅有一个公共顶点C，则以点C为旋转中心，任意旋转其中一个三角形，都有AF=BE．【解析】(1)根据题中所给的等边三角形的条件，两对边对应相等，有一个角都等于60°，变换这个60°的对应角，利用SAS证AF和BE所在的三角形全等；(2)方法同(1)，利用SAS求证两个三角形全等，进而求解；(3)方法同(1)利用SAS证AF和BE所在的三角形全等；(4)根据前面得到的结论，AF和BE所在的三角形总是全等，那么AF恒等于BE．21.A 、B 两所学校在一条东西走向公路的同旁，以公路所在直线为x 轴建立如图所示的平面直角坐标系，且点A 的坐标是(2，2)，点B 的坐标是(7，3)．(1)一辆汽车由西向东行驶，在行驶过程中是否存在一点C ，使C 点到A 、B 两校的距离相等，如果有？请用尺规作图找出该点，保留作图痕迹，不求该点坐标．(2)若在公路边建一游乐场P ，使游乐场到两校距离之和最小，通过作图在图中找出建游乐场P 的位置，并求出它的坐标．解：(1)存在满足条件的点C ；作出图形，如图所示．(2)作点A 关于x 轴对称的点A ′(2，-2)，连接A ′B ，与x 轴的交点即为所求的点P ．设A ′B 所在直线的解析式为：y =kx +b ，把(2，-2)和(7，3)代入得： 7k +b =32k +b =−2， 解得： k =1b =−4， ∴y =x -4，当y =0时，x =4，所以交点P 为(4，0)．【解析】(1)连接AB ，作出线段AB 的垂直平分线，与x 轴的交点即为所求的点；(2)找到点A 关于x 轴的对称点，连接对称点与点B 与x 轴交点即为所求作的点．。

八年级上册物理练习题及答案一、选择题1. 下列关于声音的说法中，正确的是（）A. 声音是由物体的振动产生的B. 声音的传播速度与介质的种类无关C. 声音的传播速度与温度无关D. 声音的传播速度与频率无关解析：A选项正确，因为声音是由物体的振动产生的。

B选项错误，因为声音的传播速度与介质的种类有关。

C选项错误，因为声音的传播速度与温度有关。

D选项错误，因为声音的传播速度与频率有关。

答案：A2. 下列关于声音的传播的说法中，正确的是（）A. 声音可以在真空中传播B. 声音在固体中的传播速度最快C. 声音在液体中的传播速度最快D. 声音在气体中的传播速度最快解析：B选项正确，因为声音在固体中的传播速度最快。

A选项错误，因为声音不能在真空中传播。

C选项错误，因为声音在液体中的传播速度不是最快的。

D选项错误，因为声音在气体中的传播速度不是最快的。

答案：B3. 下列关于声音的频率的说法中，正确的是（）A. 声音的频率越高，音调越高B. 声音的频率越低，音调越高C. 声音的频率越高，音调越低D. 声音的频率越低，音调越低解析：A选项正确，因为声音的频率越高，音调越高。

B选项错误，因为声音的频率越低，音调越低。

C选项错误，因为声音的频率越高，音调越高。

D选项错误，因为声音的频率越低，音调越低。

答案：A4. 下列关于声音的响度的说法中，正确的是（）A. 声音的响度与声音的频率有关B. 声音的响度与声音的振幅有关C. 声音的响度与声音的传播速度有关D. 声音的响度与声音的波长有关解析：B选项正确，因为声音的响度与声音的振幅有关。

A选项错误，因为声音的响度与声音的频率无关。

C选项错误，因为声音的响度与声音的传播速度无关。

D选项错误，因为声音的响度与声音的波长无关。

答案：B5. 下列关于声音的音色的说法中，正确的是（）A. 音色与发声体的材料有关B. 音色与发声体的形状有关C. 音色与发声体的振动频率有关D. 音色与发声体的振动幅度有关解析：A选项正确，因为音色与发声体的材料有关。

八年级数学上册练习题及答案
1. 整数运算
题目：
a) 两个整数相加得到0，其中一个整数为-15，求另一个
整数是多少？
b) 三个整数相加得到-16，其中两个整数分别为-9和12，求第三个整数是多少？
答案：
a) 另一个整数为15。

b) 第三个整数为-19。

2. 百分数
把小数转换为百分数：
a) 0.25
b) 0.075
答案：
a) 0.25 转化为百分数为25%。

b) 0.075 转换为百分数为7.5%。

3. 几何图形
题目：
计算正方形的面积和周长，其中一条边长为5 cm。

正方形的面积 = 边长× 边长= 5 cm × 5 cm = 25 平方厘米
正方形的周长= 4 × 边长= 4 × 5 cm = 20 厘米
4. 代数方程
题目：
解方程：2x + 3 = 11
答案：
2x + 3 = 11
将3移到方程右边：
2x = 11 - 3
将2移到方程右边：
x = 8 / 2
x = 4
5. 比例
题目：
已知6个苹果的价格是30元，求10个苹果的价格。

答案：
6个苹果的价格 = 30元
1个苹果的价格 = 30元÷ 6 = 5元
10个苹果的价格 = 5元× 10 = 50元
这样的例子还有很多很多，一本数学练习册包含很多章节和各种类型的问题。

希望以上的例子可以帮助您对八年级数学上册的练习题有一个初步的了解。

如果您需要更详细和全面的练习题及答案，建议您参考课本或向数学老师寻求帮助。

八年级数学上册练习题【五篇】【导语:】这篇关于八年级数学上册练习题【五篇】的文章，是特地为大家整理的，希望对大家有所帮助！第二章实数一、选择题1．在下列实数中，是无理数的为（）（A）0（B）－3.5（C）（D）2．A为数轴上表示－1的点，将点A沿数轴移动3个单位到点B，则点B所表示的实数为（）．（A）3（B）2（C）－4（D）2或－43．一个数的平方是4，这个数的立方是（）（A）8（B）－8（C）8或－8（D）4或－44．实数m、n在数轴上的位置如图1所示，则下列不等关系正确的是（）（A）n＜m（B）n2＜m2（C）n0＜m0（D）|n|＜|m|5．下列各数中没有平方根的数是（）（A）－（－2）（B）3（C）（D）－（2+1）6．下列语句错误的是（）（A）的平方根是±（B）－的平方根是－（C）的算术平方根是（D）有两个平方根，它们互为相反数7．下列计算正确的是（）．（A）（B）（C）（D）—18．估计56的大小应在（）．（A）5～6之间（B）6～7之间（C）8～9之间（D）7～8之间9．已知，那么（）（A）0（B）0或1（C）0或-1（D）0，-1或110．已知为实数,且,则的值为（）（A）3（B）（C）1（D）二、填空题11．的平方根是____________，（）2的算术平方根是____________。

12．下列实数：，，，︱－1︱，，，0.1010010001……中无理数的个数有个。

13．写出一个3到4之间的无理数。

14．计算：。

15．的相反数是______，绝对值是______。

三、解答题16．计算：17．某位同学的卧室有25平方米，共用了64块正方形的地板砖，问每块砖的边长是多少？18．如图2，一只蚂蚁沿棱长为的正方体表面从顶点A爬到顶点B，则它走过的最短路程为多少？19．如图3，一架长2.5米的梯子，斜靠在一竖直的墙上，这时，梯底距离墙底端0.7米，如果梯子的顶端沿墙下滑0.4米，那么梯子的低端将滑出多少米？20．学校要在一块长方形的土地上进行绿化，已知这块长方形土地的长=5,宽=4(1)求该长方形土地的面积．(精确到0．01)(2)若绿化该长方形土地每平方米的造价为180元，那么绿化该长方形土地所需资金为多少元?第三章位置与坐标一、选择题1．如图1，小手盖住的点的坐标可能是（）（A）（5，2）（B）（－6，3）（C）（―4，―6）（D）（3，－4）2．在平面直角坐标系中，下列各点在第二象限的是（）（A）（2，1）（B）（2，－1）（C）（－2，1）（D）（－2，－1）3．点P(—2，3)关于y轴对称的点的坐标是（）（A）(—2，—3)（B）(3，—2)（C）(2，3)（D）(2，—3)4．平面直角坐标系内，点A（，）一定不在（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限5．如果点P(在轴上，则点P的坐标为（）(A)(0，2)(B)(2，0)(C)(4，0)(D)(0，6．已知点P的坐标为(，且点P到两坐标轴的距离相等，则点P的坐标为（）(A)(3，3)(B)(3，(C)(6，(D)(3，3)或(6，7．已知点A（2，0）、点B（－，0）、点C（0，1），以A、B、C三点为顶点画平行四边形，则第四个顶点不可能在（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限8．若P（）在第二象限，则Q()在（）（A）第一象限（B）第二象限（C）第三象限（D）第四象限9．如图2是某战役中缴获敌人防御工程的坐标地图碎片，依稀可见:一号暗堡的坐标为（1，2），四号暗堡的坐标为（-3，2）．另有情报得知:指挥部坐标为（0，0），你认为敌军指挥部的位置大约是（）（A）A处（B）B处（C）C处（D）D处10．以边长为4的正方形的对角线建立平面直角坐标系，其中一个顶点位于轴的负半轴上，则该点坐标为（）（A）（2，0）（B）（0，－2）（C）（0，）（D）（0，）二、填空题11．点A在轴上，且与原点的距离为5，则点A的坐标是________．12．如图3，每个小方格都是边长为1个单位长度的正方形，如果用（0，0）表示A点的位置，用（3，4）表示B点的位置，那么用表示C点的位置.13．已知点M，将点M向右平移个单位长度得到N点，则N点的坐标为________.14．第三象限内的点，满足，，则点的坐标是．15．如图4，将AOB绕点O逆时针旋转900，得到。

10.18八年级物理练习一．选择题（共12小题，每题2分，共24分）1．如图所示为杭州亚运会吉祥物“琮琮”，根据图片信息估测图中琮琮的高度约为（）A．3mm B．3cm C．3dm D．3m2．如图所示是位于成都世园会主会场的摩天轮——天府眼，它紧邻绛溪河与植物馆，与锦云楼相互呼应，是游客游览成都世园会重要的参观点之一。

游客在箱内随摩天轮上升的过程中，下列说法正确的是（）A．以地面为参照物，游客是静止的B．以乘客为参照物，地面是静止的C．以其他的箱体为参照物，游客是静止的D．以乘坐的箱体为参照物，游客是静止的3．下列实例中，与其他三项运动形式不同的是（）A．行星转动B．小树长高C．车水马龙D．骏马奔腾4．关于错误和误差，下列说法中正确的是（）A．错误是不可避免的B．错误是由于测量工具不够精密造成的C．误差是由不规范的操作造成的D．通过多次测量取平均值可以减少误差5．如图所示，是甲、乙两个小球同时从左向右运动，每隔0.1s拍下的“频闪照片”，甲、乙两小球在0.2s～0.3s分别从a点运动到b点、从c点运动到d点。

分析“频闪照片”，下列说法正确的是（）A．甲、乙两球都做变速直线运动B．照片记录的甲球运动时间比乙球运动时间短C．从开始计时到0.3s时，甲球的平均速度比乙球大D．甲、乙两球在ab、cd段的运动中，以乙球为参照物，甲球向左运动6．所谓区间测速，是指检测机动车通过两个相邻测速监控点之间的路段（测速区间）的平均速度的方法。

如图是某交通标志牌，下列说法错误的是（）A．某小车通过该路段用了4min，没有超速B．此段路车速最高不超过60km/hC．此段路车速最低不低于60km/hD．以行驶的汽车为参照物，交通标志牌是运动的7．如图，用刻度尺测长度的方法中不合理的是（）A．B．C．D．8．某物体做匀速直线运动，由速度公式v＝可知，物体的（）A．速度与路程成正比B．速度大小恒定不变C．速度与时间成反比D．以上说法都对9．如图所示，记录了甲、乙两辆汽车在平直公路上行驶时，相同时间内通过的路程。

八年级数学练习册篇一：人教版八年级数学练习册答案新课程课堂同步练习本《数学》（人民教育版八年级第一册）参考答案第十一章全等三角形11.1全等三角形一、一.c2.c二、 1 （1）①阿布德②acdc③棉花华东（2）①∠a∠d②∠b∠e③∠acb∠dce二点一二零四三、1.对应角分别是：∠aoc和∠dob，∠aco和∠dbo，∠a和∠d.相应的边是：Ao和do、OB和OC、AC和DB2.相等，理由如下：∵△abc≌△dfe∴bc=fe∴bc-ec=fe-ec∴be=fc3.相等，理由如下：∵△abc≌△aef∴∠cab=∠fae∴∠cab―∠baf=∠fae―∠baf即∠caf=∠eab11.2全等三角形的确定（I）一、一.1002.△bad,三边对应相等的两个三角形全等（sss）3.2,△亚行≌△数模转换器，△abc≌△dcb4。

24二、1.∵bg=ce∴be=cg在△abe和△dcg中，∴△阿贝≌△dcg（sss）∴∠b=∠C2.∵d是bc中点，∴bd=cd，在△abd和△acd中，∴△阿布德≌△acd（sss）∴∠亚行=∠adc又∵∠adb+∠adc=180°∴∠adb=90°∴ad⊥bc3.提示：证书△ AEC≌ △ BFD，∠ DAB=∠ CBA，8787∠ 1 = ∠ 2.≠∠ DAB-∠ 1 = ∠ CBA-∠ 2可以得到∠ ace=∠ FDB11.2全等三角形的判定（二）一、 1 d2。

C二、1.ob=oc2.95三、 1有人建议∠ DAC=∠ DBC可以通过使用“SAS”证书获得△ 轻而快地擦掉≌ △ 中国篮球协会2.∵∠1=∠2∴∠1+∠cad=∠2+∠cad即∠bac=∠dae，在△bac和△dae中，∴△bac≌△dae（sas）∴bc=de3.（1）可添加的条件为：BC=EF或be=CF（2）∵ab∥de∴∠b=∠def，在△abc和△def中，∴△abc≌△def（sas）11.2全等三角形的判定（三）一、 1 c2。

海淀区八年级练习语 文2025.01学校 班级 姓名一、基础·运用(共15分)今年是颐和园向公众开放110周年。

班级准备制作一期关于颐和园的板报，下面是各组同学准备的材料，现在请你帮助完善。

第一部分 颐和探源 “颐和探源”组同学制作了“清．漪出锦绣”资料卡。

请阅读资料卡，完成任务。

2.文段拼音处应填入的汉字、加点字的读音，全都正确的一项是(2分)A.障 彰 xiào jìnB.嶂 张 xi āo jìngC.嶂 彰 xiào jìngD.障 张 xi āo jìn3.根据文段内容，在横线处填入成语，最恰当的一项是(2分)A. 妙手偶得B.因地制宜C. 精益求精D. 一丝不苟第二部分 颐和寻美4.下面是“颐和寻美”组的考察记录，请阅读并完成相关任务。

(4分)被联合国救科文组织列入《世界遗产名录》的颐和园，其园址选择、细节处理和建筑布局，体现了多重美学的追求。

颐和园选址于山水之问，呈现了中国古典园林所崇尚的自然山水之美；以全园制高点①佛香阁为标志的中央建筑群、阐释了中国古典园林造园艺术的人文之美②园林中树木花草的配置和栽种都颇具匠心，使颐和园的景致富于变化，极具图画之美。

(1)有同学对材料中①②两处使用的标点符号有疑问，你认为这两处的标点符号使用正确的是(2分)A. 破折号句号B. 冒号句号C. 骨号分号D. 破折号分号(2)文段中的画线句表达欠妥，请你修改。

(2分)答：5.“颐和寻美”小组同学被匾额吸引，产生探究的兴趣。

请你一起完成下面任务。

(4分)第三部分颐和新境6.“颐和新境”组准备了宣传资料、请你根据语境，依次在横线上填入短语、最恰当的一项是(2分)颐和园作为“三山五园”中保护最为完整的古典园林和唯一的世界文化遴产，近年宋在等方面成绩斐然。

从保护性修绺后的长廊到重新充相的“画中游”，古建修络技艺不断进步。

从桃柳央岸的西堤到五彩斑斓的后溪河，皇家因林特色景观体系不断完善。

八年级物理练习题及答案1. 一个物体质量为2kg，受到的力是10N，求物体的加速度。

解答：根据牛顿第二定律F=ma，可知力等于质量乘以加速度。

所以加速度等于力除以质量，即a=F/m=10N/2kg=5m/s²。

2. 一辆汽车以10m/s的速度匀速行驶了20秒，求汽车的位移。

解答：匀速运动的位移可以通过速度乘以时间来计算。

所以位移等于速度乘以时间，即位移=速度×时间=10m/s×20s=200m。

3. 一个物体从静止开始匀加速运动，经过5秒后速度为20m/s，求物体的加速度。

解答：匀加速运动的速度可以通过加速度乘以时间来计算。

所以加速度等于速度除以时间，即加速度=速度/时间=20m/s/5s=4m/s²。

4. 一个物体以10m/s²的加速度匀加速运动，经过6秒后速度为16m/s，求物体的起始速度。

解答：物体的起始速度可以通过速度减去加速度乘以时间来计算。

所以起始速度等于速度减去加速度乘以时间，即起始速度=速度-加速度×时间=16m/s-10m/s²×6s=16m/s-60m/s= -44m/s。

5. 一个物体以20m/s²的加速度匀加速运动，经过4秒后速度为36m/s，求物体的位移。

解答：物体的位移可以通过速度乘以时间加上加速度乘以时间的平方的一半来计算。

所以位移等于速度乘以时间加上加速度乘以时间的平方的一半，即位移=速度×时间+0.5×加速度×时间²=36m/s×4s+0.5×20m/s²×4s²=144m+80m=224m。

6. 对于一个静止的物体，如果受到的合力为零，那么物体的状态将保持不变，即静止或匀速直线运动。

7. 一个物体只受到重力和支持力，没有其他力作用，那么物体的合力为零，即物体处于平衡状态。

8. 牛顿第一定律也被称为惯性定律，它表明在没有外力作用时，物体将保持静止或匀速直线运动的状态。

八年级上册英语练习题及答案第一单元：Hello! 你好！练习题1. 请用所给的单词完成下列句子：a. My name is __Tom__.b. She is __eleven__ years old.c. There are __twenty__ students in my class.2. 根据所给的句子完成对话：A: __Hello, my name is John. What's your name?__B: __Hello, my name is__ __Li Ming__.3. 翻译下列句子：a. What's your name?b. How old are you?c. Where are you from? 答案1.a. Tomb. elevenc. twenty2.A: Hello, my name is John. What's your name? B: Hello, my name is Li Ming.3.a. 你叫什么名字？b. 你多大了？c. 你来自哪里？---第二单元：Family and Friends练习题1. 请用所给的单词完成下列句子：a. My __mother__ is a teacher.b. That is my __sister__.c. These are my __brothers__ and __sisters__.2. 根据所给的句子完成对话：A: __Hello, this is John. Who is this?__B: __Hello, this is__ __Mike__. __Nice to meet you.__3. 翻译下列句子：a. Who is that man?b. How many brothers and sisters do you have?c. What does your mother do?答案1.a. motherb. sisterc. brothers, sisters2.A: Hello, this is John. Who is this?B: Hello, this is Mike. Nice to meet you.3.a. 那个人是谁？b. 你有多少个兄弟和姐妹？c. 你妈妈是做什么的？---第三单元：School Life练习题1. 请用所给的单词完成下列句子：a. I go to __school__ at 8:00 a.m.b. Our __classroom__ is on the second floor.c. We have __math__, __English__, and __history__ lessons on Mondays.2. 根据所给的句子完成对话：A: __Hello, how was your first day at school?__B: __It was__ __great__. __I met a lot of new friends.__3. 翻译下列句子：a. What lessons do you have on Mondays?b. How was your first day at school?c. Do you like your new classmates?答案1.a. schoolb. classroomc. math, English, history2.A: Hello, how was your first day at school? B: It was great. I met a lot of new friends.3.a. 你星期一有什么课程？b. 你在学校的第一个日子怎么样？c. 你喜欢你的新同学吗？---以上是八年级上册英语的前三个单元的练习题及答案。

八年级数学练习册答案（精品8篇）八年级数学练习册答案（1）基础达标1、整式：-3x+2/5m;a+3b/5;m-4/4;1/π(x+y)分式：x+1/x+2;1+3/x;m-3/m;4/3-2x;2/2x+12、x=-2;x=2/3;x≠2;x≠1且x≠-23、x>1;x+y≠04、1/a-b5、(1)-2/3x(2)1/y(3)-2/ab(4)5+y/x6、B7、A8、D9、C10、D综合提升11、a+1=3,a=2a+1=1,a=0a+1=-3,a=-4a+1=-1,a=-212、5-x/x2>0x2(5-x)0x-5x13、(1)6x+4y/3x-4y(2)10x+4y/10y-5x14、p/(a/m+b/n)=pmn/an+bm(天)15、P1=MP/(1-35%)M=20/13P16、解：kda2/m2八年级数学练习册答案（2）基础达标1、B2、D3、D4、B5、A6、x/x-1-x+3/x2-1?(x+1)2x+3=x/x-1-x+1/x-1=-1/x-1=-1/x-17、a-b/a+2b÷a2-b2/(a+2b)2-1=a-b/a+2b×(a+2b)2/(a+b)(a-b)-1=a+2b/a+b-1=a+2b-a-b/a+b=b/a+ba=b=1b/a+b=1/28、(x-3/x+3+6x/x2-9)÷1/x2-9=x-3/x+3×(x2-9)+6x/x2-9×(x2-9)=(x-3)2+6x=x2+99、(1)A?B=(3x/x-2-x/x+2)(x2-4/x)=2x+8(2)若一个数是x2-4/x,与另一个数的积是2x+8,求另一个数(2x+8)÷x2-4/x=2x(x+4)/x2-4=3x/x-2-x/x+2综合提升10、(x/y-y/x)÷(x/y+y/x-2)÷(1+y/x)=x2-y2/xy÷x2+y2-2xy/xy÷x+y/x=x2-y2/xy×xy/(x-y)2×x/x+y=x+y/x-y×x/x+y=x/x+y=x/x+y=(1/2)/(1/2+1/3)=(1/2)/(5/6)=1/2×6/5=3/5 11、(1)1/n-1/n+1(2)①1-1/20XX=20XX/20XX②1-1/n+1=n/n+1(3)1/2-1/4+1/4-1/6+1/6-1/8+…+1/20XX×20XX=1/2-1/20XX=1004-1/20XX=1003/20XX八年级数学练习册答案（3）第4节分式方程答案基础达标1、B2、D3、A4、C5、(1)解：x/2x-5-5/2x-5=1x-5/2x-5=1x-5=2x-5x=0(2)解：5x-4/2x-4=2x+5/3x-6-1/215x-12/6x-12-4x+10/6x-12=-1/211x-22=-1/2(6x-12)11x-22=-3x+614x=28x=26、2x+a/x-2=12x+a/x-2+1=02x+a+x-2/x-2=03x+a-2/x-2=03x+a-2=03x=a-2x=2-a/3>0a7、1/x-1=-1/28、解：2/x+1+5/1-x=m/x2-12(x-1)-5(1+x)=m2x-2-5-5x=m-3x-7=m当x=1时，m=-10当x=-1时，m=-49、(1)通分(2)②(3)移项变号10、解：设慢车的速度是x，快车的速度是X=50慢车速度50km/h11、解：设第一批的进价是x元。

2023-2024学年八年级语文上册练习★★
周末作业(二)
题型
积累运用(30分)
课内外文言文比较 阅读(15分)
总分(45分)
得分
一、积累运用 1.默写古诗文。(共10分。答对一句得1分，满分不超过10分) (1)八方各异气， 千里殊风雨 。(曹植《梁甫行》) (2) 攀条折其荣 ，将以遗所思。 馨香盈怀袖 ，路远莫致 之。(《庭中有奇树》) (3)此物何足贵? 但感别经时 。(《庭中有奇树》)
(4)东汉末年建安时期，以“三曹”为代表，其作品真实反映了现 实生活和人民的苦难。“ 老骥伏枥 ， 志在千里 ； 烈士暮年 ， 壮心不已 ”(曹操《龟虽寿》)抒发了诗人建功立 业的理想和积极进取的精神；“ 冰霜正惨凄 ， 终岁常端正 ” [刘桢《赠从弟(其二)》]突出了松柏傲雪凌霜的美好品格； “ 柴门何萧条 ， 狐兔翔我宇 ”(曹植《梁甫行》)咏叹家园荒 芜，狐兔出没，表达了诗人强烈的激愤之情。该类作品形成了 雄健深沉、慷慨悲凉的艺术风格，文学史上称之为“建安风骨” 或“魏晋风骨”。
雕塑图片：
雕塑简介：《新四军东进》雕塑是东台市杰出乡友、全国政协 常委、中国美协副主席、中国美术馆馆长吴为山所创作。新落 成的“大铜马”为枣红色，坐西向东，高5.2米，长5.15米，宽2.07 米。雕塑由基座和骑马战士塑像两部分组成。基座上刻写的“东 进”二字在阳光下熠熠生辉，背面新四军东进纪事记录了陈毅、 粟裕等老一辈革命家率领新四军在东台浴血奋战的光辉历程。
比得上；D.结构助词，的/代词，指代所学的知识。
4.请用“/”给文中画线的句子断句。(3分) 而置州以来无人赏爱 徘徊溪上为之怅然 而 置 州 以 来 /无 人 赏 爱 / 徘 徊 溪 上 / 为 之 怅 然
5.【甲】【乙】两文都写水，其中【乙】文哪些句子是写水 的?【甲】【乙】两文共同突出了水的什么特点?(2分)(高阶 思维) 【乙】文写水的句子是：清流触石，洄悬激注。(1分) 【甲】【乙】两文共同突出了“水流湍急”的特点。(1分)