生产计划安排最优化模型
- 格式:doc
- 大小:300.00 KB
- 文档页数:13

最优化理论与方法
最优化理论与方法是一门涉及在给定约束条件下寻求最佳解的学科。
其应用广泛,可用于解决诸如生产计划、资源分配、网络设计、机器学习等领域中的问题。
最优化问题通常涉及目标函数的最大化或最小化,以及一些约束条件。
最优化理论与方法旨在寻找能够满足约束条件下使目标函数达到极值的解。
最优化问题的解可能是一个点、一条线、一个曲线,甚至可以是一个函数。
最优化方法可以分为两大类:无约束优化方法和有约束优化方法。
无约束优化方法中,最常用的是求解无约束问题的导数为零的点,即寻找目标函数的极值点。
常用的算法包括梯度下降法、牛顿法和拟牛顿法等。
有约束优化问题相对复杂,求解方法依赖于约束条件的类型。
常见的算法有拉格朗日乘子法、KKT条件、线性规划等。
最优化理论与方法在实际应用中有着广泛的应用。
例如,在生产计划中,可以使用最优化方法来确定最佳的生产量,以最大化利润或最小化成本。
在资源分配问题中,可以使用最优化方法来确定资源的最佳分配方案,以满足不同的需求。
在机器学习中,最优化方法常用于确定模型的最优参数,以提高模型的准确性和性能。
总之,最优化理论与方法为解决各种实际问题提供了一种有效的数学工具。
通过寻找目标函数的最佳解,可以提高效率、优化资源利用以及加强决策的科学性。
在未来的发展中,最优化
理论与方法将继续发挥重要作用,并在更多领域中得到广泛应用。

发电机组合生产的线形规划模型姓名:鲁成学号:2009409433 姓名:阮国淼学号:2009409434 姓名:王良泽南学号:2009401315 姓名:李操学号:2009409431摘要本文研究的是发电机组合生产中发电机使用计划的最优化问题。
通过对问题的分析和合理的假设,采用规划的理论建立了以使用发电机在每天7个时间段内总花费成本的最小值为目标函数的线性规划模型。
运用LINGO软件得到了全局最优解,对此类问题的求解提供了一种较优的方案。
问题(1),文中以发电机在每天7个时间段内总花费成本的最小值为目标函数,以用户每个时间段用电需求量不同、发电机的启动成本、发电机工作于最小功率状态时的固定的每小时成本以及发电机功率超出最小功率部分每兆瓦每小时存在的边际成本等为约束条件,建立了使得每日电力生产成本最小的线性规划模型。
在实际生产过程中,为了保护发电机,通常实际生产功率不高于额定功率的80%,且频繁开启、关闭会对发电机造成无法恢复的机械损伤,因此,据此我们对模型进行了适当优化,增加了部分生产费用来延长发电机的使用寿命。
运用LINGO求解,得出只须花费1516829.97元即可完成当日的电力生产任务。
具体结果见文中表3。
问题(2), 建立了使得在任意时刻,正在工作的发电机组都留出20%的发电能力余量且每日电力生产成本最小的线性规划模型。
运用LINGO求解,得出只须花费1915330.0元即可完成当日的电力生产任务。
具体结果见文中表4。
最后,对模型的优缺点进行了分析,并给出了模型的改进意见,对解决实际问题具有一定的指导意义。
关键词:线性规划;LINGO;最优解;模型优化Ⅰ问题重述在实际生活中,通过统计,得出用户每日电力需求情况如表1所示:表1 每日用电需求(兆瓦)时段0点—6点6点—9点9点—12点12点—14点14点—18点18点—22点22点—24点需求12000 32000 25000 36000 25000 30000 18000为了满足用户每日的电力需求,我们选用了如下四种不同类型的发电机生产电力。

第一章 线性规划模型线性规划(Linear Programming )是数学规划的一个重要组成部分,是最优化与运筹学理论中的一个重要分支和常用的方法,是最优化理论的基础性内容。
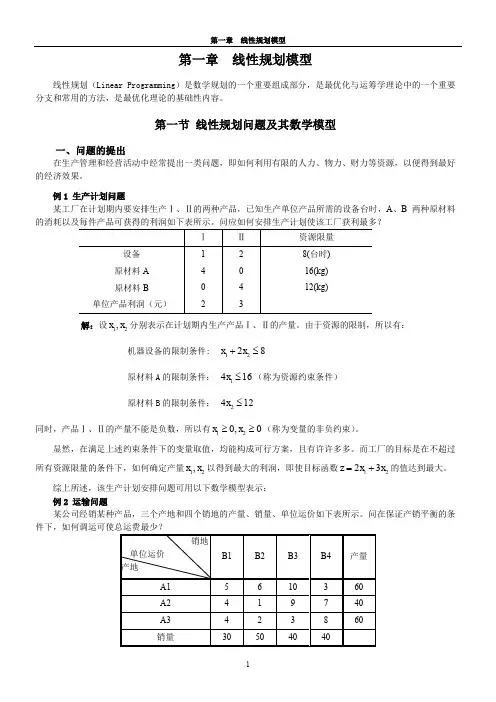
第一节 线性规划问题及其数学模型一、问题的提出在生产管理和经营活动中经常提出一类问题,即如何利用有限的人力、物力、财力等资源,以便得到最好的经济效果。
例1 生产计划问题某工厂在计划期内要安排生产Ⅰ、Ⅱ的两种产品,已知生产单位产品所需的设备台时,A 、B 两种原材料的消耗以及每件产品可获得的利润如下表所示。
问应如何安排生产计划使该工厂获利最多?解:设12,x x 分别表示在计划期内生产产品Ⅰ、Ⅱ的产量。
由于资源的限制,所以有:机器设备的限制条件: 1228x x +≤原材料A 的限制条件: 1416x ≤(称为资源约束条件) 原材料B 的限制条件: 2412x ≤同时,产品Ⅰ、Ⅱ的产量不能是负数,所以有120,0x x ≥≥(称为变量的非负约束)。
显然,在满足上述约束条件下的变量取值,均能构成可行方案,且有许许多多。
而工厂的目标是在不超过所有资源限量的条件下,如何确定产量12,x x 以得到最大的利润,即使目标函数1223z x x =+的值达到最大。
综上所述,该生产计划安排问题可用以下数学模型表示:例2 运输问题某公司经销某种产品,三个产地和四个销地的产量、销量、单位运价如下表所示。
问在保证产销平衡的条解:(1)决策变量:设(1,2,3;1,2,3,4)ij x i j ==为从产地i 运到销地j 的运量(2)目标函数:总运费最小3411min ij iji j z c x===∑∑(3)约束条件: 产量约束 销量约束 非负约束 模型为:二、线性规划问题的模型上述几例所提出的问题,可归结为在变量满足线性约束条件下,求使线性目标函数值最大或最小的问题。
它们具有以下共同的特征。
(1)每个问题都可用一组决策变量12(,,,)n x x x 表示某一方案,其具体的值就代表一个具体方案。

2003年大学生数学建模全国一等奖论文学员:吴成映王聿磊曹霞斌指导老师:朱家明露天矿生产车辆安排方案的优化模型摘要本文建立了露天矿生产车辆安排方案的优化模型,为提高设备的利用率以增加露天矿经济效益,在卡车不等待条件下且满足产量和品位要求的基础上,依据所给的两条原则分别建模制定了一个班次的生产计划:铲车的定辆定位和卡车定辆定线定次,并相应给出各生产计划的快速算法、总运量及岩矿石的产量,最终在讨论分析后,对模型做出了评价和改进。
模型Ⅰ对问题1建立了求路段车次上限、卸点车次下限、铲位矿与岩最大整车数等模型,并依据原则一分步建立了若干个线性规划模型,运用Mathematic软件求解,综合给出了生产计划:出动6辆铲车;出动13辆卡车;a相应的总运量88496.1吨公里,岩石产量32186吨,矿石产量38192吨。
模型Ⅱ对问题1建立整数规划模型,采用lingo编程法,给出了一个班次的生产计划:出动7辆铲车,铲位1、2、3、4、8、9、10各安排一辆;出动13辆卡车,具体方案为:铲位1→岩石漏81车次,2辆;铲位3→岩石漏43车次,1辆;铲位9→岩场70车次,2辆;铲位4→倒装场Ⅰ45车次,2辆;铲位8→矿石漏54车次,2辆;铲位2 →倒装场Ⅰ40车次,→矿石漏13车次,→倒装场Ⅱ15车次,3辆;铲位10 →岩场15车次,→矿石漏11车次,→倒装场Ⅱ70车次,2辆。
相应的总运量85714.86吨公里,岩石产量32186吨,矿石产量38192吨。
结果总运量优于模型Ⅰ,产量相同。
模型Ⅲ对问题2建立最优化模型,利用lingo编程法,给出生产计划:出动全部7辆,铲位1、2、3、7、8、9、10各安排一辆;出动20辆卡车,具体方案为:铲位1→倒装场Ⅰ15车,岩石漏81车;铲位2→倒装场Ⅰ66车,→岩石漏28车,→倒装场Ⅱ2车;铲位3→矿石漏20车,→岩石漏51车,→倒装场Ⅱ25车;铲位7→倒装场Ⅰ68车,→岩场28车;铲位8→矿石漏60车,→倒装场Ⅰ2车,→岩场12车,→倒装场Ⅱ22车;铲位9→倒装场Ⅰ9车,→岩场87车;铲位10→岩场33车,→倒装场Ⅱ63车。
Stip模型是一个用于描述供应链中库存和生产决策的模型。
它是一种统计模型,用于分析库存和生产策略,以实现库存管理和生产效率的最优化。
Stip模型基于统计和概率方法,考虑了库存和生产过程的随机性和不确定性,提供了有关库存策略和生产决策的详细信息。
Stip模型的主要组成部分包括需求预测、库存计划、生产计划和决策规则。
需求预测考虑了消费者的需求模式和季节性变化,并使用统计模型进行预测。
库存计划基于库存需求和可用库存量,决定最佳的库存水平和管理策略,如安全库存、补货策略等。
生产计划考虑了生产能力和生产成本,以确定最佳的生产批次、生产数量和生产时间。
此外,Stip模型还包括决策规则,用于指导库存和生产决策的实施。
这些规则基于业务目标和风险评估,允许管理者根据实际情况进行调整和优化。
Stip模型的目标是实现库存成本和生产效率的最优化,同时满足业务需求和消费者期望。
Stip模型的应用范围广泛,适用于各种类型的供应链场景,包括制造、物流、零售等。
它可以帮助企业制定合理的库存和生产策略,降低库存成本和缺货风险,提高生产效率和质量。
此外,Stip模型还可以用于分析供应链风险和不确定性,以及制定相应的应对策略。
总之,Stip模型是一个用于描述供应链中库存和生产决策的统计模型,它基于概率和统计方法,提供有关库存策略和生产决策的详细信息,以实现库存管理和生产效率的最优化。
Stip 模型的应用范围广泛,适用于各种类型的供应链场景,为企业提供合理的库存和生产策略,降低成本和风险,提高效率和竞争力。
基于asprova的某企业生产计划与排程工作的优化摘要在制造型企业中,根据己有的资源,包括工具、设备、工人等的具体情况,以及各种约束条件,对现有订单需要生产的产品制定生产计划是一项非常重要的工作。
生产计划的质量直接影响到能否给客户一个合理的可以接受的交货期,并且做到最低的库存,最短的制造提前期。
订单的完成情况会直接影响到企业的客户满意度,进而影响企业的长远发展。
由于ERP生产计划不准确,它的生产计划与排程模块很难满足企业的需要。
而APS 系统是在ERP的基础上不断发展起来的,它弥补了ERP的多种不足之处,使生产从计划到车间执行、生产调度一气呵成,它以独有的优势很好地解决了企业在生产计划与排程上的难题。
本论文首先对APS(高级计划排程)基础理论进行研究,介绍了高级计划排程的概念和基本原理,并做以详细分析说明。
然后对某一现实食品制造企业的现状与存在的问题进行论述,运用asprova软件对生产计划与排程工作进行建模与设计。
asprova的模拟结果展示了APS在生产计划与排程上的优势。
关键词:ERP ,高级计划与排程 ,asprova,设计Based On The Asprova Of A Certain Enterprise's Production Planning And Scheduling Optimization Of WorkABSTRACTIn manufacturing enterprises, according to some of their own resources, including tools, equipment, works and so on the specific circumstances, as well as variety of constraints, it is a very important job to develop the production planning & schedule of products on the existing orders .The production planning & schedule has a direct impact on giving customers a reasonable & acceptable delivery, and to achieve the lowest inventories, to create the shortest lead time. the completion of orders will have a direct impact on the customer satisfaction, thereby affecting the long-term development.For the production planning of ERP is not accurate, it is hard to meet the need of the enterprise in the production planning & scheduling. However, APS system is continually on the basis of ERP, it makes up a variety deficiencies of ERP. integration of the workshop task and the workshop work function, making the production plan to shop execution, production scheduling in one take, with the unique advantages it easily solutes the problem of enterprise in the production planning and scheduling.This article first introduces the basic theory of the APS and the differences and relations among APS, MRP and ERP. And then discusses the problems of a real food manufacturing enterprise, by using the asprova software combined with the actual situation of an enterprise to model and design production planning and scheduling. The simulation results of asprova shows the absolute advantage of the APS in production planning and scheduling.KEY WORDS: ERP,APS, asprova, design目录摘要 (I)ABSTRACT (II)1 绪论 (1)1.1论文研究的背景 (1)1.2 研究的主要内容 (2)1.3论文研究的意义 (3)2 APS相关理论 (5)2.1 APS的相关概念 (5)2.1.1 APS的起源 (5)2.1.2 APS的概念 (5)2.1.3 APS的现状及发展趋势 (6)2.2 APS的系统结构和功能模型 (7)2.2.1 APS的系统结构 (7)2.2.2 APS的功能模型 (8)2.3 APS的特征与作用范围 (9)2.3.1 APS的特征 (9)2.3.2 APS的作用范围 (10)2.4 APS与MRP、ERP的关系 (11)2.4.1 APS与MRP的关系 (11)2.4.2 APS与ERP的联系与区别 (11)2.5 APS排成要素与相关原则 (13)2.5.1 APS排程三要素 (13)2.5.2 APS排程时必须考虑的限制因素 (14)2.5.3 APS排程时的最短路径原则 (15)3 食品(方便面)制造企业概述 (16)3.1企业业务流程 (16)3.1.1总体业务流程 (16)3.1.2 生产流程 (16)3.1.3车间制造流程 (17)3.2企业情况 (18)3.3企业存在的问题 (18)IV3.3.1库存积压 (18)3.3.2 生产车间任务量大,缺乏弹性 (19)3.3.3 生产计划的制定和执行困难 (19)3.4运用asprova进行生产计划与排程 (19)4 基于该企业的APS生产排程的建模与设计 (20)4.1资源 (20)4.1.1 物料 (20)4.1.2 工人 (21)4.1.3 生产线 (21)4.1.4 机器 (22)4.1.5 仓库 (22)4.1.6 供应商 (22)4.2工艺路线 (22)4.2.1 操作工序 (22)4.2.2 工序流程图 (29)4.3 外围要素 (32)4.3.1 时间范围 (32)4.3.2 日程安排 (32)4.3.3 供需情况 (32)4.4 asprova APS的模型建立过程 (33)4.5 asprova APS在生产计划与排程上的优化与分析 (38)4.5.1 精确生产排计划与排程 (38)4.5.2 可适应的几种突发情况 (39)4.5.3 导入Asprova APS系统后给企业带来的好处 (39)4.6 案例总结 (39)5 总结 (42)致谢 (43)参考文献 (44)基于asprova的某企业生产计划与排程工作的优化 11 绪论作为企业信息中枢的ERP系统,现在已经在许多企业中用于作业处理和定单执行。
生产计划安排最优化模型 摘要 本文是针对工厂生产计划的安排对总利润的影响问题,通过对题目的分析,建立线性规划模型,利用Lingo软件对模型进行编程求出最优解,最终完整地解决这一问题。 分析题意,可知总利润=总销售利润-总存储费用,据此我们建立了本题的目标函数。同时依据题目的要求,可以得出对目标函数的约束条件可分为各种产品每个月的产量约束,各种产品每个月的存储量约束,各种产品每个月的生产时间约束,然后根据这三种约束条件可得出各个约束式,因此,已知目标函数与约束条件,再通过利用Lingo软件进行编程求出最优解,最终得出六个月的最大利润为937115元。 从Lingo软件的求解中,可以得出各个月的生产计划安排,同时我们对各个月的生产计划表进行分析,发现各个月都有不生产的产品,而这些产品销售量都符合各个月的最大需求量要求,而特别的是一月份无生产产品VII,经过对题目的分析,发现生产产品VII所需的单位设备所需台时,比生产其他产品的单位设备所需台时要耗时,因此不生产产品VII是符合最大利润要求,从而得出各个月的生产计划安排都符合题意要求。 最后根据求解结果对每个月生产情况的合理性进行了分析,得出的结论是:根据模型所建立的生产计划是科学合理的。
关键字:生产计划,线性规划,lingo问题重述 企业是一个有机的整体,企业管理是一个完整的系统,由许多子系统组成。在企业的管理中,非常关键的一部分是科学地安排生产。对于生产、库存与设备维修更新的合理安排对企业的生存和发展具有重要的意义。 已知某工厂要生产7种产品,以I,II,III,IV,V,VI,VII来表示,但每种产品的单件利润随市场信息有明显波动,现只能给出大约利润如下。 产 品 I II III IV V VI VII 大约利润/元 100 60 80 40 110 90 30 该厂有4台磨床、2台立钻、3台水平钻、1台镗床和1台刨床可以用来生产上述产品。已知生产单位各种产品所需的有关设备台时如下表。 单位所需 台时 设备 I II III IV V VI VII
磨床 0.5 0.7 / / 0.3 0.2 0.5 立钻 0.1 0.2 / 0.3 / 0.6 / 水平钻 0.2 / 0.8 / / / 0.6 镗床 0.05 0.03 / 0.07 0.1 / 0.08 刨床 / / 0.01 / 0.05 / 0.05 从1月到6月,维修计划如下:1月—1台磨床,2月—2台水平钻,3月—1台镗床,4月—1台立钻,5月—1台磨床和1台立钻,6月—1台刨床和1台水平钻,被维修的设备当月不能安排生产。 又知从1—6月市场对上述7中产品最大需求量如下表所示。 I II III IV V VI VII 1月 500 1000 300 300 800 200 100 2月 600 500 200 0 400 300 150 3月 300 600 0 0 500 400 100 4月 200 300 400 500 200 0 100 5月 0 100 500 100 1000 300 0 6月 500 500 100 300 1100 500 60 每种产品当月销售不了的每件每月存储费为5元,但规定任何时候每种产品的存储量均不能超过100件。1月初无库存,要求6月末各种产品各储存50件。 若该工厂每月工作24天,每天两班,每班8小时,问该厂应如何安排生产,可使总利润达到最大。
1. 模型的假设与符号说明 2.1 模型的假设 1. 假设工厂的设备都不是全新的; 2. 假设工厂的设备每天连续工作16小时,不受换班影响; 3. 假设工厂设备的维修不收取费用。
产 品 2.2 符号说明 Z 表示六个月的总利润 Pij 表示第i个月第j种产品的产量 Rij 表示第i个月第j种产品的库存量 Sij 表示第i个月第j种产品的销售量 Qij 表示第i个月第j种产品的最大需求量 Nki 表示第k种设备第i个月的可用数量 Xij 表示第i个月第j种产品的单位利润 Tkj 表示第k种设备第j种产品的单位所需台时 (其中i代表月份i=1,2,3…6,j代表产品的种类j=1,2,3…7,k代表设备的种类k=1,2,3…5,注:其他符号在相关位置再作假设。)
2. 问题分析 企业是一个有机的整体,企业管理是一个完整的系统,由许多子系统组成。在企业的管理中,非常关键的一部分是科学地安排生产,即生产计划。而生产计划就是一种关于企业生产运作系统总体方面的计划,是企业在计划期应达到的产品品种、质量、产量和产值等生产任务的计划和对产品生产进度的安排。 对于本问题明显是一个线性规划问题,由于各类产品的销售利润不同,生产的时间不同,因此,以各个月利润最大为目标,通过对题目数据的分析,最终求出最大总利润。从题目中可以得知,要求出这6个月的总利润,则需要求出6个月的产品销售总利润,同时要求出6个月的总存储费用。从而能够得出以下公式 : 总利润=销售总利润-总存储费用 首先从公式可以得出,要总利润最大,则销售总利润必须最大,同时总存储费用必须最小。再结合题目,可以得出对目标函数的约束条件可分为各种产品每个月的产量约束,各种产品每个月的存储量约束,各种产品每个月的生产时间约束,然后根据这三种约束条件可得出各个约束条件式子,通过利用lingo软件编程计算出最优解。
3. 模型的建立与求解 4.1 线性规划模型 依据问题分析,要求出6个月的总利润,则需要求出每个月的利润,而每个月的总利润应当等于每个月的销售利润减去每个月存储费用,然后将这6个月的利润加起来,从而得出目标函数Max Z。 根据题意可得,每个月各种产品的库存量应当等于上个月的库存量加上当月的产量减去当月的销售量,而由于1月初无库存,因此1月份的库存量当直接等于当月的产量减去当月的销售量,从而得出约束条件(1),(2)。 从题目中可知,工厂的设备每月工作24天,每天工作16小时,但是由于各种设备对各种产品的单位生产时间不同,同时每个月都有设备需要进行维修,每个月的各种设备可用数量不同,因此各种设备每个月的工作总时间不得超过该设备每个月的最大可工作时间,公式如约束条件(3)所示。 由于各个月各种的产品库存量要求不得超过100件,并且要求6月末各种产品各储存需要有50件,同时要求每个月各种产品的销售量不得超过每个月各种产品的最大需求量,因此得出约束条件(4),(5),(6)。 综合以上的分析,结合题意,建立如下的线性规划模型: 目标函数:
约束条件:
根据以上模型,利用lingo软件编写代码计算得出这6个月的最大利润为937115元。
4.2 生产计划 公司的生产计划,依据利润最大化的宗旨进行。按照Lingo求解结果,我们得到了各个月各种产品的详细生产计划表,如下: 表 1 一月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 500 500 0 50000.00 II 888 888 0 53280.00 III 383 300 83 23585.00 IV 300 300 0 12000.00 V 800 800 0 88000.00 VI 200 200 0 18000.00 VII 0 0 0 0.00 单月总利润 244865.00 表 2 二月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 700 600 100 59500.00 II 600 500 100 29500.00 III 117 200 0 16000.00 IV 0 0 0 0.00 V 500 400 100 43500.00 VI 300 300 0 27000.00 VII 250 150 100 4000.00 单月总利润 179500.00 表 3 三月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 0 100 0 10000.00 II 0 100 0 6000.00 III 0 0 0 0.00 IV 0 0 0 0.00 V 0 100 0 11000.00 VI 400 400 0 36000.00 VII 0 100 0 3000.00 单月总利润 66000.00 表 4 四月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 200 200 0 20000.00 II 300 300 0 18000.00 III 400 400 0 32000.00 IV 500 500 0 20000.00 V 200 200 0 22000.00 VI 0 0 0 0.00 VII 100 100 0 3000.00 单月总利润 115000.00 表 5 五月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 0 0 0 0.00 II 100 100 0 6000.00 III 600 500 100 39500.00 IV 100 100 0 4000.00 V 1100 1000 100 109500.00 VI 300 300 0 27000.00 VII 100 0 100 -500.00 单月总利润 185500.00 表 6 六月份生产计划表 产品 生产量 销售量 库存量 利润(元) I 550 500 50 49750.00 II 550 500 50 29750.00 III 0 50 50 3750.00 IV 350 300 50 11750.00 V 0 50 50 5250.00