当前位置：文档之家 › 单层感知器

单层感知器

  • 格式：doc
  • 大小：150.50 KB
  • 文档页数：11

下载文档原格式

  / 11

合集下载

神经网络+数学建模模型及算法简介

神经网络+数学建模模型及算法简介

人工神经网络的工作原理
感知器模型
具体的： 这样的话，我们就可以得到
WT X = 0 j
一、引例
• 思路：作一直线将两类飞蠓分开
• 例如；取A＝（1.44，2.10）和 B＝(1.10，1.16)， 过A B两点作一条直线： • y＝ 1.47x - 0.017 • 其中x表示触角长；y表示翼长． • 分类规则：设一个蚊子的数据为（x, y） • 如果y≥1.47x - 0.017，则判断蚊子属Apf类； • 如果y＜1.47x - 0.017；则判断蚊子属Af类．
oj x2
n
-1
y = f (∑ wi xi − θ )
i =1
y = f (∑wxi ) i
i=1
n
• 参数识别：假设函数形式已知，则可以从已有的 输入输出数据确定出权系数及阈值。
简单原理
人工神经网络是根据人的认识过程而开发出的 一种算法。 假如我们现在只有一些输入和相应的输出，而 对如何由输入得到输出的机理并不清楚，那么我们 可以把输入与输出之间的未知过程看成是一个“网 络”，通过不断地给这个网络输入和相应的输出来 “训练”这个网络，网络根据输入和输出不断地调 节自己的各节点之间的权值来满足输入和输出。这 样，当训练结束后，我们给定一个输入，网络便会 根据自己已调节好的权值计算出一个输出。这就是 神经网络的简单原理。
人工神经网络的分类
按网络连接的拓扑结构分类：
层次型结构：将神经元按功能分成若干层，如输入层、 中间层（隐层）和输出层，各层顺序相连 单 纯 型 层 次 型 结 构
人工神经网络的分类
按网络内部的信息流向分类：
前馈型网络：网络信息处理的方向是从输入层到各隐 层再到输出层逐层进行

人工智能实验总结

人工智能实验总结
对于同一个问题 由于搜索规模增大，宽度优先搜索和深度 优先搜索都未能得出解，宽度只显示有解， 但未能搜索出结果，深度达到了指定搜索 深度也未能找到目标，而且启发式搜索仍 然可以求出解来。
总结
宽度优先搜索法
在有解的情形总能保证搜索到最短路经，也 就是移动最少步数的路径。但宽度优先搜索法的 最大问题在于搜索的结点数量太多，因为在宽度 优先搜索法中，每一个可能扩展出的结点都是搜 索的对象。随着结点在搜索树上的深度增大，搜 索的结点数会很快增长，并以指数形式扩张，从 而所需的存储空间和搜索花费的时间也会成倍增 长。
1 2
0 1 0 1
0 0 1 1
0 1 1 0
神经网络设计
用两层神经网络来实现，其中隐层为随机 感知器层（net1），神经网络元数目设计为 3，其权值和阈值是随机的，它的输出作为 输出层（分类层）的输入；输出层为感知 器层（net2），其神经元数为1，这里仅对 该层进行训练。
程序运行结果
随机感知器层的权值向量 iw1 = 0.4267 -0.6556 -0.5439 0.9376 -0.1007 -0.2886 随机感知器层的阈值向量 b1 = 0.4074 0.0441 0.8658
运行结果分析
上面实验结果可以看出，城市数目为30的 时候，当迭代次数为100，算法收敛慢，在 迭代次数内最优解没有达到稳定，没有搜 索到最好的解。 迭代次数为200和250的时候，算法基本达 到收敛，最优解在100代以后趋于稳定，表 明搜索到问题的最优解。
运行结果
当城市数目改变的时候： CityNum=50;最大代数gnmax=100;
程序运行结果
第二层感知器层的权值向量和阈值向量 iw2 = -3 -2 2 b2 = 2

感知器算法

感知器算法
i
y = f (∑ wi xi − θ )
i =1
d
而且f为一阶跃函数， 而且 为一阶跃函数，即： 为一阶跃函数
d 1, ∑ wi xi − θ ≥ 0 i =1 y = f ( x) = = sgn( w0T x − θ ) d −1, w x − θ < 0 ∑ i i i =1
四、感知器训练算法在多类问题中的应用 就第二章中的第三种情况为例说明） （就第二章中的第三种情况为例说明） 判决规则：对于c种类型 存在k个判决函 种类型， 判决规则：对于 种类型，存在 个判决函 数 d j ( x)( j = 1, 2,⋯, k ) ，若 di ( x) > d j ( x)( j = 1, 2,⋯ , k , j ≠ i) ， x ∈ ωi 则判： 则判： 假设k=c, 多类问题的感知器算法的步骤如下： 多类问题的感知器算法的步骤如下： 假设 (1) 赋给初值： 赋给初值： 赋初值，选择正常数c, 给 Wi 赋初值，选择正常数 把训练样本 变成增广型， 变成增广型，k=0; x (2) 输入训练样本 xk，k ∈{x1 , x2 ,⋯, xn }，假定 x ∈ ωi ；
训练样本
x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 x1 x2 x3 x4 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101 1011 0111 1101 0101
W(K)Tx
+ + + 0 0 + 0 + + + -
(3) 计算 个判决函数值： 计算c个判决函数值 个判决函数值：
di ( xk ) = [Wi (k )]T xk , i = 1, 2,⋯ , c

智能控制简明教程-神经网络原理

智能控制简明教程-神经网络原理
并由神经冲动进行信息传递的神经网络。分为 单层与多层感知器，是一种具有学习能力的神 经网络。
①单层感知器
感知器模型是由美国学者 F.Rosenblatt于
1957年建立的，它是一个具有单层处理单元的 神经网络。
Hale Waihona Puke 知器的输出：学习规则：向量形式：
下面讨论单层感知器实现逻辑运算问题： a.单层感知器的逻辑“与”运算
0 0 0 -1.5 0 o 0 0 1 -0.5 0 o 0 1 0 -0.5 0 o 1 1 1 0.5 1 *
b.单层感知器的逻辑“或”运算
0 0 0 -0.5 0 o 1 0 1 0.5 1 * 1 1 0 0.5 1 * 1 1 1 1.5 1 *
c.“异或”运算线性不可分
000 011 101 110
①Hebb学习规则（无导师学习）
在Hebb学习规则中，取神经元的输出为学习 信号：
神经网络调整权值的原则： 若第i个与第j个神经元同时处于兴奋状态，则它们之间 的连接权应加强。符合心理学中条件反射的机理两 个神经元同时兴奋（输出同时为‘1’态）时w加强，
否
则应削弱。
4.3 感知器（perceptron) 感知器是模拟人的视觉，接受环境信息，
前向网络特点
1. 神经元分层排列，可多层 2. 层间无连接 3. 方向由入到出 感知网络（perceptron即为此） 应用最为广泛
注意：构成多层网络时，各层间的转移函数应 是非线性的，否则多层等价一个单层网络。
另外，隐层的加入大大提高NN对信息的处理能 力，经过训练的多层网络，具有较好的性能， 可实现X→Y的任意非线性映射的能力。
5.神经网络的学习功能
a.学习方法
学习是NN最重要的特征，学习learning，训练 training。

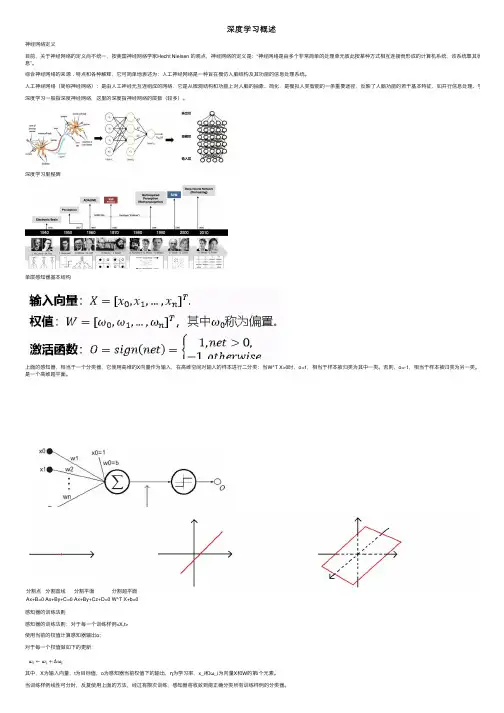
深度学习概述

深度学习概述

深度学习概述神经⽹络定义⽬前，关于神经⽹络的定义尚不统⼀，按美国神经⽹络学家Hecht Nielsen 的观点，神经⽹络的定义是：“神经⽹络是由多个⾮常简单的处理单元彼此按某种⽅式相互连接⽽形成的计算机系统，该系统靠其状态对外部输息”。

综合神经⽹络的来源﹑特点和各种解释，它可简单地表述为：⼈⼯神经⽹络是⼀种旨在模仿⼈脑结构及其功能的信息处理系统。

⼈⼯神经⽹络（简称神经⽹络）：是由⼈⼯神经元互连组成的⽹络，它是从微观结构和功能上对⼈脑的抽象、简化，是模拟⼈类智能的⼀条重要途径，反映了⼈脑功能的若⼲基本特征，如并⾏信息处理、学习、联想、深度学习⼀般指深度神经⽹络，这⾥的深度指神经⽹络的层数（较多）。

深度学习⾥程碑单层感知器基本结构上⾯的感知器，相当于⼀个分类器，它使⽤⾼维的X向量作为输⼊，在⾼维空间对输⼊的样本进⾏⼆分类：当W^T X>0时，o=1，相当于样本被归类为其中⼀类。

否则，o=-1，相当于样本被归类为另⼀类。

这两类的边是⼀个⾼维超平⾯。

分割点分割直线分割平⾯分割超平⾯Ax+B=0Ax+By+C=0Ax+By+Cz+D=0W^T X+b=0感知器的训练法则感知器的训练法则：对于每⼀个训练样例<X,t>使⽤当前的权值计算感知器输出o；对于每⼀个权值做如下的更新：其中，X为输⼊向量，t为⽬标值，o为感知器当前权值下的输出，η为学习率，x_i和ω_i为向量X和W的第i个元素。

当训练样例线性可分时，反复使⽤上⾯的⽅法，经过有限次训练，感知器将收敛到能正确分类所有训练样例的分类器。

在训练样例线性不可分时，训练很可能⽆法收敛。

因此，⼈们设计了另⼀个法则来克服这个不⾜，称为delta法则。

它使⽤梯度下降（Gradient Descent）的⽅法在假设空间中所有可能的权向量，寻找到最佳拟合训练样梯度下降与损失函数l对于多元函数o=f(x)=f(x_0,x_1,…,x_n )，其在X^′=〖[〖x_0〗^′,〖x_1〗^′,…,〖x_n〗^′]' ' 〗^T处的梯度为：梯度向量的⽅向，指向函数增长最快的⽅向。

基于BP神经网络的PID控制器设计

基于BP神经网络的PID控制器设计

基于BP神经⽹络的PID控制器设计基于BP神经⽹络的PID控制器设计班级：21班学号：2014561姓名：常临妍摘要常规PID控制技术是⼯业控制中⼀种常⽤的控制⽅法。

其结构简单、容易实现、控制效果良好，且能对相当⼀些⼯业对象或过程进⾏有效的控制，已得到⼴泛应⽤。

但其局限性在于：当控制对象不同，或被控对象具有复杂的⾮线性特性时，难以建⽴精确的数学模型。

控制器的参数难以⾃动调整以适应外界环境的变化。

且由于对象和环境的不确定性，往往难以达到满意的控制效果。

为了使控制器具有较好的⾃适应性，实现控制器参数的⾃动调整，可以借助BP神经⽹络控制的⽅法。

BP神经⽹络已被证明具有逼近任意连续有界⾮线性函数的能⼒，给⾮线性控制带来了新的思路。

利⽤⼈⼯神经⽹络的⾃适应能⼒，并结合传统的PID控制理论，构造神经⽹络PID控制器，实现控制器参数的⾃动调整。

本⽂研究了基于BP神经⽹络的PID控制器设计，利⽤BP神经⽹络的⾃适应能⼒进⾏在线参数整定。

其实现具有⾃适应性等特点，⽹络的收敛速度快，能够对⾮线性对象有很好的控制，系统的跟踪性能好。

其参数设定⽆需知道被控对象的具体参数及其数学模型，对不同的对象具有适应性。

关键词：PID控制BP神经⽹络控制器设计⼀．绪论1.1神经元⽹络PID的发展历程1934年，美国⼼理学家W.McCulloch和数学家W.Pitts⽤数学模型对神经系统中的神经元进⾏理论建模，建⽴了MP神经元模型。

MP神经元模型⾸次⽤简单的数学模型模仿出⽣物神经元活动功能，并揭⽰了通过神经元的相互连接和简单的数学计算，可以进⾏相当复杂的逻辑运算这⼀事实。

1957年，美国计算机学家F.Rosenblatt提出了著名的感知器模型。

它是⼀个具有连续可调权值⽮量的MP神经⽹络模型，经过训练可达到对⼀定输⼊⽮量模型进⾏识别的⽬的。

1959年，美国⼯程师B.Widrow和M.Hoff提出了⾃适应线性元件。

它与感知器的主要不同之处在于其神经元有⼀个线性激活函数，这允许输出可以是任意值，⽽不仅仅只是像感知器中那样只能取0或1。

智能控制智能控制试卷(练习题库)(2023版)

智能控制智能控制试卷（练习题库）1、简述智能控制的概念。

2、比较智能控制和传统控制的特点？3、智能控制的概念首次由著名学者（）提出的。

4、经常作为智能控制典型研究对象的是（）。

5、智能自动化开发与应用应当面向（）。

6、不属于智能控制是（）。

7、以下不属于智能控制主要特点的是（）。

8、以下不属于智能控制的是（）。

9、地质探矿专家系统常使用的知识表示方法为（）。

10、自然语言问答专家系统使用的知识表示方法为（）。

11、专家系统中的自动推理是基于O的推理。

12、适合专家控制系统的是（）。

13、直接式专家控制通常由O组成。

14、产生式系统的推理方式不包括（）。

15、黑板专家控制系统的组成有O16、建立专家系统，最艰难（“瓶颈”）的任务是（）。

17、产生式系统包含的基本组成O18、下列概念中不能用普通集合表示的是（）。

19、以下应采用模糊集合描述的是（）。

20、某模糊控制器的语言变量选为实际温度与给定温度之差即误差e、误差变化率4e；以及加热装置中可控硅导通角21、在论域U中，模糊集合A的支集只包含一个点u,且OAum=I,则A称为（）。

22、在模糊控制中，隶属度（）。

23、在模糊控制器的推理输出结果中，取其隶属度最大的元素作为精确值, 去执行控制的方法称为（）。

24、在温度模糊控制系统中，二维模糊控制器的输出是（）。

25、以下的集合运算性质中，模糊集合不满足的运算性质（）。

26、模糊控制方法是基于（）。

27、以下应采用模糊集合描述的是（）。

28、模糊隶属度函数曲线的形状可以为（）。

29、某模糊控制器的语言变量选为实际水位与给定水位之差即误差e,以及调节阀门开度的变化量u,故该模糊控制器30、某一隶属度函数曲线的形状可以选为（）。

31、模糊控制器的术语“正中”，可用符合O表示。

32、在模糊控制器的推理输出结果中，取其隶属度函数曲线与横坐标围成面积的重心作为输出值，去执行控制的方法称33、下列概念中不能用普通集合表示的是（）。

BP神经网络PPTppt课件


输 入 至 网 络 , 由 前 向 后 ， 逐 层 得 到 各 计 算 单 元 的 实 际 输 出 y：
对 于 当 前 层 l 的 第 j个 计 算 单 元 ,j 1,..., nl
该
单
元
的
净
输
入
实
际
输
出
n l1
n
e
t
l j
Ol l 1 ij i
i 1
O
l j
f
n
e
t
l j
1
=
1+
e
➢ 可见层
输入层 (input layer) 输入节点所在层，无计算能力
输出层 (output layer) 节点为神经元
➢ 隐含层( hidden layer) 中间层，节点为神经元
可编辑课件PPT
20
具有三层计算单 元的前馈神经网络结 构
可编辑课件PPT
21
2. 感知器神经网络(感知器)、感知器神经元
s ig n 型 函 数 ， 不 可 微 ； 对 称 硬 极 限 函 数 ；
双
极
函
数
f
net
=
sgn
net
=
1
-
1
net 0 net < 0
m atlab函 数 hardlim s
D .阈 值 函 数
f
net
=
-
net net <
其 中 , , 非 负 实 数
可编辑课件PPT
单层感知器网络
感知器神经元
可编辑课件PPT
22
2. 感知器神经网络、感知器神经元(续)
感知器神经元的传递函数

为什么三层感知器能够解决任意区域组合的分类问题（不同隐层数的感知器的分类能力）

为什么三层感知器能够解决任意区域组合的分类问题（不同隐层数的感知器的分类能⼒）主要内容有：1. 单层感知器的迭代学习算法(包含代码)2. 两层感知器解决异或问题3. 解释两层感知器分类能⼒有限的问题4. 解释为什么三层感知器能够解决任意区域组合的分类问题访问我的博客有更好的展⽰效果。

最近在准备模式识别考试,关于三层感知器能够解决任意区域组合的分类问题解释甚是有趣,这两天考完试了在此对这些内容做个总结。

单层感知器的迭代算法感知器算法属于线性分类器,单层感知器在给定数据线性可分的情况下,可以经过有限次迭代使得算法收敛我曾经写过关于感知器迭代计算学习的代码,是找到⼀个平⾯,将三维空间的两类线性可分的点分隔开来。

感知器算法的更新过程(2类问题)如下:N个属于w1,w2类的模式样本构成训练样本集{X1,X2,....X N}1. 将原始数据写成增⼴向量形式,并规范化构成增⼴向量形式是指添加⼀个维度为1的向量,如三维的样本的话，我们将会这样设置:X=[x1,x2,x3,1]T写成增⼴向量形式是为了让我们的运算能够执⾏矩阵乘法,便于编程实现。

规范化是指将w2类样本×−1接下来任取权向量初始值W(1),开始迭代2.⽤全部训练样本进⾏⼀轮迭代，计算W T(k)X i的值，并修正权向量。

分两种情况，更新权向量的值：若W^T (k) X_i \leq 0表明分类器对第i个模式做了错误分类，我们将进⾏校正，权向量校正为：W(k+1)=W(k)+cX_i \ , \quad c>0若W^T (k) X_i > 0表明分类正确，权向量不变。

W(k+1)=W(k)因此我们可以将权向量的更新规则统⼀写为:W(k+1) = \left\{\begin{matrix} W(k) \quad if \ W^{T}(k)X_i > 0 \\ W(k) + cX_i \quad if \ W^{T}(k)X_i \leq 0 \end{matrix}\right.3.分析分类结果：只要有⼀个错误分类,回到2,直⾄对所有样本正确分类。

人工神经网络理论及应用.ppt课件


ww1ij (k )
m
yi1
j1
1 yi1
w2ji e j
yi1 (1
yi1 )
uj
对比Hebb规则: 各项
如遇到隐含层多于1层，可依次类推
yi (1 yi ) y1jei
yi1(1
yi1) u j
m
yi1
1 yi1
w2jie
j
j1
演示
BP算法演示
BP学习算法评述
优点
代入上式，有 因此
ym yi1
ym (1
ym )wmi
J
T
e
e yi1
m j 1
y j (1
y j ) w2jiej
即误差进行反向传输
BP学习步骤：误差反传(隐含层)
w1
w2
u1
e1
yi1 wi1j
yi1(1 yi1)u j
un
… …
…
em
综合上述结果
y1
Δwi1j
k
dJ dwi1j
主要内容
神经元数学模型 感知器 多层前馈网络与BP算法※ BP算法评述
神经元数学模型
n
y f wjxj
j1
n
设 p wj x j 则 yi f ( pi ) j 1
作用 函数
f
(
x)
1, 0,
x0 x0
i
f (xi )
（a）
f (x)
1
0 x
(b) 作用函数
MP神经元模型
感知器(感知机)
包含感知层，连接层和反应层。
感知层：接受二值输入； 连接层：根据学习规则不断调整权值 输出层：取为对称型阶跃函数
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

单层感知器
一 、与运算
1.程序
function main()
close all
rand ('state',sum(100*clock));
X=[-1,0,0;-1,0,1;-1,1,0;-1,1,1];D=[0,0,0,1];q=1;W=[0.1,rand(1,2)];
O=[0,0,0,0];ERROR=[];R2=[0,0,0,1];t=1;
for j=1:100
for p=1:4
if W(t,:)*X(p,:)'>0
O(1,p)=1;
else
O(1,p)=0;
end
R2(1,p)=D(1,p)-O(1,p)
M=W(t,:)+q* R2(1,p)*X(p,:)
W=[W;M]
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==0 ,break,end
t=t+1
end
ERROR=[ERROR R2(1,1)+R2(1,2)+R2(1,3)+R2(1,4)]
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==0 ,break,end
end
for i=1:3
figure
hold on
grid on
x=1:t
y=W(x,i)
plot(x,y,'b--');
ylabel('w')
end
figure
hold on
grid on
for i=1:4
x=X(i,2)
y=X(i,3)
plot(x,y,'*')
end
axis([-1 2 -1 2])
a=0:1
b=[W(t,1)-W(t,2)*a]/W(t,3)
plot(a,b,'b--')
figure
hold on
grid on
x=1:j
y=ERROR(1,x);
plot(x,y,'b--')
end
2.训练结果
最终误差：0
迭代次数：8
最终权值：2.6416 1.3022
最终阈值：3.1000
误差收敛曲线
权值变化曲线
W1变化曲线

W2变化曲线
3 样本分布及分界线

阈值=0.1时 平均迭代次数
学习率
0.01 0.05 0.1 0.5 1 2 10

迭代次数
24.4 5.7 4.4 4.8 6.2 6.8 7.8

学习率=0.1时 平均迭代次数
阈值
0.01 0.05 0.1 0.5 1 2 10

迭代次数
4.8 4.1 5.1 3.1 2.4 5.2 31.5

阈值=0.1 学习率=0.1
变换函数 单极点二值函数 单极点Sigmoid 函数
迭代次数
4.8 1691.9

二 或运算
1编程
function main()
close all
rand ('state',sum(100*clock));
X=[-1,0,0;-1,0,1;-1,1,0;-1,1,1];
D=[0,1,1,1];q=0.1;
W=[0.1,rand(1,2)];
O=[0,0,0,0];
ERROR=[];R2=[0,0,0,1];
t=1;
for j=1:1000
for p=1:4
if W(t,:)*X(p,:)'>0
O(1,p)=1;
else
O(1,p)=0;
end
R2(1,p)=D(1,p)-O(1,p)
M=W(t,:)+q* R2(1,p)*X(p,:)
W=[W;M]
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==0 ,break,end
t=t+1
end
ERROR=[ERROR abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))]
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==0 ,break,end
end
for i=1:3
figure
hold on
grid on
x=1:t
y=W(x,i)
plot(x,y,'b--');
ylabel('w')
end
figure
hold on
grid on
for i=1:4
x=X(i,2)
y=X(i,3)
plot(x,y,'*')
end
axis([-1 2 -1 2])
a=0:1
b=[W(t,1)-W(t,2)*a]/W(t,3)
plot(a,b,'b--')
figure
hold on
grid on
x=1:j
y=ERROR(1,x);
plot(x,y,'b--')
end
2.训练结果
误差收敛曲线

权值变化曲线
W1变化曲线
W2变化曲线
3 样本分布及分界线
三 异或

1编程
function main()
close all
rand ('state',sum(100*clock));
X=[-1,0,0;-1,0,1;-1,1,0;-1,1,1];
D=[0,1,1,0];q=1;
W=[0.1,rand(1,2)];
O=[0,0,0,0];
ERROR=[];R2=[0,0,0,1];
t=1;
for j=1:20
for p=1:4
if W(t,:)*X(p,:)'>0
O(1,p)=1;
else
O(1,p)=0;
end
R2(1,p)=D(1,p)-O(1,p);
M=W(t,:)+q* R2(1,p)*X(p,:);
W=[W;M];
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==4 ,break,end
t=t+1;
end
ERROR=[ERROR abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))];
if abs(R2(1,1))+abs(R2(1,2))+abs(R2(1,3))+abs(R2(1,4))==4 ,break,end
end
j
ERROR
for i=1:3
figure
hold on
grid on
x=1:t;
y=W(x,i);
plot(x,y,'b--');
ylabel('w')
end
figure
hold on
grid on
for i=1:4
x=X(i,2);
y=X(i,3);
plot(x,y,'*')
end
axis([-1 2 -1 2])
a=0:1;
b=[W(t,1)-W(t,2)*a]/W(t,3);
plot(a,b,'b--')
figure
hold on
grid on
x=1:j;
y=ERROR(1,x);
plot(x,y,'b--')
end
2.训练结果
最终误差=4
误差收敛曲线
权值变化曲线
W1变化曲线

W2变化曲线