线性系统的频域分析-自动控制
- 格式:doc
- 大小:239.00 KB
- 文档页数:14


《自动控制原理》实验3.线性系统的频域分析实验三线性系统的频域分析一、实验目的1.掌握用MATLAB语句绘制各种频域曲线。
2.掌握控制系统的频域分析方法。
二、基础知识及MATLAB函数频域分析法是应用频域特性研究控制系统的一种经典方法。
它是通过研究系统对正弦信号下的稳态和动态响应特性来分析系统的。
采用这种方法可直观的表达出系统的频率特性,分析方法比较简单,物理概念明确。
1.频率曲线主要包括三种:Nyquist图、Bode图和Nichols图。
1)Nyquist图的绘制与分析MATLAB中绘制系统Nyquist图的函数调用格式为:nyquist(num,den) 频率响应w的范围由软件自动设定 nyquist(num,den,w) 频率响应w的范围由人工设定[Re,Im]= nyquist(num,den) 返回奈氏曲线的实部和虚部向量,不作图2s?6例4-1:已知系统的开环传递函数为G(s)?3,试绘制Nyquists?2s2?5s?2图,并判断系统的稳定性。
num=[2 6]; den=[1 2 5 2]; nyquist(num,den)极点的显示结果及绘制的Nyquist图如图4-1所示。
由于系统的开环右根数P=0,系统的Nyquist曲线没有逆时针包围(-1,j0)点,所以闭环系统稳定。
p =-0.7666 + 1.9227i -0.7666 - 1.9227i -0.4668图4-1 开环极点的显示结果及Nyquist图若上例要求绘制??(10?2,103)间的Nyquist图,则对应的MATLAB语句为:num=[2 6]; den=[1 2 5 2];w=logspace(-1,1,100); 即在10-1和101之间,产生100个等距离的点nyquist(num,den,w)2)Bode图的绘制与分析系统的Bode图又称为系统频率特性的对数坐标图。
Bode图有两张图,分别绘制开环频率特性的幅值和相位与角频率?的关系曲线,称为对数幅频特性曲线和对数相频特性曲线。







自动控制原理第五章线性系统的频域分析法1、基本内容和要点(l)频率特性系统的稳态频率响应,频率响应的物理概念及数学定义;求取频率特性的分析法和实验法。
(2)典型环节的频率特性比例、惯性、积分、微分、振荡、延迟环节的频率特性和对数频率特性。
非最小相位环节的频率特性。
(3)反馈控制系统的开环频率特性研究系统开环频率特性的意义。
单环系统开环对数频率持性的求取与绘制。
最小相位系统开环对数幅频特性与相频特性间的对应关系。
(4)奈奎斯特稳定判据幅角定理。
S平面与F平面的映射关系。
根据开环频率特性判别闭环系统稳定性的奈氏判据。
奈氏判据在多环系统中的应用和推广。
系统的相对稳定性。
相角与增益稳定裕量。
(5)二阶和高阶系统的频率域性能指标与时域性指标。
系统频率域性能指标。
二阶和高阶系统暂态响应性能指标与频率域性能指标间的解析关系及近似关系。
(6)系统的闭环频率特性开环频率特性与闭环频率特性间的解析关系。
用等M圆线从开环频率特性求取闭环频率特性。
用尼氏图线从开环对数频率特性求取闭环频率特性。
2、重点(l)系统稳态频率响应和暂态时域响应的关系。
(2)系统开环频率特性的绘制,最小相位系统开环频率特性的特点。
(3)奈奎斯特稳定判据和稳定裕量。
5-1引言第三章,时域分析,分析系统零、极点与系统时域指标的关系;典型二阶系统极点或和n与时域指标tp、和t、tr及稳态误差等的关系,及高阶系统的近似指标计算;第四章,根轨迹分析,研究系统某一个参数变化对系统闭环极点的影响;本章讨论系统零、极点对系统频率域指标的关系,频域指标又分开环频域指标和闭环频域指标,它们都是在频域上评价系统性能的参数。
频域分析是控制理论的一个重要分析方法。
5-2频率特性1.频率特性的基本概念理论依据定理:设线性定常系统G()的输入信号是正弦信号某(t)某int,在过度过程结束后,系统的稳态输出是与输入同频率的正弦信号,其幅值和相角都是频率的函数,即为c(t)Y()in[t()]。

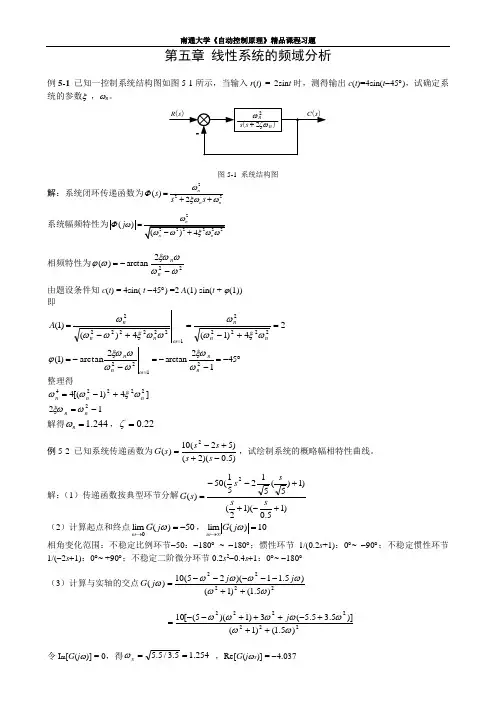
第五章 线性系统的频域分析例5-1 已知一控制系统结构图如图5-1所示,当输入r (t ) = 2sin t 时,测得输出c (t )=4sin(t -45︒),试确定系统的参数ξ ,ωn 。
图5-1 系统结构图解:系统闭环传递函数为222()2nn ns s s ωΦξωω=++ 系统幅频特性为2()j Φω相频特性为222arctan)(ωωωξωωϕ--=nn由题设条件知c (t ) = 4sin( t -45︒) =2 A (1) sin(t + ϕ(1)) 即122222224)()1(=+-=ωωωξωωωnnnA 24)1(22222=+-=nnnωξωω1222arctan)1(=--=ωωωωξωϕn n ︒-=--=4512arctan2n nωξω整理得]4)1[(422224n n n ωξωω+-= 122-=n n ωξω解得 1.244n ω=,0.22ζ=例5-2 已知系统传递函数为)5.0)(2()52(10)(2-++-=s s s s s G ,试绘制系统的概略幅相特性曲线。
解:(1)传递函数按典型环节分解)15.0)(12()1)5(51251(50)(2+-++--=s s s s s G(2)计算起点和终点50)(lim 0-=→ωωj G ,10)(lim =∞→ωωj G相角变化范围:不稳定比例环节-50:-180︒ ~ -180︒;惯性环节1/(0.2s +1):0︒~ -90︒;不稳定惯性环节1/(-2s +1):0︒~ +90︒;不稳定二阶微分环节0.2s 2-0.4s +1:0︒~ -180︒(3)计算与实轴的交点22222)5.1()1()5.11)(25(10)(ωωωωωωω++-----=j j j G2222222)5.1()1()]5.35.5(3)1)(5([10ωωωωωωω+++-+++--=j(4) 确定变化趋势 根据G (j ω)的表达式,当ω <ωx 时,I m [G (j ω)] < 0;当ω >ωx 时,I m [G (j ω)] > 0。
实验三·线性系统的频域分析
一、实验目的
1.掌握用MATLAB 语句绘制各种频域曲线。
2.掌握控制系统的频域分析方法。
二、实验内容
1.典型二阶系统
222()2n n n
G s s s ωζωω=++ 绘制出6n ω=,0.1ζ=,0.3,0.5,0.8,2的bode 图,记录并分析ζ对系统bode 图的影响。
2.系统的开环传递函数为
210()(51)(5)G s s s s =
-+ 228(1)
()(15)(610)s G s s s s s +=+++
4(/31)()(0.021)(0.051)(0.11)
s G s s s s s +=+++ 绘制系统的Nyquist 曲线、Bode 图和Nichols 图,说明系统的稳定性,并通过绘制阶跃响应曲线验证。
3.已知系统的开环传递函数为21()(0.11)
s G s s s +=+。
求系统的开环截止频率 穿越频率、幅值裕度和相位裕度。
应用频率稳定判据判定系统的稳定性。
三、实验内容及分析
1. 系统1:222()2n n n
G s s s ωζωω=++中6n ω=,(1)0.1ζ=时 Matlab 文本如下:
num=[36 0 0];
den=[1 1.2 36];
w=logspace(-2,3,100);
bode(num,den,w)
Grid
得到图像:
同理,得到其他值情况下的波特图:ξ=0.3时
ξ=0.5时
ξ=0.8时
ξ=2时
从上面的图像中可以看出:随着ξ的不断增大,波特图中震荡的部分变得越来越平滑。
而且,对幅频特性曲线来说,其上升的斜率越来越慢;对相频特性曲线来说,下降的幅度也在变缓。
2. 开环传递函数1:210()(51)(5)
G s s s s =-+ 奈奎斯特图函数及图像如下:
num=[0 10];
den=[conv([5,-1],[1,5]),0,0];
[z,p,k]=tf2zp(num,den); p
nyquist(num,den)
结果:p =0
-5.0000
0.2000
从上面的结果可知:
在右半平面根的个数P=1。
系统的Nyquist图不包围(-1,j0)点,R=0不等于P=1,闭环系统不稳定。
波特图函数及图像如下:
num=[0 10];
den=[conv([5,-1],[1,5]),0,0];
w=logspace(-2,3,100);
bode(num,den,w)
grid
从图中可以看出:幅值为零(对应频率为Wc)时,对应的相角裕度=180度+Wc时的相位值<0。
故系统不稳定。
尼克斯函数及图像如下:
num=[0 10];
den=[conv([5,-1],[1,5]),0,0];
w=logspace(-1,1,500);
[mag,phase]=nichols(num,den,w);
plot(phase,20*log10(mag))
ngrid %绘制nichols图线上的网格
阶跃响应函数及图像如上右图:
num=[0 10];
den=[conv([5,-1],[1,5]),0,0];
step(num,den)
%调用阶跃响应函数求取单位阶跃响应曲线 grid %画网格标度线 xlabel('t/s'),ylabel('c(t)')
%给坐标轴加上说明title('Unit-step Respinse of G(s)=25/(s^2+4s+25)') %给图形加上标题名
分析:曲线先平稳然后急剧上升,故闭环不稳定,验证了Nyquist 图判断结论的正确性。
开环传递函数2:228(1)
()(15)(610)s G s s s s s +=+++
奈奎斯特函数及图像如下:
num=[8 8];
den=[conv([1,15],[1,6,10]),0,0];
[z,p,k]=tf2zp(num,den); p
nyquist(num,den)
p = 0
-15.0000
-3.0000 + 1.0000i
-3.0000 - 1.0000i
从上面的结果可知:
在右半平面根的个数P=0。
系统的Nyquist图不过(-1,j0)点,R=0等于P=0,闭环系统不稳定。
波特函数及图像如下:
num=[8 8];
den=[conv([1,15],[1,6,10]),0,0];
w=logspace(-2,3,100);
bode(num,den,w)
grid
尼克斯函数及图像如上右图:
num=[8 8];
den=[conv([1,15],[1,6,10]),0,0];
w=logspace(-1,1,500);
[mag,phase]=nichols(num,den,w);
plot(phase,20*log10(mag))
ngrid %绘制nichols图线上的网格
阶跃响应函数及图像如下:
num=[8 8];
den=[conv([1,15],[1,6,10]),0,0];
step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线grid %画网格标度线
xlabel('t/s'),ylabel('c(t)') %给坐标轴加上说明
title('Unit-step Respinse of G(s)=25/(s^2+4s+25)')%给图形加上标题名
开环传递函数3:
奈奎斯特函数及图像如下:
num=[4/3 4];
den=[conv([0.02,1],conv([1,15],[1,6,10])),0];
[z,p,k]=tf2zp(num,den); p
nyquist(num,den)
p =
-50.0000
-15.0000
-3.0000 + 1.0000i
-3.0000 - 1.0000i
从上面求得的根可知该系统稳定
波特函数及图像如下:
num=[4/3 4];
den=[conv([0.02,1],conv([1,15],[1,6,10])),0]; w=logspace(-2,3,100);
bode(num,den,w)
grid
尼克斯函数及图像如下:
num=[4/3 4];
den=[conv([0.02,1],conv([1,15],[1,6,10])),0]; w=logspace(-1,1,500);
[mag,phase]=nichols(num,den,w);
plot(phase,20*log10(mag))
ngrid %绘制nichols图线上的网格
阶跃响应函数及图像:
num=[4/3 4];
den=[conv([0.02,1],conv([1,15],[1,6,10])),0];
step(num,den) %调用阶跃响应函数求取单位阶跃响应曲线
grid %画网格标度线
xlabel('t/s'),ylabel('c(t)') %给坐标轴加上说明
title('Unit-step Respinse of G(s)=25/(s^2+4s+25)') %给图形加上标题名
开环传递函数21()(0.11)
s G s s s +=+ 其在matlab 中取得的开环截止频率、穿越频率、幅值裕度和相位裕度分别为:
num=[1 1]; den=[0.1 1 0 0];
[gm,pm,wcg,wcp]=margin(num,den);
gm,pm,wcg,wcp
结果:
gm =
pm =
44.4594
wcg =
wcp =
1.2647
分析:在截至频率时,相角裕度大于零,故系统稳定。
四、实验结果与心得
本次试验主要有三大内容:
1.对二阶系统中参数ξ进行分析,实验表明:当阻尼比ξ增大时,阻尼振荡频率Wd会减小,当ξ>=1时,Wd将不复存在,系统的响应不再出现振荡。
2.利用得到的nyquist图和Boad图对系统的稳定性进行分析,需要注意的是对Nyqusit 图要补虚线。
3.利用相值和幅值裕度对系统进行判稳。
结论是:当幅值条件为零时,相值裕度大于零,则系统稳定;当相值条件为零时,幅值裕度小于零,则系统稳定。