UC矩阵练习
- 格式:xls
- 大小:21.00 KB
- 文档页数:2

矩阵专项练习题1. 题目一:矩阵的基本概念和运算简述矩阵的定义和表示方法。
以两个矩阵相加为例,详细说明矩阵相加的运算规则。
2. 题目二:矩阵的乘法和转置介绍矩阵的乘法定义和性质。
以一个具体的矩阵乘法例题,展示如何进行矩阵乘法运算。
阐述矩阵转置的定义,并给出转置矩阵的计算方法。
3. 题目三:矩阵的秩和逆解释矩阵的秩的概念和计算方法。
以一个矩阵求逆的实例,展示如何计算矩阵的逆。
讨论矩阵是否具有逆的条件。
4. 题目四:特殊的矩阵列举并解释零矩阵、单位矩阵、对角矩阵和对称矩阵的特点和性质。
以示例题的形式,演示如何判断一个矩阵是否为对角矩阵或对称矩阵。
5. 题目五:行列式和特征值特征向量介绍行列式的定义、性质和计算方法。
讲解特征值和特征向量的概念和计算方法。
通过一个实例,展示如何求解矩阵的特征值和特征向量。
6. 题目六:线性方程组和矩阵的应用以线性方程组为背景,介绍矩阵的应用。
通过矩阵的方法和行列式的方法,解决一个线性方程组的实例问题。
7. 题目七:二阶矩阵的特性阐述二阶矩阵的特性。
以二阶矩阵为例,解释如何进行二阶矩阵的运算和转置。
8. 题目八:矩阵的迹与行列式关系解释矩阵的迹的概念,并给出迹的计算方法。
探讨矩阵的迹与行列式之间的关系。
9. 题目九:矩阵的特征值与特殊矩阵讲解特殊矩阵(如零矩阵、单位矩阵、对称矩阵)的特征值的性质。
提供具体的计算例题,展示如何求解特殊矩阵的特征值。
10. 题目十:矩阵的奇异值分解简述矩阵的奇异值分解的定义和计算方法。
以一个实例,演示如何进行矩阵的奇异值分解。
总结:通过以上不同的专题练习题,我们全面了解了矩阵的基本概念和运算,如矩阵的定义、相加、相乘、转置等;深入探讨了特殊的矩阵及其性质,如零矩阵、单位矩阵、对称矩阵等;了解了矩阵的行列式、逆、秩、特征值特征向量等重要概念和计算方法,并通过实例进行了详细的演示。
这些知识点和技巧可以为我们在线性代数和相关领域的学习与应用提供基础与支持。

一、填空题:1.若,为同阶方阵,则的充分必要条件是A B 22))((B A B A B A -=-+。
BAAB =2. 若阶方阵,,满足,为阶单位矩阵,则=。
n A B C I ABC =I n 1-CAB3. 设,都是阶可逆矩阵,若,则=。
A B n ⎪⎪⎭⎫ ⎝⎛=00A B C 1-C ⎪⎪⎭⎫ ⎝⎛--0011B A 4. 设A =,则=。
⎪⎪⎭⎫ ⎝⎛--11121-A ⎪⎪⎭⎫⎝⎛21115. 设, .则。
⎪⎪⎭⎫ ⎝⎛--=111111A ⎪⎪⎭⎫⎝⎛--=432211B =+B A 2⎪⎪⎭⎫ ⎝⎛--7317336.设,则=⎪⎪⎪⎭⎫⎝⎛=300020001A 1-A ⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛310002100017.设矩阵,为的转置,则=.1 -1 32 0,2 0 10 1A B ⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭T A A B A T⎪⎪⎪⎭⎫⎝⎛-1602228. ,为秩等于2的三阶方阵,则的秩等于 2 .⎪⎪⎪⎭⎫⎝⎛=110213021A B AB 二、判断题(每小题2分,共12分)1. 设均为阶方阵,则 (k 为正整数)。
……………( × )B A 、n kk k B A AB =)(2. 设为阶方阵,若,则。
……………………………(,,A B C n ABC I =111CB A ---=× )3. 设为阶方阵,若不可逆,则都不可逆。
……………………… ( × )B A 、n AB ,A B4. 设为阶方阵,且,其中,则。
……………………… ( B A 、n 0AB =0A ≠0B =× )5. 设都是阶矩阵,且,则。
……………………( C B A 、、n I CA I AB ==,C B =√ )6. 若是阶对角矩阵,为阶矩阵,且,则也是阶对角矩阵。
…( A n B n AC AB =B n × )7. 两个矩阵与,如果秩()等于秩(),那么与等价。


急诊应急处理管理系统uc矩阵急诊应急处理管理系统UC矩阵1. 引言急诊室作为医院的门面部门,在医疗救助中起着至关重要的作用。
急诊医生需要面对各种临床情况,高效快速地做出准确判断并进行应急处理。
为了提高急诊医生的工作效率,急诊应急处理管理系统应运而生。
本文将探讨急诊应急处理管理系统中的UC矩阵,即用例图矩阵,以帮助读者全面、深入地了解该系统。
2. UC矩阵概述UC矩阵是对急诊应急处理管理系统用例图的进一步拓展,它展示了不同用户角色在系统中所涉及的用例。
UC矩阵一般由行表示不同的用户角色,列表示系统中的用例。
通过UC矩阵的分析,可以帮助开发团队和用户更好地理解系统的功能和用户间的交互。
3. UC矩阵内容在急诊应急处理管理系统中,UC矩阵可以包含以下内容:3.1 急诊医生角色急诊医生是系统的核心用户,他们的主要职责是对患者进行初步评估、及时处理急诊事件。
UC矩阵中可能涉及的用例有:3.1.1 患者登记:急诊医生可以通过系统为患者进行登记,包括个人信息、病情描述等。
3.1.2 初步评估:急诊医生根据患者的病情进行初步评估,判断是否属于急诊事件。
3.1.3 快速处理:急诊医生可以根据患者的初步评估结果进行快速处理,如注射、急救等。
3.1.4 咨询其他专家:急诊医生可以通过系统向其他专家咨询,获取更多的意见和处理建议。
3.2 辅助人员角色急诊应急处理管理系统不仅仅是为急诊医生提供支持,还需要辅助人员的配合。
UC矩阵中可能涉及的用例有:3.2.1 实时监控:辅助人员通过系统可以对急诊室的设备进行实时监控,确保设备正常运行。
3.2.2 病历记录:辅助人员可以通过系统记录患者的病历信息,包括检查结果、用药情况等。
4. UC矩阵的优势UC矩阵作为对急诊应急处理管理系统用例图的进一步拓展,具有如下优势:4.1 全面评估功能:UC矩阵清晰地展示了系统中不同用户角色的行为和用例的关系,使开发团队和用户可以全面评估系统的功能。


高中数学矩阵练习题及讲解1. 矩阵的加法设矩阵A和矩阵B如下:\[ A = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix}, \quad B = \begin{bmatrix} 5 & 6 \\ 7 & 8 \end{bmatrix} \]求矩阵A和B的和,并验证加法的交换律。
2. 矩阵的数乘给定矩阵C:\[ C = \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \] 求矩阵C与标量2的乘积。
3. 矩阵的乘法设矩阵D和矩阵E如下:\[ D = \begin{bmatrix} 2 & 3 \\ 4 & 5 \end{bmatrix}, \quad E = \begin{bmatrix} 6 & 7 \\ 8 & 9 \end{bmatrix} \]求矩阵D和E的乘积。
4. 矩阵的转置给定矩阵F:\[ F = \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix} \]求矩阵F的转置。
5. 矩阵的行列式给定矩阵G:\[ G = \begin{bmatrix} 1 & 2 \\ 3 & 4 \end{bmatrix} \] 求矩阵G的行列式。
6. 矩阵的逆给定矩阵H:\[ H = \begin{bmatrix} 4 & 7 \\ 2 & 6 \end{bmatrix} \] 求矩阵H的逆矩阵,如果H不可逆,请说明原因。
7. 线性方程组的矩阵表示考虑以下线性方程组:\[ \begin{align*}x + 2y &= 5 \\3x - y &= 1\end{align*} \]将此方程组转换为矩阵形式,并求解。
8. 特征值和特征向量给定矩阵I:\[ I = \begin{bmatrix} 3 & 1 \\ 0 & 2 \end{bmatrix} \] 求矩阵I的特征值和对应的特征向量。

矩阵变换练习题掌握矩阵变换的方法和应用矩阵变换练习题:掌握矩阵变换的方法和应用矩阵变换是线性代数中的重要内容,广泛应用于图形学、计算机视觉以及物理学等领域。
通过矩阵变换,我们可以对图形进行平移、旋转、缩放等操作,从而实现各种有趣的效果。
本文将介绍一些矩阵变换的基本方法和应用,并提供练习题来帮助读者加深理解与掌握。
一、平移变换平移变换是将图形沿着指定的方向进行移动的一种变换方法。
为了实现平移,我们可以使用二维或三维的平移矩阵。
对于二维情况下的平移变换,平移矩阵可以表示为:\[\begin{bmatrix} 1 & 0 & t_x \\ 0 & 1 & t_y \\ 0 & 0 & 1\end{bmatrix}\]其中,\(t_x\)和\(t_y\)分别表示在x轴和y轴上的平移距离。
对于三维情况下的平移变换,平移矩阵可以表示为:\[\begin{bmatrix} 1 & 0 & 0 & t_x \\ 0 & 1 & 0 & t_y \\ 0 & 0 & 1 & t_z \\ 0 & 0 & 0 & 1 \end{bmatrix}\]其中,\(t_x\)、\(t_y\)和\(t_z\)分别表示在x轴、y轴和z轴上的平移距离。
通过将图形的顶点坐标与平移矩阵相乘,即可实现平移变换。
练习题一:已知二维图形A的顶点坐标为(2, 3),应用平移变换使得A沿x轴正方向平移4个单位,沿y轴正方向平移5个单位。
请计算平移后A的顶点坐标。
练习题二:已知三维图形B的顶点坐标为(1, 2, 3),应用平移变换使得B沿x轴负方向平移2个单位,沿y轴负方向平移3个单位,沿z轴正方向平移1个单位。
请计算平移后B的顶点坐标。
二、旋转变换旋转变换是将图形绕指定点或指定轴进行旋转的一种变换方法。

1. 在R 22⨯中求矩阵⎥⎦⎤⎢⎣⎡=3021A 在基123111111,,,111000E E E ⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦41000E ⎡⎤=⎢⎥⎣⎦下的坐标。
2. 试证:在R 22⨯中矩阵123411111110,,,11011011αααα⎡⎤⎡⎤⎡⎤⎡⎤====⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦线性无关,并求⎥⎦⎤⎢⎣⎡=d c b a α在1234,,,αααα下的坐标。
3. 在R 22⨯空间中,线性变换T :()221240,2114T X X X R ⨯-⎡⎤⎡⎤=∈⎢⎥⎢⎥⎣⎦⎣⎦, 求T 在基123101111,,,000010ααα⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦41111α⎡⎤=⎢⎥⎣⎦下的矩阵表示。
4. 设T 是线性空间3R 上的线性变换,它在R 3中基123,,ααα下的矩阵表示是⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=512301321A (1)求T 在基112123123,,ααααααβββ==+=++下的矩阵表示; (2)求T 在基123,,ααα下的核与值域。
5. 求下列矩阵的Jordan 标准及其相似变换矩阵P(1)⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----211212112 , (2)⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-2000120010201012. 6. 已知矩阵310121013A -⎡⎤⎢⎥=--⎢⎥⎢⎥-⎣⎦验证A 是正规矩阵,并求A 的谱分解表达式。
7. 已知3阶矩阵1114335A x y -⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦的二重特征值2λ=对应两个线性无关的特征向量 (1)求,x y ;(2)求可逆矩阵P ,使得1P AP -为对角矩阵; (3)求A 的谱分解表达式。
8. 已知矩阵011101110A ⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦验证A 是正规矩阵,并求A 的谱分解表达式。
9. 已知矩阵024********2A ⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦验证A 是单纯矩阵,并求A 的谱分解表达式。

3.5实验题
(2)参考本章例子,设计一个例子,说明U/C矩阵的模块划分的方法
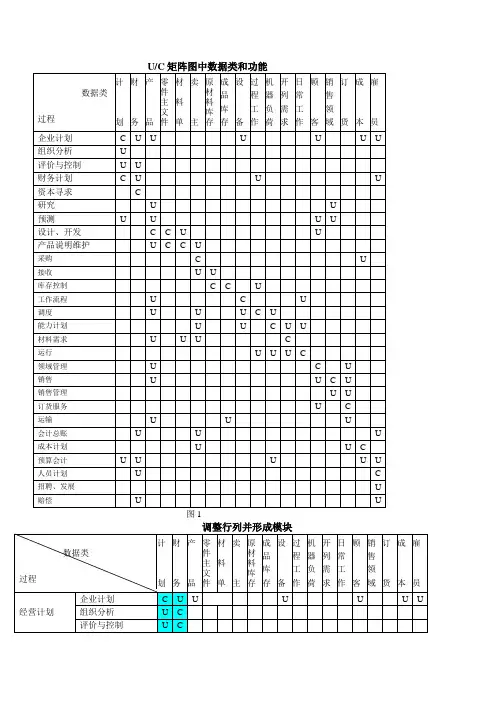
图1既是初始的矩阵图,数据类和企业过程是随机排列的,U、C在矩阵中的排列也是分散的。
我们以调换企业过程和数据类的顺序的方法尽量使UC集中到对角线上排列,既是调换矩阵的行列顺序,使得C尽量地靠近对角线,如图2所示;沿着对角线划分模块,即将C和与之紧密联系的U画在一个框中,这些框便构成了系统的功能模块,这些小模块就是一个个小系统。
图2 调整行列并形成模块
图2既是划分好的模块,从上往下依次是经营计划子系统、产品研发子系统、生产制造计划子系统、销售子系统、财务子系统和人事档案子系统。