
雅礼中学2021年上学期高一年级入学考试
数学
时量:120分钟 满分:150分
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)
1. 已知集合2{|340},{4,1,3,5}A x x x B =--<=-,则A B =( ) A. {4,1}- B. {1,5} C. {3,5} D. {1,3}
D
先求出集合A ,然后再求两个集合的交集即可 由2340x x --<解得14x -<<, 所以{}|14A x x =-<<,
又因为{}4,1,3,5B =-,所以{}1,3A B =,故选:D.
此题考查集合的交集运算,考查一元二次不等式的解法,属于基础题 2. 已知00a b >>,,则“a b >”是“11
a b b a
+>+”的( ) A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
C
根据不等式的可加性,即可证明充分性成立;再根据作差法和不等式的性质,即可证明必要性成立. 若0a b >>,则11
b a >,所以11a b b a
+>+,充分性成立. 若11a b b a
+
>+,则110a b b a +-->,即1()10a b ab ?
?-+> ???,
又00a b >>,,所以1
10ab
+>,所以0a b ->,即a b >,必要性成立. 故“a b >”是“11
a b b a
+>+”的充要条件.故选:C .
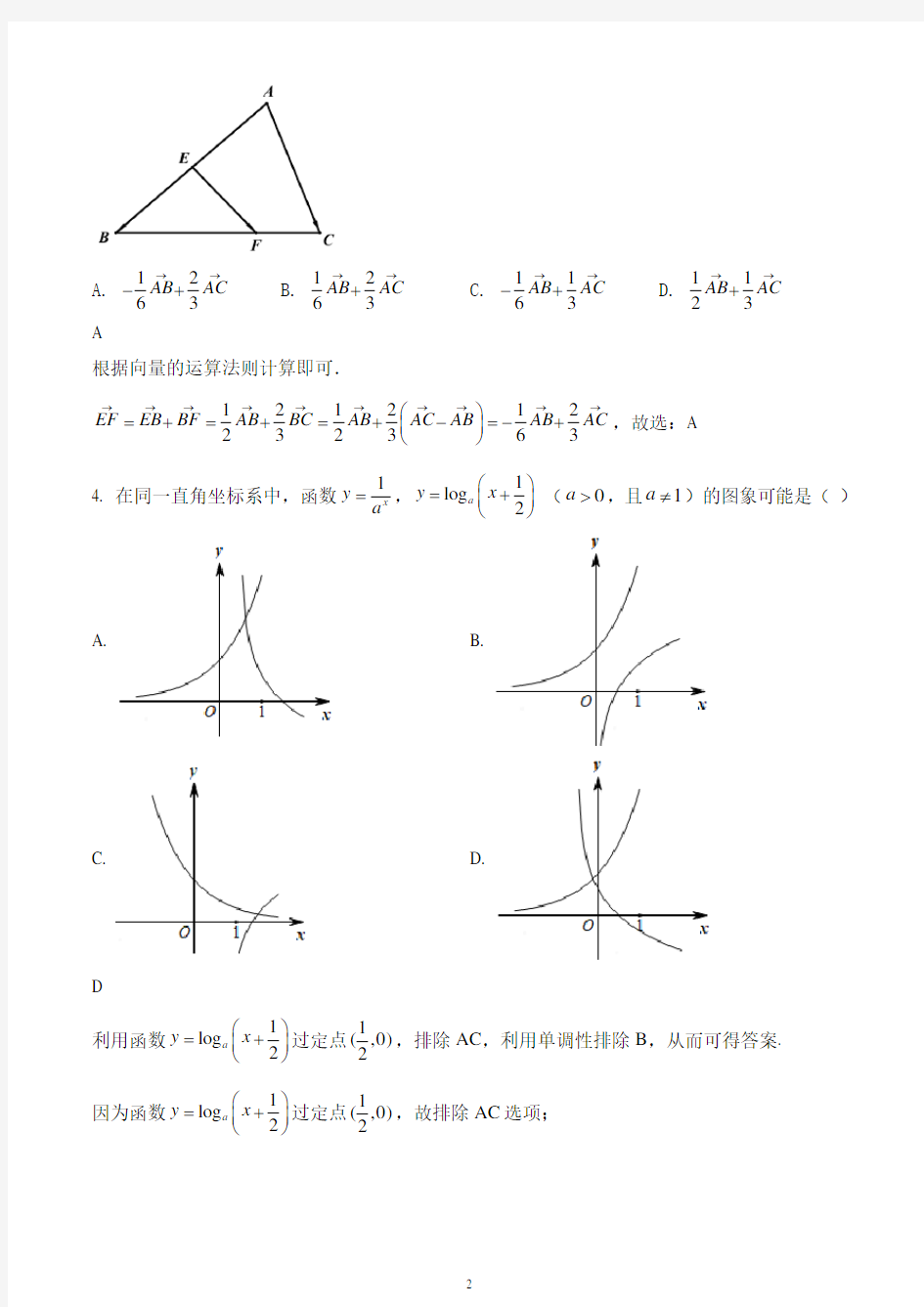
本题主要考查了充分必要条件的判断,以及不等式性质的应用,属于基础题. 3. 如图,ABC 中,E 是AB 的中点,点F 满足2BF FC →
→
=,则EF →
=( )
A. 1263AB AC →→
-+
B. 1263AB AC →→
+
C. 1163AB AC →→
-+
D. 1123
AB AC →→
+
A
根据向量的运算法则计算即可.
121212232363EF EB BF AB BC AB AC AB AB AC →
→
→
→→→→→→→??
=+=+=+-=-+ ???,故选:A
4. 在同一直角坐标系中,函数1x y a =
,1log 2a y x ?
?=+ ???
(0a >,且1a ≠)的图象可能是( ) A. B.
C. D.
D
利用函数1log 2a y x ?
?=+ ???过定点1(,0)2,排除AC ,利用单调性排除B ,从而可得答案.
因为函数1log 2a y x ?
?=+ ??
?过定点1(,0)2,故排除AC 选项;
对于B ,由图可知函数1x y a =
单调递增,可得01a <<,函数1log 2a y x ?
?=+ ??
?单调递增,
可得1a >,而01a <<与1a >不能同时成立,所以B 不合题意,排除B 选项.故选:D. 方法点睛:函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置. (2)从函数的单调性,判断图象的变化趋势; (3)从函数的奇偶性,判断图象的对称性; (4)从函数的特征点,排除不合要求的图象.
5. 已知向量()2,4a =,()1,b k =,且a 与b 的夹角为锐角,则实数k 的取值范围是( )
A. 1,2??
-+∞ ???
B. 1,22??
- ???
C. 1,2??-∞- ??
?
D. ()1,22,2??
-?+∞ ???
D
利用0a b ?>再排除同向共线即可求出.
a 与b
的夹角为锐角,
24024
a b k k ??=+>∴?≠?,解得12k >-且2k ≠,
即k 的取值范围是()1,22,2??
-?+∞ ???
.
6. 将函数()sin 2f x x x =的
图象沿x 轴向左平移()0??>个单位后得到函数()g x ,若
()g x 为偶函数,则?的最小值为( ) A. 12
π
B.
6
π
C.
4
π D.
512
π A
利用两角和与差的三角函数化简函数的解析式为一个角的一个三角函数的形式,通过平移求出平移后的函数的解析式,利用偶函数求出?的值. 函数sin 22sin(2)3
y x x x π
==+,
将函数sin 22y x x =+的图象沿x 轴向左平移?个单位后,得到函数2sin(22)3
y x π
?=++,
因为函数是偶函数,
∴2()()3
2
212
k k k Z k Z π
π
ππ
?π?+
=+
∈∴=
+∈. 当0k =时,12
π
?=
.故选:A
结论点睛:函数sin()y A x ω?=+是偶函数时,,;2
k k Z π
?π=+∈当函数sin()y A x ω?=+是奇函数
时,,.k k Z ?π=∈
7. 在ABC 中,a 、b 、c ,分别为ABC 的内角A 、B 、C 的对边,15a =、10b =、60A =?.则cos B =( )
A. 12-
B. -
C. D
利用正弦定理有
sin sin a b
A B
=求得sin B ,又22sin cos 1B B +=且三角形中大边对大角知0A B >>,即可求cos B . 由正弦定理知:sin sin a b
A B
=,即1510sin 60sin B =?,
∴sin B =
,又a b >,即π,0,2A B B ??>∈ ???,且22sin cos 1B B +=,
∴cos =
B .故选:D 关键点点睛:应用正弦定理求角的正弦值,结合三角形中内角性质--大边对大角、同角三角函数的平方关系求余弦值.
8. 已知min{,}m n 表示实数m ,n 中的较小数,若函数124()min 3log ,log f x x x ??
=+????
,当0a b
<<
时,有()()f a f b =,则 ) A. 6 B. 8 C. 9 D. 16
B
首先画出函数()f x 的图象,由图象确定当有()()f a f b =时,即214
log log 3
a b ++,再根据对
数运算公式化简求值.
作出函数()f x 的图象,如图中实线所示,由()()f a f b =可知,214
log log 3a b =+,所以
24log log 3a b +=,即222log log log ()3a b a b +==,所以8a b =.
故选:B
关键点点睛:本题一道数形结合分析问题的典型题型,关键是理解min{,}m n ,并画出函数()f x 的图象,属于中档题型.
二、多项选择题(本题共4小题,每小题5分,共20分.在每小题给出的四个选项中,有多项符合题目要求.全部选对得5分,部分选对得2分,有选错得0分.) 9. 下列结论正确的是( )
A. 在三角形ABC 中,若A B >,则sin sin A B >
B. 在锐角三角形ABC 中,不等式2220b c a +->恒成立
C. 若sin 2sin 2A B =,则三角形ABC 为等腰三角形
D. 在锐角三角形ABC 中,sin sin cos cos A B A B +>+ ABD
由正弦定理及三角形性质判断A ,由余弦定理判断B ,由正弦函数性质判断C ,利用锐角△ABC 这个条件,可得2
A B π
+>
,结合三角函数的单调性比较sin A 与cos B 大小即可判断D . ABC 中,A B a b >?>,由sin sin a b
A B
=,得sin sin A B >,A 正确; 在锐角三角形ABC 中,222
222cos 0,02b c a A b c a bc
+-=
>∴+->,B 正确; ABC 中,若sin 2sin 2A B =,则22A B =或22180A B ?+=,即A B =或90A B ?+=,ABC 为等腰三角形或直角三角形,C 错误; 在锐角三角形ABC 中,
2
A B π
+>
,
02
2
A B π
π
∴
>>
->,
sin sin 2A B π??
∴>- ???
,即sin cos A B >,同理:sin cos B A >
sin sin cos cos A B A B ∴+>+,D 正确.故选:ABD.
关键点睛:本题考查正弦定理,余弦定理,正弦函数的性质,诱导公式等,学会公式的灵活应用是解答本题的关键.
10. 已知函数()()sin 0,0,2f x A x A πω?ω??
?=+>>< ?
??的
部分图象如图所示,下列说法正确的
是( )
A. 函数()y f x =的周期为π
B. 函数()y f x =在2,36ππ??
--????
单调递减
C. 函数()y f x =的图象关于直线512
x π
=-
对称 D. 该图象向右平移6
π个单位可得2sin 2y x =的图象 ACD
先根据图像求出()y f x =的解析式,再分别验证A 、B 、C 、D 是否正确. 对于A :利用周期公式求周期;
对于B :利用复合函数“同增异减”求单调区间;
对于C :计算512f π?-?
???
,看512x π=-是否经过顶点;
对于D :利用“左加右减”判断.
由图像可知:A =2,周期24,2312T T ππππω??
=-=∴== ???
;
由
=2sin22 1212
2
f
ππ
?
π
?
?????
?+= ?
?
??
????
?
?<
??
解得:
3
π
?=
故函数()2sin2
3
f x x
π
??
=+
?
??
对于A:4
312
T
ππ
π
??
=-=
?
??
,故A正确;
对于B:当
2
36
x
ππ
-≤≤-时20
3
x
π
π-≤+≤,所以()
y f x
=在
2
,
36
ππ
??
--
??
??
上不单调.故B错误;对于C:当
5
12
x
π
=-时2
55
s2
12123
2in
f
πππ
????
=-=-
?
??
-?
?
+
?
?,即直线
5
12
x
π
=-是()
y f x
=的一条对称轴.故C正确;
对于D:()
y f x
=向右平移
6
π
个单位得到2sin222sin2
63
y x x
ππ
??
=-?+=
?
??
,故D正确.故选:ACD
求三角函数解析式的方法:
(1)求A通常用最大值或最小值;
(2)求ω通常用周期;
()求φ通常利用函数上的点带入即可求解.
11. 如图,正方形ABCD的长为2,O为边AD中点,射线OP绕点O按逆时针方向从射线OA旋转至射线OD,在旋转的过程中,记AOP
∠为x,射线OP扫过的正方形ABCD内部的区域(阴影部分)的面积为()
f x,则下列说法正确的是()
A.
1
42
f
π??
=
?
??
B. ()
f x在,
2
π
π
??
?
??
上为减函数
C. ()()4
f x f x
π
+-= D. ()
f x图象的对称轴是
2
x
π
=
AC
求出当0tan 2x <≤时,函数()f x 的解析式,可判断A 选项的正误;利用()f x 的单调性可判断B 选项的正误;利用对称性可判断C 选项的正误;利用特殊值法可判断D 选项的正误. 对于A 选项,当0tan 2x <≤时,设OP 交AB 于点E ,
tan tan AE x AOE AE OA =∠=
=,所以,()11
tan 22
f x OA AE x =?=, 0tan
24π
<≤,1
1tan 42
42f ππ??∴== ???,A 选项正确;
对于B 选项,当,2x ππ??
∈ ???时,射线OP 扫过的正方形ABCD 内部的区域(阴影部分)的面积
显然逐渐增加,即函数()f x 在,2ππ??
???
上单调递增,B 选项错误;
对于C 选项,取BC 的中点G ,连接OG ,
设射线OP 与正方形的边的交点为E ,作点E 关于直线OG 的对称点F , 则FOD x ∠=,所以,AOF x π∠=-,
将射线OF 绕O 点按顺时针方向旋转扫过正方形ABCD 的面积为S ,由对称性可知()S f x =, 因为()4S f x π+-=,即()()4f x f x π+-=,C 选项正确;
对于D 选项,由C 选项可知,()
()4f x f x π+-=,则3444
f f ππ????
+= ? ???
??
,
所以,3744
424f f f π
ππ??
????=-=≠
? ? ???
????
, 所以,函数()f x 的图象不关于直线2
x π=
对称,D 选项错误.故选:AC.
关键点点睛:本题考查函数基本性质的判断问题,在判断函数()f x 的单调性时,需要充分利用()f x 的几何意义,结合面积的对称性来求解,另外在判断某些结论不成立时,可充分利用特殊值来进行否定.
12. 设函数()y f x =和()y f x =-,若两函数在区间[],m n 上的单调性相同,则把区间[],m n 叫
做()y f x =的“稳定区间”,已知区间[]
1,2020为函数12x
y a ??
=+ ???
的“稳定区间”,则实数a 的可
能取值是( )
A. 32
-
B. 56
-
C. 0
D.
132
AB
首先求函数()f x -,根据两个函数同为增函数或同为减函数,确定绝对值里面的正负,根据恒成立求a 的取值范围.
由题意得1()2x
f x a ??=+ ???
与()2x
f x a -=+在区间[1,2020]上同增或同减.
若同增,则10,220x x a a ???+? ?????+?
在区间[1,2020]上恒成立,即1,22,a a ?
≤??
?≥-?所以1
22a --. 若同减,则10,220x x a a ???+? ?????+?在区间[1,2020]上恒成立,即2020
20201,
22,a a ???-? ????
?-?
无解, 所以A ,B 选项符合题意.故选:AB
思路点睛:本题考查指数函数单调性的综合应用,本题的关键是读懂“稳定区间”的定义,同时讨论函数同为增函数或同为减函数,去绝对值后转化为恒成立问题. 三、填空题(本题共4小题,每小题5分,共20分)
13. 已知命题“2,10x R mx x ?-+<∈”是假命题,则实数m 的取值范围是_________.
14
m ≥
求得原命题的否定,根据其为真命题,即可结合二次不等式恒成求得参数范围
若命题“2,10x R mx x ?-+<∈”是假命题,则“2,10x R mx x ?∈-+≥”为真命题, 显然0m =时,不满足题意,
故只需满足0140m m >???=-≤?,解得1
4m ≥.
故答案为:1
4
m ≥
. 本题考查根据含量词命题的真假求参数范围的问题,涉及二次不等式在R 上恒成立求参数的问题,属综合基础题.
14. 已知a 、b 满足:3a =,2b =,4a b +=,则a b -=_________.
10
将4a b +=两边平方展开可得a b ?的值,再计算2
a b -的值,进而可得a b -的值.
2
2
2
216a b a b a b +=++?=,
因为3a =,2b =, 所以3
2
a b ?=
, 所以2
2
2
3
2942102
a b a b a b +-?=+-?=-=, 可得10a b -=, 10.
15. 已知0a >,0b >,且21a b +=2a b ________.
2
22(2)222122a b a b a b ab ab =+=++=+由基本不等式计算可得结果,验证等号成立即可得解.
因为0a >,0b >,且21a b +=,
22(2)22212212112a b a b a b ab ab a b =+=++=+++=+= 当且仅当2a b =即1
1
,4
2
a
b 时,等号成立, 2a b 2. 2.
易错点睛:利用基本不等式求最值时,要注意其必须满足的三个条件: (1) “一正”就是各项必须为正数;
(2)“二定”就是要求和的最小值,必须把构成和的二项之积转化成定值;要求积的最大值,则必须把构成积的因式的和转化成定值;
(3)“三相等”是利用基本不等式求最值时,必须验证等号成立的条件,若不能取等号则这个定值就不是所求的最值,这也是最容易发生错误的地方.
16. 某市规定某工厂产生的废气必须过滤后才能排放,已知在过滤过程中,废气中的污染物P (单位:毫克/升)与过滤时间t (单位:小时)之间的函数关系式为:()0
kt
P t Pe -=(e 为自然
对数的底数,0P 为污染物的初始含量),过滤2小时后检测,发现污染物的含量为原来的16
25
,则k =______;且至少需要过滤______小时后,才能使污染物的含量不超过初始值的1
10000
.(参考数据:lg 20.3≈) (1). 5
ln 4
(2). 40 根据
2001625k p p e -=,求得k e -的值,即可得到k 的值;由0041()()51000
t p t p p =,化简整理,取以10为底的对数,计算即可得到所求最小值. 因为过滤2小时后检测,发现污染物的含量为原来的1625
, 根据题设,得
20016
25
k p p e -=, ∴45
k e -=,可得5ln
4
k =; 所以,04()()5
t p t p =
由()0041510000
t
p t p p ??
= ?
??
,得4
4()105t -,
两边取10为底对数,并整理得(13lg2)4t -,
0.14,40t t ∴?≥,
因此,至少还需过滤40小时, 故答案为:5
ln
4
,40. 四、解答题(本题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17. 已知集合3|
03x M x x +??
=
,集合22{|20N x x mx m =--<,其中0}m >. (1)当2m =时,求M N ?;
(2)若x M ∈是x ∈N 的必要不充分条件,求实数m 的取值范围. (1){23}M
N x x =-<<∣;(2)30,2??
???
.
(1)首先求出集合M ,N ,再根据交集的定义计算可得; (2)首先求出集合M ,依题意可得N M
,即可得到不等式组,解得即可;
解:(1)由
3
03
x x +<-,得33x -<<,所以{|33}M x x =-<<; 当2m =时,由2280x x --<,得24x -<<, 所以{|24}N x x =-<<. 所以{|23}M
N x x =-<<.
(2)由2220x mx m --<及0m >,得2m x m -<<.即{}|2x m x m N -<<= 因为x M ∈是x ∈N 的必要不充分条件,所以N
M
所以323
m m -≥-??≤?,且等号不同时成立,解得32m ≤.
又0m >,所以实数m 的取值范围是30,2??
???
.
本题考查必要不充分条件求参数的取值范围,一般可根据如下规则判断: (1)若p 是q 的必要不充分条件,则q 对应集合是p 对应集合的真子集; (2)p 是q 的充分不必要条件, 则p 对应集合是q 对应集合的真子集; (3)p 是q 的充分必要条件,则p 对应集合与q 对应集合相等;
(4)p 是q 的既不充分又不必要条件, q 对的集合与p 对应集合互不包含.
18. 已知函数()2
2sin cos 22222x x x f x ππ????
=-++- ? ?????
(1)求()f x 的最小正周期;
(2)求()f x 在区间[]0,π上的最小值及单调减区间.
(1)最小正周期为2π;(2)()min f x =()f x 的单调递减区间为,6ππ??
????
.
(1)利用降幂公式、诱导公式及逆用正弦二倍角公式将函数()f x 化为一个角的正弦函数,再利用周期公式,即可求出()f x 的最小正周期;
(2)先求出内层函数的值域,再结合正弦函数的图象和性质,即可求出结果.
(1)1cos ()2sin cos 222
x x x
f x +=+sin x x =+
12sin 2sin 23x x x π???
?=+=+ ? ?????
.
所以()f x 的最小正周期为2π. (2)因为[]0,x π∈,所以4,333x π
ππ??
+∈????
,
所以当433
x π
π
+=
,即x π=时,函数()f x 取得最小值由
42
3
3x π
π
π≤+
≤
,得6x ππ≤≤,所以函数()f x 的单调递减区间为,6ππ??????
. 关键点点睛:本题的关键是根据式子结构,将函数()f x 化为sin()y A x k ω?=++的形式.
19. 在ABC 中,a ,b ,c 分别是角A ,B ,C 所对的边,已知1a =,
(1,m =,()sin ,cos n A A =且m n ⊥.
(1)求角A 的大小;
(2)求ABC 周长的取值范围. (1)3
A π
=
;(2)(]2,3
(1)由题意得出
sin 0m n A A ==,从而求得A 的值; (1)由正弦定理表示出
b B =
,c C =
,利用三角恒等变换与三角形内角和定理,即可求出l a b c =++的取值范围.
解:(1)由(1,3)m =-,(sin ,cos )n A A =,且m n ⊥, 得
sin 0m n A A ==,
tan A ∴=;
又(0,)A π∈,
3
A π
∴=
;
(2)由(1)知3A π
=,1a =
,则1sin sin sin sin 3
b c a B C A π====
,
b B ∴
,c C =
,23
C A B B ππ=--=-,2(0,)3B π∈;
231sin(
)1(sin )12sin()32
6l a b c B B B B B ππ
∴=++=-=++=++, 又2(0,
)3
B π
∈,5,
666B πππ??
∴+∈ ???
, 1
sin()(62
B π∴+∈,1],
212sin()36
B π
∴<++,
ABC 周长的取值范围(]2,3.
解三角形的基本策略:一是利用正弦定理实现“边化角”,二是利用余弦定理实现“角化边”;求三角形面积的最大值也是一种常见类型,主要方法有两类,一是找到边之间的关系,利用基本不等式求最值,二是利用正弦定理,转化为关于某个角的函数,利用函数思想求最值. 20. 已知ABC 中,角A ,B ,C 所对的边长分别为a ,b ,c ,且满足cos sin =+b a C c A . (1)求A 的大小; (2)若3
cos 5B =
,5BC =,
17
BD BA =,求CD 的长. (1)π
4
A =;(2
)CD =(1)由正弦定理得sin sin cos sin sin B A C C A =+,再由()sin sin B A C =+,代入得
cos sin sin sin A C C A =,可求得A 的大小; (2)由正弦定理
sin sin AC BC
B A
=
,求得AC =7AB =,1BD =,利用余弦定理求得答案.
解:(1)在ABC 中,由正弦定理得sin sin cos sin sin B A C C A =+, 又()()sin sin πsin B A C A C =-+?=??+?, 所以()sin sin cos sin sin A C A C C A +=+
即sin cos cos sin sin cos sin sin A C A C A C C A +=+,整理得cos sin sin sin A C C A =, 因为sin 0C ≠可得cos sin A A =,又0A π<<, 所以π
4
A =;
(2)在ABC
中,4sin 5
B ==
,由4sin sin 5AC BC AC B A =?=
,解得AC =
又因为(
)cos cos cos cos sin sin 10
C A B A B A B =-+=-+=
, 所以2222cos 49AB AC BC AC BC C =+-???=,得7AB =, 由1
7
BD BA =
得17BD BA =,所以1BD =,
所以2222cos 20CD BD BC BD BC B =+-???=,
所以CD ==关键点点睛:在运用正弦定理、余弦定理解三角形时,注意由已知条件选择合适的定理,并注意角的范围.
21. 湖南省第二届张家界园林博览会于2019年9月28日至11月28在张家界园博园举办,本届园林博览会以“辉煌张家界,生态林园博”为主题,展示张家界生态之美,文化之韵,吸引更多优秀企业来张投资,从而促进张家界经济快速发展.在此博览会期间,某公司带来了一种智能设备供采购商谈采购,并决定大量投放张家界市场.已知该种设备年固定研发成本为50万元,每生产一台需另投入80元,设该公司一年内生产该设备x 万台,且全部售完.且每万台的销售
收入()G x (万元)与年产量x (万台)的函数关系式近似满足:()21802,020
20009000
70,20x x G x x x x -<≤??
=?+->??. (1)写出年利润()W x (万元)关于年产量x (万台)函数解析式(年利润=年销售收入-总成本);
(2)当年产量为多少万台时,该公司获得的利润最大?并求最大利润.
(1)()2210050,020
9000
101950,20x x x W x x x x ?-+-<≤?
=?--+>?
?;(2)当年产量为30万台,该公司获得的利润最大,最大利润为1350万元.
(1)利用()()8050W x xG x x =--可得出函数()W x 的解析式;
(2)利用二次函数求出函数()W x 在(]0,20上的最大值,利用基本不等式求得函数()W x 在
()20,+∞上的最大值,综合可得出函数()W x 的最大值及其对应的x 的值,即可得出结论.
(1)由题意可得()()8050W x xG x x =--.
当020x <≤时,()()2
1802080502010050W x x x x x x =---=-+-;
当20x >时,()2200090009000708050101950W x x x x x x x ?
?=+---=--+ ???
. 因此,()2210050,020
9000
101950,20x x x W x x x x ?-+-<≤?
=?--+>?
?
; (2)当020x <≤时,()()2
22100502251200W x x x x =-+-=--+, 则函数()W x 在(]0,20上单调递增, 当20x
时,()W x 取得最大值()max 22512001150W x =-?+=(万元);
当20x >时,(
)9000900195010195010195010W x x x x x ?
?=--
=-+≤-? ???
1350=(万元). 当且仅当900
x x
=
,即30x =时,等号成立. 综上所述,()max 1350x W =(万元).
答:当年产量为30万台时,该公司获得的利润最大,最大利润为1350万元. 思路点睛:解函数应用题的一般程序:
第一步:审题——弄清题意,分清条件和结论,理顺数量关系;
第二步:建模——将文字语言转化成数学语言,用数学知识建立相应的数学模型; 第三步:求模——求解数学模型,得到数学结论;
第四步:还原——将用数学方法得到的结论还原为实际问题的意义;
第五步:反思回顾——对于数学模型得到的数学结果,必须验证这个数学解对实际问题的合理性.
22. 设函数()x x
f x ka a -=-(0a >且1a ≠)是定义域为R 的奇函数,()312
f =.
(1)求函数()f x 的解析式;
(2)若()()222x x
g x a a mf x -=+-在[)1,+∞上的最小值为2-,求m 的值.
(1)()22x x
f x -=-;(2)2
(1)由题意得:()00f =,由此可得1k =,再代入()312
f =,解方程可得:2a =,即可求出函数()f x 的解析式;
(2)由(1)得,()()()2
222222x x x x g x m --=---+,令22x x t -=-,利用换元法转化为二次函数的最值,再分类讨论即可求出答案. 解:(1)由题意知:()00f =,
即()00
010f ka a k =-=-=,
解得:1k =,
()x x f x a a -∴=-,
由()312
f =,得:()1
312
f a a -=-=
, 即22320a a --=,
解得:2a =,或1
2
a =-(舍去),
()22x x f x -∴=-;
(2)由(1)得,()()2222222x x x x
g x m --=+--()()2
222222x x x x m --=---+,
令22x x t -=-,
易知:22x x t -=-在[)1,+∞上单调递增,
故当1≥x 时,11
3222
t -≥-=
, ∴函数()g x 转化为()2
22h t t mt =-+,对称轴为:t m =,
当3
2
m ≥
时, ()()22min 222h t h m m m ==-+=-, 即24m =,
解得2m =,或2m =-(舍去); ②当3
2m <时,()min
39324
22h h t m ??= ???=-+=-, 解得25
12
m =
(舍去); 综上所述:2m =.
关键点点睛:本题解题的关键是利用换元法和二次函数的图象与性质进行求解.