QDPSK理论误码率与实际误码率matlab仿真程序

QPSK通信系统的性能分析与matlab仿真1 绪论在当今高度信息化的社会，信息和通信已成为现代社会的“命脉”。

信息作为一种资源，只有通过广泛地传播与交流，才能促进社会成员之间的合作，推动生产力的发展，创造出巨大的经济效益。

在新技术革命的高速推动和信息高速公路的建设，全球网络化发展浪潮的推动下，通信技术得到迅猛的发展，载波通信、卫星通信和移动通信技术正在向数字化、智能化、宽带化发展。

Simulink具有适应面广、结构和流程清晰及仿真精细、效率高、贴近实际、等优点，基于以上优点Simulink已被广泛应用于控制理论和数字信号处理的复杂仿真和设计。

同时有大量的第三方软件和硬件应用于Simulink。

本文设计出一个QPSK仿真模型，以分析QPSK在高斯信道中的性能，通过此次课程设计，更好地了解QPSK系统的工作原理，传输比特错误率和符号错误率的计算。

1.1 研究背景与研究意义1.1.1 研究背景在当今高度信息化的社会，信息和通信已成为现代社会的“命脉”。

信息作为一种资源，只有通过广泛地传播与交流，才能促进社会成员之间的合作，推动生产力的发展，创造出巨大的经济效益。

信息的数字转换处理技术走向成熟，为大规模、多领域的信息产品制造和信息服务创造了条件。

高新技术层出不穷。

随着通信技术的发展，通信系统方面的设计也会越来越复杂，利用计算机软件的仿真，可以大大地降低通信过程中的实验成本。

Simulink是MATLAB最重要的组件之一，它提供一个动态系统建模、仿真和综合分析的集成环境。

在该环境中只要通过简单的鼠标操作，就可以构造出复杂的系统。

Simulink提供了一个建立模型方块图的图形用户接口，这个创建过程只需单击和拖动鼠标操作就能完成，它提供了一种更快捷、直接明了的方式，而且用户可以立即看到系统的仿真结果。

1.1.2研究意义通过完成实验的设计内容，加深对通信原理理论的理解，熟悉通信系统的基本概念，复习正交相位偏移键控(QPSK)调制解调的基本原理和误比特率的计算方法，了解调制解调方式中最基础的方法。

⽤matlab进⾏误码率仿真翻译利⽤Matlab进⾏误码率仿真PS:⼀篇英⽂⽂献的重点摘抄翻译1 简介Matlab是误码率仿真的利器。

2 采样信号的性质在Matlab中通过序列来表征连续信号。

2.1 功率定义瞬时功率为然⽽，更有⽤的⼀个概念是平均功率。

平均瞬时功率的定义Matlab的表⽰pav= sum(x.^2)/length(x)由于加的⽩噪声0均值，换句话说，就是没有直流分量。

因此就可以通过⽅差来获得信号的平均功率。

2.2 能量信号的总能量必须等于其平均功率乘以其持续时间，定义为Matlab的表⽰et= sum(x.^2)/fs.3 仿真概述仿真⼀般包括发射机，接收机和信道。

仿真结果⽤⼆维图表⽰，横坐标为归⼀化信噪⽐Eb/N0:即单位⽐特能量除以单边带噪声功率谱密度。

纵坐标为误码率，⽆量纲，⼀般为10的幂次⽅表⽰。

4 仿真流程4.1 发射机产⽣⼀个伪随机序列作为信源信息4.2 建⽴SNR将信噪⽐Eb/N0由dB转换为线性，即成⼀个⽆量纲，Matlab可以表⽰为：ebn0= 10^(snrdb/10)4.3 确定Eb⽐特能量是总能量除以信号中位数。

也可以表⽰为平均信号功率乘以⼀个⽐特的持续时间。

总之，定义为：N采样信号长度, fbit⽐特速率Matlab表⽰为：eb = sum(x.^2)/(length(x)?fb)4.4 计算N0单边带噪声功率谱密度可以表⽰为信噪⽐除以⽐特能量。

Matlab表⽰为：n0 = eb/ebn04.5 计算定义为功率谱密度乘以带宽为噪声⽅差。

、：Matlab表⽰为：pn= n0?fs/24.6 产⽣噪声可以⽤matlab⾃带的函数产⽣，这⾥我们⾃⼰产⽣n=sqrt(pn)?randn(1,length(x));4.7 添加噪声y=x+n4.8 接收机接收机收到的是已经有信道噪声的信号4.9 判断偏移量由于滤波器等其他时延设备带来的延迟，接收机和发射机信号存在延迟。

专业课程设计报告题 目：专业课程设计南昌航空大学信息工程学院20 15 年 7月 3 日姓 名：专 业： 基于MATLAB 的QPSK 调制系统的误码性能研究班级学号： 12042243 同 组 人 ：指导教师：宋高俊专业 课程设计任务书20 14－20 15 学年 第 2 学期 第 16 周－ 18 周注：1、此表一组一表二份，课程设计小组组长一份；任课教师授课时自带一份备查。

2、课程设计结束后与“课程设计小结”、“学生成绩单”一并交院教务存档。

题目 基于MATLAB 的QPSK 调制系统的误码性能研究 内容及要求〖基本要求〗理解和掌握BPSK 、QPSK 的调制与解调原理，掌握MATLAB 的编程方法，用仿真的方法（基于MATLAB ）研究BPSK 和QPSK 系统的符号错误率并作图，研究仿真实验次数与结果精确度的关系，完成课程设计报告。

进度安排2015.6.15-2015.6.21：查阅资料，方案分析与设计； 2015.6.22-2015.6.28：在MATLAB 平台下完成仿真实验； 2015.6.29-2015.7.3：完成课程设计报告。

学生姓名：指导时间：第16-18周 指导地点： E610 任务下达2015 年6月15日任务完成2015年7月3日考核方式1.评阅 □√ 2.答辩 □ 3.实际操作 □√ 4.其它□ 指导教师宋高俊系（部）主任摘要QPSK正交相移键控，是一种数字调制方式，四相相移键控信号。

在现代通信系统中，调制与解调是必不可少的重要手段。

调制就是把信号转换成适合在信道中传输的形式的一种过程。

解调则是调制的相反过程，而从已调制信号中恢复出原信号。

QPSK 技术具有抗干扰能力好、误码率低、频谱利用效率高等一系列优点。

本设计主要介绍了BPSK、QPSK的调制与解调原理，以及比较BPSK和QPSK系统的符号错误率，利用Matlab对QPSK、BPSK系统进行调制解调仿真，在Matlab中的AWGN信道中研究它们误码性能。

matlab误码率仿真代码以下是一个简单的 MATLAB 误码率仿真代码示例，用于模拟二进制传输系统的误码率。

在这个示例中，我们将使用 BPSK（二进制相移键控）调制来进行仿真。

matlab.% 设置参数。

SNR_dB = 0:1:10; % 信噪比范围。

numBits = 1e6; % 要传输的比特数。

ber = zeros(size(SNR_dB)); % 初始化误码率向量。

for i = 1:length(SNR_dB)。

% 生成随机的二进制数据。

txBits = randi([0,1],1,numBits);% BPSK调制。

txSignal = 2txBits 1;% 添加高斯噪声。

noiseVar = 10^(-SNR_dB(i)/10);noise =sqrt(noiseVar/2)(randn(1,numBits)+1irandn(1,numBits)); rxSignal = txSignal + noise;% BPSK解调。

rxBits = real(rxSignal) > 0;% 计算误码率。

ber(i) = sum(rxBits ~= txBits)/numBits;end.% 绘制误码率曲线。

semilogy(SNR_dB,ber,'o-');xlabel('SNR (dB)');ylabel('Bit Error Rate');title('BPSK误码率仿真');grid on;在这个示例中，我们首先设置了信噪比范围和要传输的比特数。

然后我们使用 for 循环来遍历不同的信噪比值。

在每个循环中，我们生成随机的二进制数据，并将其进行 BPSK 调制。

接着我们添加高斯噪声，并进行 BPSK 解调。

最后我们计算误码率，并将结果绘制成误码率曲线。

这个示例代码可以帮助你了解如何使用 MATLAB 进行简单的误码率仿真。

[键入文字]通信工程专业《通信原理》课程设计题目 QPSK的误码率仿真分析学生姓名谭夕林学号 **********所在院(系)陕西理工学院物理与电信工程学院专业班级通信工程专业 1102 班指导教师魏瑞完成地点陕西理工学院物理与电信工程学院实验室2014年 3 月 12 日通信工程专业课程设计任务书院(系) 物理与电信工程学院专业班级通信工程专业1102班学生姓名谭夕林一、课程设计题目 QPSK的误码率仿真分析二、课程设计工作自 2014 年 2 月 24 日起至 2014 年 3 月 16 日止三、课程设计进行地点: 物理与电信工程学院实验室四、课程设计的内容要求：利用仿真软件等工具，结合所学知识和各渠道资料，对QPSK在高斯通道下的误码率进行研究分析指导教师魏瑞系(教研室)通信工程系接受任务开始执行日期2014年2月24日学生签名谭夕林QPSK的误码率仿真分析谭夕林陕西理工学院物理与电信工程学院通信1102班，陕西汉中723003）指导教师：魏瑞【摘要】为实现QPSK应用到无线通信中，该文对QPSK系统性能进行了理论研究。

介绍了QPSK调制解调原理,对高斯白噪声信道的系统性能进行了研究，分析对比了在高斯白噪声信道下的系统误码性能。

为基于副载波QPSK无线激光通信系统的研究奠定了理论基础。

使用MATLAB中M语言完成QPSK的蒙特卡罗仿真，得出在加性高斯白噪声的信道下，传输比特错误率以及符号错误率。

并将比特错误率与理论值相比较，并得出关系曲线。

使用simulink搭建在加性高斯白噪声信道下的QPSK调制解调系统，其中解调器使用相关器接收机。

并计算传输序列的比特错误率。

通过多次运行仿真得到比特错误率与信噪比之间的关系。

【关键词】： QPSK，误码率，仿真，星座图【中图分类号】 TN702 [文献标志码] AQPSK BER simulation analysisTan Xilin(Grade11,Class2,Major of Communication Engineering，School of Physics and telecommunication Engineering of Shaanxi University of Technology, Hanzhong 723003,China)Tutor:Wei Rui[Abstract]For the application of the QPSK (Phase-Shift-Keying) to the wireless laser communication, this paper emphasizes the system of QPSK's performance, theoretically. In the paper, the principle of the QPSK's modulation and demodulation were introduced in brief and the performance of the system at white Gaussian noise (AWGN) channel was also analyzed carefully. The above results provide the theoretical foundation for the wireless laser communication system based on the QPSK with e the MATLAB language to complete Monte Carlo simulation of QPSK, and to obtain the transmission sequence bit error rate and symbol error rate in the additive white Gaussian noise channel, comparing it with the theoretical value, then get curve. The second aspect is to learn how to use Simulink and the functions and principles of various modules. Then we use Simulink to create the model of QPSK through additive white Gaussian noise channel. And take the advantage of the Correlator receiver to complete the operation of demodulation. Then calculate the transmission sequence bit error rate. By running the simulation repeatedly, we can get the relationship between the bit error rate and SNR.Keywords: QPSK, BER, simulation, constellation目录摘要 (3)Abstract (4)一绪论 (6)1.1 课题背景及仿真 (6)1.1.1QPSK系统的应用背景简介 (6)1.1.2QPSK实验仿真的意义 (6)1.1.3仿真平台和仿真内容 (6)二系统实现框图和分析 (7)2.1QPSK调制部分 (7)2.2QPSK解调部分 (8)三QPSK特点及应用领域 (9)3.1QPSK特点 (9)3.2误码率 (10)3.3QPSK时域信号 (10)3.4扩充认知QPSK-OQPSK (10)3.5QPSK的应用领域 (11)四使用simulink搭建QPSK调制解调系统 (12)4.1信源产生 (12)4.2QPSK系统理论搭建 (13)五仿真模型参数设置及结果 (15)5.1仿真附图及参数设置 (15)5.2仿真结果 (16)5.3误码率曲线程序及其仿真结果 (17)六仿真结果分析 (19)七总结与展望 (20)致谢 (21)参考文献 (21)一．绪论1.1课题背景及仿真：1.1.1QPSK系统的应用背景简介QPSK是英文Quadrature Phase Shift Keying的缩略语简称，意为正交相移键控，是一种数字调制方式。

QPSK（Quadrature Phase Shift Keying）调制是一种常见的数字调制方式，它可以使信号在传输时能够更有效地利用频谱资源。

在数字通信系统中，QPSK调制被广泛应用于各种应用场景中，因其具有高效利用频谱和抗干扰能力强等特点而备受青睐。

在QPSK调制中，误码率是一个非常重要的性能指标，它直接影响到系统的可靠性和稳定性。

对QPSK调制的误码率曲线进行分析和绘制是十分重要的。

1. QPSK调制原理QPSK调制是一种采用正交载波的调制方式，它将两路独立的数字信号分别调制到正交的载波上，然后再将两路调制信号叠加在一起进行传输。

在QPSK调制中，每个符号携带两个比特信息，分别代表实部和虚部，因此可以实现在单位频谱带宽内传输两倍的数据量。

QPSK 调制的信号点图形式如下图所示：（此处插入QPSK调制信号点图）2. QPSK调制误码率QPSK调制的误码率是指在传输过程中由于信道噪声或其他干扰因素引起的信号错误率。

误码率通常用比特错误率（BER）来表示，即单位时间内传输的比特中出现错误的比例。

QPSK调制的误码率曲线是描述在不同信噪比条件下系统性能的重要指标，它反映了系统在不同信噪比条件下的可靠性和稳定性。

通常情况下，我们可以通过理论分析或仿真实验来得到QPSK调制的误码率曲线。

3. Matlab绘制QPSK调制误码率曲线Matlab是一款功能强大的科学计算软件，它提供了丰富的绘图函数和工具，可以方便地进行误码率曲线的绘制。

在Matlab中，我们可以利用通信工具箱中的相关函数和工具来实现QPSK调制误码率曲线的分析和绘制。

下面我们将结合实际代码示例来演示如何使用Matlab 进行QPSK调制误码率曲线的绘制。

```matlab设置信号点数目M = 4;设置信噪比范围EbN0dB = 0:10;EbN0 = 10.^(EbN0dB/10);计算误码率ber = berawgn(EbN0,'qam',M);绘制误码率曲线semilogy(EbN0dB,ber,'linewidth',2);grid on;xlabel('Eb/N0 (dB)');ylabel('Bit Error Rate');title('QPSK Modulation BER Curve');```4. 结论通过Matlab的仿真分析和绘图，我们可以得到QPSK调制的误码率曲线。

图 14 低通滤波后的波形
图 15 误码情况（0dB）
3.误码率
在统计误码率时，考虑到程序运行时间，码元个数为：65536，在高信噪 比下统计的误码率可信度较低。 判决前的信噪比按下式计算：SNR=A2/δ
2
，其中 A 为已调信号幅度，δ
2
为
噪声方差。BPSK 的理论误码率为：0.5 ∗ erfc( ������)，其中 r=SNR=A2/δ 2 为判决时的 信噪比。2DPSK 的理论误码率为：0.5 ∗ exp(−r)。 BPSK 在-10dB,-8dB,-6dB,-4dB,-2dB,0dB,2dB,4dB,6dB,8dB,10dB 的信噪比下的误 码率依次为： 0.334625244140625 0.293212890625000 0.244171142578125 0.192596435546875 0.140975952148438 0.0857543945312500 0.0433654785156250 0.0148315429687500 0.00328063964843750 0.000488281250000000 4.57763671875000e-05 2DPSK 在-10dB,-8dB,-6dB,-4dB,-2dB,0dB,2dB,4dB,6dB,8dB,10dB 的信噪比下的 误码率依次为： 0.463904783703365 0.444800488288701 0.410727092393378 0.370138094148165 0.309910734721904 0.229083695735103 0.144426642252232 0.0688944838635844 0.0211947814145113 0.00267032883192187 0.000183108262760357 根据这两组数据以及对应的理论数据，绘制的误码率曲线如下图所示：

专业课程设计报告题目：基于MATLAB的QPSK调制系统的误码性能研究姓名：专业：通信工程班级学号：同组人：指导教师：南昌航空大学信息工程学院20 16 年 6 月 27 日专业 课程设计任务书20 15－20 16 学年 第 2 学期 第 15 周－ 18 周注：1、此表一组一表二份，课程设计小组组长一份；任课教师授课时自带一份备查。

2、课程设计结束后与“课程设计小结”、“学生成绩单”一并交院教务存档。

摘要QPSK正交相移键控，是一种数字调制方式，四相相移键控信号。

在现代通信系统中，调制与解调是必不可少的重要手段。

调制就是把信号转换成适合在信道中传输的形式的一种过程。

解调则是调制的相反过程，而从已调制信号中恢复出原信号。

QPSK技术具有抗干扰能力好、误码率低、频谱利用效率高等一系列优点。

本设计主要介绍了BPSK、QPSK的调制与解调原理，在Matlab\simulink 中对比了BPSK和QPSK系统的符号错误率，并研究了仿真试验次数与结果精度的关系。

关键词:正交相移键控调制解调 Matlab\simulink 误码性能目录第一章课程设计内容介绍 (1)1.1 设计目的 (1)1.2 MATLAB\Simulink简介 (1)1.3 通信系统基本模型 (1)第二章 MPSK调制解调原理 (2)2.1 QPSK、BPSK基本原理介绍 (2)2.2 BPSK调制原理 (2)2.3 BPSK调制原理 (4)2.4 QPSK调制原理 (5)2.5 QPSK解调原理 (6)第三章 MPSK系统误码性能研究 (7)3.1 BPSK系统及其模块参数配置 (7)3.2 QPSK系统及其模块参数配置 (10)3.3 QPSK&BPSK系统误码率对比 (11)3.4 仿真实验次数与结果精确度的关系 (12)第四章课程设计总结 (15)参考文献 (15)附录 BPSK&QPSK误码率曲线对比代码 (16)第一章课程设计内容介绍1.1 设计目的1、掌握MATLAB的编程方法和学会使用simulink仿真。

基于MATLAB的QDPSK通信系统仿真摘要针对信号与系统课程及电子信息类专业的特点, 提出将MATLAB引入到信号与系统课程的教与学中, 既能加强学生对理论知识的掌握及提高解决实际问题的能力, 又能为课堂教学及教学方法和手段的改革增添活力。

MATLAB的出现使“信号与系统”课程的计算机辅助教学更为便捷。

本文详细论述了使用MATLAB工具将“信号与系统”中复杂的理论计算和绘图等抽象问题通过编程变得简单而直观。

MATLAB的运用大大改善了“信号与系统”的教学方法和手段,丰富了教学容,取得了良好的教学效果,对于教学水平的提高十分有益利用MATLAB平台的SIMULINK功能编写了一套QDPSK通用功能模块库，并在此基础上进行了多项可视化仿真,较好地显示了数字通信的工作方式和优越性，以及采用SIMULINK进行仿真的良好的演示效果，为QDPSK系统的研究提供了一个较好的软件平台。

关键字: 通信系统; 仿真; QDPSK引言在通信与电子工程领域，系统仿真技术一直是进行新型通信协议研发、通信体制的性能研究、通信系统设计、算法分析和改进、通信信号处理、电子系统设计的重要手段。

传统的仿真技术基于C语言等计算机专业编程技术，编程的工作量大，仿真程序的可读性、可重用性、可靠性都很难适应大型复杂通信系统仿真的需要。

通信与电子工程师和科研工作者迫切需要一种仿真工具，以摆脱繁杂的编程工作，将精力和时间集中到解决科学问题、提出和验证创新思想和算法上来。

MATLAB以及Simulink科学计算、建模和仿真软件是为了适应这一要求而产生的优秀仿真平台软件，并已成为全世界科学工作者共同的学术交流工以及系统仿真界事实上的工业标准。

现在，我国教育科研部门对MATLAB的地位和重要作用也逐渐达成了共识，尤其是在硬件设施有限、科研经费不足的情况下，MATLAB的广泛应用必将大大提升我国科教事业的基础研究水平。

目录1 课程设计目的 (1)2 课程设计要求 (1)3 相关知识 (1)4 课程设计分析 (2)5 程序代码 (4)6 运行结果 (6)7 参考文献 (7)1.课程设计目的（1）加深对QDPSK系统基本理论知识的理解。

基于MATLAB的QDPSK通信系统仿真摘要: 利用MATLAB平台的SIMULINK功能编写了一套QDPSK通用功能模块库，并在此基础上进行了多项可视化仿真,较好地显示了数字通信的工作方式和优越性，以及采用SIMULINK进行仿真的良好的演示效果，为QDPSK数字通信系统的研究提供了一个较好的软件平台。

关键字: 通信系统; 仿真; QDPSK引言在通信与电子工程领域，系统仿真技术一直是进行新型通信协议研发、通信体制的性能研究、通信系统设计、算法分析和改进、通信信号处理、电子系统设计的重要手段。

传统的仿真技术基于C语言等计算机专业编程技术，编程的工作量大，仿真程序的可读性、可重用性、可靠性都很难适应大型复杂通信系统仿真的需要。

通信与电子工程师和科研工作者迫切需要一种仿真工具，以摆脱繁杂的编程工作，将精力和时间集中到解决科学问题、提出和验证创新思想和算法上来。

MATLAB以及Simulink科学计算、建模和仿真软件是为了适应这一要求而产生的优秀仿真平台软件，并已成为全世界科学工作者共同的学术交流工以及系统仿真界事实上的工业标准。

现在，我国教育科研部门对MATLAB的地位和重要作用也逐渐达成了共识，尤其是在硬件设施有限、科研经费不足的情况下，MATLAB的广泛应用必将大大提升我国科教事业的基础研究水平。

1 QDPSK技术简介1.1调制原理多进制数字相位调制又称多相制，它利用载波的多种不同相位或相位差来表征数字信息的调制方式。

QDPSK（四相相对移相调制）信号是利用前后码元之间的相对相位变化来表示数字信息。

若以前一双比特码元相位作为参考，Δφn为当前双比特码元与前一双比特码元初相差，四相相对码变换的逻辑关系如表一所示。

表一QDPSK编码与载波相位变化关系QDPSK信号的调制通常采用码变换加调相法。

先将输入的双比特码进行码形变换，再用码形变换器输出的双比特码进行四相绝对移相，所得到的输出信号便是四相相对移相信号（QDPSK信号），其调制原理如图一所示。

光通信相干调制和外差检测技术的误码率蒙特卡洛仿真matlab 蒙特卡洛方法是一种通过随机模拟来估计系统参数或性能的统计方法。

在光通信相干调制和外差检测技术的误码率蒙特卡洛仿真中，我们可以使用 MATLAB 来实现。

以下是一个基于 MATLAB 的光通信相干调制和外差检测技术的误码率蒙特卡洛仿真示例代码：```matlab% 产生随机二进制序列binary_sequence = randi([0,1],10000,1);% 进行相干调制和外差检测modulated_signal = modulate(binary_sequence,'PSK',1);received_signal = detect(modulated_signal,'PSK',1);% 计算误码率error_count = sum(binary_sequence ~= received_signal);error_rate = error_count/numel(binary_sequence);disp(['误码率为：', num2str(error_rate)]);```在上述示例代码中，我们首先产生了一个长度为 10000 的随机二进制序列。

然后，我们使用`modulate`函数对二进制序列进行相干调制，调制方式为 PSK，星座点数为 1。

接下来，我们使用`detect`函数进行外差检测。

最后，我们计算误码率，即错误比特的数量与总比特数量的比值。

你可以根据实际需求修改代码中的调制方式、检测方式、二进制序列长度等参数。

同时，你还可以使用`MonteCarlo`函数来进行多次仿真，以获得更准确的误码率估计。

请注意，上述示例代码仅提供了一个简单的误码率蒙特卡洛仿真框架，实际应用中可能需要考虑更多的因素，如信道噪声、光纤损耗等。

实验报告实验目的1.掌握BPSK信号调制、相干解调方法；2.掌握BPSK信号误码率计算。

实验内容1.BPSK信号的调制；2.BPSK信号相干解调；3.不同信噪比环境下BPSK信号误码率计算，并与理论误码率曲线对比。

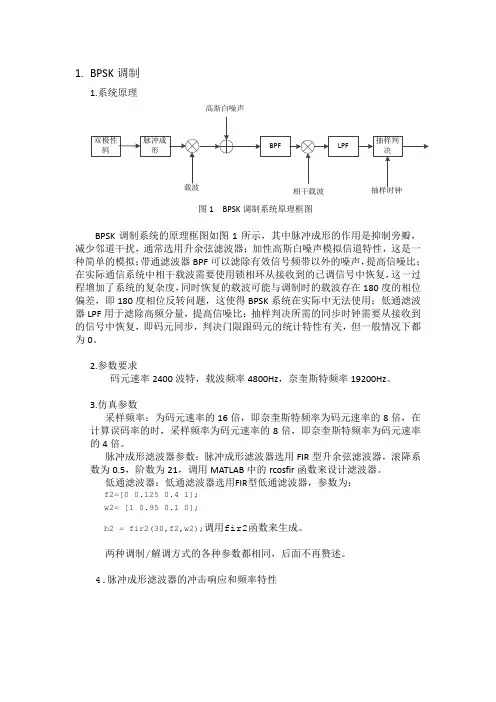
实验原理BPSK信号调制原理1.系统原理高斯白噪声图1 BPSK调制系统原理框图BPSK调制系统的原理框图如图1所示，其中脉冲成形的作用是抑制旁瓣，减少邻道干扰，通常选用升余弦滤波器；加性高斯白噪声模拟信道特性，这是一种简单的模拟；带通滤波器BPF可以滤除有效信号频带以外的噪声，提高信噪比；在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复，这一过程增加了系统的复杂度，同时恢复的载波可能与调制时的载波存在180度的相位偏差，即180°相位反转问题，这使得BPSK 系统在实际中无法使用；低通滤波器LPF 用于滤除高频分量，提高信噪比；抽样判决所需的同步时钟需要从接收到的信号中恢复，即码元同步，判决门限跟码元的统计特性有关，但一般情况下都为0。

2. 参数要求码元速率1000波特，载波频率4KHz ，采样频率为16KHz 。

BPSK 信号解调原理BPSK 信号的解调方法是相干解调法。

由于PSK 信号本身就是利用相位传递信息的，所以在接收端必须利用信号的相位信息来解调信号。

图2中给出了一种2PSK 信号相干接收设备的原理框图。

图中经过带通滤波的信号在相乘器中与本地载波相乘，然后用低通滤波器滤除高频分量，在进行抽样判决。

判决器是按极性来判决的。

即正抽样值判为1，负抽样值判为0。

图2 BPSK 解调系统原理框图BPSK 信号误码率在AWGN 信道下BPSK 信号相干解调的理论误码率为：12e P erfc =，其中r 为信噪比222na r σ=。

在大信噪比(1)r条件下，上式可近似为：r e P -=实验结果与分析BPSK信号调制根据BPSK信号产生原理，用matlab仿真BPSK信号如图3所示。

QPSK（Quadrature Phase Shift Keying，正交相移键控）是一种数字调制技术，广泛应用于无线通信系统中。

在实际应用中，由于信道的传输特性和噪声的影响，信号可能会发生误码。

因此，评估和优化QPSK系统的误码率是非常重要的。

在MATLAB中，我们可以使用以下步骤来计算QPSK系统的误码率：
1. 生成QPSK信号：首先，我们需要生成一个QPSK信号。

这可以通过MATLAB中的函数来实现，例如`qammod`函数可以生成QPSK调制信号。

2. 添加噪声：为了模拟实际信道中的噪声影响，我们需要在QPSK信号上添加高斯白噪声。

可以使用`awgn`函数来实现这一步骤。

3. 解调QPSK信号：接收到带有噪声的QPSK信号后，我们需要对其进行解调以恢复原始数据。

MATLAB中的`qamdemod`函数可以实现这一功能。

4. 计算误码率：最后，我们需要比较解调后的数据与原始数据，计算误码率。

可以使用MATLAB中的`biterr`函数来实现这一步骤。

以下是一个简单的MATLAB代码示例，用于计算QPSK系统的误码率：
通过运行上述代码，我们可以得到QPSK系统在不同信噪比下的误码率。

这对于评估和优化
QPSK系统的性能是非常有帮助的。

QPSK系统的误码率和星座图MATLAB仿真QPSK系统的误码率和星座图MATLAB仿真2011-06-22 10:29:12| 分类：编程 | 标签：qpsk matlab |字号订阅一、引言数字调制就是把数字基带信号的频谱搬移到高频处，形成适合在信道中传输的带通信号。

基本的数字调制方式有振幅键控（ASK）、频移键控（FSK）、绝对相移键控（PSK）、相对（差分）相移键控（DPSK）。

在接收端可以采用想干解调或非相干解调还原数字基带信号。

数字信号的传输方式分为基带传输和带通传输。

然而，实际中的大多数信道（如）无线信道具有丰富的低频分量。

为了使数字信号在带通信道中传输，必须用数字基带信号对载波进行调制，以使信号与信道的特性相匹配。

通信系统的抗噪声性能是指系统克服加性噪声影响的能力。

在数字通信系统中，信道噪声有可能使传输码元产生错误，错误程度通常用误码率来衡量。

因此，与分析数字基带系统的抗噪声性能一样，分析数字调制系统的抗噪声性能，也就是求系统在信道噪声干扰下的总误码率。

误码率（BER：bit error ratio）是衡量数据在规定时间内数据传输精确性的指标。

误码率是指错误接收的码元数在传输总码元数中所占的比例，更确切地说，误码率是码元在传输系统中被传错的概率，即误码率=错误码元数/传输总码元数。

如果有误码就有误码率。

误码的产生是由于在信号传输中，衰变改变了信号的电压,致使信号在传输中遭到破坏，产生误码。

噪音、交流电或闪电造成的脉冲、传输设备故障及其他因素都会导致误码（比如传送的信号是1，而接收到的是0；反之亦然）。

误码率是最常用的数据通信传输质量指标。

它表示数字系统传输质量的式是“在多少位数据中出现一位差错”。

误信率，又称误比特率，是指错误接收的比特数在传输总比特数中所占的比例，即误比特率=错误比特数/传输总比特数。

在数字通信系统中，可靠性用误码率和误比特率表示。

数字调制用“星座图”来描述，星座图中定义了一种调制技术的两个基本参数：（1）信号分布；（2）与调制数字比特之间的映射关系。

%%dpsk格雷码矩形%%等效基带调制clc;clear all;close all;%%关闭所有窗口，比如之前画的图nsymbol = 1e6;%%每种信噪比下符号数的发送符号数，10^6个数errornumber = zeros(1,10);errorratio = zeros(1,10);dataa = randi([0,1],1,2*nsymbol);%%产生1行，2*nsymbol列均匀分布的随机数datab = zeros(1,2*nsymbol);data_mod1 = zeros(1,nsymbol);%%各参量初始化data_mod2 = zeros(1,nsymbol);data_demod1 = zeros(1,nsymbol);data_demod2 = zeros(1,nsymbol);s_receive1 = zeros(1,nsymbol);s_receive2 = zeros(1,nsymbol);datab_receive = zeros(1,2*nsymbol);dataa_receive = zeros(1,2*nsymbol);datab(1) = xor(0,dataa(1));%%给定初始相位for l = 2:(2*nsymbol)%%逻辑运算datab(l) = xor(dataa(l),datab(l-1));endfor i = 1:nsymbol %%格雷码调制到星座图的映射if datab(2*i-1)==0 && datab(2*i)==0data_mod1(i) = 1;data_mod2(i) = 1;elseif datab(2*i-1)==0 && datab(2*i)==1data_mod1(i) = -1;data_mod2(i) = 1;elseif datab(2*i-1)==1 && datab(2*i)==1data_mod1(i) = -1;data_mod2(i) = -1;elseif datab(2*i-1)==1 && datab(2*i)==0data_mod1(i) = 1;data_mod2(i) = -1;endendSNR_dB = 1:10;%%%信噪比dB形式SNR = 10.^(SNR_dB/10);%%信噪比转化为线性值for loop= 1:10sigma = sqrt(1/SNR(loop));%%%根据符号功率求噪声功率s_receive1 = data_mod1+sigma * randn(1,length(data_mod1));s_receive2 = data_mod2+sigma * randn(1,length(data_mod2));%%添加复高斯白噪声for k = 1:nsymbol%%反映射if s_receive1(k)>0 && s_receive2(k)>0data_demod1(k) = 0;data_demod2(k) = 0;elseif s_receive1(k)<0 && s_receive2(k)>0data_demod1(k) = 0;data_demod2(k) = 1;elseif s_receive1(k)<0 && s_receive2(k)<0data_demod1(k) = 1;data_demod2(k) = 1;elseif s_receive1(k)>0 && s_receive2(k)<0data_demod1(k) = 1;data_demod2(k) = 0;enddatab_receive(2*k-1) = data_demod1(k);datab_receive(2*k) = data_demod2(k);enddataa_receive(1) = xor(0,datab_receive(1));for n = 2:(2*nsymbol)dataa_receive(n) = xor(datab_receive(n),datab_receive(n-1));endfor m = 1:nsymbolif (dataa_receive(2*m-1) ~= dataa(2*m-1))||(dataa_receive(2*m) ~= dataa_receive(2*m))%%统计误码个数errornumber(loop) = errornumber(loop)+1;endenderrorratio(loop) = errornumber(loop)/nsymbol; %%计算误码率endser_theory = 1-(1-qfunc(sqrt(SNR))).^2;%理论误码率，注意Q函数和误差函数的对应关系semilogy(SNR_dB,errorratio,'-k*',SNR_dB,ser_theory,'-ro');title('DPSK信号在AWGN信道下的性能（格雷码）');xlabel('信噪比/dB');ylabel('误码率');legend('误码率','理论误码率');grid on;%%坐标线。

实验报告实验目的1.掌握BPSK信号调制、相干解调方法；2.掌握扩频、解扩的方法；3.掌握BPSK扩频信号误码率计算。

实验内容1.BPSK信号的调制；2.BPSK信号扩频；3.不同信噪比环境下BPSK扩频信号误码率计算，并和理论误码率曲线对比。

实验原理BPSK信号调制原理1.系统原理双极性码脉冲成形BPF LPF抽样判决载波高斯白噪声图5 BPSK调制系统原理框图BPSK调制系统的原理框图如图1所示，其中脉冲成形的作用是抑制旁瓣，减少邻道干扰，通常选用升余弦滤波器；加性高斯白噪声模拟信道特性，这是一种简单的模拟；带通滤波器BPF可以滤除有效信号频带以外的噪声，提高信噪比；在实际通信系统中相干载波需要使用锁相环从接收到的已调信号中恢复，这一过程增加了系统的复杂度，同时恢复的载波可能和调制时的载波存在180度的相位偏差，即180°相位反转问题，这使得BPSK系统在实际中无法使用；低通滤波器LPF 用于滤除高频分量，提高信噪比；抽样判决所需的同步时钟需要从接收到的信号中恢复，即码元同步，判决门限跟码元的统计特性有关，但一般情况下都为0。

2. 参数要求码元速率1000波特，载波频率4KHz ，采样频率为16KHz 。

BPSK 信号扩频原理通信理论和通信技术的研究，是围绕着通信系统的有效性和可靠性这两个基本问题展开的，所以有效性和可靠性是设计和评价一个通信系统的主要性能指标。

通信系统的有效性，是指通信系统传输信息效率的高低。

这个问题是讨论怎样以最合理、最经济的方法传输最大数量的信息。

在模拟通信系统中，多路复用技术可提高系统的有效性。

显然，信道复用程度越高，系统传输信息的有效性就越好。

在数字通信系统中，由于传输的是数字信号，因此传输的有效性是用传输速率来衡量的。

通信系统的可靠性，是指通信系统可靠地传输信息。

由于信息在传输过程中受到干扰，收到的信息和发出的信息并不完全相同。

可靠性就是用来衡量收到信息和发出信息的符合程度。

利用Matlab进行误码率仿真PS:一篇英文文献的重点摘抄翻译1 简介Matlab是误码率仿真的利器。

2 采样信号的性质在Matlab中通过序列来表征连续信号。

2.1 功率定义瞬时功率为然而，更有用的一个概念是平均功率。

平均瞬时功率的定义Matlab的表示pav= sum(x.^2)/length(x)由于加的白噪声0均值，换句话说，就是没有直流分量。

因此就可以通过方差来获得信号的平均功率。

2.2 能量信号的总能量必须等于其平均功率乘以其持续时间，定义为Matlab的表示et= sum(x.^2)/fs.3 仿真概述仿真一般包括发射机，接收机和信道。

仿真结果用二维图表示，横坐标为归一化信噪比Eb/N0:即单位比特能量除以单边带噪声功率谱密度。

纵坐标为误码率，无量纲，一般为10的幂次方表示。

4 仿真流程4.1 发射机产生一个伪随机序列作为信源信息4.2 建立SNR将信噪比Eb/N0由dB转换为线性，即成一个无量纲，Matlab可以表示为：ebn0= 10^(snrdb/10)4.3 确定Eb比特能量是总能量除以信号中位数。

也可以表示为平均信号功率乘以一个比特的持续时间。

总之，定义为：N采样信号长度, fbit比特速率Matlab表示为：eb = sum(x.^2)/(length(x)∗fb)4.4 计算N0单边带噪声功率谱密度可以表示为信噪比除以比特能量。

Matlab表示为：n0 = eb/ebn04.5 计算定义为功率谱密度乘以带宽为噪声方差。

、：Matlab表示为：pn= n0∗fs/24.6 产生噪声可以用matlab自带的函数产生，这里我们自己产生n=sqrt(pn)∗randn(1,length(x));4.7 添加噪声y=x+n4.8 接收机接收机收到的是已经有信道噪声的信号4.9 判断偏移量由于滤波器等其他时延设备带来的延迟，接收机和发射机信号存在延迟。

在Matlab通过下式获得偏移量。