
MATLAB中关于常见的概率分布密度函数的语句及格式
MATLAB中关于常见的概率分布密度函数的语句及格式
normpdf(x,mu,sigma) 正态分布密度函数。
uifpdf(x,a,b) 均匀分布(连续)密度函数
exppdf(x,a) 指数分布密度函数
geopdf(x,p) 几何分布密度函数
binopdf(x,n,p) 二项分布密度函数
poisspdf9x,n) 泊松分布密度函数
unidpdf(x,n) 均匀分布(离散)密度函数
chi2pdf(x,3) X^2分布密度函数
fpdf(x,m,n) F分布密度函数
tpdf(x,n) t分布密度函数
一、常见连续分布的密度函数MATLAB实现
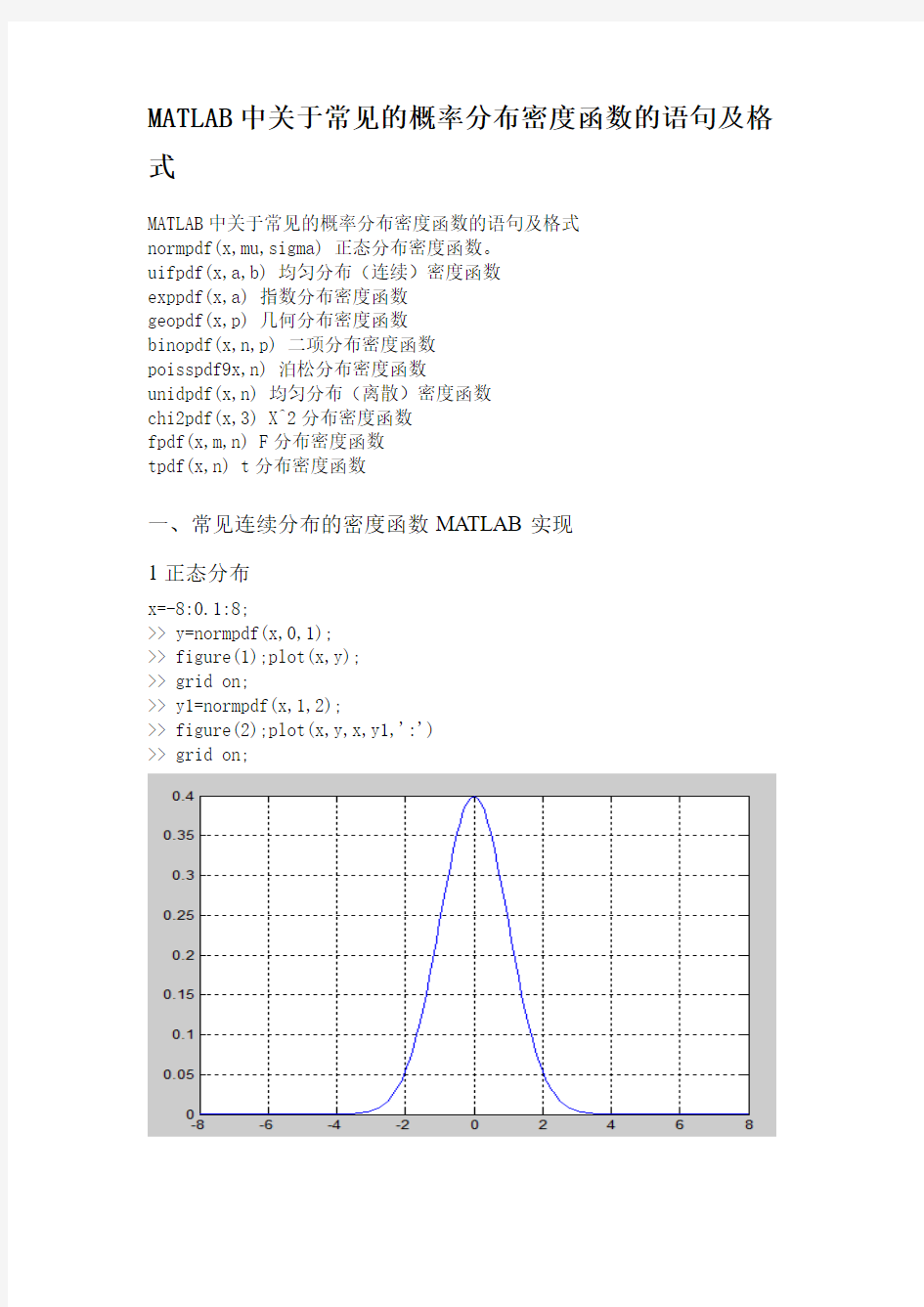
1正态分布
x=-8:0.1:8;
>> y=normpdf(x,0,1);
>> figure(1);plot(x,y);
>> grid on;
>> y1=normpdf(x,1,2);
>> figure(2);plot(x,y,x,y1,':')
>> grid on;
2均匀分布
>> clear all
>> x=-10:0.1:10;
>> r=1;
>> y=unifpdf(x,0,2*pi*r); >> plot(x,y,'r*');
>> grid on;
x=0:0.1:30;
>> y=exppdf(x,4);
>> plot(x,y,'m-.')
>> grid on
二、常见离散分布的密度函数1几何分布
x=0:30;
>> y=geopdf(x,0.5);
>> plot(x,y,'bo')
>> grid on
clear all
>> x=0:50;
>> y=binopdf(x,500,0.05); >> plot(x,y,'r*');
3泊松分布
x=0:50;
>> y=poisspdf(x,25);
>> plot(x,y,'r.');
三、三大抽样分布的密度函数
1 X*2分布
第三章 二维随机变量及其联合概率分布 考试内容: 二维随机变量的联合分布函数 / 离散型二维随机变量的联合概率分布、边缘分布和条件分布 / 连续型二维随机变量的联合概率密度、边缘密度/ 随机变量的独立性和相关性 / 常见二维随机变量的概率分布 / 两个随机变量的函数的概率分布 考试要求: 1、理解二维随机变量的联合分布函数的概念和基本性质。 2、理解二维随机变量的联合分布的概念、性质及其两种基本表达形式:离散型二维随机变量联合概率 分布和连续型二维随机变量联合概率密度。掌握已知两个随机变量的联合分布时分别求它们的边缘分布的方法。 3、理解随机变量的独立性和相关性的概念,掌握随机变量独立的条件;理解随机变量的不相关性与独 立性的关系。 4、掌握二维均匀分布和二维正态分布,理解其中参数的概率意义。 5、掌握根据两个随机变量的联合概率分布求其函数概率分布的方法。 一、知识要点 1、二维随机变量的分布函数 ),(Y X 的联合分布函数 },{),(y Y x X P y x F ≤≤=, 性质:1),(0≤≤y x F ,单调不减,右连续, 0),(=-∞-∞F ,0),(=-∞y F ,0),(=-∞x F ,1),(=+∞+∞F ; X 的边缘分布函数:),()(+∞=x F x F X ; Y 的边缘分布函数:),()(y F y F Y +∞=. 2、二维离散型随机变量),(Y X 联合分布律:ij j p y Y x X P ===),(1, ,2,1,=j i ,一般用矩形表格列出; 边缘分布律:?===∑i j ij i p p x X P 记)(, ,2,1=i j i ij j p p y Y P ?== =∑记 )(, ,2,1=j . 3、二维连续型随机变量),(Y X 若?? ∞-∞ -= x y v u v u f y x F d d ),(),(,称),(y x f 为),(Y X 的联合密度函数; ),(y x f 的性质: (1) 0),(≥y x f ; (2) 1d d ),(=?? ∞+∞-∞ +∞ -y x y x f ; (3)若),(y x f 连续,则),() ,(2y x f y x y x F =???; (4)??= ∈D y x y x f D Y X P d d ),(}),{(;
幻灯片1 正态分布 第二章 第七节 一、标准正态分布的密度函数 二、标准正态分布的概率计算 三、一般正态分布的密度函数 四、正态分布的概率计算幻灯片2 正态分布的重要性正态分布是概率论中最重要的分布, 这能够由 以下情形加以说明: ⑴ 正态分布是自然界及工程技术中最常见的分布之一, 大量的随机现象都是服从或近似服从正态分布的.能够证明, 如果一个随机指标受到诸多因素的影响, 但其中任何一个因素都不起决定性作用, 则该随机指标一定服从或近似服从正态分布. 这些性质是其它 ⑵ 正态分布有许多良好的性质, 许多分布所不具备的. ⑶ 正态分布能够作为许多分布的近似分布.幻灯片3 -标准正态分布下面我们介绍一种最重要的正态分布 一、标准正态分布的密度函数若连续型随机变量X 的密度函数为定义 则称X 服从标准正态分布,
记为标准正态分布是一种特别重要的它的密度函数经常被使用, 分布。 幻灯片4 密度函数的验证 则有 ( 2) 根据反常积分的运算有能够推出 幻灯片5 标准正态分布的密度函数的性质若随机变量 , X 的密度函数为 则密度函数的性质为: 的图像称为标准正态( 高斯) 曲线幻灯片6 随机变量 由于 由图像可知, 阴影面积为概率值。对同一长度的区间 , 若这区间越靠近 其对应的曲边梯形面积越大。标准正态分布的分布规律时”中间多, 两头少” . 幻灯片7 二、标准正态分布的概率计算 1、分布函数分布函数为幻灯片8 2、标准正态分布表书末附有标准正态分布函数数值表, 有了它, 能够解决标准正态分布的概率计算.表中给的是x > 0时,①(x)的值. 幻灯片9 如果由公式得令则幻灯片10
一十种概率密度函数 function zhifangtu(x,m) %画数据的直方图,x表示要画的随机数,m表示所要画的条数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% a=min(x); b=max(x); l=length(x); h=(b-a)/m; %量化x x=x/h; x=ceil(x); w=zeros(1,m); for i=1:l for j=1:m if (x(i)==j) %x(i)落在j的区间上,则w(j)加1 w(j)=w(j)+1; else continue end end end w=w/(h*l); z=a:h:(b-h); bar(z,w); title('直方图') function y=junyun(n) %0-1的均匀分布,n代表数据量,一般要大于1024 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% y=ones(1,n); x=ones(1,n); m=100000; x0=mod(ceil(m*rand(1,1)),m); x0=floor(x0/2); x0=2*x0+1; u=11; x(1)=x0; for i=1:n-1 x(i+1)=u*x(i)+0; x(i+1)=mod(x(i+1),m); x(i)=x(i)/m; end %x(n)单位化
x(n)=x(n)/m; y=x; function y=zhishu(m,n) %指数分布,m表示指数分布的参数,m不能为0.n表示数据量,n一般要大于1024 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% x=junyun(n); for i=1;n if (x(i)==0) x(i)=0.0001; else continue; end end u=log(x); y=-(1/m)*u; function y=ruili(m,n) %瑞利分布,m是瑞利分布的参数,n代表数据量,n一般要大于1024 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% x=junyun(n); for i=1:n if (x(i)==0) x(i)=0.0001; else continue; end end u=(-2)*log(x); y=m*sqrt(u); function y=weibuer(a,b,n) %韦布尔分布,a,b表示参数,b不能为0.n表示数据量,一般要大于1024 %a=1时,是指数分布 %a=2时,是瑞利分布%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% x=junyun(n); for i=1:n if (x(i)==0) x(i)=0.0001; else continue; end
设(X ,Y )的联合密度函数为f (x ,y ),现求Z=X+Y 的概率密度。 令{(,)|}z D x y x y z =+≤,则Z 的分布函数为: (){} {}(,)((,))Z D z z y F z P Z z P X Y z f x y dxdy f x y dx dy +∞--∞ -∞ =≤=+≤==??? ? (1.1) 固定z 和y 对积分 (,)z y f x y dx --∞ ?作换元,令x y u +=,得 (,)(,)z y z f x y dx f u y y du --∞ -∞ =-?? (1.2) 于是 ()(,)[(,)]z z Z F z f u y y dudy f u y y dy du +∞+∞ -∞-∞ -∞ -∞ =-=-???? (1.3) 由概率论定义,即得Z 的概率密度为 ()(,)Z f z f z y y dy +∞-∞ =-? (1.4) 由X 与Y 的对称性,又可得 ()(,)Z f z f x z x dx +∞-∞ =-? , (1.5) 特别的,当X 与Y 相互独立时,有 ()()()()()Z X Y X Y F z f z y f y dx f x f z x dx +∞ +∞ -∞ -∞ =-=-? ? (1.6) 其中,()X f x 、()Y f y 分别是X 和Y 的密度函数。 式(1.6)又称为()X f x 和()Y f y 的卷积,常记为*()X Y f f z 。因此式(1.6)又称为独立和分布的卷积公式。
设(X ,Y )的联合密度函数为f (x ,y ),又X Z Y =,现求X Z Y =的概率密度,Z 的分布函数为 1 2 (){} (,)(,)Z D D F z P Z z f x y dxdy f x y dxdy =≤=+???? (2.1) 而 1 (,)(,)yz D f x y dxdy f x y dxdy +∞ -∞=?? ? ? (2.2) 对于固定的z ,y ,积分 (,)yz f x y dx -∞ ?作换元x u y = (这里y>0),得 (,)(,)yz z f x y dx yf yu y du -∞ -∞ =?? (2.3) 于是 01 (,)(,)(,)z D z f x y dxdy yf yu y dudy yf yu y dydu +∞-∞+∞ -∞==????? ? (2.4) 类似的可得 2 (,)(,)(,)yz D z f x y dxdy f x y dxdy yf yu y dydu +∞ -∞-∞-∞ ==-??? ? ? ? (2.5) 故有 12 0()(,)(,)[(,)(,)][(,)]Z D D z z F z f x y dxdy f x y dxdy yf yu y dy yf yu y dy du y f yu y dy du +∞-∞ -∞ +∞-∞-∞ =+=-=?????? ? ?? (2.6) 有概率密度定义可得X Z Y = 的概率密度为 ()(,)Z f z y f yz y dy +∞ -∞ =? (2.7) 特别的,当X 与Y 相互独立时,有 ()()()Z X Y f z y f yz f y dy +∞-∞ =? (2.8)
目录 1. 均匀分布 (1) 2. 正态分布(高斯分布) (2) 3. 指数分布 (2) 4. Beta分布(:分布) (2) 5. Gamm 分布 (3) 6. 倒Gamm分布 (4) 7. 威布尔分布(Weibull分布、韦伯分布、韦布尔分布) (5) 8. Pareto 分布 (6) 9. Cauchy分布(柯西分布、柯西-洛伦兹分布) (7) 2 10. 分布(卡方分布) (7) 8 11. t分布................................................ 9 12. F分布 ............................................... 10 13. 二项分布............................................ 10 14. 泊松分布(Poisson 分布)............................. 11 15. 对数正态分布........................................
1. 均匀分布 均匀分布X ~U(a,b)是无信息的,可作为无信息变量的先验分布。
2. 正态分布(高斯分布) 当影响一个变量的因素众多,且影响微弱、都不占据主导地位时,这个变量 很可能服从正态分布,记作 X~N (」f 2)。正态分布为方差已知的正态分布 N (*2)的参数」的共轭先验分布。 1 空 f (x ): —— e 2- J2 兀 o' E(X), Var(X) _ c 2 3. 指数分布 指数分布X ~Exp ( )是指要等到一个随机事件发生,需要经历多久时间。其 中,.0为尺度参数。指数分布的无记忆性: Plx s t|X = P{X t}。 f (X )二 y o i E(X) 一 4. Beta 分布(一:分布) f (X )二 E(X) Var(X)= (b-a)2 12 Var(X)二 1 ~2
正态分布 第二章 第七节 一、标准正态分布的密度函数 二、标准正态分布的概率计算 三、一般正态分布的密度函数 四、正态分布的概率计算 幻灯片2 正态分布的重要性正态分布是概率论中最重要的分布, 这可以由 以下情形加以说明: ⑴正态分布是自然界及工程技术中最常见的分布 之一, 大量的随机现象都是服从或近似服从正态分布的. 可以证明, 如果一个随机指标受到诸多因素的影响, 但其中任何一个因素都不起决定性作用, 则该随机指标 一定服从或近似服从正态分布. 这些性质是其它 ⑵正态分布有许多良好的性质, 许多分布所不具备的. ⑶正态分布可以作为许多分布的近似分布. 幻灯片3 -标准正态分布 下面我们介绍一种最重要的正态分布 一、标准正态分布的密度函数 若连续型随机变量X的密度函数为 定义 则称X服从标准正态分布, 记为 标准正态分布是一种特别重要的 它的密度函数经常被使用, 分布。 幻灯片4 密度函数的验证 则有 (2)根据反常积分的运算有 可以推出 幻灯片5 标准正态分布的密度函数的性质
,X的密度函数为 则密度函数的性质为: 的图像称为标准正态(高斯)曲线。 幻灯片6 随机变量 由于 由图像可知,阴影面积为概率值。 对同一长度的区间 ,若这区间越靠近 其对应的曲边梯形面积越大。 标准正态分布的分布规律时“中间多,两头少”. 幻灯片7 二、标准正态分布的概率计算 1、分布函数 分布函数为 幻灯片8 2、标准正态分布表 书末附有标准正态分布函数数值表,有了它,可以解决标准正态分布的概率计算. 表中给的是x > 0时, Φ(x)的值. 幻灯片9 如果 由公式得 令 则 幻灯片10 例1 解 幻灯片11 由标准正态分布的查表计算可以求得, 当X~N(0,1)时, 这说明,X 的取值几乎全部集中在[-3,3]区间内,超出这个范围的可能性仅占不到0.3%. 幻灯片12 三、一般正态分布的密度函数 如果连续型随机变量X的密度函数为 (其中 为参数) 的正态分布,记为 则随机变量X服从参数为 所确定的曲线叫 作正态(高斯)曲线. 幻灯片13
目录 1. 均匀分布 ...................................................................................................... 1 2. 正态分布(高斯分布) ........................................................................... 2 3. 指数分布 ...................................................................................................... 2 4. Beta 分布(β分布) .............................................................................. 2 5. Gamma 分布 .............................................................................................. 3 6. 倒Gamma 分布 ......................................................................................... 4 7. 威布尔分布(Weibull 分布、韦伯分布、韦布尔分布) ..................... 5 8. Pareto 分布 ................................................................................................. 6 9. Cauchy 分布(柯西分布、柯西-洛伦兹分布) (7) 10. 2χ分布(卡方分布) (7) 11. t 分布 ......................................................................................................... 8 12. F 分布 ........................................................................................................ 9 13. 二项分布 ................................................................................................ 10 14. 泊松分布(Poisson 分布) .............................................................. 10 15. 对数正态分布 ....................................................................................... 11 1. 均匀分布 均匀分布~(,)X U a b 是无信息的,可作为无信息变量的先验分布。 1 ()f x b a =-
数学期望:随机变量最基本的数学特征之一。它反映随机变量平均取值的大小。又称期望或均值。它是简单算术平均的一种推广。例如某城市有10万个家庭,没有孩子的家庭有1000个,有一个孩子的家庭有9万个,有两个孩子的家庭有6000个,有3个孩子的家庭有3000个,则此城市中任一个家庭中孩子的数目是一个随机变量,记为X,它可取值0,1,2,3,其中取0的概率为0.01,取1的概率为0.9,取2的概率为0.06,取3的概率为0.03,它的数学期望为0×0.01+1×0.9+2×0.06+3×0.03等于1.11,即此城市一个家庭平均有小孩1.11个,用数学式子表示为:E(X)=1.11。 也就是说,我们用数学的方法分析了这个概率性的问题,对于每一个家庭,最有可能它家的孩子为1.11个。 可以简单的理解为求一个概率性事件的平均状况。 各种数学分布的方差是: 1、一个完全符合分布的样本 2、这个样本的方差 概率密度的概念是:某种事物发生的概率占总概率(1)的比例,越大就说明密度越大。比如某地某次考试的成绩近似服从均值为80的正态分布,即平均分是80分,由正态分布的图形知x=80时的函数值最大,即随机变量在80附近取值最密集,也即考试成绩在80分左右的人最多。 下图为概率密度函数图(F(x)应为f(x),表示概率密度):
离散型分布:二项分布、泊松分布 连续型分布:指数分布、正态分布、X2分布、t分布、F分布 抽样分布 抽样分布只与自由度,即样本含量(抽样样本含量)有关 二项分布(binomial distribution):例子抛硬币 1、重复试验(n个相同试验,每次试验两种结果,每种结果概率恒定———— 伯努利试验) 2、
第一章随机事件和概率 (1)排列组合公式 )! ( ! n m m P n m- =从m个人中挑出n个人进行排列的可能数。 )! (! ! n m n m C n m- =从m个人中挑出n个人进行组合的可能数。 (2)加法和乘法原理加法原理(两种方法均能完成此事):m+n 某件事由两种方法来完成,第一种方法可由m种方法完成,第二种方法可由n种方法来完成,则这件事可由m+n 种方法来完成。 乘法原理(两个步骤分别不能完成这件事):m×n 某件事由两个步骤来完成,第一个步骤可由m种方法完成,第二个步骤可由n 种方法来完成,则这件事可由m×n 种方法来完成。 (3)一些常见排列重复排列和非重复排列(有序)对立事件(至少有一个) 顺序问题 (4)随机试验和随机事件如果一个试验在相同条件下可以重复进行,而每次试验的可能结果不止一个,但在进行一次试验之前却不能断言它出现哪个结果,则称这种试验为随机试验。试验的可能结果称为随机事件。 (5)基本事件、样本空间和事件在一个试验下,不管事件有多少个,总可以从其中找出这样一组事件,它具有如下性质: ①每进行一次试验,必须发生且只能发生这一组中的一个事件; ②任何事件,都是由这一组中的部分事件组成的。 这样一组事件中的每一个事件称为基本事件,用ω来表示。 基本事件的全体,称为试验的样本空间,用Ω表示。 一个事件就是由Ω中的部分点(基本事件ω)组成的集合。通常用大写字母A,B,C,…表示事件,它们是Ω的子集。 Ω为必然事件,?为不可能事件。 不可能事件(?)的概率为零,而概率为零的事件不一定是不可能事件;同理,必然事件(Ω)的概率为1,而概率为1的事件也不一定是必然事件。 (6)事件的关系与运算①关系: 如果事件A的组成部分也是事件B的组成部分,(A发生必有事件B发生):B A? 如果同时有B A?,A B?,则称事件A与事件B等价,或称A等于B:A=B。 A、B中至少有一个发生的事件:A B,或者A+B。 属于A而不属于B的部分所构成的事件,称为A与B的差,记为A-B,也可表示为A-AB或者B A,它表示A发生而B不发生的事件。 A、B同时发生:A B,或者AB。A B=?,则表示A与B不可能同时发生,称 事件A与事件B互不相容或者互斥。基本事件是互不相容的。 Ω-A称为事件A的逆事件,或称A的对立事件,记为A。它表示A不发生的
目录 1.均匀分布 (1) 2.正态分布(高斯分布) (2) 3.指数分布 (2) 4.Beta分布(β分布) (2) 5.Gamma分布 (3) 6.倒Gamma分布 (4) 7.威布尔分布(Weibull分布、韦伯分布、韦布尔分布) (5) 8.Pareto分布 (6) 9.Cauchy分布(柯西分布、柯西-洛伦兹分布) (7) χ分布(卡方分布) (7) 10.2 11.t分布 (8) 12.F分布 (9) 13.二项分布 (10) 14.泊松分布(Poisson分布) (10) 15.对数正态分布 (11) 1.均匀分布 均匀分布~(,) X U a b是无信息的,可作为无信息变量的先验分布。
1()f x b a = - ()2 a b E X += 2 ()()12 b a Var X -= 2. 正态分布(高斯分布) 当影响一个变量的因素众多,且影响微弱、都不占据主导地位时,这个变量很可能服从正态分布,记作2~(,)X N μσ。正态分布为方差已知的正态分布 2(,)N μσ的参数μ的共轭先验分布。 22 ()2()x f x μσ-- = ()E X μ= 2()Var X σ= 3. 指数分布 指数分布~()X Exp λ是指要等到一个随机事件发生,需要经历多久时间。其中0λ>为尺度参数。指数分布的无记忆性:{}|{}P X s t X s P X t >+>=>。 (),0 x f x e x λλ-=> 1 ()E X λ = 2 1 ()Var X λ = 4. Beta 分布(β分布)
Beta 分布记为~(,)X Be a b ,其中Beta(1,1)等于均匀分布,其概率密度函数可凸也可凹。如果二项分布(,)B n p 中的参数p 的先验分布取(,)Beta a b ,实验数据(事件A 发生y 次,非事件A 发生n-y 次),则p 的后验分布(,)Beta a y b n y ++-,即Beta 分布为二项分布(,)B n p 的参数p 的共轭先验分布。 10 ()x t x t e dt ∞--Γ=? 1 1()()(1)()() a b a b f x x x a b --Γ+= -ΓΓ ()a E X a b = + 2 ()()(1) ab Var X a b a b = +++ 5. Gamma 分布 Gamma 分布即为多个独立且相同分布的指数分布变量的和的分布,解决的
利用Excel的NORMSDIST函数建立正态 分布表 董大钧,乔莉 沈阳理工大学应用技术学院、信息与控制分院,辽宁抚顺113122 摘要:利用Excel办公软件特有的NORMSDIST函数可以很准确方便的建立正态分布表、查找某分位数点的正态分布概率值,极大的提高了数理统计的效率。该函数可返回指定平均值和标准偏差的正态分布函数,将其引入到统计及数据分析处理过程中,代替原有的手工查找正态分布表,除具有直观、形象、易用等特点外,更增加了动态功能,极大提高了工作效率及准确性。 关键词:Excel;正态分布;函数;统计 引言 正态分布是应用最广泛的连续概率分布,生产与科学实验中很多随机变量的概率分布都可以近似地用正态分布来描述。例如,在生产条件不变的情况下,某种产品的张力、抗压强度、口径、长度等指标;同一种生物体的身长、体重等指标;同一种种子的重量;测量同一物体的误差;弹着点沿某一方向的偏差;某个地区的年降水量;以及理想气体分子的速度分量等等。一般来说,如果一个量是由许多微小的独立随机因素影响的结果,那么就可以认为这个量具有正态分布。从理论上看,正态分布具有很多良好的性质,许多概率分布可以用它来近似;还有一些常用的概率分布是由它直接导出的,例如对数正态分布、t分布、F分布等。在科学研究及数理统计计算过程中,人们往往要通过某本概率统计教材附录中的正态分布表去查找,非常麻烦。若手头有计算机,并安装有Excel软件,就可以利用Excel的NORMSDIST( x )函数进行计算某分位数点的正态分布概率值,或建立一个正态分布表,准确又方便。 1 正态分布及其应用 正态分布(normal distribution)又名高斯分布(Gaussian distribution),是一个在数学、物理及工程等领域都非常重要的概率分布,在统计学的许多方面有着重大的影响力。若随机变量X服从一个数学期望为μ、标准方差为σ2的高斯分布,记为N(μ,σ2 )。则其概率密度
第二章 随机变量及其分布 复习 一、随机变量. 1. 随机试验的结构应该是不确定的.试验如果满足下述条件: ①试验可以在相同的情形下重复进行;②试验的所有可能结果是明确可知的,并且不止一个;③每次试验总是恰好出现这些结果中的一个,但在一次试验之前却不能肯定这次试验会出现哪一个结果. 它就被称为一个随机试验. 2. 离散型随机变量:如果对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量.若ξ是一个随机变量,a ,b 是常数.则b a +=ξη也是一个随机变量.一般地,若ξ是随机变量,)(x f 是连续函数或单调函数,则)(ξf 也是随机变量.也就是说,随机变量的某些函数也是随机变量. 3、分布列:设离散型随机变量ξ可能取的值为: ,,,,21i x x x ξ取每一个值),2,1( =i x 的概率p x P ==)(ξ,则表称为随机变量ξ的概率分布,简称ξ的分布列. 121i 注意:若随机变量可以取某一区间内的一切值,这样的变量叫做连续型随机变量.例如:]5,0[∈ξ即ξ可以取0~5之间的一切数,包括整数、小数、无理数. 典型例题: 1、随机变量ξ的分布列为(),1,2,3(1) c P k k k k ξ== =+……,则P(13)____ξ≤≤= 2、袋中装有黑球和白球共7个,从中任取两个球都是白球的概率为1 7 ,现在甲乙两人从袋中轮流摸去一 球,甲先取,乙后取,然后甲再取……,取后不放回,直到两人中有一人取到白球时终止,用ξ表示取球的次数。(1)求ξ的分布列(2)求甲取到白球的的概率 3、5封不同的信,放入三个不同的信箱,且每封信投入每个信箱的机会均等,X 表示三哥信箱中放有信件树木的最大值,求X 的分布列。 4 已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为5 . (1)请将上面的列联表补充完整; (2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由; (3)已知喜爱打篮球的10位女生中,12345,,A A A A A ,,还喜欢打羽毛球,123B B B ,,还喜欢打乒乓球,12C C ,还喜欢踢足球,现再从喜欢打羽毛球、喜欢打乒乓球、喜欢踢足球的女生中各选出1名进行其他方面的调查,求1B 和1C 不全被选中的概率. (参考公式:2 ()()()()() n ad bc K a b c d a c b d -=++++,其中n a b c d =+++)
今天在网上找到了一些概率密度函数的总结,怕以后找不到就先转到这里,呵呵统计工具箱函数 Ⅰ-1 概率密度函数 函数名对应分布的概率密度函数 betapdf 贝塔分布的概率密度函数 binopdf 二项分布的概率密度函数 chi2pdf 卡方分布的概率密度函数 exppdf 指数分布的概率密度函数 fpdf f分布的概率密度函数 gampdf 伽玛分布的概率密度函数 geopdf 几何分布的概率密度函数 hygepdf 超几何分布的概率密度函数 normpdf 正态(高斯)分布的概率密度函数 lognpdf 对数正态分布的概率密度函数 nbinpdf 负二项分布的概率密度函数 ncfpdf 非中心f分布的概率密度函数 nctpdf 非中心t分布的概率密度函数 ncx2pdf 非中心卡方分布的概率密度函数 poisspdf 泊松分布的概率密度函数 raylpdf 雷利分布的概率密度函数 tpdf 学生氏t分布的概率密度函数 unidpdf 离散均匀分布的概率密度函数 unifpdf 连续均匀分布的概率密度函数 weibpdf 威布尔分布的概率密度函数 Ⅰ-2 累加分布函数 函数名对应分布的累加函数 betacdf 贝塔分布的累加函数 binocdf 二项分布的累加函数 chi2cdf 卡方分布的累加函数 expcdf 指数分布的累加函数 fcdf f分布的累加函数 gamcdf 伽玛分布的累加函数 geocdf 几何分布的累加函数 hygecdf 超几何分布的累加函数 logncdf 对数正态分布的累加函数 nbincdf 负二项分布的累加函数 ncfcdf 非中心f分布的累加函数 nctcdf 非中心t分布的累加函数 ncx2cdf 非中心卡方分布的累加函数 normcdf 正态(高斯)分布的累加函数 poisscdf 泊松分布的累加函数 raylcdf 雷利分布的累加函数 tcdf 学生氏t分布的累加函数 unidcdf 离散均匀分布的累加函数
目录 1、 均匀分布 ...................................................................................................... 1 2、 正态分布(高斯分布) ............................................................................... 2 3、 指数分布 ...................................................................................................... 2 4、 Beta 分布(β分布) .................................................................................. 2 5、 Gamma 分布 .................................................................................................. 3 6、 倒Gamma 分布 ............................................................................................. 4 7、 威布尔分布(Weibull 分布、韦伯分布、韦布尔分布) ................. 5 8、 Pareto 分布 ................................................................................................ 6 9、 Cauchy 分布(柯西分布、柯西-洛伦兹分布) .. (7) 10、 2 χ分布(卡方分布) (7) 11、 t 分布 ........................................................................................................ 8 12、 F 分布 ........................................................................................................ 9 13、 二项分布 ................................................................................................ 10 14、 泊松分布(Poisson 分布) .................................................................. 10 15、 对数正态分布 ....................................................................................... 11 1. 均匀分布 均匀分布~(,)X U a b 就是无信息的,可作为无信息变量的先验分布。 1 ()f x b a = -
概率论中几种常用的重要的分布摘要:本文主要探讨了概率论中的几种常用分布,的来源和他们中间的关系。其在实际中的应用。 关键词 1 一维随机变量分布 随机变量的分布是概率论的主要内容之一,一维随机变量部分要介绍六中常用分布,即( 0 -1) 分布、二项分布、泊松分布、均匀分布、指数分布和正态分布.下面我们将对这六种分布逐一地进行讨论. 随机事件是按试验结果而定出现与否的事件。它是一种“定性” 类型的概念。为了进一步研究有关随机试验的问题,还需引进一种“定量”类型的概念,即,根据试验结果而定取什么值(实值或向量值)的变数。称这种变数为随机变数。本章内将讨论取实值的这种变数——一维随机变数。 定义1.1 设X 为一个随机变数,令 F(x) P([X ( ,x)]) P([X p x]),( p xp ). 这样规定的函数F(x)的定义域是整个实轴、函数值在区间[0,1]上。它是一个普通的函数。成这个函数为随机函数X 的分布函数。 有的随机函数X 可能取的值只有有限多个或可数多个。更确切地说:存在着有限多个值或可数多个值a1,a2,..., 使得 P([ X { a1, a2 ,...}]) 1 称这样的随机变数为离散型随机变数。称它的分布为离散型分布。 【例1】下列诸随机变数都是离散型随机变数。 (1) X可能取的值只有一个,确切地说,存在着一个常数a,使P([X a]) 1 o 称这种随机变数的分布为退化分布。一个退化分布可以用一个常数 a 来确定。 (2) X可能取的值只有两个。确切地说,存在着两个常数a , b,使 P([X {a,b}]) 1.称这种随机变数的分布为两点分布。如果P([X b]) p,那么,P ([X a]) 1 p。因此,一个两点分布可以用两个不同的常数a,b及一个在区间(0,1 )内的值p来确定。 特殊地,当a,b依次为0,1时,称这两点分布为零-壹分布。从而,一个零 -壹分布可以用一个在区间(0,1)内的值p来确定。 (3) X可能取的值只有n个:a1,...,a2 (这些值互不相同),且,取每个a:值 ■. 、. 1
1.编号1,2,3的三位学生随意入座编号为 1, 2 , 3的三个座位,每位学生坐一个座位 设与座位编号相同的学生的个数是 X. (1) 求随机变量X 的分布列; (2) 求随机变量X 的数学期望和方差. 解(1)P ( X=0)= _L =1 - A 33 ; P ( X=1)=-C3 = 1 ; P ( X=3)= 2 =丄; A 3 2 A 3 6 (2) E (X ) =1 X 丄 +3 X 丄=1. 2 6 D (X ) =(1-0) 2 1 +(1-1) 2 丄+(3-1) 2 1 =1. 3 2 6 2某商场举行抽奖促销活动,抽奖规则是:从装有9个白球、1个红球的箱子中每次 随机地摸岀一个球,记下颜色后放回,摸岀一个红球可获得奖金 10元;摸岀两个红 球可获得奖金50元.现有甲、乙两位顾客,规定:甲摸一次,乙摸两次,令X 表示 甲、乙两人摸球后获得的奖金总额.求: (1 ) X 的分布列; (2) X 的均值. 解 (1 ) X 的所有可能取值为0,10,20,50,60. 9 1 9 P(X=50)= X =- 10 102 1 000 1 1 P(X=60)= 3 = . ' 103 1 000 故X 的分布列为 P (X=0 ) @ 1 = 729 10 = 1 000 P ( X=10)」X 「2 X C 2 X 丄 10 〔0 丿 10 10 9 X 一 = 243 1 000 P(X=20)= 丄 X C 2 X 丄 X ?= 10 10 10 18 1 000
729 243 18 9 (2 ) E ( X ) =0 X +10 X -243+20 X 18+50 X — +60 X 1 000 1 000 1 000 1 000 1 =3.3(兀). 1 000 ' ' 3 (本小题满分13分) 为了解甲、乙两厂的产品质量,采用分层抽样的方法从甲、乙两厂生 产的产品中分别抽出取14件和5件,测量产品中的微量元素x,y的含 (1)已知甲厂生产的产品共有98件,求乙厂生产的产品数量; (2)当产品中的微量元素x,y满足x》175 ,且y》75时,该产品为优等 品。用上述样本数据估计乙厂生产的优等品的数量; (3)从乙厂抽出的上述5件产品中,随机抽取2件,求抽取的2件产品中优等品数?的分布列极其均值(即数学期望)。 & 98 解:(1)7,5 7=35,即乙厂生产的产品数量为35件。 14 (2)易见只有编号为 2 , 5的产品为优等品,所以乙厂生产的产品中
10种概率密度函数function zhifangtu(x,m) %画数据的直方图,x表示要画的随机数,m表示所要画的条数%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% a=min(x); b=max(x); l=length(x); h=(b-a)/m; %量化x x=x/h; x=ceil(x); w=zeros(1,m); for i=1:l for j=1:m if (x(i)==j) %x(i)落在j的区间上,则w(j)加1 w(j)=w(j)+1; else continue end end end w=w/(h*l); z=a:h:(b-h); bar(z,w); title('直方图') function y=junyun(n)
%0-1的均匀分布,n代表数据量,一般要大于1024 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% y=ones(1,n); x=ones(1,n); m=100000; x0=mod(ceil(m*rand(1,1)),m); x0=floor(x0/2); x0=2*x0+1; u=11; x(1)=x0; for i=1:n-1 x(i+1)=u*x(i)+0; x(i+1)=mod(x(i+1),m); x(i)=x(i)/m; end %x(n)单位化 x(n)=x(n)/m; y=x; function y=zhishu(m,n) %指数分布,m表示指数分布的参数,m不能为0.n表示数据量,n一般要大于1024 %%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% x=junyun(n); for i=1;n if (x(i)==0) x(i)=0.0001;
两个随机变量的和与商的分布函数与密度函数 一、两个随机变量的和的分布 设(X ,Y )的联合密度函数为f (x ,y ),现求Z=X+Y 的概率密度。 令{(,)|}z D x y x y z =+≤,则Z 的分布函数为: (){} {}(,)((,))Z D z z y F z P Z z P X Y z f x y dxdy f x y dx dy +∞--∞ -∞ =≤=+≤==??? ? (1.1) 固定z 和y 对积分(,)z y f x y dx --∞ ? 作换元,令x y u +=,得 (,)(,)z y z f x y dx f u y y du --∞ -∞ =-?? (1.2) 于是 ()(,)[(,)]z z Z F z f u y y dudy f u y y dy du +∞+∞ -∞-∞ -∞ -∞ =-=-? ??? (1.3) 由概率论定义,即得Z 的概率密度为 ()(,)Z f z f z y y dy +∞ -∞ =-? 注意:积分限为?∞到+∞ (1.4) 由X 与Y 的对称性,又可得 ()(,)Z f z f x z x dx +∞ -∞ =-? 注意:积分限为?∞到+∞ (1.5) (1.4)与(1.5)相当于分别在 x z y y z x =-=-或条件下,求X 或Y 的边缘概率密度。 特别的,当X 与Y 相互独立时,有 ()()()()()Z X Y X Y f z f z y f y dy f x f z x dx +∞ +∞ -∞ -∞ =-=-? ? (1.6) 其中,()X f x 、()Y f y 分别是X 和Y 的边缘概率密度。 式(1.6)又称为()X f x 和()Y f y 的卷积公式,常记为()*()X Y f z f z 。因此式(1.6)又称为独立随机变量和的分布的卷积公式。 二、两个随机变量的商的分布 设(X ,Y )的联合密度函数为f (x ,y ),现求X Z Y =的概率密度,Z 的分布函数为