北京交通大学号与系统时域分析

北交大考研复试班-北京交通大学电子信息工程学院控制科学与工程考研复试经验分享北京交通大学是教育部直属，教育部、北京市人民政府、中国铁路总公司共建的全国重点大学，“211工程”“985工程优势学科创新平台”项目建设高校和具有研究生院的全国首批博士、硕士学位授予高校。

学校牵头的“2011计划”“轨道交通安全协同创新中心”是国家首批14个认定的协同创新中心之一。

2017年，学校正式进入国家“双一流”建设行列，将围绕优势特色学科，重点建设“智慧交通”世界一流学科领域。

北京交通大学作为交通大学的三个源头之一，历史渊源可追溯到1896年，前身是清政府创办的北京铁路管理传习所，是中国第一所专门培养管理人才的高等学校，是中国近代铁路管理、电信教育的发祥地。

1917年改组为北京铁路管理学校和北京邮电学校，1921年与上海工业专门学校、唐山工业专门学校合并组建交通大学。

1923年交通大学改组后，北京分校更名为北京交通大学。

1950年学校定名北方交通大学，毛泽东主席题写校名，著名桥梁专家茅以升任校长。

1952年，北方交通大学撤销，京唐两院独立，学校改称北京铁道学院。

1970年恢复“北方交通大学”校名。

2000年与北京电力高等专科学校合并，由铁道部划转教育部直属管理。

2003年恢复使用“北京交通大学”校名。

学校曾培养出中国第一个无线电台创建人刘瀚、中国第一台大马力蒸汽机设计者应尚才、中国第一本铁路运输专著作者金士宣、中国铁路运输经济学科的开创者许靖、中国最早的四大会计师之一杨汝梅，以及中国现代作家、文学评论家、文学史家郑振铎等一大批蜚声中外的杰出人才。

“东京审判”担任首席检察官的向哲浚，中国著名的经济学家、人口学家马寅初等都曾在学校任教。

电子信息工程学院是北京交通大学最早成立的学院之一。

学院下设信息与通信工程系、自动控制工程系、电子科学技术系、光波技术研究所、国家电工电子教学基地五个行政单位。

学院现有教职工269人，其中教授71人(含研究员)，副教授117人（含高工），具有博士学位的教师占教师总数的90.1%。

信号与系统_北京交通大学中国大学mooc课后章节答案期末考试题库2023年1.某连续周期信号如题1图所示，该信号的频谱成分有( )【图片】参考答案:直流、奇次谐波的余弦分量2.已知描述某连续时间LTI系统的状态方程的矩阵分别为【图片】【图片】【图片】【图片】则该系统的系统函数【图片】为参考答案:3行3列矩阵3.关于连续非周期信号的频域表示，正确的说法是( )参考答案:将信号表示为不同频率正弦信号的线性组合4.连续非周期信号频谱的特点是( )参考答案:连续、非周期5.已知某线性连续时间系统，其在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】；该系统在初始状态为【图片】、输入激励为【图片】作用下产生的完全响应为【图片】【图片】试求初始状态为【图片】，激励为【图片】时系统的完全响应【图片】=( ）。

参考答案:,6.连续非周期信号频谱的特点是参考答案:连续、非周期7.已知信号【图片】，其频谱【图片】在【图片】的值【图片】参考答案:88.连续周期信号【图片】是功率信号，其傅里叶变换【图片】都不存在。

参考答案:错误9.已知信号【图片】的最高频率分量为【图片】 Hz，若抽样频率【图片】，则抽样后信号的频谱一定混叠。

参考答案:错误10.连续时间周期信号【图片】的平均功率为( )参考答案:1111.利用状态变量分析法分析连续时间LTI系统时，输出方程【图片】可能与哪些因素有关参考答案:与输入和状态变量有关12.关于连续周期信号频谱的特性，正确的说法是( )参考答案:同时具有离散特性和幅度衰减特性。

13.若描述离散时间系统的差分方程为【图片】，该系统为( )。

参考答案:因果、线性时不变系统14.连续周期信号在有效带宽内各谐波分量的平均功率之和占整个信号平均功率的很大一部分。

参考答案:正确15.连续时间信号在时域展宽后，其对应的频谱中高频分量将增加。

参考答案:错误16.信号时域时移，其对应的幅度频谱不变，相位频谱将发生相移。

课程思政优秀案例——《信号与系统》：连续时间信号的时域抽样一、课程和案例的基本情况课程名称：信号与系统授课对象：电子信息类专业本科二年级学生课程性质：专业核心课程课程简介：我们已进入以信息化和智能化为主要特征的新工科时代，信号与系统课程是电子信息类专业重要的专业基础课程，为相关专业提供了重要的基础理论。

该课程主要阐述信号的时域分析和变换域分析，以及信号与系统的作用机理。

该课程具有“原理深厚、方法多元、应用广泛”等特点，蕴含了丰富的课程思政元素，课程思政与课程教学深度融合，启发了学生的辩证思维能力，熏陶了学生的科学探索精神，厚植了学生的家国情怀。

思想价值引领贯穿于课程教学全过程，课程教学改革取得了显著成效，形成了“名课程、名教材、名团队”协同推进的良好格局。

该课程囊括了各类课程称号（图1）。

图1 课程教学改革成果课程教学改革和建设水平处于全国领先地位，示范引领，为推进全国信号与系统课程建设发挥了重要作用。

牵头组织成立了覆盖全国50多所高校的“信号处理课程群”虚拟教研室，牵头撰写了“全国信号与系统课程思政教学指南”。

建设了该课程的中文和英文MOOC，选学人数约30万。

编著的教材发行20多万册，被全国200多所高校选用。

应邀在全国性教学会议做大会特邀报告20多次，在40多所高校做专题报告。

案例简介：该案例的教学内容为“连续时间信号的时域抽样”，处于课程教学的中间阶段，紧随连续信号和离散信号的时域分析和频域分析。

主要阐述“为何要进行信号抽样、信号抽样的理论分析、抽样定理的本质内容、抽样定理的工程应用”，其为连续信号的数字化分析与处理提供了理论支撑，是课程教学的重点内容之一。

没有信息化就没有现代化，而信息化的基础是数字化。

信号的时域抽样正是阐述信号数字化的基本原理和方法，其架设了现实的模拟世界与虚拟的数字世界之间的桥梁，为信息化和智能化奠定了重要的理论基础。

本讲内容的教学目标：知识传授：※了解信号的时域抽样对信息化时代的重要意义；※理解信号时域抽样定理的基本原理和本质内容；※掌握实际工程应用中常见信号的时域抽样方法。

《信号与系统》期末复习材料一、考核目标和范围通过考核使学生了解和掌握信号与系统的基本原理、概念和方法，运用数学分析的方法解决一些简单问题，使学生在分析问题和解决问题的能力上有所提高，为学生进一步学习后续课程打下坚实的基础。

课程考核的命题严格限定在教材第1—8章内，对第9、10章不做要求。

二、考核方式三、复习资源和复习方法（1）教材《信号与系统》第2版，陈后金，胡健，薛健编著，清华大学出版社，北方交通大学出版社，2003年。

结合教材习题解答参考书（陈后金，胡健，薛健，钱满义，《信号与系统学习指导与习题精解》，清华大学出版社，北京交通大学出版社，2005）进行课后习题的练习、复习。

（2）离线作业。

两次离线作业题目要熟练掌握。

（3）复习方法：掌握信号与系统的时域、变换域分析方法，理解各种变换（傅里叶变换、拉普拉斯变换、Z变换）的基本内容、性质与应用。

特别要建立信号与系统的频域分析的概念以及系统函数的概念。

结合习题进行反复练习。

四、期末复习重难点第1章信号与系统分析导论1. 掌握信号的定义及分类。

2. 掌握系统的描述、分类及特性。

3. 重点掌握确定信号及线性非时变系统的特性。

第2章信号的时域分析1．掌握典型连续信号与离散信号的定义、特性及其相互关系。

2．掌握连续信号与离散信号的基本运算。

3．掌握信号的分解，重点掌握任意连续信号分解为冲激信号的线性组合，任意离散信号分解为单位脉冲序列的线性组合。

第3章系统的时域分析1．掌握线性非时变连续时间系统时域描述。

2．掌握用卷积法计算连续时间系统的零状态响应3．掌握离散时间系统的时域描述。

4．掌握用卷积法计算离散时间系统的零状态响应。

第4章周期信号的频域分析1．掌握连续周期信号的频域分析方法。

2．掌握离散周期信号的频域分析方法。

第5章非周期信号的频域分析1．掌握常见连续时间信号的频谱，以及Fourier变换的基本性质及物理含义。

2．掌握连续非周期信号的频域分析。

3．掌握离散非周期信号的频域分析。

摘 要 分析传统教学模式下信号与系统课程教学存在的问题，提出在工程教育认证背景下的课程教学改革措施。

在改革过程中精选教学内容、引入雨课堂新技术，并采用“CDIO 国际工程教育”和“以学生为中心”的教学理念来改革教学方法，同时将形成性评价和终结性评价相结合，从而建立符合认证标准的教学模式和课程考核评价体系。

实践表明，课程教学改革取得较好的效果。

关键词 工程教育；信号与系统；雨课堂；教学改革中图分类号：G642.0 文献标识码：B 文章编号：1671-489X(2020)16-0088-03Exploration and Practice of Teaching Reform of Signal and Sys -tem Course under Background of Engineering Education //W ANG Xia, LI WeiAbstract This paper analyzes the problems existing in the teaching of signal and system course under the traditional teaching mode, and proposes the teaching reform measures under the background of engi-neering education certifi cation. In the process of reform, the teaching content is subtly selected, the new technology of rain classroom is introduced to the class, and the teaching method is reformed with the teaching concept of “CDIO international engineering education” and “student-centered”. At the same time, the formative evaluation and the summative evaluation are combined. Thus, the teaching mode and the course evaluation system conforming to the certifi cation stan-dard is established. The practice shows that the teaching reform of the course has achieved good performance.Key words engineering education; signal and system; rain classroom;teaching reform１　前言工程教育专业认证是国际通行的工程教育质量保障制度，也是实现工程教育国际互认和工程师资格国际互认的重要基础。

《信号与系统》课程研究性学习手册专题一信号时域分析1. 基本信号的产生，语音的读取与播放【研讨内容】1) 生成一个正弦信号，改变正弦信号的角频率和初始相位，观察波形变化；2) 生成一个幅度为1、基频为2Hz 、占空比为50%的周期方波，3) 观察一定时期内的股票上证指数变化，生成模拟其变化的指数信号，4) 录制一段音频信号，进行音频信号的读取与播放【题目分析】⑴正弦信号的形式为Acosg o t+书)或Asin (3 o t+，分别用MATLAB 的内部函数cos 和sin 表示，其调用形式为y A* cos(w0* t phi)、y A*sin(wo*t phi)。

生成正弦信号为y=5sin(t), 再依次改变其角频率和初相，用matlab 进行仿真。

⑵幅度为1 ,则方波振幅为0.5 ,基频wO=2Hz ,则周期T=pi ,占空比为50% , 因此正负脉冲宽度比为 1 。

(3) 将波形相似的某一段构造成一个指数函数, 在一连续时间内构造不同的2~3 个不同指数函数即可大致模拟出其变化。

(4) 录制后将文件格式转化为wav ,再用wavread 函数读取并播放,用plot 函数绘制其时域波形。

【仿真】( 1 ) 正弦信号正弦信号 1 ：A=1;w0=1/4*pi;phi=pi/16;t=-8:0.001:8;xt 仁A*si n(w0*t+phi);plot(t,xt1)title('xt 仁si n( 0.25*pi*t+pi/16)')正弦信号2 (改变1中频率)A=1;w1=1/4*pi;w2=1*pi;phi=pi/16; t=-8:0.001:8; xt 1= A*si n(w1*t+phi);xt2=A*si n(w2*t+phi);plot(t,xt1,t,xt2)正弦信号3 (改变1中相位)A=1;w=1/4*pi;phi仁pi/16;phi2=pi/4; t=-8:0.001:8; xt 1=A*si n(w*t+phi1);xt3=A*si n(w*t+phi2) plot(t,xt1,t,xt3)0.4 -0.2 -0 --0.2 --0.4 --0.6 --0.8 〜(2) 方波信号t=-100:0.01:100;T=0.5;f=1/T;y=square(2*pi*f*t,50);Plot(t,y);axis([-2 2 -3 3]);-3 1—--------- [ ------------ ■ ----------- 1- ---------- 1 ----------- 1 ----------- 1 ----------- 1 -------------------------t-2 -1.5 -1 -0.5 0 0.5 1 1.520.80.6-1 ------------- [ ---------- L-8 -6 -4(3) 模拟股票上证指数变化的指数信号x1=0:0.001:5;y1=2500+1.8*exp(x1);x2=5:0.001:10;y2=2847-1.5*exp(0.8*x2);x3=10:0.001:15;y3=2734+150*exp(-0.08*x3);x4=15:0.001:20;y4=2560-156*exp(-0.08*x4);x=[x1,x2,x3,x4];y=[y1,y2,y3,y4];plot(x,y);30002500200015001000500-500-1000-1500(4) 音频信号的读取与播放 [x,Fs,Bits]=wavread( sou nd(x,Fs,Bits) plot(x)-2000 ---------- [-------- [---------- L0 2 4 6 8 10 1214 16 18 20 'C:\Users\Ghb\Desktop\na nsheng.wav'C\Users\Ghb\Desktop\nvshe ng.wav' [x,Fs,Bits]=wavread(sou nd(x,Fs,Bits)plot(x)2. 信号的基本运算（语音信号的翻转、展缩）【研讨内容】1）将原始音频信号在时域上进行延展、压缩，2）将原始音频信号在频域上进行幅度放大与缩小，3）将原始音频信号在时域上进行翻转，【题目分析】用matlab 的wavread 函数读取录制的音频，用length 函数计算出音频文件的长度，最后计算出时间t ，然后用plot 函数输出录制的音频信号（1）延展与压缩分析把时间t 变为原来的一半，信号就被延展为原来的 2 倍，把时间他变为原来的 2 倍，信号就被压缩为原来的一半。

图2-2
3．有一离散时间信号
（1）画出
（2）求序列 学]
使之满足
解：（1）
又 比较上述两式可得： 故如图2-3所示。
[电子科技大
图2-3
4．已知 如图2-4（a），画出
和
的波形。[北
京理工大学]
解：将 反转得 如图2-4（b）所示，将它们相加、减得 ，波形如图2-4（c）、（d）所示。
图2-4 5．已知f（t）的波形如图2-5所示，令r（t）＝tu（t）。
大学]
图1-2 解：因为：
故：
y2（t）的波形如图1-3所示。
图1-3 3．将如图1-4（a）、（b）所示的连续信号展成如下形式：
给出信号
最简单的解析表达形式。[北京航空航天大学]
图1-4
解：（a）该信号可分为两段：
和
可化简为
故
，即：
（b）该信号可分为三段： 可化简为 故
，即
4．求
的值。[北京航空航天大学2006研]
，应该与齐次解有关，即系统的特征根为－1和－3，故特征方程应为 ，即a0＝4，a1＝3。
（2）设系统对激励 rzs（t），则
的零输入响应和零状态响应分别为rzi（t）和
由于
，则由线性时不变系统的微分特性可知
同时，设系统的单位冲激响应为h（t），则由线性时不变系统的叠加性 可知
由式（1）、式（2），并设
陈后金《信号与系统》（第2版）配 套模拟试题及详解
第一部分 名校考研真题 第1章 信号与系统分析导论 一、选择题
1．方程 天大学2007研] A．线性时不变 B．非线性时不变 C．线性时变 D．非线性时变 E．都不对 【答案】B
描述的系统是（ ）。[北京航空航

图 A-4
图 A-5 6. （6 分）已知系统 y ' (t ) 2 y (t ) f (t ) 的完全响应为 y (t ) ( 2e 统的零输入响应和零状态响应。 7. （6 分）已知 N=5 点滑动平均系统的输入输出关系为 的单位脉冲响应，并判断系统是否因果、稳定。
t
3e 2t ) (t ) ，求系
图 A-6
参考答案
一、解：
1. 2. 3. 4. 错误。 由序列傅立叶变换的位移特性， 离散信号经过单位延迟器后， 其幅度频谱不变。 正确。 正确。 正确。
5. 错误。 对连续周期信号取样所得离散时间序列可能是周期序列， 也可能是非周期序列。
二、解
1. 利用冲激信号的取样特性，可得 2. 系统的零状态响应为 f (k ) h(k ) ，由于 h( k ) ( k ) ( k 4) {1,1,1,1} ，故利用列 表法可得
f ' (t ) sin( t )[ (t ) (t )] cos(t )[ (t ) (t )] f ' (t ) sin( t )[ (t ) (t )] (t ) (t )
2. 将 f ( 0.5t 1) 改 写 为 f [ 0.5(t 2)] ， 先 反 转 ， 再 展 宽 ， 最 后 左 移 2 ， 即 得 f (0.5t 1) ，如图 A-8 所示。
图 A-7
3. 因为系统函数为
图 A-8
H ( j ) [ g 2 ( 5) g 2 ( 5)]e j 2 因为 g 2 (t ) 2Sa( ) ，由傅立叶变换的对称性可得： 2Sa(t ) 2g 2 ( ) 2g 2 ( )

Ionic conductances
synapses (es)
+
Chemical synapses (cs)
Gion1 Gion2
Gionm
Ges1 Ges2
Gesn
Gcs1, 1 Gcs1, 2
Gcs1, p
Gcsn, 1 Gcsn, 2
Gcsn, p
CM
++
+
++
+
++
+
++
+
Iex
Eion1 Eion2
例1 已知实信号f(t)的最高频率为fm (Hz)， 试计算对各信号f(2t)， f(t)*f(2t)， f(t)f(2t)抽样不混叠的最小抽样频率。
解： 根据信号时域与频域的对应关系及抽样定理得： 对信号f(2t)抽样时，最小抽样频率为 4fm(Hz)；
对f(t)*f(2t)抽样时，最小抽样频率为 2fm(Hz)；
信号与系统
Signals and Systems
国家精品课程主教材、北京市精品教材 《信号与系统》(第2版)
陈后金，胡健，薛健 清华大学出版社，北京交通大学出版社，2005年
系统的频域分析及其应用
连续时间系统的频率响应 连续信号通过系统响应的频域分析 无失真系统与理想低通 抽样与抽样定理 调制与解调 离散时间系统的频域分析
F( jw)
1
Fs( jw)1 T
n
F[ j(w

nws
)]
w
wm 0 wm
ws 2.5wm Fs ( jw)
F[j(wws)]
1
T F(jw)

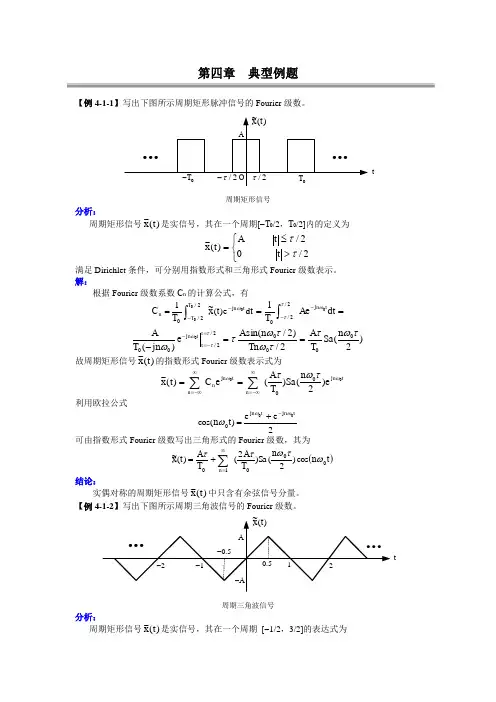
第四章 典型例题【例4-1-1】写出下图所示周期矩形脉冲信号的Fourier 级数。

t周期矩形信号分析：周期矩形信号)(~t x 是实信号，其在一个周期[-T 0/2，T 0/2]内的定义为⎩⎨⎧>≤=2/02/ )(~ττt t A t x满足Dirichlet 条件，可分别用指数形式和三角形式Fourier 级数表示。

解：根据Fourier 级数系数C n 的计算公式，有t t x T C t n T T n d e )(~1000j 2/2/0ω--⎰===--⎰t A T t n d e 10j 2/2/0ωττ 2/2/j 000e )j (ττωω=-=--t t t n n T A 2/)2/sin(00τωτωτTn n A =)2(Sa 00τωτn T A =故周期矩形信号)(~t x 的指数形式Fourier 级数表示式为t n n t n n n n T A C t x 00j 00j e )2(Sa )(e )(~ωωτωτ∑∑∞-∞=∞-∞===利用欧拉公式2e e )cos(00j j 0tn t n t n ωωω-+=可由指数形式Fourier 级数写出三角形式的Fourier 级数，其为()t n n T A T A t x n 00010cos )2(Sa )2()(~ωτωττ∑∞=+=结论：实偶对称的周期矩形信号)(~t x 中只含有余弦信号分量。

【例4-1-2】写出下图所示周期三角波信号的Fourier 级数。

t周期三角波信号分析：周期矩形信号)(~t x 是实信号，其在一个周期 [-1/2，3/2]的表达式为⎪⎩⎪⎨⎧≤<-≤=2321 )1(221 2)(~t t A t At t x满足Dirichlet 条件，可分别用指数形式和三角形式Fourier 级数表示。

解：由于该三角波信号)(~t x 的周期T 0=2，所以ππ200==T ω。

北京理工大学信号与系统实验报告6-离散时间系统的z域分析————————————————————————————————作者：————————————————————————————————日期：实验6 离散时间系统的z 域分析（综合型实验）一、 实验目的1） 掌握z 变换及其反变换的定义,并掌握ＭAT ＬＡＢ实现方法。

2） 学习和掌握离散时间系统系统函数的定义及z 域分析方法。

3） 掌握系统零极点的定义,加深理解系统零极点分布与系统特性的关系。

二、 实验原理与方法 1. z 变换序列(n)x 的z 变换定义为(z)(n)znn X x +∞-=-∞=∑ (1）Z 反变换定义为11(n)(z)z 2n rx X dz jπ-=⎰(2）MA ＴＬA Ｂ中可采用符号数学工具箱z ｔrans 函数和ｉz ｔｒans 函数计算z 变换和z 反变换： Z=ztran ｓ（Ｆ）求符号表达式Ｆ的z 变换。

Ｆ=iztra ｎｓ（Z)求符号表达式Z 的ｚ 反变换 2. 离散时间系统的系统函数离散时间系统的系统函数H(z)定义为单位抽样响应ｈ(n)的z 变换(z)(n)znn H h +∞-=-∞=∑ (３）此外连续时间系统的系统函数还可由系统输入与输出信号z 变换之比得到(z)(z)/X(z)H Y = (4)由(4）式描述的离散时间系统的系统时间函数可以表示为101101...(z)...MM NN b b z b z H a a z a z----+++=+++ (5） 3. 离散时间系统的零极点分析ＭＡTLAB 中可采用roots 来求系统函数分子多项式和分母多项式的根，从而得到系统的零极点。

此外还可采用MATL ＡB 中zpl ａne 函数来求解和绘制离散系统的零极点分布图,zp ｌane 函数的调用格式为：zplane(b,a) ｂ、a 为系统函数分子分母多项式的系数向量(行向量) zplane （z,p) z 、ｐ为零极点序列(列向量) 系统函数是描述系统的重要物理量，研究系统函数的零极点分布不仅可以了解系统单位抽样响应的变化,还可以了解系统频率特性响应以及判断系统的稳定性; 系统函数的极点位置决定了系统的单位抽样响应的波形，系统函数零点位置只影响冲激响应的幅度和相位，不影响波形。

《信号与系统》期末复习重点一、考核目标和范围通过考核使学生了解和掌握信号与系统的基本原理、概念和方法，运用数学分析的方法解决一些简单问题，使学生在分析问题和解决问题的能力上有所提高，为学生进一步学习后续课程打下坚实的基础。

课程考核的命题严格限定在教材第1—8章内，对第9、10章不做要求。

二、考核方式三、复习资源和复习方法（1）教材《信号与系统》第2版，陈后金，胡健，薛健编著，高等教育出版社，2007年。

结合教材习题解答参考书（陈后金，胡健，薛健，钱满义，《信号与系统学习指导与习题精解》，清华大学出版社，北京交通大学出版社，2005）进行课后习题的练习、复习。

（2）离线作业。

两次离线作业题目要熟练掌握。

（3）复习方法：掌握信号与系统的时域、变换域分析方法，理解各种变换（傅里叶变换、拉普拉斯变换、Z变换）的基本内容、性质与应用。

特别要建立信号与系统的频域分析的概念以及系统函数的概念。

结合习题进行反复练习。

四、期末复习重难点第1章信号与系统分析导论1. 掌握信号的定义及分类。

2. 掌握系统的描述、分类及特性。

3. 重点掌握确定信号及线性非时变系统的特性。

第2章信号的时域分析1．掌握典型连续信号与离散信号的定义、特性及其相互关系。

2．掌握连续信号与离散信号的基本运算。

3．掌握信号的分解，重点掌握任意连续信号分解为冲激信号的线性组合，任意离散信号分解为单位脉冲序列的线性组合。

第3章系统的时域分析1．掌握线性非时变连续时间系统时域描述。

2．掌握用卷积法计算连续时间系统的零状态响应3．掌握离散时间系统的时域描述。

4．掌握用卷积法计算离散时间系统的零状态响应。

第4章 周期信号的频域分析1．掌握连续周期信号的频域分析方法。

2．掌握离散周期信号的频域分析方法。

第5章 非周期信号的频域分析1．掌握常见连续时间信号的频谱，以及Fourier 变换的基本性质及物理含义。

2．掌握连续非周期信号的频域分析。

3．掌握离散非周期信号的频域分析。

计算机与信息技术学院硕士研究生入学考试自命题科目考试范围一、905 信号与系统1、连续时间信号与系统的时域分析。

（1）信号与系统基本概念；（2）信号的表示与典型信号：信号的表示、指数信号、复指数信号、正弦信号、抽样信号；（3）基本运算与变换：加法和乘法运算、信号的反转、平移与尺度变换；（4）阶跃函数和冲激函数：阶跃函数、冲激函数、冲激偶信号的定义及其关系，冲激函数的性质及运算；（5）信号的分解；（6）线性时不变连续系统：线性时不变系统的判断，线性时不变系统的表示：方框图、常系数微分方程，线性时不变系统的求解：零输入响应、零状态响应、自由响应、强迫响应、全响应的概念和求解，用卷积积分法求零状态响应，起始点的跳变；（7）单位冲激响应与阶跃响应的定义和计算；（8）卷积的定义、性质和计算，线性时不变连续系统输入输出关系。

2、连续系统的频域分析（傅里叶变换）。

（1）频谱的概念；（2）周期信号的频谱与傅里叶级数分析、函数的对称性与傅里叶系数的关系、典型周期信号的傅里叶级数；（3）非周期信号的频谱：傅里叶变换对和非周期信号频谱的特点、典型非周期信号的频谱；（4）冲激函数与阶跃函数的傅里叶变换；（5）傅里叶变换的性质和应用；（6）卷积定理；（7）周期信号的傅里叶变换；（8）连续系统的频域分析；（9）抽样信号的傅里叶变换；（10）连续时间信号抽样：理想抽样、实际抽样、抽样定理；（11）理想低通滤波器：频域特性与冲激响应、系统的物理可实现性。

3、连续系统的复频域分析（拉普拉斯变换）。

（1）拉普拉斯变换的定义与收敛域；（2）拉普拉斯变换的性质；（3）拉普拉斯反（逆）变换；（4）连续时间系统的复频域分析；（5）系统函数、系统稳定性判断、系统函数决定系统的时域与频域特性；（6）全通函数与最小相移函数；（7）拉普拉斯变换与傅里叶变换之间的关系。

4、离散时间系统的时域分析。

（1）离散时间信号：常用序列、序列基本运算、周期性等；（2）线性移不变系统：线性、移不变、因果性、稳定性；（3）离散系统的时域分析：常系数差分方程的求解方法、系统零输入响应、零状态响应、自由响应与强迫响应的计算、单位抽样响应的计算、卷积和的计算。

第6章系统的频域分析一、选择题1．选择题已知信号f（t）的最高频率，则对信号取样时，其频谱不混叠的最大取样间隔等于（）。

[北京交通大学研]A．B．C．D．【答案】A【解析】信号f（t）的最高频率为，根据Fourier变换的展缩特性可得信号的最高频率为（Hz），再根据时域抽样定理，可得对信号取样时，其频谱不混叠的最大取样间隔2．下列说法中正确的是（）。

[东南大学研]A．罗斯—霍维茨准则也能判断离散系统的稳定性B．信号经调制后带宽一定增加C．抽样频率必须是信号最高频率的2倍以上才不产生混叠D．积分器是线性运算，不改变信号的带宽【答案】AD【解析】本题考查信号与系统的综合应用。

罗斯霍维茨准则是稳定性判定准则，信号经调制后带宽不一定增加，有时只是频谱的搬移，积分运算是累加运算，也即线性运算，抽样频率必须是信号最高频率的2倍或者2倍以上才不产生混叠。

因此选择AD。

3．系统的幅频特性和相频特性如图6-1（a）、（b）所示，则下列信号通过该系统时，不产生失真的是（）。

[西安电子科技大学研]A．B．C．D．【答案】B【解析】由系统的幅频特性和相频特性可知：若输入信号的频率均处于之间，既不产生幅度失真又不产生相位失真。

只有（B）满足这一条件。

图6-1二、填空题1．已知一连续时间LTI系统的频响特性该系统的幅频特性相频特性是否是无失真传输系统______。

[北京交通大学研] 【答案】否【解析】由于的分子分母互为共轭，故有所以系统的幅度响应和相位响应分别为由于系统的相位响应不是的线性函数，所以系统不是无失真传输系统。

三、解答题1．某因果数字滤波器的零、极点如图6-2所示，并已知其H（π）=-1试求：图6-2（1）它的系统函数H（z）及其收敛域，且回答它是IIR、还是FIR的什么类型（低通、高通、带通、带阻或全通）滤波器；（2）写出图6-2（b）所示周期信号x[n研]的表达式，并求其离散傅里叶级数的系数；（3）该滤波器对周期输入x[n研]的响应y[n研]。

《信号与系统》课程研究性学习报告组长学号小组成员学号：指导教师时间2011.11信号与系统的时域分析专题研讨【目的】(1) 加深对信号与系统时域分析基本原理和方法的理解。

(2) 学会利用MA TLAB 进行信号与系统的分析。

(3) 培养学生自主学习能力，以及发现问题、分析问题和解决问题的能力。

【研讨题目】 题目1 连续信号通过系统的响应 一连续LTI 系统满足的微分方程为)()('2)(2)('3)(''t x t x t y t y t y +=++(1) 已知)(e )(3t u t x t -=，试求该系统的零状态响应)(zs t y 。

(2) 用lsim 求出该系统的零状态响应的数值解。

利用(1)所求得的结果，比较不同的抽样间隔对数值解精度的影响。

(3)用命令[x,Fsam,bits] = wavread('Yourn')；将硬盘上的语音文件Yourn.wav 读入计算机。

用命令sound(x,Fsam)；播放该语音信号；(4)用命令load model01将磁盘文件model01.mat 读入计算机后，MATLAB 的workspace 中将会新增变量den 和num 。

den 表示微分方程左边的系数，变量num 表示微分方程右边的系数。

写出磁盘文件model01.mat 定义的微分方程；(5)计算(3)中的信号通过(4)中系统的响应，播放系统输出的语音信号。

与处理前的信号比较，信号有何不同？能用已学知识解释所得结果吗？ 【题目目的】1.学会用计算机求解信号通过系统响应；2.熟悉用Matlab 处理语音信号的基本命令；求解系统的零状态响应：系统的特征方程为：032=+s s 特征根为 2,121-=-=s s ，因此系统的设冲击响应可以设为：)()e e ()(2-t t u B A t h t -+=将上述结果带入原方程待定系数法解得3,1=-=B A 带入原微分方程解出系统零状态响应为：t -23e 21e 3e 25)(*)(-+-==--t t zs t x t h y用命令“fprintf(‘%s ’,num)””fprintf(‘%s ’,den)”从磁盘读入的系统描述的微分方程为：den: 1.309536e+004 7.076334e+008 6.939120e+012 1.396319e+0178.396151e+020 5.648432e+024num: 3.162278e-003 9.235054e-014 1.649476e+007 3.566819e-0041.646178e+016 1.058969e+005 4.486709e+024【仿真结果】不同抽样间隔时的波形比较：12345678-0.100.10.20.30.40.50.6ty tT=0.512345678-0.0500.050.10.150.20.250.3t y tT=0.212345678-0.0500.050.10.150.20.250.3ty tT=0.13,载入信号波形：02468101214161820-0.8-0.6-0.4-0.200.20.40.6处理后的波形：2468101214161820-0.25-0.2-0.15-0.1-0.0500.050.10.150.20.25【结果分析】1、 从曲线看，当抽样间隔比较大的时候，改变间隔对信号的影响较大：抽样间隔小于一定的值后，再减小抽样间隔对曲线的影响就变得很小了，说明用抽样来模拟连续信号是可行的并且抽样间隔需要足够小。

第二章 连续系统的时域分析一、单项选择题X2.1（东南大学2002年考研题）一线性时不变连续时间系统，其在某激励信号作用下的自由响应为(e -3t +e -t )ε(t )，强迫响应为(1-e -2t )ε(t )，则下面的说法正确的是 。

（A ）该系统一定是二阶系统 （B ）该系统一定是稳定系统（C ）零输入响应中一定包含(e -3t +e -t )ε(t ) （D ）零状态响应中一定包含(1-e -2t )ε(t )X2.2（西安电子科技大学2005年考研题）信号f 1(t )和 f 2(t ) 如图X2.2所示，f =f 1(t )* f 2(t )，则 f (-1)等于 。

（A ）1 （B ）-1 （C ）1.5 （D ）-0.5图X2.2X2.3（西安电子科技大学2005年考研题）下列等式不成立的是 。

[])()(*)()()()(*)()()(*)()(*)()()(*)()(*)()(2121210201t f t t f D t f t t f C t f dt d t f dt d t f t f dt d B t f t f t t f t t f A ='='⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==+-δδ答案：X2.1[D]，X2.2[C]，X2.3[B]二、判断与填空题T2.1（北京航空航天大学2001年考研题）判断下列说法是否正确，正确的打“√”，错误的打“×”。

（1）若)(*)()(t h t f t y =，则)2(*)2(2)2(t h t f t y =。

[ ] （2）如果x (t )和y (t )均为奇函数，则x (t )*y (t )为偶函数。

[ ] （3）卷积的方法只适用于线性时不变系统的分析。

[ ] （4）若)(*)()(t h t f t y =，则)(*)()(t h t f t y --=-。

[ ]（5）两个LTI 系统级联，其总的输入输出关系与它们在级联中的次序没有关系。