数字信号处理算法的定点化及其C语言仿真
- 格式：doc
- 大小：46.00 KB
- 文档页数：8
下载文档原格式
合集下载
DSP中浮点转定点运算--举例及编程中的心得
DSP中浮点转定点运算--举例及编程中的⼼得5．举例及编程中的⼼得5．1举例 “第3章 DSP芯⽚的定点运算.doc”这篇⽂章中给了⼀个很简单有能说明问题的例⼦，不想动⼤脑了，直接引⽤过来如下。
这是⼀个对语⾳信号(0.3kHz~3.4kHz)进⾏低通滤波的C语⾔程序，低通滤波的截⽌频率为800Hz，滤波器采⽤19点的有限冲击响应FIR滤波。
语⾳信号的采样频率为8kHz，每个语⾳样值按16位整型数存放在insp.dat⽂件中。
例3.7 语⾳信号800Hz 19点FIR低通滤波C语⾔浮点程序复制代码代码如下:#include <stdio.h>const int length = 180 /*语⾳帧长为180点＝22.5ms@8kHz采样*/void filter(int xin[ ],int xout[ ],int n,float h[ ]); /*滤波⼦程序说明*//*19点滤波器系数*/static float h[19]={0.01218354,-0.009012882,-0.02881839,-0.04743239,-0.04584568,-0.008692503,0.06446265,0.1544655,0.2289794,0.257883,0.2289794,0.1544655,0.06446265,-0.008692503,-0.04584568,-0.04743239,-0.02881839,-0.009012882,0.01218354};static int x1[length+20];/*低通滤波浮点⼦程序*/void filter(int xin[ ],int xout[ ],int n,float h[ ]){int i,j;float sum;for(i=0;i<length;i++) x1[n+i-1]=xin[i];for (i=0;i<length;i++){sum=0.0;for(j=0;j<n;j++) sum+=h[j]*x1[i-j+n-1];xout[i]=(int)sum;}for(i=0;i<(n-1);i++) x1[n-i-2]=xin[length-1-i];}/*主程序*/void main( ){FILE *fp1,*fp2;int frame,indata[length],outdata[length];fp1=fopen(insp.dat,"rb"); /*输⼊语⾳⽂件*/fp2=fopen(outsp.dat,"wb"); /*滤波后语⾳⽂件*/frame=0;while(feof(fp1)==0){frame++;printf("frame=%d/n",frame);for(i=0;i<length;i++) indata[i]=getw(fp1); /*取⼀帧语⾳数据*/filter(indata,outdata,19,h); /*调⽤低通滤波⼦程序*/for(i=0;i<length;i++) putw(outdata[i],fp2); /*将滤波后的样值写⼊⽂件*/}fcloseall( ); /*关闭⽂件*/return(0);}例3.8 语⾳信号800Hz 19点FIR低通滤波C语⾔定点程序复制代码代码如下:#include <stdio.h>const int length=180;void filter(int xin[ ],int xout[ ],int n,int h[ ]);static int h[19]={399,-296,-945,-1555,-1503,-285,2112,5061,7503,8450,7503,5061,2112,-285,-1503,-1555,-945,-296,399}; /*Q15*/static int x1[length+20];/*低通滤波定点⼦程序*/void filter(int xin[ ],int xout[ ],int n,int h[ ]){int i,j;long sum;for(i=0;i<length;i++) x1[n+i-1]=xin[i];for (i=0;i<length;i++){sum=0;for(j=0;j<n;j++) sum+=(long)h[j]*x1[i-j+n-1];xout[i]=sum>>15;}for(i=0;i<(n-1);i++) x1[n-i-2]=xin[length-i-1];}主程序与浮点的完全⼀样。
定点数原码一位乘法c语言
定点数原码一位乘法c语言定点数原码一位乘法是一种基于原码表示法的乘法运算方法，其基本思想是将被乘数和乘数都表示为定点数，然后按照二进制一位一位地相乘，并累加得到最终结果。
以下是一个用C语言实现的定点数原码一位乘法的示例代码：```cinclude <>// 定义定点数类型typedef int fixed_point;// 定义定点数原码一位乘法函数fixed_point multiply(fixed_point a, fixed_point b) {fixed_point result = 0; // 初始化结果为0int i = 0; // 初始化位数为0while (b != 0) { // 循环计算每一位的乘积if (b & 1) { // 如果b的最低位为1result += a << i; // 将a左移i位后加到结果中}a <<= 1; // 将a左移一位b >>= 1; // 将b右移一位i++; // 位数加1}return result; // 返回结果}int main() {fixed_point a = 10; // 被乘数fixed_point b = 3; // 乘数fixed_point result = multiply(a, b); // 调用乘法函数计算结果printf("(%d %d) = %d\n", a, b, result); // 输出结果return 0;}```在上述代码中，我们定义了一个定点数类型`fixed_point`，并实现了一个`multiply`函数，该函数接收两个定点数作为参数，并返回它们的乘积。
在函数中，我们使用了一个循环来计算每一位的乘积，具体实现方式是通过左移操作将每一位的乘积加到结果中。
最后，我们在`main`函数中调用`multiply`函数，并输出结果。
第5章 数字信号处理算法的DSP实现 《DSP原理及实践应用》电子课件
第五章 数字信号处理算法的DSP实现
④运行应用程序，观察波形 将上述的三个文件添加到工程项目中，之后对工程项目 中的文件进行编译，汇编，链接，生成可以在目标系统 中运行的可执行的输出文件FIR.out。选择View->Graph>Time/Frequency命令，在打开的图形参数设置对话框中 设置参数，就可显示出高通滤波器的频谱响应，输入序 列，输出序列。 按图5-3所示进行图形参数对话框中的参数设置，生成的 高通滤波器的频谱响应如图5-4所示。
第五章 数字信号处理算法的DSP实现
5.1 数字滤波器的实现
• 数字滤波是DSP最基本的应用，它是图像处理，模式识别 ，语音处理，频谱分析等应用的基本处理算法。本节主要 介绍最常用的数字滤波器----FIR(有限冲激响应滤波器)的编 程实现方法。
第五章 数字信号处理算法的DSP实现
• 5.1.1 FIR滤波器的基本结构 图5-1是FIR滤波器的结构图，它的差分方程表达式为：
/
f s )]
sin[2n ( fc1 2n
/
f
s
)] ]
第五章 数字信号处理算法的DSP实现
• 【例5-2】 在CCS开发平台中用C语言实现FIR高通滤波器， 其阶数为30，截止频率为10Hz。构造一个输入信号，它由 频率4Hz和12Hz两个正弦信号叠加而成，设采样频率为 fs=50Hz。用设计的高通滤波器对输入序列进行滤波。
N 1
y(n) bi x(n i)
0
式中，x(n)为输入序列，y(n)为输出序列， bi 为滤波器系数，N
为滤波器的阶数。
第五章 数字信号处理算法的DSP实现
x(n)
x(n-1)
z-1
z-1
数字信号处理
DFT方法计算量太大，限制了应用。直到1965年，美 国的Cooly和Turkey提出了一种快速计算DFT的算法。例如： 当N=1024时，DFT的复数乘法次数约为105万次，Cooly和 Turkey的复数乘法次数5120次，仅为DFT的1/200。人们称 这种快速算法为快速傅里叶变换（FFT）。算法中，规定N 取2的整数次幂，因此也称基2型FFT。 目前实现FFT主 要有软件和硬件两种方法。FFT是功率谱、互谱、频率响 应函数、相干函数等经典频域分析和许多相关分析方法的 基础。
ቤተ መጻሕፍቲ ባይዱ
思考题： 1、将连续时间信号进行离散化时产生混叠的主要原因是什么？
2、叙述采样定理，并说明你对该定理是如何理解的？
3 、从波形特点上说明什么是低通、高通、带通、带阻滤波器？ 4、调制与解调的作用是什么？简述其工作原理。 5、将随时间连续变化的模拟信号转变成离散的数字信号需要经 过几个环节的变化，并说明各自的特点。
二、测试信号数字化处理的基本步骤
1) 信号调整
(预处理）
2) 模数转换 3) 数字信号分析 4) 输出结果
数字信号处理步骤简图
• 预处理
是指在数字处理之前，对信号用模拟方法进行的处
理。把信号变成适于数字处理的形式，以减小数字处理
的困难。它包括： 1. 对输人信号的幅值进行处理，使信号幅值与A／D转 换器的动态范围相适应； 2. 衰减信号中不感兴趣的高频成分，减小频混的影响； 3. 隔离被分析信号中的直流分量，消除趋势项及直流分 量的干扰等项处理。
5.4 数字信号处理基础
一、数字信号处理的主要研究内容
数字信号处理主要研究用数字序列或符号序列表示信号， 并用数字计算方法对这些序列进行处理，以便把信号变换成符 合某种需要的形式。数字信号处理的主要内容包括频谱分析与 数字滤波及信号的识别等。
基于CCS和ICETEK5509实验箱FFT算法的C语言实现与验证
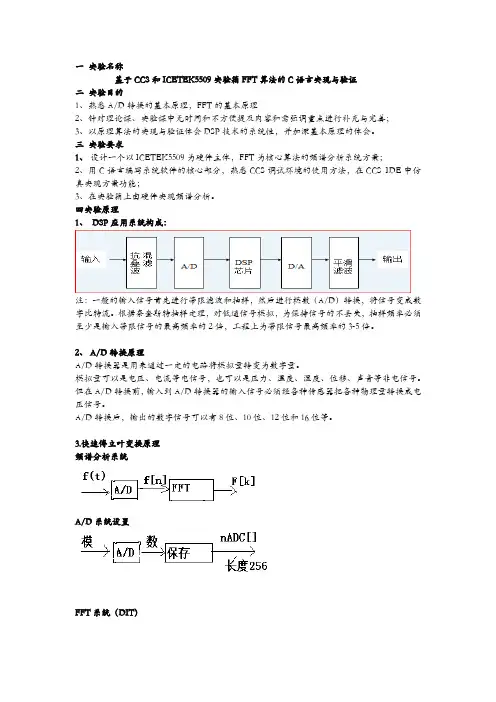
一实验名称基于CCS和ICETEK5509实验箱FFT算法的C语言实现与验证二实验目的1、熟悉A/D转换的基本原理，FFT的基本原理2、针对理论课、实验课中无时间和不方便提及内容和需强调重点进行补充与完善；3、以原理算法的实现与验证体会DSP技术的系统性，并加深基本原理的体会。
三实验要求1、设计一个以ICETEK5509为硬件主体，FFT为核心算法的频谱分析系统方案；2、用C语言编写系统软件的核心部分，熟悉CCS调试环境的使用方法，在CCS IDE中仿真实现方案功能；3、在实验箱上由硬件实现频谱分析。
四实验原理1、DSP应用系统构成：注：一般的输入信号首先进行带限滤波和抽样，然后进行模数（A/D）转换，将信号变成数字比特流。
根据奈奎斯特抽样定理，对低通信号模拟，为保持信号的不丢失，抽样频率必须至少是输入带限信号的最高频率的2倍，工程上为带限信号最高频率的3-5倍。
2、A/D转换原理A/D转换器是用来通过一定的电路将模拟量转变为数字量。
模拟量可以是电压、电流等电信号，也可以是压力、温度、湿度、位移、声音等非电信号。
但在A/D转换前，输入到A/D转换器的输入信号必须经各种传感器把各种物理量转换成电压信号。
A/D转换后，输出的数字信号可以有8位、10位、12位和16位等。
3.快速傅立叶变换原理频谱分析系统A/D系统设臵FFT系统（DIT）对于有限长离散数字{x[n]}，0≤n≤N-1，其离散谱{x[k]}可以由离散傅氏变换（DFT）求得。
不难看出，是周期性的，且周期为N，即，m，l=0，±1，±2….FFT算法可以分为按时间抽取FFT和按频率抽取FFT两大类输入也有和复数之分，一般情况下，都假定输入序列为复数。
FFT算法利用旋转因子的对称性和周期性，加快运算速度。
用定点DSP芯片实现FFT程序时，一个比较重要的问题就是防止中间结果的溢出，防止中间结果的溢出的方法就是对中间数值归一化，而不可能溢出的则不进行归一化。
【转】dsp定点运算基本方法
【转】dsp定点运算基本⽅法⽬录参考：⼀ＤＳＰ定点算数运算1 数的定标在定点DSP芯⽚中，采⽤定点数进⾏数值运算，其操作数⼀般采⽤整型数来表⽰。
⼀个整型数的最⼤表⽰范围取决于DSP芯⽚所给定的字长，⼀般为16位或24位。
显然，字长越长，所能表⽰的数的范围越⼤，精度也越⾼。
如⽆特别说明，本书均以16位字长为例。
DSP芯⽚的数以2的补码形式表⽰。
每个16位数⽤⼀个符号位来表⽰数的正负，0表⽰数值为正，l则表⽰数值为负。
其余15位表⽰数值的⼤⼩。
因此，⼆进制数0010000000000011b=8195⼆进制数1111111111111100b= -4对DSP芯⽚⽽⾔，参与数值运算的数就是16位的整型数。
但在许多情况下，数学运算过程中的数不⼀定都是整数。
那么，DSP芯⽚是如何处理⼩数的呢？应该说，DSP芯⽚本⾝⽆能为⼒。
那么是不是说DSP芯⽚就不能处理各种⼩数呢？当然不是。
这其中的关键就是由程序员来确定⼀个数的⼩数点处于16位中的哪⼀位。
这就是数的定标。
通过设定⼩数点在16位数中的不同位置，就可以表⽰不同⼤⼩和不同精度的⼩数了。
数的定标有Q表⽰法和S表⽰法两种。
表1.1列出了⼀个16位数的16种Q表⽰、S表⽰及它们所能表⽰的⼗进制数值范围。
从表1.1可以看出，同样⼀个16位数，若⼩数点设定的位置不同，它所表⽰的数也就不同。
例如，16进制数2000H=8192，⽤Q0表⽰16进制数2000H=0.25，⽤Q15表⽰但对于DSP芯⽚来说，处理⽅法是完全相同的。
从表1.1还可以看出，不同的Q所表⽰的数不仅范围不同，⽽且精度也不相同。
Q越⼤，数值范围越⼩，但精度越⾼；相反，Q越⼩，数值范围越⼤，但精度就越低。
例如，Q0 的数值范围是⼀32768到+32767，其精度为1，⽽Q15的数值范围为-1到0.9999695，精度为1/32768=0.00003051。
因此，对定点数⽽⾔，数值范围与精度是⼀对⽭盾，⼀个变量要想能够表⽰⽐较⼤的数值范围，必须以牺牲精度为代价；⽽想精度提⾼，则数的表⽰范围就相应地减⼩。
数字信号处理实验报告
数字信号处理实验报告
数字信号处理是指利用数字技术对模拟信号进行采样、量化、编码等处理后，再通过数字信号处理器进行数字化处理的技术。
在数字信号处理实验中，我们通过对数字信号进行滤波、变换、解调等处理，来实现信号的处理和分析。
在实验中，我们首先进行了数字信号采集和处理的基础实验，采集了包括正弦信号、方波信号、三角波信号等在内的多种信号，并进行了采样、量化、编码等处理。
通过这些处理，我们可以将模拟信号转换为数字信号，并对其进行后续处理。
接着，我们进行了数字信号滤波的实验。
滤波是指通过滤波器对数字信号进行处理，去除其中的噪声、干扰信号等不需要的部分，使其更加纯净、准确。
在实验中，我们使用了低通滤波器、高通滤波器、带通滤波器等多种滤波器进行数字信号滤波处理，得到了更加干净、准确的信号。
除了滤波，我们还进行了数字信号变换的实验。
数字信号变换是指将数字信号转换为另一种表示形式的技术，可以将信号从时域转换到频域，或者从离散域转换到连续域。
在实验中，我们使用了傅里叶变换、离散傅里叶变换等多种变换方式，对数字信号进行了变换处理，得到了信号的频谱信息和其他相关参数。
我们进行了数字信号解调的实验。
数字信号解调是指将数字信号转换为模拟信号的技术，可以将数字信号还原为原始信号，并进行后续处理。
在实验中，我们使用了频率解调、相干解调等多种解调方式，将数字信号转换为模拟信号，并对其进行了分析和处理。
总的来说，数字信号处理实验是一项非常重要的实验，可以帮助我们更好地理解数字信号处理的原理和方法，为我们今后从事相关领域的研究和工作打下坚实的基础。
数字信号处理
数字信号处理数字信号处理（Digital Signal Processing，简称DSP）是指通过数学运算和算法实现对数字信号的分析、处理和改变的技术。
它广泛应用于通信、音频、视频、雷达、医学图像等领域，并且在现代科技发展中发挥着重要作用。
本文将介绍数字信号处理的基本原理和应用，以及相关的算法和技术。
一、数字信号处理的基本原理数字信号处理的基本原理是将连续的模拟信号转换为离散的数字信号，再通过算法对数字信号进行处理。
这个过程主要包括信号采样、量化和编码三个步骤。
1. 信号采样：信号采样是指以一定的时间间隔对连续的模拟信号进行离散化处理，得到一系列的采样点。
通过采样，将连续的信号转换为离散的信号，方便进行后续的处理和分析。
2. 量化：量化是指对采样得到的信号进行幅度的离散化处理，将连续的幅度变为离散的幅度级别。
量化可以采用线性量化或非线性量化的方式，通过确定幅度级别的个数来表示信号的幅度。
3. 编码：编码是指对量化后的信号进行编码处理，将其转换为数字形式的信号。
常用的编码方式包括二进制编码、格雷码等，在信息传输和存储过程中起到重要作用。
二、数字信号处理的应用领域数字信号处理被广泛应用于各个领域，以下介绍几个主要的应用领域：1. 通信领域：在通信领域中，数字信号处理用于信号的调制、解调、编码、解码等处理过程。
通过数字信号处理，可以提高通信系统的性能和可靠性，实现高速、高质量的数据传输。
2. 音频和视频处理：在音频和视频处理领域，数字信号处理可以用于音频和视频的压缩、解压、滤波、增强等处理过程。
通过数字信号处理，可以实现音频和视频信号的高保真传输和高质量处理。
3. 医学图像处理：在医学图像处理领域，数字信号处理可以用于医学图像的增强、分割、识别等处理过程。
通过数字信号处理，可以提高医学图像的质量和准确性，帮助医生进行疾病的诊断和治疗。
4. 雷达信号处理：在雷达领域，数字信号处理可以用于雷达信号的滤波、目标检测、跟踪等处理过程。
DSP课程设计-基于C语言实现256点的FFT
= X1(k) + WNkX2(k)
r，k = 0，1，2， … ， N − 1
2
式中，x1(k)和 x2(k)分别为 x1(r)和 x2(r)的 N/2 的 DFT
式中，x1(k)和 x2(k)分别为 x1(r)和 x2(r)的 N/2 的 DFT。
由于对称性，WNk+N/2=-WNk。因此，N 点 DFT 可分为两部分：
对称性： WNk+N/2=-WNk 周期性：WNn(N-k)=WNk(N-n)=WN-nk 利用这些特性，既可以使 DFT 中有些项合并，减少了乘法积项，又可以将 长序列的 DFT 分解成几个短序列的 DFT。FFT 就是利用了旋转因子的对称性和 周期性来减少运算量的。 FFT 的算法是将长序列的 DFT 分解成短序列的 DFT。例如：N 为偶数时， 先将 N 点的 DFT 分解为两个 N/2 点的 DFT，使复数乘法减少一半：再将每个 N/2 点的 DFT 分解成 N/4 点的 DFT，使复数乘又减少一半，继续进行分解可 以大大减少计算量。最小变换的点数称为基数，对于基数为 2 的 FFT 算法，它 的最小变换是 2 点 DFT。 一般而言，FFT 算法分为按时间抽取的 FFT（DIT ＦＦＴ）和按频率抽取 的ＦＦＴ（DIF FFT）两大类。ＤIF FFT 算法是在时域内将每一级输入序列依 次按奇／偶分成２个短序列进行计算。而 DIF FFT 算法是在频域内将每一级输 入序列依次奇／偶分成２个短序列进行计算。两者的区别是旋转因子出现的位置 不同，得算法是一样的。在 DIF FFT 算法中，旋转因子WNk出现在输入端，而在 DIF FFT 算法中它出现在输入端。 假定序列 x(n)的点数 N 是 2 的幂，按照 DIF FFT 算法可将其分为偶序列和
数字信号处理的实现方法
数字信号处理的实现方法
数字信号处理的实现方法可以分为以下几种：
1. 基于通用计算机的数字信号处理：这是最常见的实现方法，
通过通用计算机上运行的数字信号处理软件，如MATLAB、Python等，
实现数字信号处理。
2. 基于数字信号处理器（DSP）的数字信号处理：DSP是专门用
于数字信号处理的芯片，通常具有高效的计算和低功耗的特点，适用
于高速数据流和实时控制的场合。
3. 基于单片机的数字信号处理：单片机能够对模拟信号进行采样、滤波、数字化等操作，适用于低速数据处理和非实时控制的场合。
4. FPGA实现数字信号处理：FPGA具有可编程性和高速并行计算
能力，适用于数据处理和实时控制的场合。
5. ASIC实现数字信号处理：ASIC是应用特定集成电路，可以针
对特定的应用场合进行优化设计，具有高效率和低功耗的特点，适用
于大规模的数字信号处理应用。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数字信号处理算法的定点化及其C语言仿真 周海军 赵阳 （南京邮电学院 通信工程系） 摘 要 在DSP开发应用中，使用C语言进行算法仿真既可以验证算法的正确性，也可以 为今后在实际DSP芯片上调试提供一个参考。针对定点DSP使用更为普遍的现状，本文介 绍了用C语言如何实现DSP定点算法的仿真，提供了将DSP浮点算法定点化的思想和方法。
关键词 数字信号处理 数字信号处理器 定点 浮点 Abstract Fixed-point digital signal processors are used commonly in many fi elds. It's quite important to use C language to simulate at PC platform DSP algorithms when developing DSP applications. Based on the author's rich expe rience in DSP software development, this paper concludes the methods of usin g C language to implement fix-point DSP algorithms, providing the skills of converting floating-point digital signal processing algorithms into fix-poin t versions.
Key words DSP fix-point floating-point
DSP广义上指数字信号处理理论(Digital Signal Processing)，狭义上指数字 信号处理器(Digital Signal Processor)。数字信号处理理论广泛应用于语音、图象、 遥测数据、电机控制等各个方面。现代个人通信、互联网、多媒体应用的飞速发展又推 动着数字信号处理理论的进一步发展。现代信号处理（ASP）算法越来越复杂，处理的数 据量越来越庞大。由于体系结构的限制，通用微处理器并不适合作这种高运算量的信号 处理，由此诞生了一种专门用于信号处理的芯片和系统，这就是数字信号处理器，通常 简称DSP。作为数字信号处理理论和当代大规模集成电路VLSI技术融合的结晶，数字信号 处理器（DSP）正日益广泛地应用于通信、消费类电子产品、仪器仪表、航天航空等各个 领域。在数字化浪潮的推动下，基于DSP的软硬件开发需求越来越大。国际上各大DSP芯 片制造厂商也不断推出运算速度更快、功耗更低的产品。 1. 定点DSP和浮点DSP 国际上生产DSP芯片的厂商很多，典型的有TI、AD、Motorola、DSP Group以及 AT&T、NEC等等，这些公司都有自己的由低档到高档的DSP产品系列。其中TI--德州仪器 公司占有主导地位，其产品占了45%的市场份额。 AD--模拟器件公司紧随其后，其产品 约占11%的市场份额。TI公司的TMS320系列和AD公司的ADSP系列在中国使用的也最为广泛 。表1列出了常见的两家公司的主要产品。
表1 公司 DSP芯片 定点/浮点 时钟频率(MHz) TI TMS320C2xxx 定点 20－40 TMS320C3x 浮点 33－75 TMS320C54xx 定点 40－160 TMS320C55xx 定点 160－200 TMS320C62xx 定点 150－300 TMS320C67xx 浮点 100－167 AD ADSP-21xx 定点 10－80 ADSP-21xxx(SHARC) 浮点 33－100 TigerSHARC 浮点 250
从表1可以看出，两家公司都有各自的定点产品和浮点产品。数据以定点格式工 作的DSP芯片称为定点DSP，数据以浮点格式工作的DSP称为浮点DSP。浮点DSP表示数据的 精度高，编程也比较容易，从高级语言转化为适合浮点DSP的汇编语言要方便。但是，由 于DSP大量用于嵌入式系统，很多应用场合如手机、PDA、便携式音频播放器等等，都要求
价格低廉，功耗尽量低。而浮点DSP由于内部结构较复杂，价格、功耗都不易降下 来，因此其应用反而不如定点DSP普遍。DSP芯片厂商推出的定点DSP种类也比浮点DSP种 类多，这在表1中也有体现。 定点DSP的字宽一般为16位，也有24位和20位的DSP，如摩 托罗拉的DSP563XX系 列和Zoran公司的 ZR3800X系列。显然数据字长越大单字表示的范围越大，精度越高，但 TI和AD目前的产品都是16位字长。
2. C语言在DSP开发中的应用[1][3] 为缩短软件开发周期，使用C语言开发DSP产品越来越普遍。使用汇编语言可以 充分利用DSP片内资源编出精简高效的代码。但是DSP汇编语言编程较繁杂，可读性差。 而且，一般来说，不同公司的芯片汇编语言是不同的，即使是同一家公司的芯片，由于 芯片类型不同（如定点和浮点），产品的升级换代，其汇编语言也不相同，这使得汇编 语言的可移植性也较差。所以用汇编语言开发基于DSP芯片的产品周期长，软件的修改和 升级都较困难。C语言既有高级语言的易学易懂、功能丰富、表达能力强、可移植性好的 优势，又具有低级语言的特点（比如能方便地进行位运算、地址操作）。正因为如此， 各DSP芯片厂商也都提供了相应的C优化编译器，并不断提高其编译效率，鼓励DSP开发者 选用C语言作为开发DSP应用程序的首选工具。事实上，对于有些多内核、并行化程度非 常高的DSP处理器，如TI的TMS320C62xx，完全由人手编写汇编代码反而很难有效地分配 运行资源、发挥处理器并行处理的优势。当然，现在的C编译器效率仍然不是很高，DSP 片内片外资源也有限，很多地方仍然要作人工优化。 通常DSP的开发流程如图1所示，详细过程如下： （1） 用C语言编写程序，在PC机上仿真测设，确保算法正确。尽管现在DSP厂商推出的 调试工具越来越方便，用户界面越来越友善，但比起PC编程仍然要麻烦得多。确保算法 在PC机上仿真通过，以后调试DSP汇编程序时就有一个参考，这样会方便很多。一般采用 文件的形式来仿真DSP程序的输入输出。 （2） 按照DSP的C程序编写规则改写C程序，使之适合DSP硬件。将文件读写改为真正的 I/O操作。加入中断功能。必要时在C程序中嵌入汇编语句。 （3）使用C编译器编译改写的C程序，生成DSP汇编源代码。C编译器具有优化选项，根据 需要选择不同的优化等级和优化范围。 （4）手动进行程序优化，降低程序代码大小，使流程更合理，进一步加快程序的执行速 度。评估程序能否在实际的DSP处理器上实时运行。如果不行，人工编写指令周期密集的 那些模块的汇编代码，直到满足实时要求。 （5）使用汇编器将各模块汇编成目标文件。 （6）最后将各目标文件链接成可载入DSP中联机运行调试的可执行代码。 3. DSP定点算法的C语言仿真[2] DSP开发过程的第一步是在PC机上编写C仿真程序，确保算法正确，这样可以大 大节省以后在DSP上调试的时间。对于浮点算法，使用C语言加以实现是十分方便的，编 程者只需具备C编程的知识，甚至可以完全不懂DSP。常见的数字信号处理算法也都是以 浮点形式出现。但是由于定点DSP受数值表示范围的限制，用C语言仿真定点算法或将浮 点算法定点化则要复杂的多，需要了解一些定点DSP芯片硬件操作的知识，掌握一些规则 和技巧。下面就从定点DSP数值表达、常用运算来讲述如何用C语言实现DSP定点算法的仿 真。这里假定处理器是16位的定点DSP，乘法器、累加器为32位。仿真C程序使用TURBO C编译器，那么在C程序中可用的变量只有单精度整型int （16位）和 双精度长整型
long（32位）两种形式。
3.1浮点数的定点化 3.1.1 Q格式--固定小数点的表达方式[1] 定点DSP芯片中的基本单元是16位（比特）字。当表示纯整数时其范围为-3276 8到+32767，分别对应的二进制表示为1000 0000 0000 0000和0111 1111 1111 1111。处 理器中都是采用补码形式，最左面的一位即第15位是最高有效位(MSB)，最右面的一位即 第0位是最低有效位(LSB)。MSB作符号位，如果一个数是正数，MSB为0，若为负数，MSB 为1。 当要表示小数时，必须假定一个小数点位于相邻两比特之间。比如，要表示一 个-1.0到+1.0之间的小数，我们可以假定小数点位于第14位和第15位之间。这种表达方 式称为Q15格式，因为小数点右边有15位。如果小数点右边有n位就称为Qn格式。纯整数 是一种特殊的Q0格式的小数。 将浮点算法转化为定点算法，首先就要把所有的小数经定标转化为整数。比如 浮点算法中有一个浮点数组为[ 0.25 0.5 1.125 5.75 7.0 ]，用二进制表示为[ 0.01 0.1 1.001 101.11 111.0 ]。将数组各分量左移三位，得[ 10 100 1001 101110 111000 ]，十进制表示为[ 2 4 9 46 56 ]。小数点位置在第3位，此数组 中的各分量都是Q3格式，这就是定标的过程。 浮点数和定点数的转换公式如下： 浮点数(x)转换为定点数(xq)：xq＝(int)x * 2Q 定点数( xq)转换为浮点数(x)：x=(float) xq * 2-Q 不同的Q格式所表示的数的范围不同，精度也不同。Q越大，数值范围越小，但精 度越高。例如，Q0的数值范围是-32768到+32768，其精度是1，而Q15的数值范围为-1到 0.9999695，精度为1/32768=0.00003051。对于定点数而言，数据范围和精度是一对矛盾 。 3.1.2 定标浮点数--动态小数点的表达方式 固定小数点的方式只适用于表达动态范围较小的浮点数变量，对于那些动态变 化比较大的浮点数变量采取固定小数点的表达方式，往往可能造成溢出或者精度太低。 浮点数定点化的关键是要保证精度，而与精度有直接关系的是有效数字的位数 ，与小数点的位置无关。可见，只要保证了浮点数表达的有效位数为16比特定点可以表达 的最大位数，就等于保证了浮点数定点化的最大精度。因此，可以将一个浮点数用两个 16比特字来表达。第一个字表示尾数(M)， 采用补码形式，其幅度值在16384～32767之