Spontaneous decay of an excited atom in an absorbing dielectric
- 格式:pdf
- 大小:280.86 KB
- 文档页数:28
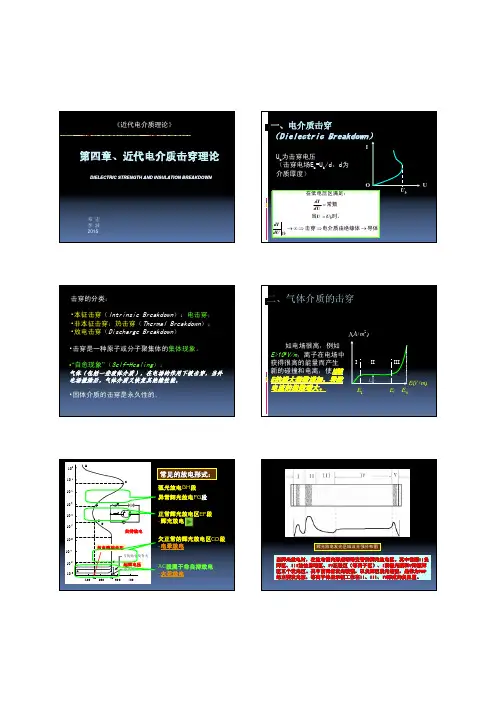
邓宏李波2015《近代电介质理论》DIELECTRIC STRENGTH AND INSULATION BREAKDOWN一、电介质击穿(Dielectric Breakdown )UIOU bU b 为击穿电压(击穿电场E b =U b /d,d为介质厚度)导体电介质由绝缘体击穿时,当常数在低电压区满足:→⇒⇒∞→==Ubb dUdI U U dUdI击穿的分类:•本征击穿(Intrinsic Breakdown ):电击穿;•非本征击穿:热击穿(Thermal Breakdown );•放电击穿(Discharge Breakdown )•击穿是一种原子或分子聚集体的集体现象。
•“自愈现象”(Self-Healing ):气体(包括一些液体介质),在电场的作用下被击穿,当外电场撤除后,气体介质又恢复其绝缘性能。
•固体介质的击穿是永久性的。
二、气体介质的击穿)/(2m A j )/(m V E IIIIII1E iE Sj bE 如电场很高,例如E>108V/m ,离子在电场中获得很高的能量而产生新的碰撞和电离,使N 随E 的增大指数增加,导致电流的指数增大。
1002003004001010 1010 10 10 10 1010100 HGFEV Vs与初始引发有关着火电压VDCA常见的放电形式:AC 段属于非自持放电-火花放电自持放电正常辉光放电区EF 段-辉光放电欠正常的辉光放电区CD 段-电晕放电起辉电压异常辉光放电FG 段弧光放电GH 段放电维持电压辉光放电发光区域及光强分布图当辉光放电时,在放电管内形成明暗交替的辉光放电区。
其中包括II 负辉区、III 法拉弟暗区、IV 正柱区(等离子区)、I 阴极光膜和V 阳极辉区五个发光区。
其中前两者发光较强,以负辉区发光最强,是作为PDP 的主要发光源,等离子体显示板工作在II 、III 、IV 形成的负阻区。
汤申特(Townsend) 碰撞游离理论1. 碰撞游离的必要条件:EVE q W L L L E q W E W W ii i =⋅≥∴⋅⋅=≥ 电荷的运动距离—为:的作用下所积累的能量一个电荷在电场(分子的游离能量)(电子的积累能量),且满足:金属电极表面逸出电子∵•多级碰撞,如果碰撞能量较小但之间间隔周期很短,可能使分子游离;•电子与受激的中性分子碰撞,中性分子回到零位状态,而电子被加速能量增大,可使下一个中性分子游离;•两个受激的分子碰撞,一个交出能量,而另一个获得能量而游离。





2011年技术物理学院08级(激光方向)专业英语翻译重点!!!作者:邵晨宇Electromagnetic电磁的principle原则principal主要的macroscopic宏观的microscopic微观的differential微分vector矢量scalar标量permittivity介电常数photons光子oscillation振动density of states态密度dimensionality维数transverse wave横波dipole moment偶极矩diode 二极管mono-chromatic单色temporal时间的spatial空间的velocity速度wave packet波包be perpendicular to线垂直be nomal to线面垂直isotropic各向同性的anistropic各向异性的vacuum真空assumption假设semiconductor半导体nonmagnetic非磁性的considerable大量的ultraviolet紫外的diamagnetic抗磁的paramagnetic顺磁的antiparamagnetic反铁磁的ferro-magnetic铁磁的negligible可忽略的conductivity电导率intrinsic本征的inequality不等式infrared红外的weakly doped弱掺杂heavily doped重掺杂a second derivative in time对时间二阶导数vanish消失tensor张量refractive index折射率crucial主要的quantum mechanics 量子力学transition probability跃迁几率delve研究infinite无限的relevant相关的thermodynamic equilibrium热力学平衡(动态热平衡)fermions费米子bosons波色子potential barrier势垒standing wave驻波travelling wave行波degeneracy简并converge收敛diverge发散phonons声子singularity奇点(奇异值)vector potential向量式partical-wave dualism波粒二象性homogeneous均匀的elliptic椭圆的reasonable公平的合理的reflector反射器characteristic特性prerequisite必要条件quadratic二次的predominantly最重要的gaussian beams高斯光束azimuth方位角evolve推到spot size光斑尺寸radius of curvature曲率半径convention管理hyperbole双曲线hyperboloid双曲面radii半径asymptote渐近线apex顶点rigorous精确地manifestation体现表明wave diffraction波衍射aperture孔径complex beam radius复光束半径lenslike medium类透镜介质be adjacent to与之相邻confocal beam共焦光束a unity determinant单位行列式waveguide波导illustration说明induction归纳symmetric 对称的steady-state稳态be consistent with与之一致solid curves实线dashed curves虚线be identical to相同eigenvalue本征值noteworthy关注的counteract抵消reinforce加强the modal dispersion模式色散the group velocity dispersion群速度色散channel波段repetition rate重复率overlap重叠intuition直觉material dispersion材料色散information capacity信息量feed into 注入derive from由之产生semi-intuitive半直觉intermode mixing模式混合pulse duration脉宽mechanism原理dissipate损耗designate by命名为to a large extent在很大程度上etalon 标准具archetype圆形interferometer干涉计be attributed to归因于roundtrip一个往返infinite geometric progression无穷几何级数conservation of energy能量守恒free spectral range自由光谱区reflection coefficient(fraction of the intensity reflected)反射系数transmission coefficient(fraction of the intensity transmitted)透射系数optical resonator光学谐振腔unity 归一optical spectrum analyzer光谱分析grequency separations频率间隔scanning interferometer扫描干涉仪sweep移动replica复制品ambiguity不确定simultaneous同步的longitudinal laser mode纵模denominator分母finesse精细度the limiting resolution极限分辨率the width of a transmission bandpass透射带宽collimated beam线性光束noncollimated beam非线性光束transient condition瞬态情况spherical mirror 球面镜locus(loci)轨迹exponential factor指数因子radian弧度configuration不举intercept截断back and forth反复spatical mode空间模式algebra代数in practice在实际中symmetrical对称的a symmetrical conforal resonator对称共焦谐振腔criteria准则concentric同心的biperiodic lens sequence双周期透镜组序列stable solution稳态解equivalent lens等效透镜verge 边缘self-consistent自洽reference plane参考平面off-axis离轴shaded area阴影区clear area空白区perturbation扰动evolution渐变decay减弱unimodual matrix单位矩阵discrepancy相位差longitudinal mode index纵模指数resonance共振quantum electronics量子电子学phenomenon现象exploit利用spontaneous emission自发辐射initial初始的thermodynamic热力学inphase同相位的population inversion粒子数反转transparent透明的threshold阈值predominate over占主导地位的monochromaticity单色性spatical and temporal coherence时空相干性by virtue of利用directionality方向性superposition叠加pump rate泵浦速率shunt分流corona breakdown电晕击穿audacity畅通无阻versatile用途广泛的photoelectric effect光电效应quantum detector 量子探测器quantum efficiency量子效率vacuum photodiode真空光电二极管photoelectric work function光电功函数cathode阴极anode阳极formidable苛刻的恶光的irrespective无关的impinge撞击in turn依次capacitance电容photomultiplier光电信增管photoconductor光敏电阻junction photodiode结型光电二极管avalanche photodiode雪崩二极管shot noise 散粒噪声thermal noise热噪声1.In this chapter we consider Maxwell’s equations and what they reveal about the propagation of light in vacuum and in matter. We introduce the concept of photons and present their density of states.Since the density of states is a rather important property,not only for photons,we approach this quantity in a rather general way. We will use the density of states later also for other(quasi-) particles including systems of reduced dimensionality.In addition,we introduce the occupation probability of these states for various groups of particles.在本章中,我们讨论麦克斯韦方程和他们显示的有关光在真空中传播的问题。

光子的能级跃迁涉及到原子物理学的知识,主要有三种过程,分别是自发辐射、受激吸收和受激辐射。
自发辐射过程:处于高能级E的一个原子自发的向低能级E跃迁,并发射一个能量为hv的光子,这种过程称为自发跃迁,由原子自发跃迁发出的光被称为自发辐射。
自发辐射的光子是自发产生的,其辐射是独立的。
受激吸收过程:处于低能态E的一个原子,在频率为v的辐射场作用下,吸收一个能量为hv的光子并向高能态E跃迁,这种过程称为受激吸收跃迁。
这个过程是非自发的,需要外来光照射,而且能够增强光的强度。
与原光子性质、状态完全相同。
受激辐射过程:处于上能级E的原子在频率为v的辐射场作用下,跃迁至低能态E ,并辐射一个能量为hv的光子。
这个过程只有在外来光子的能量恰好等于能级差时才会发生,受激辐射所发出的光子与外来光子的特性完全相同,即频率相同、相位相同、偏振方向相同、传播方向相同。
以上信息仅供参考,建议查阅物理书籍或咨询物理专业人士以获取更深入的了解。



TPO8 Lecture 4 ChemistryPro: So, are there any questions?Stu: Yes, um, Professor Harrison, you were saying that the . What exactly does that mean? I mean I understand how it organizes the elements but where’s the prediction?Pro: Ok, let’s look at our periodic table again. Ok, it groups elements into categories that , right?Stu: Uh-huh. Pro: And it is arranged according to increasing atomic nu mber, which is…Stu: The number of protons in each atom of an element.Pro: Q1Right, well, early versions of the periodic table had gaps, elements. Every time you had one more proton, you had another element. And then, oops, there’d be an atomic number, for which there was no known element.And the prediction was that an element with that atomic number existed somewhere, but it just hadn’t been found yet. And its location in the table would tell you what properties it should have. It was really pretty exciting for scientists at that time to find these missing elements and confirm their predictive properties.Q1Um, actually, that reminds of a ... of a very good example of all these, element 43. See on the table, the symbols for elements 42 and 44. Well, in early versions of the table, there was no symbol for an element 43 protons because no element with 43 protons had been discovered yet. So the periodic table had a gap between elements 42 and 44.And then in 1925, a team of chemists led by a scientist named Ida Tacke claimed that they had found element 43. They had been using a new technology called X-ray , and they were using this to examine an ore sample. And they claimed that they’d found an element with 43 protons. And they named it Masurium.Stu: Um, Professor Harrison, then, how come in my periodic table here, element 43 is Tc, that’s Technetium, right?Pro: Ok, let me add that. Actually, um, that’s the point I’m coming to. anyone believed that Tacke’d discovered a new element. X-ray spectroscopy was a new method at that time. And they were never able to isolate enough Masurium to have a weighable sample to everyone of the discovery. So they were discredited.But then, 12 years later in 1937, a different team became the first to an element using a cyclotron. And that element had…Stu: 43 protons?Pro: That’s right, but they named it Technetium to Q3emphasize that it was withtechnology. And people thought that synthesizing this element, making it artificially was the only way to get it. We still hadn’t found it.Now element 43, whether you call it Masurium or Technetium, is radioactive. Why does that matter? What is true of a radioactive element?Stu: It , it turns into other elements. Oh, so does that explain why it was missing in the periodic table?Pro: Exactly, because of its radioactive decay, element 43 . And therefore, if that ever had been on Earth, it would have decayed ages ago. So the Masurium people were wrong, and the Technetium people were right. Right? Well, that was then, now we know that element 43 does occur naturally. It can be naturally Uranium atoms that have spontaneously split. And guess what, the ore sample the Masurium group was working with had plenty of Uranium in it enough to split into of Masurium. So Tacke’s team might very well have found small amounts of Masurium in the ore sample. Q4 It’s just that once was generated from split Uranium, it decayed very quickly.Q6And you know here’s an , Ida Tacke, the chemist led the Masurium team, well, she was the first to suggest that Uranium could break up into smaller pieces, but she d idn’t know that that was the defense of her own discovery of element 43.Stu: So is my version of the periodic table wrong? Should element 43 really be called Masurium?Pro: Q5Maybe, but you know it’s hard to tell after all this time, if Ida Tacke’s group did discover element 43. They didn’t, um, publish enough detail on their methods or instruments for us to know .But I’d like to think element 43 was discovered twice. As Masurium, it was the first element discovered that occurs in nature only from spontaneous fission, and as Technetium, it was the first element discovered in a laboratory. And of course, it was an element the periodic table let us to expect existed before anyone had found it or made it.。

与激光有关的英文文献Revised at 16:25 am on June 10, 2019L a s e r t e c h n o l o g y R. E. Slusher Bell Laboratories, Lucent Technologies, Murray Hill, New Jersey 07974 Laser technology during the 20th century is reviewed emphasizing the laser’s evolution from science to technology and subsequent contributions of laser technology to science. As the century draws to a close, lasers are making strong contributions to communications, materials processing, data storage, image recording, medicine, and defense. Examples from these areas demonstrate the stunning impact of laser light on our society. Laser advances are helping to generate new science as illustrated by several examples in physics and biology. Free-electron lasers used for materials processing and laser accelerators are described as developing laser technologies for the next century.S0034-68619902802-01. INTRODUCTIONLight has always played a central role in the study of physics, chemistry, and biology. Light is key to both the evolution of the universe and to the evolution of life on earth. This century a new form of light, laser light, has been discovered on our small planet and is already facilitating a global information transformation as well as providing important contributions to medicine, industrial material processing, data storage, printing, and defense. This review will trace the developments in science and technology that led to the invention of the laser and give a few examples of how lasers are contributing to both technological applications and progress in basic science. There are many other excellent sources that cover various aspects of the lasers and laser technology including articles from the 25th anniversary of the laser Ausubell and Langford, 1987 and textbooks ., Siegman, 1986; Agrawal and Dutta, 1993; and Ready, 1997.Light amplification by stimulated emission of radiation LASER is achieved by exciting the electronic, vibrational, rotational, or cooperative modes of a material into a nonequilibrium state so that photons propagating through the system are amplified coherently by stimulated emission. Excitation of this optical gain medium can be accomplished by using optical radiation, electrical current and discharges, or chemical reactions. The amplifying medium is placed in an optical resonator structure, for example between two high reflectivity mirrors in a Fabry-Perot interferometer configuration. When the gain in photon number for an optical mode of the cavity resonator exceeds the cavity loss, as well as loss from nonradiative and absorption processes, the coherent state amplitude of the mode increases to a levelwhere the mean photon number in the mode is larger than one. At pump levels above this threshold condition,the system is lasing and stimulated emission dominates spontaneous emission. A laser beam is typically coupled out of the resonator by a partially transmitting mirror. The wonderfully useful properties of laser radiation include spatial coherence, narrow spectral emission, high power, and well-defined spatial modes so that the beam can be focused to a diffraction-limited spot size in order to achieve very high intensity. The high efficiency of laser light generation is important in many applications that require low power input and a minimum of heat generation.When a coherent state laser beam is detected using photon-counting techniques, the photon count distribution in time is Poissonian. For example, an audio output from a high efficiency photomultiplier detecting a laser field sounds like rain in a steady downpour. This laser noise can be modified in special cases, ., by constant current pumping of a diode laser toobtain a squeezed number state where the detected photons sound more like a machine gun than rain. An optical amplifier is achieved if the gain medium is not in a resonant cavity. Optical amplifiers can achievevery high gain and low noise. In fact they presently have noise figures within a few dB of the 3 dB quantum noise limit for a phase-insensitive linear amplifier, ., they add little more than a factor of two to the noise power of an input signal. Optical parametric amplifiers OPAs, where signal gain is achieved by nonlinear coupling of a pump field with signal modes, can be configured to add less than 3 dB of noise to an input signal. In an OPA the noise added to the input signal can be dominated by pump noise and the noise contributed by a laser pump beam can be negligibly small compared to the large amplitude of the pump field.2. HISTORYEinstein 1917 provided the first essential idea for the laser, stimulated emission. Why wasn’t the laser invented earlier in the century Much of the early work on stimulated emission concentrates on systems near equilibrium, and the laser is a highly nonequilibrium system. In retrospect the laser could easily have been conceived and demonstrated using a gas discharge during the period of intense spectroscopic studies from 1925 to 1940. However, it took the microwave technology developed during World War II to create the atmosphere for thelaser concept. Charles Townes and his group at Columbia conceived the maser microwave amplification by stimulated emission of radiation idea, based on their background in microwave technology and their interest in high-resolution microwave spectroscopy. Similar maser ideas evolved in Moscow Basov and Prokhorov, 1954 and at the University of Maryland Weber, 1953. The first experimentally demonstrated maser at Columbia University Gordon et al., 1954, 1955 was based on an ammonia molecular beam. Bloembergen’s ideas for gain in three level systems resulted in the first practical maser amplifiers in the ruby system. These devices have noise figures very close to the quantum limit and were used by Penzias and Wilson in the discovery of the cosmic background radiation.Townes was confident that the maser concept could be extended to the optical region Townes, 1995. The laser idea was born Schawlow and Townes, 1958 when he discussed the idea with Arthur Schawlow, who understood that the resonator modes of a Fabry-Perot interferometer could reduce the number of modes interacting with the gain material in order to achieve high gain for an individual mode. The first laser was demonstrated in a flash lamp pumped ruby crystal by Ted Maiman at Hughes Research Laboratories Maiman, 1960. Shortly after the demonstration of pulsed crystal lasers, a continuouswave CW He:Ne gas discharge laser was demonstrated at Bell Laboratories Javan et al., 1961, first at mm and later at the red nm wavelength lasing transition. An excellent article on the birth of the laser is published in a special issue of Physics Today Bromberg, 1988.The maser and laser initiated the field of quantum electronics that spans the disciplines of physics and electrical engineering. For physicists who thought primarilyin terms of photons, some laser concepts were difficult to understand without the coherent wave concepts familiar in the electrical engineering community. For example, the laser linewidth can be much narrower than the limit that one might think to be imposed by the laser transition spontaneous lifetime. Charles Townes won a bottle of scotch over this point from a colleague at Columbia. The laser and maser also beautifully demonstrate the interchange of ideas and impetus between industry, government, and university research.Initially, during the period from 1961 to 1975 there were few applications for the laser. It was a solution looking for a problem. Since the mid-1970s there has been an explosive growth of laser technology for industrial applications. As a result of this technology growth, a new generation of lasers including semiconductor diode lasers, dye lasers, ultrafast mode-locked Ti:sapphire lasers, optical parameter oscillators, and parametric amplifiers is presently facilitating new research breakthroughs in physics, chemistry, and biology.3. LASERS AT THE TURN OF THE CENTURYSchawlow’s ‘‘law’’ states that everything lases if pumped hard enough. Indeed thousands of materials have been demonstrated as lasers and optical amplifiers resulting in a large range of laser sizes, wavelengths, pulse lengths, and powers. Laser wavelengths range from the far infrared to the x-ray region. Laser light pulses as short as a few femtoseconds are available for research on materials dynamics. Peak powers in the petawatt range are now being achieved by amplification of femtosecond pulses. When these power levels are focused into a diffraction-limited spot, the intensities approach 1023 W/cm2. Electrons in these intense fields are accelerated into the relativistic range during a single optical cycle, and interesting quantum electrodynamic effects can be studied. The physics of ultrashort laser pulses is reviewed is this centennial series Bloembergen, 1999.A recent example of a large, powerful laser is the chemical laser based on an iodine transition at a wavelength of mm that is envisioned as a defensive weapon Forden, 1997. It could be mounted in a Boeing 747 aircraft and would produce average powers of 3 megawatts, equivalent to 30 acetylene torches. New advances in high quality dielectric mirrors and deformable mirrors allow this intense beam to be focused reliably on a small missile carrying biological or chemical agents and destroy it from distances of up to 100 km. This ‘‘star wars’’ attack can be accomplished during the launch phase of the target missile so that portions of the destroyed missile would fall back on its launcher, quite a good deterrent for these evil weapons. Captain Kirk and the starship Enterprise may be using this one on the Klingons At the opposite end of the laser size range are microlasers so small that only a few optical modes are contained in a resonator with a volume in the femtoliter range. These resonators can take the form of rings or disks only a few microns in diameter that use total internal reflection instead of conventional dielectric stack mirrors in order to obtain high reflectivity. Fabry-Perot cavities only a fraction of a micron in length are used for VCSELs vertical cavity surface emitting lasers that generate high quality optical beams that can be efficiently coupled to optical fibers Choquette and Hou, 1997. VCSELs may find widespread application in optical data links.4. MATERIALS PROCESSING AND LITHOGRAPHYHigh power CO2 and Nd:YAG lasers are used for a wide variety of engraving, cutting, welding, soldering, and 3D prototyping applications. rf-excited, sealed off CO2 lasers are commercially available that have output powers in the 10 to 600 W range and have lifetimes of over 10 000 hours. Laser cutting applications include sailclothes, parachutes, textiles, airbags, and lace. The cutting is very quick, accurate, there is no edge discoloration, and a clean fused edge is obtained that eliminatesfraying of the material. Complex designs are engraved in wood, glass, acrylic, rubber stamps, printing plates, plexiglass, signs, gaskets, and paper. Threedimensional models are quickly made from plastic or wood using a CAD computer-aided design computer file.Fiber lasers Rossi, 1997 are a recent addition to the materials processing field. The first fiber lasers were demonstrated at Bell Laboratories using crystal fibers in an effort to develop lasers for undersea lightwave communications. Doped fused silica fiber lasers were soon developed. During the late 1980s researchers at Polaroid Corp. and at the University of Southampton invented cladding-pumped fiber lasers. The glass surrounding the guiding core in these lasers serves both to guide the light in the single mode core and as a multimode conduit for pump light whose propagation is confined to the inner cladding by a low-refractive index outer polymer cladding. Typical operation schemes at present use a multimode 20 W diode laser bar that couples efficiently into the large diameter inner cladding region and is absorbed by the doped core region over its entire length typically 50 m. The dopants in the core of the fiber that provide the gain can be erbium for the mm wavelength region or ytterbium for the mm region. High quality cavity mirrors are deposited directly on the ends of the fiber. These fiber lasers are extremely efficient, with overall efficiencies as high as 60%. The beam quality and delivery efficiency is excellent since the output is formed as the single mode output of the fiber. These lasers now have output powers in the 10 to 40 W range and lifetimes of nearly 5000 hours. Current applications of these lasers include annealing micromechanical components, cutting of 25 to 50 mm thick stainless steel parts, selective soldering and welding of intricate mechanical parts, marking plastic and metal components, and printing applications.Excimer lasers are beginning to play a key role in photolithography used to fabricate VLSI very large scale integrated circuit chips. As the IC integrated circuit design rules decrease from mm 1995 to mm 2002, the wavelength of the light source used for photolithographic patterning must correspondingly decrease from 400 nm to below 200 nm. During the early 1990s mercury arc radiation produced enough power at sufficiently short wavelengths of 436 nm and 365 nm for high production rates of IC devices patterned to mm and mm design rules respectively. As the century closes excimer laser sources with average output powers in the 200 W range are replacing the mercury arcs. The excimer laser linewidths are broad enough to prevent speckle pattern formation, yet narrow enough, less than 2 nm wavelength width, to avoid major problems with dispersion in optical imaging. The krypton fluoride KF excimer laser radiation at 248 nm wavelength supports mm design rules and the ArF laser transition at 193nm will probably be used beginning with mm design rules. At even smaller design rules, down to mm by 2008, the F2 excimer laser wavelength at 157 nm is a possible candidate, although there are no photoresists developed for this wavelength at present. Higher harmonics of solid-state lasers are also possibilities as high power UV sources. At even shorter wavelengths it is very difficult for optical elements and photoresists to meet the requirementsin the lithographic systems. Electron beams, x-rays and synchrotron radiation are still being considered for the 70 nm design rules anticipated for 2010 and beyond.5. LASERS IN PHYSICSLaser technology has stimulated a renaissance in spectroscopies throughout the electromagnetic spectrum. The narrow laser linewidth, large powers, short pulses, and broad range of wavelengths has allowed new dynamic and spectral studies of gases, plasmas, glasses, crystals, and liquids. For example, Raman scattering studies of phonons, magnons, plasmons, rotons, and excitations in 2D electron gases have flourished since the invention of the laser. Nonlinear laser spectroscopies have resulted in great increases in precision measurement as described in an article in this volume Ha¨nsch and Walther 1999.Frequency-stabilized dye lasers and diode lasers precisely tuned to atomic transitions have resulted in ultracold atoms and Bose-Einstein condensates, also described in this volume Wieman et al., 1999. Atomicstate control and measurements of atomic parity nonconservation have reached a precision that allows tests of the standard model in particle physics as well as crucial searches for new physics beyond the standard model. In recent parity nonconservation experiments Wood et al., 1997 Ce atoms are prepared in specific electronic states as they pass through two red diode laser beams. These prepared atoms then enter an optical cavity resonator where the atoms are excited to a higher energy level by high-intensity green light injected into the cavity from a frequency-stabilized dye laser. Applied electric and magnetic fields in this excitation region can be reversed to create a mirrored environment for the atoms. After the atom exits the excitation region, the atom excitation rate is measured by a third red diode laser. Very small changes in this excitation rate with a mirroring of the applied electric and magnetic fields indicate parity nonconservation. The accuracy of the parity nonconservation measurement has evolved over several decades to a level of %. This measurement accuracy corresponds to the first definitive isolation of nuclear-spin-dependent atomic parity violation.。
光腔中两组分玻色-爱因斯坦凝聚体的受激辐射特性和量子相变黄珊;刘妮;梁九卿【摘要】研究了单模光腔中两组分玻色-爱因斯坦凝聚的基态性质和相关的量子相变.通过利用自旋相干态变换将等效赝自旋哈密顿算符对角化并求得基态能量泛函.基态能量泛函对其经典场变量进行变分并取极小值,得到光子数解和相边界曲线.通过稳定性讨论发现系统除了出现正常相和超辐射相之外,还得到了多稳的宏观量子态;受激辐射来自于原子数反转的集体态,单组分的Dicke系统中并没有此现象;受激辐射只能从一组分的原子中产生,而另外的仍保持在普通超辐射状态.通过调整相关的原子-场耦合强度和频率失谐,超辐射和受激辐射态的顺序可以在原子的两个组分之间互换.【期刊名称】《物理学报》【年(卷),期】2018(067)018【总页数】10页(P76-85)【关键词】量子相变;自旋相干态变换;能量泛函;受激辐射【作者】黄珊;刘妮;梁九卿【作者单位】山西大学, 理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原 030006;山西大学, 理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原 030006;山西大学, 理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原 030006【正文语种】中文1 引言Dicke模型描述的是N个二能级原子整体与一个单模量子化电磁场的相互作用[1].该自旋-玻色模型展示了在光与物质相互作用系统中的集体现象[2,3],并且可以发生从正常相到超辐射相的二阶相变[4−8].虽然标准Dicke模型形式简单,但是体现了丰富而独特的多体量子理论,且在量子信息等方面有广泛的研究[9],尤其在冷原子系统中讨论自旋轨道耦合的工作中也有很多丰富的研究结果[10−13].经典相变是指由于热涨落的影响导致物理系统突然发生态的改变,例如由液态到固态的变化.而Dicke模型中的量子相变描述的是在绝对零度下,当改变多粒子系统的某一序参数时,系统将从一种无序的状态连续变化到一种有序的状态.为了在实验中实现Dicke模型的量子相变,集体原子与光子的耦合强度应该与原子共振频率的数量级大小相同,这个条件很难得到满足[14−17].最近,在一个玻色-爱因斯坦凝聚(BEC)-光学腔系统中成功地观测到超辐射量子相变,实验中引入了独立的动量自旋态[3,18].因此,BEC-光学腔系统常被用来探索奇异的多体现象.近年来,利用半经典近似法对双组分BEC中量子相变进行了研究,揭示了原子对隧穿诱发的动力学[19−21].相关文献已证明:光学腔中耦合的双组分BEC具有光学、流体、多稳定性[22,23];在具有自旋自由度的双组分BEC中也可产生大量的多粒子纠缠,并且可观察到两组BEC之间的干扰[23−25].很多文献是基于Holstein-Primako ff变换,即在热力学极限(N→∞)下,将赝自旋算符转化为单模玻色算符,然后利用变分的方法研究Dicke模型的量子相变[13].本文通过玻色子算符取平均场近似后,得到一个等效赝自旋哈密顿算符,并利用自旋相干态变换将其对角化得到能量泛函,然后将求得的能量泛函对其经典场变量(复参数)变分并取极小值,从而给出基态能量和波函数的表达式.自旋相干态变分的方法可以方便地揭示多体物理系统的基态特性,既可以考虑正常赝自旋,又可以考虑反转赝自旋,同时能产生多稳的宏观量子态.在自旋为N且N→∞时,我们看到的宏观量子态就是自旋相干态.本文采用自旋相干态变分的方法,展示了两组分BECs在单模光学腔中丰富的基态相图和量子相变特性.2 模型我们考虑两团超冷原子同时与频率为ω光学腔模耦合,但两团原子之间并没有相互作用(如图1),则两组分超冷原子与光腔相互作用的有效哈密顿量[26](用自然单位~=1)可表示为式中a†,a分别表示有效光场的产生算符和湮灭算符;Sjz,Sj+,Sj−是集体赝自旋算符,自旋量子数Sj=Nj/2(j=1,2),其中Nj代表第j个组分原子数;ωj是第j个组分的原子频率;gj为第j个组分的原子与光场的耦合强度.设变分的基态波函数为玻色场的相干态|α⟩,即玻色子湮灭算符的本征态为a|α⟩= α|α⟩.在玻色场相干态表象中,方程(1)对应的哈密顿算符的期待值是一个等效的赝自旋哈密顿,即这意味着等效赝自旋哈密顿量可以通过将玻色场算符取平均场近似得到,这里经典场的变量(复数)为变分参数,因此求能量泛函的关键是通过自旋相干态变换将赝自旋哈密顿进行对角化,从而得到系统相应的本征值和本征态.本征方程为整体的态直接用两组分的自旋态直积产生本征态⟩分别为自旋算符在n方向投影的北、南极规范自旋相干态,其中是用分量极角ξj和方位角ηj描述的单位矢量.自旋相干态也可以通过旋转算符由Sz的本征态⟩生成, 即ξj,ηj是待定参数.图1 频率为ω的高精细光腔中具有频率为ω1和ω2的两组分超冷原子(白色和蓝色)的示意图Fig.1.Schematic diagram for two ensembles of ultracold atoms(white and blue)with transition frequencies ω1, ω2in an optical cavity of frequency ω.在自旋相干态变化下,原来的集体赝自旋算符Sjz,Sj+,Sj−变为[20]其中(5)式成立的条件是通过条件(7)式求得ξj和ηj,并代入到Aj(α,ξj,ηj)中,得到能量泛函为其中通过进一步求解(7)式最终求得参数,并将其代入能量泛函表达式.关于光子数的能量泛函是从(9)式可以发现:正常和反常的赝自旋态都将影响体系的多重稳定态.有四种自旋情况:两个反方向自旋(↑↑);第一个反向自旋,第二个正常自旋(↑↓);第一个正常自旋,第二个反向自旋(↓↑);两个正常自旋(↓↓).首先考虑第一种情况:两个反向自旋(↑↑),此时能量泛函为且我们假设两组分原子数目相等,为N1=N2=N/2,则基态的平均能量是对基态的平均能量对光子数γ变分,能量的极值条件为其中由此可以得出:(12)式存在光子数为零的解(γ↑↑=0),且当光子数为零时能量的二阶导是恒大于零,其区域由N↑↑表示.接下来考虑第二种情况:第一个反向自旋,第二个正常自旋(↑↓),无量纲的基态能量为其中能量的极值条件为由此可以得到有稳定的光子数为零的解(γ↑↓=0).根据能量泛函的二阶导数可以确定其稳定区域,并且用N↑↓表示,其区域范围为下面考虑第三种情况:第一个正常自旋,第二个反向自旋(↓↑). 能量泛函为能量的极值条件为此时稳定零解的区域用N↓↑表示,范围为最后一种情况:两个正常自旋↓↓.无量纲基态能量为能量的极值条件为稳定零解的区域用N↓↓表示,区域为接下来,讨论以上四种情况的非零光子数的解,统一表示为图2 极值方程Pk(γsk)=0(a1)—(a4)和平均能量曲线ε(b1)—(b4)随平均光子数γ2/N 的变化 (给定的条件是:第一组分原子与场的耦合强度为g1/ω=0.55和g2/ω=0.1,0.3,0.6,0.9,其中k=↓↓(黑线),k=↓↑(红线),k=↑↓(蓝线))Fig.2.Graphical solutions of the extremum equation Pk(γsk)=0(a1)–(a4)and the corresponding average energy curves ε (b1)–(b4)as the function of the mean photon number γ2/N for k=↓↓ (black line)and k=↓↑ (red line)(or k=↑↓ (blue line)).The plotted parameters are given by g1/ω =0.55 and g2/ω=0.1,0.3,0.6,0.9.其中k=↓↓,↑↓,↓↑,↑↑. 可以通过(17)式来数值求解光子数.在图2(a)中给出了稳定的非零光子解γsk,被称为超辐射态,其中k=↓↓(黑线),↓↑(红线),↑↓(蓝线),图2(b)为相对应的能量εsk.对于第二组分原子与场的耦合强度g2/ω=0.1时,从图2(a1)和图2(b1)可以看出只有两种情况下极值方程的解γs↓↓ 和γs↓↑ 是稳定的,即相对应的关于参数γ 的基态能量函数的二阶导数为正,此时对应的能量为局域的最小值.γs↓↑表示第二组分原子整体反转的非零光子数的稳定解.将第二组分原子与场的耦合强度提高到g2/ω=0.3(图2(a2)以及图2(b2))和g2/ω =0.6(图2(a3)和图2(b3))时,发现只有一个稳定解γs↓↓.但是当耦合强度提高到g2/ω=0.9时出现了两个稳定的解γs↓↓ 和γs↑↓ (图2(a4)和图2(b4)),γs↑↓表示来自第一组分原子反转的受激辐射解.根据图2(a4)和图2(b4),发现原子数反转的集体辐射变成了第一组分的原子反转这一有趣的现象.自旋相干态变分法的观测结果表明:除了基态可以获得稳定的宏观量子态之外,同时也获得了较高能量的稳定宏观量子态.3 讨论我们考虑不同组分原子与场的失谐分别为其中∆∈[−0.9,0.9],而原子与场的耦合不平衡参数δ表示为将(18)和(19)式代入到相对应的能量泛函,并根据极值条件可以得到正常态N↓↓和反转态N↓↑,N↑↓的相边界:正常态N↓↓和超辐射态S↓↓的平均光子数可以由相关的波函数直接求得,根据给出的自旋态,得到光子数为对于∆na(↓↓)=−1/2类似于标准Dicke模型,此时为正常相.在临界耦合强度gc↓↓前后,正常态N↓↓和超辐射态S↓↓的平均能量分别为对于另外两种态Nk,Sk,其中相对应的自旋极化k=↓↑,↑↓,它们的平均光子数为正常态的非平衡原子数为而对于超辐射态的非平衡原子数可整理为根据Pk(γsk)=0求出非零光子数γsk,将其代入到能量泛函内可以得到平均能量εk(Sk).正常态时,平均能量εk(Nk)=0.而对应零光子数解的反转自旋态的非平衡原子数∆na(↑↑)=0.5,平均能量为在N↑↑这种情况下反转自旋对应的零光子数解都是不稳定的.图3 平均光子数np和非平衡原子数∆na随原子-场耦合强度的变化(其中原子-场耦合强度g1=g2=1) (a)对应第二组分原子不存在,即ω2=0情况;(b)和(c)分别对应原子与场的失谐频率∆/ω=0.5,−0.5情况Fig.3.Variations of the average photon number npand atom population imbalance∆nawith respect to the coupling constant g1=g2=1 in the absence of the second-component atom frequency,i.e.,ω2=0(a),and atom- field frequencydetuning∆/ω=0.5(b)and∆/ω=−0.5(c).图3的(a1)和(a2)为第二组分原子不存在(ω2=0)时的平均光子数np和非平衡原子数∆na,且图3的不平衡参数δ=0.当ω2=0时,(1)式的哈密顿量可简化成标准的Dicke模型,当耦合强度达到临界条件gc=0.5会发生从正常相N↓到超辐射相S↓的量子相变,是典型的Dicke量子相变. 图3(b)和图3(c)给出了在红失谐(∆ =0.5)和蓝失谐(∆ = −0.5)时的平均光子数np和非平衡原子数∆na.在原子-场耦合强度g低于边界条件gc↓↓时,系统有稳定的零光子态,能量为最小值,即基态;在临界条件gc↓↓和gc↓↑图3(b)(或gc↑↓(图3(c))之间时,超辐射态S↓↓(黑线)和N↓↑(或N↑↓)(红线)以及N↑↑(蓝线)共存;在原子-场耦合强度g 高于临界条件gc↓↑(图3(b))或gc↑↓(图3(c))时,超辐射态S↓↓(黑线)和S↓↑(或S↑↓)(红线)以及N↑↑(蓝线)共存. 从正常相N↓↓到超辐射相S↓↓的量子相变是典型的Dicke量子相变,在临界点gc↓↓发生相变.从图3(b)可以看到,当∆/ω=0.5,出现了反转自旋极化的态N↓↑和S↓↑的情况,这是第一激发态.而在图3(c)中,对于负失谐∆/ω=−0.5,两组分发生交换,两个组分之间的自旋极化由N↓↑ 和S↓↑ 态转变为N↑↓和S↑↓,仍为第一激发态.我们观察到:当耦合强度达到临界点gc↓↑(或gc↑↓)时,系统发生正常态N↓↑(或N↑↓)到超辐射状态S↓↑(或S↑↓)的相变,这是图3呈现的一个新奇的量子相变,这是一组分BEC集体反演的整体受激辐射态.在正常态N↓↑(或N↑↓)和超辐射态S↓↑(或S↑↓)的临界点gc↓↑(或gc↑↓)并没有改变基态,且这两个态N↓↑(或N↑↓)和S↓↑(或S↑↓)是系统的集体激发态.对于给定的频率失谐∆/ω=±0.5,临界点可以根据(20)式精确地计算出gc↓↓=0.306,gc↓↑ =gc↑↓=0.433. 值得一提的是,两组分的原子集体反演的正常态N↑↑(蓝线)并未参与超辐射过程.图4为g-δ平面的相图.相变边界可以根据方程(20)准确求得.在NPts(由临界线gc↓↓限定)的区域中,存在三重零光子态,其中具有最低能量的N↓↓为基态, 该区域分为NPts(N↓↓,N↑↓,N↑↑)(I)和NPts(N↓↓,N↓↑,N↑↑)(II)两个区域, 由水平线(δ=0(a),δ=0.723(b),δ= −0.423(c))分离开.I区和II区只有一个状态不同,I区域中的状态N↑↓在II区域被替换为N↓↑.通过调整原子-场耦合强度g和原子-场耦合不平衡参数δ,可以看到从N↓↑到N↑↓同时转变(II→ I和IV → III).区域III(或区域IV)对应的态SPco(S↓↓,N↑↓,N↑↑)(或态SPco(S↓↓,N↓↑,N↑↑))是指态N↑↓(或态N↓↑)与超辐射态S↓↓共存的超辐射区域(N↑↑态指零光子的激发态),其中水平线(δ=0(a),δ=0.723(b),δ=−0.423(c))将SP超辐射区域分成两个区域(区域III和区域IV).在水平线的上面,只有第一激发态从N↓↑变化到N↑↓态,这主要是通过耦合变化引起自旋反转.在临界线gc↓↑下(区域VI),除了超辐射基态S↓↓,还有一个受激辐射态S↓↑,这是由正常态N↓↑(区域IV)变为超辐射相S↓↑. 而在临界线gc↑↓上面的区域内(区域V),同样有第一激发态正常态N↑↓(区域III)变为超辐射相S↑↓. 两个超辐射态S↑↓和S↓↑是双组分BEC中的新观测,被认为是来自较高能量原子能级的受激辐射.两个分量的稳定布居数反演态N↑↑存在于整个区域.原子与场频率的失谐仅会改变不同量子区的范围,但原子与场频率失谐和原子与场不平衡参数共同调控新的宏观多稳态.本文观察到的多稳的宏观量子态与非平衡量子相变的动力学研究一致[27,28].图4 g-δ空间的相图,其中原子与光场的频率失谐∆/ω =0(a),∆/ω =0.5(b),∆/ω = −0.5(c)Fig.4.Phase diagram in g-δ space with the atomfield frequency detuning∆/ω =0(a),∆/ω =0.5(b),∆/ω=−0.5(c).图5分别给出了平均光子数((a1)和(a2))、非平衡原子数((b1)和(b2))、平均能量((c1)和(c2))在共振条件∆ =0下随原子-场耦合常数的变化,其中非平衡参数为δ=±0.6.在非平衡参数δ=−0.6时,且当原子-场耦合强度达到临界条件gc↓↓=0.46,系统发生从正常相N↓↓到超辐射相S↓↓的量子相变.从图5(a1)—5(c1)可以看到:相比于临界值gc↓↓=0.46,第二组分具有较高的耦合值,即在临界点gc↓↑=0.55处,此时出现新的量子相变,即从集体激发态N↓↑到集体激发态S↓↑之间的相变.这种从原子数反转的正常态到超辐射态相变是由于第二组分原子的存在导致的,可通过观测非平衡原子布居数和平均能量来理解该相变.当将不平衡参数调整为δ=0.6时,在达到临界条件gc↓↓=0.26时,系统发生从正常相N↓↓到超辐射相S↓↓的量子相变,如图5(a2)—5(c2)所示.新的相变是第一个分量发生改变,在临界耦合gc↑↓ =0.401时发生从N↑↓到S↑↓的量子相变,此时集体受激辐射转移到了第一组分.负的不平衡参数δ使临界相变点gc↓↓和gc↓↑右移,而正的不平衡参数δ使临界相变点gc↓↓和gc↑↓左移,此结论与相图4中的结论是一致的.图5 在原子与场的失谐∆=0,原子-场耦合非平衡常数δ=−0.6和δ=0.6时的平均光子数np(a)、非平衡原子布居数∆na(b)和平均能量ε(c)Fig.5.Variations of the average photon number np(a),atom population imbalance∆na(b),and average energy ε(c)with respect to the atom- field frequency detuning∆=0 in the the atom- field coupling imbalan ce parameter δ= −0.6 and δ=0.6.4 结论利用自旋相干态变分方法分析了单模腔中双组分BEC的多稳宏观量子态.当调控两个组分之间的原子与场耦合不平衡参数和原子与场频率失谐时,体系出现了丰富的相图.实际上,当两个分量在正常自旋状态下时,基态显示了从正常相到超辐射相的量子相变,这是典型的Dicke模型的量子相变.当两个分量之间的原子-场耦合不平衡参数增加时,在相对较低的耦合值时,正常的自旋状态变到反转的自旋态,该状态的辐射是来自原子集体反演的受激辐射.受激辐射还可以通过操纵原子与场频率失谐产生.在特定情况下,当两组分原子与场的耦合常数消失一个或两个耦合相等时,基态和相关量子相变退回到标准Dicke模型.自旋相干态变分方法是研究原子整体与腔场相互作用系统宏观量子特性的有力工具,因为它考虑了正常和反转的赝自旋(导致多个宏观量子态),这与Dicke模型中非平衡量子相变的半经典动力学一致[29].参考文献【相关文献】[1]Dicke R H 1954 Phys.Rev.93 99[2]Colombe Y,Steinmetz T,Dubois G,Linke F,Hunger D,Reichel J 2007 Nature 450 272[3]Baumann K,Mottl R,Brennecke F,Esslinger T 2011 Phys.Rev.Lett.107 140402[4]Ritsch H,Domokos P,Brennecke F,Esslinger T 2013 Rev.Mod.Phys.85 553[5]Liang J Q,Liu J L,Li W D,Li Z J 2009 Phys.Rev.A 79 033617[6]Song L J,Yan D,Gai Y J,Wang Y B 2011 Acta Phys.Sin.60 020302(in Chinese)[宋立军,严冬,盖永杰,王玉波2011物理学报60 020302][7]Song L J,Yan D,Gai Y J,Wang Y B 2010 Acta Phys.Sin.59 3695(in Chinese)[宋立军,严冬,盖永杰,王玉波2010物理学报59 3695][8]Cao H,Fu L B 2012 Eur.Phys.J.D 66 97[9]Zhang Y C,Zhou X F,Guo G C,Zhou X,Pu H,Zhou Z W 2014 Phys.Rev.A 89 053624[10]Zhang Y,Chen G,Zhang C 2013 Sci.Rep.3 1937[11]Lian J L,Yu L,Liang J Q,Chen G,Jia S T 2013 Sci.Rep.3 3166[12]Huang Y,Hu Z D 2015 Sci.Rep.5 8006[13]Hamner C,Qu C,Zhang Y,Chang J,Gong M,Zhang C 2014 Nature Commun.5 4023[14]Emary C,Brandes T 2003 Phys.Rev.E 67 066203[15]Dimer F,Estienne B,Parkins A S,Carmichael H J 2007 Phys.Rev.A 75 013804[16]Chen G,Wang X G,Liang J Q,Wang Z D 2008 Phys.Rev.A 78 023634[17]Nagy D,Kónya G,Szirmai G,Domokos P 2010 Phys.Rev.Lett.104 130401[18]Baumann K,Guerlin C,Brennecke F,Esslinger T 2010 Nature 464 1301[19]Timmermans E 1998 Phys.Rev.Lett.81 5718[20]Pu H,Bigelow N P 1998 Phys.Rev.Lett.80 1130[21]Dong Y,Ye J W,Pu H 2011 Phys.Rev.A 83 031608[22]Sasaki K,Suzuki N,Saito H 2011 Phys.Rev.A 83 053606[23]Søensen A,Duan L M,Cirac J I,Zoller P 2001 Nature 409 63[24]Gordon D,Savage C M 1999 Phys.Rev.A 59 4623[25]Andrews M R,Townsend C G,Miesner H J,Durfee D S,Kurn D M,Ketterle W 1997 Science 275 637[26]Bhattacherjee A B 2014 Phys.Lett.A 378 3244[27]Liu N,Li J D,Liang J Q 2013 Phys.Rev.A 87 053623[28]Keeling J,Bhaseen M J,Simons B D 2010 Phys.Rev.Lett.105 043001[29]Bhaseen M J,Mayoh J,Simons B D 2012 Phys.Rev.A 85 013817。
helium: 氦 uranium: 铀gaseous state: 气态 solid liquid plasma the perfect gas law: 理想气体定律Boltzmann’s constant: 玻尔兹曼常数the most probable speed: 最概specific heat: 比热Plank’s constant: 普朗克常数quantum number: 量子数laser: 激光laser beam: n. 激光束thermonuclear fusion: 热核聚变deuterium: 氘 tritium: 氚deuteron: deuterium的原子核(=deuton) triton: tritium(氚)的原子核atomic mass unit(amu): 原子质量单位Avogadro’s number: 阿伏伽德罗常数,binding energy: 结合能Einstein’s relation between mass and energy: 爱因斯坦质能关系式electrostatic force:静电力centripetal force: 向心力valence: n.(化合)价, 原子价valence shell 价电子层nuclear force:核力spontaneous:自发的protactinium: 镤arise:出现,发生,起因于neutrino:中微子 positron:正电子sodium:钠 neon:氖negatron= electronantiparticle:反粒子 antimatter:反物质annihilate:湮灭excess n.& adj. 过度(的), 剩余, 无节制, 超额nucleate v. (使)成核 adj. 有核的 nuclear adj. 核子的, 原子能的, 核的, 中心的nucleal adj. 核子的, 原子能的, 核的, 中心的nucleant adj. 形成核的nucleus n. 原子核nuclei n. nucleus的复数nuclide n. 核素 nucleon n. 核子decay constantactivity becquerel (Bq), curie (Ci)name after: 以…命名radium n. 镭 Transmutation :核嬗变mercury:汞alchemist:炼金术士 cadmium:镉nuclear reactor:核反应堆controlled fusion reactors可控核聚变反应堆fusion :n.核聚变,熔化,熔合fission:n. [原]裂变、裂开, 分裂, rest mass:静止质量 lithium:锂the principle of conservation of momentum: 动量守恒定律in the classical and relativistic sense: 在经典及相对论意义上be of the right magnitude: 大小[数值]正好合适of the first magnitude: 头等重要的; average magnitude 平均量constantmagnitude 不变量discretemagnitude 离散量fundamental magnitude 基本量magnitude of a vector 向量的大小magnitude of stress 应力值mutual adj. 相互的, 共有的Coulomb’s relation: 库仑关系式probe n. 探针, 探测器 vt. (以探针等)探查, cross sectional area:截面面积macroscopic cross section: 宏观截面microscopic cross section: 微观截面target area:靶面积elastic scattering:弹性散射inelastic scattering:非弹性散射mean free path:平均自由程diffusion coefficient:扩散系数The dependence of absorption cross section on energy is of two type, one called 1/v, in which σa varies inversely with neutron speed, the other called resonance, where there is a very strong absorption at certain neutron energies 吸收截面关于能量的变化规律有两个:一个称为1/v 律,即微观吸收截面与中子速度成反正,另一个称为共振,即在某些能量上的吸收非常强This example shown is but one of a great variety of possible results of scattering collisions.上述实验结果仅仅是大量散射碰撞的可能结果中的一个。