2010工科数分第二学期期末试题

1. (5分) 若函数22t 02(e 1)d , 0() 0,0x t x f x x x ⎧-⎪≠=⎨⎪=⎩⎰ 求(0).f ' 2. (5分) 设()d arcsin xf x x x C =+⎰,求d .()x f x ⎰3. (10分) 设0<1()21<20<02xx f x xx x x ≤⎧⎪=-≤⎨⎪≥⎩或，求0()=()d x F x f t t ⎰.4. (10分) 设tan d n n I x x =⎰，求证：121ta (12)n n n n I x I n n --=--≥，并求55tan d I x x =⎰. 5．计算下面的积分（每小题5分，共4题20分） (1)41(1+)x x x ⎰； (2)40d 1+cos2x xx π⎰；(3)+322arctan d (1)x x x ∞+⎰; （4）222111[]d ln (1)x x x x --⎰. 6. (10分)设()f u 是连续函数，求2sin ()=(e )d x x x F x xf t t ⎰关于x 的导数。

7．(10分)设()g x 为正值连续函数，令()=||g()d (0)aa f x x t t t a --≥⎰，,判别()f x 的图形在[,]a a -上的凹凸性。

8. (10分) 证明当0x >时，有221ln(11x x x x +++>+. 9．(10分)曲线1ln(1)x y e x=++的渐近线有几条？请给出您的结论。

10．(10分)设在[1,)+∞上处处有()0f x ''≤，且(1)2,(1)3f f '==-，证明在(1,)+∞内方程()0f x =仅有一个实根。

厦门大学《高等数学》课程期末试卷学院 系 2010年级 专业主考教师：理工类教学组 试卷类型：（A 卷）11. 附加题(10分)设函数()()f x g x ，在[,]a b 上连续。

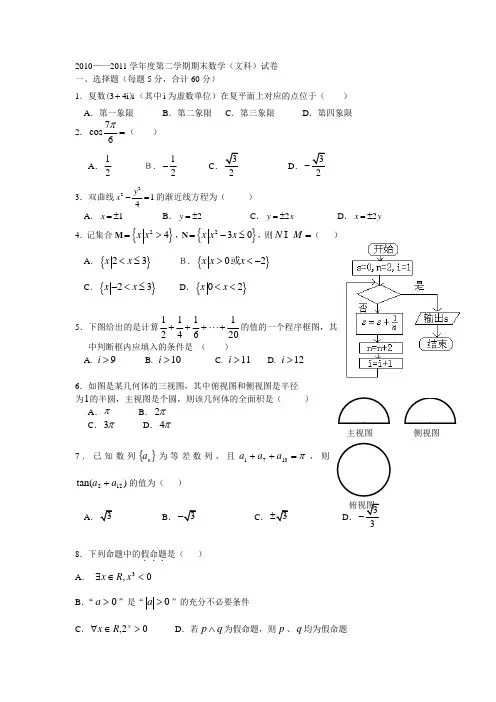
主视图侧视图2010——2011学年度第二学期期末数学（文科）试卷 一、选择题（每题5分，合计60分）1．复数34i i +()（其中i 为虚数单位）在复平面上对应的点位于（ ） A ．第一象限 B ．第二象限 C ．第三象限 D ．第四象限2．7cos6π=（ ）A ．12Ｂ．12-C ．2D ．2-3．双曲线2214yx -=的渐近线方程为（ ）A ．1x =±B ．2y =±C ．2y x =±D ．2x y =±4．记集合M {}24x x =>，N {}230x x x =-≤，则=M N （ ） A ．{}23x x <≤ Ｂ．{}02x x x ><-或 C ．{}23x x -<≤ D ．{}02x x <<5．下图给出的是计算201614121+⋅⋅⋅+++的值的一个程序框图，其中判断框内应填入的条件是 （ ）A. 9i >B. 10i >C. 11i >D. 12i >6．如图是某几何体的三视图，其中俯视图和侧视图是半径 为1的半圆，主视图是个圆，则该几何体的全面积是（ ） A ．π B ．π2 C ．π3 D ．π47．已知数列{}n a 为等差数列，且π=++1371a a a ，则)t a n (122a a +的值为（ ）A ．B ．C ．D ．3-8．下列命题中的假命题．．．是（ ） A ． 0,3<∈∃x R xB ．“0>a ”是“0>a ”的充分不必要条件C ．02,>∈∀x R xD ．若q p ∧为假命题，则p 、q 均为假命题0.00040.00030.00020.00019．已知两个不同的平面α，β和两条不重合的直线m ，n ，在下列四个命题中错误．．的是 （ ）A ．若m ∥α，n =βα ，则m ∥n Ｂ．若m ⊥α，m ⊥β，则α∥β C ．若m ∥n ，m ⊥α ，则n ⊥α D ．若m ⊥α，m ∥n ，β⊂n ，则α⊥β10．若方程()20f x -=在(,0)-∞内有解，则()y f x =的图象是（ ）11．在区间()0,1内任取两个实数，则这两个实数的和大于13的概率为A ．1718B ．79C ．29D ．11812．对任意实数,x y ，定义运算x y ax by cxy *=++，其中,,a b c 是常数，等式右边的运算是通常的加法和乘法运算。

华南农业大学期末考试试卷（A 卷）2009~2010学年第2学期 考试科目：高等数学A Ⅱ 考试类型：（闭卷）考试 考试时间： 120 分钟 学号 姓名 年级专业一、 单项选择题（本大题共5小题，每小题3分，共15分） 1．微分方程'220y y x ---=是（ ）A ．齐次方程B ．可分离变量方程C ．一阶线性方程D ．二阶微分方程2．过点(1,2,--且与直线25421x y z +-==-垂直的平面方程是（ ）A ．4250x y z +-+=B ．4250x y z ++-=C ．42110x y z +-+=D ．42110x y z ++-= 3．设(,)ln()2yf x y x x=+，则(1,1)y f =（ ） A ．0 B ．13 C ．12D ．24．若lim 0n n u →∞=，则级数1n n u ∞=∑（ ）A ．可能收敛，也可能发散B ．一定条件收敛C ．一定收敛D ．一定发散5．下列级数中发散的是（ ）A ．112n n ∞=∑ B ．11(1)n n ∞-=-∑ C ．n ∞= D ．n ∞= 二、填空题（本大题共5小题，每小题3分，共15分）1．微分方程"4'50y y y -+=的通解为______。

（今年不作要求）2．设有向量(4,3,0),(1,2,2)a b ==-，则2a b +=____________________。

3．设有向量(1,1,0),a b ==-，它们的夹角为θ，则c o s θ=____________________。

4．设x z y =，则dz =____________________。

5．设L 是圆周229x y +=（按逆时针方向绕行），则曲线积分2(22)(4)Lxy y dx x x dy -+-⎰的值为____________________。

三、计算题（本大题共7小题，每小题7分，共49分）1．已知arctan x z y =，求2,z z x x y∂∂∂∂∂。

河南理工大学 2010-2011 学年第 2 学期《工科数学分析》(下)试卷（A 卷）一、填空题（共28分，每小题4分）１．函数xyz z xy u -+=32在点()2,1,1处沿方向l （其方向角分别是00060,45,60）的方向导数 是 9/2 ．２．设0 < p < 1，计算级数()∑∞=--1121k k p p k =)20(,22<<-p pp3. 函数())sin(,22y x y x f +=在点)0,0(的泰勒公式（到二阶为止）为()()()2222,y x y x y x f +=++=ρρο４．函数()xx f 3=的幂级数展开式为∑∞=0!3ln n nn x n ．5.设()⎰-=22x xxy dy ex F ,则=')(x F ()⎰----+-223522x xxy x x dy ey ex e６．()⎰C ds x =()15532-，其中（C ）为抛物线x y =从点()0,0到点()1,1的一段弧。

7．微分方程()02='+''y y ，满足初始条件1,000='===x x y y 的特解为1ln y +=x 。

二、解答题（共50分，每小题10分）1、 设()v u ,Φ具有连续偏导数，函数()y x z ,由隐方程()bz cy az cx --Φ,=0确定，求yz b x z a∂∂+∂∂。

解：将隐方程两边全微分可得：()()()()()0,2121=-⋅Φ'+-⋅Φ'=-⋅Φ'+-⋅Φ'=--Φbdz cdy adz cdx bz cy d az cx d bz cy az cx d ………………………………………………3分 整理得：dy b a c dx b a c dz 212211Φ'+Φ'Φ'+Φ'+Φ'Φ'=……………………………………6分所以，212211,Φ'+Φ'Φ'=∂∂Φ'+Φ'Φ'=∂∂b a c y zb ac x z …………………………………………8分 y zb x z a ∂∂+∂∂=c b a c b b a c a =Φ'+Φ'Φ'+Φ'+Φ'Φ'212211,………………………………………10分2、 判定正项级数∑⎰∞=+1141n n dx x x的敛散性。

2010级高等数学（二）期末试题解答及评分标准A（本科少学时）一、选择题（本大题5个小题，每小题3分，共15分）1．22ln(23)4arccos(56)z x y x y =+++的定义域为（ D ）.Ａ．{(,)230}x y x y +>； Ｂ．22{(,)230561}x y x y x y +>+≤或； Ｃ．22{(,)561}x y x y +≤； Ｄ．22{(,)230561}x y x y x y +>+≤且.2．微分方程2220d yy dxω+=（ω是常数）的通解是函数（ Ｂ ）.Ａ．x y ωcos =； Ｂ．x C x C y ωωsin cos 21+=； Ｃ．x C ωsin 1； Ｄ．()ϕ+=x y 10sin .3．设有命题I ：函数(,)z f x y =在00(,)x y 处连续，另有命题II ：函数(,)z f x y =在00(,)x y 处的两个偏导数0000(,),(,)x y f x y f x y 存在，可以断定I 是II 的（ C ）.Ａ．充分条件 ； Ｂ．必要条件 ； Ｃ．既非充分也非必要条件 ； Ｄ．充分且必要条件.4．设区域D 由y x =、0y =及1x =所围城，令1DI d σ=⎰⎰、2DI xd σ=⎰⎰、23DI x d σ=⎰⎰、4DI xyd σ=⎰⎰，则1I 、2I 、3I 、4I 中值最大的是（ Ａ ）.Ａ．1I ； Ｂ．2I ； Ｃ．3I ； Ｄ．4I .5．设有三元方程1ln =+-xz e y z xy ，根据隐函数存在定理，存在点)1,1,0(的一个邻域，在此邻域内该方程（ D ）.A.只能确定一个具有连续偏导数的隐函数),(y x z z =；B.可确定两个具有连续偏导数的隐函数),(z y x x =和),(y x z z =；C.可确定两个具有连续偏导数的隐函数),(z x y y =和),(y x z z =；D.可确定两个具有连续偏导数的隐函数),(z y x x =和),(z x y y = .二、填空题（本大题5个小题，每小题3分，共15分）6．设22),(y x xy y x f -=+，则(,)f x y =y y y +-1)1(2 .7．设f 具有一阶连续偏导数(1)z f ≠，且(,,)z f x y z =，则dz =1x y zf dx f dy f +- .8.幂级数11(1)n n nn -∞=-∑的收敛域是11(,]22-（含端点敛散性）.9．设区域D 为环形域：2214x y ≤+≤，则22()Dx y d σ+=⎰⎰152π . 10．函数)ln(22z y x u ++=在点A )1,0,1(处沿点A 指向点B )2,2,3(-的方向导数为21.三、试解下列各题（本大题6个小题，每小题8分，共48分）11．求极限011cos()lim sin x y xy x xy →→-.解 200111()1cos()2lim lim sin x x y y xy xy x xy x xy →→→→-=⋅ （5分）12=. （8分） 12. 设sin 2arctan()z xy x y =+-，求(0,1)x z 和(0,1)y z .解 212cos 21()x z y xy x y =++-，5(0,1)2x z = （4分） 同理212cos 21()y z x xy x y =-+-，1(0,1)2yz =-. （8分） 13. 写出级数234234232432234ππππ⋅⋅⋅++++ 的通项，并判定其敛散性. 解 !nn n n u nπ= （3分）因为1lim1n n nu u e π+→∞=>，所以级数发散. （8分）14. 设f 具有二阶连续偏导数，且),(y xy f z =，求22z x∂∂，2z x y ∂∂∂.解 由于//11()z f xy yf x x∂∂=⋅=∂∂， （3分） 故//112/122)(f y f x y x z =∂∂=∂∂ （6分）//12//11/1//12//11/1/12)()(yf xyf f f xy y f y f yf y y x z ++=⎥⎦⎤⎢⎣⎡+∂∂⋅+=∂∂=∂∂∂（8分）15. 计算Dxdxdy ⎰⎰，其中D 由1xy =、y x =、2x =所围成.解 211xxDxdxdy dx xdy =⎰⎰⎰⎰ （4分）43=. （8分） 16. 已知向量a 、b 、c两两垂直，且1a = ，2b = ，3c = ，求a b c ++ .解 因为a 、b 、c两两垂直，所以0a b b c a c ⋅=⋅=⋅=（3分） 又2()()a b c a b c a b c ++=++⋅++2()a a b b c c a b b c a c =⋅+⋅+⋅+⋅+⋅+⋅22214a b c =++= （7分）从而a b c ++=（8分）四、试解下列各题（本大题2个小题，每小题6分，共12分）17.求函数22(,)8006004000033f x y x y x xy y =+----的极值点，并判定取得极大值还是极小值.解 8006x L x y =--，6006y L y x =--联立0x y L L ==得 120,80x y == （3分） 又在该点处6,1,6xx xy yy A L B L C L ==-==-==-20,0AC B A -><，故在该点处取得极大值. （6分）18. 设平面图形由抛物线)0(,2>-=a x ax y 及直线1,0,0===x x y 所围成，试确定a 的值,使此平面图形的面积最小.解曲线2y a xx =-与0y =的交点为1(0,0),(,0)a，故有所围面积为120()||A a ax x dx =-⎰112210()()a ax ax dx ax x dx =-+-⎰⎰（3分）令)()(1110112102/⎰⎰⎰⎰-++-=aa a a xdx xdx dx x a dx x a da d a A 031323=+-=a , 解得唯一驻点02)(,24//3>==aa A a 且,故当32=a 时所围成的平面图形面积最小. （6分）五、证明题（本大题2个小题，每小题5分，共10分）19．设(,)f x y 在有界闭区域D 上连续，证明：在D 上至少有一点(,)ξη，使：(,)(,)Df x y d f σξησ=⎰⎰.证明 因为(,)f x y 在有界闭区域D 上连续，所以(,)f x y 在有界闭区域D 上有最大值M 和最小值m ，即：(,)m f x y M ≤≤，从而 (,)Dm f x y d M σσσ≤≤⎰⎰，(,)Df x y d m M σσ≤≤⎰⎰ （3分）根据介值定理，在D 上至少有一点(,)ξη，使得：(,)(,)Df x y d f σξησ=⎰⎰即：(,)(,)Df x y d f σξησ=⎰⎰ . （5分）20．设)(22y x f y z -=，其中)(u f 为可导函数，验证211y zy z y x z x =∂∂+∂∂. 证明 由于)(u f 可导，故/22z xyf x f ∂=-∂, /2/22(2)2z f yf y f y f y f f ∂-⋅-+==∂ （3分） 从而 22/22/2211yzyf f y f f yf y z y x z x =++-=∂∂+∂∂. （5分）。

2009-2010第二学期工科数学分析期末试题解答(A 卷)一.1.11,65arccos(2分,2分)2.(1,2,7),4(2分,2分)3.25-,}52,51{-(2分,2分)4.∑∞=+--01)1(4)1(n nn n x ,∑∞=---+11)1(4)1(4ln n nn n x n (2分,2分)5.dy dx 2-,}2,1{-(2分,2分)6.x x y ln ,34ln(2分,2分)7.0，ππ324+，0，12+π(1分，1分，1分，1分)二.⎰=Ly dlx I μ2…………………….(2分)⎰+=15322)1(1dxx x μ……………………(6分)μμ35611532=+=⎰dx x x ……………………(9分)三.设V 在第一卦限部分为1V ⎰⎰⎰⎰⎰⎰==122486V VdVx dV x I ……………(3分)⎰⎰⎰---=yx xdzdy dx x 101010248……………..(6分)⎰⎰---=xdyy x dx x 10102)1(48………………..(7分)⎰-=1022)1(24dx x x …………………(8分)54=…………………(9分)四.令02==∂∂x xz，014=-=∂∂y yz………………(2分)解得0=x ,41=y ,得驻点)41,0(,………………..(3分)由122=+y x ，得221y x -=，代入目标函数得62+-=y y z )11(≤≤-y ………………..(4分)令012=-=y dydz，得21=y ，此时23±=x ，得两点)21,23(±………..(6分)当1±=y 时，0=x ，得两点)1,0(±………………..(7分)83941,0(=z ，42321,23(=±z ，8)1,0(=-z ，6)1,0(=z 8max =z ，839min =z ……………..(9分)五．由题意,有yXx Y ∂∂=∂∂……………………….(1分)λλλλλλλλ2121)()()33()(3)()()3()(3y x y x y y x y x y x x y y x ++--+=++--+---…….(3分)即033=--+y x y x λλ，3=λ…………………….(4分)1),()1,1(33)(3)(3),(C dy y x xy dx y x x y y x u y x ++-++-=⎰…………………….(6分)11313)(3)(3C dy y x x y dx y x xy x++-++-=⎰⎰……………………(8分)C y x yx ++-=2)(……………………(10分)注：没有加C 不扣分。

一、选择题每小题5分，共50分.⑥卷:1A ； 2B ； 3A ； 4C ； 5B ； 6D ； 7B ； 8C ； 9A ； 10B. ®卷：1D ；2D ；3A ； 4B ； 5C ； 6B ；7B ；8C ；9C ； 10D.G ）二、（微积分）（10分）求三重积分Jjj （X+y+z ）2dV,其中。

:f+y2+（z_i ）2G.Ω解原式=JJj （X2+j 2+z 2+2xy+2yz+2zr ）dVΩ=∫∫∫（x 2+y 2+z 2）dV （3分）Ω"力si110dp（7分） （10分）x=3+2tG ）二、（高数）（io 分）设直线。

：9=彳=平，直线L2：，y=ι+f .z =2+f （1）证明右与4平行.（2）求。

与4确定的平面方程.⑴证《的方向向量s ∣=（2,1,1）,取点M （1,2,3）∈L 1；（的方向向量4=（2,1」），取点M 2（3,l,2）∈L 2.向量陷%=（2,T,T ）与电不平行，所以∆1与4平行.（4分）iJk（2）所求平面的法向量W=S 1XM 1M 2=21 1=（0,4,-4）,（7分） 2-1-1 平面方程4（y-2）-4（z-3）=0,BP y-z+∖=0.（10分）G ）二、（工数）（10分）求微分方程丁〃+9-25=1的通解. 解特征方程r 2+r-2=0,特征根（=1,为=一2. 对应的齐次方程的通解Y （x ）=Ce+c 2e-2∖ （4分） 设原方程的特解/=AxeS 代入原方程，得（7分） A （x+2）e x +A （x+l ）e x -2Are r =e A ,得3A=1,BPA=-,y*=-xe r .（9分） 3,3=2信cos>∙sin^ = 2π.^1-c °s^5 I即2无+三+屯一2包-包=0∂ιΓ∂u∂v∂v∂u∂v⑥四、(10分)求曲线积分Jj(x)sinydx+(/(X)CoSy+πx)dy ,其中函数/(x)具有二阶连续导数，L 是圆周线(x-l)2+(y-π)2=l+π2上从点A(2,2π)沿逆时针方向到点0(0,0)的有向弧段. 解—=f(x)cosy+‰—=f(x)cosy.∂x ∂y方法1取从O(0,0)到Λ(2,2π)的有向线段OA:y=πx(0≤x≤2)92由格林公式，∫f ∖x)sinydr+(/(x)cos y+πx)dy=∫∫πdΛd>,=—(1+π2). 1.+OAD2又[f ,(x)Siny(Ir+(/(x)cosy+πx)dyOA =J ：(/'O)sinπx+π∙(∕(X)COSπx+πx))dx原方程的通解为 y = c 1 e r + c 2e -2v + - xe x .⑥三、(10分)通过卜二J 变换方程2』+孙栗+/票0. y = e∂x" ox∂y∂y 解 M = In Λ, V = In y ∂z ∂z 1—=—•—∂x ∂u X ∂z ∂z 1 ∂y ∂v y∂2z _ ∂2z 1 ∂z 1 ∂2z _ ∂2z 1 ∂2z _ ∂2z 1 ∂z 1 ∂x 2 ∂u 2 X 2 ∂u X 29∂x∂y ∂u∂v xy '∂y 2 ∂v 2 y 2 ∂v y 2z 1 ∂z 1 ‹∂u 2 X"∂2z 1 λ ∖∂u∂v xyr δ2z 1 ∂z 1 、力2 y 2∂v y ∖=0,2典一斗匹+典4 0, ‹∂u 2 ∂u J ∂u∂v (。

课程编号：MTH17004, MTH17006北京理工大学2010-2011学年第二学期工科数学分析期末试题（A 卷）班级_______________ 学号_________________ 姓名__________________(本试卷共6页, 十一个大题，试卷后面空白纸撕下作草稿纸)一. 填空题（每小题2分, 共10分）1. 已知3||=a ，26||=b ，72||=⨯b a，且a 与b 的夹角是钝角，则=⋅b a ______。

2. 设x yz ye y x u z ln 2++=，则=)1,1,1()grad (div u ______________。

3. 已知向量c b a,,不共面，但向量c a c b b a +++λ,,2共面，则=λ _________。

4. 设L 是曲线1,,3===z t y t x 上从)1,0,0(A 到)1,8,2(B 的一段，若将⎰++=Lzdz ydy dx x I 2化成第一类曲线积分，则有=I _________________________。

5. 变量替换x y v x u ==,可将微分方程z yzy x z x =∂∂+∂∂化成 ________________________。

二. (9分) 交换积分次序并计算⎰⎰=yyxdx xe dy I 1。

三. (9分) 求函数y y y x y x f -+=2221),(的极值和极值点。

四. (9分)设方程523=+-y xz z 确定函数),(y x z z =，求yx z∂∂∂2。

五. (9分) 在曲面xy z =上求一点，使曲面在此点处的切平面垂直于直线13211zy x =-=+，并写出切平面方程。

六. (8分) 证明方程0ln 1=+-xdy x dx yx y y 是全微分方程，并求出通解。

七. (10分) 求幂级数∑∞=-+11)1(n n x n n 的收敛域及和函数。

2009-2010学年第二学期高等数学(2)期末试卷及其答案2009 至 2010 学年度第 2 期 高等数学（下）课程考试试题册A试题使用对象 ： 2009 级 理科各 专业(本科)命题人： 考试用时 120 分钟 答题方式采用：闭卷说明：1．答题请使用黑色或蓝色的钢笔、圆珠笔在答题纸上书写工整．2．考生应在答题纸上答题，在此卷上答题作废．一．填空题（本题共15 分，共5 小题，每题 3 分） 1．已知(2,1,),(1,2,4)a mb ==r r，则当m = 时，向量a b⊥r r ．2．(,)(2,0)sin()limx y xy y →= ．3．设区域D 为22y x +≤x 2，则二重积分Dd σ=⎰⎰ ．4．函数(,),(,)P x y Q x y 在包含L 的单连通区域G 内具有一阶连续偏导数，如果曲线积分(,)(,)LP x y dx Q x y dy+⎰与路径无关，则(,),(,)P x y Q x y 应满足条件 ．5． 当p 时，级数211pn n +∞=∑收敛．二．选择题（本题共15分，共5小题，每题3 分）1．直线221:314x y z L -+-==-与平面:6287x y z π-+=的位置关系是 ．A ．直线L 与平面π平行；B ．直线L 与平面π垂直；C ．直线L 在平面π上；D ．直线L 与平面π只有一个交点，但不垂直．2． 函数(,)f x y 在点(,)x y 可微分是(,)f x y 在该点连续的（ ）．A ．充分条件； B. 必要条件； C. 充分必要条件； D. 既非充分也不必要条件 3．改变积分次序，则100(,)y dy f x y dx⎰⎰．A ．1(,)xdx f x y dy ⎰⎰； B ．11(,)dx f x y dy ⎰⎰；C ．11(,)x dx f x y dy ⎰⎰；D ．11(,)xdx f x y dy ⎰⎰4．下列级数中收敛的是 ． A ．∑∞=+1884n n nn B ．∑∞=-1884n n nn C ．∑∞=+1824n n nnD ．1248n nn n ∞=⨯∑．5．级数1...-++A. 发散B. 绝对收敛C. 条件收敛D. 既绝对收敛又条件收敛 三． 求解下列各题（本题共70分，共9小题，1~2每题7 分，3~9每题8 分）． 1．设sin uz e v=，而u xy =，v x y =- 求xz ．2．设22(,tan())u f x y xy =-，其中f 具有一阶连续偏导数，求yz ． 3．求旋转抛物面221z x y =+-在点(2,1,4)处的切平面方程及法线方程． 4．计算 22Dx d y σ⎰⎰，其中D 是由直线y x =．2x =和曲线1xy =所围成的闭区域． 5．计算L⎰，其中L 是圆周222x y a +=（0a >）．6．计算22()(sin )Lxy dx x y dy--+⎰，其中L 是上半圆周y =x 轴所围区域的边界，沿逆时针方向．7．将函数1()3f x x =+展开成(3)x -的幂级数． 8．计算曲面积分xydydz yzdzdx xzdxdy ∑++⎰⎰，其中∑为1x y z ++=，0,x =y =，0z =所围立体的外侧．9．求抛物面22z xy =+到平面10x y z +++=的最短距离．2009 至 2010 学年度第 2 期高等数学（下）课程试题A 参考答案试题使用对象： 2009 级 理科各专业(本科) 向瑞银一．填空题（本题共15 分，共5 小题，每题 3 分） 1. 1-； 2. 2； 3. π； 4.y P ∂∂=xQ ∂∂； 5.12p >二．选择题（本题共15分，共5小题，每题3 分） 1．B ； 2．A ； ３．D ； ４．C ； ５．C 三． 求解下列各题（本题共70分，共9小题，1~2每题7 分，3~9每题8 分）．1．z z u z vx u x v x∂∂∂∂∂=+∂∂∂∂∂……4分sin cos u u ye v e v=+(sin()cos())xy e y x y x y =-+-……7分 2．2212()(tan())y y uf x y f xy y∂''''=⋅-+∂ ……4分2122sec ()()yyf f xy xy '''=-+2122sec ()yf xf xy ''=-+……7分 3． 令22(,,)1F x y z xy z=+--，则法向量(2,2,1)n x y =-r，(2,1,4)(4,2,1)n=-r ……3分在点(2,1,4)处的切平面方程为 4(2)2(1)(4)0x y z -+---=．即4260x y z +--=． (6)分法线方程为214421x y z ---==-． ……8分 4．22Dx d yσ⎰⎰22121xxx dx dy y=⎰⎰……4分221/11()x xx dxy=-⎰……6分231()x x dx =-⎰322111()42x x =-94=……8分5．令cos ,sin x a y a θθ==，则sin ,cos x a y a θθ''=-=，ds θ=ad θ= ……3分20a Le ad πθ=⎰⎰ ……6分＝2aae π ……8分6．2P xy=-，1P y ∂=-∂ ，2(sin )Q x y =-+，1Q x∂=-∂ ， ……4分()0DDQ PI dxdy dxdy x y∂∂=-=∂∂⎰⎰⎰⎰ ……6分=……8分 7．1136(3)x x =++-113616x =-+ ……4分 当316x -<，即 39x -<<时，13x +013()66nn x +∞=-=-∑ ……8分8． ⎰⎰∑++zxdxdy yzdzdx xydydz=()x y z dxdydz Ω++⎰⎰⎰……4分 =1110()xx ydx dy x y z dz---++⎰⎰⎰……6分81=……8分9．设抛物面一点(,,)x y z ，它到平面的距离为1d x y z =+++满足条件220x y z +-= ……3分 拉格朗日函数为222(1)()3x y z L x y z λ+++=++- ……5分2(1)203x x y z L x λ+++=+=，2(1)203yx y z Ly λ+++=+=2(1)3z x y z L λ+++=-=，220Lx y z λ=+-=解方程组得，12x y ==-，12z =． 由问题本身知最短距离存在，所以最短距离为0.5,0.5,0.5)d --=6=……8分。