第4章 几种常见的概率分布

第四章 几种常见的概率分布

第一节 二项分布 一、二项总体 1. 定义

由非此即彼事件构成的总体，叫做二项总体(binomial population) 孵n 枚种蛋的出雏数、n 头病畜治疗后的治愈数、n 尾鱼苗的成活数等 2. 表示方法

通常给“此”事件以变量“1”，具概率φ ，给“彼”事件以变量“0”，具概率1- φ 。二项总体又称0、1总体。

● 在n 重贝努利试验中，事件A 可能发生0，1，2，…，n 次，现在我们来求事件A 恰

好发生k(0≤k ≤n)次的概率Pn(k)。 ● 先取n=4，k=2来讨论。在4次试验中，事件A 发生2次的方式有 2

4C

● 其中Ak(k=1,2,3,4)表示事件A 在第k 次试验发生；

k

A (k=1,2,3,4)表示事件A 在

第k 次试验不发生。由于试验是独立的，按概率的乘法法则，于是有

● 由于以上各种方式中，任何二种方式都是互不相容的，按概率的加法法则，在4 次试

验中，事件A 恰好发生2次的概率为

● 一般，在n 重贝努利试验中，事件A 恰好发生k(0≤k ≤n)次的概率为

k n k k

n n q p C (k)P -=n

k ,,2,1,0 =

二、二项分布

如果我们每次独立抽取二项总体的n 个个体，则所得变量X 将可能有0，1，…n ，共n+1种变量有它各自的概率而组成一个分布。这个分布就叫做二项概率分布，或简称二项分布（binomial distribution) 由此得到计算二项分布任何一项概率的通式为：p(x) =Cnx φ x(1- φ)n-x

二项分布是一种离散型随机变量的概率分布

性质

1)1(0=-∑=-n

x x n x x n C ??

∑=--=

≤m

x x

n x x n C m x P 0)1()(??

∑=--=

≥n

m

x x

n x x n

C

m x P )1()(??

∑=-=

≤≤=≤≤2

1

)()(2121m m x x

n x x n

n q p C

m k m p m x m P

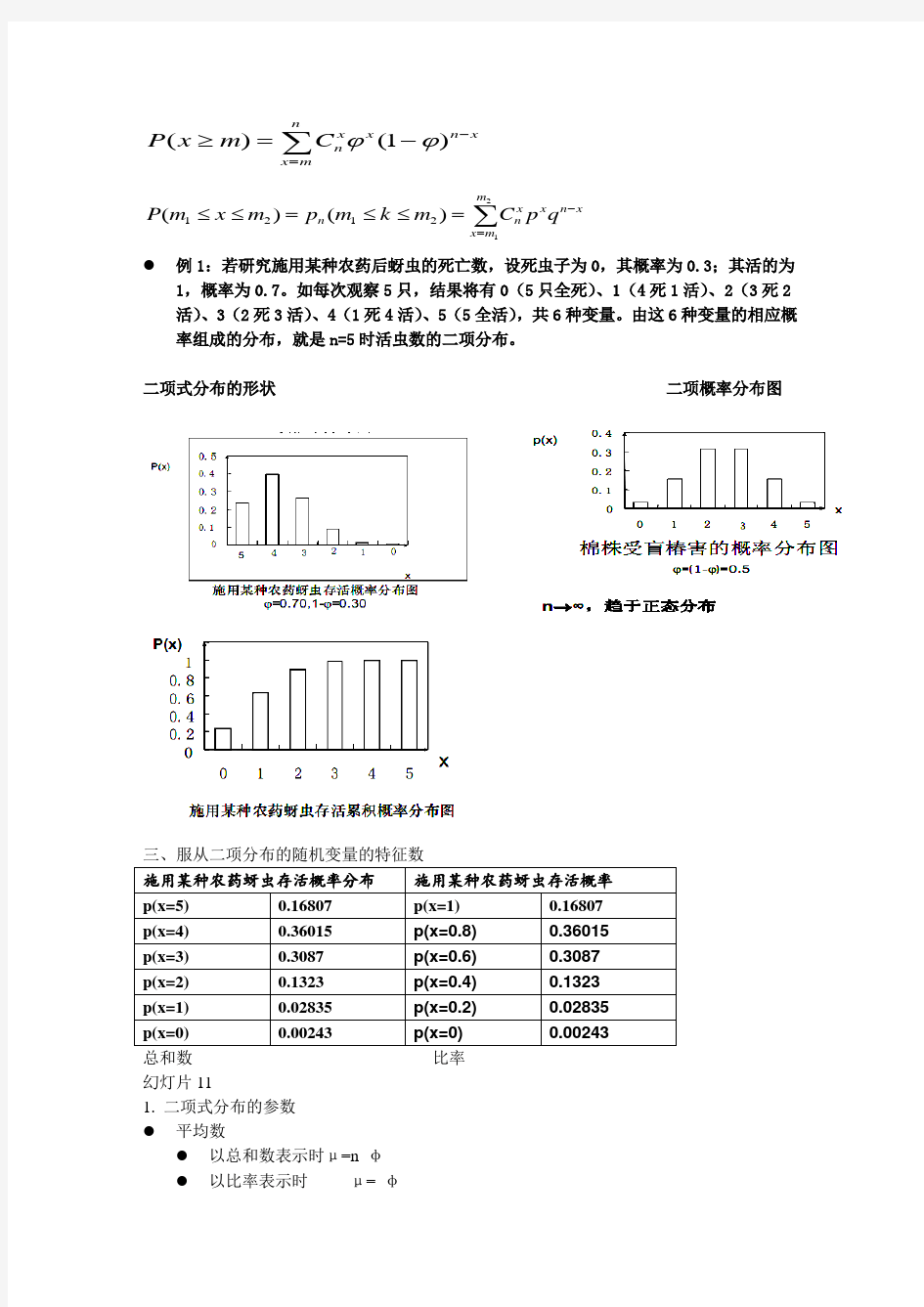
● 例1：若研究施用某种农药后蚜虫的死亡数，设死虫子为0，其概率为0.3；其活的为

1，概率为0.7。如每次观察5只，结果将有0（5只全死）、1（4死1活）、2（3死2活）、3（2死3活）、4（1死4活）、5（5全活），共6种变量。由这6种变量的相应概率组成的分布，就是n=5时活虫数的二项分布。

二项式分布的形状 二项概率分布图

三、服从二项分布的随机变量的特征数 施用某种农药蚜虫存活概率分布 施用某种农药蚜虫存活概率 p(x=5) 0.16807 p(x=1) 0.16807 p(x=4) 0.36015 p(x=0.8) 0.36015 p(x=3) 0.3087 p(x=0.6) 0.3087 p(x=2) 0.1323 p(x=0.4) 0.1323 p(x=1) 0.02835 p(x=0.2) 0.02835 p(x=0)

0.00243

p(x=0)

0.00243

总和数 比率 幻灯片11

1. 二项式分布的参数 ● 平均数

● 以总和数表示时μ=n φ ● 以比率表示时 μ= φ

●方差

●以总和数表示时σ2=n φ(1- φ)

●以比率表示时σ2= φ(1- φ)/n

2. 证明平均数、方差

3. 实例

总和数

比率

4.二项总体分布及二项分布参数比较

5. 二项分布偏斜度和峭度

四、二项分布应用实例

● 小鼠毛型受一对等位基因控制，Wv 正常直毛对wv 波浪毛为显性。以杂合基因型Wvwv

的小鼠为父本，与纯合基因型wvwv 的小鼠为母本杂交。杂交后代毛型分布符合二项分布。实验只选每窝8只的，多于或少于8

只的都淘汰，预期每窝小鼠毛型表现。

第二节 泊松分布

● 描述在一指定时间范围内或在指定的面积或体积内某一事件出现的个体数的分布 ● 泊松分布是一种离散型随机变量的概率分布

实例

调查某种猪场闭锁育种群仔猪畸形数，共记录200窝，畸形仔猪数的分布情况如下表所示。试判断畸形仔猪数是否服从泊松分布。

畸形仔猪数统计分布

解：根据泊松分布的平均数与方差相等这一特征，若畸形仔猪数服从泊松分布，则由观察数

据计算的平均数和方差就近于相等。样本均数和方差S2计算结果如下：

可以认为畸形仔猪数服从泊松分布。

幻灯片24

麦田内，平均每10 m2有1株杂草，现在要问每100m2麦田中，有0株杂草，有1株

杂草，有2株杂草，…的概率是多少？

第三节正态分布

两头少，中间多，两侧对称

一、正态分布的定义

若连续型随机变量x 的概率分布密度函数为

2

22)(21

)(σμπ

σ--

=

x e

x f -∞<μ<∞， σ> 0

其中μ为平均数，σ2为方差，则称随机变量x 服从正态分布(normal distribution)， 记为x ～N(μ,σ2)。

随机变量X 的落入任意区间（a ，b ）概率：

相应的概率分布函数为

?

∞

---

=

x

x dx

e

x F 2

22)(21

)(σμπ

σ

二、正态分布曲线

1．正态分布密度函数的图像

以x=μ为对称轴作对称分布，曲线有个最高点，以此点的横坐标为中心，向两边单调下降。 连续型随机变量的概率分布 2.

正态分布的特征

(1) 正态分布密度曲线是单峰、对称的悬钟形曲线，对称轴为x=μ；

(2) f(x)在x=μ处达到极大，极大值 ； (3) f(x)是非负函数，以x 轴为渐近线，分布从-∞至+∞；

(4) 曲线在x=μ±σ处各有一个拐点，即曲线在(-∞,μ-σ)和(μ+σ,+∞) 区间上是下凸的，在[μ-σ,μ+σ]区间内是上凸的；

(5) 正态分布有两个参数，即平均数μ和标准差σ。μ是位置参数。 当σ恒定时，μ愈大，则曲线沿x 轴愈向右移动；反之，μ愈小，曲线沿x 轴愈向左移动。σ是变异度参数，如下图所示。当μ恒定时，σ愈大，表示x 的取值愈分散， 曲线愈“胖”；σ愈小，x 的取值愈集中在μ附近，曲线愈“瘦”。

正态分布密度曲线

σ相同而μ不同的三个正态分布

μ相同而σ不同的三个正态分布

(6) 分布密度曲线与横轴所夹的面积为1，即：

1

21

)(2

2

2)(==+∞<<-∞--∞

+∞-?dx

e x P x σμπ

σ

三、标准正态分布

1. 标准正态分布定义

μ=0,σ2=1的正态分布为标准正态分布(standard normal distribution)。标准正态分布的概率密度函数及分布函数分别记作φ (u)和Φ(u)

2

221)(u e u -=

π

?

du

e u u

u ?∞

--=

22

121)(π

φ

随机变量u 服从标准正态分布，记作u ～N(0，1)

2. 标准正态分布曲线

标准正态分布密度函数曲线 分布函数曲线

00.10.20.30.40.5-3

-2

-1

-0

1

2

3

● x=0时，φ(x) 达到最大值 (1) 关于点（0，0.5）对称，该点也 ●

是它的拐点 ● (2)x 取值离原点越远，φ (x) (2) 曲线以y = 0和y = 1为渐近线； ● (3)关于y 轴对称，即φ(x)= φ (- x) (3) Ф(1.960)－Ф(－1.960) = 0.95

● (4)在x=1有两个拐点 (4) Ф(2.576)－Ф(－2.576) = 0.99 (5)曲线与x 轴间所夹面积为1 ● 由于正态分布的重要性，它的密度函数及分布函数的数值都已被编成表格备查(附表2)。 ● 注意的是多数表中只给出x ≥0的φ (x)和Ф(x)值，这是因为由它们的对称性，有：

)(1)(),()(x x x x Φ-=-Φ=-??

● 因此可容易地算出x 任意取值时φ (x)和Ф(x)的值。 3. 标准正态分布的概率计算

设u 服从标准正态分布，则u 在[u1,u2]内取值的概率为：

00.20.40.60.81-3

-2

-1

-0

1

2

3

du

e

du e

du e

u u u P u u u u u u u ?

?

?

∞

--∞

----

=

=

<≤1

22

22

1

22

12

12

121212121

)(π

π

π

＝Φ(u2)－Φ(u1)

常用关系式:

P(0≤u ≤ u1)＝Φ(u1)-0.5 P(u ≥u1) =Φ(-u1) P(｜u ｜≥u1)=2Φ(-u1)

P(｜u ｜≤ u1)=1-2Φ(-u1) P(u1≤u ≤ u2)＝Φ(u2)-Φ(u1) 幻灯片35

例：已知u ～N(0，1)，试求：

(1) P(u ＜-1.64)＝? (2) P (u ≥2.58)=?

(3) P (｜u ｜≥2.56)=? (4) P(0.34≤u ＜1.53) =? 解：

(1) P(u ＜-1.64)=0.05050

(2) P (u ≥2.58)=Φ(-2.58)=0.00494 (3) P (｜u ｜≥2.56)=2Φ(-2.56)

=2×0.00523=0.01046 (4) P (0.34≤u ＜1.53)=Φ(1.53)-Φ(0.34)

=0.93699-0.63307=0.30392

幻灯片36

4. 一般正态分布的概率计算

若随机变量 x 服从正态分布N(μ,σ2)，则x 的取值落在任意区间[x1,x2]的概率，记作P(x1≤x ≤ x2)，等于下图中阴影部分曲边梯形面积。即：

dx

e

x x x P x x

x ?--

=

<≤2

1

2

22)(2121

)(σμπ

σ

对于服从一般正态分布的随机变量X ，需先把它标准化，然后再查表。标准化方法如下：

正态分布的概率

设X ～N(μ，σ2)，令，

σ

μ

-=

X U

则U ~ N(0, 1)，即

)

(

)()(000σ

μ

σ

μ

-Φ=-<

=

这样，只要先计算U 的值，就可以从标准正态分布表中查出所需要的数值了。 例： 已知小麦穗长服从N （9.978, 1.4412），求下列概率：（1）穗长<6.536cm,（2）穗长>12.128cm,（3）穗长在8.573cm 与9.978cm 之间。 5. 几对常见的区间与其相对应的面积或概率

面积或概率 区间

μ± 1σ =0.6827 μ± 2σ =0.9545 μ± 3σ =0.9973 μ± 1.960σ =0.9500 μ± 2.576σ =0.9900

6. 正态分布的单双侧临界值 ● 上侧临界值P(U>

α

u )= α ，下侧临界值P (U <-

α

u )= α (附表3 上侧临界值)

● 若将一定曲线下面积α，平分到两侧尾区，则每侧曲线下面积为α/2, 即P(

2

α

U U > )=

α, 这时的 2

α

U U > 称为α的双侧临界值。

06811

.0)49.1()441

.1978

.9128.12()128.12(00842

.0)39.2()441

.1978

.9536.6()536.6(=-Φ=--Φ=>=-Φ=-Φ=

.015866.050000.0)1()0()

441

.1978

.9537.8()441.1978.9978.9()978.9537.8(=-=-Φ-Φ=-Φ--Φ=<

的值。页）给出了（附表。上侧临界值的称为αααu u 256 3

。

下侧临界值的称为。；同时，我们有因此，ααααααu u U P u U P -=-<=> )()(

。

双侧，也可以记为双侧临界值的称为那么平均分配到两侧，即如果将面积下侧。全部放在曲线的上侧或的单侧临界值是将面积)(,)|(|2/2/ααααααααu u u U P =>

，已知面积为α

注意：α的双侧临界值=α/2的上侧临界值 幻灯片43

● 例如，x 落在(μ-1.960σ,μ+1.960σ)之外的α为0.05，而α/2为0.025。即 ● P(x ＜μ-1.960σ)= P(x ＞μ+1.960σ)=0.025

● 例如：x 落在(μ-2.576σ,μ+2.576σ)之外的α为0.01，而α/2为0.005，即

，已知

面积为α，已知

面积为α

P(x ＜μ-2.576σ)= P(x ＞μ+2.576σ)=0.005

界值和双侧临界值。的上侧临界值、下侧临＝和例三，求01.005.0αα=

;645.105.0)1(3

05.0查表时，上侧临界值解：

==u α

96

.1)( 3

025.005.0查表＝双侧双侧临界值=u u

;

326.201.0)2(3

01.0查表时，上侧临界值==u α

;

326.201.0-=-u 所以，下侧临界值

576

.2)( 3

005.001.0查表＝双侧双侧临界值=u u

例如，已知u ～N(0,1)试求：

(1) P(u ＜-α

u )+P(u ≥

α

u )=0.10的

α

u

(2) P(-

α

u ≤u ＜αu ﹚=0.86的

α

u

解：

（1) P(u ＜-

α

u )= P(u ≥

α

u )=0.10/2=0.05=α

由附表3查得：

05

.0u =1.645

(2) P (- αu ≤u ＜ α

u )=0.86 ，α=(1- P (-

α

u ≤u ＜

α

u ))/2=

（1-0.86）/2=0.14/2=0.07 由附表3查得：

07

.0u =1.476

例如：已知猪血红蛋白含量x 服从正态分布

X~ N(12.86，1.332)，

若P(x ＜L1) =0.03, P(x ≥L2)=0.03，求L1, L2 解：由题意可知

03

.0)()33.186

.1233.186.12(

)(11=-<=-<-=<αu u P L x P L x P

=

≥)(2L x P 03

.0)()33.186

.1233.186.12(

2=≥=-≥-αu u P L x P

由附表3查得：

03

.0u =1.881,所以

(L1-12.86)/1.33=-1.881，

(L2-12.86)/1.33=1.881 即 L1 ≈10.36，L2 ≈15.36。 7.中心极限定理（独立同分布）

● 研究随机变量和的极限分布是正态分布的一类定理，称为中心极限定理。

● 假设被研究的随机变量X ，可以表示为许多相互独立的随机变量Xi 的和。如果Xi 的数

量很大，而且每一个Xi 对于X 所起的作用又很小，则X 可以被认为服从或近似地服从正态分布。 设随机变量序列

,,,,21n X X X

独立于一分布内, 且有期望和方差：

,2,1,0)(,)(2=>==k X D X E k k σμ

则对于任意实数 x,

则 Y n 为∑=n

k k

X 1

的标准化随机变量。

())

(lim x x Y P n n Φ=≤∞

→

即 n 足够大时，Y n 的分布函数近似于标准正态随机变量的分布函数

∑=n

k k X 1

μ

σn Y n n +=

),(2σμn n N 近似服从

)1,0(~N Y n 近似

σ

μ

n n X Y n

k k

n -=

∑=1

记

?∑∞--=∞→=?

????

? ??≤-x

t n k k n dt

e

x n n X P 2

1221lim πσμ

已知μ、σ，不论总体是否呈正态分布，

n 充分大，其平均数X 服从N(μ,σ2/n)

n

X n U n

i i σ

μ-=

∑=1

1

例：炮火轰击敌方防御工事 100 次, 每次轰击命中的炮弹数服从同一分布, 其数学期望为 2 , 方差为1.52. 若各次轰击命中的炮弹数是相互独立的, 求100 次轰击： (1) 至少命中180发炮弹的概率;

(2) 命中的炮弹数不到200发的概率。 幻灯片54

解 设 X k 表示第 k 次轰击命中的炮弹数

100,,2,1,5.1)(,2)(2 ===k X D X E k k

设 X 表示100次轰击命中的炮弹数, 则

,

225)(,200)(,100

1

===∑=X D X E X X k k

由中心极限定理, 有

??? ??--≈≥152001801)180(ΦX P

100

21,,,X X X 相互独立，

)

225,200(~N X

近似

)

(x Φ=

(1)

91

.0)3.1()3.1(1==--=ΦΦ

??? ??--??? ??-≈<≤15200015200200)2000(ΦΦX P

(2)

5

.0)33.13()0(=--=ΦΦ

常用的概率分布类型其特征

常用的概率分布类型及其特征 3．1 二点分布和均匀分布 1、两点分布 许多随机事件只有两个结果。如抽检产品的结果合格或不合格；产品或者可靠的工作，或者失效。描述这类随机事件变量只有两个取值，一般取0和1。它服从的分布称两点分布。 其概率分布为： 其中 Pk=P（X=Xk），表示X取Xk值的概率： 0≤P≤1。 X的期望 E（X）=P X的方差 D（X）=P（1—P） 2、均匀分布 如果连续随机变量X的概率密度函数f（x）在有限的区间[a，b]上等于一

个常数，则X服从的分布为均匀分布。 其概率分布为： X的期望 E（X）=（a+b）/2 X的方差 D（X）=（b-a）2/12 3．2 抽样检验中应用的分布 3．2．1 超几何分布 假设有一批产品，总数为N，其中不合格数为d，从这批产品中随机地抽出n件作为被检样品，样品中的不合格数X服从的分布称超几何分布。 X的分布概率为： X=0，1，…… X的期望 E（X）=nd/N

X的方差 D（X）=（（nd/N）（（N-d）/N）（（N-n）/N））（1/2）3．2．2 二项分布 超几何分布的概率公式可以写成阶乘的形式，共有9个阶乘，因而计算起来十分繁琐。二项分布就可以看成是超几何分布的一个简化。 假设有一批产品，不合格品率为P，从这批产品中随机地抽出n件作为被检样品，其中不合格品数X服从的分布为二项分布。 X的概率分布为： 0

几种常见的概率分布复习过程

几种常见的概率分布 一、 离散型概率分布 1. 二项分布 n 次独立的贝努利实验，其实验结果的分布（一种结果出现x 次的概率是多少的分布）即为二项分布 应用二项分布的重要条件是：每一种实验结果在每次实验中都有恒定的概率，各实验之间是重复独立的 平均数： (Y)np X E μ== 方差与标准差：2(1)X np P σ=- ;X σ=特例：（0-1）分布 若随机变量X 的分布律为 1(x k)p (1p)k k p -==- k=0,1；0

复抽样，抽样成功的次数X 的概率分布服从超几何分布，如福利彩票 二、 连续型概率分布 1. 均匀分布 若随机变量X 具有概率密度函数 (x)f = 则称X 在区间（a ，b ）上服从均匀分布，记为X ~ U(a ，b) 在区间（a ，b ）上服从均匀分布的随机变量X 的分布函数为 0F(x),1 x a x a a x b b a b x ? 是常数， 则称X 服从以λ 为参数的指数分布，记作~()X E λ ，X 的分布函数为 1,0(x)0,0 x e x F x λ-?-≥=?

第四章常用概率分布学习指导(定)详解

第四章 常用概率分布 [教学要求] 了解：质量控制的意义、原理和方法 熟悉：三个常用概率分布的特征。 掌握：掌握三个常用概率分布的概念；二项分布及Poisson 分布的概率 函数与累计概率、正态分布的分布函数的计算方法；医学参考值的计算。 [重点难点] 第一节 二项分布 一、二项分布的概念与特征 基本概念：如果每个观察对象阳性结果的发生概率均为 ，阴性结果的发生概率 均为（1－π）；而且各个观察对象的结果是相互独立的，那么，重复观察n 个人，发生阳性结果的人数X 的概率分布为二项分布，记作B （n ,π）。 二项分布的概率函数： X n X X n C X P --=)1()(ππ 二项分布的特征： 二项分布图的形态取决于与n ，高峰在=n 处。当接近0.5时，图形是对称的；离0.5愈远，对称性愈差，但随着n 的增大，分布趋于对称。 二项分布的总体均数为 πμn = 方差为 )1(2ππσ-=n 标准差为 )1(ππσ-=n 如果将出现阳性结果的频率记为 n X p = 则p 的总体均数为 πμ=p 标准差为 二、二项分布的应用 二项分布出现阳性的次数至多为k 次的概率为 n p ) 1(ππσ-=

∑∑==-== ≤k X k X X X e X P k X P 0 ! )()(λλ 出现阳性的次数至少为k 次的概率为 第二节 Poisson 分布的概念与特征 一、Poisson 分布的概念与特征 基本概念：Poisson 分布可以看作是每个观察对象阳性结果的发生概率 很小， 而观察例数n 很大时的二项分布。除二项分布的三个基本条件以外，Poisson 分布还要求 接近于0。有些情况 和n 都难以确定，只能以观察单位（时间、 空间、面积等）内某种稀有事件的发生数X 来近似。 Poisson 分布的概率函数： 式中，πλn =为Poisson 分布的总体均数，X 为观察单位内某稀有事件的发生次数，e 为自然对数的底，λ为常数，约等于2.71828。 Poisson 分布的特征 Poisson 分布当总体均数λ值小于5时为偏峰，λ愈小分布愈偏，随着λ增大，分布趋向对称。 Poisson 分布的总体均数与总体方差相等, 均为λ，且Poisson 分布的观察结果具有可加性。 特点：凡个体有传染性、聚集性，均不能视为二项分布或Poisson 分布。 三、Poisson 分布的应用 如果某稀有事件发生次数的总体均数为λ，那么发生次数至多为k 次的概率为 发生次数至少为k 次的概率为 ! )(X e X P X λλ -= ∑∑==---= = ≤k X k X X n X X n X n X P k X P 0 0)1()! (!! )()(ππ∑∑ ==---== ≥n k X n k X X n X X n X n X P k X P )1()! (!! )()(ππ

16种常见概率分布概率密度函数、意义及其应用

目录 1. 均匀分布 (1) 2. 正态分布（高斯分布） (2) 3. 指数分布 (2) 4. Beta分布（：分布） (2) 5. Gamm 分布 (3) 6. 倒Gamm分布 (4) 7. 威布尔分布（Weibull分布、韦伯分布、韦布尔分布） (5) 8. Pareto 分布 (6) 9. Cauchy分布（柯西分布、柯西-洛伦兹分布） (7) 2 10. 分布（卡方分布） (7) 8 11. t分布................................................ 9 12. F分布 ............................................... 10 13. 二项分布............................................ 10 14. 泊松分布（Poisson 分布）............................. 11 15. 对数正态分布........................................

1. 均匀分布 均匀分布X ~U（a,b）是无信息的，可作为无信息变量的先验分布。

2. 正态分布（高斯分布） 当影响一个变量的因素众多，且影响微弱、都不占据主导地位时，这个变量 很可能服从正态分布，记作 X~N （」f 2）。正态分布为方差已知的正态分布 N （*2）的参数」的共轭先验分布。 1 空 f （x ）： —— e 2- J2 兀 o' E(X)， Var(X) _ c 2 3. 指数分布 指数分布X ~Exp （ ）是指要等到一个随机事件发生，需要经历多久时间。其 中，.0为尺度参数。指数分布的无记忆性： Plx s t|X = P{X t}。 f （X ）二 y o i E(X) 一 4. Beta 分布（一：分布） f （X ）二 E(X) Var(X)= (b-a)2 12 Var(X)二 1 ~2

考试练习题常用概率分布教学提纲

考试练习题常用概率 分布

第四章 选择题： 1．二项分布的概率分布图在 条件下为对称图形。 A ．n > 50 B ．π=0.5 C ．n π=1 D ．π=1 E ．n π> 5 2．满足 时，二项分布B （n,π）近似正态分布。 A ．n π和n （1－π）均大于等于5 B ．n π或n （1－π）大于等于5 C ．n π足够大 D ．n > 50 E ．π足够大 3. 的均数等于方差。 A ．正态分布 B ．二项分布 C ．对称分布 D ．Poisson 分布 E ．以上均不对 4．标准正态典线下，中间95%的面积所对应的横轴范围是 。 A ．－∞到+1.96 B ．－1.96到+1.96 C ．－∞到+2.58 D ．－2.58到+2.58 E ．－1.64到+1.64 5．服从二项分布的随机变量的总体均数为 。 A ．n （1－π） B ．（n －1）π C ．n π（1－π） D ．n π 6．服从二项分布的随机变量的总体标准差为 。 A . B . （1-π）（1-π）（ -）π1 C . D . π（1-π）（π 7.设X 1,X 2分别服从以λ1,λ2为均数的Poisson 分布,且X 1与X 2独立,则X 1+X 2服从以 为方差的Poisson 分布。 A . B .λ2λ12+2λ 2λ1+ C . D . 2λ2λ1+（） 2λ2λ1+（） E .λ2λ12+2 8．满足 时，Poisson 分布Ⅱ（λ）近似正态分布。

A．λ无限大 B．λ>20 C．λ=1 D．λ=0 E．λ=0.5 9．满足时，二项分布B（n，π）近似Poisson分布。 A．n很大且π接近0 B．n→∞ C．nπ或n（1－π）大于等于5 D．n很大且π接近0.5 E．π接近0.5 10．关于泊松分布，错误的是。 A．当二项分布的n很大而π很小时，可用泊松分布近似二项分布 B．泊松分布均数λ唯一确定 C．泊松分布的均数越大，越接近正态分布 D．泊松分布的均数与标准差相等 E．如果X1和X2分别服从均数为λ1和λ2的泊松分布，且相互独立。则 X1+X2服从均数为λ1+λ2的泊松分布。 11．以下分布中，均数等于方差的分布是。 A．正态分布 B．标准正态分布 C．二项分布 D．Poisson分布 E．t 分布 12．随机变量X服从正态分布N（μ1，σ12），Y服从正态分布N（μ2，σ 2），X与Y独立，则X－Y服从。 2 A．N（μ1+μ2，σ12－σ22） B．N（μ1－μ2，σ12－σ22） C．N（μ1－μ2，σ12+σ22） D．N（0，σ12+σ22） E．以上均不对 13．下列叙述中，错误的是。 A．二项分布中两个可能结果出现的概率之和为1 B．泊松分布只有1个参数λ C．正态曲线下的面积之和为1

常用分布概率计算的Excel应用

上机实习常用分布概率计算的Excel应用利用Excel中的统计函数工具，可以计算二项分布、泊松分布、正态分布等常用概率分布的概率值、累积（分布）概率等。这里我们主要介绍如何用Excel来计算二项分布的概率值与累积概率，其他常用分布的概率计算等处理与此类似。 §3.1 二项分布的概率计算 一、二项分布的（累积）概率值计算 用Excel来计算二项分布的概率值P n(k)、累积概率F n(k)，需要用BINOMDIST函数，其格式为： BINOMDIST (number_s，trials, probability_s, cumulative) 其中 number_s：试验成功的次数k； trials：独立试验的总次数n； probability_s：一次试验中成功的概率p； cumulative：为一逻辑值，若取0或FALSE时，计算概率值P n(k)；若取1 或TRUE时，则计算累积概率F n(k)，。 即对二项分布B(n,p)的概率值P n(k)和累积概率F n(k)，有 P n(k)=BINOMDIST(k,n,p,0)；F n(k)= BINOMDIST(k,n,p,1) 现结合下列机床维修问题的概率计算来稀疏现象（小概率事件）发生次数说明计算二项分布概率的具体步骤。 例3.1某车间有各自独立运行的机床若干台，设每台机床发生故障的概率为0.01，每台机床的故障需要一名维修工来排除，试求在下列两种情形下机床发生故障而得不到及时维修的概率： （1）一人负责15台机床的维修； （2）3人共同负责80台机床的维修。 原解：（1）依题意，维修人员是否能及时维修机床，取决于同一时刻发生故障的机床数。 设X表示15台机床中同一时刻发生故障的台数，则X服从n=15,p=0.01的二项分布： X～B(15,0.01)， 而 P(X= k)= C15k(0.01)k(0.99)15-k，k = 0, 1, …, 15 故所求概率为 P(X≥2)=1-P(X≤1)=1-P(X=0)-P(X=1) =1-(0.99)15-15×0.01×(0.99)14 =1-0.8600-0.1303=0.0097 （2）当3人共同负责80台机床的维修时，设Y表示80台机床中同一时刻发生故障的台数，则Y服从n=80、p=0.01的二项分布，即 Y～B(80,0.01) 此时因为 n=80≥30, p=0.01≤0.2 所以可以利用泊松近似公式：当n很大，p较小时（一般只要n≥30,p≤0.2时），对任一确定的k,有（其中 =np）

几种常见的概率分布

几种常见的概率分布 离散型概率分布 1.二项分布 n次独立的贝努利实验，其实验结果的分布(一种结果出现x次的概率是多少的分布)即为二项分布 应用二项分布的重要条件是：每一种实验结果在每次实验中都有恒定的概率，各实验之间是重复独立的 平均数：\二E(Y)二叩 方差与标准差：▽ X = np(1- P) ; = J np(1- p) 特例：(0-1 )分布 若随机变量x的分布律为 p(x = k) = p k(1 - p)1* k=o,i ；0

复抽样，抽样成功的次数X的概率分布服从超几何分布，如福利彩票 二、连续型概率分布 1?均匀分布 若随机变量X具有概率密度函数 f（X）二 则称X在区间（a，b）上服从均匀分布，记为X?U（a，b）在区间（a，b）上服从均匀分布的随机变量X的分布函数为 x v a F（x）X— ,a 乞x b b — a , X x 2指数分布 若随机变量X具有概率密度函数f（X）= e ' x - 0其中0是常数, 0,x< 0 则称X服从以’为参数的指数分布，记作X?E（' ），X的分布函数为 F(x)=」1 -e ,x 色0 j 0,x<0 3.正态分布 正态随机变量X的概率密度函数的形式如下： 1 f （x） e 2 $ ，—：：：： x ::: 式中，」为随机变量X的均值；、；2为随机变量X的方差通常对具有均值卩，方差为62的正态概率分布，记为N （卩，62）。于是有正态随机变量X~N （ '2）。

第四章 常概率分布

第四章常用概率分布 为了便于读者理解统计分析的基本原理，正确掌握和应用以后各章所介绍的统计分析方法，本章在介绍概率论中最基本的两个概念——事件、概率的基础上，重点介绍生物科学研究中常用的几种随机变量的概率分布——正态分布、二项分布、波松分布以及样本平均数的抽样分布和t分布。 第一节事件与概率 一、事件 （一）必然现象与随机现象在自然界与生产实践和科学试验中，人们会观察到各种各样的现象，把它们归纳起来，大体上分为两大类：一类是可预言其结果的，即在保持条件不变的情况下，重复进行试验，其结果总是确定的，必然发生（或必然不发生）。例如，在标准大气压下，水加热到100℃必然沸腾；步行条件下必然不可能到达月球等。这类现象称为必然现象（inevitable phenomena）或确定性现象（definite phenomena）。另一类是事前不可预言其结果的，即在保持条件不变的情况下，重复进行试验，其结果未必相同。例如，掷一枚质地均匀对称的硬币，其结果可能是出现正面，也可能出现反面；孵化6枚种蛋，可能“孵化出0只雏”，也可能“孵化出1只雏”，…，也可能“孵化出6 只雏”，事前不可能断言其孵化结果。这类在个别试验中其结果呈现偶然性、不确定性现象，称为随机现象（random phenomena）或不确定性现象（indefinite phenomena）。 人们通过长期的观察和实践并深入研究之后，发现随机现象或不确定性现象，有如下特点：在一定的条件实现时，有多种可能的结果发生，事前人们不能预言将出现哪种结果；对一次或少数几次观察或试验而言，其结果呈现偶然性、不确定性；但在相同条件下进行大量重复试验时，其试验结果却呈现出某种固有的特定的规律性——频率的稳定性，通常称之为随机现象的统计规律性。例如，对于一头临产的妊娠母牛产公犊还是产母犊是事前不能确定的，但随着妊娠母牛头数的增加，其产公犊、母犊的比例逐渐接近1：1的性别比例规律。概率论与数理统计就是研究和揭示随机现象统计规律的一门科学。 （二）随机试验与随机事件 1、随机试验通常我们把根据某一研究目的，在一定条件下对自然现象所进行的观察或试验统称为试验（trial）。而一个试验如果满足下述三个特性，则称其为一个随机试验（random trial），简称试验： （1）试验可以在相同条件下多次重复进行； （2）每次试验的可能结果不止一个，并且事先知道会有哪些可能的结果； （3）每次试验总是恰好出现这些可能结果中的一个，但在一次试验之前却不能肯定这次试验会出现哪一个结果。 如在一定孵化条件下，孵化6枚种蛋，观察其出雏情况；又如观察两头临产妊娠母牛所

16种常见概率分布概率密度函数、意义及其应用

目录 1.均匀分布 (1) 2.正态分布（高斯分布） (2) 3.指数分布 (2) 4.Beta分布（β分布） (2) 5.Gamma分布 (3) 6.倒Gamma分布 (4) 7.威布尔分布(Weibull分布、韦伯分布、韦布尔分布) (5) 8.Pareto分布 (6) 9.Cauchy分布（柯西分布、柯西-洛伦兹分布） (7) χ分布（卡方分布） (7) 10.2 11.t分布 (8) 12.F分布 (9) 13.二项分布 (10) 14.泊松分布（Poisson分布） (10) 15.对数正态分布 (11) 1.均匀分布 均匀分布~(,) X U a b是无信息的，可作为无信息变量的先验分布。

1()f x b a = - ()2 a b E X += 2 ()()12 b a Var X -= 2. 正态分布（高斯分布） 当影响一个变量的因素众多，且影响微弱、都不占据主导地位时，这个变量很可能服从正态分布，记作2~(,)X N μσ。正态分布为方差已知的正态分布 2(,)N μσ的参数μ的共轭先验分布。 22 ()2()x f x μσ-- = ()E X μ= 2()Var X σ= 3. 指数分布 指数分布~()X Exp λ是指要等到一个随机事件发生，需要经历多久时间。其中0λ>为尺度参数。指数分布的无记忆性：{}|{}P X s t X s P X t >+>=>。 (),0 x f x e x λλ-=> 1 ()E X λ = 2 1 ()Var X λ = 4. Beta 分布（β分布）

Beta 分布记为~(,)X Be a b ，其中Beta(1,1)等于均匀分布，其概率密度函数可凸也可凹。如果二项分布(,)B n p 中的参数p 的先验分布取(,)Beta a b ，实验数据（事件A 发生y 次，非事件A 发生n-y 次），则p 的后验分布(,)Beta a y b n y ++-，即Beta 分布为二项分布(,)B n p 的参数p 的共轭先验分布。 10 ()x t x t e dt ∞--Γ=? 1 1()()(1)()() a b a b f x x x a b --Γ+= -ΓΓ ()a E X a b = + 2 ()()(1) ab Var X a b a b = +++ 5. Gamma 分布 Gamma 分布即为多个独立且相同分布的指数分布变量的和的分布，解决的

第4章 常见概率分布.

第四章常用概率分布 一、二项分布的概念和特征 概念 分布:随机变量的取值规律分布函数:描述分布的规律 变量类型 连续型变量 离散型变量如:正态分布 如:二项分布,泊松分布 思考 例1.假设有5只实验小白鼠,要求它们同种属、同性别、体重相近,且给小白鼠注射一定剂量的毒物时,他们有相同的死亡率80%,存活率为20%。那么这5只小白鼠实验后全部死亡的概率是多少?有一只白小鼠存活的概率是多少?2只小白鼠存活的概率是多少? 例1.假设有5只实验小白鼠,要求它们同种属、同性别、体重相近, 且给小白鼠注射一定剂量的毒物时,他们有相同的死亡率80%, 存活率为20%。那么这5只小白鼠实验后全部死亡的概率是多少? 有一只白小鼠存活的概率是多少?2只小白鼠存活的概率是多少? P 死 =0.8 P 活 =0.2 P 1 =0.8×0.8×0.8×0.8×0.8 P 2 = P 3 = 1 5 C 2 5

C 0.2×0.8 4 =0.082 0.2 2 ×0.8 3 =0.020 =0.8 5 =0.328 该实验有三个特点: 1.各次实验是彼此独立的; 2.每次实验只有二种可能的结果,或死亡或生存; 3.每次实验小白鼠死亡和生存的概率是固定的。 具备以上三点,即从阳性率为π的总体中随机抽取大小为n的样本, 则出现“阳性”数为X的概率分布即呈现二项分布,记作B(n,p。 概率分布函数 二项分布的概率函数P (X 可用公式 X n X X n C X P - - = 1 ( ( p p 其中 ! ( ! ! X n X n C X n - = 对于任何二项分布,总有 ( 1 = ? = n X X P 例2.临床上用针灸治疗某型头疼,有效的概率为60%,现以该疗法治疗3例,其中2例有效的概率是多大? 分析:治疗结果为有限和无效两类,每个患者是否有效不受其他病例的影响,有效概率均为0.6,符合二项分布的条件。

各种概率分布介绍

一、引言 Bayes统计起源于英国学者托马斯.贝叶斯（Thomas Bayes,1702～1761）死后发表的一篇论文“论有关机遇问题的求解”。在此论文中他提出了著名的贝叶斯公式和一些归纳推理方法，随后拉普拉斯（Laplace,P.C.1749～1827）不仅重新发现了贝叶斯定理，阐述的远比贝叶斯更为清晰，而且还用它来解决天体力学、医学统计以及法学问题。之后虽有一些研究和应用但由于其理论尚不完整，应用中出现一些问题，致使贝叶斯方法长期未被接受。直到二战后，瓦尔德(Wald,A.1902～1950)提出统计决策函数论后又引起很多人对贝叶斯研究方法的兴趣。因为在这个理论中，贝叶斯解被认为是一种最优决策函数。在Savage,L.J.(1954)、Jeffreys,H.(1961)、Good,I.J(1950)、Lindley,D.V(1961)、Box,G.E.P.&Tiao,G.C.(1973)、Berger,J.O.(1985)等贝叶斯学者的努力下，对贝叶斯方法在观点、方法和理论上不断的完善。另外在这段时期贝叶斯方法在工业、经济、管理等领域内获得一批无可非议的成功应用。贝叶斯统计的研究论文与著作愈来愈多，贝叶斯统计的国际会议经常举行。如今贝叶斯统计已趋成熟，贝叶斯学派已发展成为一个有影响的学派，开始打破了经典统计学一统天下的局面。 贝叶斯统计是在与经典统计的争论中发展起来的,现已成为统计学中不可缺少的一部分.贝叶斯统计与经典统计的主要区别就是是否利用先验信息。贝叶斯统计重视已出现的样本观测值，对尚未发生的样本观测值不予考虑。近几年来对贝叶斯统计的广泛应用，使得贝叶斯统计在可靠性问题中起到越来越重要的作用。尤其是对产品的失效率以及产品寿命的检验中，更是离不开贝叶斯统计。本文主要是探索串联系统和并联系统的可靠性，以及可靠性增长模型的Bayes估计，这些都表现出了Bayes统计在可靠性中的广泛应用。 二、绪论 （一）统计学及其发展历程 人类的统计活动源远流长，自从有了数的概念，有了计数活动，就有了统计。但作为一门学科的统计学，它的出现却晚得多。英国学者配第（W.Petty）《政治算术》一书的问世，标志着统计学的开端。 概率论是统计学的重要起源之一。14世纪时，在工商业比较繁荣的意大利以及地中海岸其他地区，由于赌博游戏盛行和保险活动的萌起。人们

概率论中几种常用的重要的分布

概率论中几种常用的重要的分布 摘要：本文主要探讨了概率论中的几种常用分布，的来源和他们中间的关系。其在实际中的应用。 关键词 1 一维随机变量分布 随机变量的分布是概率论的主要内容之一，一维随机变量部分要介绍六中常用分布，即( 0 －1) 分布、二项分布、泊松分布、均匀分布、指数分布和正态分布． 下面我们将对这六种分布逐一地进行讨论． 随机事件是按试验结果而定出现与否的事件。它是一种“定性”类型的概念。为了进一步研究有关随机试验的问题，还需引进一种“定量”类型的概念，即，根据试验结果而定取什么值（实值或向量值）的变数。称这种变数为随机变数。本章内将讨论取实值的这种变数—— 一维随机变数。 定义1.1 设X 为一个随机变数，令 ()([(,)])([]),()F x P X x P X x x =∈-∞=-∞+∞p p p . 这样规定的函数()F x 的定义域是整个实轴、函数值在区间[0,1]上。它是一个普通的函数。成这个函数为随机函数X 的分布函数。 有的随机函数X 可能取的值只有有限多个或可数多个。更确切地说：存在着有限多个值或可数多个值12,,...,a a 使得 12([{,,...}])1P X a a ∈= 称这样的随机变数为离散型随机变数。称它的分布为离散型分布。 【例1】下列诸随机变数都是离散型随机变数。 （1）X 可能取的值只有一个，确切地说，存在着一个常数a ,使([])1P X a ==。称这种随机变数的分布为退化分布。一个退化分布可以用一个常数a 来确定。 （2）X 可能取的值只有两个。确切地说，存在着两个常数a ，b ，使([{,}])1P X a b ∈=.称这种随机变数的分布为两点分布。如果([])P X b p ==，那么，([])1P X a p ===-。因此，一个两点分布可以用两个不同的常数,a b 及一个在区间（0,1）内的值p 来确定。 特殊地，当,a b 依次为0,1时，称这两点分布为零-壹分布。从而，一个零-壹分布可以用一个在区间（0，1）内的值p 来确定。 （3）X 可能取的值只有n 个：12,...,a a （这些值互不相同），且，取每个i a 值

第四章 常用概率分布

第四章常用概率分布 为了便于理解统计分析的基本原理，正确掌握和应用以后各章所介绍的统计分析方法，本章在介绍概率论中最基本的两个概念——事件、概率的基础上，重点介绍生物科学研究中常用的几种随机变量的概率分布——正态分布、二项分布、波松分布以及样本平均数的抽样分布和t分布。 第一节排列与组合 一、乘法原理 如果一个过程分两个阶段进行，第一阶段有m种做法，第二阶段有n种做法，且第一阶段与第二阶段的任一种做法配成整个事件的一种做法，那么整个过程应该有mn种做法。 二、排列 从n个不同的元素中，任意取出r个不同的元素（0＜r≤n）按一定顺序排成一列，这样的一列元素，叫做从n个不同的元素中取r个不同的元素组成的一种排列。记做Pn r P n r=n(n-1)---(n-r+1)=n!/(n-r)! 例1：从1、2、3、4、5、6、7任取3个不同的数字组成3位数中，有几个是偶数？ 3×6×5＝90 如果容许重复，则P n r =n r 例2：体育彩票6位数的排列数有106，加上特征数共有106C51 例3 用0、1、2－－－9组成3位数 （1）如考虑数字可重复，可以组成多少不同的3位数？ （2）3位数中数字没有重复的有几个？ （3）3个数字相同的有几个？ （4）只有2个相同的有几个？ 解 1）百位9种，十位10种，个位10种 9×10×10 （2）百位9种，十位9种，个位8种 9×9×8 （3）百位9种，9×1×1 （4）百位与十位相同9×9，百位与个位相同9×9，十位与个位相同9×9 9×9＋9×9＋9×9＝243 三、组合 设有n个不同的元素，从它们中间任取r个构成一组，不考虑r元素的次序，记做C n r C n r=P n r/r!= n!/(n-r)!r! 例：5本不同的数学书，8本不同的物理书，任取2 本数学书，4本物理书的取法C52C84＝700 第二节事件与概率 一、事件 （一）必然现象与随机现象 在自然界与生产实践和科学试验中，观察到各种现象，归纳起来，大体上分为两大类：必然现象（inevitable phenomena）或确定性现象（definite phenomena）：可预言其结果的，即在保持条件不变的情况下，重复进行试验，其结果总是确定的，必然发生（或必然

考试练习题常用概率分布

第四章 选择题： 1．二项分布的概率分布图在条件下为对称图形。 A．n > 50 B．π=0.5 C．nπ=1 D．π=1 E．nπ> 5 2．满足时，二项分布B（n,π）近似正态分布。 A．nπ和n（1－π）均大于等于5 B．nπ或n（1－π）大于等于5 C．nπ足够大D．n > 50 E．π足够大 3. 的均数等于方差。 A．正态分布B．二项分布C．对称分布D．Poisson分布E．以上均不对4．标准正态典线下，中间95%的面积所对应的横轴范围是。 A．－∞到+1.96 B．－1.96到+1.96 C．－∞到+2.58 D．－2.58到+2.58 E．－1.64到+1.64 5．服从二项分布的随机变量的总体均数为。 A．n（1－π）B．（n－1）πC．nπ（1－π）D．nπ 6．服从二项分布的随机变量的总体标准差为。 7.设X1,X2分别服从以λ1,λ2为均数的Poisson分布,且X1与X2独立,则X1+X2服从以 为方差的Poisson分布。 8．满足时，Poisson分布Ⅱ（λ）近似正态分布。 A．λ无限大B．λ>20 C．λ=1 D．λ=0 E．λ=0.5 9．满足时，二项分布B（n，π）近似Poisson分布。 A．n很大且π接近0 B．n→∞C．nπ或n（1－π）大于等于5 D．n很大且π接近0.5 E．π接近0.5 10．关于泊松分布，错误的是。 A．当二项分布的n很大而π很小时，可用泊松分布近似二项分布 B．泊松分布均数λ唯一确定 C．泊松分布的均数越大，越接近正态分布 D．泊松分布的均数与标准差相等 E．如果X1和X2分别服从均数为λ1和λ2的泊松分布，且相互独立。则X1+X2服从均数为λ1+λ2的泊松分布。 11．以下分布中，均数等于方差的分布是。 A．正态分布B．标准正态分布C．二项分布D．Poisson分布E．t分布12．随机变量X服从正态分布N（μ1，σ12），Y服从正态分布N（μ2，σ22），X与Y 独立，则X－Y服从。 A．N（μ1+μ2，σ12－σ22）B．N（μ1－μ2，σ12－σ22） C．N（μ1－μ2，σ12+σ22）D．N（0，σ12+σ22）E．以上均不对 13．下列叙述中，错误的是。 A．二项分布中两个可能结果出现的概率之和为1 B．泊松分布只有1个参数λ C．正态曲线下的面积之和为1 D．服从泊松分布的随机变量，其取值为0到n的概率之和为1 E．标准正态分布的标准差为1 14．据既往经验，注射破伤风抗毒素异常发生率为5‰，某医院一年接种600人次，无1例发生异常，该情况发生的可能性P（X=0）应等于。

16种常见概率分布概率密度函数、意义及其应用

均匀分布 .................................... 1 .... 正态分布（高斯分布） ....................... 2 ... 指数分布 .................................... 2 .... Beta 分布（ 分布） .......................... 2 ... Gamma 分布 .................................. 3 .... 倒 Gamma 分布 威布尔分布 （Weibull 分布、韦伯分布、韦布尔分布 ） .............................................. 5.. Pareto 分布 ................................ 6 .... Cauchy 分布（柯西分布、柯西 .................. - 洛伦 兹分布） 7.. 2 分布（卡方分布） ......................... 7. t 分布 ......................................................................................................... 8.. F 分布 ......................................................................................................... 9.. 二项分布 ....................................................................................................... 1..0. 泊松分布（ Poisson 分布） .............................................................................................. 1..0. 对数正态分布 ..................................................................................................... 1..1.. 均匀分布 均匀分布 X ~U （a,b ） 是无信息的，可作为无信息变量的先验分布 1 f （x ） 目 录 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 1. .4.