100以内数的平方、立方表

平方数的规律及100之内的整数平方表112=121122=144132=169142=196152=225 162=256172=289182=324192=361202=400 212=441222=484232=529242=576252=625 262=676272=729282=784292=841302=900 312=961322=1024332=1089342=1156352=1225 2222236=129637=136938=144439=152140=1600 412=1681422=1764432=1849442=1936452=2025 462=2116472=2209482=2304492=2401502=2500 512=2601522=2704532=2809542=2916552=3025 562=3136572=3249582=3364592=3481602=3600 612=3721622=3844632=3969642=4096652=4225 662=4356672=4489682=4624692=4761702=4900 712=5041722=5184732=5329742=5476752=5625 2222276=577677=592978=608479=624180=6400 812=6561822=6724832=6889842=7056852=7225 862=7396872=7569882=7744892=7921902=8100 912=8281922=8464932=8649942=8836952=9025 962=9216972=9409982=9604992=98011002=10000规律：(1)完整平方数的个位数字只好是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字同样.(3)(2)奇数的平方的个位数字是奇数，十位数字是偶数.(4)假如完整平方数的十位数字是奇数,则它的个位数字必定是6；反之，假如完整平方数的个位数字是6，则它的十位数字必定是奇数.(5)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(6)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.完整平方数的形式必以下两种之一:3n,3n+1.不可以被5整除的数的平方5n±1型,能被5整除的数的平方5n型.平方数的形式拥有以下形式16n,16n+1,16n+4,16n+9.完整平方数的各位数字之和的个位数字只好是0,1,3,4,6,7,9.(没有2,5,8)假如数p能整除a,但p的平方不可以整除a,a不是完整平方数.在两个相的整数的平方数之的全部整数都不是完整平方数.(12)一个正整数n是完整平方数的充足必需条件是n有奇数个因数(包含1和n).一个数假如是另一个整数的完整立方（即一个整数的三次方,或整数乘以它自己乘以它自己）那么我就称个数完整立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000,等. 假如正整数x,y, z 足不定方程x2+y2=z2,就称x,y,z一勾股数.x,y必然是一个奇数另一个偶数，不行能同奇数或同偶数.z 和z2必然都是奇数.五常的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841技巧：(a+b)2=a2+ b2+ 2ab(a－b)2=a2+b2－2ab ||||||a ×ab×b2×a×b a×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=16988 2=(90-2)2=902+22－2×90×2=8100+4－360=7744用：①算能力，使算更快更正确；②估某数的平方根所的范，在判断某个大的数n能否是数能够小其可能因子的范,只要3到之的全部数能否是n的因子即可，超的都不用了.比如，判断2431能否22因此49<<50,2+4+3+1=10不可以被3整数，因49=2401<2431<2500=50,除,2341的个位既非0又非5,故只要7到47之的全部数可否整除2431即可，而53,59,61,67⋯⋯等更大的数都不用了，上2431=1117.③增添数字的熟习程度，比方162=256=28，322=1024=210，642=4096=212,此外一些特别构造的数字应当切记，如882=7744, 2211=121,22=484,(121和484从左到右与从右到左看是同样的) 2222212=144,21=441,13=169,31=961,(a左右颠倒后a也左右颠倒).。

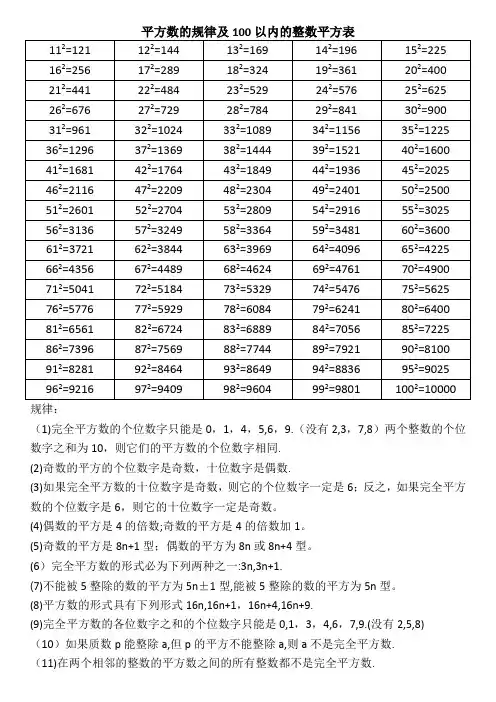
规律：（1)完全平方数的个位数字只能是0，1，4，5,6，9.（没有2,3，7,8）两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数，则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数。

(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1。

(5)奇数的平方是8n+1型；偶数的平方为8n或8n+4型。

(6）完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型。

(8)平方数的形式具有下列形式16n,16n+1，16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1，3，4,6，7,9.(没有2,5,8)（10）如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.（11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12）一个正整数n是完全平方数的充分必要条件是n有奇数个因数（包括1和n）.一个数如果是另一个整数的完全立方（即一个整数的三次方，或整数乘以它本身乘以它本身），那么我们就称这个数为完全立方数，也叫做立方数,如0,1，8，27,64，125，216,343，512，729，1000等。

如果正整数x,y,z满足不定方程x2+y2=z2，就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数。

五组常见的勾股数:32+42=52;52+122=132;72+242=252;82+152=172;202+212=2929+16=25；25+144=169；49+576=625; 64+225=289；400+441=841记忆技巧：（a+b)2= a2 + b2+2ab（a－b)2=a2+b2 －2ab｜| ｜｜｜｜a×ab×b2×a×ba×ab×b2×a×b例：132=（10+3)2=102+32+2×10×3=100+9+60=169882=(90-2）2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可,超过的都不必检查了。

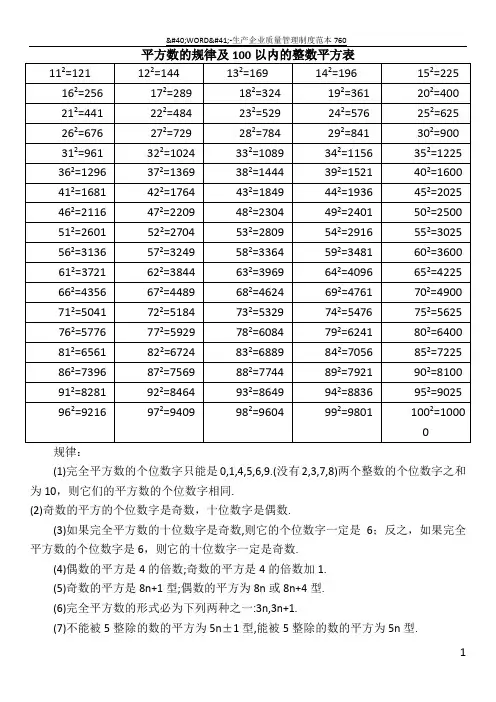
规律：(1)完全平方数的个位数字只能是0,1,4,5,6,9.(没有2,3,7,8)两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2= a2 + b2 + 2ab (a－b)2=a2 + b2 －2ab| | | | | |a×a b×b 2×a×b a×a b×b 2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50 ,2+4+3+1=10不能被3整除, 2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212 ,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).信你自己罢！只有你自己是真实的，也只有你能够创造你自己。

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。

如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。

㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。

(2 列出开发利用方案编制所依据的主要基础性资料的名称。

如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。

对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。

二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。

2、国内近、远期的需求量及主要销向预测。

㈡产品价格分析
1、国内矿产品价格现状。

2、矿产品价格稳定性及变化趋势。

三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。

2、矿区矿产资源概况。

3、该设计与矿区总体开发的关系。

㈡该设计项目的资源概况
1、矿床地质及构造特征。

2、矿床开采技术条件及水文地质条件。

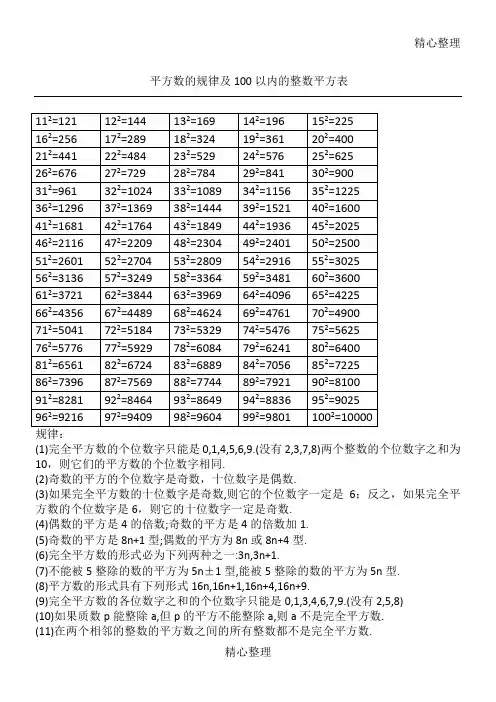
精心整理平方数的规律及100以内的整数平方表(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1.(5)奇数的平方是8n+1型;偶数的平方为8n或8n+4型.(6)完全平方数的形式必为下列两种之一:3n,3n+1.(7)不能被5整除的数的平方为5n±1型,能被5整除的数的平方为5n型.(8)平方数的形式具有下列形式16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是0,1,3,4,6,7,9.(没有2,5,8)(10)如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数.(11)在两个相邻的整数的平方数之间的所有整数都不是完全平方数.精心整理精心整理(12)一个正整数n是完全平方数的充分必要条件是n有奇数个因数(包括1和n).一个数如果是另一个整数的完全立方（即一个整数的三次方,或整数乘以它本身乘以它本身）,那么我们就称这个数为完全立方数,也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000等.如果正整数x,y,z满足不定方程x2+y2=z2,就称x,y,z为一组勾股数.x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数.z 和z2必定都是奇数.五组常见的勾股数：32+42=52；52+122=132；72+242=252；82+152=172；202+212=2929+16=25；25+144=169；49+576=625；64+225=289；400+441=841记忆技巧：(a+b)2=a2+b2+2ab(a－b)2=a2+b2－2ab||||||a×ab×b2×a×ba×ab×b2×a×b例：132=(10+3)2=102+32+2×10×3=100+9+60=169882=(90-2)2=902+22－2×90×2=8100+4－360=7744用处：①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围，在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了.例如，判定2431是否为质数，因为492=2401<2431<2500=502,所以49<<50,2+4+3+1=10不能被3整除,2341的个位既非0又非5,故只需检查7到47之间的所有质数能否整除2431即可，而53,59,61,67……等更大的质数都不用检查了，实际上2431=1117.③增加对数字的熟悉程度，比如162=256=28，322=1024=210，642=4096=212,另外一些特殊结构的数字应该牢记，如882=7744,112=121,222=484,(121和484从左到右与从右到左看是一样的)122=144,212=441,132=169,312=961,(a左右颠倒后a2也左右颠倒).精心整理。

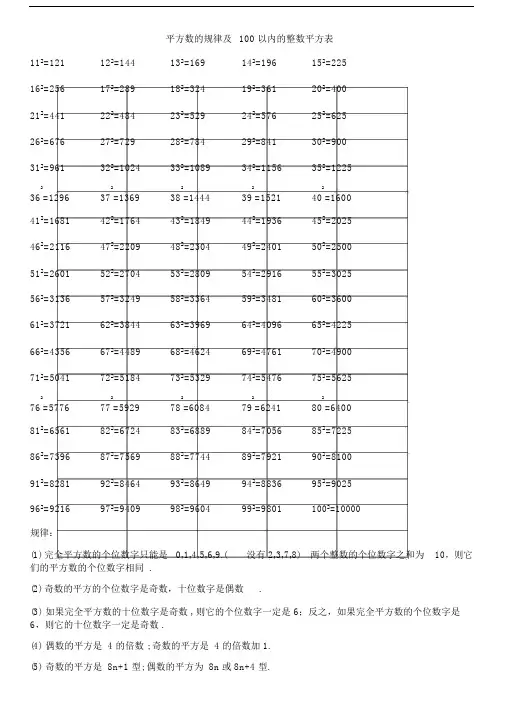
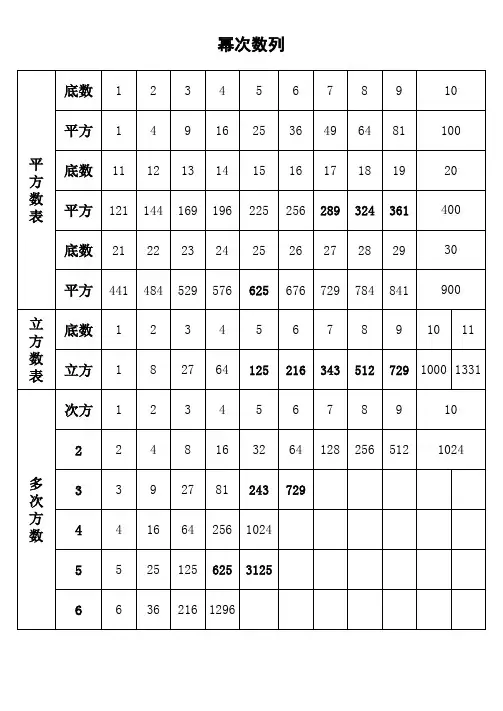
平方数的规律及100 以内的整数平方表112=121 122=144 132=169 142=196 152=225162=256 172=289 182=324 192=361 202=400212=441 222=484 232=529 242=576 252=625262=676 272=729 282=784 292=841 302=900312=961 322=1024 332=1089 342=1156 352=12252 2 2 2 236 =1296 37 =1369 38 =1444 39 =1521 40 =1600412=1681 422=1764 432=1849 442=1936 452=2025462=2116 472=2209 482=2304 492=2401 502=2500512=2601 522=2704 532=2809 542=2916 552=3025562=3136 572=3249 582=3364 592=3481 602=3600612=3721 622=3844 632=3969 642=4096 652=4225662=4356 672=4489 682=4624 692=4761 702=4900712=5041 722=5184 732=5329 742=5476 752=56252 2 2 2 276 =5776 77 =5929 78 =6084 79 =6241 80 =6400812=6561 822=6724 832=6889 842=7056 852=7225862=7396 872=7569 882=7744 892=7921 902=8100912=8281 922=8464 932=8649 942=8836 952=9025962=9216 972=9409 982=9604 992=9801 1002=10000规律：(1) 完全平方数的个位数字只能是 0,1,4,5,6,9.( 没有 2,3,7,8) 两个整数的个位数字之和为10，则它们的平方数的个位数字相同 .(2) 奇数的平方的个位数字是奇数，十位数字是偶数.(3)如果完全平方数的十位数字是奇数 , 则它的个位数字一定是 6；反之，如果完全平方数的个位数字是6，则它的十位数字一定是奇数 .(4)偶数的平方是 4 的倍数 ; 奇数的平方是 4 的倍数加 1.(5)奇数的平方是 8n+1 型; 偶数的平方为 8n 或 8n+4 型.(6)完全平方数的形式必下列两种之一 :3n,3n+1.(7)不能被 5 整除的数的平方 5n±1 型, 能被 5 整除的数的平方 5n 型 .(8)平方数的形式具有下列形式 16n,16n+1,16n+4,16n+9.(9)完全平方数的各位数字之和的个位数字只能是 0,1,3,4,6,7,9.(没有2,5,8)(10)如果数 p 能整除 a, 但 p 的平方不能整除 a, a 不是完全平方数 .(11)在两个相的整数的平方数之的所有整数都不是完全平方数.(12) 一个正整数 n 是完全平方数的充分必要条件是n 有奇数个因数 ( 包括 1 和 n).一个数如果是另一个整数的完全立方（即一个整数的三次方, 或整数乘以它本身乘以它本身）那么我就称个数完全立方数, 也叫做立方数，如0,1,8,27,64,125,216,343,512,729,1000, 等 .如果正整数x,y,z 足不定方程x2+y2=z2 , 就称x,y,z 一勾股数.x,y 必然是一个奇数另一个偶数，不可能同奇数或同偶数.z 和 z2必定都是奇数.五常的勾股数：32+42=52； 52 +122=132；72+242=252； 82 +152=172；202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841技巧：(a+b) 2= a 2 + b 2 +2ab (a －b) 2=a2 + b 2 －2ab| | | | | |a × a b×b 2 ×a×b a ×a b ×b 2 ×a×b例： 132=(10+3) 2 =102+32 +2×10×3=100+9+60=169882=(90-2) 2 =902+22－2×90×2=8100+4－360=7744用：① 算能力，使算更快更准确；②估某数的平方根所的范，在判定某个大的数n 是不是数可以小其可能因子的范 , 只需 3 到之的所有数是不是 n 的因子即可，超的都不必了 . 例如，判定 2431 是否2 2所以 49<<50 ,2+4+3+1=10 不能被 3 整除 , 2341 的个位既非 0 数，因 49 =2401<2431<2500=50,又非 5, 故只需 7 到 47 之的所有数能否整除2431 即可，而 53,59,61,67 ⋯⋯等更大的数都不用了，上 2431=1117. ③增加数字的熟悉程度，比如 162=256=28，322 =1024=210，642=4096=212 , 另外一些特殊结构的数字应该牢记，如882=7744,2 211 =121,22 =484,(121 和 484 从左到右与从右到左看是一样的)2222 212 =144,21 =441,13 =169,31 =961,(a 左右颠倒后 a 也左右颠倒 ).。

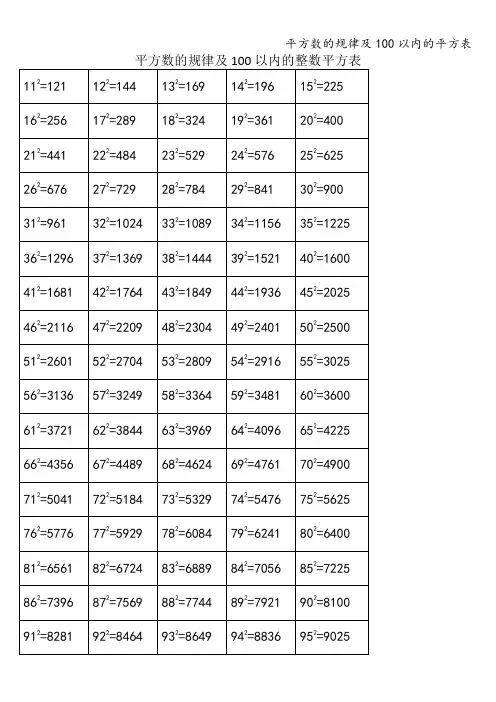
（1)完全平方数的个位数字只能是0，1，4,5，6,9.（没有2,3，7,8）两个整数的个位数字之和为10，则它们的平方数的个位数字相同.(2)奇数的平方的个位数字是奇数，十位数字是偶数。

(3）如果完全平方数的十位数字是奇数,则它的个位数字一定是6；反之，如果完全平方数的个位数字是6,则它的十位数字一定是奇数.(4)偶数的平方是4的倍数;奇数的平方是4的倍数加1。

(5）奇数的平方是8n+1型；偶数的平方为8n或8n+4型。

(6）完全平方数的形式必为下列两种之一：3n,3n+1.（7)不能被5整除的数的平方为5n±1型，能被5整除的数的平方为5n型.（8）平方数的形式具有下列形式16n,16n+1,16n+4，16n+9。

（9）完全平方数的各位数字之和的个位数字只能是0,1,3，4,6，7,9.(没有2，5，8)（10）如果质数p能整除a,但p的平方不能整除a,则a不是完全平方数. (11）在两个相邻的整数的平方数之间的所有整数都不是完全平方数.（12）一个正整数n是完全平方数的充分必要条件是n有奇数个因数（包括1和n)。

一个数如果是另一个整数的完全立方（即一个整数的三次方，或整数乘以它本身乘以它本身），那么我们就称这个数为完全立方数,也叫做立方数,如0，1,8,27，64,125，216,343，512,729,1000等。

如果正整数x,y，z满足不定方程x2+y2=z2 ,就称x,y,z为一组勾股数。

x,y必然是一个为奇数另一个为偶数，不可能同时为奇数或同时为偶数。

z和z2必定都是奇数。

五组常见的勾股数:32+42=52；52+122=132 ;72+242=252；82+152=172 ;202+212=2929+16=25；25+144=169；49+576=625； 64+225=289； 400+441=841记忆技巧：（a+b）2= a2 + b2 + 2ab (a－b）2=a2 + b2 －2ab｜ | | | ｜｜a×a b×b 2×a×b a×a b×b 2×a×b例:132=(10+3）2=102+32+2×10×3=100+9+60=169882=(90—2)2=902+22－2×90×2=8100+4－360=7744用处:①训练计算能力，使计算更快更准确；②估计某数的平方根所处的范围,在判定某个较大的数n是不是质数时可以缩小其可能因子的筛选范围,只需检查3到之间的所有质数是不是n的因子即可，超过的都不必检查了。