数独的直观式解题技巧

数独的技巧和规律数独直观法解题技巧主要有：唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法、余数测试法等。

数独解法全是由规则衍生出来的。

基本解法分为两类思路，一类为排除法，一类为唯一法。

更复杂的解法，最终也会归结到这两大类中。

1、基础摒除法基础摒除法就是利用1～9的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。

基础摒除法可以分为行摒除、列摒除、九宫格摒除。

2、唯一解法当某行已填数字的宫格达到8个，那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。

成为行唯一解。

3、唯余解法唯余解法就是某宫格可以添入的数已经排除了8个,那么这个宫格的数字就只能添入那个没有出现的数字。

4、区块摒除法区块摒除法是基础摒除法的提升方法,是直观法中使用频率最高的方法之一。

所谓区块，就是将行分成3个三个相连的小方块构成,列也是分成3个三个相连的小方块构成.九宫格同样被看成由3个三个相连的小方块构成，如下面示意图：区块摒除法的核心思想如下面解释(以行为例),对于在列也是相同的道理。

5、撑点定位法当某个小九宫格中有一行已有3个数字时，我们将这3个数所在的行称为“撑”。

这时，在该行另外两个小九宫格上的另外两行寻找该小九宫格没有的数字，将该数的位置称为“点”。

那么，“点”上的数字在“撑”所在的九宫格中必然位于“撑”和“点”所在行以外的另一行；同时，“点”上的数字在“撑”和“点”以外的另一九宫格中位于“撑”所在的行上。

6、余数测试法所谓余数测试法就是在某行或列，九宫格所填数字比较多,剩余2个或3个时，在剩余宫格添入值进行测试的解题方法。

7、候选数法候选数法解题的过程就是逐渐排除不合适的候选数的过程，当某个宫格的候选数排除到只有一个数的时候，那么这个数就是该宫格的唯一的一个候选数，这个候选数就可以解了。

8、链数删减法找出某一列、某一行或某一个九宫格中的某三个宫格候选数中，相异的数字不超过3个的情形，进而将这3个数字自其它宫格的候选数中删减掉的方法就叫做三链数删减法。

数独解题技巧1.直观法（1）单元限定法：此处的单元指的是行、列或者是小九宫格。

使用此种方法时有三种情况：当某行、列、小九宫格有八个单元格中已有数字，空白处必定为唯一缺少的数字。

（2）单元排除法：在某一单元（行、列、小九宫格）中找到能填入某一数字的唯一位置，也就是把单元中其他的空白位置都排除掉。

（3）区块排除法：a)当某数字在某个小九宫格中可填入的位置正好都在同一行上，因为该小九宫格中必须要有该数字，所以这一行中不在该小九宫格内的单元格上将不能再出现该数字。

b)在某数字在某个小九宫格中可填入的位置正好都在同一列上，因为该小九宫格中必须要有该数字，所以这一列中不在该小九宫格内的单元格上将不能再出现该数字。

c)当某数字在某行中可填入的位置正好都在同一小九宫格上，因为该行中必须要有该数字，所以该小九宫格中不在该行内的单元格上将不能再出现该数字。

d)当某数字在某列中可填入的位置正好都在同一小九宫格上，因为该列中必须要有该数字，所以该小九宫格中不在该列内德单元格上将不能再出现该数字。

（4）唯一余解法：如果某一单元格所在的行、列、小九宫格中共出现了八种不同的数字，那么该单元格可以确定地填入还未出现过的数字。

（5）矩形排除法：如果一个数字在某两行中能填入的位置正好在同样地两列中，则这两列上其他的单元格中将不能再出现这个数字；或者如果一个数字在某两列中能填入的位置正好在同样地两行中，则这两行的其他的单元格中将不能再出现这个数字。

（6）直观扫描法（7）逐行、逐列扫描法2.候选数法（1）显示唯一法：扫描候选数栅格表，如果哪个单元格中只剩下一个候选数，就可以应用显示唯一法，在该单元格中填入这个数字，并在相应行、列、小九宫格的候选数中删除该数字。

（2）隐式唯一法：若一个单元格内德候选数不止一个，但该单元格所在的行、列、小九宫格内，只有它含有某一个数字，那么这个单元格就可以直接填这个数字。

（3）显式对法：指在一个行、列、小九宫格中，如果有两个单元格都包含且只包含相同的两个候选数，则这两个候选数字不能再出现在该行、列、小九宫格的其他单元格的候选数中。

数独游戏技巧：1-9九宫格数独口诀与解题技巧心得分享九宫格数独口诀技巧首先确认中间的数字，中间的确认了，其他的就都好说了。

1.九宫格数独是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

2.数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件。

3.利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

4.这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

5.数独解法全是由规则衍生出来的，基本解法分为两类思路，一类为排除法，一类为唯一法。

更复杂的解法，最终也会归结到这两大类中。

6.数独直观法解题技巧主要有唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法，余数测试法等数独的规则在空格内填入数字1-9，使得每行、每列和每个宫内数字都不重复。

注意：数独题目满足条件的答案是唯一的。

数独的元素数独的元素主要包括行、列和宫。

这三者划分出数独有三种不同形态的区域，而数独规则就是要求在这些区域内出现的数字都为1~9。

元素坐标图：行：数独盘面内横向一组九格的区域，用字母表示其位置；列：数独盘面内纵向一组九格的区域，用数字表示其位置；宫：数独盘面内3×3格被粗线划分的区域，用中文数字表示其位置。

格的坐标：利用表示行位置的字母和表示列位置的数字定位数独盘面内每个格子的具体位置，如A3格，F8格等。

数独技巧1.宫内排除法排除法就是利用数独中行、列和宫内不能填入相同数字的规则，利用已出现的数字对同行、同列和同宫内其他格进行排斥相同数字的方法。

宫内排除法就是将一个宫作为目标，用某个数字对它举行排除，最终得到这个宫内只有一格出现该数字的方法。

技巧透露表现图：宫内排除法如上图所示，A2、B4和F7三格内的1都对三宫进行排除，这时三宫内只有C9格可以填入1，本图例就是对三宫运用的排除法。

数独九宫格骨灰级解题技巧
1、数独盘面是个九宫，每一宫又分为九个小格，在这八十一格中给出一定的已知数字和解题条件。

2、利用逻辑和推理，在其他的空格上填入1-9的数字，使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

3、这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳方式。

4、数独解法全是由规则衍生出来的，基本解法分为两类思路，一类为排除法，一类为唯一法，更复杂的解法，最终也会归结到这两大类中。

5、数独直观法解题技巧主要有唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法，余数测试法等。

6、除此之外还可以利用宫内排除法，行列排除法，区块排除法，宫内数对占位法，唯余解法，行列区块法，行列内数对占位法，数组占位法，显性数对，显性数组。

首先确认中间的数字，中间的确认了，其他的就都好说了。

一、数独简介数独是一种以数字为表现形式的逻辑推理谜题。

数独起源于18世纪末的瑞士，后在美国发展、并在日本得以发扬光大。

1783年，瑞士数学家欧拉发明了一种拉丁方块的游戏，这就是现代数独的雏形。

1984年，在日本游戏杂志上出现了“数独”游戏，提出了“独立的数字”的概念，意思就是“这个数字只能出现一次”，并将这个游戏命名为“数独”（sudoku ）。

数独一次的命名也就源于日本语，我们直接把日语中“数独”这两个同音字引用过来，也就成为了对其的命名。

每一道合格的数独谜题都有且仅有唯一答案，推理方法也以此为基础，任何无解或多解的题目都是不合格的二、数独规则标准数独的规则一般只有三点：1、数独中每行内的数字为1-9且不重复；2、数独中每列内的数字为1-9且不重复；3、数独中每宫内的数字为1-9且不重复。

三、数独元素标准数独的基本元素包括单元格、行、列、宫、区、区块、已知数、候选数等等。

单元格：简称格，是数独盘面中最小的格子，只可以填入一个数字； 行：数独盘面中横向9个单元格的总称； 列：数独盘面中纵向9个单元格的总称；宫：数独盘面中粗线划分出的9格单元格的总称；区：填入一组1-9数字的区域，行、列、宫、都是区的一种具体表现形式； 区块：某宫中横向或者纵向3个并排单元格的总称； 已知数：数独题目初始给出的数字；候选数：某空单元格中目前还可以填入的数字。

IH G F E D C B A数独直观解法，指的是我们在解数独的时候，不需要标记候选数，直接可以凭借直观判断填出格内得数的方法。

（有时候标记会大大增加解题效率，不能说标记就不属于直观解法）单区唯一解法、简单排除法、单元排除法、区块排除法、数组占位法、多区唯一解法第一节 单区唯一解法一、什么是单区唯一解法单区唯一解法，顾名思义“单区”指的是一行、一列或者一宫，“唯一解”指的是某格内只有唯一一个解。

由于数独规则的要求，数独中每行、每列及每一宫内数字都为1-9,。

数独解题技巧数独是一种基于逻辑的数字填充游戏，需要将数字填入一个9x9的网格中，使得每行、每列和每个宫格中都没有重复的数字。

解决数独谜题需要一定的技巧和策略，下面介绍一些常用的解题思路和技巧：1. 直观法* 唯余法：利用数独中每格内都只有9种数字的可能性，如果某格中有8种数字都不能填，只能填入唯一未出现数字的方法。

* 行列区块法：利用行列排除，在某行或列内制造出一个区块，利用该区块对该区块所在宫的其他格进行删除的方法。

2. 基础摒除法基础摒除法是利用1～9的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。

基础摒除法可以分为行摒除、列摒除、九宫格摒除。

实际寻找解的过程为：寻找九宫格摒除解：找到了某数在某一个九宫格可填入的位置只余一个的情形；意即找到了该数在该九宫格中的填入位置。

寻找列摒除解：找到了某数在某列可填入的位置只余一个的情形；意即找到了该数在该列中的填入位置。

3. 区块摒除法区块摒除法指的是利用数对、数组等区块，在某行或列内制造出一个区块，利用该区块对该区块所在宫的其他格进行删除的方法。

4. X-Wing法X-Wing法是一种高级解法，用于解决一些难度较大的数独谜题。

它可以在不使用直观法的情况下，通过逻辑推理得到正确答案。

这种方法需要在不同的行和列中寻找两个数字，它们的位置可以确定其他数字的位置。

这种方法需要一定的观察力和逻辑推理能力。

5. Swordfish法Swordfish法是一种更高级的解法，用于解决一些特别复杂的数独谜题。

这种方法需要观察多行、多列和多个九宫格，并使用逻辑推理来确定正确的数字。

这种方法需要极高的观察力和逻辑推理能力。

总之，解决数独谜题需要多种方法和技巧的综合运用。

直观法是最常用的方法之一，但也需要结合其他方法和技巧进行解题。

对于初学者来说，需要多加练习和学习，不断提高自己的解题能力和技巧水平。

数独解题方法大全首先，数独候选数法解题技巧主要有:唯一候选数法、隐性唯一候选数法、区块删减法、数对删减法、隐性数对删减法、三链数删减法、隐性三链数删减法、矩形顶点删减法、三链列删减法、关键数删减法、关连数删减法。

数独这个数字解谜游戏,完全不必要用到算术!会用到的只是推理与逻辑。

解题方法分两大类：直观法和候选数法。

直观法就是不需要任何辅助工具，从接到数独谜题的那一刻起就可以立即开始解题。

绝不猜测。

数独直观法解题技巧主要有:唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法，余数测试法.候选数法就是解数独题目需先建立候选数列表，根据各种条件，逐步安全的清除每个宫格候选数的不可能取值的候选数，从而达到解题的目的。

使用候选数法一般能解比较复杂的数独题目,但是候选数法的使用没用直观法那么直接，需要先建立一个候选数列表的准备过程。

所以实际使用时可以先利用直观法进行解题，到无法用直观法解题时再使用候选数方法解题。

候选数法解题的过程就是逐渐排除不合适的候选数的过程，所以在进行候选数删除的时候一定要小心，确定安全的删除不合适的候选数，否则,很多时候只有重新做题了.有了计算机软件的帮助，使得候选数表的维护变得轻松起来。

一、直观法:1、唯一解法:当某行已填数字的宫格达到8个，那么该行剩余宫格能填的数字就只剩下那个还没出现过的数字了。

成为行唯一解.当某列已填数字的宫格达到8个,那么该列剩余宫格能填的数字就只剩下那个还没出现过的数字了。

成为列唯一解.当某九宫格已填数字的宫格达到8个，那么该九宫格剩余宫格能填的数字就只剩下那个还没出现过的数字了。

成为九宫格唯一解。

下面是例题：A行已经添入8个数字，A行只有数字3没有出现过，所以A9=3，这是行唯一解.第1列已经添入8个数字，第1列只有数字5没有出现过，所以E1=5，这是列唯一解.在A8所在九宫格区域已经添入8个数字，只有数字9没有出现过，所以A8=9，这是九宫格唯一解.2、基础摒除法基础摒除法就是利用1 ～9 的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。

数独技巧数独顾名思义——每个数字只能出现一次。

数独是一种源自18世纪末的瑞士，后在美国发展、并在日本得以发扬光大的数字谜题。

数独盘面是个九宫，每一宫又分为九个小格。

在这八十一格中给出一定的已知数字和解题条件，利用逻辑和推理，在其他的空格上填入1-9的数字。

使1-9每个数字在每一行、每一列和每一宫中都只出现一次。

这种游戏全面考验做题者观察能力和推理能力，虽然玩法简单，但数字排列方式却千变万化，所以不少教育者认为数独是训练头脑的绝佳数独技巧数独基本元素示意图单元格：数独中最小的单元，标准数独中共有81个；行：横向9个单元格的集合；列：纵向9个单元格的集合；宫：粗黑线划分的区域，标准数独中为3×3的9个单元格的集合；已知数：数独初始盘面给出的数字；数独解法全是由规则衍生出来的，基本解法分为两类思路，一类为排除法，一类为唯一法。

更复杂的解法，最终也会归结到这两大类中。

下边以图示简单介绍几种解法，只要你花几分钟看一遍，马上就可以开始做数独了。

数独直观法解题技巧主要有：唯一解法、基础摒除法、区块摒除法、唯余解法、矩形摒除法、单元摒除法,余数测试法等。

基础摒除法就是利用1～9的数字在每一行、每一列、每一个九宫格都只能出现一次的规则进行解题的方法。

基础摒除法可以分为行摒除、列摒除、九宫格摒除。

实际寻找解的过程为：寻找九宫格摒除解：找到了某数在某一个九宫格可填入的位置只余一个的情形；意即找到了该数在该九宫格中的填入位置。

寻找列摒除解：找到了某数在某列可填入的位置只余一个的情形；意即找到了该数在该列中的填入位置。

寻找行摒除解：找到了某数在某行可填入的位置只余一个的情形；意即找到了该数在该行中的填入位置。

看能用基础摒除法确定Ｂ２、Ｃ８、Ｅ７、Ｆ６、Ｉ５的数字吗？数独技巧A4=9,则Ａ行其它格排除９，G1=9,第1列排除数字９，D3=9,第3列排除数字9。

数独技巧由基础摒除法，第A1所在的九宫格内９只有一个唯一的位置，即确定B2=9。

数独突破口：几种常见技巧与方法数独题目100题 - 独数题目：如何快速找到解题的突破口？数独作为一种逻辑游戏，解题的过程常常需要玩家找到解题的突破口。

以下是几种常用的方法，帮助玩家快速找到解题的突破口：1.区块分析法：这是数独解题中常用的一种方法。

通过观察整个数独盘面，将数字分为不同的区块，然后在每个区块中分析可能的数字。

当某个区块内只有一个数字可能性时，就可以立即填入，从而为整个数独解题找到突破口。

2.唯一余数法：这也是一种常用的数独解题技巧。

当某个单元格内只能填入一个数字时，就可以立即填入这个数字。

这个数字可能是通过排除其他所有可能的数字后得出的。

这种方法在解题初期和中期特别有效。

3.候选数法：通过观察每个单元格的可能数字，将每个单元格的候选数字列出，然后根据数独的规则，逐步排除不可能的候选数字。

当某个单元格的候选数字只剩下一个时，就可以填入这个数字，从而为解题找到突破口。

4.数对与数组法：在数独中，如果某两个单元格内只能填入同一组数字，那么这两个单元格就构成了一个数对。

如果某几个单元格内只能填入同一组数字，那么这些单元格就构成了一个数组。

通过观察和分析数对和数组，可以找出一些隐藏的线索，从而快速找到解题的突破口。

5.直观法：这是一种不依赖任何辅助工具，直接通过观察数独盘面来寻找线索的方法。

虽然这种方法需要较高的逻辑能力和数独经验，但一旦找到线索，就可以迅速找到解题的突破口。

以上这些方法并不是孤立的，而是可以相互配合使用的。

在解数独题目时，玩家可以根据自己的习惯和实际情况，选择适合自己的方法，也可以综合运用多种方法，找到解题的突破口。

同时，需要注意的是，数独解题并不是一蹴而就的过程，往往需要耐心和细心。

玩家在解题时，不要急于求成，要一步步地分析，逐步接近正确答案。

只有这样，才能真正享受数独带来的乐趣和挑战。

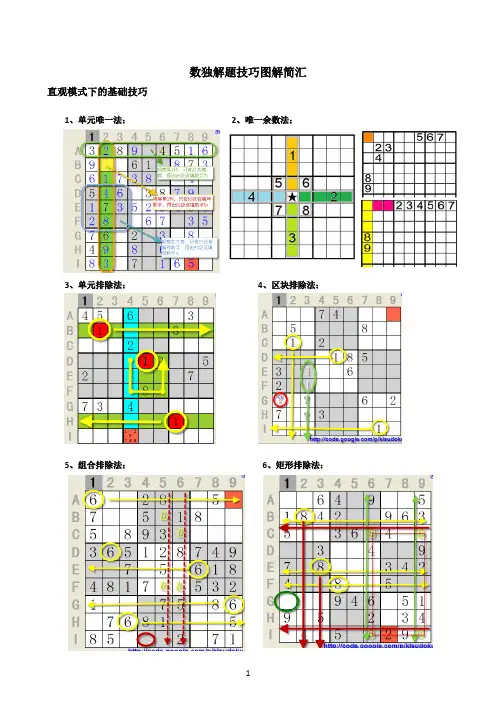
数独解题技巧图解简汇直观模式下的基础技巧1、单元唯一法：2、唯一余数法：3、单元排除法：4、区块排除法：5、组合排除法：6、矩形排除法：7、数对占位排除法：候选数模式下的解题技巧1、显式唯一数法：如某格只包含一个候选数，2、隐式唯一数法：如某格所含候选数字在该单元即可将该数字填入该单元格。

格只出现一次，则该格即可填入该数字。

3、区块删除法：先确定某区块一定包含某个数字，再以此为已知条件对相关区其他单元格进行该数字删除。

4、显式数对法：利用一组显性数对，对所在区其他单元格内的与显性数对数字相同的候选数进行删除。

显性数对为格外删除。

5、隐式数对法：在同一区中只有两个单元格出现某两个候选数字，且该区其他单元格均不包含这两个候选数，则可将该两格内的其他候选数进行删除。

隐性数对为格内删除。

6、显式三数集法：利用一组显性数组对所在区其他单元格内的与显性数组数字相同的候选数进行删除。

该行既含359显式三数集也含17隐式数对，二者均可将4和6两格中359进行删除。

7、隐式三数集法：在同一区中只有三个单元格出现某三个候选数字（每格至少包含其中的两个数字），且该区其他单元格均不包含这三个候选数，则可将该三格内的其他候选数进行删除。

该H行既含589隐式三数集也含1234显式四数集，二者均可将H1、H3中134进行删除。

8、显式四数集法：该行既含89隐式数对也含2356显式四数集，二者均可将D3、D7中356进行删除。

9、隐式四数集法：该行既含2489隐式四数集也含17显式数对，二者均可将A4A6A7A8中17进行删除。

10、矩形对角线法：如果一个数字正好出现且只出现在某两行的相同的两列上，则这个数字就可以从这两列上其他的单元格的候选数中删除。

或，如果一个数字正好出现且只出现在某两列的相同的两行上，则这个数字就可以从这两行上的其他单元格的候选数中删除。

在B G两行中，7都出现两次，且都位于第2列和在第1列和第7列上，数字9出现两次且只出第7列上，故第2列中的A2，第7列中的C7，D7 现在行C和行G上，故行C上的[C4] 和[C5]和E7的候选数7均可删除。