高考数列总复习(完整)

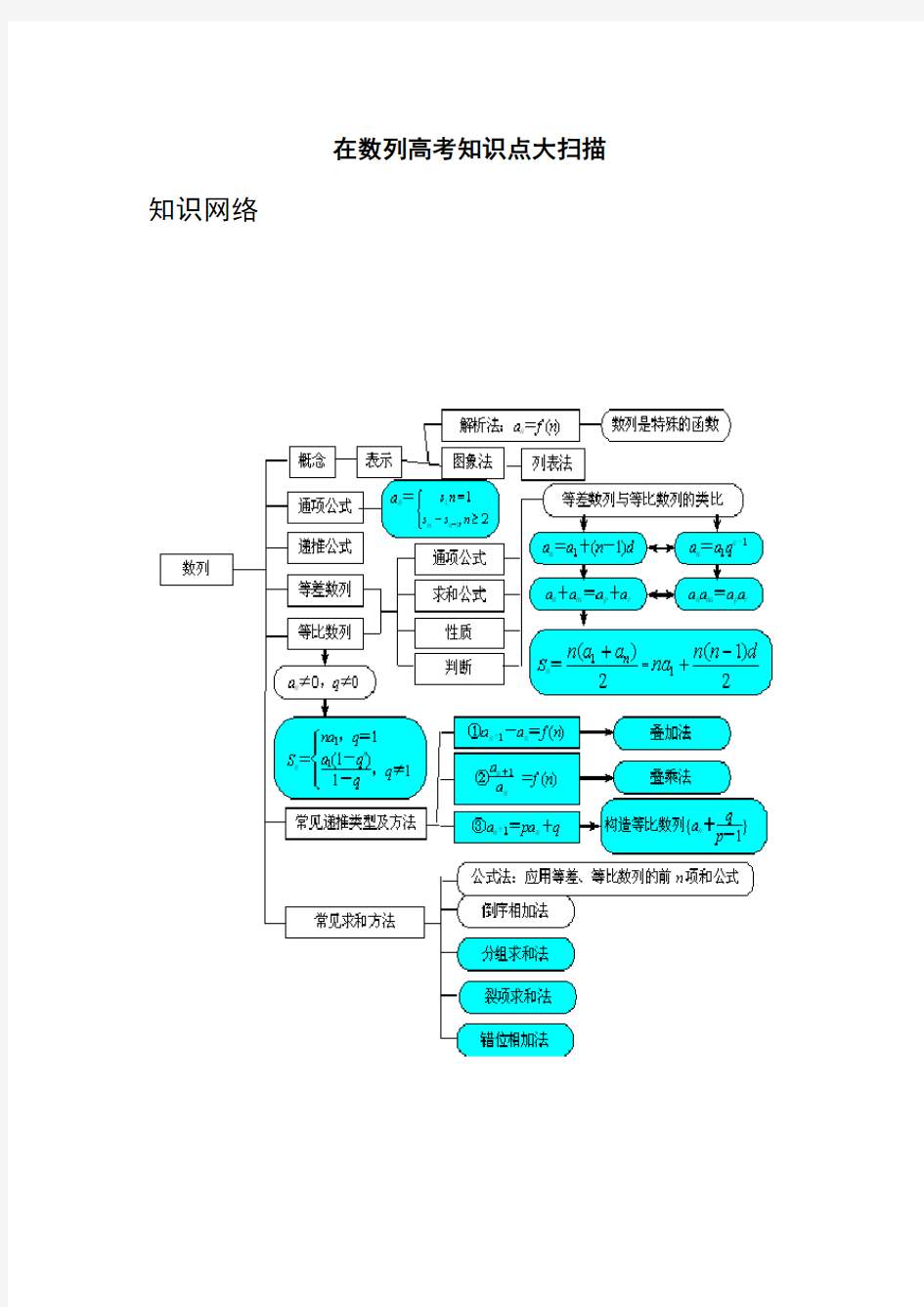
在数列高考知识点大扫描知识网络

数列基本概念

数列是一种特殊函数，对于数列这种特殊函数，着重讨论它的定义域、值域、增减性和最值等方面的性质，依据这些性质将数列分类：

依定义域分为：有穷数列、无穷数列； 依值域分为：有界数列和无界数列；

依增减性分为递增数列、递减数列和摆动数列。

数列的表示方法：列表法、图象法、解析法（通项公式法及递推关系法）； 数列通项：()

n

a f n =

2、等差数列

1、定义当n N ∈,且2n ≥时，总有1,()n n a a d d +-=常，d 叫公差。

2、通项公式1(1)n

a a n d =+-

3、前n 项和公式

由1211,n

n n n n S a a a S a a a -=+++=+++ ，

相加得12n n

a a S n +=

，还可表示为1(1)

,(0)2

n n n S na d d -=+≠，是n 的二次函数。 特别的，由1212n n a a a -+=可得21(21)n n S n a -=-。

4、由三个数a ，A ，b 组成的等差数列可以看成最简单的等差数列，则A 称为a 与b 的

等差中项．若2

a c

b +=

，则称b 为a 与c 的等差中项． 5、等差数列的性质：

（1）m n p q +=+（m 、n 、p 、*

q ∈N ），则m n

p q a a a a +=+； 特别地，若2n p q =+（n 、p 、*

q ∈N ），则2n

p q a a a =+．

（2）n S ，2n n S S -，32n n S S -成等比数列． （3）若项数为()

*2n n ∈N ，则S S nd -=偶奇

，．

（4）若项数为()*

21n n -∈N ，则()2121n n S n a -=-，1

S n S n =

-奇偶

3、等比数列

1、 定义当n N ∈,且2n

≥时，总有

1

(0)n

n a q q a -=≠ , q 叫公比。 2、 通项公式：

11n n

m

n m a a q a q --

==, 在等比数列中，若

2m n p q r

+=+= , 则

2m n p q r a a a a a ?=?=.

3、 、在a 与b 中间插入一个数G ，使a ，G ，b 成等比数列，则G 称为a 与b 的等比中

项．若2

G ab =，则称G 为a 与b 的等比中项． 4、 等比数列的前n 项和的性质：

（1）m n p q +=+（m 、n 、p 、*

q ∈N ），则m n p q a a a a ?=?；若{}n a 是等比数列，且2n p q =+（n 、p 、*q ∈N ），则2

n

p q a a a =?．

（2）n S ，2n n S S -，32n n S S -成等比数列。

5、 前n 项和公式: 由12231,n

n n n n S a a a qS a a a a +=+++=++++ ，两式相减，

当1q ≠时，11(1),(1)11n n a a q a q S q q q

--==≠--；当1q =时，1n s na =。

关于此公式可以从以下几方面认识：

①

不能忽视11(1)11n n a a q

a q S q q

--==

--成立的条件：1q ≠。特别是公比用字母表示时，要分类讨论。

② 公式推导过程中，所使用的“错位相消法”，可以用在相减后所得式子能够求和的情形。 如，公差为

d

的等差数列

{}

n a ，

212n

n n S a x a x a x =+++ ，则

23

121n n n n n xS a x a x a x a x +

-=+++ ，

相减得2

11(1)n n n n S x a x dx

dx a x +-=+++- ，

当1x ≠时，111(1)(1)1n n n n dx x S x a x a x x -+--=+--，12112

(1)1(1)

n n n n a x a x dx x S x x +---=+--

当1x =时，

第一节等差数列的概念、性质及前n 项和

题根一等差数列{a n }中，6

9121520a a a a +++=，求S 20

[思路]等差数列前n 项和公式11()(1)

22

n n

a a n n n S na d +-=

=+：

1、 由已知直接求a 1，公差d.

2、 利用性质q p n m a a a a q p n m +=+?+=+

[请你试试 1——1]

1、 等差数列{a n }满足12

1010a a a +++= ，则有（）

A 、1101

0a a +> B 、21000a a +< C 、3990a a += D 、5151a =

2、 等差数列中,a 3+a 7-a 10=8,a 11-a 4=4,求13S 。

第1变求和方法——倒序相加法

[变题1] 等差数列{a n }共10项，12

3420a a a a +++=，12360n n n n a a a a ---+++=，求S n.

[思路] 已知数列前四项和与后四项和，结合通项性质，联想S n 公式推导方法。

[请你试试 1——2]

1、 等差数列{a n }前n 项和为18 ，若1S =3

, 123n n n a a a --++=, 求项数n .

2、 求和12

2n

n

n n n S n C C C =+++ 。

第2变已知前n 项和及前m 项和，如何求前n+m 项和

[变题2] 在等差数列{a n }中，S n =a,S m =b,(m>n)，求S n+m 的值。 [思路]

,,m m n S S S +n 下标存在关系：m+n=m+n, 这与通项性质q

p n m a a a a q p n m +=+?+=+是否有关？

[请你试试 1——3]

1、 在等差数列{a n }中，15S =6，55S =9，求S 15。

2、在等差数列{a n }中，1S =3

，3S =9，求S 12。

第3变已知已知前n 项和及前2n 项和，如何求前3n 项和

[变题3] 在等差数列{a n }中，20S =10

，40S =20，求S 30

[思路] 由2030,,S S S 10寻找102030,,S S S S S --1020之间的关系。

[请你试试 1——4]

1、在等差数列{a n }中，12

3a a +=，346a a +=，求78a a +

第二节等比数列的概念、性质及前n 项和

题根二等比数列{a n } ，5

74,6a a ==, 求a 9。

[思路] 1、由已知条件联立，求，从而得

2、由等比数列性质，知成等比数列。

[请你试试2 ——1]

等比数列{a n } ，10,2a q >=，若

，则_______。

第1变连续若干项之和构成的数列仍成等比数列

[变题2] 等比数列{a n } ，12

34562,6a a a a a a ++=++=，求101112a a a ++。

[思路] 等比数列中，连续若干项的和成等比数列。

[请你试试2——2]

1、等比数列{a n } ，1q ≠-时，242,6S S ==，求6S 。

2、等比数列{a n } ，1q

≠-时，261,21S S ==，求4S 。

第三节常见数列的通项求法

一、公式法

例1 已知数列{}n a 满足1232n n n a a +=+?，12a =，求数列{}n a 的通项公式。

二、累加法

例2 已知数列{}n a 满足1121

1n n a a n a +=++=，，求数列{}n a 的通项公式。

例3 已知数列{}n a 满足112313n n n a a a +=+?+=，，求数列{}n a 的通项公式。

三、累乘法

例4已知数列{}n a 满足112(1)53n n n a n a a +=+?=，，求数列{}n a 的通项公式。

四、作差法

例5（数列{n a }的前n 项和为n S ，且满足11a =，2(1)n n S n a =+.求{n a }的通项公式

五，构造法

例6数列{}n a 中，若21=a ，n

n

n a a a +=+11，求数列{}n a 的通项公式n a 。

例7数列{}。求通项中n n n n a a a a a ,12,1,11+==+

第四节常见数列求和方法

1．直接法：即直接用等差、等比数列的求和公式求和。 （1）等差数列的求和公式：d n n na a a n S n n 2

)

1(2)(11-+=+=

（2）等比数列的求和公式?????≠--==)

1(1)1()1(11q q

q a q na S n

n （切记：公比含字母时一定要讨论）

2．公式法：

222221

(1)(21)

1236

n

k n n n k n =++=++++=

∑

2

33333

1

(1)1232n

k n n k n =+??=++++=????∑ 3．错位相减法：比如{}{}.,,2211的和求等比等差n n n n b a b a b a b a +++ 4．裂项相消法：把数列的通项拆成两项之差、正负相消剩下首尾若干项。 常

见

拆

项

公

式

：

1

1

1)1(1+-

=+n n n n ；

1111()(2)22n n n n =-++)1

21

121(21)12)(12(1+--=+-n n n n !)!1(!n n n n -+=?

5．分组求和法：把数列的每一项分成若干项，使其转化为等差或等比数列，再求和。

6．合并求和法：如求2

2222212979899100-++-+- 的和。 7．倒序相加法：

8．其它求和法：如归纳猜想法，奇偶法等 （二）主要方法：

1．求数列的和注意方法的选取：关键是看数列的通项公式； 2．求和过程中注意分类讨论思想的运用； 3．转化思想的运用； （三）例题分析： 例1．

2．错位相减法求和 例2．已知，求数列｛a n ｝的前n 项和S n .

3.裂项相消法求和

例3.求和)

12)(12()2(5343122

22+-+

+?+?=n n n S n

4.倒序相加法求和

例4求证：n n

n n n n n C n C C C 2)1()12(53210+=+++++

求值：

5．其它求和方法

还可用归纳猜想法，奇偶法等方法求和。 例5．已知数列{}n n n n S n a a 求],)1([2,---=。

第四节递推数列的通项公式及前n 项和综合

例1．数列{n a }的前n 项和为n S ，且满足11a =，2(1)n n S n a =+.

（1）求{n a }的通项公式；（2）求和T n =1211123(1)n

a a n a ++++ .

例2 ．已知数列}{n a ，a 1=1，点*))(2,(1N n a a P n n ∈+在直线012

1

=+-

y x 上. （1）求数列}{n a 的通项公式； （2）函数)2*,(1

111)(321≥∈++++++++=

n N n a n a n a n a n n f n

且 ，求函数)(n f 最小值.

例3 ．设数列{}n a 的前n 项和为n S ，且1n n S c ca =+-，其中c 是不等于1-和0的实常数.

（1）求证: {}n a 为等比数列；

（2）设数列{}n a 的公比()q f c =，数列{}n b 满足()()111,,23

n n b b f b n N n -==∈≥，试写出1n b ??

????

的通项公式，并求12231n n b b b b b b -+++ 的结果.

例4．已知数列{}n a 的前n 项的和为n S ，且()0,21≠≥?=-n n n n S n S S a ，9

21=

a . （1）求证：?

??

??

?n S 1为等差数列； （2）求数列{}n a 的通项公式．

例5．已知数列{}n a 是首项为11

4a =

，公比14q =的等比数列，设123log n n b a +=()n *∈N ，数列{}n c 满足n n n c a b =?.

（Ⅰ）求证：数列{}n b 成等差数列；

（Ⅱ）求数列{}n c 的前n 项和n S ；

2020年高考理科数学《数列》题型归纳与训练及参考答案

2020年高考理科数学《数列》题型归纳与训练 【题型归纳】 等差数列、等比数列的基本运算 题组一 等差数列基本量的计算 例1 设S n 为等差数列{a n }的前n 项和，若a 1=1，公差d =2，S n ＋2?S n =36，则n = A ．5 B ．6 C ．7 D ．8 【答案】D 【解析】解法一：由题知()21(1) 2 1n S na d n n n n n n ==+-=-+，S n ＋2=(n ＋2)2，由S n ＋2?S n =36得，(n ＋2)2?n 2=4n ＋4=36，所以n =8. 解法二：S n ＋2?S n =a n ＋1＋a n ＋2=2a 1＋(2n ＋1)d =2＋2(2n ＋1)=36，解得n =8.所以选D ． 【易错点】对S n ＋2?S n =36，解析为a n ＋2，发生错误。 题组二 等比数列基本量的计算 例2 在各项均为正数的等比数列{a n }中，若28641,2a a a a ==+，则a 6的值是________． 【答案】4 【解析】设公比为q (q ≠0)，∵a 2=1，则由8642a a a =+得6422q q q =+，即42 20q q --=，解得q 2=2， ∴4 624a a q ==. 【易错点】忘了条件中的正数的等比数列. 【思维点拨】 等差（比）数列基本量的计算是解决等差（比）数列题型时的基础方法，在高考中常有所体现，多以选择题或填空题的形式呈现，有时也会出现在解答题的第一问中，属基础题.等差(比)数列基本运算的解题思路： (1)设基本量a 1和公差d (公比q )． (2)列、解方程组：把条件转化为关于a 1和d (q )的方程(组)，然后求解，注意整体计算，以减少运算量．

高考理科数学《数列》题型归纳与训练

高考理科数学《数列》题型归纳与训练 【题型归纳】 等差数列、等比数列的基本运算 题组一 等差数列基本量的计算 例1 设S n 为等差数列{a n }的前n 项和，若a 1=1，公差d =2，S n ＋2?S n =36，则n = A ．5 B ．6 C ．7 D ．8 【答案】D 【解析】解法一：由题知()21(1) 2 1n S na d n n n n n n ==+-=-+，S n ＋2=(n ＋2)2，由S n ＋2?S n =36得，(n ＋2)2?n 2=4n ＋4=36，所以n =8. 解法二：S n ＋2?S n =a n ＋1＋a n ＋2=2a 1＋(2n ＋1)d =2＋2(2n ＋1)=36，解得n =8.所以选D ． 【易错点】对S n ＋2?S n =36，解析为a n ＋2，发生错误。 题组二 等比数列基本量的计算 例2 在各项均为正数的等比数列{a n }中，若28641,2a a a a ==+，则a 6的值是________． 【答案】4 【解析】设公比为q (q ≠0)，∵a 2=1，则由8642a a a =+得6422q q q =+，即42 20q q --=，解得q 2=2， ∴4 624a a q ==. 【易错点】忘了条件中的正数的等比数列. 【思维点拨】 等差（比）数列基本量的计算是解决等差（比）数列题型时的基础方法，在高考中常有所体现，多以选择题或填空题的形式呈现，有时也会出现在解答题的第一问中，属基础题.等差(比)数列基本运算的解题思路： (1)设基本量a 1和公差d (公比q )． (2)列、解方程组：把条件转化为关于a 1和d (q )的方程(组)，然后求解，注意整体计算，以减少运算量．

高考数学数列题型专题汇总

高考数学数列题型专题 汇总 公司内部档案编码：[OPPTR-OPPT28-OPPTL98-OPPNN08]

高考数学数列题型专题汇总 一、选择题 1、已知无穷等比数列{}n a 的公比为q ，前n 项和为n S ，且S S n n =∞ →lim .下列 条件中，使得()*∈q a （B ）6.07.0,01-<<-q a （D ）7.08.0,01-<<-

A ．{}n S 是等差数列 B ．2{}n S 是等差数列 C ．{}n d 是等差数列 D ．2{}n d 是等差数列 【答案】A 二、填空题 1、已知{}n a 为等差数列，n S 为其前n 项和，若16a =，350a a +=，则 6=S _______.. 【答案】6 2、无穷数列{}n a 由k 个不同的数组成，n S 为{}n a 的前n 项和.若对任意 *∈N n ，{}3,2∈n S ，则k 的最大值为________. 【答案】4 3、设等比数列{}n a 满足a 1+a 3=10，a 2+a 4=5，则a 1a 2a n 的最大值 为 . 【答案】64 4、设数列{a n }的前n 项和为S n .若S 2=4，a n +1=2S n +1，n ∈N *，则 a 1= ，S 5= . 【答案】1 121

数列题型及解题方法归纳总结

累加累积 归纳猜想证明 掌握了数列的基本知识，特别是等差、等比数列的定义、通项公式、求和公式及性质，掌握了 典型 题型的解法和数学思想法的应用，就有可能在高考中顺利地解决数列问题。 一、典型题的技巧解法 1、求通项公式 (1)观察法。(2)由递推公式求通项。 对于由递推公式所确定的数列的求解，通常可通过对递推公式的变换转化成等差数列或等比数列问题。 ⑴递推式为a n+i =3+d 及a n+i =qa n (d ，q 为常数) 例1、 已知｛a n ｝满足a n+i =a n +2，而且a i =1。求a n 。 例1、解 ■/ a n+i -a n =2为常数 ??? ｛a n ｝是首项为1，公差为2的等差数列 /? a n =1+2 (n-1 ) 即 a n =2n-1 1 例2、已知｛a n ｝满足a n 1 a n ，而a 1 2，求a n =? 佥 1 2 解■/^ = +是常数 .■-傀｝是以2为首顶，公比为扌的等比数 把n-1个等式累加得： .' ? an=2 ? 3n-1-1 ji i ? / ] — 3 ⑷ 递推式为a n+1=p a n +q n (p ，q 为常数) s 1 1 【例即己知何沖.衍二右札+ 吧求％ 略解在如十冷)*的两边乘以丹得 2 严‘ *珞1 = ~〔2怙血)+1.令亠=2n 召 则也€%乜于是可得 2 2 n b n 1 n 1 n b n 1 b n (b n b n 1)由上题的解法，得：b n 3 2(—) ? a . n 3(—) 2(—) 3 3 2 2 3 ★说明对于递推式辺曲=+屮，可两边除以中叫得蹲= Q 計/斗引辅助财如(%=芒.徼十氣+护用 (5) 递推式为 a n 2 pa n 1 qa n 知识框架 数列 的概念 数列的分类 数列的通项公式 数列的递推关系 函数角度理解 (2)递推式为 a n+1=a n +f (n ) 1 2 例3、已知｛a n ｝中 a 1 a n 1 a n 1 ，求 a n . 4n 2 1 等差数列的疋义 a n a n 1 d(n 2) 等差数列的通项公式 a n a 1 (n 1)d 等差数列 等差数列的求和公式 S n (a 1 a n ) na 1 n(n 1)d 2 2 等差数列的性质 a n a m a p a q (m n p q) 两个基 本数列 等比数列的定义 a n 1 q(n 2) 等比数列的通项公式 a n n 1 a 1q 数列 等比数列 a 1 a n q 3(1 q ) (q 1) 等比数列的求和公式 S n 1 q 1 q / n a 1(q 1) 等比数列的性质 S n S m a p a q (m n p q) 公式法 分组求和 错位相减求和 裂项求和 倒序相加求和 解：由已知可知a n 1 a n (2n 1)(2n 1)夕2n 1 2n 令n=1，2，…，(n-1 )，代入得(n-1 )个等式累加，即(a 2-a 1) + 1广 K z 1】、 =-[(1-" + J J 5 _■ 冷(一 Jr ★ 说明 只要和f ( 1) +f (2) 入，可得n-1个等式累加而求a n 。 ⑶ 递推式为a n+1=ps n +q (p , q 为常数) 1 a n a 1 (1 2 +?…+f 例 4、｛a n ｝中，ai 1，对于 n > 1 (n € N) 有a n (a 3-a 2) + ? + (a n -a n-1) L )也 2n 1 4n 2 (n-1 )是可求的，就可以由 a n+1=a n +f (n )以n=1，2，…， 3a n 1 2 ，求 a n ? 数列 求和 解法一： 由已知递推式得 a n+1=3a n +2，a n =3a n-1+2。两式相减：a n+1-a n =3 (a n -a n-1) 因此数列｛a n+1-a n ｝是公比为3的等比数列，其首项为 a 2-a 1= (3X 1+2) -1=4 --a n+1 -a n =4 ? 3 - a n+1 =3a n +2 - - 3a n +2-a n =4 ? 3 即 a n =2 ? 3 -1 解法_ : 上法得｛a n+1-a n ｝是公比为 3 的等比数列，于是有： a 2-a 1=4， a 3-a 2=4 ? 3， a 4-a 3=4 ? 3 ? 3 ， 数列的应用 分期付款 其他

高中数学数列复习题型归纳解题方法整理

数列 一、等差数列与等比数列 1.基本量的思想： 常设首项、（公差）比为基本量，借助于消元思想及解方程组思想等。转化为“基本量”是解决问题的基本方法。 2.等差数列与等比数列的联系 1）若数列{}n a 是等差数列，则数列}{n a a 是等比数列，公比为d a ，其中a 是常数，d 是{}n a 的公差。 （a>0且a ≠1）； 2）若数列{}n a 是等比数列，且0n a >，则数列{}log a n a 是等差数列，公差为log a q ，其中a 是常数且 0,1a a >≠，q 是{}n a 的公比。 3）若{}n a 既是等差数列又是等比数列,则{}n a 是非零常数数列。 3.等差与等比数列的比较

4、典型例题分析 【题型1】等差数列与等比数列的联系 例1 （2010陕西文16）已知{}是公差不为零的等差数列，a1＝1，且a1，a3，a9成等比数列.（Ⅰ）求数列{}的通项;（Ⅱ）求数列{2}的前n项和. 解：（Ⅰ）由题设知公差d≠0， 由a1＝1，a1，a3，a9成等比数列得12 1 d + ＝ 18 12 d d + + ， 解得d＝1，d＝0（舍去），故{}的通项＝1+（n－1）×1＝n. (Ⅱ)由（Ⅰ）知2m a=2n，由等比数列前n项和公式得 2+22+23+…+22(12) 12 n - - 21-2. 小结与拓展：数列{}n a是等差数列，则数列} {n a a是等比数列，公比为d a，其中a是常数，d是{}n a的公差。（a>0且a≠1）. 【题型2】与“前n项和与通项”、常用求通项公式的结合 例2 已知数列{}的前三项与数列{}的前三项对应相同，且a1＋2a2＋22a3＋…＋2n－1＝8n对任意的n∈N*都成立，数列{＋1－}是等差数列．求数列{}与{}的通项公式。 解：a1＋2a2＋22a3＋…＋2n－1＝8n(n∈N*) ① 当n≥2时，a1＋2a2＋22a3＋…＋2n－2－1＝8(n－1)(n∈N*) ② ①－②得2n－1＝8，求得＝24－n， 在①中令n＝1，可得a1＝8＝24－1， ∴＝24－n(n∈N*)．由题意知b1＝8，b2＝4，b3＝2，∴b2－b1＝－4，b3－b2＝－2， ∴数列{＋1－}的公差为－2－(－4)＝2，∴＋1－＝－4＋(n－1)×2＝2n－6，

高考数学数列知识点及题型大总结

20XX 年高考数学数列知识点及题型大总结 等差数列 知识要点 1．递推关系与通项公式 m n a a d n a a d d n a a d m n a a d n a a d a a m n n n m n n n n --= --= --=-+=-+==-+1; )1()()1(1111变式：推广：通项公式：递推关系： 为常数） 即：特征：m k m kn n f a d a dn a n n ,(,)(), (1+==-+= ),为常数，（m k m kn a n +=是数列{}n a 成等差数列的充要条件。 2．等差中项： 若c b a ,,成等差数列，则b 称c a 与的等差中项，且2 c a b +=；c b a ,,成等差数列是c a b +=2的充要条件。 3．前n 项和公式 2 )(1n a a S n n += ； 2)1(1d n n na S n -+= ) ,()(,)2(22212为常数即特征：B A Bn An S Bn An n f S n d a n d S n n n +=+==-+= 是数列 {}n a 成等差数列的充要条件。 4．等差数列 {}n a 的基本性质),,,(*∈N q p n m 其中 ⑴q p n m a a a a q p n m +=++=+，则若反之，不成立。 ⑵d m n a a m n )(-=- ⑶m n m n n a a a +-+=2

⑷n n n n n S S S S S 232,,--仍成等差数列。 5．判断或证明一个数列是等差数列的方法： ①定义法： ）常数）（*+∈=-N n d a a n n (1?{}n a 是等差数列 ②中项法： )22 1*++∈+=N n a a a n n n （?{}n a 是等差数列 ③通项公式法： ),(为常数b k b kn a n +=?{}n a 是等差数列 ④前n 项和公式法： ),(2为常数B A Bn An S n +=?{}n a 是等差数列 练习：1．等差数列 {}n a 中， ) (3 1 ,1201191210864C a a a a a a a 的值为则-=++++ A ．14 B ．15 C ．16 D ．17 165 1203232)(32) 2(3 1 318999119=?==-=+-=-a d a d a a a a 2．等差数列 {}n a 中，12910S S a =>，，则前10或11项的和最大。 解：0912129 =-=S S S S ， 003011111121110>=∴=∴=++∴a a a a a a ，又，， ∴ {}n a 为递减等差数列∴1110S S =为最大。 3．已知等差数列{}n a 的前10项和为100，前100项和为10，则前110项和为－110 解：∵ ，，，，，1001102030102010S S S S S S S --- 成等差数列，公差为D 其首项为 10010=S ，前10项的和为10100=S 解

数列高考题型分类汇总

题型一 1．设{a n }是公比为正数的等比数列a 1 =2，a 3 =a 2 +4． （Ⅰ）求{a n }的通项公式； （Ⅱ）设{b n }是首项为1，公差为2的等差数列，求数列{a n +b n }的前n项和S n ． 题型二 2．已知数列{a n }、{b n }、{c n }满足． （1）设c n =3n+6，{a n }是公差为3的等差数列．当b 1 =1时，求b 2 、b 3 的值； （2）设，．求正整数k，使得对一切n∈N*，均有b n ≥b k ； （3）设，．当b 1=1时，求数列{b n }的通项公式． 题型三 3．已知数列{an}满足a1=0，a2=2，且对任意m、n∈N*都有a2m﹣1+a2n﹣1=2am+n ﹣1+2（m﹣n）2 （1）求a 3，a 5 ； （2）设b n =a 2n+1 ﹣a 2n﹣1 （n∈N*），证明：{b n }是等差数列； （3）设c n =（a n+1 ﹣a n ）q n﹣1（q≠0，n∈N*），求数列{c n }的前n项和S n ． 题型四 4．已知数列{an}满足，，n∈N×． （1）令b n =a n+1 ﹣a n ，证明：{b n }是等比数列； （2）求{a n }的通项公式． 5．设数列{an}的前n项和为Sn=2an﹣2n， （Ⅰ）求a 1，a 4 （Ⅱ）证明：{a n+1 ﹣2a n}是等比数列； （Ⅲ）求{a n }的通项公式． 6．在数列{a n }中，a 1 =1，．

（Ⅰ）求{a n }的通项公式； （Ⅱ）令 ，求数列{b n }的前n 项和S n ； （Ⅲ）求数列{a n }的前n 项和T n ． 7．已知数列{a n }的首项， ，n=1，2，3，…． （Ⅰ）证明：数列是等比数列； （Ⅱ）求数列的前n 项和S n ． 8.在数列{}n a 中，10a =，且对任意*k N ∈k N ∈，21221,,k k k a a a -+成等差数列， 其公差为k d 。 (Ⅰ)若k d =2k ，证明21222,,k k k a a a -+成等比数列（*k N ∈）； (Ⅱ)若对任意*k N ∈，21222,,k k k a a a -+成等比数列，其公比为k q . 设1q ≠1.证明11k q ????-??是等差数列； 9.设数列{}n a 的前n 项和为,n S 已知11,a =142n n S a +=+ （I ）设12n n n b a a +=-，证明数列{}n b 是等比数列 （II ）求数列{}n a 的通项公式。 10. 设数列{}n a 的前n 项和为n S ，已知()21n n n ba b S -=- （Ⅰ）证明：当2b =时，{}12n n a n --?是等比数列； （Ⅱ）求{}n a 的通项公式

人教版高中数列知识点总结(知识点+例题)

人教版高中数列知识点总结(知识点+例题) Lesson6 数列 知识点1：等差数列及其前n 项 1．等差数列的定义 2．等差数列的通项公式 如果等差数列{a n }的首项为a 1，公差为d ，那么它的通项公式a n ＝a 1＋(n －1) d . 3．等差中项 a ＋b 如果 A ＝2 ，那么A 叫做a 与b 的等差中项． 4．等差数列的常用性质 (1)通项公式的推广：a n ＝a m ＋（n-m ）d ，(n ，m ∈N *) ． (2)若{a n }为等差数列，且k ＋l ＝m ＋n ，(k ，l ，m ，n ∈N *) ，则 (3)若{a n }是等差数列，公差为d ，则{a 2n }也是等差数列，公差为. (4)若{a n }，{b n }是等差数列，则{pa n ＋qb n }也是等差数列． (5)若{a n }是等差数列，公差为d ，则a k ，a k ＋m ，a k ＋2m ，…(k ，m ∈N *) 是公差为的等差数列． 5．等差数列的前n 项和公式 n (a 1＋a n )n (n －1) 设等差数列{a n }的公差d ，其前n 项和S n 或S n ＝na 1＋22. 6．等差数列的前n 项和公式与函数的关系 d d 2? S n 2＋ a 1－2n . 数列{a n }是等差数列?S n ＝An 2＋Bn ，(A 、B 为常数) ． ?? 7．等差数列的最值 在等差数列{a n }中，a 1>0，d 0，则S n 存在最小值． [难点正本疑点清源] 1．等差数列的判定 (1)定义法：a n －a n －1＝d (n ≥2) ； (2)等差中项法：2a n ＋1＝a n ＋a n ＋2.

高考数列专题总结(全是精华)

数列专题复习（0929） 一、证明等差等比数列 1． 等差数列的证明方法： （1）定义法：1n n a a d +-=(常数) （2）等差中项法：112(2)n n n a a a n +-+=≥ 2．等比数列的证明方法： （1）定义法： 1 n n a q a +=(常数) （2）等比中项法：211(2)n n n a a a n +-=≥ 例1.设｛a n ｝为等差数列，S n 为数列｛a n ｝的前n 项和，已知S 7＝7，S 15＝75， T n 为数列｛ n S n ｝的前n 项和，求T n ． 解：设等差数列｛a n ｝的公差为d ，则 S n =na 1＋21 n （n －1）d ．∴S 7＝7，S 15＝75，∴???=+=+,7510515,721711d a d a 即???=+=+,57,131 1d a d a 解得a 1＝－2，d ＝1．∴ n S n ＝a 1＋21（n －1）d ＝－2＋21 （n －1）． ∵ 2111=-++n S n S n n ，∴数列｛n S n ｝是等差数列，其首项为－2，公差为21 ， ∴T n ＝ 41n 2－4 9 n ． 例2．设数列{a n }的首项a 1=1，前n 项和S n 满足关系式： 3tS n －（2t +3）S n －1=3t （t >0，n =2，3，4，…） 求证：数列{a n }是等比数列； 解：（1）由a 1=S 1=1，S 2=1+a 2，得a 2=t t a a t t 323,32312+= + 又3tS n －（2t +3）S n －1=3t ① 3tS n －1－（2t +3）S n －2=3t ② ①－②得3ta n －（2t +3）a n －1=0 ∴ t t a a n n 33 21+= -，（n =2，3，…） 所以{a n }是一个首项为1，公比为t t 33 2+的等比数列. 练习：已知a 1=2，点(a n ,a n+1)在函数f (x )=x 2+2x 的图象上，其中=1，2，3，… （1） 证明数列｛lg(1+a n )｝是等比数列； （2） 设T n =(1+a 1) (1+a 2) …(1+a n )，求T n 及数列｛a n ｝的通项； 答案 .(2) 2 1 3n n T -=,2 1 31n n a -=-; 二．通项的求法 （1）利用等差等比的通项公式 (2)累加法：1()n n a a f n +-= 例3．已知数列{}n a 满足211=a ，n n a a n n ++=+211，求n a 。 解：由条件知：1 1 1)1(112 1+-=+=+= -+n n n n n n a a n n 分别令)1(,,3,2,1-??????=n n ，代入上式得)1(-n 个等式累加之，即 )()()()(1342312--+??????+-+-+-n n a a a a a a a a )111()4131()3121()211(n n --+??????+-+-+-=所以n a a n 1 11-=- 211=a ，n n a n 1231121-=-+=∴ （3）构造等差或等比 1n n a pa q +=+或1()n n a pa f n +=+ 例4．已知数列{}n a 满足*111,21().n n a a a n N +==+∈ 求数列{}n a 的通项公式； 解：* 121(),n n a a n N +=+∈ 112(1),n n a a +∴+=+ {}1n a ∴+是以112a +=为首项，2为公比的等比数列。 12.n n a ∴+= 即 *21().n n a n N =-∈ 例5．已知数列{}n a 中，11a =,1111 ()22 n n n a a ++=+，求n a . 解：在1111 ()22 n n n a a ++= +两边乘以12+n 得：112(2)1n n n n a a ++?=?+ 令2n n n b a =?，则11n n b b +-=,解之得：111n b b n n =+-=-,所以1 22 n n n n b n a -= =.

高考数学 题型全归纳：数列在生活中的应用(含答案)

数列在生活中的应用 在实际生活和经济活动中，很多问题都与数列密切相关。如分期付款、个人投资理财以及人口问题、资源问题等都可运用所学数列知识进行分析，从而予以解决。与此同时,数列在艺术创作上也有突出的作用! 数学家华罗庚曾经说过：宇宙之大，粒子之微，火箭之速，化工之巧，地球之变，日用之繁，无处不用数学。这是对数学与生活关系的精彩描述。 首先, 我重点分析等差数列、等比数列在实际生活和经济活动中的应用。 （一）按揭货款中的数列问题 随着中央推行积极的财政政策，购置房地产按揭货款（公积金贷款）制度的推出，极大地刺激了人们的消费欲望，扩大了内需，有效地拉动了经济增长。 众所周知，按揭货款（公积金贷款）中都实行按月等额还本付息。这个等额数是如何得来的，此外若干月后，还应归还银行多少本金，这些人们往往很难做到心中有数。下面就来寻求这一问题的解决办法。 若贷款数额a0元,贷款月利率为p,还款方式每月等额还本付息a元.设第n月还款后的本金为an,那么有: a1=a0(1+p)-a, a2=a1(1+p)-a, a3=a2(1+p)-a, ...... an+1=an(1+p)-a,.........................(*) 将（*）变形，得（an+1-a/p）/（an-a/p）=1+p. 由此可见，{an-a/p}是一个以a1-a/p为首项，1+p为公比的等比数列。日常生活中一切有关按揭货款的问题，均可根据此式计算。 （二）有关数列的其他经济应用问题 数列知识除在个人投资理财方面有较为广泛的应用外，在企业经营管理上也是不可或缺的。一定做过大量的应用题吧！虽然这些应用题是从实际生活中抽象出的略高于生活的问题，但他们是数学习题中最能反映数学知识与实际生活密切关系的一类问题。因此，解答应用问题有助于我们对数学在日常生活中广泛应用的理解和认识。 (三)数列在艺术中的广泛应用

数列题型及解题方法归纳总结99067

知识框架 111111(2)(2)(1)(1)()22()n n n n n n m p q n n n n a q n a a a q a a d n a a n d n n n S a a na d a a a a m n p q --=≥=?? ←???-=≥?? =+-??-?=+=+??+=++=+??两个基等比数列的定义本数列等比数列的通项公式等比数列数列数列的分类数列数列的通项公式函数角度理解 的概念数列的递推关系等差数列的定义等差数列的通项公式等差数列等差数列的求和公式等差数列的性质1111(1)(1) 11(1)() n n n n m p q a a q a q q q q S na q a a a a m n p q ---=≠--===+=+???? ? ???????????????? ??? ???????????? ???? ????????????? ?????? ? ?? ?? ?? ?? ??????????? 等比数列的求和公式等比数列的性质公式法分组求和错位相减求和数列裂项求和求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用其他??????? ? ? 掌握了数列的基本知识，特别是等差、等比数列的定义、通项公式、求和公式及性质，掌握了典型题型的解法和数学思想法的应用，就有可能在高考中顺利地解决数列问题。 一、典型题的技巧解法 1、求通项公式 （1）观察法。（2）由递推公式求通项。 对于由递推公式所确定的数列的求解，通常可通过对递推公式的变换转化成等差数列或等比数列问题。 (1)递推式为a n+1=a n +d 及a n+1=qa n （d ，q 为常数） 例1、 已知{a n }满足a n+1=a n +2，而且a 1=1。求a n 。 例1、解 ∵a n+1-a n =2为常数 ∴{a n }是首项为1，公差为2的等差数列 ∴a n =1+2（n-1） 即a n =2n-1 例2、已知{}n a 满足11 2 n n a a +=，而12a =，求n a = （2）递推式为a n+1=a n +f （n ） 例3、已知{}n a 中112a = ，12141 n n a a n +=+-，求n a . 解： 由已知可知)12)(12(11-+= -+n n a a n n )1 21 121(21+--=n n 令n=1，2，…，（n-1），代入得（n-1）个等式累加，即（a 2-a 1）+（a 3-a 2）+…

数列题型与解题方法归纳总结

.下载可编辑. 知识框架 111111(2)(2)(1)(1)()22()n n n n n n m p q n n n n a q n a a a q a a d n a a n d n n n S a a na d a a a a m n p q --=≥=?? ←???-=≥?? =+-??-?=+=+??+=++=+??两个基等比数列的定义本数列等比数列的通项公式等比数列数列数列的分类数列数列的通项公式函数角度理解 的概念数列的递推关系等差数列的定义等差数列的通项公式等差数列等差数列的求和公式等差数列的性质1111(1)(1) 11(1)() n n n n m p q a a q a q q q q S na q a a a a m n p q ---=≠--===+=+???? ? ???????????????? ??? ???????????? ???? ????????????? ?????? ? ?? ?? ?? ????????????? 等比数列的求和公式等比数列的性质公式法分组求和错位相减求和数列裂项求和求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用其他??????? ? ? 掌握了数列的基本知识，特别是等差、等比数列的定义、通项公式、求和公式及性质，掌握了典型题型的解法和数学思想法的应用，就有可 能在高考中顺利地解决数列问题。 一、典型题的技巧解法 1、求通项公式 （1）观察法。（2）由递推公式求通项。 对于由递推公式所确定的数列的求解，通常可通过对递推公式的变换转化成等差数列或等比数列问题。 (1)递推式为a n+1=a n +d 及a n+1=qa n （d ，q 为常数） 例1、 已知{a n }满足a n+1=a n +2，而且a 1=1。求a n 。 例1、解 ∵a n+1-a n =2为常数 ∴{a n }是首项为1，公差为2的等差数列 ∴a n =1+2（n-1） 即a n =2n-1 例2、已知{}n a 满足11 2 n n a a +=，而12a =，求n a =？ （2）递推式为a n+1=a n +f （n ） 例3、已知{}n a 中112a = ，12141 n n a a n +=+-，求n a . 解： 由已知可知)12)(12(11-+= -+n n a a n n )1 21 121(21+--=n n 令n=1，2，…，（n-1），代入得（n-1）个等式累加，即（a 2-a 1）+（a 3-a 2）+… +（a n -a n-1）

高考数列解题技巧归纳总结

高考数列解题技巧归纳总结 知识框架 111111(2)(2)(1)(1)()22()n n n n n n m p q n n n n a q n a a a q a a d n a a n d n n n S a a na d a a a a m n p q --=≥=?? ←???-=≥?? =+-??-?=+=+??+=++=+??两个基等比数列的定义本数列等比数列的通项公式等比数列数列数列的分类数列数列的通项公式函数角度理解 的概念数列的递推关系等差数列的定义等差数列的通项公式等差数列等差数列的求和公式等差数列的性质1111(1)(1) 11(1)() n n n n m p q a a q a q q q q S na q a a a a m n p q ---=≠--===+=+???? ? ???????????????? ??? ???????????? ???? ????????????? ?????? ? ?? ?? ?? ?? ??????????? 等比数列的求和公式等比数列的性质公式法分组求和错位相减求和数列裂项求和 求和倒序相加求和累加累积归纳猜想证明分期付款数列的应用其他??????? ? ? 掌握了数列的基本知识，特别是等差、等比数列的定义、通项公式、求和公式及性质，掌握 了典型题型的解法和数学思想法的应用，就有可能在高考中顺利地解决数列问题。 一、典型题的技巧解法 1、求通项公式 （1）观察法。（2）由递推公式求通项。 对于由递推公式所确定的数列的求解，通常可通过对递推公式的变换转化成等差数列或等比数列问题。 (1)递推式为a n+1=a n +d 及a n+1=qa n （d ，q 为常数） 例1、 已知{a n }满足a n+1=a n +2，而且a 1=1。求a n 。 解 ∵a n+1-a n =2为常数 ∴{a n }是首项为1，公差为2的等差数列 ∴a n =1+2（n-1） 即a n =2n-1 例2、已知{}n a 满足11 2 n n a a +=，而12a =，求n a =？

高中数学最全数列总结及题型精选

高中数学：数列及最全总结和题型精选 一、数列的概念 （1）数列定义：按一定次序排列的一列数叫做数列； 数列中的每个数都叫这个数列的项。记作n a ，在数列第一个位置的项叫第1项（或首项），在第二个位置的叫第2项，……，序号为n 的项叫第n 项（也叫通项）记作n a ； 数列的一般形式：1a ，2a ，3a ，……，n a ，……，简记作 {}n a 。 （2）通项公式的定义：如果数列}{n a 的第n 项与n 之间的关系可以用一个公式表示，那么这个公式就叫 这个数列的通项公式。 例如：①：1 ，2 ，3 ，4， 5 ，… ②：5 14131211，，，，… 说明： ①{}n a 表示数列，n a 表示数列中的第n 项，n a = ()f n 表示数列的通项公式； ② 同一个数列的通项公式的形式不一定唯一。例如，n a = (1)n -=1,21 ()1,2n k k Z n k -=-?∈?+=? ； ③不是每个数列都有通项公式。例如，1，，，，…… （3）数列的函数特征与图象表示： 从函数观点看，数列实质上是定义域为正整数集N +（或它的有限子集）的函数()f n 当自变量n 从1开始 依次取值时对应的一系列函数值(1),(2),(3),f f f ……，()f n ，……．通常用n a 来代替()f n ，其图象是一群孤立点。 （4）数列分类：①按数列项数是有限还是无限分：有穷数列和无穷数列；②按数列项与项之间的大小关系分：递增数列、递减数列、常数列和摆动数列。 例：下列的数列，哪些是递增数列、递减数列、常数列、摆动数列 （1）1，2，3，4，5，6，… (2)10, 9, 8, 7, 6, 5, … (3) 1, 0, 1, 0, 1, 0, … (4)a, a, a, a, a,… （5）数列{n a }的前n 项和n S 与通项n a 的关系：1 1(1)(2)n n n S n a S S n -=?=? -?≥ 二、等差数列 (一)、等差数列定义：一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数，那么这个数列就叫等差数列，这个常数叫做等差数列的公差，公差通常用字母d 表示。用递推公式表示为1n n -或1(1)n n a a d n +-=≥ 例：等差数列12-=n a n ，=--1n n a a (二)、等差数列的通项公式：1(1)n a a n d =+-； 说明：等差数列（通常可称为A P 数列）的单调性：d 0>为递增数列，0d =为常数列，0d < 为递减数列。 例：1.已知等差数列{}n a 中，124971 16a a a a ，则，==+等于（ ） A ．15 B ．30 C ．31 D ．64 2.{}n a 是首项11a =，公差3d =的等差数列，如果2005n a =，则序号n 等于 （A ）667 （B ）668 （C ）669 （D ）670 3.等差数列12,12+-=-=n b n a n n ，则n a 为 n b 为 （填“递增数列”或“递减数列”） (三)、等差中项的概念： 定义：如果a ，A ，b 成等差数列，那么A 叫做a 与b 的等差中项。其中2 a b A +=

数列题型及解题方法归纳总结

知识框架 掌握了数列的基本知识，特别是等差、等比数列的定义、通项公式、求和公式及性质，掌握了典型题型的解法和数学思想法的应用，就有可能在高考中顺利地解决数列问题。 一、典型题的技巧解法 1、求通项公式 （1）观察法。（2）由递推公式求通项。 对于由递推公式所确定的数列的求解，通常可通过对递推公式的变换转化成等差数列或等比数列问题。 (1)递推式为a n+1=a n +d 及a n+1=qa n （d ，q 为常 数） 例1、已知{a n }满足a n+1=a n +2，而且a 1=1。求a n 。 例1、解∵a n+1-a n =2为常数∴{a n }是首项为1，公差为2的等差数列 ∴a n =1+2（n-1）即a n =2n-1 例2、已知{}n a 满足11 2n n a a +=，而12a =，求 n a =？ （2）递推式为a n+1=a n +f （n ） 例3、已知{}n a 中112 a = ，12 141 n n a a n +=+ -，求n a . 解：由已知可知 )12)(12(11-+= -+n n a a n n )1 21 121(21+--=n n 令n=1，2，…，（n-1），代入得（n-1）个等式累加，即（a 2-a 1）+（a 3-a 2）+…+（a n -a n-1） ★ 说明只要和f （1）+f （2）+…+f （n-1）是可求的，就可以由a n+1=a n +f （n ）以n=1，2，…，（n-1）代入，可得n-1个等式累加而求a n 。 (3)递推式为a n+1=pa n +q （p ，q 为常数） 例4、{}n a 中，11a =，对于n ＞1（n ∈N ）有 132n n a a -=+，求n a . 解法一：由已知递推式得a n+1=3a n +2，a n =3a n-1+2。两式相减：a n+1-a n =3（a n -a n-1） 因此数列{a n+1-a n }是公比为3的等比数列，其首项为a 2-a 1=（3×1+2）-1=4 ∴a n+1-a n =4·3n-1∵a n+1=3a n +2∴3a n +2-a n =4·3n-1 即a n =2·3n-1-1 解法二：上法得{a n+1-a n }是公比为3的等比数列，于是有：a 2-a 1=4，a 3-a 2=4·3，a 4-a 3=4·32，…，a n -a n-1=4·3n-2， 把n-1个等式累加得：∴an=2·3n-1-1 (4)递推式为a n+1=pa n +qn （p ，q 为常数） )(3 2 11-+-=-n n n n b b b b 由上题的解法， 得：n n b )3 2(23-=∴ n n n n n b a )31(2)21(32 -== (5)递推式为21n n n a pa qa ++=+ 思路：设21n n n a pa qa ++=+,可以变形为： 211()n n n n a a a a αβα+++-=-， 想 于是{a n+1-αa n }是公比为β的等比数列，就转化 为前面的类型。 求n a 。 (6)递推式为S n 与a n 的关系式 系；（2）试用n 表示a n 。 ∴)2121( )(1 2 11 --++- +-=-n n n n n n a a S S ∴1 11 2 1 -+++ -=n n n n a a a ∴ n n n a a 2 1 211+= + 上式两边同乘以2n+1得2n+1a n+1=2n a n +2则{2n a n }是公差为2的等差数列。 ∴2n a n =2+（n-1）·2=2n 数列求和的常用方法： 1、拆项分组法：即把每一项拆成几项，重新组合分成几组，转化为特殊数列求和。

数学高考大题题型归纳必考题型例题

数学高考大题题型归纳必考题型例题 1数学高考大题题型有哪些 必做题： 1.三角函数或数列（必修4，必修5） 2.立体几何（必修2） 3.统计与概率（必修3和选修2-3） 4.解析几何（选修2-1） 5.函数与导数（必修1和选修2-2） 选做题： 1.平面几何证明（选修4-1） 2.坐标系与参数方程（选修4-4） 3.不等式（选修4-5） 2数学高考大题题型归纳 一、三角函数或数列 数列是高中数学的重要内容，又是学习高等数学的基础。高考对本章的考查比较全面，等差数列，等比数列的考查每年都不会遗漏。有关数列的试题经常是综合题，经常把数列知识和指数函数、对数函数和不等式的知识综合起来，试题也常把等差数列、等比数列，求极限和数学归纳法综合在一起。探索性问题是高考的热点，常在数列解答题中出现。本章中还蕴含着丰富的数学思想，在主观题中着重考查函数与方程、转化与化归、分类讨论等重要思想，以及配方法、换元法、待定系数法等基本数学方法。 近几年来，高考关于数列方面的命题主要有以下三个方面;(1)数列本身的有关知识，其中有等差数列与等比数列的概念、性质、通项公式及求和公式。(2)数列与其它知识的结合，其中有数列与函数、方程、不等式、三角、几何的结合。(3)数列的应用问题，其中主要是以增长率问题为主。试题的难度有三个层次，小题大都以基础题为主，解答题大都以基础题和中档题为主，只有个别地方用数列与几何的综合与函数、不等式的综合作为最后一题难度较大。 二、立体几何 高考立体几何试题一般共有4道(选择、填空题3道，解答题1道)，共计总分27分左右，考查的知识点在20个以内。选择填空题考核立几中的计算型问题，而解答题着重考查立几中的逻辑推理型问题，当然，二者均应以正确的空间想象为前提。随着新的课程改革的进一步实

数列常见题型总结经典(超级经典)

高中数学《数列》常见、常考题型总结 题型一 数列通项公式的求法 1．前n 项和法（知n S 求n a ）?? ?-=-11n n n S S S a )2()1(≥=n n 例1、已知数列}{n a 的前n 项和212n n S n -=，求数列|}{|n a 的前n 项和n T 1、若数列}{n a 的前n 项和n n S 2=，求该数列的通项公式。 2、若数列}{n a 的前n 项和32 3-= n n a S ，求该数列的通项公式。 3、设数列}{n a 的前n 项和为n S ，数列}{n S 的前n 项和为n T ，满足22n S T n n -=， 求数列}{n a 的通项公式。 2.形如)(1n f a a n n =-+型（累加法） （1）若f(n)为常数,即：d a a n n =-+1,此时数列为等差数列，则n a =d n a )1(1-+. （2）若f(n)为n 的函数时，用累加法. 例 1. 已知数列｛a n ｝满足)2(3 ,1111≥+==--n a a a n n n ,证明2 13-=n n a

1. 已知数列{}n a 的首项为1，且*12()n n a a n n N +=+∈写出数列{}n a 的通项公式. 2. 已知数列}{n a 满足31=a ，)2() 1(11≥-+ =-n n n a a n n ，求此数列的通项公式. 3.形如 )(1n f a a n n =+型（累乘法） （1）当f(n)为常数，即：q a a n n =+1（其中q 是不为0的常数），此数列为等比且n a =11-?n q a . （2）当f(n)为n 的函数时,用累乘法. 例1、在数列}{n a 中111,1-+= =n n a n n a a )2(≥n ，求数列的通项公式。 1、在数列}{n a 中1111,1-+-= =n n a n n a a )2(≥n ，求n n S a 与。 2、求数列)2(1232,11 1≥+-==-n a n n a a n n 的通项公式。