多项式插值理论

第六章 多项式插值理论

一、区间[a , b ]上的一般插值理论 (从有限维子空间出发的逼近方法)

① 对无限维函数空间的一个元素f (x ) 进行逼近，关于f (x ) 的情况仅知道一部分

(1、若干点的函数值或导数值已知； 2、满足一些控制方程)

② 选择一个由固定基函数张成的有限维函数子空间 基函数性质: ??

??

?、线性无关、完备的条件、满足基本的函数已知321

③ 选择n X 中的元素)()(~x P x f n 或，在一定的约束条件下，使)(~

x f 良好的逼近()x f ,

即 令)(~

x f = n n c c c φφφ+++ 2211关于()x f 在插值区间上有不大的误差（包括一定的光滑性逼近）。 ④ 良好逼近的判断

ε<-f f ~

e .g . Tchebychef

f 范数，|| f || = |)(|max x f b

x a ≤≤ 称为一致逼近。

⑤ 约束条件: （依据对()x f 的了解来确定）

i / 插值约束

)()(~

i i x f x f = 1n i ≤≤ i x ∈ (a , b ) 且i x 互不相同；

ii / 插值与光滑性混合约束

(1)、 )()(~

i i x f x f = 1k i ≤≤ i x ∈(a , b ) 且i x 互不相同

(2)、 )()(~

i i x f x f '=' 1k i ≤≤ i x ∈(a,b) 且互不相同

(3)、 )(~

x f 的二阶导数存在

iii / 变分约束 （以下两种约束不再具有严格的插值含义，这里可能仅知道被插函数

满足某些控制方程）

依据|| f -f ~||在n X 中为最小的条件，即确定常数n c c c 21, 使f ~

的解由下列形式的极小化问题得到：

|| f -0f ~|| = min{|| f -f ~||：f ~

n X ∈}

Note ：这里的||·|| 不局限于切比雪夫范数和2－范数，可能是某种内积定义的范数；这也是固体力学求近似解的基本方法（如，有限元就是能量的变分）。 iv / 正交约束

根据f -f ~

与n 个给定基函数)(,),(),(21x x x n φφφ 的正交条件，确定常数：

i c , 1n i ≤≤。即

< f -f ~

,0)()](~

)([=->=

?

dx x x f x f i b

a

i φφ 1n i ≤≤

{}n n Span X φφφ,,,21 =

这是Galerkin 方法的基础。

Note :

1）、约束条件可组合使用，如在有限元的计算中，构造位移形状函数时，应用插值或光

滑性约束条件与变分约束的组合。

2）、仅对插值约束问题，实际构成求解下列方程组：

???

?

?=+++=+++)

()()()()

()()()(221

111212111n n n n n n n n x f c x c x c x x f c x c x c x φφφφφφ 3）、若选取X n = Span {n x x x ,,,,12 } 则称为Lagrange 多项式插值。 二 、Lagrange 多项式插值

1、多项式插值的一般定理

Weierstrass （维尔斯托拉斯）定理：

设[a , b ]为任意给定的闭区间，ε为任意小常数，f (x )为 [a ,b ]上的任意连续函数，则

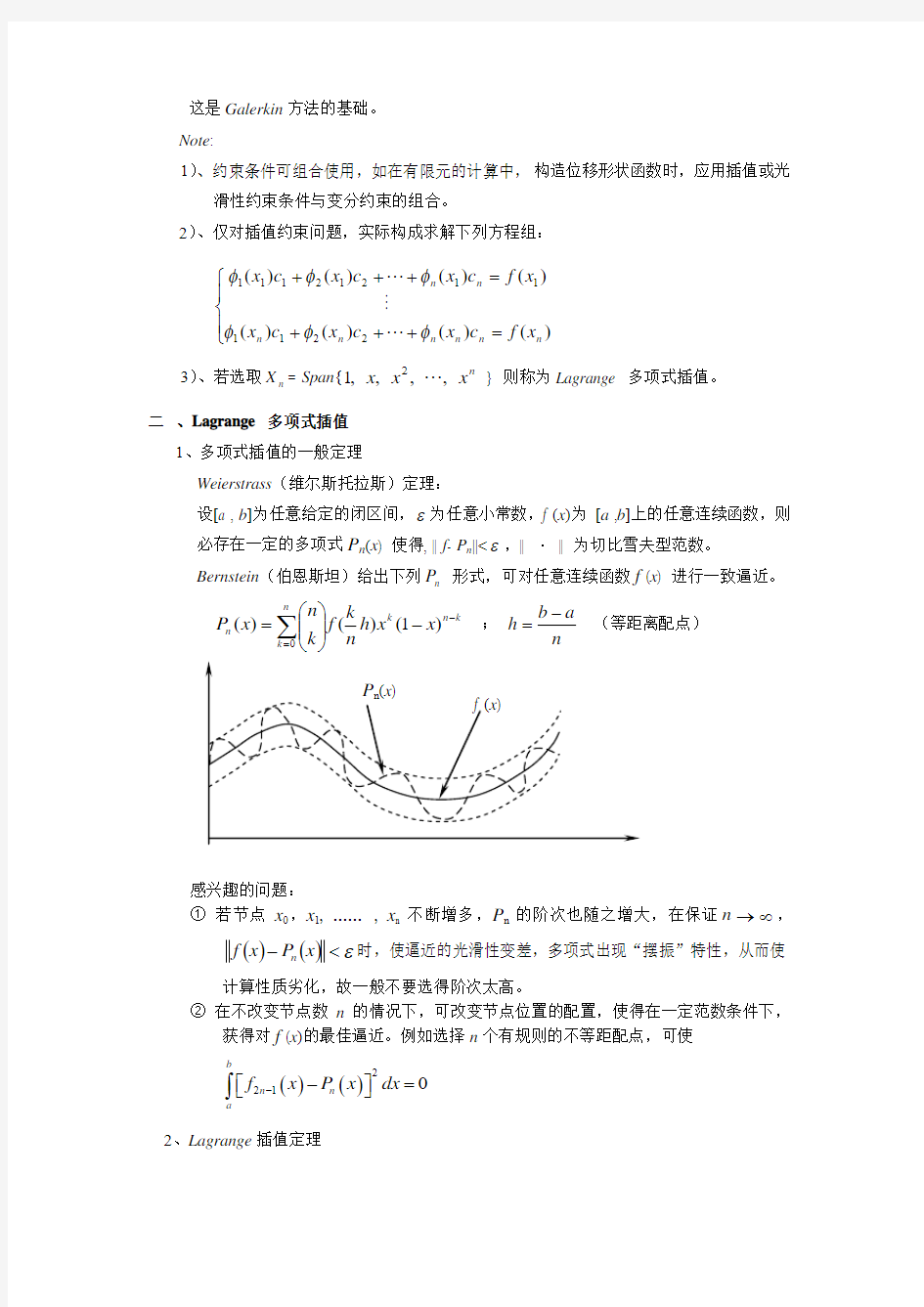
必存在一定的多项式P n (x ) 使得, || f - P n ||<ε，|| · || 为切比雪夫型范数。 Bernstein （伯恩斯坦）给出下列n P 形式，可对任意连续函数f (x ) 进行一致逼近。 k n k n

k n x x h n k f k n x P -=-???

? ??=∑)1()()(0 ； n a b h -=（等距离配点）

感兴趣的问题：

① 若节点x 0，x 1, …… , x n 不断增多，P n 的阶次也随之增大，在保证∞→n ，

()()ε<-x P x f n 时，使逼近的光滑性变差，多项式出现“摆振”特性，从而使

计算性质劣化，故一般不要选得阶次太高。

② 在不改变节点数n 的情况下，可改变节点位置的配置，使得在一定范数条件下，

获得对f (x )的最佳逼近。例如选择n 个有规则的不等距配点，可使

()()2

210b

n n a

f x P x dx --=?

???? 2、Lagrange 插值定理

在n +1个不相等的实数n x x x <<< 10上，取被规定值的n 次多项式P n (x ) 是存在且唯一的。意思是说，不论你用什么多项式形式或各种方法构造逼近函数，结果都是唯一的，都可化为统一的形式。这样，就有Lagrange 插值的标准基函数（Canonical Base Function ）:

11001101()()

()()()()()

()()()()()()()

()()()

()

n

n i i i i i n i i i i i i i i n i n p f x l x x x x x x x x x w x l x x x w x x x x x x x x x w x x x x x x x =-+-+=----=

='-----=---∑

① 第i 个基函数在x i 点取值为 1，在 x j ( j ≠i )的点取值为 0，即 ② 在区间 [a ,b ]上为 n 次多项式。

③ P n 为基函数的线性组合，其系数为被插函数在型值点的函数值。（仅有典则基有此性

质）。

④ {}n l l l ,,,10 称为n 次多项式线性空间上的典则基。

⑤ 还有许多多项式基函数，如{1，x ,…x n

}（并不满足插值系数就是函数点值的性质）；

再如：正交多项式基：Legender 或 Tchebycheff 基等。正交多项式可类比Euchilid 几何空间上的正交坐标轴，在那里几何上的正交性是自然的；在函数空间中的正交多项式是指在内积定义下的正交性，如带权正交基函数定义为：

()

()???≠=∞<=>=

a

j i j i 0,φρφφφ

⑥ 计算时如何选择基，则依据对计算的方便和高精度少运算量的原则来决定；在插值时

用典则基比较方便。

注意：这里并不是分片插值基函数，而是全域上的；分片插值见下段。 3、误差估计（包括这种误差估计式） 4、分段拉氏插值

有上节所述，多项式在整个区间[ a ,b ]上插值，随着节点的增多（n →∞, h →0）会使逼近函数的图形产生激烈的起落（也与型值有关）。这是不希望的，克服的办法采用分段插值，

l i (x

()()

??

?≠===j i j i x l ij

j i 01)(δ

即:

()???????≤≤+++≤≤+++≤≤+++=++++++ m

m m

m m m m

m m m m m m m m x x x x a x a a x x x x a x a a x x x x a x a a x S 213322*********

或 00223232()()

()()()()

()()()

()

m

i

m i

i m

i i

m m i m m

i i

m m i m

f x l x x x x S x f x l x x x x f x l x x x x ===?≤≤???

=≤≤?

??≤≤??

∑∑∑ 常用的m = 1分段线性插值 ：

M = 2分段二次插值 ：

Note : 不保证节点导数的存在。 5、有限元常用的在标准区间上的插值形式：

在区间 [ x i+1，x i+2 ]上，作标准变换

[ -1，1 ]

()

()122

1

2

++=+-==

?=∑i i i i k k k i x x h h dx l x x ξ

()()()()

ξξξξ+=-=12

1121

21l l ()()11121≤≤-+=ξξξξk k l ???==-=2111k k k ξ -1 1

l 1

1

l 2

在标准区间[-1，1]上，作函数插值：

()()()∑

=+=

2

1

k k k i l x f S ξξ 函数的近似积分：

()()

??

-≈++1

1

2

2

1

ξξd h s dx x f i

x x i i 三、Hermite （埃尔米特）插值

1、区间 [a , b ] 上满足插值与光滑性约束的插值

约束条件：

()()

()()

()()()()

b f b P b f b P a f a P a f a P '='='='=

由拉氏插值定理可以得到如下启迪：

① 能唯一构造一个三次多项式：3

32210)(x a x a x a a x p +++=

② 可以写成一种典则基形式：

)()()()()()()()()(21112010x b p x a p x b p x a p x p ΦΦΦΦ'+'++=

其中，x 1= a , x 2 = b 时，()x ??Φ为区间 [a , b ] 上的三次多项式，且

?????

?

?≤≤=Φ'=Φ=Φ'≤≤=Φ2

1002

11100j ,i )x ()x ()x (j ,i )x (ij i

i j i j i ij j i δ

δ （这里的 i ,j 指的是区间的两端点）

寻找方法：)(0x i Φ在节点（边界点）上的要求类似于)(x l i ，但要是三次多项式且还要

满足前两个条件，故可选：2

0()()()i i x ax b l x Φ=+

易验证： 00()0;()0

()i j i j x x i j 'Φ=Φ=≠

于是选择常数a , b 满足： 2()()1()[()2()()]0

i i i i i i i i i i ax b l x l x al x ax b l x ?+=?

?'++=?? (i =j )

j

i j i i i i i i x x x x l )

x (l x b )x (l a --=

'+='-=?

212

同理可得：)(1x i Φ

留作作业。

最终，??

?

???

?

???

???---=---=--+--=

--+--=222122

1132203

210)()()()()())(()()()](2)[()()()()](2)[()()(b a b x a x x b a b x a x x a b x b a b a x x b a x a b a b x x ΦΦΦΦ

唯一性证明略.

2、 拉格朗日分段线性插值在节点处改进为一阶导函数连续的Hermite 插值。

该问题实际上是上述Hermite 插值的简单推广，只要取[a , b ]为[x i+1 , x i+2 ] 即可。

由此获得分段的Hermite 插值多项式。该插值是在每个节点有两个参数，即 f (x i +1) 及 f ′(x i +1) 情况下得到的，同时具有节点一阶导数连续的内嵌性。 3、 有限元常用的标准区间上的Hermite 插值

① 在节点坐标系上，x 轴的原点在梁的第一个节点，x 轴的正向指向第二个节点，元素长度为l ，即在[ 0, l ]上做Hermite 插值。 在[ 0，l ]上：

??????

?

???

???+

-=+

-=-=+-=23

22123

2113

2203210

2)(2)(3)(2)(31l x l x l x l x x l x l x l

x l x ΦΦΦΦ 在[-1 ，1 ] 上：

?????

???

??

?=-+=Φ=--=Φ=-+=Φ=+-=Φ4

2212

2113

32013

101181

118132413241N ))((N

))((N

)(N )(ξξξξξξξξ()()()()

()()()()()()()()

ξξξξξξξ4232211112

1

0N x f N x f N x f N x f x f x f )(S i i i i k k i k k k i +++++=+'++'+=Φ'+Φ=∑∑

2

11

()

()(1)2

i k k k k k x x l l ξξξξ+===

+∑ （亚参元） 4、 在节点上仅已知函数值（即不知导数值）情况下的Hermite 插值

方法可以很多，但三次多项式是唯一的。举例一种：

22

011

1

()()()k k k k k k s x r x q x ===Φ+Φ∑∑

（r 1, r 2, q 1, q 2）可以这样来选择：()()i i S x f x = f 为被插函数 1≤ i ≤4 即：243211++=<<<=i i x x x x x x ，联立方程求解后获得被插函数的系数。 这样的插值存在且唯一。该例说明，不一定梁元问题必须选节点导数作未知参数。 5、 保证节点高阶导数一致的Hermite 插值（略） 四、多变量函数的逼近 1、几点基本认识

● 多变量函数逼近的一般理论要落后很多，许多提法简单；很重要的问题，尚未获得

很好的解决。

● 在一个随机网格上（二维区域?，随机存在 p 0， p 1， ….，p n 个不同的节点）寻找

一个关于x , y 变量都是n 次的多项式p (x , y )，满足下列插值约束：

()()()

n i y ,x p p f p P i i i i i n ≤≤==0

P (x , y )具有以下形式：P (x , y )=

∑=n

j ,i j i ij

y x a

其解存在，但不保证解的唯一性。

●

在随机网格上构成光滑（即可微）的分片拉格朗日插值函数，分片埃尔米特插值函数，有些情况下可能不存在。关键在于配置节点p i ，以及分片插值函数在各片的边界上如何连续，为构成光滑的逼近函数，节点的配置必须具有某种规律性。（一般为矩形网格或三角形网格）

2、矩形网格上的拉格朗日逼近函数

设 ?(){}d y c ,b x a :y ,x R ≤≤≤≤=?2

d

y y y c b x x x a m y n x =<<<=∏=<<<=∏ 1010::

拉格朗日插值：

设： (){}(){}次多项式

次多项式m m i y l n n i x l i

i ≤≤≤≤0:?0:?

其中：

m

k i y l n k i x l ik

k

i

ik

k i ≤≤=≤≤=,0)(?,0)(?δ

δ

则：()()()

)(?)(?,,,00y l x l l y x l y x f y x p j i ij m

j n i ij

i

i

==

∑≤≤≤≤

是一个x 方向n 次，y 方向m 次的多项式，其满足插值条件： p ( x i , y i ) = f (x i , y i ) 0≤ i ≤n ; 0≤ j ≤m

而且是唯一的，ij l (x , y )在工程上称为形状函数，在数学上称为基函数。

3、分片拉格朗日多项式：将x 方向和y 方向的分片拉格朗日多项式的基函数相乘，再称以常数并求和可构成二维情况的分片拉格朗日多项式。若x , y 方向的分片多项式的次数相同，则得到矩形域上的分片双线性、分片双二次等拉格朗日多项式。 即：()()()∑≤≤≤≤Φ=

n

j n i ij

j

i

y ,x y ,x f y ,x S 00

对于双线性分片插值，则()=Φy ,x ij 1

(1)(1)4

i i x y ξη++ 4、分片双三次 Hermite 插值多项式: 插值约束：

)y ,x (y x f

)y ,x (y x p )y ,x (y

f

)y ,x (y

p )y ,x (x f

)y ,x (x p )y ,x (f )y ,x (p j i 2j i n 2j i j i n

j i j i n

j i j i n ???=?????=????=??=

(-1,-1)

(1,-1)

(1,1)

(-1,1)

存在且唯一

??????

??

???

?

?ΦΦ???+ΦΦ??+ΦΦ??+ΦΦ=∑∑∑

∑

====n

j ,i 1j 1i j i 2n

0j ,i 1j 0i j i n

0j ,i 0j 1i j i n 0

j ,i 0j 0i j i n )

y ()x ()y ,x (y x f )y ()x ()y ,x (y

f

)y ()x ()y ,x (x f

)y ()x ()y ,x (f )y ,x (p

5、张量积空间 (矩形域?上)

上述的二维插值基函数，可以用以下数学空间理论来描述。 设：[][]d ,c C Y ,b ,a C X ==, ()

[][]()d ,c b ,a R y ,x j i ?∈

{}{}

N N N N ,,,S p a n Y ,,,S p a n X ψψψ=ΦΦΦ= 2121

Y

M X N ??维子空间维子空间

N N Y X ? 的张量积的定义：

即N N Y X ?是由)x (i Φ 1≤ i ≤ N 和()y j ψ 1≤ j ≤ M 乘积的一切线性组合构成的，因为它由N , M 个函数的一切线性组合所构成，所以N N Y X ?是一个线性空间。不过它仍是

[]

2R C ?Ω的子空间，因为它的元素是连续函数乘积之和。

应当注意，如果我们以上所讲的基函数{}{

}N N ,,,ψψΦΦ 11是指分片插值函数中的典则基。这些基函数具有在一个子区间上有值，而且在其余区间上为0。即：

数学上称这些函数有“局部支撑”或“支紧集”函数。只有这样函数的线性组合，在一个区间上构成一个规定阶次的多项式函数，而且它们是线性独立的。这些函数的线性组合构成的函数在区间上或边界上的连续性不同。从这个角度看N N Y X ?显然是[

]2

R C ?Ω的子空

间。

如果我们选择的基函数{

}{}

M N

y ,y

,y ,,x ,x ,x , 2

211则在?与上构成一个N ?M 阶多

项式。

6、 矩形网格上的插值函数举例

ⅰ/四节点双线性插值（拉格朗日）

}N ,N ,N ,N {span )}

1)(1(4

1

),1)(1(41),1)(1(41),1)(1(41{span Y X b

y

)}1(21),1(21{span Y a x

)}1(21),1(21{span X xy c y c x c c u xy c y c x c c u }

xy ,y ,x ,1{Y X }y ,1{span Y }x ,1{span X 4321N N N N 8765y 4321x N N N N =η+ξ-η+ξ+η-ξ+η-ξ-=?=

ηη+η-==

ξξ+ξ-=??

??

???+++=+++==?==位移关系待定系数法获得与节点

1

111

11432111i )

1)(1(41

N N v N v N v N v v N u N u N u N u u i

i i i i 4

43322114

4332211++--++-=η-=ξ=ηη+ξξ+=??

?+++=+++=

ii/ 九节点双二次拉格朗日插值：

可与节点参数直接对应N N k i

k

3i k 1k N k i k

3i k 1k N N

N 2N 2N Y X 3,2,1i Y 3,2,1i X Y X }y ,y ,1{Y }x ,x ,1{X ????

?

??

????

??????????=η-ηη-η∏

=??????????=ξ-ξξ-ξ∏

=??==≠=≠=

作业：给出N 9的具体形式，并验证其在矩形域上的气泡特性。

ⅲ/ 八节点非完全二次拉格朗日插值函数

内部9节点对其他单元不构成作用，工程上不太喜欢用。仅采用8节点不完全二次多项式插值。

N 9 气泡函数

1

2

3

2 3

}y ,y ,1{Y }x ,x ,1{X 2N 2N ==

在N N Y X ?中去掉2

2

y x 项。 可采用待定系数方法，亦可用典则 基函数（形状函数）构造法，如下：

角点1为例分析：选

))((ηξ--114

1时，在节点5，8处不为零 而为21

)

1)(1)(1(41

N )1)(1)(1(41

N 21N 21)1)(1(41N i i i i i 851-ηη+ξξηη+ξξ+=-ξ-η-η-ξ-=--η-ξ-=

作业：构造其拉格朗日型形状基函数

7、 三角网格上的插值函数

① 可采用单项式基 {1,,}{1,,N N X x Y y ==

② 可采用（节点）形状函数基（面积坐标）一般多用线性元 ③ 用节点导数参数的三次多项式（板弯问题中已见过）

边中点：

)1(2

1

N )1(21N )1(21N )

1(21

N 6i

66

i 6

8i 88i 87i 77i 75i 55i 5ξ+η-η

η-η=ξ-η-ηη-η=η+ξ-ξξ-ξ=η-ξ-ξξ-ξ=∏∏

∏

∏

≠≠≠

≠N 5的形状函数

故：

8、关于有限元插值收敛性问题

收敛性：当元素尺寸趋近于零时，（换言之，当节点数目或节点位移的数量趋于无穷大时）最后的解答如果能无限的逼近准确解，那么这样的位移函数（或形状函数）就称为收敛的。

C1较C2有更好的收敛性；

C3趋向于某一确定值，不是该问题的解答（元素设计有问题时）

C4虽收敛，但不是单调收敛，它不能构成准确解的上界或下界（C4对应非协调元） C5发散（连续性条件不满足，或不能通过分片检验）。

●

从最小势能原理出发的位移有限元素法，已知近似解的势能总大于真实解势能，同时，无限维位移场函数用有限个自由度进行插值，且限定了位移场的形态，这相当于限制了单元的变形能力，故一般计算的刚阵偏大（硬），而计算的位移一般偏小。

●

从变分运算对象的位能泛函∏，取决于弹性体的位移和应变，而应变也就是位移的某种导数（一阶的或二阶的），故为收敛性需要，可以自然想到应当使位移函数及其某种导数能够“无限的接近”真实的位移及其导数（只要满足某种误差限即可）。

●

不论元素的性态多么复杂， 当元素尺寸趋于零时，真实位移及其导数总是趋于某一常数，故从收敛性角度而言：

① 对形状函数的第一要求应当是：

函数本身及其某种导数应在元素上连续，并含有常数部分（ 包含刚体位移）： 轴力杆：1，x 平面应力元素：1, x , y 空间应力元素：1, x , y , z 平面刚架元素：2

1x ,x ,

平板弯曲元素：2

2

1y ,xy ,x ,y ,x ,

② 对形状函数的第二条要求：元素之间的位移协调。不仅节点处的位移应协调，沿整个内边界上的位移都应是协调的，这是最小位能原理所要求的基本前提。

可能的收敛曲线

③从收敛的快速性上要求：

插值多项式次数尽可能取高。

拉格郞日插值法总结

拉格朗日插值公式 2008-04-26 20:58 一．线性插值(一次插值） 已知函数f(x)在区间[xk ,xk+1 ]的端点上的函数值yk =f(xk ), yk+1 = f(xk+1 ),求一个一次函数y=P1 (x)使得yk =f(xk ),yk+1 =f(xk+1 ), 其几何意义是已知平面上两点(xk ,yk ),(xk+1 ,yk+1 ),求一条直线过该已知两点。 1. 插值函数和插值基函数 由直线的点斜式公式可知： 把此式按照yk 和yk+1 写成两项: 记 并称它们为一次插值基函数。该基函数的特点如下表： 从而 P1 (x) = yk lk (x) + yk+1 lk+1 (x) 此形式称之为拉格朗日型插值多项式。其中, 插值基函数与yk 、yk+1 无关，而由插值结点xk 、xk+1 所决定。一次插值多项式是插值基函数的线性组合, 相应的组合系数是该点的函数值yk 、yk+1 . 例1: 已知lg10=1,lg20=1.3010, 利用插值一次多项式求lg12的近似值。 解: f(x)=lgx,f(10)=1,f(20)=1.3010, 设 x0 =10 ,x1 =20 ,y0 =1 ,y1 =1.3010 则插值基函数为：

于是, 拉格朗日型一次插值多项式为: 故: 即lg12 由lg10 和lg20 两个值的线性插值得到,且具有两位有效数字(精确值lg12=1.0792). 二．二次插值多项式 已知函数y=f(x)在点xk-1 ,xk ,xk+1 上的函数值yk-1 =f(xk-1 ),yk =f(xk ), yk+1 =f(xk+1 ), 求一个次数不超过二次的多项式P2 (x), 使其满足, P2 (xk-1 )=yk-1 , P2 (xk )=yk , P2 (xk+1 )=yk+1 . 其几何意义为:已知平面上的三个点 (xk-1 ,yk-1 ),(xk ,yk ),(xk+1 ,yk+1 ), 求一个二次抛物线, 使得该抛物线经过这三点。 1.插值基本多项式 有三个插值结点xk-1 ,xk ,xk+1 构造三个插值基本多项式，要求满足： (1) 基本多项式为二次多项式；(2) 它们的函数值满足下表： 因为lk-1 (xk )= 0,lk-1 (xk+1 )=0, 故有因子(x-xk )(x-xk+1 ), 而其已经是一个二次多项式, 仅相差一个常数倍, 可设 lk-1 (x)=a(x-xk )(x-xk+1 ), 又因为 lk-1 (xk-1 )=1 ==> a(xk-1 -xk )(xk-1 -xk+1 )=1 得

牛顿插值法原理及应用

牛顿插值法 插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式，就称它为插值多项式。当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。为了克服这一缺点，提出了牛顿插值。牛顿插值通过求各阶差商，递推得到的一个公式： f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x0 )...(x-xn-1)+Rn(x)。 插值函数 插值函数的概念及相关性质[1] 定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点 x0,x1,…xn上取值分别为y0,y1,…yn （设a≤ x1≤x2……≤xn≤b)。若在函数类中存在以简单函数P(x) ，使得P(xi)=yi,则称P(x) 为f(x)的插值函数. 称x1,x2,…xn 为插值节点，称[a,b]为插值区间。 定理：n次代数插值问题的解存在且唯一。

牛顿插值法C程序 程序框图#include void main() { float x[11],y[11][11],xx,temp,newton; int i,j,n; printf("Newton插值:\n请输入要运算的值:x="); scanf("%f",&xx); printf("请输入插值的次数(n<11):n="); scanf("%d",&n); printf("请输入%d组值:\n",n+1); for(i=0;i

Lagrang插值多项式

第5章 实验四Lagrange 插值多项式 实验目的：理解Lagrange 插值多项式的基本概念，熟悉Lagrange 插值多项 式的公式及源代码，并能根据所给条件求出Lagrange 插值多项式，理解龙格现象。 5.1 Lagrange 插值多项式 Lagrange 插值多项式的表达式： 1,,2,1,) ()()(, )()(1 11 1+=--==∏ ∑+≠=+=n i x x x x x l x l y x L n i j j j i j i n i i i 。 其中)(x l i 被称为插值基函数，实际上是一个n 次多项式。)(x l i 的这种表示具有较好的对称性。公式具有两大优点：（1）求插值多项式，不需要求解线性方程组，当已知数据点较多时，此公式更能显示出优越性。（2）函数值可以用符号形式表示，数据点未确定的纵坐标可用多项式表示。 5.2 Lagrange 插值多项式源代码I % 功能： 对一组数据做Lagrange 插值 % 调用格式：yi=Lagran_(x,y,xi) % x,y 数组形式的数据表 % xi:待计算y 值的横坐标数组 % yi 用Lagrange 插值算出的y 值数组 function fi=Lagran_(x,f,xi) fi=zeros(size(xi)); np1=length(f); for i=1:np1 z=ones(size(xi)); for j=1:np1 if i~=j,z=z.*(xi-x(j))/(x(i)-x(j));end end fi=fi+z*f(i); end return

例5.1 已知4对数据（1.6，3.3），（2.7，1.22），（3.9，5.61），（5.6，2.94）。写出这4个数据点的Lagrange 插值公式，并计算出横坐标xi=[2.101,4.234]时对应的纵坐标。 解：4个数据点的Lagrange 插值公式为： ) 9.36.1(*)7.26.5(*)6.16.5() 9.3(*)7.2)(6.1(* 94.2) 6.59.3(*) 7.29.3(*)6.19.3() 6.5(*) 7.2(*)6.1(*9.3) 6.5 7.2(*)9.37.2(*)6.17.2() 6.5(*)9.3(*)6.1(*22.4) 6.56.1(*)9.36.1(*) 7.26.1() 6.5(*)9.3(*) 7.2(* 3.3)(3------+ ------+ ------+ ------=x x x x x x x x x x x x x L 清单5.1 clear x=[1.6, 2.7, 3.9, 5.6]; y=[3.3, 1.22, 5.61, 2.94]； xi=[2.101,4.234]; yi=Lagran_(x,y,xi); xx=1.5:0.05:6.5; yy=Lagran_(x,y,xx); plot(xx,yy,x,y,'o') 其结果为： yi = 1.0596 6.6457 x g (x ):-, d a t a p o i n t s :o 图5.1 插值多项式曲线图

多项式插值法和拉格朗日插值

多项式插值法和拉格朗日插值 教案一多项式插值法和拉格朗日插值 基本内容提要 1 多项式插值法的基本概念 2 插值多项式的存在性与唯一性分析 3 拉格朗日插值多 项式的构造及截断误差 4 截断误差的实用估计式 5 逐次线性插值法教学目的和要求 1 熟练掌握多项式插值法的基本概念 2 理解插值多项式的存在性与唯一性 3 掌握拉 格朗日插值法 4 掌握截断误差的估计方法 5 理解逐次线性插值法的基本思想，掌握Aitken逐次线性插值法 6 掌握运用拉格朗 日插值法处理问题的基本过程教学重点 1 拉格朗日插值基函数及拉格朗日插值多项式的构造 2 拉格朗日插值多项式的截断 误差分析 3 逐次线性插值法的基本思想教学难点 1 插值多项式存在唯一性条件的讨论分析 2 插值误差的分析与估计 3 Aitken逐次线性插值法的计算过程课程类型新知识理论课教学方法 结合提问，以讲授法为主教学过程 问题引入 实际问题中许多变量间的依赖关系往往可用数学中的函数概念刻画，但在多数情况下，这些函数的表达式是未知的，或者函数已知，但形式十分复杂。基于未知函数或复杂函数 的某些已知信息，如何构造这些函数的近似表达式？如何计算这些函数在其它点处的函数值？所构造的近似表达式与真实函数的误差是多少？插值理论与方法就是解决这些问题的 有效工具之一。 §2.1 多项式插值 2.1.1 基本概念 假设f(x)是定义在区间[a,b]上的未知或复杂函数，但已知该函数在点a≤x0 P(xi)=yi,i=0,1,2,L,n,即在给定点xi处，P(x)与f(x)是相吻合的。 (2.1) 把P(x)称为f(x)的插值多项式（函通常把上述x0 数）， f(x)称为被插函数。[a,b]称为插值区间，条件（2.1）称为插值条件，并把 求P(x)的过程称为插值法。

拉格朗日插值法理论及误差分析

浅析拉格朗日插值法 目录： 一、 引言 二、 插值及多项式插值的介绍 三、 拉格朗日插值的理论及实验 四、 拉格朗日插值多项式的截断误差及实用估计式 五、 参考文献 一、引言 插值在数学发展史上是个古老问题。插值是和拉格朗日（Lagrange ）、牛顿（Newton ）、高斯（Gauss ）等著名数学家的名字连在一起的。在科学研究和日常生活中，常常会遇到计算函数值等一类问题。插值法有很丰富的历史渊源，它最初来源人们对天体研究——有若干观测点（我们称为节点）计算任意时刻星球的位置（插值点和插值）。现在，人们在诸如机械加工等工程技术和数据处理等科研都有很好的应用，最常见的应用就是气象预报。插值理论和方法能解决在实际中当许多函数表达式未知或形式复杂，如何去构造近似表达式及求得在其他节点处的值的问题。 二、插值及多项式插值 1、插值问题的描述 设已知某函数关系()y f x =在某些离散点上的函数值： 插值问题：根据这些已知数据来构造函数()y f x =的一种简单的近似表达式，以便于计算点,0,1,,i x x i n ≠= 的函数值()f x ，或计算函数的一阶、二阶导数值。 x 0x 0 y y 1 y 1 n y -n y 1 x 1 n x -n x

2、插值的几何意义 插值的几何意义如图1所示： 图1 3、多项式插值 3.1 基本概念 假设()y f x =是定义在区间,a b ????上的未知或复杂函数，但一直该函数在点01n a x x x b ≤<<<≤ 处的函数值01,,n y y y 。找一个简单的函数，例如函数 ()P x ，使之满足条件 (),0,1,2,, i P x y i n == （3.1） 通常把上述01n x x x <<< 称为插值节点，把()P x 称为()f x 的插值多项式，条件（3.1）称为插值条件，并把求()P x 的过程称为插值法。 3.2 插值多项式的存在性和唯一性 如果插值函数是如下m 次的多项式： 1 011()m m m m m P x a x a x a x a --=+++ 那么插值函数的构造就是要确定()m P x 表达式中的m+1个系数 011,,,m m a a a a - 。由于插值条件包含n+1独立式，只要m=n 就可证明插值函数多项式是唯一存在。 实际上，由n+1个插值条件可得

插值多项式简介

在离散数据的基础上补插连续函数，使得这条连续曲线通过全部给定的离散数据点。插值是离散函数逼近的重要方法，利用它可通过函数在有限个点处的取值状况，估算出函数在其他点处的近似值。 早在6世纪，中国的刘焯已将等距二次插值用于天文计算。17世纪之后，I.牛顿，J.-L.拉格朗日分别讨论了等距和非等距的一般插值公式。在近代，插值法仍然是数据处理和编制函数表的常用工具，又是数值积分、数值微分、非线性方程求根和微分方程数值解法的重要基础，许多求解计算公式都是以插值为基础导出的。 插值问题的提法是：假定区间[a，b］上的实值函数f（x）在该区间上n＋1个互不相同点x0，x1……xn 处的值是f [x0］，……f（xn），要求估算f（x）在[a，b］中某点的值。其做法是：在事先选定的一个由简单函数构成的有n＋1个参数C0，C1，……Cn的函数类Φ(C0，C1，……Cn)中求出满足条件P（xi）＝f（xi）（i＝0，1，…… n）的函数P(x)，并以P()作为f()的估值。此处f（x）称为被插值函数，c0，x1，……xn 称为插值结(节)点，Φ(C0，C1，……Cn)称为插值函数类，上面等式称为插值条件，Φ（C0，……Cn）中满足上式的函数称为插值函数，R（x）＝ f（x）－P（x）称为插值余项。当估算点属于包含x0，x1……xn 的最小闭区间时，相应的插值称为内插，否则称为外插。 多项式插值这是最常见的一种函数插值。在一般插值问题中，若选取Φ为n次多项式类，由插值条件可以唯一确定一个n次插值多项式满足上述条件。从几何上看可以理解为：已知平面上n＋1个不同点，要寻找一条n次多项式曲线通过这些点。插值多项式一般有两种常见的表达形式，一个是拉格朗日插值多项式，另一个是牛顿插值多项式。 埃尔米特插值对于函数f（x），常常不仅知道它在一些点的函数值，而且还知道它在这些点的导数值。这时的插值函数P（x），自然不仅要求在这些点等于f(x）的函数值，而且要求P（x）的导数在这些点也等于f（x)的导数值。这就是埃尔米特插值问题，也称带导数的插值问题。从几何上看，这种插值要寻求的多项式曲线不仅要通过平面上的已知点组，而且在这些点（或者其中一部分）与原曲线“密切”，即它们有相同的斜率。可见埃尔米特插值多项式比起一般多项式插值有较高的光滑逼近要求。 分段插值与样条插值为了避免高次插值可能出现的大幅度波动现象，在实际应用中通常采用分段低次插值来提高近似程度，比如可用分段线性插值或分段三次埃尔米特插值来逼近已知函数，但它们的总体光滑性较差。为了克服这一缺点，一种全局化的分段插值方法——三次样条插值成为比较理想的工具。见样条函数。 三角函数插值当被插函数是以2π为周期的函数时，通常用n阶三角多项式作为插值函数，并通过高斯三角插值表出。 插值（Interpolation），有时也称为“重置样本”，是在不生成像素的情况下增加图像像素大小的一种方法，在周围像素色彩的基础上用数学公式计算丢失像素的色彩。有些相机使用插值，人为地增加图像的分辨率。插值：用来填充图像变换时像素之间的空隙。 如果您认为本词条还有待完善，需要补充新内容或修改错误内容，请编辑词条 贡献者（共4名）： zy19842006、laner6810、明明我心521、lewuyang 问题的描述与基本概念

拉格朗日多项式插值

拉格朗日多项式插值法浅析 摘要 拉格朗日插值多项式是一种最常见的多项式插值法，也是一种最常用的逼近工具。“学以致用 ”是每一门学科都致力追求的境界，数学自然也不例外。下面，探讨拉格朗日插值法的基本原理、如何构造拉格朗日多项式、拉格朗日多项式的误差界，并用 MATLAB 程序来实现这一数学算法的自动化，为复杂的分析研究提供了一条数学算法的捷径。 【关键词】：拉格朗日多项式 算法实现 MATLAB 在科学研究和实际的工程设计中，几乎所有的问题都可以用)(x f y =来表示其某种内在规律的数量关系。但理想化的函数关系在实际工程应用中是很难寻找 的，对于那些没有明显解析式的函数关系表达式则只能通过实验观察的数据，利用多项式对某一函数的进行逼近，使得这个逼近函数能够反映)(x f 的特性，而且利用多项式就可以简便的计算相应的函数值。例如我们不知道气温随日期变化的具体函数关系，但是我们可以测量一些孤立的日期的气温值，并假定此气温随日期变化的函数满足某一多项式。这样，利用已经测的数据，应用待定系数法便可以求得一个多项式函数f （x ）。应用此函数就可以计算或者说预测其他日期的气温值。一般情况下，多项式的次数越多，需要的数据就越多，而预测也就越 准确。当然，构造组合多项式方法比较多，如线性方程求解、拉格朗日系数多项式以及构造牛顿多项式的分段差分和系数表等等，这里只对拉格朗日多项式插值法进行深入探讨。 一、拉格朗日多项式插值算法基本原理 函数)(x f y =在区间[a,b]上有定义,在是[ a,b]上取定的 N + 1个互异节点, 且在这些点处的函数值)(0x f , )(1x f ,…,)(n x f 为已知, 即 yi =f (xi ) , (N i ...1,0=)，若存在一个和)(x f 近似的函数)(x P N ，满足 )()(i i N x f x P = (N i ...1,0=) （1） 则称 φ(x) 为 f (x) 的一个插值函数, 点i x 为插值节点，（1）称为插值条件, 区间[a,b]称为插值区间, 而误差函数)()(x P x f E N N -=称为插值余项。即是求一个不超过N 次多项式0111...)(a x a x a x a x P N N N N N ++++=-- (N i ...1,0=) 满足 )()(i i N x f x P = (N i ...1,0=)

Lagrange插值多项式

宁夏师范学院数学与计算机科学学院 《数值分析》实验报告 实验序号：1实验项目名称：Lagrange插值多项式

end L(k,:)=V; end C=y*L 五、实验结果与数据处理 1.（1）清单： >> clear >> clf >> x=[1,2,2.5]; >> y=x+2./x; >> [C,L]=lagran(x,y); C = 0.4000 -1.2000 3.8000 >> xx=[1.5,1.2]; >> yy=polyval(C,xx) yy = 2.9000 2.9360 （2）清单 >> clear,clf >> x=[0.5,1,3,5]; >> y=x+2./x; >> [C,L]=lagran(x,y); C = -0.2667 2.5333 -6.3333 7.0667 >> xx=[1.5,1.2]; >> yy=polyval(C,xx) yy = 2.3667 2.6539 2. 清单： >> x=0:pi/16:pi/2; >> y=x.*sin(x); >> [C,L]=lagran(x,y); C = Columns 1 through 8 -0.0001 -0.0003 0.0089 -0.0005 -0.1663 -0.0001 1.0000 -0.0000 Column 9 >> xx=0:pi/16:pi/2; >> yy=polyval(C,xx); >> plot(xx,yy,'b',x,y,'.') >> hold on >> a=polyfit(x,y,4)

>> grid on 六、分析与讨论 通过本次的实验，我初步掌握了 综合运用专业及基础知识，解决实际数学问题的能力，运行过程中有几处错误，但照提示改过就出结果了。 七、教师评语

多项式插值理论

第六章 多项式插值理论 一、区间[a , b ]上的一般插值理论 (从有限维子空间出发的逼近方法) ① 对无限维函数空间的一个元素f (x ) 进行逼近，关于f (x ) 的情况仅知道一部分 (1、若干点的函数值或导数值已知； 2、满足一些控制方程) ② 选择一个由固定基函数张成的有限维函数子空间 基函数性质: ?? ?? ?、线性无关、完备的条件、满足基本的函数已知321 ③ 选择n X 中的元素)()(~x P x f n 或，在一定的约束条件下，使)(~ x f 良好的逼近()x f , 即 令)(~ x f = n n c c c φφφ+++ 2211关于()x f 在插值区间上有不大的误差（包括一定的光滑性逼近）。 ④ 良好逼近的判断 ε<-f f ~ e .g . Tchebychef f 范数，|| f || = |)(|max x f b x a ≤≤ 称为一致逼近。 ⑤ 约束条件: （依据对()x f 的了解来确定） i / 插值约束 )()(~ i i x f x f = 1n i ≤≤ i x ∈ (a , b ) 且i x 互不相同； ii / 插值与光滑性混合约束 (1)、 )()(~ i i x f x f = 1k i ≤≤ i x ∈(a , b ) 且i x 互不相同 (2)、 )()(~ i i x f x f '=' 1k i ≤≤ i x ∈(a,b) 且互不相同 (3)、 )(~ x f 的二阶导数存在 iii / 变分约束 （以下两种约束不再具有严格的插值含义，这里可能仅知道被插函数 满足某些控制方程） 依据|| f -f ~||在n X 中为最小的条件，即确定常数n c c c 21, 使f ~ 的解由下列形式的极小化问题得到： || f -0f ~|| = min{|| f -f ~||：f ~ n X ∈} Note ：这里的||·|| 不局限于切比雪夫范数和2－范数，可能是某种内积定义的范数；这也是固体力学求近似解的基本方法（如，有限元就是能量的变分）。 iv / 正交约束 根据f -f ~ 与n 个给定基函数)(,),(),(21x x x n φφφ 的正交条件，确定常数： i c , 1n i ≤≤。即 < f -f ~ ,0)()](~ )([=->= ? dx x x f x f i b a i φφ 1n i ≤≤ {}n n Span X φφφ,,,21 =

多项式与插值

多项式 多项式的表达 MatLab中用按降幂排列的多项式系数组成的行向量表示多项式,如: p(x)=x^3-2x-5被表示为: p = [1 0 –2 –5]; 多项式的根 r = roots(p) r = 2.0946 –1.0473 + 1.1359i –1.0473 – 1.1359i 根被储存为列向量． 若要由方程的根构造多项式，则 p2 = poly(r) p2 = 1 8.8818e-16 – 2 –5 多项式估计 可以用多项式估计出多项式在某一点的值： polyval(p,5) ans = 110 同样也可以估计矩阵多项式的值p(X) = X^3 – 2X – 5I, X = [2 4 5; –1 0 3; 7 1 5]; Y = polyvalm(p,X) Y = 377 179 439 111　81 136 490 253 639 卷积 多项式相乘是一个卷积的过程,conv() a = [1 2 3]; b = [4 5 6]; c = conv(a,b) c = 4 13 28 27 18 多项式相除是其逆过程，用deconv():

[q,r] = deconv(c,a) q = 4 5 6 r = 0 0 0 0 0 多项式曲线逼近 polyfit(x,y,n)能用多项式逼近由x,y向量提供的数据,n是其阶数,如: x = [1 2 3 4 5]; y = [5.5 43.1 128 290.7 498.4]; p = polyfit(x,y,3) p = –0.1917 31.5821 –60.3262 35.3400 将图画出 x2 = 1:.1:5; y2 = polyval(p,x2); plot(x,y,’o’,x2,y2) grid on 分式多项式分解 residue()可将分式多项式分解如下:

拉格朗日插值公式的证明及其应用讲解

拉格朗日插值公式的证明及其应用 摘要: 拉格朗日(Lagrange)插值公式是多项式中的重要公式之一,在理论和实践中都有着广泛的应用.本文阐述了Lagrange 插值的基本理论，譬如：线形插值，抛物插值，Lagrange 多项式等.然后将线形插值，抛物插值，Lagrange 多项式插值分别应用到高中知识中，并且学会用计算机程序来编写.插值法的思想与中国剩余定理一脉相承, 体现了代数中"线性化" (即表示为求和和数乘的形式) 这一基本思路, 大巧若拙.本文的目的是通过介绍拉格朗日插值公式的推导，唯一性，证明过程及其在解题与实际生活问题中的应用来寻找该公式的优点，并且引人思考它在物理，化学等领域的应用.通过实际鉴定过程，利用插值公式计算生活中的成本问题，可以了解它的计算精度高,方法快捷. 关键词： 拉格朗日插值公式 唯一性 证明 解题应用 资产评估 曲线插值问题，直观地说，认为已知的一批数据点()n k k k f x 0,=是准确的，这些数据点所表现的 准确函数关系()x f 是未知的，在这种情况下要作一条近似曲线()x P 且点点通过这些点，插值问题不仅要讨论这种近似曲线()x P 的构造方法，还要讨论点增多时这种近似曲线()x P 是否稳定地收敛于未知函数()x f ，我们先研究一种简单常用的插值——拉格朗日插值. 一.定义，推导及其在解题中的应用 １.线性插值 １.１. 线性插值的定义 假定已知区间[]1,+k k x x 的端点处的函数值()k k x f y =, ()11++=k k x f y ,要求线性插值多项式()x L 1使它满足()k k y x L =1, ()111++=k k y x L ． ()x L y 1=的几何意义:通过两点()k k y x ,和()11,++k k y x 的直线， 如图１所示，()x L 1的表达式由几何意义直接给出，即 ()()k k k k k k x x x x y y y x L ---+ =++111 (点斜式)， 图１ ()11111++++--+--= k k k k k k k k y x x x x y x x x x x L (两点式)． y=L 1x () y=f x () y k+1 y k x k+1 x k o y x

几种常用的插值方法

几种常用的插值方法 数学系 信息与计算科学1班 李平 指导老师：唐振先 摘要:插值在诸如机械加工等工程技术和数据处理等科学研究中有许多直接的应用,在很多领域都要用插值的办法找出表格和中间值,插值还是数值积分微分方程数值解等数值计算的基础。本文归纳了几种常用的插值方法,并简单分析了其各自的优缺点。 关键词:任意阶多项式插值,分段多项式插值。 引言:所谓插值,通俗地说就是在若干以知的函数值之间插入一些未知函数值,而插值函数的类型最简单的选取是代数多项式。用多项式建立插值函数的方法主要用两种：一种是任意阶的插值多项式,它主要有三种基本的插值公式：单项式,拉格朗日和牛顿插值；另一种是分段多项式插值,它有Hermite 和spine 插值和分段线性插值。 一．任意阶多项式插值： 1.用单项式基本插值公式进行多项式插值： 多项式插值是求通过几个已知数据点的那个n-1阶多项式,即P n-1(X)=A 1+A 2X+…A n X n-1,它是一个单项式基本函数X 0,X 1…X n-1的集合来定义多项式,由已知n 个点（X,Y ）构成的集合,可以使多项式通过没数据点,并为n 个未知系数Ai 写出n 个方程,这n 个方程组成的方程组的系数矩阵为Vandermonde 矩阵。 虽然这个过程直观易懂,但它都不是建立插值多项式最好的办法,因为Vandermonde 方程组有可能是病态的,这样会导致单项式系数不确定。另外,单项式中的各项可能在大小上有很大的差异,这就导致了多项式计算中的舍入误差。 2.拉格朗日基本插值公式进行插值： 先构造一组插值函数L i （x ） =011011()()()() ()()()() i i n i i i i i i n x x x x x x x x x x x x x x x x -+-+-------- ，其中i=0，… n.容易看出n 次多项式L i （x ）满足L i （x ）=1，（i=j ）；L i （x ）=0，（i ≠j ），其中i=0，1…n ，令L i （x ）=0()n i i i y l x =∑这就是拉格朗日插值多项式。与单项式基本

hermite插值多项式的例题

例 若()f x 在[a,b]上有三阶连续导数，且已知()f x 在[,]a b 上两个互异的 点01,x x 上的函数值01(),()f x f x 和一阶导数值' 0()f x ，试求满足条件 ''001100()(),()(),()()H x f x H x f x H x f x === 的插值多项式，并估计误差。 解 由给定的3 个插值条件，显然可确定一个次数不超过2次的埃尔米特插值多项式()H x ， 又有()H x 应满足插值条件()()i i H x f x =，(0,1)i =，而节点01,x x 上的线性插值函数1()N x 也满足插值条件1()(),(0,1)i i N x f x i ==，故可设101()()()()H x N x A x x x x -=--，其中A 为待定常数，上式又可记为 101000101()()()() ()()[,]()()H x N x A x x x x f x x x f x x A x x x x =+--=+-+-- 为了确定常数A ，对上式求导，得 '0110()[,][()()]H x f x x A x x x x =+-+-， 令0x x =代入，且注意插值条件'' 001010()[,]()()H x f x x A x x f x =+-=, 于是有'01010[,]()f x x f x A x x -=-，即多项式()H x 为 '010******** [,]()()()()[,]()()f x x f x H x f x x x f x x x x x x x x -=+-+--- ， 当然也可先采用拉格朗日多项式构造，同样得到满足相同条件的插值多项式()H x 余项为(3)201()()()()6 f R x x x x x ξ=--。

多项式插值

多项式插值典型算法及其应用 一、任务简介 (2) 1.1任务题目 (2) 1.2任务目的 (2) 1.3任务案例 (2) 二、总体设计 (3) 三、算法原理 (4) 3.1分段线性插值 (4) 3.2保形插值 (4) 3.3三次样条插值 (5) 3.4最邻近点插值 (9) 3.5分片线性插值 (9) 3.6双线性插值 (9) 四、算法介绍 (11) 4.1分段线性插值 (11) 4.2保形插值 (12) 4.3三次样条插值 (13) 4.4最邻近点插值 (14) 4.5分片线性插值 (15) 4.6双线性插值 (16) 五、软件功能 (16) 六、运行结果 (17) 6.1主界面 (17) 6.2二级界面 (17) 6.3程序结果 (18) 七、个人总结 (22) 八、参考资料 (23) 附录 (23)

一、任务简介 1.1任务题目 多项式插值典型算法及其应用 1.2任务目的 基于MATLAB图形界面对测试案例利用分段线性插值、保型插值、三次样条插值、最邻近点插值、分片线性插值、双线性插值实现。 1.3任务案例 案例一、数控机床加工零件 待加工零件的外形根据工艺要求由一组数据（x,y）给出（在平面情况下），用数控机床加工时刀具必须沿这些数据点前进，并且由于刀具每次只能沿x方向或y方向走非常小的一步，所以需要将已知数据加密，得到加工所要求的步长很小的（x,y）坐标。 图1是待加工零件的轮廓线，表1给出了轮廓线上x每间隔0.2（长度单位）的加工坐标x,y（顺时针方向为序，由轮廓线的左右对称性，表中只给出右半部的数据），假设需要得到x或y坐标每改变0.05时的坐标，试完成加工所需的加密数据，画出曲线。 图1、零件的轮廓线（x间隔0.2） 0 0.2 0.4 0.6 0.8 1 1.2 5 4.71 4.31 3.68 3.05 2.5 2.05 1.4 1.6 1.8 2 2.2 2.4 2.6 1.69 1.4 1.18 1 0.86 0.74 0.64 2.8 3 3.2 3.4 3.6 3.8 4 0.57 0.5 0.44 0.4 0.36 0.32 0.29 4.2 4.4 4.6 4.8 5 4.8 4.6 0.26 0.24 0.2 0.15 0 -1.4 -1.96

牛顿插值法原理及应用

牛顿插值法原理及应用

牛顿插值法 插值法是利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式，就称它为插值多项式。当插值节点增减时全部插值基函数均要随之变化，这在实际计算中很不方便。为了克服这一缺点，提出了牛顿插值。牛顿插值通过求各阶差商，递推得到的一个公式： f(x)=f[x0]+f[x0,x1](x-x0)+f[x0,x1,x2](x-x0)(x-x1)+...f[x0,...xn](x-x 0)...(x-xn-1)+Rn(x)。 插值函数 插值函数的概念及相关性质[1] 定义：设连续函数y-f(x) 在区间[a,b]上有定义，已知在n+1个互异的点 x0,x1,…xn上取值分别为y0,y1,…yn （设a≤ x1≤x2……≤xn≤b)。若在函数类中存在以简单函数P(x) ，使得P(xi)=yi,则称P(x) 为f(x)的插值函数. 称x1,x2,…xn 为插值节点，称[a,b]为插值区间。 定理：n次代数插值问题的解存在且唯一。

牛顿插值法C程序 程序框图#include void main() { float x[11],y[11][11],xx,temp,newton; int i,j,n; printf("Newton插值:\n请输入要运算的值:x="); scanf("%f",&xx); printf("请输入插值的次数(n<11):n="); scanf("%d",&n); printf("请输入%d组值:\n",n+1); for(i=0;i

插值与多项式逼近的数组计算方法实验

插值与多项式逼近的数组计算方法实验【摘要】计算机软件中经常要用到库函数，如） （x cos，x e，它们 sin，） （x 是用多项式逼近来计算的。虽然目前最先进的逼近方法是有理函数（即多项式的商），但多项式逼近理论更适于作为数值分析的入门课程。在已知数据具有高精度的情况下，通常用组合多项式来构造过给定数据点的多项式。构造组合多项式的方法有许多种，如线性方程求解、拉格朗日系数多项式以及构造牛顿多项式的方分和系数表。 关键字泰勒级数、拉格朗日插值法、牛顿插值法、帕德逼近 一、实验目的 1.通过具体实验，掌握泰勒级数、拉格朗日插值法、牛顿插值法、帕德逼近的编程技巧。 2.比较各插值方法的优劣并掌握。 二、实验原理 1.泰勒级数 在数学中，泰勒级数（英语：Taylor series）用无限项连加式——级数来表示一个函数，这些相加的项由函数在某一点的导数求得。 如果在点x=x 具有任意阶导数，则幂级数 称为在点x 处的泰勒级数。 =0，得到的级数 在泰勒公式中，取x 称为麦克劳林级数。函数的麦克劳林级数是x的幂级数，那么这种展开

是唯一的，且必然与的麦克劳林级数一致。 2.拉格朗日插值法 如对实践中的某个物理量进行观测，在若干个不同的地方得到相应的观测值，拉格朗日插值法可以找到一个多项式，其恰好在各个观测的点取到观测到的值。这样的多项式称为拉格朗日（插值）多项式。数学上来说，拉格朗日插值法可以给出一个恰好穿过二维平面上若干个已知点的多项式函数。 在平面上有(x 1,y 1)(x 2,y 2)...(x n ,y n )共n 个点，现作一条函数f （x ）使其图像经过这n 个点。 作n 个多项式p i (x),i=1,2,3...,n,使得 最后可得 3.牛顿插值法 插值法利用函数f (x)在某区间中若干点的函数值，作出适当的特定函数，在这些点上取已知值，在区间的其他点上用这特定函数的值作为函数f (x)的近似值。如果这特定函数是多项式，就称它为插值多项式。利用插值基函数很容易得到拉格朗日插值多项式，公式结构紧凑，在理论分析中甚为方便，但当插值节点增减时全部插值基函数均要随之变化，整个公式也将发生变化， 这在实际计算中是很不方便的，为了克服这一缺点，提出了牛顿插值。 牛顿插值通过求各阶差商，递推得到的一个公式： 10121()()()()()()N N N N P x P x a x x x x x x x x --=+----L 牛顿插值与拉格朗日插值具有唯一性。 4.帕德逼近 它不仅与逼近论中其他许多方法有着密切的关系，而且在实际问题特别是许多物理问题中有着广泛的应用。设是在原点某邻域内收敛的、具有复系数的麦克劳林级数。欲确定一个有理函数，式中,使得前次方的系数为0，即使得 此处约定qk ＝0（k>n ）。虽然所求得的Pm(z)和Qn(z)不惟一，但是比式却总是惟一的。有理函数称为F(z)的(m,n)级帕德逼近,记为(m/n)。由(m/n)所形成的阵列称为帕德表。

5次lagrange插值函数多项式

5次拉格朗日插值多项式函数%% 求取五次Lagrange多项式L5(x). clear;clc; X = [0.4 0.55 0.65 0.80 0.95 1.05]; Y = [0.41075 0.57815 0.69675 0.90000 1.000000 1.25382]; % 求取插值基函数：L0_(x). syms x la_0 = 1; for ii = 2:length(X) if(ii == 1) continue else L_0 = (x-X(ii))/(X(1)-X(ii)); la_0 = la_0*L_0; end end L0_x = collect(la_0); % 求取插值基函数：L1_(x). la_1 = 1; for ii = 1:length(X) if (ii == 2) continue else L_1 = (x-X(ii))/(X(2)-X(ii)); la_1 = la_1*L_1; end end L1_x = collect(la_1); % 求取插值基函数：L2_(x). la_2 = 1; for ii = 1:length(X) if (ii == 3) continue else L_2 = (x-X(ii))/(X(3)-X(ii)); la_2 = la_2*L_2; end end L2_x = collect(la_2); % 求取插值基函数：L3_(x). la_3 = 1;

for ii = 1:length(X) if (ii == 4) continue else L_3 = (x-X(ii))/(X(4)-X(ii)); la_3 = la_3*L_3; end end L3_x = collect(la_3); % 求取插值基函数：L4_(x). la_4 = 1; for ii = 1:length(X) if (ii == 5) continue else L_4 = (x-X(ii))/(X(5)-X(ii)); la_4 = la_4*L_4; end end L4_x = collect(la_4); % 求取插值基函数：L5(x). la_5 = 1; for ii = 1:length(X) if (ii == 6) continue else L_5 = (x-X(ii))/(X(6)-X(ii)); la_5 = la_5*L_5; end end L5_x = collect(la_5); % 求取五次Lagrange多项式函数. Lagrange5_x = eval(collect(L0_x*Y(1)+L1_x*Y(2)+L2_x*Y(3)+L3_x*Y(4)+L4_x*Y(5)+L5_x*Y(6 ))) P = sym2poly(Lagrange5_x); % 得到五次Lagrange多项式函数的系数向量. K1 = polyval(P,0.596); % 进行多项式求值. fprintf('f(0.596)的值为：f(1.8) = %f\n',K1); K2 = polyval(P,0.99); % 进行多项式求值. fprintf('f(0.99)的值为：f(1.8) = %f\n',K1);

hermite插值多项式的例题

例若()f x 在[a,b]上有三阶连续导数，且已知()f x 在[,]a b 上两个互异的 点01,x x 上的函数值01(),()f x f x 和一阶导数值' 0()f x ，试求满足条件 ' ' 001100()(),()(),()()H x f x H x f x H x f x === 的插值多项式，并估计误差。 解由给定的3 个插值条件，显然可确定一个次数不超过2次的埃尔米特插值多项式()H x ， 又有()H x 应满足插值条件()()i i H x f x =，(0,1)i =，而节点01,x x 上的线性插值函数 1()N x 也满足插值 条件 1()(),(0,1) i i N x f x i ==，故可设1 ( ) ()()()H x N x A x x x x -=--，其中A 为待定常数，上式又可记为 101000101()()()() ()()[,]()()H x N x A x x x x f x x x f x x A x x x x =+--=+-+-- 为了确定常数A ，对上式求导，得 ' 0110()[,][()()]H x f x x A x x x x =+-+-， 令0x x =代入，且注意插值条件'' 001010()[,]()()H x f x x A x x f x =+-=, 于是有 ' 01010 [,]() f x x f x A x x -= -，即()H x 为 ' 010******** [,]() ()()()[,]()()f x x f x H x f x x x f x x x x x x x x -=+-+ --- ， 当然也可先采用拉格朗日多项式构造，同样得到满足相同条件的插值多项式()H x 余项为(3) 2 01() ()()()6 f R x x x x x ξ=--。

插值多项式汇总

请求高手帮忙给个hermite插值法和拉格朗日插值法的matlab程序，要求实现x=[-5.0000 -3.8889 -2.7778 -1.6667 -0.5556 0.5556 1.6667 2.7778 3.8889 5.0000]; y=[0.0385 0.0620 0.1147 0.2647 0.7642 0.7642 0.2647 0.1147 0.0620 0.0385];这组数据的两个插值函数，满意的话我还会加分，不胜感激！ Matlab函数M文件Lagrange程序 function yy=lagrange(x,y,xi) m=length(x);n=length(y); if m~=n,error('向量x与y的长度必须一致');end s=0; for i=1:n z=ones(1,length(xi)); for j=1:n if j~=i z=z .*(xi-x(j))/(x(i)-x(j)); end end s=s+z*y(i); end yy=s; 上面是拉格朗日插值法，其中xi为要计算的数值比如 x=[0 3 5 9 31]; y=[2 7 10 12 15]; xi=[1 4 7] ; yi=Lagrange(x,y,xi) 这是要求在1,4,7处的值。 hermite程序我没有。 三次样条插值函数的MATLAB程序 matlab的spline x = 0:10; y = sin(x); xx = 0:.25:10; yy = spline(x,y,xx); plot(x,y,'o',xx,yy)

function f = Hermite(x,y,y_1,x0) syms t; f = 0.0; if(length(x) == length(y)) if(length(y) == length(y_1)) n = length(x); else disp('y和y的导数的维数不相等！'); return; end else disp('x和y的维数不相等！'); return; end for i=1:n h = 1.0; a = 0.0; for j=1:n if( j ~= i) h = h*(t-x(j))^2/((x(i)-x(j))^2); a = a + 1/(x(i)-x(j)); end end f = f + h*((x(i)-t)*(2*a*y(i)-y_1(i))+y(i)); if(i==n) if(nargin == 4) f = subs(f,'t',x0); else f = vpa(f,6); end end end