最近对蛮力分治实验报告
- 格式:doc
- 大小:111.00 KB
- 文档页数:6

分治法实验报告
石家庄经济学院
《算法设计与分析》实验报告
姓名:
班级:
学号:
指导教师:
完成日期:
一、实验名称
分治法实验
二、实验目的
1. 掌握分治法的基本思想、求解问题的基本步骤;
2. 掌握分支算法的一般模式;
3. 根据问题采取有效的分解和合并的方式,能够分析确定问题的阈值;
4. 掌握分治算法的时间复杂度,并能利用C语言实现算法。
三、实验内容及要求
1. 大整数乘法。
要求:
(1) 求解两个n位的二进制整数的乘法,设n=2k;
(2) 利用分治的思想分析和求解问题;
(3) 利用C语言实现算法,要求结果正确。
2. 矩阵相乘(选做)
(1) 求解两个n阶方阵的乘法,设n=2k;
(2) 可利用基本的分解方法或者STRANSSEN方法求解;
(3) 利用C语言实现算法,要求结果正确。
四、问题分析及算法设计
1. 大整数乘法
问题分析:
算法设计:
算法复杂度分析:
2. 矩阵乘法
问题分析:
算法设计:
算法复杂度分析:
五、代码及运行结果
六、实验总结
(要求总结本次实验遇到的问题及解决方法,收获和不足,300字以上,提交报告时删去此行)
教师评语:
成绩:优良中及格不及格。

实验1、《分治算法实验》一、实验目的1. 了解分治策略算法思想2. 掌握快速排序、归并排序算法3. 了解其他分治问题典型算法二、实验内容1.编写一个简单的程序,实现归并排序。
2. 编写一段程序,实现快速排序。
3. 编写程序实现循环赛日程表。
设有n=2k个运动员要进行网球循环赛。
现要设计一个满足以下要求的比赛日程表:(1)每个选手必须与其它n-1个选手各赛一次(2)每个选手一天只能赛一场(3)循环赛进行n-1天三、算法思想分析1.归并排序先是将待排序集合分成两个大小大致相同的集合,分别对每个集合进行排序,递归调用归并排序函数,再是调用合并函数,将两个集合归并为一个排好序的集合。
2.快速排序先是选择关键数据作为比较量,然后将数组中比它小的数都放到它的左边,比它大的数放大右边,再对左右区间重复上一步,直至各个区间只有一个数。
3.循环赛日程表先将选手分为两部分,分别排序,再将两部分合并,合并时由于循环赛的规律得知直接将左上角的排序表复制到右下角,左下角的排序表复制到右上角即可。
分成两部分时需要利用递归不断分下去直至只剩下一位选手。
四、实验过程分析1.通过归并算法我对分治算法有了初步的实际操作经验,快速排序与归并算法有很大的相似点,但是在合并时的方法不一样,而循环赛日程表则是思路问题,这个题目编程难点应该在于合并时数组调用的for循环的次数以及起始位置问题。
2.对于分治算法一般是将大规模问题分解为小问题,通过递归不断分下去,然后对每个小规模用一个函数去求解。
适用于小规模独立且易解,可以合并到大问题具有最优子结构的问题。
3.归并排序和快速排序熟悉书本及PPT基本没有问题,循环赛日程表则是纠结了很久,一开始算法思路并不是十分清晰所以错了很多次,后来想了很久再观察PPT的循环赛日程表得知最终算法,编写代码中遇到了一个小问题,有一部分选手未排序,如图所示:图中有部分选手未排序,即左下角排序出现了问题,后来直接静态调试,自己按照代码用实际数据去试了一遍,发现是排序时的for循环的次数不对。

分治思想实验报告总结分治思想是一种重要的问题求解方法,它将一个问题划分为多个子问题,并通过分别解决子问题来解决原始问题。
本次实验通过选择三个不同的问题,利用分治思想进行求解,并对实验结果进行总结。
首先,我们选择了经典的归并排序问题。
归并排序是一种稳定的排序算法,它将一个无序的序列分为两个子序列,分别进行排序,然后将两个有序的子序列合并成一个有序的序列。
在实验中,我们随机生成了一个长度为100的整数数组,并利用分治思想实现了归并排序算法。
实验结果显示,排序后的数组是按照从小到大的顺序排列的,证明了归并排序算法的可行性。
然后,我们选择了求解最大子序列和问题。
给定一个整数序列,我们要找到一个连续子序列,使得其元素之和最大。
为了解决这个问题,我们采用了分治思想的方法。
将整个序列分为两个子序列,分别求解左子序列的最大子序列和、右子序列的最大子序列和以及横跨左右子序列的最大子序列和,然后取最大值作为整个序列的最大子序列和。
通过实验,我们发现该方法能够正确求解最大子序列和问题,并且在时间效率上也比较高。
最后,我们选择了计算斐波那契数列问题。
斐波那契数列是一个经典的递归问题,其中第n个数的值等于前两个数的和。
在实验中,我们通过分治思想实现了斐波那契数列的计算方法。
具体而言,在求解第n个数的时候,我们将其划分为求解第n-1个数和第n-2个数两个子问题,然后将两个子问题的结果相加。
实验结果表明,该方法能够正确地计算出斐波那契数列的值,并且时间效率也相对较高。
综上所述,分治思想是一种行之有效的问题求解方法。
通过将问题划分为多个子问题并分别解决,可以大大简化问题的求解过程,提高求解效率。
然而,分治思想并不是适用于所有的问题,它对问题的划分和合并过程有一定的要求。
因此,在实际应用中,我们需要根据具体的问题来选择合适的求解方法。
最后,本次实验不仅增加了我们对分治思想的理解,还提高了我们的编程实践能力。

算法综合实验报告学号: 1004111115 姓名:李宏强一、实验内容:分别用动态规划、贪心及分支限界法实现对TSP问题(无向图)的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:(包括程序的数据结构、函数组成、输入/输出设计、符号名说明等)1、动态规划法(1)数据结构:利用二进制来表示集合,则集合S可由一个十进制数x相对应,此x所由一个十进制数x相对应,此x所对应的二进制数为y,如果y的第k位为1,则表示k存在集合S中。
例如:集合S={0,1}(其子集合为{}{0}{1}{01}),我们用二进制数11(所对应十进制数为3)表示S,11中右手边第1个数为1表示0在集合S中,右手边第二个数为1表示1在集合S中,其他位为0表示其它数字不在集合S中;同理,集合S={0,2}(其子集合为{}{0}{2}{02}可用二进制数101(所对应十进制数为5)表示(右手边第1个数为1表示0在集合S中,右手边第二个数为0表示1不在集合S中,右手边第3个数为1表示2在集合S中,则说明0,2在集合中,1不在集合中。
利用邻接矩阵表示任意两点之间的距离例如:mp[i][j]表示点i,j两点之间的距离。
(2)函数组成输入函数in()利用动态规划法算法实现的求解函数solve()主函数main()(3)输入/输出设计本程序可以通过键盘进行输入、屏幕进行输出。
(根据实际程序情况,还可以选择随机产生输入数据、将输出数据输出到文件等其它方式)这里采用随机产生输入数据,将数据输出在屏幕上的方式。
(4)符号名说明n 表示顶点个数。
mp[i][j] 表示顶点i和顶点j之间的距离。
dp[i][j] 表示顶点i经过集合S(用二进制表示的数为j)后回到起始点的最短路径和。
(5)算法描述某一个点i不经过任意点回到起始点的最短路径和为mp[i][0](默认初始点为0)dp[i][0] = mp[i][0]; (1<=i<n)点i经过集合S(二进制表示的数为j)的最短路径和为从点i经过集合S中的某一点k后再从该点出发,经过集合S-{k}的最小值。

一. 实验目的及实验环境实验目的:熟练掌握运用分治法解决问题。
实验环境:windows下的Ubuntu虚拟机二. 实验内容利用分治法求一个数组的最大值、最小值(要求:数组的大小和数组的长度随机产生)三.方案设计分治法解决问题就是要将原问题分解成小问题,再将小问题分解成更小的问题,以此类推,直到最终分解的问题能够一步解决即可。
代码要求最后要输出数组的最大值、最小值。
所以,在用分治法求最值的函数max_min()中,需要将设置参数int *max,int *min。
即void max_min(int a[],int m,int n,int *max,int *min)。
这样就可以直接得到最大值、最小值。
该函数使用递归来实现,而递归的终止条件是最后分得的数组中只有一个或两个元素,当分得的数组元素个数大于2时,就进行递归调用。
四.测试数据及运行结果正确的3组运行结果:出现的错误:若将代码中的随机数函数返回值的类型改变,则会出现错误结果,甚至编译不通过。
五.总结1.实验过程中遇到的问题及解决办法;实验过程中,用分治法求最大值、最小值时,如果用返回值求最大值和最小值,则需要两个函数。
这样就会导致代码冗余,不会达到代码的复用性功能。
所以要将两个功能用一个函数直接实现就可以使用参数指针的形式。
2.对设计及调试过程的心得体会。
算法设计的课内实验既要实现实验的功能,还要讲究代码中算法的精妙、简单以及它的效率。
不能同其他高级语言的课内实验一样仅仅考虑如何完成该实验的功能,这样就可以真正地体验到算法与设计这门课的意义。
平时做实验时我们可以用不同算法实现,这样不仅可以积累平常上课学到的知识,还可以为以后的算法设计能力奠定基础。
平常更多地进行思考,可以让我们在求职时更受益。
六.附录:源代码(电子版)#include<stdio.h>#include<stdlib.h>#include<time.h>void max_min(int a[],int m,int n,int *max,int *min){int middle,hmax,hmin,gmax,gmin;if(m==n){ *max=a[m];*min=a[m];}else if(m==n-1){if(a[m]>a[n]){*max=a[m];*min=a[n];}else{*max=a[n];*min=a[m];}}else{max_min(a,m,middle,&gmax,&gmin);max_min(a,middle+1,n,&hmax,&hmin);if(gmax>hmax)*max=gmax;else*max=hmax;if(gmin<hmin)*min=gmin;else*min=hmin;}}int main(){int i;int max,min;srand((unsigned)time(NULL));int n=rand()%10+1;printf("数组的个数:%d\n",n);int a[n];for(i=0;i<n;i++){a[i]=rand()%50+1;printf("%d\t",a[i]);}max_min(a,0,n-1,&max,&min);printf("最大数:%d,最小数:%d\n",max,min);retur n 0;}。
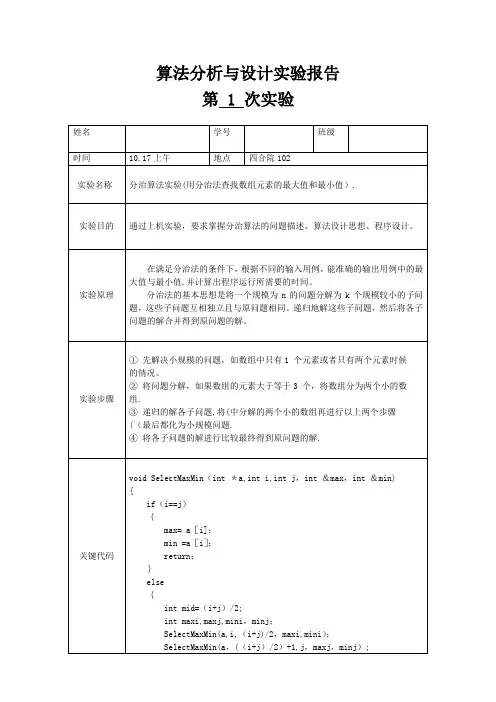
算法分析与设计实验报告第 1 次实验if(maxi>maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}srand((unsigned int)time(NULL));cout <〈”随机产生的数据(0—100):”;for(int i=0; i〈m; i++)a[i] = rand()%100;测试结果附录:完整代码SelectMaxMin.cpp:#include <iostream>#include <ctime>#include 〈cstdio>#include <iomanip>#include 〈cstdlib〉using namespace std;void SelectMaxMin(int *a,int i,int j,int &max,int &min) {if(i==j){max= a[i];min =a[i];return;}else{int mid=(i+j)/2;int maxi,maxj,mini,minj;SelectMaxMin(a,i,(i+j)/2,maxi,mini);SelectMaxMin(a,((i+j)/2)+1,j,maxj,minj);if(maxi〉maxj)max=maxi;elsemax=maxj;if(mini<minj)min=mini;elsemin=minj;return;}}int main(){clock_t start,end,over;start=clock();end=clock();over=end—start;start=clock();//freopen("in。
txt",”r",stdin);//freopen(”out。
txt”,”w",stdout);int m;cout 〈<"Please input the number : ”;cin>〉 m;int a[m];srand((unsigned int)time(NULL));cout 〈〈 "随机产生的数据(0-100):";for(int i=0; i〈m; i++)a[i] = rand()%100;for(int i=0; i〈m; i++)cout <〈 a[i] 〈< " ";cout 〈< endl;int max,min;SelectMaxMin(a,0,m-1,max,min);cout 〈< "max = " 〈〈 max 〈〈 endl;cout <〈”min = " <〈 min 〈〈 endl;end=clock();printf(”The time is %6.3f”,(double)(end-start—over)/CLK_TCK); }。


算法——蛮⼒法之最近对问题和凸包问题 上次的博客写到⼀半宿舍停电了。
然⽽今天想起来补充完的时候发现博客园并没有⾃动保存哦,微笑。
最近对问题 ⾸先来看最近对问题,最近对问题描述的就是在包含n个端的集合中找到距离最近的两个点,当然问题也可以定义在多维空间中,但是这⾥只是跟随书上的思路实现了⼆维情况下的最近对问题。
假设所有讨论的点是以标准的笛卡尔坐标形式(x,y)给出的,那么在两个点P i=(X i,Y i)和P j=(X j,Y j)之间的距离是标准的欧⼏⾥得距离: d(P i,P j)=sqrt( (X1-X2)2+(Y1-Y2)2 )蛮⼒法的思路就是计算出所有的点之间的距离,然后找出距离最⼩的那⼀对,在这⾥增加效率的⼀种⽅式是只计算点下标 i<j 的那些对点之间的距离,这样就避免了重复计算同⼀对点间距离。
下⾯是蛮⼒法解决最近对问题的算法:使⽤蛮⼒法求平⾯中距离最近的两点BruteForceClosetPoints(P)//输⼊:⼀个n(n≥2)的点的列表P,P i=(X i,Y i)//输出:距离最近的两个点的下标index1和index2dmin <— ∞for i <— 1 to n-1 do for j <— i+1 to n do d <— sqrt( (X i-X i)2+(Y j-Y j)2 ) if d<dmin dmin=d; index1=i; index2=j;return index1,index2 该算法的关键步骤是基本操作虽然是计算两个点之间的欧⼏⾥得距离,但是求平⽅根并不是像加法乘法那么简单。
上⾯算法中,开平⽅函数导数恒⼤于0,它是严格递增的,因此我们可以直接只计算(X i-X i)2+(Y j-Y j)2,⽐较d2的⼤⼩关系,这样基本操作就变成了求平⽅。
平⽅操作的执⾏次数是: n(n-1)∈Θ(n2)因此,蛮⼒法解决最近对问题的平均时间复杂度是Θ(n2) 下⾯是该算法的c++代码实现部分,在实现这个算法时,我碰到了三个问题: ⼀是:怎么表⽰⼀个点集,因为最终返回的下标是集合中点的下标,要⽤的数据结构就是⼀维数组,但是点的xy坐标⼜要怎么表⽰呢,这⾥我在头⽂件中创建了struct类型的点结构,该结构拥有的成员变量就是x代表的横坐标和y代表的纵坐标,这样就可以直接创建该结构的⼀位数组进⾏计算了。

分治思想实验报告总结引言分治法是一种非常重要的算法设计思想,它将一个大规模问题划分为多个相同或相似的子问题,然后逐一解决子问题,并将子问题的解合并为原问题的解。
分治法的应用非常广泛,例如在排序算法、图像处理、机器学习等领域都有着重要的地位。
本实验通过具体的案例来验证分治思想的有效性和实用性。
首先,我们将通过合并排序算法来理解分治法的基本思想和步骤。
然后,我们将通过求解给定数列的最大子数组和问题来进一步探讨使用分治法解决问题的过程和效果。
实验步骤与结果合并排序算法合并排序算法是一种典型的使用分治思想的排序算法。
它的基本思路是将待排序的序列划分成两个大小相等(或相差不超过1)的子序列,然后对子序列进行排序,最后将两个已排序的子序列合并为一个有序序列。
具体步骤如下:1. 将待排序序列划分为两个大小相等(或相差不超过1)的子序列;2. 对两个子序列分别进行递归调用,继续划分和排序;3. 将排好序的两个子序列合并起来。
经过实验,我们验证了合并排序算法的正确性,且其时间复杂度为O(nlogn)。
最大子数组和问题最大子数组和问题是一个常见的问题,它的目标是在给定的一个数列中找出连续的一段子数组,使得这段子数组的元素之和尽可能大。
为了解决这个问题,我们使用了分治法并设计了以下算法:1. 将给定的数列划分为左右两部分;2. 分别对左右两部分进行递归求解,得到左右两部分的最大子数组和;3. 考虑跨越中点的情况,即计算包含中点元素的最大子数组和;4. 取上述三种情况中的最大值作为结果返回。
经过实验,我们发现该算法可以在较短时间内求解较大规模的问题,并得出正确的结果。
总结本实验通过合并排序算法和最大子数组和问题的案例,验证了分治思想在算法设计中的有效性和实用性。
分治法能够将一个大规模的问题划分为多个相似的子问题,这些子问题可以并行求解,从而提高效率。
同时,分治法也能够降低问题的复杂度,使得问题的求解更加简便和直观。
然而,分治法在某些情况下可能并不适用,例如问题的分解和合并过程会带来额外的开销,从而降低了效率。

平⾯最近点对问题(分治)平⾯最近点对问题是指:在给出的同⼀个平⾯内的所有点的坐标,然后找出这些点中最近的两个点的距离.⽅法1:穷举1)算法描述:已知集合S中有n个点,⼀共可以组成n(n-1)/2对点对,蛮⼒法就是对这n(n-1)/2对点对逐对进⾏距离计算,通过循环求得点集中的最近点对2)算法时间复杂度:算法⼀共要执⾏ n(n-1)/2次循环,因此算法复杂度为O(n2)代码实现:利⽤两个for循环可实现所有点的配对,每次配对算出距离然后更新最短距离.for (i=0 ; i < n ;i ++){for(j= i+1 ; j<n ;j ++){点i与点j的配对}}⽅法2:分治1) 把它分成两个或多个更⼩的问题;2) 分别解决每个⼩问题;3) 把各⼩问题的解答组合起来,即可得到原问题的解答。
⼩问题通常与原问题相似,可以递归地使⽤分⽽治之策略来解决。
在这⾥介绍⼀种时间复杂度为O(nlognlogn)的算法。
其实,这⾥⽤到了分治的思想。
将所给平⾯上n个点的集合S分成两个⼦集S1和S2,每个⼦集中约有n/2个点。
然后在每个⼦集中递归地求最接近的点对。
在这⾥,⼀个关键的问题是如何实现分治法中的合并步骤,即由S1和S2的最接近点对,如何求得原集合S中的最接近点对。
如果这两个点分别在S1和S2中,问题就变得复杂了。
为了使问题变得简单,⾸先考虑⼀维的情形。
此时,S中的n个点退化为x轴上的n个实数x1,x2,...,xn。
最接近点对即为这n个实数中相差最⼩的两个实数。
显然可以先将点排好序,然后线性扫描就可以了。
但我们为了便于推⼴到⼆维的情形,尝试⽤分治法解决这个问题。
假设我们⽤m点将S分为S1和S2两个集合,这样⼀来,对于所有的p(S1中的点)和q(S2中的点),有p<q。
递归地在S1和S2上找出其最接近点对{p1,p2}和{q1,q2},并设 d = min{ |p1-p2| , |q1-q2| } 由此易知,S中最接近点对或者是{p1,p2},或者是{q1,q2},或者是某个{q3,p3},如下图所⽰。

T S P问题分析动态规划-分支界限法-蛮力法算法综合实验报告学号: 1004111115 姓名:李宏强一、实验内容:分别用动态规划、贪心及分支限界法实现对TSP问题(无向图)的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:(包括程序的数据结构、函数组成、输入/输出设计、符号名说明等)1、动态规划法(1)数据结构:①利用二进制来表示集合,则集合S可由一个十进制数x相对应,此x所对应的二进制数为y,如果y的第k位为1,则表示k存在集合S中。
例如:集合S={0,1}(其子集合为{}{0}{1}{01}),我们用二进制数11(所对应十进制数为3)表示S,11中右手边第1个数为1表示0在集合S中,右手边第二个数为1表示1在集合S中,其他位为0表示其它数字不在集合S中;同理,集合S={0,2}(其子集合为{}{0}{2}{02}可用二进制数101(所对应十进制数为5)表示(右手边第1个数为1表示0在集合S中,右手边第二个数为0表示1不在集合S中,右手边第3个数为1表示2在集合S中,则说明0,2在集合中,1不在集合中。
②利用邻接矩阵表示任意两点之间的距离例如:mp[i][j]表示点i,j两点之间的距离。
(2)函数组成①输入函数in()②利用动态规划法算法实现的求解函数solve()③主函数main()(3)输入/输出设计本程序可以通过键盘进行输入、屏幕进行输出。
(根据实际程序情况,还可以选择随机产生输入数据、将输出数据输出到文件等其它方式)这里采用随机产生输入数据,将数据输出在屏幕上的方式。
(4)符号名说明① n 表示顶点个数。
② mp[i][j] 表示顶点i和顶点j之间的距离。
③ dp[i][j] 表示顶点i经过集合S(用二进制表示的数为j)后回到起始点的最短路径和。
(5)算法描述①某一个点i不经过任意点回到起始点的最短路径和为mp[i][0](默认初始点为0)dp[i][0] = mp[i][0]; (1<=i<n)②点i经过集合S(二进制表示的数为j)的最短路径和为从点i经过集合S中的某一点k后再从该点出发,经过集合S-{k}的最小值。
第1篇一、实验目的1. 了解伐树过程中树木受力的基本原理。
2. 掌握树木受力分析的方法。
3. 提高对树木力学特性的认识。
二、实验原理在伐树过程中,树木受到的主要力有:重力、拉力、剪力、摩擦力等。
本实验通过搭建简易的伐树模型,分析伐树过程中树木受力的变化规律,从而为实际伐树作业提供理论依据。
三、实验器材1. 钢筋一根,长度约为2m。
2. 钢丝一根,长度约为1m。
3. 轴承两个。
4. 定滑轮一个。
5. 重物若干,质量约为50kg。
6. 弹簧测力计一个。
7. 直尺一把。
8. 记录本一本。
四、实验步骤1. 将钢筋一端固定在支架上,另一端穿过轴承,并穿过定滑轮。
2. 将钢丝穿过轴承,并连接在钢筋的另一端。
3. 将重物挂在钢丝上,调整重物位置,使钢丝处于水平状态。
4. 使用弹簧测力计测量钢丝的拉力。
5. 在树木根部施加一定的压力,使树木倾斜。
6. 记录伐树过程中钢丝的拉力变化情况。
7. 分析伐树过程中树木受力的变化规律。
五、实验数据1. 钢丝初始拉力:F1 = 100N2. 伐树过程中钢丝最大拉力:F2 = 200N3. 伐树过程中钢丝最小拉力:F3 = 150N六、实验结果分析1. 在伐树过程中,钢丝的拉力随着树木倾斜角度的增加而增大。
这是由于树木受到的重力、拉力、剪力等力的作用,使得钢丝的受力状态发生变化。
2. 在伐树过程中,树木受到的重力、拉力、剪力等力的作用相互影响,使得树木的受力状态复杂。
通过实验数据可以看出,在伐树过程中,钢丝的拉力变化较大,说明树木受力状态不稳定。
3. 在伐树过程中,摩擦力对树木受力的影响不容忽视。
实验结果表明,摩擦力对树木受力有缓冲作用,使得树木在倾斜过程中受力相对平稳。
七、实验结论1. 伐树过程中,树木受力状态复杂,主要包括重力、拉力、剪力、摩擦力等。
2. 在伐树过程中,钢丝的拉力随着树木倾斜角度的增加而增大,树木受力状态不稳定。
3. 摩擦力对树木受力有缓冲作用,使得树木在倾斜过程中受力相对平稳。
算法综合实验报告学号:姓名:一、实验内容:分别用蛮力、动态规划、贪心及分支限界法实现对TSP问题或者0-1背包问题的求解,并至少用两个测试用例对所完成的代码进行正确性及效率关系上的验证。
二、程序设计的基本思想、原理和算法描述:1、蛮力法(1)数据结构:使用一维数组存储物品的价值和重量还有下标。
(2)函数组成除主函数外还有一个subset()函数,在此函数中列出所有的子集列出子集的同时求解最大价值,并且物品总重量要小于背包总容量。
(3)输入/输出设计首先通过键盘输入物品的总重量,再输入背包总容量,依次输入每个物品的重量,对应输入相应重量的价值,循环直至输入所有物品的重量和价值。
最后输出物品的最大价值。
本程序通过键盘进行输入、屏幕进行输出。
(根据实际程序情况,还可以选择随机产生输入数据、将输出数据输出到文件等其它方式)(4)符号名说明w[1001]为物品重量的集合,v[1001]为物品价值的集合,n为物品数量,m为背包总容量,x[1001]用来存储物品是否装入背包,0为不装入,1为装入。
用a[1001]来存储下标,用下标找出所有子集。
(5)算法描述采用增量构造的方法来构造出物品的所有子集,对物品的下标应用此方法进行构造,下标与物品相对应,选出子集时物品的重量加之前重量小于背包总重量时将价值加上去,最后选出能装入背包的物品的最大值。
2、 动态规划法(1)数据结构:使用一维数组存储各个物品价值,重量,使用一个二维数组存储动态规划的整体求解的表,并以背包容量为最大列号,物品个数为最大行号。
(2)函数组成:除主函数外由两个函数组成,一个是求解两个数中的大的一个的函数,另一个则是进行动态规划求解的函数,在使用动态规划方法具体求解时调用求最大值函数,在主程序之中调用动态规划函数。
(3)输入/输出设计:首先通过键盘输入物品的总重量,再输入背包总容量,依次输入每个物品的重量,对应输入相应重量的价值,循环直至输入所有物品的重量和价值。
分治法算法分析作业吴迪2011-3-29本次是第一次算法作业,该部分容包含3个题目的程序代码,分析文档,说明图片等容目录引言 (3)1算法性能比较 (3)1.1问题分析 (3)1.2源程序代码 (3)1.3运行示例 (8)1.4数据分析 (8)(单次录入数据具有较大随机误差,只看增长趋势) (8)2循环赛问题 (9)2.1问题描述 (9)2.2问题分析 (9)2.3 源程序 (10)2.4运行示例 (11)3最大最小值问题 (12)3.1问题描述与分析 (12)3.2源程序 (13)3.3运行示例 (14)引言任何一个可以用计算机求解的问题所需的计算时间都与其规模有关。
问题的规模越小,越容易直接求解,解题所需的计算时间也越少。
分治法是计算机科学中经常使用的一种算法。
设计思想是,将一个难以直接解决的大问题,分割成一些规模较小的相同问题,以便各个击破,分而治之。
但是不是所有问题都适合用分治法解决。
当求解一个输入规模为n且取值又相当大的问题时,使用蛮力策略效率一般得不到保证。
因此分治策略将问题划分成k个子问题分别求解合并能有效提高计算效率。
1算法性能比较1.1问题分析比较插入排序,合并排序和快速排序性能。
算法性能比较通常是从时间复杂度的角度进行的。
排序算法的复杂度主要和算法中的比较次数和元素交换或移动次数有关。
因而在不同大小规模的问题过统计这两者之和来评判算法的优劣。
同时也可以证明各种算法的时间复杂度与问题规模n之间的关系。
特别说明:本程序中考虑到不同规模的乱序数据输入过程比较复杂,编写了一个规模n的整型数据随机排列函数,能够直接生成指定大小的1-n无序整数列。
1.2源程序代码//2011年3月19日0:20:02//main test.cpp for test#include<iostream>#include<time.h>using namespace std;//全局标记比较次数和移动次数int count_compare=0;int count_move = 0;int count_all(){return count_compare+count_move;}void clear_count(){count_compare=0;count_move = 0;}//insert sortvoid insert_element(int a[],int size,int element) //size before insertion {int i=0;for(i=size-1;i>=0;i--){count_compare++;if(element<a[i]){ a[i+1]=a[i];count_move++;}else break;}a[i+1]=element;count_move++;}void InsertSort(int a[],int size){for(int i=1;i<size;i++){insert_element(a,i,a[i]);}}//merge sortvoid Merge(int c[],int d[], int l, int m, int r){int i = l, j = m+1, k = l;while(i <= m && j <= r){count_compare++;if(c[i] <= c[j]){d[k++]=c[i++];count_move++;}else{ d[k++]=c[j++];count_move++;}}count_compare++;if(i > m){for(int q = j; q <= r; q ++){d[k++] = c[q];count_move++;}}elsefor(int q = i; q <= m; q ++){d[k++] = c[q];count_move++;}}void Copy(int a[],int b[],int l,int r){for(int i=l;i<=r;i++){a[i]=b[i];count_move++;}}void MergeSort(int a[],int left,int right,int size) {if(left < right){count_compare++;int i = (right + left)/2;int p=size; //this is important,mind the value! int *b=new int[p];MergeSort(a, left, i,size);MergeSort(a, i+1, right,size);Merge(a, b, left, i, right);Copy(a,b,left,right);}}//quick sortvoid swap(int a[],int i,int j){int temp=a[i];a[i]=a[j];a[j]=temp;count_move+=3;}int partition(int a[],int p,int r){int i=p,j=r+1;int x=a[p];while(true){while(a[++i]<x&&i<r) count_compare++;while(a[--j]>x) count_compare++;count_compare++;if(i>=j) break;swap(a,i,j);}a[p] =a[j];a[j] = x;count_move++;return j;}void QuickSort(int a[],int p ,int r){if (p < r){int q= partition(a, p , r);QuickSort(a,p,q-1);QuickSort(a,q+1,r);}count_compare++;}//showvoid show_array(int a[],int size) //显示一个数组的所有元素{for(int i=0;i<size;i++){cout << a[i] << " ";}cout << endl;}//random arrayvoid RandomArray(int a[],int size) //随机生成数组含n个元素,其元素各不相同{srand(time(NULL));for(int i=0;i<size;i++) a[i]=0;for(int i=1;i<=size;i++){int p=rand()%size;while(a[p]!=0) {p=(++p)%size;}a[p]=i;}show_array(a,size);}//copy arrayvoid CopyArray(int a[],int b[],int size){for(int i=0;i<size;i++) b[i]=a[i];}int main(){int*a;int *temp_a;int size=4;cin>>size;a=new int [size];temp_a = new int [size];RandomArray(temp_a,size);CopyArray(temp_a,a,size);show_array(a,size);InsertSort(a,size);show_array(a,size);cout << "插入排序比较次数为" << count_compare << endl; cout << "插入排序移动次数为" << count_move << endl; cout << "总规模为" << count_all() << endl;clear_count();CopyArray(temp_a,a,size);show_array(a,size);MergeSort(a,0,size-1,size);show_array(a,size);cout << "合并排序比较次数为" << count_compare << endl; cout << "合并排序移动次数为" << count_move << endl; cout << "总规模为" << count_all() << endl;clear_count();CopyArray(temp_a,a,size);show_array(a,size);QuickSort(a,0,size-1);show_array(a,size);cout << "快速排序比较次数为" << count_compare << endl; cout << "快速排序移动次数为" << count_move << endl; cout << "总规模为" << count_all() << endl;show_array(a,size);system("pause");return 0;}}1.3运行示例1.4数据分析(单次录入数据具有较大随机误差,只看增长趋势)问题规模(n)排序总复杂度规模(T(n))插入排序合并排序快速排序10 57 105 5020 221 280 12230 367 461 23840 946 660 37150 1394 879 43280 3261 1570 856100 4694 2064 1064200 22912 4718 2447500 130133 13668 73681000 504254 30309 1700310000 43898103 401968 225489根据列表分析,插入算法平均复杂度为, 合并算法平均复杂度为, 快速排序算法平均复杂度为,但是排序算法最坏情况下复杂度仍为,为了验证这一点,取n=1000的已排好数组,快排总规模变为503497,取n=10000的已排好数组,快排总规模变为50034997。
实验三蛮力法排序(四号黑体)【一】实验目的(小四黑体)1.采用蛮力法实现序列排序;2.分析各种方法的优缺点。
【二】实验内容(小四黑体)1.采用蛮力排序算法对序列排序;2.编程实现选择排序与冒泡排序;3.分析比较2种算法的时间复杂度;4.试着改进冒泡排序,使算法在序列达到有序状态时停止运行。
【三】实验步骤(代码、结果)(小四黑体)#include <stdio.h>#include <stdlib.h>#include <math.h>void SelectionSort(int a[],int n){int i,j,t,temp;for(i=0; i<=n-2; i++){t=i;for(j=i+1; j<=n-1; j++){if(a[j]<a[t]){t=j;}}temp=a[i];a[i]=a[t];a[t]=temp;}}void BubbleSort(int a[],int n){int i,j,temp;for(i=0; i<=n-2; i++){for(j=0; j<=n-2-i; j++){if(a[j+1]<a[j]){temp=a[j];a[j]=a[j+1];a[j+1]=temp;}}}}void BubbleSort1(int a[],int n){int falg=1;int i,temp;while(falg){falg=0;for(i=0;i<n;i++){if(a[i+1]<a[i]){temp=a[i];a[i]=a[i+1];a[i+1]=temp;falg=1;}}n--;}}void print(int a[],int n){int i;for(i=0; i<n; i++){printf("%d ",a[i]);}}int main(){printf("学号:Z09315221 姓名:谭召\n"); int a[10]= {10,20,15,17,13,9,5,4,2,7}; //int a[10]= {1,2,3,4,5,6,7,8,9,1};SelectionSort(a,10);BubbleSort(a,10);BubbleSort1(a,10);print(a,10);return 0;}【四】实验结果分析(小四黑体)选择排序的基本思想是对待排序的记录序列进行n-1遍的处理,第i遍处理是将L[i..n]中最小者与L[i]交换位置。
《算法设计与分析》实验报告一学号: 1004091130姓名: 金玉琦 日期: 2011-10-13得分:一、实验内容:最近对问题,即找出一个点集合中距离最近的点对,分别运用蛮力法和分治法性能解决该问题,对两种算法进行性能比较。
二、所用算法的基本思想及复杂度分析:1.分治法1)基本思想我们用分治法解决最近对问题,就是将集合S 分成两个子集S 1和S2,每个子集中有n/2个点。
然后在每个子集中递归的求其最接近的点对,在求出每个子集的最接近点对后,关键问题是如何实现分治法中的合并步骤,如果组成S 的最接近点对的2个点都在S1中或都在S2中,则问题很容易解决。
但是,如果这2个点分别在S1和S2中,则对于S1中任一点p ,S2中最多只有n/2个点与它构成最接近点对的候选者,仍需计算才能得到准确结果。
2)复杂度分析应用分治法求解含有n 个点得最近对问题,其时间复杂性可由下面的递推式表示:T (n )=2T (n /2)+f (n )合并子问题的解的时间f (n )=O (1),由通用分治递推式的主定理可得,T (n )=O (nlog 2n )2.蛮力法1)基本思想蛮力法求解最近对问题的过程是:分别计算每一对点之间的距离,然后找出距离最小的一对,为了避免对同一对点计算两次距离,只考虑i<j 的那些点对(P i ,P j )。
2)复杂度分析算法的基本操作是计算两个点的欧几里得距离。
注意到在求欧几里得距离时,避免了球平方根操作,原因是:如果被开方的数越小,则它的平方根也越小。
所以,算法的基本操作就是求平方,其执行次数为:T(n)=∑-=11n i ∑+=n i j 12 =2∑-=-11)(n i i n =n (n-1)=O (n 2) 三、源程序及注释:#define LENGTH 10000#define min(X,Y) ((X)<(Y)?(X):(Y))#include <FLOAT.H>#include <WINDOWS.H>#include <TIME.H>#include <MATH.H>#include <algorithm>#include <IOSTREAM>using namespace std;struct point{double x;double y;};point points[LENGTH*2];// point tempLeft[LENGTH];// point tempRight[LENGTH];//排序int cmpp(point a,point b){if(a.x!=b.x) return a.x<b.x;return a.y<b.y;}//求距离的平方,在这不用求出距离,直接求出平方少计算一次,效果相同double Distence(point a,point b){return (a.x-b.x)*(a.x-b.x)+(a.y-b.y)*(a.y-b.y);}//蛮力法函数double ClosestPoints(int n,point p[],int &index1,int &index2) {double minDist=DBL_MAX;double temp;for (int i=0;i<n;i++)for (int j=i+1;j<=n;j++){temp=Distence(p[i],p[j]);if(temp<minDist){minDist=temp;index1=i;index2=j;}}return sqrt(minDist);}//分治法函数double DivPoints(point p[],int begin,int end){int i,j;int n=end-begin+1;int m=(begin+end)/2;if(n==2)return Distence(p[begin],p[end]);//两个点返回距离if(n==3)//三个点直接求最近点并返回距离{double d1=Distence(p[begin],p[begin+1]);double d2=Distence(p[begin+1],p[end]);double d3=Distence(p[begin],p[end]);if(d1<=d2&&d1<=d3)return d1;else if(d2<=d3)return d2;else return d3;}double left=DivPoints(p,begin,m);double right=DivPoints(p,m+1,end);double d=min(left,right);int k,l,flag=0;//找到以m为中心的与m横坐标距离小于sqrt(d)的点for(i=begin;i<=end;i++){if(flag==0&&(p[m].x-p[i].x)<=sqrt(d)){flag=1;k=i;}if((p[i].x-p[m].x)<=sqrt(d))l=i;}for (i=k;i<=m;i++){for (j=m+1;j<=l&&fabs((p[j].y-p[i].y))<sqrt(d);j++){if(Distence(p[i],p[j])<=d)d=Distence(p[i],p[j]);}}// for(i=begin;i<=m;i++)// if((p[m].x-p[i].x)<=sqrt(d))// tempLeft[k++]=p[i]; //将m左侧与m水平距离小于d的点放入tempLeft中// for(i=m+1;i<=end;i++)// if((p[i].x-p[m].x)<=sqrt(d))// tempRight[l++]=p[i]; //将m右侧与m水平距离小于d的点放入tempRight中// //将tempLeft和tempRight按y升序排列// sort(tempLeft,tempLeft+k,cmpy);// sort(tempRight,tempRight+l,cmpy);// double md=DBL_MAX;// for(i=0;i<k;i++)// for(j=0;j<l&&fabs(tempLeft[i].y-tempRight[j].y)<=sqrt(d);j++) // {// if(Distence(tempLeft[i],tempRight[j])<=md)// md=Distence(tempLeft[i],tempRight[j]);// }return d;}//主函数void main(){LARGE_INTEGER begin,end,frequency;int n;int index1,index2;double forcedist,divdist;cout<<"输入随机点个数:";cin>>n;cout<<endl;//生成随机数srand(time(0));for (int i=0;i<n;i++){points[i].x=rand();points[i].y=rand();}//蛮力法求最近对时间QueryPerformanceFrequency(&frequency);QueryPerformanceCounter(&begin);forcedist=ClosestPoints(n,points,index1,index2);QueryPerformanceCounter(&end);cout<<"最短距离是:"<<forcedist<<"两个点是:("<<points[index1].x<<","<<points[index1].y<<")和("<<points[index2].x<<","<<points[index2].y<<")"<<endl;cout<<"蛮力法求解时间"<<(double)(end.QuadPart-begin.QuadPart)/frequency.QuadPart<<"s"<<endl;//分治法求最近对时间QueryPerformanceCounter(&begin);sort(points,points+n,cmpp); //对点对排序divdist=sqrt(DivPoints(points,0,n-1));QueryPerformanceCounter(&end);cout<<"最短距离是:"<<divdist<<endl;cout<<"分治法求解时间"<<(double)(end.QuadPart-begin.QuadPart)/frequency.QuadPart<<"s"<<endl;}四、运行输出结果:五、调试和运行程序过程中产生的问题、采取的措施及获得的相关经验教训:1在点的个数比较少的时候,蛮力法所用时间时间比分治法少,点数比较多的情况下,分治法的优势就很明显了,所用时间明显比蛮力法少。
2.在输入一个点的时候程序会崩溃,因为返回值是无穷大,分治法的合并过程中会出错。
3.分治法中,借鉴别人的做法,没有产生P1和P2两个子点集,这样节省了空间,而且将整个点集排序之后就没有必要划分成两个点集。
上述代码中被注释部分是将整个点集划分成两个子集的做法。