北师大版八年级上册数学寒假作业

北师大版八年级上册数学寒假作业答案（2021最新版）作者：______编写日期：2021年__月__日一、选择1.B2.A3.C4.C5.B6.B7.C8.D9.C10.D11.B二、填空12.①②③④13.①②14.；15.且；或216.；17.且；18.-1；19.；20.；；；21.2；222.或-223.且三、计算24.2；25.3；26.；27.；28.；29.；30.；31.；四、解分式方程32.；33.（增根）；34.（增根）；35.（增根）；36.；37.或-1五、用分式方程解应用题38.步行：6千米/小时；自行车：18千米/小时39.原计划每小时加工150个40.原来这个两位数是6341.船在静水中的速度是19千米/小时42.规定日期为6天43.今年用水价格为元/m344.项目家电种类购买数量（台）原价购买总额（元）政府补贴返还比例补贴返还总金额（元）每台补贴返还金额（元）冰箱4000013%5200电视机1500013%1950电视：10台；冰箱：20台一、选择1——8CDDCDDCB二、填空题9.110.46000000011.1812.13.14.（0，3）15.y=-1.5x+3.516.10元17.5418.（4，2）三、解答题19.解：（1）将，代入得：∴∴一次函数的解析式为（2）将的图象向上平移6个单位得，当时，∴平移后的图象与x轴交点的坐标为.20.解：甲：众数为10.8，平均数为10.9，中位数为10.85.乙：众数为10.9，平均数为10.8，中位数为10.85.分析：从众数上看，甲的整体成绩优于乙的整体成绩；从平均数上看，乙的平均成绩优于甲的平均成绩；从中位数看，甲、乙的成绩一样好.21.解：（1）四边形OCED是菱形.∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形，又在矩形ABCD中，OC=OD，∴四边形OCED是菱形.（2）连结OE.由菱形OCED得：CD⊥OE，∴OE∥BC又CE∥BD∴四边形BCEO是平行四边形∴OE=BC=8∴S四边形OCED=22.解（1）令y=0，得x=∴A点坐标为（，0）.令x=0，得y=3∴B点坐标为（0，3）.（2）设P点坐标为（x，0），依题意，得x=±3.∴P点坐标为P1（3，0）或P2（-3，0）.∴S△ABP1==S△ABP2==.∴△ABP的面积为或.23.（1）证明：都是等腰直角三角形∴AC=BC，EC=DC在中，AC=BCEC=DC≌（2）解：由（1）可得AE=BD，又，即是直角三角形24.解：（1）甲厂的收费y（元）与印制数量x（份）之间的函数关系式为y=x+1000乙厂的收费y（元）与印制数量x（份）之间的函数关系式为y=2x（2）根据题意：若找甲厂印制，可以印制的份数x满足3000=x+1000得x=2000若找乙厂印制，可以印制的份数x满足3000=2x得x=1500又2000>1500∴找甲厂印制的宣传材料多一些.（3）根据题意可得x+10001000当印制数量大于1000份时，在甲厂印刷合算.25.解：（1）由题可得，当y1=y2时，即-x+70=2x-38∴3x=108，∴x=36当x=36时，y1=y2=34，所以该药品的稳定价格为36元/件，稳定需求量为34万件.（2）令y1=0，得x=70，由图象可知，当药品每件价格在大于36元小于70元时，该药品的需求量低于供应量.（3）设政府对该药品每件价格补贴a元，则有解得所以政府部门对该药品每件应补贴9元.。

专题一勾股定理及其逆定理一、填空题1．△ABC，∠C=90°，a=9，b=12，则c=__________。

2．△ABC，AC=6，BC=8，当AB=__________时，∠C=90°。

3．等边三角形的边长为6 cm，则它的高为__________。

4．△ABC中，∠C=90°，∠A=30°，则BC∶AC∶AB=__________。

5．直角三角形两直角边长分别为3 和4，则斜边上的高为__________。

6．等腰三角形的顶角为120°，底边上的高为3，则它的周长为__________。

7．若直角三角形两直角边之比为3∶4，斜边长为20，则它的面积为__________。

8．等腰三角形的两边长为2和4，则底边上的高为__________。

9．如图1，在高2米，坡角为30°的楼梯表面铺地毯，地毯的长至少需________米。

10．若一个三角形的三边长分别为3，4，x，则使此三角形是直角三角形的x2的值是__________。

图1 图2 图3 图4二、选择题11．下列各组数中，不能构成直角三角形的一组是（）A．1，2，5B．1，2，3C．3，4，5 D．6，8，1212．如图2，△ABC中AD⊥BC于D，AB=3，BD=2，DC=1，则AC等于（）A．6 B．6C．5D．413．已知三角形的三边长之比为1∶1∶2，则此三角形一定是（）A．锐角三角形B．钝角三角形C．等边三角形D．等腰直角三角形14．直角三角形的斜边比一直角边长2 cm，另一直角边长为6 cm，则它的斜边长（）A．4 cm B．8 cm C．10 cm D．12 cm15．如图3，以三角形三边为直径向外作三个半圆，若较小的两个半圆面积之和等于较大的半圆面积，则这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．锐角三角形或钝角三角形三、解答题18、在某山区需要修建一条高速公路，在施工过程中要沿直线AB打通一条隧道，动工前，应先测隧道BC的长，现测得∠ABD=150°，∠D=60°，BD=10 k m，请根据上述数据，求出隧道BC的长。

八年级上册数学北师大版寒假作业答案2022 2022年八年级上册数学北师大版寒假作业答案如下：1、第一章：数的基本概念1) 第1题：1.25， 1/4，0.25， 2/82) 第2题：复数：5的共轭复数为：5+i3) 第3题：运算法则：交换律2、第二章：分数1) 第4题：加减法：2/5+1/5=3/52) 第5题：乘法：1/3*3/5=3/153) 第6题：除法：＜2/5＞÷＜1/2＞=4/53、第三章：小数1) 第7题：计算：3.7-2.86=0.842) 第8题：除法：2.5÷0.1=253) 第9题：乘法：4.7*1.3=6.114、第四章：数的级数1) 第10题：能量守恒定理：能量守恒定律表明，能量在它的转换过程中，总是保持不变。

2) 第11题：真现定理：真现定理指出，等差数列的和等于该数列的首项与末项的积除以2。

3) 第12题：映射定理：映射定理指出：如果集合A和B相等，那么任意两个从A到B的映射都是相等的。

5、第五章：比例1) 第13题：应用题：如果珊瑚的重量是0.35千克，它的长度是20厘米，那么它的宽度是：7厘米2) 第14题：对比概念：比例是由一组相对比例关系组成的概念。

3) 第15题：比例法：两个比例相等时，相应比例尺寸也相等。

6、第六章：数的因式分解1) 第16题：因子：一个正整数可以分解为两个或两个以上的质因数的乘积。

2) 第17题：因子的乘积：两个或多个因子相乘，得到的积称为因子的乘积。

3) 第18题：内括号：使用内括号将一组数列分组，有助于表达算式的含义。

7、第七章：方程与不等式1) 第19题：方法：解一元二次不等式的方法是先把该不等式视为一元二次方程，再把该方程化成一元二次不等式，最后求其解。

2) 第20题：求解：2x-5<7，解：2x<12， x<63) 第21题：应用题：蔡先生派发了数份礼物，每份礼物总价180元，其中书60元，买2本，买其它礼物一共花了多少钱？花了120元。

八年级上册寒假作业（三）姓名： 年 月 日1.将△ABC 的三个顶点坐标的横坐标乘以－1，纵坐标不变，则所得图形与原图的关系是( )A ．关于x 轴轴称B ．关于y 轴对称C ．关于原点对称D ．将原图向x 轴的负方向平移了1个单位2.实数a 、b 在数轴上对应点的位置如图，则2a b a --的结果是( )A 、2a-bB 、b-2aC 、bD 、-b 3.如果梯子的底端离建筑物5米，13米长的梯子可以达到建筑物的高度是（ ）A ．12米B ．13米C ．14米D ．15米4.直线l 与直线y ＝4x －3相交于y 轴上一点，且与直线y ＝－5x ＋8平行，则直线l 的表达式为__5.如图，在△ABC 中，CE 平分∠ACB ，CF 平分△ABC 的外角∠ACD ，且EF ∥BC 交AC 于点M ，若EF ＝5，则CE 2＋CF 2＝____．6.△ABC 中，已知∠A ＝60°，∠B ＝80°，则∠C 的外角的度数是____．7. 化简① ⎪⎭⎫ ⎝⎛-÷⨯631205315 ② ()()()120201021214.31-⎪⎭⎫ ⎝⎛--+---π8.某超市计划购进一批甲、乙两种玩具，已知5件甲种玩具的进价与3件乙种玩具的进价的和为231元，2件甲种玩具的进价与3件乙种玩具的进价的和为141元．(1)求每件甲种、乙种玩具的进价分别是多少元？(2)如果购进甲种玩具有优惠，优惠方法是：购进甲种玩具超过20件，超出部分可以享受7折优惠，若购进x(x>0)件甲种玩具需要花费y 元，请你求出y 与x 的函数关系式．0b a八年级上册寒假作业姓名： 年 月 日1.设n 为正整数，且n<65<n ＋1，则n 的值为( )A ．5B ．6C ．7D ．82. 放学以后，萍萍和晓晓从学校分手，分别沿东南方向和西南方向回家，•若萍萍和晓晓 走的速度都是40米/分，萍萍用15分钟到家，晓晓用20分钟到家，萍萍家和晓晓家的距离为（ ）A ．600米B ．800米C ．1000米D ．不能确定3.若直线y ＝kx ＋b 经过第二、三、四象限，则( )A ．k >0，b >0B ．k >0，b <0C ．k <0，b >0D ．k <0，b <04.若如图，在平面直角坐标系中，长方形OABC 的顶点A ，C 的坐标分别为(10，0)，(0，4)，5.点D 是OA 的中点，点P 在BC上运动，当△ODP 是腰长为5的等腰三角形时，点P 的坐标为5.若3a -+（b+2）2=0，则点M （a ，b ）关于y 轴的对称点的坐标为_______．6. 若x ，y 满足2x －1＋1－2x ＋y ＝4，求x y ＝7.解方程组1) ⎩⎨⎧=-=+52223y x y x （2）257320x y x y -=⎧⎨-=⎩8.已知A 地在B 地正南方向3千米处，甲、乙两人分别从两地向正北方向匀速直行，他们与A 地的距离s (千米)与所行时间t (时)之间的关系如图，其中l 2表示甲运动的过程，l 1表示乙运动的过程，根据图象回答：(1)甲和乙哪一个在A 地，哪一个在B 地？(2)追者用多长时间追上被追者？哪一个是追者？(3)求出表示甲、乙的函数表达式．八年级上册寒假作业姓名： 年 月 日1.直角三角形两直角边长分别为5和12,则它斜边上的高是（ ）A ．1330B ．524C ．512D ．1360 2.如图，AB ∥CD ，AD 和BC 相交于点O ，∠A ＝20°，∠COD ＝100°，则∠C 的度数是( ) A ．80° B ．70° C ．60° D ．50°3.直角三角形两条直角边的长分别为8和6，则斜边上的高为 ( )A 、2.4B 、4.8C 、1.2D 、104.直线y ＝k 1x ＋b 1(k 1>0)与y ＝k 2x ＋b 2(k 2<0)相交点(－2，0)，且两直线与y 轴围成的三角形面积为4，那么b 1－b 2＝____．5.直线l 与直线y ＝4x －3相交于y 轴上一点，且与直线y ＝－5x ＋8平行，则直线l 的表达式为____ ．6.若实数a 、b 满足,02)2(2=-+-a b a 则b+2a= 。

八年级北师大寒假数学作业1.引言1.1 介绍八年级北师大寒假数学作业的重要性八年级北师大寒假数学作业对学生的学习发展具有重要的意义。

通过寒假数学作业，学生可以巩固和复习在上学期学习的数学知识，增强数学基础，为下学期的学习打下良好的基础。

寒假数学作业也可以帮助学生培养独立学习的能力和解决问题的能力，提高学生的数学思维和分析能力。

而且，数学作业也是检验学生对数学知识掌握程度的一种方式，通过认真完成寒假数学作业，可以帮助学生发现自己在数学学习中存在的问题，及时进行调整和改进。

八年级北师大寒假数学作业不仅是对学生学习成绩的一种促进，更是锻炼学生学习态度和方法的重要途径。

学生应当认真对待寒假数学作业，树立正确的学习态度，把寒假数学作业作为提高自身数学水平的重要机会。

1.2 强调学生认真对待寒假数学作业的必要性学生认真对待寒假数学作业的必要性非常重要，这不仅是为了完成老师布置的任务，更重要的是为了巩固学习成果，提高数学水平，培养良好的学习习惯。

在寒假期间，学生通常容易被各种娱乐活动吸引，而忽视了数学作业的重要性。

数学作业是巩固学习成果，提高解决问题的能力和思维能力的有效途径。

而且，认真对待数学作业还能够帮助学生培养自觉学习的习惯，提高学习的主动性和积极性。

认真对待数学作业可以帮助学生养成严谨的思维方式，提高解决问题的能力，培养逻辑思维和数学思维。

我们在这篇文章中将重点强调学生认真对待寒假数学作业的必要性，希望通过这篇文章的阐述，能够唤起学生对数学作业的重视，培养良好的学习习惯和方法。

1.3 提出文章的目的和结构本文旨在探讨八年级北师大寒假数学作业的重要性，强调学生认真对待寒假数学作业的必要性，并提出解决数学作业困难的方法。

文章包括引言、正文和结论三个部分。

通过本文的阐述，我们希望读者能够意识到寒假数学作业的重要性，认真对待数学作业，并在学习中形成良好的习惯和方法，从而提高数学学习的效果和成绩。

2.正文2.1 寒假数学作业的内容和要求寒假数学作业的内容和要求：寒假数学作业是为了巩固学生在上学期所学习的数学知识，并为下学期的学习打下基础。

全国免费客户服务电话：400-715-6688地址：西安经济技术开发区凤城一路8号御道华城A 座10层八年级数学练习11、一个长方形的长为x 米，宽为50米，如果它的周长不小于280米，那么x 应满足的不等式为 ；2、点A （－5，y 1）、B （－2，y 2）都在直线y = －2x 上，则y 1与y 2的关系是 ；3、如果一次函数y =（2－m ）x ＋m 的图象经过第一、二、四象限，那么m 的取值范围是 ； A ．若a －b ＝0，则a ＝b ＝0 B ．若a －b ＞0，则a ＞b C ．若a －b ＜0，则a ＜b D ．若a －b ≠0，则a ≠b5、如果关于x 的不等式(a+1)x>a+1的解集为x<1，则a 的取值范围是（ ） A.a<0 B.a<-1 C.a>1 D.a>-16、若x ＞ｙ，则ax ＞ay ，那么a 一定为（ ） A ．a ＞0 B ．ａ＜0 C ．ａ≥0 D ．a ≤0 7.如果不等式组 ⎩⎨⎧>-<+mx x x 145 的解集是x>2，则m 的取值范围是( )A.m ≥2B.m ≤2C.m=2D.m ＜2 8、下列各式中,不能分解因式的有 ( )①9x 2-y 2;② b 2-9a 2;③ a 2+2ab －b 2;④－x 2+25y 2;⑤ 7a 2-7b 2⑥ x 2－x+41A. 2个B. 1个C. 3个D. 4个 10、若分式方程5156-=+--x k x x （其中k 为常数）产生增根，则增根是（ ） A.x=6 B.x=5 C.x=k D.无法确定11、在梯形ABCD 中，AD ∥BC ，AC 与BD 相交于O ，如果AD ∶BC=1∶3，那么下列结论正确的是（ ） A.S △COD =9S △AOD B.S △ABC =9S △ACD C.S △BOC =9S △AOD D.S △DBC =9S △AOD12、如图，在△ABC 中，若∠AED ＝∠B ，DE ＝6，AB ＝10，AE ＝8，则BC 的长为（ ） A ．415 B ．7 C ．215 D ．524 13、如图，在□ABCD 中，E 为CD 中点，AE 与BD 相交于点O ，S △DOE =12cm 2，则S △AOB 等于 cm 2. 14、如图，下列结论：①∠A >∠ACD ；②∠B+∠ACB=180°-∠A ； ③∠B+∠ACB<180°； ④∠HEC>∠B 。

初中数学试卷金戈铁骑整理制作一、选择题1、以下法中，正确的选项是〔〕A ．任何数的平方都是正数B．正数的倒数必小于个正数C．等于它自己的数必是非数D．零除以任何一个数都等于零2、假定 m 是一个整数的平方数，那么和m 相且比它大的那个平方数是〔〕A ． m＋ 2 m＋ 1B ．m＋ 1C． m2＋ 1D．以上都不3、假定 a， b 数，以下命中正确的选项是〔〕A ．假定 a＞ b， a2＞ b2B．假定 a＞｜ b｜， a2＞b2C．假定｜ a｜＞ b， a2＞b2D．假定 a＞ 0，a＞ b， a2＞ b24、全体小数所在的会合是〔〕A ．分数会合B．有理数会合C．数会合D．无理数会合5、无理数 4 6的在 ()A．8和9之B．9 和 10 之C．10 和 11 之D．11 和 12 之6、以下法正确的选项是()A ．无穷小数都是无理数B ．根号的数都是无理数C．开方开不尽的数是无理数 D ．π是无理数，故无理数也可能是有限小数7、数a、b、c在数上的地点如所示，化|a+b|-|c-b|的果是 ()A ． a+cB ． -a-2b+c C．a+2b-c D． -a-c8、a-b=2 3 -1,ab= 3 , (a+1)(b-1)的()A ．3B．3 3C．2 2D．22二、填空题9．以下各数中：－1，7， 3.14159 ，π，10，－34，，0. 3，38，16，2.121122111222⋯430其 中 有 理 数 有 ___________________________ ； 无 理 数 有_________________________________ 。

10．在 数中 最小的数是________；在 整数中 最小的数是________。

11． 数 a ，b 在数 上所 的点的地点如 所示，2a___________0，a ＋b__________0，－｜ b － a ｜ ________0 ，化 ｜ 2a ｜－｜ a ＋b ｜＝ ________。

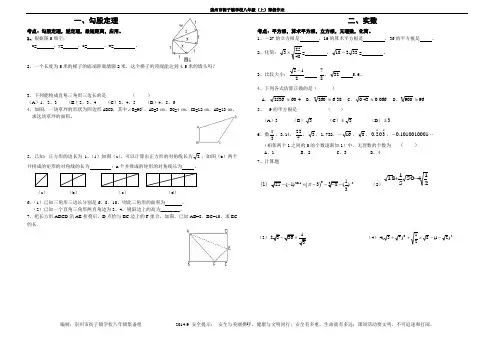
一、勾股定理考点：勾股定理，逆定理，最短距离，应用。

1、根据图5填空：x= ，y= ，z= ，w= 。

2、一个长度为5米的梯子的底端距离墙脚2米，这个梯子的顶端能达到4.5米的墙头吗？3、下列能构成直角三角形三边长的是（）（A）1、2、3 （B）2、3、4 （C）3、4、5 （D）4、5、64、如图，一块草坪的形状为四边形ABCD，其中∠B=90º，AB=3㎝，BC=4㎝，CD=12㎝，AD=13㎝，求这块草坪的面积。

5、已知：正方形的边长为1。

（1）如图（a），可以计算出正方形的对角线长为2；如图（b）两个并排成的矩形的对角线的长为；n个并排成的矩形的对角线长为。

6、（1）已知三角形三边长分别是6，8，10，则此三角形的面积为。

（2）已知一个直角三角形两直角边为3、4，则斜边上的高为________。

7、把长方形ABCD沿AE折叠后，D点恰与BC边上的F重合，如图，已知AB=8，BC=10，求EC 的长．二、实数考点：平方根，算术平方根，立方根，无理数，化简。

1、－27的立方根是，16的算术平方根是，36的平方根是。

2、化简：48253⨯= ，32318-= 。

3、比较大小：215-87，32 5.6。

4、下列各式估算正确的是（）A、4.602536≈ B、38.62603≈ C、066.043.0≈ D、969003≈5、9的平方根是（）（A）3 （B）3（C）3±（D）3±6、数3π，3.14，722，3，1.732，16-，8，••32.0，⋅⋅⋅-1010010001.0（相邻两个1之间的0的个数逐渐加1）中，无理数的个数为 ( )A、1B、2C、3D、47、计算题(1)()0201123125(1)38()3π---⨯----（2）214505118-+（3）123363-+（4）20)21(821)73(4--⨯++（a）（b）（c）（d）三、平面直角坐标考点；点坐标，对称。

八年级上册数学寒假作业答案北师大版[模版仅供参考，切勿通篇使用]权威发布，请访问初中二年级网。

一、选择题1.下列四个说法中，正确的是A.一元二次方程有实数根;B.一元二次方程有实数根;C.一元二次方程有实数根;D.一元二次方程x2+4x+5=a有实数根.【答案】D2.一元二次方程有两个不相等的实数根，则满足的条件是A. =0B. >0C.【答案】B3.已知方程的两个解分别为、，则的值为A. B.【答案】D4.方程 x2 + x – 1 = 0的一个根是A. 1 –B.C. –1+D.【答案】D5.已知一元二次方程 x2 + x ─ 1 = 0，下列判断正确的是A.该方程有两个相等的实数根B.该方程有两个不相等的实数根C.该方程无实数根D.该方程根的情况不确定【答案】B6.若是方程 =4的两根，则的值是【答案】D7.关于x的一元二次方程x2-6x+2k=0有两个不相等的实数根，则实数k的取值范围是.≤【答案】B8.一元二次方程x2-4=0的解是=2，x2=-2 =-2 =2 D. x1=2，x2=0【答案】A9.一元二次方程的两根之积是A.-1B. -2【答案】B10.方程的估计正确的是A. B.C. D.【答案】B11.一元二次方程的解是 .A. ，B. 。

C. ，D. 。

【答案】A12.方程=x-5的解是=5 =5或x=6 =7 =5或x=7【答案】D二、填空题1. 已知关于x的一元二次方程有实数根，则m的取值范围是 .【答案】2.已知x1、x2为方程x2+3x+1=0的两实根，则x12+8x2+20=__________.【答案】-13.设x1、x2 是一元二次方程x2+4x-3=0的两个根。

2x1+a =2，则a= ▲ .【答案】84.一元二次方程的解为___________________.【答案】5.方程的解是▲ .【答案】6.若关于x的方程x2-mx+3=0有实数根，则m的值可以为___________.【答案】7.如果方程ax2+2x+1=0有两个不等实数根，则实数a的取值范围是【答案】a8.已知α、β是一元二次方程x2-4x-3=0的两实数根，则代数式= .【答案】-69.若实数m满足m2- m + 1 = 0，则 m4 + m-4 = .【答案】6210.一元二次方程x2-5x+6=0 的两根分别是x1,x2, 则x1+x2等于A. 5B. 6C. -5D. -6【答案】A11.关于x的一元二次方程-x2+x+1-m2=0无实数根，则m的取值范围是_______________。

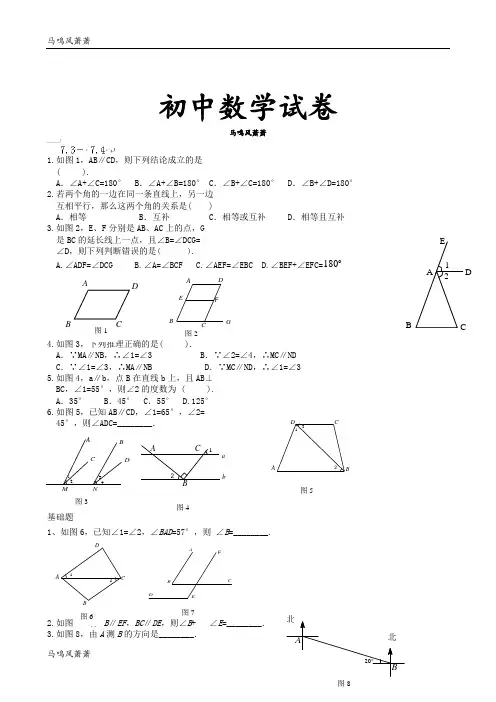
FA B C D E G 图2初中数学试卷马鸣风萧萧1.如图1，AB∥CD，则下列结论成立的是 ( ).A ．∠A+∠C=180°B ．∠A+∠B=180°C ．∠B+∠C=180°D ．∠B+∠D=180° 2.若两个角的一边在同一条直线上，另一边 互相平行，那么这两个角的关系是( )A ．相等B ．互补C ．相等或互补D ．相等且互补 3.如图2，E 、F 分别是AB 、AC 上的点，G 是BC 的延长线上一点，且∠B=∠DCG= ∠D，则下列判断错误的是( ).A.∠ADF=∠DCGB.∠A=∠BCF C .∠AEF=∠EBC D .∠BEF+∠EFC=1804.如图3，下列推理正确的是( ).A ．∵MA∥NB，∴∠1=∠3B ．∵∠2=∠4，∴MC∥NDC ．∵∠1=∠3，∴MA∥NBD ．∵MC∥ND，∴∠1=∠3 5.如图4，a∥b，点B 在直线b 上，且AB⊥ BC ，∠1=55°，则∠2的度数为 ( ). A ．35° B ．45° C．55° D.125° 6.如图5，已知AB∥CD，∠1=65°，∠2=45°，则∠ADC=________．基础题1、如图6，已知∠1=∠2，∠BAD =57°，则 ∠B =________.2.如图7，若AB ∥EF ，BC ∥DE ，则∠B + ∠E =________．3.如图8，由A 测B 的方向是________． A B CD4321M N图321ABCab图4231ABC D 图5图1 A B CD 21A B C D图6FAB C D E 图7A北北ABCDE 124.已知：如图，∠B =∠C.（1）若AD ∥BC,求证：AD 平分∠EAC; (2)若∠B+∠C+∠ABC=180°,AD 平分 ∠EAC,求证AD ∥BC.5.已知：如图，∠1=∠B ，∠A =32°.求： ∠2的度数．6.如图，∠B+∠BCD+∠D=360， 求证：∠1=∠2．7.现有下列命题，其中真命题的个数是（ ）①（-5）2的平方根是-5；②近似数3.14×103有3个有效数字；③单项式3x 2y 与单项式-2xy 2是同类项；④正方形既是轴对称图形，又是中心对称 图形． A ．1 B ．2 C ．3 D ．48.如图,在梯形ABCD 中,AD ∥BC,∠D= 120°,∠DCA=20°,求∠BCA 和∠DAC 的 度数.DCBA9.如图，A 、B 之间是一座山，要修一条铁 路通过A 、B 两地，在A 地测得铁路走向 是北偏东58°11′．如果A 、B 两地同时 开工开隧道，那么在B 地按北偏西多少度 施工，才能使铁路隧道在山腹中准确接 通？ 1ABCD2A BCD E 1 32 4FA B C DE图4图1DA B C7.5三角形内角和定理1已知，如图1，△ABC 中，∠B=∠DAC，则 ∠BAC 和∠ADC 的关系是( ).A ．∠BAC＜∠ADCB ．∠BAC=∠ADC C ．∠BAC＞∠ADCD ．不能确定2.对于△ABC，下列命题中是假命题的为 ( ) .A.若∠A+∠B=∠C，则△ABC 是直角三角 形B.若∠A+∠B＞∠C，则△ABC 是锐角三角 形C.若∠A+∠B＜∠C，则△ABC 是钝角三角 形D.若∠A=∠B=∠C，则△ABC 是斜三角形 3.在△ABC 中，已知∠A+∠C=2∠B，∠C－∠A=80°，则∠C 的度数是( ). A ．60° B．80° C．100° D ．120°4.如图2，∠A、∠DOE 和∠BEC 的大小关系是( ).A ．∠A＞∠DOE＞∠BECB ．∠DOE＞∠A＞∠BEC C ．∠BEC＞∠DOE＞∠AD ．∠DOE＞∠BEC＞∠A5.如图3，∠B=∠C，则∠ADC 与∠AEB 的关系是( ).A ．∠ADC＞∠AEB B.∠ADC=∠AEBC ．∠ADC＜∠AEBD ．不能确定基础题1.在△ABC 中，∠A∶∠B∶∠C=1∶2∶3，则∠C=________．2.△ABC 中，若∠A=30°，∠B=21∠C，则∠B=________，∠C=________．3.△ABC 中，∠B=40°，∠C=60°，AD 是 ∠A 的平分线，则∠DAC 的度数为_____．4.△ABC 中，∠C=90°，CD⊥AB，∠B=63°， 则∠DCA=________．5.如图4，点D 在△ABC 边BC 的延长线上， DE⊥AB 于E ，交AC 于F ，∠B=50°， ∠CFD=60°，则∠ACB=________．6.已知：如图，A B∥CD，AD∥BC，∠1=50°，∠2=80°．求∠C 的度数．7.已知：如图，D 是△ABC 的∠C 的外角平 分线与BA 的延长线的交点．AB C D EO图2 21ABCD图3 A B CDE ABC D北北求证：∠BAC＞∠B．8.已知：如图，在△ABC 中，BD 、CE 是∠B、∠C 的平分线，且相交于点O ．求证：∠BOC=90°+21∠A．9.如图，已知DE ∥BC ，CD 是∠ACB 的平分 线，∠B ＝70°，∠ACB ＝50°， 10.求∠EDC和∠BDC 的度数.A BCDE11.如图，AB ∥CD ，EF ⊥AB 于O ，∠2＝135 °，求∠1的度数．下面提供三个思路： （1）过F 作FH ∥AB ，（2）延长EF 交CD 于I ； （3）延长GF 交AB 于K ．请你利用三个思路中的两个思路，求∠1的度数．DABC E A BC DEO。