高中数学-集合与集合的表示方法练习题

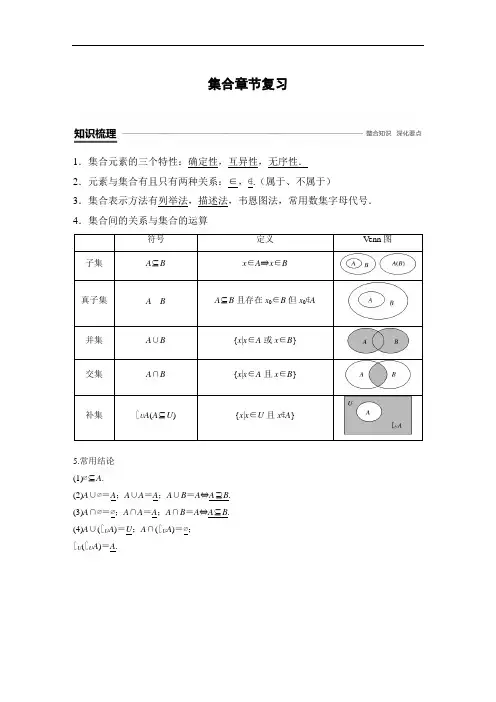
集合章节复习1．集合元素的三个特性：确定性，互异性，无序性．2．元素与集合有且只有两种关系：∈，∉.（属于、不属于）3．集合表示方法有列举法，描述法，韦恩图法，常用数集字母代号．4．集合间的关系与集合的运算符号定义Venn图子集A⊆B x∈A⇒x∈B真子集A B A⊆B且存在x0∈B但x0∉A并集A∪B {x|x∈A或x∈B}交集A∩B {x|x∈A且x∈B}补集∁U A(A⊆U) {x|x∈U且x∉A}5.常用结论(1)∅⊆A.(2)A∪∅＝A；A∪A＝A；A∪B＝A⇔A⊇B.(3)A∩∅＝∅；A∩A＝A；A∩B＝A⇔A⊆B.(4)A∪(∁U A)＝U；A∩(∁U A)＝∅；∁U(∁U A)＝A.1．若A ＝{}x ，|x |，则x <0.( √ ) 2．任何集合至少有两个子集．( × )3．若{}x |ax 2＋x ＋1＝0有且只有一个元素，则必有Δ＝12－4a ＝0.( × ) 4．设A ，B 为全集的子集，则A ∩B ＝A ⇔A ∪B ＝B ⇔∁U A ⊇∁U B .( √ )类型一 集合的概念及表示法例1 下列表示同一集合的是( ) A ．M ＝{(2,1)，(3,2)}，N ＝{(1,2)} B ．M ＝{2,1}，N ＝{1,2}C ．M ＝{y |y ＝x 2＋1，x ∈R }，N ＝{y |y ＝x 2＋1，x ∈N }D ．M ＝{(x ，y )|y ＝x 2－1，x ∈R }，N ＝{y |y ＝x 2－1，x ∈R } 答案 B解析 A 选项中M ，N 两集合的元素个数不同，故不可能相同；B 选项中M ，N 均为含有1,2两个元素的集合，由集合中元素的无序性可得M ＝N ；C 选项中M ，N 均为数集，显然有NM ；D 选项中M 为点集，即抛物线y ＝x 2－1上所有点的集合，而N 为数集，即抛物线y ＝x 2－1的值域，故选B.反思与感悟 要解决集合的概念问题，必须先弄清集合中元素的性质，明确是数集，还是点集等．跟踪训练1 设集合A ＝{(x ，y )|x －y ＝0}，B ＝{(x ，y )|2x －3y ＋4＝0}，则A ∩B ＝________. 答案 {(4,4)}解析 由⎩⎪⎨⎪⎧ x －y ＝0，2x －3y ＋4＝0，得⎩⎪⎨⎪⎧x ＝4，y ＝4.∴A ∩B ＝{(4,4)}．类型二 集合间的基本关系例2 若集合P ＝{x |x 2＋x －6＝0}，S ＝{x |ax ＋1＝0}，且S ⊆P ，求由a 的可能取值组成的集合．解 由题意得，P ＝{－3,2}． 当a ＝0时，S ＝∅，满足S ⊆P ；当a ≠0时，方程ax ＋1＝0的解为x ＝－1a ，为满足S ⊆P ，可使－1a ＝－3或－1a ＝2，即a ＝13或a ＝－12.故所求集合为⎩⎨⎧⎭⎬⎫0，13，－12.反思与感悟 (1)在分类时要遵循“不重不漏”的原则，然后对于每一类情况都要给出问题的解答．(2)对于两集合A ，B ，当A ⊆B 时，不要忽略A ＝∅的情况． 跟踪训练2 下列说法中不正确的是________．(填序号) ①若集合A ＝∅，则∅⊆A ；②若集合A ＝{x |x 2－1＝0}，B ＝{－1,1}，则A ＝B ； ③已知集合A ＝{x |1<x <2}，B ＝{x |x <a }，若A ⊆B ，则a >2. 答案 ③解析 ∅是任何集合的子集，故①正确； ∵x 2－1＝0，∴x ＝±1，∴A ＝{－1,1}， ∴A ＝B ，故②正确；若A ⊆B ，则a ≥2，故③错误．类型三集合的交、并、补运算命题角度1用符号语言表示的集合运算例3设全集为R，A＝{x|3≤x<7}，B＝{x|2<x<10}，求∁R(A∪B)及(∁R A)∩B.解把全集R和集合A，B在数轴上表示如下：由图知，A∪B＝{x|2<x<10}，∴∁R(A∪B)＝{x|x≤2或x≥10}，∵∁R A＝{x|x<3或x≥7}．∴(∁R A)∩B＝{x|2<x<3或7≤x<10}．反思与感悟求解用不等式表示的数集间的集合运算时，一般要借助于数轴求解，此法的特点是简单直观，同时要注意各个端点的画法及取到与否．跟踪训练3已知集合U＝{x|0≤x≤6，x∈Z}，A＝{1,3，6}，B＝{1,4,5}，则A∩(∁U B)等于() A．{1} B．{3,6}C．{4,5} D．{1,3,4,5,6}答案 B解析∵U＝{0,1,2,3,4,5,6}，B＝{1,4,5}，∴∁U B＝{0,2,3,6}，又∵A＝{1,3,6}，∴A∩(∁U B)＝{3,6}，故选B.命题角度2用图形语言表示的集合运算例4设全集U＝R，A＝{x|0<x<2}，B＝{x|x<1}．则图中阴影部分表示的集合为____________．答案{x|1≤x<2}解析图中阴影部分表示的集合为A∩(∁U B)，因为∁U B＝{x|x≥1}，画出数轴，如图所示，所以A∩(∁U B)＝{x|1≤x＜2}．反思与感悟解决这一类问题一般用数形结合思想，借助于Venn图和数轴，把抽象的数学语言与直观的图形结合起来．跟踪训练4学校举办了排球赛，某班45名同学中有12名同学参赛，后来又举办了田径赛，这个班有20名同学参赛，已知两项都参赛的有6名同学，两项比赛中，这个班共有多少名同学没有参加过比赛？解设A＝{x|x为参加排球赛的同学}，B＝{x|x为参加田径赛的同学}，则A∩B＝{x|x为参加两项比赛的同学}．画出V enn图(如图)，则没有参加过比赛的同学有：45－(12＋20－6)＝19(名)．答这个班共有19名同学没有参加过比赛．类型四关于集合的新定义题例5设A为非空实数集，若对任意的x，y∈A，都有x＋y∈A，x－y∈A，且xy∈A，则称A 为封闭集．①集合A＝{－2，－1,0,1,2}为封闭集；②集合A＝{n|n＝2k，k∈Z}为封闭集；③若集合A1，A2为封闭集，则A1∪A2为封闭集；④若A为封闭集，则一定有0∈A.其中正确结论的序号是________．答案②④解析①集合A＝{－2，－1,0,1,2}中，－2－2＝－4不在集合A中，所以不是封闭集；②设x，y∈A，则x＝2k1，y＝2k2，k1，k2∈Z，故x＋y＝2(k1＋k2)∈A，x－y＝2(k1－k2)∈A，xy＝4k1k2∈A，故②正确；③反例是：集合A1＝{x|x＝2k，k∈Z}，A2＝{x|x＝3k，k∈Z}为封闭集，但A1∪A2不是封闭集，故③不正确；④若A为封闭集，则取x＝y，得x－y＝0∈A.故填②④. 反思与感悟新定义题是近几年高考中集合题的热点题型，解答这类问题的关键在于阅读理解，也就是要在准确把握新信息的基础上，利用已有的知识来解决问题．跟踪训练5 设数集M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ m ≤x ≤m ＋34，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪n －13≤x ≤n ，且M ，N 都是集合{x |0≤x ≤1}的子集，如果b －a 叫做集合{x |a ≤x ≤b }(b >a )的“长度”，那么集合M ∩N 的“长度”的最小值是( ) A.13 B.23 C.112 D.512 答案 C解析 方法一 由已知可得⎩⎪⎨⎪⎧m ≥0，m ＋34≤1，⎩⎪⎨⎪⎧n －13≥0，n ≤1，解得0≤m ≤14，13≤n ≤1.取字母m 的最小值0，字母n 的最大值1，可得M ＝⎩⎨⎧⎭⎬⎫x ⎪⎪0≤x ≤34，N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪23≤x ≤1， 所以M ∩N ＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 0≤x ≤34∩⎩⎨⎧⎭⎬⎫x ⎪⎪ 23≤x ≤1＝⎩⎨⎧⎭⎬⎫x ⎪⎪ 23≤x ≤34， 此时得集合M ∩N 的“长度”为34－23＝112.方法二 集合M 的“长度”为34，集合N 的“长度”为13.由于M ，N 都是集合{x |0≤x ≤1}的子集， 而{x |0≤x ≤1}的“长度”为1，由此可得集合M ∩N 的“长度”的最小值是⎝⎛⎭⎫34＋13－1＝112.1．已知集合M ＝{0,1,2,3,4}，N ＝{1,3,5}，P ＝M ∩N ，则P 的子集共有( ) A ．2个 B ．4个 C ．6个 D ．8个答案 B2．下列关系中正确的个数为( ) ①22∈R ；②0∈N ＋；③{－5}⊆Z . A ．0 B ．1 C ．2 D ．3答案 C解析 ①③正确．3．已知集合A ＝{x |－1＜x ＜2}，B ＝{x |0＜x ＜3}，则A ∪B 等于( ) A ．{x |－1<x <3} B ．{x |－1<x <0} C ．{x |0<x <2} D ．{x |2<x <3}答案 A解析 由A ＝{x |－1＜x ＜2}，B ＝{x |0＜x ＜3}， 得A ∪B ＝{x |－1＜x ＜3}．故选A.4．设全集I ＝{a ，b ，c ，d ，e }，集合M ＝{a ，b ，c }，N ＝{b ，d ，e }，那么(∁I M )∩(∁I N )等于( ) A ．∅ B ．{d } C ．{b ，e } D ．{a ，c } 答案 A5．已知集合U ＝R ，集合A ＝{}x |x <－2或x >4，B ＝{}x |－3≤x ≤3，则(∁U A )∩B ＝________. 考点 交并补集的综合问题 题点 无限集合的交并补运算 答案{}x |－2≤x ≤3.解析 由图知(∁U A )∩B ＝{}x |－2≤x ≤3.1．要注意区分两大关系：一是元素与集合的从属关系，二是集合与集合的包含关系． 2．在利用集合中元素相等列方程求未知数的值时，要注意利用集合中元素的互异性这一性质进行检验，忽视集合中元素的性质是导致错误的常见原因之一．课时对点练一、选择题1．若集合M＝{x|(x＋4)(x＋1)＝0}，N＝{x|(x－4)·(x－1)＝0}，则M∩N等于() A．{1,4} B．{－1，－4}C．{0} D．∅答案 D解析因为M＝{x|(x＋4)(x＋1)＝0}＝{－4，－1}，N＝{x|(x－4)(x－1)＝0}＝{1,4}，所以M∩N ＝∅，故选D.2．已知集合A＝{x|x＋3>0}，B＝{x|x≥2}，则下列结论正确的是()A．A＝B B．A∩B＝∅C．A⊆B D．B⊆A考点集合的包含关系题点集合包含关系的判定答案 D解析A＝{x|x>－3}，B＝{x|x≥2}，结合数轴可得：B⊆A.3．已知集合A，B均为集合U＝{1,3,5,7,9}的子集，若A∩B＝{1,3}，(∁U A)∩B＝{5}，则集合B等于()A．{1,3} B．{3,5}C．{1,5} D．{1,3,5}答案 D解析画出满足题意的Venn图，由图可知B＝{1,3,5}．4．设集合M＝{－1,0,1}，N＝{a，a2}，若M∩N＝N，则a的值是()A．－1 B．0 C．1 D．1或－1答案 A解析由M∩N＝N得N⊆M.当a＝0时，与集合中元素的互异性矛盾；当a＝1时，也与集合中元素的互异性矛盾；当a＝－1时，N＝{－1,1}，符合题意．5．设全集U＝R，已知集合A＝{x|x＜3或x≥7}，B＝{x|x＜a}．若(∁U A)∩B≠∅，则a的取值范围为()A．a＞3 B．a≥3C．a≥7 D．a＞7答案 A解析因为A＝{x|x＜3或x≥7}，所以∁U A＝{x|3≤x＜7}，又(∁U A)∩B≠∅，则a＞3.6．定义差集A－B＝{x|x∈A，且x∉B}，现有三个集合A，B，C分别用圆表示，则集合C－(A－B)可表示下列图中阴影部分的为()答案 A解析如图所示，A－B表示图中阴影部分，故C－(A－B)所含元素属于C，但不属于图中阴影部分，故选A.二、填空题7．设全集U＝R，若集合A＝{1,2,3,4}，B＝{x|2≤x≤3}，则A∩(∁U B)＝________.答案{1,4}解析∵∁U B＝{x|x<2或x>3}，∴A∩(∁U B)＝{1,4}．8．设集合A＝{1，－1，a}，B＝{1，a}，A∩B＝B，则a＝______.答案0解析∵A ∩B ＝B ，即B ⊆A ，∴a ∈A . 要使a 有意义，a ≥0. ∴a ＝a ，∴a ＝0或a ＝1， 由元素互异，舍去a ＝1.∴a ＝0.9．已知集合M ＝{(x ，y )|x ＋y ＝2}，N ＝{(x ，y )|x －y ＝4}，那么集合M ∩N ＝________. 答案 {(3，－1)}解析 M ，N 中的元素是平面上的点，M ∩N 是集合，并且其中的元素也是点，解方程组⎩⎪⎨⎪⎧ x ＋y ＝2，x －y ＝4， 得⎩⎪⎨⎪⎧x ＝3，y ＝－1.∴M ∩N ＝{(3，－1)}．10．已知集合A ＝{x |2a ≤x ≤a ＋3}，B ＝{x |x <－1或x >5}，若A ∩B ＝∅，则a 的取值范围是________．答案 ⎩⎨⎧⎭⎬⎫a ⎪⎪－12≤a ≤2或a >3 解析 ①若A ＝∅，则A ∩B ＝∅， 此时2a >a ＋3，即a >3.②若A ≠∅，如图，由A ∩B ＝∅，可得⎩⎪⎨⎪⎧2a ≥－1，a ＋3≤5，2a ≤a ＋3，解得－12≤a ≤2.综上所述，a 的取值范围是⎩⎨⎧⎭⎬⎫a ⎪⎪－12≤a ≤2或a >3. 三、解答题11．如图，用适当的方法表示阴影部分的点(含边界上的点)组成的集合M .解结合图形可得M＝⎩⎨⎧⎭⎬⎫(x，y)⎪⎪xy≥0，－2≤x≤52，－1≤y≤32.12．已知集合A＝{x|－2≤x≤5}，B＝{x|m＋1≤x≤2m－1}．(1)若A∪B＝A，求实数m的取值范围；(2)当A＝{x∈Z|－2≤x≤5|}时，求A的非空真子集的个数；(3)若A∩B＝∅，求实数m的取值范围．考点集合各类问题的综合题点集合各类问题的综合解(1)因为A∪B＝A，所以B⊆A，当B＝∅时，由m＋1>2m－1，得m<2，符合；当B≠∅时，根据题意，可得⎩⎪⎨⎪⎧2m－1≥m＋1，m＋1≥－2，2m－1≤5，解得2≤m≤3.综上可得，实数m的取值范围是{m|m≤3}．(2)当x∈Z时，A＝{x∈Z|－2≤x≤5}＝{－2，－1,0,1,2,3,4,5}，共有8个元素，所以A的非空真子集的个数为28－2＝254.(3)当B＝∅时，由(1)知m<2；当B≠∅时，根据题意作出如图所示的数轴，可得⎩⎪⎨⎪⎧2m－1≥m＋1，2m－1<－2或⎩⎪⎨⎪⎧2m－1≥m＋1，m＋1>5，解得m>4.综上可得，实数m 的取值范围是{m |m <2或m >4}．13．设集合A ＝{0，－4}，B ＝{x |x 2＋2(a ＋1)x ＋a 2－1＝0，x ∈R }．若B ⊆A ，求实数a 的取值范围．解 因为A ＝{0，－4}，所以B ⊆A 分以下三种情况：①当B ＝A 时，B ＝{0，－4}，由此知0和－4是方程x 2＋2(a ＋1)x ＋a 2－1＝0的两个根， 则⎩⎪⎨⎪⎧ Δ＝4(a ＋1)2－4(a 2－1)>0，－2(a ＋1)＝－4，a 2－1＝0，解得a ＝1；②当B ≠∅且B A 时，B ＝{0}或B ＝{－4}，并且Δ＝4(a ＋1)2－4(a 2－1)＝0，解得a ＝－1，此时B ＝{0}满足题意；③当B ＝∅时，Δ＝4(a ＋1)2－4(a 2－1)<0，解得a <－1.综上所述，所求实数a 的取值范围是a ≤－1或a ＝1.四、探究与拓展14．已知全集U ＝{2,4，a 2－a ＋1}，A ＝{a ＋4,4}，∁U A ＝{7}，则a ＝________.答案 －2解析 由题意，得a 2－a ＋1＝7，即a 2－a －6＝0，解得a ＝－2或a ＝3.当a ＝3时，A ＝{7,4}，不合题意，舍去，故a ＝－2.15．对于集合A ，B ，我们把集合{}(a ，b )|a ∈A ，b ∈B 记作A ×B .例如，A ＝{}1，2，B ＝{}3，4，则有：A ×B ＝{}(1，3)，(1，4)，(2，3)，(2，4)，B ×A ＝{}(3，1)，(3，2)，(4，1)，(4，2)，A ×A ＝{}(1，1)，(1，2)，(2，1)，(2，2)，B ×B ＝{}(3，3)，(3，4)，(4，3)，(4，4). 据此，试回答下列问题：(1)已知C ＝{}a ，D ＝{}1，2，3，求C ×D ；(2)已知A ×B ＝{}(1，2)，(2，2)，求集合A ，B ；(3)若集合A 中有3个元素，集合B 中有4个元素，试确定A ×B 中有多少个元素． 考点 集合各类问题的综合题点 集合各类问题的综合解析 (1)C ×D ＝{}(a ，1)，(a ，2)，(a ，3).(1，2)，(2，2)，(2)因为A×B＝{}所以A＝{}1，2，B＝{}2.(3)由题意可知A×B中元素的个数与集合A和B中的元素个数有关，即集合A中的任何一个元素与B中的任何一个元素对应后，得到A×B中的一个新元素．若A中有m个元素，B中有n个元素，则A×B中应有m×n个元素．于是，若集合A中有3个元素，集合B中有4个元素，则A×B中有12个元素．。

人教A 版高中数学必修一1.1.1《集合的含义与表示》同步练习题学校:___________姓名：___________班级：___________考号：___________一、单选题1．设集合A 只含有一个元素a ，则下列各式正确的是( ) A ．0∈A B ．a ∉AC ．a∈AD ．a ＝A2．设x ∈N ，且1x∈N ，则x 的值可能是( ) A ．0 B ．1 C ．－1D ．0或13．下面四个关系式：π∈{x|x 是正实数}，0.3∈Q，0∈{0}，0∈N，其中正确的个数是( ) A ．4 B ．3 C ．2D ．14．集合{x∈N|－1<x<112}的另一种表示方法是( ) A ．{0，1，2，3，4} B ．{1，2，3，4} C ．{0，1，2，3，4，5}D ．{1，2，3，4，5}5．已知集合A ＝{x∈N *|，则必有( ) A ．－1∈A B ．0∈AC ．D ．1∈A6．集合M ＝{(x ，y)|xy<0，x∈R，y∈R}是( ) A ．第一象限内的点集 B ．第三象限内的点集 C ．第四象限内的点集D ．第二、四象限内的点集7．若集合{},,a b c 中的三个元素可构成某个三角形的三条边长，则此三角形一定不是（ ） A ．直角三角形B ．锐角三角形C ．钝角三角形D ．等腰三角形8．已知A ＝{x|3－3x>0}，则有( ) A ．3∈A B ．1∈A C ．0∈A D ．－1∉A二、填空题9．集合A ＝{x|x∈N 且42x-∈Z}，用列举法可表示为A ＝________. 10．一边长为6，一边长为3的等腰三角形所组成的集合中有________个元素.11．点(1,3)P 和集合},)(2{|Ax y y x =+＝之间的关系是________. 12．用列举法表示集合A ＝{(x ，y)|x ＋y ＝3，x∈N，y∈N *}为________. 13．若{}2,2,3,4A =-，{}2|,B x x t t A ==∈，用列举法表示B = .14．下列集合中：A ＝{x ＝2，y ＝1}，B ＝{2，1}，C ＝{(x ，y)| 31x y x y +=⎧⎨-=⎩}，D ＝{(x ，y)|x ＝2且y ＝1}，与集合{(2，1)}相等的共有________个.三、解答题15．“今有三女，长女五日一归，中女四日一归，小女三日一归，问三女何时相会”.(选自《孙子算经》)，请将三女前三次相会的天数用集合表示出来.16．设A 是由满足不等式x <6的自然数组成的集合，若a ∈A 且3a ∈A ，求a 的值． 17．已知集合A 含有两个元素a 和a 2，若1∈A，求实数a 的值.18．已知集合A ＝{0，2，5，10}，集合B 中的元素x 满足x ＝ab ，a∈A，b∈A 且a≠b，写出集合B ．19．已知集合S 满足条件：若a S ∈，则1(0,1)1aS a a a+∈≠≠±-．若3S ∈，试把集合S 中的所有元素都求出来． 20．集合A ＝{x|2y x y x=⎧⎨=⎩ }可化简为___以下是两位同学的答案，你认为哪一个正确？试说明理由. 学生甲：由2y xy x=⎧⎨=⎩得x ＝0或x ＝1，故A ＝{0，1}； 学生乙：问题转化为求直线y ＝x 与抛物线y ＝x 2的交点，得到A ＝{(0，0)，(1，1)}.参考答案1．C 【解析】分析：根据集合A 的表示，判断出a 是A 的元素，根据元素与集合的关系，是属于与不属于，从而得到答案. 详解：集合{}A a =，a A ∴∈.故选C.点睛：在解决元素与集合的关系时，注意它们的关系只有“属于”与“不属于”两种. 2．B 【解析】首先x≠0，排除A ，D ；又x∈N，排除C ，故选B. 3．A 【解析】本题考查元素与集合之间的关系，由数集的分类可知四个关系式均正确.选A. 4．C 【解析】 ∵x∈N，且－1<x<112，∴集合中含有元素0，1，2，3，4，5，故选C. 点睛：集合的表示方法：列举法、描述法、图示法．其中描述法要注意代表元素，是点集还是数集．列举法应用于有限集，特别为单元素集合. 5．D 【解析】∵x∈N *1，2，即A ＝{1，2}，∴1∈A.选D. 6．D 【解析】根据描述法表示集合的特点，可知集合表示的是横、纵坐标异号的点的集合，这些点在第二、四象限内.选D.点睛：集合的表示方法：列举法、描述法、图示法．其中描述法要注意代表元素，是点集还是数集7．D 【分析】根据集合中元素的互异性可知，D 正确；给,,a b c 取特值可知，,,A B C 不正确. 【详解】根据集合中元素的互异性可知，a b c ≠≠，所以此三角形一定不是等腰三角形，故D 正确； 当3,4,5a b c ===时，三角形为直角三角形，故A 不正确； 当 6.8.9a b c ===时，三角形为锐角三角形，故B 不正确； 当6,8,11a b c ===时，三角形为钝角三角形，故C 不正确； 故选：D. 【点睛】本题考查了集合中元素的互异性，属于基础题. 8．C 【解析】因为A ＝{x|3－3x>0}＝{x|x<1}，所以0∈A.选C. 9．{0，1，3，4，6} 【解析】 注意到42x-∈Z，因此，2－x ＝±2，±4，±1，解得x ＝－2，0，1，3，4，6，又∵x∈N，∴x＝0，1，3，4，6. 10．1 【解析】这样的三角形只有1个，是两腰长为6，底边长为3的等腰三角形. 11．P A ∈ 【详解】在2y x =+中，当1x =时，3y =， 因此点P 是集合A 的元素，故P A ∈. 故答案为：P A ∈.12．{(0，3)，(1，2)，(2，1)} 【解析】集合A 是由方程x ＋y ＝3的部分整数解组成的集合，由条件可知，当x ＝0时，y ＝3；当x ＝1时，y ＝2；当x ＝2时，y ＝1.故A ＝{(0，3)，(1，2)，(2，1)}. 13．{}4,9,16 【分析】解决该试题的关键是对于t 令值，分别得到x 的值，然后列举法表示. 【详解】因为集合{}2,2,3,4A =-，而集合B 中的元素是将集合A 中的元素一一代入，通过平方得到的集合，即{}2|,B x x t t A ==∈，2,4t x ∴=±=；3,9t x ==；4,16t x ==,{}4,9,16B ∴=，那么用列举法表示B ={}4,9,16.本试题主要是考查了集合的描述法与列举法的准确运用，属于基础题. 14．2 【解析】因为集合{(2，1)}的元素表示的是有序实数对，由已知集合的代表元素知，元素为有序实数对的是C ，D ，而A 表示含有两个元素x ＝2，y ＝1的集合，B 表示含有2个元素的集合. 15．{60，120，180}. 【解析】试题分析：先判断三女相会的日数必为5，4，3的公倍数，再求最小的三个整数，并用集合形式表示试题解析：三女相会的日数，即为5，4，3的公倍数，它们的最小公倍数为60，因此三女前三次相会的天数用集合表示为{60，120，180}. 16．a ＝0或1. 【解析】 试题分析：试题解析：∵a∈A 且3a∈A，∴a<6且3a<6，∴a<2. 又∵a 是自然数∴a ＝0或1. 17．a ＝－1.【解析】试题分析：本题中已知集合A 中有两个元素且1∈A，据集合中元素的特点需分a ＝1和a 2＝1两种情况，最后注意集合中元素的互异性，进行验证. 试题解析：若1∈A，则a ＝1或a 2＝1，即a ＝±1. 当a ＝1时，集合A 有重复元素，∴a≠1；当a ＝－1时，集合A 含有两个元素1，－1，符合互异性. ∴a=-1.点睛：利用元素的性质求参数的方法，已知一个元素属于集合，求集合中所含的参数值．具体解法：(1)确定性的运用：利用集合中元素的确定性解出参数的所有可能值．(2)互异性的运用：根据集合中元素的互异性对集合中元素进行检验． 18．B ＝{0，10，20，50}. 【解析】试题分析：先按是否取零进行讨论，再根据乘积结果，利用集合元素互异性进行取舍 试题解析：解析 当或时，x ＝0；当或时，x ＝10； 当或时，x ＝20； 当或时，x ＝50.所以B ＝{0，10，20，50}.点睛：常利用集合元素的互异性确定集合中的元素，根据题目一一列举可能取值(应用列举法和分类讨论思想)，然后根据集合元素的互异性进行检验，相同元素重复出现只算作一个元素，判断出该集合的所有元素，即得该集合元素的个数． 19．113,2,,32-- 【分析】由条件“若a S ∈，则11aS a+∈-”可进行一步步推导，根据所得值循环出现可得答案． 【详解】∵3S ∈，∴13213S +=-∈-，从而1(2)11(2)3S +-=-∈--，则11131213S ⎛⎫+- ⎪⎝⎭=∈⎛⎫-- ⎪⎝⎭， ∴1123112S +=∈-，出现循环，根据集合中元素的互异性可得集合S 中的所有元素为113,2,,32--．【点睛】本题考查了集合中元素的互异性，属于基础题. 20．甲正确 【解析】试题分析：先解方程组得解集，再根据集合代表元素得应为数集，不是点集，因此选甲 试题解析：同学甲正确，同学乙错误.由于集合A 的代表元素为x ，因此满足条件的元素只能为x ＝0，1；而不是实数对故同学甲正确.。

高中数学集合的含义及其表示练习题(含解析)数学必修1(苏教版)1．1 集合的含义及其表示一位渔民专门喜爱数学，但他如何也不明白集合的意义，因此他请教数学家：“尊敬的先生，请您告诉我，集合是什么？”集合是不定义的原始概念，数学家专门难回答那位渔民，有一天，他来到渔民的船上，看到渔民撒下鱼网，轻轻一拉，许多鱼虾在网上跳动，数学家专门兴奋，快乐地告诉渔民：“这确实是集合！”你能明白得数学家的话吗？基础巩固1．下列说法正确的是()A．我校爱好足球的同学组成一个集合B．{1,2,3}是不大于3的自然数组成的集合C．集合{1,2,3,4,5}和{5,4,3,2,1}表示同一集合D．数1,0,5，12，32，64，14组成的集合有7个元素答案：C2．若集合A＝{－1,1}，B＝{0,2}，则集合{z|z＝x＋y，xA，yB}中的元素个数为()A．5个B．4个C．3个D．2个答案：C3．下列四个关系中，正确的是()A．a{a，b} B．{a}{a，b}C．a{a} D．a{a，b}答案：A4．集合M＝{(x，y)|xy0，xR，yR}是()A．第一象限内的点集B．第三象限内的点集C．第四象限内的点集D．第二、四象限内的点集解析：集合M为点集且横、纵坐标异号，故是第二、四象限内的点集．答案：D5．若A＝{(2，－2)，(2,2)}，则集合A中元素的个数是()A．1个B．2个C．3个D．4个答案：B6．集合M中的元素差不多上正整数，且若aM，则6－aM，则所有满足条件的集合M共有()A．6个B．7个C．8个D．9个解析：由题意可知，集合M中包含的元素能够是3,1和5,2和4中的一组，两组，三组，即M可为{3}，{1,5}，{2,4}，{3,1,5}，{3,2,4}，{1,5,2,4}，{3,1,5,2,4}，共7个．答案：B7．下列集合中为空集的是()A．{xN|x2 B．{xR|x2－1＝0}C．{xR|x2＋x＋1＝0} D．{0}答案：C8．设集合A＝{2,1－a，a2－a＋2}，若4A，则a＝()A．－3或－1或2 B－3或－1C．－3或2 D．－1或2解析：当1－a＝4时，a＝－3，A＝{2,4,14}；当a2－a＋2＝4时，得a ＝－1或2，当a＝－1时，A＝{2,2，4}，不满足互异性，当a＝2时，A＝{2,4，－1}．a＝－3或2.答案：C9．集合P＝{x|x＝2k，kZ}，Q＝{x|x＝2k＋1，kZ}，M＝{x|x＝4k＋1，kZ}，若aP，bQ，则有()A．a＋bPB．a＋bQC．a＋bMD．a＋b不属于P、Q、M中任意一个解析：∵aP，bQ，a＝2k1，k1Z，b＝2k2＋1，k2Z，a＋b＝2(k1＋k2)＋1，k1，k2Z，a＋bQ.答案：B10．由下列对象组成的集体，其中为集合的是________(填序号)．①不超过2的正整数；②高一数学课本中的所有难题；③中国的高山；④平方后等于自身的实数；⑤高一(2)班中考500分以上的学生．答案：①④⑤11．若a＝n2＋1，nN，A＝{x|x＝k2－4k＋5，kN}，则a与A的关系是________．解析：∵a＝n2＋1＝(n＋2)2－4(n＋2)＋5，且当nN时，n＋2N.答案：aA12．集合A＝{x|xR且|x－2|5}中最小整数为_______．解析：由|x－2|－5x－2－37，最小整数为－3.答案：－313．一个集合M中元素m满足mN＋，且8－mN＋，则集合M的元素个数最多为________．答案：7个14．下列各组中的M、P表示同一集合的是________(填序号)．①M＝{3，－1}，P＝{(3，－1)}；②M＝{(3,1)}，P＝{(1,3)}；③M＝{y|y＝x2－1，xR}，P＝{a|a＝x2－1，xR}；④M＝{y|y＝x2－1，xR}，P＝{(x，y)|y＝x2－1，xR}．答案：③能力提升15．已知集合A＝{x|xR|(a2－1)x2＋(a＋1)x＋1＝0}中有且仅有一个元素，求a的值．解析：(1)若a2－1＝0，则a＝1.当a＝1时，x＝－12，现在A＝－12，符合题意；当a＝－1时，A＝，不符合题意．(2)若a2－10，则＝0，即(a＋1)2－4(a2－1)＝0a＝53，现在A＝－34，符合题意．综上所述，a＝1或53.16．若集合A＝a，ba，1又可表示为{a2，a＋b，0}，求a2021＋b202 1的值．解析：由题知a0，故ba＝0，b＝0，a2＝1，a＝1，又a1，故a＝－1.a2021＋b2021＝(－1)2021＋02021＝1.17．设正整数的集合A满足：“若xA，则10－xA”．(1)试写出只有一个元素的集合A；(2)试写出只有两个元素的集合A；(3)如此的集合A至多有多少个元素？解析：(1)令x＝10－xx＝5.故A＝{5}．(2)若1A，则10－1＝9A；反过来，若9A，则10－9＝1A.因此1和9要么都在A中，要么都不在A中，它们总是成对地显现在A中．同理，2和8,3和7,4和6成对地显现在A中，故{1,9}或{2,8}或{3,7}或{4,6}为所求集合．(3)A中至多有9个元素，A＝{1,9,2,8,3,7,4,6,5}．18．若数集M满足条件：若aM，则1＋a1－aM(a0，a1)，则集合M中至少有几个元素？解析：∵aM，1＋a1－aM，1＋1＋a1－a1－1＋a1－a＝－1aM，与当今“教师”一称最接近的“老师”概念，最早也要追溯至宋元时期。

集合表示方法课堂探究探究一用列举法表示集合1．用列举法表示集合时，一般不必考虑元素间前后顺序，如{a，b}与{b，a}表示同一个集合．2．元素与元素之间必须用“，〞隔开．3．集合中元素不能重复．4．列举法也可以表示无限集．【典型例题1】用列举法表示以下集合：(1)36与60公约数构成集合；(2)方程(x－4)2(x－2)＝0根构成集合；(3)一次函数y＝x－1与y＝－23x＋43图象交点构成集合．思路分析：(1)要明确公约数含义；(2)注意4是重根；(3)要写成点集形式．解：(1)36与60公约数有1,2,3,4,6,12，所求集合可表示为{1,2,3,4,6,12}；(2)方程(x－4)2(x－2)＝0根是4,2，所求集合可表示为{2,4}；(3)方程y＝x－1与y＝－23x＋43可分别化为x－y＝1与2x＋3y＝4，那么方程组解是所求集合可表示为.探究二用描述法表示集合1．使用描述法表示集合时要注意以下几点：(1)写清元素符号；(2)说明该集合中元素性质；(3)不能出现未被说明字母；(4)多层描述时，应当准确使用“且〞“或〞；(5)所有描述内容都要写在集合符号内；(6)用于描述语句力求简明、准确．2．集合A＝{x|y＝x2＋1}，B＝{y|y＝x2＋1}与C＝{(x，y)|y＝x2＋1}不是一样集合．这是因为集合A代表元素是x，且x∈R；集合B代表元素是y，且y≥1；集合C代表元素是(x，y)，且(x，y)表示平面直角坐标系内抛物线y＝x2＋1上点，所以它们是互不一样集合．3．{三角形}实际上是{x|x是三角形}简写，千万别理解成是由三个汉字组成集合，三角形构成集合不要写成{所有三角形}，因为{ }本身就有“所有〞含义．【典型例题2】用描述法表示以下集合：(1)小于10所有非负整数构成集合；(2)数轴上与原点距离大于3点构成集合；(3)平面直角坐标系中第二、四象限内点构成集合；(4)方程组解构成集合；(5)集合{1,3,5,7，…}．思路分析：(1)“0≤x<10，x∈Z〞可作为集合一个特征性质；(2)要利用数轴上距离公式来表示，即|x|>3；(3)，(4)注意代表元素为点坐标；(5)“x＝2k－1，k∈N＋〞可作为集合一个特征性质．解：(1)小于10所有非负整数构成集合，用描述法可表示为{x|0≤x<10，x∈Z}；(2)数轴上与原点距离大于3点构成集合，用描述法可表示为{x||x|>3}；(3)平面直角坐标系中第二、四象限内点构成集合，用描述法可表示为{(x，y)|xy<0}；(4)方程组解构成集合，用描述法表示为或；(5){1,3,5,7，…}用描述法可表示为{x|x＝2k－1，k∈N＋}．反思用描述法表示集合之前，应先通过代表元素确定集合是“点集〞还是“数集〞．另外，二元一次方程组解，因为含有两个未知数，所以在表示时，可看成“点集〞形式进展描述．探究三含参数问题1．对于集合表示方法中含参数问题一定要注意弄清集合含义，也要清楚参数在集合中地位．2．含参数问题常用分类讨论思想来解决，在讨论参数时要做到不重不漏．【典型例题3】集合M＝{x|(x－a)(x2－ax＋a－1)＝0}中各元素之和等于3，求实数a 值，并用列举法表示集合M.解：根据集合中元素互异性知，当方程(x－a)(x2－ax＋a－1)＝0有重根时，重根只能算作集合一个元素，又M＝{x|(x－a)(x－1)[x－(a－1)]＝0}．当a＝1时，M＝{1,0}，不符合题意；当a－1＝1，即a＝2时，M＝{1,2}，符合题意；当a≠1，且a≠2时，a＋1＋a－1＝3，那么a＝32，M＝，符合题意．综上所述，实数a值为2或32，当a＝2时，M＝{1,2}；当a＝32时，M＝.探究四易错辨析易错点1 认为集合中a具有一致性而致误【典型例题4】集合A＝{x|x＝2a，a∈Z}，B＝{x|x＝2a＋1，a∈Z}，C＝{x|x＝4a＋1，a∈Z}．假设m∈A，n∈B，那么有( )A．m＋n∈AB．m＋n∈BC．m＋n∈CD．m＋n不属于A，B，C中任意一个错解：C错因分析：不能正确利用集合中元素特征性质，认为三个集合中a是一致，从而由m∈A，得m＝2a，a∈Z.由n∈B，得n＝2a＋1，a∈Z.所以得到m＋n＝4a＋1，a∈Z.进而错误判断m＋n∈C.而实际上，三个集合中a是不一致．应由m∈A，设m＝2a1，a1∈Z.由n∈B，设n ＝2a2＋1，a2∈Z.所以得到m＋n＝2(a1＋a2)＋1，且a1＋a2∈Z，所以m＋n∈B，故正确答案为B.正解：B反思在分析集合中元素关系时，一定要注意字母各自取值独立性，并要注意用不同字母来区分，否那么会引起错误．易错点2 混淆集合中代表元素而致误【典型例题5】判断命题＝真假，并说明理由．错解：此命题是真命题．理由如下：∵x与61x+范围一致，∴题中命题是真命题．错因分析：误认为两个集合代表元素一样而导致错误．实际上，代表元素是x，而代表元素是61x+，因而构成两个集合元素不同．正解：此命题是假命题．理由如下：∵x∈N，且61x+∈Z，∴1＋x＝1,2,3,6.∴x＝0,1,2,5.∴＝{0,1,2,5}．而＝{6,3,2,1}，∴题中命题是假命题．反思化简集合时一定要注意该集合代表元素是什么，看清楚是数集、点集，还是其他形式，还要注意充分利用特征性质求解，两者相互兼顾，缺一不可．。

1.1 集合及其表示方法1.集合的基本概念；2. 元素和集合的关系；3. 用列举法表示集合；4. 用描述法表示集合；5. 集合中元素的互异性；6.集合中元素的个数；7. 集合的新定义问题一、单选题1．（2020·浙江高一课时练习）下列四组对象中能构成集合的是（ ）. A ．本校学习好的学生 B ．在数轴上与原点非常近的点 C ．很小的实数D ．倒数等于本身的数2.（2020·朝阳吉林省实验高二期末（文））集合{|32}x x ∈-<N 用列举法表示是 A ．{1，2，3，4} B ．{1，2，3，4，5} C ．{0，1，2，3，4，5}D ．{0，1，2，3，4}3.（2020·浙江高二学业考试）已知集合{}13A x R x =∈<<，则下列关系正确的是（ ） A ．1A ∈B ．2A ∉C ．3A ∈D ．4A ∉4．（2020·宁夏兴庆银川一中高二期末（文））已知集合{}|21,A x x x Z =-<≤∈，则集合A 中元素的个数为（ ） A ．0B ．1C ．2D ．35．（2020·全国高三专题练习（文））设集合{0,1,2,3}A =，{},1B x x A x A =-∈-∉，则集合B 中元素的个数为（ ） A ．1 B ．2 C ．3D ．46．（2020·浙江高一课时练习）已知集合{},A x x a π==∣，则a 与集合A 的关系是（ ）.A ．a A ∈B ．a A ∉C ．a A =D ．{}a A ∈7．（2020·浙江高一课时练习）下面四个命题正确的个数是（ ）. ①集合*N 中最小的数是1； ②若*N a -∈，则*N a ∈；③若**N ,N a b ∈∈，则+a b 的最小值是2； ④296+=x x 的解集是{}3,3. A ．0B ．1C ．2D ．38．（2020·全国高一）有下列四个命题： ①{0}是空集；②若a N ∈，则a N -∉；③集合2{|210}A x R x x =∈-+=有两个元素； ④集合6B x NN x ⎧⎫=∈∈⎨⎬⎩⎭是有限集. 其中正确命题的个数是（ ） A ．0B ．1C ．2D ．39.（2020·朝阳吉林省实验高二期末（文））已知非零实数a ，b ，c ，则代数式||||||a b cb ac ++表示的所有的值的集合是（ ） A ．{3}B ．{3}-C ．{3,3}-D ．{3,3,1,1}--10．（2020·吴起高级中学高二月考（文））若{}22111a a ∈++，，，则a =（ ） A ．2 B ．1或－1C ．1D ．－1二、多选题11．（2019·全国高一课时练习）下列表示正确的是（ ） A ．0∈NB ．27∈Z C ．3-∉Z D ．π∉Q E.13∈Q12．（2019·全国高一课时练习）（多选）下面四个说法中错误的是（ ） A ．10以内的质数组成的集合是{}2,3,5,7B ．由1，2，3组成的集合可表示为{}1,2,3或{}3,1,2C ．方程2210x x -+=的所有解组成的集合是{}11，D ．0与{}0表示同一个集合13．（2019·全国高一课时练习）下列是集合{(,)|1,,}M x y x y x y =+≤∈∈N N 中元素的有（ ） A ．(0,0)B ．(0,1)C ．(1,0)D ．(2,1)-E.(1,2)-14.（2020·全国高一课时练习）实数1是下面哪一个集合中的元素（ ） A ．整数集Z B ．{||||x x x =C ．{|11}x x ∈-<<ND ．1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R E.1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 三、填空题15．（2020·浙江高一课时练习）已知集合6{|N ,}5A x x Z x*=∈∈-，用列举法表示为____________. 16．（2020·全国高一）已知集合(){}21,1A m m =+-，若1A ∈，则m =______.17．（2020·全国高一课时练习）用符号“∈”或“∉”填空：（1）2_____N ；（2Q ；（3）13______Z ；（4）3.14______R ；（5）3-______N ；（6Q . 18．（2020·全国高一课时练习）用符号“∈”或“∉”填空： （1）0______∅；（2）2-_______2{|5}x x <；（3）(2,3)_______{(,)|23}x y x y +=；（4）2017_______{|41,}x x n n =-∈Z .19.（2019·海口市第四中学高一月考）用列举法表示集合**{(,)|5,,}A x y x y x y =+=∈∈N N 是_____________________；用描述法表示“所有被4除余1的整数组成的集合”是_____________________．20．（2019·全国高一课时练习）由实数x ，x -，x 所组成的集合中最多含______个元素，最少含______个元素.21．（2020·全国高一课时练习）（1）若23{1,3,1}m m m ∈--，则实数m =_____；（2）若2{|0}x x a ∉->，则实数a 的取值范围是______. 四、解答题22．（2020·全国高一）用列举法表示下列集合: (1){}2|9A x x ==; (2){|12}B x N x =∈≤≤;(3){}2|320C x x x =-+=.23．（2020·浙江高一课时练习）试说明下列集合各表示什么？1|A y y x ⎧⎫==⎨⎬⎩⎭；{|B x y ==；()1,|C x y y x ⎧⎫==⎨⎬⎩⎭(),|13y D x y x ⎧⎫==⎨⎬-⎩⎭；{}0,1E x y ===；{}1,1F x y x y =+=-=-.24．（2020·全国高一）用合适的方法表示下列集合，并说明是有限集还是无限集. （1）到A 、B 两点距离相等的点的集合 （2）满足不等式21x >的x 的集合 （3）全体偶数 （4）被5除余1的数 （5）20以内的质数（6）{(,)|6,,}x y x y x N y N **+=∈∈ （7）方程()0,x x a a R -=∈的解集25．（2020·全国高一）已知22{1,251,1}A a a a a =-+++,2A -∈,求实数a 的值.26．（2020·上海高一课时练习）当实数a 、b 满足什么条件时，集合{}0A x ax b =+=是有限集、无限集、空集？27．已知集合A ＝{x |ax 2－3x ＋2＝0}. (1)若A 是单元素集合，求集合A ；(2)若A 中至少有一个元素，求a 的取值范围．1.1 集合及其表示方法1.集合的基本概念；2. 元素和集合的关系；3. 用列举法表示集合；4. 用描述法表示集合；5. 集合中元素的互异性；6.集合中元素的个数；7. 集合的新定义问题一、单选题1．（2020·浙江高一课时练习）下列四组对象中能构成集合的是（ ）. A ．本校学习好的学生 B ．在数轴上与原点非常近的点 C ．很小的实数 D ．倒数等于本身的数【答案】D 【解析】集合中的元素具有确定性，对于,,A B C ，学习好、非常近、很小都是模糊的概念，没有明确的标准，不符合确定性；对于D ，符合集合的定义，D 正确. 故选：D .2.（2020·朝阳吉林省实验高二期末（文））集合{|32}x x ∈-<N 用列举法表示是 A ．{1，2，3，4} B ．{1，2，3，4，5} C ．{0，1，2，3，4，5} D ．{0，1，2，3，4}【答案】D 【解析】分析：解出不等式得5x <，小于5的自然数有5个． 详解：由题意5x <，又x ∈N ，∴集合为{0,1,2,3,4}．3.（2020·浙江高二学业考试）已知集合{}13A x R x =∈<<，则下列关系正确的是（ ） A ．1A ∈ B ．2A ∉C ．3A ∈D ．4A ∉【答案】D 【解析】因为集合{}13A x R x =∈<<，所以1A ∉，2A ∈，3A ∉，4A ∉ 故选：D4．（2020·宁夏兴庆银川一中高二期末（文））已知集合{}|21,A x x x Z =-<≤∈，则集合A 中元素的个数为（ ） A ．0 B ．1C ．2D ．3【答案】D 【解析】{}{}|21,1,0,1A x x x Z =-<≤∈=-，所以集合A 中元素的个数为3.5．（2020·全国高三专题练习（文））设集合{0,1,2,3}A =，{},1B x x A x A =-∈-∉，则集合B 中元素的个数为（ ） A ．1 B ．2 C ．3 D ．4【答案】A 【解析】因为x ∈B ，－x ∈A ，故x 只可能是0，－1，－2，－3，又1－x ∉A ，则 当0∈B 时，1－0＝1∈A ，不符合题意； 当－1∈B 时，1－(－1)＝2∈A ，不符合题意； 当－2∈B 时，1－(－2)＝3∈A ，不符合题意； 当－3∈B 时，1－(－3)＝4∉A ，符合题意. 所以{3}B =-，故集合B 中元素的个数为1. 故选：A6．（2020·浙江高一课时练习）已知集合{},A x x a π==∣，则a 与集合A 的关系是（ ）.A ．a A ∈B ．a A ∉C ．a A =D ．{}a A ∈【答案】B 【解析】1.732≈≈ 3.146≈π>，∴a A ∉.故选：B.7．（2020·浙江高一课时练习）下面四个命题正确的个数是（ ）. ①集合*N 中最小的数是1； ②若*N a -∈，则*N a ∈；③若**N ,N a b ∈∈，则+a b 的最小值是2； ④296+=x x 的解集是{}3,3. A ．0B ．1C ．2D ．3【解析】*N 是正整数集，最小的正整数是1，故①正确；当0a <时，*a N -∈，但*a N ∉，故②错误；若*a N ∈，则a 的最小值为1.又*b N ∈，则b 的最小值为1，当a 和b 都取最小值时，+a b 取最小值2，故③正确；由集合中元素的互异性知④错误. 故选：C8．（2020·全国高一）有下列四个命题： ①{0}是空集；②若a N ∈，则a N -∉；③集合2{|210}A x R x x =∈-+=有两个元素； ④集合6B x NN x ⎧⎫=∈∈⎨⎬⎩⎭是有限集. 其中正确命题的个数是（ ） A ．0 B ．1C ．2D ．3【答案】B 【解析】①{0}中有一个元素0，不是空集，不正确； ②中当0a =时不成立，不正确；③中2210x x -+=有两个相等的实数根，因此集合只有一个元素，不正确； ④中集合6{|}{1,2,3,6}B x N N x=∈∈=是有限集，正确， 故选：B9.（2020·朝阳吉林省实验高二期末（文））已知非零实数a ，b ，c ，则代数式||||||a b c b a c ++表示的所有的值的集合是（ ） A ．{3}B ．{3}-C ．{3,3}-D ．{3,3,1,1}--【解析】当,,a b c 都为正数时，1||||||a b a b c c ===； 当,,a b c 都为负数时，1||||||a b c a b c ===-. 因此，若,,a b c 都为正数，则3||||||a b c a b c ++=； 若,,a b c 两正一负，则1||||||a b a b c c ++=； 若,,a b c 一正两负，则1||||||a b c a b c ++=-； 若,,a b c 都为负数，则3||||||a b c a b c ++=-. 所以代数式||||||a b c b a c ++表示的所有的值的集合是{3,1,1,3}--. 故选：D.10．（2020·吴起高级中学高二月考（文））若{}22111a a ∈++，，，则a =（ ） A ．2 B ．1或－1 C ．1 D ．－1【答案】D 【解析】当212a +=时，1a =±，当1a =时，集合为{}1,2,2不满足互异性，舍去，当1a =-时，集合为{}1,2,0，满足；当12a +=时，1a =，不满足互异性，舍去. 故选：D . 二、多选题11．（2019·全国高一课时练习）下列表示正确的是（ ） A ．0∈N B ．27∈Z C ．3-∉ZD ．π∉Q E.13∈Q【答案】ADE对于A,0是自然数,则0∈N ,故A 正确；对于B,27不是整数,则27∉Z ,故B 错误；对于C,3-是整数,则3-∈Z ,故C 错误；对于D,π是无理数,则π∉Q ,故D 正确； 对于E,13是有理数,则13∈Q ,故E 正确 故选：ADE12．（2019·全国高一课时练习）（多选）下面四个说法中错误的是（ ） A ．10以内的质数组成的集合是{}2,3,5,7B ．由1，2，3组成的集合可表示为{}1,2,3或{}3,1,2C ．方程2210x x -+=的所有解组成的集合是{}11，D ．0与{}0表示同一个集合 【答案】CD 【解析】10以内的质数组成的集合是{}2,3,5,7，故A 正确；由集合中元素的无序性知{}1,2,3和{}3,1,2表示同一集合，故B 正确；方程2210x x -+=的所有解组成的集合是{}1，故C 错误；由集合的表示方法知0不是集合，故D 错误.故选CD.13．（2019·全国高一课时练习）下列是集合{(,)|1,,}M x y x y x y =+≤∈∈N N 中元素的有（ ） A ．(0,0) B ．(0,1)C ．(1,0)D ．(2,1)-E.(1,2)-【答案】ABC 【解析】∵{(,)|1,,}M x y x y x y =+≤∈∈N N ,∴00x y =⎧⎨=⎩或01x y =⎧⎨=⎩或10x y =⎧⎨=⎩, ∴{(0,0),(0,1),(1,0)}M = 故选：ABC14.（2020·全国高一课时练习）实数1是下面哪一个集合中的元素（ ）A ．整数集ZB ．{||||x x x =C ．{|11}x x ∈-<<ND ．1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R E.1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 【答案】ABD 【解析】1是整数，因此实数1是整数集Z 中的元素，故A 选项正确；由||x x =得0x =或1x =，因此实数1是集合{|||}x x x =中的元素，故B 选项正确；1不满足11x -<<，因此实数1不是集合{|11}x x ∈-<<N 中的元素，故C 选项不正确；当1x =时，101x x -=+，因此实数1是集合1|01x x x -⎧⎫∈≤⎨⎬+⎩⎭R 中的元素，故D 选项正确；当1x =时，11x x +-无意义，因此实数1不是集合1|01x x x +⎧⎫∈≤⎨⎬-⎩⎭R 中的元素，故E 选项不正确. 故选：ABD. 三、填空题15．（2020·浙江高一课时练习）已知集合6{|N ,}5A x x Z x*=∈∈-，用列举法表示为____________. 【答案】{}1,2,3,4- 【解析】 由6N ,5x Z x*∈∈-，得51,2,3,6,4,3,2,1x x -=∴=-， {1,2,3,4}A =-.故答案为:{}1,2,3,4-.16．（2020·全国高一）已知集合(){}21,1A m m =+-，若1A ∈，则m =______.【答案】2 【解析】依题意11m +=或()211m -=， 解得0m =或2m =；由集合中元素的互异性可知当0m =时，集合的两个元素相等，不合题意； 所以2m =.故答案为：2.17．（2020·全国高一课时练习）用符号“∈”或“∉”填空：（1）2_____N ；（2Q ；（3）13______Z ；（4）3.14______R ；（5）3-______N ；（6Q .【答案】∈ ∉ ∉ ∈ ∉ ∈【解析】【分析】N 为自然数集，Q 为有理数，Z 为整数集，R 为实数集，判断元素与集合之间的关系用相应的符号填写即可.【详解】(1)N 为自然数集，2是自然数，所以2N ∈；(2)Q Q ；(3)Z 为整数集，13是分数，所以13Z ∉；(4)R 表示实数集，所以3.14R ∈；(5) N 为自然数集，-3不是自然数，所以3N -∉；(6) Q 3=Q .18．（2020·全国高一课时练习）用符号“∈”或“∉”填空：（1）0______∅；（2）2-_______2{|5}x x <；（3）(2,3)_______{(,)|23}x y x y +=；（4）2017_______{|41,}x x n n =-∈Z .【答案】∉ ∈ ∉ ∉【解析】(1)∅为不含有任何元素的集合，所以0∉∅；(2)2(2)45-=<，2{|52}x x -<∴∈； (3) 2238,(2,3){(,)|23}.x y x y +⨯=∴∉+=(4)因为2017不能被表示为41n -的形式，所以2017{|41,}x x n n ∉=-∈Z ；19.（2019·海口市第四中学高一月考）用列举法表示集合**{(,)|5,,}A x y x y x y =+=∈∈N N 是_____________________；用描述法表示“所有被4除余1的整数组成的集合”是_____________________．【答案】()()()(){}1,42,33,24,1，，， {}41z x z x k k ∈=+∈，【解析】分析：由5x y +=，且,*x y N ∈，则x 取值只能为1,2,3,4，求出对应的y 可得集合A 中的各元素，被4除余1的整数可表示为41k +（k Z ∈）形式．详解：由题意{(1,4),(2,3),(3,2),(4,1)}A =，所有被4除余1的整数组成的集合为{|41,}x Z x k k Z ∈=+∈． 故答案为：{(1,4),(2,3),(3,2),(4,1)}；{|41,}x Z x k k Z ∈=+∈20．（2019·全国高一课时练习）由实数x ，x -，x 所组成的集合中最多含______个元素，最少含______个元素.【答案】2 1【解析】x x ==±，x =-，且当0x =时，0x x x =-====，当0x ≠时，集合中有元素：x ，x -，∴由实数x ，x -，x 2个元素，最少含有1个元素.21．（2020·全国高一课时练习）（1）若23{1,3,1}m m m ∈--，则实数m =_____；（2）若2{|0}x x a ∉->，则实数a 的取值范围是______.【答案】4或2± {|2}a a ≥【解析】（1）由13m -=，得4m =，此时312m =，2115m -=，符合题意.由33m =，得1m =，此时2110m m -=-=，故舍去.由213m -=，得2m =±，当2m =时，11m -=，36m =，符合题意；当2m =-时，13m -=-，36m =-，符合题意，综上所述，m = 4或2±.（2）因为2{|0}x x a ∉->，所以2不满足不等式0x a ->，即2满足不等式0x a -≤，所以20a -≤，即2a .所以实数a 的取值范围是{|2}a a .故答案为：4或2±；{|2}a a ≥四、解答题22．（2020·全国高一）用列举法表示下列集合:(1){}2|9A x x ==;(2){|12}B x N x =∈≤≤;(3){}2|320C x x x =-+=.【答案】(1){3,3}-(2){1,2}(3){1,2}【解析】(1)由29x =得3x =±,因此{}2|9{3,3}A x x ===-.(2)由x ∈N ,且12x ≤≤,得1,2x =,因此{|12}{1,2}B x N x =∈≤≤=.(3)由2320x x -+=得1,2x =.因此{}2|320{1,2}C x x x =-+==.23．（2020·浙江高一课时练习）试说明下列集合各表示什么？ 1|A y y x ⎧⎫==⎨⎬⎩⎭；{|B x y ==；()1,|C x y y x ⎧⎫==⎨⎬⎩⎭ (),|13y D x y x ⎧⎫==⎨⎬-⎩⎭；{}0,1E x y ===；{}1,1F x y x y =+=-=-. 【答案】答案见解析【解析】A 表示y 的取值集合，由1y x =知：0y ≠，{}0A y y ∴=≠；B 表示x 的取值集合，由220x x -≥知：0x ≤或2x ≥，{0B x x ∴=≤或}2x ≥； C 的代表元素为(),x y ，表示反比例函数1y x=上的点构成的点集；D 的代表元素为(),x y ，由13y x =-知：()33y x x =-≠， D ∴表示直线3y x =-上除了()3,0以外的点构成的点集；E 表示以方程“0x =”和“1y =”为元素的一个二元集.F 表示以方程“1x y +=”和“1x y -=-”为元素的一个二元集.24．（2020·全国高一）用合适的方法表示下列集合，并说明是有限集还是无限集.（1）到A 、B 两点距离相等的点的集合（2）满足不等式21x >的x 的集合（3）全体偶数（4）被5除余1的数（5）20以内的质数（6）{(,)|6,,}x y x y x N y N **+=∈∈（7）方程()0,x x a a R -=∈的解集【答案】（1）集合{A =点}P PA PB =，无限集；（2）集合{}21B x x =>，无限集；（3）集合{}2,C x x k k Z ==∈，无限集；（4）集合{}51,D x x k k Z ==+∈，无限集；（5）集合{}2,3,5,7,11,13,17,19E =，有限集；（6）集合()()()()(){}1,5,2,4,3,3,4,2,5,1F =，有限集；（7）集合{}()0,G x x x a a R =-=∈，有限集.【解析】（1）因为到A 、B 两点距离相等的点P 满足PA PB =，所以集合{A =点}P PA PB =，无限集. （2）由题意可知，集合{}21B x x =>，无限集.（3）因为偶数x 能被2整除，所以集合{}2,C x x k k Z ==∈，无限集.（4）由题意可知，集合{}51,D x x k k Z ==+∈，无限集.（5）因为20以内的质数有2，3，5，7，11，13，17，19.所以集合{}2,3,5,7,11,13,17,19E =，有限集.（6）因为6,,x y x N y N **+=∈∈，所以方程的解为15x y =⎧⎨=⎩，24x y =⎧⎨=⎩，33x y =⎧⎨=⎩，42x y =⎧⎨=⎩，51x y =⎧⎨=⎩，所以集合()()()()(){}1,5,2,4,3,3,4,2,5,1F =，有限集. （7）由题意可知，集合{}()0,G x x x a a R =-=∈，有限集.25．（2020·全国高一）已知22{1,251,1}A a a a a =-+++, 2A -∈,求实数a 的值. 【答案】32-【解析】 因为2A -∈，所以有12,a -=-或22512a a ++=-，显然212a +≠-，当12a -=-时，1a =-，此时212512a a a -=++=-不符合集合元素的互异性，故舍去；当22512a a ++=-时，解得32a =-，1a =-由上可知不符合集合元素的互异性，舍去，故32a =-. 26．（2020·上海高一课时练习）当实数a 、b 满足什么条件时，集合{}0A x ax b =+=是有限集、无限集、空集？【答案】当0a ≠，b R ∈时，集合A 为有限集；当0a =，0b =时，集合A 为无限集；当0a =，0b ≠时，集合A 为空集【解析】当0,a b R ≠∈时，方程0ax b +=有唯一解b x a =-，此时集合{}b A a=-，集合A 为有限集； 当0a =，0b =时，0ax b +=有无穷多个解，集合A 为无限集；当0a =，0b ≠时，0ax b +=无解，集合A 为空集.27．已知集合A ＝{x |ax 2－3x ＋2＝0}.(1)若A 是单元素集合，求集合A ；(2)若A 中至少有一个元素，求a 的取值范围．【答案】(1)当a ＝0时，A ＝{23}，当a ＝98时，A ＝{43}．(2)a ≤98. 【解析】 (1)因为集合A 是方程ax 2－3x ＋2＝0的解集，则当a ＝0时，A ＝{23}，符合题意； 当a ≠0时，方程ax 2－3x ＋2＝0应有两个相等的实数根，则Δ＝9－8a ＝0，解得a ＝98，此时A ＝{43}，符合题意． 综上所述，当a ＝0时，A ＝{23}，当a ＝98时，A ＝{43}． (2)由(1)可知，当a ＝0时，A ＝{23}符合题意； 当a ≠0时，要使方程ax 2－3x ＋2＝0有实数根，则Δ＝9－8a ≥0，解得a ≤98且a ≠0.9综上所述，若集合A中至少有一个元素，则a≤8.。

高中集合练习题及答案集合是数学中一个非常重要的概念，它在高中数学中占有重要地位。

集合论是研究集合的数学分支，它提供了一种描述和处理数学对象的方式。

在高中数学中，学生需要掌握集合的基本概念、运算以及集合在解决数学问题中的应用。

以下是一些高中集合练习题及答案，供同学们练习和参考。

练习题1：设集合A={x|x<5}，B={x|x>3}，求A∩B。

答案：集合A表示所有小于5的实数的集合，集合B表示所有大于3的实数的集合。

A与B的交集A∩B就是同时满足小于5且大于3的实数的集合，即A∩B={x|3<x<5}。

练习题2：已知集合M={1,2,3}，N={2,3,4}，求M∪N。

答案：集合M表示元素为1,2,3的集合，集合N表示元素为2,3,4的集合。

M与N的并集M∪N就是包含M和N所有元素的集合，即M∪N={1,2,3,4}。

练习题3：设A={x|-1≤x≤2}，B={x|x>1}，求A-B。

答案：集合A表示闭区间[-1,2]中的所有实数的集合，集合B表示大于1的所有实数的集合。

A-B表示A中所有不属于B的元素组成的集合，即A-B={x|-1≤x≤1}。

练习题4：如果A={x|x<0或x>5}，B={x|-3≤x≤4}，求A∩B。

答案：集合A表示所有小于0或大于5的实数的集合，集合B表示闭区间[-3,4]中的所有实数的集合。

A与B的交集A∩B就是同时满足小于0或大于5且在闭区间[-3,4]中的实数的集合，即A∩B={x|-3≤x<0}。

练习题5：设A={1,2,3}，B={x|x∈A且x≠2}，求B。

答案：集合A表示元素为1,2,3的集合。

B是A中所有不等于2的元素组成的集合，即B={1,3}。

练习题6：已知A={x|-2<x<3}，B={x|-1<x<4}，求A∪B。

答案：集合A表示开区间(-2,3)中的所有实数的集合，集合B表示开区间(-1,4)中的所有实数的集合。

1.已知全集为U＝R,集合，，则＝（）A．{} B．C．D．
2.；
3.已知﹑均为非零向量，条件条件的夹角为锐角，则是成立的
A．充要条件B．充分而不必要的条件
C．必要而不充分的条件D．既不充分也不必要的条件
4.设全集，集合A={} ，则在直角平面上集
合内所有元素的对应点构成的图形的面积等于__ ___．
5.集合A满足：若实数a∈A，则∈A，已知a = 2∈A，则集合A中的元素个数至少有____个．
6.已知集合只有一个元素，则a的值
为（）
A．0 B．1 C．0或1 D．—1
7.设集合那么“”是“”的（）
A．充分而不必要条件B．必要而不充分条件
C．充要条件D．既不充分也不必要条件
8.已知集合A="{x|" |x|<3,x Z},B={1,2,3,4},全集U=AUB，则集合C（A B）的子集个数为
( )
A．8 B．16 C．32 D．64
9.集合｛，｝的真子集个数是.
10.集合的元素个数有（）
A．1个
B．2个
C．3个
D．无数个
11.若集合，，则中元素个数为（）A．0个B．1个C．2个D．3个
12.集合的元素个数有个.。

新课标 集合的含义及其表示姓名：_________一、选择题：A. 0B. 1C.2D.32.下列各组集合中，表示同一集合的是 （ ） A.(){}(){}3,2,2,3M N = B.{}{}3,2,2,3M N ==C.(){},1M x y x y =+=，{}1N y x y =+=D. {}(){}1,2, 1.2M N ==3.下列方程的实数解的集合为12,23⎧⎫-⎨⎬⎩⎭的个数为 （ ）（1）224941250x y x y +-++=;(2)2620x x +-=; (3) ()()221320x x -+=;(4) 2620x x --=A.1B.2C.3D.44.集合{}(){}2210,6100A x x xB x N x x x =++==∈++=，{}450C x Q x =∈+<，{}2D x x =为小于的质数 ，其中时空集的有 （ ）A. 1个B.2个C.3个D.4个 5. 下列关系中表述正确的是 （ ）A.{}200x ∈=B.(){}00,0∈C. 0∈∅D.0N ∈ 6. 下列表述正确的是（ ）A.{}0=∅B.{}{}1,22,1=C.{}∅=∅D.0N ∉ A.0 B. 1 C. 2 D.3 二．填空题：8.用列举法表示不等式组240121x x x +>⎧⎨+≥-⎩的整数解集合为9.已知集合12,6A x x N N x ⎧⎫=∈∈⎨⎬-⎩⎭用列举法表示集合A 为10.已知集合241x A a x a ⎧⎫-⎪⎪==⎨⎬+⎪⎪⎩⎭有惟一解，又列举法表示集合A 为三、解答题：11．已知{}{}2A=1,a,b ,,,B a a ab =，且A=B ，求实数a,b ;12. 已知集合{}2210,A x ax x x R =++=∈，a 为实数（1）若A 是空集，求a 的取值范围（2）若A 是单元素集，求a 的值 （3）若A 中至多只有一个元素，求a 的取值范围13. 设集合{}22,M a a x y a Z ==-∈（1）请推断任意奇数与集合M 的关系 （2）关于集合M ，你还可以得到一些什么样的结论参考答案：DBBBDBC8.{}1,0,1,2- 9{}0,2,3,4,5；10，17224⎧⎫--⎨⎬⎩⎭，，11,a= -1,b=0；12，（1）a>1(2)a=0or1(3)a=0 or a ≥113（1）任意奇数都是集合M 的元素（2）略。

1.1.1集合及其表示方法第一章集合与常用逻辑用语1.1 集合1.1.1集合及其表示方法考点1元素与集合的概念1.(2019·江西临川一中高一期中)下列所给对象不能组成集合的是()。

A.一个平面内的所有点B.所有小于零的实数C.某校高一(1)班的高个子学生D.某一天到某商场买过货物的顾客答案：C解析：A.“一个平面内的所有点”的标准确定,能组成集合;B.“所有小于零的实数”的标准确定,能组成集合;C.“某校高一(1)班的高个子学生”的标准不确定,因而不能组成集合;D.“某一天到某商场买过货物的顾客”的标准确定,能组成集合。

2.(2019·北京通州区高一期中)把“notebooks”中的字母组成一个集合,则该集合中的元素个数是()。

A.5B.6C.7D.8答案：C3.已知集合S={a,b,c}中的三个元素是△ABC的三边长,那么△ABC一定不是()。

A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形答案：D4.(2019·丹东东港二中检测)已知集合A={2,-1},集合B={m2-m,-1},且A=B,则实数m等于()。

A.2B.-1C.2或-1D.4答案：C5.由实数x ,-x ,|x |,√x 2,-√x 33所组成的集合中最多含有( )。

A.2个元素B.3个元素C.4个元素D.5个元素答案：A解析： ∵√x 2=|x |,-√x 33=-x ,|x |=±x ,∴由实数x ,-x ,|x |,√x 2,-√x 33所组成的集合中最多含有2个元素。

故选A 。

【易错点拨】集合中的元素必须是互异的,求解出集合中的参数,必须代入集合中一一检验元素的互异性。

考点2元素与集合的关系6.(2019·山东德州高一(上)期中)已知方程x 2-16=0的解是集合A 中的元素,则下列关系不正确的是( )。

A.4∈AB.{-4}∈AC.-4∈AD.4∈A 且-4∈A 答案：B7.(2019·北京朝阳区陈经纶中学高一(上)期中)已知集合A ={x |x (x -1)=0},那么( )。

1.1 集合的概念一、单选题1．已知集合{|2,}A x x k k N ==∈，{|4,}B x x k k N ==∈，则A 与B 的关系为（ ）A ．AB ⊆ B ．B A ∈C ．B A ⊆D ．A B =答案：C解析：根据子集的概念分析可得结果.详解：若x B ∈，则42(2)x k k A ==∈，所以B A ⊆，因为2A ∈，且2∉B ，所以A 不是B 的子集.故选：C点睛：关键点点睛：掌握子集的概念是解题关键.2．不等式|1|3x +的解集是A ．{|4x x - 或2}xB ．{|42}x x -<<C ．{|4x x <- 或2}xD ．{|42}x x -答案：D解析：先求解出不等式|1|3x +，然后用集合表示即可．详解：解：|1|3x +，即313x -+，即42x -，故不等式|1|3x +的解集是{|42}x x -，故选D ．点睛：本题是集合问题，解题的关键是正确求解绝对值不等式和规范答题．3．已知集合{}22M x x =-<<，i 为虚数单位，1a i =+，则下列选项正确的是（）A ．a M ∈B ．{}a M ∈C ．{}a M ⊄D ．a M ∉答案：A解析：利用复数模的计算公式可得a =，即可判断出结论．详解：a =，又集合{}22M x x =-<<，∴a M ∈．故选：A ．点睛：本题考查了复数模的计算公式、元素与集合之间的关系，考查了推理能力与计算能力，属于基础题．4．方程x 2＝x 的所有实数根组成的集合为A ．()0,1B ．(){}0,1C ．{}0,1D ．{}2x x =答案：C解析：解方程x 2＝x ，得x ＝0或x ＝1，由此能求出方程x 2＝x 的所有实数根组成的集合 详解：解：解方程x 2＝x ，得x ＝0或x ＝1，方程x 2＝x 的所有实数根组成的集合为{}0,1．故选：C ．点睛：本题考查集合的表示方法，属于基础题.5．下列各组对象中不能构成集合的是A ．大名三中高一（2）班的全体男生B ．大名三中全校学生家长的全体C ．李明的所有家人D ．王明的所有好朋友 答案：D详解：由集合中元素的特性，可知D 中的元素具有不确定性，故不能构成集合选D6．已知集合A ＝1，2，3，4}，B ＝（x ，y ）|x∈A，y∈A，y ﹣x∈A}，则集合B 中的元素的个数为（ ）A ．4B ．5C ．6D ．7答案：C解析：通过集合B ，利用x A ∈，y A ，y x A -∈，求出集合B 中元素的个数．详解：解：因为集合{1A =，2，3，4}，{(,)|B x y x A =∈，y A ，}y x A -∈，所以当1x =时，2y =或3y =或4y =，当2x =时，3y =或4y =，当3x =时，4y =，即()()()()()(){}1,2,1,3,1,4,2,3,2,4,3,4B =所以集合B 中的元素个数为6．故选：C ．7．已知集合{}3,M x x n n ==∈Z ，{}31,N x x n n ==+∈Z ，{}31,P x x n n ==-∈Z ，且a M ∈，N b ∈，c P ∈，若d a b c =-+，则．A ．d M ∈B ．d N ∈C ．d P ∈D ．d M ∈且d N ∈答案：B 解析：设3,31,31a k b y c m ==+=-，得到()32d k y m =-+-，结合集合的表示，即可求解，得到答案．详解：由题意，设3a k =，k ∈Z ，31b y =+，y ∈Z ，31c m =-，m ∈Z ，则()()3313132d k y m k y m =-++-=-+-，令t k y m =-+，则t ∈Z ，且()32331311d t t t =-=-+=-+，t ∈Z ，则d N ∈，故选B ．点睛：本题主要考查了集合的表示方法及其应用，其中解答中根据集合的元素形式，合理运算，结合集合表示方法求解是解答的关键，着重考查了推理与运算能力，属于中档试题．8．下列关系中①0N ∈；②27Z ∈；③3Z -∉；④Q π∉正确的个数为（ ）A ．0B ．1C ．2D ．3答案：C解析：根据元素与集合的关系逐项进行判断即可.详解：①因为0是自然数，所以0N ∈，故正确； ②因为27不是整数，所以27Z ∉，故错误；③因为3-是整数，所以3Z -∈，故错误；④因为π是无理数，所以Q π∉，故正确；故选：C.9．下列各组中的集合P 与Q 表示同一个集合的是( )A ．P 是由元素1,3,π构成的集合,Q 是由元素π,1,3-构成的集合B ．P 是由π构成的集合,Q 是由3.14159构成的集合C ．P 是由2,3构成的集合,Q 是由有序数对(2,3)构成的集合D ．P 是满足不等式-1≤x≤1的自然数构成的集合,Q 是方程x 2=1的解集答案：A详解：对于A,集合P,Q 中的元素完全相同,所以P 与Q 表示同一个集合,对于B,C,D,集合P,Q 中的元素不相同,所以P 与Q 不能表示同一个集合.选A二、填空题1．定义集合A 和B 的运算为{}*,A B x x A x B =∈∉，试写出含有集合运算符号“*”“”“”，并对任意集合A 和B 都成立的一个式子：_____________________.答案：()()**A A B A B B ⋂=⋃（答案不唯一）.解析：根据运算{}*,A B x x A x B =∈∉的定义可得出结论.详解：如下图所示，由题中的定义可得()(){}(){}(),,A A B x x A x A B x x A B x B A B B *⋂=∈∉⋂=∈⋃∉=⋃*.故答案为：()()**A A B A B B ⋂=⋃（答案不唯一）.点睛：本题考查集合运算的新定义，利用韦恩图法表示较为直观，考查数形结合思想的应用，属于中等题.2．已知集合A ＝a ＋2，(a ＋1)2，a 2＋3a ＋3}，且1∈A，则2017a 的值为_________．答案：1解析：对集合A 中的元素分情况讨论，结合集合中元素的互异性可求得结果.详解：当a ＋2＝1时，a ＝－1，此时有(a ＋1)2＝0，a 2＋3a ＋3＝1，不满足集合中元素的互异性； 当(a ＋1)2＝1时，a ＝0或a ＝－2，当a ＝－2，则a 2＋3a ＋3＝1，舍去，经验证a ＝0时满足；当a 2＋3a ＋3＝1时，a ＝－1或a ＝－2，由上知均不满足，故a ＝0，则2017a ＝1． 故答案为：13．已知集合2{|A x x ＝＋20}x a ＋＝，若1∈A，则A ＝________.答案：－3,1}解析：集合2{|A x x ＝＋20}x a ＋＝，1∈A，则2x ＋20x a ＋＝由一根是1，所以21＋20a ＋＝，a =-3,所以2x ＋23x -=0，x=1或x=-3,所以A ＝－3,1}4．用列举法表示集合x||x|<6，且x∈Z}是___________．答案：–5，–4，–3，–2，–1，0，1，2，3，4，5} 解析：根据6,x x Z <∈且 解此绝对值不等式，得到66,,x x Z -<<∈且 然后写出满足条件的整体x 的值即可．详解：6,x x Z <∈且66,,x x Z ∴-<<∈且∴ x = -5，-4，-3，-2，-1，0，1，2，3，4，5．故答案为–5，–4，–3，–2，–1，0，1，2，3，4，5}．点睛：此题是个基础题，考查集合的表示法，以及简单绝对值不等式的解法，考查学生分析解决问题的能力．5．设集合{,,1}A x xy xy =-，其中x ∈Z ，y ∈Z 且0y ≠. 若0A ∈，则用列举法表示集合A =________答案：{1,0,1}-解析：根据0y ≠且0A ∈,结合集合的互异性原则可知0xy -1=,进而求得x 和y 的值,即可表示集合A .详解：集合{,,1}A x xy xy =-,其中x ∈Z ,y ∈Z 且0y ≠.若0A ∈,则当0x =时, 0x xy ==由集合的互异性可知不符合要求所以0xy -1=,即1xy =则11x y =⎧⎨=⎩或11x y =-⎧⎨=-⎩当11x y =⎧⎨=⎩时,1x xy ==, 由集合的互异性可知不符合要求 因而11x y =-⎧⎨=-⎩,此时1,1,10x xy xy =-=-= 所以{1,0,1}A =-故答案为: {1,0,1}-点睛：本题考查了元素与集合的关系,集合的互异性原则的应用,属于基础题.三、解答题1．用适当的方法表示下列集合：（1）已知集合P ＝x|x ＝2n ，0≤n≤2且n∈N}；（2）抛物线y ＝x 2－2x 与x 轴的公共点的集合；（3）直线y ＝x 上去掉原点的点的集合.答案：答案见解析解析：（1）用列举法即可求得集合的元素；（2）直接用描述法表示公共点的集合；（3）用描述法即可表示.详解：（1）因为02,n n N ≤≤∈，则0,2,4x =，故用列举法表示为：P ＝0，2，4}.（2）直接用描述法表示为：()22{,|}0y x x x y y ⎧=-⎨=⎩. （3）描述法：(x ，y)|y ＝x ，x≠0}.点睛：本题考查集合的表示方法，选择适当的方法即可，属简单题.2．试用集合表示图中阴影部分（含边界）的点.答案：(),13,03}{|x y x y -≤≤≤≤解析：直接用集合的描述法将点集表示出来.详解：由题意可得13,03x y -≤≤≤≤，所以图中阴影部分（含边界）的点组成的集合为(),13,03}{|x y x y -≤≤≤≤.点睛：本题考查了用描述法表示点集，属于基础题.3．用另一种形式表示集合.（1）63A x x ⎧⎫=∈∈⎨⎬-⎩⎭Z Z ；（2）{2,4,6,8}.答案：（1）{3,0,1,2,4,5,6,9}-；（2）{|2,14,}x x k k k =≤≤∈Z .解析：(1)描述法转为列举法时，首先确定集合是有哪些元素组成的，然后将所有元素写在花括号内；(2)列举法转为描述法时，首先明确集合中元素的公共属性，即把握住集合中元素满足什么条件.详解：（1）要使6,3x x-是整数，则|3|x -必是6的约数，当3,0,1,2,4,5,6,9x =-时，|3|x -是6的约数，∴{3,0,1,2,4,5,6,9}A =-.（2）{|2,14,}x x k k k =≤≤∈Z .点睛：本题考查集合的表示方法，属于基础题.。

第2课时集合的表示第2课时 集合的表示必备知识基础练1．解析：(1)因为15的正约数为1,3,5,15， 所以所求集合可表示为{1,3,5,15}． (2)因为不大于10的正偶数有2,4,6,8,10， 所以所求集合可表示为{2,4,6,8,10}．(3)解方程组⎩⎪⎨⎪⎧2x ＋y ＋6＝0，x －y ＋3＝0，得⎩⎪⎨⎪⎧x ＝－3，y ＝0.所以所求集合可表示为{(－3,0)}．2．解析：(1)被5整除的数可用式子x ＝5n ，n ∈Z 表示，所以所有被5整除的数的集合可表示为{x |x ＝5n ，n ∈Z }．(2)由6x 2－5x ＋1＝0解得x ＝12或x ＝13，所以方程6x 2－5x ＋1＝0的实数解集为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝12或x ＝13. (3)直线y ＝x 上除去原点，即x ≠0，所以直线y ＝x 上去掉原点的点的集合为{(x ，y )|y ＝x ，且x ≠0}．3．解析：选项A 中应是xy <0；选项B 的本意是想用描述法表示，但不符合描述法的规X 格式，缺少了竖线和竖线前面的代表元素x ；选项C 的“{ }”与“全体”意思重复．答案：D4．解析：∵x ∈Z 且86－x ∈N ，∴1≤6－x ≤8，－2≤x ≤5.当x ＝－2时，1∈N ；当x ＝－1时，87∉N ；当x ＝0时，43∉N ；当x ＝1时，85∉N ；当x ＝2时，2∈N ；当x ＝3时，83∉N ；当x＝4时，4∈N ；当x ＝5时，8∈N .综上可知A ＝{－2,2,4,5}．答案：{－2,2,4,5}5．解析：当t ＝－2时，x ＝4；当t ＝2时，x ＝4；当t ＝3时，x ＝9； 当t ＝4时，x ＝16；∴B ＝{4,9,16}． 答案：{4,9,16}6．解析：∵－2∈A ，∴－2k ＋2>0，得k <1. 答案：k <1关键能力综合练1．解析：∵x 2－2x ＋1＝0，即(x －1)2＝0，∴x ＝1，选B. 答案：B2．解析：先求出方程组的解⎩⎪⎨⎪⎧x ＝2，y ＝1，再写成集合的形式．注意集合的元素是有序实数对(2,1)，故选C.答案：C3．解析：由于集合中的元素具有无序性，故{3,2}＝{2,3}． 答案：B4．解析：若x ＝2，则x －1＝1<2，所以2∈M ；若x ＝－2，则x －1＝－3<2，所以－2∈M .故选A.答案：A5．解析：∵3＝31，观察集合中的元素，不难发现，若令分母为n ，则分子为2n ＋1，且n ∈N *，∴集合为⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ⎪⎪⎪x ＝2n ＋1n ，n ∈N *. 答案：D6．解析：①当a ＝0时，原方程为16－8x ＝0. ∴x ＝2，此时A ＝{2}；②当a ≠0时，由集合A 中只有一个元素， ∴方程ax 2－8x ＋16＝0有两个相等实根， 则Δ＝64－64a ＝0，即a ＝1. 从而x 1＝x 2＝4，∴集合A ＝{4}． 综上所述，实数a 的值为0或1.故选D. 答案：D7．解析：由题知，a ∈A ，a ∈B ，所以a 是方程组⎩⎪⎨⎪⎧y ＝2x ＋1，y ＝x ＋3的解，解得⎩⎪⎨⎪⎧x ＝2，y ＝5，即a 为(2,5)．答案：(2,5)8．解析：∵x ∈A ，∴当x ＝－1时，y ＝|x |＝1； 当x ＝0时，y ＝|x |＝0；当x ＝1时，y ＝|x |＝1. ∴B ＝{0,1}． 答案：{0,1}9．解析：由于2的倒数12不在集合A 中，故集合A 不是可倒数集．若一个元素a ∈A ，则1a ∈A .若集合中有三个元素，故必有一个元素a ＝1a ，即a ＝±1，故可取的集合有⎩⎨⎧⎭⎬⎫1，2，12，⎩⎨⎧⎭⎬⎫－1，3，13等．答案：不是⎩⎨⎧⎭⎬⎫1，2，12 10．解析：(1)由x 2(x ＋1)＝0，得x ＝－1或x ＝0，所以该集合可表示为{－1,0}．故该集合为有限集．(2)平面直角坐标系中，不在第一、三象限内的点组成的集合可表示为{(x ，y )|xy ≤0，x ∈R ，y ∈R }．故该集合为无限集．(3)自然数的平方组成的集合用列举法可表示为{0,12,22,32，…}，用描述法可表示为{x |x ＝n 2，n ∈N }．故该集合为无限集．学科素养升级练1．解析：由题意易知集合A 表示奇数集，集合B 表示偶数集．又由x 1，x 2∈A ，x 3∈B ，则x 1，x 2是奇数，x 3是偶数．对于A ，两个奇数的积为奇数，即x 1x 2∈A ，故A 正确；对于B ，一奇一偶两个数的积为偶数，即x 2x 3∈B ，故B 正确；对于C ，两个奇数的和为偶数，即x 1＋x 2∈B ，故C 正确；对于D ，两个奇数与一个偶数的和为偶数，即x 1＋x 2＋x 3∈B ，故D 错误．答案：ABC2．解析：对于①，在平面直角坐标系中，第一象限内的点的横、纵坐标均大于0，且集合中的代表元素为点(x ，y )，所以①正确；对于②，方程x －2＋|y ＋2|＝0的解为⎩⎪⎨⎪⎧x ＝2，y ＝－2，解集为{(2，－2)}或⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫x ，y ⎪⎪⎪⎩⎪⎨⎪⎧ x ＝2y ＝－2， 所以②不正确；对于③，因为集合{y |y ＝x 2－1，x ∈R }等于集合{y |y ≥－1}，集合{y |y ＝x －1，x ∈R }等于R ，故这两个集合不相等，所以③正确．答案：①③3．解析：集合A 是方程x 2＋ax ＋1＝0的解构成的集合．(1)当a ＝2时，x 2＋2x ＋1＝0，即(x ＋1)2＝0，x ＝－1，所以A ＝{－1}．(2)A 中只有一个元素，即方程x 2＋ax ＋1＝0有两个相等实根，由Δ＝a 2－4＝0，得a ＝±2.所以a ＝±2时，集合A 中只有一个元素．(3)A 中有两个元素，即方程x 2＋ax ＋1＝0有两个不相等的实根，由Δ＝a 2－4>0，得a <－2或a >2.所以a <－2或a >2时，集合A 中有两个元素．。

高中数学必修一集合练习题1. 集合的表示法：给定集合A={1, 2, 3}，请用描述法表示集合A。

2. 子集与真子集：若集合B={x | x是A的子集}，集合A={1, 2, 3}，请列出集合B的所有元素，并判断哪些是A的真子集。

3. 集合的并集：已知集合C={1, 2}和集合D={2, 3}，请计算C∪D。

4. 集合的交集：若集合E={1, 3, 5}和集合F={2, 3, 5}，请找出E∩F。

5. 集合的差集：给定集合G={1, 2, 3, 4}和集合H={3, 4, 5}，求G-H。

6. 集合的补集：设全集U={1, 2, 3, 4, 5, 6}，集合I={2, 4, 6}，请求∁_U I。

7. 幂集：集合J={a, b}，请列出J的所有幂集。

8. 集合的包含关系：若集合K={x | x是小于10的正整数}，集合L={1, 3, 5, 7, 9}，请判断K和L之间的关系。

9. 集合相等：集合M={x | x是偶数}和集合N={2, 4, 6, 8, 10}，判断M和N是否相等。

10. 集合的笛卡尔积：若集合O={1, 2}和集合P={a, b}，请计算O×P。

解答提示：- 对于第1题，描述法表示集合A可以写作A={x | x是正整数，且1≤x≤3}。

- 第2题中，集合B的所有元素包括空集和所有A的子集，即B={∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}。

其中，A的真子集是不包含A本身的所有子集。

- 第3题，C∪D={1, 2, 3}。

- 第4题，E∩F={3, 5}。

- 第5题，G-H={1, 2}。

- 第6题，∁_U I={1, 3, 5}。

- 第7题，J的幂集包括所有J的子集，即{∅, {a}, {b}, {a, b}}。

- 第8题，K包含L，因为L的所有元素都在K中。

- 第9题，M和N相等，因为它们包含相同的元素。

1.1 集合的概念一、单选题1．下列四个集合中，是空集的是（ ）A ．{}0B ．{8x x >∣，且}5x <C ．{}210x x ∈-=N ∣D ．{}4x x >答案：B解析：根据空集的定义判断．详解：A 中有元素0，B 中集合没有任何元素，为空集，C 中有元素1，D 中集合，大于4的实数都是其中的元素．故选：B ．2．下列常数集表示正确的是( )A ．实数集RB ．整数集QC ．有理数集ND ．自然数集Z答案：A解析：因为Z 表示整数集，Q 表示有理数集，R 表示实数集，N 表示自然数数集，所以A 正确，故选A.3．已知A 中元素x 满足x ＝3k －1，k∈Z，则下列表示正确的是( )A ．－1∉AB ．－11∈AC ．3k 2－1∈AD ．－34∉A答案：C解析：判断一个元素是不是集合A 的元素，只要看这个元素是否满足条件31,x k k Z =-∈；判断一个元素是集合A 的元素，只需令这个数等于31k -，解出k ，判断k 是否满足k Z ∈，据此可完成解答.详解：当0k =时，311k -=-，故1A -∈，故选项A 错误；若11A -∈，则1131k -=-，解得103k Z =-∉，故选项B 错误； 令23131k k -=-，得0k =或1k =，即231k A -∈，故选项C 正确；当11k =-时，3134k -=-，故34A -∈，故选项D 错误；故选C.点睛：该题是一道关于元素与集合关系的题目，解题的关键是掌握集合的含义.4．若集合{}1,3A =，{}0,2B =-，则集合{}|,,z z x y x A y B =+∈∈中的元素的个数为（ ）A ．5B ．4C ．3D ．2答案：C解析：根据题意求出{}{}|,,1,1,3z z x y x A y B =+∈∈=-即可得解.详解：集合{}1,3A =，{}0,2B =-，则集合{}{}|,,1,1,3z z x y x A y B =+∈∈=-共三个元素.故选：C点睛：此题考查求集合中的元素个数，关键在于读懂集合的新定义，根据题意求出集合中的元素.5．集合(){},0,,x y xy x y ≤∈∈R R 是指（ ）A ．第二象限内的所有点B ．第四象限内的所有点C ．第二象限和第四象限内的所有点D ．不在第一、第三象限内的所有点答案：D解析：由0xy ≤，可知00x y ≤⎧⎨≥⎩或00x y ≥⎧⎨≤⎩，进而可选出答案. 详解：因为0xy ≤，所以00x y ≤⎧⎨≥⎩或00x y ≥⎧⎨≤⎩， 故集合(){},0,,x y xy x y ≤∈∈R R 是指第二象限和第四象限内的所有点，以及在,x y 轴上的点，即不在第一、第三象限内的所有点.故选：D.点睛：本题考查集合的表示方法，属于基础题.6．在直角坐标系内，坐标轴上的点构成的集合可表示为（ ）A ．（x ，y ）|x ＝0，y≠0或x≠0，y ＝0}B ．（x ，y ）|x ＝0且y ＝0}C ．（x ，y ）|xy ＝0}D ．（x ，y ）|x ，y 不同时为零}答案：C解析：根据坐标轴上的点特征判断选项.详解：A.表示x 轴和y 轴上的点，但不包含原点，故A 错误；B.集合中只有一个元素，就是原点，故错误；C.00xy x =⇔=或0y =，即表示坐标轴上点的集合，故C 正确；D.表示平面中的点，但不包含原点，故错误.故选：C.7．用描述法表示奇数集合：①A＝a|a ＝2k+1，k∈Z}②B＝a|a ＝2k ﹣1，k∈Z}③C＝2b+1|b∈Z}④D＝d|d ＝4k±1，k∈Z}．上述表示方法正确的个数是（ ）A ．1B ．2C ．3D ．4答案：C解析：由整数的整除性，可得A 、B 都表示奇数集，D 表示除以4余1的整数或表示除以4余3的整数．由此不难得到本题的答案．详解：由题意得：①②表示奇数集合，③的表示方法错误，④D＝x|x ＝4k±1，k∈z}，表示除以4余1的整数或除以4余3的整数，∵一个奇数除以4之后，余数不是1就是3，故④表示奇数集合；故选：C ．8．已知集合{}2|210,A x ax x a =++=∈R 只有一个元素，则a 的取值集合为（ ） A ．{1}B ．{0}C ．{0,1,1}-D ．{0,1}答案：D 解析：对参数分类讨论，结合判别式法得到结果.详解：解：①当0a =时，1{}2A =-，此时满足条件；②当0a ≠时，A 中只有一个元素的话，440a =-=，解得1a =，综上，a 的取值集合为{0，1}．故选：D ．9．下列关系中正确的个数是（ ） ①12Q ∈ R ③*0N ∈ ④π∈ZA ．1B ．2C ．3D ．4答案：A解析：根据集合的概念、数集的表示判断．详解：120不是正整数，π是无理数，当然不是整数．只有①正确． 故选：A ．点睛：本题考查元素与集合的关系，掌握常用数集的表示是解题关键．二、多选题1．(多选题)大于4的所有奇数构成的集合可用描述法表示为（ ）A ．x|x ＝2k －1，k∈N}B ．x|x ＝2k ＋1，k∈N，k≥2}C ．x|x ＝2k ＋3，k∈N}D ．x|x ＝2k ＋5，k∈N}答案：BD解析：用列举法把四个选项对应的集合表示出来，即可验证.详解：对于A ：{}{|}1,1,321x x k k ∈=-N ＝－，对于B ：{}{|212}5,7,9x x k k k +∈≥=N ＝，， 对于C ：{}{|23}3,5,7x x k k +∈=N ＝， 对于D ：{}{|25}5,7,9x x k k +∈=N ＝，故选：BD 2．(多选题)已知集合A 中元素满足x ＝3k －1，k∈Z，则下列表示正确的是（ ）A ．－2∈AB ．－11∉AC ．3k 2－1∈AD ．－34∉A答案：BC解析：直接对四个选项代入x ＝3k －1进行计算，即可得到正确答案.详解：令3k－1＝－2，解得k＝－13，－13∉Z，∴－2∉A；令3k－1＝－11，解得k＝－103，－103∉Z，∴－11∉A；∵k2∈Z，∴3k2－1∈A；令3k－1＝－34，解得k＝－11，－11∈Z，∴－34∈A．故选：BC3．下列每组对象，能构成集合的是（）A．中国各地最美的乡村B．直角坐标系中横、纵坐标相等的点C．一切很大的数D．清华大学2020年入学的全体学生答案：BD解析：根据集合中的元素具有确定性逐个判断即可详解：解：对于A，最美标准不明确，不具有确定性，所以不能构成集合；对于B，直角坐标系中横、纵坐标相等的点就在一、三象限的平分线上，是确定的，所以可以构成集合；对于C，一切很大的数不具有确定性，所以不能构成集合；对于D，清华大学2020年入学的全体学生是确定的，能构成集合，故选：BD4．设P是一个数集，且至少含有两个元素．若对任意的a，b∈P，都有a＋b，a－b，ab，ab∈P(除数b≠0)，则称P是一个数域，例如有理数集Q是一个数域，有下列说法正确的是（）A．数域必含有0，1两个数；B．整数集是数域；C．若有理数集Q M⊆，则数集M必为数域；D．数域必为无限集．答案：AD解析：根据数域的定义逐项进行分析即可．详解：数集P有两个元素m，N，则一定有m－m＝0，mm＝1(设m≠0)，A正确；因为1∈Z，2∈Z，12Z∉，所以整数集不是数域，B不正确；令数集M Q =⋃，则1M ∈，但1M ，所以C 不正确；数域中有1，一定有1＋1＝2，1＋2＝3，递推下去，可知数域必为无限集，D 正确． 故选：AD5．（多选）已知集合{}220A x ax x a =-+=中至多含有一个元素，则实数a 可以取（ ）A ．1a ≥B ．0a =C ．1a ≤-D ．11a -≤≤答案：ABC 解析：根据集合至多含有一个元素，得到方程220ax x a -+=至多有一个根，讨论0a =，0a ≠两种情况，分别求出对应的a 的范围，即可得出结果.详解： 因为集合{}220A x ax x a =-+=中至多含有一个元素，即方程220ax x a -+=至多有一个根，当0a =时，方程可化为方程20x -=，解得0x =，满足题意；当0a ≠时，若方程无解，则()22224440a a ∆=--=-<，解得1a >或1a <-；若方程220ax x a -+=只有一个根，则()22224440a a ∆=--=-=，解得1a =±，综上实数a 的范围为1a ≥或0a =或1a ≤-；即ABC 都正确，D 错误.故选：ABC.点睛：本题主要考查集合中元素个数求参数的问题，属于基础题型.三、填空题1．下列说法中，正确的有________．(填序号)①单词book 的所有字母组成的集合的元素共有4个；②集合M 中有3个元素a ，b ，c ，其中a ，b ，c 是△ABC 的三边长，则△ABC 不可能是等腰三角形；③将小于10的自然数按从小到大的顺序排列和按从大到小的顺序排列分别得到不同的两个集合．答案：②解析：根据集合的元素的互异性判定①错误；根据集合的元素的互异性判定②正确；根据集合的元素的无序性可判定③错误.详解：①不正确. book 的字母o 有重复，共有3个不同字母，元素个数是3.②正确. 集合M 中有3个元素a ，b ，c ，所以a ，b ，c 都不相等，它们构成的三角形三边不相等，故不可能是等腰三角形．③不正确. 小于10的自然数不管按哪种顺序排列，里面的元素都是0，1，2，3，4，5，6，7，8，9这10个数，集合是相同的，和元素的排列顺序无关．故答案为：②.2．已知集合[][],14,9A t t t t =+⋃++，0A ∉，存在正数λ，使得对任意a A ∈，都有A a λ∈，则t 的值是____________答案：1或3-解析：根据t 所处的不同范围，得到[],1a t t ∈+和[]4,9a t t ∈++时，aλ所处的范围；再利用集合A 的上下限，得到λ与t 的等量关系，从而构造出方程，求得t 的值. 详解：0A ∉，则只需考虑下列三种情况：①当0t >时，[][],14,9a t t t t ∈+++ 11111,,941a t t t t ⎡⎤⎡⎤∴∈⎢⎥⎢⎥+++⎣⎦⎣⎦又0λ> ,,941a t t t t λλλλλ⎡⎤⎡⎤⇒∈⎢⎥⎢⎥+++⎣⎦⎣⎦A a λ∈ 914t t t t λλ⎧≥⎪⎪+∴⎨⎪≤+⎪+⎩且419t t t t λλ⎧≥+⎪⎪+⎨⎪≤+⎪⎩ 可得：()()()()()()991414t t t t t t t t λλ⎧+≤≤+⎪⎨++≤≤++⎪⎩ ()()()914t t t t λ∴=+=++ 1t ⇒=②当90t +<即9t <-时，与①构造方程相同，即1t =，不合题意，舍去③当1040t t +<⎧⎨+>⎩即41t -<<-时 可得：11t t t t λλ⎧≥⎪⎪+⎨⎪≤+⎪⎩且4994t t t t λλ⎧≥+⎪⎪+⎨⎪≤+⎪+⎩()()()149t t t t λ∴=+=++ 3t ⇒=-综上所述：1t =或3-点睛：本题考查利用集合与元素的关系求解参数的取值问题，关键在于能够通过t 的不同取值范围，得到a 与a λ所处的范围，从而能够利用集合的上下限得到关于λ的等量关系，从而构造出关于t 的方程；难点在于能够准确地对t 的范围进行分类，对于学生的分析和归纳能力有较高的要求，属于难题.3．如果集合A ＝x|ax 2－2x －1＝0}只有一个元素则a 的值是_____________答案：0或－1解析：当0a =时，12A ⎧⎫=-⎨⎬⎩⎭符合题意；当0a ≠时，一元二次方程判别式440,1a a ∆=+==-.4．集合{}28160A x kx x =-+=∣，若集合A 中只有一个元素，则由实数k 的值组成的集合为________.答案：{}0,1解析：分0k =和0k ≠两种情况，分别讨论集合A ，进而可求出答案.详解：当0k =时，方程28160kx x -+=可化为8160x -+=，解得2x =，满足题意；当0k ≠时，要使集合{}28160A xkx x =-+=∣中只有一个元素， 则方程28160kx x -+=有两个相等的实数根，所以64640k ∆=-=，解得1k =，此时集合{4}A =，满足题意.综上所述，0k =或1k =，即实数k 的值组成的集合为{}0,1.故答案为：{}0,1.点睛：本题考查单元素的集合，注意讨论方程28160kx x -+=中k 是否为0，属于基础题.5．已知集合{}2,1,0,1P =--，集合{},Q y y x x P ==∈，则Q =______．答案：{}2,1,0解析：将2,1,0,1x =--分别代入y x =中，得到y 的值，即可求得集合Q ，得到答案． 详解：由题意，将2x =-，1-，0，1分别代入y x =中，得到2,1,0y =，所以{}2,1,0Q =．故答案为{}2,1,0．点睛：本题主要考查了集合的表示方法及应用，着重考查了推理与运算能力，属于基础题．四、解答题1．试用恰当的方法表示下列集合.（1）使函数12y x =-有意义的x 的集合； （2）不大于12的非负偶数；（3）满足不等式*(3)2x x -≤∈N 的解集；（4）由大于10小于20的所有整数组成的集合.答案：（1）{|2}x x ∈≠R ；（2）{0,2,4,6,8,10,12}或{|2,x x n n =∈N 且7}n <；（3）{1,2,3,4,5}或{}*|5,x x x ≤∈N ；（4）{|1020}x x ∈<<Z 或{11,12,13,14,15,16,17,18,19}. 解析：（1）用描述法表示；（2）、（3）、（4）既可用描述法也可用列举法.详解：（1）要使函数12y x =-有意义，必须使分母20x -≠，即2x ≠. 因此所求集合用描述法可表示为{|2}x x ∈≠R .（2）∵不大于12是小于或等于12，非负是大于或等于0，∴不大于12的非负偶数集用列举法表示为{0,2,4,6,8,10,12}.用描述法表示为{|2,x x n n =∈N 且7}n <.（3）满足()*32x x -≤∈N 的解是1，2，3，4，5. 用列举法表示为{1,2,3,4,5}，用描述法表示为{}*|5,x x x ≤∈N . （4）设大于10小于20的整数为x ，则x 满足条件x ∈Z 且1020x <<.故用描述法可表示为{|1020}x x ∈<<Z ，用列举法表示为{11,12,13,14,15,16,17,18,19}.点睛：本题考查集合的表示方法，属于基础题.2．设2y x ax b =-+，{}|0A x y x =-=，{|0}B x y ax =-=，若{3,1}A =-，试用列举法表示集合B ．答案：{33B =---+解析：将2y x ax b =-+带入集合A 的方程化简整理，由{3,1}A =-利用韦达定理求出参数,a b ，再利用一元二次方程的解法求解集合B.详解：将2y x ax b =-+代入集合A 中的方程并整理得2(1)0x a x b -++=.因为{3,1}A =-，所以方程2(1)0x a x b -++=的两根为-3，1，由韦达定理得311,31,a b -+=+⎧⎨-⨯=⎩ 解得3,3,a b =-⎧⎨=-⎩所以233y x x =+-.将233y x x =+-，3a =-代入集合B 中的方程并整理得2630x x +-=，解得3x =--或3x =-+{33B =---+.点睛：本题考查了集合的表示方法，准确的利用韦达定理求参数是解题的关键，属于一般难度的题.3．已知集合A 的元素全为实数，且满足：若a A ∈，则11a A a+∈-．若2a =，求出A 中其他所有元素．答案：113,,23-- 解析：根据定义依次计算即可得答案.详解：解：因为若a A ∈，则11a A a +∈-， 所以当2a =时，11a a +=-12312A +=-∈-； 当3a =-时，11a a +=-131132A -=-∈+， 当12a =-时，11a a +=-11121312A -=∈+， 当13a =时，11a a +=-1132113A +=∈-， 综上A 中其他所有元素为：113,,23--. 点睛：本题考查集合的元素的求解，是基础题.。

高中数学必修一练习题（一）集合（详细答案）班号姓名集合的含义与表示1．下面的结论正确的是()A．a∈Q，则a∈NC．某2－1＝0的解集是{－1，1}2．下列说法正确的是()A．某班中年龄较小的同学能够形成一个集合B．由1，2，3和9，1，4组成的集合不相等C．不超过20的非负数组成一个集合D．方程某2－4＝0和方程|某－1|＝1的解构成了一个四元集3．用列举法表示{(某，y)|某∈N＋，y∈N＋，某＋y＝4}应为()A．{(1，3)，(3，1)}B．{(2，2)}D．{(4，0)，(0，4)}B．a∈Z，则a∈ND．以上结论均不正确C．{(1，3)，(3，1)，(2，2)}4．下列命题：(1)方程某－2＋|y＋2|＝0的解集为{2，－2}；(2)集合{y|y＝某2－1，某∈R}与{y|y＝某－1，某∈R}的公共元素所组成的集合是{0，1}；(3)集合{某|某－1<0}与集合{某|某>a，a∈R}没有公共元素．其中正确的个数为()A．0B．1C．2D．35．对于集合A＝{2，4，6，8}，若a∈A，则8－a∈A，则a的取值构成的集合是________．6．定义集合A某B＝{某|某＝a－b，a∈A，b∈B}，若A＝{1，2}，B＝{0，2}，则A某B中所有元素之和为________．7．若集合A＝{－1，2}，集合B＝{某|某2＋a某＋b＝0}，且A＝B，则求实数a，b的值．8．已知集合A＝{a－3，2a－1，a2＋1}，a∈R.(1)若－3∈A，求实数a的值；(2)当a为何值时，集合A的表示不正确．集合间的基本关系1．下列关系中正确的个数为()①0∈{0}；②{0}；③{(0，1)}{(0，1)}；④{(a，b)}＝{(b，a)}．A．1 B．2C．3D．42．已知集合A＝{某|－1BB．ABC．BAD．AB3．已知{1，2}M{1，2，3，4}，则符合条件的集合M的个数是()A．3B．4C．6D．8M，则a的取值为()4．集合M＝{1，2，a，a2－3a－1}，N＝{－1，3}，若3∈M且NA．－1 B．4C．－1或－4D．－4或15．集合A中有m个元素，若在A中增加一个元素，则它的子集增加的个数是__________．6．已知M＝{y|y＝某2－2某－1，某∈R}，N＝{某|－2≤某≤4}，则集合M与N之间的关系是________．7．若集合M＝{某|某2＋某－6＝0}，N＝{某|(某－2)(某－a)＝0}，且NM，求实数a的值．8．设集合A＝{某|a－2＜某＜a＋2}，B＝{某|－2＜某＜3}，(1)若A B，求实数a的取值范围；(2)是否存在实数a使BA并集与交集1．A∩B＝A，B∪C＝C，则A，C之间的关系必有()A．ACB．CAC．A＝CD．以上都不对2．A＝{0，2，a}，B＝{1，a2}，A∪B＝{0，1，2，4，16}，则a的值为()A．0B．1C．2D．43．已知全集U＝R，集合M＝{某|－2≤某－1≤2}和N＝{某|某＝2k－1，k∈N某}的关系的韦恩(Venn)图如图所示，则阴影部分所示的集合的元素共有()A．2个B．3个C．1个D．无穷多个4．设集合M＝{某|－3≤某＜7}，N＝{某|2某＋k≤0}，若M∩N≠，则k 的取值范围是()A．k≤3B．k≥－3C．k＞6D．k≤65．已知集合M＝{某|－35}，则M∪N＝________，M∩N＝________．6．已知集合A＝{(某，y)|y＝某2，某∈R}，B＝{(某，y)|y＝某，某∈R}，则A∩B中的元素个数为___．7．已知集合A＝{某|某2＋p某＋q＝0}，B＝{某|某2－p某－2q＝0}，且A∩B＝{－1}，求A∪B.8．已知A＝{某|某3}，B＝{某|4某＋m<0，m∈R}，当A∩B＝B时，求m的取值范围．集合的补集运算1．已知全集U＝{1，2，3，4，5，6，7，8}，M＝{1，3，5，7}，N ＝{5，6，7}，则U(M∪N)＝()A．{5，7}B．{2，4}C．{2，4，8}D．{1，3，5，6，7}2．已知全集U＝{2，3，5}，集合A＝{2，|a－5|}，若UA＝{3}，则a的值为()A．0B．10C．0或10D．0或－103．已知全集U＝R，集合A＝{某|－2≤某≤3}，B＝{某|某＜－1或某>4}，那么集合A∩(UB)等于()A．{某|－2≤某＜4}B．{某|某≤3或某≥4}C．{某|－2≤某＜－1}D．{某|－1≤某≤3}4．如图所示，U是全集，A，B是U的子集，则阴影部分所表示的合是()A．A∩BB．A∪BC．B∩(UA)D．A∩(UB)5．已知全集S＝R，A＝{某|某≤1}，B＝{某|0≤某≤5}，则(SA)∩B＝________．6．定义集合A某B＝{某|某∈A，且某B}，若A＝{1，2，3，4，5}，B＝{2，4，5}，则A某B的子集的个数是________．7．已知全集U＝R，A＝{某|－4≤某≤2}，B＝{某|－12}，(1)求A∩B；(2)求(UB)∪P；(3)求(A∩B)∩(UP)．8．已知集合A＝{某|2a－2集参考答案集合的含义与表示1．选C对于A，a属于有理数，则a属于自然数，显然是错误的，对于B，a属于整数，则a属于自然数当然也是错的，对于C的解集用列举法可用它来表示．故C正确．2．选CA项中元素不确定；B项中两个集合元素相同，因集合中的元素具有无序性，所以两个集合相等；D项中两个方程的解分别是±2，0，2，由互异性知，可构成一个三元集．3．选C某＝1时，y＝3；某＝2时，y＝2；某＝3时，y＝1.某＝2，某－2＝0，4．选A(1)故解集为{(2，－2)}，而不是{2，－2}；y＝－2.|y＋2|＝0(2)集合{y|y＝某2－1，某∈R}表示使y＝某2－1有意义的因变量y的范围，而y＝某2－1≥－1，故{y|y＝某2－1，某∈R}＝{y|y≥－1}．同理集合{y|y＝某－1，某∈R}＝R.结合数轴(图1)知，两个集合的公共元素所组成的集合为{y|y≥－1}；(3)集合{某|某－1<0}表示不等式某－1<0的解集，即{某|某<1}．而{某|某>a，a∈R}就是某>a的解集．结合图2，当a≥1时两个集合没有公共元素；当a＜1时，两个集合有公共元素，形成的集合为{某|a5．解析：当a＝2时，8－a＝6∈A；a＝4时，8－a＝4∈A；a＝6时，8－a＝2∈A；a＝8时，8－a＝0A.∴所求集合为{2，4，6}．答案：{2，4，6}6．解析：A某B＝{1，－1，2，0}，∴A某B中所有元素之和为1－1＋2＋0＝2.答案：27．解：由题意知－1，2是方程某2＋a某＋b＝0的两个根，1－a＋b＝0，由根与系数的关系可知有故有a＝－1，b＝－2.4＋2a＋b＝0，当a－3＝－3时，a＝0，集合A＝{－3，－1，1}，满足题意；当2a－1＝－3时，a＝－1，集合A＝{－4，－3，2}，满足题意；当a2＋1＝－3时，a无解．综上所述，a＝0或a＝－1.(2)若元素不互异，则集合A的表示不正确若a－3＝2a－1，则a＝－2；若a－3＝a2＋1，则方程无解；若2a－1＝a2＋1，则方程无解．综上所述，a＝－2.集合间的基本关系1．选C①、②、③均正确；④不正确．a≠b时，(a，b)与(b，a)是不同的元素．2．C3．选A符合条件的集合M有{1，2}，{1，2，3}，{1，2，4}共3个．4．选B(1)若a＝3，则a2－3a－1＝－1，即M＝{1，2，3，－1}，显然NM，不合题意．(2)若a2－3a－1＝3，即a＝4或a＝－1(舍去)，当a＝4时，M＝{1，2，4，3}，满足要求．5．解析：由2m＋1－2m＝2·2m－2m＝2m.答案：2m6．解析：∵y＝(某－1)2－2≥－2，∴M＝{y|y≥－2}，∴NM.答案：NM7．解：由某2＋某－6＝0，得某＝2或某＝－3.因此，M＝{2，－3}．若a＝2，则N＝{2}，此时NM；若a＝－3，则N＝{2，－3}，此时N＝M；若a≠2且a≠－3，则N＝{2，a}，此时N不是M的子集，故所求实数a的值为2或－3.a－2>－2，a－2≥－2，8．解：(1)借助数轴可得，a应满足的条件为或解得0≤a≤1.a＋2≤3，a＋2<3，a－2≤－2，(2)同理可得a应满足的条件为得a无解，所以不存在实数a使BA.a＋2≥3，并集与交集1．选AA∩B＝AAB，B∪C＝CBC，∴AC.a＝4，2．选D∵A＝{0，2，a}，B＝{1，a2}，A∪B＝{0，1，2，4，16}，则∴a＝4.a＝16.23．选AM＝{某|－1≤某≤3}，N＝{某|某＝2k－1，k∈N某}，∴M∩N ＝{1，3}．kk4．选D因为N＝{某|2某＋k≤0}＝{某|某≤－}，且M∩N≠，所以－≥－3k≤6.225．解析：借助数轴可知：M∪N＝{某|某>－5}，M∩N＝{某|－3－5}{某|－3y＝某2，某＝0，某＝1，6．解析：由得或答案：2y＝某，y＝0y＝1.7．解：因为A∩B＝{－1}，所以－1∈A且－1∈B，将某＝－1分别代入两个方程，得1－p＋q＝0p＝3，解得.所以A＝{某|某2＋3某＋2＝0}＝{－1，－2}，1＋p－2q＝0q＝2B＝{某|某2－3某－4＝0}＝{－1，4}，所以A∪B＝{－1，－2，4}．m8.解：由题知，B＝{某|某4m所以由数轴(如图)可得－≤－2，所以m≥8，即m的取值范围是m≥8. 4集合的补集运算1．选CM∪N＝{1，3，5，6，7}．∴U(M∪N)＝{2，4，8}．2．选C由UA＝{3}，知3A，3∈U.∴|a－5|＝5，∴a＝0或a＝10.3．选D由题意可得，UB＝{某|－1≤某≤4}，A＝{某|－2≤某≤3}，所以A∩(UB)＝{某|－1≤某≤3}．端点处的取舍易出错．4．选C阴影部分表示集合B与集合A的补集的交集．因此，阴影部分所表示的集合为B∩(UA)．5．解析：由已知可得SA＝{某|某>1}，∴(SA)∩B＝{某|某>1}∩{某|0≤某≤5}＝{某|1答案：{某|16．解析：由题意知A某B＝{1，3}．则A某B的子集有22＝4个．答案：47．解：借助数轴，如图．(1)A∩B＝{某|－15(2)∵UB＝{某|某≤－1或某>3}，∴(UB)∪P＝{某|某≤0或某≥}．255(3)UP＝{某|0228．解：RB＝{某|某≤1或某≥2}≠，∵ARB，∴分A＝和A≠两种情况讨论．(1)若A＝，此时有2a－2≥a，∴a≥2.2a－2＜a2a－2综上所述，a≤1或a≥2.。

1.1 集合的概念一、单选题1．设集合{1,2,3}A =，{2,3,4}B =，{|}M x x ab a A b B ==∈∈,,，则M 中的元素个数为（ ）A ．5B ．6C ．7D ．8答案：C解析：根题意求出集合M 即可得出.详解：{1,2,3}A =，{2,3,4}B =，{}{|}2,3,4,6,8,9,12M x x ab a A b B ∴==∈∈=,,， 所以M 中的元素个数为7.故选：C.2．下列语句能构成集合的是A ．大于2且小于8的实数全体B ．某班中性格开朗的男生全体C ．所有接近1的数的全体D ．某校高个子女生全体答案：A解析：根据集合元素的确定性进行判断.详解：选项A:符合集合元素的确定性，可以构成集合；选项B:确定不了什么叫性格开朗，故不能构成集合；选项C:确定不了接近1的数的标准是什么，故不能构成集合；选项D:不符合集合的确定性，因为不知道高个子女生的标准是什么，故不能构成集合，因此本题选A.点睛：本题考查了集合元素的确定性，准确理解集合元素的确定性是解题的关键.3．下列集合符号运用不正确的是( )A ．2Z ∈B ．}{}{1,2,31,2⊆C ．{}12⋂∅=∅，D ．N R R ⋃=答案：B解析：根据集合知识,逐项分析,即可求得答案.详解：对于A,由2Z ∈,故A 正确;对于B,因为}{}{1,21,2,3⊆,故B 错误;对于C,因为{}12⋂∅=∅，,故C 正确; 对于D,因为N R R ⋃=,故D 正确.故选:B.点睛：解题关键是掌握集合的基础知识,考查了分析能力,属于基础题.4．下列说法正确的有（ ）①NBA 联盟中所有优秀的篮球运动员可以构成集合；②*0N ∈；③集合{}2| 1 y y x =-与集合(){}2,| 1 x y y x =-是同一个集合；④空集是任何集合的真子集.A ．0个B ．1个C ．2个D ．3个答案：A解析：根据集合的定义，元素与集合的关系，列举法和描述法的定义以及空集的性质分别判断命题的真假．详解：对于①，优秀的篮球队员概念不明确，不能构成集合，错误；对于②，元素与集合的关系应为属于或不属于，即0∉N *，错误；对于③，集合{}2|1{|1}y y x y y =-=≥-是数集，集合（x ，y ）|y=x 2-1}表示的是满足等式的所有点，不是同一个集合，错误；对于④，空集是任何非空集合的真子集，错误；故选A ．点睛：本题考查集合的确定性，元素与集合的关系，列举法和描述法表示集合以及空集的有关性质，属于基础题．5．集合{|13}A x Z x =∈-<<的元素个数是（ ）A ．1B ．2C ．3D ．4答案：C解析：根据集合A 的代表元素及需满足的条件，用列举法表示出集合A ，即可得到结果. 详解：解：{}{|13}0,1,2A x Z x =∈-<<=所以集合A 中含有3个元素故选：C点睛：本题考查列举法表示集合及集合元素的个数问题，属于基础题.6．下列关系式中，正确的关系式有几个(1）2∈Q (2）0∉N (3）1，2} (4)φ=0} A ．0B ．1C ．2D ．3 答案：B详解：(1)因为2为无理数，所以错；（2）O 属于N ，错；（3）正确；（4）{}0φ⊆,错.7．若集合A=｛-1，1｝，B=｛0，2｝，则集合｛z ︱z=x+y,x∈A,y∈B｝中的元素的个数为（ ）A ．5B ．4C ．3D ．2 答案：C详解：，，或是，，根据集合元素的互异性，集合为，共含有3个元素，故选C. 考点：元素与集合8．已知集合{A =第二象限角}，{B =钝角}，{C =小于180°的角}，则A ，B ，C 关系正确的是（ ）A ．B AC =⋂B ．AC C ．C C =B ∪D ．A B C ==答案：C解析：由集合A ，B ，C ，求出B 与C 的并集，判断A 与C 的包含关系，以及A ，B ，C 三者之间的关系即可．详解：由题意得B A C ⋂，故A 错误； A 与C 互不包含，故B 错误；由{B =钝角}{小于180°的角}，所以C C =B ∪，故C 正确 .由以上分析可知D 错误．故选：C ．9．下列说法中正确的是（ ）A ．联合国所有常任理事国(共5个）组成一个集合B ．宜丰二中年龄较小的学生组成一个集合C ．{}1,2,3与{}2,1,3是不同的集合D ．由1,0,5,1,2,5组成的集合有六个元素答案：A解析：根据集合中的元素的性质逐一判断可得选项.详解：年龄较小不确定，所以B 选项错误；{1,2,3}与{2,1,3}是相同的集合，故C 错误；由1,0,5,1,2,5组成的集合有4个元素，故D 错误；故选：A.点睛：本题考查集合中的元素的性质和判断两个集合是否是同一集合，属于基础题.二、多选题1．下列与集合1(,)|30x y M x y x y ⎧+=⎧⎫=⎨⎨⎬--=⎩⎭⎩表示同一个集合的有（ ） A ．{(2,1)}-B ．{2,1}-C ．{(,)|2,1}x y x y ==-D ．{2,1}x y ==- E.{(1,2)}-答案：AC 解析：解方程组可得集合中的元素为有序数对(2,1)-，根据集合的表示方法可得答案. 详解：由1,30x y x y +=⎧⎨--=⎩得2,1,x y =⎧⎨=-⎩即(){}2,1M =-， 所以根据集合的表示方法知A ，C 与集合M 表示的是同一个集合，故选：AC.点睛：本题考查同一集合问题，考查集合的表示方法，属于基础题.2．（多选题）设集合{}1,A x x a x R =-<∈，{}15,B x x x R =<<∈，则下列选项中，满足A B =∅的实数a 的取值范围的有（ ）A ．[]0,6B ．(][),24,-∞+∞C ．(][),06,-∞+∞ D ．[)8,+∞答案：CD 解析：先解集合A 得{}11A x a x a =-<<+，再根据题意求解即可.详解： 由题得{}11A x a x a =-<<+，{}15,B x x x R =<<∈，又因为A B =∅，所以11a +≤ 或15a -≥，即0a ≤或6a ≥.所以满足题意的有选项C ，D.故选：CD.点睛：本题考查绝对值不等式的解法，集合的交集运算，是中档题.3．下列是集合{(,)|1,,}M x y x y x y =+≤∈∈N N 中元素的有（） A ．(0,0) B ．(0,1) C ．(1,0) D ．(2,1)-E.(1,2)-答案：ABC解析：用列举法表示集合,进而判断选项即可详解：∵{(,)|1,,}M x y x y x y =+≤∈∈N N ,∴00x y =⎧⎨=⎩或01x y =⎧⎨=⎩或10x y =⎧⎨=⎩,∴{(0,0),(0,1),(1,0)}M =故选ABC点睛：本题考查列举法表示集合,考查点集,考查元素与集合的关系4．下面表示同一个集合的是（ ）A ．{}2|10,,P x x x R Q =+=∈=∅B ．{2,5},{5,2}P Q ==C ．{(2,5)},{(5,2)}P Q ==D ．{|21,},{|21,}P x x m m Z Q x x m m Z ==+∈==-∈答案：ABD解析：对选项中的集合元素逐一分析判断即可.详解：A 选项中，集合P 中方程210x +=无实数根，故P Q ==∅，表示同一个集合；B 选项中，集合P 中有两个元素2，5，集合Q 中页有两个元素2，5，表示同一个集合；C 选项中，集合P 中有一个元素是点(2,5)，集合 Q 中有一个元素是点(5,2)，元素不同，不是同一集合；D 选项中，集合{|21,}P x x m m Z ==+∈表示所有奇数构成的集合，集合{|21,}Q x x m m Z ==-∈也表示所有奇数构成的集合，表示同一个集合.故选：ABD.5．已知非空集合M 满足：①{2,1,21,,3,4}M ⊆--，②若x M ∈，则2x M ∈，则满足上述要求的集合M 有（ ）A ．1,1,{}2,4-B ．1,2,{}2,4-C ．{1,1}-D ．{1}答案：CD解析：由集合M 的元素所满足的两个性质，找出集合M 的元素，从而确定集合M 有哪些可能．详解：由题意可知3M ∉且4M ∉，而-2或2与4同时出现，所以2M -∉且2M ∉，所以满足条件的非空集合M 有{1,1}-，{1}.故选：CD ．点睛：本题考查满足条件的集合的求法，考查元素与集合的关系，是基础题．三、填空题1．含有三个实数的集合既可表示成,,1b a a ⎧⎫⎨⎬⎩⎭又可表示成{}2,,0a a b +，20142015a b +=______.答案：1解析：根据两个集合的相等关系，可求得,a b 的值，即可得解.详解： 由题意可知，两个集合相等，{}2,,1,,0b a a a b a ⎧⎫=+⎨⎬⎩⎭，由0a ≠所以只能是0ba=，即0b =，所以{}{}2,0,1,,0a a a =， 由集合互异性可知1a ≠，则21a =，解得1a =-，符合题意，所以20142015101a b +=+=，故答案为：1.本题考查了集合相等的应用，由集合互异性和相等求参数，属于基础题.2．已知集合A 中元素x 满足2x ＋a>0，a∈R.若1∉A ，2∈A，则实数a 的取值范围为________．答案：42a -<≤-解析：根据已知条件列不等式组，解不等式组求得a 的取值范围.详解：因为1∉A ，2∈A，所以210220a a ⨯+≤⎧⎨⨯+>⎩， 即42a -<≤-.故答案为：42a -<≤-3．用描述法表示所有偶数组成的集合__________．答案：{}2,x x n n Z =∈解析：利用描述法的定义求解即可详解： 解：所有偶数组成的集合为{}2,x x n n Z =∈， 故答案为：{}2,x x n n Z =∈4．设集合{}22,,A x x =，若1A ∈，则x 的值为___________.答案：1-解析：根据集合中元素的互异性可知，1x ≠，再根据1A ∈，可得1x =-.详解：根据集合中元素的互异性可知，2x x ≠，所以1x ≠且0x ≠，因为1A ∈，所以21x =，解得1x =-或1x =（舍），故答案为：1-点睛：本题考查了集合中元素的互异性，考查了元素与集合的关系，属于基础题.5．用描述法表示被4除余3的正整数集合：______．答案：x|x ＝4n+3，n∈N}解析：设该数为x ，则该数x 满足x ＝4n+3，n∈N；再写成集合的形式.设该数为x ，则该数x 满足x ＝4n+3，n∈N；∴所求的正整数集合为x|x ＝4n+3，n∈N}．故答案为：x|x ＝4n+3，n∈N}．点睛：本题主要考查集合的表示方法，属于基础题.四、解答题1．用适当的方法表示下列集合：（1）B=（x ，y ）|x+y=4，x∈N*，y∈N*}；（2）不等式3x-8≥7-2x 的解集；答案：（1）列举法：{}(1,3),(2,2),(3,1)B =；（2）描述法：{}|3x x ≥.解析：（1）根据代表元素的特征将元素一一列举即可.（2）根据描述法表示集合即可求解.详解：（1）B=（x ，y ）|x+y=4，x∈N*，y∈N*}{}(1,3),(2,2),(3,1)=.（2）3x-8≥7-2x 解得3x ≥，所以不等式的解集为{}|3x x ≥.2．已知集合A=x|x=m 2-n 2，m∈Z，n∈Z}．求证：（1）3∈A；（2）偶数4k-2（k∈Z）不属于A ．答案：（1）见解析；（2）见解析.详解：试题分析：（1）由3=22-12即可证得；（2）设4k-2∈A，则存在m ，n∈Z，使4k-2=m 2-n 2=（m+n ）（m-n ）成立，分当m ，n 同奇或同偶时和当m ，n 一奇，一偶时两种情况进行否定即可.试题解析：（1）∵3=22-12，3∈A；（2）设4k-2∈A，则存在m ，n∈Z，使4k-2=m 2-n 2=（m+n ）（m-n ）成立，1、当m ，n 同奇或同偶时，m-n ，m+n 均为偶数，∴（m-n ）（m+n ）为4的倍数，与4k-2不是4的倍数矛盾．2、当m ，n 一奇，一偶时，m-n ，m+n 均为奇数，∴（m-n ）（m+n ）为奇数，与4k-2是偶数矛盾．综上4k-2不属于A ．3．由实数组成的集合A 具有如下性质：若a A ∈，b A ∈且a b <，那么1a A b+∈.（1）若集合A 恰有两个元素，且有一个元素为43，求集合A ；（2）是否存在一个含有元素0的三元素集合A ；若存在请求出集合，若不存在，请说明理由.答案：（1）4{4,}3A =或44{,}39A =或4{3A =；（2）存在，A =. 解析：（1）根据题意设集合4{,}3A x =，然后分类讨论x 与43的大小，根据集合的性质解出x ，即可得解；（2）假设存在一个含有元素0的三元素集合A {0,,}a b =，根据集合中元素的性质可知，0a <，0b <，进一步可知，1A ∈，不妨设集合{,0,1},(0A x x =>且1)x ≠，再根据集合中元素的性质可求得结果.详解：（1）集合A 恰有两个元素且43A ∈.不妨设集合4{,}3A x =， 当43x <时，由集合A 的性质可知，314x A +∈，则314x x +=或34143x +=， 解得4x =(舍)或49x =，所以集合44{,}39A = 当43x >时，由集合A 的性质可知，413A x +∈，则413x x +=或44133x +=，解得36x =或36x =(舍)或4x =所以集合4{,4}3A =或43{,}36A +=综上所述：4{4,}3A =或44{,}39A =或4{3A =. （2）假设存在一个含有元素0的三元素集合A {0,,}a b =，即0A ∈，当0a >时，则10a +无意义，当0b >时，则10b +无意义， 所以0a <，0b <，并且01A a +∈，01A b +∈，即1A ∈， 不妨设集合{,0,1},(0A x x =>且1)x ≠，当1x >时，由题意可知，11A x+∈，若11x x +=，即210x x --=，解得x =或x =(舍)，此时集合A =； 若111x +=，则10x =不成立； 若110x+=，即1x =-(舍)， 当01x <<时，由题意可知，1x A +∈，若10x +=，则1x =-（舍），若11x +=，则0x =（舍），若1x x +=，则10=不成立，综上所述，集合A 是存在的，A =. 点睛：本题考查了元素与集合的关系，考查了分类讨论思想，属于中档题.。

1.已知集合N={1，2，3，4，…，n}，A为非空集合，且A N，定义A的“交替和”如下：将集合A中的元素按由大到小排列，然后从最大的数开始，交替地减、加后续的数，直到最后一个数，并规定单元素集合的交替和为该元素，例如集合{1，2，5，7，8}的交替和为8-7+5-2+1=5，集合{4}的交替和为4，当n=2时，集合N={1，2}的非空子集为{1}，{2}，{1，2}，记三个集合的交替和的总和为S2=1+2+（2-1）=4，则n=3时，集合N={1，2，3}的所有非空子集的交替和的总和S3=（）；集合N={1，2，3，4，…，n}的所有非空子集的交替和的总和S n=（）。

2.已知集合A={1，2，3，4，5}，B={（x，y）|x∈A，y∈A，x-y∈A}，则B中所含元素的个数为[ ] A．3B．6C．8D．103.定义集合运算：A⊙B={z|z=xy（x+y），x∈A，y∈B}，设集合A={0，1}，B={2，3}，则集合A⊙B的所有元素之和为[ ]A.0B.6C.12D.184.对于正整数a，b，存在唯一一对整数q和r，使得a=bq+r，0≤r＜b。

特别地，当r=0时，称b能整除a，记作b|a，已知A={1，2，3，…，23}，(1)存在q∈A，使得2011=91q+r（0≤r＜91），试求q，r的值；(2)求证：不存在这样的函数f：A→{1，2，3}，使得对任意的整数x，y∈A，若|x-y|∈{1，2，3}，则f（x）≠f（y）；(3)若B A，card（B）=12（card（B）指集合B中的元素的个数），且存在a，b∈B，b＜a，b|a，则称B为“和谐集”。

求最大的m∈A，使含m的集合A的有12个元素的任意子集为“和谐集”，并说明理由。

5.已知集合，且2∈A，3A，则实数a的取值范围是（）。

6.如图，与复平面中的阴影部分（含边界）对应的复数集合是[ ]A.B.C.D.7.设P、Q为两个非空实数集合，定义集合P+Q={a+b|a∈P，b∈Q}，若P={0，2，5}，Q={1，2，6}，则P+Q中元素的个数是[ ]A．9B．8C．7D．6。

数学高中集合大题练习题及讲解集合是数学中描述对象的集合体，是高中数学中的重要组成部分。

以下是一些集合相关的大题练习题及讲解：### 练习题1：集合的运算设集合A = {1, 2, 3}，集合B = {2, 3, 4}，求以下集合运算的结果：1. A ∪ B（A并B）2. A ∩ B（A交B）3. A - B（A减B）讲解：1. A ∪ B表示A和B中所有元素的集合，不重复地列出，即{1, 2, 3, 4}。

2. A ∩ B表示A和B中共有的元素，即{2, 3}。

3. A - B表示A中有而B中没有的元素，即{1}。

### 练习题2：子集与幂集设集合S = {a, b, c}，求：1. S的所有子集。

2. S的幂集。

讲解：1. S的所有子集包括空集以及S中所有元素的所有组合，即：∅，{a}，{b}，{c}，{a, b}，{a, c}，{b, c}，{a, b, c}。

2. S的幂集是S所有子集的集合，即：{∅, {a}, {b}, {c}, {a, b}, {a, c}, {b, c}, {a, b, c}}。

### 练习题3：集合的包含关系设集合A = {1, 2, 3}，集合B = {2, 3, 4, 5}，判断A是否是B的子集，并说明理由。

讲解：A不是B的子集，因为A中的元素1不在B中。

子集的定义是如果集合A的所有元素都在集合B中，那么A是B的子集。

### 练习题4：集合的相等集合A = {1, 2, 3}和集合C = {3, 2, 1}是否相等？为什么？讲解：集合A和C相等。

根据集合的性质，集合的元素是无序的，即元素的排列顺序不影响集合的相等性。

### 练习题5：描述法和列举法用描述法表示集合{x | x是小于10的正整数}，并用列举法表示集合{x | x是偶数}。

讲解：1. 描述法表示为{x | x ∈ N, 1 ≤ x < 10}，其中N表示自然数集合。

2. 列举法表示为{2, 4, 6, 8, 10}。