Computer Graphics Group

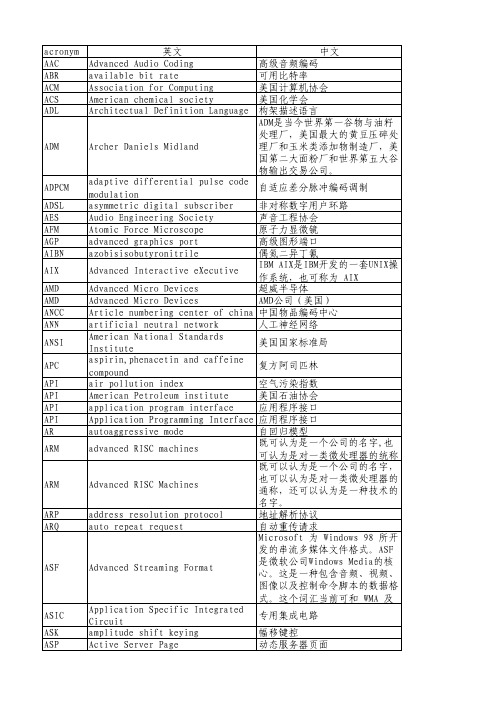
acronym英文中文AAC Advanced Audio Coding高级音频编码ABR available bit rate可用比特率ACM Association for Computing美国计算机协会ACS American chemical society美国化学会ADL Architectual Definition Language构架描述语言ADM Archer Daniels Midland ADM是当今世界第一谷物与油籽处理厂，美国最大的黄豆压碎处理厂和玉米类添加物制造厂，美国第二大面粉厂和世界第五大谷物输出交易公司。

ADPCM adaptive differential pulse codemodulation自适应差分脉冲编码调制ADSL asymmetric digital subscriber非对称数字用户环路AES Audio Engineering Society声音工程协会AFM Atomic Force Microscope原子力显微镜AGP advanced graphics port高级图形端口AIBN azobisisobutyronitrile偶氮二异丁氰AIX Advanced Interactive eXecutive IBM AIX是IBM开发的一套UNIX操作系统，也可称为 AIXAMD Advanced Micro Devices超威半导体AMD Advanced Micro Devices AMD公司（美国）ANCC Article numbering center of china中国物品编码中心ANN artificial neutral network人工神经网络ANSI American National StandardsInstitute美国国家标准局APC aspirin,phenacetin and caffeinecompound复方阿司匹林API air pollution index空气污染指数API American Petroleum institute美国石油协会API application program interface应用程序接口API Application Programming Interface应用程序接口AR autoaggressive mode自回归模型ARM advanced RISC machines 既可认为是一个公司的名字,也可认为是对一类微处理器的统称ARM Advanced RISC Machines 既可以认为是一个公司的名字，也可以认为是对一类微处理器的通称，还可以认为是一种技术的名字。

Set Up Your MXI -Express x4 System This document explains what you will need to set up variousMXI-Express x4 hardware configurations.The products covered by this guide are the NI PCIe-8371/8372 and NI PXIe-8370/8374. For the remainder of this manual the termMXI-Express x4 product refers to any of these products.Additional compatible products are included in subsequent tables, but are not covered in this manual.TerminologyThe following terms may be used throughout this document:•Host PC —A host computer with at least one PCI Express x4 or wider slot available.Note Using a PCI Express slot wider than x4 may result in negotiation down to x1 width, and therefore limiting bandwidth. This is uncommon in newer PCs.•Expansion Chassis —An expansion chassis of any of the following types:–CompactPCI Express chassis –PXI Express chassis –NI HDD RAID •MXI-Express x4 copper cable —Standard PCI Express specification compliant cable with x4 PCIe connectors.Note Refer to the Cabling section for details. Most MXI-Express kits include the cable, but not all.•Host Board —The MXI-Express x4 board of a cabled pair of boards that is closer to the CPU.™Set Up Your MXI-Express x4 System •Target Board —The MXI-Express x4 board of a cabled pair of boards that is farther from the CPU.•Cabled Pair —Two MXI-Express x4 boards that are connected with a single cable.Connecting a PC to an Expansion ChassisUsing a MXI-Express x4 Copper CableRefer to the Terminology section for more detail on the items in this list.Equipment Needed❑Host PC❑Expansion chassis❑MXI-Express x4 copper cable❑ A MXI-Express x4 host board and target board that is appropriate for the host system slot and target chassis. Refer to Table 1 for moreinformation.Note For full PXI or PXI Express functionality, refer to the Software Installation andConfiguration section for more information.Table 1. MXI-Express x4 Connectivity Support from a Host PC Using a x4 Copper Cable From HostTargets Slot TypeProduct PXI ExpressChassisHDD RAID NI PXIe-8370NI HDD-8263NI HDD-8264NI HDD-8265PCI Express x4NI PCIe-8371✓✓✓✓PCI Express x4NI PCIe-8372✓✓✓✓Note : For installation instructions and other information about the NI HDD series of products, refer to their respective user manuals.© National Instruments Corporation 3Set Up Your MXI-Express x4 System Connecting Additional Expansion Chassis to a System Using a MXI-Express x4 Copper CableRefer to the Terminology section for more detail on the items in this list.Equipment Needed❑Chassis to daisy-chain from❑Expansion chassis to daisy-chain to❑MXI-Express x4 copper cable❑ A MXI-Express x4 host board and target board that is appropriate for the host system slot and target chassis. Refer to Table 2 for moreinformation.Note For full PXI or PXI Express functionality, refer to the Software Installation andConfiguration section of for more information.Table 2. MXI-Express x4 Connectivity Support from a Chassis Using a x4 Copper Cable From ChassisTargets Slot TypeProduct PXI ExpressChassisHDD RAID NI PXIe-8370NI HDD-8263NI HDD-8264NI HDD-8265PXI Express x4NI PXIe-8374✓✓✓✓PXI Express x4NI 8262—✓✓✓Note : For installation instructions and other information about the NI HDD series of products, refer to their respective user manuals.Installation and ConfigurationThis section explains how to unpack, install, and configure theMXI-Express x4 hardware and software.UnpackingYour MXI-Express x4 cards are shipped in antistatic packages to preventelectrostatic damage (ESD) to the devices. ESD can damage severalcomponents on the device.To avoid such damage in handling the device, take the followingprecautions:•Ground yourself using a grounding strap or by holding a groundedobject.•Touch the antistatic package to a metal part of the computer chassisbefore removing the device from the package.Remove the device from the package and inspect the device for loosecomponents or any sign of damage. Notify NI if the device appearsdamaged in any way. Do not install a damaged device into the computer orinto a PXI Express or CompactPCI Express chassis.Store the device in the antistatic envelope when not in use.Set Up Your MXI-Express x4 © National Instruments Corporation 5Set Up Your MXI-Express x4 System Hardware InstallationThe following are general instructions for installing the MXI-Express x4cards. Consult your computer user manual or technical reference manualfor specific instructions and warnings.Installing an NI PCIe-8371/8372Complete the following steps to install the NI PCIe-8371/8372 in yourcomputer.1.Power off your computer.Caution To protect both yourself and the computer from electrical hazards, your computershould remain off until you finish installing all hardware as instructed.2.Remove the top cover or access port to the PCI Express expansion slots.3.Touch the metal part of the power supply case inside the computer to discharge any static electricity that might be on your clothes or body.4.Unplug the computer and wait 30 seconds to allow the energy stored in the computer’s power supply to fully dissipate.5.Select any available PCI Express expansion slot (x4 or wider).Note Using a PCI Express slot wider than x4 may result in negotiation down to x1 width,which will reduce throughput performance. This is rare in modern systems.Note The BIOS or motherboard may not support the NI PCIe-8371/8372 in a slot intendedfor a graphics card.Note Not all PCI Express expansion slots that have x4 or wider physical connectors areelectrically capable of x4 PCI Express operation. Check with the motherboardmanufacturer to verify that the slot is capable of x4 PCI Express operation.6.Locate the metal bracket that covers the cut-out in the back panel of thecomputer for the slot you have selected. Remove and save thebracket-retaining screw and the bracket cover.7.Line up the NI PCIe-8371/8372 with the slot on the back panel. Slowlylower the NI PCIe-8371/8372 until its card-edge connector is restingon the expansion slot receptacle. Using slow, evenly distributedpressure, press the NI PCIe-8371/8372 straight down until it seats inthe expansion slot, as shown in Figure 1.8.Secure the NI PCIe-8371/8372 to the back panel rail using a bracketretaining screw.Set Up Your MXI-Express x4 System 9.Replace the computer cover.10.Plug the computer back in.Figure 1. Installing the NI PCIe-8371/8372Installing the Low-Profile Bracket on the NI PCIe-8371 (Optional)To install the NI PCIe-8371 in a host computer that requires a low-profileheight card, the front bracket must be replaced with the low-profile bracketincluded with your kit. Complete the following steps to replace the bracket.1.Remove the standard height front bracket already installed on yourNI PCIe-8371 card by removing the two 4-40 × 1/4 inch Phillips headscrews that attach the bracket to the card. Note that the two mountingtabs for the standard height bracket rest against the front side of thecard, which is the side upon which the cable receptacle connectorhousing rests. Set the two screws aside to re-use when installing thelow-profile bracket.1NI PCIe-8371/83722PCI Express x4 Card-Edge Connector 3PCI Express Slot (x4 or wider)© National Instruments Corporation 7Set Up Your MXI-Express x4 SystemFigure 2. Removing the Standard Height Bracket from the NI PCIe-8371CautionWhen removing the bracket, be careful not to remove or lose the EMI gasket onthe cable receptacle connector housing.2.Fit the low-profile bracket onto the NI PCIe-8371. Note that thetwo mounting tabs that the screws thread into rest against the back sideof the card for the low-profile bracket. Ensure that the front bracketLED bulb is situated in the display hole correctly.3.Align the mounting holes on the card with the threaded holes on themounting tabs of the bracket, and insert the screws from the front side.4.Tighten each screw to a maximum torque of 3.6 lb · in. (0.407 N · m).Set Up Your MXI-Express x4 System Installing an NI PXIe-8370 or NI PXIe-8374Table 3 provides information on which PXI Express MXI-Express x4boards are compatible with which chassis slot types.Note For this section, all of the above products will be referred to as an “NI PXI Express board”.Complete the following steps to install the NI PXI Express board in yourPXI Express or CompactPCI Express chassis.1.Power off your PXI Express or CompactPCI Express chassis, but leaveit plugged in while installing the NI PXI Express board. The powercord grounds the chassis and protects it from electrical damage whileyou install the module.Caution To protect both yourself and the chassis from electrical hazards, leave the chassis off until you finish installing the NI PXI Express board.2.Remove or open any doors or covers blocking access to the slot in which you intend to install the NI PXI Express board.3.Touch a metal part of the chassis to discharge any static electricity that might be on your clothes or body.4.Make sure the injector/ejector handle is in its downward position.Be sure to remove all connector packaging and protective caps fromretaining screws on the module. Align the NI PXI Express board withthe card guides on the top and bottom of the system controller slot.CautionDo not raise the injector/ejector handle as you insert the NI PXI Express board.It will not insert properly unless the handle is in its downward position so that it does not interfere with the injector/ejector rail on the chassis, as shown in Figure 3.5.Hold the handle as you slowly slide the module into the chassis untilthe handle catches on the injector/ejector rail.Table 3. NI MXI-Express x4 PXI Express Board Slot Type Compatibility© National Instruments Corporation 9Set Up Your MXI-Express x4 System 6.Raise the injector/ejector handle until the module firmly seats into thebackplane receptacle connectors. The front panel of the NI PXIExpress board should be even with the front panel of the chassis.Note LEDs on the back side of the NI PXIe-8370 will light, indicating the presence of 5V auxiliary power. Refer to the LED Indicators section for details.7.Tighten the bracket-retaining screws on the top and bottom of the front panel to secure the NI PXI Express board to the chassis.8.Replace or close any doors or covers to the chassis.Figure 3 shows an NI PXI Express board just before installation in thesystem controller slot of a National Instruments PXI Express chassis.Figure 3. Example NI PXI Express Board Installation Into a PXI Express Chassis 1PXI Express/CompactPCI Express Chassis 2NI PXI Express board 3Ejector Handle in Down Position 4Injector/Ejector RailSet Up Your MXI-Express x4 System CablingMXI-Express x4 is available with copper cables of various lengths. Table 4shows the MXI-Express x4 copper cables 1 available from NationalInstruments.Connect the MXI-Express x4 cable to both MXI-Express x4 cards. Thecables have no polarity, so either end may be connected to either card.CautionDo not remove the cable after the system is powered on. Doing so can hangor cause errors in applications communicating with devices behind MXI-Express x4. If a cable becomes unplugged, plug it back into the system. (You may need to restart your computer.)Powering On the MXI-Express x4 System1.Power-on all of the expansion chassis in any order you choose.2.Power-on the host.Note There are no requirements on how MXI-Express x4 expansion chassis are powered up relative to each other, as long as they are all on before the computer is powered on.3.Observe the LED status on the NI PCIe-8371, NI PCIe-8372,NI PXIe-8370 and NI PXIe-8374 where applicable. A properlyconnected and powered up system should report a valid link and powerstatus on all of these boards once the host PC is powered on. Refer tothe LED Indicators section for more information.Typical PCI-PCI bridges and switches are used to add PCI devices to a PCIhierarchy in which all the bridges and devices are contained within a singlechassis. Because of this, BIOSes and operating systems make theassumption that all PCI devices in the entire hierarchy will be available assoon as code execution begins at power-up time. This assumption meansthat all of the expansion chassis must be turned on before the host PC for the BIOS and OS to correctly configure a MXI-Express x4 system.1 For more information, refer to the Terminology section.Table 4. National Instruments MXI-Express x4 Copper Cables Cable Length(Meters)Description Part Number 3 mMXI-Express x4 copper cable 779725-037 m MXI-Express x4 copper cable779725-07Powering Off the MXI-Express x4 SystemBecause operating systems and drivers commonly make the assumptionthat PCI devices will be present in the system from power-up topower-down, it is important to not power off the expansion chassis untilafter the host PC is powered off. Powering off the expansion chassis whilethe host is still on can cause crashes or hangs. However, once the host pc ispowered off, the order that the expansion chassis are powered off is notimportant.Note To power down the chassis while the host computer or host chassis is on, you mayneed to hold the power button for at least four seconds. However, this behavior cannot beguaranteed.LED IndicatorsThe LEDs on MXI-Express x4 cards give status information about powersupplies and link state. The NI PCIe-8371 and NI PXIe-8374 haveone tri-color LED on the panel, indicating power and link status. TheNI PCIe-8372 has two tri-color LEDs on the panel, indicating power andlink status for each port. The NI PXIe-8370 has two LEDs, one for powersupply status and one for link state.Table 5. LED Status Descriptions of MXI-Express x4 ProductsBoard LED Color MeaningNI PCIe-8371 (199994x-01L) NI PXIe-8374 (193970x-02L)PWR/LINK Off Power is offBlinking Red Power is out of specSolid Amber Power is within spec;no link to chassisSolid Green Power is within spec;link establishedNI PCIe-8372 (194591x-01L)PWR/LINK Off Power is offSolid Red Power is out of specSolid Amber Power is within spec;no link to chassisSolid Green Power is within spec;link established© National Instruments Corporation11Set Up Your MXI-Express x4 SystemTable 5. LED Status Descriptions of MXI-Express x4 Products (Continued)Board LED Color MeaningNI PXIe-8370 (194402x-02)PWR Off No powerBlinking Red Power is out of specSolid Green Power is within specLINK Off Link not establishedSolid Green Link establishedRefer to Figure4 for onboard LED locations.Figure 4. NI PXIe-8374 (193970x-02L) Onboard LED LocationsLink Good LEDs—LEDs that indicate a successful cable link (LED 0) andbackplane link (LED 4).Link Activity LEDs—LEDs that indicate link activity on the cable link(LED 0) and the backplane link (LED 4).Set Up Your MXI-Express x4 © National Instruments Corporation 13Set Up Your MXI-Express x4 System The NI PXIe-8370 also has a vertical column of 16 LEDs on the back panelof the card near the front connector, as shown in Figure 5. These LEDsprovide additional information about the link status of the PCI Expresslanes on the module to the backplane. Each group of four LEDscorresponds to one of the four PCI Express links to the backplane.Figure 5. NI PXIe-8370 Back Side LED LocationsNotesIf you are using a chassis (such as the NI PXIe-1062) that directly links thePXI Express board, the LEDs to that slot will not illuminate until you have a PXI Express board installed and linked.If you are using the NI PXIe-1062 chassis, you will notice that the last group of LEDs has an LED (PORT 3) illuminated even if no boards are populated in the slots. Since theNI PXIe-1062 uses the last link for a PCI Express to PCI bridge for PXI communication, this link should always be active. Different chassis topologies will give different defaultbehaviors. Contact your chassis’ manufacturer for more information on your chassis’topology.1Back Panel LEDsSet Up Your MXI-Express x4 System Software Installation and ConfigurationInstallationMXI-Express x4 is based on PCI Express technology, using PCI Expressswitches and/or bridges to enable control of a PXI Express chassis from aPC or another PXI Express chassis with an available PCI Express orPXI Express slot. This technology will be recognized as a collection ofPCI-to-PCI bridges to the operating system, and should automatically haveCompactPCI Express level support without any additional software.Note For full PXI/PXI Express functionality such as chassis and controller identification, trigger routing, and slot detection, install the PXI Platform Services software included with your kit. This software also can be found at /updates by searching forPXI Platform Services .For operating system support, refer to the KnowledgeBase 53399AQ7,PXI Platform Services Operating System Support at /kb .Configuring Your SystemNote The following requires the PXI Platform Services software andMeasurement &Automation Explorer (MAX), included on your PXI PlatformServices CD or your driver CD.For information on configuring your system in MAX, open MAX andnavigate to Help»Help Topics»PXI.LabVIEW, National Instruments, NI, , the National Instruments corporate logo, and the Eaglelogo are trademarks of National Instruments Corporation. Refer to the Trademark Information at/trademarks for other National Instruments trademarks. Other product and companynames mentioned herein are trademarks or trade names of their respective companies. For patentscovering National Instruments products/technology, refer to the appropriate location: Help»Patentsin your software, the patents.txt file on your media, or the National Instruments Patent Noticeat /patents. Refer to the Export Compliance Information at /legal/export-compliance for the National Instruments global trade compliance policy and how toobtain relevant HTS codes, ECCNs, and other import/export data.© 2006–2011 National Instruments Corporation. All rights reserved.371976C-01Jul11。

1.2计算机科学与技术重要国际学术会议一、A类会议二、B类会议1.3自动化重要国际学术会议一、A类会议二、B类会议数据挖掘相关的权威期刊和会议-----------------------------------------------[Journals]1.ACM Transactions on Knowledge Discovery from Data (TKDD)2.IEEE Transactions on Knowledge and Data Engineering (TKDE)3.Data Mining and Knowledge Discovery4.Knowledge and Information Systems5.Data & Knowledge Engineering[Conferences]1.SIGMOD:ACM Conference on Management of Data (ACM)2.VLDB:International Conference on Very Large Data Bases (Morgan Kaufmann/ACM)3.ICDE:IEEE International Conference on Data Engineering (IEEE Computer Society)4.SIGKDD:ACM Knowledge Discovery and Data Mining (ACM)5.WWW:International World Wide Web Conferences (W3C)6.CIKM:ACM International Conference on Information and Knowledge Management (ACM)7.PKDD:European Conference on Principles and Practice of Knowledge Discovery in Databases (Springer-Verlag LNAI)JournalsACM TKDD /DMKD/content/1573-756X/?p=859c3e83455d41679ef1be783 e923d1d&pi=0IEEE TKDE /organizations/pubs/transactions/tkde.htm ACM TODS /tods/VLDB Journal /ACM Tois /pubs/tois/ConferencesSigKDD /ICDM /~icdm/SDM /meetings/sdm08/PKDD /VLDB /SigMod /sigmod/ICDE http://www.ipsi.fraunhofer.de/tcde/conf_e.htmlWWW /conferencesOnline Resources网址集合/Computers/Software/Databases/Data_Mining// A google co-op search engine for Data Mining/coop/cse?cx=006422944775554126616%3Aixcd3tdxkke Data Mining, University of Houston/boetticher/CSCI5931%20Data%20Mining.htmlData Mining Program, University of Central Florida / Data Mining Group, University of Dortmundhttp://www-ai.cs.uni-dortmund.de/index.htmlData Mining, MIT OCW/OcwWeb/Sloan-School-of-Management/15-062Data-MiningSpri ng2003/CourseHome/Data Mining Group, Tsinghua /dmg.html KDD oral presentations video Data Mining Events Feed /DataMiningEvents ToolsWeka /ml/weka/Rapid Miner(Yale) /content/view/3/76/lang,en/IlliMine /Alpha Miner http://www.eti.hku.hk/alphaminerPotter's Wheel A-B-C /abc/。

Artificial Intelligence a Driving force for Human Computer Interaction(HCI) in EducationIntroductionComputer games have made a tremendous contribution to entertainment industry in the recent years. Production of computer games requires input of different stakeholders including designers, artists, programmers, etc. Innovation and creativity are key aspects in game formulation. The imaginative vision of an artist can be formulated into logical design of a game which is eventually translated into computer game by a game designer and programmer. When I was six years old in the first year at Elementary/primary school, two of the subjects we had namely “Physical Education” and “Story Telling” were very much liked by children in the class. “Story Telling” was more popular than “Physical Education”. The stories were logically constructed and they developed the children’s critical thinking ability. The stories were narrated using animals of different behaviors as actors. For example, the rabbit represented the tricky creature, and tortoise represented a creature that always acts in hiding. Today all the narrative stories can be translated into computer games using the concept of virtual reality. These game programmes can greatly enhance children in learning real life skills. Game creation should match the target audience for the game. For example, games in which actors continuously act violence against each other is not appropriate for little children as it instills violence in their mind-set which becomes difficult to transform in the future.Sesame street was born to educate children through entertainment. At that time in the late ‘60s, the entertainment media of choice was television.. In more recent years, Sesame asked the same question regarding the potential for interactive entertainment media to be used for educational purposes. The variety of entertainment media today might be considered a, “vast wasteland”, because these media could have potential for education children and adults. Unfortunately little has been achieved through utilizing them for educational purpose. In the Sesame workshop model, the production of educational media required the integration of expertise in the media production, educational content (curriculum), and research with children. These varied expertises can achieve a common goal, the educational package for content delivery to children. This particular approach to interactive education used constructivist’s paradigm in which children learn through heuristic approach. The interface development for educational content delivery should suit the target group. For example, preschool children can not read text, their content should include media such as sound, graphics, animation, and video. [8]Motivation for Computer GamesNowadays, computer games have become a dominating form of entertainment due to their higher level of attractiveness to game players. [3].Computer games in the twenty first century have gained more popularity over its traditional counterpart games due to a number of reasons.-they attract people by creating the illusion of being immersed in an imaginative virtual world with computer graphics and sound [2].-the goals of computer games are typically more interactive than that of traditional games, which brings players a stronger desire to win the game.-computer games, usually designed with an optimal level of information complexity, can easily provoke players’ curiosity. Consequently, computer games intrinsically motivate players by bringing them more fantasy, challenge, and curiosity, which are the three main elements contributing the fun in games [9].-Computer games stimulate the players critical thinking to approach problem solvingTrying to understand entertainment is worthwhile for a number of reasons: [6] -Entertainment defines society’s culture. The shared enjoyment of music, stories, games, and other entertainment experiences help to bind people together.-Entertainment is a cornerstone of communication of communication. Much true understanding is achieved through storytelling.-Entertainment is a cornerstone of discovery. Play is how we examine, manipulate things and ideas. Composers play with melody lines, mathematicians play with equations, and architects play with designs.-We are most alive when entertained. Persons who are well and truly entertained are focused, alert, alive, and are enjoying themselves.In addition to the above points given by Jesse we can also say that entertainment is a tool for socializing people of different cultural background when there is a common value all can get from it. Entertainment can be used by society to fight against harmful cultural practices.Many people in society do not see entertainment as a valuable discipline that needs to be developed.Human Computer Interaction“Human Computer Interaction (HCI) is often misunderstood to represent Human Computer Interface; there are those who imagine HCI is a science of building form-based GUIs. This limiting (and generally inaccurate) perspective does not represent what HCI can do and what it can not contribute. HCI researchers consider the point of how technology can contribute to the human endeavor and how computing can integrate with and expand human physical, intellectual and social abilities”. [7].Interfaces involve the virtual, social domain (GUI) as well as the physical domain.[3]. Each of these interfaces can compliment the other depending on the game application. The graphical user interface should be designed to reflect human centered interaction style. Game boards when used with game objects retain social richness of traditional desktop games where physical objects are covered using camera so that dynamic and visual rich game boards can be realized with game objects on the display to blend GUI with tangible interfaces.Artificial IntelligenceMost of electronic games seem to have artificial intelligence features for interacting with human.[10]. The important characteristics of artificial intelligence in game are it’s behaviors (which need to be similar to human’s behavior), and the intelligence (which should not be too much that no human will beat the game). The game developers are therefore called to incorporate the above behaviors when designing specific game player’s requirements.Most artificial intelligence problems that programmers face fall into three groups. At the lowest level is the problem of physical movement – movement, making turns, walking, etc. This characteristic is called locomotion or motor skills. Moving up one level is a higher-level view of unit movement, where the unit has to decide how to get from point A to point B, avoiding obstacles and/or other units. This group is called steering or task generation. At the highest level of AI is the actual thinking. The third and the highest stage is where the unit decides what to do and uses its ability to move around and plan directions to carry out its wishes. [13]A number of paradigms have emerged for interactive narratives. One of the approaches is provided in the “Holodeck” [12], where the user is immersed in a virtual environment while participating in a story that is initiated within his environment. Another approach is in “interactive TV” in which the user is an active spectator having external influence on the story to the unfolding plot. [4]Another approach we can mention is “immersive mixed reality”, in which, a user is not only immersed in the story but also features as a character it its visual presentation, which allows the user to see himself or herself playing an active role in the interactive narrative. In this approach, the user’s image is normally captured in real time and immersed into a virtual environment populated by the autonomous virtual actors with which he or she interacts in the story. [5] Interactive storytelling uses artificial intelligence (AI) techniques to generate real time narratives featuring synthetic characters. Unlike the early systems in which the users were interacting with virtual characters like IMPROV [11] OR kidsroom [1], they are based on a long term narrative drive and maintain the overall consistency of the plot while taking into account user interaction [4].Neural Networks in GamesNeural networks have made significant contribution in the field of artificial intelligence by closely simulating intelligence in the physical sense. Researchers have discovered the basic building blocks of the brain and have found that, at a biological level, it is just a real dense graph.[13]. On the order of billions or trillions of nodes and each node is connected to the thousands of others. The processing unit of a biological neuron is soma which receives input from the dendrites and outputs to the axon. The digital version is similar to the biological neuron with a network of nodes connected with edges.Neural nets can be trained to know solution to each problem. This is important for them to ensure that the correct answer is generated for whatever action they perform.AxonDendritesSomaRule-Based Artificial IntelligenceThe physical world is governed by a set of rules. Without rules AI application would have a lot of problems. However, the rule-based AI can lessen this problem. Rules can be formulated to simulate real world or imaginary events. In life every person seeks protection in case there is danger. Human beings are usually courageous in actions, but courage can also be contradiction in terms as it can cost the life of the human. We can define a set of rules that govern how a rate can successfully tie a bell at the neck of a cat. In this situation, the rat has to analyze the set of rules of what to do. The rat can successfully tie the bell when the cat is asleep and when the bell doesn’t hit the gong. When either the cat notices the rat or the bell bits the gong, the rat should escape at the highest possible speed to avoid attack and subsequent destruction by the cat. When approaching the cat the rat should walk slowly so that the bell doesn’t hit the gong. Rules for the above Cartoon GameIF [Cat == Asleep] AND [Gong_Hit_Bell == False]THEN [Bell_Game == Successful]IF [Gong_Hit_Bell == True] OR [Cat == Awake]THEN [Rat_Walk == Very Fast] AND [Bell_Game == Unsuccessful]Conclusion and RecommendationComputer Entertainment has not been fully utilized to address real world problems. Computer entertainment has been directed to activities such as playing game to refresh one’s mind or get rid of boredom, entertaining children regardless of whether or not theentertainment offers room for critical thinking. For video games in mobile phones. All the above contribute positively to society.The researcher wants to point out that games offer a lot of educational values that have not been envisioned. An open area of research can be developing multimedia based computer entertainment platform for fight against HIV in developing countries. Millions of the lives of people have been claimed in the world by the deadly virus which they acquire mainly because of lack of information regarding its danger to humanity. International communities (Donors) have spent multibillion dollars in fight against HIV in countries especially in sub-Saharan Africa and Asia. Computer entertainment has high potential of making contribution to public education of HIV awareness and dangers. Computer entertainment can be used to enlighten the youth in high schools and universities on the need to guard against HIV, using entertainment approach can be effective because entertainment is center of attraction for young people. To develop such would need input of a number of stakeholders including students from high schools and universities, educationists, teachers, systems designers and programmers, artists, and parents.References[1] A.F. Bobick et al, “The kidsroom: A perceptually-based interactive and immersive story environment”, Technical Report 398, MIT Media Lab Perceptual Computer Section, 1996.[2] AMORY, A. NAICKER, K., VINCENT, J., AND ADAMS, C. 1999. The use ofcomputer games as an educational tool: Identification of appropriate game types andelements. British J. of Educational Technology. 30, 4 (1999), 311-321. [3] Carsten et al, Pervasive Games: Bringing Computer Entertainment back to the Real World, ACM Computers in Entertainment, Vol. 3, No. 3, July 2005, Article 4A. [4] Cavazza et al, “Character-based interactive storytelling”, IEEE Intelligent systems, special issue on AI in interactive environment, 2002, p.p. 17-24.[5] Charles et al, “Compelling experiences in mixed reality interactive storytelling”, ACE 2004, June 3-5, 2004, Singapore[6] Jesse Schell, Understanding Entertainment: Story and Gameplay are One, ACM Computers in Entertainment, Vol. 3, No. 1, January 2005, Article 6A[7] Joshua B. Gross, Crossroads, The ACM Student Magazine Issue 12.2, Winter 2005.[8] Glenda L. Revelle, “Education via Entertainment Media: The Sesame workshopapproach”, ACM Computers in Entertainment, Vol. 1, No. 1, October 2003, Article07.[9] MALONE, T. W. 1981. Toward a theory of intrinsically motivating instruction.Cognitive Science 4, 13 (1981),333-369.[10] Nitiwat, “Artificial Intelligence based on fuzzy behavior for game programming”,ACE’04, June 3-5, 2004, Singapore.[11] Perlin K and Goldberg A, “Improv: A system for scripting interactive actors invirtual world”, Computer Graphics; Vol. 29 No. 3, 1996.[12] Swartout et al, “Toward the Holodeck: Integrating graphics, sound, character and story”, in the proceedings of the autonomous agents 2001 conference, 2001. [13] Walsh Peter, “Artificial Intelligence”, Advanced 3D game programming withDirectX 9.0, 2003。

DRIVER VERSION: 30.0.101.1121 BETADATE: November 16, 2021NOTE: The driver version numbering has rolled over from 100.9999 to 101.1069. This requires the use of all 7-digits instead of 4-digits for the driver build number. For more information, see Understanding the Intel® Graphics Driver Version Number.GAMING HIGHLIGHTS1:•Fix for crash in Battlefield 2042* on 11th Generation Intel® Core™ Processors with Intel® Iris® X e graphics. KEY ISSUES FIXED:•Minor graphic anomalies seen in Shadow of the Tomb Raider* (DX11).•Error message seen when running Rise of the Tomb Raider* (DX12) on Intel® Iris® X e Discrete graphics.Get a front row pass to gaming deals, contests, betas, and more with Intel Software Gaming Access.*2 Are you still experiencing an error preventing the driver update? Look here for why and a solution.KNOWN ISSUES:•Intermittent crash or hang may be seen in Call of Duty: Black Ops Cold War* (DX12), Far Cry 6* (DX12), The Sims 4* (hot plug or unplug of external display).•Minor graphic anomalies may be observed in Dark Souls 3*, F ar Cry 6* (DX12), Metro Exodus* (DX12), Microsoft Flight Simulator* (during installation), Mount & Blade II: Bannerlord*, Red Dead Redemption 2* (DX12), The Surge 2* (Vulkan), Tom Clancy’s Ghost Recon Breakpoint*.•“Update driver” p op-up error may be seen while launching Battlefield 1* after upgrading from 30.0.100.9955 or older drivers due to the driver version roll-over.•[11th Generation Intel® Core™ Process ors with Intel® Iris® Xe graphics]: Crash or hang may be seen in Breathedge*, Detroit: Become Human* (Vulkan), FIFA 21*, NBA 2K21* (DX12) (when switching resolution from 1920 x 1080 to 1600 x 900 and 1280 x 720), The Ascent.•[11th Generation Intel® Core™ Processors with Intel® Iris® Xe graphics]: Black screen may be seen in Arma 3* (when changing display mode to windowed or full screen).•[11th Generation Intel® Core™ Processors with Intel® Iris® Xe graphics]: Minor graphic anomalies may be seen in Adobe Premiere Pro 2020 during video playback, Baldur’s Gate 3* (Vulkan), Call of the Duty: Vanguard* (DX12), Call of the Sea*, Crysis Remastered*, Elex*, Just Cause 4 *, Red Dead Redemption* (Vulkan), The Ascent.•[Intel® Iris® X e Discrete graphics]: Intermittent crash or hang may be seen in Conan Exiles* (Low End Laptop Mode” in game settings), Forza Horizon 4* (DX12), Forza Motorsport 6* (DX12), Spyro: Reignited Trilogy*.•[Intel® Iris® X e Discrete graphics]: Minor graphic anomalies may be observed in Assassin’s Creed Valhalla* (DX12), Code Vein*, Death Stranding* (DX12), Microsoft Flight Simulator*, GRID 2019* (DX12).•[11th and 12th Generation Intel® Core™ Processors]: Display is getting blanked out with 4K@60hz resolution connected via dock.•[12th Generation Intel® Core™ Processors with Intel® UHD graphics]: Minor graphic anomalies may be observed in Netflix* after quickly unplugging and re-plugging external displays during video playback.•[12th Generation Intel® Core™ Processors with Intel® UHD graphics]: Intermittent crash or hang may be seen in Marvel’s Avengers* (DX12), Metro Exodus* (DX12) (after changing quality), Shadow of the Tomb Raider* (Dx12), The Sims 4* (when loading save file).•[12th Generation Intel® Core™ Processors with Intel® UHD graphics]: Minor graphic anomalies may be observed in Gears 5*, Genshin Impact*, Ring of Elysium* (DX12), Wolfenstein: Youngblood* (Vulkan).CONTENTS OF THE PACKAGE:•Intel® Graphics Driver•Intel® Display Audio Driver 10.26.0.11 (6th Gen and related Pentium Silver and Celeron processors)•Intel® Display Audio Driver 10.27.0.11 (7th, 8th, 9th, 10th Gen Intel® Core™ processors)•Intel® Display Audio Driver 11.1.0.19 (10th Gen Intel® Core™ processors with Iris Plus Graphics)•Intel® Display Audio Driver 11.2.0.9 (Intel® Co re™ Processors with Intel® Hybrid Technology)•Intel® Media SDK Runtime (21.0.1.35)•Intel® oneVPL6 GPU Runtime (21.0.2.5)•Intel® Graphics Compute Runtime for OpenCL* Driver•Intel® Graphics Command Center (installed via Microsoft* Store)•Vulkan*3 Runtime Installer•Intel® Graphics Driver Installer (1.0.542)•OneAPI Level Zero Loader and Validation Layer•Intel® Graphics Compute Runtime for OneAPI Level Zero specificationOPERATING SYSTEM SUPPORT:SUPPORTED APIs:If you are uncertain of which Intel processor is in your computer, Intel recommends using the Intel Processor Identification Utility or Intel Driver & Support Assistant to identify your Intel processor.Be sure to check out , where you’ll find recommended in-game settings for your Intel Graphics system for many more of your favorite games.Note:1.Intel Labs conducts independent testing of supported titles on Intel platforms to ensure playability. Please refer topublisher system requirements to ensure compatibility with your system.2.Graphics Driver Smart Installer Enhancement allows end-users to upgrade systems with OEM DCH drivers to newerIntel generic DCH drivers. OEM customizations are preserved during this upgrade process, in accordance with Microsoft* DCH driver design principles (ref er to Microsoft documentation, “Extension INF Publishing Whitepaper”to learn more). The installer will continue to restrict OEM non-DCH to Intel Generic non-DCH upgrades as well as OEM non-DCH to Intel Generic DCH driver upgrades. End-users will continue to be referred to OEM websites.WARNING: Installing this Intel generic graphics driver will overwrite your Computer Manufacturer (OEM) customized driver. OEM drivers are handpicked, customized, and validated to resolve platform-specific issues, enable features and enhancements, and improve system stability. The generic driver’s intention is to temporarily test new features, game enhancements, or check if an issue is resolved. Once testing is complete Intel advises reinstalling the OEM driver until they validate it and release their own version.Any graphics issues found using Intel generic graphics drivers should be reported directly to Intel. Corporate customers should always use OEM drivers and report all issues through the vendor they purchased the platforms and support through.3.Product is conformant with the Vulkan* 1.2 specification. Vulkan* and the Vulkan* logo are registered trademarksof the Khronos Group Inc*.4.In the Intel Graphics Command Center (System > Driver), the ‘Microsoft Di rectX* version refers to the operatingsyst em’s DirectX version. The DirectX 12 API is supported but some optional features may not be available.Applications using the DirectX 12 API should query for feature support before using specific hardware features.Please note that DirectX12 is only supported on Windows 10 and DirectX11.3 support is also available onsupported Microsoft* operating systems.5.One API Level Zero API version is supported on 6th generation Intel® Core™ processors and above. Note that Intel®Atom processors are not supported.6.Intel® One API Video Processing Library GPU Runtime* release – more details belowa.Intel® OneAPI Video Processing Library Specification:https://spec.oneapi.io/versions/latest/elements/oneVPL/source/index.htmlb.Upgrading from Intel® Media SDK to Intel® oneAPI Video Processing Library7.See the Windows Subsystem for Linux Installation Guide for Windows 10 onwards for more details about how toinstall a supported Linux distribution.More on Intel ProcessorsFor more information on the Intel Core processor family, Intel Xeon E processor family,and 12th Generation Intel Core processors, please visit:12th Gen Intel® Core™ ProcessorsIntel® Cor e™ Processor FamilyIntel® Xeon® E ProcessorsIntel® GraphicsWe continuously strive to improve the quality of our products to better serve our users and appreciate feedback on any issues you discover and suggestions for future driver releases. If you have an issue to submit, please follow the guidance found here Default level information for reporting Graphics issues.Intel, the Intel logo, Celeron, Intel Core, Iris, Pentium and Xeon are trademarks of Intel Corporation or its subsidiaries in the U.S. and/or other countries.* Other names and brands may be claimed as the property of others.。

献给CV和CG入门者之科研经验浅问细答兼与大家探讨吴怀宇hywu@, huaiyuwu@中国科学院内容为什么做科研？－科研的几个好处以及几个误区1科研容易还是很难？－科研要过的几个关2科研从哪里开始？－选题的重要性以及如何选题3科研也分档次吗？－创新的几个层次以及如何获4得好的idea科研也有捷径吗？－科研中的一些技巧5科研，Re-search。

那首先，how to search？－查6阅和阅读paper的技巧其次，我们如何出牛文章？7科研也需要气氛，也需要扎堆吗？－Coffee Break的8作用与建议征求为什么做科研？1z科研的唯一源泉是你的兴趣和理想。

科研的几个好处z有利于身心健康。

科研时大脑发出阿尔法脑电波，和僧人入静时发出的脑电波是一样的，对人的身心健康很有好处，因此很多学者非常长寿z证明自己的智商至少是正常的，甚至位于Top 10％z以后不容易受骗。

并有机会站在全球科技的前沿，了解世界科学水平发展的现状，为自己今后人生的规划打下扎实的基础！z在自己年轻时，有一个真正有技术含量的锻炼机会。

睿智渊博、见多识广的导师将潜移默化、言传身教地教你学会做人、做事z更多、更强大的…如为祖国的四化做贡献、为人类摆脱黑暗而奋斗，等等科研的几个误区z搞科研的人都是天才，自己只是个“跑龙套”的z总觉得自己倒霉,导师分了个很难的课题。

z好高骛远，嫌课题太小。

z不关心和自己研究方向没有直接联系的领域发展情况z对权威专家的论点深信不疑；或盲目推翻权威（如爱因斯坦的相对论已被“民科们”推翻了无数次）z期望看一篇论文马上就能用，希望投一篇文章马上就能中z光看论文,不动手实验z当实验结果和预想不符时就马上放弃原来想法z很多人老是说自己基础如何如何差，担心搞不定。

从来就没有太晚的时候，人都是逼出来的。

科研容易还是很难？2z搞科研需要亮剑精神，需要闯关！¾很难！闯不过，便裹足不前。

¾容易！闯过了，就一马平川搞科研必须要过的几个关z1、查文献，跟踪学科前沿(选题)z2、读懂论文。

1、研究方向和团队带头人●概况浙江大学动画与感知课题组(Computer Animation &Perception Group)的主要研究方向有基于动作捕获技术的计算机动画、基于感知的自然人机交互、个性化制鞋CAD技术与系统、多通道融合的场景感知与理解等。

●团队带头人✧耿卫东教授计算机应用专业和数字化艺术设计专业的博士生导师，曾先后在德国信息技术国家研究中心媒体通讯研究所、香港理工大学多媒体创新中心等大学和研究机构访问进修。

2004年入选浙江省新世纪151人计划第二层次，2007年入选国家新世纪人才计划，研究成果“交互式数字媒体引擎关键技术研究及产业化”2010年获上海市科技进步三等奖。

电子信箱：gengwd@2、近年的代表性论著：1.Bingwen Jin, Hao Lei, and Weidong Geng*, Accurate IntrinsicCalibration of Depth Camera with Cuboids, European Conference on Computer Vision (ECCV), Springer International Publishing, 20142.Bingwen Jin and Weidong Geng*, Correspondence specificationlearned from master frames for automatic inbetweening, Multimedia Tools and Applications, 1-17, 20143.Bingwen Jin, Linglong Feng, and Weidong Geng*, A Hybrid Approachto Animating the Murals with Dunhuang Style. International Workshop on Multimedia Signal Processing (MMSP), IEEE, 20144.Li M J, Geng W D*. Evaluation Fitness of Footwear Using HybridSimulation[J]. Applied Mechanics and Materials. 2014, 462: 1055-10615.Li M J, Geng W D*. The Extension of Geodesics[J]. Applied Mechanicsand Materials. 2013, 333: 95-104.6.李萌坚，耿卫东*，潘云鹤. 基于扩展测地线的鞋楦围长测量[J]. 计算机辅助设计与图形学学报. 2013, 25(10).7.R. Fan, S. Xu, and W. Geng*, “Example-Based Automatic Music-DrivenConventional Dance Motion Synthesis.,”IEEE Transactions on Visualization and Computer Graphics, vol. 18, pp. 501-515, 2012.8.高飞, 王青, 耿卫东*,潘云鹤，三维动态脚型测量方法，中国科学：信息科学，2011年6月9.李启雷,金文光,耿卫东*,基于无线惯性传感器的人体动作捕获方法，浙江大学学报(工学版), 02期, pp 280-285, 2012.10.X. Liang, Z. Wang, W. Geng*, F. Multon, “A motion-based userinterface for the control of virtual humans performing sports”, International Journal of Virtual Reality, vol. 10(3), 1-8, 2011.11.Qilei Li, Wenguang Jin, Weidong Geng*, Virtual Avatar Control UsingMotion Sensors, Journal of Computers, Vol 6, No 2 (2011), 184-18912.J. Xu, X. Li, Y. Ren, and W. Geng*, “Performance-driven animationof hand-drawn cartoon faces,”Computer Animation and Virtual Worlds, vol. 22, no. 5, pp. 471-483, 2011.13.张翔, 梁秀波, 樊儒昆, 耿卫东*, “数据驱动的夸张动作生成,”计算机辅助设计与图形学学报, no. 9, pp. 1468-1474, 2010.14.樊儒昆, 傅晶, 程司雷, 张翔, 耿卫东*, “动作与音乐的节奏特征匹配模型,”计算机辅助设计与图形学学报, no. 6, pp. 990-996, 2010.15.梁秀波, 张顺, 李启雷, 张翔, 耿卫东*, “运动传感驱动的3D直观手势交互”，计算机辅助设计与图形学学报，no. 3, pp.521-526, 2010.16.耿卫东，三维游戏引擎设计与实现[M]，浙江大学出版社，2008-10-07，ISBN:17.耿卫东，艺术化绘制的图形学原理和方法[M]，浙江大学出版社和Springer-Verlag GmbH，2010-01-15，ISBN:18.耿卫东，The Algorithms and Principles of Non-photorealisticGraphics[M]，浙江大学出版社和Springer，2010-01-15，ISBN:3、团队的网站介绍//capggeng/。

大学计算机基础缩写词1.ALU：Arithmetic Logic Unit算术逻辑单元2.CPU：Central Processing Unit中央处理单元3.CISC技术：ComplexInstructionSetComputer复杂指令系统计算机4.RISC技术：ReducedInstructionSetComputer精减指令系统计算机5.RAM：Random Access Memory6.BIOS：Basic Input/output system7.CMOS：complementary metal-oxide semiconductor互补金属氧化物半导体8.SDRAM：Synchronous DRAM同步动态随机存储器9.DDR：Dual Date Rate10.SDRAM：双倍速率11.掩膜ROM：Masked ROM12.PROM：Programmable ROM可编程PROM13.EPROM：Erasable PROM可擦除PROM14.ROM：Read Only Memory15.VLSI：Very Large Scale Integration，超大规模集成电路16.EISA：Extended Industry Standard Architecture17.ISA：Industrial Standard Architecture总线18.VESA：Video Electronics Standards Association即视频电子标准协会总线19.PCI：peripheral component interconnect总线20.AGP ：Accelerated Graphics Port总线B：Universal Serial Bus总线22.DBMS：Database Management System数据库管理系统23.IDE：Integrated Drive Electronics电子集成驱动器24.SCSI硬盘：Small Computer System Interface小型计算机系统接口25.RAID：Redundant Array of Independent Disks独立磁盘冗余阵列26.SSD：Solid States Disk固态存储器27.BCD码：Binary Coded Decimal，用二进制代码表示的十进制数28.PCB：Process Control Block进程控制块29.DMA：Direct Memory Access直接存取方式30.FAT：File Allocation Table文件分配表31.DBP：Dos Boot Record操作系统引导记录区32.BPB：BIOS Parameter Block，BIOS参数块33.NTFS：New Technology File System34.MBR：Master Boot Record主引导记录35.DPT：Disk Partition Table硬盘分区表36.GUI：Graphics User Interface图形用户界面37.Windows NT：NT，New Technology38.PCM：Pulse Coded Modulation脉冲编码调制39.DRM：Digital Rights Management数字版权管理40.MIDI：Musical Instrument Digital Interface41.RGB：Red、Green、Blue42.CMYK：Cyan、Magenta、Yellow、blacK43.HSB：Hue、Saturation、Brightness色相、饱和度、明度44.GIF：Graphics Interchange Format45.JPEG：Joint Photographic Experts Group46.MPEG：Moving picture experts group47.TIFF：Tagged Image File Format48.PNG：Portable Network Graphic可移植的网络图像49.AVI：Audio Video Interleaved，音频视频交叉存取格式50.ADSL：Asymmetrical Digital Subscriber Line非对称数字用户环路51.ARP ：Address Resolution Protocol 地址解析协议52.ATM ：Asynchronous Time division multiplexing异步传输模式53.BBS：Bulletin Board System电子公告栏54.CDMA：Code Division Multiple Access码分多址接入技术55.CERNET：China Education and Research Network中国教育和科研网56.CGWNET：China Great Wall Network中国长城网57.ChinaGBN：China Gold Bridge Network中国金桥信息网58.CIETNET：China International Economy Trade Network中国国际经济贸易互联网59.CMNET：China Mobile Network中国移动互联网CNET：China NetCom Network中国网通公用互联网61.CSTNET ：China Science and Technique NetWork中国科技网62.CSS ：Cascading Style Sheets层叠样式表63.DDN：Digital Data Network数字数据网64.DHCP：Dynamic Host Configuration Protocol动态主机配置协议65.DNS：Domain Name System域名解析系统66.DWDM：Dense Wavelength Division Multiplexing密集波分复用67.FDDI：Fiber Distributed Data Interface光纤分布式数据接口68.FTP ：File Transfer Protocol文件传输协议69.GPRS：General Packer Radio Service通用无线分组业务70.GPS：Global Position System全球定位系统71.HTML：Hypertext Markup Language超文本标记语言72.HTTP：Hypertext Transfer Protocol超文本传输协议73.ICMP：Internet Control Message Protocol因特网控制报文协议74.IGMP：Internet Group Management Protocol因特网组管理协议75.IMAP：Internet Mail Access Protocol Internet邮件访问协议76.IP：Internet Protocol 网际协议77.IPX/SPX：Internetwork Packet eXchange/Sequences Packet NETW ARE eXchange客户端/服务器的协议群78.ISDN：Integrated Services Digital Network综合业务数字网N：Local Area Network局域网80.MAC：Medium Access Control媒体接入控制81.MAN ：Metropolitan Area Network城域网82.MIME：Multipurpose Internet Mail Extensions多用途Internet函件扩展标准BEUI：NetBIOS Extended User Interface NetBios增强用户接口84.OSI/RM：Open Systems Interconnection Reference Model开放系统互联基本参考模型85.POP ：Post Office Protocol邮局协议86.PPP：Point to Point Protocol点对点协议87.RARP：Reverse Address Resolution Protocol逆地址解析协议88.RSS：Really Simple Syndication描述和同步网站内容的格式89.SMTP ：Simple Mail Transfer Protocol简单邮件传送协议90.SNMP：Simple Network ManagementProtocol简单网络管理协议91.TCP：Transmission Control Protocol传输控制协议92.UDP：User Datagram Protocol用户数据报协议93.UNINET：China Unicom Network中国联通互联网94.URL：Uniform Resource Locator统一资源定位器95.WAN：Wide Area Network广域网96.WWW： World Wide Web万维网。