
考点六 二次函数与函数的最值
知识梳理
1.二次函数
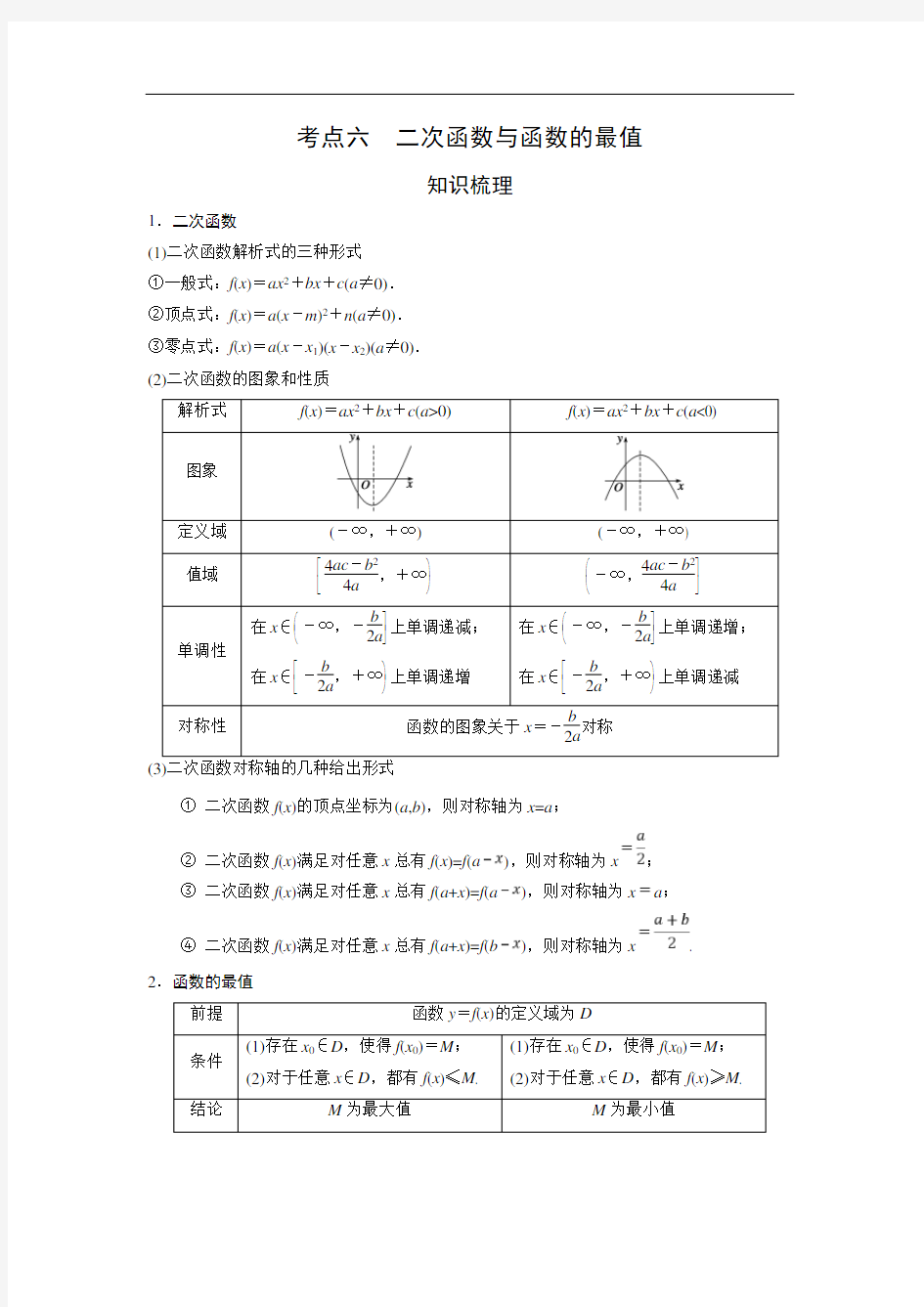
(1)二次函数解析式的三种形式 ①一般式:f (x )=ax 2+bx +c (a ≠0). ②顶点式:f (x )=a (x -m )2+n (a ≠0). ③零点式:f (x )=a (x -x 1)(x -x 2)(a ≠0). (2)二次函数的图象和性质
解析式
f (x )=ax 2+bx +c (a >0)
f (x )=ax 2+bx +c (a <0)
图象
定义域 (-∞,+∞)
(-∞,+∞)
值域
???
?4ac -b 24a ,+∞ ?
???-∞,4ac -b 24a
单调性
在x ∈????-∞,-b
2a 上单调递减; 在x ∈???
?-b
2a ,+∞上单调递增 在x ∈????-∞,-b
2a 上单调递增; 在x ∈???
?-b
2a ,+∞上单调递减 对称性
函数的图象关于x =-b
2a
对称
① 二次函数f (x )的顶点坐标为(a ,b ),则对称轴为x =a ; ② 二次函数f (x )满足对任意x 总有f (x )=f (a ),则对称轴为x ; ③ 二次函数f (x )满足对任意x 总有f (a +x )=f (a ),则对称轴为x a ;
④ 二次函数f (x )满足对任意x 总有f (a +x )=f (b ),则对称轴为x
.
2.函数的最值
前提 函数y =f (x )的定义域为D
条件 (1)存在x 0∈D ,使得f (x 0)=M ; (2)对于任意x ∈D ,都有f (x )≤M .
(1)存在x 0∈D ,使得f (x 0)=M ; (2)对于任意x ∈D ,都有f (x )≥M .
结论
M 为最大值
M 为最小值
说明:闭区间上的二次函数必有最值. 求二次函数在闭区间上的最值主要有三种类型:定轴定区间、轴动区间定、轴定区间动,不论哪种类型,核心是函数对称轴与给定区间的相对位置关系的讨论.一般分为:对称轴在区间的左边,中间,右边三种情况.当含有参数时,要依据对称轴与区间的关系进行分类讨论.
典例剖析
题型一 二次函数的解析式
例1 二次函数的图象过点(0,1),对称轴为x =2,最小值为-1,则它的解析式为________. 答案 f (x )=1
2
(x -2)2-1
解析 依题意可设f (x )=a (x -2)2-1, 又其图象过点(0,1),∴4a -1=1,∴a =1
2.
∴f (x )=1
2
(x -2)2-1.
变式训练 已知二次函数f (x )的图象经过点(4,3),它在x 轴上截得的线段长为2,并且对任意x ∈R ,都有f (2-x )=f (2+x ),求f (x )的解析式. 答案 f (x )=x 2-4x +3
解析 ∵f (2-x )=f (2+x )对x ∈R 恒成立,∴f (x )的对称轴为x =2. 又∵f (x )图象被x 轴截得的线段长为2,∴f (x )=0的两根为1和3. 设f (x )的解析式为f (x )=a (x -1)(x -3)(a ≠0).
又∵f (x )的图象过点(4,3),∴3a =3,a =1.∴所求f (x )的解析式为f (x )=(x -1)(x -3), 即f (x )=x 2-4x +3.
解题要点 二次函数解析式的求法
根据已知条件确定二次函数解析式,一般用待定系数法,选择规律如下:
(1)已知三个点坐标,宜选用一般式;
(2)已知顶点坐标、对称轴、最大(小)值等,宜选用顶点式; (3)已知图象与x 轴两交点坐标,宜选用零点式. 题型二 二次函数的图象和性质
例2 两个二次函数f (x )=ax 2+bx +c 与g (x )=bx 2+ax +c 的图象可能是________.(填序号)
①
② ③
④
答案 ④
解析 函数f (x )图象的对称轴为x =-b 2a ,函数g (x )图象的对称轴为x =-a 2b ,显然-b
2a 与-
a
2b
同号,故两个函数图象的对称轴应该在y 轴的同侧.只有④满足. 变式训练 如果函数f (x )=x 2+(a +2)x +b (x ∈[a ,b ])的图象关于直线x =1对称,则函数f (x )的最小值为________. 答案 5
解析 由题意知?????
-a +22=1,a +b =2,
得?????
a =-4,
b =6.
则f (x )=x 2-2x +6=(x -1)2+5≥5. ∴ f (x )的最小值为5.
题型三 闭区间上二次函数最值
例3 函数f (x )=2x 2-2ax +3在区间[-1,1]上最小值记为g (a ),求g (a )的函数表达式. 解析 当a <-2时,函数f (x )的对称轴x =a
2<-1,则g (a )=f (-1)=2a +5;②当-2≤a ≤2
时,函数f (x )的对称轴x =a 2∈[-1,1],则g (a )=f ????a 2=3-a 22;③当a >2时,函数f (x )的对
称轴x =a
2>1,则g (a )=f (1) =5-2a .
综上所述,g (a )=?????2a +5(a <-2),3-a
2
2(-2≤a ≤2),5-2a (a >2).
变式训练 设函数y =x 2-2x ,x ∈[-2,a ],若函数的最小值为g (a ),求g (a ). 解析 ∵函数y =x 2-2x =(x -1)2-1, ∴对称轴为直线x =1,
当-21时,函数在[-2,1]上单调递减,在[1,a ]上单调递增,则当x =1时,y 取得最小值,即y min =-1.
综上,g (a )=?
????a 2-2a ,-2 -1,a >1. 解题要点 二次函数在闭区间上的最值主要有三种类型:轴定区间定、轴动区间定、轴定区间动,不论哪种类型,解决的关键是考察对称轴与区间的位置关系,当含有参数时,要依据对称轴与区间的位置关系进行分类讨论 题型四 二次函数恒成立问题 例4 对于任意实数x ,函数f (x )=(5-a )x 2-6x +a +5恒为正值,则a 的取值范围是________. 答案 (-4,4) 解析 由题意可得? ???? 5-a >0,36-4(5-a )(a +5)<0, 解得-4<a <4. 变式训练 已知a 是实数,函数f (x )=2ax 2+2x -3在x ∈[-1,1]上恒小于零,求实数a 的取值范围. 解析 2ax 2+2x -3<0在[-1,1]上恒成立. 当x =0时,适合; 当x ≠0时,a <32????1x -132-16, 因为1 x ∈(-∞,-1]∪[1,+∞), 当x =1时,右边取最小值12,所以a <1 2. 综上,实数a 的取值范围是? ???-∞,12. 解题要点 1.二次函数在R 上恒成立的两个常见结论:设f (x )=ax 2+bx +c ,则对于x ∈R , 二次函数f (x )>0恒成立, 二次函数f (x )<0恒成立 . 2.对于二次函数在某区间上恒成立问题,可以采取分离参数法,然后根据a > f (x )恒成立,则a > f (x )max ,a 当堂练习 1.若二次函数f (x )满足f (x +1)-f (x )=2x ,且f (0)=1,则f (x )的表达式为______________. 答案 f (x )=x 2-x +1 解析 设 f (x )=ax 2+bx +c (a ≠0),由题意得??? ?? c =1, a (x +1)2+ b (x +1)+ c -(ax 2+bx +c )=2x . 故???? ? 2a =2,a +b =0,c =1, 解得???? ? a =1, b =-1, c =1, 则f (x )=x 2-x +1. 2.已知f (x )=x 2+bx +c 且f (-1)=f (3),则f (-3)、c 、f (5 2) 的大小关系是______________. 答案 c <f (5 2 )<f (-3) 解析 选.由已知可得二次函数图象关于直线x =1对称.又f (-3)=f (5),c =f (0)=f (2),二次函数在区间(1,+∞)上单调递增,故有f (-3)=f (5)>f (5 2)>f (2)=f (0)=c . 3. 函数y =2x 2-8x +2在区间[-1,3]上的值域为________. 答案 [-6,12] 解析 y =2(x -2)2-6.当x =2时,y 最小为-6;当x =-1时,y 最大为12. 4.已知f (x )=x 2-2mx +5在[2,+∞)上是增函数,则实数m 的取值范围是________. 答案 (-∞,2] 5.若二次函数f (x )=ax 2+bx +c (a ≠0)满足f (x +1)-f (x )=2x ,且f (0)=1. (1)求f (x )的解析式; (2)若在区间[-1,1]上,不等式f (x )>2x +m 恒成立,求实数m 的取值范围. 解析 (1)由f (0)=1,得c =1,∴f (x )=ax 2+bx +1. 又f (x +1)-f (x )=2x , ∴a (x +1)2+b (x +1)+1-(ax 2+bx +1)=2x ,即2ax +a +b =2x . ∴? ????2a =2,a +b =0.∴?????a =1,b =-1. 因此,所求解析式为f (x )=x 2-x +1. (2)f (x )>2x +m 等价于x 2-x +1>2x +m ,即x 2-3x +1-m >0,要使此不等式在区间[-1,1]上恒成立,只需使函数g (x )=x 2-3x +1-m 在区间[-1,1]上的最小值大于0即可. ∵g (x )=x 2-3x +1-m 在区间[-1,1]上单调递减, ∴g (x )min =g (1)=-m -1,由-m -1>0,得m <-1. 因此满足条件的实数m 的取值范围是(-∞,-1). 课后作业 一、 填空题 1.函数y =2x 2-6x +3,x ∈[-1,1],则y 的最小值是________. 答案 -1 解析 函数y =2x 2-6x +3的图象的对称轴为x =3 2>1,∴函数y =2x 2-6x +3在x ∈[-1,1] 上为单调递减函数,∴y min =2-6+3=-1. 2.已知a ,b ,c ∈R ,函数f (x )=ax 2+bx +c .若f (0)=f (4)>f (1),则下列说法正确的是________.(填序号) ①a >0,4a +b =0 ②a <0,4a +b =0 ③a >0,2a +b =0 ④a <0,2a +b =0 答案 ① 解析 由f (0)=f (4)可知x =-b 2a =2,∴b +4a =0,又f (0)>f (1)知f (x )先减后增,即a >0. 3.函数f (x )=ax 2+ax -1在R 上恒满足f (x )<0,则a 的取值范围是________. 答案 -4 解析 当a =0时,f (x )=-1在R 上恒有f (x )<0; 当a ≠0时,∵f (x )在R 上恒有f (x )<0,∴? ??? ?