
第6章相似三角形的判定
(一)知识点梳理
1、相似三角形:各角分别相等,各边成比例的两个三角形相似。
2、相似三角形判定定理:
3、分析方法:
(1)先确定是哪两个三角形
(2)根据已知条件确定使用的判定定理 (3)找出所缺条件 (4)证明相似 (5)得出结论 (二)题型分类全解
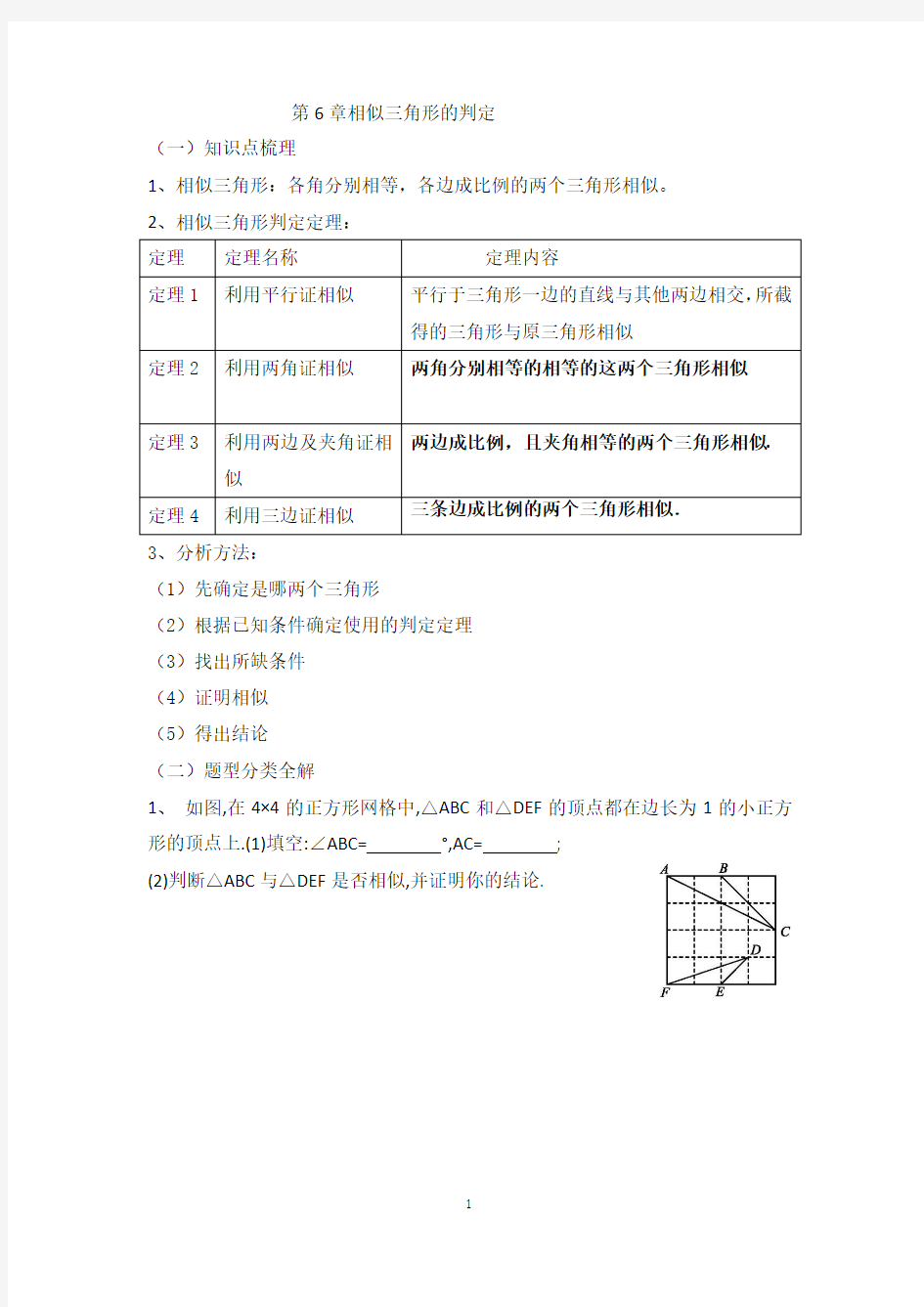
1、 如图,在4×4的正方形网格中,△ABC 和△DEF 的顶点都在边长为1的小正方形的顶点上.(1)填空:∠ABC= °,AC= ; (2)判断△ABC 与△DEF 是否相似,并证明你的结论.
2、如图,在?ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD 交于点G.若=,BE=4,求CE的长.
3、已知:如图,在Rt△ABC和Rt△A'B'C'中,∠C=∠C'=90°,=.
求证:Rt△ABC∽Rt△A'B'C'.
4、如图,在△ABC中,∠C=90°,AB=10,BC=6,点P从点A出发,沿折线AB—BC向终点C运动,在AB上以每秒5个单位长度的速度运动,在BC上以每秒3个单位长度的速度运动.点Q从点C出发,沿CA方向以每秒个单位长度的速度运动.P,Q两点同时出发,当点P停止运动时,点Q也随之停止.设点P运动的时间为t秒.
(1)求线段AQ的长(用含t的代数式表示);
(2)连接PQ,当PQ与△ABC的一边平行时,求t的值
5、如图,AB为☉O的直径,点C在☉O上,AD⊥CD于点D,且AC平分∠DAB.
求证:(1)直线DC是☉O的切线;
(2)AC2=2AD·AO.
6、如图所示,在△ABC中,AB=AC,AD为BC边上的中线,DE⊥AB于点E.
(1)求证:△BDE∽△CAD;
(2)若AB=13,BC=10,求线段DE的长.
7、如图,在△ABC中,AF⊥BC,CE⊥AB,垂足分别为F,E.求证:△BEF∽△BCA.
8、如图,在△ADE中,AD=AE,C为DE延长线上一点,B为ED延长线上一点,∠DAE=40°,则当∠BAC=°时,△BDA∽△AEC.
9、如图,O是△ABC内一点,D,E,F分别为OA,OB,OC上的点,且==.
求证:△DEF∽△ABC.
10、在△ABC中,P是AB上的动点(点P异于点A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有条.
(二)才华展示
1、如图,四边形ABCD是矩形,E是边BC延长线上的一点,AE与CD相交于点F,则图中的相似三角形共有()
A. 4对
B. 3对
C. 2对
D. 1对
2、如图,在矩形ABCD中,AB=,BC=,点E在对角线BD上,且BE=1.8,连接AE并
延长交DC于点F,则=.
3、如图,在△ABC中,AB=8,BC=4,CA=6,CD∥AB,BD是∠ABC的平分线,交AC于点
E.求AE的长.
1、在△ABC中,AB=6,AC=5,点D在边AB上,且AD=2,点E在边AC上,当AE=________ 时,以A、D、E为顶点的三角形与△ABC相似
2、如图,在锐角三角形ABC 中,点D ,E 分别在边AC ,AB 上,AG ⊥BC 于点G ,AF ⊥DE 于点F ,∠EAF =∠GAC.
(1)求证:△ADE ∽△ABC ; (2)若AD =3,AB =5,求AG
AF
的值.
1、 在三角形纸片ABC 中,AB =8,BC =4,AC =6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC 相似的是( )
2、经过三
边都不相等的三角形的一个顶点的线段把三角形分成两个小三角形,如果其中一个是等腰三角形,另外一个三角形和原三角形相似,那么把这条线段定义为原三角形的“和谐分割线”.如图,线段CD是△ABC的“和谐分割线”,△ACD为等腰三角形,△CBD和△ABC相似,∠A=46°,则∠ACB的度数为___________
1、如图,在⊙O中,直径AB=12,弦CE⊥AB,垂足为D,AD∶DB=1∶2,则弦CE=________.
2、如图,四边形ABCD是矩形,连接AC,过点B作BF⊥AC并延长交AD于点E,交CD的延长线于点G,求证:△GED∽△GCF.
三垂直长存在的图形背景
1、如图点A 、B 分别在反比例函数x y 1=
(x>0),x
a
y =(x<0)的图象上.若OA ⊥OB , OA
OB
=2,则a 的值为( ) A. -4 B. 4 C. -2 D. 2
2、如图,已知AB是⊙O的直径,直线l1、l2分别与⊙O相切于点A、B,点P 是切线l1上的一点,连接PO,作QO⊥PO交切线l2于点Q.
(1)求证:△APO∽△BOQ;
(2)连接PQ,试判段直线PQ与⊙O的位置关系,并说明理由.
1、如图,△ABC和△ADE均为等边三角形,点D在BC边上,DE与AC交于点F.
(1)写出图中的相似三角形;
(2)求证:AE2=AF?AC.
2、如图,在△ABC中,AB=AC,点E在边BC上移动(点E不与点B、C重合),
满足∠DEF=∠B,且点D、F分别在边AB、AC上.
(1)求证:△BDE∽△CEF;
(2)当点E移动到BC的中点时,求证:FE平分∠DFC
… 相似三角形的判定练习题 1、如图,点D 在△ABC 的边AC 上,添加 条件,可判定△ADB 与△ABC 相似。 2、如图,在△ABC 中.∠ACB=90°,CD ⊥AB 于点D ,则图中相似三角形有 。 3、如图,在?ABCD 中,E 、F 分别是AD 、CD 边上的点,连接BE 、AF ,他们相交于G ,延长BE 交CD 的延长线于点H ,则图中的相似三角形是 。 4、如图,P 为线段AB 上一点,AD 与BC 交干E ,∠CPD=∠A=∠B ,BC 交PD 于E ,AD 交PC 于G ,则图中相似三角形 有 。 & 5、如图,已知AB=AC ,∠A=36°,AB 的中垂线MD 交AC 于点D 、交AB 于点M .下列结论: ①BD 是∠ABC 的平分线;②△BCD 是等腰三角形;③△ABC ∽△BCD ;④△AMD ≌△BCD .正确的有 。 6、如图,在Rt △ABC 中,AB=AC ,D 、E 是斜边BC 上两点,且∠DAE=45°,将△ADC 绕点A 顺时针旋转90°后,得到△AFB ,连接EF ,下列结论中正确的是 ①∠EAF=45°;②△ABE ∽△ACD ;③EA 平分∠CEF ;④BE 2 +DC 2 =DE 2 7、如图,在△ABC 中,∠ACB=90°,∠A=30°,将△ABC 绕点C 顺时针旋转得到△A′B′C,点B′在AB 上,A′B′交AC 于F ,则图中与△AB'F 相似的三角形有(不再添加其它线段)是 。 8、如图,在正方形ABCD 中,E 是BC 的中点,F 是CD 上一点,且CF= 4 1 CD ,下列结论:①∠BAE=30°,②△ABE ∽△AEF ,③AE ⊥EF ,④△ADF ∽△ECF .其中正确的为 。 、 9、在△ABC 中,∠C=90°,D 是边AB 上一点(不与点A ,B 重合),过点D 作直线与另一边相交,使所得的三角形与原三角形相似,这样的直线有 条。 10、在△ABC 中,AB=6,AC=4,P 是AC 的中点,过P 点的直线交AB 于点Q ,若以A 、P 、Q 为顶点的三角形和以A 、B 、C 为顶点的三角形相似,则AQ 的长为 11、如图,AD ∥BC ,∠D=90°,DC=7,AD=2,BC=4.若在边DC 上有点P 使△PAD 和△PBC 相似,求PD 的值。 ? # 12、如图,在矩形ABCD 中,对角线AC 、BD 相交于点G ,E 为AD 的中点,连接BE 交AC 于F ,连接FD ,若∠BFA=90°,求证:①△ BEA ∽△ACD ;②△FED ∽△DEB ;③△CFD ∽△ABG # 13、如图,△ABC 与△AFG 是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC 分别与AF ,AG 相交于点D ,E .找出图中所有不全等的相似三角形并证明。 ! % 14、如图,四边形ABCD 是平行四边形.O 是对角线AC 的中点,过点O 的直线EF 分别交AB 、DC 于点E 、F ,与CB 、AD 的延长线分 别交于点G 、H . (1)写出图中所有不全等的两个相似三角形(并选择一种情况证明); (2)除AB=CD ,AD=BC ,OA=OC 这三对相等的线段外,图中还有多对相等的线段, 请选出其中一对加以证明. ]
相似三角形的判定练习 【知能点分类训练】 知能点1 角角识别法 1.如图1,(1)若OA OB =_____,则△OAC∽△OBD,∠A=________. (2)若∠B=________,则△OAC∽△OBD,________与________是对应边. (3)请你再写一个条件,_________,使△OAC∽△OBD. 2.如图2,若∠BEF=∠CDF,则△_______∽△________,△______∽△_______. (1) (2) (3) 3.如图3,已知A(3,0),B(0,6),且∠ACO=?∠BAO,?则点C?的坐标为________,?AC=_______. 4.已知,如图4,△ABC中,DE∥BC,DF∥AC,则图中共有________对相似三角形.5.下列各组图形一定相似的是(). A.有一个角相等的等腰三角形 B.有一个角相等的直角三角形 C.有一个角是100°的等腰三角形 D.有一个角是对顶角的两个三角形 6.如图5,AB=BC=CD=DE,∠B=90°,则∠1+∠2+∠3等于(). A.45° B.60° C.75° D.90° (4) (5) (6) 7.如图6,若∠ACD=∠B,则△_______∽△______,对应边的比例式为_____________,∠ADC=________. 8.如图,在△ABC中,CD,AE是三角形的两条高,写出图中所有相似的三角形,简要说明理由.
9.如图,D ,E 是AB 边上的三等分点,F ,G 是AC 边上的三等分点,?写出图中的相似三角形,并求出对应的相似比. 10.如图,在直角坐标系中,已知点A (2,0),B (0,4),在坐标轴上找到点C (1,0)?和点D ,使△AOB 与△DOC 相似,求出D 点的坐标,并说明理由. 【综合应用提高】 11.已知:如图是一束光线射入室内的平面图,?上檐边缘射入的光线照在距窗户 2.5m 处,已知窗户AB 高为2m ,B 点距地面高为1.2m ,求下檐光线的落地点N?与窗户的距离NC . 12.如图,等腰直角三角形ABC 中,顶点为C ,∠MCN=45°,试说明△BCM ∽△ANC . 13.在ABCD 中,M ,N 为对角线BD 的三等分点,连接AM 交BC 于E ,连接EN 并延长交AD 于F .(1)试说明△AMD ∽△EMB ;(2)求FN NE 的值.
初三数学相似三角形 (一)相似三角形是初中几何的一个重点,同时也是一个难点,本节复习的目标是: 1. 理解线段的比、成比例线段的概念,会根据比例线段的有关概念和性质求线段的长或两线段的比,了解黄金分割。 2. 会用平行线分线段成比例定理进行有关的计算、证明,会分线段成已知比。 3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。 4. 能熟练运用相似三角形的有关概念解决实际问题 本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。 本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。 相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在10%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。 (二)重要知识点介绍: 1. 比例线段的有关概念: 在比例式 ::中,、叫外项,、叫内项,、叫前项,a b c d a b c d a d b c a c ==() b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。 把线段AB 分成两条线段AC 和BC ,使AC 2 =AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。 2. 比例性质: ①基本性质: a b c d ad bc =?= ②合比性质: ±±a b c d a b b c d d =?= ③等比性质: ……≠……a b c d m n b d n a c m b d n a b ===+++?++++++=()0 3. 平行线分线段成比例定理: ①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。 则 ,,,…AB BC DE EF AB AC DE DF BC AC EF DF ===
第一节:相似形与相似三角形 基本概念: 1.相似形:对应角相等,对应边成比例的两个多边形,我们称它们互为相似形。 2.相似三角形:对应角相等,对应边成比例的两个三角形,叫做相似三角形。 1.几个重要概念与性质(平行线分线段成比例定理) (1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知a ∥b ∥c, A D a B E b C F c 可得 EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB =====或或或或 等. (2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C 由DE ∥BC 可得:AC AE AB AD EA EC AD BD EC AE DB AD = ==或或.此推论较原定理应用更加广泛,条件是平行. (3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线. (4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. (5)①平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。 ②比例线段:四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即b a =d c ,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。 2.比例的有关性质 ①比例的基本性质:如果 d c b a =,那么ad=b c 。如果ad=bc (a ,b ,c , d 都不等于0),那么 d c b a =。 ②合比性质:如果 d c b a =,那么d d c b b a ±=±。
相似三角形经典模型总结 经典模型 【精选例题】“平行型” 【例1】 如图,111EE FF MM ∥∥,若AE EF FM MB ===, 则1 11 1 1 1 :::_________AEE EE F F FF M M MM CB S S S S ?=四边形四边形四边形 【例2】 如图,AD EF MN BC ∥∥∥,若9AD =, 18BC =,::2:3:4AE EM MB =,则 _____EF =,_____MN = 【例3】 已知,P 为平行四边形ABCD 对角线,AC 上一点,过点P 的 直线与AD ,BC ,CD 的延长线,AB 的延长线分别相交于点E ,F ,G ,H 求证: PE PH PF PG = M 1F 1E 1M E F A B C M N A B C D E F P H G F E D C B A
【例4】 已知:在ABC ?中,D 为AB 中点,E 为AC 上一点,且 2AE EC =,BE 、CD 相交于点F , 求BF EF 的值 【例5】 已知:在ABC ?中,12AD AB = , 延长BC 到F ,使1 3 CF BC =,连接FD 交AC 于点E 求证:①DE EF = ②2AE CE = 【例6】 已知:D ,E 为三角形ABC 中AB 、BC 边上的点,连接DE 并延长交AC 的延长线于点F ,::BD DE AB AC = 求证:CEF ?为等腰三角形 【例7】 如图,已知////AB EF CD ,若AB a =,CD b =,EF c =,求证: 111c a b =+. F E D C B A 【例8】 如图,找出ABD S ?、BED S ?、BCD S ?之间的关系,并证明你的结论. F E D C B A 【例9】 如图,四边形ABCD 中,90B D ∠=∠=?,M 是AC 上一点,ME AD ⊥于点E ,MF BC ⊥于点F 求证: 1MF ME AB CD += F E D C B A A B C D F E F E D C B A
相似三角形基本类型一、“X”型. B C B C 二、“子母”,“A型”,“斜A ”. B B B (双垂直K型)三、“K”型
C B (三垂直K 型) A C D B C A B D 四、共享型 A B E C D
A B E B B 1.在△ABC 和△ADE 中,∠BAD=∠CAE ,∠ABC=∠ADE. A B E
1.如图,已知∠1=∠2,∠3=∠4,求证∠ABE=∠ACD. A B D 2. A B P 3.如图,已知C 是线段AB 上的任意一点(端点除外),分别以AC 、BC 为斜边并且在AB 的 同一侧作等腰直角△ACD 和△BCE ,连结AE 交CD 于点M ,连结BD 交CE 于点N ,给出以下三个结论:①MN ∥AB ;②1MN =1AC +1 BC ;③M N≤14AB ,其中正确结论的个数 是( ) A .0 B .1 C .2 D .3
F E C B B' C' 4.如图,Rt △AB 'C ' 是由Rt △ABC 绕点A 顺时针旋转得到的,连结CC ' 交斜边于点E , CC ' 的延长线交BB ' 于点F . (1)证明:△ACE ∽△FBE ; (2)设∠ABC =α,∠CAC ' =β,试探索α、β满足什么关系时,△ACE 与△FBE 是全 等三角形,并说明理由. 5.
A D B 6.在等边△ABC 中,D 为BC 边上一点,E 为AC 边上一点,且∠ADE=60°,BD=3,CE=2,则△ABC 的边长为_________. A B C D 7. 0 90A E ∠=∠=°, 1 2 EDB C ∠= ∠. (1)当AB=AC 时,①∠EBF=_________.
相似三角形的判定练习题 1、如图,点D在△ABC的边AC上,添加条件,可判定△ADB与△ABC相似。 2、如图,在△ABC中.∠ACB=90°,CD⊥AB于点D,则图中相似三角形有。 3、如图,在?ABCD中,E、F分别是AD、CD边上的点,连接BE、AF,他们相交于G,延长BE交CD的延长线于点H,则图中 的相似三角形是。 4、如图,P为线段AB上一点,AD与BC交干E,∠CPD=∠A=∠B,BC交PD于E,AD交PC于G,则图中相似三角形 有。 5、如图,已知AB=AC,∠A=36°,AB的中垂线MD交AC于点D、交AB于点M.下列结论: ①BD是∠ABC的平分线;②△BCD是等腰三角形;③△ABC∽△BCD;④△AMD≌△BCD.准确的有。 6、如图,在Rt△ABC中,AB=AC,D、E是斜边BC上两点,且∠DAE=45°,将△ADC绕点A顺时针旋转90°后,得到△AFB, 连接EF,下列结论中准确的是①∠EAF=45°;②△ABE∽△ACD;③EA平分∠CEF;④BE2+DC2=DE2 7、如图,在△ABC中,∠ACB=90°,∠A=30°,将△ABC绕点C顺时针旋转得到△A′B′C,点B′在AB上,A′B′交AC于F,则图 中与△AB'F相似的三角形有(不再添加其它线段)是。 8、如图,在正方形ABCD中,E是BC的中点,F是CD上一点,且CF= 4 1 CD,下列结论:①∠BAE=30°,②△ABE∽△AEF, ③AE⊥EF,④△ADF∽△ECF.其中准确的为。 9、在△ABC中,∠C=90°,D是边AB上一点(不与点A,B重合),过点D作直线与另一边相交,使所得的三角形与原三角形相 似,这样的直线有条。 10、在△ABC中,AB=6,AC=4,P是AC的中点,过P点的直线交AB于点Q,若以A、P、Q为顶点的三角形和以A、B、C 为顶点的三角形相似,则AQ的长为 11、如图,AD∥BC,∠D=90°,DC=7,AD=2,BC=4.若在边DC上有点P使△PAD和△PBC相似,求PD的值。 12、如图,在矩形ABCD中,对角线AC、BD相交于点G,E为AD的中点,连接BE交AC于F,连接FD,若∠BFA=90°,求 证:①△BEA∽△ACD;②△FED∽△DEB;③△CFD∽△ABG 13、如图,△ABC与△AFG是两个全等的等腰直角三角形,∠BAC=∠F=90°,BC分别与AF,AG相交于点D,E.找出图中所有 不全等的相似三角形并证明。 14、如图,四边形ABCD是平行四边形.O是对角线AC的中点,过点O的直线EF分别交AB、DC于点E、F,与CB、AD的 延长线分别交于点G、H. (1)写出图中所有不全等的两个相似三角形(并选择一种情况证明); (2)除AB=CD,AD=BC,OA=OC这三对相等的线段外,图中还有多对相等的线段,请选出其中一对加以证明.
2019-2020 年中考数学《相似三角形的判定》专题练习含解析考点分类汇编 学习要求 1.掌握相似三角形的判定定理. 2.能通过证三角形相似,证明成比例线段或进行计算. 课堂学习检测 一、填空题 1. ______三角形一边的______和其他两边 ______,所构成的三角形与原三角形相似. 2.如果两个三角形的______对应边的 ______,那么这两个三角形相似. 3.如果两个三角形的______对应边的比相等,并且______相等,那么这两个三角形相似. 4.如果一个三角形的______角与另一个三角形的______,那么这两个三角形相似. 5.在△ ABC 和△ A′B′ C′中,如果∠ A= 56°,∠ B=28°,∠ A′= 56°,∠ C′=28°,那么这两个三角形能否相似的结论是______.理由是 ________________.6.在△ ABC 和△ A'B′ C′中,如果∠ A= 48°,∠ C=102°,∠ A′= 48°,∠ B′=30°,那么这两个三角形能否相似的结论是______.理由是 ________________.7.在△ ABC 和△ A'B′ C′中,如果∠ A= 34°, AC= 5cm, AB= 4cm,∠ A′= 34°,A'C′= 2cm, A′B′= 1.6cm,那么这两个三角形能否相似的结论是______,理由是____________________ . 8.在△ ABC 和△ DEF 中,如果 AB= 4,BC= 3,AC=6;DE= 2.4,EF= 1.2,FD = 1.6,那么这两个三角形能否相似的结论是____________,理由是 __________________.9.如图所示,△ABC 的高 AD ,BE 交于点 F,则图中的相似三角形共有______对. 第 9 题图第 10 题图 10.如图所示,□ABCD 中, G 是 BC 延长线上的一点, AG 与 BD 交于点 E,与 DC 交于点 F ,此图中的相似三角形共有______对. 二、选择题 11.如图所示,不能判定△ ABC∽△ DAC 的条件是 ( ) A .∠ B=∠ DAC B.∠ BAC=∠ ADC C. AC 2= DC· BC D. AD2= BD· BC 第 11 题第 12 题 12.如图,在平行四边形 ABCD 中, AB= 10, AD= 6,E 是 AD 的中点,在 AB 上取一点 F ,使△ CBF ∽△ CDE ,则 BF 的长是 ( ) A . 5 B . 8.2 C. 6.4 D . 1.8 13.如图所示,小正方形的边长均为 1,则下列选项中阴影部分的三角形与△ABC 相似的是 ( )
D C B A D C B A C B A C B A C B C P 《相似三角形中分类讨论思想的运用》 一、温故知新: 1. 已知△ABC 的三边长分别是4、6、8,△DEF 的一条边为24,如果△DEF 与△ABC 相似,则相似比为 2.两个相似三角形的面积之比是9:25,其中一个三角形一边上的高是6,那么另一个三角形对应边上的高为 3.已知线段AB=2,P 是线段AB 的黄金分割点,则AP 的长为 问题:什么是分类讨论?为什么要分类? 二、新知学习: 题组一: 1.例1.如图所示,在ABC ?中,AB=6,AC=4,P 是AC 的中点,过P 点的直线交AB 于点Q ,若使APQ ?与ABC ?相似,则AQ 的长为 2.变式一:如图所示, 在ABC ?中,P 是AC 上一点,过P 点的直线截ABC ?交AB 于点Q ,使截得的三角形与原三角形相似,则满足这样的直线有 条. 3. 变式二:如图所示,在ABC ?中,P 是AC 上一点,过P 点的直线截ABC ?,使截得的三角形与原三角形相似,则满足这样的直线最多有 条. 探究:如果ABC ?是直角三角形,点P 直角边上或点P 在斜边上上述结论还成立吗?等腰三角形呢? 题组二: 1.例2: 己知菱形ABCD 的边长是3,点E 在直线AD 上,DE =1,联结BE 与对角 线AC 相交于点M ,则MC AM = C B C B C B
2.变式一: 等腰ABC 中,AB=AC=10,BC=16,点P 在BC 边上,若PA 与腰垂直,则BP= . 3. 变式二: 在△ABC 中∠B=25°,AD 是BC 边上的高,并且AD 2=BD ·DC,则∠BCA= . 题组三 1.在矩形ABCD 中,AB=4,AD=5,P 是射线BC 上的一个动点,作PE ⊥AP ,PE 交射线DC 于点E ,射线AE 交射线BC 于点F ,设BP=x ,CE=y .求y 关于x 的函数解析式,并写出它的定义域;(点P 与点B 、C 都不重合), 2.已知AB=2,AD=4,∠DAB=90°,AD∥BC(如图).E 是射线BC 上的动点(点E 与点B 不重合),M 是线段DE 的中点.联结BD ,交线段AM 于点N ,如果以A 、N 、D 为顶点的三角形与△BME 相似,求线段BE 的长. 三、课后反思: 1. 相似三角形中有哪些几何情境需要分类讨论?分类的原则是什么? 2. 请积累你运用分类讨论思想解决的数学问题. A C D A C D
①定理:三条平行线截两条直线,所得的对应线段成比例,如图:l 1∥l 2∥l 3。 则,,,…AB BC DE EF AB AC DE DF BC AC EF DF === ②推论:平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例。 ③定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边。 ○4推论:如果一条直线平行于三角形的一条边,截其它两边(或其延长线),那么所截得的三角形与原三角形相似.推论○4的基本图形有三种情况,如图其符号语言:∵DE ∥BC ,∴△ABC ∽△ADE ; 知识点二、相似三角形的判定
判定定理1:两角对应相等,两三角形相似. 符号语言: 拓展延伸: (1)有一组锐角对应相等的两个直角三角形相似。 (2)顶角或底角对应相等的两个等腰三角形相似。 例题1.如图,直线DE 分别与△ABC 的边AB 、AC 的反向延长线相交于D 、E ,由ED ∥BC 可以推出 AD AE BD CE = 吗?请说明理由。(用两种方法说明) 例题2.(射影定理)已知:如图,在△ABC 中,∠BAC=90°,AD ⊥BC 于D. 求证:(1)2AB BD BC =?;(2)2AD BD CD =?;(3)CB CD AC ?=2 例题3.如图,AD 是Rt ΔABC 斜边BC 上的高,DE ⊥DF ,且DE 和DF 分别交AB 、AC 于E 、F.则 BD BE AD AF =例题精讲 A E D B C A B C D
吗?说说你的理由. 例题4.如图,在平行四边形ABCD 中,已知过点B 作BE ⊥CD 于E,连接AE ,F 为AE 上一点,且∠BFE=∠C (1) 求证:△ABF ∽△EAD ; (2)若AB=4,∠BAE=30°,求AE 的长;3分之8倍根号3 (3)在(1)(2)条件下,若AD=3,求BF 的长。 2分之3倍根号3 随练: 一、选择题 1.如图,△ABC 经平移得到△DEF ,AC 、DE 交于点G ,则图中共有相似三角形( )D A . 3对 B . 4对 C . 5对 D . 6对 2.如图,已知DE ∥BC ,EF ∥AB ,则下列比例式中错误的是( )C A D C B E F G F E D C B A
相似三角形的判定 中考要求 重难点 1.相似定义,性质,判定,应用和位似 2.相似的判定和证明 3.相似比的转化 课前预习 相似三角形的由来 两千六百多年前,埃及有个国王,想知道已经给他盖好了的大金字塔的实际高度,于是,命令祭司们去丈量.可是,没有一个祭司知道该怎样测量,往这个问题面前,祭司们个个束手无策.既然,人是不可能爬到那么高大的塔顶上去的;即使爬上去了,由于塔身是斜的,又怎样来量呢?一时,金字塔的高度成了一个难题.国王一气之下,杀死了几个祭司,同时悬赏求解答. 有一个叫法涅斯的学者,看到国王的招字后,决心解決这个难题.他想了好几个解题的方案,但都行不通.失败并没使他灰心.法涅斯索性来到外面,一边踱步,一边思索著解決的辦法,以致撞到树上.于是,他转了个圈,又走下去.太阳把他的影子投到地上,他走到那里,影子也跟到那里.这时,他突然看到自己的影子,于是想:是不是可以请太阳来帮忙呢?在古埃及人的眼里,太阳是万能的,太阳能给人温暖,能帮助人们确定方向,法涅斯眼前一亮,他清楚记得,早上和傍晚每个物体都拖著一个长长的影子,而中午每个物体的影子都很短…那么,是不是有一个时刻,物体的影子就等于物体的高度怩?﹁他自言自
语起来. 想到这里,法涅斯就找了一根竿子,竖在太阳底下,认真观察、测量起來.经过几天的观察、测量,法涅斯终于证实了自己的想法一有一个时候,物体的影子等于物体的高度.于是,他去测量好金字塔底边的长度,并把数据记下来.然后,他毫不犹豫地揭下了悬挂的招字.国王得到“有人揭下招字”的报告后,高兴万分,派人把法涅斯召进王官,盛情款待,一切准备停当后,国王选择了一个风和日丽的日子,举行测塔仪式.测塔这天,国王在祭司们的陪同下,和法捏斯一起来到金字塔旁.看热闹的人黑压压一片,喧闹着,拥挤著,他们等待着壮观的一刻到来,法涅斯站在测塔指挥台上,俨然像个天使,一动也不动地注视着自己的影子.看看时间快到了,太阳光给每一个在旁的人和巨大的金字塔都投下了黑黑的影子.当法涅斯确定他自己的影子已等于他的身高时,便发出了测塔的命令。这时,助手们立即测出了金字塔的阴影CD 的长.接着,法涅斯十分准确地算出了金字塔的高度,最后,他还把测量金字塔高度的秘密告訴大家.场上,发出一阵热烈的观呼声.当然,法涅斯利用了相似三角形的原理测得了塔高.在法捏斯以前,还沒有人知道这个原理呢!法捏斯第一次发现、利用这个原理.在那个时代,这是一个伟大的创举! 在这个基础上,法涅斯进一步研究,得出一个法则:在任意两個对应角相等的三角形中,对应边的比率也相等.从而,找到了在任何季节里,在任何时候都能测塔高的方法. 例题精讲 模块一 相似三角形的判定 ?角对应相等、边对应成比例,三角形相似 对应角相等,对应边成比例的三角形叫做相似三角形. 如图,在ABC △与A B C '''△中,',','A A B B C C ∠=∠∠=∠∠=∠, ''''''AB BC AC A B B C A C == ,则ABC △与A B C '''△相似,记作ABC A B C '''△∽△,符号∽读作“相似于” . A ' B ' C ' C B A 相似三角形对应边的比叫做相似比.全等三角形的相似比是1.“全等三角形”一定是“相似形”,“相似形”不一定是“全等形”. 【例1】 如图,已知四边形ABCD 是平行四边形.求证:MEF MBA △∽△. M F E D C B A
初三数学相似三角形典型例题(含答案)
————————————————————————————————作者:————————————————————————————————日期:
初三数学相似三角形 (一)相似三角形是初中几何的一个重点,同时也是一个难点,本节复习的目标是: 1. 理解线段的比、成比例线段的概念,会根据比例线段的有关概念和性质求线段的长或两线段的比,了解黄金分割。 2. 会用平行线分线段成比例定理进行有关的计算、证明,会分线段成已知比。 3. 能熟练应用相似三角形的判定和性质解答有关的计算与证明题。 4. 能熟练运用相似三角形的有关概念解决实际问题 本节的重点内容是相似三角形的判定定理和性质定理以及平行线分线段成比例定理。 本节的难点内容是利用判定定理证明两个三角形相似以及相似三角形性质的应用。 相似三角形是平面几何的主要内容之一,在中考试题中时常与四边形、圆的知识相结合构成高分值的综合题,题型常以填空、选择、简答或综合出现,分值一般在10%左右,有时也单独成题,形成创新与探索型试题;有利于培养学生的综合素质。 (二)重要知识点介绍: 1. 比例线段的有关概念: 在比例式::中,、叫外项,、叫内项,、叫前项,a b c d a b c d a d b c a c ==() b 、d 叫后项,d 叫第四比例项,如果b=c ,那么b 叫做a 、d 的比例中项。 把线段AB 分成两条线段AC 和BC ,使AC 2=AB ·BC ,叫做把线段AB 黄金分割,C 叫做线段AB 的黄金分割点。 2. 比例性质: ①基本性质:a b c d ad bc =?= ②合比性质:±±a b c d a b b c d d =?= ③等比性质: ……≠……a b c d m n b d n a c m b d n a b ===+++?++++++=()0
《相似三角形》判定与性质测试卷 一、细心填一填(共30分) 1.已知:如图,在ABC △中,DE ∥BC ,DE 分别与AB 、AC 相交于D 、E ,:1:3AD AB =.若2DE =,则BC =_________. 第1题图 第2题图 第6题图 第7题图 2.在□ABCD 中,E 为CD 上一点,连接AE 、BD,且AE 、BD 交于点F ,S △DEF :S △ABF =4:25,则DE :AB=_________. 3.已知789x y z ==,则x y z x z +++的值为 . 4.在一张由复印机复印出来的纸上,一个多边形图案的一条边由原来的1cm 变成2cm ,那么这次复印出来的多边形图案面积是原来的 . 5.已知,,,a b c d 是成比例线段,且3,6,15,a cm b cm c cm d ===则= . 6.如图,路灯距离地面8米,身高1.6米的小明站在距离灯的底部(点O )20米的A 处,则小明的影子AM 长为 米. 7.如图,∠DAB=∠CAE,请你再补充一个条件___ (写一个即可)使得△ABC ∽△ADE. 8.在ΔABC 中,AB =4,BC =9,AC =8,在AC 上取一点M ,当AM 的长为 时,ΔAMB∽ΔABC. 9.如图,已知L 1//L 2//L 3,下列比例式中不成立的是 . (填序号及可) ① BC CE DF AD = ②AF BC BE AD = ③CE AD DF BC = ④CE BE DF AF = 第9题图 第11题图 第13题图 10.已知AD 为Rt △ABC 斜边BC 上的高,且AB=15cm ,BD=9cm ,则AD= ,CD= . 二、选择题 (每题3分,共30分) 11.如图,在Rt △ABC 中,AD ⊥BC 与D ,DE ⊥AB 与E ,若AD=3,DE=2,则AC=( ) A 、2 21 B 、215 C 、29 D 、15 12.下列三角形中,一定相似的是( ) A .两个等腰三角形 B .两个直角三角形 C .两个等边三角形 D .两个钝角三角形
相似三角形的判定的习题分类编选 一、利用“两角对应相等的两个三角形相似”证明三角形相似. 1.如图,(1)当∠C=_________时,△OAC∽△OBD.(2)当∠B=_________时,△OAC∽△ODB。 (3)当∠A=_____________,△OAC与△OBD相似. 2.如图2,若∠BEF=∠CDF,则△_____,_∽△_______,△_____∽△______. 3.下列各组图形一定相似的是(). A.有一个角相等的等腰三角形 B.有一个角相等的直角三角形 C.有一个角是100°的等腰三角形 D.有一个角是对顶角的两个三角形 4.如图3,已知A(2,0),B(0,4),且∠ACO=?∠BAO,?则点C?的坐标为________ 5.如图4,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC,DE∥BC,那么与△ABC相似的三角形有______个 图1 图2 图3 图4 图5 图 6 6在△ABC中,M是AB上一点,若过M的直线所截得的三角形与原三角形相似,则满足条件的直线最多有_____条.7.如图5,在△ABC中,CD,AE是三角形的两条高,则图中的相似三角形有_______对. 8.如图6,等腰直角三角形ABC中,顶点为C,∠MCN=45°,图中有______对相似三角形 9.如图,△ABC和△DEF均为正三角形,D,E分别在AB,BC上, 则图中与△DBE相似的三角形是________. 10、如图,在△ABC和△ADE中,∠BAD=∠CAE,∠ABC=∠ADE. 写出图中两对相似三角形(不得添加辅助线);并证明这两对三角形相似. 11、如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F. (1)求证:⊿ABD≌⊿BCE。 (2)求证:⊿AEF∽⊿BEA (3)求证:BD2=AD·DF。 12、如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B. (1)求证:△ADF∽△DEC。(2)若AB=4,AD=33,AE=3,求AF的长. 13如图,四边形ABCD是平行四边形,点F在BA的延长线上,连接CF交AD?于点E. 求证:△CDE∽△FAE.
相似三角形 一.选择题 1.如图,D、E分别是AB、AC上两点,CD与BE相交于点O,下列条件中不能使△ABE和△ACD相似的是() A.∠B=∠C B.∠ADC=∠AEB C.BE=CD,AB=AC D.AD:AC=AE:AB 2.如图,△ACD和△ABC相似需具备的条件是() A. B. C.AC2=AD?AB D.CD2=AD?BD 3.如图,在等边三角形ABC中,D为AC的中点,,则和△AED(不包含△AED)相似的三角形有() A.1个 B.2个 C.3个 D.4个 4.如图,已知点P是Rt△ABC的斜边BC上任意一点,若过点P作直线PD与直角边AB或AC相交于点D,截得的小三角形与△ABC相似,那么D点的位置最多有() A.2处 B.3处 C.4处 D.5处 5.如图,在矩形ABCD中,E、F分别是CD、BC上的点.若∠AEF=90°,则一定有() A.△ADE∽△ECF B.△BCF∽△AEF C.△ADE∽△AEF D.△AEF∽△ABF 6.在△ABC中,∠ACB=90°,用直尺和圆规在AB上确定点D,使△ACD∽△CBD,根据作图痕迹判断,正确的是()
A. B. C. D. 7.如图,点D,E分别在△ABC的AB,AC边上,增加下列条件中的一个:①∠AED=∠B,②∠ADE=∠C,③,④,⑤AC2=AD?AE,使△ADE与△ACB一定相似的有() A.①②④ B.②④⑤ C.①②③④ D.①②③⑤ 8.如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为() A.3:4 B.9:16 C.9:1 D.3:1 9.如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交AD的延长线于点E.若AB=12,BM=5,则DE的长为() A.18 B.C. D. 10.如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论: ①BE=2AE;②△DFP∽△BPH;③△PFD∽△PDB;④DP2=PH?PC 其中正确的是() A.①②③④ B.②③ C.①②④ D.①③④ :S 11.如图,在平行四边形ABCD中,E为CD上一点,连接AE、BE、BD,且AE、BD交于点F,S △DEF =4:25,则DE:EC=() △ABF
知识梳理 相似三角形的概念 对应角相等,对应边成比例的三角形,叫做相似三角形. 相似用符号“∽”表示,读作“相似于”. 相似三角形对应边的比叫做相似比(或相似系数). 相似三角形对应角相等,对应边成比例. 注意: ①对应性:即两个三角形相似时,通常把表示对应顶点的字母写在对应位置上,这样写比较容易 找到相似三角形的对应角和对应边. ②顺序性:相似三角形的相似比是有顺序的. ③两个三角形形状一样,但大小不一定一样. ④全等三角形是相似比为1的相似三角形.二者的区别在于全等要求对应边相等,而相似要求对 应边成比例. 相似三角形的基本定理 定理:平行于三角形一边的直线和其它两边(或两边延长线)相交,所构成的三角形与原 三角形相似. 定理的基本图形: 用数学语言表述是:
BC DE // , ADE ∽ABC . 相似三角形的等价关系 (1)反身性:对于任一ABC 有ABC ∽ABC . (2)对称性:若ABC ∽'''C B A ,则'''C B A ∽ABC . (3)传递性:若ABC ∽C B A '',且C B A ''∽C B A ,则ABC ∽C B A . 三角形相似的判定方法 1、定义法:对应角相等,对应边成比例的两个三角形相似. 2、平行法:平行于三角形一边的直线和其它两边(或两边的延长线)相交,所构成的三角 形与原三角形相似. 3、判定定理1:如果一个三角形的两个角与另一个三角形的两个角对应相等,那么这两 个三角形相似.简述为:两角对应相等,两三角形相似. 4、判定定理2:如果一个三角形的两条边和另一个三角形的两条边对应成比例,并且夹 角相等,那么这两个三角形相似.简述为:两边对应成比例且夹角相等,两三角形相似. 5、判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这 两个三角形相似.简述为:三边对应成比例,两三角形相似.(在遇到两个三角形的三边都知道的情况优先考虑,把边长分别从小到大排列,然后分别计算他们的比值是否相等来判断是否相似) 6、判定直角三角形相似的方法: (1)以上各种判定均适用. (2)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似. (3)直角三角形被斜边上的高分成的两个直角三角形与原三角形相似. 直角三角形中,斜边上的高是两直角边在斜边上射影的比例中项。每一条直角边是这条直角边在斜边上的射影和斜边的比例中项。 公式 如图,Rt △ABC 中,∠BAC=90°,AD 是斜边BC 上的高,则有射影定理如下: (1)(AD )2=BD ·DC , (2)(AB )2=BD ·BC , (3)(AC )2=CD ·BC 。 证明:在 △BAD 与△ACD 中,∠B+∠C=90°,∠DAC+∠C=90°,∴∠B=∠DAC ,又∵∠ BDA=∠ADC=90°,∴△BAD ∽△ACD 相似,∴ AD/BD =CD/AD ,即 (AD )2=BD ·DC 。其余类似可证。 注:由上述射影定理还可以证明勾股定理。由公式(2)+(3)得: (AB )2+(AC )2=BD ·BC+CD ·BC =(BD+CD)·BC=(BC )2, 即 (AB )2+(AC )2=(BC )2。 这就是勾股定理的结论。 判断相似三角形的几条思路: 1 条件中若有平行线,可采用相似三角形的基本定理 2 条件中如果有一对等角,可再找一对等角(用判定1)或再找夹边成比例。(用判定2)3条件中若有两边对应成比例,可找夹角相等(直角可以直接得出相似)4条件中若有一对直角,可考虑在找一对等角或证明斜边,直角边对应成比例。5条件中若
《相似三角形的判定》专题练习 1.下列命题中正确的是( ) ① 任意两个等腰三角形都相似 ② 任意两个直角三角形都相似 ③ 任意两个等边三角形都相似 ④ 任意两个等腰直角三角形都相似 A .①③ B .①④ C .②④ D .③④ 2.在△ABC 和△A 1B 1C 1中,有下列条件:① 1111AB BC A B B C =,② 1111 BC AC B C A C = ,③∠A =∠A 1 ,④∠B =∠B 1 ,⑤∠C =∠C 1 ,如果从中任取两个条件组成一组,那么能判断△ABC ∽△A 1B 1C 1的有( ) A .4组 B .5组 C .6组 D .7组 3.在等腰△ABC 和等腰△DEF 中,∠A 与∠D 是顶角,下列判断正确的是( ) ①∠A =∠D 时,两三角形相似; ②∠A =∠ E 时,两三角形相似; ③EF DE BC AB =时,两三角形相似; ④∠B =∠E 时,两三角形相似。 A .1个 B .2个 C .3个 D .4个 4.如图,P 是Rt △ABC 的斜边BC 上异于B ,C 的一点,过P 点作直线截△ABC ,使截得的三角形与△ABC 相似,满足这样条件的直线共有( ) A .1条 B .2条 C .3条 D .4条 5.如图所示,点E 是 ABCD 的边BC 延长线上的一点,AE 与CD 相交于点F ,则图中相似三角形共有( ) A .2对 B .3对 C .4对 D .5对 6.如图,锐角△ABC 的高CD 和B E 相交于点O ,图中与△ODB 相似的三角形有( ) A .4个 B .3个 C . 2个 D .1个 (第4题图) (第5题图) (第6题图) 7.如图,在大小为4×4的正方形网格中,是相似三角形的是( ) ① ② ③ ④ A .①和② B .①和③ C .②和③ D .②和④ 8.如图,若A 、B 、C 、P 、Q 、甲、乙、丙、丁都是方格纸中的格点,为使△PQR∽△ABC,则点R 应是甲、乙、丙、 丁四点中的( ) A .甲 B .乙 C .丙 D .丁 9.如图:点P 是△ABC 边AB 上一点(AB >AC ),下列条件不一定能使△ACP ∽△ABC 的是( )
相似三角形分类整理 (超全)
第一节:相似形与相似三角形 基本概念: 1.相似形:对应角相等,对应边成比例的两个多边形,我们称它们互为相似形。 相似三角形:对应角相等,对应边成比例的两个三角形,叫做相似三角形。 1.几个重要概念与性质(平行线分线段成比例定理) (1)平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例. 已知a ∥b ∥c, A D a B E b C F c 可得EF BC DE AB DF EF AC BC DF EF AB BC DF DE AC AB EF DE BC AB = ====或或或或 等. (2)推论:平行于三角形一边的直线截其它两边(或两边的延长线)所得的对应线段成比例. A D E B C 由DE ∥BC 可得: AC AE AB AD EA EC AD BD EC AE DB AD ===或或.此推论较原定理应用更加广泛,条件是平行. (3)推论的逆定理:如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例.那么这条直线平行于三角形的第三边. 此定理给出了一种证明两直线平行方法,即:利用比例式证平行线. (4)定理:平行于三角形的一边,并且和其它两边相交的直线,所截的三角形的三边与原三角形三边对应成比例. (5)①平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似。 ②比例线段:四条线段a ,b ,c ,d 中,如果a 与b 的比等于c 与d 的比,即b a =d c ,那么这四条线段a ,b ,c ,d 叫做成比例线段,简称比例线段。 2.比例的有关性质 ①比例的基本性质:如果 d c b a =,那么ad=b c 。如果ad=bc (a ,b ,c , d 都不等于0),那么 d c b a =。