matlab中有关膨胀与腐蚀的解释

膨胀与腐蚀对偶证明
膨胀与腐蚀是一对互为对偶的概念。

在数学中，对偶是指一个概念与它的对立面之间的关系。

对偶是一种反转的过程，通过它可以将一个概念转化成另一个概念。

在图像处理中，膨胀和腐蚀是两个重要的操作，它们可以用来改变图像的形态和结构。

膨胀是一种形态学操作，用来增强图像的亮度和粗细。

它将每个像素与它的邻域进行比较，并将像素的值设置为邻域的最大值。

这样做可以使图像中的白色区域变得更大和更连通。

腐蚀是一种形态学操作，用来减小图像的亮度和粗细。

它将每个像素与它的邻域进行比较，并将像素的值设置为邻域的最小值。

这样做可以使图像中的黑色区域变得更大和更连通。

膨胀和腐蚀是互为对偶的操作。

这意味着，对一个图像进行膨胀操作，然后对结果进行腐蚀操作，可以得到原始图像。

同样地，对一个图像进行腐蚀操作，然后对结果进行膨胀操作，也可以得到原始图像。

这对偶关系证明了膨胀和腐蚀是可以互相替代的操作。

膨胀和腐蚀是图像处理中常用的操作，它们可以用来改善图像的质量和结构，同时也可以用来提取图像中的关键信息。

通过理解它们的对偶关系，可以更好地掌握它们的应用和技巧。

- 1 -。

膨胀腐蚀练习题膨胀腐蚀是数字图像处理中的一种基本操作，常用于图像分割、特征提取等领域。

通过对图像中的像素进行膨胀或腐蚀操作，可以改变像素点的形态，从而实现对图像的处理和分析。

在本篇文章中，我们将介绍一些关于膨胀腐蚀的基础知识，并提供一些练习题供读者巩固理解。

1. 什么是膨胀腐蚀操作？膨胀和腐蚀是一种基于邻域的操作，主要用于二值图像或灰度图像的处理。

膨胀操作可以增大图像中物体的边界线或者填充图像中的孔洞，而腐蚀操作则可以减小物体的边界线或者去除图像中的噪点。

这两种操作在形态学图像处理中非常常见。

2. 膨胀操作的原理膨胀操作基于邻域像素的最大值，即通过对邻域内的像素进行比较，选取其中的最大值作为输出像素的灰度值。

膨胀操作可以将物体的边缘变得更加粗糙。

一般情况下，膨胀操作使用一个称为结构元的模板进行操作。

练习题1：请使用3×3的结构元对下面的二值图像进行膨胀操作。

（插入一副二值图像示例）3. 腐蚀操作的原理腐蚀操作基于邻域像素的最小值，即通过对邻域内的像素进行比较，选取其中的最小值作为输出像素的灰度值。

腐蚀操作可以将物体的边缘变得更加细小。

与膨胀操作类似，腐蚀操作也使用结构元进行操作。

练习题2：请使用3×3的结构元对下面的灰度图像进行腐蚀操作。

（插入一副灰度图像示例）4. 膨胀腐蚀的应用膨胀腐蚀操作在图像分割和特征提取中有着广泛的应用。

膨胀操作可以将目标物体的边缘向外扩展，从而更好地分割出目标。

腐蚀操作可以去除图像中的噪点或者不需要的细节，以便更好地进行特征提取和分析。

练习题3：请使用适当的结构元对下面的彩色图像进行膨胀腐蚀操作，以实现目标物体的分割和去除噪点。

（插入一副彩色图像示例）5. 总结膨胀腐蚀是数字图像处理中常用的操作之一，通过对图像中像素的处理，可以改变图像的形态并提取感兴趣的特征。

本文简要介绍了膨胀腐蚀操作的原理和应用，并提供了一些练习题供读者巩固学习。

希望本文能为读者理解膨胀腐蚀操作提供帮助。

膨胀和腐蚀的特点
膨胀和腐蚀是图像处理中常用的操作，它们有各自独特的特点。

首先是膨胀操作。

膨胀操作是将图像中的物体边界向外扩张，可以用来填平物体内部的空洞、使物体边界变粗、连接相邻物体等。

其算法是将一个结构元素在图像上滑动，若结构元素的所有像素都是图像中某个物体的像素，则将结构元素的中心像素赋为该物体像素。

可以看出，膨胀操作会使物体变大，因此需要慎重使用。

其次是腐蚀操作。

腐蚀操作是将图像中的物体边界向内收缩，可以用来去除物体中的噪声、使物体边界变细、分离相邻物体等。

其算法与膨胀操作类似，将一个结构元素在图像上滑动，若结构元素的所有像素都是图像中某个物体的像素，则将结构元素的中心像素保持原来的像素值。

可以看出，腐蚀操作会使物体变小，因此也需要谨慎使用。

除了以上的特点，膨胀和腐蚀还有一些其他值得注意的点。

首先是结构元素的选择。

结构元素的大小、形状会影响膨胀和腐蚀的效果。

在选择结构元素时，需要根据实际需求进行调整。

其次是多次操作的效果。

多次膨胀操作会使物体越来越大，多次腐蚀操作会使物体越来越小。

因此，需要根据实际需求进行操作的次数。

在实际应用中，膨胀和腐蚀常常结合使用，可以用来进行形态学处理、边缘检测、图像分割等操作。

需要在实际需求和效果之间进行平衡和
选择，才能达到最佳的处理效果。

总之，膨胀和腐蚀是图像处理中常用且重要的操作，具有各自独特的
特点。

在使用时需要注意结构元素的选择、操作次数等因素，才能发
挥其最大的作用。

形态学运算中腐蚀，膨胀，开运算和闭运算：1. 腐蚀是一种消除边界点，使边界向内部收缩的过程。

可以用来消除小且无意义的物体。

2. 膨胀是将与物体接触的所有背景点合并到该物体中，使边界向外部扩张的过程。

可以用来填补物体中的空洞。

3. 先腐蚀后膨胀的过程称为开运算。

用来消除小物体、在纤细点处分离物体、平滑较大物体的边界的同时并不明显改变其面积。

4. 先膨胀后腐蚀的过程称为闭运算。

用来填充物体内细小空洞、连接邻近物体、平滑其边界的同时并不明显改变其面积。

5. 通常，由于噪声的影响，图象在阈值化后所得到边界往往是很不平滑的，物体区域具有一些噪声孔，背景区域上散布着一些小的噪声物体。

连续的开和闭运算可以有效地改善这种情况。

有时需要经过多次腐蚀之后再加上相同次数的膨胀，才可以产生比较好的效果。

6. 腐蚀操作会去掉物体的边缘点，细小物体所有的点都会被认为是边缘点，因此会整个被删去。

再做膨胀时，留下来的大物体会变回原来的大小，而被删除的小物体则永远消失了。

7. 膨胀操作会使物体的边界向外扩张，如果物体内部存在小空洞的话，经过膨胀操作这些洞将被补上，因而不再是边界了。

再进行腐蚀操作时，外部边界将变回原来的样子，而这些内部空洞则永远消失了。

图像膨胀的Matlab实现：可以使用imdilate函数进行图像膨胀,imdilate函数需要两个基本输入参数，即待处理的输入图像和结构元素对象。

结构元素对象可以是strel函数返回的对象，也可以是一个自己定义的表示结构元素邻域的二进制矩阵。

此外，imdilate还可以接受两个可选参数：PADOPT(padopt) ——影响输出图片的大小、PACKOPT(packopt).——说明输入图像是否为打包的二值图像(二进制图像)。

举个实例如下：步骤1，首先创建一个包含矩形对象的二值图像矩阵。

>> BW=zeros(9,10);>> BW(4:6,4:7) =1BW =0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 1 1 1 1 0 0 00 0 0 1 1 1 1 0 0 00 0 0 1 1 1 1 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0步骤2，使用一个3×3的正方形结构元素对象对创建的图像进行膨胀。

matlab 图像处理工具函数一(2009-10-20 09:49:33)转载标签：matlab 图像处理工具函数教育分类：学习资料图像处理函数详解——strel功能：用于膨胀腐蚀及开闭运算等操作的结构元素对象(本论坛随即对膨胀腐蚀等操作进行讲解)。

用法：SE = strel(shape,parameters)创建由指定形状shape对应的结构元素。

其中shape的种类有arbitrary''pair''diamond''periodicline''disk''rectangle''line''square''octagon参数parameters一般控制SE的大小。

例子：se1 = strel('square',6)% 创建6*6的正方形se2 = strel('line',10,45)% 创建直线长度10，角度45se3 = strel('disk',15)% 创建圆盘半径15se4 = strel('ball',15,5)% 创建椭圆体，半径15，高度5图像处理函数详解——roipoly功能：用于选择图像中的多边形区域。

用法：BW = roipoly(I,c,r)BW = roipoly(I)BW = roipoly(x,y,I,xi,yi)[BW,xi,yi] = roipoly(...)[x,y,BW,xi,yi] = roipoly(...)BW = roipoly(I,c,r)表示用向量c、r指定多边形各点的X、Y坐标。

BW选中的区域为1，其他部分的值为0.BW = roipoly(I)表示建立交互式的处理界面。

BW = roipoly(x,y,I,xi,yi)表示向量x和y建立非默认的坐标系，然后在指定的坐标系下选择由向量xi，yi指定的多边形区域。

形态学运算中腐蚀，膨胀，开运算和闭运算(针对二值图而言)6.1腐蚀腐蚀是一种消除边界点，使边界向内部收缩的过程。

可以用来消除小且无意义的物体。

腐蚀的算法：用3x3的结构元素，扫描图像的每一个像素用结构元素与其覆盖的二值图像做“与”操作如果都为1,结果图像的该像素为1。

否则为0。

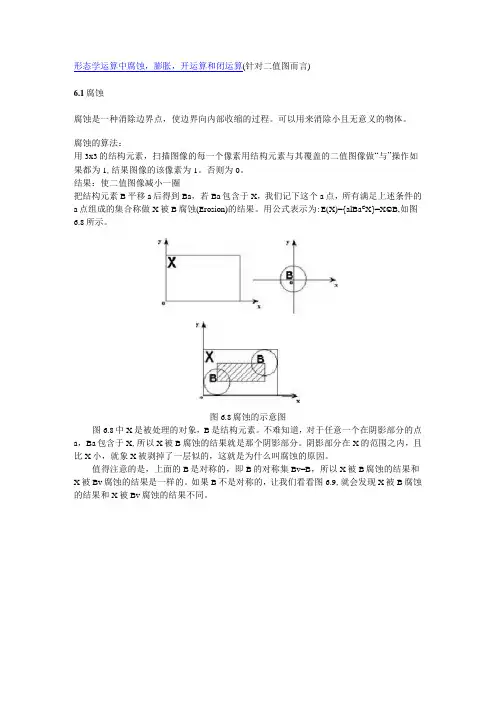
结果：使二值图像减小一圈把结构元素B平移a后得到Ba，若Ba包含于X，我们记下这个a点，所有满足上述条件的a点组成的集合称做X被B腐蚀(Erosion)的结果。

用公式表示为:E(X)={alBa C X}=X©B,如图6.8所示。

图6.8腐蚀的示意图图6.8中X是被处理的对象，B是结构元素。

不难知道，对于任意一个在阴影部分的点a，Ba包含于X,所以X被B腐蚀的结果就是那个阴影部分。

阴影部分在X的范围之内，且比X小，就象X被剥掉了一层似的，这就是为什么叫腐蚀的原因。

值得注意的是，上面的B是对称的，即B的对称集Bv=B，所以X被B腐蚀的结果和X被Bv腐蚀的结果是一样的。

如果B不是对称的，让我们看看图6.9,就会发现X被B腐蚀的结果和X被Bv腐蚀的结果不同。

y图6.9结构元素非对称时，腐蚀的结果不同图6.8和图6.9都是示意图，让我们来看看实际上是怎样进行腐蚀运算的。

在图6.10中，左边是被处理的图象X （二值图象，我们针对的是黑点），中间是结构元素B ，那个标有origin 的点是中心点，即当前处理元素的位置，我们在介绍模板操作时也有过类似的概念。

腐蚀的方法是，拿B 的中心点和X 上的点一个一个地对比，如果B 上的所有点都在X 的范围内，则该点保留，否则将该点去掉；右边是腐蚀后的结果。

可以看出，它仍在原来X 的范围内，且比X 包含的点要少，就象X 被腐蚀掉了一层。

o Q Q Q o & QO Qo Q o O oooo o o o o o 0- 0 O 0 o o •• • ■ Oo o oo o o 0 o o o o o 0 0 o o o ••o o o oo o o o ■ ■ o o 0 0 o o o ••o 0 0 oo o o 0 ■ • ♦ o QQ Q ■0 0 & o Q Q Q 0 0 * * 0 0 0 O 0 0 • ♦ ♦■ 0 Q Q ◎ 00o o ■ •0 0 o O ■ ■ ■ ■ *« O Q Qo o■ ■ ■ ■ Q Q c- O■ * ■ o GO O O O o o •o o ■ •• ■ o o o o O oO ■ ■ ■o 0o O O o O ♦<Q 0■••■ o a o o O o O o o 0 0 o 0oO o oooo\>o0 00o o o o 0 0 0'originFEX e 6图6.10腐蚀运算 图6.11为原图，图6.12为腐蚀后的结果图，能够很明显地看出腐蚀的效果。

matlab 形态学填充孔洞-概述说明以及解释1.引言1.1 概述在图像处理领域，孔洞是指图像中的空白区域或空洞，这些空洞可能会对图像处理和分析造成困难。

Matlab形态学填充孔洞是一种常用的图像处理方法，通过填充这些孔洞，可以改善图像质量、优化图像分割结果，并且对于图像识别和分析具有重要意义。

本文将介绍Matlab形态学填充孔洞的基本概念、应用场景以及实现方法，以帮助读者全面了解并掌握这一重要的图像处理技术。

通过学习本文内容，读者将能够在实际应用中灵活运用Matlab形态学填充孔洞的方法，提高图像处理的效率和准确性。

1.2 文章结构文章结构部分的内容可以描述整篇文章的结构安排和内容安排，包括各个章节的主题和内容概要。

例如："文章结构部分将介绍本文的整体结构安排，包括引言、正文和结论三个部分的主要内容。

在引言部分，将对Matlab形态学填充孔洞的概述、文章的组织结构和文章的目的进行详细阐述。

在正文部分，将分别介绍Matlab形态学填充孔洞的基本概念、应用场景和实现方法。

在结论部分，将对整篇文章进行总结，阐明形态学填充孔洞的意义，并展望未来的发展方向。

通过对文章结构的介绍，读者可以清晰地了解到本文的内容安排和主题方向，从而更好地理解整个文章的脉络和逻辑。

"1.3 目的本文旨在介绍在Matlab中如何使用形态学填充方法来填补图像中的孔洞。

通过对形态学填充孔洞的基本概念和实现方法进行详细阐述，读者将能够了解到如何利用这一技术来处理图像中存在的空洞问题。

同时，本文还将探讨形态学填充孔洞在实际应用中的场景，并对该技术的意义和未来发展进行展望。

通过本文的阅读，读者将能够掌握Matlab中形态学填充孔洞的具体方法和应用技巧，为图像处理领域的实践工作提供有益的参考和指导。

2.正文2.1 Matlab形态学填充孔洞的基本概念形态学填充孔洞是一种图像处理技术，用于填充图像中的黑色孔洞，使其变得更加完整和连续。

1、实验目的学习常见的数学形态学运算基本方法，了解腐蚀、膨胀、开运算、闭运算取得的效果，培养处理实际图像的能力，并为课堂教学提供配套的实践机会。

2、实验要求利用MatLab工具箱中关于数学形态学运算的函数，计算本指导书中指定二值图像进行处理。

3、实验设备与软件1.LC-PC计算机系统2.MatLab软件/语言包括图像处理工具箱(Image Processing Toolbox)3.实验所需要的图片4.4、实验内容与步骤1.调入并显示图像Plane2.jpg；2.选取合适的阈值，得到二值化图像Plane2-2.jpg；3.设置结构元素；4.对得到的二值图像Plane2-2.jpg进行腐蚀运算；5.对得到的二值图像Plane2-2.jpg进行膨胀运算；6.对得到的二值图像Plane2-2.jpg进行开运算；7.对得到的二值图像Plane2-2.jpg进行闭运算；8.将两种处理方法的结果作比较；5、实验过程及结果程序代码：I=imread('1.jpg');%读入图像level = graythresh(I); %得到合适的阈值bw = im2bw(I,level); %二值化SE = strel('square',3); %设置膨胀结构元素BW1 = imdilate(bw,SE); %膨胀SE1 = strel('arbitrary',eye(5)); %设置腐蚀结构元素BW2 = imerode(bw,SE1); %腐蚀BW3 = bwmorph(bw, 'open'); %开运算BW4 = bwmorph(bw, 'close'); %闭运算imshow(I)figure,imshow(bw);title('原图');figure,imshow(BW1);title('膨胀');figure,imshow(BW2);title('腐蚀');figure,imshow(BW3);title('开运算');figure,imshow(BW4);title('闭运算');6、思考题/问答题1.结合实验内容，评价腐蚀运算与膨胀运算的效果。

文章内容：一、腐蚀与膨胀的定义和作用在图像处理和计算机视觉中，腐蚀和膨胀是常用的图像形态学处理操作，用于图像的边缘检测、特征提取等。

腐蚀是一种图像变换操作，通过对图像中每个像素的局部邻域应用结构元素来改变原始图像，使得图像中的物体缩小或者断开。

腐蚀操作通常用于消除图像中的小型噪声、分割图像中的物体等。

相反，膨胀则是通过对图像中每个像素的局部邻域应用结构元素来扩张原始图像，使得图像中的物体增大或连接。

膨胀操作通常用于填充图像中的孔洞、连接断开的物体等。

二、matlab 中腐蚀与膨胀的实现在matlab中，我们可以使用imerode函数来实现腐蚀操作，使用imdilate函数来实现膨胀操作。

这两个函数都需要指定一个结构元素作为参数，该结构元素通常是一个二值矩阵，用于描述要应用于图像的变换。

在实现腐蚀和膨胀操作时，我们可以通过调整结构元素的形状和大小，来达到不同的效果。

使用一个较小的正方形结构元素可以对图像进行细化处理，而使用一个较大的圆形结构元素可以对图像进行填充处理。

三、结构元素的选择和影响在进行腐蚀和膨胀操作时，结构元素的选择对最终的处理效果有很大的影响。

对于不同形状和大小的结构元素，它们在图像上的操作效果也会有所不同。

当我们想要消除图像中的小噪点时，可以选择一个较小的结构元素来进行腐蚀操作；当我们想要填充图像中的孔洞时，可以选择一个较大的结构元素来进行膨胀操作。

在实际应用中，我们可以通过试验不同的结构元素来找到最适合的处理效果。

四、个人观点和理解在我看来，腐蚀和膨胀操作是图像处理中非常实用且重要的一部分。

通过合理选择结构元素和调整参数，我们可以对图像进行精细化的操作，从而达到我们想要的效果。

腐蚀和膨胀操作也可以结合使用，来实现更复杂的图像处理需求。

在实际应用中，我发现腐蚀和膨胀操作在物体识别、图像分割等领域有着很好的效果，可以有效提高图像处理的准确性和鲁棒性。

总结：通过本文的介绍，我们了解了腐蚀和膨胀在图像处理中的基本原理和实现方法。

先膨胀后腐蚀的运算解释说明以及概述1. 引言1.1 概述在图像处理和形态学图像分析领域，先膨胀后腐蚀的运算被广泛应用。

该运算是一种基于形态学思想的操作，它通过对图像进行膨胀和腐蚀两个步骤的组合操作，能够改变图像的形状、大小、结构等特征。

这种运算方法具有一定的特点和优势，已被证明在许多应用场景中具有重要价值。

1.2 文章结构本文将首先介绍先膨胀后腐蚀的运算的定义和原理，在此基础上详细解释其具体步骤，并提供实例进行说明。

接着，将探讨该运算在图像处理、形态学图像分析以及模式识别等领域中的应用。

同时，本文还会与其他相关运算进行比较分析，并对不同尺寸结构元素对先膨胀后腐蚀结果影响进行深入研究。

最后，通过总结与展望来评估先膨胀后腐蚀运算的局限性和未来发展趋势。

1.3 目的本文旨在深入探讨先膨胀后腐蚀的运算，全面了解其原理、特点和应用领域，以及与其他相关运算的比较分析。

通过本文的阐述，读者将能够理解并掌握先膨胀后腐蚀运算，并能在实际应用中灵活运用该方法。

对于图像处理、形态学图像分析以及模式识别等领域的研究人员和工程师而言，本文将为他们提供有价值的参考和指导。

以上是“1. 引言”部分的内容，请根据需要进行修改和补充。

2. 先膨胀后腐蚀的运算解释说明：2.1 膨胀操作定义与原理：膨胀是形态学图像处理中的基本运算之一，它可以用来增强图像中亮度较高的区域。

膨胀操作基于结构元素，通过将结构元素沿着图像的每个像素进行平移，并找出覆盖范围内的最大值作为输出像素的灰度值。

这意味着，通过膨胀操作，图像中亮度较高的区域将会逐渐扩展。

膨胀操作可以用数学形式描述如下：D = A ⊕B其中，D表示进行膨胀后所得到的图像，A表示待处理的原始图像，B表示结构元素。

2.2 腐蚀操作定义与原理：与膨胀相反，腐蚀是一种可以去除图像中亮度较低区域的操作。

它同样依赖于结构元素，并根据在覆盖范围内找出最小值作为输出像素的灰度值。

因此，通过连续进行多次腐蚀操作，亮度较低或细小的细节将会不断被消除。

膨胀运算和腐蚀运算
膨胀运算和腐蚀运算是数字图像处理中常用的形态学图像处理技术。

它们是基于图像的形状和结构特征来操作，能够在图像中识别和增强物体的形态。

下面是膨胀运算和腐蚀运算的简要解释：
1. 膨胀运算是对图像进行扩张和增大的一种操作。

它的基本思想是利用一个结构元素在图像中滑动，当结构元素与原始图像上的像素重合时，取结构元素内最大的像素值作为该像素点的新像素值。

因此，膨胀运算可以使目标物体变得更加坚定、更加圆滑，同时可以去除孔洞和内部噪声，使物体形态更加清晰明了。

2. 腐蚀运算是一种对图像进行收缩和缩小的操作。

它的基本思想是利用结构元素在图像上滑动，当结构元素完全覆盖要处理的像素时，取结构元素内最小的像素值作为该像素点的新像素值。

因此，腐蚀运算可以使物体边缘变得更加精细和明显，同时可以消除细节和孤立的小物体，使边缘和形态更加清晰和明了。

总的来说，膨胀和腐蚀是图像处理中常用的两种基本形态学操作，常常配合使用，以达到更好的图像增强、物体分割、形态分析等目的。

1/ 1。

matlab形态学腐蚀膨胀sobel算子边缘检测Title: Image Processing with MATLAB: Morphological Erosion, Dilation, and Sobel Edge DetectionMATLAB, a powerful tool for numerical computation and visualization, is widely used in image processing tasks. Among the various operations, morphological erosion and dilation, as well as Sobel edge detection, play crucial roles in extracting meaningful information from images.MATLAB作为一种强大的数值计算和可视化工具，在图像处理任务中得到了广泛应用。

在众多操作中，形态学腐蚀、膨胀以及Sobel边缘检测在从图像中提取有意义信息方面发挥着至关重要的作用。

Morphological erosion is a process that removes pixels from the boundaries of objects in an image, effectively 'shrinking' them. This operation is useful in eliminating small, noisy elements while preserving larger structures.形态学腐蚀是一个过程，它从图像中对象的边界移除像素，从而有效地“缩小”它们。

这种操作在消除小的噪声元素同时保留较大结构方面非常有用。

On the other hand, morphological dilation enlarges objects by adding pixels to their boundaries. This helps to fill small gaps or holes within objects, enhancing their connectivity and visibility.另一方面，形态学膨胀通过向对象边界添加像素来扩大对象。

膨胀、腐蚀、开、闭运算，你这么解释，小学生都看得懂了膨胀、腐蚀、开、闭运算，你这么解释，小学生都看得懂了！看过我前面一些章节内容的小伙伴肯定已经不止一次遇到过这几个词了。

对图像的形态学处理也避不开这几个。

但是想要准确理解他们的意思似乎不是那么简单。

首先，这四个运算都是用一个结构元对需要处理的region进行相应的形态学变换后得到想要的处理后的region。

就像你要对一个数做减法，你需要给他一个减数，这样'被减数-减数=差'，才能求出差。

膨胀：就是把region变大，变大的方式就是用一个结构元的中心点在原来的region轮廓上游走一遍，所走过的区域加上原来的region 区域就是膨胀后的区域，如下图（图 3-14-1），如果我原来的region 是左边的大矩形，结构元是右边的cell。

图 3- 14 -1那么结构元的中心点就是圆心了，让cell在大矩形的轮廓上游走一圈，就是下图（图3-14-2）这样了：图 3-14-2游走途径的像素点再加上regionSource原来覆盖的区域一起，就是膨胀后的区域了。

其实就是这个矩形各个方向再往外扩大这个小圆的半径，拐角部分的直角变成了圆角，如下图（图3-14-3）。

（像极了原本90斤的女朋友后来变成了120斤，体积大了一圈，棱角变圆了，真是一个悲伤的故事~~）。

图3-14-3膨胀弄懂了，腐蚀也就不难了。

腐蚀：就是把region变小。

变小的方式就是用一个结构元的中心点在原来的region内部游走一遍，（注意这里不是轮廓了）。

当中心点到某个位置，整个结构元都在region内部的时候，所有符合这个条件的点，合在一起就是新的腐蚀后的区域了。

还是用原来的regionSource和cell，腐蚀的话就是下图（图 3-14-4）这样：图 3-14-4外面红色矩形是原来的regionSource，圆形就是结构元cell，为了满足所有的点都在regionSource内部，这个cell最边缘的位置也就是图中的位置了，那么cell的圆心所在位置就是腐蚀后的region，那么整个regionSource内所有符合这些条件的点就是图中绿色矩形了。

matlab腐蚀结构元素-回复什么是腐蚀结构元素？在图像处理领域中，腐蚀（Erosion）是一种常用的形态学运算，用于处理二值化图像中的噪声和边缘。

腐蚀操作基于一个特定的结构元素（Structuring Element），该结构元素决定了腐蚀操作的效果和范围。

本文将详细介绍腐蚀结构元素的概念、属性以及在MATLAB中的使用方法。

一、腐蚀操作简介腐蚀是形态学中的一种基本操作，其目的是通过从对象的边缘去除一个结构元素，来改变或减小对象的形状。

腐蚀操作通常在二值化图像上进行，其中白色代表对象，黑色代表背景。

腐蚀操作通过将结构元素与图像中的各个像素进行比较，如果结构元素完全包含在对象像素上，则该像素不变，否则该像素会被置为背景色。

二、腐蚀结构元素的属性在进行腐蚀操作之前，需要定义一个结构元素。

腐蚀结构元素具有以下几个属性：形状、大小和中心。

1. 形状：腐蚀结构元素可以是任意形状的，常见的形状有线条、矩形、圆形等。

不同的形状具有不同的特性，适用于不同场景。

2. 大小：腐蚀结构元素的大小一般由用户指定，大小决定了腐蚀的程度。

较小的结构元素能够更好地去除噪声，但可能会导致物体缩小或完全消失。

3. 中心：腐蚀结构元素的中心位置对腐蚀操作的效果有着重要影响。

不同的中心位置会导致不同的腐蚀结果。

三、MATLAB中的腐蚀结构元素MATLAB提供了丰富的图像处理工具包，其中包含了用于腐蚀操作的函数。

下面将介绍在MATLAB中如何定义和使用腐蚀结构元素。

1. 定义结构元素MATLAB提供了两种定义腐蚀结构元素的方式：strel函数和offsetstrel函数。

- 使用strel函数：strel函数可以创建一个平面上的结构元素。

函数的语法如下：matlabse = strel(shape,parameters)其中，shape参数是结构元素的形状，可以是'disk'、'rectangle'、'line'等；parameters参数是结构元素的参数，如大小、角度等。

《深度探讨：Matlab中的腐蚀、膨胀、开运算和闭运算》在图像处理领域，腐蚀、膨胀、开运算和闭运算是常用的图像处理技术。

它们可以帮助我们对图像进行形态学处理，从而对图像进行特定的操作和增强。

本文将从简单入手，深入探讨Matlab中的腐蚀、膨胀、开运算和闭运算的原理、应用和个人观点。

1. 腐蚀腐蚀是一种图像形态学处理操作，其主要作用是“侵蚀”目标的边界。

在Matlab中，可以使用im erode函数来进行腐蚀操作。

腐蚀操作可以帮助我们去除图像中的细小细节或者连接目标，使得图像中的目标变得更加清晰和突出。

腐蚀操作的核心思想在于利用一个结构元素对图像进行扫描，当结构元素与图像相交时，输出图像的对应像素值将取决于结构元素中的最小像素值。

2. 膨胀相对于腐蚀，膨胀是一种图像形态学处理操作，其主要作用是“膨胀”目标的边界。

在Matlab中，可以使用im dilate函数来进行膨胀操作。

膨胀操作可以帮助我们连接图像中的细小裂缝或者增强目标的边界，使得图像中的目标变得更加完整和饱满。

膨胀操作的核心思想在于利用一个结构元素对图像进行扫描，当结构元素与图像相交时，输出图像的对应像素值将取决于结构元素中的最大像素值。

3. 开运算开运算是腐蚀操作和膨胀操作的结合，其主要作用是先进行腐蚀操作，然后进行膨胀操作。

在Matlab中，可以使用im open函数来进行开运算。

开运算可以帮助我们去除图像中的噪声或者平滑图像中的目标，使得图像中的目标更加清晰和稳定。

开运算的核心思想在于先利用腐蚀操作去除细小细节，然后利用膨胀操作连接目标。

4. 闭运算闭运算是膨胀操作和腐蚀操作的结合，其主要作用是先进行膨胀操作，然后进行腐蚀操作。

在Matlab中，可以使用im close函数来进行闭运算。

闭运算可以帮助我们填充图像中的小洞或者平滑图像中的目标边界，使得图像中的目标更加完整和稳定。

闭运算的核心思想在于先利用膨胀操作连接裂缝，然后利用腐蚀操作去除小洞。

数字图像处理实验编程实现膨胀运算或者腐蚀运算姓名：学好：0904210239指导老师：王韬时间：2012年5月编程实现膨胀运算或者腐蚀运算一、实验原理腐蚀：是一种消除连通域的边界点，使边界向内收缩的处理。

设计一个结构元素，结构元素的原点定位在待处理的目标像素上，通过判断是否覆盖，来确定是否该点被腐蚀掉。

膨胀：是将与目标区域的背景点合并到该目标物中，使目标物边界向外部扩张的处理。

设计一个结构元素，结构元素的原点定位在背景像素上，判断是否覆盖有目标点，来确定是否该点被膨胀为目标点。

二、实验步骤腐蚀：1）扫描原图，找到第一个像素值为1的目标点；2）将预先设定好形状以及原点位置的结构元素的原点移到该点；3）判断该结构元素所覆盖范围内的像素值是否全部为1：如果是，则腐蚀后图像中的相同位置上的像素值为1；如果不是，则腐蚀后图像中的相同位置上的像素值为0；4）重复2）和3），直到所有原图中像素处理完成。

膨胀：1）扫描原图，找到第一个像素值为0的背景点；2）将预先设定好形状以及原点位置的结构元素的原点移到该点；3）判断该结构元素所覆盖范围内的像素值是否存在为1的目标点：如果是，则膨胀后图像中的相同位置上的像素值为1；如果不是，则膨胀后图像中的相同位置上的像素值为0；4）重复2）和3），直到所有原图中像素处理完成。

三、实验程序# include <afxwin.h># include <windows.h># include <iostream.h># include <stdlib.h># include <math.h># define PI 3.14159265typedef struct{double re;double im;}COMPLEX;COMPLEX Add(COMPLEX c1,COMPLEX c2){COMPLEX c;c.re=c1.re+c2.re;c.im=c1.im+c2.im;return c;}COMPLEX Sub(COMPLEX c1,COMPLEX c2){COMPLEX c;c.re=c1.re-c2.re;c.im=c1.im-c2.im;return c;}COMPLEX Mul(COMPLEX c1,COMPLEX c2){COMPLEX c;c.re=c1.re*c2.re-c1.im*c2.im;c.im=c1.re*c2.im+c2.re*c1.im;return c;}int nWidth;int nHeight;int nColorBits;int nColor;int nLen;int nByteWidth;BYTE * lpBitmap;BYTE * lpBits;void OpenFile(CString FileName);void SaveFile(CString FileName);void fushi();void pengzhang();void OpenFile(CString FileName){HANDLE hFile= ::CreateFile(FileName,GENERIC_READ,FILE_SHARE_READ,NULL,OPEN_EX ISTING,FILE_ATTRIBUTE_NORMAL,NULL);if(hFile==0){printf("不能调开文件，请重新选择! \n");return;}DWORD WriteNum;BITMAPFILEHEADER BFH;ReadFile(hFile,&BFH,14,&WriteNum,NULL);if((BFH.bfType!='MB')||(WriteNum!=sizeof(BITMAPFILEHEADER))){printf("不是BMP位图文件或数据有误! \n");return;}nLen = GetFileSize(hFile,NULL)-sizeof(BITMAPFILEHEADER);lpBitmap= new BYTE[nLen];ReadFile(hFile,lpBitmap,nLen,&WriteNum,NULL);BITMAPINFOHEADER * BIH = ((BITMAPINFOHEADER*)lpBitmap);nWidth = BIH ->biWidth;nHeight = BIH ->biHeight;nColorBits= BIH ->biBitCount;nByteWidth= (nWidth*nColorBits+31)/32*4;nColor = (nColorBits>8)?0:(1<<nColorBits);lpBits = lpBitmap + sizeof(BITMAPINFOHEADER) +sizeof(RGBQUAD)*nColor;CloseHandle(hFile);}void SaveFile(CString FileName){HANDLE hFile= ::CreateFile(FileName,GENERIC_WRITE,FILE_SHARE_WRITE,NULL,CREAT E_ALWAYS,FILE_ATTRIBUTE_NORMAL,NULL);if(hFile ==0){printf("不能创建文件，请重新选择! \n");return;}unsigned long WriteNum;BITMAPFILEHEADER BFH;BFH.bfType = 'MB';BFH.bfSize = nLen + sizeof(BITMAPFILEHEADER);BFH.bfOffBits = sizeof(BITMAPFILEHEADER) +sizeof(BITMAPINFOHEADER) + nColor * sizeof(RGBQUAD);BFH.bfReserved1 = BFH.bfReserved2 = 0;WriteFile(hFile,&BFH,sizeof(BITMAPFILEHEADER),&WriteNum,NULL);WriteFile(hFile,(BITMAPINFOHEADER* )lpBitmap,nLen,&WriteNum,NULL);CloseHandle(hFile);}void fushi(){unsigned char * data,* lpDst,* temp ;//分别指向源图像和缓存图像的指针temp=new BYTE[256*256];//暂时分配内存，以保存新图像for (int i=1;i<nHeight-1;i++){for (int j=1;j<nWidth-1;j++){data=(lpBits+nByteWidth*j+i);//指向原图像第j行第i个像素的指针lpDst=(temp+nByteWidth*j+i);//指向目标图像第j行第i个像素的指针*lpDst=255;//目标图像中的当前点先赋成白色if(*data==255){if( *(data-1)==0 || *(data+1)==0 ||*(data-nByteWidth)==0 || *(data+nByteWidth)==0 ||*(data-nByteWidth-1)==0 || *(data-nByteWidth+1)==0 ||*(data+nByteWidth-1)==0 || *(data+nByteWidth+1)==0)*lpDst=0;}else*lpDst=0;}}for(i=0;i<nHeight;i++){for(int j=0;j<nWidth;j++){data=(lpBits+nByteWidth*j+i);lpDst=(temp+nByteWidth*j+i);* data = * lpDst;}delete temp;//释放空间}void pengzhang(){unsigned char * data,* lpDst,* temp ;//分别指向源图像和缓存图像的指针temp=new BYTE[256*256];//暂时分配内存，以保存新图像for (int i=1;i<nHeight-1;i++){for (int j=1;j<nWidth-1;j++){data=(lpBits+nByteWidth*j+i);//指向原图像第j行第i个像素的指针lpDst=(temp+nByteWidth*j+i);//指向目标图像第j行第i个像素的指针*lpDst=0;//目标图像中的当前点先赋成黑色if(*data==0){if( *(data-1)==255 || *(data+1)==255 ||*(data-nByteWidth)==255 || *(data+nByteWidth)==255 ||*(data-nByteWidth-1)==255 || *(data-nByteWidth+1)==255 ||*(data+nByteWidth-1)==255 || *(data+nByteWidth+1)==255)*lpDst=255;}else*lpDst=255;}}for(i=0;i<nHeight;i++){for(int j=0;j<nWidth;j++){data=(lpBits+nByteWidth*j+i);lpDst=(temp+nByteWidth*j+i);* data = * lpDst;}}delete temp;//释放空间}{char OpenFileName[100];char SaveFileName[100];printf("输入待处理的图像路径: \n");gets(OpenFileName);printf("保存处理图像结果的路径: \n");gets(SaveFileName);OpenFile(OpenFileName);cout<<"选择：1腐蚀，2膨胀"<<endl;int n;cin>>n;switch(n){case 1:fushi();break;case 2:pengzhang();break;}SaveFile(SaveFileName);return 0;}四、实验结果原图像：腐蚀后：膨胀后：。

在MATLAB中，可以使用图像处理工具箱进行图像的灰度值二值化、膨胀和腐蚀操作。

以下是一个简单的示例代码，展示如何进行这些操作：
读取图像
img = imread('image.png');
转换为灰度图像
gray_img = rgb2gray(img);
二值化图像
binary_img = imbinarize(gray_img);
显示原始图像和二值化图像
subplot(1,2,1);
imshow(gray_img);
title('原始图像');
subplot(1,2,2);
imshow(binary_img);
title('二值化图像');
膨胀操作
se = strel('disk', 5); % 创建结构元素
dilated_img = imdilate(binary_img, se);
显示膨胀后的图像
figure;
imshow(dilated_img);
title('膨胀后的图像');
腐蚀操作
eroded_img = imerode(binary_img, se);
显示腐蚀后的图像
figure;
imshow(eroded_img);
title('腐蚀后的图像');
在上述代码中，首先读取图像并将其转换为灰度图像。

然后，使用imbinarize函数将灰度图像二值化。

接着，使用strel函数创建结构元素，并使用imdilate函数对二值化图像进行膨胀操作。

最后，使用imerode函数对二值化图像进行腐蚀操作。