glossary_arch

何地方 ap- 加强或引申意义 appraise 评价 用在 p 前 apo- 离开 apogee 远地 点 ar- 含 at,to 意,加强 意义 arrange 安排 用在 r 前 arch- 主要的，首位的 archenemy 头号敌人 as- 含 at,to 意,加强 意义 assort 分类 用在 s 前 at- 含 at,to 意,加强 意义 attract 吸引 用在 t 前 auto- 自己，自动 autobiography 自传 back- 反的，向后的 backstroke 仰泳 be- 1. 使...，使成为. .. belittle 使缩小，贬低 be- 2. 加以...，用... bespangle 用小亮片装饰 be- 3. 在 below 在... 下面 be- 4. 加强及引申意 义 befall 降临，发生 bene- 善，好 benediction 祝福 bi- 两，二 bimonthly 双月刊 by- 旁，侧，非正式 byroad 小路，僻径 centi- 百分之一，厘 centimetre 厘米 circum- 周围，环境 circumpolar 极地周围的 co- 共同 cooperation 合作 用在元音字前 col- 1. 共同 collocate 并置，并列 用 在l前 col- 2. 加强或引申意 义 collate 校对 用在 l 前
com- 1. 共同 combine 联合，结合 用在 b,m,p 前 com- 2. 加强或引申意 义 commix 混合 用在 b,m,p 前 con- 1. 共同 concolorous 同色的 con- 2. 加强或引申意 义 confirm 使坚定 contra- 反对，相反 contradict 反驳，相矛盾 cor- 1. 共同，互相 correspond 共鸣 用在 r 前 cor- 2. 加强或引申意 义 corrupt 腐败，败坏 用 在r前 counter- 反对，相反 counterattack 反攻，反击 de- 1. 否定，非，相 反 deprecatory 反对的 de- 2. 除去，取消， 毁 deflower 摧残，蹂躏 de- 3. 离开 depart 离 去 de- 4. 向下，降低 devaluate 贬值 de- 5. 使成...，加强 意义 delimit 划定界限 deca- 十 decameter 十 米 deci- 十分之一 decigram 十分之一克 demi- 半 demigod 半神 半人 di- 二，双 dioxide 二 氧化物 dia- 贯通，对穿，透 过 diameter 直径 dif- 1. 不，无，相反 diffidence 无自信 用在 f 前 dif- 2. 分开，离，散 diffract 分散 用在 f 前 dis- 1. 不，无，相反

2013.12.12abbreviation n.abidevt. vt. abolish vt. absenta. absorptionn. abstract a. n. absurda. abundancen. accessoryn. a. accordn. acknowledge vt.acquaint vt. actionn. adherevi. adjacent a. adjoinvt. adjustablea.administrationn. ( )admirationn.adoption n. adorevt. advantageous a.advertisevt. vi. advocate n. vt. aeriala. aerospacen.affirmvt. agitationn. agreeablea. alas int. albumn. alerta. algebra n.aliena. n. alignmentn. allieda. allowancen alongsideprep.ally n.alterationn.alternatevt. a.amateur a. n.ambassadorn.ambient a.ambiguousa.ambitiousa.amplea.amplituden.amusementn.analogue n.analogy n.analytic(al) a.anniversary n.announce vt.annually ad.anoden.answervi.antarctica. n.antenna n.antique a. n.anybody n.apparent a.appendix n.applaud vt. vi.applause n.appreciable a.appreciation n.apt a.arc n.arch n. vt.architectn.arctica. n.arrayvt. n.ascendvi.ascertainvt.ascribe vt.ashoread.ass n.assassinate vt.assault vt. n.assertvt.assessmentn.assumptionn.assurancen.astonishment n.astronomyn.atom n.attachmentn.attendancen.attendantn.attorney n.audience n.authorn.automate vt.availvt. n.availability n. ( )aviation n.awakevi.awfula.awkward a.axiala.axis n.axle n.( )baby n.bachelor n.baconn.bacteriumn.badgen.bafflevt. n.bait n.balcony n.bald a.balletn.bamboon.bandage n.banditn.bank vi.bankern.bankrupt a. vt.banquet n.barelyad.bargen.barleyn.barometern.baronn.barrena.baseball n.basement n.basinn.battery n.battlevi. vt.bazaarn.bead n.beam vi.bearing n.bed n. ( )beetlen.beforehandad.bend vt. vi.bestowvt.between ad.bewarevt.&vi.bewilder vt.bid vt. vi.bishopn.( )bitternessn.blacksmithn.blastn.blazevt. vi.bleachvt. vi.blindn.blockn.blondn.blousen.blue a.blunder vi. n.blushvi. n.boardvt.( )body n. ( )boilern.bore n.bounda.bourgeoisa.box n.boycott vt.&n.bracen. vt.brandvt.breakdownn.breakfastvi.breedn.( )briben. vt.bridegroomn.bridgevt.bridlen. vt.brightnessn.broaden vt.&vi.bronzen.broodvt. vi.Buddhism n.budgetn.buffalo n.bug n.buglen.bull n.bulletinbump vt. vi. n.bureaucracy n.burglar n.burialn.burnern.busheln. ( )butt n.buzz vi.( )bypassn. vt.by-productn.cablen.calculus n.calibration n.can vt.cane n.( )cancelvt.capabilityn.capacitance n.capacitorn.1cape n. captive a.carryvt.cartoon n. cartridgen.cataloguevt. catalyst n. category n. catervi. Catholic a. n.caution n. vt. cautious a. cavityn. cementvt. vi. censorvt. cerealn. certaintyn.challengen.champion n. characterize vt. charcoal n. chargen. vt. charmn. vi. charter vt. n. chatter vi.&n. cheatn. checkn.cherish vt. ( ) chestnut n. chillvi.chip n. choicen. a. chop n. chordn.( ) vi. chorusvt.&vi. Christn. ( ) Christiana. cigarn. circular n. circulation n. ( ) circusn.cite vt.civilian n. a.claimn.clampn. vt.clap n.clashn.claspvt.classic n. a.clatter n.cleanliness n.clearing n.( )clientn.climaxn.( )clingvi.clinicn.clip vt. n.clip vt.cloakvt.clockwisea.&ad.closetn.cloudya.clownn.( )cluster n. vt.clutchvt. vi.coachvt.cock n.coefficient n.coffinn.coherent a.coin vt. ( )coincide vi.coke n. vt.&vi.collaborate vi.collide vi.colonial a.colonist n.combatvt. vi.combustionn.comedyn.commence vt. vi.commend vt.commissionn.commodityn.commonplace a. n.commonsense a.commonwealth n.compact a. vt.comparablea.compatiblea.compensatevt.&vi.compensation n.competitive a.competitorn.complaintn.complementvt. n.( )completionn.complexityn. ( )complication n.complimentn. vt.complyvi.composer n.compositea. n.composition n.comprehendvt.compression n.compulsorya.conceit n.conceive vt.concentrate vt.&vi.conceptionn.concern n.concert n.concessionn.confidencen.confidential a.confirmation n.conform vt. vi.confront vt.conquerorn.consciousnessn.consequence n. ( )consequenta.conservative a.consistenta.console n.consolidate vt. vi.constituent a. n.constitutevt.constitution n.( )constraintn.construction n. ( )consuln.consumer n.consumption n. ( )contend vi. vt.context n.continental a.contradictvt.contrary n.contrast vt. vi.controversy n.conventionn. ( )convert vt.conveyvt.convictionn.cooperative a. n.coordinatea. n.correctlyad.correlaten.correlation n.correspondencen.corrosionn.corrupt vt. a.cosmica.cosmosn.couchn.counsel n.countn.counter a.&ad. ( )courageousa.courteousa.courtesy n.cowarda.crab n. vi.crackvi.&vt.cradlen.craftn.crankn. vi.crashvi.creditvt.&n.crisisn.crispa.criterionn.crooked a.crossa.cruelty n.cruisevi. vt.cubica.cuckoon.curlya.currency n.2currentlyad. customn. customarya.cuttern. cylinder n. ( )damn vt. n. datumn. dazzlevt.&vi. deafenvt.deal vi. dealern. dean n.( ) decayvt. decidedlyad. decimal a. decisive a. declaration n.decline vt. decomposevt.&vi. decorativea.decreen. dedicate vt. deem vt. vi. deepenvt.default n.&vi. deficiencyn. deficienta. definevt. ( ) deflect vt.&vi.( ) deflectionn. deformvt. deformation n.defy vt. degradation n.degrade vt. delegate n.deliberatea.deliberately ad.denialn.denotevt.denounce vt.dentist n.dependantn.deposit n.depositionn.depressionn.deprive vt. ( )deputyn. a.derivationn.descendantn.descent n.desertvt. ( )designatevt.desolate a.dessert n.destine vt.destiny n.destructive a. ( )detachvt. ( )detailn.detainvt.detectiven.detector n.develop vt. ( )deviate vt.( )deviationn.devotion n.devourvt.diagnose vt. ( )dictator n.dieseln.diet n.difficulta.dignity a. ( )diminish vt.dine vi. vt.dioxide n.diploma n.diplomatica.directoryn.disagreement n.disappearancen.disastrousa.discern vt.discount n.discoursen.discriminationn.disgrace n.disillusion n. vt.dismayn.dismiss vt.disorder n.dispatch vt. n.disperse vt.( )displace vt.displacement n.disregardvt. n.dissatisfaction n.dissipatevt. vi.dissolve vt. ( )distinct a.distinctlyad.distinguish v.distort vt.distortionn.distract vt. ( )disturbance n.diverge vi.diversionn.divertvt. vi.divinea.dizzya.dock vt.doctrine n.documentary a.dome n.domestic a.dominant a. n.dominate vt.doom n. vt.doubtlessad.dove n.drainvi.( )drainage n.draman.drastic a.drawback n.dreadful a.dry a.duke n.duplicaten. vt.dust n.dwarfn.dwelln. vi.dynamic(al) a.dynamon.ear n.( )earnings n.earthenware n.eastward a.&ad.echo vt. ( )eclipse n.( )ecology n.economically ad.economicsn.edit vt.editorialn.Egyptian a. n.ejectvt.elapsevi.( )elbowvt.electrician n.electroden.electronics n.elegant a.( )elementala.elevate vt. ( )elevationn.ellipticala.eloquencen.embarrassvt.embassy n.embodyvt.embrace vt.embroideryn.emergevi.emigrate vi.emission n.empiricala.enchant vt.enclosuren.end n.endanger vt.endeavor vi.&n.endowvt.endurancen.energetica.energize vt.engagevt. ( )engagementn.enhance vt.enlightenvt.enrichvt.enrollvt. vi.enterprisen.entertainmentn.entitle vt.entreat vt.&vi.3entryn. environmentala.episode n. epochn.( ) equation n.equator n. equilibrium n.equivalenta. ( ) erecta.erosion n. errandn. escortn.&vt. essence n. essentiala. establishvt.estaten. eternal n. evaporatevt. vi.even a. evenlyad. everlasting a. evil n. evolutionn. ( )excelvt. vi. exceptvt. exceptional a. excessn. excessively ad. exclamation n.exclusivea. excursionn. excusevt. executionn.executiven. exemplifyvt. ( ) exertvt. ( ) exilevt. n. expectvt. expeditionn.expenditure n.( )expelvt.experimentallyad.experimentation n.expirevi.explicit a.exploration n.expositionn.extinct a.extinguishvt.extran.extract vt. n.extractionn.extraordinarily ad.extravagant a.extreme n.fabricatevt.fabrication n.facilitatevt.faction n.fair a.fake n. a.fall vi.fantastica.fascinatevt. vi.fastener n.faultlessa.fearless a.feel vi.fell vt. ( )fellowshipn.feminine a.fencen. ( ) vi.ferrous a.ferryn. vt.fertile a.( )fighter n.filament n.fill vt. ( )filtervi.filthn.finance vt.finelyad.finitea.fireplacen.firework n.firmness n.first-ratea.fission n.fitness n.fitting a. n.fixture n.flaken.flamevi. vt.flankn.flannel n.flap vt.&n. vi.flaskn.flatten vt.flatter vt.flavour vt.flaw n.flee vi. vt.flexible a.flightn.flingvi.&vt.( )floatn.flockvi.fluctuatevi. vt.fluctuation n.flushn.flutter vi.( )flux n.fly v.foam n.followvt. ( )follower n.footpath n.fore ad. a.foreign a.foresee vt.forgevt. ( )formala.formerly ad.formidablea.formulatevt.formulation n.forsake vt.fort n.forthcoming a.fortress n.forumn.forward ad. vt.fossiln. a.fostervt.foul a.fowl n.fraction n.fracture n. vi.fragile a.fragrant a.fraila.frameworkn.freight n.frequencyn.frequent a.freshen vt.fret vt.&vi.( )friction n.frightn.frightfula.fringen.fro ad.frockn.( )frustratevt.furious a.further vt.fury n.fuse n.fuss n. vi.gamblen. vt.gangster n.gap n.garagen.garlicn.garment n.gathervt.gatheringn.gear n.generalizationn.generalizevt. vi.generate vt.generosityn.geographical a.( )geology n. ( )geometrical a.germ n.gesture vi.( )gigantic a.gingern.gleamn. vi.glidern.globala.glorify vt. ( )glossary n.glue vt.gnaw vt. vi.goddess n.goodness n.gorilla n.gorgeous a.gossipn.governvt.grab vt.&vi.gracious a.gradient n. a.gramophonen.granite a.grantn.graphite n.grasshopper n.4grassya. grateful a.graveln. grazevi. ( ) greasen. greedn.griefn. grim a. grin vi.grindvt. grooven. vt. gropevi.( ) grossa.( ) groven. growlvi.( ) grumble vi. gruntvi. guiltn. guitarn.gust n. guttern.hail vt. vi. halvevt.ham n. ( ) hampervt. handbook n.handicap vt. handout n. handya. harbour vt. hard a.( )hardya. harmoniousa. harp n. harsha. hatchvt. haughty a. haul vt. hauntvt. vi. hazardvt. n. head vt. ( )vi. heading n. headlong a.&ad. ( ) headquarters n. hearthn.heatern.heartya.heavevt.( )Heavenn.heighten vt.hemispheren.henceforthad.heraldad.herb n.herd vt. vi.hesitate vi.hide n.hike vi.hindrancen.hingen.hip n.hiss n. vi.historiann.historic a.hit n. ( )hitherto ad.hoarsea.( )hoe vt.&vi.hoistvt. vi.hollowvt. vi.homelya.homogeneous a.hook vt.hop vi. ( )horizon n.horn n.hose n.hospitality n.hostage n.hostess n.hostile a.houndn.housen.hovervi.howl n. vi.hug vt. n.hull n.hum n. vt.humanitarian a. n.humanity n.humidity n.hurl vt. vi.hurrahint.hurricanen.hurt n.hush n. int.hydraulica.hydrocarbon n.hymn n.hypothesisn.ice vt. vi.icy a.idealism n.ideally ad.identicala.identificationn.idiotn.idleness n.ignitevt. vi.ignorancen.illiteratea. n.illuminatevt.illusion n.imitationn.immerse vt.immigratevt.( )immortal a.impartvt.impartiala.implementn. vt.implore vt.imposevi.impress vt.improper a.impulse n.impurity n.inaccessible a.inaccuratea.inadequatea.inasmuch ad.inauguratevt.incapablea.incense n.incidencen.incidentally ad.inclination n.incline n.inclusivea.incompatible a.incompletea.incorporate vt.incrediblea.indefinitea.indicativea.indignation n.indispensablea.individuala.indoora.inducevt.inductionn.indulge vt. ( )vi.industrious a.inertia n.inevitablyad.infectvt.infectiousa.infervt.&vi.inferencen.inferior n.infinite n. ( )infinitelyad.infinity n.inflationn.influencen.ingeniousa.ingenuityn.ingredientn.inherent a.initial a.initiallyad.initiate vt.initiativea. n.injectvt.inlanda.inletn. vt.innovationn.innumerable a.inorganica.inputvt. n.insertvi.( )insight n.insignificanta.insistenta.inspectorn.inspiration n.instability n.installment n.instantaneousa.instructorn.instrumental a.insulate vt.insulatorn.intaken.integral a.integratevt.5ntegrityn. intellectn. intenta. interact vi. interconnect vt. intercourse n.interfacen.interior n. a. intermediate n.interpretvt. vi. intervenevi. interviewvt.intonationn.introducevt. ( ) invalid n. a. invariablyad. inverselyad.invoice n. ion n.irregularity n. irrespective a.irrigationn. irritate vt. Islamn. ivoryn. jack n. jam n. vt. jealousy n. jean n. jellyn. jerk vt. vi. Jesusn.jewelleryn. jinglevt.&vi.( )jog vt. ( )jug n. junction n.junglen. juniorn. Jupiter n. kerneln.( )kidnapvt.kidneyn.kilowatt n. ( )kindlevt. vi.kinetic a. ( )kit n.knightn.lace vi.landscapen.largely ad.late a.latenta.lathen. vt.latitude n.lattice n.laundry n.leaflet n.leakage n.leasen.legislation n.lengthn.lengthen vt. vi.leopard n.lessenvt. vi.levern.liabilityn.liablea. ( )lighter n.likelihoodn. ( )likeness n.lily n.limb n.limestonen.limp vi. n.line vt.lineara.linern.lingervi.liningn.( )lipstick n.literal a. ( )literallyad.literary a.littern. vi.lobbyn. ( )locality n.location n.locomotivea.locustn.lodging n.loftya.log n.longing n. a.longituden.loosely ad.loosenvi.loungen.( )lubricatevt. vi.luminous a.lump vt.( ) vi.lunara.luncheon n.luxuriousa.magician n.magistraten.magnetn. ()magnetismn.magnify vt.magnituden.maid n.maidenn.main n.maintenance n.majesty n.makeupn.malicen.mammaln.manifest vt. a.manipulatevt.mansion n.manuscriptn.maplen.marginn.marginal a.marketvt.( )Mars n.marshn.marshal n.martyrn.marveln. vt.masculinea.massacre n.massive a.mast n. vt.maturevt. vi.measurement n.( )mechanicsn.mechanismn.meditate vt.melancholyn.&a. ( )melodyn.membershipn.menacevt.&vi.&n.( )mend vt.merchandise n.merciful a.mercury n.meritvt. vi. ( )mesh n.mess vt.message n.metallic a. n.metallurgyn.metropolitan a. n.microprocessorn.microscopic a.microwaven.mightya.migrate vi.mild a.( )milkya.millionaire n.minglevt. vi.miniaturen. a.minimize vt.mint n.mint n.mirrorn.mishief n.misern.miseryn.misfortunen.missionaryn.mist n. vi.mistress n.mittenn.mixern.mob vi.mobilize vt. vi.mock n. vt.moderatelyad.modesty n.modification n.modulate vt. ( )modulen.moleculara.momentarya.monarch n.monk n.monopoly n.monster n.monstrousa.moor vt.mop n.morality n.mortgage n. vt.Moslemn.&a. ( )6mosquen.moss n. moteln. motivea. motorway n. mountv. n. mountainous a.move n. multiplicationn.multituden. municipala. murmurn. muscular a.muse vi. mustard n.mute n. mystery n.napkinn. ( ) narrationn.negative a. negligiblea. negotiatevi. neighbouring a.nest vi. vt.net vt. network n. neutron n.nice a. nickeln. nickname n. nightmaren.nominate vt.norm n. normalizationn.northward(s) ad. a.nose n. ( ) notable n.noteda.notifyvt.notionn.notoriousa.notwithstanding prep.noughtn.nourish vt.nourishment n. ()novela.novelty n.nucleus n.numbervt.numericala.nun n.nursery n.nut n.oar n. vi. ( )oath n.obediencen.obedient n.objectiven. a.obligationn.obligevt.obscure a.observation n.observe vi.obstinatea.occurrencen.offence n.offensivea.offervt. vi.offsetn. vt.offspringn.ohm n.oliven.onward(s)a. ( )opaquea.operationn.opiumn.optical a.optimism n.optimum n.optionn.orchard n.orchestran.ordinarilyad.orientn.orientation n.originatevi. vt.ornament n. vt.ornamentala. n.otherwisead.oughtv.auxoutbreak n.( )outcome n.outermosta.outlawn.outletn. ( )outline vt.outside prep.oval a. n.over prep. ( )overall a. n.overestimate vt.overflow vt.overhang vt. vi.overhear vt.overlap vt. vi.overload vt.overlook vt.overseas ad. ( )overtake vt.overthrowvt. n.overwhelmvt.overwhelming a.oxiden.oxidize vt.oystern.pace vi.( )pacific a.pal n.pamphlet n.paneln.( )panicn.pant vi.panther n.pantryn.pantsn.papervt. ( )parachuten.paradevt. ( )paragraphn.paralyse vt.parametern. ( )participant n. a.participate vi. vt.particulara.partitionn.passport n.pasture n.patenta. n.pathetic a.patriot n.patriotica.patroln. n.patronn.pattern vt.peacock n.peak n.( )peck vt.&vi.peculiarity n.pedaln.pedestriann.pedlarn.( )peel n.peer vi.penalty n.penetration n.pendulum n.( )perceptionn.perchn.( )perfect vt.perfectionn.periln.perimetern. ( )periodic n.periodicaln.peripherala.perishvi.perpendiculara. n.( )perpetuala.perplex vt.persecutevt.perseverevi.persist vi.persistence n.personality n.personneln.persuasionn.pertinenta.pest n.petition n. vt.pettya.photoelectrica.photography n.physicallyad.picklen.pier n.( )piercevt.pilgrim n.pineapplen.piousa.pipe n.piraten.pistonn.7pitchn. plaguen. plaina. plastic a. plateau n. platform n. plea n. pleadvt. vi. pledgen. vt. pluckvt. ( ) plumpvt. plunder v.&n. pneumatica. poke vt. ( ) polara. ( ) polarity n. ( ) politics n. poll n. vi. polymer n. pondervt. vi.pop vi.( )pope n.( ) popularityn.porcelainn. a. pore n. portable a.pose vt.( ) position n. positive a. positivelyad. possibility n. postala. postulatevt. poultry n.practicable a.prairie n. preachvt. precede vt. vi. predecessor n. predictionn.predominant a.pregnant a.prejudicen.prescription n.presentation n.preservation n.presetvt.preside vi.pressn.pressure n.prestige n.presumablyad.presume vt.prevalenta.preventionn.prey vi. vi.prickvt. ( ) n.primitivea.principally ad.printer n.priority n.prismn. ( )proben. vt.proceedingn.producer n.productivea.productivity n.proficiency n.proficienta.profitablea.profound a.program vi.prohibition n.projectorn.prolong vt.promotionn.promptly ad.propagandan.propagatevt.propagation n.propelvt.propellern.propera.prophecy n.prophet n.proposition n.propulsionn.prosen.protonn.prototypen.proverb n.province n.provisionn.provoke vt.prudent a.psychologyn.puff vi. vt. ( )pulleyn.pumpkin n.punchvt. n.puppyn.purifyvt. ( )pyjamas n.( )qualificationn.qualify vt.qualitative a.quantify vt.quantitative a.quarterlya. ad.quartzn.quenchvt.questvt. vi.question vt.questionable a.questionnairen.quivervi.( )radiala.radiant a.radiator n.radical a.radiusn.raisevt.raisinn.rallyn.&vt.&vi.( )ramblevi.ranchn.( )randomn. a.rangevt.rap n. vt.rapidity n.rapture n.rascaln.rash a.rate n. vt.rational a.rattlevt.reactor n.realistica.realization n.( )rear vt.reasonvt.rebukevt.receiver n.recipen.reciprocala.reckless a.reckonvi. vt.reclaim vt.recognition n.recommendationn.reconcilevt.recreationn.rectanglen.rectify vt.reed n.reef n.reel vt.referee n.( )referencen.refinery n.refrain vi.refreshment n.( )refugee n.regenerative a.regimen.regiment n.regularityn.regulate vt.regulationn.reignn.rejectvt.relayvt.religion n.remaindern. ( )repayvt.&vi.repealvt. n.repelvt.replace vt.replacement n.reportn.representationn.representativea.reproducevt.reproduction n. ( )reptile n.requisitea. n.resemblance n.resentvt.reservation n.reserve n.residevi.resident n.residual a.resignvt.resignation n.resolute a.respectable a.8response n.responsible a. restrain vt. resultanta. resumen.( )retailn. a. retardvt. retirementn.retortvt.&vi. revealvt. revenue n. reverse n. revivevt.&vi. revolve vt.&vi.( ) ridicule vi.&n. rigorous a.( ) rim n. ( ) rinsevt.riot n.&vi.rip vi. ripplen. roam vt. rollern. Romann. romance n. romantic a. rooster n. rotatevt.&vi.( ) roundabouta.routine a. n.row n. royalty n. ruby n.rule n.ruthless a. safeguardn. salmonn. salutevt. sandwich vt. sardine n. satelliten. satisfaction n.satisfactorilyad.saturationn. ( )Saturnn.scan n.scandal n.scar n.scarcity n.scarlet n. a.schemevt. vi.scholarship n.scoffvt.&vi.scopen.scorchvi.scoutvt.scramble vi.&n.scrapn. vt.scratch n.scripturen.scrubn.&vt.sculpturen. ( )seam n.seaport n.seaside n. ( )secondvt.second-hand n.section n.seeminglyad.segment n.selectionn.senator n.sensationn.senselessa.sensible a.sensitivity n. ( )sensorn.sentimentn.sequence n.sermonn.serpent n. ()set n. ( )settlementn. ( )severea.shabbya.shaden.( )shadowy a.shadya.shaftn.( )sham n. vt.shamevt.shameful a.sharkn.sharply ad.shatter vt.sheera.shelln.sheriff n.shipbuilding n. ( )shipment n.shipwreckn.shortage n.shortcut n.shorten vt.shorthandn.shouldv.aux.shoulder vt.shovevt. vi.( )shoveln. vt.showervi. vt.shrilla. vt.shrimpn.( )shrinen.shrubn.shrugvt.&vi. ( ) n.shutter n. ( )shuttle n.( )sideways ad.siegen.sift vt. vi.sightn.sign n.significant a.signify vt.silicon n. ( )similarityn.simplea.simplicityn.simultaneous a.sincerityn.singular a.sink n.( )sirenn.sitting-room n.situated a.situationn.( )skeleton n.skip vi.skyscrapern.slacka.slander n.&vt.slangn.slap vt. n.slaughtervt.&n.slavevi. vt.sliden.slim a.slit vt. n.slumber n.smartvi.smashvt.smuggle vt. vi.snackn.snailn.snap vt.sneervi.&n.sneezevi.sniffvi. vt.snob n.snobbish a.snorevi.sociologyn.sodiumn.sofa n.softenvt. vi.softness n.software n.( )solara.solidarityn.solidify vt.&vi.solo n.sophisticateda.sorrowfula.southwardsad.sovereignn. a.souvenir n.soy n.spacious a.span n.( )spatial a.specializevt.species n.specificationn.specimen n.spectaclen.spectatorn.spectrum n.speculatevi.sphericala.spicen.spilln.( )spirala. ( )spiten.splashvt. vi. n.splitn.spokesmann.squashvt. n.squatvi.&vt.( )squeeze n.stabilityn.stagger vi. vt.stainlessa.stairway n.stalkn.stalln.stammer vt. n.standardize vt.startvt.stationeryn.statisticsn.steadya.9teakn. stealvt.stem n. ( ) stereon. a. sternn.stew vt. vi. n. stiffa.stiffnessn.stillnessn. stingn. vt. stitchn. vt. stonen. ( ) storage n. stormn. vt.&vi. stouta. straightenvt. vi.straightforward a. ad.straitn.strange a. strayvi. a. streamlinen. strength n. stridevi. n. strifen.striking a. stripn.strivevi. strolln. stubborn a. studion. stuffya. sturdya. subdividevt. subduevt. subject vt. subordinate a. subscribevi.subscripta. n.subscription n.subsequenta. subsequently ad.subsidiarya.substancen.substantial a.subtlea.successionn. ( )successorn.suffice vi.suicide n.&vi.&vt.suit vt. vi.suitcase n.sullena.summary a.summitn.summonvt. ( )superba.superficial a.superiority n. ( )supersonica.superstition n.supervisevt.&vi.supplementn.support vt.suppress vt.surpass vt.surplus n. ( )survival n.suspiciousa.sweeten vt. vi.sweetnessn.swellvi.&vt.switchn.( )symmetrical a.symmetry n. ( )symphony n.symposiumn.symptom n.synthesisn.systematica.systematicallyad.tabulate vt.tack n. vt.tacklevt. n.tact n.tactics n.tanglevt.tankern.tape vt.tapern.tar n.team vi.teasevt.telexn.temptvt.tensile a.terminal n.terminatevt.&vi.terminology n.terrace n.terrify vt.terroristn.testify v.Thanksgiving n.theatre n.theftn. ( )themen.theorem n.theoryn.thereafterad.therein ad.thereof ad.thermal a.thesisn.thicken vt. ( )thighn.thorough a.thoughtless a.thrashvt. vi.threshvt.thresholdn.thrifty a.thrillvt.&vi.( )through prep.ticketn.( )ticklevt.tighten vt.&vi.( )tightly ad.tile n.tilt vt.&vi.( )timelya.tiresome a.toad n.tokenn.tolerant a.tone n.torment n. vt.torpedo n.torquen. ( ) ( )toss vi.tow vt.&n.towards prep.towervi.trackvi.tradevi.tradern.tradesmann.tragica.trampvt.&vi.&n.trample vt.&vi.&n.tranquil a.transaction n.transformvt.transitionn.transmission n.transplantvt.&vi.transversea. n.traverse vt.treadvi.&vt.treasurern.trenchn.triangulara.tribute n.triflevi.trigger n. vt.triumphanta.trivial a.trolley n.troopn.tropicn.tropical a.trot vi.&n.( )troublesome a.tuberculosis n.tug vi. n.tulipn.tuna n.turtlen.tutorvt.twilight n.twistv.tyranny n.tyrantn.ultimate a.ultrasonica. n.ultraviolet a. n.unanimousa.( )uncertaina.underestimatevt.underlinevt.undertakevt.undertaking n.underwearn.undesirable a.uneasya.unemployment n.unfita.unfoldvt. vi.uniformlyad.uniquea.universally ad.unlimiteda.unlockvt.unpaida.10。

한중영 철강사전
(version 2.0) 영문 A0 transformation A0 transformation A1 transformation A1 transformation A2 transformation A2 transformation A3 transformation A3 transformation A4 transformation A4 transformation Abrasion test Abrasion test Abrasion test Absorbed energy Accelerated cooling Accuracy Accuracy Acetylene Acetylene Acetylene gas welding Acicular structure Acicular structure Acid Bessemer converter Acid Bessemer process Acid electric-arc furnace Acid refractory Addition agent 중국어 한자 A0转变 钢中渗碳体的磁性转变 A1转变 钢的共析转变 A2转变 铁的磁性转变 A3转变 铁的同素转变 A4转变 ?铁?铁转变 磨耗试验 磨蚀试验 磨损试验 吸收能量 加速冷却 精确度 准确度 电石气 乙炔 乙炔焊 针状结构 针状组织 酸性转炉<钢> 酸性转炉法<钢> 酸性电弧炉 酸性耐火材料 添加剂 后吹 After blow 후취(後吹) (碱性底吹转炉炼钢法的后期操作) After treatment 후처리 补充处理 After treatment 후처리 二次处理 After treatment 후처리 后处理 Age hardening 시효경화 时效硬化 Aging 시효 陈化 Aging 시효 老化 Aging 시효 时效 Air cooling 공냉 空气冷却 Air shear 에어시어 风动剪 Alloy 합금 合金<冶> Alloy steel 합금강 合金钢 Alloy tool steel 합금공구강 合金工具钢 Alumina 알루미나 矾土 Alumina 알루미나 铝氧 Alumina 알루미나 氧化铝 Alumina silica refractory 알루미나 실리카계 내화물 硅酸铝耐火材料 Aluminous cement 알루미나시멘트 矾土水泥 Aluminous cement 알루미나시멘트 高铝水泥 AMF alloy AMF합금 AMF耐蚀合金 Angle 앵글 角钢 <压> Angles ㄱ형강 角钢<压> Anisotropic 이방성(異方性) 各向异性的 Anisotropic 이방성(異方性) 有向性的 Annealing 소둔 退火 Annealing 어닐링 退火 Annealing furnace 어닐링로 退火炉 Anthracite coal 무연탄 无烟煤 Apparent porosity 외관기공율 表观气孔度 Apparent porosity 외관기공율 视气孔度 Apparent specific gravity 외관비중 表观比重 Apparent specific gravity 외관비중 视比重 Arc gouging 아크가우징 电弧表面切割 Arc voltage 아크전압 电弧电压 Arc welding 아크용접 电弧焊接 Arc welding 아크용접 弧焊 Arc welding electrode 아크용접봉 电弧焊用焊条 Arch 아치 拱 Arch 아치 拱顶 Arch 아치 炉拱 Argon oxygen decarburization AOD 氩-氧脱碳<钢> Arsenic 비소 砷 Artificial aging 고온시효 人工时效 Artificial graphite 인조흑연 人造石墨 Ash content 회분 灰分含量, 含灰量 Atmospheric corrosion resistance 내후성 抗大气腐能力 Atmospheric corrosion resistance 내후성 耐候性 Atomization 아토마이제이션 粉化 Atomization 아토마이제이션 雾化 Austenite 오스테나이트 奥氏体<金> Austenite grain size 오스테나이트 입도 奥氏体晶粒度 Austenitic stainless steel 오스테나이트계 스테인리스강 奥氏体不锈钢 Austenitic steel 오스테나이트강 奥氏体钢 Austenitizing 오스테나이트화 奥氏体化 Automatic welding 자동용접 自动焊接 Back up roll 백업롤 支撑辊 Bainite 베이나이트 贝氏体 한글 A0변태 A0변태 A1변태 A1변태 A2변태 A2변태 A3변태 A3변태 A4변태 A4변태 마찰(마모)시험 마찰(마모)시험 마찰(마모)시험 흡수에너지 가속냉각 정확도 정확도 아세틸렌 아세틸렌 아세틸렌용접 침상조직 침상조직 산성노저취입전로 산성노저취입전로법 산성아크로 산성내화물 첨가물 2004. 2. 11/POSCO-China 중국어 병음 A0 zhuan bian gang zhong shen tan ti de ci xing zhuan bian A1 zhuan bian gang de gong xi zhuan bian A2 zhuan bian tie de ci xing zhuan bian A3 zhuan bian tie de tong su zhuan bian A4 zhuan bian tie tie zhuan bian mo hao shi yan mo shi shi yan mo sun shi yan xi shou neng liang jia su leng que ห้องสมุดไป่ตู้ing que du zhun que du dian shi qi yi que yi que han zhen zhuang jie gou zhen zhuang zu zhi suan xing zhuan lu<gang> suan xing zhuan lu fa<gang> suan xing dian hu lu suan xing nai huo cai liao tian jia ji hou chui(jian xing di chui zhuan lu lian gang fa de hou qi cao zuo) bu chong chu li er ci chu li hou chu li shi xiao ying hua chen hua lao hua shi xiao kong qi leng que feng dong jian he jin<ye> he jin gang he jin gong ju gang fan tu lv yang yang hua lv gui suan lv nai huo cai liao fan tu shui ni gao lv shui ni AMF nai shi he jin jiao gang<ya> jiao gang<ya> ge xiang yi xing de you xiang xing de tui huo tui huo tui huo lu wu yan mei biao guan qi kong du shi qi kong du biao guan bi zhong shi bi zhong dian hu biao mian qie ge dian hu dian ya dian hu han jie hu han dian hu han yong han tiao gong gong ding lu gong yan-yang tuo tan<gang> shen ren gong shi xiao ren zao shi mo hui fen han liang,han hui liang kang da qi fu shi neng li nai hou xing fen hua wu hua ao shi ti<jin> ao shi ti jing li du ao shi ti bu xiu gang ao shi ti gang ao shi ti hua zi dong han jie zhi cheng gun bei shi ti

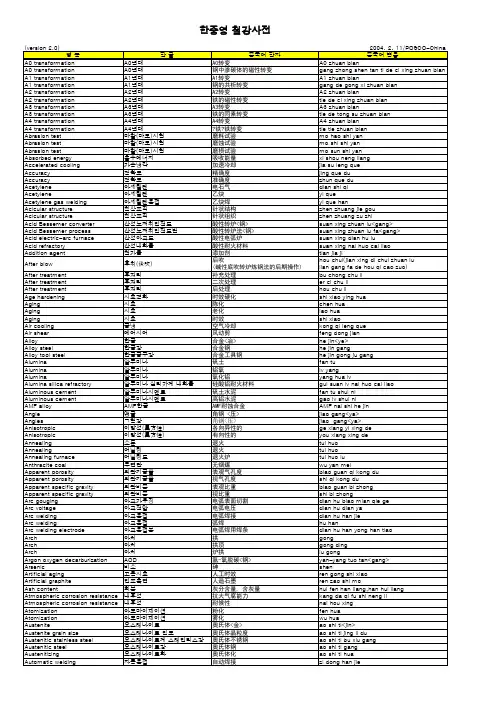
旅游的词汇很多，大师平时多看看都有好处。

这里面有我们讲义上的那几个诗句，还有四字词是按字母挨次排的。

TOURISM1.1 话题扩充1. accommodations n. 膳宿；住房[glossary] [扩展]adjoining room [ ] n.相邻的房间single room - a room with one bed for one person n. 单人房〔一张床〕twin room - a room with two beds for two people n. 双人房〔两张床〕double room - a room for two persons with a double bed n. 双人房〔一张床〕triple room - a room for three persons, usually consisting of twin beds (or double bed)plus a roll-away cot n. 三人房standard room n. 尺度间deluxe room [ ] n. 豪华间luxury suite[ ] n. 豪华套房presidential suite [ ] n. 总统套房ocean front - a room directly facing the ocean n. 面朝海洋的房间ocean view -a room from which it is possible to secure a view of the ocean (usuallylocated on the side of the hotel) 海景房wet bar小吧台n. 〔旅馆房间里有自来水和水槽的小吧台〕book/ reserve a room v. 订房booth n. 餐厅中的包厢或火车座bowling alley [ ] n. 保龄球场check in v. 入住check out v. 结账、退房close-circuit television [ ] n. 闭路电视deposit[ ] n. 预定金discotheque [ ] n. 迪斯科舞厅front desk; reception desk n. 前台gym [ ] n. 健身房hotel registration form n. 旅馆登记表karaoke [ ] n. 卡拉OKlobby n. 大堂make a reservation预订massage parlor [ ] n. 按摩室, (挂按摩院招牌的)倡寮pool table n. 台球桌stay at v. 在。

地下室平面圖
詞性
名詞 名詞 名詞 名詞 動詞 名詞 名詞
形容詞
項次 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 order scale
中文名稱 設計 親密性 私密性 公共性 構想 模距 幾何構圖 層次 漸進 平衡 主導 交替 裝飾 側影 鋪面 天際線 動線 投射 紋脈 生態 踏步 樓梯 牆 窗 門 穹頂 圓拱 都市 帳蓬 城市 應力 應變 樑 柱 構架 鉸接 輥接
詞性 N N N N N N N N N N V N N N N N N N N N N N N N N N N N N N N N N N N N N
屋頂平面圖
室內 （的） 名詞
名詞 名詞 名詞 名詞 名詞 名詞 名詞 名詞
比例 物理性的 心理性的 重複性 重複 研究 反應
名詞 動詞 名詞 動詞
項次 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107
英文名稱 design intimacy privacy publicity concept modulor geometry hierarchy recession balance dominate transparency decoration silhouette pavement skyline circulation projection contex ecology steps stairs wall window door dome arch urban tent city Stress Strain Beam Column Frame Hinge Roller

(a)esthet = feeling 感觉 例：anesthetic n.麻醉剂
sens, sent = feel 感觉 例：sensor n.传感器
pass = feeling 感情 例：passion n.热情，激情
path = feeling, suffering, illness 感情，痛苦，病 例：sympathy n.同情；同感
sume, sumpt = take 拿，取 例：consumer n.消费者；顾客
rap, rapt, rav = snatch 捕，夺 例：rape v.强奸；抢夺
ten, tent,tain,tin = hold 拿住 例：continent n.大陆；大洲
habit, hibit= have,hold,dwell 拥有，居住 例：cohabit v.同居
emper, imper = command 命令，统治 例：emperor n.皇帝 [emper 命令，-or 者；“发布命令者”→统治者→]
agog = lead 引导 例：pedagogue n.教师
duc, duct = lead, bring 引导，带来 例：introduce n.介绍，引荐
crit, cris = judge, discern 判断，分辨 例：critique n.评论 v.批判；评论
judg, judic = judge 判断 例：judgment n.判断；辨别力
chrom = color 颜色 例：chromosome n.染色体
chron = time 时间 例：chronograph n.计时器
calc = stone 石头 例：calculate v.计算

魔方词典--------------------------------------------------------------------- 0 — 9~' 魔方某面或某层逆时针转动("~"代表某个字母)。

# blindfoldcubing专用标记。

以此来表示角块与边块的颜色、位置关系。

(~) 括号内字母表示高阶魔方以某几层为一个单位同时向一定方向转动。

- blindfoldcubing专用标记。

以此来表示角块需要逆时针旋转。

+ blindfoldcubing专用标记。

以此来表示角块需要顺时针旋转。

1 blindfoldcubing专用标记。

某角块颜色需要顺时针旋转归位或某边块未归位。

15 Tilt的角度。

也包括30和45。

1st Layer 请参考“First Layer”。

1ｘ1ｘ2 请参考“Marvin Boob”。

~2 魔方某面或某层转动180度。

例：R2；S'2。

2 blindfoldcubing专用标记。

某角块颜色需要逆时针旋转归位。

2ｘ2ｘ2 请参考“Rubik's Pocket Cube”。

2ｘ2ｘ3 请参考“Slim Tower”和“Franken Tower”。

2-Second Penalty 2003年由提议开始正式列为世界魔方比赛规则。

选手虽完成还原但某面或某层未完全归位且超过一定限度会被施与完成时间增加两秒的处罚。

2nd Layer 请参考“Second Layer”。

3ｘ3ｘ1 请参考“Rubik's Layer”。

3ｘ3ｘ2 请参考“Magic Domino”。

3ｘ3ｘ3 请参考“Rubik's Cube”。

3ｘ3ｘ5 请参考“Grown Tower”。

3ｘ4ｘ4 请参考“Specter Cube”。

3-Cycle 魔方某三色块作一定规则的循环置换。

3rd Layer 运用LBL还原魔方的第三层。

三阶魔方的最后一层。

Week 1Mondayabort v.中止;使流产absurd a.荒谬的abundance n.丰盛academician n.院士accession n.就职;正式加入accessory n.附件;装饰品accommodate vt.留宿;使……适应accountability n.负责accountable a.负有责任的accounting n.会计行业accusation n.控告accustom vt.使习惯于activate vt.激活actuality n.实际addict n.吸毒成瘾的人;对……入迷的人addicted a.上了瘾的addictive a.使人上瘾的adhere vi.粘附;坚持adherence n.遵守adjacent a.邻近的adjoin v.与……毗连administer vt.管理;施行admittance n.进入admittedly ad.公认地adolescence n.青春(期)adolescent n.青少年a.青春期的,青少年的advancement n.推动advantageous a.有利的adventurer n.冒险者adventurous a.大胆的;充满新鲜事物的adverse a.不利的aerial a.空气中的n.天线aerospace n.航空affiliate v.(使)隶属于n.附属机构affirm vt.断言affix v.粘上n.词缀afflict vt.折磨aggravate vt.使加重,使恶化aggregate v.使聚集;合计a.合计的n.合计airborne a.空降的;飞行中的aisle n.通道alien a.外国的;不相容的;陌生的n.外国人;外星人alienate vt.离间allege vt.宣称allegedly ad.据说alleviate vt.减轻allocate vt.分配allotment n.分配aloft ad.在高处alternate v.(使)交替ambiguity n.含糊不清ambiguous a.含糊不清的amend vt.修改ample a.富裕的;丰满的amplify vt.放大;详述analogy n.类比analytical a.分析的anew ad.重新animate a.有生命的vt.使具活力animated a.栩栩如生的;生气勃勃的Tuesdayannoyance n.烦恼(事) anonymous a.匿名的;无名的apparatus n.器械;机构appease vt.平息appendix n.附录;阑尾appraisal n.估计;评价appraise v.估价;评价appropriation n.拨专款;挪用apt a.恰当的;有……倾向的arch n.拱门v.(使)成弓形armour n.盔甲;装甲array vt.排列arrogance n.傲慢arrogant a.骄傲自大的artful a.精巧的;巧妙的articulate v.明确表达a.善于表达的;口齿清楚的artifact n.人工制品artwork n.艺术品ascend vt.攀登vi.上升ascertain vt.查明ascribe vt.把……归因于assault n./vt.袭击assertive a.坚定自信的assimilate v.(使)同化assurance n.信心;保证;保险attendant n.服务人员a.伴随的attributable a.可归因于……的authenticity n.真实性authoritative a.权威性的authorize vt.授权automation n.自动化autonomous a.自治的autonomy n.自治(权)avail n.效用availability n.可用性avert vt.转移(目光等);避免aviation n.航空avoidance n.避免axis n.轴;坐标轴baffle vt.使困惑ballet n.芭蕾舞;芭蕾舞剧;芭蕾舞团ballot n.投票总数;选票v.(使)投票表决bankruptcy n.破产barren a.贫瘠的;不孕的;没有结果的batch n.一批;一批生产的量battalion n.营batter v.连续猛击n.面糊beforehand ad.预先behavio(u)ral a.行为的beneficiary n.受惠者bewilder vt.使迷惑bias n.偏见vt.使有偏见bilingual a.熟悉两种语言的binder n.装订者;活页夹blaze vi.熊熊燃烧;迸发n.光辉bleed vi.流血vt.榨取bless vt.为……祈神赐福blink v.眨(眼睛) vi.闪亮blunder vi.跌跌撞撞地走;犯愚蠢的错误n.愚蠢的错误blunt a.钝的;率直的vt.使变钝;使减弱Wednesdayblush vi./n.脸红boastful a.好自夸的boycott n./vt.抵制brace n.大括号;支架vt.支住bracket n.括号;等级breach n.违背;缺口vt.违反breakdown n.破裂;故障;分类brew vt.酿造;冲泡(茶等) n.啤酒brewery n.啤酒厂briefing n.情况介绍会brighten vt.使发光brink n.边缘brood n.(雏鸡等)一窝;一个家庭的所有孩子vi.孵蛋;焦虑,忧思bruise n.青肿;伤痕v.(使)出现伤痕vt.挫伤buck n.美元vi.猛然弓背跃起bully v.欺负n.恃强欺弱者bureaucracy n.官僚体制;官僚主义bureaucrat n.官僚(主义)者bureaucratic a.官僚(主义)的bust n.胸部vt.打破buzz vi./n.(发出)嗡嗡声calling n.使命感;职业cape n.海角capsule n.胶囊;太空舱caption n.说明文字;字幕cardinal a.最重要的n.红衣主教carve vt.雕刻;切casualty n.伤员;受害人cater v.承办酒席vi.迎合caution n.小心;警告vt.提醒cavity n.洞certification n.证明certify vt.证明;颁发证书给charitable a.慈善的cherish vt.珍爱;怀有chord n.和弦;弦chorus n.合唱队;副歌;齐声vt.齐声说chronic a.慢性的;积习难改的chronicle n.年代记circulation n.发行量;循环;流通clamp n.夹具vt.夹紧clarification n.澄清clarity n.清楚clasp n.扣环;紧握vt.扣紧;握紧classified a.分类的;保密的clearance n.清除;批准;(支票的)兑现;间隙clear-cut a.明显的climax n.高潮cluster n.串;群v.群集clutch n.离合器coalition n.结合;同盟cognitive a.认知的coherent a.有条理的cohesion n.内聚力coincide vi.同时发生;相符;重叠coincidence n.巧合;一致collaboration n.合作;勾结collide vi.碰撞;冲突commemorate vt.纪念commend v.称赞Thursdaycommentary n.实况报道;评论(文章) commodity n.商品commonplace n.平常的事a.普通的commonwealth n.英联邦;联合体compassionate a.有同情心的competence n.能力compile vt.编写complement vt.补充n.补充;补语complexion n.肤色complexity n.复杂性;难题complication n.使复杂化的事物;并发症compliment v.赞美n.问候comply vi.遵从composite a.混合成的n.合成物compulsory a.强制的;必修的conceited a.自负的conceive v.构思;怀胎conception n.构想;怀孕concise a.简洁的concurrently ad.同时地condemnation n.谴责confer v.商讨;授予(某人) confidential a.机密的conform vi.遵守;符合conformity n.遵守confrontation n.对抗congressman n.国会议员conqueror n.征服者conscientious a.认真的consecutive a.连续的consequent a.作为结果的conserve v.保存,保护console v.安慰consolidate vt.巩固;合并conspicuous a.明显的constituent a.形成的n.成分;选民constrain vt.限制constrict v.(使)束紧consultancy n.咨询公司;专家咨询consultative a.咨询的contemplate vt.思量;注视contempt n.轻视contend v.竞争,斗争;坚决主张contention n.争辩;论点continuance n.连续contradict vt.反驳;相矛盾contrive vt.设法做到;谋划convene v.召集;集会converge vi.聚集;汇合conversion n.变换;皈依convertible a.可改变的cooperative a.合作的;配合的n.合作企业cordial a.热情友好的corporate a.公司的correlate vt.使相互关联correlation n.相互关系corrode v.(受)腐蚀corrupt a.堕落的vt.使堕落councilor n.(州、市、镇等的)议员counterclockwise a./ad.逆时针方向的(地) Fridaycounterpart n.与另一方作用相当的物courageous a.勇敢的coverage n.覆盖范围;新闻报道crackdown n.严厉打击cradle n.摇篮;发源地vt.轻轻地抱credible a.可信的criterion n.标准culminate vi.以……告终cultivation n.耕作;教养cumulative a.累积的customary a.习惯的dart n.飞镖;急驰vi.猛冲dazzle vt.使眩目;使倾倒decimal a.十进位的n.小数decisive a.决定性的;果断的decree n.法令;裁决vt.判决dedicate vt.把(一生等)献给;题献词于(著作等)上dedication n.奉献;献词deduce vt.推论deduction n.推论;扣除deem vt.认为default n.不履行;弃权vi.不履行defection n.背叛defective a.有缺点的defendant n.被告defiance n.违抗deficient a.缺乏的;有缺陷的definitive a.最可靠的degenerate v.衰退a.衰退的degrade vt.降低……的身份denote vt.指示denounce vt.谴责;告发deplore vt.哀叹;痛惜deploy v.部署;施展deport vt.把……驱逐出境deprive vt.剥夺derail v.使……出轨descendant n.后裔descent n.下降;血统designate vt.标示;指派desirability n.值得向往desirous a.渴望的despatch v.派遣;发送n.急件despise vt.鄙视destined a.命中注定的;以……为目的地的destiny n.命运;天命detach vt.拆卸detain vt.耽搁;拘留detention n.拘留deteriorate vi.恶化deterioration n.恶化;变坏deviate vi.背离diagnosis n.诊断dictator n.独裁者differentiate v.区别;表明……间的差别diffuse v.扩散;传播a.冗长的dilute vt./a.稀释(的)diminish v.减少,降低disable vt.使伤残;使无效Week 2Mondaydiscern v.辨别;看出disciplinary a.纪律处分的disciplined a.受过训练的disclose vt.揭露disclosure n.揭发discreet a.谨慎的discrepancy n.不符合discrete a.分离的discriminate v.区别vi.歧视dismay vt./n.(使)失望dismissal n.解雇;不予考虑dispense v.分配;配(药)disperse v.(使)分散displace vt.取代;迫使……离开家园disposition n.性情;排列;意向disregard vt./n.忽视,漠视disrupt n.扰乱distill vt.蒸馏;吸取distinguishable a.可辨别的distort vt.扭曲;歪曲distracted a.思想不集中的diversion n.转移;临时绕行路divert vt.使转向;转移;使娱乐dividend n.分红;被除数divine a.神的dodge v.躲闪dole v.发给domain n.领地;领域dominance n.优势domination n.支配;优势donate v.捐赠doom n.厄运vt.注定dread vt.惧怕n.担忧drought n.旱灾dub vt.配音;起绰号dubious a.怀疑的duplicate vt.重复n.复制品a.复制的dwell vi.居住dweller n.居民eccentric a.古怪的n.古怪的人eclipse n.(日、月)食vt.使暗淡eject vt.喷射,弹出;驱逐elapse vi.消逝elastic n.松紧带a.有弹性的;灵活的elasticity n.弹性electrician n.电工elevate vt.提拔;举起elicit vt.诱出eligible a.有恰当资格的;合适的eloquent a.口才流利的;明白显示出的emancipate vt.解放embark vi.上船(或飞机、汽车等);从事embed vt.把……嵌入;使深留脑中embody vt.体现;包括emigrant n.移民emission n.散发物enclosure n.圈占地;附件endanger vt.危害endeavo(u)r vi./n.努力endorse vt.赞同;宣传Tuesdayendow vt.资助enforcement n.执行;强制enrol(l)ment n.注册ensue vi.接着发生entail vt.使成为必要entrust v.委托envisage vt.想象equator n.赤道eradicate vt.连根拔除erase vt.擦掉erupt vi.喷发;爆发escort n.护送者v.护送essence n.本质;精髓esteem vt./n.尊重evacuate vt.转移evaporate v.(使)蒸发;消失evoke vt.唤起exceptional a.卓越的;例外的execution n.履行exemplary a.典范的exempt a.被豁免的vt.免除exhaustion n.耗尽;精疲力竭expend vt.花费,消耗expenditure n.经费;耗费expire vi.死亡;期满exposition n.展览会exquisite a.精美的;敏锐的;感觉强烈的extinct a.灭绝的;已废弃的extract v.取出;获得n.摘录;提出物extravagant a.奢侈的;放肆的,过度的fabricate vt.捏造;装配fabulous a.极好的;寓言中的facet n.琢面;一个方面falsehood n.谎言fatality n.死亡feast n.盛宴;节日vi.尽情地吃feat n.功绩;技艺fellowship n.伙伴关系;联谊会feminine a.女性的;女子气的ferry n.渡船v.渡运finite a.有限的fitting a.适合的n.设备;附件;试衣fixture n.固定装置;固定在某位置的人flap v.拍动;振翅n.片状垂悬物;激动flare vi.突发n.闪光信号灯flatter vt.奉承;使显得更漂亮flip v.轻抛;轻拍;快速翻动n.轻弹flush v.冲洗vi./n.脸红a.齐平的flutter v.快速跳动;拍翅;飘动foam n.泡沫vi.起泡沫foil n.箔;陪衬vt.挫败foremost a.最重要的foresight n.远见formulate vt.构想出;确切表达fort n.城堡forthcoming a.即将发生的;现成的;乐于提供消息的foster a.收养(孩子)的vt.收养,养育(非亲生子);培养,促进,助长foul a.发臭的;令人不愉快的;恶劣的v.弄脏;对……犯规n.犯规Wednesdayfracture n.裂缝v.(使)断裂fragile a.易碎的;脆弱的fright n.惊骇;恐怖的经历fringe n.刘海;外围funding n.基金furious a.暴怒的;强烈的fury n.暴怒fuse n.导火线v.熔化fusion n.融合galaxy n.星系;银河系gasp n./v.喘气v.喘着气说出generalize/-ise v.概括generosity n.慷慨giggle vi./n.咯咯笑glare vi.发强光;怒目而视n.刺眼的光;怒视gleam n.微光;流露vi.闪烁;流露glide vi.滑动glossary n.词汇表gorge n.峡谷gossip n.流言蜚语;爱说长道短的人vi.传播流言蜚语gracious a.仁慈的granted conj.因为graphic a.图表的grease n.油脂vt.用油脂涂;给……加润滑油grieve vt.使悲伤vi.感到悲痛grill vt.烧烤;拷问n.烤架;烧烤餐馆groan vi./n.呻吟groove n.槽grope vi.摸索guardian n.监护人;守卫者hamper vt.妨碍handicap vt.妨碍n.不利条件hasty a.草率的;匆忙的hatch vi.孵出vt.孵;筹划n.舱门;开口haunt vt.常出没于;萦绕在……心头n.常去的地方hawk n.鹰hazardous a.危险的heighten v.加强hemisphere n.(地球的)半球heritage n.遗产hesitant a.犹豫不决的hierarchical a.等级制的hierarchy n.等级制度;统治集团hike vi./n.徒步旅行n.增加hinge n.铰链,合叶vi.取决于hoist vt.举起homogeneous a.同种类的honorary a.名誉的hop vi.单足跳跃;齐足跳跃n.蹦跳;短程航行hospitality n.殷勤hound n.猎犬v.烦扰hover vi.翱翔;徘徊humane a.人道的humanism n.人道主义humanist n.人道主义者humanitarian a.人道主义的n.人道主义者hurl vt.猛投;大声叫骂ignite v.点燃;激起illicit a.违禁的illuminate vt.照明,照亮;阐明Thursdayimitation n.模仿;赝品immerse vt.使浸没;使沉浸在immunize vt.使免疫impair vt.损害impart vt.赋予;告知imperative a.必要的n.必要的事imperialism n.帝国主义imperialist n.帝国主义者impetus n.推动;推动力imprison vt.关押impromptu a./ad.即席的(地) inaugurate vt.为……举行就职典礼; 为……举行落成仪式;开创inborn a.天生的incentive n.刺激incidentally ad.顺便提一句inclusive a.包括一切的incompatible a.不一致的,不相容的incorporate vt.把……合并;包含incur vt.招致indefinite a.含糊的indicative a.指示的;陈述的indignant a.愤怒的indignation n.愤怒induction n.感应inductive a.归纳的;电感的indulge v.纵容;沉溺于infectious a.传染(性)的;有感染力的infinity n.无限inflict vt.使遭受打击infringe v.违反;侵犯ingenious a.灵巧的;巧妙的inhabit vt.居住于inhibit vt.阻止initiate vt.创始;使初步了解;接纳inject vt.注入;注射inlet n.进口;水湾innovation n.革新;新方法innumerable a.无数的instal(l)ment n.分期付款instantaneous a.瞬间的institutional a.公共机构的instrumental a.用乐器演奏的insulate vt.使绝缘;使隔离insurgency n.起义integral a.构成整体所必需的intellect n.智力;才智非凡的人intelligible a.可理解的intent n.意图a.专心的interactive a.互相作用的;交互式的interim n.间歇a.暂时的intermediate a.中间的;中级的intervene vi.干涉;干扰intolerance n.不容忍;过敏intolerant a.不能容忍的intricate a.错综复杂的intrigue vi.耍阴谋intrinsic a.固有的intuition n.直觉invalid a.无效的n.病弱者Fridayinvaluable a.非常宝贵的invariably ad.不变地invert vt.使倒转;使倒置investigator n.调查员investor n.投资者irrespective a.不顾及的irritate vt.激怒isolation n.脱离jealousy n.妒忌jeopardize vt.危及jerk n./v.猝然一动jog v./n.慢跑;轻轻碰撞judicial a.司法的junction n.枢纽kidnap vt.诱拐lace n.蕾丝(花边);鞋带vt.用系带束紧lame a.跛的lash v.猛烈抨击n.鞭梢;鞭打;睫毛lawsuit n.诉讼layoff n.解雇leaflet n.传单v.(向……)散发传单legalization n.合法化legend n.传说;传奇人物legislative a.立法的legislator n.立法者legitimate a.法律认可的;合情合理的vt.使合法lever n.杠杆;手段levy vt./n.征税liability n.责任;债务likelihood n.可能(性)linger vi.逗留;继续存留literal a.逐字的;字面意义的locality n.地区locomotive n.机车lofty a.高傲的;高尚的;高耸的lounge n.休息厅lubricate vt.使润滑luminous a.发光的,发亮的lunar a.月的lure n.诱饵;诱惑物vt.引诱magistrate n.地方法官magnify vt.放大;夸大magnitude n.巨大majesty n.陛下;雄伟make-up n.化妆品;组成malicious a.有恶意的manoeuvre v.转动n.策略manifest a.显而易见的vt.表明;显现manuscript n.手稿;手抄本massacre n.大屠杀;(比赛等)惨败vt.大规模屠杀;彻底击败mastermind n.出谋划策者vt.策划maturity n.成熟mediate v.调解medieval a.中世纪的melody n.旋律memorize vt.熟记,记住menace n.威胁;具有危险性的人(或物) vt.威胁merge v.(使)结合merger n.合并midst n.中部Week 3Mondaymigrant n.移民;候鸟militant a.激进的n.激进分子mingle v.(使)混合vi.相交往miniature n.缩影a.小型的minimal a.最小的minimize vt.使减小到最低限度misfortune n.不幸;灾难mobilise/-ize v.动员;调动mock v.嘲笑a.假装的;模拟的momentary a.瞬息间的momentum n.动量;势头monetary a.货币的,金融的monopoly n.垄断;垄断物mortal a.终有一死的;致命的motel n.汽车旅馆mourn v.哀悼;对……感到痛心muddy a.泥泞的;暗淡的vt.使沾上烂泥multitude n.大量;群众murmur v./n.小声说(话)mute a.哑的;缄默的mutter v./n.轻声低语,小声抱怨naive a.天真的;幼稚的necessitate vt.使成为必要neglectful a.疏忽的negligible a.微不足道的negotiable a.可谈判的neutralize vt.使中立;使无效nominal a.名义上的;象征性的nominate vt.提名,任命nominee n.被提名者,被任命者normalize v.标准化notable a.显著的n.名人notation n.记号noteworthy a.值得注意的notorious a.臭名昭著的novelty n.新奇事物;新奇(感) nuisance n.令人讨厌的东西nurture vt./n.养育nutrition n.营养obedience n.听从obedient a.服从的obscure a.费解的;不著名的vt.掩盖offset vt./n.抵消offspring n.子女omission n.省略onset n.开始oppress vt.压迫;使(心情等)沉重optic a.眼的optimism n.乐观(主义)orient n.东方vt.以……为方向(目标);使适应oriental a.东方的orientation n.方向originate vi.起源于vt.创造oust vt.剥夺outdate vt.使过时outrage n.暴行;义愤vt.激怒outreach v.超过;比……到达更远overflow n.容纳不下的物v.漫出;挤满overhear vt.无意中听到Tuesday overlap n.重叠v.部分重叠oversee vt.监督oversight n.疏忽;负责overstate vt.言过其实overt a.公开的overthrow n.推翻v.摒弃overturn v.推翻overwhelming a.势不可挡的pact n.条约parachute n.降落伞v.跳伞paralyze vt.使瘫痪parliamentary a.议会的partition n.分割vt.隔开passer-by n.过路人patent a.专利的vt.得到……的专利权pathetic a.可怜的;无用的patriot n.爱国者patriotic a.爱国的patrol vt.巡逻n.巡查patron n.赞助人;顾客peculiarity n.特点;怪癖;奇特pedal n.踏板v.踩踏板;骑(自行车)peel n.外皮vt.削……的皮vi.剥落peg n.小钉,桩vt.用钉子钉pendulum n.摇摆不定的事态perfume n.香水vt.使充满芳香;洒香水于periodical n.期刊perish v.死亡;消亡permeate v.弥漫;感染permissible a.容许的perpetual a.永久的;无休止的perplex vt.迷惑persecution n.迫害;困扰persistent a.坚持不懈的persuasive a.有说服力的petitioner n.请求者pirate n.海盗;侵犯版权者vt.盗用plaster vt.在……上抹灰泥plateau n.高原;稳定期plea n.恳求;借口plead v.恳求;申诉;为……辩护plight n.苦境poke vt./n.戳vi.伸出polar a.极地的;完全相反的pollutant n.污染物质ponder v.考虑populate v.居住于portfolio n.文件夹;有价证券组合portray vt.描绘;扮演posture n.姿势;看法vi.故作姿态practicable a.可实施的preach v.讲道;说教precede vt.先于precedent n.惯例preclude vt.阻止;排除predecessor n.前任;前身prediction n.预言predominant a.占主导地位的;显著的premise n.前提Wednesdaypremium n.额外费用;保险费a.售价高的presentation n.呈交;介绍preservation n.保护;保持preside vi.主持presidential a.总统的presume vt.假定,推测vi.擅自行事presumption n.假定,推测;冒昧,放肆,擅作主张pretext n.借口prevalent a.流行的preview n.预演;预告片v.为(影视节目)写预评prey n.捕获物;受害者v.捕食privacy n.隐私;个人自由privileged a.有特权的probability n.概率,可能性proceeding n.会议记录profitable a.有利可图的;有益的profound a.知识渊博的;深奥的prolong vt.延长prone a.易于……的;俯卧的propaganda n.宣传propagate vt.传播v.繁殖propel vt.推进proposition n.建议;命题prosecute vi.起诉vt.继续从事prosecution n.起诉;执行prospective a.预期的provincial a.省的;狭隘的provocative a.挑衅的;挑逗的proximity n.接近publicize/-ise v.宣扬punctuality n.准时punctuate v.加标点pursuit n.追赶;追求;消遣quantify vt.确定……的数量quantitative a.(数)量的queer a.奇怪的quench vt.扑灭;止渴quota n.定额radiant a.辐射的;光辉灿烂的;容光焕发的radiate v.辐射;流露random a.任意的rap n.斥责vt.严厉批评rash a.轻率的n.皮疹;令人不快的事物rating n.等级;收视率reactionary a.反动的n.反动分子reassure vt.使放心rebellion n.反叛rebound n./v.反弹recede vi.退去;逐渐减弱receptor n.接收器recipe n.烹饪法;诀窍reciprocal a.相互的reckless a.鲁莽的reclaim v.要求归还;开垦reconciliation n.和解;协调recount①v.重数recount②v.叙述rectify vt.纠正recur vi.再发生Thursdayrecyclable a.可循环使用的redundant a.过剩的;被解雇的reel n.卷轴v.卷referee n.裁判;介绍人;仲裁者refrain vi.抑制refreshment n.饮料,点心refuge n.避难处;庇护refund v.退还n.退款refute vt.驳斥regime n.统治;政治制度regiment n.团;大量regulatory a.监管的rehearsal n.排练rehearse v.排练;讲述,默诵reign vi.统治;成为最重要的rein n.缰绳rejoice vi.感到高兴relay v.传送;转播n.接力赛reliance n.依靠relieve vt.减轻;调剂;接替relish n.享受;调味品vt.从……中获得乐趣remainder n.余下的部分reminiscence n.回忆;回忆录remnant n.残留部分renewable a.可更新的renowned a.闻名的repay vt.归还;报答repel vt.击退;排斥;使厌恶reproach n./vt.责备reproduce v.复制;繁殖resemblance n.相似resentment n.愤恨reside vi.居住residential a.居住的;需要在某地居住的resignation n.辞职;听任resourceful a.富于智谋的respectable a.可敬的respondent n.回答者;被告responsive a.反应积极的restoration n.恢复;修复restructure v.改组resultant a.因此发生的resume①n.摘要;简历resume②v.继续retailer n.零售商retention n.保留retort v./n.回嘴retreat vi./n.撤退;退缩retrieval n.挽回;数据检索retrieve vt.取回;挽回;检索retrospect n.回顾retrospective a.回顾的;有追溯效力的revelation n.揭示;被揭示的真相revenge n.报仇reversible a.可反转的revert v.恢复(原状);(指财产等)归还revive v.(使)苏醒rigorous a.严密的;严格的rim n.边,缘rivalry n.竞争Fridayromance n.恋爱(关系);浪漫气氛rot v.(使)腐烂routinely ad.例行公事地royalty n.王族(成员);版税rupture n./v.破裂;断绝sabotage n./v.阴谋破坏sacred a.神圣的;宗教的safeguard vt.保护salute v./n.敬礼;致意saturate vt.使充满;使湿透savage a.野蛮的;残暴的n.野蛮人vt.乱咬;激烈抨击scar n.(伤)疤;(精神上的)创伤vt.给……留下伤痕(或创伤) scarcity n.缺乏;稀少scent n.香味;香水;臭迹vt.嗅到scorn v./n.轻蔑,鄙视scramble vi./n.爬行,攀登;争夺scrap n.碎片vt.废弃scrub v.擦洗;取消scrutiny n.详细检查sculpture n.雕刻(作品);雕刻术segregate vt.使隔离segregation n.分离sensation n.感觉;轰动sensational a.极好的sensitivity n.敏感性sentiment n.感情,情绪serial a.连续的n.连续剧setback n.挫折sexy a.性感的shatter vi.碎裂vt.使粉碎;使破灭shutter n.快门;百叶窗shuttle n.梭子vt.短程穿梭运送sieve n.筛子v.筛,滤signify vt.表示vi.要紧simplistic a.显得过于简单的simulate vt.假装;模仿simultaneous a.同时发生的situate vt.使坐落于situated a.坐落在……的;处于……境地的sizable a.相当大的skeptical a.怀疑的skip vi./n.蹦跳vt.略过,跳过slack a.松(弛)的;萧条的n.松弛部分vi.懈怠slash vt.砍;大幅度削减n.斜线号slaughter vt./n.屠杀;屠宰slot n.狭缝v.把……放入狭长开口中slump vi.突然倒下;暴跌n.萧条期smuggle vt.走私snatch v.抢夺sneak vi.溜vt.偷偷地做sneaker n.鬼鬼祟祟的人;胶底运动鞋sniff n./v.以鼻吸气;嗅sober a.未醉的v.(使)醒酒socialize vt.使适合社会需要sociologist n.社会学家solo n.独唱(曲) a./ad.单独的（地）soluble a.可溶的;可解决的sovereign n.君主a.至高无上的;具有独立主权的sovereignty n.最高统治权;国家的主权spacious a.宽广的Week 4Mondaysparkle vi.闪耀speciality n.专业specialization n.专业化,专门化spectacle n.眼镜;壮观的景象;演出spectator n.观众spectrum n.谱;范围speculation n.推断;投机活动speculative a.投机的spice n.香料;趣味v.加香料于;使增添趣味spiral n.螺旋线a.螺旋的vi.盘旋上升;不断急剧地上升sprinkle vt.洒stabilize/-ise v.(使)稳定,(使)稳固stalk n.茎vt.悄悄地跟踪stall n.摊棚;畜栏v.(使)停转standby n.备用物standoff n.僵持局面staple①n.订书钉vt.用订书钉钉staple②n.主食;主要产品a.主要的stern n.船尾a.严厉的stimulus n.刺激(物)stipulate v.规定stitch n.一针;针法v.缝straightforward a.坦率的;简单的strand vt.使搁浅n.(线等的)股,缕; (论据、思想等的)一个组成部分stray vi.迷路;分心a.迷路的streamline vt.使成流线型;使效率更高strive vi.努力stubborn a.顽固的;难对付的stumble vi./n.绊倒stump n.树桩;残根v.使为难;作巡回演说stun vt.使震惊;打昏subjective a.主观(上)的submission n.服从;提交subordinate a.次要的;下级的n.下级vt.使处于次要地位subscribe vi.订阅vt.捐助subscriber n.订阅者subscription n.订购;捐助subsidiary a.附属的n.附属机构successor n.接替人sue vt.控告vi.要求suffice vi.足够suite n.套间;家具summon vt.召唤;召集;鼓起superiority n.优越supersonic a.超音速的supplementary a.增补的suppress vt.压制;查禁surpass vt.超过susceptible a.易受影响的;过敏的;能经受……的suspension n.暂停suspicious a.猜疑的;可疑的swamp n.沼泽vt.淹没swap n./v.交换symmetrical a.对称的symmetry n.对称(性);整齐symphony n.交响乐symposium n.专题讨论会;专题论文集tablet n.药片;碑;(竹)简tack n.大头钉vt.钉住Tuesdaytakeoff n.起飞;起跳tan v.(使)晒成棕褐色tangle n./v.(使)缠结tariff n.关税;价目表tease vt.戏弄;挑逗n.(爱)戏弄他人者temperament n.气质temporal a.时间的;世俗的tempt vt.引诱tentative a.试探(性)的terminate v.停止termination n.终止terrace n.梯田;阶梯看台terrain n.地势terrify vt.使惊吓terrorism n.恐怖主义terrorist n.恐怖分子testify v.作证;表明testimony n.证词texture n.质地thereafter ad.之后thermal a.热的;保暖的thesis n.论文threshold n.门槛;入门tickle n.痒vt.使发痒;逗乐tilt v./n.(使)倾斜timely a.及时的timid a.胆怯的tolerant a.宽容的;耐……的tow vt./n.拖,拉toxic a.有毒的tract n.大片tragic a.悲惨的;悲剧的transcend vt.超出transcribe v.抄写;改编transient a.短暂的;临时的transistor n.晶体管;晶体管收音机transit n.运输transition n.过渡traverse vt.横渡trench n.沟tribute n.颂词trigger n.(枪的)扳机;起因vt.触发triple a.三部分的;三倍的vt.使增至三倍trivial a.琐碎的tuck vt.把……夹入tug v.用力拖(或拉) n.拖船tuition n.教学tumble vi.跌倒;翻滚n.暴跌turbulence n.动荡;湍流turbulent a.动荡的;汹涌的turnout n.出席人数;投票人数turnover n.营业额tutorial a.家庭教师的unanimous a.全体一致的underestimate vt./n.低估underlying a.含蓄的underscore vt.画底线;强调underway a.在进行中;在行进中的undutiful a.未尽职的;不顺从的unfold v.展开;展现Wednesdayunification n.统一unify vt.使联合;使相同unilateral a.单方面的unlawful a.违法的unprecedented a.空前的unsettle vt.使人不安unveil v.除去……的面纱;为……揭幕upcoming a.即将来临的update v.更新n.最新信息upfront a.直率的upgrade vt.提升uphold vt.支撑;支持upside n.好的一面utilization n.利用vacancy n.空;空缺vaccinate vt.给……接种疫苗validate v.使生效validity n.有效性vein n.静脉;叶脉;纹理;方式velocity n.速度venerable a.可敬的vent n.通风孔ventilate vt.使通风;把……公开venue n.聚集地点verbal a.用言辞的;口头的;动词的verdict n.裁定;结论verge n.边缘vi.接近versatile a.多才多艺的;多用途的versus prep.与……相对vicinity n.周围地区vicious a.恶毒的;恶劣的victorious a.胜利的virgin n.处女a.未经开发的,未经使用的;处女的virtuous a.有道德的;自命清高的visibility n.可见性;可见度visionary a.有远见的;空想的visualize/-ise vt.想象vocal a.嗓音的;直言不讳的vocational a.职业的void n.真空;空虚感a.缺乏的;无效的vow n.誓约vt.发誓vulgar a.粗野的;庸俗的vulnerable a.易受伤的;易受攻击的warfare n.战争;斗争warrant vt.使有必要n.正当理由;授权令wasteland n.荒地watertight a.防水的;严密的weary a.疲劳的,厌倦的vi.厌烦wedge vt.把……楔牢n.楔子well-being n.健康;幸福well-off a.富裕的whereby ad.借以whirl n.旋转wholesale n./ad.批发withhold vt.抑制wreckage n.失事wrench vt.猛拧;挣脱;扭伤n.扳手;痛苦wretched a.极不愉快的;令人苦恼的zigzag n.之字形Thursdayabandon vt.放弃;遗弃abnormal a.异常的abolish vt.废除absorb vt.吸收;使全神贯注;同化abundant a.丰盛的accelerate v.(使)加快accept v.接受;认可access n.通道;接近的机会accessible a.易接近的;可到达的accommodation n.住处,膳宿accord n.一致;协议vi.相符合accordance n.一致account n.叙述;账户accumulate v.积累acknowledge vt.承认……的权威acquire vt.取得acute a.敏锐的;急性的;严重的address n.地址;演说vt.向……作讲话adequate a.足够的;恰当的affection n.喜爱afford vt.买得起;提供agenda n.议事日程aggressive a.侵略的;进取的alert a.警觉的n.警戒alliance n.结盟allowance n.津贴alter vt.改变alternative n.可供选择的事物a.两者择一的ambition n.雄心;野心ambitious a.有雄心的;有野心的announce vt.宣告;声称anticipate vt.预料anxiety n.焦虑;渴望appearance n.露面;外观appliance n.电器applied a.实用的arbitrary a.专断的;任意的assemble v.(人)集合;(物)装配asset n.优点;财产;资产assign vt.分配;指派assist v.帮助astronomer n.天文学家attach vt.把……固定;与……有关联attitude n.态度;姿势attribute vt.把……归因于n.属性authentic a.真正的;可靠的awkward a.笨拙的;尴尬的;不方便的blame vt.责备;把……归咎于n.责任bloodshed n.人员伤亡boiler n.锅炉boom vi.发出隆隆声;繁荣n.隆隆声boring a.令人厌烦的bound v./n.跳(跃)breakthrough n.突破breed v.繁殖;饲养;引起n.品种brilliant a.卓越的budget n.预算v.编预算a.低廉的bulk n.容积;大量a.大量的bump n.碰撞;隆起v.碰;颠簸地行驶Fridaycabinet n.陈列柜;内阁cancel vt.取消candidate n.候选人;考生capacity n.容量;能力career n.生涯;职业challenge vt.向……挑战n.挑战(书);质疑chip vt.削下n.碎片;炸土豆条circuit n.环行,环行道;电路citizenship n.公民权claim vt.声称;要求;夺去n.索赔clap v.拍(手) n.鼓掌clash n.冲突;不协调;撞击声coarse a.粗糙的;粗劣的collapse v./n.倒坍;崩溃collision n.碰撞combat n.战斗combine v.联合n.联合企业(或团体);联合收割机comment n.批评v./n.评论commission n.委员会;佣金;委托commitment n.承诺;奉献compact a.紧密的,结实的n.协议compatible a.能和睦相处的;兼容的compel vt.强迫compensate v.弥补;补偿compensation n.补偿(或赔偿)的款物; 补偿compete vi.竞争competitive a.竞争的;有竞争力的competitor n.竞争者complain v.抱怨complaint n.抱怨;疾病complicated a.复杂的composer n.作曲者comprehension n.理解(力);理解练习comprehensive a.综合的compress vt.压紧comprise vt.由……组成computerize v.用电脑处理conceal vt.隐藏concede v.(不情愿地)承认;让步;允许concern n.关心;重要的事vt.涉及;使担心conclusion n.推论;结尾;缔结condemn vt.谴责;宣判condense v.浓缩;压缩confirm vt.证实;批准confirmation n.确认confront vt.遭遇;面对Confucian a.儒家的,孔子的confuse vt.使困惑;混淆consent vi./n.同意consequently ad.因此,所以conservation n.保存conservative a.保守的n.保守的人consider v.认为;考虑;关心considerable a.相当大的considerate a.体贴的consist vi.由……组成;在于consistent a.一致的,符合的constant a.不变的n.常数constitute link v.组成constitution n.组成;宪法;体格Week 5Mondayconsult v.请教;商议vt.查询consultant n.顾问;会诊医师consumption n.消费(量);挥霍contaminate vt.弄脏contest vt.争夺;争辩n.争夺context n.环境contradiction n.矛盾;反驳contrary a.相反的n.相反contrast n.对比contribute v.捐款;有助于controversy n.争论convenience n.便利conventional a.普通的;习惯的convey vt.运输,传送convince vt.使确信cooperation n.合作cope vi.对付,应付cord n.细绳;灯芯绒裤court n.法庭;球场crash v./n.碰撞,撞击n.碰撞声critical a.批评的crucial a.决定性的crude a.天然的;粗糙的cruise v.巡航crush n./vt.压碎vt.镇压current a.流行的;现在的n.潮流;流curse v.诅咒,咒骂n.祸害debate v./n.辩论decay v./n.腐烂vi.衰败deceive v.欺骗decent a.得体的decline vi./n.下降,衰退v.婉拒decorate vt.装饰decrease v./n.减少deficit n.赤字defy vt.违抗;挑delegation n.代表团delete vt.删除deliver v.拯救;接生;宣布demanding a.要求高的denial n.否认;拒绝给予deny vt.否认;拒绝depart vi.离开;背离depend vi.依靠;决定于dependence n.依靠depict vt.描绘;描述deposit vt.使沉淀;存放n.沉积物;押金;存款depress vt.按下;使沮丧;使不景气derive v.起源于;取得descend v.下降destruction n.破坏destructive a.破坏(性)的devote vt.献身,致力于dictate v.口授;命令differ vi.不同于;发生分歧dilemma n.困境dim a.昏暗的;模糊的v.(使)变暗淡dine vi.进(正)餐disaster n.灾难;彻底的失败discard vt.抛弃Tuesdaydisguise vt./n.假扮;伪装disorder n.凌乱;骚乱;失调display n./vt.陈列;显示dispose vt.排列vi.处理distinction n.差别distress n.忧虑;贫困;危难vt.使忧虑dominant a.占优势的dominate v.支配donation n.捐赠;捐款doubtful a.怀疑的drag vt.拖,拉drain v.排走n.耗竭;排水沟drift vi./n.漂流economic a.经济(学)的economical a.节约的economics n.经济学;经济情况economist n.经济学家economy n.经济;节约efficiency n.效率elaborate v.精心制作;详述a.精心制作的elegant a.优美的emergency n.紧急情况emphasize v.强调encounter v./n.遭遇endure v.忍受;持续enforce vt.执行;强迫engage v.吸引住;雇用enhance vt.提高enlarge v.扩大;放大enrich vt.使富裕;充实enrol(l) v.注册ensure vt.保证entertainment n.娱乐;招待entitle vt.给……权利epidemic a.传染性的n.流行病equivalent a.相等的;相同的erode v.腐蚀error n.错误estimate v./n.估计;评价eternal a.永恒的exaggerate v.夸大exceed vt.超过exception n.例外excess n.过量a.额外的excessive a.过度的exclaim v.呼喊exclude vt.不包括exclusive a.独有的excursion n.远足execute vt.实施;执行exhibit v.展览n.展览品expand v.膨胀;展开expel vt.驱逐;排出;把……开除explicit a.直言的;清楚明白的explore v.探测expose vt.暴露;揭露;使(照片)曝光extend vt.伸展;提供extinguish vt.熄灭;消灭facial a.面部的facilitate vt.促进Wednesdayfake n.假货;骗子a.假的v.伪装fantastic a.异想天开的;奇异的fantasy n.想象,幻想fascinate vt.迷住fashion n.方式;流行款式fatal a.致命的feasible a.可行的fiction n.小说;虚构的事file v.把……归档;排成纵队行进n.文件;档案finance n.财政,资金v.为……提供资金flexible a.易弯曲的;灵活的fluctuate vi.波动foresee vt.预见forestry n.林学formal a.形式上的;正式的format n.设计;版式vt.使格式化fraction n.小部分;分数frontier n.边境;尖端function n.功能;重大聚会furnish vt.布置;提供gamble v./n.赌博gaze vi./n.凝视gear n.设备vt.使适应generate vt.产生genetic a.遗传(学)的n.遗传学genuine a.名副其实的;真诚的glow n.光辉vi.发光grant n.拨款vt.同意grief n.悲伤;伤心事grim a.严厉的;讨厌的grip vt.握紧;吸引住……的注意gross a.总的;粗鲁的n.总额guarantee v./n.保证guard vt.守卫n.警卫harness vt.给(马)上挽具n.马具haul vt./n.拖n.拖运heave v.举起;扔n.举起highlight vt.强调hinder vt.妨碍historical a.历史(上)的hostile a.敌对的humanity n.人类;人性;人道;人文学科humble a.谦虚的;卑贱的vt.贬低ideal n.理想a.理想的;想象的identical a.同一的identify vt.鉴定illegal a.非法的imaginary a.虚构的imagination n.想象力;创造力immune a.对……免疫的;免除的;不受影响的imply vt.暗示impose vt.把……强加于;征(税等) impress vt.给……留下深刻印象impression n.印记;印象impulse n.冲动;推动力inadequate a.不充足的incidence n.发生率incident n.发生的事incline v.(使)倾斜;(使)倾向于n.斜坡indifferent a.冷漠的Thursdayindispensable a.必需的induce vt.引起;引诱inevitable a.不可避免的inferior a.下级的n.下级influence n.影响力vt.影响influential a.有很大影响的inform vt.通知inherent a.固有的inherit vt.继承;由遗传而得到inner a.内部的;内心的input vt.输入inquiry n.打听;调查。

Rows of pointed arches upon delicate shafts form a typical wall decoration known as blind arcading. Niches with pointed arches and containing statuary are a major external feature. The pointed arch lent itself to elaborate intersecting shapes which developed within window spaces into complex Gothic tracery forming the structural support of the large windows that are characteristic of the style
法国巴黎圣母院
Amiens Cathedral is the masterpiece of French Gothic architecture. It is a Roman Catholic cathedral and seat of the Bishop of Amiens . It is situated on a slight ridge overlooking the River Somme in the administrative capital of the Picardy region of France. The cathedral is the tallest complete cathedral in France.
Characteristics of Gothic churches and cathedrals

with attenuation bias is less in magnitude than the absolute value of the parameter. Augmented Dickey-Fuller Test: A test for a unit root that includes lagged changes of the variable as regressors. Autocorrelation: See serial correlation. Autoregressive Conditional Heteroskedasticity (ARCH): A model of dynamic heteroskedasticity where the variance of the error term, given past information, depends linearly on the past squared errors. Autoregressive Process of Order One [AR(1)]: A time series model whose current value depends linearly on its most recent value plus an unpredictable disturbance. Auxiliary Regression: A regression used to compute a test statistic—such as the test statistics for heteroskedasticity and serial correlation—or any other regression that does not estimate the model of primary interest. Average: The sum of n numbers divided by n.

air-tight double glazing window 密闭双层玻璃窗multiple glazing 多层玻璃; 多层玻璃窗multiple-glazing unit 多层玻璃窗outside glazing 外装玻璃法patent glazing 专利装玻璃配件; 无油灰镶玻璃法plate glazing 平板压光plate glazing calender 平板抛光机; 平板砑光机putty glazing 油灰镶玻璃法puttyless glazing 无油灰镶玻璃法rebate of glazing 镶嵌玻璃槽口reflecting glazing 反射窗玻璃salt glazing 盐釉self-glazing 自动研光spray glazing 喷釉法spraying glazing 喷釉anti-burglary glazing 防盗玻璃窗attack resisting glazing 防盗窗玻璃bead glazing 压条装配玻璃法body wetting before glazing 补水copper glazing 铜条嵌镶玻璃copperlight glazing 铜条嵌镶玻璃copperlite glazing 铜条装配玻璃corrugated roof glazing 瓦楞玻璃屋面direct glazing 无窗框安装法double glazing unit 双层中空玻璃double-glazing 双层玻璃13X 13X 分子筛3A 3A 分子筛4A 4A 分子筛abbeive 阻黏剂，防黏剂，分离剂ablation 脱离，切除，消融abrasion 磨耗，磨损，磨蚀abrasion hardness 磨蚀硬度abrasion index 磨损指数abrasion tester 磨损实验机accelerateagingtest 加速老化实验acetate 乙酸盐，乙酸酯，乙酸根，乙酸基acetone 丙酮acid resistance 耐酸性acoustic 声学的acrylic resin 丙烯酸类树脂acrylic 丙烯酸，亚克利acrylics 丙烯酸acrylonitrile 丙烯腈activation 激活activator 活化剂adduct 加（成化）合物adhere 黏合，黏附adhesion 老化实验，老化检验adhesion 黏合adhesion failure 黏合破坏adhesion of rubber to metal 橡胶和金属粘结adhesion promoter 黏合增进剂，助黏剂adhesive 黏合剂adsorbent 吸附剂adsorption 吸附affinity 亲和性aluminum oxide 氧化铝aluminum profile 铝型材aluminum section 铝型材aluminum shim/butyl spacer 铝带丁基胶条，实唯高胶条aluminum spacer 铝间隔条，槽铝式ambient noise 环境噪音ambient temperature 环境温度amorphous 无定性的，非晶质的angstroms 埃anhydrite 无水石膏an nealed glass 原片，普通玻璃an nealing 退火，退火的an nealing lehr （隧道氏）退火窑（炉）an nealing point 退火温度（相当黏度为1018 泊）anodize 阳极氧化anomaly 异常AFG （American Float Glass ）美国浮发玻璃公司Agate 玛瑙Aging 陈化，老化aging resistance 耐老化性，老化性能aging test 老化实验argon filled 充氩气air adsorption 气体吸附air barrier 防漏气隔离层，隔离屏障，气挡air curing 空气硫化，空气熟化air drying 风干air filled 充空气air infiltration 空气渗透air infiltration 空气渗透air side 浮法玻璃生产中朝上的玻璃面air space 空气层airflow 气流alabaster 雪花石膏，雪花石膏制的aldehydes 醛aliphatic 脂（肪）族化合物salkali 碱alkali metal salt 碱金属盐alkali resistance 耐碱性alkalinity 碱性，碱度alligatoring 鳄纹alumina 氧化铝aluminoborosilicate glass 铝硼硅酸盐玻璃aluminosilicate glass 铝硅酸盐玻璃aluminum 铝anticracking agent 防裂剂（橡胶）antimony oxide 氧化镝antioxidant 抗氧化剂application table 操作台aqueous 水的，含水的，水成的argon 氩气arsenic 砷arsenic trisulfide 三氧化砷arsenious oxide 五氧化二砷art glass 艺术玻璃，镶嵌玻璃大气或臭氧asphalt 沥青柏油ASTM 美国中空玻璃检测标Atmospheric or ozone cracking （作用）龟裂，自然龟裂Atmospheric pressure 大气压（力）Attenuation 衰减物Autoclave 高压釜Bback-bone 主链，主要成分，骨干，骨架back-fill 反填充，回填充bacteria 细菌barium crown glass 钡冕玻璃barium oxide 氧化钡barometric pressure 气压base基胶batch house 料房，配料车间bath 瑶池，池炉bending strength 弯曲强度bent glass 弯玻璃，弯玻bent spacer 连续弯管金属隔条bentonite 膨润土，皂土，浆土benzene 苯benzene ring 苯环beryllium 铍Bicherous smiotios pocess 比切罗克斯法，间歇压延法（平板玻璃）bitumen 沥青，柏油bleeding 增塑剂等渗出表面形成薄膜baistering 起泡，气泡blocks 玻璃支撑快bromine 溴brookfield synchro-lectric visosimetre 布鲁克菲尔德单圆筒黏度计brookfiled test 布鲁克菲尔德检测Btu 英国热量单位（=256Cal ）Bubbing 起泡Bloom 起霜白化blown ware 吹制的玻璃制品blue-line drawing 蓝图blush 起霜白化boiler gages 锅炉表bond breakage键断裂bond strength 键强度bonding agent 键合剂，黏合剂borate 硼酸盐borax硼砂boric acid 硼酸boric oxide 氧化硼boron 硼borosilicate cwn 硼硅酸盐冕玻璃brosiliceglass 硼硅酸盐bow 弯曲弓形box spacer 槽铝式隔条brglass 防弹玻璃breakage 炸裂breaking stress 极限应力，破裂应力breather tube 呼吸管brewsters布鲁斯特，（光弹性单位）bullet resistant glass 防弹玻璃bull 's e后ye圆玻璃，圆快玻璃butadiene 丁二烯butyl 丁基胶butylene 丁烯C Cadmium 镉Calcareous 钙质，含钙的石灰的Calcium peroxide 过氧化钙Calcium carbonate碳酸钙CAN/CGSB-12.8-97 加拿检测标准大中空玻璃Canal arch 通道拱Capillary 毛细管Capillary tube unit 安装毛细管的中空玻璃Carbon black 碳黑carbon dioxide 二氧化碳Cardinal IG 美国卡迪诺中空玻璃公司catalyst 催化剂，触媒，固化剂cathode阴极caulk 堵缝，填隙cavity thickness 空腔厚度Celsius 摄氏cement 水泥，胶结剂，胶结，封接CEN 欧洲中空坡璃标准centigrade 摄氏centipoise 厘泊（黏度单位）centre in tension 中央张力centre of the glass 玻璃中央chain stopper 链终止剂，止链剂chalcogenide glass 硫属玻璃chalking 粉化，起垩Charles ' s La查w 里定理checking 龟裂checking sunlight 日晒引起的龟裂chemical fogging 化学雾chemical resistance 耐化学性chemical strengthened glass 化学钢化玻璃chlorine 氯chord 弦chords 弦circumference 圆周，周围clay 粘土，粘土质的clear glass 白玻，透明玻璃coadsorption 共吸附coating technology 镀膜技术cobalt 钴coefficient of expansion 膨胀系数cohesion 内聚cohesive failure 内聚失败cold edge 冷边cold flexibility 冷挠曲性cold flow 冷流cold resistant 抗冷性，耐冷度compatibility 相容性compatible spacer 相容间隔条compound curve 复合曲线（玻璃）compression modulus 压缩模量compression set 永入性破坏compressive strength 压强度compressive stress 压应力concave 凹的condensation 冷凝condensation gutter 冷凝水收集槽，沟conduction 传导conductivity 传导container stability （=shelf life ）货架寿命contamination 污染continuos film 平整的薄膜，无断裂或针眼convection 对流conventional hot melt 普通热融胶，常规热融胶convex 凸cool light 冷光cooling 冷却copolymer （二元）共价物copper 铜comer key 插角correlation 相关corrosion resistance 抗腐蚀能力cracking 裂化，裂解，断裂，裂纹creep 蠕变critical temperature 临界温度crosslink 化学交联cross-linking agent 交联剂crown glass 冕法玻璃，人工吹制成的玻璃片crystal glass 晶质玻璃crystal structure 晶体结构crystallization 结晶，结晶作用，晶化cullet 碎玻璃，废玻璃（料）cumene hydroperoxide 氢过氧化枯烯curative 固化剂，硬化剂cure time 固化时间curing agent 触媒，固化剂curing mechanism 固化机制curtain wall 幕墙curved glass 异型玻璃cyclic wind loading 周期性风荷载cycling 循环cylinder glass 筒形玻璃，（吹制或拉制）D，圆筒法平板玻璃Damping 缓冲，减震，阻尼Daylight 日光Dead air 静止空气Dead load 自重Decibel （dB）分贝Decorative glass 装饰玻璃，镶嵌玻璃Deflection 挠度，挠曲Delaminate 分层，脱层Delinerate 描绘，叙述，描外形Density 密度Depth 深度Desiccant 分子筛Design load 设计荷载Desorption 解吸附Dew point 露点Diameter 直径Diamond pyramid 金刚石锥硬度标Diaphram 横膈膜，隔膜，膜片Dichromate 重铬酸盐Dicing 骰子Dielectric 电介体，电介质；介电的Diffusion 扩散Diisocyanates 二异氰酸盐Diluent 稀释剂，冲淡剂Dilute 稀释Dilution 稀释Dimethyl ketone 二甲丙酮DIN 1286 德国中空玻璃标准1286Dip coat 浸涂Disentangle 解开，清理Dispersion 色散，弥散]distribution 分布distortion 扭曲，畸变disulfide 二硫化物divider 除数，间隔物，隔板，划分者dolomite 白云石door-light 镶嵌玻璃drain line 流浆线道drawn glass 拉制玻璃drawn sheet glass 拉制平板玻璃drum 55 加仑铁桶dry time 缺胶接头DSE 等同双道密封Dispersion 分散(作用) ，分散体，色散，离差Dual panes unit 双玻中空玻璃Dual panes 双玻中空玻璃Dual seal 双道密封Dual-sealed units 双道密封中空玻璃Dlurability 耐久性Durometer 硬度詈，硬度测验器Dynamic fatigue 动态疲劳EEdge clearance 边部间隙Edge cover 边部遮盖Edge of glass 玻璃边部Edge seal 边部密封Edge seal height 边部密封高度Edgetech IC 美国艾杰中空玻璃技术××公司Elastic solid 弹性固体Elasticity 弹性Elastomer 高弹性Electromagetic 电磁的Elements 元素，自然界的风，雨，雪和雷电等Elongation 延伸Emery 刚玉粉，刚砂Emulsion 乳状液Enamel glass 釉彩玻璃Encyclopedia 百科全书Endothermic 吸热的Energy efficiency 能源效率Energy star 美国能源明星计划ENR 室外噪音评定ER ( energy rating )能源等级评定Erosion 腐蚀Ethylene 乙烯EWNR(exterior wall noise rating ) 外墙噪音评定Exhaling air 呼出空气Exothermic 放热的Exterior glazing 室外安装玻璃Factory glazed 工厂安装玻璃Fahrenheit 华氏Failure analysis （water immersion technique）失败分析Far ir 远红外Fatigue strength （疲劳强度）Faying surfaces 接触面Feeder 进料器，加料器Feldspar 长石Feldspathic 长石质的Fenestration 门窗Fiberglass 玻璃钢Filler 填料Filter cake 滤饼Fin 毛刺Fire-retardant material 阻燃材料Flame resistant 耐燃性（的）Flame retardant 阻燃剂Flash point 闪点，闪燃点Flat glass 平板玻璃Flaw 缺陷Flexible 弹性的Flexible silicone foam 弹性硅酮微孔间隔条，超级间隔条Flint glass 火石玻璃，无色玻璃Float glass 浮法玻璃Float process 浮法工艺Flow out 流出Flow point 玻璃的流动温度Fluorine 氟Fluxe 溶剂Fluxing agent 助熔剂Fog 雾Fogging unit 内侧雾化的中空玻璃Foot 英尺Forming roll 压延辊Four sides curtain wall 全隐式幕墙Fractography 断口组织试验，断口组织的显微镜观察Fracture 破碎，断面，断裂，破坏FRAME 计算机模拟热流的软件Frequency 频率Front end 窑前端Front gable –wall 前脸墙，端墙Frost poin 霜点Ft/reel 英尺/ 轴Fulcrum 支点Fumed silica 热解法二氧化硅，火成二氧化硅Fungi 霉菌Furnace 炉，窑Furnace floor 炉底，窑床Fusion 熔融，熔化GGallon 加仑Gas 气体，惰性气体Gas retention 惰性气体保持能力Gas –filled unit 充惰性气体的中空玻璃Gasket 玻璃密封胶条Geometry 几何Geolrgian bar 美隔条Germicidal 杀菌的Girth 曲线周长Glass blowetr 玻璃灯工，玻璃吹制工Glass breakage 玻璃炸裂Glass crtain wall 玻璃幕墙Glass edge seal 玻璃边缘密封Glass modulus 玻璃态模量Glass phase 玻璃相Glass point 玻璃点Glass ribbon 玻璃带，玻璃条Glass transit temperature 玻璃化温度Glass washer 玻璃清洗机Glassblowing 玻璃吹制Glass-making 玻璃制造Glassware 玻璃器皿Glazing bead 玻璃压条Glazing material 玻璃，玻璃密封材料Glazing rabbet 玻璃镶嵌槽Glazing system 玻璃装配系统Glossary 小辞典，词汇表Goblet 小料块(玻璃)料滴Gouges 表GPR (gas permeance rate ) 气体渗透率Green strength 初始湿强度Greenhouse 温室Grinding hardness 研磨硬度Grit 压痕硬度Grout 薄浆(水泥)GS(galvanized steel ) 镀锌钢Gun consistency 适用从胶枪嘴向外打胶的松软度Gypum 石膏HH.B.Fuller 美国富乐公司H.H(high temperature high humidity) 高温高温Hard coat 硬度膜Hardness 硬度Heat flow 热流Heat mirror 热境Heat press roller 热(辊)压机Heat resistance 抗热Heat treated 热处理Heating 供热Heat-seal 熔焊，熔接，热封Heat-strengthened glass 热增强玻璃，半钢化玻璃Heat-treated glass 热处理玻璃Hermetic 气密的Hertz(HZ) 赫兹Heterogeneous 不均匀的，多相的Hiding power 遮盖的，覆盖力，盖底力，被覆盖High humidity testing 高湿试验HIGS 北美中空玻璃标准HI-TR 耐高热HMB 热融丁基胶Holiday 空胶，露布，露白，露胶Hook 钩Horizontal 水平的，卧式的Hot melt 热融胶Hot melt butyl 热融丁基胶Hot melt sealant 热融密封胶Humidity 温度Humidity aging 温度老化HVAC 中央空调Hydrocarbon 碳水化合物Hydrolytic 水解Hydrolytic resistance 抗水解Hydrolyzability 水解Hydrophilic action 亲水性， (的)反应，吸湿反应Hydroxides 氢氧化物Hydroxy 羟基Ideal Gas Law 理想气体定律）北美中空玻璃制造联盟LGMA （lnsulating Glass Manufuracturing Alliance LGU中空玻璃单元Impact 冲击Impact resistance 抗冲击Impact strength 抗冲击强度Impart 给予，分给Impeller 叶轮Imperial 英制Incandescent lamp 白炽灯Inch 英寸Incident noise 入射噪音IIndentation hardness 压痕硬度Inert gas 惰性气体Infrared 红外线Ingredient 组分，成分Inhaling air 吸入空气Initial 初始的Initial dew point 初始露点Inorganic 无机的Inside temperature 室内温度Insulating block 保温材料块Insulating glass 中空玻璃Insulating value 保温值Insulation material 保温材料Intensity 强度；密（集）度LnterceptTM U 型间隔条TM Interior glazing 室内安装玻璃Intelayer 夹胶，夹层Internal reflection 内反射Internal strain 内应变Internal stresse 内应力Iodine 碘Ion exchange 离子交换Ion exchange process 离子交换反应LR 红外线Iron oxide 氧化铁Isocyanate 异氰酸盐（酯）Isoprene 异戊二烯，丁二烯，甲基-1 Isostere（电子）等排物Isotherm 等温线Jamp 边框KKaolin 高岭土Kiln bottom 窑底Knurl roll 压花辊LLading （用勺子）舀（玻璃液）Laminated glass 夹层玻璃Lap point 搭接点，搭接面Lap shear 搭接剪切实验LBNL （lawrence Berkerly National Laboratory）美国劳伦斯伯克利国家实验室Le Joint Francais（LJF）法国乐杰福密封胶××公司Lead crystal 铅晶质玻璃Lead oxide 氧化铅Lead peroxide 过氧化铅Lead –alkali –silicate glass 铅碱硅盐酸玻璃Leaded glass 含铅玻璃Lehr 退火窑（炉）Leq 等效声音级别Life exqectancy 寿命期望值，期望寿命Lifting 提升，举起，升起Limestone 石灰石Lindemann glass 林德曼玻璃（含X 射线含锂铍硼玻璃）Linear thermal coefficient of expansion 先性膨胀系数Lip 瓶口Lite 玻璃Lithia 氧化锂Live load 活载荷，活负载Load 荷载，载荷，负荷Load average 平均荷载Location block 定位块Logarithmics 对数Longevity 长久性，寿命Long-wave 长波Low-Eglass 低辐射玻璃Low-emissivty coatings 低辐射镀膜Low-emissvity glass 低辐射玻璃LOW-TR 耐低热Lump 起疙瘩，胶团，块nanometer 纳米National Fenestration Rating Council 美国国家门窗等级评定委员会negative pressure 负压Neolithic 新石器时代的，过时的neoprene 氯丁橡胶，氯丁二烯橡胶neutral 中性NFPA 美国国家放火署NERC 美国门窗等级评定委员会niter 硝石nitrile rubber 丁腈橡胶nitrogen 氮气noble metal 贵金属noise 噪音noise control 噪声控制noise factor 噪声系数noise figure 噪声疲劳noise insulation factor 隔噪声因子noise level 噪声级noise limitation 噪声限度noise meter 噪生计noise muffler 噪声衰减器noise pollution 噪声污染noise reduction 噪声降低noise reduction coefficient 降(低)噪(声)系数nominal strain 名义应变nominal stress 名义应力noncollapisible 不可收缩的，不可折叠的noncrystalline 非晶体的nondrying 不干性nonductile 不可展伸的nonsag 非下垂nonskinning 表层不固化的nonstaining 不污染的nontoxic 无毒NR(noise reduction) 降噪NRC(national research Council of Canada) 加拿大国家研究院Nylon 尼龙QQuality 质量Qualitycontrol 质量控制Quantity 数量Quartz 石英R ＆D(research ＆development) 研究与开发Rabbet platform 玻璃镶嵌槽底片Radiation 辐射Radii 半径(单数) Radiology 放射线Radius 半径(单数) Rapid dew point drop 漏点下降快Reactive 反应型的Reactive hot melt 反应型热融胶，湿气固化热融胶Reactor 反应堆real-time 实时refining end 澄清部，澄清带reflective glass 反射镀膜玻璃refraction 折射refractive index 折射的，折射指数，折射率relative humidity(r.h) 相对湿度residentail building 名用住宅底层建筑residual water 残余水resistor 电阻，电阻器resonnating 共振，共鸣reverberation 混响reverse dual seal 逆向双道密封rh 相对湿度rheological 流变的rheological agent 流变剂rheological characteristic 流变特性ribbon glass 带状玻璃，玻璃带rigidity 刚性rod 棒料，棒，条roller press 辊压rolling machine 压铸机rolled glass 压延玻璃room temperature 室温residential 民用的RTV(room temperature vulcanizing) 室温硫化Rupture 破裂，断裂，裂缝，裂口，洞穿Rutile titanium dioxide 金红石型二氧化钛R-value 热阻S Saflex 首诺胶片Sag 下垂度sagging 下垂度salt spray test 喷盐实验sand 石英砂，砂子saturation equilibrium 饱和均衡schematic 示意图scrap glass 废玻璃scratch 划伤scratch hardness 刮痕硬度，划痕硬度screw spline 螺丝连接槽，连接键sea level 海平面sealant 密封胶sealed failure 密封失败sealed insulating glass 密封中空玻璃Sealed lnsulating Glass Manufacturers Associations Sealed space 密封空腔] Secondary seal 第二道密封Secondary sealant 第二道密封胶Seed 灰泡小气泡Selenide 硒化物Self-cleaning glass 自清洁玻璃Semiconducting glass 半导体玻璃Service termpreature 工作温度Setting block 玻璃支撑块SE6（sulfur hexaflouride ）六氟化硫Shear 剪切Shear strength 剪切强度Shelf aging 搁置老化Shelf life 货架寿命SHGC 增阳系数Shore hardness A 邵氏硬度A Short vinyl 短胶Short wavelength 短波波长Shrinkage 收缩Shut-off gate 闸门，供料机闸砖（供料机上用）SIGMA 美国中空玻璃制造商协会Silanol 硅烷醇Silica gel 硅胶美国中空玻璃制造商协会Silicate glass 硅酸盐玻璃Silicone carbide 炭化硅Silicone structural seal 硅酮结构胶Silicone weatherseal 硅酮耐候胶Silicone 硅酮胶Sill 窗台（板），窗口Silimanite 硅线石Simulation 模拟Single pane 单片玻璃Skid 托盘Slab (厚)板玻璃，玻璃砖Slag 炉底玻璃；炉渣，矿渣Sloped glazed 倾斜似玻璃装配Slot 缝Slump 下垂度Smart glass 智能玻璃Smart window 智能窗Snap-oncover cap 扣入式外盖Soda(sodium carbonate) 碳酸钠Soda ash 苏打灰Soda ash glass 钠玻璃Soda lime glass 钠钙玻璃Soda-lime-silica glass 钠钙硅酸盐玻璃Sodium gydroxide 氢氧化钠，苛性钠，烧碱Sodium oxide 氧化钠Sodium si9licate 钠硅酸盐Soft coat 软镀膜Softening point 软化点，软化温度Solar energy 太阳能Solar rediation 太阳辐射Solar tranmittance 太阳投射比Solar transmission 太阳投射Solidify 使凝固，凝结，固化Sovent 溶剂Sound 声音Sound absorption 声吸收Sound absorption coefficient 吸声系数Sound contral glass 声控玻璃Sound diffusion 声发散Soun energy 声能Sound energy density 声能密度Sound energy fllux 声能通量Sound grating 声栅Sound level 声级Sound proof 不透声的Sound source 声源Sound spectrum 声谱Sound wave 声波Soupy 胶浆的Spacer 间隔条，中空玻璃间隔条Spacer depth 间隔条深度，间隔条高度Spacer height 间隔条高度Spacer width 间隔条宽度Spandrel glass 安装在建筑物外墙不见光的无光泽玻璃Sparklike 芬兰斯巴莱克公司Specific adhesion 特性黏合，比黏合Specific gravity 比重Specific heat 比熟Specimen 样品Spectrophotometry 分光光度测定(法)Splotch 污点，(渍，痕) ，斑点Spout 料盘，流料槽Spout cover 供料池盖砖Spun glass 玻璃纤维，玻璃丝Sputter-coated low –e 阴极溅射低辐射镀膜Ss(stainless steel) 不锈钢Stained glass 彩色玻璃Stainless steel 不锈钢Stainless steel spacer 不锈钢间隔条Standard deviation 标准差Starved joint 缺胶接头Stc(sound transmission coefficient) 声透射系数Stearic acid 硬脂酸，十八(烷)酸Sticky 胶黏的Stiffener 加强筋Stiffness 挺度，劲度，僵硬度Straight chain 直链Strain 应变Stain point 应变点Stree 应力Structural design 结构设计Structural sealant glazed system(SSG) 结构胶玻璃装配系统Structural strength 结构强度Substrate 基材Sulfides 硫化物Sulfric acod 硫酸Super spacer 超级间隔条Surface flaw 表面缺陷Surface in compression 表面压应力Surface temperature 表面温度Surface tension 表面张力Suspended glazing 吊挂似玻璃装配Swiggle stripTM 实维高胶条、舒适胶条Synthetic 人工复合TTack free 表干Tangent 正切Target 靶Tear strength 剪切强度Technical data 技术数据Tellurite glass 碲玻璃Tempered glass 钢化玻璃Tensile modulus 拉伸模量Tensile streength 拉伸强度Tension 张力拉伸Terminology 术语Test apparatus 实验仪器Tetrahedral 四面体的Tetramethyl 四甲基Tetramethyl thiuram disulfide 二硫化四甲基秋兰姆Thermal aging 热老化Thermal analysis 热分析Thermal break 热炸裂Thermal conductance 热传导Thermal conductivity coefficient 热传导系数Thermal contraction 热收缩Thermal diffusivity 热扩散系数Thermal energy 热能Thermal shock 热冲击Thermal shock resistance 抗热冲击阻力Thermal syrain 热应变Shermal stress 热应力Thermal value 热值Thermo set 热固Thermocouple 电热偶Thermoplastic 热塑Thiokol 聚硫胶，聚硫橡胶，乙硫橡胶Thiuram type accelerator 秋兰姆类促进剂Thixotrope 触变胶Thixotropic 触变（的），具有触变作用的Thixotropic agent 触变剂Thixotropy 触变性Thixotropy factor 触变系数Thixotropy index 触变指数Thorium 钍Threshold 限度，界限Tin catalyst 锡触媒Tint glass 本体着色玻璃Tint 着色，色彩，色调Titania 氧化钛Titanium dioxide 二氧化钛，钛白Toluene 甲苯Toughened gloass 强化玻璃Transformation temperature （玻璃的）转变温度Translucent 半透明的Transparency 透明度Transverse seam 横向缝Tray bar 接料板Tray roiier 传送辊Triple pane unit 三玻中空窗Triple panes 三玻中空窗Trowel 镘刀，抹平刀Trowelling 抹涂，镘涂Tubing 管，管道，制管Tungsten 钨Tweel 炉闸口Two sides curtain wall 半隐式幕墙Two-component 双组分UUltimate elongation 极限伸长Ultraviolet 紫外线Ultravioet light 紫外线灯Ultraviolet-transmitting glass 透紫外线玻璃Unalterate 未改变的，不变的Undestructive argon 非破坏性氩气分析仪Undulating current 波荡电流Uniform loading 均匀负荷Uniform thickness 均匀厚度United inches 玻璃的一个边长和边宽之和UOP 美国环球分子筛公司Uv-lamp 紫外线灯U-value U 值Ventilation 通风Vertical 垂直的，立式的Vertical mullion 竖框Vibrate 振动Vinyl 乙烯基，聚氯乙烯Virus 病毒Viscoelasticity 黏弹性Viscometer 黏度计Viscosimeter 黏度计Viscosity 黏度Viscous 黏（滞）的Visible 可见的Visible light 可见光Vistanex 聚异丁烯Visual distortion 视觉变形Vitreous 熔融状，玻璃状的，玻化Volatile 挥发的，易挥发的Volatile fogging 挥发化学物Volatile outgassing 挥发气体外泄Vulcanization 硫化，硬化Vulcanize 硫化，硬化WWaisting 细腰玻璃Warm edge 暖边Warm edge technology 暖边技术Warp 玻璃状板；光学扭曲，翘曲Warranty 质保书Water immersion 浸水Wavelength 波长Weather cycling 气候循环实验，气候循环检测Weatherometer 老化实验机Wedge 锲，锲入Weep 漏（泄渗）水Weep hole 排水孔Weep slot 槽形排水孔WET（warm edge technology）暖边技术Wetting 润湿White room 绝尘室，无尘室Wind load 风荷载Windborne 住链，主要成分；骨干；骨架Wire glass 夹丝玻璃Work life 操作时间XXenon gas 疝气x-ray leaded glass 防X 射线含铅玻璃x-ray protction 防X 射线x-ray shielding X 射线屏障xylene 二甲苯Yield strength 屈服强度Yong ＇s modulus 杨模量ZZeolite 沸石Zinc oxide 氧化锌Zirconium oxide 氧化锆γ-glycidoxpropyltimethoxysilane - 环氧丙γ氧丙基三甲氧基硅脘IIdeal Gas Law 理想气体定律LGMA ( lnsulating Glass Manufuracturing Alliance )北美中空玻璃制造联盟LGU 中空玻璃单元Impact 冲击Impact resistance 抗冲击Impact strength 抗冲击强度Impart 给予，分给Impeller 叶轮Imperial 英制Incandescent lamp 白炽灯Inch 英寸Incident noise 入射噪音Indentation hardness 压痕硬度Inert gas 惰性气体Infrared 红外线Ingredient 组分，成分Inhaling air 吸入空气Initial 初始的Initial dew point 初始露点Inorganic 无机的Inside temperature 室内温度Insulating block 保温材料块Insulating glass 中空玻璃Insulating value 保温值Insulation material 保温材料Intensity 强度；密（集）度LnterceptTM U 型间隔条TM Interior glazing 室内安装玻璃Intelayer 夹胶，夹层Internal reflection 内反射Internal strain 内应变Internal stresse 内应力Iodine 碘Ion exchange 离子交换Ion exchange process 离子交换反应LR 红外线Iron oxide 氧化铁Isocyanate 异氰酸盐（酯）Isoprene 异戊二烯，丁二烯，甲基-1 Isostere（电子）等排物Isotherm 等温线。

A Useful Glossary for Personal Data（个人资料有用词汇）name 姓名aliss 别名pen name 笔名date of birth 出生日期birthdate 出生日期born 生于birthplace 出生地点birthday 生日age 年龄native place 籍贯province 省city 市autonomous region 自治区prefecture专区county县nationality 民族；国籍citizenship 国籍duel citizenship 双重国籍address 地址current address 目前住址pressent address 目前住址permanent address 永久住址postal code 邮政编码home phone 住宅电话office phone 办公电话Tel.电话sex 性别male 男female 女Mr.先生Miss 小姐Mrs.太太Ms (小姐或太太)height 身高cm. 厘米ft. 英尺in 英寸weight 体重kg 公斤lbs 磅marital status 婚姻状况family status 家庭状况married 已婚single 未婚unmarried 未婚divorced 离异separated 分居number of children 子女人数none 无street 街lane 胡同，巷road 路district 区house number 门牌health 健康状况bloodtype 血型A A型B B型O O型excellent （身体）极佳very good 很好good 好strong 强壮short-sighted 近视far-sighted 远视color-blind 色盲ID card 身份证No. 号码date of availability 可到职时间available 可到职membership 会员、资格president 会长director 理事standing director 常务理事secretary-general 秘书长society 学会association 协会research society 研究会January (Jan.) 一月February (Feb.) 二月March (Mar.)三月April(Apr.) 四月May 五月June 六月July 七月August (Aug.)八月September (Sept.) 九月October (Oct.)十月November (Nov.) 十一月December (Dec.) 十二A Useful Glossary for Educational Background（教育程度有用词汇）education 学历educational background 教育程度educational history 学历currculum 课程major 主修minor 副修educational highlights 课程重点部分curriculum included 课程包括specialized courses 专门课程courses taken 所学课程courses completed 所学课程special training 特别训练social practice 社会实践part-time jobs 业余工作summer jobs 暑期工作vacation jobs 假期工作refresher course 进修课程extracurricular activies 体育活动recreational activities娱乐活动academic activities 学术活动social activities 社会活动rewards 奖励scholarship 奖学金"Three Goods" student "三好"学生excellent League member 优秀团员excellent leader 优秀干部student council 学生会off-job training 脱产培训in-job training 在职培训educational sustem 学制academic year 学年semester 学期（美）term 学期（英）president 校长vice-president 副校长acdemic dean 教务员department chairman 系主任professor 教授associate professor 副教授guest professor 客座教授lecturer 讲师teching assistant 助教research fellow 研究员rearch assistant 助理研究员supervisor 论文导师principal 中学校长（美）headmaster 中小学校长（英）master 小学校长（美）dean of students 教务长dean of students 教导主任teacher 教师probation teacher 代课教师tutor 家庭教师governess 女家庭教师intelligence quotient 智商pass 及格fial 不及格marks 分数grades 分数scores 分数ecamination 考试grade 年级class 班级monitor 班长vice-monitor 副班长commissary in charge of studies 学习委员commissary in charge of entertaainment 文娱委员commissary in charge of sports 体育委员commissary in charge of physical labour 劳动委员Party branch secretary 党支部书记League branch secretary 团支部书记commissary in charge of organization组织委员commessary in charge of publicity 宣传委员degree 学位post doctorate 博士后doctor (Ph.D) 博士maeter 硕士bachelor 学士student 学生graduate student 研究生abroad student 留学生returned student 回国留学生foreign student 外国留学生undergraduate 大学肄业生；（尚未取得学位的）大学生senior 大学四年级学生；高中三年级学生Junior 大学三年级学生；高中二年级学生sophomore 大学二年级学生；高中一年级学生freshman大学一年级学生guest student 旁听生（英）auditor 旁听生（美）government-supported student 公费生commoner 自费生extern 走读生day-student 走读生intern 实习生prize fellow 奖学金生boarder 寄宿生classmate 同班同学schoolmate 同校同学graduate 毕业生Stating Your Education（说明教育程度）Useful Courses for English teaching include:Psychology,teaching methodology,phonectics,rhetorie,grammar,composition.对英语教学有用课程包括：心理学、教学方法论、语音学、修辞学、语法、写作。

英语词根表(完整版)The assembly of English word roots词根 释义 凡例及注解 注意事项a- 1. 无，不，非 -azonic 非地带性的a- 2. 含in,at等意义 -asleep 在熟睡中a- 3. 加强意义 -aloud 高声地ab-离去，相反，不 -abuse 滥用ac-含at,to意,加强意义 -accustom 使习惯用在c,k,q前ad-含at,to意,加强意义 -adventure 冒险用在d,h,j,m,v前af-含at,to意,加强意义 -afforest 造林，绿化用在f前ag-含at,to意,加强意义 -aggrandize 增大用在g前air-空中的 -airline 航空公司al- 1. 含at,to意,加强意义 -allocate 分配用在l前al- 2. 构成副词 -almost 几乎amphi-两，双 -amphibian 水陆两用车an- 1. 无，不 -anarchistic 无政府的an- 2. 含at,to意,加强意义 -annotate 注解用在n前ante-前，先 -anteroom 接待室anthropo-有关人的 -anthropophagus 吃人族anti-反对，相反，防止 -antibiotics 抗生素用于a前省iany-任何 -anywhere 任何地方ap-加强或引申意义 -appraise 评价用在p前apo-离开 -apogee 远地点ar-含at,to意,加强意义 -arrange 安排用在r前arch-主要的，首位的 -archenemy 头号敌人as-含at,to意,加强意义 -assort 分类用在s前at-含at,to意,加强意义 -attract 吸引用在t前auto-自己，自动 -autobiography 自传back-反的，向后的 -backstroke 仰泳be- 1. 使...，使成为... -belittle 使缩小，贬低be- 2. 加以...，用... -bespangle 用小亮片装饰be- 3. 在 -below 在...下面be- 4. 加强及引申意义 -befall 降临，发生bene-善，好 -benediction 祝福bi-两，二 -bimonthly 双月刊by-旁，侧，非正式 -byroad 小路，僻径centi-百分之一，厘 -centimetre 厘米circum-周围，环境 -circumpolar 极地周围的co-共同 -cooperation 合作用在元音字前col- 1. 共同 -collocate 并置，并列用在l前col- 2. 加强或引申意义 -collate 校对用在l前con-1. 共同 -concolorous 同色的con-2. 加强或引申意义 -confirm 使坚定contra-反对，相反 -contradict 反驳，相矛盾cor- 1. 共同，互相 -correspond 共鸣用在r前cor- 2. 加强或引申意义 -corrupt 腐败，败坏用在r前counter-反对，相反 -counterattack 反攻，反击de- 1. 否定，非，相反 -deprecatory 反对的de- 2. 除去，取消，毁 -deflower 摧残，蹂躏de- 3. 离开 -depart 离去de- 4. 向下，降低 -devaluate 贬值de- 5. 使成...，加强意义-delimit 划定界限deca-十 -decameter 十米deci-十分之一 -decigram 十分之一克demi-半 -demigod 半神半人di-二，双 -dioxide 二氧化物dia-贯通，对穿，透过 -diameter 直径dif- 1. 不，无，相反 -diffidence 无自信用在f前dif- 2. 分开，离，散 -diffract 分散用在f前dis- 1. 不，无，相反 -dislike 不喜欢dis- 2. 取消，除去 -disappear 消失dis- 3. 加强意义 -disannul 使无效，废除dis- 4. 分开，离，散 - distract 分心dys-不良，恶，困难 -dyspepsia 消化不良e- 1. 加强或引申意义 -evaluate 评价e- 2. 出，外 -erupt 喷出ef-出，离去 -efflux 流出用在f前electro-有关电的 -electrograph 电传电报em- 1. 置...之内 -embosom 藏于胸中，怀抱用在b,m,p前em- 2. '配（饰）以...'-embroider 镶边用在b,m,p前em- 3. 致使... -empurple 使发紫用在b,m,p前en- 1. 置...之中 -encage 关入笼中en- 2. '配（饰）以...'-enchain 用链锁住en- 3. 致使... -enlarge 使扩大，放大en- 4. 'in'或加强意义 -enregister 登记endo-内 -endoparasite 体内寄生虫epi-在...上面 -epidermis 表皮equi-相等，同等 -equilateral 正多边形eu-优，善，好 -euphonic 声音优的every-每一 -everyday 每天ex- 1. 出，外 -excavate 挖出，发掘ex- 2. 前任的，以前的 -ex-mayor 前任市长ex- 3. 使（做）... -expurgate 使清洁exo-外，外部-exotic 外来的extra-以外，超过 -extraterritorial 治外法权的for-禁止，离去，克制-forbear 忍受fore-前，先，预先 -foreground 前景geo-地质，地球-geology 地质学hecto-一百 -hectopascal 百帕hemi-半 -hemisphere 半球hepta-七-heptagon 七角形hetero-异-heterosexual 异性的hexa-六-hexangular 有六角的high-高，大，主要 -highway 高速路holo-全-hologram 全息图homo-同 -homonym 同音字hyper-超过，过多，太甚-hyperacid 胃酸过多的hypo-下，低，次，少-hypotension 低血压ideo-观念，意义 -ideograph 会意字il-1. 不，无，非 -illegal 非法的用在l前il-2. 使成...，加强意义 -illuminate 照耀用在l前im- 1. 不，无，非 -immoral 不道德的用在b,m,p前im- 2. 向内，入 -imprison 投入狱中，监禁用在b,m,p前im- 3. 使成...，加强意义-imparadise 使登天堂用在b,m,p前in- 1. 不，无，非 -inhuman 不人道的in- 2. 内，入 -inbreak 入侵in- 3. 使成...，加强意义 -inflame 燃烧infra-下，低 -infrared 红外线（低于红线）inter-1. 在...之间，..际-interoceanic 大洋之间的inter-2. 互相 -interview 会见intra-在内，内部-intrastate 州内的intro-向内，入内 -intromit 插入ir- 1. 不，无irregular 不规则的用在r前ir- 2. 向内，入irrigate 灌入水，灌溉用在r前iso-等，同 -isotope 同位素kilo-千-kilowatt 千瓦macro-大，宏，长 -macroclimate 大气候magni-大，长 -magnify 扩大用于a前省imal-恶，不良，失 -malfunction 故障mega-百万-megabyte 兆字节meta- 1. 超-metachemistry 超级化学meta- 2. 变化 -metagenesis 世代交替micro-微-microwave 微波mid-中 -midsummer 仲夏milli-1. 千分之一，毫milligram 千分之一克milli-2. 千-millipede 千足虫，多足虫mini-小 -minipark 小型公园mis-误，错，恶，不 -misspell 拼错mono-单一，独-monoxide 一氧化物multi-多 -multimedia 多媒体的用于a前省i neo-新-neoimpressionism 新印象派no-无 -nothing 没事non-1. 不 -nonsmoker 不抽烟的人non-2. 非 -nonmetal 非金属non-3. 无 -nonpayment 无力支付ob-逆，反，非，倒-object 反对oc-逆，反，非，倒-occupy 占领用在c前octa-八-octagon 八角形of-逆，反，非，倒-offend 触犯用在f前omni-全，总，公，都-omnibus 公共汽车op-逆，反，非，倒-opposite 相反的用在p前out-1. 胜过，超过 -outrun 跑过，追过out-2. 过度，太甚-outdream 做梦太多out-3. 外，出 -outdoor 户外的out-4. 除去 -outcast 开除的，遗弃的over-1. 过度，太甚-overpraise 过奖over-2. 在上，在外，从上-overbridge 天桥over-3. 颠倒，反转-overthrow 推翻paleo-古，旧-paleozoology 古动物学pan-全，泛-pantheism 泛神论para-1. 半，类似，准-parallel 平行的para-2. 辅助，副 -paramilitary 辅助军事的para-3. 旁，靠近，外 -parasite 寄生虫para-4. 错误，伪-paradox 似是而非para-5. 防，避开，保护-parasol 遮阳伞para-6. 超过 -paramount 至上的pen-几乎，相近，相似-penultimate 倒数第二个penta-五-pentagram 五角星形per-1. 贯穿，通，透 -persist 坚持per-2. 加强意义 -perturb 扰乱per-3. 过，高 -perchloride 高氯化物peri-周围，外层，靠近-pericarp 果皮用于a前省ipoly-多 -polyfunctional 多功能的post-后 -postscript 后记pre-1. 前 -prefix 前缀pre-2. 预先 -prepay 预付pro-1. 向前，在前 -prologue 前言，序言pro-2. 代理，代替-procurator 代理人pro-3. 拥护，亲，赞成 -pro-British 亲英的proto-原始-protoplasm 原生质，细胞质pseudo-假-pesudonym 假名quadr-四-quadruped 四足动物quinque-五-quinquesection 五等分用于a前省e re- 1. 回，向后 -reclaim 收回re- 2. 再，重复，重新-reconsider 重新考虑re- 3. 相反，反对 -revolt 反叛，造反retro-向后，回，后 -retrospect 回顾se-离开，分开 -secede 脱离，退出semi-半 -semimonthly 半月刊sept-七-septuple 七倍的sex-六-sexto 六开本Sino-中国-Sino-Tibetan 汉藏语系some-某-sometime 某时step-后，继-stepfather 继父stereo-立体 -stereosonic 立体声的sub-1. 下 -submarine 海面下的sub-2. 次，亚，准，半 -subtropics 亚热带sub-3. 稍，略，微-subarid 略干燥的sub-4. 副，分支，下级-subworker 副手，助手sub-5. 接近-subarctic 近北极圈的sub-6. 更进一层，再-sublet 转租，再租suc-使成...，加强意义 -succeed 成功用在c前suf-使成...，加强意义 -suffocate 窒息用在f前sup-使成...，加强意义 -support 支持用在p前super- 1. 超，超级-superpower 超级大国super- 2. 上 -superstructure 上层建筑super- 3. 过度，过多 -superexcitation 过度兴奋supra-超，上 -suprarenal 肾上腺的sur- 1. 上，外，超-surcharge 超载sur- 2. 使成...，加强意义 -surround 包围用在r前sym-共同，相同 -symmetry 对称用在b,m,p前syn-共同，相同 -synthesis 合成tele-2. 远程-telemetry 远距离测量tetra-四-tetrachord 四弦乐器trans- 1. 越过，横过，超-translucent 半透明的trans- 2. 转移，变换-transport 运输tri-三-triangle 三角twi-二，两 -twin 双胞胎ultra-1. 极端ultrathin 极薄的ultra-2. 超，以外 -ultramarine 海外的un- 1. 不 -unfortunate 不幸的un- 2. 无 -unmanned 无人驾驶的un- 3. 非 -unartificial 非人工的un- 4. 未-uncivilized 未开化的un- 5. 相反动作，取消 -unbutton 解开钮扣un- 6. 由...中弄出 -unbosom 吐露（心事）under- 1. 下 -underworld 下层社会under- 2. 内（用于衣服）-undershirt 帖身内衣under- 3. 不足，少-underestimate 估计不足under- 4. 副，次-underking 副王，小王uni-单一 -unicorn 独角兽vice-副 -vice-manager 副经理with-向后，相反 -withdraw 撤回，撤退-'s- 1. 所有格(a)today's 今日的-'s- 2. 店铺(n)greengrocer's 菜场-a- 构成复数名词 (n)stadia 体育馆单数以um结尾-ability- 可...性 (n)dependability 可靠性-able- 可...的 (a)inflammable 易燃的-ably- 可...地 (ad)suitably 合适地-aceous- 有...性质的 (a)carbonaceous 含碳的-acious- 具有...的，多...的 (a)sagacious 聪明的-acity- 性质等（抽象）(n)veracity 诚实，真实-acle- 构成名词 (n)manacle 手铐-acy- 性质等（抽象）(n)fallacy 谬误-ade- 1. 行为等 (n)blockade 封锁-ade- 2. 物（...制成）(n)lemonade 柠檬水-ade- 3. 人和集体 (n)cavalcade 骑兵队-age- 1. 集合名词 (n)foliage 叶子-age- 2. 场所、地点 (n)orphanage 孤儿院-age- 3. 费用 (n)postage 邮资-age- 4. 行为 (n)pilgrimage 朝圣-age- 5. 状态，身分 (n)reportage 报告文学-age- 6. 物 (n)carriage 马车，客车厢-ain- 人 (n)chieftain 酋长，头子-aire- 1. 人 (n)millionaire 百万富翁-aire- 2. 物 (n)questionnaire 调查问卷-al- 1. 有...性质的 (a)continental 大陆的-al- 2. 行为（抽象）(n)withdrawal 撤退-al- 3. 人 (n)rival 竟争者-al- 4. 物 (n)manual 手册-ality- ..性，（抽象）(n)technicality 技术性-ally- 方式，程度等 (ad)conditionally 有条件地-an- 1. 属于...的 (a)metropolitan 大都市的-an- 2. 人 (n)publican 旅店主人-ance- 情况等（抽象）(n)buoyance 浮力-ancy- 情况等（抽象）(n)elegancy 优美，高雅-aneity- 性质等（抽象）(n)contemporaneity 同时代-aneous- 有...性质的 (a)subterraneous 地下的-ant- 1. 属于...的 (a)luxuriant 奢华的-ant- 2. 人 (n)participant 参与者-ant- 3. 物 (n)excitant 兴奋剂-ar- 1. 有...性质的 (a) consular 领事的-ar- 2. 人 (n)liar 说谎的人-ar- 3. 物 (n)altar 祭坛-ard- 人（贬义）(n)bastard 私生子-arian- 1. 人 (n)parliamentarian 国会议员-arian- 2. 兼形容词 (n,a)vegetarian 吃素者（的）-arily- 有...性质地 (ad)extraordinarily 不寻常地-arium- 场所，...馆(n)planetarium 天文馆-ary- 1. 有...性质的 (a)customary 习惯的-ary- 2. 场所，地点 (n)apiary 养蜂场-ary- 3. 人 (n)secretary 书记，秘书-ary- 4. 物 (n)glossary 词汇表-asm- 性质（抽象）(n)sarcasm 讥讽-ast- 人 (n)enthusiast 热心者-aster- 人（卑称）(n)medicaster 江湖医生-ate- 1. 做，造成 (v)activate 激活-ate- 2. 有...性质的 (a)private 私人的-ate- 3. 人 (n)graduate 毕业生-ate- 4. 职位，职权(n)professoriate 教授职位-ate- 5. 构成化学名词 (n)acetate 醋酸盐-atic- 有...性质的 (a)diagrammatic 图解的-ation- 1. 行为，情况(n)invitation 邀请-ation- 2. 行为的过程(n)reformation 改革-ative- 与...有关的 (a)affirmative 肯定的-ator- 做...工作的人，物 (n)calculator 计算机-atory- 1. 具有...的 (a)exclamatory 感叹的-atory- 2. 场所，地点 (n)observatory 天文台-cian- ...学家(n)clinician 临床医学专家-cracy- 统治(n)bureaucracy 官僚主义-crat- 参加者，支持者(n)democrat 民主主义者-cy- 性质，状态(n)infancy 幼年期-dom- 1. 情况，身分 (n)freedom 自由-dom- 2. 领域，...界 (n)sportsdom 体育界-ed- 1. 构成过去式 (v)showed 展示规则动词-ed- 2. 构成过去分词 (v)published 出版规则动词-ed- 3. 已完成的 (a)destroyed 毁灭的-ee- 受动者(n)employee 雇员-eer- 关系者，管理者(n)volunteer 志愿者-en- 1. 含...的，...制的 (a)golden 含金的-en- 2. 使成为 (v)widen 加宽-ence- 性质，状态，行为 (n)existence 存在-ent- 有...性质的 (a)deterrent 妨碍的-er- 1. 人 (n)fighter 战士-er- 2. ...的住民(n)villager 村民-er- 3. 制作者(n)hatter 帽商-er- 4. 物 (n)harvester 收割机-er- 5. 更... (a,ad)better 更好的比较级-ern- 在...方的 (a)northern 北方的-es- 1. 构成复数名词 (n)bushes 灌木单数或原型尾-es- 2. 第三人称单数(v)does 做ch,is,o,s,sh,x,z-ese- ...民族的 (a)Japanese 日本的-ess- 阴性 (n)airhostess 空姐-est- 最... (a,ad)nicest 最佳的最高级-et- 小 (n)floweret 小花-fold- ...倍的，...重的 (a)multifold 多倍的-ful- 1. 有...性质的 (a)beautiful 美丽的-ful- 2. ...的量(n)teaspoonful 一茶匙-fully- 有...性质地 (ad)carefully 小心地-fy- 使...化 (v)electrify 通电-graph- 信号 (n)electrograph 电传真-hood- 性质，状态(n)childhood 童年-i- 构成复数名词 (n)fungi 真菌单数以us结尾-ial- 1. ...的 (a)industrial 工业的-ial- 2. 行为（抽象）(n)trial 审判-ial- 3. 人 (n)official 官员-ial- 4. 物 (n)material 材料-ian- 1. ...的 (a)antemeridian 午前的-ian- 2. ...民族的 (a)Canadian 加拿大的-ian- 3. ...的人，...学家(n)custodian 保管人-ibility- 可...性 (n)responsibility 责任-ible- 可...的 (a)possible 可能的-ibly- 可...地 (ad)terribly 可怕地-ic- 1. ...的 (a)basic 基本的-ic- 2. ...的人 (n)critic 批评家-ic- 3. 学科(n)logic 逻辑学-ical- ...的 (a)identical 全等的-ice- 行为，动作，状态(n)service 服务-icious- 具有...的，多...的 (a)suspicious 可疑的-icity- 性质(n)authenticity 真实性-ics- 学科(n)physics 物理学-ies- 1. 构成复数名词 (n)counties 县单数以y结尾-ies- 2. 第三人称单数(v)cries 哭原型以y结尾-ing- 1. 构成现在分词 (v)hoping 希望-ing- 2. 正在进行的 (a)developing 发展中的-ing- 3. 构成名词 (n)feeling 感觉-ious- 具有...特性的 (a)glorious 光荣的-ise- 使...化 (v)surprise 使惊愕BrE-ish- 1. ...民族的 (a)Turkish 土耳其的-ish- 2. 有点...的 (a)tallish 稍高的-ish- 3. 有...性质的 (a)foolish 笨的-ish- 4. 造成，致使 (v)finish 结束-ism- 主义，学说，状态(n) socialism 社会主义-ist- ...主义者，...家(n)novelist 小说家-it- ...的动作 (n)pursuit 追求-ity- 性质，状态(n)solidarity 团结-ium- （化学）元素名(n)calcium 钙-ive- 有...性质的 (a)attractive 迷人的-ize- 使...化 (v)initialize 初始化AmE-kin- 小 (n)princekin 小王子-less- 无，没有，不 (a)hopeless 绝望的-let- 小 (n)booklet 小册子-like- 似...的 (n)catlike 猫样的-ling- 小（轻蔑）(n)starling 小星星-logy- 学科(n)astrology 占星术-ly- 1. 像...的 (a)friendly 友好的-ly- 2. 方式，程度等 (ad)chiefly 首要地-ly- 3. 每隔...发生的 (a)monthly 每月一次的-ment- 行为，结果，手段(n)implement 工具-most- 最... (a)utmost 极端的不是最高级-ness- 性质，状态，程度(n)illness 疾病-or- 1. 人 (n)emperor 皇帝-or- 2. 物 (n)tractor 拖拉机-or- 3. 状态，性质(n)color 颜色AmE-ory- 1. 有...效果的 (a)satisfactory 令人满意的-ory- 2. ...的处所(n)category 目录-our- 状态，性质(n)favour 好感BrE-ous- 具有...特性的 (a)dangerous 危险的-que- 概念(n)techique 技巧-ress- 阴性 (n)actress 女演员-ry- 1. 性质，行为 (n)rivalry 敌对-ry- 2. 境遇，身份(n)slavery 奴役-ry- 3. 种类 (n)jewelry 宝石-ry- 4. 行业(n)forestry 林业-s- 1. 构成复数名词 (n)rockets 火箭-s- 2. 第三人称单数(v)plays 玩-s- 3. 构成副词 (ad)indoors 在家-ship- 1. 动作 (n)courtship 求爱-ship- 2. 身份(n)citizenship 公民身份-ship- 3. 关系(n)friendship 友谊-sion- 动作，状态(n)revision 复习-sis- 性质，状态，动作 (n)crisis 危机-some- 引起的 (a)troublesome 烦人的-teen- 十... (num)fifteen 十五13~19-th- 1. 行为，结果(n)death 死亡-th- 2. 第... (num)sixth 第六基数个位≥4-tic- 有...性质的 (a)romantic 浪漫的-tion- 行为，状态，情况(n)contribution 贡献-tious- 有...性质的 (a)cautious 谨慎的-ty- 1. 性质，情况(n)safety 安全-ty- 2. ...十 (num)ninety 九十20, 30, ..., 90-ure- 结果，动作，过程(n)procedure 程序-ves- 构成复数名词 (n)calves 幼仔单数以f,fe结尾-ward- 向，向...的 (prep,a)backward 向后-wards- 向 (ad)skywards 朝上地-y- 1. 充满，有...性质(a)handy 手巧的-y- 2. 亲昵(n)kitty 猫咪-yst- 1. 人 (n)analyst 分析者-yst- 2. 物 (n)catalyst 催化剂注：1. 本表共收录英文词根410个（含一形多义及变体），其中前辍224个，后辍186个。

Unit 11Abdicate退位，辞职，正式放弃2Abolish废除，取消3Accomplice共犯4Acquittal无罪释放，履行（职责）5Adjourn休会，休庭6Adjudicate裁定，判决7Anarchy无政府状态，混乱，无秩序8Apolitical不关心政治的，非政治的9Apologist辩护者，辩解者10Arbitrate仲裁，公断11Aristocracy贵族，贵族阶级12Asylum政治（避难）13Autocracy专制独裁，独裁政体14Autonomous自治的，有自治权的15Barter物物交换，以物易物16Bourgeois资产阶级，中产阶级17Broker经纪人18Bureaucracy官僚主义，官僚总称19Burglary盗窃（罪）20Cede割让，放弃21Cession割让，转让22Chaos无秩序，混乱23Chauvinism沙文主义24Clique派系，小集团25Coalition联合体，联盟26Codify（法律）编辑成典，编纂27Coin28Collusion29Communal30Compact31Complicity32Concede33Conspiracy34Constituent35Decree36Default37Denotation38Depose39Disaffected40Discount41Discrimination42Imperial43Monarchy 44Plot45Property 46V assal47Affiliate 48Alimony 49Amnesty 50Annuity 51Arbiter52Beneficiary 53Bequeath 54Bicaeral 55Bullion56Cabal57Canvass 58Clientele 59Clout60Coup61Defray62Demise63Despot64Regal 65Regicide66Actuarial67Arraign68Barrister69Camaraderie70Codicil71Connivance72Covenant73Decapitate74Dregs75Dross76Minion77ArrearsUnit 2 1. Carnage78Confiscate79Demote80Dissident81Economy82Edict83Embezzlement84Emissary85Endorse86Entrepreneur 87Exculpate88Expatriate89Faction]90Functionary 91Hegemony92Illlicit93Impeach94Impunity95Inaugurate96Indict97Insurance98Interrogate99Invalidate 100Lien101Nullify 102Relegate 103Embargo 104Entail 105Exonerate 106Extraditon 107extralegal 108Factitious 109Felon110Ferocity111Fetter112Fugitive113Impute114Incarcerate 115Infraction 116Inquisitor 117Jingoist118Larceny119Limbo120Mace121Disenfranchise 122Disseminate 123Dossier124Emolument 125Enfranchise 126Exchequer 127Extort128Filch129Filibuster130Firebrand131Forensic132Franchise133Gentry134Immure135Incendiary136Indenture137Insolvent138Internecine139Interregnum140Junta141Litigation142Docket143Enclave144Gerontocracy145Gerrymander146JurisprudenceUnits 31.Deposition2.lucre3.machiavellian4.magisterial5.mandate6.mandatory7.manifest8.manifestation9.manifesto10.m arsal11.m ediate12.m onetary13.n epotism14.o rdinance15.p artisan partizan16.p erjury17.p olarize18.p robe19.p rosecution20.r eactionary21.r ecession22.r eciprocal23.r ecompense24.r elease25.r enounce26.r epel27.r epellent28.r esignation29.r etract30.r evoke31.s anction32.s tatus quo33.c ountermand34.m agnate35.m anacle36.m ercantile37.m issive38.m ulct39.o ptician40.p erquisite41.p iscatorial42.p olitec43.p olity44.p olygamist45.p roletarian46.p roscribe47.p unitive 48.p urge49.q uorum50.r ecidivism51.r ecidivist52.r emiss53.r emission54.r eprieve55.r esidue56.m alefactor57.m alfeasance58.m ayhem59.m oratoriu,60.n umismatist61.p erfidious62.p illory63.p lenary64.p otentate65.p rerogative66.p roviso67.r ider68.s edition69.s ervile70.s ervitude71.s inecure72.m anumit73.m averick74.m ilieu75.o ligarchy76.p lutocracy77.q uislingunit 41.accuse2.ally3.anachronistic4.apostate5.betray6.boycott7.bribe8.budget9.civil10.c oercion11.c ommerce12.c ommerce13.c ommercial 14.c ontract15.c onviction16.d efend17.d iplomacy18.d iscipline19.d omestic20.g uilt21.h ierarchy22.i ndex23.l egislation24.l egislature25.o ration26.p olitician27.p ractitioner28.r ebel29.s heriff30.s orority31.s tatute32.s tatutory33.s tipend34.s tock35.s ubsidy36.t estimony37.t ribute38.t urbulence39.t urmoil40.t urncoat41.t ycoon42.t yranny43.u pheaval44.u prising45.u surp46.u topia47.v erdict48.w itness49.a nachronism50.c onvulsion51.e ndemic52.s ignatory53.s uffragist54.s urveillalnce55.t hrall56.t ithe57.u ltimtum 58.u nderbid59.u nfetter60.u sury61.v enal62.v endor vie63.c oterie64.h aggle65.s late66.s uborn67.s ubpoena68.t estator69.t ribunal70.v enue71.w rit72.v ouchsafeunit 51.alchemy2.altruistic3.amphitheater4.anthem5.arch6.artifact artefact7.artisan8.ascetic9.haroque10.b rochure11.c arnal12.c arve13.c aste14.c lose-up15.c onjure16.c onnotation17.c ontext18.c onvert19.c reed20.c urator21.c ursive22.d evout23.d idactic24.d octrine25.d ogma26.e cologist27.e ffigy28.e galitarian 29.e goism30.e lixir31.l egalism32.a blution33.a dage34.a mulet35.a phorism36.a pparition37.a sceticism38.a theism39.b astion40.b enediction41.c elestial42.c horeography43.c limactic44.c ollage45.c onsecrate46.c redo47.d efeatist48.d ictum49.d octrinaire50.a pothegm apophthegm51.a rcade52.b ackdrop53.b lasphemy54.b ugaboo55.b urlesque56.c elibte57.c loister58.c onundrum,59.c ornice60.d eify61.d elineate62.d esecrate63.d iva64.e gotistical65.b ehemoth66.c entaur67.d efrock68.d emoniac69.d iadem70.d iorama71.e cclesiasticunit 6 1.embroider2.epic3.facade4.fluency5.fresco6.hallowed7.heresy8.humanitarian9.icon10.i deology11.i mpiety12.i mpious13.i ncarnate14.i ncarnation15.l egend16.m aterialism17.m aternal18.m axim19.m editation20.m etropolis21.m onastic22.n ominal23.o mnipresent24.o mnipresent25.o mniscient26.o rator27.o rthodox28.e ndearment29.e pilogue30.e pitaph31.e thos32.e xistential33.f atalism34.f igurine35.h edonist36.h eterodox37.h istrionic38.h orticultural39.i mprecation40.i ncantation41.i ncorporeal42.i nfernal43.i nviolable44.i nvocation 45.l ectern46.m onotheism47.n eophyte48.n ether49.o dyssey50.o racular51.o rdain52.o rdination53.e mboss54.e pigram55.f anfare56.f rieze57.g enealogy58.h ermitage59.h omily60.k ismet61.m alediction62.o belisk63.e pistemologist64.f ancier65.f iligree66.g ambit67.g argoyle68.i nfidel69.n ecromancy70.n irvana71.o ratoriounit 71.dirge2.elegy3.panoramic4.pastoral5.philatelist6.pious7.platitude8.platonic9.pragmatist10.p rologue11.r ecluse12.r everent13.r otunda14.s acrifice15.s anctuary16.s ermon 17.s train18.t hematic19.t rait20.v enerable21.w izardry22.p acifist23.p alette24.p atriarch25.p atrician26.p enance27.p odiatrist28.p odium29.p reamble30.p recept31.p rofane32.p roscenium33.p urgatory34.p epertoire35.r equiem36.r ococo37.s ect38.s eminary39.s pectral40.s treak41.t alisman42.t eetotalism43.t heocracy44.t rilogy45.u nction46.v eneration47.p aean48.p arochial49.p astiche50.p ontifical51.p urport52.r ecapitulate53.s acrilegious54.s cenario55.s chism56.s tipple57.s tratum58.s tygian59.t hespian60.u nfrock 61.p erdition62.p relate63.p roselytizeunit 81.abstract2.academic3.allegory4.alliteration5.analogy6.anecdote7.anecdote8.annals9.annotate10.a nthology11.a nticlimax12.a ntithesis13.a rchetype14.a rtistic15.b ibliography16.c aption17.c aricature18.c ategory19.c ircumlocution20.c liche21.c oda22.c ode23.c olloquial24.c onnoisseur25.d ata26.d epict27.d erivative28.d esign29.d iary30.d isciple31.d iscourse32.d issertation33.e mpirical34.e nigma35.e pitome36.e xcerpt37.g enre38.g ist39.g lossary40.i diom 41.j argon42.l ampoon43.l yric44.a ddendum45.a lias46.a nalogous47.a rgot48.c ameo49.c anto50.c ategorical51.c ognate52.c outh53.d oggerel54.e pistle55.e tymology56.f acsimile57.f elicitous58.f igurative59.h ieroglyphic60.o rthography61.a nthropomorphic62.b ard63.c ompendum compend64.d enouement65.e pithet66.e uphemism67.e xpletive68.f elicity69.h yperbole70.i ndite71.a lmanacunit 91.lexicographer2.lexicon3.liaison4.linguistic5.malapropism6.metaphor7.motif8.multilingual9.narrative10.n urture11.o bjective12.o bjectivity 13.p aradox14.p aralelism15.p edagogy16.p ortrait17.p ortray18.p recis19.p rototype20.p seudonym21.p undit22.q uintessence23.r hetoric24.r hyme25.s atire26.s cript27.s imile28.s ketch29.s oliloquy30.s onnet31.s tanza32.s tereotype33.s yntax34.t reatise35.t ruism36.u nderstatement37.u ndertone38.v erbalize39.v ernacular40.b ignette41.k en42.l imn43.l ineage44.m entor45.m iscelany46.n eologism47.o bituary48.o nomatopoeia49.p antomime50.p aradigm51.p arlance52.p edagogue53.p eruse54.p hilology55.p icaresque56.p rosody 57.r ubric58.s aga59.s avant60.s kit61.t irade62.t ome63.t ravesty64.v erismilitude65.v erity66.w itticism67.y arn68.l ineament69.m inuscule70.o pus71.p aragon72.p ariah73.p atois74.p eroration75.p olyglot76.s olecism77.v entriloquist78.l itotes79.r unic80.v irtuosounit 101.acoustic2.acrophobia3.aesthetic4.amphibian5.amputate6.angular7.antropoid8.anthropology9.antibiotic10.a ntidote11.a ntiseptic12.a ntler13.a pe14.a postrophe15.a pproximation16.a rchaeology17.a ria18.a t length19.b allet 20.b y birtue of21.c hoir22.c onsequently23.c onsonance24.d itty25.l est26.n everthleless27.o pera28.o rchestra29.p arenthesis30.p unctuate31.r ote32.s core33.s onata34.t erminology35.a bscission36.a cetic acid37.a lluvial38.a mnesia39.a nemia40.a nodyne41.a poplexy42.a quiline43.a rithmetic44.a xiom45.c adence46.c arillon47.e thnology48.f inale49.i nsofar50.l ibretto51.p ertain52.r endition53.r eprise54.s yncopation55.t empo56.t imber57.v audeville58.v elocity59.a nalgesic60.a pothecary61.a rchipelago62.c antata63.c rescendo 64.g amut65.m adrigal66.a phasia67.a rboretum68.f luted69.s poonerismunit 111.artery2.asteroid3.avalalnche4.billow5.burgeon6.capillary7.carnivorous8.cascade9.catharsis10.c entigrade11.c erebral12.c hronic13.c ompound14.c oncept15.c onifer16.c orrelation17.c orrode18.c orrosive19.c osmic20.c riteria21.d efoliate22.d egenerate23.d elta24.d issection25.e bb26.l ava27.a rrhythmic28.a septic29.a stigmatism30.a stral31.a ureole32.b enign33.c anine34.c anker35.c arat36.c arcinogen 37.c ardiology38.c arrion39.c athartic40.c entripetal41.c hasm42.c iliated43.c laustrophobia44.c lavicle45.c ompute46.c oncave47.c oncentric48.c ontagion49.c onvex50.c orporeal51.d emoented52.d emographic53.d isquistion54.d orsal55.d rone56.t ouchstone57.a rroyo58.a tavism59.a utopsy60.b ifurcate61.b ilious62.b rawn63.c arapace64.c artography65.c ataract66.c auterize67.c erebration68.c rux69.d eciduous70.d ecomposition71.d elirium72.d ermatologist73.d yspeptic74.c adaver75.c lime76.c ontusion77.c ynosureunit 121.entity2.erode3.ethnic4.euthanasia5.expertise6.fleck7.foliage8.formulate9.fungi10.g alaxy11.g erminate12.g rotto13.h ibernate14.h over15.i ncubate16.i nsomnia17.i nterdisciplinary18.i ntuition19.k ernel20.l abyrinth21.l atitude22.e clipse23.e ddy24.e jaculation25.e llipse26.e lllipsis27.e questrian28.e quine29.e uphony30.e we31.e xcise32.f acet33.f erret34.f ester35.f leece36.f rond37.f ruition38.g adfly39.g eneric40.g enesis41.g estate42.g narled43.g raphic44.h erbivorous45.h interland46.h ydrophobia 47.i sthmus48.k noll49.l ancet50.l eaven51.e ugenic52.f ebrile53.f loe54.g all55.g irth56.h erpetologist57.i gneous58.i nsalubrious59.k inetic60.l aceration61.e metic62.e ncroachment63.e ntomology64.e quinox65.f auna66.f lora67.l ackles68.h irsute69.h ummock70.h umus71.h ypochondriac72.i chthyology73.i mbecility74.k leptomaniac75.l agoonunit 131.liquid2.luminous3.lunar4.magnitude5.mammal6.maritime7.mirage8.molecule9.myopic10.o piate11.o rientation12.p late13.p anacea14.p arameter 15.p erimetter16.p henoenon17.p hobia18.p hoenix19.p hysiological20.p igment21.p ith22.p lacebo23.l eeway24.l ibido25.l umen26.m ammoth27.m atrix28.m rcurial29.m eteoric30.m ite31.m olt32.m omentum33.m orbid34.m ote35.n ebulous36.o bstetrician37.o lfactory38.o mnivorous39.o ptometrist40.o sseous41.o ssify42.o void43.p alpitate44.p apyrus45.p arity46.p athological47.p ediatrician48.p erceptive49.p ercussion50.p eriphery51.p lasticity52.p lumage53.p otion54.m angy55.m arsupial56.m egalomania57.m esmerize58.m nemonic 59.m onochromatic60.n ettle61.o bsequy62.o culist63.o rnithologist64.p aleontology65.p aranoia66.p etilential67.p hysiognomy68.l eonine69.m enagerie70.m icrocosm71.n omenclature72.o af73.p alimpest74.p enumbraunit 141.prey2.principle3.projectile4.promontory5.proportion6.psyche7.psychiatrist8.psychosis9.respiration10.s atellite11.s cope12.s emblance13.s eminal14.s pectrum15.s pherule16.s pleen17.s tatic18.s ubliminal19.s uture20.t actile21.t heoretical22.t herapeutic23.t heral24.t itle25.t undra26.t yphoon27.v estige 28.v irus29.v iscous30.a ppellation31.p recipitous32.p ropagate33.p ropulsive34.p rotuberance35.p sychopathic36.p ulmonary37.r avine38.r efraction39.r esponsiveness40.r ivulet41.s aline42.s alubrious43.s ensitization44.s eptic45.s lough46.s olstice47.s oluble48.s omnambulist49.s pawn50.s tanch51.s ucculent52.t angential53.t errestrial54.t opography55.t orso56.t raumatiuc57.u ndulating58.u rsine59.v enom60.v entral61.v isage62.v iscid63.p oultice64.p recipice65.p rophylactic66.p rovenance67.p ulsate68.r amification69.r everberate70.s accharine71.s eismic72.s idereal73.s olvent74.s omatic75.s ylvan76.s ymbiosis77.t axonomist78.t ravail79.u nguent80.v iper81.v isceral82.v ivisection83.p terodactyl84.q uadruped85.s imian86.t alon87.t arantula88.v itriolicunit 151.accessory2.adjunct3.adulterate4.akin5.alloy6.apex7.cleft8.cogponent10.c ompress11.c onduit12.d ecelerate13.d ehydrate14.d ilute15.d isembark16.d rake17.e mbryonic18.e ndocrine19.f atorable20.h ybrid21.h ybridization22.i mmunity23.m ete24.m osaic25.m ucus26.p atent 27.p eptide28.p recipitate29.r eaper30.r etina31.s luice32.s perm33.s yndrome34.s ynthesis35.s ynthetic36.u nearth37.v accinate38.w help39.w hiff40.y ield41.a morphous42.a naerobic43.a nneal44.a ppurtenances45.a utomaton46.c areen47.c hassis48.c oncatenate49.f illy50.i ncandescent51.l evee52.l og53.m acerate54.m atrilineal55.p ropellant propellent56.q uarantine57.r epercussion58.s alvage59.s lag60.t adpole61.t iller62.v aporize63.v ise64.v ortex65.w arble66.w hinny67.w horl68.w indfall69.c alorific70.c entrifugal 71.c onservatory72.c ulvert73.i ncrustation74.l igneous75.p araphernalia76.p hylum77.p recipitant78.p lverize79.s eine80.s melt81.s older82.v eneer83.v itreous84.g erminal85.s extant86.v erdigrisunit 161.anesthetic2.asphalt3.bolster4.brocade5.bulb6.carpenter7.catalyst8.caulk9.caustic10.c omposition11.c onstruction12.c revice13.d ebris14.d esiccate15.d issolve16.f erment17.f ilter18.f law19.f oil20.f rame21.f riction22.f usion23.h atch24.i llusion25.i nfiltrate26.i ngest27.i rrigate 28.j uncture29.m edium30.m ine31.o re32.p ebble33.r adiation34.r adium35.r amp36.r emmant37.s culpture38.s eep39.s tatue40.s ubstitute41.s urvey42.t exture43.t hermometer44.a perture45.a piary46.c argo47.d ismantle48.d issolution49.d istill50.d uctile51.e qualizer52.f ilings53.f ission54.f lax55.f ulcrum56.g laze57.g ouge58.h allucination59.h oist60.h one61.i mbue62.i mplode63.k it64.m etallurgical65.m otility66.o rb67.f ift68.f ubble69.s oot70.s ponge71.t rickle 72.d ie73.e gress74.f issure75.f lail76.g alvanize77.h iatus78.h omeostasis79.i sotope80.m etalloid81.m etamorphosis82.h one83.i mbue84.i plode85.k it86.m etallurgical87.m otility88.o rb89.r ift90.r ubble91.s oot92.s ponge93.t rickle94.d ie95.e gress96.f issure97.f lail98.g alvanize99.h iatus100.homeostasis 101.isotope102.metalloid103.metamorphosis 104.orifice105.turquoise106.acclivity107.flotsam108.guy109.gyroscope110.purchaseunit 171.aggressive2.annex3.annihilate4.armada5.assault6.beleaguer7.beset8.carnage9.dispatch10.e mancipate11.f ortify12.i ncursion13.i nvasion14.m artial15.m artyr16.m ilitant17.m ilitary18.m issile19.o nslaught20.r etreat21.s caffold22.t orque23.t ransmit24.v anguard25.a ccoutrements26.a trocity27.b arrage28.b ellicose29.b esiege30.c aliber calibre31.c atapult32.c itadel33.c ommandeer34.d etrerent35.d isband36.f eint37.f orage38.f oray39.h olster40.i mpale41.i mplosion42.i ndentation43.i nsurgent44.i nsurrection45.m uster46.p rotrude47.r ampant48.r eparation 49.r out50.s cabbard51.s kirmish52.s quash53.t amp54.a djutant55.a rsenal56.a ttrition57.b elligerent58.b randish59.b ulwark60.c apitulate61.c enturion62.c ohorts63.c onscript64.d eploy65.d etontion66.d islodge67.e spionage68.f iasco69.f usillade70.h olocaust71.m utinous72.r econnaissance73.s entinel74.s pangle75.s tratagem76.w aylay77.c ordon78.s tratifiedunit 181.barb2.brooch3.brush4.circlet5.cuisine6.culinary7.echelon8.embark9.fleet10.g ale11.g usty12.p edestal13.r ampart 14.r egiment15.r eserve16.s avory17.s ear18.s torage19.v ogue20.c arafe21.c onflagration22.c onveyance23.c rypt24.d inghy25.d ingy26.d ormer27.g armer28.g renade29.r efectory30.r epository31.r ostrum32.s avor33.s having34.s ilt35.s tochade36.s will37.t rappings38.t rinket39.u nsavory40.v ertex41.w armonger42.z enith43.a mazon44.d ais45.d ecollete46.e picure47.f odder48.g alleon49.g astronomy50.p rovender51.q uay52.r egimen53.r endezvous54.r ig55.s artorial56.s cavenge57.s hard 58.s herbet59.s kiff60.s toke61.s urfeit62.s ustenance63.t ipple64.t rajectory65.t rough66.t ureen67.v enison68.]victuals69.w arren70.d eclivity71.e paulet72.r aimentunit 191.accommodate2.ballast3.balm4.chalice5.gourmet6.gruel7.hoard8.hoe9.jet lag10.j unk11.l oophole12.l umber13.m ausoleum14.m iser15.p alatable16.r ealm17.r elic18.r etouch19.s age20.s pruce21.t hreshole22.t ire23.a lcove24.a limentary25.b auble26.b lazon27.c istern28.c olander 29.c ollation30.d arn31.g avel32.g ourmand33.g ratuitous34.g raze35.g rill36.g uise37.h aven38.i dyllic39.i ndigenous40.n autical41.n avigable42.p endant43.p estle44.p oncho45.p otable46.r epast47.r ung48.s ash49.s awdust50.s cent51.s ubsistence52.t assel53.t enement54.a viary55.c ondiments56.d omicile57.g ranary58.g ratuity59.i ndigence60.i nebriated61.j unket62.p all63.p allet64.p arquet65.p eregrination66.p eripatetic67.p yre68.r egatta69.v iand70.g azetteunit 20 1.aboriginal 2.abyss3.adolescent4.agenda5.amenity6.archives7.athlete8.bask9.bathe10.b in11.c hampion12.c omestible13.f arewell14.f estive15.f ete16.f orebear17.f orality18.i tinerary19.j ubilation20.k aleidoscope21.n ovice22.p astime23.p ickings24.p itch25.p ool26.r ite27.s hear28.s heathe29.s lab30.t in31.t int32.t orrent33.v ampire34.a ncestry35.b acchanal36.b egrudge37.b ivouac38.c aldron cauldron39.c oiffure40.d agger41.d esolate42.g nome43.h ilarity44.b ovel45.i tinerant 46.i tinerate47.k indergarten48.m iasma49.m ores50.o rgy51.p laque52.p ugilist53.r evelry54.s ecular55.s heath56.t rident57.w anderlust58.w ithdrawn59.z ephyr60.b oon61.c arousal62.d eluge63.h orde64.i conoclastic65.j ollity66.l oe67.n atation68.n ostrum69.q uagmire70.r egale71.s pate72.s patula73.t ract74.b ouillon75.c ornucopia76.o bsidian77.t oga78.t onsureunit 211.assuption2.cognitiveplain4.confirm5.conjecture6.corroborate7.deduce8.definition9.demon10.d emonstrate 11.d ialectic12.d isprove13.e laborate14.e lucidate15.e xtrovert16.f allacy17.f ascination18.f ractious19.h ypothesis20.h ypothetical21.i lluinate22.i llustrate23.i nduce24.i nfer25.i nterpretation26.i ntrovert27.p ostulate28.r ash29.r ationale30.r ationalize31.r ebuttal32.r efute33.s ophist34.s ophistry35.s pecify36.s peculation37.s upposition38.s urmise39.u nravel40.v ex41.v exation42.c holeric43.c ontrovert44.c rabbed45.c rotchety46.d ialectical47.d isabuse48.i ndignation49.i rate50.m etaphysical51.p osit52.t esty53.w rath54.c ognizance 55.d ichotomy56.e xtrapolation57.f allacious58.f uror59.i rascible60.p etulant61.p ique62.p utative63.r atiocination64.r ile65.s uppositious66.s yllogism67.t antrum68.f eiustyunit 221.agitate2.assiduous3.charitable4.charitlyplement6.cultivated7.decorous8.exalt9.extol10.i ndustrious11.i nfamous12.i nflexible13.i nsight14.i ntractable15.i rritation16.l aud17.o bdurate18.o bstinate19.o bstreperous20.o dious21.r efractory22.t enacious23.v anity24.w illful25.a ccolade26.a damant27.a dulation28.a stute29.b igotry 30.c avalier31.c avil32.d espicable33.d ogged34.d ogmatic35.e ulogistic36.f idelity37.h ard-nosed38.h eadstrong39.h ospitable40.i gnoble41.i mperious42.m alignant43.n otoriety44.p anache45.p erspicacious46.q uerulous47.r ecalcitrant48.r ectitude49.s curvy50.s plenetic51.t enacity52.v eracious53.c lairvoyant54.e ncomiastic55.e ncomium56.e ulogy57.e uphoria58.f roward59.g affe60.n efarious61.o blique62.o dium63.p anegyric64.p eremptory65.p ertinacious66.p robity67.r hapsodize68.s currilous69.v eritable70.r ibalduni 231.abhor2.alert3.antipathy4.arrogance5.asperity6.attentive7.bearing8.caution9.circumspect10.c omplacent11.c omprehend12.c onceit13.c oncentrate14.d isgust15.d umbfound16.i ntegrity17.i rksome18.l oathe19.m eticulous20.o verbearing21.p rudent22.r epulsion23.r esentment24.r evulsion25.r uthless26.s crupulous27.s eriousness28.t ension29.t entative30.v aunted31.v aunting32.v igilant33.a bominate34.e xecrable35.e xecrate36.f ixate37.g ingerly38.h aughtiness39.h ubris40.i nsolence41.i nsularity42.o verweening43.p ore44.p resumptuous45.p retentious46.r eflect 47.r igor48.r uminate49.s mug50.t emperament51.t hwart52.t ouchy53.t ruculence54.d iscretion55.d isinclination56.d our57.d raconian58.g eniality59.i ncisive60.i nvidious61.p ugnacity62.r epugnance63.s adistic64.s tringent65.s upercilious66.t ransport67.u nbridled68.v ainglorious69.v irulentuni 241.adventurous2.avarice3.avaricious4.baffle5.belittle6.bewilder7.bold8.brazen9.candor10.c ommitment11.c ompassion12.c onfound13.c onfusion14.c ontempt15.c ovetous16.c oy17.d epreciate18.d espise19.d isdain20.d isparage 21.i ntrepid22.j eer23.p erplexed24.p luck25.p roficient26.r idicule27.s arcasm28.s atirical29.s coff30.s corn31.s light32.t imidity33.v alor34.w ince35.b alk36.b awdy37.b efuddled38.c alculated39.c anny40.c omely41.r avenous42.d eride43.f oolhardy44.g ibe45.l ewd46.m ordant47.m uddle48.p ert49.p rowess50.q ualms51.q uizzical52.r apacious53.c upidity54.r ecreant55.s alacious56.s ensual57.s kittish58.d erision59.e mpathy60.f lout61.g amely62.i gnominy63.l ascivious64.l echery 65.l ibidinous66.p rurient67.p uissant68.p unctilious69.p usillanious70.q uandary71.q uip72.r apt73.s ardonic74.t aunt75.t emerity76.t imorous77.v oraciousunit 251.impotent2.rejoice3.relish4.reverie5.secretive6.sensation7.serenity8.smirk。

分享】写英文简历中可能用到的单词A Useful Glossary for Personal Data（个人资料有用词汇）name 姓名aliss 别名pen name 笔名date of birth 出生日期birth date 出生日期born 生于birthplace 出生地点birthday 生日age 年龄native place 籍贯province 省city 市autonomous region 自治区prefecture专区county县nationality 民族；国籍citizenship 国籍duel citizenship 双重国籍address 地址current address 目前住址present address 目前住址permanent address 永久住址postal code 邮政编码home phone 住宅电话office phone 办公电话Tel.电话sex 性别male 男female 女Mr.先生Miss 小姐Mrs.太太Ms (小姐或太太)height 身高cm. 厘米ft. 英尺in 英寸weight 体重kg 公斤lbs 磅marital status 婚姻状况family status 家庭状况married 已婚single 未婚unmarried 未婚divorced 离异separated 分居number of children 子女人数none 无street 街lane 胡同，巷road 路district 区house number 门牌health 健康状况blood type 血型A A型B B型O O型excellent （身体）极佳very good 很好good 好strong 强壮short-sighted 近视far-sighted 远视color-blind 色盲 ID card 身份证No. 号码date of availability 可到职时间available 可到职membership 会员、资格president 会长director 理事standing director 常务理事secretary-general 秘书长society 学会association 协会research society 研究会January (Jan.) 一月February (Feb.) 二月March (Mar.)三月April(Apr.) 四月May 五月June 六月July 七月August (Aug.)八月September (Sept.) 九月October (Oct.)十月November (Nov.) 十一月December (Dec.) 十二月喜欢鱼 2005-09-13 20:09--------------------------------------------------------------------------------A Useful Glossary for Educational Background（教育程度有用词汇）education 学历educational background 教育程度educational history 学历curriculum 课程major 主修minor 副修educational highlights 课程重点部分curriculum included 课程包括specialized courses 专门课程courses taken 所学课程courses completed 所学课程special training 特别训练social practice 社会实践part-time jobs 业余工作summer jobs 暑期工作vacation jobs 假期工作refresher course 进修课程extracurricular activies 体育活动recreational activities娱乐活动academic activities 学术活动social activities 社会活动rewards 奖励scholarship 奖学金"Three Goods" student "三好"学生excellent League member 优秀团员excellent leader 优秀干部student council 学生会off-job training 脱产培训in-job training 在职培训educational sustem 学制academic year 学年semester 学期（美）term 学期（英）president 校长vice-president 副校长acdemic dean 教务员department chairman 系主任professor 教授associate professor 副教授guest professor 客座教授lecturer 讲师teaching assistant 助教research fellow 研究员rearch assistant 助理研究员supervisor 论文导师principal 中学校长（美）headmaster 中小学校长（英）master 小学校长（美）dean of students 教务长dean of students 教导主任 teacher 教师probation teacher 代课教师tutor 家庭教师governess 女家庭教师intelligence quotient 智商pass 及格fail 不及格marks 分数grades 分数scores 分数examination 考试grade 年级class 班级monitor 班长vice-monitor 副班长commissary in charge of studies 学习委员commissary in charge of entertainment 文娱委员commissary in charge of sports 体育委员commissary in charge of physical labour 劳动委员Party branch secretary 党支部书记League branch secretary 团支部书记commissary in charge of organization组织委员commessary in charge of publicity 宣传委员degree 学位post doctorate 博士后doctor (Ph.D) 博士master 硕士bachelor 学士student 学生graduate student 研究生abroad student 留学生returned student 回国留学生foreign student 外国留学生undergraduate 大学肄业生；（尚未取得学位的）大学生senior 大学四年级学生；高中三年级学生Junior 大学三年级学生；高中二年级学生sophomore 大学二年级学生；高中一年级学生freshman大学一年级学生guest student 旁听生（英）auditor 旁听生（美）government-supported student 公费生commoner 自费生extern 走读生day-student 走读生intern 实习生prize fellow 奖学金生boarder 寄宿生classmate 同班同学schoolmate 同校同学graduate 毕业生喜欢鱼 2005-09-13 20:10-------------------------------------------------------------------------------- Useful Glossary for Work Experience（工作经历有用词汇）work experience 工作经历work history 工作经历occupational history 工作经历professional 职业经历employment 工作employment history 工作经历experience 经历business experience 工作经历specific experience 具体经历employment record 工作经历business history 工作经历employment experience工作经历business background 工作经历position 职位job title 职位responsibilities 职责duties 职责second job 第二职业achievements 工作成就，业绩administer 管理assist 辅助adapted to 适应于accomplish 完成（任务等）appointed 被任命的adept in 善于analyze 分析authorized 委任的；核准的behave 表现break the record 打破记录control 控制breakthrough 惊人的进展，关键问题的解决conduct 经营，处理cost 成本；费用create 创造demonstrate 证明，示范decrease 减少design 设计develop 开发，发挥devise 设计，发明direct 指导double 加倍，翻一番earn 获得，赚取effect 效果，作用eliminate 消除enlarge 扩大enrich 使丰富exploit开发（资源，产品）enliven 搞活establish 设立（公司等）；使开业；确立evaluation 估价，评价execute 实行，实施expand 推广；扩大expedite 加快；促进export 出口found 创立generate 产生good at 擅长于guide 指导；操纵implement 完成，实施import 进口improve 改进，提高increase 增加influence 影响initiate 创始，开创introduce 采用，引进innovate 改革，革新inspired 受启发的；受鼓舞的install 安装invest 投资integrate 使结合；使一体化invent 发明justified 经证明的；合法化的launch 开办（新企业）lead 领导lengthen 延长lessen 减少（生产成本）level 水平localize 使地方化manage 管理，经营make 制造maintain 保持；维修manufacture 制造modernize 使现代化mastered 精通的motivate 促进，激发negotiate 谈判nominated 被提名的；被任命的operate 操作，开动（机器等），经营（厂矿）originate 创始，发明organize 组织overcome 克服（困难等）participate in 参加perfect 使完善；改善perform 执行，履行plan 计划promote 生产，制造profit 利润promote 推销（商品）；创立（企业等）be promoted to 被提升为be proposed as 被提名为；被推荐为provide 提供，供应raise 提高reach 达到realize 实现（目标等）；获得（利润）receive 收到，得到，接受reckon 计算（成本等）recognize 认清（职责等）recommended 被推荐的；被介绍的reconsolidate 重新巩固；重新整顿reconstruct 重建recorded 记载的recover 恢复；弥补rectify 整顿，调整redouble 加倍，倍增reduce 减少，降低（成本等）refine 精练，精制reform 改革registered 已注册的regenerate 更新，使更生regularize 使系统化regulate 控制（费用等）re handle 重铸；重新处理rehash 以新形式处理（旧材料）reinforce 加强renew 重建，换新renovate 革新；修理repair 修复，修补replace 接替，替换representative 代表，代理人research 调查，研究resolve 解决set 创造（纪录等）settle 解决（问题等）shorten 减低......效能show 显示,表明significant 重要的,有效的simplify 简化,精简sort out 清理speed up 加速sponsor 主办spread 传播,扩大solve 解决standard 标准,规格streamline 把......设计流线型strengthen 加强,巩固study 研究succeed 成功supervise 监督,管理supply 供给,满足(需要)systematize 使系统化target 目标,指标test 试验,检验top 头等的,最高的total 总数,总额translate 翻译,转化travel 旅行well-trained 训练有素的type 打字unify 使成一体,统一use 使用，运用utilize 利用valuable 有价值的useful 有用的verify 证实,证明vivify 使活跃work 工作,起作用worth 使......钱的,有......价值的advanced worker 先进工作者working model 劳动模范excellent Party member 优秀党员excellent League member 优秀团员喜欢鱼 2005-09-13 20:11-------------------------------------------------------------------------------- A Useful Glossary for Other Contents（其它内容有用词汇）应聘职位objective 目标career objective 职业目标employment objective 工作目标position wanted 希望职位job objective 工作目标position applied for 申请职位position sought 谋求职位position desired 希望职位A Useful Glossary for Personal Characters（个人品质有用词汇）able 有才干的，能干的active 主动的，活跃的adaptable 适应性强的adroit 灵巧的，机敏的aggressive 有进取心的alert 机灵的ambitious 有雄心壮志的amiable 和蔼可亲的amicable 友好的analytical 善于分析的apprehensive 有理解力的aspiring 有志气的，有抱负的audacious 大胆的，有冒险精神的capable 有能力的，有才能的careful 办理仔细的candid 正直的charitable 宽厚的competent能胜任的confident 有信心的conscientious 认真的，自觉的considerate 体贴的constructive 建设性的contemplative 好沉思的cooperative 有合作精神的creative 富创造力的dashing 有一股子冲动劲的，有拼搏精神的dedicated 有奉献精神的devoted 有献身精神的dependable 可靠的diplomatic 老练的，有策略的disciplined 守纪律的discreet （在行动、说话等方面）谨慎的dutiful 尽职的dynamic 精悍的earnest 认真的well-educated 受过良好教育的efficient 有效率的energetic 精力充沛的enthusiastic 充满热情的expressively 善于表达faithful 守信的，忠诚的forceful （性格）坚强的frank直率的，真诚的friendly 友好的frugal 俭朴的generous 宽宏大量genteel有教养的gentle 有礼貌的hard-working 勤劳的hearty 精神饱满的honest 诚实的hospitable 殷勤的 humble 恭顺的humorous 有幽默impartial 公正的independent 有主见的industrious 勤奋的ingenious 有独创性的initiative 首创精神have an inquiring mind爱动脑筋intellective 有智力的intelligent 理解力强的inventive有发明才能，有创造力的just 正直的kind-hearted 好心的knowledgeable 有见识的learned 精通某门学问的liberal 心胸宽大的logical 条理分明的loyal 忠心耿耿的methodical 有方法的modest 谦虚的motivated 目的明确的objective 客观的open-minded 虚心的orderly 守纪律的original 有独创性的painstaking 辛勤的，苦干的，刻苦的practical 实际的precise 一丝不苟的persevering 不屈不挠的punctual 严守时刻的purposeful 意志坚强的qualified 合格的rational 有理性的realistic 实事求是的reasonable 讲道理的reliable 可信赖的responsible 负责的self-conscious 自觉的selfless 无私的sensible 明白事理的sincere 真诚的smart 精明的spirited 生气勃勃的sporting 光明正大的steady 踏实的straightforward 老实的strict 严格的systematic 有系统的strong-willed 意志坚强的sweet-tempered 性情温和的temperate 稳健的tireless 孜孜不倦的喜欢鱼 2005-09-13 20:12-------------------------------------------------------------------------------- A Useful Glossary for Other Contents（其它内容有用词汇）科研成果scientific achievements 科研成果publications 发表作品daily 日报evening news 晚报periodical 期刊magazine 杂志monthly 月刊weekly 周刊bimonthly 双月刊，半月刊yearly book 年鉴，年刊 biweekly 双周刊，半周刊journal 学刊，学报issue （报刊）期号be published 出版be carried 登载publishing house 出版社press 出版社invention 发明innovation 革新patent 专利A Useful Glossary for Other Contents（其它内容有用词汇）业余爱好hobbies 业余爱好interests 兴趣，爱好go dancing 跳舞go boating 划船go fishing 钓鱼listening to pop music 听流行音乐listening classical music 听古典音乐listening symphony 听交响乐do some clay sculptures 搞泥塑reading 阅读singing 唱歌writing fiction 写小说dog training 训狗marionette puppet making 制作木偶skating 滑冰skiing 滑雪do boxing 拳击see films 看电影traveling 旅游walking in the countryside 在乡间散步take pictures 拍照play cards 打扑克play chess 下棋play bridge 打桥牌go to the theater 看戏play 话剧drama 戏剧opera 歌剧Peking opera 京剧play basketball 打篮球 play volleyball 打排球play football 踢足球play tennis 打网球play table tennis 打乒乓球play golf 打高尔夫球play badminton 打羽毛球swimming 游泳wrestling 摔跤bike riding 骑单车jogging 慢跑cooking 烹调sewing 缝纫drawing 画画long distance running 长跑collecting stamps 集邮collecting coins 收藏硬币collecting lithographs 收藏字画collecting antiques 收藏古董collecting toys 收藏玩具collecting seashells 收藏海贝horseback riding 骑马hiking 长途徒步旅行camping 宿营bowling 滚木球play the piano 弹钢琴play the guitar 弹吉他play the violin 拉小提琴play the flute 吹笛子play the pipe 奏管乐play the accordion 拉手风琴。

a- 1. 无，不，非azonic 非地带性的a -2. 含in,at等意义asleep 在熟睡中a- 3. 加强意义aloud 高声地ab- 离去，相反，不abuse 滥用ac-含at,to意,加强意义accustom 使习惯用在c,k,q前ad-含at,to意,加强意义adventure 冒险用在d,h,j,m,v前af-含at,to意,加强意义afforest 造林，绿化用在f前ag-含at,to意,加强意义aggrandize 增大用在g前air-空中的airline 航空公司al-1.含at,to意,加强意义allocate 分配用在l前al-2.构成副词almost 几乎amphi- 两，双amphibian 水陆两用车an-1. 无，不anarchistic 无政府的an-2.含at,to意,加强意义annotate 注解用在n前ante- 前，先anteroom 接待室anthropo- 有关人的anthropophagus 吃人族anti- 反对，相反，防止antibiotics 抗生素用于a前省iany- 任何anywhere 任何地方ap- 加强或引申意义appraise 评价用在p前apo- 离开apogee 远地点ar- 含at,to意,加强意义arrange 安排用在r前arch- 主要的，首位的archenemy 头号敌人as- 含at,to意,加强意义assort 分类用在s前at- 含at,to意,加强意义attract 吸引用在t前auto- 自己，自动autobiography 自传back- 反的，向后的backstroke 仰泳be- 1. 使...，使成为... belittle 使缩小，贬低be- 2. 加以...，用... bespangle 用小亮片装饰be- 3. 在below 在...下面be- 4. 加强及引申意义befall 降临，发生bene- 善，好benediction 祝福bi- 两，二bimonthly 双月刊by- 旁，侧，非正式byroad 小路，僻径centi- 百分之一，厘centimetre 厘米circum- 周围，环境circumpolar 极地周围的co- 共同cooperation 合作用在元音字前col- 1.共同collocate 并置，并列用在l前col- 2.加强或引申意义collate 校对用在l前com-1.共同combine 联合，结合用在b,m,p前com-2.加强或引申意义commix 混合用在b,m,p前con- 1.共同concolorous 同色的con- 2.加强或引申意义confirm 使坚定contra- 反对，相反contradict 反驳，相矛盾cor- 1. 共同，互相correspond 共鸣用在r前cor- 2. 加强或引申意义corrupt 腐败，败坏用在r前counter- 反对，相反counterattack 反攻，反击de- 1. 否定，非，相反deprecatory 反对的de- 2. 除去，取消，毁deflower 摧残，蹂躏de- 3. 离开depart 离去de- 4. 向下，降低devaluate 贬值de- 5. 使成...，加强意义delimit 划定界限deca- 十decameter 十米deci- 十分之一decigram 十分之一克demi- 半demigod 半神半人di- 二，双dioxide 二氧化物dia- 贯通，对穿，透过diameter 直径dif- 1. 不，无，相反diffidence 无自信用在f前dif- 2. 分开，离，散diffract 分散用在f前dis- 1. 不，无，相反dislike 不喜欢dis- 2. 取消，除去disappear 消失dis- 3. 加强意义disannul 使无效，废除dis- 4. 分开，离，散distract 分心dys- 不良，恶，困难dyspepsia 消化不良e- 1. 加强或引申意义evaluate 评价e- 2. 出，外erupt 喷出ef- 出，离去efflux 流出用在f前electro- 有关电的electrograph 电传电报em- 1. 置...之内embosom 藏于胸中，怀抱用在b,m,p前em- 2. '配（饰）以...' embroider 镶边用在b,m,p前em- 3. 致使... empurple 使发紫用在b,m,p前en- 1. 置...之中encage 关入笼中en- 2. '配（饰）以...' enchain 用链锁住en- 3. 致使... enlarge 使扩大，放大en- 4. 'in'或加强意义enregister 登记endo- 内endoparasite 体内寄生虫epi- 在...上面epidermis 表皮equi- 相等，同等equilateral 正多边形eu- 优，善，好euphonic 声音优的every- 每一everyday 每天ex- 1. 出，外excavate 挖出，发掘ex- 2. 前任的，以前的ex-mayor 前任市长ex- 3. 使（做）... expurgate 使清洁exo- 外，外部exotic 外来的extra- 以外，超过extraterritorial 治外法权的for- 禁止，离去，克制forbear 忍受fore- 前，先，预先foreground 前景geo- 地质，地球geometry 大地测量术，几何hecto- 一百hectopascal 百帕hemi- 半hemisphere 半球hepta- 七heptagon 七角形hetero- 异hetero*ual 异性的hexa- 六hexangular 有六角的high- 高，大，主要highway 高速路holo- 全hologram 全息图homo- 同homonym 同音字hyper- 超过，过多，太甚hyperacid 胃酸过多的hypo- 下，低，次，少hypotension 低血压ideo- 观念，意义ideograph 会意字il- 1. 不，无，非illegal 非法的用在l前il- 2. 使成...，加强意义illuminate 照耀用在l前im- 1. 不，无，非immoral 不道德的用在b,m,p前im- 2. 向内，入imprison 投入狱中，监禁用在b,m,p前im- 3. 使成...，加强意义imparadise 使登天堂用在b,m,p前in- 1. 不，无，非inhuman 不人道的in- 2. 内，入inbreak 入侵in- 3. 使成...，加强意义inflame 燃烧infra- 下，低infrared 红外线（低于红线）inter- 1. 在...之间，..际interoceanic 大洋之间的inter- 2. 互相interview 会见intra- 在内，内部intrastate 州内的intro- 向内，入内intromit 插入ir- 1. 不，无irregular 不规则的用在r前ir- 2. 向内，入irrigate 灌入水，灌溉用在r前iso- 等，同isotope 同位素kilo- 千kilowatt 千瓦macro- 大，宏，长macroclimate 大气候magni- 大，长magnify 扩大用于a前省imal- 恶，不良，失malfunction 故障mega- 百万megabyte 兆字节meta- 1. 超metachemistry 超级化学meta- 2. 变化metagenesis 世代交替micro- 微microwave 微波mid- 中midsummer 仲夏milli- 1. 千分之一，毫milligram 千分之一克milli- 2. 千millipede 千足虫，多足虫mini- 小minipark 小型公园mis- 误，错，恶，不misspell 拼错mono- 单一，独monoxide 一氧化物multi- 多multimedia 多媒体的用于a前省ineo- 新neoimpressionism 新印象派no- 无nothing 没事non- 1. 不nonsmoker 不抽烟的人non- 2. 非nonmetal 非金属non- 3. 无nonpayment 无力支付ob- 逆，反，非，倒object 反对oc- 逆，反，非，倒occupy 占领用在c前octa- 八octagon 八角形of- 逆，反，非，倒offend 触犯用在f前omni- 全，总，公，都omnibus 公共汽车op- 逆，反，非，倒opposite 相反的用在p前out- 1. 胜过，超过outrun 跑过，追过out- 2. 过度，太甚outdream 做梦太多out- 3. 外，出outdoor 户外的out- 4. 除去outcast 开除的，遗弃的over- 1. 过度，太甚overpraise 过奖over- 2. 在上，在外，从上overbridge 天桥over- 3. 颠倒，反转overthrow 推翻paleo- 古，旧paleozoology 古动物学pan- 全，泛pantheism 泛神论para- 1. 半，类似，准parallel 平行的para- 2. 辅助，副paramilitary 辅助军事的para- 3. 旁，靠近，外parasite 寄生虫para- 4. 错误，伪paradox 似是而非para- 5. 防，避开，保护parasol 遮阳伞para- 6. 超过paramount 至上的pen- 几乎，相近，相似penultimate 倒数第二个penta- 五pentagram 五角星形per- 1. 贯穿，通，透persist 坚持per- 2. 加强意义perturb 扰乱per- 3. 过，高perchloride 高氯化物peri- 周围，外层，靠近pericarp 果皮用于a前省i poly- 多polyfunctional 多功能的post- 后postscript 后记pre- 1. 前prefix 前缀pre- 2. 预先prepay 预付pro- 1. 向前，在前prologue 前言，序言pro- 2. 代理，代替procurator 代理人pro- 3. 拥护，亲，赞成pro-British 亲英的proto- 原始protoplasm 原生质，细胞质pseudo- 假pesudonym 假名quadr- 四quadruped 四足动物quinque- 五quinquesection 五等分用于a前省e re- 1. 回，向后reclaim 收回re- 2. 再，重复，重新reconsider 重新考虑re- 3. 相反，反对revolt 反叛，造反retro- 向后，回，后retrospect 回顾se- 离开，分开secede 脱离，退出semi- 半semimonthly 半月刊sept- 七septuple 七倍的- 六to 六开本Sino- 中国Sino-Tibetan 汉藏语系some- 某sometime 某时step- 后，继stepfather 继父stereo- 立体stereosonic 立体声的sub- 1. 下submarine 海面下的sub- 2. 次，亚，准，半subtropics 亚热带sub- 3. 稍，略，微subarid 略干燥的sub- 4. 副，分支，下级subworker 副手，助手sub- 5. 接近subarctic 近北极圈的sub- 6. 更进一层，再sublet 转租，再租suc- 使成...，加强意义succeed 成功用在c前suf-使成...，加强意义suffocate 窒息用在f前sup- 使成...，加强意义support 支持用在p前super- 1. 超，超级superpower 超级大国super- 2. 上superstructure 上层建筑super- 3. 过度，过多superexcitation 过度兴奋supra- 超，上suprarenal 肾上腺的sur- 1. 上，外，超surcharge 超载sur- 2. 使成...，加强意义surround 包围用在r前sym- 共同，相同symmetry 对称用在b,m,p前syn- 共同，相同synthesis 合成tele- 1. 电telecommunication 电信tele- 2. 远程telemetry 远距离测量tetra- 四tetrachord 四弦乐器trans- 1. 越过，横过，超translucent 半透明的trans- 2. 转移，变换transport 运输tri- 三triangle 三角twi- 二，两twin 双胞胎ultra- 1. 极端ultrathin 极薄的ultra- 2. 超，以外ultramarine 海外的un- 1. 不unfortunate 不幸的un- 2. 无unmanned 无人驾驶的un- 3. 非unartificial 非人工的un- 4. 未uncivilized 未开化的un- 5. 相反动作，取消un*** 解开钮扣un- 6. 由...中弄出unbosom 吐露（心事）under- 1. 下underworld 下层社会under- 2. 内（用于衣服）undershirt 帖身内衣under- 3. 不足，少underestimate 估计不足under- 4. 副，次underking 副王，小王uni- 单一unicorn 独角兽vice- 副vice-manager 副经理with- 向后，相反withdraw 撤回，撤退-'s 1. 所有格(a) today's 今日的-'s 2. 店铺(n) greengrocer's 菜场-a 构成复数名词(n) stadia 体育馆单数以um结尾-ability 可...性(n) dependability 可靠性-able 可...的(a) inflammable 易燃的-ably 可...地(ad) suitably 合适地-aceous 有...性质的(a) carbonaceous 含碳的-acious 具有...的，多...的(a) sagacious 聪明的-acity 性质等（抽象）(n) veracity 诚实，真实-acle 构成名词(n) manacle 手铐-acy 性质等（抽象）(n) fallacy 谬误-ade 1. 行为等(n) blockade 封锁-ade 2. 物（...制成）(n) lemonade 柠檬水-ade 3. 人和集体(n) cavalcade 骑兵队-age 1. 集合名词(n) foliage 叶子-age 2. 场所、地点(n) orphanage 孤儿院-age 3. 费用(n) postage 邮资-age 4. 行为(n) pilgrimage 朝圣-age 5. 状态，身分(n) reportage 报告文学-age 6. 物(n) carriage 马车，客车厢-ain 人(n) chieftain 酋长，头子-aire 1. 人(n) millionaire 百万富翁-aire 2. 物(n) questionaire 调查问卷-al 1. 有...性质的(a) continental 大陆的-al 2. 行为（抽象）(n) withdrawal 撤退-al 3. 人(n) rival 竟争者-al 4. 物(n) manual 手册-ality ..性，（抽象）(n) technicality 技术性-ally 方式，程度等(ad) conditionally 有条件地-an 1. 属于...的(a) metropolitan 大都市的-an 2. 人(n) pubican 旅店主人-ance 情况等（抽象）(n) buoyance 浮力-ancy 情况等（抽象）(n) elegancy 优美，高雅-aneity 性质等（抽象）(n) contemporaneity 同时代-aneous 有...性质的(a) subterraneous 地下的-ant 1. 属于...的(a) luxuriant 奢华的-ant 2. 人(n) participant 参与者-ant 3. 物(n) excitant 兴奋剂-ar 1. 有...性质的(a) consular 领事的-ar 2. 人(n) liar 说谎的人-ar 3. 物(n) altar 祭坛-ard 人（贬义）(n) * 私生子-arian 1. 人(n) parliamentarian 国会议员-arian 2. 兼形容词(n,a) vegetarian 吃素者（的）-arily 有...性质地(ad) extraordinarily 不寻常地-arium 场所，...馆(n) planetarium 天文馆-ary 1. 有...性质的(a) customary 习惯的-ary 2. 场所，地点(n) apiary 养蜂场-ary 3. 人(n) secretary 书记，秘书-ary 4. 物(n) glossary 词汇表-asm 性质（抽象）(n) sarcasm 讥讽-ast 人(n) enthusiast 热心者-aster 人（卑称）(n) medicaster 江湖医生-ate 1. 做，造成(v) activate 激活-ate 2. 有...性质的(a) private 私人的-ate 3. 人(n) graduate 毕业生-ate 4. 职位，职权(n) professoriate 教授职位-ate 5. 构成化学名词(n) acetate 醋酸盐-atic 有...性质的(a) diagrammatic 图解的-ation 1. 行为，情况(n) invitation 邀请-ation 2. 行为的过程(n) reformation 改革-ative 与...有关的(a) affirmative 肯定的-ator 做...工作的人，物(n) calculator 计算机-atory 1. 具有...的(a) exclamatory 感叹的-atory 2. 场所，地点(n) observatory 天文台-cian ...学家(n) clinician 临床医学专家-cracy 统治(n) bureaucracy 官僚主义-crat 参加者，支持者(n) democrat 民主主义者-cy 性质，状态(n) infancy 幼年期-dom 1. 情况，身分(n) freedom 自由-dom 2. 领域，...界(n) sportsdom 体育界-e 构成复数名词(n) larvae 幼虫单数以a结尾-ed 1. 构成过去式(v) showed 展示规则动词-ed 2. 构成过去分词(v) published 出版规则动词-ed 3. 已完成的(a) destroyed 毁灭的-ee 受动者(n) employee 雇员-eer 关系者，管理者(n) volunteer 志愿者-en 1. 含...的，...制的(a) golden 含金的-en 2. 使成为(v) widen 加宽-ence 性质，状态，行为(n) existence 存在-ent 有...性质的(a) deterrent 妨碍的-er 1. 人(n) fighter 战士-er 2. ...的住民(n) villager 村民-er 3. 制作者(n) hatter 帽商-er 4. 物(n) harvester 收割机-er 5. 更... (a,ad) better 更好的比较级-ern 在...方的(a) northern 北方的-es 1. 构成复数名词(n) bushes 灌木单数或原型结尾ch,is,o,s,sh,x,z -es 2. 第三人称单数(v) does 做-ese ...民族的(a) Japanese 日本的-ess 阴性(n) airhostess 空姐-est 最... (a,ad) nicest 最佳的最高级-et 小(n) floweret 小花-fold ...倍的，...重的(a) multifold 多倍的-ful 1. 有...性质的(a) beautiful 美丽的-ful 2. ...的量(n) teaspoonful 一茶匙-fully 有...性质地(ad) carefully 小心地-fy 使...化(v) electrify 通电-graph 信号(n) electrograph 电传真-hood 性质，状态(n) childhood 童年-i 构成复数名词(n) fungi 真菌单数以us结尾-ial 1. ...的(a) industrial 工业的-ial 2. 行为（抽象）(n) trial 审判-ial 3. 人(n) official 官员-ial 4. 物(n) material 材料-ian 1. ...的(a) antemeridian 午前的-ian 2. ...民族的(a) Canadian 加拿大的-ian 3. ...的人，...学家(n) custodian 保管人-ibility 可...性(n) responsibility 责任-ible 可...的(a) possible 可能的-ibly 可...地(ad) terribly 可怕地-ic 1. ...的(a) basic 基本的-ic 2. ...的人(n) critic 批评家-ic 3. 学科(n) logic 逻辑学-ical ...的(a) identical 全等的-ice 行为，动作，状态(n) service 服务-icious 具有...的，多...的(a) suspicious 可疑的-icity 性质(n) authenticity 真实性，可靠性-ics 学科(n) physics 物理学-ies 1. 构成复数名词(n) counties 县单数以y结尾-ies 2. 第三人称单数(v) cries 哭原型以y结尾-ing 1. 构成现在分词(v) hoping 希望-ing 2. 正在进行的(a) developing 发展中的-ing 3. 构成名词(n) feeling 感觉-ious 具有...特性的(a) glorious 光荣的-ise 使...化(v) surprise 使惊愕BrE-ish 1. ...民族的(a) Turkish 土耳其的-ish 2. 有点...的(a) tallish 稍高的-ish 3. 有...性质的(a) foolish 笨的-ish 4. 造成，致使(v) finish 结束-ism 主义，学说，状态(n) socialism 社会主义-ist ...主义者，...家(n) novelist 小说家-it ...的动作(n) pursuit 追求-ity 性质，状态(n) solidarity 团结-ium （化学）元素名(n) calcium 钙-ive 有...性质的(a) attractive 迷人的-ize 使...化(v) initialize 初始化AmE-kin 小(n) princekin 小王子-less 无，没有，不(a) hopeless 绝望的-let 小(n) booklet 小册子-like 似...的(n) catlike 猫样的-ling 小（轻蔑）(n) starling 小星星-logy 学科(n) astrology 占星术-ly 1. 像...的(a) friendly 友好的-ly 2. 方式，程度等(ad) chiefly 首要地-ly 3. 每隔...发生的(a) monthly 每月一次的-ment 行为，结果，手段(n) implement 工具-most 最... (a) utmost 极端的不是最高级-ness 性质，状态，程度(n) illness 疾病-or 1. 人(n) emperor 皇帝-or 2. 物(n) tractor 拖拉机-or 3. 状态，性质(n) color 颜色AmE-ory 1. 有...效果的(a) satisfactory 令人满意的-ory 2. ...的处所(n) category 目录-our 状态，性质(n) favour 好感BrE-ous 具有...特性的(a) dangerous 危险的-que 概念(n) techique 技巧-ress 阴性(n) actress 女演员-ry 1. 性质，行为(n) rivalry 敌对-ry 2. 境遇，身份(n) slavery 奴役-ry 3. 种类(n) jewelry 宝石-ry 4. 行业(n) forestry 林业-s 1. 构成复数名词(n) rockets 火箭-s 2. 第三人称单数(v) plays 玩-s 3. 构成副词(ad) indoors 在家-ship 1. 动作(n) courtship 求爱-ship 2. 身份(n) citizenship 公民身份-ship 3. 关系(n) friendship 友谊-sion 动作，状态(n) revision 复习-sis 性质，状态，动作(n) crisis 危机-some 引起的(a) troublesome 烦人的-teen 十... (num) fifteen 十五13~19-th 1. 行为，结果(n) death 死亡-th 2. 第... (num) sixth 第六基数个位≥4 -tic 有...性质的(a) romantic 浪漫的-tion 行为，状态，情况(n) contribution 贡献-tious 有...性质的(a) cautious 谨慎的-ty 1. 性质，情况(n) safety 安全-ty 2. ...十(num) ninety 九十20, 30, ..., 90-ure 结果，动作，过程(n) procedure 程序-ves 构成复数名词(n) calves 幼仔单数以f,fe结尾-ward 向，向...的(prep,a) backward 向后-wards 向(ad) skywards 朝上地-y 1. 充满，有...性质(a) handy 手巧的-y 2. 亲昵(n) kitty 猫咪-yst 1. 人(n) analyst 分析者-yst 2. 物(n) catalyst 催化剂。

air-tight double glazing window 密闭双层玻璃窗multiple glazing 多层玻璃; 多层玻璃窗multiple-glazing unit 多层玻璃窗outside glazing 外装玻璃法patent glazing 专利装玻璃配件; 无油灰镶玻璃法plate glazing 平板压光plate glazing calender 平板抛光机; 平板砑光机putty glazing 油灰镶玻璃法puttyless glazing 无油灰镶玻璃法rebate of glazing 镶嵌玻璃槽口reflecting glazing 反射窗玻璃salt glazing 盐釉self-glazing 自动研光spray glazing 喷釉法spraying glazing 喷釉anti-burglary glazing 防盗玻璃窗attack resisting glazing 防盗窗玻璃bead glazing 压条装配玻璃法body wetting before glazing 补水copper glazing 铜条嵌镶玻璃copperlight glazing 铜条嵌镶玻璃copperlite glazing 铜条装配玻璃corrugated roof glazing 瓦楞玻璃屋面direct glazing 无窗框安装法double glazing unit 双层中空玻璃double-glazing 双层玻璃13X 13X分子筛3A 3A分子筛4A 4A分子筛abbeive阻黏剂，防黏剂，分离剂ablation脱离，切除，消融abrasion磨耗，磨损，磨蚀abrasion hardness磨蚀硬度abrasion index磨损指数abrasion tester磨损实验机accelerateagingtest加速老化实验acetate乙酸盐，乙酸酯，乙酸根，乙酸基acetone丙酮acid resistance耐酸性acoustic声学的acrylic resin丙烯酸类树脂acrylic丙烯酸，亚克利acrylics丙烯酸acrylonitrile丙烯腈activation激活activator活化剂adduct加（成化）合物adhere黏合，黏附adhesion老化实验，老化检验adhesion黏合adhesion failure黏合破坏adhesion of rubber to metal橡胶和金属粘结adhesion promoter黏合增进剂，助黏剂adhesive黏合剂adsorbent吸附剂adsorption吸附affinity亲和性aluminum oxide氧化铝aluminum profile铝型材aluminum section铝型材aluminum shim/butyl spacer铝带丁基胶条，实唯高胶条aluminum spacer铝间隔条，槽铝式ambient noise环境噪音ambient temperature环境温度amorphous无定性的，非晶质的angstroms埃anhydrite无水石膏an nealed glass原片，普通玻璃an nealing退火，退火的an nealing lehr（隧道氏）退火窑（炉）an nealing point退火温度（相当黏度为1018泊）anodize阳极氧化anomaly异常AFG（American Float Glass）美国浮发玻璃公司Agate玛瑙Aging 陈化，老化aging resistance 耐老化性，老化性能aging test老化实验argon filled充氩气air adsorption气体吸附air barrier防漏气隔离层，隔离屏障，气挡air curing空气硫化，空气熟化air drying风干air filled充空气air infiltration空气渗透air infiltration空气渗透air side浮法玻璃生产中朝上的玻璃面air space空气层airflow气流alabaster雪花石膏，雪花石膏制的aldehydes醛aliphatic脂（肪）族化合物salkali碱alkali metal salt碱金属盐alkali resistance耐碱性alkalinity碱性，碱度alligatoring鳄纹alumina氧化铝aluminoborosilicate glass铝硼硅酸盐玻璃aluminosilicate glass铝硅酸盐玻璃aluminum铝anticracking agent防裂剂（橡胶）antimony oxide氧化镝antioxidant抗氧化剂application table操作台aqueous水的，含水的，水成的argon氩气arsenic砷arsenic trisulfide三氧化砷arsenious oxide五氧化二砷art glass艺术玻璃，镶嵌玻璃asphalt沥青柏油ASTM美国中空玻璃检测标Atmospheric or ozone cracking大气或臭氧（作用）龟裂，自然龟裂Atmospheric pressure大气压（力）Attenuation衰减物Autoclave高压釜Bback-bone 主链，主要成分，骨干，骨架back-fill 反填充，回填充bacteria细菌barium crown glass钡冕玻璃barium oxide氧化钡barometric pressure气压base基胶batch house料房，配料车间bath瑶池，池炉bending strength弯曲强度bent glass弯玻璃，弯玻bent spacer连续弯管金属隔条bentonite膨润土，皂土，浆土benzene苯benzene ring苯环beryllium铍Bicherous smiotios pocess比切罗克斯法，间歇压延法（平板玻璃）bitumen沥青，柏油bleeding增塑剂等渗出表面形成薄膜baistering起泡，气泡blocks玻璃支撑快bromine溴brookfield synchro-lectric visosimetre布鲁克菲尔德单圆筒黏度计brookfiled test布鲁克菲尔德检测Btu英国热量单位（=256Cal）Bubbing起泡Bloom起霜白化blown ware吹制的玻璃制品blue-line drawing蓝图blush起霜白化boiler gages锅炉表bond breakage键断裂bond strength键强度bonding agent键合剂，黏合剂borate硼酸盐borax硼砂boric acid硼酸boric oxide氧化硼boron硼borosilicate cwn硼硅酸盐冕玻璃brosiliceglass硼硅酸盐bow弯曲弓形box spacer槽铝式隔条brglass防弹玻璃breakage炸裂breaking stress极限应力，破裂应力breather tube呼吸管brewsters布鲁斯特，（光弹性单位）bullet resistant glass防弹玻璃bull’s eye后圆玻璃，圆快玻璃butadiene丁二烯butyl丁基胶butylene丁烯CCadmium镉Calcareous钙质，含钙的石灰的Calcium peroxide过氧化钙Calcium carbonate碳酸钙CAN/CGSB-12.8-97加拿检测标准大中空玻璃Canal arch通道拱Capillary毛细管Capillary tube unit安装毛细管的中空玻璃Carbon black碳黑carbon dioxide二氧化碳Cardinal IG 美国卡迪诺中空玻璃公司catalyst 催化剂，触媒，固化剂cathode 阴极caulk 堵缝，填隙cavity thickness 空腔厚度Celsius 摄氏cement 水泥，胶结剂，胶结，封接CEN 欧洲中空坡璃标准centigrade摄氏centipoise 厘泊（黏度单位）centre in tension 中央张力centre of the glass 玻璃中央chain stopper 链终止剂，止链剂chalcogenide glass 硫属玻璃chalking 粉化，起垩Charles ’s Law 查里定理checking 龟裂checking sunlight 日晒引起的龟裂chemical fogging 化学雾chemical resistance 耐化学性chemical strengthened glass 化学钢化玻璃chlorine 氯chord 弦chords弦circumference 圆周，周围clay 粘土，粘土质的clear glass 白玻，透明玻璃coadsorption 共吸附coating technology 镀膜技术cobalt 钴coefficient of expansion 膨胀系数cohesion 内聚cohesive failure 内聚失败cold edge 冷边cold flexibility 冷挠曲性cold flow 冷流cold resistant 抗冷性，耐冷度compatibility 相容性compatible spacer 相容间隔条compound curve 复合曲线（玻璃）compression modulus 压缩模量compression set 永入性破坏compressive strength 压强度compressive stress 压应力concave 凹的condensation 冷凝condensation gutter 冷凝水收集槽，沟conduction 传导conductivity 传导container stability (=shelf life ) 货架寿命contamination 污染continuos film 平整的薄膜，无断裂或针眼convection 对流conventional hot melt 普通热融胶，常规热融胶convex 凸cool light 冷光cooling 冷却copolymer （二元）共价物copper 铜comer key 插角correlation 相关corrosion resistance 抗腐蚀能力cracking 裂化，裂解，断裂，裂纹creep 蠕变critical temperature 临界温度crosslink 化学交联cross-linking agent 交联剂crown glass 冕法玻璃，人工吹制成的玻璃片crystal glass 晶质玻璃crystal structure 晶体结构crystallization 结晶，结晶作用，晶化cullet 碎玻璃，废玻璃（料）cumene hydroperoxide 氢过氧化枯烯curative 固化剂，硬化剂cure time 固化时间curing agent 触媒，固化剂curing mechanism 固化机制curtain wall 幕墙curved glass 异型玻璃cyclic wind loading 周期性风荷载cycling 循环cylinder glass 筒形玻璃，（吹制或拉制），圆筒法平板玻璃DDamping 缓冲，减震，阻尼Daylight 日光Dead air 静止空气Dead load 自重Decibel （dB）分贝Decorative glass 装饰玻璃，镶嵌玻璃Deflection 挠度，挠曲Delaminate 分层，脱层Delinerate 描绘，叙述，描外形Density 密度Depth 深度Desiccant 分子筛Design load 设计荷载Desorption 解吸附Dew point 露点Diameter 直径Diamond pyramid 金刚石锥硬度标Diaphram 横膈膜，隔膜，膜片Dichromate 重铬酸盐Dicing 骰子Dielectric 电介体，电介质；介电的Diffusion 扩散Diisocyanates 二异氰酸盐Diluent 稀释剂，冲淡剂Dilute 稀释Dilution 稀释Dimethyl ketone 二甲丙酮DIN 1286 德国中空玻璃标准1286 Dip coat 浸涂Disentangle 解开，清理Dispersion 色散，弥散]distribution 分布distortion 扭曲，畸变disulfide 二硫化物divider 除数，间隔物，隔板，划分者dolomite 白云石door-light 镶嵌玻璃drain line 流浆线道drawn glass 拉制玻璃drawn sheet glass 拉制平板玻璃drum 55加仑铁桶dry time 缺胶接头DSE 等同双道密封Dispersion 分散（作用），分散体，色散，离差Dual panes unit 双玻中空玻璃Dual panes 双玻中空玻璃Dual seal 双道密封Dual-sealed units 双道密封中空玻璃Dlurability 耐久性Durometer 硬度詈，硬度测验器Dynamic fatigue 动态疲劳EEdge clearance 边部间隙Edge cover 边部遮盖Edge of glass 玻璃边部Edge seal 边部密封Edge seal height 边部密封高度Edgetech IC 美国艾杰中空玻璃技术有限公司Elastic solid 弹性固体Elasticity 弹性Elastomer 高弹性Electromagetic 电磁的Elements 元素，自然界的风，雨，雪和雷电等Elongation 延伸Emery 刚玉粉，刚砂Emulsion 乳状液Enamel glass 釉彩玻璃Encyclopedia 百科全书Endothermic 吸热的Energy efficiency 能源效率Energy star 美国能源明星计划ENR 室外噪音评定ER （energy rating ）能源等级评定Erosion 腐蚀Ethylene 乙烯EWNR(exterior wall noise rating ) 外墙噪音评定Exhaling air 呼出空气Exothermic 放热的Exterior glazing 室外安装玻璃FFactory glazed 工厂安装玻璃Fahrenheit 华氏Failure analysis (water immersion technique) 失败分析Far ir 远红外Fatigue strength (疲劳强度)Faying surfaces 接触面Feeder 进料器，加料器Feldspar 长石Feldspathic 长石质的Fenestration 门窗Fiberglass 玻璃钢Filler 填料Filter cake 滤饼Fin 毛刺Fire-retardant material 阻燃材料Flame resistant 耐燃性（的）Flame retardant 阻燃剂Flash point 闪点，闪燃点Flat glass 平板玻璃Flaw 缺陷Flexible 弹性的Flexible silicone foam 弹性硅酮微孔间隔条，超级间隔条Flint glass 火石玻璃，无色玻璃Float glass 浮法玻璃Float process 浮法工艺Flow out 流出Flow point 玻璃的流动温度Fluorine 氟Fluxe 溶剂Fluxing agent 助熔剂Fog 雾Fogging unit 内侧雾化的中空玻璃Foot 英尺Forming roll 压延辊Four sides curtain wall 全隐式幕墙Fractography 断口组织试验，断口组织的显微镜观察Fracture 破碎，断面，断裂，破坏FRAME 计算机模拟热流的软件Frequency 频率Front end 窑前端Front gable – wall 前脸墙，端墙Frost poin 霜点Ft/reel英尺/轴Fulcrum支点Fumed silica 热解法二氧化硅，火成二氧化硅Fungi 霉菌Furnace 炉，窑Furnace floor 炉底，窑床Fusion 熔融，熔化GGallon 加仑Gas 气体，惰性气体Gas retention 惰性气体保持能力Gas –filled unit 充惰性气体的中空玻璃Gasket 玻璃密封胶条Geometry 几何Geolrgian bar 美隔条Germicidal 杀菌的Girth 曲线周长Glass blowetr 玻璃灯工，玻璃吹制工Glass breakage 玻璃炸裂Glass crtain wall 玻璃幕墙Glass edge seal 玻璃边缘密封Glass modulus 玻璃态模量Glass phase 玻璃相Glass point 玻璃点Glass ribbon 玻璃带，玻璃条Glass transit temperature 玻璃化温度Glass washer 玻璃清洗机Glassblowing 玻璃吹制Glass-making 玻璃制造Glassware 玻璃器皿Glazing bead 玻璃压条Glazing material 玻璃，玻璃密封材料Glazing rabbet 玻璃镶嵌槽Glazing system 玻璃装配系统Glossary 小辞典，词汇表Goblet 小料块（玻璃）料滴Gouges 表GPR (gas permeance rate )气体渗透率Green strength 初始湿强度Greenhouse 温室Grinding hardness 研磨硬度Grit 压痕硬度Grout 薄浆（水泥）GS(galvanized steel ) 镀锌钢Gun consistency 适用从胶枪嘴向外打胶的松软度Gypum 石膏HH.B.Fuller 美国富乐公司H.H(high temperature high humidity) 高温高温Hard coat 硬度膜Hardness 硬度Heat flow 热流Heat mirror 热境Heat press roller 热（辊）压机Heat resistance 抗热Heat treated 热处理Heating 供热Heat-seal 熔焊，熔接，热封Heat-strengthened glass 热增强玻璃，半钢化玻璃Heat-treated glass热处理玻璃Hermetic 气密的Hertz(HZ) 赫兹Heterogeneous 不均匀的，多相的Hiding power 遮盖的，覆盖力，盖底力，被覆盖High humidity testing 高湿试验HIGS 北美中空玻璃标准HI-TR 耐高热HMB 热融丁基胶Holiday 空胶，露布，露白，露胶Hook 钩Horizontal 水平的，卧式的Hot melt 热融胶Hot melt butyl 热融丁基胶Hot melt sealant 热融密封胶Humidity 温度Humidity aging 温度老化HVAC 中央空调Hydrocarbon 碳水化合物Hydrolytic 水解Hydrolytic resistance 抗水解Hydrolyzability 水解Hydrophilic action 亲水性，（的）反应，吸湿反应Hydroxides 氢氧化物Hydroxy 羟基IIdeal Gas Law理想气体定律LGMA（lnsulating Glass Manufuracturing Alliance）北美中空玻璃制造联盟LGU中空玻璃单元Impact 冲击Impact resistance抗冲击Impact strength 抗冲击强度Impart 给予，分给Impeller叶轮Imperial英制Incandescent lamp白炽灯Inch 英寸Incident noise 入射噪音Indentation hardness压痕硬度Inert gas惰性气体Infrared红外线Ingredient组分，成分Inhaling air吸入空气Initial初始的Initial dew point初始露点Inorganic无机的Inside temperature室内温度Insulating block 保温材料块Insulating glass中空玻璃Insulating value保温值Insulation material保温材料Intensity强度；密（集）度LnterceptTM U 型间隔条TM Interior glazing室内安装玻璃Intelayer夹胶，夹层Internal reflection内反射Internal strain内应变Internal stresse内应力Iodine碘Ion exchange离子交换Ion exchange process离子交换反应LR红外线Iron oxide氧化铁Isocyanate异氰酸盐（酯）Isoprene异戊二烯，丁二烯，甲基-1 Isostere（电子）等排物Isotherm等温线LJamp 边框KKaolin高岭土Kiln bottom窑底Knurl roll压花辊LLading （用勺子）舀（玻璃液）Laminated glass夹层玻璃Lap point搭接点，搭接面Lap shear搭接剪切实验LBNL (lawrence Berkerly National Laboratory)美国劳伦斯伯克利国家实验室Le Joint Francais(LJF)法国乐杰福密封胶有限公司Lead crystal铅晶质玻璃Lead oxide氧化铅Lead peroxide过氧化铅Lead –alkali –silicate glass铅碱硅盐酸玻璃Leaded glass含铅玻璃Lehr退火窑（炉）Leq等效声音级别Life exqectancy寿命期望值，期望寿命Lifting提升，举起，升起Limestone石灰石Lindemann glass林德曼玻璃（含X射线含锂铍硼玻璃）Linear thermal coefficient of expansion先性膨胀系数Lip瓶口Lite 玻璃Lithia氧化锂Live load活载荷，活负载Load荷载，载荷，负荷Load average平均荷载Location block定位块Logarithmics对数Longevity长久性，寿命Long-wave长波Low-Eglass低辐射玻璃Low-emissivty coatings低辐射镀膜Low-emissvity glass低辐射玻璃LOW-TR耐低热Lump起疙瘩，胶团，块Nnanometer纳米National Fenestration Rating Council美国国家门窗等级评定委员会negative pressure负压Neolithic新石器时代的，过时的neoprene氯丁橡胶，氯丁二烯橡胶neutral中性NFPA美国国家放火署NERC美国门窗等级评定委员会niter硝石nitrile rubber丁腈橡胶nitrogen氮气noble metal贵金属noise噪音noise control噪声控制noise factor噪声系数noise figure噪声疲劳noise insulation factor隔噪声因子noise level噪声级noise limitation噪声限度noise meter噪生计noise muffler噪声衰减器noise pollution噪声污染noise reduction噪声降低noise reduction coefficient降（低）噪（声）系数nominal strain名义应变nominal stress名义应力noncollapisible不可收缩的，不可折叠的noncrystalline 非晶体的nondrying不干性nonductile不可展伸的nonsag非下垂nonskinning表层不固化的nonstaining不污染的nontoxic无毒NR(noise reduction)降噪NRC(national research Council of Canada) 加拿大国家研究院Nylon尼龙QQuality质量Qualitycontrol质量控制Quantity数量Quartz石英RR＆D(research ＆development)研究与开发Rabbet platform玻璃镶嵌槽底片Radiation辐射Radii半径（单数）Radiology放射线Radius半径（单数）Rapid dew point drop漏点下降快Reactive反应型的Reactive hot melt反应型热融胶，湿气固化热融胶Reactor反应堆real-time实时refining end 澄清部，澄清带reflective glass反射镀膜玻璃refraction折射refractive index折射的，折射指数，折射率relative humidity(r.h)相对湿度residentail building名用住宅底层建筑residual water残余水resistor电阻，电阻器resonnating共振，共鸣reverberation混响reverse dual seal逆向双道密封rh相对湿度rheological流变的rheological agent流变剂rheological characteristic流变特性ribbon glass带状玻璃，玻璃带rigidity刚性rod棒料，棒，条roller press辊压rolling machine压铸机rolled glass压延玻璃room temperature室温residential民用的RTV(room temperature vulcanizing)室温硫化Rupture破裂，断裂，裂缝，裂口，洞穿Rutile titanium dioxide金红石型二氧化钛R-value热阻SSaflex首诺胶片Sag下垂度sagging下垂度salt spray test喷盐实验sand石英砂，砂子saturation equilibrium饱和均衡schematic示意图scrap glass废玻璃scratch划伤scratch hardness刮痕硬度，划痕硬度screw spline螺丝连接槽，连接键sea level海平面sealant密封胶sealed failure密封失败sealed insulating glass密封中空玻璃Sealed lnsulating Glass Manufacturers Associations美国中空玻璃制造商协会Sealed space密封空腔]Secondary seal 第二道密封Secondary sealant 第二道密封胶Seed灰泡小气泡Selenide 硒化物Self-cleaning glass 自清洁玻璃Semiconducting glass半导体玻璃Service termpreature工作温度Setting block玻璃支撑块SE6（sulfur hexaflouride）六氟化硫Shear剪切Shear strength 剪切强度Shelf aging搁置老化Shelf life货架寿命SHGC增阳系数Shore hardness A邵氏硬度AShort vinyl短胶Short wavelength 短波波长Shrinkage收缩Shut-off gate闸门，供料机闸砖（供料机上用）SIGMA美国中空玻璃制造商协会Silanol硅烷醇Silica gel硅胶Silicate glass 硅酸盐玻璃Silicone carbide炭化硅Silicone structural seal 硅酮结构胶Silicone weatherseal硅酮耐候胶Silicone硅酮胶Sill 窗台（板），窗口Silimanite 硅线石Simulation 模拟Single pane 单片玻璃Skid托盘Slab （厚）板玻璃，玻璃砖Slag炉底玻璃；炉渣，矿渣Sloped glazed倾斜似玻璃装配Slot 缝Slump 下垂度Smart glass 智能玻璃Smart window 智能窗Snap-oncover cap 扣入式外盖Soda(sodium carbonate) 碳酸钠Soda ash苏打灰Soda ash glass钠玻璃Soda lime glass钠钙玻璃Soda-lime-silica glass 钠钙硅酸盐玻璃Sodium gydroxide氢氧化钠，苛性钠，烧碱Sodium oxide氧化钠Sodium si9licate 钠硅酸盐Soft coat 软镀膜Softening point 软化点，软化温度Solar energy太阳能Solar rediation 太阳辐射Solar tranmittance 太阳投射比Solar transmission 太阳投射Solidify 使凝固，凝结，固化Sovent 溶剂Sound 声音Sound absorption 声吸收Sound absorption coefficient吸声系数Sound contral glass声控玻璃Sound diffusion 声发散Soun energy 声能Sound energy density 声能密度Sound energy fllux 声能通量Sound grating 声栅Sound level 声级Sound proof 不透声的Sound source 声源Sound spectrum 声谱Sound wave 声波Soupy 胶浆的Spacer 间隔条，中空玻璃间隔条Spacer depth 间隔条深度，间隔条高度Spacer height间隔条高度Spacer width间隔条宽度Spandrel glass安装在建筑物外墙不见光的无光泽玻璃Sparklike芬兰斯巴莱克公司Specific adhesion特性黏合，比黏合Specific gravity 比重Specific heat 比熟Specimen 样品Spectrophotometry 分光光度测定（法）Splotch污点，（渍，痕），斑点Spout 料盘，流料槽Spout cover 供料池盖砖Spun glass 玻璃纤维，玻璃丝Sputter-coated low –e 阴极溅射低辐射镀膜Ss(stainless steel) 不锈钢Stained glass 彩色玻璃Stainless steel 不锈钢Stainless steel spacer 不锈钢间隔条Standard deviation 标准差Starved joint 缺胶接头Stc(sound transmission coefficient) 声透射系数Stearic acid硬脂酸，十八（烷）酸Sticky 胶黏的Stiffener 加强筋Stiffness 挺度，劲度，僵硬度Straight chain 直链Strain 应变Stain point 应变点Strength 强度Stree应力Structural design结构设计Structural sealant glazed system(SSG)结构胶玻璃装配系统Structural strength 结构强度Substrate基材Sulfides 硫化物Sulfric acod 硫酸Super spacer 超级间隔条Surface flaw 表面缺陷Surface in compression 表面压应力Surface temperature 表面温度Surface tension 表面张力Suspended glazing 吊挂似玻璃装配Swiggle stripTM 实维高胶条、舒适胶条Synthetic 人工复合TTack free 表干Tangent 正切Target 靶Tear strength 剪切强度Technical data 技术数据Tellurite glass 碲玻璃Tempered glass 钢化玻璃Tensile modulus 拉伸模量Tensile streength 拉伸强度Tension 张力拉伸Terminology 术语Test apparatus 实验仪器Tetrahedral 四面体的Tetramethyl 四甲基Tetramethyl thiuram disulfide 二硫化四甲基秋兰姆Thermal aging 热老化Thermal analysis 热分析Thermal break 热炸裂Thermal conductance 热传导Thermal conductivity coefficient 热传导系数Thermal contraction 热收缩Thermal diffusivity 热扩散系数Thermal energy热能Thermal shock 热冲击Thermal shock resistance 抗热冲击阻力Thermal syrain 热应变Shermal stress 热应力Thermal value 热值Thermo set 热固Thermocouple 电热偶Thermoplastic热塑Thiokol 聚硫胶，聚硫橡胶，乙硫橡胶Thiuram type accelerator 秋兰姆类促进剂Thixotrope 触变胶Thixotropic 触变（的），具有触变作用的Thixotropic agent 触变剂Thixotropy 触变性Thixotropy factor 触变系数Thixotropy index 触变指数Thorium 钍Threshold 限度，界限Tin bath 锡槽Tin catalyst 锡触媒Tint glass 本体着色玻璃Tint 着色，色彩，色调Titania 氧化钛Titanium dioxide 二氧化钛，钛白Toluene 甲苯Toughened gloass 强化玻璃Transformation temperature （玻璃的）转变温度Translucent 半透明的Transparency 透明度Transverse seam 横向缝Tray bar 接料板Tray roiier 传送辊Triple pane unit 三玻中空窗Triple panes三玻中空窗Trowel镘刀，抹平刀Trowelling 抹涂，镘涂Tubing 管，管道，制管Tungsten 钨Tweel炉闸口Two sides curtain wall 半隐式幕墙Two-component 双组分UUltimate elongation 极限伸长Ultraviolet 紫外线Ultravioet light 紫外线灯Ultraviolet-transmitting glass 透紫外线玻璃Unalterate 未改变的，不变的Undestructive argon 非破坏性氩气分析仪Undulating current 波荡电流Uniform loading均匀负荷Uniform thickness 均匀厚度United inches 玻璃的一个边长和边宽之和UOP美国环球分子筛公司Uv-lamp 紫外线灯U-value U值VVentilation 通风Vertical 垂直的，立式的Vertical mullion 竖框Vibrate 振动Vinyl 乙烯基，聚氯乙烯Virus 病毒Viscoelasticity 黏弹性Viscometer 黏度计Viscosimeter黏度计Viscosity 黏度Viscous 黏（滞）的Visible 可见的Visible light 可见光Vistanex 聚异丁烯Visual distortion 视觉变形Vitreous 熔融状，玻璃状的，玻化Volatile 挥发的，易挥发的Volatile fogging 挥发化学物Volatile outgassing 挥发气体外泄Vulcanization 硫化，硬化Vulcanize硫化，硬化WWaisting 细腰玻璃Warm edge 暖边Warm edge technology 暖边技术Warp 玻璃状板；光学扭曲，翘曲Warranty 质保书Water immersion 浸水Wavelength 波长Weather cycling 气候循环实验，气候循环检测Weatherometer 老化实验机Wedge 锲，锲入Weep 漏（泄渗）水Weep hole 排水孔Weep slot 槽形排水孔WET(warm edge technology) 暖边技术Wetting 润湿White room 绝尘室，无尘室Wind load 风荷载Windborne 住链，主要成分；骨干；骨架Wire glass 夹丝玻璃Work life 操作时间XXenon gas 疝气x-ray leaded glass 防X射线含铅玻璃x-ray protction 防X射线x-ray shielding X射线屏障xylene 二甲苯YYield strength 屈服强度Yong＇s modulus 杨模量ZZeolite 沸石Zinc oxide 氧化锌Zirconium oxide 氧化锆γ-glycidoxpropyltimethoxysilane γ-环氧丙氧丙基三甲氧基硅脘IIdeal Gas Law理想气体定律LGMA（lnsulating Glass Manufuracturing Alliance）北美中空玻璃制造联盟LGU中空玻璃单元Impact 冲击Impact resistance抗冲击Impact strength 抗冲击强度Impart 给予，分给Impeller叶轮Imperial英制Incandescent lamp白炽灯Inch 英寸Incident noise 入射噪音Indentation hardness压痕硬度Inert gas惰性气体Infrared红外线Ingredient组分，成分Inhaling air吸入空气Initial初始的Initial dew point初始露点Inorganic无机的Inside temperature室内温度Insulating block 保温材料块Insulating glass中空玻璃Insulating value保温值Insulation material保温材料Intensity强度；密（集）度LnterceptTM U 型间隔条TM Interior glazing室内安装玻璃Intelayer夹胶，夹层Internal reflection内反射Internal strain内应变Internal stresse内应力Iodine碘Ion exchange离子交换Ion exchange process离子交换反应LR红外线Iron oxide氧化铁Isocyanate异氰酸盐（酯）Isoprene异戊二烯，丁二烯，甲基-1Isostere（电子）等排物Isotherm等温线。