塑胶热膨胀计算公式

零件热装孔膨胀量计算公式引言。

在工程设计和制造中，热装孔膨胀量是一个非常重要的参数。

它是指在零件热装孔的过程中，由于温度变化导致孔的尺寸发生变化的现象。

为了有效地控制零件的尺寸变化，需要准确地计算热装孔膨胀量。

本文将介绍零件热装孔膨胀量的计算公式，并对其进行详细的解析。

热装孔膨胀量计算公式。

零件热装孔膨胀量可以通过以下公式来计算：ΔL = α L ΔT。

其中，ΔL为热装孔膨胀量，单位为米；α为材料的线膨胀系数，单位为1/℃；L为热装孔的长度，单位为米；ΔT为温度变化量，单位为℃。

以上公式是根据线膨胀系数的定义和热膨胀原理推导出来的。

线膨胀系数是一个材料特性参数，它描述了材料在单位温度变化下长度的变化量。

通过这个公式，我们可以准确地计算出零件在热装孔过程中的尺寸变化量。

公式解析。

1. 线膨胀系数。

线膨胀系数是一个材料的重要特性参数。

它描述了材料在温度变化下长度的变化量。

线膨胀系数的大小与材料的性质有关，通常可以在材料的技术手册或标准中找到。

在实际计算中，需要根据具体的材料来确定其线膨胀系数。

2. 热装孔长度。

热装孔长度是指在零件热装孔的过程中，孔的长度。

在实际计算中，需要准确地测量热装孔的长度，并将其代入到公式中进行计算。

3. 温度变化量。

温度变化量是指在零件热装孔的过程中，温度的变化量。

在实际计算中，需要准确地测量温度的变化量，并将其代入到公式中进行计算。

通过以上公式的解析，我们可以看到热装孔膨胀量的计算是一个比较简单的过程。

只需要准确地测量材料的线膨胀系数、热装孔的长度和温度变化量，就可以通过公式计算出热装孔膨胀量。

应用实例。

为了更好地理解热装孔膨胀量的计算公式，我们可以通过一个应用实例来进行说明。

假设有一块钢材，在温度从20℃升高到100℃的过程中，其线膨胀系数为1.2×10^-5/℃，热装孔的长度为10cm。

我们需要计算在这个过程中，钢材的热装孔膨胀量。

根据上述公式，我们可以进行如下计算：ΔT = 100℃ 20℃ = 80℃。

thermal expansion coefficient物体由于温度改变而有胀缩现象。

其变化能力以等压(p一定)下，单位温度变化所导致的体积变化，即热膨胀系数表示热膨胀系数有体膨胀系数β和线膨胀系数热α。

体膨胀系数β=ΔV/(V*ΔT)，线膨胀系数α=ΔL/(L*ΔT)，式中ΔV为所给温度变化ΔT下物体体积的改变，V为初始体积；ΔL为所给温度变化ΔT下物体长度的改变，L为初始长度。

严格说来，上式只是温度变化范围不大时的微分定义式的差分近似；准确定义要求ΔV与ΔT无限微小，这也意味着，热膨胀系数在较大的温度区间内通常不是常量。

温度变化不是很大时，α就成了常量，利用它，可以把固体和液体体积膨胀表示如下：Vt=V0(1+3αΔT)，而对理想气体，Vt=V0(1+0.00367ΔT)；Vt、V0分别为物体末态和初态的体积对于可近似看做一维的物体，长度就是衡量其体积的决定因素，这时的热膨胀系数可简化定义为：单位温度改变下长度的增加量与的原长度的比值，这就是线膨胀系数。

对于三维的具有各向异性的物质，有线膨胀系数和体膨胀系数之分。

如石墨结构具有显著的各向异性，因而石墨纤维线膨胀系数也呈现出各向异性，表现为平行于层面方向的热膨胀系数远小于垂直于层面方向。

宏观热膨胀系数与各轴向膨胀系数的关系式有多个，普遍认可的有Mrozowski算式：α=Aαc+(1-A)αaαa,αc分别为a轴和c轴方向的热膨胀率，A被称为“结构端面”参数。

编辑本段各种金属的线性膨胀系数测定温度条件及单位：20℃，10^-6K^-1金属名称元素符号线性热膨胀系数金属名称元素符号线性热膨胀系数铍Be 12.3 铝Al 23.2锑Sb 10.5 铅Pb 29.3铜Cu 17.5 镉Cd 41.0铬Cr 6.2 铁Fe 12.2锗Ge 6.0 金Au 14.2铱Ir 6.5 镁Mg 26.0锰Mn 23.0 钼Mo 5.2镍Ni 13.0 铂Pt 9.0银Ag 19.5 锡Sn 2.0 编辑本段常见液体的体膨胀系数测定温度条件：20℃，单位：1/℃（1/K）汞（水银）0.00018水0.000208丙三醇（甘油）0.00050浓硫酸0.00055乙二醇0.00057苯胺0.00085二甲苯0.00085汽油0.00095松节油0.00100煤油0.00100甲苯0.00108乙醇（酒精）0.00109乙酸0.00110溴0.00110正辛烷0.00114三氯乙烯0.00117甲醇0.00118二硫化碳0.00119四氯化碳0.00122正庚烷0.00124苯0.00125氯仿0.00127乙酸乙酯0.00138丙酮0.00143乙醚0.00160。

物体的膨胀与热膨胀系数的计算物体的膨胀是指物体在受热或受冷时发生的体积变化。

膨胀是一个普遍存在的现象，我们可以通过热膨胀系数来计算物体的膨胀程度。

一、膨胀与热膨胀系数的概念热膨胀系数是一个用于衡量物体在温度变化下的膨胀程度的物理量。

它表示单位温度变化时物体相对于其原始长度或体积的变化比例。

膨胀系数通常用α表示，单位是1/℃或℃^-1。

对于长度膨胀，我们用线膨胀系数α_l表示；对于体积膨胀，我们用体积膨胀系数α_v表示。

二、线膨胀系数的计算公式线膨胀系数α_l可以通过以下公式进行计算：α_l = ΔL / (L * ΔT)其中，ΔL表示长度变化量，L表示原始长度，ΔT表示温度变化量。

三、体积膨胀系数的计算公式体积膨胀系数α_v可以通过以下公式进行计算：α_v = ΔV / (V * ΔT)其中，ΔV表示体积变化量，V表示原始体积，ΔT表示温度变化量。

四、膨胀系数的实际应用膨胀系数在工程学、物理学等领域有着广泛的应用。

例如，建筑工程中，膨胀系数的计算可以帮助我们预测建筑材料在不同温度下的膨胀和收缩，从而避免因温度变化引起的损害；在热力学研究中，膨胀系数可以用来计算物体在热力学循环中的温度变化和体积变化。

膨胀系数还可以用于设计热膨胀补偿装置，例如管道系统中的膨胀节，用来克服由于温度变化而引起的管道的热膨胀。

五、常见物体的膨胀系数不同物体的膨胀系数各不相同，下面是一些常见物体的线膨胀系数α_l的范围：- 铝：23×10^-6/℃- 铜：16×10^-6/℃- 黄铜：18×10^-6/℃- 钢：12×10^-6/℃- 玻璃：8×10^-6/℃- 混凝土：7×10^-6/℃对于体积膨胀系数α_v，可以通过以下公式与线膨胀系数α_l之间进行转换：α_v = 3α_l六、总结物体的膨胀是受热或受冷时发生的体积变化现象，可以通过热膨胀系数来计算物体的膨胀程度。

热学解题技巧热膨胀和热传导的计算热学解题技巧：热膨胀和热传导的计算热学是物理学的重要分支，研究能量传递和转换的规律。

在热学问题解题过程中，热膨胀和热传导是两个重要的计算内容。

本文将介绍有关热膨胀和热传导计算的一些技巧和方法。

热膨胀的计算：热膨胀是指物体由于温度升高而引起的尺寸变化。

在计算热膨胀问题时，我们首先需要了解两个重要的物理量，即热膨胀系数和温度变化量。

热膨胀系数是描述物体膨胀或收缩程度的物理量，通常用符号α表示。

不同物质的热膨胀系数存在差异，因此在计算之前需要查阅相关资料或者题目中已给出。

热膨胀系数的单位是1/℃（开尔文）。

温度变化量是指物体温度的变化程度，通常用符号ΔT表示。

将物体的初温度记为T1，末温度记为T2，则温度变化量ΔT等于T2减去T1的差。

在计算物体的热膨胀量时，我们可以使用如下公式：ΔL = αL0ΔT 其中，ΔL表示物体的长度变化量，α是物体的热膨胀系数，L0是物体的初始长度，ΔT是温度变化量。

这个公式可以用于计算线性膨胀、面积膨胀和体积膨胀的情况。

在实际计算时，需要根据题目中给出的具体条件选择适当的公式进行计算。

热传导的计算：热传导是指物体内部或不同物体之间发生的热量传递过程。

在计算热传导问题时，我们需要了解几个重要的物理量，包括热传导系数、面积、厚度和温度差。

热传导系数是描述物质导热性能的物理量，通常用符号λ表示。

不同物质的热传导系数也存在差异，因此在计算之前需要查阅相关资料或者题目中已给出。

热传导系数的单位是W/(m·℃)（瓦特/米·开尔文）。

面积是指热传导过程中参与传热的物体或物体表面的面积。

通常用符号A表示，其单位是平方米（m^2）。

厚度是指热传导物体的厚度，通常用符号d表示，其单位是米（m）。

温度差是指热传导过程中参与传热的物体（或者不同物体之间）的温度差，通常用符号ΔT表示。

在计算热传导问题时，我们可以使用如下公式：Q = λAΔT/d其中，Q表示传热速率或单位时间内传热的热量，λ是物质的热传导系数，A是热传导面积，ΔT是传热物体之间的温度差，d是传热物体的厚度。

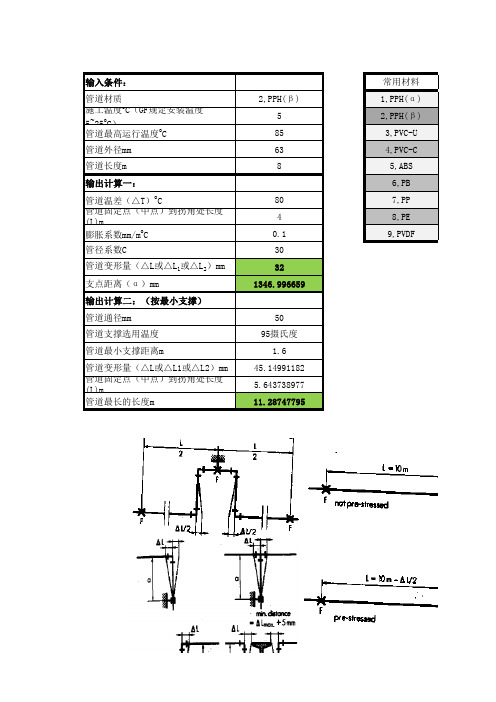
输入条件：常用材料管道材质2,PPH(β)1,PPH(α)施工温度o C（GF规定安装温度52,PPH(β) 5~25o C）管道最高运行温度o C853,PVC-U 管道外径mm634,PVC-C 管道长度m85,ABS 输出计算一：6,PB管道温差（△T）o C807,PP管道固定点（中点）到拐角处长度48,PE (L)m膨胀系数mm/m o C0.19,PVDF 管径系数C30管道变形量（△L或△L1或△L2）mm32支点距离（α）mm1346.996659输出计算二：（按最小支撑）管道通径mm50管道支撑选用温度95摄氏度管道最小支撑距离m 1.6管道变形量（△L或△L1或△L2）mm45.14991182管道固定点（中点）到拐角处长度5.643738977(L)m管道最长的长度m11.28747795膨胀系数mm/m o C管径系数C0.1330公称直径mm管道外径法兰公称压力0.1302532PN10 0.0833.53240PN10 0.07354050PN10 0.132.75063PN10 0.13106575PN10 0.15308090PN10 0.226100110PN10 0.1821.7100125PN10125140PN10150160PN10150180PN10200200PN10200225PN10250250PN10300315PN10350355PN10400400PN10450450PN3.2500500PN3.2550560PN3.2600600PN3.2700700PN3.2800800PN3.2PP,PE,PVDF管道最小支撑距离备注40摄氏度60摄氏度80摄氏度95摄氏度1.8 1.6 1.5 1.31.9 1.7 1.6 1.41.9 1.7 1.6 1.42.4 2.12 1.62.4 2.12 1.62.8 2.5 2.3 1.93.2 2.8 2.7 2.43.2 2.8 2.7 2.43.2 2.8 2.7 2.43.2 2.8 2.7 2.43.2 2.8 2.7 2.44 3.5 3.3 2.94 3.5 3.3 2.94 3.5 3.3 2.94 3.5 3.3 2.94.4 3.8 3.5 3.24.4 3.8 3.5 3.2可与DN450 PN10法兰配套 4.4 3.8 3.5 3.2可与DN500 PN10法兰配套 4.4 3.8 3.5 3.2可与DN600 PN10法兰配套 4.4 3.8 3.5 3.24.4 3.8 3.5 3.24.4 3.8 3.5 3.24.4 3.8 3.5 3.2。

机台吨位时间1805.9机台吨位开合模时间K1 成型热膨胀系数1mm/℃12.8120 5.2K2 射出速率系数3000150 5.6V 射出速率（cm 3/s)100180 5.9 塑胶密度（g/cm3)0.92250 6.9m 产品总重（g)（整模含水口）2302857.33007.53207.8注塑机台成本＝每分钟机台成本/60*注塑周期时间/模穴数吨位（T）功率每小时成本每分钟成本7511.05350.58310011.05400.66715015.18500.83318017.08550.91722024.8760 1.00028028.6375 1.25045031.581051.750例：100吨机台注塑8穴PP按头周期20秒＝0.667/60*20/8＝0.02778开合模时间3.0锁模力计算=500kg/cm3*投影面cm2*模具穴数*安全系数例：某ABS胶件，长12cm宽8cmm,中间有一个4*3cm孔，模具1*2锁模力＝500*（12*8－4*3）*2*1.1 ＝ 84000kg≈90~100吨机台10.7射胶时间最大壁厚2.2胶料热导系数0.065Tc 熔胶温度℃215Tm 模具温度℃40Tx 热变形温度℃85成型热膨胀系数ABS： 0.000078热变形温度℃PC: 130 ℃PP： 0.000128ABS： 88PMMA：0.000085AS： 95PA： 0.000120HDPE：80PE： 0.000195LDPE：50POM： 0.000149PCTA：75AS： 0.000070PMMA：100POM： 120PP： 85K胶： 75射出速率系数ABS： 60胶料热导系数PC: 0.105mm2sec-1PP： 0.000128ABS： 0.08PMMA：0.000085POM： 0.06PA： 0.000120PP: 0.065PE： 0.000195PS: 0.08POM： 0.000149LDPE: 0.096AS： 0.000070HDPE: 0.08PMMA: 0.075PA6: 0.092PA66: 0.07PA6+30%GF: 0.063PA66+30%GF: 0.06冷却时间8.7保压时间8.6生产周期时间26.2。

thermal expansion coefficient物体由于温度改变而有胀缩现象。

其变化能力以等压(p一定)下，单位温度变化所导致的体积变化，即热膨胀系数表示热膨胀系数有体膨胀系数β和线膨胀系数热α。

体膨胀系数β=ΔV/(V*ΔT)，线膨胀系数α=ΔL/(L*ΔT)，式中ΔV为所给温度变化ΔT下物体体积的改变，V为初始体积；ΔL为所给温度变化ΔT下物体长度的改变，L为初始长度。

严格说来，上式只是温度变化范围不大时的微分定义式的差分近似；准确定义要求ΔV与ΔT无限微小，这也意味着，热膨胀系数在较大的温度区间内通常不是常量。

温度变化不是很大时，α就成了常量，利用它，可以把固体和液体体积膨胀表示如下：Vt=V0(1+3αΔT)，而对理想气体，Vt=V0(1+0.00367ΔT)；Vt、V0分别为物体末态和初态的体积对于可近似看做一维的物体，长度就是衡量其体积的决定因素，这时的热膨胀系数可简化定义为：单位温度改变下长度的增加量与的原长度的比值，这就是线膨胀系数。

对于三维的具有各向异性的物质，有线膨胀系数和体膨胀系数之分。

如石墨结构具有显著的各向异性，因而石墨纤维线膨胀系数也呈现出各向异性，表现为平行于层面方向的热膨胀系数远小于垂直于层面方向。

宏观热膨胀系数与各轴向膨胀系数的关系式有多个，普遍认可的有Mrozowski算式：α=Aαc+(1-A)αaαa,αc分别为a轴和c轴方向的热膨胀率，A被称为“结构端面”参数。

编辑本段各种金属的线性膨胀系数测定温度条件及单位：20℃，10^-6K^-1金属名称元素符号线性热膨胀系数金属名称元素符号线性热膨胀系数铍Be 12.3 铝Al 23.2锑Sb 10.5 铅Pb 29.3铜Cu 17.5 镉Cd 41.0铬Cr 6.2 铁Fe 12.2锗Ge 6.0 金Au 14.2铱Ir 6.5 镁Mg 26.0锰Mn 23.0 钼Mo 5.2镍Ni 13.0 铂Pt 9.01银Ag 19.5 锡Sn 2.0 编辑本段常见液体的体膨胀系数测定温度条件：20℃，单位：1/℃（1/K）汞（水银）0.00018水0.000208丙三醇（甘油）0.00050浓硫酸0.00055乙二醇0.00057苯胺0.00085二甲苯0.00085汽油0.00095松节油0.00100煤油0.00100甲苯0.00108乙醇（酒精）0.00109乙酸0.00110溴0.00110正辛烷0.00114三氯乙烯0.00117甲醇0.00118二硫化碳0.00119四氯化碳0.00122正庚烷0.00124苯0.00125氯仿0.00127乙酸乙酯0.00138丙酮0.00143乙醚0.00160。

常用塑料的热膨胀系数1哎，说到塑料的热膨胀系数，这事儿我可真得好好说说。

你知道，我最近在帮朋友装修房子，他问我：“这塑料管子能埋墙里吗？会不会冬天一冷就裂了，夏天一热就变形啊？”我一听，得，这问题挺专业啊，我得给他好好讲讲。

2首先，咱们得搞清楚啥是热膨胀系数。

简单来说，就是材料在受热时体积或长度的变化程度。

塑料作为一种常用材料，它的热膨胀系数对咱们日常生活影响还真不小。

比如说，塑料容器、塑料管道，甚至是塑料家具，都会受到温度变化的影响。

3我记得有一次，我在家里用塑料盒加热食物，结果拿出来的时候，发现盒子竟然有点变形了。

我心想，这塑料的热膨胀系数还真不是盖的，连微波炉的热量都能让它变形。

4我那朋友听了，更担心了：“那这塑料管子，会不会冬天一冷就变脆，夏天一热就变软啊？”我告诉他，不同的塑料，热膨胀系数也不一样。

比如，聚乙烯（PE）的热膨胀系数就比较低，适合做管道；而聚氯乙烯（PVC）的热膨胀系数就比较高，受温度影响更大。

5我给他举了个例子：“你看，冬天的时候，室外的PVC管道可能会变硬变脆，一不小心就容易裂；而夏天，它们又可能会变软，甚至变形。

所以，选材料的时候，得根据实际情况来。

”我那朋友听了，若有所思地点点头。

6我还告诉他，现在市面上有很多改性塑料，它们的热膨胀系数可以调整到接近金属，这样就能更好地适应温度变化。

我那朋友眼睛一亮：“那这改性塑料得多贵啊？”我笑了笑：“价格嘛，肯定会比普通塑料贵点，但考虑到使用寿命和安全性，还是很划算的。

”7我那朋友听了我的解释，终于松了口气：“行，那我就用你说的那个聚乙烯管子，虽然贵点，但放心。

”我点点头：“对，选材料，不能只看价格，还得考虑性能和安全性。

”8通过这次经历，我发现，塑料的热膨胀系数对咱们的生活影响还真挺大的。

别看塑料轻巧方便，但在使用的时候，还是得根据具体情况选择合适的材料。

9所以，我想说的是，下次你们在选择塑料制品的时候，不妨多留意一下它们的热膨胀系数。

c17300 热膨胀系数热膨胀系数是描述物体在温度变化下尺寸变化的一个物理量。

它表示单位温度变化下物体长度、面积、体积等属性的变化。

下面我们将详细介绍热膨胀系数的定义、计算方法和应用。

1. 定义：热膨胀系数是指物体的长度、面积或体积在温度变化下单位温度变化所引起的相对变化。

常用的热膨胀系数有线膨胀系数、面膨胀系数和体膨胀系数。

线膨胀系数表示单位长度的物体在温度变化前后的长度增加或减小的比例。

面膨胀系数表示单位面积的物体在温度变化前后的面积增加或减小的比例。

体膨胀系数表示单位体积的物体在温度变化前后的体积增加或减小的比例。

2. 计算方法：线膨胀系数的计算方法为：线膨胀系数= ΔL / (L0 × ΔT)，其中ΔL为温度变化前后的长度变化值，L0为温度变化前的长度，ΔT为温度变化。

面膨胀系数和体膨胀系数的计算方法类似。

面膨胀系数= ΔA / (A0 × ΔT)，体膨胀系数= ΔV / (V0 × ΔT)，其中ΔA为温度变化前后的面积变化值，A0为温度变化前的面积，ΔV为温度变化前后的体积变化值，V0为温度变化前的体积。

热膨胀系数通常以摄氏度（℃）或开尔文（K）为单位。

摄氏度和开尔文的温度变化是一一对应的，所以在温度变化时可以通用。

3. 应用：热膨胀系数在工程和科学研究中具有广泛的应用。

以下是一些常见的应用领域：(1) 结构工程：在建筑物和桥梁等结构工程中，考虑到温度变化对构件的影响是非常重要的。

通过测量材料的热膨胀系数，可以设计出更稳定和安全的结构。

(2) 电子技术：电子设备中的元件在工作时会产生热量，温度的变化会对元件的性能产生影响。

了解材料的热膨胀系数可以设计出更稳定的电子设备和电路。

(3) 制造业：在机械制造和精密加工中，精确控制材料的尺寸变化对产品的质量至关重要。

热膨胀系数可以帮助制造业准确预测材料在不同温度下的尺寸变化，并采取相应的措施来保证产品质量。

(4) 材料科学研究：热膨胀系数是研究材料热力学性质的重要参数之一。

热的膨胀和膨胀系数的计算材料的热膨胀是指由于温度的升高，材料的长度、面积或体积增加的现象。

膨胀系数是一个材料的性质，用来描述其对温度变化的敏感度。

本文将介绍热膨胀的基本原理以及如何计算膨胀系数。

一、热膨胀的原理根据热力学原理，物质的温度升高会导致分子的热运动增强，分子之间的相互作用力减弱，使材料的体积、长度或面积增大。

不同材料的热膨胀性能可能有所不同，这取决于其结构、成分和弹性模量等因素。

热膨胀是一种普遍存在于物质中的现象，对于工程设计和材料选择具有重要意义。

二、线膨胀系数的计算线膨胀系数（α）是描述材料在一定温度下单位长度的膨胀量。

通常用公式表示为：ΔL = αL₀ΔT其中，ΔL是材料长度的变化量，L₀是初始长度，ΔT是温度的变化量。

根据单位换算，线膨胀系数的单位通常是1/℃或者K⁻¹。

线膨胀系数可以通过实验测量或者查阅资料获得，常见材料的线膨胀系数如下：- 钢：11x10⁻⁶ /℃- 铝：23x10⁻⁶ /℃- 铜：16x10⁻⁶ /℃- 玻璃：8x10⁻⁶ /℃三、体膨胀系数的计算体膨胀系数（β）用于描述材料在一定温度下单位体积的膨胀量。

通常用公式表示为：ΔV = βV₀ΔT其中，ΔV是材料体积的变化量，V₀是初始体积，ΔT是温度的变化量。

与线膨胀系数类似，体膨胀系数的单位也是1/℃或者K⁻¹。

体膨胀系数可以通过实验测量或者查阅资料获得，常见材料的体膨胀系数如下：- 钢：3x10⁻⁵ /℃- 铝：7x10⁻⁵ /℃- 铜：5x10⁻⁵ /℃- 玻璃：9x10⁻⁶ /℃四、应用实例假设我们有一根长度为1m的铁管，将其加热到100℃，我们可以根据铁的线膨胀系数计算出其长度的变化量：ΔL = αL₀ΔT= 11x10⁻⁶ /℃ x 1m x 100℃= 0.011m因此，铁管的长度将增加0.011m。

同样地，我们也可以计算铁管的体积变化量：ΔV = βV₀ΔT= 3x10⁻⁵ /℃ x (1m)³ x 100℃= 0.03m³铁管的体积将增加0.03m³。