Special Topics II Algorithms and Numerical Recipes of Integration

Hilbert空间中广义变分不等式的近似-似投影算法陈方琴;夏福全【摘要】In this paper, we consider the proximal projected-like method for solving generalized variational inequalities in Hilbert spaces. This method includes proximal method and projected-like method. At first, we obtain temporary iteration points by using proximal method, and then by using the projected-like method, we project the temporary point onto the feasible set of generalized variational inequalities to get the next iterative point. Under the assumptions that the set-valued mapping is maximal monotone, we prove that every weak accumulation point of the sequence is a solution of variational inequalities. Finally, under the condition that the distance-like function is a special function, we prove that the sequence has a unique weak accumulation point.%在Hilbert空间中研究了广义变分不等式解的近似-似投影算法,该算法包含了近似点算法和似投影算法.首先通过近似算法,获得暂时迭代点,然后利用似投影算法将该暂时的迭代点投影到广义变分不等式的可行集上,获得下一步的迭代点.在集值映象为极大单调的条件下,证明了迭代序列的任意弱聚点都是变分不等式的解.最后,在取特殊的似距离泛函的情况下证明了序列具有唯一的弱聚点.【期刊名称】《四川师范大学学报（自然科学版）》【年(卷),期】2012(035)003【总页数】6页(P297-302)【关键词】近似点算法;似投影算法;似距离泛函;极大单调映象【作者】陈方琴;夏福全【作者单位】四川师范大学数学与软件科学学院,四川成都 610066;四川师范大学数学与软件科学学院,四川成都 610066【正文语种】中文【中图分类】O176.3;O178设H为Hilbert空间，X为H中的非空闭凸子集，T：X→2H为集值映射.本文研究下列广义的变分不等式问题：求x*∈X，w*∈T(x*)，使得本文始终假设广义变分不等式问题(1)的解集S非空，并且X∩int(dom(T))≠Ø，或int(X)∩dom(T)≠Ø，其中广义变分不等式问题(1)在经济平衡、运筹学、数学物理等方面都有着广泛的应用［1］.同时，广义变分不等式问题(1)也和许多非线性问题有密切的关系，如相补问题、平衡问题、不动点理论等［2-3］.特别地，当 T是真凸下半连续泛函 f：H→R∪{+∞}的次微分时，广义变分不等式问题(1)退化为下列非光滑约束优化问题因此，对广义变分不等式问题(1)的研究无论是理论还是应用都很有意义.当集值映象T是强单调或者可行集X具有某种特殊结构(比如X是盒子)时，已有很多的有效算法计算广义变分不等式问题(1)的解［4-5］.但是，当集值映象T不是强单调或者可行集X不具有某种特殊结构时，广义变分不等式问题(1)的有效算法却不多.在这种情况下，应用最广泛的算法是投影算法，例如文献［6］.然而，一般情况下投影算子本身难以计算(事实上，必须要求解一个优化问题才能找到投影)，这使得投影型算法难以实现.如何降低投影算子的计算难度或者如何实现投影成为众多数学和应用数学工作者关注的问题.最近，A.Auslender等［7-8］为了克服这一难点，引入了似距离泛函，定义了似投影算子，并在映射T是极大单调以及T在X的有界集上有界的条件下得到迭代序列{xk}的凸组合的极限点是广义变分不等式问题(1)的解.另一方面，广义变分不等式问题(1)也等价于下列的变分包含问题：求x*∈X使得其中，NX是闭凸集X的正规对偶算子，其定义为：显然广义变分不等式问题(1)是下列问题的特例：其中，A是Hilbert空间H到自身的一个集值映射.对于(3)式的求解算法有很多(参见文献［9-11］)，其中最常见的方法之一是近似点算法，它的一般形式为然而，上式的精确解一般难以计算，特别当A为非线性算子时更困难.为了克服上述难点，近年有很多文献提出了非精确的近似点算法.具体方法是在上式中添加容许误差，从而计算上式的近似解(参见文献［12-13］).受上述工作的启发，本文在Hilbert空间中研究了广义变分不等式问题(1)的近似-似投影算法.该算法包含有非精确的近似点算法，即在近似点算法中包含有误差ξ，它满足一个容易验证的条件(5)(见算法2.1).应用非精确的近似点算法，获得暂时的迭代点.然后应用似投影算子，将暂时的迭代点投影到广义变分不等式的可行集上，获得下一步的迭代点，进而构造出变分不等式的迭代序列.本文在集值映象T是极大单调的条件下证明了迭代序列的有界性，也证明了迭代序列的弱聚点都为广义变分不等式问题(1)的解.最后，在取特殊的似距离泛函的情况下证明了序列的弱收敛性.本文只假设T是极大单调映射，去掉了T在X的有界集上有界的条件.因此，本文的结果推广了文献［7］中的相应结果.1 预备知识文中R+代表全体正实数.首先介绍A.Auslender等［7］给出的似投影算子的定义及性质：定义1.1 对任给的g∈H，x∈X，定义似投影算子P(g，x)如下：其中d：X×X→R+∪{+∞}为给定的泛函，且对任意的y∈X都有：(d1)d(·，y)是X上的真凸下半连续泛函且有d(y，y)=0，▽1d(y，y)=0，其中▽1d(·，y)是d(·，y)的梯度.(d2)domd(·，y)⊂X，dom∂1d(·，y)=X，其中∂1d(·，y)是d(·，y)的次梯度映象. (d3)d(·，y)在X上ρ强凸，即存在ρ＞0对于任意的y∈X都有设D(X)表示满足条件(d1)～(d3)的所有泛函的集合.易知，若d∈D(X)，则对于任意的g∈H，x∈X都有P(0，x)=x.也需要下面的似距离泛函.定义1.2［8］ X是Hilbert空间H的闭凸子集，d∈D(X)，称泛函F：X×X→R+∪{+∞}为由d诱导的近似距离.若F在X×X上为有限值，且存在σ＞0，γ∈(0，1］，使得对任意的a，b∈X有：引理1.1［8］假设d∈D(X)，F是满足定义1.2的似距离泛函，P是定义2.1中的似投影算子，则对于任意的τ∈X，y∈X都有定义1.3 设X是一个Hilbert空间H的非空子集，T：X→2H为集值映射，称(i)T为单调的，如果对任意的x，y∈X，u∈T(x)，v∈T(y)有(ii)T为极大单调的，如果T为单调映射，并且对于任何的单调映射只要满足都有引理 1.2［14］假设η∈［0，1)且μ=若v=u+ξ，其中‖ξ‖2≤η2(‖u‖2+‖v‖2)，则2 近似-似投影算法及其性质在本节中，首先介绍广义变分不等式问题(1)的近似-似投影算法;然后再研究该算法的一些有用性质.选取正实数序列{λk}和正数η∈［0，1)，构造下列的迭代算法：算法2.11)选取初始点z0∈H.令k=0.2)求xk∈X，使得其中，ξk∈H满足3)若gk+ωk=0，则算法停止，否则令其中4)令k=k+1，然后回到第2步.令A=T+NX，其中NX是由(2)式定义的闭凸集X的正规对偶算子，若T为极大单调映象且dom(NX)∩intdom(T)≠Ø，则A为极大单调映象.从而(I+λkA)-1有意义且是单值的［15］.由(4)式知xk=(I+λkA)-1(zk+ξk)，从而序列{xk}、{zk}有定义. 本文总假设T是极大单调集值映射，η∈［0，1)，现介绍算法2.1产生的迭代序列的一些性质.且序列{λk}满足性质2.1 若则证明令v=λk(gk+ωk)，u=zk-xk，将其带入引理1.2就可以得到性质(i)和(ii).对于(iii)一方面利用Cauchy-Schwarz不等式及(i)有另一方面由(ii)可知注2.1 在算法2.1的第3步中，若gk+ωk= 0，则-ωk∈NX(xk)，从而有因此，xk是广义变分不等式问题(1)的解.另一方面，若gk+ωk≠0，由性质2.1(ii)知由T的伪单调性知对于任意的x*∈S，又因为gk∈NX(xk)则可得性质2.2 设且对任意k都有gk+ωk≠0，则且序列{F(x*，zk)}收敛.证明在引理1.1中，令τ=x*，g=βk(gk+ ωk)，结合(6)式有从而由定义2.2(ii)，上式等于这里由(10)式可得.另一方面所以将(11)～(12)式相结合有由(7)式，上式等于由(7)、(9)式以及可知从而即序列{F(x*，zk)}单调递减.又根据似距离泛函F的定义知对任意的k都有F(x*，zk)≥0，故序列{F(x*，zk)}收敛.性质2.3 假设序列{λk}满足(8)式，则存在一个常数ζ＞0使得证明如果gk+ωk=0，则上式成立.现假设gk +ωk≠0.由性质2.1(ii)有因为λk∈［α1，α2］，所以令性质2.4 假设序列{λk}满足(8)式且1-则证明若gk+ωk≠0，则由(8)、(13)和(14)式以及性质2.1(iii)可知，对于任意的k 有对上式取极限并由序列{F(x*，zk)}的收敛性得性质2.5 假设{xk}、{zk}是由算法2.1产生的两个无限序列，{λk}满足(8)式，则{xk}、{zk}都有界且具有相同的弱聚点.证明由性质2.2和定义1.2(iii)知序列{zk}有界，利用性质2.4和性质2.1(i)，可得所以有因为{zk}有界，从而可得{xk}有界.由(15)式知{xk}和{zk}具有相同的弱聚点.3 收敛性分析定理3.1 如果由算法2.1产生的序列{xk}是有限序列，则序列最后一项为广义变分不等式问题(1)的解.证明若序列{xk}为有限序列，则对于序列的最后一项算法2.1将在第3步停止，故有gk+ωk= 0.由注2.1知xk∈X且是广义变分不等式问题(1)的解.现在假设由算法2.1产生的序列{xk}是无限序列，下面将证明{xk}的弱聚点是广义变分不等式问题(1)的解.定理3.2 设{xk}是由算法2.1产生的序列，则{xk}的任意弱聚点都是广义变分不等式问题(1)的解.证明假设是{}的任意一个弱聚点，由此可以得到一个{xk}的子列弱收敛于.不失一般性，假设xk=(弱收敛).因为{xk}⊂X，所以∈X.由性质2.5知对于所有的v∈H，任意选取u∈T(v)+NX(v)，则存在点ω'∈T(v)和g'∈NX(v)，使得ω'+g'=u.因此，两个不等式相加有因为ω'+g'=u，所以由于‖ωk+gk‖→0，且{xk}有界，故有对(16)式取极限所以故存在使由NX的定义知从而所以是广义变分不等式问题(1)的解.当似距离泛函F(x，y)具有特殊结构时，将证明算法2.1产生的迭代序列{zk}、{xk}弱收敛于广义变分不等式问题(1)的解.下面推论的证明与R.T.Rockafellar［16］中证明序列收敛的方法一样.推论3.1 令F(x，y)=m‖x-y‖2，其中常数则由算法2.1产生的序列{zk}有唯一的弱聚点，从而{xk}和{zk}弱收敛.证明对于任意的x*∈S，由性质2.2知{m‖x*-zk‖2}收敛，下面证明序列{zk}有唯一的弱聚点.假设是{zk}的两个弱聚点，{zkj}和{zki}是{zk}的两个子序列且分别弱收敛于由性质2.5知是序列{xk}的弱聚点.再由定理3.2知根据性质2.2知序列和收敛.令则分别对(17)～(18)式取极限，由于{zkj}、{zki}分别弱收敛于所以〈和都收敛于0.由α1、α2、θ的定义可得由(19)和(20)式可得从而θ=0，故所以{zk}的所有子列具有相同的弱聚点，从而{zk}弱收敛，由性质2.5知{xk}弱收敛.参考文献［1］Fang Y P，Huang N J.Variational-like inequalities with generalized monotone mappings in Banach spaces［J］.Optim Theo Appl，2003，118(2)：327-338.［2］吴定平.随机变分不等式和随机相补问题［J］.四川师范大学学报：自然科学版，2005，28(5)：535-537.［3］张石生.变分不等式和相补问题理论及应用［M］.上海：科学技术文献出版社，1991.［4］Auslender A，Teboulle M.Interior gradient and proximal methods for convex and coinc optimization［J］.SIAM J Optim，2006，16：697-725. ［5］Xia F Q，Huang N J，Liu Z B.A projected subgradient method for solving generalized mixed variational inequalities［J］.Oper Research Lett，2008，36：637-642.［6］Solodov M V，Svaiter B F.A new projection method for variational inequality problems［J］.SIAM J Control Optim，1999，37(3)：765-776. ［7］Auslender A，Teboulle M.Projected subgradient menthods whih non-euclidean distances for non-differentiable convex minimization and variational inequalities［J］.Math Program，2009，120：27-48.［8］Auslender A，Teboulle M.Interior projection-like methods for monotone variational inequalities［J］.Math Program，2005，A104：39-68.［9］Eckstein J，Bertsekas D P.On the Douglas-Rachford splitting method and the proximal point algorithm for maximal monotone operators［J］.Math Program，1992，55：293-318.［10］Eckstein J，Svaiter B F.A family of projective splitting methods forthe sum of two maximal monotone operators［J］.Math Pro-gram，2008，111：173-199.［11］Eckstein J，Ferris M.Smooth methods of mulitipliers forcomplementarity problems［J］.Math Program，1999，86：65-90. ［12］Solodov M V，Svaiter B F.Error bounds for proximal point subproblems and associated inexact proximal point algorithms［J］.Math Program，2002，88：371-389.［13］Solodov M V，Svaiter B F.A hybrid projection-proximal point algorithm［J］.J Convex Anal，1999，6：59-70.［14］Solodov M V，Svaiter B F.A unified framework for some inexact proximal point algorithms［J］.Numer Funct Anal Optim，2001，22：1013-1035.［15］Minty G.A theorem on monotone sets in Hilbert spaces［J］.J Math Anal Appl，1967，97：434-439.［16］Rockafellar R T.Monotone operators and the proximal point algorithm［J］.SIAM J Control Optim，1976，14：877-898.［17］Ding X P，Xia F Q.A new class of completely generalized quasi-variational inclusions in Banach spaces［J］.J Comput Appl Math，2002，147：369-383.［18］Xia F Q，Huang N J.Variational inclusions with general H-monotone operators in Banach spaces［J］.Comput Math Appl，2007，54：24-30. ［19］Rockafellar R T，Bets R J.Variational Analysis［M］.New York：Springer-Verlag，1988.［20］Teboulle M.Convergence of proximal-like algorithms［J］.SIAM J Optim，1997，7：1069-1083.。

一类改进的谱共轭梯度法景书杰;李亚敏;牛海峰【摘要】谱共轭梯度法有两个方向控制参数,是解决大规模无约束优化问题的有效方法.本文提出了一个改进的谱参数θk,它不同于现有的θk.新算法在任何线搜索下都满足著名的共轭条件:dTk yk-1=0.新方法的搜索方向在任何线搜索下都是充分下降的.在一般假设下,我们证明该方法在改进的Wolfe线搜索是全局收敛的.【期刊名称】《洛阳师范学院学报》【年(卷),期】2019(038)002【总页数】5页(P1-5)【关键词】无约束优化;谱共轭梯度法;下降条件;谱参数;Wolfe线搜索【作者】景书杰;李亚敏;牛海峰【作者单位】河南理工大学数学与信息科学学院,河南焦作454000;河南理工大学数学与信息科学学院,河南焦作454000;河南理工大学数学与信息科学学院,河南焦作454000【正文语种】中文【中图分类】O221.20 引言考虑无约束优化问题(0.1)其中f(x)在Rn→R上是连续可微的函数，Rn表示n维欧式空间. 我们定义g(x)=▽f(x)是f(x)在xk处的梯度向量，且令gk=g(xk).由于非线性共轭梯度法(简称CG法)迭代简单有效，全局收敛性和低内存需求，故它是解决问题(0.1)的最有效的迭代方法之一，特别是在科学和工程计算中的大规模优化问题中. 在解决问题(0.1)的迭代算法中得到序列{xk}，它的一般迭代格式如下xk+1=xk+αkdk(0.2)其中xk是当前迭代点，αk为步长.这里βk∈Rn为共轭参数，不同的CG法是由不同形式的共轭参数βk决定. 本文被以下共轭参数所吸引：它们的βk公式[1-4]如下这里代表Euclidean范数，yk:=gk+1-gk.PRP和HS是公认的最有效的两个CG法，但它们的收敛性都不是很好. 已有很多关于收敛性的研究[5-11]. 这些CG法都有良好的收敛性和数值表现，然而它们构造复杂且难以理解，不像经典的CG法[1-4,12-15], 形式简单，容易应用，所以工程师们也很少把它们应用到科学和生产等研究中. 因此，Rivaie等[16]给出了一个形式简单的共轭参数为方便起见，我们称它为RMIL法.2012年，Rivaie等[16]提出RMIL法的共轭参数，定义为(0.3)这里yk-1=gk-gk-1.显然(0.4)Rivaie等[16]验证了该方法产生的搜索方向dk是充分下降的，并在精确线搜索下建立了该算法的全局收敛性. 数值试验表明，RMIL法具有线性收敛速率，比其它CG法更有效.2001年，Birgin 和Martinez[17]提出了谱共轭梯度法(SCG法)，即将谱梯度方法和CG法的思想结合起来，搜索方向dk的迭代格式如下(0.5)其中这里θk是谱参数；sk-1=xk-xk-1；yk-1=gk-gk-1. 令人惊奇的是, SCG法在很多情况下优于经典的CG法. 但SCG法产生的搜索方向dk不满足下降条件并且没有证明算法是否是全局收敛性的. 故已有学者对此进行研究，使其修正的SCG法产生搜索方向dk是下降方向，并在一般假设下建立算法的全局收敛性.Zhang等在文献 [18] 给出一个修正的FR共轭梯度法(MFR)，搜索方向dk如下dk=-θkgk+βkdk-1其中显然，对k≥1，有成立. 即搜索方向dk是不依赖于任何线搜索的充分下降方向. Zhang等[18]证明了MFR法对于一般的目标函数在Wolfe线搜索或Armijo线搜索下也具有全局收敛性.2008年，Yu等[19]修正谱Perry共轭梯度法得到一个新的SCG法，称为DSP-CG法.的公式如下这里数值试验表明，对于任何的线搜索DSP-CG法都是下降方法. Yu等[19]证明了DSP-CG法对一般目标函数在Wolfe线搜索下是全局收敛性的.最近，Deng等[20]改进了SCG算法，给出混合的θk和βk公式，定义为:这里η是一个给定的小常数. 参数θk和βk的选择使得搜索方向dk既是充分下降的也是拟牛顿方向. 在Armijo线搜索下验证了改进的SCG算法的全局收敛性. 数值试验证实了改进的SCG算法比现存的算法更有效和稳定.本文将展示一个改进的谱参数θk，进而结合文献[16] 中的构造一个新的SCG法，我们称它为SRMIL法. 该方法的搜索方向dk不需要任何线搜索都是充分下降的.我们建立了在修正的Wolfe线搜索下SRMIL法的全局收敛性.1 谱参数θk及算法下降性下面我们给出谱参数θk的选取方法. 我们给出的谱参数θk不依赖于任何线搜索而满足著名的共轭条件：给式(0.3)的两边同乘yk-1，可得因此所以(1.1)本文用SRMIL法解决问题(0.1)，该方法中xk和dk的迭代格式分别选用(0.2)和(0.5). 用式(0.3)计算βk，用式(1.1)计算θk. 故有SRMIL法满足著名的共轭条件. 算法:Step 0：给定初始值x0∈Rn，ε>0，令0<ρ<σ<1，令k:=0,d0=-g0.Step 1：计算gk；若则停止，否则转Step 2.Step 2：计算步长αk>0，使其满足修正的Wolfe线搜索[21]：(1.2)Step 3：利用式(0.3)，式(0.5)，式(1.1)，分别计算Step 4：令xk+1=xk+αkdk，求gk+1，并用(0.3)试求令令k:=k+1，转Step 1.基本假设H[22](H1)目标函数f(x)在水平集l0={x∈Rn|f(x)≤f(x0)} 上有下界，其中x0为初始点.(H2)目标函数f(x)在水平集l0的一个邻域N内连续可微，且梯度函数g(x)满足Lipschitz连续，即存在常数L>0，使(1.3)引理1.1 若假设 H 成立，则修正的 Wolfe 线搜索(1.2)是可行的，故必存在αk>0满足条件(1.2).证明类似于文献 [19] 中引理1的证明，这个结果的证明是显然的.下面给出算法的充分下降条件.引理1.2 设序列{gk}和{dk}由算法生成，则对任意k≥0，(1.4)和(1.5)成立.证明用数学归纳法证明.(i)当k=0时，有d0=-g0，则有成立.(ii)假设有成立. 当k=k+1时，由式(0.4)，式(0.5)和式(1.1)有(1.6)综上，式(1.4)得证.由式(1.6)，显然有式(1.5)成立.2 全局收敛性引理2.1[23] 若假设H成立，则由算法生成的序列{gk}和{dk}满足Zoutendijk条件(2.1)证明由式(1.2)和式(1.3)，可得因此将上式的两边取平方得由式(1.2)和假设H，可得<+∞定理2.1 若假设H成立，序列{gk}由迭代算法(0.2)和(0.5)产生，则有(2.2)证明我们用反证法证明，反设结论不成立，则必存在常数γ>0，使得对式(0.5)变形得(2.3)把(2.3)的两边取平方模，并移项得上式两边除以得再利用式(1.5)，得(2.4)注意到当k=0时，d0=-g0，所以，由式(2.4)得所以显然，这与引理2.1中的(2.1)矛盾，故参考文献【相关文献】[1] Polak E,Ribiere G. Note Sur la Convergence de Methodes de DirectionsConjugees[J].Rev. Francaise Informat. Recherche Operationelle, 1969, 16(3): 35-43.[2] Polyak B T. The Conjugate Gradient Method in Extreme Problems[J]. USSR Computational Mathematics and Mathematical Physics, 1969, 9(4): 94-112.[3] Hestenes M R,Steifel E. Method of Conjugate Gradient for Solving Linear Equations[J]. J. Res. Nat. Bur. Stand., 1952, 49: 409-436.[4] Liu Y,Storey C. Efficient Generalized Conjugate Gradient Algorithms Part 1: Theory[J]. J. Comput. Appl. Math., 1992, 69(1):129-137.[5] 戴彧虹,袁亚湘．非线性共轭梯度法[M]．上海：上海科学技术出版社,2000．[6] Hager W W,Zhang H. A New Conjugate Gradient Method with Guaranteed Descent and an Efficient Line Search[J]. SIAM J.Optim., 2005, 16:170-192.[7] Hager W W,Zhang H. A Survey of Nonlinear Conjugate Gradient Methods,PacificJ.Optim.,2006,2:35-58.[8] Yuan G,Lu X. A Modified PRP Conjugate Gradient Method,Ann. Oper. Res., 2009, 166:73-90.[9] Wei Z X,Li G Y, Qi L Q. New Nonliner Conjugate Gradient Formulas for Large-scale Unconstrained Optimization Problems[J]. Appl. Math. Comput., 2006, 179(2): 407-430. [10] Dai Z F,Wan F H . Another Improved Wei-Yao-Liu Nonlinear Conjugate Gradient Method with Sufficient Descent Property[J]. Appl. Math. Comput.,2012, 218(14): 7421-7430.[11] Huang H,Lin S H .A Modified Wei-Yao-Liu Conjugate Gradient Method forUnconstrained Optimization[J]. Appl. Math. Comput., 2014, 231(2): 179-186.[12] Fletcher R,Reeves C. Function Minimization by Conjugate Gradients[J]. The Comput. J. 1964, 7(2): 149--154.[13] Dai Y H,Yuang Y X. A Nonlinear Conjugate Gradient Method with a Strong Global Convergence Property[J].SIAM J. Optim., 1999, 10(1): 177-182.[14] Fletcher R. Practical Methods of Optimization vol 1: Unconstrained Optimization[M]. New York: John Wiley & Sons, 1987.[15] Wei Z X,Yao S G, Liu L Y. The Convergence Properties of Some New Conjugate Gradient Methods[J]. Appl. Math. Comput., 2006, 183(2): 1341-1350.[16] Rivaie M, Mamat M, June L W,et al. A New Class of Nonliner Conjugate Gradient Coefficients with Global Convergence Properties[J]. Appl. Math. Comput., 2012, 218(22): 11323-11332.[17] Birgin E G,Martinez J M. A Spectral Conjugate Gradient Method for Unconstrained Optimization[J]. Appl.Math.Optim., 2001, 43(2): 117-128[18] Zhang L,Zhou W J,Li D H.Global Convergence of a Modified Fletcher-Reeves Conjugate Gradient Method with Armijo-type Line Search[J]. Numer. Math. 2006, 104: 561-572.[19] Yu G H,Guan L T,Chen W F,Spectral Conjugate Gradient Methods with Sufficient Descent Property for Large-scale Unconstrained Optimization,Optim. Methods Softw., 2008, 23:275-293.[20] Deng S H,Wan Z,Chen X H,An Improved Spectral Conjugate Gradient Algorithm for Non-conve Unconstrained Optimization Problems,J. Optim. Theory Appl., 2013, 157:820-842.[21] Wang C Y,Chen Y Y, Du Shouqiang.Futher Insight into the Shamanskii Modification of Newton Method[J]. Appl. Math. Comput., 2006, 180(1): 46-52.[22] 简金宝, 江羡珍, 尹江华. 非线性共轭梯度法研究进展[J]. 玉林师范学院学报, 2016, 37(2):3-10.[23] Zoutendijk G. Nonlinear Programming,Computational Methods,in integer and Nonlinear Programming [M]. Amsterdam: North-Holland, 1970.。

9;s Guarded Command Language GCL 2] is a weakest-precondition based method of describing computations and their meaning; here we extend it to probabilistic programs, those that implement random algorithms, and we give examples of its use. Most sequential programming languages contain a construct for `deterministic' choice, where the program selects one from a number of alternatives in some predictable way: for example, in
Part of this report is a `transliteration' of another report 16] from generalised substitutions 1] to guarded commands. The case study (Rabin's algorithm) has not appeared before.
explicit operator: the construct this u that chooses between the alternatives unpredictably and, as a speci cation, indicates abstraction from the issue of which will be executed. The customer will be happy with either this or that ; and the implementor may choose between them according to his own concerns. Early research on probabilistic semantics took a di erent route: demonic choice was not regarded as fundamental | rather it was abandoned altogether, being replaced by probabilistic choice 9, 4, 3, 8, 7]. Thus probabilistic semantics was divorced from the contemporaneous work on speci cation and re nement, because without demonic choice there is no means of abstraction. More recently however it has been discovered 6, 15] how to bring the two topics back together, taking the more natural approach of adding probabilistic choice, while retaining demonic choice. In fact deterministic choice is a special case of probabilistic choice, which in turn is a re nement of demonic choice. We give the resulting probabilistic extension of GCL the name `pGCL'. Section 2 gives a brief and shallow overview of

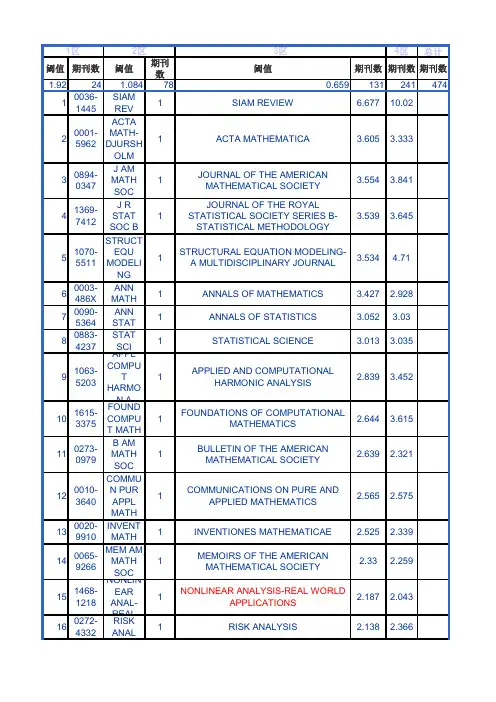
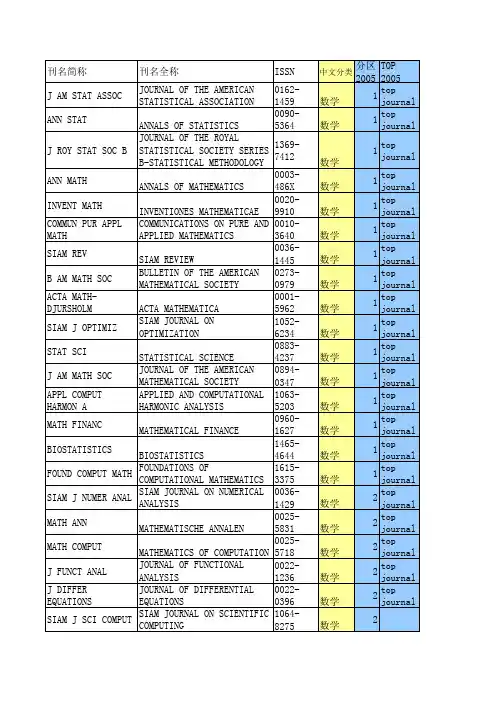
4区总计阈值期刊数阈值期刊数阈值期刊数期刊数期刊数1.9224 1.084780.65913124147410036-1445SIAMREV1SIAM REVIEW 6.67710.0220001-5962ACTAMATH-DJURSHOLM1ACTA MATHEMATICA 3.605 3.33330894-0347J AMMATHSOC1JOURNAL OF THE AMERICANMATHEMATICAL SOCIETY3.554 3.84141369-7412J RSTATSOC B1JOURNAL OF THE ROYALSTATISTICAL SOCIETY SERIES B-STATISTICAL METHODOLOGY3.539 3.64551070-5511STRUCTEQUMODELING1STRUCTURAL EQUATION MODELING-A MULTIDISCIPLINARY JOURNAL3.5344.7160003-486XANNMATH1ANNALS OF MATHEMATICS 3.427 2.92870090-5364ANNSTAT1ANNALS OF STATISTICS 3.052 3.0380883-4237STATSCI1STATISTICAL SCIENCE 3.013 3.03591063-5203APPLCOMPUTHARMON A1APPLIED AND COMPUTATIONALHARMONIC ANALYSIS2.8393.452101615-3375FOUNDCOMPUT MATH1FOUNDATIONS OF COMPUTATIONALMATHEMATICS2.6443.615110273-0979B AMMATHSOC1BULLETIN OF THE AMERICANMATHEMATICAL SOCIETY2.639 2.321120010-3640COMMUN PURAPPLMATH1COMMUNICATIONS ON PURE ANDAPPLIED MATHEMATICS2.565 2.575130020-9910INVENTMATH1INVENTIONES MATHEMATICAE 2.525 2.339140065-9266MEM AMMATHSOC1MEMOIRS OF THE AMERICANMATHEMATICAL SOCIETY2.33 2.259151468-1218NONLINEARANAL-REAL1NONLINEAR ANALYSIS-REAL WORLDAPPLICATIONS2.187 2.043160272-4332RISKANAL1RISK ANALYSIS 2.138 2.3661区2区3区170162-1459J AMSTATASSOC1JOURNAL OF THE AMERICANSTATISTICAL ASSOCIATION2.126 1.992180964-1998J RSTATSOC ASTAT1JOURNAL OF THE ROYALSTATISTICAL SOCIETY SERIES A-STATISTICS IN SOCIETY2.123 2.11191540-3459MULTISCALEMODELSIM1MULTISCALE MODELING &SIMULATION2.122 2.009200073-8301PUBLMATH-PARIS1PUBLICATIONS MATHEMATIQUES DEL IHES2.112 2.143211064-8275SIAM JSCICOMPUT1SIAM JOURNAL ON SCIENTIFICCOMPUTING2.06 1.569221536-867XSTATA J1Stata Journal 2.024 2.222230266-5611INVERSEPROBL1INVERSE PROBLEMS 1.973 1.88240165-0114FUZZYSETSYST1FUZZY SETS AND SYSTEMS 1.924 1.759250025-5610MATHPROGRAM2MATHEMATICAL PROGRAMMING 1.908 1.707260218-2025MATHMODMETHAPPL S2MATHEMATICAL MODELS & METHODSIN APPLIED SCIENCES1.894 1.635270895-4798SIAM JMATRIXANAL A2SIAM JOURNAL ON MATRIX ANALYSISAND APPLICATIONS1.835 1.368281052-6234SIAM JOPTIMIZ2SIAM JOURNAL ON OPTIMIZATION 1.716 1.629290036-1429SIAM JNUMERANAL2SIAM JOURNAL ON NUMERICALANALYSIS1.704 1.609300960-3174STATCOMPUT2STATISTICS AND COMPUTING 1.7 1.429310735-0015J BUSECONSTAT2JOURNAL OF BUSINESS & ECONOMICSTATISTICS1.678 1.779320027-3171MULTIVARBEHAVRES2MULTIVARIATE BEHAVIORALRESEARCH1.677 1.412330938-8974JNONLINEAR SCI2JOURNAL OF NONLINEAR SCIENCE 1.663 1.149341085-3375ABSTRAPPLANAL2Abstract and Applied Analysis 1.66 1.318351687-1812FIXEDPOINTTHEORY A2Fixed Point Theory and Applications 1.634 1.634360036-1410SIAM JMATHANAL2SIAM JOURNAL ON MATHEMATICALANALYSIS1.587 1.316370033-3123PSYCHOMETRIKA2PSYCHOMETRIKA 1.585 1.772380272-4979IMA JNUMERANAL2IMA JOURNAL OF NUMERICALANALYSIS1.577 1.481390012-7094DUKEMATH J2DUKE MATHEMATICAL JOURNAL 1.569 1.537400176-4276CONSTRAPPRO2CONSTRUCTIVE APPROXIMATION 1.567 1.119410036-1399SIAM JAPPLMATH2SIAM JOURNAL ON APPLIEDMATHEMATICS1.531 1.425421239-6095BOREALENVIRON RES2ANNALES ACADEMIAE SCIENTIARUMFENNICAE-MATHEMATICA1.522 1.803430091-1798ANNPROBAB2ANNALS OF PROBABILITY 1.506 1.789440885-7474J SCICOMPUT2JOURNAL OF SCIENTIFIC COMPUTING 1.505 1.557450178-8051PROBABTHEORY REL2PROBABILITY THEORY AND RELATEDFIELDS1.499 1.533461435-9855J EURMATHSOC2JOURNAL OF THE EUROPEANMATHEMATICAL SOCIETY1.498 1.404470021-7824J MATHPUREAPPL2JOURNAL DE MATHEMATIQUESPURES ET APPLIQUEES1.475 1.295481069-5869JFOURIER ANALAPPL2JOURNAL OF FOURIER ANALYSIS ANDAPPLICATIONS1.459 1.034490363-0129SIAM JCONTROLOPTIM2SIAM JOURNAL ON CONTROL ANDOPTIMIZATION1.454 1.518500307-904XAPPLMATHMODEL2APPLIED MATHEMATICAL MODELLING 1.442 1.579510029-599XNUMERMATH2NUMERISCHE MATHEMATIK 1.441 1.321520022-040XJDIFFERGEOM2JOURNAL OF DIFFERENTIALGEOMETRY1.437 1.583531930-8337INVERSEPROBLIMAG2Inverse Problems and Imaging 1.436 1.074540362-546XNONLINEARANAL-THEOR2NONLINEAR ANALYSIS-THEORYMETHODS & APPLICATIONS1.434 1.536550025-5718MATHCOMPUT2MATHEMATICS OF COMPUTATION 1.431 1.313561019-7168ADVCOMPUT MATH2ADVANCES IN COMPUTATIONALMATHEMATICS1.427 1.488570749-159XNUMERMETHPART DE2NUMERICAL METHODS FOR PARTIALDIFFERENTIAL EQUATIONS1.342 1.404580096-3003APPLMATHCOMPUT2APPLIED MATHEMATICS ANDCOMPUTATION1.326 1.317590022-0396JDIFFEREQUATIONS2JOURNAL OF DIFFERENTIALEQUATIONS1.321 1.277600001-8708ADVMATH2ADVANCES IN MATHEMATICS 1.317 1.177610764-583XESAIM-MATHMODELNUM2ESAIM-MATHEMATICAL MODELLINGAND NUMERICAL ANALYSIS-MODELISATION MATHEMATIQ1.301 1.218620926-6003COMPUT OPTIMAPPL2COMPUTATIONAL OPTIMIZATION ANDAPPLICATIONS1.296 1.35631465-3060GEOMTOPOL2GEOMETRY & TOPOLOGY 1.295 1.295641016-443XGEOMFUNCTANAL2GEOMETRIC AND FUNCTIONALANALYSIS1.285 1.246651557-4679INT JBIOSTAT2International Journal of Biostatistics 1.284 1.284661559-3940COMMAPPMATHCOM SC2Communications in Applied Mathematicsand Computational Science1.281 1.562671931-6690BAYESIANANAL2Bayesian Analysis 1.277 1.65680925-5001JGLOBALOPTIM2JOURNAL OF GLOBAL OPTIMIZATION 1.27 1.196691056-3911JALGEBRAICGEOM2JOURNAL OF ALGEBRAIC GEOMETRY 1.2670.932700012-9593ANN SCIECOLENORM S2ANNALES SCIENTIFIQUES DE LECOLE NORMALE SUPERIEURE1.253 1.46711016-3328COMPUTCOMPLEX2COMPUTATIONAL COMPLEXITY 1.253 1.122721948-206XANALPDE2Analysis & PDE 1.226 1.172730024-6115P LONDMATHSOC2PROCEEDINGS OF THE LONDONMATHEMATICAL SOCIETY1.205 1.324740025-5831MATHANN2MATHEMATISCHE ANNALEN 1.196 1.297751539-6746COMMUN MATHSCI2Communications in MathematicalSciences1.192 1.412760002-9327AM JMATH2AMERICAN JOURNAL OFMATHEMATICS1.188 1.057770897-3962JINTEGRAL EQUAPPL2Journal of Integral Equations andApplications1.188 1.188780956-7925EUR JAPPLMATH2EUROPEAN JOURNAL OF APPLIEDMATHEMATICS1.185 1.022790294-1449ANN I HPOINCARE-AN2ANNALES DE L INSTITUT HENRIPOINCARE-ANALYSE NON LINEAIRE1.184 1.271800022-1236JFUNCTANAL2JOURNAL OF FUNCTIONAL ANALYSIS 1.175 1.082811061-8600JCOMPUTGRAPHSTAT2JOURNAL OF COMPUTATIONAL ANDGRAPHICAL STATISTICS1.173 1.056820895-7177MATHCOMPUTMODEL2MATHEMATICAL AND COMPUTERMODELLING1.172 1.346830925-7721COMPGEOM-THEORAPPL2COMPUTATIONAL GEOMETRY-THEORY AND APPLICATIONS1.1710.725840960-1627MATHFINANC2MATHEMATICAL FINANCE 1.171 1.246850893-9659APPLMATHLETT2APPLIED MATHEMATICS LETTERS 1.168 1.371860304-4149STOCHPROCAPPL2STOCHASTIC PROCESSES AND THEIRAPPLICATIONS1.168 1.01871386-1999EXTREMES2Extremes 1.158 1.263880377-0427JCOMPUT APPLMATH2JOURNAL OF COMPUTATIONAL ANDAPPLIED MATHEMATICS1.145 1.112891230-3429TOPOLMETHOD NONLAN2Topological Methods in NonlinearAnalysis1.1390.733901133-0686TEST-SPAIN2TEST 1.134 1.125910022-247XJ MATHANALAPPL2JOURNAL OF MATHEMATICALANALYSIS AND APPLICATIONS1.133 1.001921070-5325NUMERLINEARALGEBR2NUMERICAL LINEAR ALGEBRA WITHAPPLICATIONS1.128 1.168930010-437XCOMPOS MATH2COMPOSITIO MATHEMATICA 1.125 1.187941040-7294J DYNDIFFEREQU2Journal of Dynamics and DifferentialEquations1.1160.733950167-9473COMPUT STATDATAAN2COMPUTATIONAL STATISTICS & DATAANALYSIS1.115 1.028961050-5164ANNAPPLPROBAB2ANNALS OF APPLIED PROBABILITY 1.114 1.091970044-2275ZANGEWMATHPHYS2ZEITSCHRIFT FUR ANGEWANDTEMATHEMATIK UND PHYSIK1.1110.951980944-2669CALCVARPARTIAL DIF2CALCULUS OF VARIATIONS ANDPARTIAL DIFFERENTIAL EQUATIONS1.107 1.235990075-4102J REINEANGEWMATH2JOURNAL FUR DIE REINE UNDANGEWANDTE MATHEMATIK1.107 1.0421000022-2526STUDAPPLMATH2STUDIES IN APPLIED MATHEMATICS 1.090.8191011935-7524ELECTRON JSTAT2Electronic Journal of Statistics 1.09 1.1541020002-9947T AMMATHSOC2TRANSACTIONS OF THE AMERICANMATHEMATICAL SOCIETY1.084 1.0931030360-5302COMMUN PARTDIFF EQ3COMMUNICATIONS IN PARTIALDIFFERENTIAL EQUATIONS1.0780.8941040219-5305ANALAPPL3Analysis and Applications 1.072 1.141050003-1305AMSTAT3AMERICAN STATISTICIAN 1.0640.961060168-9274APPLNUMERMATH3APPLIED NUMERICAL MATHEMATICS 1.0550.9671070176-4268JCLASSIF3JOURNAL OF CLASSIFICATION 1.0350.7191081078-0947DISCRETECONTDYN-A3DISCRETE AND CONTINUOUSDYNAMICAL SYSTEMS1.0350.9131090095-8956J COMBTHEORY B3JOURNAL OF COMBINATORIALTHEORY SERIES B1.030.8921100022-3239JOPTIMIZTHEORY APP3JOURNAL OF OPTIMIZATION THEORYAND APPLICATIONS1.023 1.0621111292-8119ESAIMCONTROPTIMCA3ESAIM-CONTROL OPTIMISATION ANDCALCULUS OF VARIATIONS1.0210.7581120024-3795LINEARALGEBRA APPL3LINEAR ALGEBRA AND ITSAPPLICATIONS1.0170.9741131350-7265BERNOULLI3BERNOULLI 1.017 1.051141556-1801NETWHETEROGMEDIA3Networks and Heterogeneous Media 1.0020.6581150303-6898SCANDJ STAT3SCANDINAVIAN JOURNAL OFSTATISTICS0.992 1.1181160010-2571COMMENTMATHHELV3COMMENTARII MATHEMATICIHELVETICI0.980.8621171042-9832RANDOMSTRUCTALGOR3RANDOM STRUCTURES &ALGORITHMS0.974 1.0341181017-0405STATSINICA3STATISTICA SINICA0.973 1.0171191548-159XDYNAMPARTDIFFEREQ3Dynamics of Partial Differential Equations 0.970.7811200047-259XJMULTIVARIATEANAL3JOURNAL OF MULTIVARIATEANALYSIS0.9690.8791210022-2518INDIANAU MATHJ3INDIANA UNIVERSITY MATHEMATICSJOURNAL0.9660.8861221661-6952JNONCOMMUTGEOM3Journal of Noncommutative Geometry0.960.8251231937-5093KINETRELATMOD3Kinetic and Related Models0.9360.6771241022-1824SELMATH-NEWSER3Selecta Mathematica-New Series 0.9170.8791251687-2770BOUNDVALUEPROBL3Boundary Value Problems 0.9110.9111261474-7480J INSTMATHJUSSIEU3Journal of the Institute of Mathematics ofJussieu0.909 1.0221271584-2851CARPATHIAN JMATH3Carpathian Journal of Mathematics0.9030.9061280179-5376DISCRETECOMPUT GEOM3DISCRETE & COMPUTATIONALGEOMETRY0.9010.9381291583-5022FIXEDPOINTTHEOR-RO3Fixed Point Theory 0.90.971300391-173XANNSCUOLANORM-SCI3ANNALI DELLA SCUOLA NORMALESUPERIORE DI PISA-CLASSE DISCIENZE0.880.6951311753-8416JTOPOL3Journal of Topology0.880.8681320373-3114ANNMATPURAPPL3ANNALI DI MATEMATICA PURA EDAPPLICATA0.8780.8381331531-3492DISCRETECONTDYN-B3DISCRETE AND CONTINUOUSDYNAMICAL SYSTEMS-SERIES B0.8660.9211341424-3199J EVOLEQU3JOURNAL OF EVOLUTION EQUATIONS0.8650.8831350925-9899JALGEBRCOMB3JOURNAL OF ALGEBRAICCOMBINATORICS0.8640.7521360095-4616APPLMATHOPT3APPLIED MATHEMATICS ANDOPTIMIZATION0.8630.9521370254-9409JCOMPUT MATH3JOURNAL OF COMPUTATIONALMATHEMATICS0.8620.9781380196-8858ADVAPPLMATH3ADVANCES IN APPLIEDMATHEMATICS0.8580.8431391380-7870LIFETIME DATAANAL3LIFETIME DATA ANALYSIS0.8570.9151400219-1997COMMUNCONTEMP3COMMUNICATIONS INCONTEMPORARY MATHEMATICS0.8550.5741410044-2267ZAMM-ZANGEWMATHME3ZAMM-Zeitschrift fur AngewandteMathematik und Mechanik0.8530.8631421083-6489ELECTRON JPROBAB3ELECTRONIC JOURNAL OFPROBABILITY0.8510.7131430926-2601POTENTIALANAL3POTENTIAL ANALYSIS0.850.9431441930-5311J MODDYNAM3Journal of Modern Dynamics0.8490.9421450944-6532JCONVEX ANAL3JOURNAL OF CONVEX ANALYSIS0.8480.8231461017-1398NUMERALGORITHMS3NUMERICAL ALGORITHMS0.847 1.0421471687-1847ADVDIFFEREQU-NY3Advances in Difference Equations 0.8450.8451480035-9254J RSTATSOC C-APPL3JOURNAL OF THE ROYALSTATISTICAL SOCIETY SERIES C-APPLIED STATISTICS0.8440.8281491023-6198JDIFFEREQUAPPL3JOURNAL OF DIFFERENCEEQUATIONS AND APPLICATIONS0.8330.81500378-4754MATHCOMPUTSIMULA3MATHEMATICS AND COMPUTERS INSIMULATION0.8320.7381510218-1274INT JBIFURCATCHAOS3INTERNATIONAL JOURNAL OFBIFURCATION AND CHAOS0.8290.7551521877-0533SET-VALUEDVARANAL3Set-Valued and Variational Analysis0.8290.7911530025-5874MATH Z3MATHEMATISCHE ZEITSCHRIFT0.8210.7491540209-9683COMBINATORICA3COMBINATORICA0.8170.6711550021-7670J ANALMATH3JOURNAL D ANALYSEMATHEMATIQUE0.8140.7831561941-4889J GEOMMECH3Journal of Geometric Mechanics0.8120.8121570924-6703DISCRETEEVENTDYN S3DISCRETE EVENT DYNAMICSYSTEMS-THEORY ANDAPPLICATIONS0.8110.6411580020-3157ANN ISTATMATH3ANNALS OF THE INSTITUTE OFSTATISTICAL MATHEMATICS0.8110.8571590166-218XDISCRETE APPLMATH3DISCRETE APPLIED MATHEMATICS0.8110.7951600024-6107J LONDMATHSOC3JOURNAL OF THE LONDONMATHEMATICAL SOCIETY-SECONDSERIES0.8050.7891610963-5483COMBPROBABCOMPUT3COMBINATORICS PROBABILITY &COMPUTING0.8040.7781620167-8019ACTAAPPLMATH3ACTA APPLICANDAE MATHEMATICAE0.80.8991630213-2230REVMATIBEROA3REVISTA MATEMATICAIBEROAMERICANA0.7990.8521641527-5256JSYMPLECTGEOM3Journal of Symplectic Geometry0.7990.8481650170-4214MATHMETHOD APPLSCI3MATHEMATICAL METHODS IN THEAPPLIED SCIENCES0.7970.7431660232-704XANNGLOBANALGEOM3ANNALS OF GLOBAL ANALYSIS ANDGEOMETRY0.7950.7141671050-6926J GEOMANAL3JOURNAL OF GEOMETRIC ANALYSIS0.7950.7611681382-6905J COMBOPTIM3JOURNAL OF COMBINATORIALOPTIMIZATION0.7910.6641691079-8986B SYMBLOG3BULLETIN OF SYMBOLIC LOGIC0.790.6091700246-0203ANN I HPOINCARE-PR3ANNALES DE L INSTITUT HENRIPOINCARE-PROBABILITES ETSTATISTIQUES0.7850.8971711387-5841METHODOLCOMPUT APPL3METHODOLOGY AND COMPUTING INAPPLIED PROBABILITY0.780.7531721073-7928INTMATHRESNOTICE3INTERNATIONAL MATHEMATICSRESEARCH NOTICES0.775 1.0141731534-0392COMMUN PURAPPLANAL3COMMUNICATIONS ON PURE ANDAPPLIED ANALYSIS0.7740.6921740143-3857ERGODTHEORDYNSYST3ERGODIC THEORY AND DYNAMICALSYSTEMS0.7730.7021751463-9963INTERFACEFREEBOUND3INTERFACES AND FREE BOUNDARIES0.7690.7951760021-9045JAPPROXTHEOR3JOURNAL OF APPROXIMATIONTHEORY0.7650.6811770097-3165J COMBTHEORY A3JOURNAL OF COMBINATORIALTHEORY SERIES A0.7640.8261780269-9648PROBABENGINFORMSC3PROBABILITY IN THE ENGINEERINGAND INFORMATIONAL SCIENCES0.7630.6421790308-1087LINEARMULTILINEAR A3LINEAR & MULTILINEAR ALGEBRA0.7620.7271801935-9179ELECTRON RESANNOUNC3Electronic Research Announcements inMathematical Sciences0.7610.5241810319-5724CAN JSTAT3CANADIAN JOURNAL OF STATISTICS-REVUE CANADIENNE DESTATISTIQUE0.7550.6711821345-4773JNONLINEARCONVEX A3Journal of Nonlinear and Convex Analysis0.7520.9331830001-8678ADVAPPLPROBAB3ADVANCES IN APPLIED PROBABILITY0.750.6791840306-7734INTSTATREV3INTERNATIONAL STATISTICALREVIEW0.7480.541851471-082XSTATMODEL3STATISTICAL MODELLING0.7470.8951860723-0869EXPOMATH3EXPOSITIONES MATHEMATICAE0.7450.9021870195-6698EUR JCOMBIN3EUROPEAN JOURNAL OFCOMBINATORICS0.7380.6771881424-9286MILAN JMATH3Milan Journal of Mathematics 0.7380.221890219-8916JHYPERBOLDIFFEREQ3Journal of Hyperbolic DifferentialEquations0.7370.7961900008-0624CALCOLO3CALCOLO0.7360.8081910026-2285MICHMATH J3MICHIGAN MATHEMATICAL JOURNAL0.7340.9481920373-0956ANN IFOURIER3ANNALES DE L INSTITUT FOURIER0.7320.551930006-3835BIT3BIT NUMERICAL MATHEMATICS 0.7310.7241941536-1365ADVNONLINEARSTUD3ADVANCED NONLINEAR STUDIES0.7290.6441950143-9782J TIMESERANAL3JOURNAL OF TIME SERIES ANALYSIS0.7290.7611960289-2316JPN JMATH3Japanese Journal of Mathematics0.7290.6151971079-9389ADVDIFFERENTIALEQU3Advances in Differential Equations0.7270.7271980033-569XQ APPLMATH3QUARTERLY OF APPLIEDMATHEMATICS0.7260.5241990257-0130QUEUEINGSYST3QUEUEING SYSTEMS0.7260.7172001029-242XJINEQUAL APPL3JOURNAL OF INEQUALITIES ANDAPPLICATIONS0.7260.7262011073-2780MATHRESLETT3MATHEMATICAL RESEARCH LETTERS0.7230.7432021431-0643DOCMATH3Documenta Mathematica 0.7210.7332030933-7741FORUMMATH3FORUM MATHEMATICUM0.7130.6072040378-3758J STATPLANINFER3JOURNAL OF STATISTICAL PLANNINGAND INFERENCE0.7110.7162050272-4960IMA JAPPLMATH3IMA JOURNAL OF APPLIEDMATHEMATICS0.710.7762060021-2172ISR JMATH3ISRAEL JOURNAL OF MATHEMATICS0.710.7452071004-8979NUMERMATH-THEORY ME3Numerical Mathematics-Theory Methodsand Applications0.7080.6922081705-5105INT JNUMERANALMOD3International Journal of NumericalAnalysis and Modeling0.7050.6242090021-9002J APPLPROBAB3JOURNAL OF APPLIED PROBABILITY0.7040.6322101065-2469INTEGRTRANSFSPEC F3INTEGRAL TRANSFORMS ANDSPECIAL FUNCTIONS0.7030.7592111071-5797FINITEFIELDSTH APP3FINITE FIELDS AND THEIRAPPLICATIONS0.7010.5862121139-1138REVMATCOMPLUT3Revista Matematica Complutense 0.7010.6672131452-8630APPLANALDISCRMATH3Applicable Analysis and DiscreteMathematics0.70.7542141019-8385COMMUN ANALGEOM3COMMUNICATIONS IN ANALYSIS ANDGEOMETRY0.6950.6872151385-0172MATHPHYSANALGEOM3MATHEMATICAL PHYSICS ANALYSISAND GEOMETRY0.6920.8062161735-0654IRAN JFUZZYSYST3Iranian Journal of Fuzzy Systems0.69 1.0562170305-0041MATHPROCCAMBRIDGE3MATHEMATICAL PROCEEDINGS OFTHE CAMBRIDGE PHILOSOPHICALSOCIETY0.6860.6932181239-629XANNACADSCIFENN-M3ANNALES ACADEMIAE SCIENTIARUMFENNICAE-MATHEMATICA0.6850.6752191524-1904APPLSTOCHMODELBUS3APPLIED STOCHASTIC MODELS INBUSINESS AND INDUSTRY0.6830.692200308-2105P ROYSOCEDINB A3PROCEEDINGS OF THE ROYALSOCIETY OF EDINBURGH SECTION A-MATHEMATICS0.6810.6792211683-3511APPLCOMPUT MATH-BAK3Applied and Computational Mathematics0.680.5512221083-4362TRANSFORMGROUPS3TRANSFORMATION GROUPS0.680.6882230921-7134ASYMPTOTICANAL3ASYMPTOTIC ANALYSIS0.6780.4132240894-9840JTHEORPROBAB3JOURNAL OF THEORETICALPROBABILITY0.6770.6812250001-9054AEQUATIONESMATH3Aequationes Mathematicae0.6760.5112260163-0563NUMERFUNCANALOPT3NUMERICAL FUNCTIONAL ANALYSISAND OPTIMIZATION0.6740.7112270973-5348MATHMODELNATPHENO3Mathematical Modelling of NaturalPhenomena0.6740.6332280233-1888STATISTICS3STATISTICS0.6670.7242292090-8997JFUNCTSPACEAPPL3Journal of Function Spaces andApplications0.6670.6672301063-8539J COMBDES3JOURNAL OF COMBINATORIALDESIGNS0.6640.622310003-6811APPLANAL3APPLICABLE ANALYSIS 0.6630.7442320025-584XMATHNACHR3MATHEMATISCHE NACHRICHTEN0.6630.6822331021-9722NODEA-NONLINEARDIFF3NODEA-NONLINEAR DIFFERENTIALEQUATIONS AND APPLICATIONS0.6590.5382341793-5253JTOPOLANAL4Journal of Topology and Analysis0.6590.6592351068-9613ELECTRON TNUMERANA4ELECTRONIC TRANSACTIONS ONNUMERICAL ANALYSIS0.6490.82361937-0652ALGEBRNUMBERTHEOR4Algebra & Number Theory0.6480.5392370895-4801SIAM JDISCRETEMATH4SIAM JOURNAL ON DISCRETEMATHEMATICS0.6470.6482380037-1912SEMIGROUPFORUM4SEMIGROUP FORUM0.6460.732391110-757XJ APPLMATH4Journal of Applied Mathematics0.6430.6562400024-6093B LONDMATHSOC4BULLETIN OF THE LONDONMATHEMATICAL SOCIETY0.6430.5412411661-7738J FIXPOINTTHEORY A4Journal of Fixed Point Theory andApplications0.6420.7762420515-0361ASTINBULL4Astin Bulletin0.6410.4862430022-250XJ MATHSOCIOL4JOURNAL OF MATHEMATICALSOCIOLOGY0.6410.682440008-414XCAN JMATH4CANADIAN JOURNAL OFMATHEMATICS-JOURNAL CANADIENDE MATHEMATIQUES0.640.5482451661-7207GROUPGEOMDYNAM4Groups Geometry and Dynamics 0.6360.5082460026-9255MONATSHMATH4MONATSHEFTE FUR MATHEMATIK0.6360.6162471864-8258ADVCALCVAR4Advances in Calculus of Variations0.6350.6882481609-3321MOSCMATH J4Moscow Mathematical Journal0.6340.472491745-9737J MATHMUSIC4Journal of Mathematics and Music0.6280.192500033-5606Q JMATH4QUARTERLY JOURNAL OFMATHEMATICS0.6250.6172511369-1473AUSTNZ JSTAT4AUSTRALIAN & NEW ZEALANDJOURNAL OF STATISTICS0.6250.4362521077-8926ELECTRON JCOMB4ELECTRONIC JOURNAL OFCOMBINATORICS0.6230.6382530013-0915PEDINBURGHMATHSOC4PROCEEDINGS OF THE EDINBURGHMATHEMATICAL SOCIETY0.6210.4152540021-8693JALGEBRA4JOURNAL OF ALGEBRA0.620.6132550002-9939P AMMATHSOC4PROCEEDINGS OF THE AMERICANMATHEMATICAL SOCIETY0.6170.6112561432-2994MATHMETHOD OPERRES4MATHEMATICAL METHODS OFOPERATIONS RESEARCH0.6170.4812571472-2739ALGEBRGEOMTOPOL4Algebraic and Geometric Topology 0.6160.5582580926-2245DIFFERGEOMAPPL4DIFFERENTIAL GEOMETRY AND ITSAPPLICATIONS0.6120.6462590022-4049J PUREAPPLALGEBRA4JOURNAL OF PURE AND APPLIEDALGEBRA0.610.5672601865-2433J K-THEORY4Journal of K-Theory0.610.752610007-4497B SCIMATH4BULLETIN DES SCIENCESMATHEMATIQUES0.6060.6312620126-6705BMALAYSMATHSCI SO4Bulletin of the Malaysian MathematicalSciences Society0.6050.7792630039-3223STUDMATH4STUDIA MATHEMATICA0.6040.62640219-4937STOCHDYNAM4Stochastics and Dynamics 0.60.7462650026-1335METRIKA4METRIKA0.5980.6742660022-4812JSYMBOLICLOGIC4JOURNAL OF SYMBOLIC LOGIC0.5920.5622670714-0045SURVMETHODOL4Survey Methodology 0.5920.9272681382-4090RAMANUJAN J4RAMANUJAN JOURNAL0.5890.5112690927-2852APPLCATEGORSTRUCT4APPLIED CATEGORICALSTRUCTURES0.5890.62700214-1493PUBLMAT4PUBLICACIONS MATEMATIQUES0.5890.662710025-5645J MATHSOCJPN4JOURNAL OF THE MATHEMATICALSOCIETY OF JAPAN0.5880.632721938-7989STATINTERFACE4Statistics and Its Interface0.5880.7022730168-0072ANNPUREAPPLLOGIC4ANNALS OF PURE AND APPLIEDLOGIC0.5880.452740893-4983DIFFERINTEGRAL EQU4Differential and Integral Equations0.5840.5842750030-8730PAC JMATH4PACIFIC JOURNAL OF MATHEMATICS0.5840.6262761392-6292MATHMODELANAL4Mathematical Modelling and Analysis 0.5830.4632770364-9024JGRAPHTHEOR4JOURNAL OF GRAPH THEORY0.5820.524。

《Python编程实用技巧》IntroductionAre you a Python enthusiast? Do you want to enhance your Python programming skills and become a more proficient developer? Look no further because "《Python编程实用技巧》" is here to help you! In this article, we will explore the contents of this book, discuss its significance, and present you with a comprehensive review. Whether you are a beginner or an experienced programmer, "《Python编程实用技巧》" is a must-read resource that will greatly benefit you in your Python journey. Chapter 1: Introduction to the Book1.1 What is "《Python编程实用技巧》"?"《Python编程实用技巧》" is a groundbreaking book that aims to provide practical tips and techniques for Python programming. It covers a wide range of topics, from fundamental concepts to advanced tricks, enabling readers to enhance their Python skills effectively. This book is authored by experienced Python developers who have a deep understanding of the language and its unique features.1.2 Importance of "《Python编程实用技巧》"Python is a popular programming language known for its simplicity and versatility. However, mastering Python requires more than just a basic understanding of its syntax. "《Python编程实用技巧》" fills the gap by providing readers with actionable advice and expert insights into Python programming. Whether you are writing scripts, developing web applications, or working on data analysis, this book will equip you with the necessary skills to solve complex problems efficiently. Chapter 2: Key Features of "《Python编程实用技巧》"2.1 Comprehensive Coverage of Python Language Features"《Python编程实用技巧》" covers a wide range of Python language features, including variables, data types, control flow, functions, classes, and modules. Each topic is explained in detail, ensuring readers have a solid foundation in Python programming.2.2 Advanced Techniques and Best PracticesApart from the basics, this book also delves into advanced techniques and best practices that separate an ordinary programmer from an exceptional one. It covers topics such as error handling, debugging,code optimization, and writing efficient algorithms. By mastering these techniques, readers can write cleaner, more optimized code that performs better and is easier to maintain.Chapter 3: Learning Python with Practical Examples 3.1 Practical Examples and Hands-on Approach "《Python编程实用技巧》" follows a practical approach to learning Python. Each concept is illustrated with real-world examples, making it easier for readers to understand and apply the knowledge in their own projects. Learning by doing is an effective method, and this book capitalizes on it to ensure readers can immediately put their newly acquired skills to practice.3.2 Strengthening Python Skills Through ProjectsTo further reinforce the concepts learned, "《Python编程实用技巧》" provides project-based exercises. These exercises challenge readers to apply their knowledge and think critically to solve problems. By completing these projects, readers can build confidence in their abilities and gain valuable hands-on experience in Python programming.Chapter 4: Strategies for Effective Python Development4.1 Code Organization and ModularityOne key aspect of effective Python development is code organization and modularity. "《Python编程实用技巧》" teaches readers how to structure their code for better maintainability and reusability. It covers topics such as choosing appropriate variable names, writing modular code with functions and classes, and applying design patterns for better code structure.4.2 Debugging and Error HandlingDebugging is an inevitable part of software development, and "《Python编程实用技巧》" equips readers with effective debugging techniques. It explains how to use Python's built-in debugging tools and third-party libraries to identify and fix errors. Furthermore, the book provides insights into error handling, teaching readers how to handle exceptions gracefully and build robust applications.Chapter 5: Optimizing Python Code for Performance5.1 Profiling and Performance Analysis"《Python编程实用技巧》" recognizes the importance of writing code that performs well. To optimize Python code for performance, the book introduces readers to profiling and performance analysis techniques. It explains how to identify bottlenecks in code execution and provides strategies for optimizing performance, such as using appropriate data structures and algorithms.5.2 Utilizing Python's Special FeaturesPython offers numerous powerful features that can enhance code performance. "《Python编程实用技巧》" explores these features, including list comprehensions, generator expressions, and built-in functions like map, filter, and reduce. By leveraging these features effectively, readers can write Python code that executes faster and utilizes system resources more efficiently.Chapter 6: Exploring Advanced Python Topics6.1 Metaprogramming and ReflectionFor those seeking to dive deeper into Python, "《Python编程实用技巧》" covers advanced topics such as metaprogramming and reflection.These topics allow developers to write code that modifies itself and introspects its own structure. By understanding metaprogramming and reflection, readers can unlock new possibilities in Python development.6.2 Concurrency and ParallelismAs applications become more complex, the need for concurrent and parallel execution arises. "《Python编程实用技巧》" introduces readers to Python's concurrency and parallelism capabilities, such as threading, multiprocessing, and asynchronous programming. By utilizing these techniques, developers can write applications that take advantage of modern computer architectures and provide better performance. Chapter 7: ConclusionIn conclusion, "《Python编程实用技巧》" is an invaluable resource for anyone looking to enhance their Python programming skills. With its comprehensive coverage of Python language features, practical examples, and expert insights, this book caters to both beginners and experienced programmers. By applying the knowledge gained from this book, readers can write cleaner, more optimized Python code and develop robust applications efficiently. So, what are you waiting for? Dive into "《Python编程实用技巧》" and take your Python programming to the next level!。

1)
给出了非等温的纤维悬浮聚合物熔体领域的多尺度模型，该多尺度模型建立在聚合物大分子尺 度、增韧纤维尺度和宏观流场尺度的耦合上。 通过对4:1平板收缩流的数值模拟，验证了该多尺度 模型在纤维增韧聚合物复合材料加工过程中的有效性。 最后得到了各个尺度上的应力分布信息， 其中宏观流场的法向应力差和剪应力分别关于拐角平分线大致呈对称和反对称分布，而纤维产生的 法向应力差和剪应力则由于纤维的旋转取向运动而在下游产生逆序应力结构，聚合物哑铃大分子则 由于其黏性远小于基体溶液黏性，故而产生层状的法向应力差和剪应力分布。 对于对复合材料性 能影响很大的增韧纤维情况，也得到了其运动规律和取向分布，纤维大体沿流动方向取向，在壁面 处受到强剪切作用而沿壁面取向，在对称线上沿单轴拉伸，在下游区域，由于拐角效应纤维出现旋 转取向运动。 由温度影响聚合物熔体应力的数值结果可知，即使在流动阶段，较低的温度仍有助 于提升熔体的黏弹性。 关键词 纤维取向，黏弹性，多尺度
*
徐鉴君*,+,2)
(天津城市建设学院基础学科部, 天津 300384)
(南开大学数学科学学院, 天津 300071)
+
**
(麦吉尔大学数学与统计学系, H3A2K6)
液态粒子的固化成型是自然界与工业生产领域普遍存在的重要现象。 本文在平均场的概念下 对雾化液粒的凝固过程提出了一个简化的液-固-气-雾(LSGF)数学模型，并在小过冷度的条件下，求 出了有关初值问题的一致有效渐近解。 结果表明：整个动力学过程可以分为两个相互联结的时间 阶段。 （1）液粒初始温度分布的瞬态过渡阶段。 在这个阶段，凝固尚未正式启动，只是系统内 的温度从任意给定的初始分布迅速调整到某一特定空间分布。 （2）液粒向固粒转变阶段。 在这一 阶段，液－固两相开始分离，相界面逐渐向液粒中心传播，直至液相完全消失。 进而以铜为例， 讨论了液态粒子在不同生长条件与一些重要物理参数下的凝固时间与凝固过程中的温度分布的演化 规律。 关键词 Gibbs-Thomson 公式, 过冷度, 无量纲化, 界面条件, 渐近展开, 零级近似解, 内解, 外 解, 一致有效渐近解

Algorithm Design Techniques and Analysis: English VersionExercise with AnswersIntroductionAlgorithms are an essential aspect of computer science. As such, students who are part of this field must master the art of algorithm design and analysis. Algorithm design refers to the process of creating algorithms that solve computational problems. Algorithm analysis, on the other hand, focuses on evaluating the resources required to execute those algorithms. This includes computational time and memory consumption.This document provides students with helpful algorithm design and analysis exercises. The exercises are in the formof questions with step-by-step solutions. The document is suitable for students who have completed the English versionof the Algorithm Design Techniques and Analysis textbook. The exercises cover various algorithm design techniques, such as divide-and-conquer, dynamic programming, and greedy approaches.InstructionEach exercise comes with a question and its solution. Read the question carefully and try to find a solution withoutlooking at the answer first. If you get stuck, look at the solution. Lastly, try the exercise agn without referring to the answer.Exercise 1: Divide and ConquerQuestion:Given an array of integers, find the maximum possible sum of a contiguous subarray.Example:Input: [-2, -3, 4, -1, -2, 1, 5, -3]Output: 7 (the contiguous subarray [4, -1, -2, 1, 5]) Solution:def max_subarray_sum(arr):if len(arr) ==1:return arr[0]mid =len(arr) //2left_arr = arr[:mid]right_arr = arr[mid:]max_left_sum = max_subarray_sum(left_arr)max_right_sum = max_subarray_sum(right_arr)max_left_border_sum =0left_border_sum =0for i in range(mid-1, -1, -1):left_border_sum += arr[i]max_left_border_sum =max(max_left_border_sum, left_b order_sum)max_right_border_sum =0right_border_sum =0for i in range(mid, len(arr)):right_border_sum += arr[i]max_right_border_sum =max(max_right_border_sum, righ t_border_sum)return max(max_left_sum, max_right_sum, max_left_border_s um+max_right_border_sum)Exercise 2: Dynamic ProgrammingQuestion:Given a list of lengths of steel rods and a corresponding list of prices, determine the maximum revenue you can get by cutting these rods into smaller pieces and selling them. Assume the cost of each cut is 0.Lengths: [1, 2, 3, 4, 5, 6, 7, 8]Prices: [1, 5, 8, 9, 10, 17, 17, 20]If the rod length is 4, the maximum revenue is 10.Solution:def max_revenue(lengths, prices, n):if n ==0:return0max_val =float('-inf')for i in range(n):max_val =max(max_val, prices[i] + max_revenue(length s, prices, n-i-1))return max_valExercise 3: Greedy AlgorithmQuestion:Given a set of jobs with start times and end times, find the maximum number of non-overlapping jobs that can be scheduled.Start times: [1, 3, 0, 5, 8, 5]End times: [2, 4, 6, 7, 9, 9]Output: 4Solution:def maximum_jobs(start_times, end_times):job_list =sorted(zip(end_times, start_times))count =0end_time =float('-inf')for e, s in job_list:if s >= end_time:count +=1end_time = ereturn countConclusionThe exercises presented in this document provide a practical way to master essential algorithm design and analysis techniques. Solving the problems without looking at the answers will expose students to the type of problems they might encounter in real life. The document’s solutionsprovide step-by-step instructions to ensure that students can approach the problems with confidence.。

2 2 2 2 2 2 2
数学 0196-6774数学 0178-4617数学 0027-3171 0964-1998 数学 0012-9593 1061-8600 0021-7824 1050-5164 数学 数学 数学 数学
2 2 2 2 2 2
数学 1017-0405数学 0294-1449 数学 0218-2025 数学
数学 0029-599X数学 0012-7094数学 0075-4102 数学
INTERNATIONAL JOURNAL OF BIFURCATION AND CHAOS AMERICAN JOURNAL OF AM J MATH MATHEMATICS ANNALS OF PROBABILITY ANN PROBAB ADVANCES IN MATHEMATICS ADV MATH SIAM JOURNAL ON SIAM J MATH ANAL MATHEMATICAL ANALYSIS STOCHASTIC PROCESSES AND STOCH PROC APPL THEIR APPLICATIONS RISK ANALYSIS RISK ANAL INVERSE PROBLEMS INVERSE PROBL AMERICAN STATISTICIAN AM STAT JOURNAL OF BUSINESS & J BUS ECON STAT ECONOMIC STATISTICS STRUCTURAL EQUATION STRUCT EQU MODELING-A MODELING MULTIDISCIPLINARY JOURNAL SIAM JOURNAL ON MATRIX SIAM J MATRIX ANALYSIS AND APPLICATIONS ANAL A PROBABILITY THEORY AND PROBAB THEORY REL RELATED FIELDS MEMOIRS OF THE AMERICAN MEM AM MATH SOC MATHEMATICAL SOCIETY JOURNAL OF ALGORITHMS J ALGORITHM ALGORITHMICA ALGORITHMICA MULTIVARIATE BEHAVIORAL MULTIVAR BEHAV RESEARCH RES JOURNAL OF THE ROYAL J ROY STAT SOC A STATISTICAL SOCIETY SERIES STA A-STATISTICS IN SOCIETY ANNALES SCIENTIFIQUES DE L ANN SCI ECOLE ECOLE NORMALE SUPERIEURE NORM S JOURNAL OF COMPUTATIONAL J COMPUT GRAPH AND GRAPHICAL STATISTICS STAT JOURNAL DE MATHEMATIQUES J MATH PURE APPL PURES ET APPLIQUEES ANNALS OF APPLIED ANN APPL PROBAB PROBABILITY STATISTICA SINICA STAT SINICA ANNALES DE L INSTITUT ANN I H POINCAREHENRI POINCARE-ANALYSE NON AN LINEAIRE MATHEMATICAL MODELS & MATH MOD METH METHODS IN APPLIED APPL S SCIENCES INT J BIFURCAT CHAOS

国外计算机编程经典书籍1.《代码大全》（Code Complete）作者Steve McConnell。

这本书是软件开发领域的经典之作，涵盖了软件构建过程中的各个方面，包括设计、编码、调试等。

2.《计算机程序的构造和解释》（Structure and Interpretation of Computer Programs）作者Harold Abelson和Gerald Jay Sussman。

这本书被誉为计算机科学教育的经典教材，深入讲解了程序设计的基本原理和方法。

3.《算法导论》（Introduction to Algorithms）作者ThomasH. Cormen、Charles E. Leiserson、Ronald L. Rivest和Clifford Stein。

这本书是关于算法和数据结构的权威指南，被广泛应用于计算机科学教育和专业领域。

4.《设计模式，可复用面向对象软件的基础》（Design Patterns: Elements of Reusable Object-Oriented Software）作者Erich Gamma、Richard Helm、Ralph Johnson和John Vlissides。

这本书介绍了面向对象设计中的23种设计模式，对软件开发具有重要的指导作用。

5.《Clean Code: A Handbook of Agile Software Craftsmanship》作者Robert C. Martin。

这本书强调编写整洁、可读、可维护代码的重要性，是软件工程师必读的经典之作。

6.《编程珠玑》（Programming Pearls）作者Jon Bentley。

这本书以一系列有趣的问题和解决方案展示了高效编程的技巧和方法，对提高编程技能有很大帮助。

以上列举的书籍只是众多优秀计算机编程书籍中的一部分，它们涵盖了计算机科学领域的各个方面，对于想要深入了解编程和软件开发的人来说，都是非常值得阅读和学习的经典之作。

六年级计算机科学英语阅读理解30题1<背景文章>A computer is an amazing device that has become an essential part of our daily lives. It consists of several important components, each with its own unique function.One of the most crucial parts is the Central Processing Unit (CPU). The CPU is often considered the "brain" of the computer. It executes instructions and performs calculations. It fetches data from the memory, processes it, and then stores the results back in the memory.Memory, also known as Random - Access Memory (RAM), is another vital component. RAM is a temporary storage space. When you open a program or a file, it is loaded into the RAM. This allows the CPU to access the data quickly. However, the data stored in RAM is lost when the computer is turned off.The hard disk drive (HDD) or solid - state drive (SSD) is a long - term storage device. It stores all your programs, files, and operating system. The hard disk has a large capacity, which means it can hold a huge amount of data. For example, you can store your photos, videos, and documents on it.The motherboard is like a big circuit board that connects all the components together. It provides the electrical connections and pathwaysfor data to travel between different parts of the computer.1. <问题1>What is the function of the CPU in a computer?A. It only stores data permanently.B. It executes instructions and does calculations.C. It is only used to connect other components.D. It only displays the information on the screen.答案：B。

c++ 信奥赛常用英语在C++ 信奥赛中（计算机奥林匹克竞赛），常用英语词汇主要包括以下几方面：1. 基本概念：- Algorithm（算法）- Data structure（数据结构）- Programming language（编程语言）- C++（C++ 编程语言）- Object-oriented（面向对象）- Function（函数）- Variable（变量）- Constants（常量）- Loops（循环）- Conditional statements（条件语句）- Operators（运算符）- Control structures（控制结构）- Memory management（内存管理）2. 常用算法与数据结构：- Sorting algorithms（排序算法）- Searching algorithms（搜索算法）- Graph algorithms（图算法）- Tree algorithms（树算法）- Dynamic programming（动态规划）- Backtracking（回溯）- Brute force（暴力破解）- Divide and conquer（分治）- Greedy algorithms（贪心算法）- Integer array（整数数组）- Linked list（链表）- Stack（栈）- Queue（队列）- Tree（树）- Graph（图）3. 编程实践：- Code optimization（代码优化）- Debugging（调试）- Testing（测试）- Time complexity（时间复杂度）- Space complexity（空间复杂度）- Input/output（输入/输出）- File handling（文件处理）- Console output（控制台输出）4. 竞赛相关：- IOI（国际信息学奥林匹克竞赛）- NOI（全国信息学奥林匹克竞赛）- ACM-ICPC（ACM 国际大学生程序设计竞赛）- Codeforces（代码力）- LeetCode（力扣）- HackerRank（黑客排名）这些英语词汇在信奥赛领域具有广泛的应用，掌握这些词汇有助于提高选手之间的交流效率，同时对提升编程能力和竞赛成绩也有很大帮助。

大学印象最深刻的科目英语作文My most impressive subject in university is definitely Computer Science. It is a subject that has fascinated me from the beginning, and I have thoroughly enjoyed studying it.Why do you find Computer Science so interesting?Well, for one, it is a subject that is constantly evolving and changing. There is always something new to learn, and the field is always expanding. Additionally, Computer Science has many practical applications in today's world, and I find it exciting to be a part of an industry that is making such a significant impact on society.What are some of the topics you have studied in Computer Science?I have studied a wide variety of topics in Computer Science, ranging from programming languages and algorithms to data structures and computer networks. I have also had the chance to explore more specialized areas, such as artificial intelligence and machine learning.What has been your favorite project or assignment in Computer Science?One of my favorite projects was developing a mobile app that could help people track their daily water intake. It was a challenging project that required me to use my knowledge of both programming and user interface design. But in the end, it was extremely rewarding to see something that I had created being used by others.中文翻译：我在大学中最深刻的科目是计算机科学。

代码特征自动提取方法史志成1,2，周宇1,2,3+1.南京航空航天大学计算机科学与技术学院，南京2100162.南京航空航天大学高安全系统的软件开发与验证技术工信部重点实验室，南京2100163.南京大学软件新技术国家重点实验室，南京210023+通信作者E-mail:***************.cn 摘要：神经网络在软件工程中的应用极大程度上缓解了传统的人工提取代码特征的压力。

已有的研究往往将代码简化为自然语言或者依赖专家的领域知识来提取代码特征，简化为自然语言的处理方法过于简单，容易造成信息丢失，而引入专家制定启发式规则的模型往往过于复杂，可拓展性以及普适性不强。

鉴于以上问题，提出了一种基于卷积和循环神经网络的自动代码特征提取模型，该模型借助代码的抽象语法树（AST ）来提取代码特征。

为了缓解因AST 过于庞大而带来的梯度消失问题，对AST 进行切割，转换成一个AST 序列再作为模型的输入。

该模型利用卷积网络提取代码中的结构信息，利用双向循环神经网络提取代码中的序列信息。

整个流程不需要专家的领域知识来指导模型的训练，只需要将标注类别的代码作为模型的输入就可以让模型自动地学习如何提取代码特征。

应用训练好的分类编码器，在相似代码搜索任务上进行测试，Top1、NDCG 、MRR 的值分别能达到0.560、0.679和0.638，对比当下前沿的用于代码特征提取的深度学习模型以及业界常用的代码相似检测工具有显著的优势。

关键词：代码特征提取；代码分类；程序理解；相似代码搜索文献标志码：A中图分类号：TP391Method of Code Features Automated ExtractionSHI Zhicheng 1,2,ZHOU Yu 1,2,3+1.College of Computer Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China2.Key Laboratory for Safety-Critical Software Development and Verification,Ministry of Industry and Information Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China3.State Key Laboratory for Novel Software Technology,Nanjing University,Nanjing 210023,ChinaAbstract:The application of neural networks in software engineering has greatly eased the pressure of traditional method of extracting code features manually.Previous code feature extraction models usually regard code as natural language or heavily depend on the domain knowledge of experts.The method of transferring code into natural计算机科学与探索1673-9418/2021/15(03)-0456-12doi:10.3778/j.issn.1673-9418.2005048基金项目：国家重点研发计划（2018YFB1003902）；国家自然科学基金（61972197）；中央高校基本科研业务费专项资金（NS2019055）；江苏高校“青蓝工程”。

一种求解正交约束问题的投影梯度方法童谣;丁卫平【摘要】The orthogonality constrained problems has wide applications in eigenvalue problems, sparse principal component analysis, etc. However, it is challenging to solve orthogonality constrained problems due to the non-convexity of the equality constraint. This paper proposes a projection gradient method using Gram-Schmidt process to deal with the orthogonality constraint. The time complexity is bounded by O ( r2 n), which is lower than the classical SVD. Some primary numerical results verified the validity of the proposed method.%摘正交约束优化问题在特征值问题、稀疏主成分分析等方面有广泛的应用。

由于正交约束的非凸性，精确求解该类问题具有一定的困难。

本文提出了一种求解正交约束优化问题的投影梯度算法。

该算法采用施密特标准正交化方法处理正交约束，其时间复杂度为 O ( r2 n)，比传统 SVD 分解复杂度低，且实现简单。

数值实验验证了算法的有效性。

【期刊名称】《湖南理工学院学报（自然科学版）》【年(卷),期】2015(000)002【总页数】5页(P5-9)【关键词】正交约束优化;投影梯度算法;邻近点算法;施密特标准正交化【作者】童谣;丁卫平【作者单位】福州大学数学与计算机科学学院，福州 350108;湖南理工学院数学学院，湖南岳阳 414006【正文语种】中文【中图分类】O224正交约束优化模型在科学与工程计算相关领域有广泛应用, 譬如: 线性和非线性特征值问题[1,2], 组合优化问题[3,4], 稀疏主成分分析问题[5,6], 人脸识别[7], 基因表达数据分析[8], 保角几何[10,11], 1-比特压缩传感[12～14], p-调和流[15～18], 等等, 都离不开正交约束优化模型.一般地, 正交约束优化问题有如下形式:其中F( X)是ℝn×r→ℝ的可微函数, Q是对称正定阵, I是r×r单位阵, n≥r. 由于Q是对称正定的, 可设Q=LT L. 令Y=LX, 则(1)可转化为:线性约束优化问题的求解技术已经比较成熟, 为了简化问题(2)的形式, 我们主要考虑求解如下正交约束优化问题:由于正交约束的非凸性, 精确求解问题(1)或(3)具有一定的挑战. 目前为止, 还没有有效的算法可以保证获取这类问题的全局最优解(除了某些特殊情况, 如: 寻找极端特征值). 由于保持正交约束可行性的计算代价太大, 为了避免直接处理非线性约束, 人们提出了很多方法, 将带约束的优化问题转化成无约束的优化问题求解. 这些方法中, 最常用的有罚函数方法[21,22]和增广拉格朗日方法[19,20].罚函数方法将正交约束违背作为惩罚项添加到目标函数中, 把约束优化问题(3)转化为如下无约束优化问题:其中ρ＞0为罚参数. 当罚参数趋于无穷大时, 罚问题(4)与原问题(3)等价. 为了克服这个缺陷, 人们引入了标准增广拉格朗日方法. Wen和Yang等[23]提出用Lagrange方法求解问题并证明了算法收敛于问题的可行解(在正则条件下, 收敛到平衡点). 最近, Manton [24,25] 等提出了解决正交约束问题的Stiefel manifold 结构方法: Osher [26] 等提出一种基于Bregman迭代的SOC算法. SOC算法结合算子分裂与Bregman迭代方法, 将正交约束问题转化为交替求解一个无约束优化问题和一个具有解析解的二次约束优化问题, 该方法获得了不错的数值实验效果. SOC算法在处理矩阵正交约束的子问题时,使用了传统的SVD分解, 其时间复杂度为O( n3).在本文中, 我们提出一种新的处理正交约束的算法, 该算法计算复杂性比传统的SVD分解要低. 根据问题(3)约束条件的特殊性, 我们将问题求解过程分解为两步: 第一步, 采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 第二步, 将预测点投影到正交约束闭子集上. 基本的数值结果说明了这种正交闭子集投影梯度算法优越于经典增广Lagrange算法.本节给出求解正交约束优化问题的正交闭子集上的投影梯度算法(简记为POPGM). 该方法分为两步: 首先, 采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 然后, 将预测点投影到正交闭子集上, 其中投影算子是一个简单的斯密特标准正交化过程. 为此, 我们先简要介绍邻近点算法.1.1 经典邻近点算法求解无约束优化问题的方法有很多, 包括: 最速下降法, Barzilai-Borwein method[30], 外梯度方法[31],等等. 这里, 我们介绍一种有效的求解算法, 邻近点算法(Proximal Point Algorithm, 简记为PPA)[27,28]. 最初, Rockafellar等[32]提出了求解变分不等式问题的PPA算法. 对于抽象约束优化问题:1.2 投影梯度算法现在给出本文提出的邻近点正交约束投影梯度算法(POPGM):Step 0. 给定初始参数r0＞0, v=0.95, 初始点X0∈Ω, 给定ε＞0, ρ＞1, 令k=0. 注: 子问题(10)等价于求解如下单调变分不等式变分不等式(12)可采用下述显示投影来获得逼近解:由于(11)和(13)均有显示表达式, 可知和Xk都是易于求解的. 另外, 由于r<<n, 与传统SVD分解方法的时间复杂度O( n3)相比, 本文所提出的在正交约束闭子集上投影梯度法的计算时间花费更少, 这是因为(11)式处理正交约束的时间复杂度仅需O( r2 n).本节通过实例来说明POPGM算法的有效性. 实验测试环境为Win7系统,Intel(R)Core i3, CPU .20GHz, RAM 2.0GB, 编程软件为MATLAB R2012b.测试问题及数据取自Yin0. 给定对称矩阵A∈ℝn×n , 和酉矩阵V∈ℝn×r , 当V 是前r个最大特征值所对应特征空间的一组正交基时, 函数Trace(VT AV)达到最大值. 该问题可以考虑为求解如下正交约束优化问题:其中λ1≥λ2≥…≥λr 是我们要提取A的r个最大的特征值, A∈ℝn×n 为对称正定矩阵.实验数据:, 其中, 即中的元素服从均匀分布.实验参数:,ρ=1.6, ε=1.0e-5.初始点: X0=randn(n, r), X0=orth(X0).终止条件: .下面采用三种算法求解上述问题, 分别是本文的POPGM算法, Yin0的algorithm 2(简记为Yin’s Algo.)与MATLAB工具包中的“eigs”函数. 表中的FP/FY/FE 分别表示通过运行POPGM、Yin’s Algo和Eigs所求得的r个最大特征值之和, 即目标函数值; win表示两种算法对比, 所获得的目标函数值之差; err表示可行性误差, 即: e.表1给出了对于固定r=6, n 在500到5000之间变化时, 三种算法在求解问题的迭代次数(iter)与CPU时间(cput)的对比结果. 由表1可知, POPGM迭代次数受矩阵维数影响不大. 随着矩阵维数的增大, POPGM算法与Yin’s Algo.相比, 当n≤2000时, POPGM不仅时间上有优势, 而且提取效果也较好(win＞0); n≥3000时, POPGM时间花费略多, 但提取效果有明显优势. POPGM与“eigs”相比, 随着维数n的增大, 时间优势逐渐变大, 但提取变量的解释能力也逐渐减弱. 由实验结果可知, 当矩阵维数n较大时, POPGM有较好的表现.表2列出了固定n=3000, 提取特征值的个数r在1到23之间变化时POPGM的运行结果. 由表2可以看出, 当r越小, POPGM计算花费时间越少; 随着r增大, FP 增大, 时间花费也在增大; 当r取5到7时, 花费时间合适, 且提取效果较好.表3列出了固定提取r=6, 将POPGM算法框架中的正交化过程替换成SVD分解, 对比两种处理正交约束方法的求解结果. 由表3可知, 在POPGM算法框架下, 在正交约束闭子集上的投影算子比传统的SVD分解在运算时间上要节约很多; 同时, 两种方法所提取的特征之和保持一致, 不随维数变化而变化,时间优势随矩阵维数增大而增大. 可见, 本文提出的处理正交约束的方法非常有效.本文研究求解一类正交约束优化问题的快速算法. 结合邻近点算法和施密特标准正交化过程, 本文提出了基于邻近点算法的非精确投影梯度算法, 算法采用邻近点算法求解松弛的无约束优化问题, 得到预测点; 然后, 将预测点投影到正交约束闭子集上. 与传统的增广拉格朗日法、罚函数方法的主要区别在于POPGM在每一步迭代中通过在正交约束集上投影得到迭代解, 并且避免使用SVD分解, 加快了算法的运行速度. 数值实验说明本文提出的POPGM有较好的综合表现.【相关文献】[1] Edelman A., As T., Arias A., Smith T., et al. The geometry of algorithms with orthogonality constraints [J]. SIAM J. Matrix Anal. Appl., 1998, 20 (2): 303～353[2] Caboussat A., Glowinski R., Pons V. An augmented lagrangian approach to the numerical solution of a non-smooth eigenvalue problem [J]. J. Numer. Math., 2009, 17 (1): 3～26[3] Burkard R. E., Karisch S. E., Rendl F. Qaplib-a quadratic assignment problem library [J]. J. Glob. Optim., 1997, 10 (4): 291～403[4] Loiola E. M., de Arbreu N. M. M., Boaventura –Netto P. O., et al. A survey for thequadratic assignment problem[J]. Eur. J. Oper. Res., 2007, 176 (2): 657～690[5] Lu Z. S., Zhang Y. An augmented lagrangian approach for sparse principal component analysis[J]. Math. Program., Ser. A., 2012, 135: 149～193[6] Shen H., Huang J. Z. Sparse principal component analysis via regularized low rank matrix approximation[J]. J. Multivar. Anal., 2008, 99 (6): 1015～1034[7] Hancock P. Burton A., Bruce V. Face processing: human perception and principal components analysis[J]. Memory Cogn., 1996, 24: 26～40[8] Botstein D. Gene shavingas a method for identifying distinct sets of genes with similar expression patterns[J]. Genme Bil., 2000, 1: 1～21[9] Wen Z., Yin W. T. A feasible method for optimization with orthogonality constraints[J]. Math. Program., 2013, 143(1-2): 397～434[10] Gu X., Yau S. Computing conformal structures of surfaces[J]. Commun. Inf. Syst., 2002, 2 (2): 121～146[11] Gu X., Yau S. T. Global conformal surface parameterization[C]. In Symposium on Geometry Processing, 2003: 127～137[12] Boufounos P. T., Baraniuk R. G. 1-bit compressive sensing [C]. In Conference on information Sciences and Systems (CISS), IEEE, 2008: 16～21[13] Yan M., Yang Y., Osher S. Robust 1-bit compressive sensing using adaptive outlier pursuit [J]. IEEE Trans, Signal Process, 2012, 60 (7): 3868～3875[14] Laska J. N., Wen Z., Yin W., Baraniuk R. G. Trust, but verify: fast and accurate signal recovery from 1-bit compressive measurements [J]. IEEE Trans. Signal Process, 2011, 59 (11): 5289[15] Chan T. F., Shen J. Variational restoration of nonflat image features: models and algorithms [J]. SIAM J. Appl. Math., 2000, 61: 1338～1361[16] Tang B., Sapiro G., Caselles V. Diffusion of general data on non-flat manifolds via harmonic maps theory: the direction diffusion case [J]. Int. J. Comput. Vis., 2000, 36: 149～161[17] Vese L. A., Osher S. Numerical method for p-harmonic flows and applications to image processing[J]. SIAM J. Numer. Anal., 2002, 40 (6): 2085～2104[18] Goldfarb D., Wen Z., Yin W. A curvilinear search method for the p-harmonic flow on spheres [J]. SIAM J. Imaging Sci., 2009, 2: 84～109[19] Glowinski R., Le Tallec P. Augmented Lagrangian and operator splitting methods in nonlinear mechanics [J]. SIAM Studies in Applied Mathematics, Society for Industrial and Applied Mathematics(SIAM), Philadelphia, PA, 1989, 9[20] Fortin M., Glowinski R. Augmented Lagrangian methods: applications to the numerical solution of boundary-value problems [J]. North Holland, 2000, 15[21] Nocedal J., Wright S. J. Numerical Optimization[M]. Springer, New York, 2006[22] Brthuel F., Brezis H., Helein F. Asymptotics for the minimization of a ginzburg-landau functional [J]. Calc. Var. Partial. Differ. Equ., 1993, 1 (2): 123～148[23] Wen Z., Yang C., Liu X. Trace-penalty minimization for large-scale eigenspace computation [J]. J. Scientific Comput., to appear[24] Manton J. H. Optimization algorithms exploiting unitary constraints [J]. IEEE Trans. Signal Process, 2002, 50 (3): 635～650[25] Absil P. -A., Mahony R., Sepulchre R. Optimization algorithms on matrix manifolds [M]. Princeton University Press, Princeton, 2008[26] Lai R., Osher S. A splitting method for orthogonality constrained problem [J]. J Sci Comput., 2014, 58 (2): 431～449[27] He B. S., Fu X. L. and Jiang Z. K. Proximal point algorithm using a linear proximal term [J]. J. Optim. Theory Appl., 2009, 141: 209～239[28] He B. S., Yuan X. M. Convergence analysis of primal-dual algorithms for a saddle-point problem: From contraction perspective [J]. SIAM J. Imaging Sci., 2012, 5: 1119～149 [29] Barzilai J., Borwein J. M. Two-point step size gradient methods [J]. IMA J. Numer. Anal., 1988, 8: 141～148[30] Korpelevich G. M. The extragradient method for finding saddle points and other problems [J]. Ekonomika Matematicheskie Metody, 1976, 12: 747～756[31] Rockafellar R. T. Monotone operators and the proximal point algorithms [J]. SIAM J. Cont. Optim., 1976, 14: 877～898。

第1篇As a candidate for the position of Marketing Manager, your task is to design a comprehensive marketing strategy for a new fitness app, FitActive. The app aims to provide users with personalized workout plans, nutrition guidance, and community support to help them achieve their fitness goals. The app will be launching in a few months and will be competing in a highly competitive market. Your strategy should cover the following areas:1. Market Analysis- Identify the target market for FitActive.- Analyze the competitive landscape, including key competitors and their strengths and weaknesses.- Determine the unique selling points (USPs) of FitActive.2. Brand Positioning- Define the brand identity of FitActive.- Develop a brand message that resonates with the target audience.- Create a logo and visual identity for the app.3. Product Launch- Outline the pre-launch activities, including the beta testing phase.- Design a launch event that generates buzz and attracts early adopters.- Plan the official launch date and time.4. Customer Acquisition- Develop a multi-channel acquisition strategy to reach the target audience.- Implement targeted online advertising campaigns.- Identify and leverage influencers and brand ambassadors to promote the app.5. Customer Retention- Design a loyalty program to encourage repeat usage.- Implement customer feedback mechanisms to continuously improve the app.- Develop content and resources to keep users engaged and motivated.6. Public Relations and Partnerships- Develop a PR strategy to generate media coverage and public interest.- Identify potential partnerships that can enhance the app's value proposition.- Plan events and sponsorships that align with the brand's values.7. Budgeting and ROI Analysis- Estimate the marketing budget required for the first year.- Outline key performance indicators (KPIs) to measure the success of the marketing strategy.- Conduct a cost-benefit analysis to ensure the strategy isfinancially viable.1. Market AnalysisTarget Market:FitActive's target market is divided into two primary segments:- Fitness Enthusiasts: Individuals who are already engaged in regular exercise and are looking for a more personalized approach to fitness.- Sedentary Individuals: Those who are new to exercise or have struggled to maintain a consistent fitness routine.Competitive Landscape:- MyFitnessPal: Offers a comprehensive diet and exercise tracking system.- Nike Training Club: Provides workout plans and videos, with a focus on Nike products.- Fitbit: Combines fitness tracking with social features and challenges.Strengths and Weaknesses:- MyFitnessPal: Strong brand recognition, extensive user base, but limited workout options.- Nike Training Club: High-quality content, integration with Nike products, but limited to Nike users.- Fitbit: Popular for tracking, but lacks personalized workout plans and nutrition guidance.USPs of FitActive:- Personalized Workout Plans: Tailored to individual fitness levels and goals.- Nutrition Guidance: Integrates diet plans with exercise routines.- Community Support: Offers a platform for users to connect, share progress, and motivate each other.2. Brand PositioningBrand Identity:FitActive is a brand that empowers individuals to take control of their health and fitness journey through personalized support and community.Brand Message:"Transform your fitness journey with FitActive – where personalized plans, expert nutrition, and a supportive community make achieving your goals easier than ever."Logo and Visual Identity:The logo should be sleek, modern, and easy to recognize. It should incorporate imagery that represents fitness, such as a person running or lifting weights. The color scheme should be vibrant and energetic, reflecting the brand's positive and empowering message.3. Product LaunchPre-Launch Activities:- Beta Testing: Invite a select group of users to test the app and provide feedback.- Social Media Teasers: Share sneak peeks and behind-the-scenes content to build anticipation.- Influencer Partnerships: Collaborate with fitness influencers to create buzz around the app.Launch Event:- Date and Time: The official launch event will take place on thefirst Friday of the launch month, at 6 PM local time.- Location: A fitness studio or community center with high foot traffic.- Activities: A panel discussion with fitness experts, live workout sessions, and interactive challenges.4. Customer AcquisitionMulti-Channel Acquisition Strategy:- Online Advertising: Invest in search engine marketing (SEM), social media advertising (Facebook, Instagram, Twitter, LinkedIn), and display ads.- Email Marketing: Develop an email marketing campaign to reach potential users who have shown interest in fitness-related content.- Content Marketing: Create valuable content, such as blog posts, infographics, and videos, that educate and engage users.Targeted Online Advertising Campaigns:- Google Ads: Use keywords related to fitness, exercise, and wellness to reach individuals searching for fitness solutions.- Social Media Ads: Target ads based on user interests, demographics, and behaviors.- Retargeting: Use retargeting campaigns to reach individuals who have visited the app's website but haven't converted.Influencer and Brand Ambassador Partnerships:- Fitness Influencers: Partner with fitness influencers to showcase the app's features and benefits.- Brand Ambassadors: Recruit fitness enthusiasts to share their experiences with the app and encourage others to try it.5. Customer RetentionLoyalty Program:- Points System: Users earn points for completing workouts, sharing progress, and engaging with the app's content.- Rewards: Offer rewards such as discounts on fitness equipment, personalized workout plans, and exclusive access to events.Customer Feedback Mechanisms:- In-App Surveys: Conduct regular surveys to gather feedback on the app's features and user experience.- Email Feedback: Send out periodic feedback requests to encourage users to share their thoughts and suggestions.Content and Resources:- Educational Content: Provide valuable content, such as workout guides, nutrition tips, and fitness challenges.- Community Engagement: Host live Q&A sessions with fitness experts, encourage user-generated content, and organize challenges to keep users engaged.6. Public Relations and PartnershipsPR Strategy:- Press Releases: Send out press releases to announce the app's launch, major updates, and achievements.- Media Outreach: Reach out to fitness and wellness publications, blogs, and podcasts to secure coverage.- Social Media Outreach: Engage with media influencers and fitness bloggers to share their experiences with FitActive.Potential Partnerships:- Fitness Brands: Collaborate with fitness brands to offer exclusive deals and promotions.- Health Clubs: Partner with local health clubs to offer joint membership packages.- Corporate Wellness Programs: Work with corporate wellness programs to provide employees with access to FitActive.Events and Sponsorships:- Fitness Events: Sponsor local fitness events and participate in health fairs.- Charity Events: Partner with charity organizations to host fitness-related events and raise awareness for health-related causes.7. Budgeting and ROI AnalysisMarketing Budget Estimation:- Year 1: $500,000- Online Advertising: $200,000- Influencer Partnerships: $100,000- Public Relations and Partnerships: $50,000- Customer Retention Programs: $50,000- Miscellaneous: $50,000Key Performance Indicators (KPIs):- User Acquisition: Number of new users acquired through marketing channels.- User Retention: Percentage of users who continue to use the app after the first month.- Engagement: Number of daily active users and average session duration.- Conversion Rate: Percentage of users who sign up for a premium subscription.Cost-Benefit Analysis:- Costs: Total marketing budget for the first year.- Benefits: Expected revenue from premium subscriptions, in-app purchases, and partnerships.- ROI: Calculate the return on investment based on the difference between benefits and costs.In conclusion, the comprehensive marketing strategy for FitActive involves a multifaceted approach that targets both customer acquisition and retention. By leveraging a strong brand identity, personalized user experience, and strategic partnerships, FitActive aims to establish itself as a leading fitness app in the competitive market.第2篇As a new eco-friendly fashion brand, we are looking to establish our presence in the market and appeal to environmentally conscious consumers. Your task is to design a comprehensive marketing strategy that will effectively launch our brand, increase brand awareness, and drive sales. Please consider the following aspects in your strategy:1. Brand Positioning and Identity (500 words)a. Define the core values and mission of the brand.b. Explain how the brand's products align with these values and the eco-friendly ethos.c. Create a unique value proposition that differentiates the brand from competitors.d. Design a brand identity, including a logo, color scheme, and typography that convey the brand's message and appeal to the target audience.2. Target Audience Analysis (500 words)a. Identify the primary demographic, geographic, and psychographic characteristics of our target audience.b. Explain how the brand's eco-friendly approach resonates with this audience.c. Analyze the consumer behavior and preferences of the target audience in relation to fashion and sustainability.d. Discuss potential challenges in engaging this audience and how to overcome them.3. Market Research and Competitor Analysis (500 words)a. Conduct a SWOT analysis of the market and identify key opportunities and threats.b. Analyze the competitive landscape, including direct and indirect competitors.c. Identify the strengths and weaknesses of our competitors in terms of marketing strategies and product offerings.d. Discuss how our marketing strategy can capitalize on these insights and differentiate our brand.4. Digital Marketing Strategy (1000 words)a. Outline a comprehensive digital marketing plan, including social media, email marketing, content marketing, and search engineoptimization (SEO).b. Identify the key platforms where our target audience is most active and how we will leverage them to increase brand awareness and engagement.c. Develop a content calendar that includes blog posts, videos, infographics, and other content types that align with our brand message and target audience.d. Discuss how we will measure the success of our digital marketing efforts and adjust the strategy accordingly.Social Media Strategy:- Choose three social media platforms and explain how we will utilize them to engage with our audience.- Develop a content strategy for each platform, including types of content, frequency, and engagement tactics.- Discuss how we will measure the performance of our social media campaigns and use insights to optimize future content.Email Marketing Strategy:- Explain the role of email marketing in our overall strategy and how it will be used to nurture leads and convert sales.- Design an email marketing campaign that includes welcome series, product updates, and exclusive offers.- Discuss how we will segment our email list and personalize communications to increase engagement and conversions.Content Marketing Strategy:- Outline a content marketing plan that includes blog posts, videos, and infographics.- Discuss how we will create content that educates, informs, andinspires our target audience.- Explain how we will promote our content and measure its impact on brand awareness and conversions.SEO Strategy:- Discuss how we will optimize our website and content for search engines to increase organic traffic.- Identify keywords and phrases that are relevant to our target audience and incorporate them into our website and content.- Explain how we will measure the success of our SEO efforts and use insights to refine our strategy.5. Traditional Marketing and Public Relations (PR) Strategy (500 words)a. Identify traditional marketing channels that are effective for reaching our target audience, such as print, outdoor, and television advertising.b. Develop a traditional marketing campaign that includes advertising creatives, media placements, and budget allocations.c. Discuss how we will leverage PR to increase brand visibility and credibility, including press releases, media interviews, and influencer partnerships.d. Explain how we will measure the success of our traditional marketing and PR efforts and use insights to refine our strategy.6. Retail and Distribution Strategy (500 words)a. Outline a retail strategy that includes brick-and-mortar locationsand online sales channels.b. Discuss how we will ensure that our products are accessible and convenient for our target audience.c. Explain how we will manage inventory and logistics to maintainproduct availability and customer satisfaction.d. Discuss how we will measure the performance of our retail and distribution channels and use insights to optimize future operations.7. Customer Experience and Satisfaction Strategy (500 words)a. Describe how we will ensure a positive customer experience from the moment they discover our brand to post-purchase support.b. Discuss how we will collect and analyze customer feedback to improve our products and services.c. Explain how we will implement a loyalty program to encourage repeat purchases and foster brand loyalty.d. Discuss how we will measure customer satisfaction and use insights to enhance the overall customer experience.8. Conclusion and Next Steps (250 words)Summarize the key components of your marketing strategy and outline the next steps for implementation. Discuss how you will monitor the progress of the strategy and make necessary adjustments to ensure its success.In your response, please provide a detailed plan that addresses each of the above aspects, showcasing your understanding of marketing principles, strategic thinking, and your ability to create a cohesive and effective marketing strategy for an eco-friendly fashion brand.第3篇Introduction:This document provides a comprehensive set of interview questions and scenarios tailored for a Senior Software Engineer role. The questions are designed to assess the candidate's technical expertise, problem-solving skills, experience, and cultural fit within the team and organization. The document is divided into several sections, each focusing on different aspects of the role.Section 1: Technical Skills and Knowledge1. Programming Languages and Frameworks:- What programming languages are you proficient in, and which one do you consider your strongest?- Can you explain the difference between synchronous and asynchronous programming in JavaScript?- Describe how you would implement a RESTful API using Node.js and Express.- What is a closure, and how do you use it in JavaScript?2. Data Structures and Algorithms:- Explain the difference between a stack and a queue.- How would you implement a binary search tree from scratch?- Describe the time and space complexity of a quicksort algorithm.- What is the purpose of a hash table, and how does it work?3. Database Management:- What are the differences between SQL and NoSQL databases?- Describe how you would optimize a SQL query for performance.- What are the primary data types in MongoDB, and how do you use them?- How do you handle data consistency in a distributed database system?4. Software Design Patterns:- Explain the Singleton design pattern and when it is appropriate to use it.- What is the Observer pattern, and how do you implement it in Java?- Describe the use case of the Factory pattern in software development.- How would you implement the Command pattern in a web application?5. Version Control:- What is your preferred version control system, and why?- Describe how you would resolve a merge conflict in Git.- How do you manage branches and tags in a repository?- What is the purpose of the `.gitignore` file, and how do you use it?Section 2: Problem-Solving and Algorithmic Thinking1. Coding Challenges:- Write a function to find the intersection of two arrays.- Implement a binary search algorithm to find a specific element in an unsorted array.- Write a program to reverse a string in-place.- Describe how you would implement a caching mechanism in a web application.2. Logic Puzzles:- A man starts at the bottom of a well that is 100 meters deep. Every hour, he climbs 10 meters, but then slides down 6 meters. How long will it take him to reach the top?- You are in a race with a friend, and you are 20 meters behind. You can run at a speed of 10 meters per second, but your friend can run at 15 meters per second. How long will it take you to catch up?3. Scenario-Based Questions:- You are working on a project where a critical component is not functioning as expected. How would you approach troubleshooting and resolving the issue?- Describe a situation where you had to optimize a piece of code. What techniques did you use, and how did they improve performance?- How would you design a scalable system to handle a high volume of concurrent requests?Section 3: Experience and Professional Growth1. Professional Experience:- Can you describe a challenging project you have worked on, and what role you played in its success?- What have you learned from a project that did not go as planned?- Describe a time when you had to work with a team member who had a different approach to problem-solving. How did you handle the situation?2. Continuous Learning:- How do you stay updated with the latest trends and technologies in software engineering?- What programming books or resources have had the biggest impact on your career?- Describe a technical challenge you have faced and how you overcame it.3. Soft Skills and Teamwork:- How would you handle a situation where you disagree with a colleague's approach to a problem?- Describe a time when you had to lead a team on a project. What were your key responsibilities, and how did you ensure the team's success?- What is your preferred communication style, and how do you adapt to different team dynamics?Section 4: Cultural Fit and Company Values1. Company Culture:- What are the values of our company, and how do they align with your personal values?- Describe a work environment where you were most productive. What made it effective?- How do you approach feedback and constructive criticism?2. Collaboration and Teamwork:- How would you contribute to a team that is currently facing a challenging deadline?- Describe a time when you had to collaborate with a cross-functional team. What was your role, and how did you ensure effective communication?- What are your expectations for teamwork and collaboration in a professional setting?3. Long-Term Goals:- What are your long-term career goals, and how do you see this role contributing to those goals?- Describe your ideal work environment and what you look for in a company.- How do you envision your growth and development within our organization?Conclusion:This document provides a comprehensive set of interview questions and scenarios for a Senior Software Engineer role. By thoroughly preparing for these questions, candidates can demonstrate their technical expertise, problem-solving skills, experience, and cultural fit within the team and organization. Good luck with your interview!。

&RS\ULJKW E\ 6SDWLDO $XWRPDWLRQ /DERUDWRU\6$/$ 0HVKIUHH 0HWKRG IRU ,QFRPSUHVVLEOH )OXLG '\QDPLFV 3UREOHPV, 7VXNDQRY 9 6KDSLUR 6 =KDQJA Meshfree Method for Incompressible Fluid Dynamics ProblemsI.Tsukanov a∗,V.Shapiro a,S.Zhang ba Spatial Automation LaboratoryUniversity of Wisconsin-Madison1513University AvenueMadison,WI53706,U.S.A.b General Motors R&D CenterWarren,MI48090,U.S.A.Accepted for publication in Int.Journal forNumerical Methods in EngineeringAbstractWe show that meshfree variational methods may be utilized for solution of incompressiblefluid dynamics prob-lems using the R-function method(RFM).The proposed approach constructs an approximate solution that satisfiesall prescribed boundary conditions exactly using approximate distancefields for portions of the boundary,transfiniteinterpolation,and computations on a non-conforming spatial grid.We give detailed implementation of the methodfor two common formulations of the incompressiblefluid dynamics problem:first using scalar stream function for-mulation and then using vector formulation of the Navier-Stokes problem with artificial compressibility approach.Extensive numerical comparisons with commercial solvers and experimental data for the benchmark back-facing stepchannel problem reveal strengths and weaknesses of the proposed meshfree method.Keywords:meshfree method,distancefield,solution structure,Navier-Stokes problem,stream function,artificialcompressibility approach1Introduction1.1Towards meshfree solution of computationalfluid dynamics problemsModeling of the incompressiblefluidflow involves solution of the Navier-Stokes equations inside a geometric domain. The interaction between thefluid and the boundary of the geometric domain,in terms of the mathematical model is described by boundary conditions,formulated for viscousfluid as known velocity profile at the inlet and zero velocity at the walls.The nature of this problem makes its treatment difficult:the solution algorithm needs to incorporate two distinct types of information—(1)analytical information that describes the Navier-Stokes equations and func-tions given as boundary conditions;and(2)geometric information about boundaries where the boundary conditions are prescribed.Conventional methods of engineering analysis solve this problem by employingfirst,the spatial dis-cretization of the geometric domain(a mesh that conforms to the boundary of the geometric domain),and second,the discretization of the Navier-Stokes equations and the boundary conditions over the discretized geometry domain.The resulting approximation,therefore,unifies both functional and geometric information.Such approach,despite its wide usage,has some drawbacks.For example,it is well known that the construction of a“good”mesh is a difficult and time consuming task.In engineering practice design iterations require efficient feedback from the analysis results to the geometric model.However,employment of conforming meshes for solution of engineering problems is not quite suitable for design purposes,because the spatial grid restricts changes of the parameters of the geometric model such that it is difficult or even impossible to change the shape of the model without remeshing.∗Corresponding author.E-mail:igor@These difficulties in the conventional approaches led to the development of methods which use non-conforming1 meshes or no meshes at all.These new meshfree(sometimes they are also called meshless)methods represent a solu-tion of the problem by linear combination of basis functions which may be constructed over meshes not conforming to the shape of the geometric model[3,23,4,17,8,21,25,18,7,9].However,the employment of non-conforming spatial discretization makes the treatment of boundary conditions more difficult.Proposed remedies include the combination of Element Free Galerkin Method(EFG)[4]withfinite element shape functions near the boundary[17],the use of modified variational principle[20],window or correction functions that vanish on the boundary[9],and Lagrange multipliers.Although these techniques appear promising,they often contradict the meshfree nature of the approxi-mation near the boundary,introduce additional constraints on solutions,or lead to systems with an increased number of unknowns[13].Several promising transformation-based approaches to satisfying essential boundary conditions at desired nodal locations have been recently proposed and compared by J.-S.Chen[8].The meshing problem can be substantially simplified by employment of the Cartesian grid methods[42,1,11,5]. These methods represent the geometric model by a hierarchical set of cubical/rectangular cells that simplify computa-tion of the partial derivatives using afinite difference scheme.Instead of requiring that cells conform to the boundaries of the domain,the geometric model of the domain is approximated by quad/octtree spatial decompositions to any prescribed accuracy.This approach is accompanied by introduction of additional sources of errors and potentially exponential(in the subdivision depth)increase in computational cost.In contrast to Cartesian grid methods,immersed boundary methods[24,14,15]solve the problem using a uniform non-conforming grid of points that cover the geometric model.Influence of the boundaries and boundary conditions is accounted for by modification of the differential equation of the problem,based on special case analysis.In this paper,we describe a method that also relies on a non-conforming uniform rectangular grid,but goes sub-stantially further.All prescribed boundary conditions are satisfied exactly by transfinitely interpolating individual boundary conditions inversely proportional to the approximate distance to each boundary portion.The technique can be applied systematically to any and all boundary value problems using the theory of R-functions[30],and the result-ing interpolant can be combined with just about any standard numerical solution method.The method is demonstrated with variational methods applied to the solution of incompressiblefluid dynamics problems:first using scalar stream function formulation,and then using vector formulation of the Navier-Stokes problem with artificial compressibility approach.1.2Brief History of the MethodKantorovich showed that Dirichlet boundary conditions could be satisfied exactly using functions vanishing on the boundary of a geometric object[16].He proposed to represent a solution satisfying Dirichlet boundary conditionu|∂Ω=ϕin the following form:u=ωNi=1C iχi+ϕ,(1)whereωis a function taking on zero value on the boundary of the domain;{χi}N i=1is a system of linearly independent basis functions;{C i}N i=1is a vector of unknown coefficients andϕis a function given as a boundary condition. Different sets of the coefficients{C i}N i=1give different functions u but all of them satisfy the prescribed boundary condition.Numerical values of the unknown coefficients can be obtained via variational or projectional methods. Application of Kantorovich’s method was limited to very simple geometric domains,because at that time it was unclear how to construct functionωfor arbitrary geometric domains.Several years later,Rvachev proposed that functions taking on zero value on the boundary of a geometric domain can be constructed for virtually any geometric object using R-functions[27,28,34].Informally,R-functions serve as a construction toolkit transforming a set-theoretic description of the boundary of a geometric object into a real valued function whose zero set coincides with the boundary.Detailed discussion on R-functions and construction techniques is outside of the scope of this paper,but it can be found in numerous references[28,34,35,26,29]and will be illustrated in section2.2.Functions constructed using R-functions are differentiable everywhere except a finite number of points[28,35]and behave as distances to the boundaries near the boundary points.We will refer 1This should not be confused with the another commonly used terminology of“conforming/non-conformingfinite element”.In this paper the non-conformance of the spatial grid to the shape of the geometric domain means that the grid is extended beyond,and unconstrained by the boundary of the geometric domain.to such functions as approximate distancefields.Besides techniques based on the theory of R-functions[28],other methods may also be applied for construction of approximate distancefields.For example,the level set method [33,32]results in a distance-like functions,albeit defined at a discrete set of points and usually implicitly.In contrast, the approximate distancefields constructed using R-functions are explicitly defined at all points of the space.The successful employment of the level set method to model holes and inclusions was discussed in[38].Similar technique was used to model crack development and propagation in[37].Approximate distancefields can be used for interpolation of the functions and their derivatives prescribed on the boundary pieces of a geometric object[31].Representation of boundaries of a geometric object by approximate distancefields made possible the extension of the Kantorovich’s method into the R-function method(RFM).The RFM allows the satisfaction of many types of boundary conditions exactly by employing solution structures that incorporate boundary conditions,approximate distancefields,and basis functions with unknown coefficients[30]. RFM is essentially a meshfree method because it places no restriction on the choice of the basis functions:they can be constructed over conforming or non-conforming mesh.For example,finite elements can be used as basis functions;in this case,RFM can be viewed as an enhancedfinite element method that treats all given boundary conditions exactly. But in this paper,all computations were performed over a uniform rectangular grid of B-splines and performed within the SAGE system developed by authors[41].In[36],we showed that the method is particularly effective in dealing with moving and deforming boundaryconditions.Figure1:Parametrization of the geometry of a back facing step channel1.3Scope and outlineThis paper serves two purposes.First,the application of the RFM to Computational Fluid Dynamics(CFD)is illus-trated through two different formulations;second,the numerical properties(accuracy and convergence)of the RFM, applied to these formulations,are investigated.The paper will show that the RFM approach to CFD provides a unique andflexible method to link both the functional and geometric information in a unified manner.It will also be shown that the artificial compressibility approach gives good results for low Reynolds numberflow(Re<400).For higher Reynolds numbersflows the RFM needs to be implemented either with Finite V olume(FV)/Finite Difference(FD) numerical schemes or using the regularization approach described in[10].Throughout the paper,we assume thatflow is laminar,fluid is Newtonian,and we focus on two-dimensional problems.In this case incompressible two dimensional viscousflow is described by Navier-Stokes equations and the continuity equation[19]:u ∂u∂x+v∂u∂y−1Re∇2u=−Eu∂p∂x;u ∂v∂x+v∂v∂y−1Re∇2v=−Eu∂p∂y∂u ∂x +∂v∂y=0,(2)where variables u and v are the velocity components in the x and y coordinate directions respectively,p is thepressure variable,Re=23u max2h inletνand Eu=Pρu2maxare Reynolds and Euler numbers respectively.We explorethe accuracy of the RFM and its convergence properties,solving a standard textbook benchmark problem:an incom-pressible viscousfluidflow in a two-dimensional back-facing step channel,whose parametrization is shown in Figure 1.For this problem experimental data[2],as well as the computer simulation results given by the conventionalfluiddynamics systems,are available.For concreteness we let the geometric parameters take on the following numericalvalues:L inlet=5,L channel=12,h inlet=0.5and s=0.471.In order to simplify the comparison of the RFM modeling results with experimental data,we use the same ratio between h inlet and s as in[2].Boundary conditions areformulated as a parabolic velocity profile with u max=1.5at the inlet and zero velocity at the walls of the channel.Most meshfree methods employ some variational principle in order to solve the problem,and the RFM is no ex-ception.Since RFM treats the given boundary conditions exactly,the variational principle is applied to the differentialequation(s)of the problem only.Because viscousfluidflows do not conserve energy,we employ a least squares method.In the paper we discuss the application of the RFM to two different formulation of the incompressiblefluid dynamics problem:stream function and artificial compressibility formulations.The stream function formulation discussed in Section2substantially simplifies the initial problem reducing the system of the Navier-Stokes and continuity equations to a single equation.We use the stream function formulation as an introductory example in order to explain the concept of the RFM solution structure and the RFM solution procedure. The velocity profiles given by the RFM are in good agreement with the experimental data for Reynolds number100. For higher Reynolds numbers the RFM overestimates the position of the reattachment point.The accuracy of the modeling results can be improved by applying the RFM to the primitive variables of the Navier-Stokes equations via an artificial compressibility approach,detailed in Section3.In contrast to the stream function formulation,the artificial compressibility formulation allows modeling offluidflows in channels with arbitrary geo-metric shape including multiple connected channels.Further,it can be easily extended to model three-dimensional and turbulentflows.Since the artificial compressibility formulation leads to solution of a vector problem,application of the RFM to this formulation of incompressiblefluid dynamics problem results in vector solution structures whose construction we explain in Section3.2.Section2.5and Section3.4contain the analysis of the RFM modeling results and their comparison with exper-imental data and numerical results obtained using the commercialfluid analysis system Fluent.Distributions of the velocity components and the pressurefield given by the RFM are in good agreement with experimental data,however the employment of variational methods appears to raise some issues.These observations and possible ways to improve effectiveness of the method are discussed in Section4.2RFM with stream function formulation2.1Stream function formulation and solutionIntroduction of a stream functionψsuch that u=∂ψ∂y and v=−∂ψ∂xallows us to satisfy the continuity equation andto exclude the pressure p from the momentum equations.Substitution of the stream functionψinstead of derivatives of velocity components gives a differential equation for the stream function[19]:1 Re ∇4ψ−∂ψ∂y∂∂x∇2ψ+∂ψ∂x∂∂y∇2ψ=0.(3)Boundary conditions for the stream function at the inlet can be derived from the velocity profile at the inlet which is usually known:ψ|inlet=sV(x,y)cos(n,V)dS,(4)where V=u i+v j is the velocity vector and n is the normal vector to the inlet section.Assuming a parabolic profile for the u component of the velocity vector,as shown in Figure1,with u max=1.5and v=0at the inlet,we obtain the boundary condition for stream function as:ψ|inlet=2h2inlety3+3h inlety2;∂ψ∂n|inlet =0.(5)On the walls of the channel the stream function should satisfy the following boundary conditions:ψ|lower wall =0;ψ|upper wall =h inlet .(6)Since we are dealing with viscous flow,velocity is assumed to be zero on all walls.This condition is expressed in terms of homogeneous Neumann boundary condition for the stream function:∂ψ∂n |walls =0.(7)Boundary conditions for the stream function at the outlet can be derived from two conditions:(a)the total discharge at the outlet should be the same as at the inlet,and (b)the velocity components at the outlet should respectively be:v =0,and u should possess a parabolic profile as is shown in Figure 1.After simplification we get:ψ|outlet =m −y 33+h inlet −s 2y 2+h inlet sy +k ;m =6h inlet (h inlet +s )3;k =m 4 3s 2h inlet +s 3 ;∂ψ∂n |outlet=0.(8)The geometry of the channel,equation (3)together with boundary conditions (4–8)constitutes a complete mathe-matical formulation of the problem.The first steps of solving this problem with RFM are construction of approximate distance fields for boundary pieces and the RFM solution structure for the problem.The solution structure interpolates all given boundary conditions over the specified geometry,but also includes a set of basis functions with undetermined coefficients.The subsequent solution procedure will determine the coefficients that best approximate the govern-ing differential equation in some sense.The solution structure,as well as approximate distance fields,are usually constructed automatically without user’s intervention,but below we show all the construction details manually and explicitly.2.2Theory of R -functions and approximate distance fieldsThe theory of R -functions was originally developed in Ukraine by V .L.Rvachev and his students [28,26,29].A complete list of references through 2001can be found in [22].A brief English summary of the theory of R -functions written by Shapiro in 1988[34]is available as a technical report.An R -function is real-valued function whose sign is completely determined by the signs of its arguments.For example,the function xyz can be negative only when the number of its negative arguments is odd.A similar property is possessed by functions x +y + xy +x 2+y 2and xy +z +|z −yx |,and so on.Such functions ‘encode’Boolean logic functions and are called R -functions .Every Boolean function is a companion to infinitely many R -functions,which form a branch of the set of R -functions.For example,it is well known that min(x 1,x 2)is an R -function whose companion Boolean function is logical “and”(∧),and max(x 1,x 2)is an R -function whose companion Boolean function is logical “or”(∨).But the same branches of R -functions contain many other functions,e.g.x 1∧αx 2≡11+α x 1+x 2− x 21+x 22−2αx 1x 2 ;x 1∨αx 2≡11+α x 1+x 2+x 21+x 22−2αx 1x 2 ,(9)where α(x 1,x 2)is an arbitrary symmetric function such that −1<α(x 1,x 2)≤1.The precise value of αmay or may not matter,and often it can be set to a constant.For example,setting α=1yields the min and max respectively,but setting α=0results in much nicer functions ∨0and ∧0that are analytic everywhere except when x 1=x 2=0.Similarly,R -functionsx 1∧m αx 2≡(x 1∧αx 2)(x 21+x 22)m 2;x 1∨m αx 2≡(x 1∨αx 2)(x 21+x 22)m 2(10)(a)(b)Figure2:(a)Halfspaces that constitute a CSG representation of the channel;(b)the corresponding approximate distancefield(a)(b)Figure3:Approximate distancefields for the portions of the boundary where non-slip boundary conditions are pre-scribed:(a)for the car presented in Figure23(b);(b)for the car presented in Figure23(c)are analytic everywhere except the origin(x1=x2=0),where they are m times differentiable.Many other systems of R-functions are studied in[28].The choice of an appropriate system of R-functions is dictated by many considerations, including simplicity,continuity,differential properties,and computational convenience.Just as Boolean functions,R-functions are closed under ing R-functions,any object defined by a predicate on“primitive”geometric regions(e.g.regions defined by a system of inequalities)can now also be represented by a single inequality,or equation.The latter can be evaluated,differentiated,and possesses many other useful properties.In particular:•the functions are constructed in a‘logical’fashion and can be controlled through intuitive user-defined parame-ters;•functions can be normalized,in which case they behave as distance functions near the boundary of the object and can be differentiated everywhere[28,35];•functions can also be constructed for individual cells and cells complexes,given prescribed values for the func-tions and their gradients;•the functions can be used to define time-varying geometry and used for modeling various complex physical phenomena.Theory of R-functions provides the connection between logical and set operations on geometric primitives and analytic constructions.For every logical or set-theoretic construction,there is a corresponding approximate distance function with the above properties.Furthermore,the translation from logical and set-theoretic description is a matter of simple syntactic substitution that does not require expensive symbolic computations.For example,the geometric domain of the channel in Figure2(a)can be defined as a Boolean(Constructive Solid Geometry)combination of six primitives:Ω=(f1∪f2)∩f3∩f4∩f5∩f6,where x denotes the regularized complement of x,and individual primitives f1through f6are defined by the following inequalities:f1=y≥0;f2=x−L inlet≥0;f3=y−s≥0;f4=L inlet+L channel−x≥0;f5=h inlet−y≥0;f6=x≥0Naturally,all numeric constants can be viewed as specific values for some parameters(size,position,etc.).The constructed Boolean representation can be translated into the approximate distancefield shown in Figure2(b)using R-functions:ω=(f1∨0f2)∧0f3∧0f4∧0f5∧0f6,(11) which is also parameterized by h inlet,s,L inlet and L channel.This example clearly shows that any Boolean representation may be translated into the corresponding approximate distancefield.Similarly,boundary representation of a solid is a union of solid’s faces,each face is a subset of some surface bounded by edges,and so on.This logical description can also be directly translated into a function such that is zero for every point on the boundary and positive elsewhere. Our recent results[35,41]indicate that such functions can be constructed directly from the commercially available solid modeling representations,as well as from a variety of other geometric data structures,such as cell complexes. For example,Figures3(a)and(b)show approximate distancefields for the portions of the boundary where non-slip boundary conditions are prescribed(compare to the car shapes in Figures23(b)and(c)respectively).In the next Section we explain the usage of approximate distancefields for construction of the RFM solution structures and transfinite interpolation of the prescribed boundary conditions.2.3RFM solution structure for stream functionA solution structure is a function that satisfies exactly all prescribed boundary conditions.In general,any RFM solution structure can be represented as a sum of two functions:ψ=ψ0+ψ1(12) whereψ0satisfies homogeneous boundary conditions and contains necessary degrees of freedom in order to approxi-mate the differential equation of the problem;functionψ1interpolates the functions given as boundary conditions(5),Figure4:The RFM solution structure that satisfies boundary conditions(4-8)exactly(6)and(8).The interpolation term is constructed using the transfinite interpolation method[31]which is a generaliza-tion of the inverse distance weighting technique;it matches all specified boundary conditions and extends them inside the domain by some arbitrary but well behaved function.For the problem considered here,it takes:ψ1=ψoutletω2outlet+ψinletω2inlet+ψupper wallω2upper wall+ψlower wallω2lower wall1ω2outlet+1ω2inlet+1ω2upper wall+1ω2lower wall,(13)whereωoutlet,ωinlet,ωupper wall andωlower wall are approximate distancefields that describe outlet,inlet and walls of the channel as it is shown in Figure4.Rasing these functions to the second power assures that boundary condition∂ψ∂n|whole boundary =0is satisfied.Functionψ0in the solution structure(12)serves for approximation of the differential equation of the problem.In our case it can be represented as a product of the second power of an approximate distance to the boundary of the channelωand unknown functionΦwhose sole purpose is the approximation of the differential equation of theproblem:ψ0=ω2Φ.Sinceωtakes on zero value on boundary of the geometric domain,ψ0vanishes on the boundary together with itsfirst normal derivative.Therefore,regardless of the chosen functionΦ,functionψ0satisfies thehomogeneous boundary conditions exactly.In many practical situations functionΦcannot be determined exactly,which is why it is usually represented by a linear combination of basis functions{χi}N i=1:Φ=Ni=1C iχi.(14)The basis functions{χi}N i=1have to be smooth enough in order to approximate the differential equation of the problem. Thus,the RFM solution structure(12)may be rewritten as follows:ψ=ψoutletω2outlet+ψinletω2inlet+ψupper wallω2upper wall+ψlower wallω2lower wall1ω2outlet+1ω2inlet+1ω2upper wall+1ω2lower wall+ω2Ni=1C iχi.(15)This solution structure corresponds to the space that contains functions satisfying the prescribed boundary conditions and is sufficiently complete in the sense of being able to approximate the exact solution with an arbitrary degree of accuracy[30].Employment of the RFM solution structures to represent a solution of a physical problem offers several advantages. In particular:an RFM solution structure treats the prescribed boundary conditions exactly;an RFM solution structure contains no information about the differential equation of the problem which means that the same solution structure can be used to represent solutions of different physical problems with similar types of boundary conditions;basis functions in the solution structure can be constructed over a mesh conforming or non-conforming to a geometric model;solution structure can be easily adjusted to a new geometric model—only approximate distancefields have to be reconstructed in order to represent the boundary pieces of new geometric model;an RFM solution structure can be evaluated and differentiated at any point inside the computational domain;finally,an RFM solution structure can be integrated over the geometric model using adaptive numerical procedures[41].2.4Computation of the coefficients in the solution structureSince the RFM solution structure satisfies the given boundary conditions exactly,to solve the problem we need to find the set of the unknown coefficients{C i}N i=1in the RFM solution structure that gives the best approximation to the differential equation of the boundary value problem.Numerical values of these coefficients can be determined via variational or projectional methods.The differential equation(3)for the stream function contains non-linear terms that have to be linearized before the solution method is applied.After substitution of solution structure(12)into differentialequation (3)and application of Newton-Kantorovich linearization scheme we obtain:1Re ∇4ψn +10− ∂ψn +10∂y ∂∇2ψn 0∂x +∂ψn 0∂y ∂∇2ψn +10∂x −∂ψn +10∂x ∂∇2ψn 0∂y −∂ψn 0∂x ∂∇2ψn +10∂y−∂ψn +10∂y ∂∇2ψ1∂x −∂ψ1∂y ∂∇2ψn +10∂x +∂ψn +10∂x ∂∇2ψ1∂y +∂ψ1∂x ∂∇2ψn +10∂y=−1Re ∇4ψ1+∂ψ1∂y ∂∇2ψ1∂x −∂ψ1∂x ∂∇2ψ1∂y −∂ψn 0∂y ∂∇2ψn 0∂x +∂ψn 0∂x ∂∇2ψn 0∂y .(16)This equation is formulated for the function ψ0satisfying the homogeneous boundary conditions ψ0|∂Ω=0,∂ψ0∂n |∂Ω=0.Equation (16)is solved by an iterative algorithm,and the superscripts n +1and n in the equation denote solutions at the current and previous iterations respectively.The iterative process finishes as soon as the difference between twoconsecutive solutions becomes sufficiently small.At each iteration the least squares method is applied to equation (16)minimizing the residual of the equation:F = Ω1Re ∇4ψn +10− ∂ψn +10∂y ∂∇2ψn 0∂x +∂ψn 0∂y ∂∇2ψn +10∂x −∂ψn +10∂x ∂∇2ψn 0∂y −∂ψn 0∂x ∂∇2ψn +10∂y −∂ψn +10∂y ∂∇2ψ1∂x −∂ψ1∂y ∂∇2ψn +10∂x +∂ψn +10∂x ∂∇2ψ1∂y +∂ψ1∂x ∂∇2ψn +10∂y+1Re ∇4ψ1−∂ψ1∂y ∂∇2ψ1∂x +∂ψ1∂x ∂∇2ψ1∂y +∂ψn 0∂y ∂∇2ψn 0∂x −∂ψn 0∂x ∂∇2ψn 0∂y 2d Ω→min.(17)From the necessary condition of the existence of minimum ∂F ∂C i =0,i =1,...,N we obtain a system of linear equations AC =B whose solution gives the numerical values of the unknown coefficients in the solution structure.Elements of the matrix A and vector B are defined as follows:a ij = Ω 1Re ∇4 ω2χi − ∂∂y ω2χi ∂∇2ψn 0∂x +∂ψn 0∂y ∂∂x ∇2 ω2χi −∂∂x ω2χi ∂∇2ψn 0∂y −∂ψn 0∂x ∂∂y ∇2 ω2χi −∂∂y ω2χi ∂∇2ψ1∂x −∂ψ1∂y ∂∂x ∇2 ω2χi +∂∂x ω2χi ∂∇2ψ1∂y +∂ψ1∂x ∂∂y ∇2(ωχi ) 1Re ∇4 ω2χj − ∂∂y ω2χj ∂∇2ψn 0∂x +∂ψn 0∂y ∂∂x ∇2 ω2χj −∂∂x ω2χj ∂∇2ψn 0∂y −∂ψn 0∂x ∂∂y ∇2 ω2χj −∂∂y ω2χj ∂∇2ψ1∂x −∂ψ1∂y ∂∂x ∇2 ω2χj +∂∂x ω2χj ∂∇2ψ1∂y +∂ψ1∂x ∂∂y∇2 ω2χj d Ω;(18)b i = Ω 1Re ∇4 ω2χi − ∂∂y ω2χi ∂∇2ψn 0∂x +∂ψn 0∂y ∂∂x ∇2 ω2χi −∂∂x ω2χi ∂∇2ψn 0∂y −∂ψn 0∂x ∂∂y ∇2 ω2χi −∂∂y ω2χi ∂∇2ψ1∂x −∂ψ1∂y ∂∂x ∇2 ω2χi +∂∂x ω2χi ∂∇2ψ1∂y +∂ψ1∂x ∂∂y ∇2 ω2χi −1Re ∇4ψ1+∂ψ1∂y ∂∇2ψ1∂x −∂ψ1∂x ∂∇2ψ1∂y −∂ψn 0∂y ∂∇2ψn 0∂x +∂ψn 0∂x ∂∇2ψn 0∂yd Ω(19)Integrals (18)and (19)are computed using adaptive integration algorithm based on the Gauss-Legendre quadrature rule in conjunction with hierarchical space decomposition technique [41].。

A Peer-to-Peer Spatial Cloaking Algorithm for AnonymousLocation-based Services∗Chi-Yin Chow Department of Computer Science and Engineering University of Minnesota Minneapolis,MN cchow@ Mohamed F.MokbelDepartment of ComputerScience and EngineeringUniversity of MinnesotaMinneapolis,MNmokbel@Xuan LiuIBM Thomas J.WatsonResearch CenterHawthorne,NYxuanliu@ABSTRACTThis paper tackles a major privacy threat in current location-based services where users have to report their ex-act locations to the database server in order to obtain their desired services.For example,a mobile user asking about her nearest restaurant has to report her exact location.With untrusted service providers,reporting private location in-formation may lead to several privacy threats.In this pa-per,we present a peer-to-peer(P2P)spatial cloaking algo-rithm in which mobile and stationary users can entertain location-based services without revealing their exact loca-tion information.The main idea is that before requesting any location-based service,the mobile user will form a group from her peers via single-hop communication and/or multi-hop routing.Then,the spatial cloaked area is computed as the region that covers the entire group of peers.Two modes of operations are supported within the proposed P2P spa-tial cloaking algorithm,namely,the on-demand mode and the proactive mode.Experimental results show that the P2P spatial cloaking algorithm operated in the on-demand mode has lower communication cost and better quality of services than the proactive mode,but the on-demand incurs longer response time.Categories and Subject Descriptors:H.2.8[Database Applications]:Spatial databases and GISGeneral Terms:Algorithms and Experimentation. Keywords:Mobile computing,location-based services,lo-cation privacy and spatial cloaking.1.INTRODUCTIONThe emergence of state-of-the-art location-detection de-vices,e.g.,cellular phones,global positioning system(GPS) devices,and radio-frequency identification(RFID)chips re-sults in a location-dependent information access paradigm,∗This work is supported in part by the Grants-in-Aid of Re-search,Artistry,and Scholarship,University of Minnesota. Permission to make digital or hard copies of all or part of this work for personal or classroom use is granted without fee provided that copies are not made or distributed for profit or commercial advantage and that copies bear this notice and the full citation on thefirst page.To copy otherwise,to republish,to post on servers or to redistribute to lists,requires prior specific permission and/or a fee.ACM-GIS’06,November10-11,2006,Arlington,Virginia,USA. Copyright2006ACM1-59593-529-0/06/0011...$5.00.known as location-based services(LBS)[30].In LBS,mobile users have the ability to issue location-based queries to the location-based database server.Examples of such queries include“where is my nearest gas station”,“what are the restaurants within one mile of my location”,and“what is the traffic condition within ten minutes of my route”.To get the precise answer of these queries,the user has to pro-vide her exact location information to the database server. With untrustworthy servers,adversaries may access sensi-tive information about specific individuals based on their location information and issued queries.For example,an adversary may check a user’s habit and interest by knowing the places she visits and the time of each visit,or someone can track the locations of his ex-friends.In fact,in many cases,GPS devices have been used in stalking personal lo-cations[12,39].To tackle this major privacy concern,three centralized privacy-preserving frameworks are proposed for LBS[13,14,31],in which a trusted third party is used as a middleware to blur user locations into spatial regions to achieve k-anonymity,i.e.,a user is indistinguishable among other k−1users.The centralized privacy-preserving frame-work possesses the following shortcomings:1)The central-ized trusted third party could be the system bottleneck or single point of failure.2)Since the centralized third party has the complete knowledge of the location information and queries of all users,it may pose a serious privacy threat when the third party is attacked by adversaries.In this paper,we propose a peer-to-peer(P2P)spatial cloaking algorithm.Mobile users adopting the P2P spatial cloaking algorithm can protect their privacy without seeking help from any centralized third party.Other than the short-comings of the centralized approach,our work is also moti-vated by the following facts:1)The computation power and storage capacity of most mobile devices have been improv-ing at a fast pace.2)P2P communication technologies,such as IEEE802.11and Bluetooth,have been widely deployed.3)Many new applications based on P2P information shar-ing have rapidly taken shape,e.g.,cooperative information access[9,32]and P2P spatio-temporal query processing[20, 24].Figure1gives an illustrative example of P2P spatial cloak-ing.The mobile user A wants tofind her nearest gas station while beingfive anonymous,i.e.,the user is indistinguish-able amongfive users.Thus,the mobile user A has to look around andfind other four peers to collaborate as a group. In this example,the four peers are B,C,D,and E.Then, the mobile user A cloaks her exact location into a spatialA B CDEBase Stationregion that covers the entire group of mobile users A ,B ,C ,D ,and E .The mobile user A randomly selects one of the mobile users within the group as an agent .In the ex-ample given in Figure 1,the mobile user D is selected as an agent.Then,the mobile user A sends her query (i.e.,what is the nearest gas station)along with her cloaked spa-tial region to the agent.The agent forwards the query to the location-based database server through a base station.Since the location-based database server processes the query based on the cloaked spatial region,it can only give a list of candidate answers that includes the actual answers and some false positives.After the agent receives the candidate answers,it forwards the candidate answers to the mobile user A .Finally,the mobile user A gets the actual answer by filtering out all the false positives.The proposed P2P spatial cloaking algorithm can operate in two modes:on-demand and proactive .In the on-demand mode,mobile clients execute the cloaking algorithm when they need to access information from the location-based database server.On the other side,in the proactive mode,mobile clients periodically look around to find the desired number of peers.Thus,they can cloak their exact locations into spatial regions whenever they want to retrieve informa-tion from the location-based database server.In general,the contributions of this paper can be summarized as follows:1.We introduce a distributed system architecture for pro-viding anonymous location-based services (LBS)for mobile users.2.We propose the first P2P spatial cloaking algorithm for mobile users to entertain high quality location-based services without compromising their privacy.3.We provide experimental evidence that our proposed algorithm is efficient in terms of the response time,is scalable to large numbers of mobile clients,and is effective as it provides high-quality services for mobile clients without the need of exact location information.The rest of this paper is organized as follows.Section 2highlights the related work.The system model of the P2P spatial cloaking algorithm is presented in Section 3.The P2P spatial cloaking algorithm is described in Section 4.Section 5discusses the integration of the P2P spatial cloak-ing algorithm with privacy-aware location-based database servers.Section 6depicts the experimental evaluation of the P2P spatial cloaking algorithm.Finally,Section 7con-cludes this paper.2.RELATED WORKThe k -anonymity model [37,38]has been widely used in maintaining privacy in databases [5,26,27,28].The main idea is to have each tuple in the table as k -anonymous,i.e.,indistinguishable among other k −1tuples.Although we aim for the similar k -anonymity model for the P2P spatial cloaking algorithm,none of these techniques can be applied to protect user privacy for LBS,mainly for the following four reasons:1)These techniques preserve the privacy of the stored data.In our model,we aim not to store the data at all.Instead,we store perturbed versions of the data.Thus,data privacy is managed before storing the data.2)These approaches protect the data not the queries.In anonymous LBS,we aim to protect the user who issues the query to the location-based database server.For example,a mobile user who wants to ask about her nearest gas station needs to pro-tect her location while the location information of the gas station is not protected.3)These approaches guarantee the k -anonymity for a snapshot of the database.In LBS,the user location is continuously changing.Such dynamic be-havior calls for continuous maintenance of the k -anonymity model.(4)These approaches assume a unified k -anonymity requirement for all the stored records.In our P2P spatial cloaking algorithm,k -anonymity is a user-specified privacy requirement which may have a different value for each user.Motivated by the privacy threats of location-detection de-vices [1,4,6,40],several research efforts are dedicated to protect the locations of mobile users (e.g.,false dummies [23],landmark objects [18],and location perturbation [10,13,14]).The most closed approaches to ours are two centralized spatial cloaking algorithms,namely,the spatio-temporal cloaking [14]and the CliqueCloak algorithm [13],and one decentralized privacy-preserving algorithm [23].The spatio-temporal cloaking algorithm [14]assumes that all users have the same k -anonymity requirements.Furthermore,it lacks the scalability because it deals with each single request of each user individually.The CliqueCloak algorithm [13]as-sumes a different k -anonymity requirement for each user.However,since it has large computation overhead,it is lim-ited to a small k -anonymity requirement,i.e.,k is from 5to 10.A decentralized privacy-preserving algorithm is proposed for LBS [23].The main idea is that the mobile client sends a set of false locations,called dummies ,along with its true location to the location-based database server.However,the disadvantages of using dummies are threefold.First,the user has to generate realistic dummies to pre-vent the adversary from guessing its true location.Second,the location-based database server wastes a lot of resources to process the dummies.Finally,the adversary may esti-mate the user location by using cellular positioning tech-niques [34],e.g.,the time-of-arrival (TOA),the time differ-ence of arrival (TDOA)and the direction of arrival (DOA).Although several existing distributed group formation al-gorithms can be used to find peers in a mobile environment,they are not designed for privacy preserving in LBS.Some algorithms are limited to only finding the neighboring peers,e.g.,lowest-ID [11],largest-connectivity (degree)[33]and mobility-based clustering algorithms [2,25].When a mo-bile user with a strict privacy requirement,i.e.,the value of k −1is larger than the number of neighboring peers,it has to enlist other peers for help via multi-hop routing.Other algorithms do not have this limitation,but they are designed for grouping stable mobile clients together to facil-Location-based Database ServerDatabase ServerDatabase ServerFigure 2:The system architectureitate efficient data replica allocation,e.g.,dynamic connec-tivity based group algorithm [16]and mobility-based clus-tering algorithm,called DRAM [19].Our work is different from these approaches in that we propose a P2P spatial cloaking algorithm that is dedicated for mobile users to dis-cover other k −1peers via single-hop communication and/or via multi-hop routing,in order to preserve user privacy in LBS.3.SYSTEM MODELFigure 2depicts the system architecture for the pro-posed P2P spatial cloaking algorithm which contains two main components:mobile clients and location-based data-base server .Each mobile client has its own privacy profile that specifies its desired level of privacy.A privacy profile includes two parameters,k and A min ,k indicates that the user wants to be k -anonymous,i.e.,indistinguishable among k users,while A min specifies the minimum resolution of the cloaked spatial region.The larger the value of k and A min ,the more strict privacy requirements a user needs.Mobile users have the ability to change their privacy profile at any time.Our employed privacy profile matches the privacy re-quirements of mobiles users as depicted by several social science studies (e.g.,see [4,15,17,22,29]).In this architecture,each mobile user is equipped with two wireless network interface cards;one of them is dedicated to communicate with the location-based database server through the base station,while the other one is devoted to the communication with other peers.A similar multi-interface technique has been used to implement IP multi-homing for stream control transmission protocol (SCTP),in which a machine is installed with multiple network in-terface cards,and each assigned a different IP address [36].Similarly,in mobile P2P cooperation environment,mobile users have a network connection to access information from the server,e.g.,through a wireless modem or a base station,and the mobile users also have the ability to communicate with other peers via a wireless LAN,e.g.,IEEE 802.11or Bluetooth [9,24,32].Furthermore,each mobile client is equipped with a positioning device, e.g.,GPS or sensor-based local positioning systems,to determine its current lo-cation information.4.P2P SPATIAL CLOAKINGIn this section,we present the data structure and the P2P spatial cloaking algorithm.Then,we describe two operation modes of the algorithm:on-demand and proactive .4.1Data StructureThe entire system area is divided into grid.The mobile client communicates with each other to discover other k −1peers,in order to achieve the k -anonymity requirement.TheAlgorithm 1P2P Spatial Cloaking:Request Originator m 1:Function P2PCloaking-Originator (h ,k )2://Phase 1:Peer searching phase 3:The hop distance h is set to h4:The set of discovered peers T is set to {∅},and the number ofdiscovered peers k =|T |=05:while k <k −1do6:Broadcast a FORM GROUP request with the parameter h (Al-gorithm 2gives the response of each peer p that receives this request)7:T is the set of peers that respond back to m by executingAlgorithm 28:k =|T |;9:if k <k −1then 10:if T =T then 11:Suspend the request 12:end if 13:h ←h +1;14:T ←T ;15:end if 16:end while17://Phase 2:Location adjustment phase 18:for all T i ∈T do19:|mT i .p |←the greatest possible distance between m and T i .pby considering the timestamp of T i .p ’s reply and maximum speed20:end for21://Phase 3:Spatial cloaking phase22:Form a group with k −1peers having the smallest |mp |23:h ←the largest hop distance h p of the selected k −1peers 24:Determine a grid area A that covers the entire group 25:if A <A min then26:Extend the area of A till it covers A min 27:end if28:Randomly select a mobile client of the group as an agent 29:Forward the query and A to the agentmobile client can thus blur its exact location into a cloaked spatial region that is the minimum grid area covering the k −1peers and itself,and satisfies A min as well.The grid area is represented by the ID of the left-bottom and right-top cells,i.e.,(l,b )and (r,t ).In addition,each mobile client maintains a parameter h that is the required hop distance of the last peer searching.The initial value of h is equal to one.4.2AlgorithmFigure 3gives a running example for the P2P spatial cloaking algorithm.There are 15mobile clients,m 1to m 15,represented as solid circles.m 8is the request originator,other black circles represent the mobile clients received the request from m 8.The dotted circles represent the commu-nication range of the mobile client,and the arrow represents the movement direction.Algorithms 1and 2give the pseudo code for the request originator (denoted as m )and the re-quest receivers (denoted as p ),respectively.In general,the algorithm consists of the following three phases:Phase 1:Peer searching phase .The request origina-tor m wants to retrieve information from the location-based database server.m first sets h to h ,a set of discovered peers T to {∅}and the number of discovered peers k to zero,i.e.,|T |.(Lines 3to 4in Algorithm 1).Then,m broadcasts a FORM GROUP request along with a message sequence ID and the hop distance h to its neighboring peers (Line 6in Algorithm 1).m listens to the network and waits for the reply from its neighboring peers.Algorithm 2describes how a peer p responds to the FORM GROUP request along with a hop distance h and aFigure3:P2P spatial cloaking algorithm.Algorithm2P2P Spatial Cloaking:Request Receiver p1:Function P2PCloaking-Receiver(h)2://Let r be the request forwarder3:if the request is duplicate then4:Reply r with an ACK message5:return;6:end if7:h p←1;8:if h=1then9:Send the tuple T=<p,(x p,y p),v maxp ,t p,h p>to r10:else11:h←h−1;12:Broadcast a FORM GROUP request with the parameter h 13:T p is the set of peers that respond back to p14:for all T i∈T p do15:T i.h p←T i.h p+1;16:end for17:T p←T p∪{<p,(x p,y p),v maxp ,t p,h p>};18:Send T p back to r19:end ifmessage sequence ID from another peer(denoted as r)that is either the request originator or the forwarder of the re-quest.First,p checks if it is a duplicate request based on the message sequence ID.If it is a duplicate request,it sim-ply replies r with an ACK message without processing the request.Otherwise,p processes the request based on the value of h:Case1:h= 1.p turns in a tuple that contains its ID,current location,maximum movement speed,a timestamp and a hop distance(it is set to one),i.e.,< p,(x p,y p),v max p,t p,h p>,to r(Line9in Algorithm2). Case2:h> 1.p decrements h and broadcasts the FORM GROUP request with the updated h and the origi-nal message sequence ID to its neighboring peers.p keeps listening to the network,until it collects the replies from all its neighboring peers.After that,p increments the h p of each collected tuple,and then it appends its own tuple to the collected tuples T p.Finally,it sends T p back to r (Lines11to18in Algorithm2).After m collects the tuples T from its neighboring peers, if m cannotfind other k−1peers with a hop distance of h,it increments h and re-broadcasts the FORM GROUP request along with a new message sequence ID and h.m repeatedly increments h till itfinds other k−1peers(Lines6to14in Algorithm1).However,if mfinds the same set of peers in two consecutive broadcasts,i.e.,with hop distances h and h+1,there are not enough connected peers for m.Thus, m has to relax its privacy profile,i.e.,use a smaller value of k,or to be suspended for a period of time(Line11in Algorithm1).Figures3(a)and3(b)depict single-hop and multi-hop peer searching in our running example,respectively.In Fig-ure3(a),the request originator,m8,(e.g.,k=5)canfind k−1peers via single-hop communication,so m8sets h=1. Since h=1,its neighboring peers,m5,m6,m7,m9,m10, and m11,will not further broadcast the FORM GROUP re-quest.On the other hand,in Figure3(b),m8does not connect to k−1peers directly,so it has to set h>1.Thus, its neighboring peers,m7,m10,and m11,will broadcast the FORM GROUP request along with a decremented hop dis-tance,i.e.,h=h−1,and the original message sequence ID to their neighboring peers.Phase2:Location adjustment phase.Since the peer keeps moving,we have to capture the movement between the time when the peer sends its tuple and the current time. For each received tuple from a peer p,the request originator, m,determines the greatest possible distance between them by an equation,|mp |=|mp|+(t c−t p)×v max p,where |mp|is the Euclidean distance between m and p at time t p,i.e.,|mp|=(x m−x p)2+(y m−y p)2,t c is the currenttime,t p is the timestamp of the tuple and v maxpis the maximum speed of p(Lines18to20in Algorithm1).In this paper,a conservative approach is used to determine the distance,because we assume that the peer will move with the maximum speed in any direction.If p gives its movement direction,m has the ability to determine a more precise distance between them.Figure3(c)illustrates that,for each discovered peer,the circle represents the largest region where the peer can lo-cate at time t c.The greatest possible distance between the request originator m8and its discovered peer,m5,m6,m7, m9,m10,or m11is represented by a dotted line.For exam-ple,the distance of the line m8m 11is the greatest possible distance between m8and m11at time t c,i.e.,|m8m 11|. Phase3:Spatial cloaking phase.In this phase,the request originator,m,forms a virtual group with the k−1 nearest peers,based on the greatest possible distance be-tween them(Line22in Algorithm1).To adapt to the dynamic network topology and k-anonymity requirement, m sets h to the largest value of h p of the selected k−1 peers(Line15in Algorithm1).Then,m determines the minimum grid area A covering the entire group(Line24in Algorithm1).If the area of A is less than A min,m extends A,until it satisfies A min(Lines25to27in Algorithm1). Figure3(c)gives the k−1nearest peers,m6,m7,m10,and m11to the request originator,m8.For example,the privacy profile of m8is(k=5,A min=20cells),and the required cloaked spatial region of m8is represented by a bold rectan-gle,as depicted in Figure3(d).To issue the query to the location-based database server anonymously,m randomly selects a mobile client in the group as an agent(Line28in Algorithm1).Then,m sendsthe query along with the cloaked spatial region,i.e.,A,to the agent(Line29in Algorithm1).The agent forwards thequery to the location-based database server.After the serverprocesses the query with respect to the cloaked spatial re-gion,it sends a list of candidate answers back to the agent.The agent forwards the candidate answer to m,and then mfilters out the false positives from the candidate answers. 4.3Modes of OperationsThe P2P spatial cloaking algorithm can operate in twomodes,on-demand and proactive.The on-demand mode:The mobile client only executesthe algorithm when it needs to retrieve information from the location-based database server.The algorithm operatedin the on-demand mode generally incurs less communica-tion overhead than the proactive mode,because the mobileclient only executes the algorithm when necessary.However,it suffers from a longer response time than the algorithm op-erated in the proactive mode.The proactive mode:The mobile client adopting theproactive mode periodically executes the algorithm in back-ground.The mobile client can cloak its location into a spa-tial region immediately,once it wants to communicate withthe location-based database server.The proactive mode pro-vides a better response time than the on-demand mode,but it generally incurs higher communication overhead and giveslower quality of service than the on-demand mode.5.ANONYMOUS LOCATION-BASEDSERVICESHaving the spatial cloaked region as an output form Algo-rithm1,the mobile user m sends her request to the location-based server through an agent p that is randomly selected.Existing location-based database servers can support onlyexact point locations rather than cloaked regions.In or-der to be able to work with a spatial region,location-basedservers need to be equipped with a privacy-aware queryprocessor(e.g.,see[29,31]).The main idea of the privacy-aware query processor is to return a list of candidate answerrather than the exact query answer.Then,the mobile user m willfilter the candidate list to eliminate its false positives andfind its exact answer.The tighter the spatial cloaked re-gion,the lower is the size of the candidate answer,and hencethe better is the performance of the privacy-aware query processor.However,tight cloaked regions may represent re-laxed privacy constrained.Thus,a trade-offbetween the user privacy and the quality of service can be achieved[31]. Figure4(a)depicts such scenario by showing the data stored at the server side.There are32target objects,i.e., gas stations,T1to T32represented as black circles,the shaded area represents the spatial cloaked area of the mo-bile client who issued the query.For clarification,the actual mobile client location is plotted in Figure4(a)as a black square inside the cloaked area.However,such information is neither stored at the server side nor revealed to the server. The privacy-aware query processor determines a range that includes all target objects that are possibly contributing to the answer given that the actual location of the mobile client could be anywhere within the shaded area.The range is rep-resented as a bold rectangle,as depicted in Figure4(b).The server sends a list of candidate answers,i.e.,T8,T12,T13, T16,T17,T21,and T22,back to the agent.The agent next for-(a)Server Side(b)Client SideFigure4:Anonymous location-based services wards the candidate answers to the requesting mobile client either through single-hop communication or through multi-hop routing.Finally,the mobile client can get the actualanswer,i.e.,T13,byfiltering out the false positives from thecandidate answers.The algorithmic details of the privacy-aware query proces-sor is beyond the scope of this paper.Interested readers are referred to[31]for more details.6.EXPERIMENTAL RESULTSIn this section,we evaluate and compare the scalabilityand efficiency of the P2P spatial cloaking algorithm in boththe on-demand and proactive modes with respect to the av-erage response time per query,the average number of mes-sages per query,and the size of the returned candidate an-swers from the location-based database server.The queryresponse time in the on-demand mode is defined as the timeelapsed between a mobile client starting to search k−1peersand receiving the candidate answers from the agent.On theother hand,the query response time in the proactive mode is defined as the time elapsed between a mobile client startingto forward its query along with the cloaked spatial regionto the agent and receiving the candidate answers from theagent.The simulation model is implemented in C++usingCSIM[35].In all the experiments in this section,we consider an in-dividual random walk model that is based on“random way-point”model[7,8].At the beginning,the mobile clientsare randomly distributed in a spatial space of1,000×1,000square meters,in which a uniform grid structure of100×100cells is constructed.Each mobile client randomly chooses itsown destination in the space with a randomly determined speed s from a uniform distribution U(v min,v max).When the mobile client reaches the destination,it comes to a stand-still for one second to determine its next destination.Afterthat,the mobile client moves towards its new destinationwith another speed.All the mobile clients repeat this move-ment behavior during the simulation.The time interval be-tween two consecutive queries generated by a mobile client follows an exponential distribution with a mean of ten sec-onds.All the experiments consider one half-duplex wirelesschannel for a mobile client to communicate with its peers with a total bandwidth of2Mbps and a transmission range of250meters.When a mobile client wants to communicate with other peers or the location-based database server,it has to wait if the requested channel is busy.In the simulated mobile environment,there is a centralized location-based database server,and one wireless communication channel between the location-based database server and the mobile。