
`
中考说明:从07到13年我们发现各区模拟和中考中有很多考题通过距离来限制动点的位置.比如寻找等腰三角形的顶点等等. 一、线段定值问题:
初中知识涉及点到点的距离,点到线的距离,平行线的距离,距离问题可分为以下几类: ① 动点P 到定点O 的距离等于定长d ,其实就是作圆(如图1). ② 动点P 到定直线l 的距离等于定长d ,其实就是作平行线(如图2). ③ 动点P 到两定平行直线的距离倍差,其实是作平行线(图略). ④ 动点到两相交直线的距离相等,其实就是作角平分线.(如图3)
⑤ 动点到三角形三边的距离相等,其实就是三角形的内切圆圆心和旁切圆圆心(如图4).
P
d O
图1图2P 2
P 1
l
d d
图3 角平分线
角平分线
角平分线
角平分线
图4
I 3I 2
I 1
I
二、线段最值问题: 题型一:
已知AB a =,AC b =,其中a b <,求BC 的最值.如图,以点A 为圆心,线段AB 为半径作圆, A ⊙交直线AC 于点1B 、2B ,当点B 与点
1B 重合时,BC 取到最大值为a b +;当点B 和点2B 重合时,BC 取到最小值为b a -.
点评:首尾相连线段求最值,其实就是旋转共线,不重则大,重叠则小.
题型二:
在直线l 上找一点P ,使得其到直线同侧两点A B 、的距离之和最小,如图所示.作点A (或B )关于直线l 的对称点,再连接另一点与对称点,与l 的交点即为P 点.
题型三:
直线12l l 、交于O ,P 是两直线间的一点,在直线12l l 、上分别找一点
A B 、,使得PAB △的周长最短.如图所示,作P 点关于12l l 、的对称点12P P 、,连接12P P ,与12l l 、分别交于A
B 、两点,即为所求. 第二轮复习之
函数图像上点的存在性问题 中的距离、面积与角度
题型一:存在问题中的距离
B 1
B 2
C
B A A'
B
P
A
l O B A
P 2
P 1P l 2
l 1
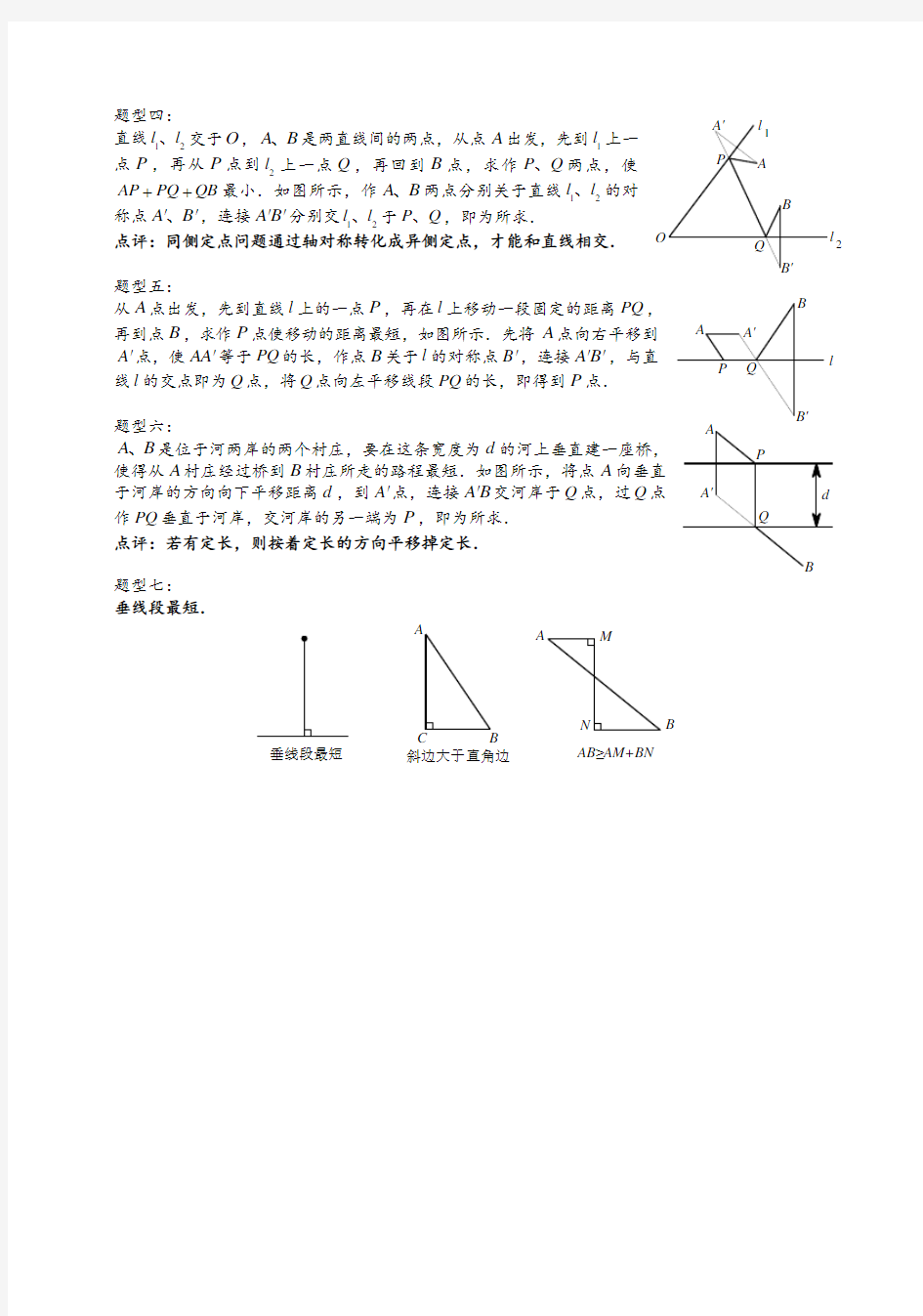
题型四:
直线12l l 、交于O ,A B 、是两直线间的两点,从点A 出发,先到1l 上一点P ,再从P 点到2l 上一点Q ,再回到B 点,求作P Q 、两点,使AP PQ QB ++最小.如图所示,作A B 、两点分别关于直线12l l 、的对称点A B ′′、,连接A B ′′
分别交12l l 、于P Q 、,即为所求. 点评:同侧定点问题通过轴对称转化成异侧定点,才能和直线相交.
题型五:
从A 点出发,先到直线l 上的一点P ,再在l 上移动一段固定的距离PQ ,再到点B ,求作P 点使移动的距离最短,如图所示.先将A 点向右平移到A ′点,使AA ′等于PQ 的长,作点B 关于l 的对称点B ′,连接A B ′′,与直线l 的交点即为Q 点,将Q 点向左平移线段PQ 的长,即得到P 点.
题型六:
A B 、是位于河两岸的两个村庄,要在这条宽度为d 的河上垂直建一座桥,使得从A 村庄经过桥到B 村庄所走的路程最短.如图所示,将点A 向垂直于河岸的方向向下平移距离d ,到A ′点,连接A B ′交河岸于Q 点,过Q 点作PQ 垂直于河岸,交河岸的另一端为P ,即为所求. 点评:若有定长,则按着定长的方向平移掉定长.
题型七:
垂线段最短.
AB ≥AM+BN
N
B
M
A
斜边大于直角边
C B A
垂线段最短
O
l 1l 2
Q
P
B'A'B
A
B'
A'Q
P
B
A
l
【例1】 在平面直角坐标系xOy 中,抛物线223y mx mx n =++经过(35)P ,,(02)A ,两点.
⑴求此抛物线的解析式;
⑵设抛物线的顶点为B ,将直线AB 沿y 轴向下平移两个单位得到直线l ,直线l 与抛物线的对称轴交于C 点,求直线l 的解析式;
⑶在⑵的条件下,求到直线OB 、OC 、BC 距离相等的点的坐标.
【例2】 已知抛物线21y ax bx =++经过点()13A ,
和点()21B ,. ⑴求此抛物线解析式;
⑵点C 、D 分别是x 轴和y 轴上的动点,求四边形ABCD 周长的最小值;
⑶过点B 作x 轴的垂线,垂足为E 点.点P 从抛物线的顶点出发,先沿抛物线的对称轴到达F 点,再沿FE 到达E 点,若P 点在对称轴上的运动速度是它在直线FE 上运动速度的2倍,试确定点F 的位置,使得点P 按照上述要求到达E 点所用的时间最短.(要
求:简述确定F 点位置的方法,但不要求证明)
y x
3
31
221
O 1
F
G
y x
E H D 1
O
C
B
A
典题精练
中考说明:经过分析统计近三年北京模拟题和外地中考题,发现二次函数综合题中涉及面积的题目所占比例极大,其原因大致有两点:一是面积可以通过底和高来限制线段,二是特殊图形面积计算也是中考的考查点.
【例3】 抛物线2
23y x x =--+与x 轴交于点A 、B (点A 在点B 右
侧),与y 轴交于点C ,若点E 为第二象限抛物线上一动点,
连接BE 、CE ,求四边形BOCE 面积的最大值,并求此时E 点的坐标.
【例4】 如图,已知抛物线21
2
y x bx c =++(b ,c 是常数,且0c <)与x 轴分别交于点A ,B (点
A 位于点
B 的左侧),与y 轴的负半轴交于点
C ,点A 的坐标为(10)-,.
⑴ b = ,点B 的横坐标为 (上述结果均用含c 的代数式表示);
⑵ 连接BC ,过点A 作直线AE BC ∥,与抛物线21
2
y x bx c =++交于点E .点D 是x
轴上一点,其坐标为()20,,当C ,D ,E 三点在同一直线上时,求抛物线的解析式;
⑶ 在⑵的条件下,点P 是x 轴下方的抛物线上的一动点,连接PB ,PC ,设所得△PBC 的面积为S .
①求S 的取值范围;
②若△PBC 的面积S 为整数,则这样的△PBC 共有 个.
典题精练
题型二:存在问题中的面积
E
x
O
y
C
B
A
O D C B A y x
1.【存在问题中的角度---特殊角】
中考说明:单个特殊角θ一般指30?、45?、60?等,初中阶段主要考察如何利用特殊角度去构造特殊三角形,从而解决相关问题;初高中衔接知识是特殊直线tan y x m θ=?+与抛物线()20y ax bx c a =++≠的交点.
【例5】 如图,在平面直角坐标系xOy 中,点P 为抛物线2
y x =上一动点,点A 的坐标为()42,,若点P 使
45AOP =?∠,请求出点P 的坐标.
典题精练
构造特殊三角形
特殊角度
45°
30°
题型三:存在问题中的角度
A
x
O y
2.【存在问题中的角度---构造角度相等或角度和】
【例6】 在平面直角坐标系xOy 中,抛物线2y x bx c =++与x 轴交
于A B ,两点(点A 在点B 的左侧),与y 轴交于点C ,点
B 的坐标为(30),
,将直线y kx =沿y 轴向上平移3个单位长度后恰好经过B C ,两点. ⑴求直线BC 及抛物线的解析式;
⑵设抛物线的顶点为D ,点P 在抛物线的对称轴上,且APD ACB ∠=∠,求点P 的坐标;
⑶连接CD ,求OCA ∠与OCD ∠两角和的度数.
1
1
37–2
3
–2–4
x
y
55O
题型一 存在问题中的距离 巩固练习
【练习1】 在平面直角坐标系xOy 中,抛物线2y x bx c =++经过()20A ,、()40B ,两点,直线
1
22
y x =
+交y 轴于点C ,且过点(8)D m ,
. ⑴求抛物线的解析式;
⑵在x 轴上找一点P ,使CP DP +的值最小,求出点P 的坐标; ⑶将抛物线2y x bx c =++左右平移,记平移后点A 的对应点为A ',点B 的对应点为B ',当四边形A B DC ''的周长最小时,求抛物线的解析式及此时四边形A B DC ''周长的最小值.
复习巩固
题型二 存在问题中的面积 巩固练习
【练习2】 如图,正比例函数和反比例函数的图象都经过点()33A ,,把直线OA 向下平移后,
与反比例函数的图象交于点()6B m ,,与x 轴、y 轴分别交于C 、D 两点. ⑴求m 的值;
⑵求过A 、B 、D 三点的抛物线的解析式;
⑶若点E 是抛物线上的一个动点,是否存在点E ,使凸
四边形OECD 的面积1S 是四边形OACD 面积S 的2
3
?若
存在,求点E 的坐标;若不存在,请说明理由.
题型三 存在问题中的角度 巩固练习
【练习3】 如图,点P 是直线l :22y x =--上的点,过点P 的另一条直线m 交抛物线2y x =于
A 、
B 两点.
⑴ 若直线m 的解析式为13
22
y x =-+,求A ,B 两点的坐标;
⑵ ① 若点P 的坐标为()2t -,.当PA AB =时,请直接写出点A 的坐标;
② 试证明:对于直线l 上任意给定的一点P ,在抛物线上能找到点A ,使得PA AB
= 成立.
⑶ 设直线l 交y 轴于点C ,若AOB △的外心在边AB 上,且BPC OCP ∠=∠,求点P 的 坐标.
m
函数对称性的解题方法归纳 讲函数的对称性主要是讲奇偶函数图像的对称性,函数与反函数图像的对称性。前者是函数自身的性质,而后者是函数的变换问题。下文中我们均简称为函数的变换性。函数的对称性在近几年高考中屡见不鲜,对于解决其它问题也很有帮助,同时也是数学美的很好体现。现通过函数自身的对称性和不同函数之间的对称变换这两个方面来探讨函数对称性有关的性质。 1. 函数自身的对称性探究 设函数 )2()2(),()(x f x f x f +=-∞+-∞上满足在,)7()7(x f x f +=-,且在闭区间[0,7]上只有0)3()1(==f f (1)试判断函数)(x f y =的奇偶性; (2)试求方程0)(=x f 在闭区间[-2005,2005]上根的个数并证明你的结论。 分析:由)7()7(),2()2(x f x f x f x f +=-+=-可得:函数图象既关于x =2对称,又关于x =7对称,进而可得到周期性,然后再继续求解,而本题关键是要首先明确函数的对称性,因此,熟悉函数对称性是解决本题的第一步。 定理1 函数)(x f y =的图像关于直线x =a 对称的充要条件是)()(x a f x a f -=+即)2()(x a f x f -= 证明(略) 推论 函数)(x f y =的图像关于y 轴对称的充要条件是)()(x f x f -= 定理2 函数)(x f y =的图像关于点A (a ,b )对称的充要条件是 b x a f x f 2)2()(=-+ 证明(略) 推论 函数)(x f y =的图像关于原点O 对称的充要条件是0)()(=-+x f x f 偶函数、奇函数分别是定理1,定理2的特例。 定理3 ①若函数)(x f y =的图像同时关于点A (a ,c )和点B (b ,c )成中心对称(b a ≠),则)(x f y =是周期函数,且b a -2是其一个周期。
例1: 在梯形ABCD中,AD∥BC,AB=AD=DC=2cm,BC=4cm,在等腰△PQR中,∠QPR=120°,底边QR=6cm,点B、C、Q、R在同一直线l上,且C、Q两点重合,如果等腰△PQR 以1cm/秒得速度沿直线l箭头所示方向匀速运动,t秒时梯形ABCD与等腰△PQR重合部分得面积记为S平方厘米 (1)当t=4时,求S得值 (2)当,求S与t得函数关系式,并求出S得最大值 25、(1)t=4时,Q与B重合,P与D重合, 重合部分就就是=
例2:如图,直线与两坐标轴分别相交于A 、B 点,点M就就是线段AB 上任意一点(A 、B两点除外),过M 分别作MC ⊥OA于点C,M D⊥O B于D 、 (1)当点M在AB 上运动时,您认为四边形O CMD 得周长就就是否发生变化?并说明理由; (2)当点M 运动到什么位置时,四边形O CMD 得面积有最大值?最大值就就是多少? (3)当四边形OC MD 为正方形时,将四边形OCM D沿着x轴得正方向移动,设平移得距离为,正方形OCMD 与△AOB 重叠部分得面积为S 、试求S 与得函数关系式并画出该函数得图象、 解:(1)设点M 得横坐标为x,则点M 得纵坐标为-x+4(0 函数的对称性 知识梳理 一、对称性的概念及常见函数的对称性 1、对称性的概念 ①函数轴对称:如果一个函数的图像沿一条直线对折,直线两侧的图像能够完全重合,则称该函数具备对称性中的轴对称,该直线称为该函数的对称轴。 ②中心对称:如果一个函数的图像沿一个点旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,该点称为该函数的对称中心。 2、常见函数的对称性(所有函数自变量可取有意义的所有值) ①常数函数;②一次函数;③二次函数;④反比例函数;⑤指数函数;⑥对数函数;⑦幂函数;⑧正弦函数; ⑨正弦型函数sin()y A x ω?=+既是轴对称又是中心对称;⑩余弦函数;⑾正切函数;⑿耐克函数; ⒁绝对值函数:这里主要说的是(||)y f x =和|()|y f x =两类。前者显然是偶函数,它会关于y 轴对称;后者是把x 轴下方的图像对称到x 轴的上方,是否仍然具备对称性,这也没有一定的结论,例如|ln |y x =就没有对称性,而|sin |y x =却仍然是轴对称。 ⒂形如(0,)ax b y c ad bc cx d +=≠≠+的图像是双曲线,其两渐近线分别直线d x c =- (由分母为零确定)和直线a y c =(由分子、分母中x 的系数确定),对称中心是点(,)d a c c -。 二、抽象函数的对称性 【此类问题涉及到了函数图象的两种对称性,一种是同一函数自身的对称性,我们称其为自对称;另一种是两个函数之间的对称性 ,我们称其为互对称。】 1、函数)(x f y =图象本身的对称性(自对称问题) (1)轴对称 ①)(x f y =的图象关于直线a x =对称 ?)()(x a f x a f -=+ ?)2()(x a f x f -= ?)2()(x a f x f +=- 课题:正弦函数、余弦函数的图象和性质(五)——正弦函数图象的对称性 教材:人教版全日制普通高级中学数学教科书(必修)第一册(下) 【教学目标】 1.使学生掌握正弦函数图象的对称性及其代数表示形式,理解诱导公式 x x sin )sin(=-π(∈x R )与x x sin )2sin(-=-π(∈x R )的几何意义,体会正 弦函数的对称性. 2.在探究过程中渗透由具体到抽象,由特殊到一般以及数形结合的思想方法,提高学生观察、分析、抽象概括的能力. 3.通过具体的探究活动,培养学生主动利用信息技术研究并解决数学问题的能力,增强学生之间合作与交流的意识. 【教学重点】 正弦函数图象的对称性及其代数表示形式. 【教学难点】 用等式表示正弦函数图象关于直线2 π =x 对称和关于点)0,(π对称. 【教学方法】 教师启发引导与学生自主探究相结合. 【教学手段】 计算机、图形计算器(学生人手一台). 【教学过程】 一、复习引入 1.展示生活实例 对称在自然界中有着丰富多彩的显现,各种对称图案、对称符号也都十分普遍(见下图). 2.复习对称概念 初中我们已经学习过轴对称图形和中心对称图形的有关概念: 轴对称图形——将图形沿一条直线折叠,直线两侧的部分能够互相重合; 中心对称图形——将图形绕一个点旋转180°,所得图形与原图形重合. 3.作图观察 请同学们用图形计算器画出正弦函数的图象(见右图),仔细观察正弦曲线是否是对称图形?是轴对称图形还是中心对称图形? 4.猜想图形性质 经过简单交流后,能够发现正弦曲线既是轴对称图形也是中心对称图形,并能够猜想出一部分对称轴和对称中心.(教师点评并板书) 如何检验猜想是否正确? 我们知道, 诱导公式x x sin )sin(-=-(∈x R ),刻画了正弦曲线关于原点对称,而x x cos )cos(=-(∈x R ),刻画了余弦曲线关于y 轴对称. 从这两个特殊的例子中我们得到一些启发,如果我们能够用代数式表示所发现的对称性,就可以从代数上进行严格证明. 今天我们利用图形计算器来研究正弦函数图象的对称性.(板书课题) 二、探究新知 分为两个阶段,第一阶段师生共同探讨正弦曲线的轴对称性质,第二阶段学生自主探索正弦曲线的中心对称性质. (一)对于正弦曲线轴对称性的研究 第一阶段,实例分析——对正弦曲线关于直线2 π =x 对称的研究. 1.直观探索——利用图形计算器的绘图功能进行探索 请同学们在同一坐标系中画出正弦曲线和直线 2 π = x 的图象,选择恰当窗口并充分利用画图功能对问 题进行探索研究(见右图),在直线2 π =x 两侧正弦函 数值有什么变化规律? 给学生一定的时间操作、观察、归纳、交流,最后得出猜想:当自变量在2 π =x 左右对称取值时,正 弦函数值相等. 二次函数图象的几何变换 内容基本要求略高要求较高要求二次函数 1.能根据实际情境了解二次函数 的意义; 2.会利用描点法画出二次函数的 图像; 1.能通过对实际问题中的情境分 析确定二次函数的表达式; 2.能从函数图像上认识函数的性 质; 3.会确定图像的顶点、对称轴和 开口方向; 4.会利用二次函数的图像求出二 次方程的近似解; 1.能用二次函数 解决简单的实际 问题; 2.能解决二次函 数与其他知识结 合的有关问题; (1)具体步骤: 先利用配方法把二次函数化成2 () y a x h k =-+的形式,确定其顶点(,) h k,然后做出二次函数 2 y ax =的图像,将抛物线2 y ax =平移,使其顶点平移到(,) h k.具体平移方法如图所示: (2)平移规律:在原有函数的基础上“左加右减”. 二、二次函数图象的对称变换 二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1. 关于x轴对称 2 y ax bx c =++关于x轴对称后,得到的解析式是2 y ax bx c =---; ()2 y a x h k =-+关于x轴对称后,得到的解析式是()2 y a x h k =---; 2. 关于y轴对称 2 y ax bx c =++关于y轴对称后,得到的解析式是2 y ax bx c =-+; ()2 y a x h k =-+关于y轴对称后,得到的解析式是()2 y a x h k =++; 3. 关于原点对称 2 y ax bx c =++关于原点对称后,得到的解析式是2 y ax bx c =-+-; ()2 y a x h k =-+关于原点对称后,得到的解析式是()2 y a x h k =-+-; 函数中的面积问题 1.如图,在直角梯形ABCD 中,AD BC ∥,90B ∠?=, 6AD cm =,8AB cm =,14BC cm =.动点P Q 、都从点C 出发,点P 沿C B →方 向做匀速运动,点Q 沿C D A →→方向做匀速运动,当P Q 、其中一点到达终点时,另一点也随之停止运动. (1)求CD 的长; (2)若点P 以1/ cm s 速度运动,点Q 以22/cm s 的速度运动,连接BQ PQ 、,设 BQP 面积为2S cm (),点P Q 、运动的时间为t s () ,求S 与t 的函数关系式,并写出t 的取 值范围; (3)若点P 的速度仍是1/cm s ,点Q 的速度为/acm s ,要使在运动过程中出现 PQ DC ∥,请你直接写出a 的取值范围. 解析:(1)过D 点作DH BC ⊥,垂足为点H , 则有8DH AB cm ==,6BH AD cm == ∴1468CH BC BH cm =-=-= 在Rt DCH 中,CD ==. (2)当点P Q 、运动的时间为t s () ,则PC t =. ①当Q 在CD 上时,过Q 点作QG BC ⊥,垂足为点G , 则由点Q 的速度为/s ,得QC =. 又∵DH HC =,DH BC ⊥, ∴45C ∠?=. ∴在Rt QCG 中,·sin sin 452QG QC C t ∠?===. 又∵14BP BC PC t =-=-, ∴211 (14)21422 BPQ S BP QG t t t t == -=- 当Q 运动到D 点时所需要的时间4t = == ∴2 1404S t t t =-≤(<). ②当Q 在DA 上时,过Q 点作QG BC ⊥,垂足为点G , 则8QG AB cm ==,14BP BC PC t =-=-. ∴11 (14)856422 BPQ S BP QG t t ==-=- 课题:函数图像的对称变换(2课时) 学情分析:相对于函数图象的平移变换,对称变换是学生的难点,对于具体函数,学生还有一定的思路,但结论性的结果,学生掌握的不是很好。 教学目标: (1) 通过具体实例的探讨与分析,得到一些对称变换的结论。 (2) 通过一定的应用,加强学生对对称变换结论的理解。 (3) 能数形结合解决想过题目。 教学过程: 欣赏图片,感受对称 一、师生共同分析讨论完成下列结论的形成。 1、(1)函数()y f x =-与()y f x =的图像关于 对称; (2)函数()y f x =-与()y f x =的图像关于 对称; (3)函数()y f x =--与()y f x =的图像关于 对称. 2、奇函数的图像关于 对称,偶函数图像关于 对称. 3、(1)若对于函数()y f x =定义域内的任意x 都有()()f a x f b x +=-,则 ()y f x =的图像关于直线 对称. (2)若对于函数()y f x =定义域内的任意x 都有()2()f a x b f a x +=--,则()y f x =的图像关于点 对称. 4、对0a >且1a ≠,函数x y a =和函数log a y x =的图象关于直线 对 称. 5、要得到()y f x =的图像,可将()y f x =的图像在x 轴下方的部分以 为轴翻折到x 轴上方,其余部分不变. 6、要得到()y f x =的图像,可将()y f x =,[)0,x ∈+∞的部分作出,再利用偶函数的图像关于 的对称性,作出(),0x ∈-∞时的图像. 二、学生先独立完成,再分析点评 2 3、函数x y e =-的图象与函数 的图象关于坐标原点对称. 4、将函数1()2x f x +=的图象向右平移一个单位得曲线C ,曲线C '与曲线C 关于直线y x =对称,则C '的解析式为 . 5、设函数()y f x =的定义域为R ,则函数(1)y f x =-与(1)y f x =-的图像的关系为关 于 对称. 6、若函数()f x 对一切实数x 都有(2)(2)f x f x +=-,且方程()0f x =恰好有四个不同实根,求这些实根之和为 . 二、典例教学 【例1】填空题: (1 (2)对于定义在R 上的函数()f x ,有下列命题,其中正确的序号为 . ①若函数()f x 是奇函数,则(1)f x -的图象关于点(1,0)A 对称;②若对x R ∈,有 §2.2由面积产生的函数关系问题 图形运动的过程中,求面积随某个量变化的函数关系,是中考数 学的热点问题. 计算面积常见的有四种方法,一是规则图形的面积用面积公式; 二是不规则图形的面积通过割补进行计算;三是同高(或同底)三角形 的面积比等于对应边(或高)的比;四是相似三角形的面积比等于相似 比的平方. 前两种方法容易想到,但是灵活使用第三种和第四种方法,可以 使得运算简单. 一般情况下,在求出面积S关于自变量x的函数关系后,会提出在 什么情况下(x为何值时),S取得最大值或最小值. 关于面积的最值问题,有许多经典的结论. 1.周长一定的矩形,当正方形时,面积最大. 2.面积一定的矩形,当正方形时,周长最小. 3.周长一定的正多边形,当边数越大时,面积越大,极限值是圆. 4.如图1,锐角△ABC的内接矩形DEFG的面积为y, AD=x,当点D 是AB的中点时,面积y最大. 5.如图2,点P在直线AB上方的抛物线上一点,当点P位于AB 的中点E的正上方时,△PAB的面积最大. 6.如图3,△ABC中,∠A和对边BC是确定的,当AB=AC时,△ABC 的面积最大. 图1 图2 图3 x2+bx+c的图象与如图所示,在平面直角坐标系中,二次函数y=-1 4 坐标轴交于A、B、C三点,其中点A的坐标为(0, 8),点B的坐标为(-4, 0). (1) 求该二次函数的表达式及点C的坐标; (2) 点D的坐标为(0, 4),点F为该二次函数在第一象限内图象上的动点,连结CD、CF,以CD、CF为邻边作平行四边形CDEF.设平行四边形CDEF的面积为S. ①求S的最大值; ②在点F的运动过程中,当点E落在该二次函数的图象上时,请直接写出此时S的值. 请打开几何画板文件名“16淮安27”,拖动点F在第一象限内的抛物线上运动,观察△CDF的面积随点F变化的函数图象,可以体验到,当点F的横坐标为3时,△CDF的面积最大;当点F的横坐标为7时,点E落在抛物线上. 1.把点F的横坐标x设为自变量,用x表示△CDF的面积. 2.连结OF“割补”△CDF比较简便. 3.如果设点F的坐标为(m, n),根据FE与CD平行且相等,通过坐标平移可以表示点E的坐标,再把点F、E的坐标分别代入抛物线的解析式,联立方程组求m的值. 正弦函数图象的对称轴与对称中心 Revised on November 25, 2020 函数 )sin(?ω+=x A y 图象的对称轴与对称中心 新疆民丰县一中 亚库普江·奥斯曼 摘要: 新课标高中数学教材上函数的性质就着重讲解了单调性、奇偶性、周期性,但在考试测验甚至高考中不乏的会出现函数对称性、连续性、凹凸性的考查。尤其是对称性,因为教材上对它有零散的介绍,例如二次函数的对称轴、反此例函数的对称性、三角函数的对称性,因而考查的频率一直比较高。以我的经验看,这方面一直是教学的难点,尤其是轴象函数的对称性判断。所以这里我对高中阶段所涉及的函数)sin(?ω+=x A y 的对称性知识提出自己的观点。 关键词:对称轴,对称中心,正弦型函数 函数轴对称:如果一个函数的图象沿一条直线对折,直线两则的图像能够完全重合,则称该函数具备对称性中的轴对称,该直线称为该函数的对称轴。 中心对称:如果一个函数的图像沿一个点折旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,该点称为该函数的对称中心。 正弦函数x y sin =的图像既是轴对称又是中心对称,它的图象关于过最值点且垂直于x 轴的直线分别成轴对称图形; x y sin =的图象的对称轴是经过其 图象的“峰顶点”或“谷底点”,且平行于y 轴的无数条直线;它的图象关于x 轴 的交点分别成中心对称图形。 ∴正弦函数x y sin =的对称轴方程为2 π π+ =k y ,对称中心点为 (0,πk ),其中 Z k ∈。 正弦型函数 )sin(?ω+=x A y 是由正弦函数x y sin =演变而成。 函数对称性 一知识点精讲: I 函数)(x f y =图象本身的对称性(自身对称) 1、)()(x b f x a f -=+?)(x f y =图象关于直线2 2)()(b a x b x a x +=-++=对称 证明:函数)(x f y =图象上的任一点00(,)P x y (满足00()f x y =)关于直线a b x +=的对称点为 (Q a b +∴点Q 推论1推论2推论32、f ((Q a b +∴点Q 推论1推论2推论3II 1、y 2、y 345.函数证明:函数()y f a x =+图象上的任一点00(,)P x y (满足00()f a x y +=)关于直线2b a x -= 的对称点为00(,)Q b a x y --,Q 000[()]()f b b a x f a x y ---=+= ∴点Q 在函数()y f b x =-的图象上;反之函数()y f b x =-的图象上任一点关于直线2 b a x -= 的对称点也在函数()y f a x =+图象上.从而函数()y f a x =+与()y f b x =-的图象关于直线2 b a x -=对称. 推论1:函数)(x a f y +=与)(x a f y -=图象关于直线0=x 对称 推论2:函数)(x f y =与)2(x a f y -=图象关于直线a x =对称 推论3:函数)(x f y -=与)2(x a f y +=图象关于直线a x -=对称 6若函数)(x f y =的定义域为R ,则函数()y f a x =+与()y f b x =--的图象关于点( ,0)2 b a -对称. 证明:函数()y f a x =+图象上的任一点00(,)P x y (满足00()f a x y +=)关于点(,0)2 b a -的对称点为00(,)Q b a x y ---,Q 000[()]()f b b a x f a x y ----=-+=- ∴点Q 在函数()y f b x =--的图象上;反之函数()y f b x =--的图象上任一点关于点(,0)2 b a -的对称点也在函数()y f a x =+图象上.从而函数()y f a x =+与()y f b x =--的图象关于点(,0)2b a -对称. 二典例解析: 11x (log 2f 解析:)(x f -(log f 234 5 解析:的,故6、设y )2(x f =解析:)2(x f 是由2 1=x ,=x 7个实根之和为解析:)(x f y =的图象关于直线3=x 对称,故五个实根,有两对关于直线3=x 对称,它们的和为12,还有一个根就是3。故这5个实根之和为15,正确答案为15 8、设函数)(x f y =的定义域为R ,则下列命题中, ①若)(x f y =是偶函数,则)2(+=x f y 图象关于y 轴对称; ②若)2(+=x f y 是偶函数,则)(x f y =图象关于直线2=x 对称; ③若)2()2(x f x f -=-,则函数)(x f y =图象关于直线2=x 对称; ④)2(-=x f y 与)2(x f y -=图象关于直线2=x 对称, 其中正确命题序号为_______。 解析:①错)2(+=x f y 关于直线2-=x 对称,②对③错若)2()2(x f x f -=-,则函数)(x f y =图象关于直线0=x 对称;④对正确答案为②④ C D A P O B 2019版中考数学专题复习图形面积问题训练鲁教版 一、填空题 1.已知如图所示,正方形ABCD 的边长为1,以AB 为直径作半圆,以点A 为圆心,AD 为半径画弧.那么图中阴影部分的面积为_______. 答案: 8 π 2.如图,在正方形ABCD 内有一折线段,其中AE ⊥EF ,EF ⊥FC,并且AE=6,EF=8,FC=10,则正方形与其外接圆之间形成的阴影部分的面积为________。 答案:80π-160 3.如图,在直角三角形ABC 中,∠ABC=90°,AC=2,BC=3,以点A 为圆心,AB 为半径画 弧,交AC 于点D ,则阴影部分的面积是 . 答案: 3 2_ 16 π 为圆心,、、,分别以,中,如图,在C B A a BC AC C ==?=∠?90ABC Rt 4. 以为半径画弧,三条弧与边所围成的阴影部分面积为。1 2 AC AB 答案:( 12 _18 π)a 2 5.如图(9),半圆的直径10AB =,P 为AB 上一点,点C D ,为半圆的三等分点,则阴影部分的面积等于_______. 答案: 6.如图,AB 为半圆O 的直径,C 、D 、E 、F 是的五等分点,P 是AB 上的任意一点.若AB =4,则图中阴影部分的面积为 . 7.如图,⊙O 的半径为5,直径AB ⊥CD ,以B 为圆心,BC 长为半径作⌒CED ,则⌒CED 与⌒CAD 围成的新月形ACED (阴影部分)的面积为_72 二、选择题 8.如图,正方形ABCD 内接于⊙O ,直径MN ∥AD ,则阴影部分的面积占圆面积: A.12 B. 14 C. 16 D. 18 答案: B 9.如图,在Rt △ABC 中,∠ACB =90o.点P 是半圆弧AC 的中点,连接BP 交AC 于点D ,若半圆弧的圆心为O ,点D , 点E 关于圆心O 对称.则图中的两个阴影部分的面积S 1,S 2 之间的关系是( ) A .S 1<S 2 B .S 1>S 2 C .S 1=S 2 D .不确定 A C O E (第7题图) A O B C D E F P O A C D E P S 2 S 1 (第10题) 函数的对称性 一、教学目标 函数图象的对称性是一类函数的特性,是函数性质的重要方面,它包括自身对称和两个函数图象之间的对称,理解掌握函数对称性,对数学问题的解决有很大的帮助,对也是数形结合思想的重要体现。 1.自身对称函数,函数图象本身具有对称轴或是对称中心,该函数的图象是轴对称图形或是中心对称图形,奇函数与偶函数是最典型的两类函数,其它自身对称的函数都可以由奇偶函数平移得到; 2.两个函数图象的对称,是指两个图形之间的关系,它们之间存在某种关联,即它们关于某一点对称或是关于某一条直线对称,研究其中一个函数的性质就可知另一个函数的特点(互为反函数的两个函数图象)。 二、举例分析 例1. 设()f x 是定义在R 上的函数, (1)若对任意x R ∈,都有()()f a x f b x -=+成立,则函数()f x 的图象关于直线2 a b x +=对称; (2)若对任意x R ∈,都有()()22f x f a x b +-=,则函数()f x 的图象关于点(),a b 成中心对称。 选题目的:通过此题的学习,让学生明白一个道理,函数()f x 的图象是轴对称或是中心对称,函数解析式()f x 应满足一关系式是什么,并能通过奇偶函数的平移获得理解这种关系式的钥匙。 思路分析: (1)要证明()f x 图象上任意一点()00,P x y 关于直线2 a b x +=对称的点()00,Q a b x y +-也在()f x 的图象上。 事实上,()()()()00000y f x f a a x f b a x f a b x ==--=+-=+-????????,即得点()00,Q a b x y +-也在()f x 的图象上。 特别地,当,a b 都为0时,就是偶函数的特征了。 创作编号: GB8878185555334563BT9125XW 创作者: 凤呜大王* 函数)sin(?ω+=x A y 图象的对称轴与对称中心 新疆民丰县一中 亚库普江·奥斯曼 摘要: 新课标高中数学教材上函数的性质就着重讲解了单调性、奇偶性、周期性,但在考试测验甚至高考中不乏的会出现函数对称性、连续性、凹凸性的考查。尤其是对称性,因为教材上对它有零散的介绍,例如二次函数的对称轴、反此例函数的对称性、三角函数的对称性,因而考查的频率一直比较高。以我的经验看,这方面一直是教学的难点,尤其是轴象函数的对称性判断。所以这里我对高中阶段所涉及的函数)sin(?ω+=x A y 的对称性知识提出自己的观点。 关键词:对称轴,对称中心,正弦型函数 函数轴对称:如果一个函数的图象沿一条直线对折,直线两则的图像能够完全重合,则称该函数具备对称性中的轴对称,该直线称为该函数的对称轴。 中心对称:如果一个函数的图像沿一个点折旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,该点称为该函数的对称中心。 正弦函数x y sin =的图像既是轴对称又是中心对称,它的图象关于过最值点且垂直于x 轴的直线分别成轴对称图形; x y sin =的图象的对称轴是经过其图象的“峰顶点”或“谷底点”,且平行于y 轴的无数条直线;它的图象关于x 轴的交点分别成中心对称图形。 ∴正弦函数x y sin =的对称轴方程为 2 π π+ =k y ,对称中心点为(0,πk ),其中 Z k ∈。 正弦型函数)sin(?ω+=x A y 是由正弦函数 x y sin =演变而成。 一般只要知道正弦函数x y sin =图象的对称轴与对称中心就可以快速准确的求出正弦型函数 面积问题(中考数学压轴) 一、解答题(共1道,每道100分) 1.如图,在锐角三角形ABC中,BC=12,△ABC的面积为48,D,E分别是边AB,AC上的两个动点(D不与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.(1)当正方形DEFG的边GF在BC上时,求正方形DEFG的边长;(2)设DE=x,△ABC与正方形DEFG重叠部分的面积为y,试求y关于x的函数关系式,写出x的取值范围,并求出y的最大值. 答案:(1)当正方形DEFG的边GF在BC上时,如图(1), 过点A作BC边上的高AM,交DE于N,垂足为M. ∵S△ABC=48,BC=12, ∴AM=8, ∵DE∥BC,△ADE∽△ABC, ∴, 而AN=AM-MN=AM-DE, ∴,解之得DE=4.8. ∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8, (2)分两种情况: ①当正方形DEFG在△ABC的内部时,如图(2), △ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积, ∵DE=x, ∴y=x2, 此时x的范围是0<x≤4.8, ②当正方形DEFG的一部分在△ABC的外部时, 如图(2),设DG与BC交于点Q,EF与BC交于点P,△ABC的高AM交DE于N, ∵DE=x,DE∥BC, ∴△ADE∽△ABC, 即, 而AN=AM-MN=AM-EP, ∴, 解得. 所以,即, 由题意,x>4.8,且x<12,所以4.8<x<12; 因此△ABC与正方形DEFG重叠部分的面积需分两种情况讨论, 当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04, 当4.8<x<12时,因为, 所以当时,△ABC与正方形DEFG重叠部分的面积的最大值为二次函数的 最大值:;因为24>23.04,所以△ABC与正方形DEFG重叠部分 的面积的最大值为24. 解题思路:(1)根据题意,作出图示;分析可得:AM=8,且△ADE∽△ABC,进而可得 ,解可得答案.(2)分两种情况:①当正方形DEFG在△ABC的内部时,② 当正方形DEFG的一部分在△ABC的外部时,依据平行线以及正方形的性质,可得二次函数,再根据二次函数的性质,解可得重合部分的面积,比较可得面积的最大值. 试题难度:三颗星知识点:中考压轴之面积问题 正弦函数图象的对称轴 与对称中心 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】 函数 )sin(?ω+=x A y 图象的对称轴与对称中心 新疆民丰县一中 亚库普江·奥斯曼 摘要: 新课标高中数学教材上函数的性质就着重讲解了单调性、奇偶性、周期性,但在考试测验甚至高考中不乏的会出现函数对称性、连续性、凹凸性的考查。尤其是对称性,因为教材上对它有零散的介绍,例如二次函数的对称轴、反此例函数的对称性、三角函数的对称性,因而考查的频率一直比较高。以我的经验看,这方面一直是教学的难点,尤其是轴象函数的对称性判断。所以这里我对高中阶段所涉及的函数)sin(?ω+=x A y 的对称性知识提出自己的观点。 关键词:对称轴,对称中心,正弦型函数 函数轴对称:如果一个函数的图象沿一条直线对折,直线两则的图像能够完全重合,则称该函数具备对称性中的轴对称,该直线称为该函数的对称轴。 中心对称:如果一个函数的图像沿一个点折旋转180度,所得的图像能与原函数图像完全重合,则称该函数具备对称性中的中心对称,该点称为该函数的对称中心。 正弦函数x y sin =的图像既是轴对称又是中心对称,它的图象关于过最值点且垂直于x 轴的直线分别成轴对称图形; x y sin =的图象的对称轴是经过其 图象的“峰顶点”或“谷底点”,且平行于y 轴的无数条直线;它的图象关于x 轴 的交点分别成中心对称图形。 ∴正弦函数x y sin =的对称轴方程为2 π π+ =k y ,对称中心点为 (0,πk ),其中 Z k ∈。 正弦型函数 )sin(?ω+=x A y 是由正弦函数x y sin =演变而成。 三角函数图象的对称性质及其应用 观察三角函数的图象,不难发现它们都具有对称性 ,虽然历届高考中关于三角函数图象的对称性问题屡有涉及,但教材中却是一个盲点。为此,本文谈谈三角函数图象的对称性质及其应用。 一、正弦曲线和余弦曲线都是轴对称图形 性质1、函数)sin(?ω+=x A y 和)cos(?ω+=x A y 的图象关于过最值点且垂直于x 轴的直线分别成轴对称图形; )sin(?ω+=x A y 对称轴方程的求法是:令1)sin(±=+?ωx ,得 2ππ?ω+=+k x )(Z k ∈,则ω ?π22)12(-+= k x ,所以函数)sin(?ω+=x A y 的图象的对称轴方程为ω?π22)12(-+=k x ; )cos(?ω+=x A y 对称轴方程的求法是:令1)cos(±=+?ωx ,得π?ωk x =+)(Z k ∈,则ω?π-= k x ,所以函数)cos(?ω+=x A y 的图象的对称轴方程为ω?π-=k x 。 例1、函数)62sin(3π+ =x y 图象的一条对称轴方程是( ) (A )0=x (B )32π=x (C )6π-=x (D )3π=x 解:由性质1知,令1)62sin(3±=+ πx 得262πππ+=+k x )(Z k ∈,即62ππ+=k x )(Z k ∈,取1=k 时,3 2π=x ,故选(B )。 例2、函数)3 3cos(21)(π+=x x f 的图象的对称轴方程是 解:由性质1知, 令1)33cos(±=+ πx 得ππk x =+33)(Z k ∈,即93ππ-=k x )(Z k ∈,所以)3 3cos()(π+=x x f 的图象的对称轴方程是9 3ππ-=k x )(Z k ∈。 二、正弦曲线和余弦曲线都是中心对称图形 性质2、函数)sin(?ω+=x A y 和)cos(?ω+=x A y 的图象关于其与x 轴的交点分别成中心对称图形; )sin(?ω+=x A y 的对称中心求法是:令0)sin(=+?ωx ,得 1 定义编辑数学术语 正弦函数是三角函数的一种. 定义与定理 定义:对于任意一个实数x 都对应着唯一的角(弧度制中等于这个实数) ,而这个角又对应 着唯一确定的正弦值Sin X ,这样,对于任意一个实数X都有唯一确定的值Sin X与它对应, 按照这个对应法则所建立的函数,表示为f(x)=sin X ,叫做正弦函数。 正弦函数的定理:在一个三角形中,各边和它所对角的正弦的比相等,即a/Sin A=b/Sin B=c/Sin C 在直角三角形ABC中,/ C=90 ,y为一条直角边,r为斜边,X为另一条直角边(在坐标 系中,以此为底),贝U Sin A=y∕r,r= √( x^2+y^2) 2 性质 编辑图像 图像是波形图像(由单位圆投影到坐标系得出) ,叫做正弦曲线(Sine curve) 正弦函数X∈& 定义域 实数集R 值域 [-1,1] (正弦函数有界性的体现) 最值和零点 ①最大值:当X=2k ∏+ ( ∏/2) , k ∈Z 时,y(max)=1 ②最小值:当X=2k ∏+ (3∏/2), k∈Z 时,y(min)=-1 零值点:( kπ ,0) ,k∈Z 对称性 既是轴对称图形,又是中心对称图形。 1) 对称轴:关于直线X= ( π /2) +kπ , k∈Z 对称 2) 中心对称:关于点(k ∏ , 0), k∈Z对称 周期性最小正周期:y=SinX T=2 π 奇偶性 奇函数(其图象关于原点对称) 单调性 在[-∏∕2+2k ∏ , ∏∕2+2k ∏], k∈Z 上是单调递增. 在[∏∕2+2k ∏ , 3∏∕2+2k ∏], k ∈Z 上是单调递减. 3 正弦型函数及其性质 编辑 正弦型函数解析式:y=Asin (ω x+ φ )+h 函数对称性 一 知识点 I 函数图象本身的对称性(自身对称) 若,则具有周期性;若,则具有对称性:“内同表示周期性,内反表示对称性”。 1、图象关于直线对称 推论1:的图象关于直线对称 推论2、的图象关于直线对称 推论3、的图象关于直线对称 2、的图象关于点对称 推论1、的图象关于点对称 推论2、的图象关于点对称 推论3、的图象关于点对称 II 两个函数的图象对称性(相互对称)(利用解析几何中的对称曲线轨迹方程理解) 1、与图象关于Y轴对称 2、与图象关于原点对称函数 3、函数与图象关于X轴对称 4、函数与其反函数图象关于直线对称 5.函数与图象关于直线对称 推论1:函数与图象关于直线对称 推论2:函数与图象关于直线对称 推论3:函数与图象关于直线对称 二典例解析: 1、定义在实数集上的奇函数恒满足,且时, ,则________。 2、已知函数满足,则图象关于__________对称。 3、函数与函数的图象关于关于__________对称。 4、设函数的定义域为R,且满足,则的图象关于__________对称。 5、设函数的定义域为R,且满足,则的图象关于__________对称。 6、设的定义域为R,且对任意,有,则关于__________对称,图象关于 __________对称,。 7、已知函数对一切实数x满足,且方程有5个实根,则这5个实根之和为() A、5 B、10 C、15 D、18 8、设函数的定义域为R,则下列命题中,①若是偶函数,则图象关于y 轴对称;②若是偶函数,则图象关于直线对称;③若,则函数图象关于直线对称;④与图象关于直线对称,其中正确命题序号为_______。 2016中考数学复习-二次函数与三角形的面积问题 二次函数与三角形的面积问题 1.运用 2铅垂高 水平宽? = s; 2.运用y; 3.将不规则的图形分割成规则图形,从而便于求出图形的总面积。 类型一:三角形的某一条边在坐标轴上或者与坐标轴平行 例1.已知:抛物线的顶点为D(1,-4),并经过点E(4,5),求: (1)抛物线解析式; (2)抛物线与x轴的交点A、B,与y轴交点C; (3)求下列图形的面积△ABD、△ABC、△ ABE、△OCD、△OCE。 一般地,这类题目的做题步骤:1.求出二次函数的解析式;2.求出相关点的坐标;3.求出相关线段的长;4.选择合适方法 求出图形的面积。 训练1.如图所示,已知抛物线() 02 ≠++=a c bx ax y 与x 轴相交于 两点A ()0,1 x , B ()0,2 x ()2 1 x x <,与y 轴负半轴相交于点C ,若抛物线 顶点P 的横坐标是1,A 、 B 两点间的距离为4,且△ABC 的面积为6。 (1)求点A 和B 的坐标; (2)求此抛物线的解析式; (3)求四边形ACPB 的面积。 类型二:三角形三边均不与坐标轴轴平行,做三角形的铅垂高。(歪歪三角形拦腰来一刀) 关于2 铅垂高 水平宽?= ? S 的知识点:如图1,过△ABC 的 三个顶点分别作出与水平线垂直的三条直线,外侧两条直线之间的距离叫△ABC 的“水平宽”(a ),中间的这条直线在△ABC 内部线段的长度叫△ABC 的“铅垂高(h )”. x A B O C y B 铅垂高 水平宽 h a 图1 我们可得出一种计算三角形面积的新方法:ah S ABC 2 1= ?,即 三角形面积等于水平宽与铅垂高乘积的一半. 想一想:在直角坐标系中,水平宽如何求?铅垂高如何求? 例2.如图2,抛物线顶点坐标为点C (1,4),交x 轴于点A (3,0),交y 轴于点B .(1)求抛物线和直线AB 的解析式;(2)点P 是抛物线(在第一象限内)上的一个动点,连结PA ,PB ,当P 点运动到顶点C 时,求△CAB 的铅垂高CD 及CAB S ?;(3)是否存在一点P ,使S △PAB =8 9 S △CAB ,若存在,求出P 点的坐标;若不存在,请说明理由. 解题思路:求出直线AB 的解析式是为了求出D .点的纵坐标.....D y ; 铅垂高D C y y CD -=,注意线段的长度非负性;分析P 点在直线AB 的上方还是下方? 图-2 x C O y A B D 1 1 关于函数图像对称性的问题 胡春林 指导老师:刘荣玄 【摘要】函数图象的对称性反映了函数的特性,是研究函数性质的一个重要方面,函数图象的对称性包括一个函数图象自身的对称性与两个函数图象之间的对称性。 【关键词】函数图像对称性轴对称中心对称 一、函数自身的对称性的问题 函数是中学数学教学的主线,是中学数学的核心内容,也是一个高中数学的基础。函数的性质是高考的重点与热点,函数的对称性是函数的一个基本性质,也是难点,对称关系不仅广泛存在于数学问题之中,而且利用对称性往往能更简捷地使问题得到解决,对称关系还充分体现了数学之美。本文拟通过函数自身的对称性和不同函数之间的对称性这两个方面来探讨函数与对称有关的性质的一些思考。 例题1. 函数y = f (x)的图像关于点A (a ,b)对称的充要条件是 f (x) + f (2a-x) = 2b 证明:(必要性)设点P(x ,y)是y = f (x)图像上任一点,∵点P( x ,y)关于点A (a ,b)的对称点P ‘(2a-x,2b-y)也在y = f (x)图像上,∴2b-y = f (2a-x) 即y + f (2a-x)=2b故f (x) + f (2a-x) = 2b,必要性得证。 (充分性)设点P(x0,y0)是y = f (x)图像上任一点,则y0 = f (x0) ∵ f (x) + f (2a-x) =2b∴f (x0) + f (2a-x0) =2b,即2b-y0 = f (2a-x0) 。 故点P‘(2a-x0,2b-y0)也在y = f (x) 图像上,而点P与点P‘关于点A (a ,b)对称,充分性得征。例题2 ①若函数y = f (x) 图像同时关于点A (a ,c)和点B (b ,c)成中心对 (a≠b),则y = f (x)是周期函数,且2| a-b|是其一个周期。 ②若函数y = f (x) 图像同时关于直线x = a 和直线x = b成轴对称(a≠b),则y = f (x)是周期函数, 且2| a-b|是其一个周期。 ③若函数y = f (x)图像既关于点A (a ,c) 成中心对称又关于直线x =b成轴对称(a≠b),则y = f (x)是周期函数,且4| a-b|是其一个周期。 ①②的证明留给读者,以下给出③的证明:函数的对称性
北京--正弦函数图象的对称性(檀晋轩)CASIO
超经典二次函数图象的平移和对称变换总结
中考数学专题复习-函数中的面积问题
函数图象的对称变换
中考数学面积问题压轴题
正弦函数图象的对称轴与对称中心
(完整word)高考专题函数对称性
2019版中考数学专题复习图形面积问题训练鲁教版
函数的对称性完美
正弦函数图象的对称轴与对称中心
面积问题(中考数学压轴)
正弦函数图象的对称轴与对称中心
三角函数图象的对称性
正弦函数的图像和性质
函数对称性
2016中考数学复习-二次函数与三角形的面积问题
关于函数图像对称性问题