计算机算法基础(第三章) 第三章 贪心方法
- 格式:ppt
- 大小:536.50 KB
- 文档页数:75

贪心法刘培liupei@Outline引入:活动选择问题 什么是贪心法贪心法的适用范围 贪心法证明几道习题活动选择问题S={1,2,…,n}为n项活动的集合si和fi分别表示活动i开始和结束时间(1<=i<=n)活动i和活动j相容当且仅当si>=fj或sj>=fi求两两相容的最大活动集活动选择问题活动选择问题1活动选择问题算法Greedy Select1. n←length[S];2. A←{1};3. j←1;4. for i←2 to n5.do if si≥fjA ←A∪{i};6. then7. j ←i;8. return A.贪心法定义A greedy algorithm always makes the choice that looks best at the moment. That is , it makes a locally optimal choice in the hope that this choice will lead to a globally optimal solution.--《算法导论》贪心法在每一步都做出一个局部最优的选择,以期在总体上仍然达到最优。
贪心法适用范围考虑这样一类问题:会有一个最优的目标—最大/最小求最大活动集会有一个或者多个约束条件求两两相容的最大活动集需要一系列的步骤去完成—多步判断每步选择一个任务不需要考虑之前或者之后的步骤—贪心选择 按完成时间排序,从左向右扫描,不回溯贪心法适用范围满足优化原则的组合优化问题若满足贪心选择性质得最优解,否则得近似解 什么是组合优化问题X 有穷的变量集合—活动集合S ={<si,fi>|1<=i<=n}Y 有穷的值集合—相容活动集A的规模{1,…,n}f(x) 目标函数—max |A|G 约束条件集合—si>=fj或sj>=fi(1<=i<j<=n)一个组合优化问题的解是对变量集X的一组赋值g:X->Y,并且在满足G中约束条件的前提下使得目标函数f(x)取得最大(小)值贪心法适用范围优化原则一个最优决策序列的任何子序列本身一定是相对于子序列的初始和结束状态的最优的决策序列例:从北京经过广州到海南的最短距离,肯定包括北京到广州的最短距离,以及广州到海南的最短距离活动选择问题贪心法适用范围贪心选择性质—正确性所求问题的最优解,可以通过一系列的局部最优解的选择,即贪心选择得到满足贪心选择得到最优解,否则为近似解需要证明,一般采用数学归纳法对选择步骤归纳对问题规模归纳础)设S={1,2,…,n}是活动集,活动按截止时间递增顺序排序.k=1, 证明存在最优解包含活动1.任取最优解A, A中的活动按照截止时间递增的顺序排列. 如果A的第一个活动为j,j≠1,令A’= (A−{j})∪{1}, 由于f1≤fj, A’也是最优解,且含有1.骤)假设命题对k为真,证明对k+1也为真.算法执行到第k步, 选择了活动i1=1, i2, …, ik, 根据归纳假设存在最优解A包含i1= 1, i2, …, ik,A中剩下的活动选自集合S’={ i | i∈S, si≥fk},且A= {i1, i2, …, ik}∪B, B是S’的最优解.若不然, S’的最优解为B*, B*的活动比B多,那么B*∪{1, i2, …, ik}是S 的最优解,且比A的活动多,与A 的最优性矛盾.根据归纳基础,存在S’的最优解B’含有S’中的第一个活动,设为ik+1, 且|B’|=|B|, 于是{i1 , i2, …, ik} ∪B’={i1 , i2, …, ik, ik+1} ∪(B’-{ik+1})也是原问题的最优解.部分背包问题问题描述背包的重量限制为bn 件物品,重量和价值分别为wi ,vi ,物品可以分割 求满足背包重量限制的条件下,装入物品的最大价值问题抽象目标函数约束条件 贪心思想物品按照vi/wi 进行排序,由高到低装入背包∑=n i i i x v 1max ∑=≤n i i i b x w 1其他背包问题考虑如果每种物品不止有一件(有限或无限件)且可分割,能不能用贪心算法?线性规划问题(目标函数和约束条件都是线性函数)—部分背包问题—贪心算法整数规划问题(xi均为非负整数)—一般背包问题—搜索与剪枝/ 动态规划0-1规划问题—0-1背包问题—搜索与剪枝/ 动态规划其他背包问题Loading问题n个集装箱1,2,…,n 装上轮船,集装箱i的重量wi, 轮船装载重量限制为c,无体积限制.问如何装使得上船的集装箱最多?不妨设wi≤c.0-1背包问题的限制形式: vi=1贪心思想将集装箱按照从轻到重排序,轻者先装证明:对问题规模进行归纳经典贪心法三个经典的贪心图算法(注意正确性证明)Prim算法(最小生成树)(教材194页) 对连接两个集合的最小边进行贪心选择 Kruskal算法(最小生成树)(教材196页) 对连接两个集合的最小边进行贪心选择 Dijkstra算法(单源最短路径)(教材187页)选择下一个离单源最近的结点贪心法得到近似解地图着色问题相邻的区域着不同的颜色,要求使用的颜色尽量少一般采用回溯法解决如果地图比较大,会采用贪心法求近似解不满足贪心选择性质,只能得到近似解贪心法得到近似解地图着色问题贪心选择While 存在未被着色的区域选择一种新颜色C选择一个未着色的区域A,用C着色考察其他所有未着色区域,如果不与着色为C的区域相邻,就用C着色贪心法得到近似解贪心法、动态规划与回溯技术习题安装雷达 区间覆盖 拆墙钓鱼安装雷达1328海上有N个扫描点雷达扫描范围d至少要安装几个雷达才能将N个点都覆盖住安装雷达1328对什么进行贪心选择?怎么排序?按横坐标排序从左到右扫描?安装雷达区间覆盖拆墙1230魔术师表演穿墙 墙都是水平的 最多能穿k面墙 最少拆几面墙才能保证魔术师安全通过?拆墙1230对什么进行贪心?如何排序? 拆哪面墙?最长的?跨越不安全的列最多的?拆墙1230拆掉右端点最靠右的墙,为什么?钓鱼1042John准备去钓鱼。

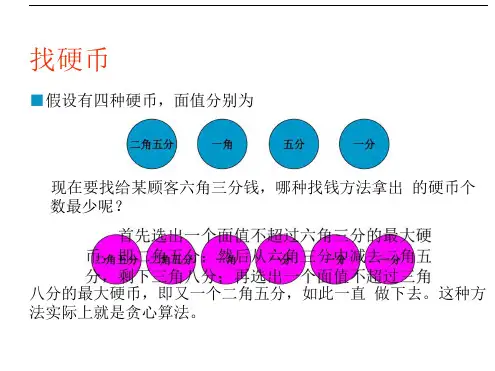
找硬币■假设有四种硬币,面值分别为现在要找给某顾客六角三分钱,哪种找钱方法拿出的硬币个数最少呢?八分的最大硬币,即又一个二角五分,如此一直做下去。
这种方法实际上就是贪心算法。
再找硬币■若硬币的面值改为一分、五分和一角一分3 种,而要找个顾客的是一角五分钱。
■还用贪心算法,将找个顾客1个一角一分的硬币和4个一分的硬币。
■然而,3个五分的硬币显然才是最好的找法。
贪心算法的特点■贪心算法总是作出在当前来看是最好的选择。
■就是说,贪心算法并不从整体最优上来考虑,所作出的选择只是某种意义上的局部最优选择。
■当然希望贪心算法得到的最终结果是最优的。
■可是贪心算法并不能保证最终结果是最优的。
■不过,在许多情况下,应用贪心算法能够得到整体最优解;并且在一些情况下,即使得到的不是最优解,也是一个很好的近似解。
贪心算法的一般框架■G reedy Algorithm(parameters) {■初始化;■重复执行以下的操作:■选择当前可以选择的(相容)最优解;■将所选择的当前解加入到问题的解中;■直至满足问题求解的结束条件。
■}最小生成树■设G = (V, E)是一个无向连通带权图,即一个网络。
E的每条边(v, w)的权为c[v][w]o■如果G的一个子图G是一棵包含G的所有顶点的树,则称G为G的生成树。
■生成树的各边的权的总和称为该生成树的耗费。
■在G的所有生成树中,耗费最小的生成树称为G 的最小(优)生成树。
树的基本性质.■连通无回路的图G称为树。
已■树是点比边多-的连通图,G连通且q二p-l。
■ ■树是点比边多一的无回路图:G无回路且q二p-1■树若添条边就有回路:G无回路,但对任意的u, veV(G),若uv纟玖G),贝ijG+uv中恰有一条回路■树若减条边就不连通:G连通,但对VeeE(G), G-e不连通。
■ n个顶点的连通图的生成树含有n-1条边。
最小生成树的贪心选择性质■令G中权最小的边为ei。
首先必定有图G的一棵最小生成树包含了■MM?■ Prim算法的做法:在保证连通的前提下依次选出权重较小的n-1条边(在实现中体现为n个顶点的选择)。



贪婪算法(贪⼼算法)贪⼼算法简介:@anthor:QYX 贪⼼算法是指:在每⼀步求解的步骤中,它要求“贪婪”的选择最佳操作,并希望通过⼀系列的最优选择,能够产⽣⼀个问题的(全局的)最优解。
贪⼼算法每⼀步必须满⾜⼀下条件: 1、可⾏的:即它必须满⾜问题的约束。
2、局部最优:他是当前步骤中所有可⾏选择中最佳的局部选择。
3、不可取消:即选择⼀旦做出,在算法的后⾯步骤就不可改变了。
贪⼼算法的定义:贪⼼算法是指在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,只做出在某种意义上的局部最优解。
贪⼼算法不是对所有问题都能得到整体最优解,关键是贪⼼策略的选择,选择的贪⼼策略必须具备⽆后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
解题的⼀般步骤是:1.建⽴数学模型来描述问题;2.把求解的问题分成若⼲个⼦问题;3.对每⼀⼦问题求解,得到⼦问题的局部最优解;4.把⼦问题的局部最优解合成原来问题的⼀个解。
如果⼤家⽐较了解动态规划,就会发现它们之间的相似之处。
最优解问题⼤部分都可以拆分成⼀个个的⼦问题,把解空间的遍历视作对⼦问题树的遍历,则以某种形式对树整个的遍历⼀遍就可以求出最优解,⼤部分情况下这是不可⾏的。
贪⼼算法和动态规划本质上是对⼦问题树的⼀种修剪,两种算法要求问题都具有的⼀个性质就是⼦问题最优性(组成最优解的每⼀个⼦问题的解,对于这个⼦问题本⾝肯定也是最优的)。
动态规划⽅法代表了这⼀类问题的⼀般解法,我们⾃底向上构造⼦问题的解,对每⼀个⼦树的根,求出下⾯每⼀个叶⼦的值,并且以其中的最优值作为⾃⾝的值,其它的值舍弃。
⽽贪⼼算法是动态规划⽅法的⼀个特例,可以证明每⼀个⼦树的根的值不取决于下⾯叶⼦的值,⽽只取决于当前问题的状况。
换句话说,不需要知道⼀个节点所有⼦树的情况,就可以求出这个节点的值。
由于贪⼼算法的这个特性,它对解空间树的遍历不需要⾃底向上,⽽只需要⾃根开始,选择最优的路,⼀直⾛到底就可以了。

第3章贪心算法贪心算法一般来说是解决“最优问题”,具有编程简单、运行效率高、空间复杂度低等特点。
是程序竞赛中的一个有力武器,受到广大同学们的青睐。
贪心算法一般是求“最优解”这类问题的。
最优解问题可描述为:有n个输入,它的解是由这n个输入的某个子集组成,并且这个子集必须满足事先给定的条件。
这个条件称为约束条件。
而把满足约束条件的子集称为该问题的可行解。
这些可行解可能有多个。
为了衡量可行解的优劣,事先给了一个关于可行解的函数,称为目标函数。
目标函数最大(或最小)的可行解,称为最优解。
贪心算法的正确性证明虽然不容易,但一些常见的方法还是值得总结的。
1.构造法根据描述的算法,用贪心的策略,依次构造出一个解,可证明一定是合法的解。
即用贪心法找可行解。
2.反证法用贪心的策略,依次构造出一个解S1。
假设最优解S2不同与S1,可以证明是矛盾的。
从而S1就是最优解。
3.调整法用贪心的策略,依次构造出一个解S1。
假设最优解S2不同与S1,找出不同之处,在不破坏最优性的前提下,逐步调整S2,最终使其变为S1。
从而S1也是最优解。
3.1 构造法构造法就是从一个空的解开始,根据贪心策略,逐步将新的内容加入原有的解中,直到满足要求或无法将新的元素加入为止。
也可以将使用相反的手段,即先将整个解设定为一个最大的集合,然后,用贪心策略逐步从原有解中取出元素,直至满足要求或无法取出元素为止。
本节例题将介绍第一种贪心的例子。
3.1.1 〖案例1〗订票一家票务办公室为音乐会售票。
它们以出售某一固定数量的连号票(简称套票)来替代常见的单张票销售。
票务办收到了大量的购票订单。
套票的订单以该套票中最小的座位号作为标识。
然而票务办并不能满足所有的订单,而且如果他们完全按照观众的要求来分·60· ACM 程序设计培训教程配座位,就会出现很多空位。
为此票务办采取了如下的座位分配和价格策略:如果一个订单被接受且完全按照观众的要求安排座位,那么观众就要付全价(每套票2 petaks);如果一个订单虽被接受但是至少有一个座位与观众的要求不同,那么顾客只需付半价(每套票1 petaks)。

计算机基础知识了解计算机算法的动态规划和贪心算法计算机基础知识:了解计算机算法的动态规划和贪心算法计算机算法是指在计算机科学中为解决问题而设计的一系列计算步骤。
它是实现特定功能的工具,在计算机科学和软件工程中扮演着重要的角色。
动态规划和贪心算法是计算机算法中常见的两种策略。
本文将详细介绍这两种算法的原理和应用。
一、动态规划算法动态规划算法(Dynamic Programming),又称动态优化算法,是一种将复杂问题分解为更简单子问题的方法,并使用子问题的解来构建原问题的解。
它通常适用于具有重叠子问题和最优子结构性质的问题。
动态规划算法的基本步骤如下:1. 定义问题的状态:将原问题划分为若干个子问题,找出子问题与原问题之间的关系;2. 构造状态转移方程:通过递推或迭代的方式,计算出子问题的解;3. 解决问题:根据状态转移方程,从子问题的解中推导出原问题的最优解;4. 构建解的过程:根据所得的最优解,记录下每一步的决策,以便后续的重建。
动态规划算法的经典应用之一是背包问题。
背包问题是在限定容量的背包中选择合适的物品,使得物品的总价值最大。
通过动态规划算法,我们可以通过计算子问题的解来得到背包问题的最优解。
二、贪心算法贪心算法(Greedy Algorithm)是一种基于贪心策略的算法。
它通过每一步的局部最优选择来达到整体最优解。
贪心算法在每一步的选择中都做出当前最好的选择,而不考虑对后续步骤的影响。
贪心算法的基本思想是:1. 定义问题的解空间和评价标准:确定问题的解空间以及如何评价每个解的好坏;2. 构建解的过程:逐步构建解,每一步都选择当前最优的子解,直到得到最终的解;3. 检查解的有效性:验证得到的解是否符合问题的要求。
贪心算法的经典应用之一是最小生成树问题。
最小生成树问题是在一张无向连通图中选择一棵权值最小的生成树。
贪心算法可以通过每次选择权值最小的边来构建最小生成树。
三、动态规划与贪心算法的比较动态规划算法和贪心算法有相似之处,但也存在一些明显的差异。


贪心算法1:贪心的概念最优装载问题贪心算法的原理:贪心算法总是做出当前最好的选择,也就是说,它期望通过局部最优选择从而得到全局最优的解决方案。
1. 没有后悔药,一旦做出选择,不可以后悔;2. 有可能得到的不是最优解,而是最优解的近似解。
3. 选择什么样的贪心策略,直接决定算法的好坏。
贪心策略的基本思想定义:贪心法是一种解决最优问题的策略。
它是从问题的初始解出发,按照当前最佳的选择,把问题归纳为更小的相似的子问题,并使子问题最优,再由子问题来推导出全局最优解。
使用贪心方法需要注意局部最优与全局最优的关系,选择当前状态的局部最优并不一定能推导出问题的全局最优。
贪心算法求解的三个步骤:a、确定贪心策略b、根据贪心策略,一步一步得到局部最优解c、将局部最优解合并起来就得到全局最优解贪心策略的特点1.贪心选择性质:所求问题的整体最优解可以通过一系列局部最优的选择来达到,这样的选择称为贪心选择。
这些选择只依赖于以往所做过的选择,决不依赖于将来的选择。
2.最优子结构性质:当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。
例题说明:例题:有一个3*3的方格,每个格子有一个正整数,要求从每行格子中取一个数,使得取出来的3个数字之和最大(贪心)。
题目修改:规定从左下角出发,每次只能向上或向右移动一格,现在要求找出一条路径使得从左下角到达右上角所经过的格子中的数字之和最大,求最大值。
贪心方法:3→14→12→5→8=42(每次都找向上或者向右最大的一个)最优解:3→6→20→9→8=46局部最优无法带来全局最优,这就是不具备贪心选择性质。
什么样的问题能用贪心来求解:利用贪心算法求解的问题往往具有两个重要的特性:贪心选择性质和最优子结构性质。
(1)贪心选择所谓贪心选择性质是指原问题的整体最优解可以通过一系列局部最优的选择得到。
(2)最优子结构当一个问题的最优解包含其子问题的最优解时,称此问题具有最优子结构性质。

第三章贪心法3.1排队接水源程序名water.???(pas,c,cpp )可执行文件名water.exe 输入文件名water.in 输出文件名water.out【问题描述】有n 个人在一个水龙头前排队接水,假如每个人接水的时间为Ti ,请编程找出这n 个人排队的一种顺序,使得n 个人的平均等待时间最小。
【输入】输入文件共两行,第一行为n ;第二行分别表示第1个人到第n 个人每人的接水时间T1,T2,…,Tn ,每个数据之间有1个空格。
【输出】输出文件有两行,第一行为一种排队顺序,即1到n 的一种排列;第二行为这种排列方案下的平均等待时间(输出结果精确到小数点后两位)。
【样例】water.in water.out 103278149610556121991000234335599812291.90【算法分析】平均等待时间是每个人的等待时间之和再除以n ,因为n 是一个常数,所以等待时间之和最小,也就是平均等待时间最小。
假设是按照1~n 的自然顺序排列的,则这个问题就是求以下公式的最小值:∑∑==⎪⎪⎭⎫ ⎝⎛=+⋯⋯+++⋯⋯++++++=ni i j j n T T T T T T T T T T total 1121321211)()()(如果用穷举的方法求解,就需要我们产生n 个人的所有不同排列,然后计算每种排列所需要等待的时间之和,再“打擂台”得到最小值,但这种方法需要进行n!次求和以及判断,时间复杂度很差!其实,我们认真研究一下上面的公式,发现可以改写成如下形式:∑=--+=++⋯⋯+-+-+=ni in n T i n T T T n T n nT total 11321)1(2)2()1(这个公式何时取最小值呢?对于任意一种排列k1,k2,k3,…,kn ,当1k T ≤2k T ≤3k T ≤…≤nk T 时,total 取到最小值。
如何证明呢?方法如下:因为nj i k k k k k T T j n T i n T n nT total +⋯++-+⋯++-+⋯+-+=)1()1()1(21假设i<j ,而i k T <jk T ,这是的和为total1,而把ki 和kj 互换位置,设新的和为total2,则:))(())(1())(1())1()1(()1()1(12i j i j i j j i i j k k k k k k k k k k T T i j T T j n T T i n T j n T i n T j n T i n total total total --=-+---+-=+-++--+-++-=-=∆我们发现上述△total 恒大于0,所以也说明了任何次序的改变,都会导致等待时间的增加。
【算法1-3】贪⼼算法贪⼼算法的含义贪⼼算法(⼜称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。
也就是说,不从整体最优上加以考虑,算法得到的是在某种意义上的局部最优解。
简单举例说明最最简单的举个例⼦:我有n张纸币,然后你要拿出10张纸币,使得相加最⼤,那么⼤家都会选择从⼤到⼩拿10张纸币,这样相加⼀定是最⼤的。
这可以说是贪⼼算法的⼀种体现。
但是⼤家发现没有,这个⽅法是我们看到之后⽴马想到的,没有经过严谨证明的,当然⼤家会觉得这个很简单的问题,⼲嘛还要证明呢?很多情况下,在类似的算法题中,我们都会有种想当然的情况,有些时候贪⼼确实是对的,但是有些时候你的想当然可能就是错的。
所谓贪⼼算法的证明主要就是在求得局部最优解,在我的理解中就是,在可能出现的任何情况下,贪⼼⼀点不会得到坏的结果,那么贪⼼往往就是最优解。
拿之前的例⼦举例,我不抽10张最⼤的纸币,我就随机抽10张,这种情况下,如果抽出来的10张中没有最⼤⾯值的纸币,这时候我⽤最⼤⾯值的纸币代替其中最⼩的那张,这样的策略是使得最后相加变⼤的,即便原先就有最⼤⾯值,⽆法代替,但是没有代替也没有使得最后的结果变糟糕,只是平了罢了。
所以,如果在可能出现的任何情况下,贪⼼⼀点不会得到坏的结果,那么贪⼼往往就是最优解难⼀点的例⼦说明背包问题:有⼀个背包,背包容量是M=150。
有7个物品,物品可以分割成任意⼤⼩。
要求尽可能让装⼊背包中的物品总价值最⼤,但不能超过总容量。
这个问题答案也很明显,既然物品可以分割成任意⼤⼩,要使得装⼊背包中的物品总价值最⼤,那么肯定会先装(价值/质量)最⼤的物品吧。
简单来说就是,同样的质量,要使得其价值最⼤,就是使得其单位价值最⼤。
⼤家可能会想,那这样的话凡是都贪⼼⼀下好像不是不可,但其实这个贪⼼有点靠感觉,就是往往你遇到贪⼼的题就知道要⽤贪⼼算法了。
⼤家可以想⼀下,同样是前⾯的背包问题,去掉“物品可以分割成任意⼤⼩”这句话的话,这个题⽬还可以⽤贪⼼吗?是不能的,举个极端例⼦,只有两个货物能装进背包⾥,其他五个质量都⼤于150,第⼀个货物质量是2,总价值是22;第⼆个货物质量是149,总价值是1490,按照贪⼼算法的话,那么得出的答案就是22,因为贪⼼算法认为要先装单位价值最⼤的货物,但是很明显我可以直接装第⼆个货物,这样价值就是1490了。