Hierarchical Object-Oriented Petri Net Modeling Method based on Ontology
- 格式:pdf
- 大小:101.36 KB
- 文档页数:5

收稿日期:2009-04-16;修回日期:2009-06-08。
基金项目:四川省教育厅应用基础项目(08Z A029)。
作者简介:陈晓亮(1984-),男,四川成都人,硕士研究生,主要研究方向:Petri 网理论及应用; 宋文(1956-),男,四川洪雅人,教授,CCF 高级会员,主要研究方向:Petri 网理论及应用; 陈东(1983-),男,四川简阳人,硕士研究生,主要研究方向:Petri 网理论及应用。
文章编号:1001-9081(2009)10-2833-05基于Petri 网B /S 体系架构的在线评测系统建模与验证陈晓亮,宋 文,陈 东(西华大学数学与计算机学院,成都610039)(xhu_chenxl@ )摘 要:在线评测系统可以看作网络环境下,实现动态事务处理的一个有代表性的系统。
针对传统的软件设计建模方案很难兼顾系统静态结构的描述和动态行为的分析,采用P /T 网构建了一类B /S 架构的在线评测系统层次模型。
根据系统功能,提出了保证系统功能正确性应具有的重要性质,继而用S_不变量对其进行了分析、验证。
关键词:Petri 网;在线评测;B /S 架构;P /T 系统;S_不变量中图分类号:TP311 文献标志码:AM odeli n g and ver i f i ca ti on of on li n e judge system w ithB /S ba sed on Petr i netsCHE N Xiao 2liang,S ONG W en,CHEN Dong(School of M athe m atics and Co m puter Engineering,X ihua U niversity,Chengdu S ichuan 610039,China )Abstract:Online judge syste m is a rep resentative syste m in dyna m ic transacti on p r ocessing under net w ork envir on ment .The p r operties of static structure and dyna m ic behavi or were not considered by the conventi onal design method of s oft w are .A hierarchical model of online judge with B /S was constructed by P /T nets .According t o the functi on,s ome i m portant qualities were p resented t o guarantee the correctness of syste m.The analysis and verificati on of the model are shown by S_invariants .Key words:Petri net;online judge;B r owser/Server (B /S )architecture;Place /Transiti on net;S_invariant0 引言Petri 网采用可视化图形描述,但却被形式化的数学方法所支持,是一种结构化的离散事件系统(D iscrete Event Dyna m ic Syste m,DE DS )描述工具。

A transformation method of OPM Model to CPNModel for System Concept DevelopmentWenlu Zhou1,a,Feng Yang1,b,Yifan Zhu1,c1College of Information System and ManagementNational University of Defense TechnologyChangsha, Hunan,410072,Chinaa***************,b*****************,c**************.cnAbstract—Modeling languages for concept development in System Engineering usually provide a static model and lack computational capability. We introduce and implement a method combing the Object Process Methodology (OPM), a holistic modeling language well suited to describe the concept model, and Coloured Petri Net (CPN), an executable modeling language supporting elaborate simulation and analysis to make the process of System Engineering more continuous. Not only the basic entities and links, but also the hierarchical properties are converted from OPM to CPN according to the rules we proposed. Application in a simple air defense system demonstrates the process develop a concept model of OPM to a preliminary simulation model of CPN by using this method.Keywords—Object Process Methodology; Coloured Petri Nets; transformation; System EngineeringI.I NTRODUCTIONConcept development is the primary and important phase in System Engineering, since the change of it costs less and affects more. A lot of modeling languages were introduced to help understanding structures and behaviors of a system and developing a conceptual model in this phase, such as Unified Modeling Language (UML)/System Modeling Language (SysML), Object Process Methodology (OPM) and so on. Despite these languages trying to describe the dynamic behaviors of a system, they are still providing a static model and cannot fully describe the quantitative aspects. It may need simulation of the system model to explore the behaviors of the system and validate the conceptual model as well.Viewing system as a whole, OPM is more consistent with the ideal of System Engineering. It provides a holistic and hierarchical model to describe a system while UML/SysML presents different aspects of a system in separated diagrams. Although the dynamic logic of an OPM model can be checked by animation, it still cannot deal with computational behavior, which is needed in many cases.There are a lot of researches aimed at addressing this issue. S. Bolshchikov etc.[1] propose two concepts: Vivid OPM and OPM Matlab Layer, the second of which can creates Matlab code from an OPM model added a numerical computational layer and make it possible to simulate system’s behavior quantitatively. F. Simon etc.[2] suggest the possibility of combining the executable meta-language called Object-Process Network (OPN) with modeling languages including OPM. Rengzhong Wang[3] proposed a holistic modeling method for architecture development by combining the capabilities of OPM, Coloured Petri Net (CPN) and feature model. Additional information defined with CPN semantics is extended in OPM, following by mapping this model to a CPN model according rules proposed. It is a significant exploration; however, there were some shortcomings could be improved. The additional information made it more difficult for architects to build a correct OPM model and it did not mention how to convert a hierarchical OPM model to a CPN model with subnets.In this paper, a method transforming an OPM model to a CPN model by mapping OPM notations to CPN is developed and implemented. Section 2 briefly introduces the theory of OPM and CPN and points out the significance of the transformation from OPM to CPN. We introduce the transformation method in section 3, which mainly concerns the logical relationship between the different elements and procedure links in the OPM and does not need any additional information for the convert. It can also turn a hierarchical OPM model into a CPN model with subnets and keep the capability of describing complex systems of OPM to some degree. Section 4 presents an example to explain the application of the convert. Section 5 contains the conclusions and future work.II.OPM AND CPNA.Object-Process MethodologyObject-Process Methodology (OPM) is a holistic modeling language for understanding and developing systems developed by Dori [4]. It combines the object-oriented and process-oriented concepts and describes structure and behavior aspects of a system in a holistic model.Entities and links are the main building blocks of OPM. Entities include states and things (Objects and Processes). Objects are existing things, and processes are things that transform the objects by generating, consuming, or affecting them. States are situations at which the objects can exist, and belong to the objects. There are two types of links: structural links and procedural links. Structure links express the static,First International Conference on Information Science and Electronic Technology (ISET 2015)persistent relationship among objects or processes, while procedural links express the dynamics behavior of a system.OPM adopts detail decomposition rather than aspect decomposition to manage the systems’ complexity resulting in a holistic hierarchical model. OPM contains two representation modes, the graphic and textual which are semantically equivalent. Object-Process CASE tool (OPCAT) is a software environment supporting system development and lifecycle using OPM [5]B.Coloured Petri NetsColoured Petri Nets (CP-nets or CPN) is a graphical oriented language for design, specification, simulation and verification of discrete event systems [6]. It combines the capabilities of Petri nets with the programming languages and has the ability to establish a hierarchical model.The building blocks of CPN are places, transitions, tokens and arcs. Places describe the state of the system and transitions describe the actions. Arcs indicate how the state changes when the transitions occur and are presented with arc expressions. Each place contains a set of marks called tokens carrying data values which belongs to a given type corresponding to the place. The types of data values are referred as colour sets which make the tokens distinguishable from each other.CPN Tools is a mature tool supporting editing, simulation and analysis of CPN. The inscription language is Standard ML. It has different simulation modes. Monitors can be used to observe, inspect, control or modify the simulation [7]. As for analysis, CPN Tools supports state space analysis and performance analysis.C.Strengths and WeaknessesOPM and CPN have their own strengths and weaknesses. OPM is well suited to describe the concept model in system development since it provides various general semantics to describe different systems and makes them easy to understand. The view taking a system as a whole is the nature of System Engineering. However, it cannot provide enough numeric analysis which is necessary in the following assessment and validation. CPN, on the other hand, is able to support elaborate simulation and analysis especially for concurrency, however it is difficult to build a completed and correct CPN model form the very beginning. Since the two modeling languages have their own strengths in system development and neither of them can demand the needs of system design and validation alone, it is a nature thought to combine them together to complement each other. The capability of establishing a hierarchical model ensures the possibility to describe complicated systems and is crucial for the transformation.III.M ETHODAccording to the introduction above, there is a nature relationship between OPM and CPN. They both have a graphic representation. The essence of CPN is a state machine and OPM also describe the states of a system and their transformations through processes. As OPM does not have a precise mathematically definition like CPN, it is hard to give a logical representation of the covert method. One possible way is mapping the building blocks between OPM and CPN, so that models constructed by them can transform from OPM to CPN. The method is implemented by transforming the xml files.A.The Conversion of Entities and LinksThe entities in OPM are objects, processes and states. Processes are converted to transitions in CPN, since they both describe the behavior of change in a system. States are mapped to places, with the name in the format of “O_S”, where “O” stands for the name of the object the state belongs to and “S” represents the name of the state. Objects that are connected to the process without states are mapped to places. If an object connected to the process has one or more states, it does not need to be converted to a CPN place, because the procedural links will change the end to its states. Objects do not have a procedural link will not be mapped to CPN.As CPN is mainly concerned the behavior aspect of a system, structural links are not mapped to CPN. Those procedural links are divided into four types for the convert to CPN: (1) consumption links, (2) instrument links, (3) result links and (4) process links.Consumption links include consumption link and consumption event link which link from an object or a state to a process. These links are mapped to arcs from places to transitions. If the source of the link is an object with states, then build a set of arcs the sources of which are places converted from every single state of the object and add a XOR relationship among the arcs. Instead of an OR relationship, a XOR relationship fixes the number of tokens consumed in the transition. The conversion of links in following part will use a XOR relationship instead of an OR relationship as well. The XOR relationship is represented by the structure of CPN. The destinations of the set of arcs are different new transitions with the name of “P_Transition”, where “P” is the name of the source place. Then link those transitions to a new place named with the original object and then connect this new place to the transition converted from the original process as shown in the Table 1. If there is only one state of the source object, just change the source of the link to the place converted from the state.Instrument links include agent link, instrument link, effect link, instrument event link and condition link. Agent link and effect link connect an object to a process, and the rest link from an object or a state to a process. Those objects and state can trigger the process without being transformed, so the links are mapped to bidirectional arcs between places and transitions. If the source is object with states, it is similar as the consumption links except that the set of arcs are bidirectional. See Table 1.Result link which connect a process to an object or a state, are mapped to arcs from transitions to places. If the destination of the link is an object with states, then build a set of arcs the destination of which are places converted from very state of the object and the source of which is the transition converted from the process. There is a XOR relationship among the arcs which is represented by the arc expression. To build a XORrelationship, a new colour set will be declared with the name of “Xor_O”, where “O” is the name of the object. The colour set is a type of integer with the range of 0 to m-1, where m stands for the number of the states in the object. Then there will be a variable named “xor_O” which is a type of “Xor_O” and the value of it indicating a particular state. The arc expression is “if xor_O = i then 1`n else empty” where i is the number representing each states. Once the transition fires, the variable “xor_O” will be given a random value and if it equals the number representing the state, it will pass the token to the place transformed from the state, else it will pass nothing. Table 1 shows the case.Process links include invocation link and exception link, which connect two processes. A new place will be added between the two transitions converted from the processes with the name of “T1 Trigger_Event” or “T2_Exception”, where “T1” and “T2” represents the name of destination process and source process respectively. A process link is mapped to a link from the source transition to the addition place and a link from the place to the destination transition. See Table 1.TABLE I.S PECIAL CASES IN CONVERSION OF LINKSOPMCPNconsumption linkA can be s1 or s2.B consumes A .instrument linkC can be s1 or s2.D requires C .result linkF can be s1 or s2. E yields F .invocation linkG invokes H .B. The Conversion of HierarchyIn OPM, the main mechanism to manage systems’ complexity and to build a hierarchical model is in-zooming/out-zooming makes a set of lower-level things enclosed with a thing visible /invisible. There will be a new OPD for each thing that is zoomed in and the set of OPDs will be connected by the zoomed in things. In CPN, the main mechanism is substitution transitions. A substitution transition is a transition that stands for a whole page of net structure. The places related to the substitution transition are socket places. The places in subpages functioning as the interface through which subpages communicate with their parent pages are called port places. Port places are marked with an In-tag, Out-tag or I/O-tag representing an input port, output port or Input/output port respectively. Each port place of the subpageis assigned to a socket place of the substitution transition and they are functionally identical.Since in-zooming/out-zooming is prior for processes, those processes zoomed in will be mapped to substitution transition and objects zoomed in will not be mapped to CPN. The rules for turning a hierarchical OPM model to a CPN model with subnets are as follows. • A process which is zoomed in will be mapped to a substitution transition.•If the main process i.e. zoomed in process is enclosed with one or more sub-processes, the subpage will not contain the transition converted from the main process, and only presented the sub-transitions.•If the main process is not contained in the subpage, those links connected to it will be change to the sub-process. If the main process is the destination of a link which is a type of consumption links, instrument links and process links, then change the destination of the link to the first sub-process. If the main process is the source of a link, which is a type of result links and process links, then change the source of the link to the last sub-process. The order of the sub-processes is defined by their locations as the timeline in an OPD flows from the top to the bottom. The first sub-process is the one at the top and the last sub-process is the one at the bottom within the main process.•If an object appears in both parent OPD and zoomed in OPD and satisfies the condition of transforming to a place, the object in parent OPD will be a socket place and the object in zoomed in OPD will be a port place. The tag of the place is defined according to the relationship between the object and the main process. If there is only a type of consumption links, it will be an In-tag marked with the place and if there is only a type of result links, it will be an Out-tag. If there is a type of instrument links, it will be an I/O-tag. It is the same with the states within an object which appears in both parent OPD and zoomed in OPD.•The newly added places in the transformation of consumption links and process links will also considered in the conversion of hierarchy if the links appears in both parent OPD and zoomed in OPD.There are some additional rules for completing the CPN model.• The default declaration of the colour sets and variables is defined to ensure the integrity of model logic and make it possible to run. The default colour set is “INT” which is a type of integer and a default variable is “n” which is a type of “INT”. All the places are type INT and all the arc expressions are “n” which means each token carrying an integer as its data value. User-defined declarations and arc expressions can also be used to solve the specific problems. • Places without any arc from a transition to itself will have initial tokens. The default initial mark is “1`1”,which means there is one token the data value of which is one. Only one of those places transformed from a set of states in an object will have an initial token indicating the object state at the beginning. •If a process has no input which means it is not the destination of any links, there will be an additional place named “P Start”, where “P” stands for the name of the process and the place will connect to the transition converted from the process.IV. A PPLICATION IN A S IMPLE A IR D EFENSE S YSTEMFig. 1.OPD of Air Defense SystemFig. 2.OPD of the in-zoomed Detecting processFig. 3. OPD of the in-zoomed Guide&Attack processAn air defense system consists of searching radar, tracking radar, missile and command centre. Searching radar is respond for detecting the target and reporting it to the command centre, tracking radar is respond for tracking the target accurately andguiding the missile to attack the target. Missile is the weapon to attack and command centre is respond for communicating and control. We simplify the model and ignore the command centre assuming that the radars and missile can communicate well with each other. The OPM model of the simple air defense system is shown in Figure 1. The detecting process and guide and attack process can be zoomed into a new OPDand details shown in Figure 2 and Figure 3.Fig. 4.CPN of Air Defense SystemFig. 5.Subnet of the Detecting processFig. 6. Subnet of the Guide&Attack processAfter the transformation, we can get corresponding CPN shown in Figure 4, 5 and 6.It can be simulated and validated the correctness of its logic. Additional formulations and possibilities can be added into the arc expressions and the model can calculate the measurement concerned during thesimulation, like the position and speed of the target and the missile, how different possibilities of detecting affect the time of finding the target and so on.V.C ONCLUSION AND F URTHER W ORKIn this paper, we introduce and implement a method transforming an OPM model to a CPN model by mapping OPM notations to CPN. Not only the basic entities and links, but also the hierarchical properties are converted from OPM to CPN according to the rules we proposed. Combing the capabilities of describing concepts of OPM and the capabilities of simulation and analysis of CPN, it can help develop a model from concepts to details in System Engineering. Application in a simple air defense system demonstrates the process develop a concept model of OPM to a preliminary simulation model of CPN by using this method. It can make the process of concept development more continuous to some degree and make it easier to develop, analysis and validate the model.Further work based on this research might include following topics:•Transformation of the concept of time in OPM to builda timed CPN model.•Transformation based on meta-model and formulation definition of OPM and CPN.A CKNOWLEDGMENTThis research was supported by Natural Science Foundation of China (61074107,91324014).R EFERENCES[1]Bolshchikov, S., Renick, A., Somekh, J., & Dori, D. OPM Model-Driven Animated Simulation with Computational Interface to Matlab-Simulink.[2]Simona, F., Pinheiro, G., & Loureiro, G. (2007). Towards AutomaticSystems Architecting. In Complex Systems Concurrent Engineering (pp.117-130). Springer London.[3]Wang, R. (2012). Search-based system architecture development using aholistic modeling approach.[4]Dori, D. (2002). Object-Process Methodology: A Holistic SystemsParadigm; with CD-ROM (Vol. 1).[5]Dori, D., Reinhartz-Berger, I., & Sturm, A. (2003, April). OPCAT-ABimodal Case Tool for Object-Process Based System Development.In ICEIS (3) (pp. 286-291).[6]Jensen, K. (1997). A brief introduction to coloured petri nets. In Toolsand Algorithms for the Construction and Analysis of Systems (pp. 203-208). Springer Berlin Heidelberg.[7]Wells, L. (2006, October). Performance analysis using CPN tools.InProceedings of the 1st international conference on Performance evaluation methodolgies and tools (p. 59). ACM.。

基于TLA的业务流程形式化分析摘要:本文先分析了业务流程形式化分析与验证的主要研究现状,提出基于tla的业务流程形式化分析的优势。
探讨如何对tla 理论体系进行扩展,以bpel为例研究如何对主流的业务流程的描述语言进行转换。
关键词:行为时序逻辑;业务流程;形式化分析;bpel中图分类号:tp301文献标识码:a文章编号:1007-9599 (2013) 07-0000-021引言行为时序逻辑tla[1,2]是由leslielamport于1990年提出的一种基于行为逻辑与线性时态逻辑的新的逻辑方法。
通过leslielamport与一些学者的研究,compaq、microsoft公司检测工具的开发,行为时序逻辑tla,其描述语言tla+[1,2]与检测工具tlc[1,2]逐步得以完善。
本文对如何使用行为时序逻辑对电子商务环境下的业务流程进行形式化分析进行了探讨。
2业务流程形式化分析与验证的研究现状近期的研究开始关注对业务流程的规范和验证,如利用petri网、自动机、进程代数规范和验证业务服务流程的bpel模型[3,4]。
xiaochuanyi[5]利用有色petri网来设计和验证web业务服务流程,一个流程可以转换到一个对等的cp-nets模型,然后用cpn工具分析验证,检验流程的正确性。
yanpingyang[6,7]把bpel转换到层次有色网,再利用cpn工具验证。
chunouyang[8]提供了比较完整地从bpel控制流到petri网的映射。
xiangfu[9]把bpel转换成自动机,进而转换成promela语言,再利用模型验证工具spin进行验证。
wombacher等人[10]用一种扩展逻辑表达式的自动机于对业务进行形式化建模,kochutk等人[11]提出一个基于petri网的设计和验证框架,可用于bpel进程的可视化、创建和验证,文献[12]给出了一套完整的、形式化的petri网语义,将bpel进程自动转换为petri网模型,可用多种验证工具对bpel进程做自动分析。

0 型系统||type 0 system1 型系统||type 1 system2 型系统||type 2 system[返]回比矩阵||return ratio matrix[返]回差矩阵||return difference matrix[加]权函数||weighting function[加]权矩阵||weighting matrix[加]权因子||weighting factor[数字模拟]混合计算机||[digital-analog] hybrid computer[最]优化||optimizations 域||s-domainw 平面||w-planez [变换]传递函数||z-transfer functionz 变换||z-transformz 平面||z-planez 域||z-domain安全空间||safety space靶式流量变送器||target flow transmitter白箱测试法||white box testing approach白噪声||white noise伴随算子||adjoint operator伴随系统||adjoint system半实物仿真||semi-physical simulation, hardware-in-the-loop simulation 半自动化||semi-automation办公信息系统||office information system, OIS办公自动化||office automation, OA办公自动化系统||office automation system, OAS饱和特性||saturation characteristics报警器||alarm悲观值||pessimistic value背景仿真器||background simulator贝叶斯分类器||Bayes classifier贝叶斯学习||Bayesian learning备选方案||alternative被动姿态稳定||passive attitude stabilization被控变量||controlled variable; 又称“受控变量”。

doi:10.3969/j.issn.1671-1122.2020.09.006基于随机Petri网的系统安全性量化分析研究毋泽南1,田立勤1,2,陈楠2(1.青海师范大学计算机学院,西宁 810000;2.华北科技学院计算机学院,北京 101601)摘 要:针对日益频发的网络攻击事件,如何准确有效地对攻击事件进行实验推断,并对网络安全相应指标进行量化分析,已成为近年来的研究热点。
文章结合网络系统安全性评估需求,对网络系统安全性评估的主要指标及求解方法进行了论述。
在此基础上研究了利用随机Petri网对网络系统安全性进行建模分析的方法和步骤,并结合模型的马尔可夫性给出了网络系统安全性指标的计算方法。
最后,通过具体实例对模型的正确性进行验证。
结果表明,利用随机Petri网对网络系统安全性进行建模分析是合理有效的,为网络系统安全性评估相关研究提供了新思路。
关键词:网络系统安全;随机Petri网;马尔可夫性;安全评估中图分类号:TP309 文献标志码: A 文章编号:1671-1122(2020)09-0027-05中文引用格式:毋泽南,田立勤,陈楠.基于随机Petri网的系统安全性量化分析研究[J]. 信息网络安全,2020,20(9):27-31.英文引用格式:WU Zenan, TIAN Liqin, CHEN Nan. Research on Quantitative Analysis of System Security Based on Stochastic Petri Net[J]. Netinfo Security, 2020, 20(9): 27-31.Research on Quantitative Analysis of System Security Based onStochastic Petri NetWU Zenan1, TIAN Liqin1,2, CHEN Nan2(1. School of Computer, Qinghai Normal University, Xining 810000, China;2.School of Computer, North ChinaInstitute of Science and Technology, Beijing 101601, China)Abstract: In response to the increasing frequency of network attack events, how to accurately and effectively perform experimental inference on the attack events andquantitatively analyze the corresponding indicators of network security has become a researchhotspot in recent years. This paper discusses the main indicators and solving methods ofnetwork system security assessment in conjunction with the needs of network system securityassessment. On this basis, the methods and steps of stochastic Petri nets for modeling andanalyzing network system security are studied, and the calculation method of network systemsecurity indicators is given in conjunction with the Markov property of the model. Finally, thecorrectness of the model is verified by specific examples. The results show that it is reasonableand effective to use stochastic Petri nets to model and analyze the network system security,收稿日期:2020-7-16基金项目:国家重点研发计划[2018YFC0808306];河北省重点研发计划[19270318D];河北省物联网监控工程技术研究中心项目[3142018055];青海省物联网重点实验室项目[2017-ZJ-Y21]作者简介:毋泽南(1991—),男,河南,博士研究生,主要研究方向为网络实体信任评估、用户行为认证;田立勤(1970—),男,陕西,教授,博士,主要研究方向为网络安全、物联网可靠性分析;陈楠(1994—),男,安徽,硕士研究生,主要研究方向为用户行为认证。
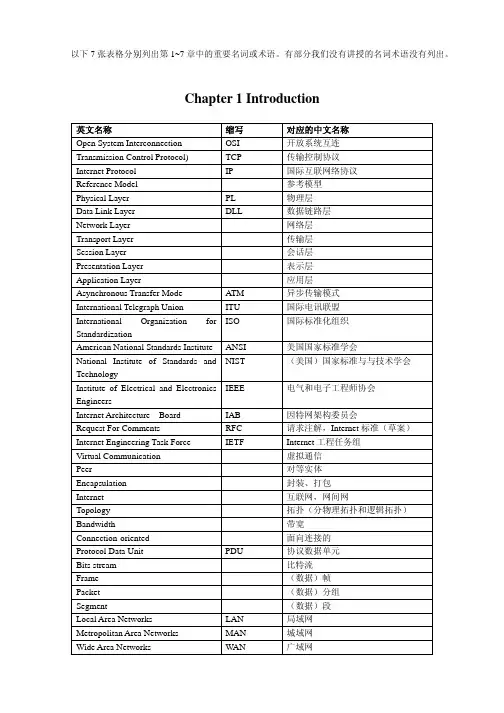

Mission Reliability Modeling for Equipment System Based on the Operational Viewpoint ofDoDAF 2.0Lin Shaoyang,College of Information System and Management National University of Defense TechnologyChangsha, P. R. China***************************Wu XiaoyueCollege of Information System and Management National University of Defense TechnologyChangsha, P. R. ChinaAbstract—Currently, Department of Defense Architecture Framework (DoDAF) 2.0 is widely used in many aspects of the architecture-related modeling fields. Due to the highly complex structure of architecture, its reliability became a pivotal issue. However, DoDAF 2.0 is lack of a specific viewpoint to model the reliability of the architecture. This paper introduces an approach to deal with reliability modeling method related missions posed by Equipment System (ES), which is an obvious characterized architecture. OV-1, OV-5a and OV-6c of DoDAF 2.0's operational viewpoint are extracted and extended as the modeling framework. Use case diagram, class diagram and sequence diagram of Unified Modeling Language (UML) are picked to present the products mentioned. The study also regulates a series of standards for each extended product in detail, in order to collect requisite reliability-related parameters for further analysis and calculation. Later, the proposed model is applied to an ES as an example to verify its availability.Keywords-reliability modeling; equipment system; mission reliability; equipment system; operational viewpoint; DoDAF2.0I.I NTRODUCTIONEquipment System (ES) is made up of wide ranges of correlative and function-complementary equipment, which integrate into an organic integrity of diverse categories, structures and scales, according to the claim of optimal placement and operational capability, thus making up a large high-level system, namely System of Systems (SoS) or architecture.Reliability is a key performance parameter in system design, so has become a basis factor affecting mission success [1]. Mission is the foundation of ES, since all member of ES are related with each other as a whole by the same target—achieving the specific destination. Mission reliability refers to the probability that a system will perform its specified mission in its mission section [2]. Therein, mission section is the profile to the events and time sequence the mission has to follow. Mission reliability reflects the ability of fulfilling the task successfully, thus playing a big part in ES operational effectiveness.On the basis of multi-view method, Architecture Framework (AF) provides a collection of normalized modeling process and description method, which standardizes the contents contained to ensure the unified understanding and comparing principal from all stakeholders [3]. Currently DoDAF 2.0 of U.S. is often adopted as descriptive model in military field [4-6]. Nonetheless, no specialized reliability modeling viewpoint or product arises in DoDAF 2.0.Several reliability modeling methods have been used in the mission reliability analysis. Fault tree analysis is suitable in describing non-repairable systems in [7–9], but its limitations become apparent when conducted to quantitative issues. Bayesian Networks were developed as a logic graphical representation [10–11], and it has shown its agile computation efficiency. This approach is also applied in the proposed methodology. Later, state-space models, namely Markov chains and Petri nets, appear as main methods for analyzing system's dynamic reliability [12-14]. However, it has the state space growth explosion problem.Yet, methods mentioned above show weakness on describing ES, since ES usually has great amount of units of different levels and complicated logical relations. On the other hand, product sets of DoDAF 2.0 do not supply all sufficient data for ES reliability analysis. In the paper, we propose a reliability modeling framework based on the operational viewpoint of DoDAF 2.0, viewing to probe into a reliability modeling framework to ES.For the rest of the paper, section II introduces DoDAF 2.0 and its operational viewpoint. Section III demonstrates the processed reliability modeling product set and its UML description in detail. Section IV describes the application of this approach to an ES as a case study. Section V summarizes the paper and gives a perspective to further research.II.D O DAF2.0A ND I TS O PERATIONAL V IEWPOINTDoDAF 2.0 is a graphical and tabular description for SoS. It provides general guidance for development, usage and management of DoD architectures with an emphasis on interoperability and integration between constituentInternational Conference on Logistics Engineering, Management and Computer Science (LEMCS 2014)systems in SoS [15]. In total, 8 viewpoints and 52 products are built in DoDAF 2.0.Viewpoint replaces "view" of antecedent versions, in order to coordinate with ISO. These viewpoints are further classified for describing the overarching aspects for every viewpoint (All Viewpoint, AV), requirements and deployments (Capability Viewpoint, CV), data relationships and alignment structure (Data and Information Viewpoint, DIV), operation scenarios and activities (Operational Viewpoint, OV), relationships between OV&CV and projects being implemented (Project Viewpoint, PV), performers, activities services and their exchanges (Service Viewpoint, SvcV), applicable principals (Standard Viewpoint, StdV), and the composition, interconnectivity and context (System Viewpoint, SV),as Fig.1 demonstrating. Each of these views has a well-defined product set in accordance with different perspectives.The DoDAF 2.0 viewpoints reside in a presentation layer, underlying which there is a data layer where defining attributes and relationships of the architecture can be documented [16]. There is a natural and straight correspondence between AF and UML [3]. Additionally, DoDAF 2.0 formalism is increasingly being supported by other commercially available architecting tools, in which documents, sheets, matrices and such structured presentations are employed to narrow development cycle, e.g. DOORs of Telelogic, Requisite Pro of Rational and Caliber RM of Borland. One of the advantages UML possesses is that not only does it allow capturing DoDAF 2.0's data layer but also supports modeling and simulation on purpose of verification.OV describes the missions and activities, operational elements, and resource flow exchanges required to conduct operations [16]. OV is adept at tracing system's dynamic behaviors and transformation, and just such character makes it quiet suitable for modeling ES mission reliability. OV has 9 products in total, involved capturing organization relationships, resource flows, state transition and other architecture's characters. For mission reliability modeling, this paper provides a tailored product set, including OV-1, OV-5a and OV-6c to model ES's mission reliability, and it would be elaborately discussed in nextFigure 1. DoDAF 2.0 eight viewpoints.III.M ISSION R ELIABILITY M ODEL U NDER OVProduct SetThe clipped product set of ES mission reliability model is shown in Fig. 1.OV-1 aims at describing the contents and processes of the mission(s) that ES has to fulfill. Graph of jpg is recommended as the storage format. Its visualized representation enables further reliability modeling, meanwhile offering information particularly concerned by high-level decision makers during their decision process. OV-1's contents depend on the unique objective and application of specific ES. In general, it may involve operation processes, organization hierarchy, geographical distribution and operational expectations including what missions will emerge, which unit(s) will undertake, what sequences should be complied with et al, and also the interaction with external environment and systems. The links between two elements are suggested but not limited as one of the follows:∙Control: Control link from A to B means B's activity is managed by A's instructions.∙TrackInfo: TrackInfo link represents the information flow movements.∙Assistance: Assistance link from A to B indicates that if B gets failed, A would make up.∙Affirm: Affrim link reports the lower equipment's being- state and attack-complete state from lowerlevel to the command center.The relationships of the elements on the diagram sometimes convey their relative position, although this is not specifically captured in the semantics. Since each ES differs, we do not set specific rules for OV-1.OV-5a is a newly created product in DoDAF 2.0, in order to describe mission constituents and their hierarchical structure. Through the decomposition it can be cleared that the duty each mission should accomplish and unnecessary redundancy that can be eliminated. Thus the model could be simplified and efficiency may be improved as well. To clarify the affect that lower-level failure brought about to higher missions, logic connections are introduced into OV-5a. Currently 'AND' gate and 'OR' gate are mainly considered. They can be defined as follows.Def. 1AND gate: Only when all nodes under AND gate succeed does mission above the gate succeed, as Fig. 2(a).Def. 2OR gate: As long as at least one of the nodes under OR gate succeeds will mission above the gate succeed, as Fig. 2(b).OV-6c depicts the sequence and information exchanges between phases. Through constant refining to the mission process, execution order and rules would be gradually precise and accurate. UML sequence diagram is adopted as representation standard. Sequence division is consistent with divided layered graph of OV-5a. On top of the graph is ES' object, accompanied by its relevant lifeline. Specific time points are labeled on left of the lifeline labels. Bars on the lifeline stand for its duration time. Solid arrow line is message transiting between objects.In each phase's sequence diagram, time propels in terms of lifeline. In reality, lifeline is finite and does not fit for long-time phase. Thus object's lifeline should be regulated in more details. As Fig. 3 shows, on left of the object A's lifeline, t11represents A's start time and similarly t12 end time, while t21 is the time message 1 from another object arrives. t22 on the right indicates message 2 leaving time.A N DP 1P 2AO RP 1P 2BFigure 2. (a) AND gate example. (b) OR gate examplemessage 2O bj ect A t 11t12t 22message 1t 21Figure 3. OV-5a UML sequence diagram representationIV. UML D EFINITIONa. OV-5a UML normalizationOV-5a describes the operations that are normally conducted in the different nodes. The extended use-case and class diagram provides a means of breaking down activities to lower level activities as well as indicating the nodes that perform the activities. It includes node, activity, link and logic relation. Their normalized data definition is shown in table 2 (a)-(d).b. OV-5a UML normalizationThe OV-6c is used to define time based behavioral scenarios between operational elements. The interactions can be service operations as well as the interactions defined on OV-5a diagrams. There are three types of elements in OV-6c: node, lifeline and message transit. Therein, node data definition is the same as OV-5a. Lifeline can be potentially described by the messageArrivingTime and messageLeavingTime attributes of message transit. Table 3 illustrates the data definition for message transit.TABLE I.ES M ISSION R ELIABILITY M ODELTABLE II.(A)D ATA D EFINITION F OR N ODETABLE III. (A) D ATA D EFINITION M ESSAGE TRANSITV.C ASE S TUDYAn ES is presented in this part as a detailed illustration to the proposed model. The system basically consists of five parts: Ground Based Interceptor (GBI), X band Ground Based Rader (GBR), Battle Management and Command, Control & Communications (BM/C3) system, Upgraded Early Warning Radar (UEWR), and Defense Support Program/Space-Based Infrared System (DSP/SBIRS) [17].GBI is an up-to-date kinetic energy antipersonnel weapon intercepting ballistic missile warheads in its midcourse outside the atmosphere and destroying it through straightly impact. Traditional GBI consists of Exoatmospheric Kill Vehicle (EKV) and two booster rockets.GBR is X band phased array radar, and it is the main fire control radar of the system, deployed at the same place with GBI. It mainly involves surveillance, capture, trace, identification, fire control assistance and damage evaluation.BM/C3 is the brain of system, connecting all constituent systems organically. It mainly involves in receiving data from each detector to analyze the striking missile's parameters (like speed, trajectory, point of fall et. al), calculating "sweet point", directing UEWR and GBR to trace and capture the target, giving launch orders to GBI, offering revised target information to the flying interceptor, evaluation intercepting effect, and so on. BM/C3 is also deployed with GBI and GBR.UWER is upgraded phased array radar used to detect and track ballistic missile and provide early warnings. It detects and traces ballistic missile initial flight and provides GBR rough azimuth information.DSP supplies early warnings for the system. Via merging data from two or more DSPs, ballistic trajectory can be forecasted. Furthermore, compared with foregone missiles' infrared characteristics, the ballistic version can be confirmed. Currently, DSP is gradually replaced by SBIRS, which consists of two kinds satellites: Lower Earth Orbit (LEO) and High Earth Orbit (HEO). Highly flexible infrared sensor technique of HEO conveys strategy, the launch and flight of theatre ballistic missile, global theatre infrared data and processed intelligence. LEO satellites are equipped with two kind sensors: the capture one is to observe flame during the rocket launch phase; the other trace one could keep in track with the locked target from its midcourse until back into the atmosphere.Fig. 4 is the OV-1 model of the system. Substantially the system functions in such procedures:1: Early warning phase1) DSP/SBIRS detects the booster's plume when the striking ballistic missiles launches, and traces until its booster rocker turning off. Via repeater satellite or earth station, DSP/SBIRS sends trackinfo back to BM/C3for predicting the striking missile's incoming direction as well as impact area. Pertinent data would also be sent to UEWR.2) After gets information of ballistic position, UEWR will search and detect associative airspace to trace the striking missile. When discovering missile warhead, it will track robustly and send trackinfo to BM/C3.2: Interception decision phase1) BM/C3formulates operations management plan, including intercepting pattern, interceptor quantity, calculating effective acting distance, thus preliminarily ascertaining GBI's launch direction and moment. Meanwhile BM/C3should send control information to GBI and receive affirm to get its authorization.2) BM/C3 sends trackinfo got from UEWR to GBR to guide its search. Through detecting and tracing ballistic warhead, GBR would retrieve more precise information for BM/C3decision. Meanwhile, GBR would generate warhead image by sufficient data it has collected.3) BM/C3conducts target identification and threat evaluation to verify the warhead version, the trajectory and the impact point. On this basis, interception decision about GBI's launch moment and estimated interception point is made. When the accuracy of the estimated interception point is within the appointed scope (20km), BM/C3 would give GBI launching orders targeting on the estimated interception point.3:Interception implementation phase1) As soon as receiving orders, GBI launches immediately. After that, GBR precisely tracks GBI and warhead, returns revised objective data back to BM/C3 to update GBI's flight.2) When GBI reaches the estimated airspace, EKV separates with the booster rocket. Then EKV compares the target information detected with former images provided by GBR to verify and target objective, thus destroying it through straight collision.4: Interception effectiveness evaluation1) During the GBI collision, GBR collects interception data sending back to BM/C3.2) BM/C3evaluated the interception effectiveness. If failed, BM/C3 has to decide whether to conduct a second interception.According to the procedure, its operational activities decomposition can be depicted like Fig. 5(a). Furthermore, Fig. 5(b) shows the class diagram for the case "EKV attack". On purpose of saving space, some of the class attribute values and operations have been omitted. For the proposed model of OV-6c, the above mentioned interception decision phase is hired as an example, and it is shown in Fig. 6.VI.C ONCLUSIONDoDAF 2.0 is a rife model framework for ES. The paper proposes a mission reliability modeling method based on the operational viewpoint of DoDAF 2.0 and illustrates the UML normalization. An ES is an example of highly complex and adaptive ES characterized by a loosely coupled federation of constituent systems. The proposed model succeeds in describing ES reliability structure, proving the methods validity. For further research, transition mechanism between OV-5a and OV-5b can be investigated in terms of enriching the product set and heterogeneous representation. Besides, UML entities can be enlarged for more abundant and convenient details. More importantly, system view's product can also be used on mission reliability modeling.A CKNOWLEDGMENTThe paper is partly supported by National Natural Science Foundation of China under grant no. 71071159.Figure 4.OV-1 modelD S P /S B I R Sdet ect pl um et racem i ssi l est ore dat asend i nf o.recei ve com m andU E W Rsearchw arheadG B IG B Rl aunch gi ve orders<extends><extends>revi se fli ghtseparat eboost ersE K V at t ack<extends><extends><extends>recei vei nf o.cal cul at edeci degenerat ei m ageFigure 5. (a) OV-5a modelactivityIDnodeContained activityDescription successrulesE K VA t t acknodeId ofActivity linkIn linkToprerequisitesuccessProbability startTime endTimeE K V S eparat enodeId ofActivity linkIn linkToprerequisitesuccessProbability startTime endTimeA t t ackO rdermessageType messageIdmessageFrom: GBR, UEWR messageArrivingTime Fl i ght P osi t i onE K V posi t i oni ngmessageType messageIdmessageFrom: GBR messageArrivingTimeR evi sed Fl i ght ANDmessageType messageId messageFrom messageTomessageArrivingTime messageLeavingTimeTarget V eri ficat i on ANDFigure 5. (b) OV-5a class diagram for the case "EKV attack"U E W RG B RB M /C 31: controlAuthorizationG B I6: launch decision order(position,time)3: traceMessage5: traceMessagewarhead image4: traceMessage 2: af f i r m at i onFigure 6. OV-6c Sequence diagram for interception decision phaseR EFERENCES[1] Reliability primer for command, control, communications,computer, intelligence, surveillance, and reconnaisssance (C4ISR) facilities. available at: http: // www. usace. ary. mil /publications/ armytm/tm5-698-3/entire.pdf.2005a.[2] Chul Kim, “Analysis for mission reliability of a combat tank ,”IEEE Transactions on Reliability, vol. 38, no. 2, pp 242-245, 1989. [3] Robert K. Garrett, Steve A., Neil T Baron, “Managing theinterstitials, a system of systems framework suited for the ballistic missile defense system ,” Systems Engineering, vol 14,no. 1, pp. 87-108,2011.[4] Yang Kewei and Tan Yuejin, Architecture RequirementsTechnique and Method. Peking: Science Press, 2010.[5] Shu Yu, Research on weapon equipment architecture modelingmethod and application based on the capability requirements, Ph.D. Dissertation, National University of Defense Technology, 2009. [6] Jiang Zhiping, Research on architecture verification method andkey technique for C4ISR system based on CADM, Ph.D. Dissertation, National University of Defense Technology, 2007. [7] Bobbio A., Portinale L, “Improving the analysis of dependablesystems by mapping fault trees into Bayesian networks ,” Reliability Engineering & System Safety, vol. 71, no. 5, pp 249-260, 2001.[8] Hichem Boudali, Joanne,Bechta Dugan, “Dynamic fault treemodels for fault tolerant computer systems ,” IEEE Transaction On Reliability, vol. 41, no. 3, pp 363-377, 1992.[9] Huang Chin-Yu, Chang Yung-Ruei, “An improved decompositionscheme for assessing the reliability of embedded systems by using dynamic fault trees,” Reliability Engineering & System Safety, vol 92, no. 10, pp 1403-1412, 2007.[10] Boudali H., Dugan J. B, “A discrete-time Bayesian networkreliability modeling and analysis framework ,” Reliability Engineering & System Safety, vol 87, no. 6, pp 337-349, 2005. [11] Hichem Boudali, Joanne Bechta Dugan, “A continuous-timeBayesian network reliability modeling and analysis framework ,” IEEE Transaction On Reliability, vol 55, no. 1, pp 34-41, 2006. [12] Jau-Yeu Menq, Pan-Chio Tuan, “Discrete Markov ballistic missiledefense system modeling ,” European Journal of Operational Research, vol 178, no. 1, pp 560-578, 2007.[13] Kim K, Park S, “Phased-mission system reliability under Markovenvironment ,” IEEE Transaction On Reliability, vol 43, no. 5, pp 301-309, 1994.[14] Abidin E.Olmez, “Mission centric reliability analysis of C4ISRarchitectures using petri net ,” In Proceedings of IEEE International Conference on Systems, Man and Cybernetics, pp 587-592, 2003. [15] Department of Defense Architecture Working Group, DoDArchitecture Framework 2.0, Volume 2: Architecture and Models, available at: /Portals/0/Documents/DODAF/DoDAF_v2-02_web.pdf[16] Biswas, A, Hayden, J, Phillips, MS, Bhasin, KB, Putt, C, &Sartwell, T, “Applying DoDAF to NASA orion mission communication and navigation architecture. In Proceedings of IEEE Aerospace Conference, pp 1-9, 2008.[17] Wang Minle and Li Yong, Ballistic Missile PenetrationEffectiveness Analysis. Peking: National Defense Industry Press, 2010.。

Winfrid G. SchneeweissPetri Nets for Reliability Modeling(in the Fields of EngineeringSafety and Dependability)LiLoLe-Verlag GmbH (Publ.Co.Ltd.)Serving Life-Long LearningPrologThis book of LiLoLe-V erlag (=publisher) was prepared with life-long learning in mind. This means easy reading as tol the level of presentation ( tutorial, rather than research type)l the didactics of explanationsl complete solutions of all the exercises(important for self-study)l the quality and number of the figuresl the text layoutl the size of the letters (still legible in case of deteriorated sight)l the size of the book ( useful as a little intellectual refresher that can be mastered during a single week)Here comes a book to be read for earnest study and professional use, or just for fun at any age from, say, 17.Table of contentsPreface1 Introduction1.1The main aim of this book1.2A preliminary description of Petri nets1.3How to work with this book2Basics of Petri nets2.1Definition of Petri nets2.2State graphs of Petri nets (reachability graphs)2.3A chess board pattern for drawing Petri nets2.4Modeling basic switching phenomena2.5Inhibit edges2.6Exercises3Special aspects of Petri nets with reliability modeling 3.1Petri nets of state graphs3.2Petri nets of fault trees and success trees3.3The different meanings of tokens3.4Exercises4Non-repairable systems4.1Systems without redundancy4.2Systems with cold standby4.3Systems with hot standby4.4Exercises5Repairable systems I; basic aspects5.1Repair after a diagnosis process5.2Repair priorities; simple cases5.3Toward a systematic design of modules5.4Integrating fault tree and success tree5.5Exercises6Repairable system II; aspects of refined maintenance 6.1Limited maintenance6.2Preventive maintenance6.3Repair priorities; more complex cases6.4Modeling the waiting for and the production of spares 6.5Materialistic aspects of medical care6.6Exercises7Cost/benefit aspects7.1Basic performance modeling via Petri nets7.2Refinements of the basic reward model7.3Exercises8aspects of timeliness8.1A single working unit8.2A pair of working units8.3Exercises9Phased missions9.1Different operational phases9.2Changes of redundancy structure9.3Repairs in several phases9.4Exercises10The design of large Petri nets10.1Hierarchical decomposition10.2Design in several phases10.3Engineering test of Petri net designs10.4Exercises11Comments on the theory of Petri nets11.1A few general aspects for reading PN literature 11.2State of the art as apparent from textbooks11.3Exercises12Tools for Petri nets applications12.1Tools known from literature12.2Tool derivable from this text12.3Exercises13On limits of the modeling approach presented here 14Solutions of the exercises15Appendix15.1basic vocabulary of graph theory15.2Glossary of terms of dependability modeling ReferencesNotationIndexPrefacePetri nets as introduced in the PhD thesis of Carl Petri in 1962 [Petr62] have proved to be the best graph-based tool for investigating or rather, modeling the dynamics of systems incorporating switching operations of any kind. Roughly speaking, Petri nets show the flow of (abstract) objects, their creation and their vanishing. The delay of flow is modeled explicitly by the parameter of so-called transitions which are one of the two types of nodes of a Petri net. The above objects are called tokens stored in so-called places, which are the other type of ON nodes. Thus a PN is a bipartite graph with a dynamic marking of one kind of its nodes. The placesThe switching operations concerning changes of that marking are mostly triggered by a logical conjunction, i.e., AND operation, based on the marking of certain neighboring places of a transition. The detailed explanations of all this will follow in subsection 2.1. The reader should here only have a rough idea of token usually drawn as bold face dots, wandering by certain local switching operations through a network, namely our Petri net, allowing also for changes in the total number of tokens. PNs are certainly no mass flow graphs with tokens as quanta of mass and they are also no state graphs, since simultaneous activities are possible in more than one part of a given PN. Rather, the state graph of a PN is the so-called reachability graph expressing which markings can be reached form an initial one.All of the above, hopefully, lets it appear plausible or even obvious that PNs are exceptionally well suited to improve reliability(dependability)modeling. (By dependability we mean the broad field of studying the fact that systems and or missions can fail; including keywords as reliability, maintainability, fault tolerance etc. [Lapr92]The study of Petri nets in reliability modeling is not new; see e.g. [Matr95], [Schn90], [SaTrPu96]. However, similar to other fields of engineering practitioners are hardly aware of them and certainly don’t use them as they could and should. Of course, it is helpful to be familiar with enough mathematics to be able to understand and hopefully apply the existing deep theory of Petri nets[AjMa95], [CBCMT93], [BaKr96]. Yet, even without mathematics, PNs (or at least the class to be presented very carefully here) are by far the best graphical tool for reliability modeling.Petri nets are typically a very good means for an interdisciplinary study of safety and/or reliability aspects of complex engineering systems where neither the specific jargon of electronics engineers nor that of mechanical engineers nor that of physicists or chemists can be of immediate use for a mixed team of all the above specialists. In contrast to the unproductive discussions on terminology of such mixed teams, it is this author’s experience that only a few hours of teaching on Petri nets to the extent of the contents of chapter 2 results in a firm, generally accepted basis for a detailed discussion of all discrete dynamic phenomena of a given complex system such as an aero plane or a production plant. Furthermore, PNs are not only a guide to Monte-Carlo simulations of the reliability-related behavior of (complex) systems, but almost a complete documentation of it.The only thing PNs usually don not readily offer is the foundation for a formal (theoretical) treatment of such systems. In that area the best text book is probably[SaTrPu96]. For non-repaired systems are also [Schn99, 1].Many readers will have come across Petri nets prior to reading this text. They should not be bewildered by the fact that a number of small details are different here. This is intended since theauthor feels that certain terms of standard notation and nomenclature, including pictures are not well adapted to reliability modeling, and possibly to further fields of engineering.l There is, e.g., the term “safe” for a PN where only at most one token per place is allowed. We propose the much more obvious term of a Boolean marking. Similarly, so-called “liveness” of any kind [Reis85] is not considered important in the field of reliability modeling. Typically, there will be branches of a PN where nothing ever happens due to an early decision for a triggering token to go elsewhere.l Furthermore, often different symbols are used for different types of transitions, as to there switching delays (not in [Reis85]), while the very existence of switching delays, as an extra marking of the transitions, is not explicitly introduced. We do introduce that important aspect of PNs for modeling real world phenomena and we see no reason for having different symbols for different types of transitions, All is very adequately expressed by small squares for the transitions in which the relevant delay is enscribed; typically 0 for the so-called immediate transitions.l Finally, this author feels that terming a PN “bounded” or “pure” or “ordinary” is superfluous since everybody will understand the only slightly longer terms” with a bound for the maximum number of tokens in any place” or “free from cycles of length 2” or “without edges of non-unity weight” respectively.For a deeper understanding of the last paragraph the reader is advised to study [BaKr96] and there the introduction to Part III: “Time-Augmented Petri Nets”. That introduction begins with the bewildering paragraph “Petri nets involve no notion of time, since it is not defined at what point in time a transition will fire. Analyzing the performance of a system with a Petri net is thus not possible… For performance or quantitative analysis the temporal(time) behavior of the system has to be part of the Petri net description…”. Remarks of this kind and the fact that the term stochastic Petri net that should, in our opinion, encompass any randomness in a PN, but not be confined as, e.g. in [SaTrPu96] for PNs with an exponential firing delay of most or all transitions are the reasons practitioners have hitherto often turned their interest to less confusing methodologies of analysis.As to PN pictures we will show 3 styles of drawing, all of which have their pros and cons. Which one is preferred is largely a matter of taste. Beside any (round) node for a “place” I we willp, but only i; likewise beside any (square) node for a “transition” i we will not not writeit, but simply i. This makes PN pictures clearer.writeiIt is my sincere pleasure to express my gratitude for the help I experienced when preparing this text. Thanks to my secretary, Elke Lenske, for her patient work with LaTeX, to Edmund Palmowski for his expert coral Draw-based figures. To Mary Harrwo for linguistic help with part of the text, and to Uwe K. Rakowsky for his engaged proof reading. Finally, I thank carl Adam Petri for his friendly permission to dedicate this book to him.1 IntroductionLearning about a new scientific subject as complex as Petri nets is a process that needs a preliminary introduction, as given in this chapter. In later chapters more formal aspects will be added to deepen understanding.In subsection 1.1 we will explain in some detail why there has been an ever growing need for a book such as this. Then we will try to explain (in subsection 1.2) what Petri nets are in a non-technical way, some might call “philosophical”. Finally, subsection 1.3 will contain a few hints on how to use this book.1.1 The main aim of this bookThis book will demonstrate the enormous usefulness of (almost) mathfree Petri net theory in the field of dependability, encompassing those well known “ilities” such as reliability, maintainability, availability, performability etc. The author has searched the existing literature for a number of years to find an easy access to understand at least the simpler aspects of PN theory. Others such as the well known computer pioneer Konrad Zuse[Zuse82] obviously had much the same intention. Usually one ends up with volumous conference proceedings, mostly of Springer Verlage [Mars93], full of advanced refinements and almost always full of papers with pages of definitions. Unfortunately this is also true for a well-meant introductory texts such as Reisig’s book[Reis85].Consequently engineers largely feel THA T PNs are objects of study exclusively for mathematicians and theoretical computer scientists. This author feels a strong motivation toward freeing the simpler parts of the Petri nets theory from the myth of being useless for practitioners. Again, PNs which encompass much more than fault trees and state graphs (known from Markov modeling) will be shown to be a graphical aid for understanding safety and reliability in a unified way at any depth needed.1.2 A preliminary description of Petri netsPetri nets are usually introduced by lengthy definitions and lots of mathematical symbolism. However, a sufficient understanding is possible without that much math notation if one is willing to first look at a fairly simple class of PNs. Let us do that in this subsection. The following definitions are used.1) A PN with a time-variable Boolean marking for the “places” is a bipartite digraph where anyplace )(i p i can “contain” at most one token; see, e.g. fig.1.1Fig. 1.1 PN with a Boolean marking. Places (round nodes) and transitions(square nodes) are numbered separately.2) Any transition )(j t j is enabled once all the places with edges pointing at j t are marked.Then it will switch or “fire” after a delay j D (written in it) whereby all input (or predecessor) places of j t loose their token and all output (or successor) places received a token; see fig. 1.2.Fig. 1.2; Switching of a transitions j t ; a) j t not enabled; b) j t enabled; c) j t at a time at least j D after enabling.Hint: In slightly more general PNs switching means subtracting a token from every input place, and adding a token to every output place (of a transition).Example 1.1: Switching in a very simple PNIn fig. 1.1, 1t is obviously enabled. Hence, at most by 1D later 1t will switch and 3p will receive a token while p and 2p loose theirs. Now both 2t and 3t are enabled and we have to consider the alternatives 32D D < and 32D D >. (Let us assume that it does not matter to which alternative 32D D = is added.) If 32D D <, then by 2D later 5p will receive a token ,and 3p and 4p will loose theirs. If 32D D >, then 2p will become marked again and 3p will be emptied. All in all this PN ends up with only 5p or both 2p and 4p marked, respectively.The above example has shown the following important features of PNs all of which are true also for wider classes of PNs.1) The number of token s in a PN need not be constant.2) The switching delays of the transitions can determine strongly the sequencing of thetransitions’ switching in a PN.3) There can exist absorbing states of a PN where no further switching is possible.Notice that the above Boolean marking may an undesirable feature, e.g., for counting operations. In fig. 1.3 the number of cycles of a token is counted by the number of tokens in 2p . D can be a random cycle time. Both PNs of fig.1.3 a, b, are equivalent.Fig. 1.3: PNs of a cyclic process during its 5th cycle1.3 How to work with this bookThis book is best read straight through. One may omit chapters 7-9, the sections on exercises and more lengthy examples. However, the reader should be careful about avoiding the exercises, since they will help substantially in finding points of still insufficient understanding. A little repetition might be helpful and the solutions of the exercises at the end of the book (see section14) informative.It would be useless to read any parts of this book prior to a thorough study of chapter 2 and 3 where the basic concepts of the type of Petri nets used here are introduced informally and formally with utmost care.For readers not familiar with basic concepts of graph theory a short appendix is enclosed; see subsection 15.1. In order to avoid any ambiguity on terms of dependability, subsection 15.2 should serve as an ad-hoc dictionary.This textbook can also serve as the basic text of a one-semester 1-to-2 hours per week course where one chapter (including the exercises) may be covered per lecture.Written by a processor of a distance study university, who has included many pictures and many examples, this book should also be well suited for self-study.。



IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 52, NO. 2, APRIL 2005595Petri Net Models, Functional Abstractions, and Reduction Techniques: Applications to the Design of Automated Manufacturing SystemsRichard Zurawski, Member, IEEEAbstract—The use of generic models in the synthesis of flexible manufacturing systems (FMSs) systems, which allows for rapid modeling and analysis, does not ease the verification task difficulty. Even though generic modules can be verified separately, the verification of the interconnections between modules requires the whole model to be considered. A potential solution is to replace the generic modules with their functional abstractions which realize the external functional behavior of these modules. The number of places and transitions involved in realizing the required functionality is, typically, a fraction of that used to represent complete components. This reduces the complexity of the components of the modeled system, and thus the complexity of the verification model. The verification task can then focus on the correctness of the interfaces, rather then on the internal nature of the components. This paper presents new results that allow for systematic construction of functional abstractions for a class of Petri net models which can be used to represent the primary components of the automated-guided-vehicle-based FMSs. Index Terms—Flexible manufacturing systems (FMSs), formal modeling, formal validation, functional abstractions, Petri nets, reduction techniques.I. INTRODUCTION ETRI NETS, as graphical and mathematical tools, provide a uniform environment for modeling, formal analysis, and design of discrete-event systems. One of the major advantages of using Petri nets is that the same model can be used for the analysis of behavioral properties as well as performance evaluation. Petri nets as a graphical tool provide a powerful communication medium between the user, typically, the requirements engineer, and the customer. Complex requirements specifications can be represented graphically using Petri nets instead of using ambiguous textual descriptions, or mathematical notations difficult to understand by the customer. The interactive graphical simulation of Petri net models of systems allows one to study the dynamics of the modeled systems. As mathematical tools, Petri nets allow for the formal analysis of the modeled systems. Petri nets possess a number of properties, which when interpreted in the context of the modeled system, allow the system designer to identify the presence or absence of the application domain specific functional properties of the system under design.Manuscript received March 22, 2002; revised November 28, 2003. Abstract published on the Internet January 13, 2005. The author was with The University of Tokyo, Tokyo, Japan. He is now with ISA Corporation, San Francisco, CA 94501 USA (e-mail: r.zurawski@). Digital Object Identifier 10.1109/TIE.2005.844225PThe recognition of these factors has led to numerous attempts to model and analyze industrial automated systems such as simple production lines, job shops, robotic assembly cells, flexible manufacturing systems (FMSs), etc [25]. However, most of these works were done at academic and research institutions. The notable exception was work by Hitachi Ltd. which developed a Petri-net-based sequence controller [13]. One of the reasons why Petri nets are largely confined to academic and research institutions is the difficulty involved in constructing Petri net models. Constructing Petri net models of systems, especially large-scale systems, is not a trivial task. It requires a great deal of experience. No methodology is yet available which would allow for fully automatic construction of Petri net models. In the past two decades, numerous approaches to the systematic construction of Petri net models of industrial automated systems have been proposed, and the work in this area still continues. These approaches are classified into bottom-up, top-down, and hybrid approaches. The most significant developments adopting the bottom-up and top-down approaches were reported in [14], [15], [4], [22], [6], [5], and [23]. These developments drew substantially from the earlier results proposed in [10] [21], [11], [12], [3], [18], [1], and [8]. The approaches presented in [4], [6], [14], [15], and [21] have mainly academic value and are not suitable for modeling realistic large scale manufacturing systems. The approaches presented in [5] and [23] are also restricted to small-scale systems. However, these approaches are, by far, the most mature attempts to model systematically manufacturing systems resulting in models which retain the required correctness properties. A comprehensive overview of these approaches is provided in [2]. In the mentioned approaches, the modeling effort concentrates on the construction of Petri net models of systems which retain the required correctness properties irrespective of the modeling stage and the adopted technique. These techniques, however, require the designer to be able to project the constructed Petri net structures onto structural and functional properties of the systems modeled. This, however, is not a trivial task, as indicated by applications restricted to very simple systems. For this reason, these approaches have mainly academic value, although they provide a framework for systematic construction of reusable models. From our observations, at the requirements specification stage, the customer or system developer tends to concentrate on the global functionality of the system, which involves the functionality of the constituent components and interactions between components. The synthesis of a design model of a0278-0046/$20.00 © 2005 IEEE596IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 52, NO. 2, APRIL 2005system with a focus on its global functionality would benefit from using objects representing typical components of industrial automated systems. To address this issue, functionality of selected primary components of an automated-guided-vehicle (AGV)-based FMS were defined in [27], based on the study of components of actual systems. This functionality reflects invariant functional properties of these components, represented at a certain level of abstraction. Petri net models representing functionality of these components were introduced in [26]. The availability of these generic models allows for rapid construction of models of FMSs and subsequent analysis focusing on the major functional properties of these systems, as well as their approximate performance. The knowledge of the approximate performance helps at the early stages of a system design to select these alternatives which are likely to meet the performance requirements. The level of detail of the models can be increased at the later design stages to suit specific application domains. The use of generic models, however, does not ease the verification task difficulty. Even though a design model of a system can be constructed fairly rapidly by using predefined objects, checking the model for its logical correctness may still be a computationally and intellectually challenging task. Although, the logical correctness of the individual objects can be established separately (from other objects), the need to check the correctness of the interactions (interfaces) between objects requires the whole model of the system to be considered. This is due to the fact that specific facets of the modeled system functionality are realized by specific facets of the individual objects functionality and certain interactions among those objects. Thus, the complexity of a design model may be such that the model is no longer amenable to analysis by inspection, or even computer-assisted analysis. An approach abating the verification task difficulty by reducing complexity of design models was proposed in [26]. This approach is based on replacing objects in the design model with their functional abstractions. Functional abstractions represent external functional behavior, or functionality, of the objects. This functionality defines the way an object responds to its inputs. Functional abstractions of objects, obtained using the approach presented in [26], employ less places and transitions then the actual objects to realize the required functionality. By replacing in the design model objects by less complex functional abstractions, the number of places and transitions can be substantially reduced. As a consequence, the number of place (transition) invariants, and places (transitions) in the corresponding invariant supports, and the size of the reachability set can be substantially reduced as well. As a result, the verification task difficulty can be eased substantially. Since functional abstractions of objects retain the functionality of the actual objects the verification effort can focus on the correctness of the interactions among components of the system, without paying attention to the correctness of the components themselves. An additional advantage of using functional abstractions is the compact representation of the model of a system. This helps to comprehend architecture and functionality of complex systems. In addition, if the size of the net permits, when using Petri nets to represent design models, it allows one to analyze dynamic behavior of the system andconduct validation of the interfaces between components by using interactive graphical simulation. The technique proposed in [26] is restricted to objects with a particular type of interaction with environment (or more precisely, a model of the environment with which the object interacts with interfaces), or other objects. In general, for the models proposed in [24], this is a valid assumption. However, this type of interaction is too restrictive to model realistic systems. For this reason, in this paper, we demonstrate the applicability of this technique to other types of interaction with the environment, or objects. These extensions allow to construct functional abstractions of Petri net models of more realistic, in terms of their functionality, components of flexible manufacturing systems, and other systems as well. At this development stage, this method is restricted to a class of Petri net models which allows for representing unidirectional flow of physical resources and control information/data. This property is characteristic of the primary components of automated guided vehicle based flexible manufacturing systems, Petri net models of which were introduced in [27]. A description of this class of Petri net models is provided in Section II. In order to introduce the concept of functionality of an object and represent it in a form of functional abstraction, temporal Petri nets [20] were adopted in this work. The description of functionality, or external functional behavior of an object, requires the concept of eventuality to be introduced. As this property cannot be expressed using ordinary Petri nets, temporal Petri nets are used in our work. Temporal Petri nets are overviewed in Section III. The concepts of functionality and functional abstractions are discussed in Section IV. The application of reduction techniques to the construction functional abstractions is presented in Section V. Techniques allowing for systematic construction of functional abstractions are introduced in Section VI. Finally, in Section VII, an example of applying the techniques to obtain functional abstraction of a Petri net model of a machining station is presented. II. A CLASS OF PETRI NET MODELS Many components of automated manufacturing systems can be viewed, at a certain level of structural abstraction, as a collection of space resources, such as buffers, machining areas, etc. In addition, they can also be characterized by an unidirectional flow of physical resources and (control) information/data. For instance, parts are delivered to a machining station, and removed from the station after machining. The information incoming to a subsystem may result in the execution of the operations internal to this subsystem, thus changing its state, or in the release of the requested physical resources or information/data. The released information, if it is a request for a resource, may result in the requested resource to be allocated to the subsystem. This also points to the fact that the progression of the unidirectional flow of resources may be controlled by the components themselves or a mix of events external to the components and components themselves. This view of the manufacturing system components is reflected in the structure of a class of Petri net models which are discussed in this section. This class includes two types ofZURAWSKI: PETRI NET MODELS, FUNCTIONAL ABSTRACTIONS, AND REDUCTION TECHNIQUES597(a)(b) Fig. 1. (a) Types of subnets. (b) Types of subnets.Fig. 2. Petri net model.models. Models which are composed of one or more subnets which are shown in Fig. 1(a), and models which are composed of one or more subnets shown in Fig. 1(b). Fig. 1 also shows and , respecthe input and output interface places tively. These are the places via which the model interacts with its environment. The first subnet [Fig. 1(a)] can be used to describe the primary components which can handle one part type. In place transition Petri nets, adopted in this work, tokens have no identity. To construct a model of a primary component which can handle one part type only, the subnets are combined into a model by sharing transitions in a way as shown in Fig. 2. In Fig. 2, two subnets were combined together into a larger subnet or model reflecting desired functionality. It should be noted that the composition of the interface places associatedwith the common transition should reflect the required functionality. Thus, after merging all interface places associated with the merged transitions may be retained, or some of them, or none. The second subnet [Fig. 1(b)] can be used to describe the primary components which can handle different part types. As already mentioned, in place transition Petri nets, adopted in this work, tokens have no identity. This identity, however, is required to distinguish amongst different types of parts. Thus, in order to obtain a Petri net model of a primary component that can handle part types, Petri net models of the primary component that can handle one part type only can be combined into a single net. This is achieved by the sharing of common places resulting in place ., as shown in Fig. 1(b). If we consider subnets which are shown in Fig. 1(a) and combine them by sharing places which correspond to place , then the subnet shown in Fig. 1(b) will be obtained. It will be explained further in this section why merging involves places which correspond to place in Fig. 1(a). Petri net models of the primary components represent flows of two types of objects. These are atomic and compound objects. The atomic objects represent physical resources, such as carts, pallets, tools, etc., as well as control information, data, etc. The flows of atomic objects which represent physical resources are modeled by one or more separate paths. These paths always begin with an input interface place and end with an output interface place, and do not contain any loops. For instance, in the model of a machining station, Fig. 3, the flow of parts is represented by a single path. Parts enter the station, are machined and then removed (this is discussed later in this section). In the same model, the flow of carts is represented by two separate paths. Carts after unloading are returned to the central storage or material handling system. After machining of parts is completed, carts are delivered to the machining station, loaded, and leave the station. In Fig. 1(a), a single path of flow of an atomic may be represented by a path involving input interface place , transition , internal place , transition , and interface . In Fig. 1(a), two separate paths of flow output place of an atomic object may be represented by a path which con, transition , and output intertains input interface place . The other path may be represented by input face place , transition , and output interface place interface place . The flow of the atomic objects which represent control information/data is modeled by two types of paths. Paths that begin and end with a transition, and paths that begin with a transition and end with an output interface place. The former type represents the flow of the control information which is internal to the model. Each place that belongs to the path of this type has one input and one output transition only. This path realizes control of the progression of the flow, internal to the model, of physical resources. In Fig. 1(a), this path is represented by transition , internal place , and transition . To explain this, consider Fig. 2. A token present on the input interface place may represent an area through which parts enter machining station, for instance. The progression of the flow of a token along , , , , , , and is the path which involves and . The controlled by the presence of tokens on places presence or absence of tokens on those places is controlled by the temporal characteristics of the activities which are modeled598IEEE TRANSACTIONS ON INDUSTRIAL ELECTRONICS, VOL. 52, NO. 2, APRIL 2005Fig. 3. Petri net model of a machining station.by the net. Places and in Fig. 2 model space resources of a component. For instance, in a machining station, they might be pallet input storage area, machining area, pallet output storage area, etc. The capacity of the space resources is typically limited. The machining area of a machining station may have space for one pallet only, for instance, whereas pallet input and output storage areas may have a much higher capacity. For this reason, a progression of a token through places which represent space resources must be controlled to reflect their storage capacity. In Fig. 2, this is achieved by the presence or absence of tokens and . This explains why places corresponding on places in Fig. 1(a) are merged to result in place . In to place represent the same space Fig. 1(b), places resource, though associated with a different type of parts. The maximum number of tokens on place represents the capacity of this space resource. The other type of paths (paths that begin with a transition and end with an output interface place) describes the flow of the control information which represents, in general, a request for a service or resource. This control information is released to the environment of the model; it will be called in this paper the request control information. Paths of this type are modeled by a transition, output interface place, and a directed arc. In Fig. 1(a), this may be represented by a path which and output interface place . The involves transition compound objects involve two or more atomic objects. An example of a compound object is the pair “request control information-flow of a physical resource”. For the class of Petri net models discussed in this paper, the path of flow of a compound object consists of two separate sections. For instance, in Fig. 2 this may be represented by the following two separate paths , , and , . The first path may model a request for a physical resource and the second a requested resource delivered. To illustrate these concepts, an example of a machining station will be used. The description of functionality of machining station can be found in [27]. The Petri net model of a machining station that can handle one part type is shown in Fig. 3. This station comprises a number of space resources; input and output storage areas for pallets, a machining area, cart unload and load areas, and a cart departure area. In this model, it is assumed that the cart unload, load, and departure areas, as well as the machining area, can accommodate only one physical object. A maximum of one token is allowed to be present in places MA-S, LDA-S. The input and output storage areas for pallets can accommodate more than one pallet. A maximum of tokens are allowed to be present in places ISA-S, OSA-S at a time. In the model shown in Fig. 3, a pallet present in the unload area (atoken is present in place ULA) is removed from the cart (operation represented by firing transition UL) and transferred into the input storage area (place SA-IN), provided that there is a space in this area (at least one token is present in place ISA-S). The empty cart is then removed from the unload area (a token is present in place ULA-EC). If the machining area is empty (a token is present in place MA-S), then a pallet is moved (modeled by firing transition TO-MA) to this area (a token is present in place MA1), and the request for a set of tools is generated (a token is present in place RQ-T). Once the set of tools has been delivered to the machining area, the parts are being machined (represented by firing transition M). After machining (a token is present in place MA2), the pallet, loaded with machined parts, is moved to the output storage area (a token is present in place SA-OUT), provided that there is a space in this area (at least on token is present in place OSA-S). When the pallet is moved to the output storage area (modeled by firing transition TO-SA), a request for an empty cart is generated by the machining station (a token is present in place RQ-EC). Also, the set of tools is released by the machining station (a token is present in place T-REL). The delivered empty cart (a token is present in place EC-DEL) is loaded with a pallet in the load area (modeled by firing transition LD), provided that this area is empty (a token is present in place LDA-S). After loading, the cart is moved from the load area (place LDA) to the cart departure area (place DA). This event is modeled by transition TO-DA. In order to obtain a Petri net model of the machining station that can handle part types, Petri net models of the machining station that can handle one part type can be combined into a single net. This is achieved by the sharing of common places; ISA-S, MA-S, OSA-S, and LDA-S. In this model, one can distinguish paths of flow of four objects. These objects are pallets (the movement of parts can be identified with the movement of pallets, assuming that each type of parts is allocated a dedicated group of pallets), carts, the request for a set of tools—the requested set of tools delivered, and the request for an empty cart—requested empty cart delivered. The last two objects are compound ones, representing the pair request for a resource (service)—requested resource (service) delivered. The path of flow of pallets is modeled by the following sequence of places and transitions: ULA, UL, SA-IN, TO-MA, MA1, M, MA2, TO-SA, SA-OUT, LD, LDA, TO-DA, and DA. The paths of flow of carts are modeled by ULA, UL, ULA-EC and EC-DEL, LD, LDA, TO-DA, DA. The path of flow of a set of tools is represented by T-DEL, M, MA2, TO-SA, T-REL. The path of flow of the pair the request for a set ofZURAWSKI: PETRI NET MODELS, FUNCTIONAL ABSTRACTIONS, AND REDUCTION TECHNIQUES599tools—the requested set of tools delivered is represented by TO-MA, RQ-T and T-DEL, M. The path of flow of the pair the request for an empty cart—the requested empty cart delivered is modeled by TO-SA, RQ-EC and EC-DEL, LD. It was mentioned that the progression of the unidirectional flow of resources may be controlled by the components themselves, or a mix of events external to the components and comand are removed from ponents themselves. If places Fig. 2, then the progression of the flow of tokens along the path , , , , , , is clearly controlled informed by and ternally by the presence or absence of tokens on places . In the case of timed Petri nets, this would also depend on temporal characteristics of transitions , , and . However, with places and retained, the progression of the flow of tokens depends also on external events, in addition to the presand . This is because ence or absence of tokens on places firing of transitions and depends on the presence of tokens and . Let us assume that on the input interface places the net shown in Fig. 2 is a part of a larger net, with places and connected to the rest of the net via transitions which are live. The presence of tokens on these two places can be determined by some (random) process reflecting dynamics of the rest of the net. Another way to ensure the presence of tokens on and may involve a mechanism, reflected in the places net structure, which ensures the presence of tokens on these two places only if they are required to progress the flow of tokens in the net shown in Fig. 2. This would, obviously, reflect some functionality of the modeled system. Using the example of a flexible manufacturing system, a machining station would generate request for empty carts to load pallets with machined parts. In the net of Fig. 2, the request would be modeled, for instance, . Delivered cart represented by by transition and place connected to transition which models some activplace ities involving the delivered cart. Those two paths constitute a compound object. A token would eventually appear on place as a result of a presence of a token on place , and some mechanism realized by the environment to which the net of Fig. 2 is interfaced. In this paper, the discussion and the proposed method for systematic construction of functional abstractions of Petri net models of components are restricted to the latter type of control of progression of the unidirectional flow of resources within the components. III. TEMPORAL PETRI NETS This section presents an overview of a class of Petri nets, temporal Petri nets (TPN), which were introduced in [19] and [20]. This class uses a variant of propositional temporal logic of linear time [7], [9], [16] as a language for specifying the temporal constraints on the behavior of a Petri net. The temporal Petri net is ; where is an ordinary Petri net as a pair defined in [17], and is a formula having the following syntax. and , are 1) Propositions: , , and , where atomic propositions. 2) Atomic propositions are formulas. , , , 3) If and are formulas then so are , , , , , .and mean that there is at The atomic propositions , least one token in place in the current marking, transition is firable in the current marking, and transition fires in the current marking, respectively. Symbols , , , and represent the Boolean connectives. The formula , “ next “, means that becomes true in the next marking. The formula , “henceforth”, means that becomes true in every marking , “eventureached from the current marking. The formula ally”, means that becomes true at some marking reachable , “precede”, from the current marking. The formula means that becomes true prior to becoming true in some marking reachable from the current marking. The formula , “either-or”, means that becomes true prior to becoming true, or becomes true prior to becoming true, in some marking reachable from the current marking. , where is the set of all (finite and Let is the set of all finite infinite) sequences of elements of . sequences of elements of , including the empty element . is the set of all infinite sequences of elements of . Let , be sequences of elements of . , denote the length of , . The length , of , is denoted by , for every integer . The concatenation of and , where , is finite if both sequences are finite, i.e., , ; infinite , ; not defined if if one sequence is infinite, i.e., both sequences are infinite, i.e., , . The formal seman, where is a tics of TPN is given as follows. Let marking of PN, be a set of all finite firing sequences from , a set of all infinite firing sequences from , and a set of all (infinite and finite) firing sequences from . Then . Let be a marking of , and is a possibly infinite firing sequence from . For each , , let and be the sequences such that and . is the prefix of with length , and is a postfix of excluding . Let be a marking reachable from by firing . For a means that is satisfied by the pair of formula , and , where denotes a valid formula: 1) 2) 3) 4) 5) 6) 7) ; 8) 9) 10) 11) ; for every ; for some ; iff for some and for some ; iff for some 12) and for some or for some and for some . iff iff iff and iff ; iff is firable in iff and iff not iff iff iff ; ; ; and or implies; ;The formula of a temporal TPN imposes restrictions on possible firing sequences of PN. The possible firing sequences from marking can be defined as follows .。
●愿景英文(V1S10n),指组织中共同愿望的景象,共同的理想与目标。
是对以后景象的全面而且清晰的设想与描画,包括企业价值、流程、组织价构、信息技术、岗位职责和企业环境等。
建立愿景的注意要点或步骤:1、建立良好的团队(Cast your team)2、定义项目范畴和目标(Project scope and objectives)3、学习更广博的知识,超越以往所知,从以往不了解的领域中获得改进的思路。
(Build profound knowledge)4、站在以后,以以后为起点,反观现在,突破原本的思维模式,进行逆向思维。
( stand in the future)5、建立以企业战略方针为导向的愿景、●头脑风暴法头脑风暴法(Brainstorming),从20世纪到50年代开始流行。
常用在决策的早期时期,以解决组织中的新咨询题或重大咨询题。
头脑风暴法是通过讨论会,产生新的方法与建议它一样只产生方案,而不进行决策。
脑力激荡法的具体操作如下:1、召集有关人员参加的人员能够是同一行业的专家,也能够是不同行业的人员,甚至能够是毫不有关的人员。
人数在7—10人之间为好。
2、选择一个合格的召集人士持头脑风暴法的召集人应该具备下列条件:(1) 了解召集的目的;(2) 把握脑力激荡法的原则;(3) 善于引导大伙儿摸索和发表观点;(4) 自己不发表倾向性观点;(5) 善于阻止相互间的评判和批判。
3、选择一个舒服的地点选择的地点应该具备下列条件:(1) 一间温度适宜、安静、光线柔和的办公室或会议室;(2) 严禁电话或来人干扰;(3) 有一架性能良好的录音机;(4) 有一块白板或白纸夹板,以及相应的书写工具。
4、召集人宣布会议开始召集人在会议开始时要清目的、拟解决的咨询题、会议规则(如相互之间不评论等等);再让每个人考虑10分钟。
5、在脑力激荡中应注意以下几点:(1)尽可能使每个人把个种方案讲出来,不管那个方案听起来多么可笑或不切实际;(2)要求每个人对自己讲出来的方案简单讲明一下;(3)鼓舞由他人的方案引出新的方案;(4)把全过程都录音;(5)把每一种方案写在白板上,使每个人都能看见,以利于激发出新的方案。
基于HCPN的面向方面NVP建模与分析孙晓星;虞慧群【期刊名称】《计算机工程》【年(卷),期】2012(038)016【摘要】Aiming at detecting the design faults at early development stage and reducing the overhead that N-version Programming(NVP) fault tolerance strategy may bring into a system, this paper proposes an aspect-onented modeling method based on Hierarchical Colored Petri Net(HCPN). NVP is modularized into an aspect sub-module and woven into a final executable HCPN. An aspect-oriented NVP model is built through a case study of searching system using this method. Analysis result verifies the correctness and effectiveness of this NVP model.%为能够在软件开发早期检测设计故障,降低N版本编程(NVP)容错策略给系统带来的额外开销,提出一种基于层次着色Petri网(HCPN)的面向方面NVP建模方法,将NVP模块转化为方面子模块,并编织为可执行的HCPN.运用该建模方法对网络搜索实例建立面向方面的NVP 模型,结果验证了该NVP模型的正确性和有效性.【总页数】4页(P61-64)【作者】孙晓星;虞慧群【作者单位】华东理工大学计算机科学与工程系,上海200237;华东理工大学计算机科学与工程系,上海200237;上海市计算机软件评测重点实验室,上海201112【正文语种】中文【中图分类】TP311【相关文献】1.一种基于UML的面向方面建模框架研究 [J], 牛言涛;刘畅;姚玉霞2.基于MOF面向方面建模工具的研究与实现 [J], 贺蕾;方义秋;葛君伟;左向科3.基于HCPN的城市轨道交通CBTC联锁系统建模研究 [J], 于潇4.基于AADL的智能交通系统面向方面建模 [J], 覃华;张立臣5.基于HCPN的发电企业项目管理工作流建模 [J], 高翔;赵霁因版权原因,仅展示原文概要,查看原文内容请购买。
Hierarchical Object-Oriented Petri Net Modeling Method based onOntologyXiaoning Feng, Zhuo Wang, Guisheng YinInstitute of Computer Science and Technology,Harbin Engineering University, Harbin 150001, Chinafengxiaoning@AbstractThis paper presents a Hierarchical Object-Oriented Petri Net(HOOPN) modeling method based on Ontology that should not only enable sharing Petri nets models on the Semantic Web but also present a high level Petri net. Previous work on formal methods for representing Petri nets mainly focuses on modeling and analyzing aspects or formats for Petri net model interchange. However, such efforts do not provide a suitable model description for using Petri nets on the Semantic Web. This paper uses the HOOPN with the Ontology concepts as a starting point for implementing the Petri net ontology. Moreover this paper uses HOOPN as the Petri net model method. HOOPN supports a wide range of Object-Oriented features including abstract, encapsulated and modularized objects, object interaction by message passing, inheritance, and polymorphism.Keywords Hierarchical object-oriented Petri net; Ontology; modeling method1. IntroductionThe main idea of this paper is to propose a suitable way for Hierarchical Object-Oriented Petri Net (HOOPN) to be used with the Ontology concept to enable full semantic interoperability of HOOPN models. Currently, Petri net interoperability is possible at the level of syntax for model sharing. Many researchers think it would be very useful if Petri net researchers could share their Petri net model descriptions. That way more software tools could be used for analyzing the same Petri net model [1, 2] .So far, almost all Petri net modeling method have been mainly focused on tool-specific, but with very low (or without any) general acceptance. The Petri Net Markup Language (PNML) [3] is a recent Petri net community effort that tries to provide XML-based model sharing. A particularly important advantage of this approach is that XML documents can be easily transformed using extensible style sheet Language Transformations (XSLT) into other formats (that need not necessarily be XML-based). A suitable way to represent Petri nets is needed in order to reuse them more effectively on the Semantic Web. It requires defining the Petri net ontology for semantic description of Petri net concepts and their relationships. The Petri net ontology enables describing a Petri net using Semantic Web languages. We defined the Petri net ontology using experience from Hierarchical Object-Oriented Petri net formal descriptions. They indicate very useful directions for selecting key Petri net concepts and specifying their mutual relations. The PNML is of primary importance here – it is closely related to the Petri net ontology.On the other hand we choose the Hierarchical Petri Net as the modeling method. Petri net is used widely to analyze and model various systems formally. Many Petri nets mania devote their efforts to enhancing and extending the expressive power of Petri nets. One such effort is to extend Petri nets with object-oriented concepts. An object-oriented paradigm provides excellent concepts to model real-world problems. Although several high-level Petri nets with the concept of objects are suggested, these nets do not fully support the object-oriented concepts. In this paper, we propose a hierarchical object-oriented Petri net (HOOPN). The formal syntax and semantics of HOOPN are explained in detail.The concepts of object-oriented paradigm such as encapsulation, inheritance, etc., have been widely used in the system modeling because they allow us to describe systems easily, intuitively, and naturally. Designers who are familiar with formal methods have come to understand the usefulness of the object-oriented concepts. Along with this trend, object-oriented formal methods have also become of particular interest to researchers in recent years, and many experts have suggested object-oriented formal methods such as object Petri nets (OPN) [4], VDM++ [5], Object-Z [6], etc. Among these studies, research on OPN formalism has been actively studied to extend Petri nets formalism to OPN such as OBJSA [7], COOPN/2 [8], and LOOPN++ [9].In this paper, we formally define hierarchical object-oriented Petri net (HOOPN), a high-level Petri net that supports object-oriented concepts. Modeling features in HOOPN support information hidingthrough optimized interfaces; abstraction through abstract places, transitions and tokens; polymorphism through dynamic binding of abstract tokens; inheritance through properties shared among classes; and interaction through message passing. We also propose two analysis methods for HOOPN models-unfolding of HOOPN to lower-level Petri nets for structural analysis and incremental reachability analysis for behavioral analysis. We apply HOOPN modeling and analysis methods to an example system in order to demonstrate its effectiveness.2. Hierarchical object-oriented Petri net andOntology The purpose of designing HOOPN is to aid in the modeling and analysis of object-oriented software systems and to bridge the gap between formal treatment of Petri nets and object-oriented approach for the modeling, analysis, and prototyping of complex software systems. 2.1 Definition of the HOOPN A HOOPN model is a variant Petri-net representation that corresponds to a class in object-oriented paradigm. The HOOPN is composed of several parts: object identification place (OIP) is a unique identifier of a class; internal object net (ION) is a net to depict the behaviors (methods) of a class; and data dictionary (DD) declares the attributes of a class.The formal definition of HOOPN is given as follows:Definition 2.1 HOOPN is a 3-tuple ),,(DD ION OIP HOOPN = satisfying the requirements below:OIP is a special place which is defined as a 1-tuple ),,,(0status M pid oip OIP =, where· oip is a variable for the unique name of a HOOPN,· pid is a unique process identifier to distinguish multiple instances of a class, which contains return address, ·0 is a function giving tokens with specific values to OIP, M · status is a flag variable to specify the state of OIP. ION is a variant CPN representing the changes in the values of attributes and the behaviors of methods. It will be formally defined in Definition 2.2. DD is a declaring part for variables, token types, and functions. The general structure of HOOPN is shown in Fig. 1.Fig.1 General structure of HOOPNDefinition 2.2 An internal structure ofHOOPN:,where()0,,,,,,,,M F E G N K A T P ION =M P and T are finite sets of places and transitions, respectively, A is a finite set of arcs such that , ∅===A T A P T P I I I K is a function mapping from P to a set of token types declared in DD, N , G , and E mean the functions of nodes,guards, and arc expressionsF is a special arc from any transitions to OIP, and notated as a body frame of ION 0 is a function giving an initial marking to any place. When modeling a system using several HOOPN features, defined in the above, we also need some means to represent abstract information (i.e., abstract state and abstract action) and interactions between subsystems. The following definitions are supporting such means.Definition 2.3 A set of places in HOOPN is defined as },{ABP PIP P =, where Primitive place (PIP) is a basic place torepresent local states of a system, the same as in basic Petri nets.An abstract place represents an abstract state, where),_,(action state refine pn ABP =· pn is the name of an abstract place, · refine_state is a flag variable denoting the refinement of an ABP, · action is the static reaction imitating the internal behaviors of ABP. The ABP is to represent abstract information (state), and can be refined in further modeling step. In order to indicate whether the refined information is modeled using HOOPN features, the flag variable “refine_state ” has a value such as true or false. The abstract place is depicted with bold-lined circle in HOOPN model.Definition 2.4 A set of transitions in HOOPN, where },,{COT ABT PIT T = Primitive transition (PIT ) is a basic transition, the same as in basic Petri nets. An abstract transition , where ),_,(action transition refine tn ABT =· tn is the name of an abstract transition, · refine_transition has the same meaning as in the definition of ABP, and · action is the static reaction imitating the internal behaviors of ABT . A communicative transition is a transition representing a method calling, where ),_,,(action type comm get tar tn COT =· tn is the name of a communicative transition, · target is a flag variable denoting whether the called method by COT was modeled (a “yes” value) or not (a “no” value), · comm._type is also a flag variable representingwhether the interaction of COT is synchronous (a“SYNC” value) or asynchronous (a “ASYN”value)· action is the static reaction reflecting the execution results of the called method.In general, when the model includes abstract information (behavior and states), it is difficult to simulate the system behavior represented in this model. However, it is possible to simulate the model with abstract information in HOOPN. The variable “action” is represented with algebraic expression to define the post-condition of abstract behavior. This variable is used to obtain an artificial effect, as if the actual execution of the abstract place or abstract transition had occurred. In HOOPN model, ABT and COT are represented with bold-lined rectangle and double-lined rectangle, respectively.Token types in HOOPN are described in DD, and classified into two categories: primitive type and abstract type. The primitive type is the same as that of CPN, while the abstract type is a compound of primitive types. The abstract type is required to express the states of the abstract place. The abstract type is declared with “complex” type or “record” type. The token type of a HOOPN model which is represented with abstract information should be also represented with the abstract token type, since the token type expressed with detailed information does not adequately represent the states of abstract behaviors in the model. When the designer declares the token type in detail at the abstract level, it is still acceptable. However, such representation for abstract states is not concise, and can cause changes in further refinements. The type of the abstract token is declared with the prefix “complex”. This type is decomposed into several subtypes (primitive types) of tokens in refined models.The definition of DD is very straightforward, is written in a textual grammar such as CPN ML. .(a) HOOPN model ‘Client’(b) Refinement of ‘Client’Fig. 2. Logical concept of HOOPN behavior.2.2. Behavioral semantics of HOOPNBehavioral semantics of HOOPN does not violate the semantics of CPN formalism such as binding, firing, and so on. However, it should be defined for behavioral semantics of some features of HOOPN which are not supported in CPN formalism. Before describing in detail the formal semantics of HOOPN, we explain the overall behavior of HOOPN models.As shown in Fig.2, the HOOPN model “Client” at the left side contains the abstract place Ap, and the model at the right side represents the refinement of the abstract place. When a token is given to OIP “Client” of the left-side model in Fig.2, a transition among T1, T2, and T3 is enabled and fired. At the entry point of the abstract place Ap, the token is transferred to the OIP of the refinement model when the value of the variable “refine_state”, defined inDefinition 2.3, is true (Step 1 in Fig. 2). After the completion of internal behavior of the refined model (Step 2), the token flows to the OIP Ap through the body frame of the refined model (Step 3), and then returned to the abstract place Ap carrying with the execution results (Step 4).2.2.1. Behavioral semantics of OIP. As explained above, the binding and firing actions of OIP are constrained by the variables which define the state ofOIP. The behavioral semantics of OIP is defined as follows:•∈∀OIP t and if status = “pre”)(:)(t B t Var v ∈∀ )(X M or for such that OIP.pid.return = if status = “post”)(•X M X X where means a set of variables appearing inthe guard function and the arc expression of t , and means the binding of t . )(t Var )(t B 2.2.2. Behavioral semantics of abstract place. The abstract place shows different behaviors depending on that the abstraction is refined or not. When the abstraction was refined, the binding and firing occur from the abstraction to its refined model. Otherwise, a transition among ABP · will be fired. The behavioral semantics of ABP is defined as follows:)(OIP M such that ABP.pn = OIP.oip if refine_state = true R(action); ∈∀t ABP · :B(t) if refine_state= falsewhere R(action) means an evaluation of the expression which is defined in variable “action” ofABP.2.2.3. Behavioral semantics of abstract transition. The abstract transition shows different behaviors depending on that the abstraction is refined or not. When the abstraction was refined, the binding and firing occur from the abstraction to its refined model. Otherwise, a place among ABT ·will be marked. The behavioral semantics of ABT is defined as follows:)(OIP M such that ABT.pn = OIP.oip if refine_state = trueR(action);)()(ABT M ABT M •−∧•+ if refine_state= falsewhere )()(ABT M ABT M •−∧•+ means the addition of tokens to output places and deletion of tokens from input places by the firing of the ABT.2.2.4. Behavioral semantics of communicative transitionThe interactions between HOOPN models (i.e., classes/objects) are occurred differently depending on the type of the communication and whether the interacting model is drawn or not. This behavior of COT is defined as follows: if target = true,such that Cot.tn = Oip.oip if sync = “SYNC”)(OIP M such that Cot.tn = OIP.oip if sync = “ASYN”)(OIP M )()(COT M COT M •−∧•+ if target = false,R(action); )()(COT M COT M •−∧•+ if sync = “SYNC” )()(COT M COT M •−∧•+ if sync = “ASYN”2.2.5. Behavior of inheriting component. HOOPN supports the inheritance mechanism of object-oriented paradigm more concretely than other OPN formalisms. When a HOOPN model is defined with general common properties, its child models can also be defined that inherit the common properties. This concept allows to reduce the complexity of drawn models, and allows to reuse the parent model.3. Conclusion and further worksThe main idea of this paper is that the Petri net ontology should provide the necessary Petri netinfrastructure for the Semantic Web. The infrastructure understands Petri nets sharing using XML-based ontology languages (i.e., RDFS and OWL). We presented the HOOPN ontology. That way, we can exploit potentials of current Petri net tools in the context of the Semantic Web.The maturity and popularity of object-oriented paradigms have steadily increased. One of the main requirements in modeling and analysis for complex and large software systems is that the design models should be unambiguous, precise, and verifiable. To fulfill these requirements, experts have suggested several methods which combine object-oriented method with formal methods. Although a number of high-level Petri nets with the concepts of objects were suggested with a clear idea in specific concerns, they did not fully support sufficient features that are needed in modeling of systems with object-oriented concepts.To solve this problem, we suggest a high-level object-oriented Petri net HOOPN, which supports most features of object-oriented concepts with clear semantics. Further, we describe the modeling and analysis methods for system models, and making it possible to develop a complex system incrementally and iteratively. This has been achieved from such bases as encapsulated and modularized objects, abstract information modeling, decomposition and refinement approach, and incremental reachability analysis.In order to enhance the applicability of HOOPN formalism to other domains, further studies should be performed to extend the HOOPN. An extending issue to be cognized is the creation of a timed- HOOPN formalism to represent the timing constraints in real-time system modeling. If we introduce the semantics of conventional time Petri nets to those of internal object net (ION) of HOOPN, it is not difficult to model the timing behavior of a system. However, when we consider the approach to modeling the timing constraints in object-oriented paradigm, this issue may not be solved by simple introduction of time Petri nets semantics. Another considerable issue is methodological consolidation between HOOPN modeling method and UML-based object-oriented modeling paradigm. HOOPN can represent the object structure and state transition of an object-oriented system. Thus, we consider that HOOPN model can substitute the object diagram and state transition diagram in unified modeling language. However, the representation scheme for the relationship among objects is required in such substitution.Reference [1] H ong Jang-Eui, Bae Doo-Hwan. Software modelingand analysis using a hierarchical object-oriented Petrinet. Information Sciences, 2000, 130:133-164[2] GASEVIC Dragan. Reusing Petri Nets Through theSemantic Web. ESWS 2004:Europen semantic web symposium 2004. vol 3053:284-298[3] B illington. The Petri Net Markup Language: Concepts,Technology and Tools. In Proceedings of the 24thInternational Conference on Applications and Theoryof Petri Nets, Eindhoven, The Netherlands (2003).483-505[4] R Bastide. Approaches in unifying Petri nets and theobject-oriented approach. Proceeding of theInternational Workshop on Object-orientedProgramming and Models of Concurrency, Turin, Italy, June, 1995,http://wrcm.dsi.unimi.it/PetriLab/ws95/home.html. [5] D Harel, E Gery. Executable object modeling withstate chart. Proceedings of the 18th InternationalConference on Software Engineering, Germany,March 1996, pp. 246-257.[6] S A Schuman. Formal Object-oriented Development,Springer, Berlin, 1997.[7] E Battiston, F D Cindio, G Mauri. OBJSA Nets: aclass of high-level nets having objects as domains, in:APN'88, Lecture Notes in Computer Science, vol. 340, 1998, pp. 20-43.[8] O Biberstein, D Buchs. An object-orientedspecification language based on hierarchical algebraicPetri nets, in: Proceedings of the IS-CORE WorkshopAmsterdam, September 1994 94-76.[9] C Lakos, C Keen. LOOPN++: a new language forobject-oriented Perti nets. Technical Report R94-4,Networking Research Group, Australia, April 2004.。