课题:4.1函数
学习目标:
1、初步掌握函数概念,能判断两个变量间的关系是否可看作函数。
2、根据两个变量间的关系式,给定其中一个量,相对应地会求出另一个量的值。
3、会对一个具体实例实行概括抽象成为数学问题。
学法指导
主动地从事观察、操作、交流、归纳等探索活动,形成自己对数学知识的理解和有效的学习模式。
探究过程
一、同学们,你们坐过摩天轮吗?当你坐在摩天轮上时,人的高度随时在变化,那么变化是否有规律呢?
摩天轮上一点的高度h与旋转时间t之间有一定的关系。请看下图,反映了旋转时间t(分)与摩天轮上一点的高度h(米)之间的关系。
大家从图上能够看出,每过6分钟摩天轮就转一圈。高度h完整地变化一次。而且从图中大致能够判断给定的时间所对应的高度h。下面根据图5-1实行填表:
t/分0 1 2 3 4 5 ……h/米
思考:对于给定的时间t,相对应的高度h确定吗?
在这个问题中,我们研究的对象有几个?分别是什么?
生活中充满着许很多多变化的量,你了解这些变量之间的关系吗?如:弹簧的长度与所挂物体的质量,路程的距离与所用时间……了解这些关系,能够协助我们更好地理解世界。下面我们就去研究一些相关变量的问题。
二、新课。
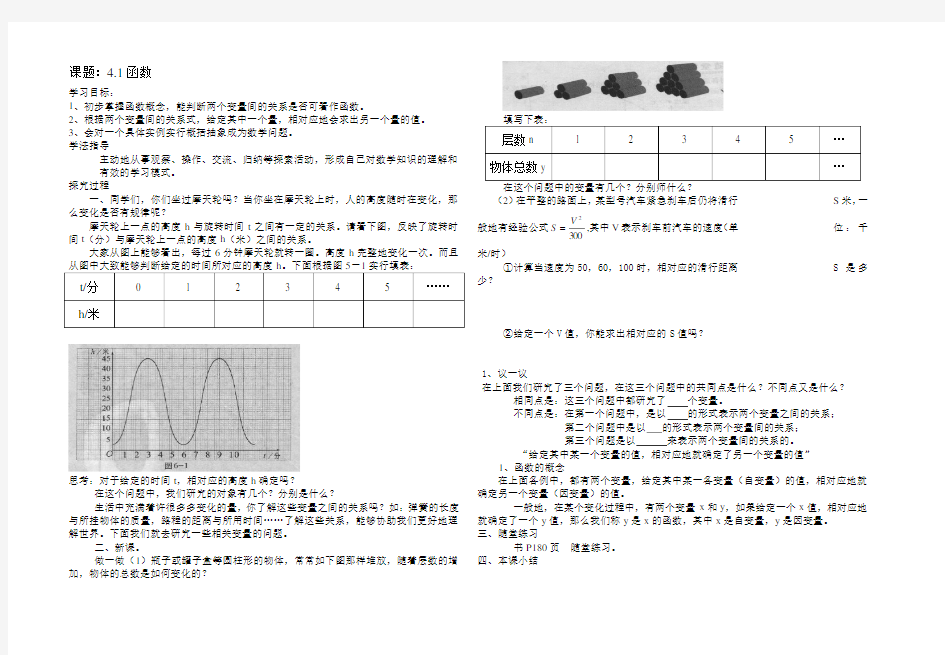
做一做(1)瓶子或罐子盒等圆柱形的物体,常常如下图那样堆放,随着层数的增加,物体的总数是如何变化的?
层数n 1 2 3 4 5 …
物体总数y …
在这个问题中的变量有几个?分别师什么?
(2)在平整的路面上,某型号汽车紧急刹车后仍将滑行S米,一
般地有经验公式
300
2
V
S ,其中V表示刹车前汽车的速度(单位:千米/时)
①计算当速度为50,60,100时,相对应的滑行距离S是多少?
②给定一个V值,你能求出相对应的S值吗?
1、议一议
在上面我们研究了三个问题,在这三个问题中的共同点是什么?不同点又是什么?
相同点是:这三个问题中都研究了个变量。
不同点是:在第一个问题中,是以的形式表示两个变量之间的关系;
第二个问题中是以的形式表示两个变量间的关系;
第三个问题是以来表示两个变量间的关系的。
“给定其中某一个变量的值,相对应地就确定了另一个变量的值”
1、函数的概念
在上面各例中,都有两个变量,给定其中某一各变量(自变量)的值,相对应地就确定另一个变量(因变量)的值。
一般地,在某个变化过程中,有两个变量x和y,如果给定一个x值,相对应地就确定了一个y值,那么我们称y是x的函数,其中x是自变量,y是因变量。
三、随堂练习
书P180页随堂练习。
四、本课小结
解函数方程的几种方法 李素真 摘要:本文通过给出求解函数方程的基本方法,来介绍函数方程,探索通过构造函数方程求解其它问题的方法,以获得新的解题思路。 关键词:函数方程;换元法;待定系数法;解方程组法;参数法 含有未知函数的等式叫做函数方程,能使函数方程成立的函数叫做函数方程的解,求函数方程的解或证明函数方程有无解的过程叫解函数方程。 函数方程的解法有换元法(或代换法)、待定系数法、解方程组法、参数法。 1.换元法 换元法是将函数的“自变量”或某个关系式代之以一个新的变量(中间变量),然后找出函数对中间变量的关系,从而求出函数的表达式。 例1 已知x x f x sin )2(+=,求)(x f 。 解:令u x =2 )(0>u ,则u x log 2=,于是可得,)log sin()log ()(222 u u u f += )(0>u ,以x 代替u ,得)log sin(log 2 )(22u x x f += )0(>x 。 例2 已知x x x x f 212ln )1(+=+ )0(>x ,求)(x f 。 解:令t x x =+1,则11-=t x )1(>t ,于是12ln 112111 2 ln )(+=-+-=t t t t f , 即1 2ln )(+=x x f 。 例3 已知x x f 2cos )cos 1(=+,求)(x f 。 解:原式可以化为 1cos 22cos )cos 1(2+==+x x x f ,令t x =+cos 1,]2,0[∈t ,则换元后有1)1(2)(2 --=x t f ]2,0[∈x 。 2.待定系数法
待定系数法适用于所求函数是多项式的情形。当我们知道了函数解析式的类型及函数的某些特征,用待定系数法来解函数方程较为简单。一般首先确定多项式的次数,写出它的一般表达式,然后由已知条件,根据多项式相等的条件确定待定系数。 例4 已知)(x f 为多项式函数,且422)1()1(2+-=-++x x x f x f ,求)(x f 。 解:由于)1(+x f 与)1(-x f 不改变)(x f 的次数,而它们的和是2次的,所以)(x f 为二次函数,故可设c bx x a x f ++=2)(,从而有 由已知条件得 422)(22222+-=+++x x c a bx x a 根据两个多项式相等的条件得 22=a ,22-=b ,4)(2=+c a ,由此得1=a ,1-=b ,1=c ,故有1)(2+-=x x x f 。 例5 已知)(x f 是x 的二次函数,且x x x f f 242)]([-=,求)(x f 。 解:因为c 是x 的二次函数,故可设c bx x a x f ++=2)(,由此,c c bx x a b c bx x a a c x bf x f a x f f ++++++=++=)()()()()]([2222 将上式化简并代入x x x f f 242)]([-=,得x x c bc c a x b abc x ab c a b a x b a x a 2)()2()2(24222223243-=+++++++++ 比较对应项的系数有 ?????????=++=+-=++==0 0222021222223c bc c a b abc ab c a b a b a a ,解之得?????-===101c b a ,故1)(2-=x x f 。 3.解方程组法 此方法是将函数方程的变量或关系式进行适当的变量代换,得到新的函数方程,然后与原方程联立,解方程组,即可求出所求的函数。
1、设',()..E R f x E a e ?是上有限的可测函数,证明:存在定义在'R 上的一列连续函数 {}n g ,使得lim ()()..n n g x f x a e →∞ =于E 。 证明:因为()f x 在E 上可测,由鲁津定理是,对任何正整数n ,存在E 的可测子集n E , 使得1 ()n m E E n -< , 同时存在定义在1R 上的连续函数()n g x ,使得当n x E ∈时,有()()n g x f x =所以对任意的0η>,成立[||]n n E f g E E η-≥?-由此可得 1[||]()n n mE f g n m E E n -≥≤-< ,因此lim [||]0n n mE f g n →∞-≥=即()()n g x f x ?, 由黎斯定理存在{}n g 的子列{}k n g ,使得lim ()()k n k g x f x →∞ =,..a e 于E 2、设()(,)f x -∞∞是上的连续函数,()g x 为[,]a b 上的可测函数,则(())f g x 是可测函数。 证明:记12(,),[,]E E a b =-∞+∞=,由于()f x 在1E 上连续,故对任意实数1,[]c E f c >是 直线上的开集,设11 [](,)n n n E f c αβ∞ =>=,其中(,)n n αβ是其构成区间(可能是有限 个 , n α可 能为 -∞ n β可有为 +∞ )因此 22221 1 [()][]([][])n n n n n n E f g c E g E g E g αβαβ∞ ∞ ==>= <<= ><因为g 在2E 上可 测,因此22[],[]n n E g E g αβ><都可测。故[()]E f g c >可测。 3、设()f x 是(,)-∞+∞上的实值连续函数,则对于任意常数a ,{|()}E x f x a =>是一开集,而{|()}E x f x a =≥总是一闭集。 证明:若00,()x E f x a ∈>则,因为()f x 是连续的,所以存在0δ>,使任意(,)x ∈-∞∞, 0||()x x f x a δ-<>就有, 即任意00U(,),,U(,),x x x E x E E δδ∈∈?就有所以是 开集若,n x E ∈且0(),()n n x x n f x a →→∞≥则,由于()f x 连续,0()lim ()n n f x f x a →∞ =≥, 即0x E ∈,因此E 是闭集。 4、(1)设2121 (0,),(0,),1,2, ,n n A A n n n -==求出集列{}n A 的上限集和下限集 证明:lim (0,)n n A →∞ =∞设(0,)x ∈∞,则存在N ,使x N <,因此n N >时,0x n <<,即
深度专注力的奥秘 “作为企业管理者,当前最忧心的到底是什么?我想宏观上一定是不确定的大环境,特别在疫情的蔓延之下,全球不确定性的因素变得更多、更复杂。而在微观上,当我们自身的时间、所获取的信息,乃至于我们的行为和行为背后的思维及逻辑,都已经碎片化的时候,作为企业管理者,其实就越需要保持专注力。” 5月23日晚,《中外管理》管理百家大讲堂之共克时艰“复商”进行时(总40期)上,《中外管理》杂志社社长、总编杨光在开播之时首先分享了上述观点。 那么,管理者如何运用“深度专注力”,事半功倍完成最重要的事情?被称为“鹰妈”的TCL集团副总裁、TCL大学执行校长许芳女士,首先从“鹰的视角”分享了她对“深度专注力”的精准思考。 而颠覆性时代,人才的特质发生了哪些变化?人才画像应做哪些“增补”和“删减”?未来领导者的人才识别技术如何打造?从技能到自我觉知的学习演化,又怎么解?DDI中国华北区董事总经理朱彦昌分享了他独门的人才“人脸识别术”。 以下为许芳和朱彦昌在直播中的部分精彩观点回顾: 许芳精彩观点集萃 ◆我们活在信息时代,但是不要活在信息里,我们活在支离破碎的环境下,要尽量保持专注力。 ◆在支离破碎的环境下,一般会有三种不同的思维模式,一种是Being(存在模式),一种是Doing(行动模式),一种是Distracting(杂念模式),保持专注的前提是先认知、了解自己的思维模式。 ◆专注力在未来会成为一种稀缺资源。
◆想要保持在原位都必须加速奔跑,更何况要超过别人,那就需要拼命地奔跑。做企业同样如此,要超越竞争对手,你就要比竞争对手跑得更快。其实拼命不是解决问题的根本方法。 ◆生产力的真谛,是可以自由的追求真正的梦想。 ◆工业时代,效率至上,然而如今把赢仅仅归结为在竞争中打败对手,这已经不能满足当下的需求了。 ◆因为企业竞争的核心要素发生了改变,过去的成本领先、效率领先,要让步给创新、技术,甚至是链接和生态圈,也就是大家要协同共赢,这会成为未来企业发展的最核心要素。 ◆如果根据激情和专注两个维度建立四象限,那么第一个象限就是渴望区,那是你既有激情,又非常精专,工作游刃有余的区域,反之对角线的就是苦差区,不精专也不想干。还有你可能是专精,但是没有激情,那就是无趣区。另外一个是你有激情做,可是并不精专,那就是干扰区。 ◆如果要提高生产力,就要知道自己最有激情和最擅长、最专业做的事情是什么。对于渴望区的事情,要加倍去做。 ◆时间是固定的,但能量是弹性的。 ◆充足的睡眠对提高效率很重要,如果没有足够的睡眠,工作效率一定不高,要学会劳逸结合。 ◆停下来思考很重要,反思是我们个人取得进步的一个非常有用的加速器。 ◆每个人的时间、资源是有限的,你不可能满足所有人要求、做所有的事情、让所有人认同你,所以要确定谁是你最需要直接关注的人,把重要、紧急的事情提前安排在日程表当中。
一般地,对于函数f(x) ⑴如果对于函数f(x)定义域内的任意一个x,都有f(x)=f(-x)或f(x)/f(-x)=1那么函数f(x)就叫做偶函数。关于y轴对称,f(-x)=f(x)。 ⑵如果对于函数f(x)定义域内的任意一个x,都有f(-x)=-f(x)或f(x)/f(-x)=-1,那么函数f(x)就叫做奇函数。关于原点对称,-f(x)=f(-x)。 ⑶如果对于函数定义域内的任意一个x,都有f(x)=f(-x)和f(-x)=-f(x),(x∈R,且R关于原点对称.)那么函数f(x)既是奇函数又是偶函数,称为既奇又偶函数。 ⑷如果对于函数定义域内的存在一个a,使得f(a)≠f(-a),存在一个b,使得f(-b)≠-f(b),那么函数f(x)既不是奇函数又不是偶函数,称为非奇非偶函数。 定义域互为相反数,定义域必须关于原点对称 特殊的,f(x)=0既是奇函数,又是偶函数。 说明:①奇、偶性是函数的整体性质,对整个定义域而言。 ②奇、偶函数的定义域一定关于原点对称,如果一个函数的定义域不关于原点对称,则这个函数一定不具有奇偶性。 (分析:判断函数的奇偶性,首先是检验其定义域是否关于原点对称,然后再严格按照奇、偶性的定义经过化简、整理、再与f(x)比较得出结论) ③判断或证明函数是否具有奇偶性的根据是定义。 ④如果一个奇函数f(x)在x=0处有意义,则这个函数在x=0处的函数值一定为0。并且关于原点对称。 ⑤如果函数定义域不关于原点对称或不符合奇函数、偶函数的条件则叫做非奇非偶函数。例如f(x)=x3【-∞,-2】或【0,+∞】(定义域不关于原点对称) ⑥如果函数既符合奇函数又符合偶函数,则叫做既奇又偶函数。例如f(x)=0 注:任意常函数(定义域关于原点对称)均为偶函数,只有f(x)=0是既奇又偶函数
合肥学院 计算机科学与技术系 课程设计报告 2013~2014学年第二学期 课程数据结构与算法 课程设计名称图的深度优先遍历算法的实现 学生姓名陈琳 学号1204091022 专业班级软件工程 指导教师何立新 2014 年9 月 一:问题分析和任务定义 涉及到数据结构遍会涉及到对应存储方法的遍历问题。本次程序采用邻接表的存储方法,并且以深度优先实现遍历的过程得到其遍历序列。
深度优先遍历图的方法是,从图中某顶点v 出发: (1)访问顶点v ; (2)依次从v 的未被访问的邻接点出发,对图进行深度优先遍历;直至图中和v 有路径相通的顶点都被访问; (3)若此时图中尚有顶点未被访问,则从一个未被访问的顶点出发,重新进行深度优先遍历,直到图中所有顶点均被访问过为止。 二:数据结构的选择和概要设计 设计流程如图: 图1 设计流程 利用一维数组创建邻接表,同时还需要一个一维数组来存储顶点信息。之后利用创建的邻接表来创建图,最后用深度优先的方法来实现遍历。 图 2 原始图 1.从0开始,首先找到0的关联顶点3 2.由3出发,找到1;由1出发,没有关联的顶点。 3.回到3,从3出发,找到2;由2出发,没有关联的顶点。 4.回到4,出4出发,找到1,因为1已经被访问过了,所以不访问。
所以最后顺序是0,3,1,2,4 三:详细设计和编码 1.创建邻接表和图 void CreateALGraph (ALGraph* G) //建立邻接表函数. { int i,j,k,s; char y; EdgeNode* p; //工作指针. printf("请输入图的顶点数n与边数e(以逗号做分隔符):\n"); scanf("%d,%d",&(G->n),&(G->e)); scanf("%c",&y); //用y来接收回车符. for(s=0;s
[语言文化]英语演讲词含意化程度和性质的控制[复制链接] 黑色礼服 大家网博士后 积分 38216 帖子 9056 精华 87 经验 28243 点 威望 0 点 金币 27993 ?串个门 ?加好友 ?打招呼 ?发消息 1楼 发表于 2010-4-20 19:35:28|只看该作者|倒序浏览 摘要:结合演讲本身的特点和含意控制理论诠释如何通 过遣词造句对英语演讲词实现含意化程度和性质的控制,从 而提高英语演讲质量、英语语用能力和鉴赏能力。一、引言含 意是语言被运用时必然会呈现的一种普遍现象,但并不构成语 言系统的一部分,只有在语言被运用时才会呈现出来。含意 化过程是语言运用时必然会经历的一个过程,它不会自然地满 足语言运用者的要求,而要语言运用者自觉去把握,对含意 化过程加以控制,就是对含意运用的控制。含意本体论的研究 表明,对含意的控制主要有三个方面:控制含意化的程度、含 意化的方式和含意化的性质。[1]演讲词作为“为讲而写”的 特殊语篇,具有其独特的语体特色。本文试图结合演讲本身的 特点和含意控制理论诠释如何通过遣词造句对英语演讲词实 现含意化程度和性质的控制,从而提高英语演讲质量、英语 语用能力和鉴赏能力。二、含意化程度的控制对含意化程 度的掌握可以考虑如下因素:受话人的知识状况、有关内容在 话语中的地位和作用、说话行文的审美要求。[1] 含意化程度 的控制主要是对含意量的控制。对于演讲而言,可包括听众的 知识状况、演讲的内容和目的等。西方演讲界有句格言“听众 永远是对的”提醒演讲者:演讲者看似处于主动地位,其实听 众并非是完全的被动者。成功的演讲最基本的是善于把握听 众。语言的简洁、充实是(英语)演说词必须遵循的原则。演讲, 特别是信息性演讲,应力求话语完备、明了。演讲稿材料的搜 集,固然是“以十当一”,越多越好,但运用材料要“以一当 十”,越精越好,言简意赅,扣紧主题,使演讲词具有较高的 含意性,概括性强并有相当的表现力。例如,杨振宁教授在一 次演讲中用十二个字干净利落地讲述复杂的核子理论基石 “规范场”概念———“物理学家所追求的物质结构”。按常 规,这十二个字对于一个复杂的科学概念来讲似乎不完备,含 意性过高,难于领会,但其语言朴素晓畅,简洁之中包含极高 的智商,略有物理知识的人都会觉得浅显易懂,更不用说在场 的学者了。这十二个字还达到了杨振宁教授演讲的目的:激发 对科学问题的探索兴趣。这十二个字简洁而充实,富含意蕴, 貌似的不完备中透出完备,表现空间宽广,含意化的程度控 制适当。相反,在一些政治和社会生活演讲中,存在泡沫化的 泛情主义,过分追求华丽辞藻和形式,以为可达到鼓动、渲染 目的,反而造成话语含意性过低,没有把握好含意化程度。 语言与措辞是分不开的,下面就如何寓简洁的语言以充实之美 谈谈英语演讲词含意化程度的控制。首先,英语演讲词往往
证明函数单调性的方法总结 导读:1、定义法: 利用定义证明函数单调性的一般步骤是: ①任取x1、x2∈D,且x1 ②作差f(x1)-f(x2),并适当变形(“分解因式”、配方成同号项的和等); ③依据差式的符号确定其增减性. 2、导数法: 设函数y=f(x)在某区间D内可导.如果f′(x)>0,则f(x)在区间D内为增函数;如果f′(x) 注意:(补充) (1)若使得f′(x)=0的x的值只有有限个, 则如果f ′(x)≥0,则f(x)在区间D内为增函数; 如果f′(x) ≤0,则f(x)在区间D内为减函数. (2)单调性的判断方法: 定义法及导数法、图象法、 复合函数的单调性(同增异减)、 用已知函数的单调性等 (补充)单调性的有关结论 1.若f(x),g(x)均为增(减)函数, 则f(x)+g(x)仍为增(减)函数. 2.若f(x)为增(减)函数, 则-f(x)为减(增)函数,如果同时有f(x)>0,
则 为减(增)函数, 为增(减)函数 3.互为反函数的两个函数有相同的单调性. 4.y=f[g(x)]是定义在M上的函数, 若f(x)与g(x)的'单调性相同, 则其复合函数f[g(x)]为增函数; 若f(x)、g(x)的单调性相反, 则其复合函数f[g(x)]为减函数.简称”同增异减” 5. 奇函数在关于原点对称的两个区间上的单调性相同; 偶函数在关于原点对称的两个区间上的单调性相反. 函数单调性的应用 (1)求某些函数的值域或最值. (2)比较函数值或自变量值的大小. (3)解、证不等式. (4)求参数的取值范围或值. (5)作函数图象. 【证明函数单调性的方法总结】 1.函数单调性的说课稿 2.高中数学函数的单调性的教学设计 3.导数与函数的单调性的教学反思
#include
edgenode *p; printf("node:%c\n",ga[i].vertex); visited[i]=1; p=ga[i].link; while(p!=NULL) { if(!visited[p->adjvex]) { Dfsl(p->adjvex); } p=p->next; } } void main() { int i; Creatadjlist( ga); printf("请输入需要遍历的顶点:\n"); scanf("%d",&i); Dfsl(i); }
高中三角函数公式大全 三角函数公式 两角和公式 sin(A+B) = sinAcosB+cosAsinB sin(A-B) = sinAcosB-cosAsinB cos(A+B) = cosAcosB-sinAsinB cos(A-B) = cosAcosB+sinAsinB tan(A+B) =tanAtanB -1tanB tanA + tan(A-B) =tanAtanB 1tanB tanA +- cot(A+B) =cotA cotB 1-cotAcotB + cot(A-B) =cotA cotB 1cotAcotB -+ 倍角公式 tan2A =A tan 12tanA 2- Sin2A=2SinA?CosA Cos2A = Cos 2A-Sin 2A=2Cos 2A-1=1-2sin 2A 三倍角公式 sin3A = 3sinA-4(sinA)3 cos3A = 4(cosA)3-3cosA tan3a = tana ·tan(3π+a)·tan(3 π-a) 半角公式 sin(2A )=2 cos 1A - cos(2A )=2 cos 1A + tan(2A )=A A cos 1cos 1+- cot( 2A )=A A cos 1cos 1-+ tan(2 A )=A A sin cos 1-=A A cos 1sin + 和差化积 sina+sinb=2sin 2b a +cos 2 b a -
sina-sinb=2cos 2b a +sin 2 b a - cosa+cosb = 2cos 2b a +cos 2 b a - cosa-cosb = -2sin 2b a +sin 2 b a - tana+tanb=b a b a cos cos )sin(+ 积化和差 sinasinb = -2 1[cos(a+b)-cos(a-b)] cosacosb = 2 1[cos(a+b)+cos(a-b)] sinacosb = 2 1[sin(a+b)+sin(a-b)] cosasinb = 2 1[sin(a+b)-sin(a-b)] 诱导公式 sin(-a) = -sina cos(-a) = cosa sin( 2 π-a) = cosa cos(2 π-a) = sina sin(2 π+a) = cosa cos(2 π+a) = -sina sin(π-a) = sina cos(π-a) = -cosa sin(π+a) = -sina cos(π+a) = -cosa tgA=tanA =a a cos sin 万能公式 sina=2 )2 (tan 12tan 2a a + cosa=2 2 )2(tan 1)2(tan 1a a +-
习题1.1 1.证明下列集合等式. (1) ()()()C A B A C B A \\=; (2) ()()()C B C A C B A \\\ =; (3) ()()()C A B A C B A \\\=. 证明 (1) )()C \B (c C B A A = )()( c c C B A A B A = c C A B A )()( = )(\)(C A B A = . (2) c C B A A )(C \B)(= )()(c c C B C A = =)\()\(C A C A . (3) )(\C)\(B \c C B A A = c c C B A )( = )(C B A c = )()(C A B A c = )()\(C A B A =. 2.证明下列命题. (1) ()A B B A = \的充分必要条件是:A B ?; (2) ()A B B A =\ 的充分必要条件是:=B A ?; (3) ()()B B A B B A \\ =的充分必要条件是:=B ?. 证明 (1) A B A B B B A B B A B B A c c ==== )()()()\(的充要条 是:.A B ? (2) c c c c B A B B B A B B A B B A ===)()()(\)( 必要性. 设A B B A =\)( 成立,则A B A c = , 于是有c B A ?, 可得.?=B A 反之若,?≠B A 取B A x ∈, 则B x A x ∈∈且, 那么B x A x ?∈且与c B A ?矛盾.
充分性. 假设?=B A 成立, 则c B A ?, 于是有A B A c = , 即.\)(A B B A = (3) 必要性. 假设B B A B B A \)()\( =, 即.\c C A B A B A == 若,?≠B 取,B x ∈ 则,c B x ? 于是,c B A x ? 但,B A x ∈ 与c C A B A =矛盾. 充分性. 假设?=B 成立, 显然B A B A \= 成立, 即B B A B B A \)()\( =. 3.证明定理1.1.6. 定理1.1.6 (1) 如果{}n A 是渐张集列, 即),1(1≥??+n A A n n 则{}n A 收敛且 ∞ =∞ →=1 ;lim n n n n A A (2) 如果{}n A 是渐缩集列, 即),1(1≥??+n A A n n 则{}n A 收敛且 ∞ =∞ →= 1 . lim n n n n A A 证明 (1) 设),1(1≥??+n A A n n 则对任意 ∞ =∈ 1 ,n n A x 存在N 使得,N A x ∈ 从而 ),(N n A x N ≥?∈ 所以,lim n n A x ∞ →∈ 则.lim 1 n n n n A A ∞→∞ =? 又因为 ∞ =∞ →∞ →??1 ,lim lim n n n n n n A A A 由此可见{}n A 收敛且 ∞ =∞ →= 1 ;lim n n n n A A (2) 当)1(1≥??+n A A n n 时, 对于, lim n n A x ∞ →∈存 )1(1≥?<+k n n k k 使得 ),1(≥?∈k A x k n 于是对于任意的,1≥n 存在0k 使得n n k >0, 从而,0 n n A A x k ?∈ 可见.lim 1 ∞ =∞ →?n n n n A A 又因为,lim lim 1 n n n n n n A A A ∞ →∞ →∞ =?? 所以可知{}n A 收敛且 ∞ =∞ →=1 .lim n n n n A A 4.设f 是定义于集合E 上的实值函数,c 为任意实数,证明: (1) ??? ???+≥=>∞ =n c f E c f E n 1][1 ; (2) ?? ? ???+<=≤∞ =n c f E c f E n 1][1 ; (3) 若))(()(lim E x x f x f n n ∈?=∞ →,则对任意实数c 有 ?????? ->=????? ?->=≥∞→∞=∞ =∞ =∞ =k c f E k c f E c f E n n k n N n N k 1lim 1][111 . 证明 (1) 对任意的[],c f E x >∈ 有,)(c x f > 则存在+ ∈Z n 使得n c x f 1)(+ ≥成
龙源期刊网 https://www.doczj.com/doc/95102063.html, 激发优势深度融合均衡发展 作者:张道琼 来源:《安徽教育科研》2019年第17期 摘要:六安路小学教育集团在管理上做到宏观把控,在活动策划、师德建设、课程开发、教师专业成长等方面做到中观指导,在班子建设与执行层面做到微观细化落实,追求多校区深度融合、优势共享、均衡发展的集团化办学之路。集团主要从提炼理念、变革机制、优化师资、完善制度、汇聚资源优势、打造信息平台等方面实现优质教育的整体跨越。 关键词:集团化;管理;实践 所谓集团化办学,是指以促进义务教育优质均衡发展为目标,以创新办学体制和管理体制为动力,科学整合、合理放大优质教育资源,充分发挥优质教育资源的影响、辐射、示范和带动作用,不断缩小义务教育城乡和校际差距,不断满足人民群众日益增长的优质化、多样化教育需求,实现从“学有所教”到“学有优教”的转变。 从2011年开始,六安路小学(以下简称“六小”)就开始了一校多区的集团化办学探索之旅。在集团化办学管理探索实践中,经过认真调研、广泛征求意见,学校制定了六小集团目标发展规划,确立了集团办学的目标体系: 立足集团建设,核心理念一元化; 立足集团发展,人力资源一体化; 立足集团管理,管理运行扁平化; 立足学生发展,校区特色多元化; 立足课堂研究,教学模式多样化; 立足现代技术,运作方式数字化。 学校根据集团发展目标体系,立足集团化办学,兼顾各校区的校情、资源,使集团力求在管理上做到宏观把控,在活动策划、师德建设、课程开发、教师专业成长等方面做到中观指导,在班子建设与执行层面做到微观细化落实,追求多校区的优势共享、深度融合、均衡发展。 一、提炼核心理念,为集团长远发展打下文化根基
函数f (x)一致连续的条件及应用 (数学与应用数学2003级 张志华 指导教师 刘敏思) 内容摘要:本文比较全面的总结了判断函数的一致连续性的条件,并结合具体例子对这些方法加以应用,而且对基本初等函数的一致连续性作了较为完整的讨论,还将一元函数的一致连续性推广到二元函数上去. 关 键 词:一致连续 拟可导函数 基本初等函数 二元函数 Abstract :This paper is more completely to summarize the methods of judging uniform continuity of functions, and apply them to analyze some examples, moreover, we discuss uniform continuity of fundamental primary functions in detail, and extend these methods to the case of functions of two variables. Key words: uniform continuity perederivatable functions fundamental primary functions functions of two variables 1.引言 函数的一致连续性是数学分析课程的重要理论,弄清函数的一致连续性的概念和熟练掌握判断函数一致连续的方法是学好这一理论的关键.一般的数学分析教材中只给出一致连续的概念和判断函数在闭区间上一致连续的.G 康托定理,内容篇幅较少,不够全面和深入;虽然有些论文对函数一致连续性的判断作了一些拓展和补充,但是显得不够系统和应用得不够广泛.因此,对一般数学分析教材中这一部分内容并结合一部分论文资料,作一个比较系统和全面的总结,并作适当的拓展,如将一元函数的一致连续性推广到二元函数上去,无疑这一工作是十分必要和具有现实意义的. 2.预备知识 2.1一致连续和非一致连续的定义 一致连续:设()f x 为定义在区间I 上的函数.若对任给的0ε>,存在()0δδε=>,使得对任何,x x I '''∈,只要x x δ'''-<,就有()()f x f x ε'''-<,则称 函数()f x 在区间I 上一致连续.
函数导数公式及证明
复合函数导数公式
) ), ()0g x ≠' ''2 )()()()() ()()f x g x f x g x g x g x ?-=?? ())() x g x , 1.证明幂函数()a f x x =的导数为''1()()a a f x x ax -== 证: ' 00()()()()lim lim n n x x f x x f x x x x f x x x →→+-+-== 根据二项式定理展开()n x x + 011222110(...)lim n n n n n n n n n n n n n x C x C x x C x x C x x C x x x ----→+++++-= 消去0n n n C x x - 11222110...lim n n n n n n n n n n x C x x C x x C x x C x x ----→++++= 分式上下约去x 112211210 lim(...)n n n n n n n n n n x C x C x x C x x C x -----→=++++ 因0x →,上式去掉零项 111 n n n C x nx --== 12210()[()()...()]lim n n n n x x x x x x x x x x x x x x ----→+-+++++++=
12210 lim[()()...()]n n n n x x x x x x x x x x ----→=+++++++ 1221...n n n n x x x x x x ----=++++ 1n n x -= 2.证明指数函数()x f x a =的导数为'ln ()x x a a a = 证: ' 00()()()lim lim x x x x x f x x f x a a f x x x +→→+--== 0(1)lim x x x a a x →-= 令1x a m -=,则有log (1)a x m =-,代入上式 00(1)lim lim log (1)x x x x x a a a a m x m →→-==+ 1000 ln ln lim lim lim ln(1)1ln(1)ln(1)ln x x x x x x m a m a a a a m m m a m →→→===+++ 根据e 的定义1lim(1)x x e x →∞ =+ ,则1 0lim(1)m x m e →+=,于是 1 ln ln lim ln ln ln(1) x x x x m a a a a a a e m →===+ 3.证明对数函数()log a f x x =的导数为''1 ()(log )ln a f x x x a == 证: '0 0log ()log ()() ()lim lim a a x x x x x f x x f x f x x x →→+-+-== 00log log (1)ln(1) lim lim lim ln a a x x x x x x x x x x x x x a →→→+++===
数学课堂深度教学引领深度学习 前天,期末成绩一出来,张艺曦妈妈立刻给我发了一条信息:汪老师,张艺曦成绩为什么总是90分左右,老是提不上呀?我立即回复:他基础知识掌握不错,可是学的不够深入,不会活学活用。和她妈妈聊过以后,我也意识到,我班就有一部分学生,感觉他们基础知识学习不错,可是,稍有变化和拓展,就显得束手无策,甚至抱怨“老师没讲过”“我没见过”等等。其实学生以前也学习过类似的一些知识,但是就没有人愿意去思索,去挖掘。同时我也认真反思自己的课堂教学,有太多浮于表面的东西,学生自主学习能力不强,学习过程中无法深入挖掘课本当中深层次内容,相关知识无法得到拓展,使得数学学习效率相对低。再说,咱学校数学一周7节课,有的更少。课堂上又有新知,又要有拓展,还想有深度,这样完成教学任务和教学进度,数学老师真的不容易。所以我们只有让课堂教学有深度,让学生深度学习,提高40分钟的效率。
我今天说的深度教学并不是要加深教学知识的深度与难度,而是指在教师的引导下,学生超越表层的知识符号学习,进入知识内在的逻辑形式和意义领域,充分调动大脑思考,透彻掌握知识并能活学活用。 我们五年级的数学课堂进行深度教学,可以从四方面入手: 一、深度解读,抓住数学学科知识本质 读透教材,把握学科本质是深度教学的根本,教师只有读懂读透教材才能抓住学科知识本质进行教学。否则教师课堂教学没有准确把握知识的本质,只停留在肤浅的表层进行教学。 俗话说:不打无准备之仗。仓促上阵,哪能不败呢?所以,在上课之前,必须要认真备课,钻研教材,读懂读透教材。只有对教材进行深度解读,做到心中有底,上课才会从容,才会忙而不乱,这是课堂上进行深度教学的重要保障。 如教学方程这一单元时,大家都知道现在的解方程的依据是等式的性质,可是当未知数出现在减数
证明函数单调性的方法总结归纳 1、定义法: 利用定义证明函数单调性的一般步骤是: ①任取x1、x2∈D,且x1②作差f(x1)-f(x2),并适当变形(“分解因式”、配方成同号项的和等); ③依据差式的符号确定其增减性. 2、导数法: 设函数y=f(x)在某区间D内可导.如果f′(x)>0,则f(x)在区间D 内为增函数;如果f′(x)注意:(补充) (1)若使得f′(x)=0的x的值只有有限个, 则如果f ′(x)≥0,则f(x)在区间D内为增函数; 如果f′(x) ≤0,则f(x)在区间D内为减函数. (2)单调性的判断方法: 定义法及导数法、图象法、 复合函数的单调性(同增异减)、 用已知函数的单调性等 (补充)单调性的有关结论 1.若f(x),g(x)均为增(减)函数, 则f(x)+g(x)仍为增(减)函数. 2.若f(x)为增(减)函数, 则-f(x)为减(增)函数,如果同时有f(x)>0,
则 为减(增)函数, 为增(减)函数 3.互为反函数的两个函数有相同的单调性. 4.y=f[g(x)]是定义在M上的函数, 若f(x)与g(x)的单调性相同, 则其复合函数f[g(x)]为增函数; 若f(x)、g(x)的单调性相反, 则其复合函数f[g(x)]为减函数.简称”同增异减” 5. 奇函数在关于原点对称的两个区间上的单调性相同; 偶函数在关于原点对称的两个区间上的单调性相反. 函数单调性的应用 (1)求某些函数的值域或最值. (2)比较函数值或自变量值的大小. (3)解、证不等式. (4)求参数的取值范围或值. (5)作函数图象. 搜集整理,仅供参考学习,请按需要编辑修改
上机实验报告 学院:计算机与信息技术学院 专业:计算机科学与技术(师范)课程名称:数据结构 实验题目:深度优先遍历(邻接矩阵)班级序号:师范1班 学号:201421012731 学生姓名:邓雪 指导教师:杨红颖 完成时间:2015年12月25号
一、实验目的: 1﹒掌握图的基本概念和邻接矩阵存储结构。 2﹒掌握图的邻接矩阵存储结构的算法实现。 3﹒掌握图在邻接矩阵存储结构上遍历算法的实现。 二、实验环境: Windows 8.1 Microsoft Visual c++ 6.0 二、实验内容及要求: 编写图的深度优先遍历邻接矩阵算法。建立图的存储结构,能够输入图的顶点和边的信息,并存储到相应存储结构中,而后输出图的邻接矩阵。 四、概要设计: 深度优先搜索遍历类似于树的先根遍历,是树的先根遍历的推广。假设初始状态是图中所有的顶点未曾被访问,则深度优先遍历可从图的某个顶点V出发,访问此顶点,然后依次从V的未被访问的邻接点出发深度优先遍历图,直至图中所有和V有路径相通的顶点都被访问到;若此时图中尚有顶点未被访问,则另选图中的一个未被访问的顶点,重复上述过程,直至图中所有顶点都被访问到为止。 以图中无向图G4为例,深度优先遍历图的过程如图所示。假设从顶点V1出发进行搜索,在访问了顶点V1后,选择邻接点V2。因为V2未曾访问,则从V2出发进行搜索。依次类推,接着从V4,V8,V5出发进行搜索。在访问了V5之后,由于V5的邻接点已都被访问,则搜索回到V8。由于同样的理由,搜索继续回到V4,V2直至V1,此时由于V1的另一个邻接点为被访问,则搜索又从V1到V3,再继续进行下去。由此得到顶点的访问序列为: V1 V2 V4 V8 V5 V3 V6 V7 五、代码 #include
求函数解析式常用的方法 求函数解析式常用的方法有:待定系数法、换元法、配凑法、消元法、特殊值法。 以下主要从这几个方面来分析。 (一)待定系数法 待定系数法是求函数解析式的常用方法之一,它适用于已知所求函数类型(如一次函数,二次函数,正、反例函数等)及函数的某些特征求其解析式的题目,它在函数解析式的确定中扮演着十分重要的角色。其方法:已知所求函数类型,可预先设出所求函数的解析式,再根据题意列出方程组求出系数。 例1:已知()f x 是二次函数,若(0)0,f =且(1)()1f x f x x +=++试求()f x 的表达式。 解析:设2()f x ax bx c =++ (a ≠0) 由(0)0,f =得c=0 由(1)()1f x f x x +=++ 得 22(1)(1)1a x b x c ax bx c x ++++=++++ 整理得22(2)()1ax a b x a b c ax b c x c +++++=++++ 得 212211120011()22 a a b b a b c c b c c f x x x ?=?+=+????++=+?=????=?=??? ∴=+ 小结:我们只要明确所求函数解析式的类型,便可设出其函数解析式,设法求出其系数即可得到结果。类似的已知f(x)为一次函数时,可设f(x)=ax+b(a≠0);f(x)为反比例函数时,可设f(x)= k x (k≠0);f(x)为
二次函数时,根据条件可设①一般式:f(x)=ax2+bx+c(a≠0) ②顶点式:f(x)=a(x-h)2+k(a≠0) ③双根式:f(x)=a(x-x1)(x-x2)(a≠0) (二)换元法 换元法也是求函数解析式的常用方法之一,它主要用来处理不知道所求函数的类型,且函数的变量易于用另一个变量表示的问题。它主要适用于已知复合函数的解析式,但使用换元法时要注意新元定义域的变化,最后结果要注明所求函数的定义域。 例2 :已知1)1,f x =+求()f x 的解析式。 解析: 1视为t ,那左边就是一个关于t 的函数()f t , 1t =中,用t 表示x ,将右边化为t 的表达式,问题即可解决。 1t = 2220 1 ()(1)2(1)1()(1)x t f t t t t f x x x ≥∴≥∴=-+-+=∴=≥ 小结:①已知f[g(x)]是关于x 的函数,即f[g(x)]=F(x),求f(x)的解析式,通常令g(x)=t ,由此能解出x=(t),将x=(t)代入f[g(x)]=F(x)中,求得f(t)的解析式,再用x 替换t ,便得f(x)的解析式。 注意:换元后要确定新元t 的取值范围。 ②换元法就是通过引入一个或几个新的变量来替换原来的某些变量的解题方法,它的基本功能是:化难为易、化繁为简,以快速实现未知向已知的转换,从而达到顺利解题的目的。常见的换元法是多种多样的,如局部换元、整体换元、三角换元、分母换元等,它的应用极为广泛。 (三)配凑法 已知复合函数[()]f g x 的表达式,要求()f x 的解析式时,若[()]f g x 表达式右边易配成()g x 的运算形式,则可用配凑法,使用