Discrete Pseudo-Control Sets for Optimal Control Problem

这里 x1 (n) 和 x2 (n) 分别表示两竞争种群在第n代的种群密度， ri (n)(i = 1, 2) 表示两种群的内禀增长 率， ai (n)(i = 1, 2) 为种内竞争系数， bi (n)(i = 1, 2) 为种间竞争系数 ri (n) , ai (n) , bi (n) , ci (n) , di (n) ,
DOI: 10.12677/aam.2020.98133
1135
应用数学进展
张杰华
ei (n) , αi (n) , βi (n) , γ i (n) (i = 1, 2) 均为非负有界的概周期序列，并且 0 < ei (k ) < 1。本文的目的旨在
通过适当的分析手法，得到保证系统(2)永久持续生存、概周期解的存在唯一性和全局吸引性的充分条件。
2
(
t
)
x2
(
t
)
并对该系统的动力学行为进行了研究。 众多研究表明，当种群世代不重叠或数量很少时，用差分方程来刻画离散时间模型比连续的更符合 实际。考虑到在实际生态系统中，生态系统经常被不可预测的因素所干扰，这将可能使某些生物参数发 生改变，破坏生态的平衡，这就需要人类对其进行开发和管理，从而更好的预测和控制生态系统所受的
lim sup x (n) ≤
n→+∞
bl
.
引理2.2 [10] 设{x (n)} 满足 x (n +1) ≥ x (n) exp{a (n) − b (n) x (n)} , n ≥ N0 , N0 ∈ N , lim sup x (n) ≤ x*
且 x ( N0 ) > 0 ，其中 a (n) ， b (n) 为非负序列且有正的上下界，则
i=0

•2 Dynamics analysis of spatial compliant parallel mechanism (空间全柔性并联机构动力学分析） 1）Dynamics analysis n+n 结构（采用了名词化结构） the analysis of dynamics 复合名词？ air pollution=the pollution of the air(复合名词） power generation 发电 =the generation of the power
: a module for amplifying displacement
temperature control valve 温度控制阀 复合名词 2） 名词连用现象（复合名词）：Displacement amplifier module ，Closed Loop Design Method 前面的名 词 修饰限定作用，词量少而信息量大，使更加客观和静态 3）使用了偏正结构，中心词为Design Method ，其与均 为修饰限定作用
面向生物工程的精密定位机构及其动力学特性研究 Study on 可以省去
Precision Positioning Mechanism 复合名词
Bio-engineering 合成词
(复合单元法在变截面梁自由振动分析中的应用) Composite Element Method 名词连用 Free Vibration Analysis 复合名词 • 20 Study on Precision Positioning Mechanism for
Bio-engineering and It 's Dynamic Characteristic
英语标题的格式

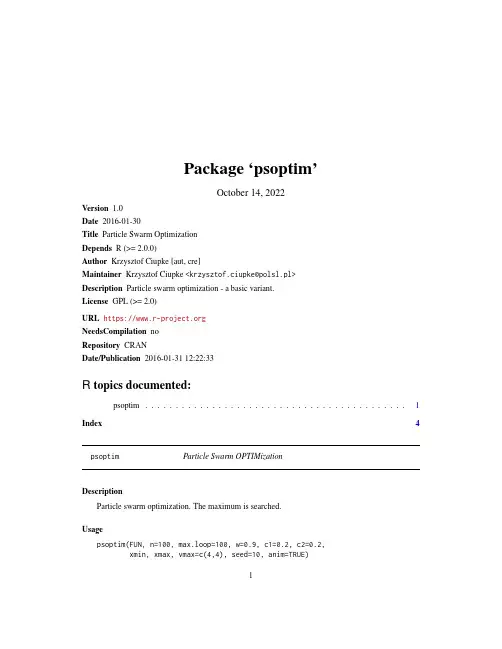
Package‘psoptim’October14,2022Version1.0Date2016-01-30Title Particle Swarm OptimizationDepends R(>=2.0.0)Author Krzysztof Ciupke[aut,cre]Maintainer Krzysztof Ciupke<*************************>Description Particle swarm optimization-a basic variant.License GPL(>=2.0)URL https://NeedsCompilation noRepository CRANDate/Publication2016-01-3112:22:33R topics documented:psoptim (1)Index4 psoptim Particle Swarm OPTIMizationDescriptionParticle swarm optimization.The maximum is searched.Usagepsoptim(FUN,n=100,max.loop=100,w=0.9,c1=0.2,c2=0.2,xmin,xmax,vmax=c(4,4),seed=10,anim=TRUE)1ArgumentsFUN the optimized function with a vector as parametern number of particlesmax.loop maximal number of iterationsw inertia weightc1coefficient of the self-recognition componentc2coefficient of the social componentxmin vector of position constraints-minimal valuesxmax vector of position constraints-maximal valuesvmax vector of velocity constraints in each directionseed seed for random valuesanim logical;if TRUE(dafault),animation of the optimization process is shown DetailsThe i-th particle velocity v in j-th direction is calculated in t iteration according to:v[ij](t+1)=w*v[ij](t)+c1*r1*(xP[ij](t)-x[ij](t))+c2*r2*(xS[j](t)-x[ij](t)).where:r1and r2are random values,w is inertia weight,c1is a coefficient of the self-recognition component and c2is a coefficient of the social component.xP denotes so far best position of the particle and xS-the best position among the swarm.The new position(coordinates)is calculated as:x[ij](t+1)=x[ij](t)+v[ij](t+1).In the current version of the package,the function works without checking the correctness of the given arguments.ValueA list with the two components:sol solution,i.e.the best set of parameters found.val the bestfitness function found.Author(s)Krzysztof Ciupke,<krzysztof.ciupke at polsl.pl>ReferencesAbraham A,Guo H,Liu H.(2006)Swarm Intelligence:Foundations,Perspectives and Applications in Nedjah N,Mourelle L.(eds.):"Swarm Intelligent Systems",Springer,Berlin Heidelberg,pp.3-25.Banks A,Vincent J,Anyakoha C.(2007)A review of particle swarm optimization.Part I:back-ground and development.Natural Computing,vol.6,No.4,pp.467-484.Dorigo M,Stutzle T.(2004)Ant Colony Optimization,MIT Press.Eberhart R,Yuhui S.(2001)Particle swarm optimization:developments,applications and re-sources,Congress on Evolutionary Computation.Seoul,Korea.Examplesn<-50m.l<-50w<-0.95c1<-0.2c2<-0.2xmin<-c(-5.12,-5.12)xmax<-c(5.12,5.12)vmax<-c(4,4)g<-function(x){-(20+x[,1]^2+x[,2]^2-10*(cos(2*pi*x[,1])+cos(2*pi*x[,2]))) }psoptim(FUN=g,n=n,max.loop=m.l,w=w,c1=c1,c2=c2,xmin=xmin,xmax=xmax,vmax=vmax,seed=5,anim=FALSE)Indexpsoptim,14。

"鞭" "链" "倾斜" "横过" "点" "酸；尖，刺，顶"
"角" "边" "棒" "长椅" "管道" "孔" "远" "近" "做"
microminimini, min pusill
gran
long
curt
lat
fil, fili fibr line
flagell
caten
bias clin, cliv
abl, abili apt, ept
labor
liber
ploy us, util
pol(y)
fatig lass
ardu
corp, corpor som
stetho
dors
man, manu chiro
digit dactyl(o)
palp tact, tag, tig, ting touch
oscul
act ag fabric fac, fic
"适应，能力"
"劳动" "自由" "用"
"卖" "疲劳"
"困难" "身体"
"胸" "背"#34;摸，接触"
"吻，接触" "钉" "锤" "臂" "武器，士兵"
"编织"

求助：谁能帮我详细解读一下，理解了两阶段极大似然估计的方法，却看不懂这个？R> loglik.marg <- function(b, x) sum(dgamma(x, shape = b[1], scale = b[2],+ log = TRUE))R> ctrl <- list(fnscale = -1)R> b1hat <- optim(b1.0, fn = loglik.marg, x = dat[, 1], control = ctrl)$parR> b2hat <- optim(b2.0, fn = loglik.marg, x = dat[, 2], control = ctrl)$parR> udat <- cbind(pgamma(dat[, 1], shape = b1hat[1], scale = b1hat[2]),+ pgamma(dat[, 2], shape = b2hat[1], scale = b2hat[2]))R> fit.ifl <- fitCopula(udat, myMvd@copula, start = a.0)fitCopula {copula} R DocumentationEstimation of the Parameters in Copula ModelsDescriptionFits a copula model to multivariate data belonging to the unit hypercube. The data can be pseudo-observations constructed from empirical or parametric marginal distribution functions, or true observations from the copula.UsageloglikCopula(param, x, copula, hideWarnings)fitCopula(copula, data, method = c("mpl", "ml", "itau", "irho"),start = NULL, lower = NULL, upper = NULL,optim.method = "BFGS", optim.control = list(maxit=1000),estimate.variance = NA, hideWarnings = TRUE)Argumentsparam a vector of parameter values.x, data n x d-matrix of (pseudo-)observations (for "mpl" and "ml" with valuesnecessarily in [0,1]) from the copula to be estimated,where n denotes the sample size and d the dimension. Considerapplying the function pobs() first in order to obtain values in [0,1]. method a character string specifying the method; can be either "ml" (maximum likelihood), "mpl" (maximumpseudo-likelihood), "itau" (inversion of Kendall's tau),and "irho" (inversion of Spearman's rho). The last three methodsassume that the data are pseudo-observations (scaled ranks),while the first method assumes that the data are observationsfrom the unknown copula. The default is "mpl".start a vector of starting values for param.lower, upper bounds on the variables for the "Brent" or "L-BFGS-B" method. optim.control a list of control parameters to be passed to optim(*, control=optim.control).optim.method the method for optim().estimate.variance logical; if true (as by default, if the optimization converges), the asymptotic variance is estimated.loglikCopula() returns the log likelihood evaluated at the given value of "param". The return value of fitCopula() is an object of class "fitCopula" (see there), containing slots (among others!)estimate the estimate of the parameters.var.est large-sample (i.e., asymptotic) variance estimate of the parameter estimator (filled with NA if estimate.variance = FALSE).copula the fitted copula.The summary() method for "fitCopula" objects returns a S3 “class” "summary.fitCopula", simply a list with components method, loglik, and convergence, all three from corresponding slots of the "fitCopula" objects, and coefficients a matrix of estimated coefficients, standard errors, t values and p-values. NoteIn the multiparameter elliptical case and when the estimation is based on Kendall's tau or Spearman's rho, the estimated correlation matrix may not always be positive-definite. If it is not, the correction proposed by Rousseeuw and Molenberghs (1993) is applied and a warning message given.If method "mpl" in fitCopula() is used and if start is not assigned a value, estimates obtained from method "itau" are used as initial values in the optimization.If methods "itau" or "itau" are used in fitCopula(), an estimate of the asymptotic variance (if available for the copula under consideration) will be correctly computed only if the argument data consists of pseudo-observations (see pobs()).For the t copula with df.fixed=FALSE (see ellipCopula()), the methods "itau" and "irho" cannot be used in fitCopula(). For the methods "ml" and "mpl", when start is not specified, the starting value for df is set to copula@df, typically 4. Also, the asymptotic variance cannot (yet) be estimated for method "mpl".To implement the “inference functions for margins” method (see, e.g., Joe 2005), the data need to be pseudo-observations obtained from fitted parametric marginal distribution functions and method needs to be set to "ml". The returned large-sample variance will then underestimate the true variance.Finally, note that the fitting functions generate error messages because invalid parameter values are tried during the optimization process (see optim()). When the number of parameters is one and the parameter space is bounded, using optim.method="Brent" is likely to give less warnings. Furthermore, from experience,optim.method="Nelder-Mead" is sometimes a more robust alternative to optim.method="BFGS".ReferencesGenest, C. (1987). Frank's family of bivariate distributions. Biometrika 74, 549–555. Genest, C. and Rivest, L.-P. (1993). Statistical inference procedures for bivariateArchimedean copulas. Journal of the American Statistical Association 88, 1034–1043. Rousseeuw, P. and Molenberghs, G. (1993). Transformation of nonpositive semidefinite correlation matrices. Communications in Statistics: Theory and Methods 22, 965–984.Genest, C., Ghoudi, K., and Rivest, L.-P. (1995). A semiparametric estimation procedure of dependence parameters in multivariate families of distributions. Biometrika82, 543–552.Joe, H. (2005). Asymptotic efficiency of the two-stage estimation method for copula-based models. Journal of Multivariate Analysis 94, 401–419.Demarta, S. and McNeil, A. J. (2005). The t copula and related copulas. International Statistical Review 73, 111–129.Genest, C. and Favre, A.-C. (2007). Everything you always wanted to know about copula modeling but were afraid to ask. Journal of Hydrologic Engineering 12, 347–368.Kojadinovic, I. and Yan, J. (2010). Comparison of three semiparametric methods for estimating dependence parameters in copula models. Insurance: Mathematics and Economics 47, 52–63.See AlsoCopula, mvdc for fitting multivariate distributions including the margins aka “meta copula”s;gofCopula.For maximum likelihood of (nested) archimedean copulas: emle, etc.Examplesgumbel.cop <- gumbelCopula(3, dim=2)(Xtras <- copula:::doExtras())n <- if(Xtras) 200 else 64set.seed(7) # for reproducibilityx <- rCopula(n, gumbel.cop)## "true" observationsu <- pobs(x) ## pseudo-observations## inverting Kendall's taufit.tau <- fitCopula(gumbel.cop, u, method="itau")fit.taucoef(fit.tau)# named vector## inverting Spearman's rhofit.rho <- fitCopula(gumbel.cop, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(gumbel.cop, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(gumbel.cop, x, method="ml")fit.ml # print()ing works via summary() ...## and of that, what's the log likelihood (in two different ways):(ll. <- logLik(fit.ml))stopifnot(all.equal(as.numeric(ll.),loglikCopula(coef(fit.ml), x=x, copula=gumbel.cop)))## a multiparameter exampleset.seed(6)normal.cop <- normalCopula(c(0.6,0.36, 0.6),dim=3,dispstr="un") x <- rCopula(n, normal.cop) ## "true" observationsu <- pobs(x) ## pseudo-observations## inverting Kendall's taufit.tau <- fitCopula(normal.cop, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop, u, method="mpl")fit.mplcoef(fit.mpl) # named vectorstr(sf.mpl <- summary(fit.mpl))coef(sf.mpl)# the matrix, with SE, t-value, ...## maximum likelihoodfit.ml <- fitCopula(normal.cop, x, method="ml")fit.ml## with dispstr="toep"normal.cop.toep <- normalCopula(c(0, 0), dim=3, dispstr="toep") ## inverting Kendall's taufit.tau <- fitCopula(normal.cop.toep, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop.toep, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop.toep, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(normal.cop.toep, x, method="ml")fit.ml## with dispstr="ar1"normal.cop.ar1 <- normalCopula(c(0), dim=3, dispstr="ar1")## inverting Kendall's taufit.tau <- fitCopula(normal.cop.ar1, u, method="itau")fit.tau## inverting Spearman's rhofit.rho <- fitCopula(normal.cop.ar1, u, method="irho")fit.rho## maximum pseudo-likelihoodfit.mpl <- fitCopula(normal.cop.ar1, u, method="mpl")fit.mpl## maximum likelihoodfit.ml <- fitCopula(normal.cop.ar1, x, method="ml")fit.ml## a t copula with variable df (df.fixed=FALSE):(tCop <- tCopula(c(0.2,0.4,0.6), dim=3, dispstr="un", df=5))set.seed(101)x <- rCopula(n, tCop) ## "true" observationsu <- pobs(x) ## pseudo-observations## maximum likelihood; start := (rho[1:3], df)(tc.ml <- fitCopula(tCop, x, method="ml", start=c(0,0,0, 10)))(tc.ml. <- fitCopula(tCop, x, method="ml")) # without 'start'## maximum pseudo-likelihood; the asymptotic variance cannot be estimated (tc.mpl <- fitCopula(tCop, u, method="mpl", estimate.variance=FALSE,start= c(0,0,0,10)))if(Xtras) { ##---- typically not run with CRAN checking: ---## without start:(tc.mp. <- fitCopula(tCop, u, method="mpl", estimate.variance=FALSE))all.eqCop <- function(x,y, ...) {x@fitting.stats$counts <- y@fitting.stats$counts <- NULLall.equal(x,y, ...) }stopifnot(all.eqCop(tc.ml , tc.ml., tolerance= .005),all.eqCop(tc.mpl, tc.mp., tolerance= .005))## same t copula but with df.fixed=TRUE (--> use same data!)(tC.f <- tCopula(c(0.2,0.4,0.6), dim=3, dispstr="un", df=5, df.fixed=TRUE))## maximum likelihood; start := rho[1:3] -------------(tcF.ml <- fitCopula(tC.f, x, method="ml", start=c(0,0,0)))(tcF.ml. <- fitCopula(tC.f, x, method="ml"))# without 'start'stopifnot(all.eqCop(tcF.ml,tcF.ml., tolerance= 4e-4))## the (estimated, asymptotic) var-cov matrix:vcov(tcF.ml)## maximum pseudo-likelihood; the asymptotic variance cannot be estimated (tcF.mpl <- fitCopula(tC.f, u, method="mpl", estimate.variance=FALSE,start=c(0,0,0)))(tcF.mp. <- fitCopula(tC.f, u, method="mpl", estimate.variance=FALSE)) stopifnot(all.eqCop(tcF.mpl,tcF.mp., tolerance= 1e-5))}## end{typically not run ...}。

discrete phase methodThe Discrete Phase Method (DPM) is a numerical technique used to simulate dynamic systems that involve multiple interacting phases, such as fluid-structure interaction or particle-based systems. It is a discretization method that treats each phase separately and solves the equations of motion for each phase using a time-stepping scheme.In the DPM, the system is divided into distinct phases, and each phase is represented by a set of particles or fluid elements. The motion of each particle or fluid element is determined by applying forces and torques to it, which are computed based on the interactions between the phases. The motion of each phase is then updated in discrete time steps using numerical integration techniques, such as the Verlet algorithm or the leapfrog method.The DPM has several advantages. First, it allows for efficient simulation of systems with multiple interacting phases by treating each phase separately. This reduces the computational cost compared to fully coupled methods. Second, it provides flexibility in representing each phase using particles or fluid elements, depending on the system being simulated. Third, it can handle complex geometries and boundary conditions, as each phase is treated independently.However, the DPM also has some limitations. One of the main challenges is dealingwith the coupling between phases, as the motion of one phase can influence the motion of another phase. This coupling needs to be accurately modeled to ensure the accuracy of the simulation. Additionally, the DPM may not be suitable for simulating systems with strong hydrodynamic interactions between phases, as it treats each phase separately and does not account for the continuous nature of fluids.Overall, the Discrete Phase Method is a valuable tool for simulating dynamic systems with multiple interacting phases. It provides an efficient and flexible approach for modeling such systems, but care must be taken to accurately model the coupling between phases and account for any specific characteristics of the system being simulated.。

第38卷 第8期西南师范大学学报(自然科学版)2013年8月V o l .38 N o .8 J o u r n a l o f S o u t h w e s t C h i n aN o r m a lU n i v e r s i t y (N a t u r a l S c i e n c eE d i t i o n )A u g.2013文章编号:10005471(2013)08002504解变分不等式的两种新的投影算法①郑 莲, 苟清明长江师范学院数学与计算机科学学院,重庆涪陵408100摘要:运用A r m i j o 型线性搜寻程序构造了一类新的超平面.借助这些超平面,运用不同的投影方式,建立了一类新的二次投影算法和自适性投影算法.在较弱的条件下,这些算法是全局收敛的.数值试验证明这些新算法是有效的.关 键 词:变分不等式;二次投影算法;自适性投影算法;收敛性中图分类号:O 177.91文献标志码:A考虑变分不等式问题V I (F ,C ):求x *ɪC ,使得<F (x *),y -x *>ȡ0 ∀y ɪC(1)其中C 是R n 的一个非空闭凸子集,F 是从R n 到自身的连续映射,<㊃,㊃>和 . 分别表示Rn的内积和范数.设S 表示V I (F ,C )的解集.我们假设S 是非空的,且F 满足<F (y ),y -x *>ȡ0 ∀y ɪC ,x *ɪS (2)投影型算法是解决变分不等式问题的一类简洁有效的方法,已被广泛研究.文献[1]介绍了二次投影算法.文献[2]运用不同的线性搜寻程序,构造了一类新的超平面,改进了文献[1]的算法.为了修正算法,一些研究者考虑了自适性投影算法,该方法主要是通过改变步长参数或搜寻方向来改善其有效性,见文献[3].本文运用A r m i j o 型线性搜寻程序构造了一类新的超平面.借助这些超平面,运用不同的投影方式,建立了一类新的二次投影算法和自适性投影算法.在较弱的条件下,这些算法被证明是全局收敛的.数值试验证明这些新算法是有效的.1 算法及预备知识设μ>0是一个参数.定义r μ(x )=x -ᵑC (x -μF (x )).算法1 选取x 0ɪC ,μ,α1>0,θɪ(0,1),σɪ(0,μ-1),α2ȡ0和α1ʂα2.令k =0.步骤1 计算r μ(x k ).如果r μ(xk )=0,则停止;否则,转到步骤2.步骤2 计算z k =x k -ηk r μ(xk ),其中ηk =θm k ,m k 是满足<F (x k )-F (x k -θmr μ(x k )),r μ(x k )>ɤσ r μ(xk ) 2(3)的最小的非负整数m .如果F (z k )=0,则停止;否则,转到步骤3.步骤3 计算步长ρk =γk ηk <r μ(x k ),F (z k )> d k2(4) 步骤4 计算x k +1=ᵑC (x k -ρk d k)(5)其中①收稿日期:20120616基金项目:重庆市教委重点资助项目(k j 111309).作者简介:郑 莲(1974),女,重庆涪陵人,副教授,主要从事非线性分析的研究.Copyright ©博看网. All Rights Reserved.d k =γk F (z k )+λk F (x k ) γk =α1 r μ(x k ) F (z k ) λk =α2 r μ(x k ) F (x k )(6)令k =k +1,转到步骤1.注1 算法1中的搜寻程序(3)与文献[3]中的相应搜寻程序是不一样的.在搜寻m 的过程中,算法1每次试验只需估算函数值,而在文献[3]中,每次试验都需要计算投影和估算函数值.由式(4)和(6)得到x k -ρk d k=x k -<x k -z k ,d k >-λk ηk <F (x k ),r μ(x k )> d k2d k =ᵑ췍H k (x k )其中췍H k ={v ɪR n:h k (v )=0}是由函数h k (v )=<v -z k ,d k >-λk ηk <F (x k ),r μ(x k )>(7)定义的超平面.算法2 选取x 0ɪC ,θɪ(0,1),σɪ(0,μ-1),μ,α1>0和α2ȡ0.令k =0.步骤1和步骤2与算法1相同.步骤3 计算x k +1=ᵑC k(x k ),其中C k ={v ɪC :h k (v )ɤ0},h k (v )由式(7)定义.令k =k +1,转到步骤1.注2 在算法1中,x k 被先投影到췍H k 再投影到C 上.而在算法2中,x k 被直接投影到C k =C ɘH k上.取α1=0,则算法2退化为文献[1]中的算法2.2.文献[1]的算法2.2中的σ只能在区间(0,1)内取值,而算法2中的σ可以取任意的正数.事实上,在数值试验部分,我们取σ=10.算法2与文献[2]中的算法是不同的,主要区别在于所构造的超平面不相同.引理1 设x *ɪS ,函数h k 由式(7)定义,则h k (x k )ȡ(μ-1-σ)ηk γk r μ(x k ) 2 h k (x *)ɤ0特别地,如果r μ(xk )ʂ0,则h k (x k )>0.证 由文献[2]的引理2.1和式(3),得到h k (x k )=<x k -z k ,d k >-λk ηk <F (x k ),r μ(x k )>=γk ηk <F (z k ),r μ(x k )>ȡ(μ-1-σ)ηk γk r μ(x k ) 2ȡ0由于σ<μ-1,如果r μ(xk )ʂ0,那么h k (x k )>0.根据条件(2),得到h k (x *)=<x *-z k ,d k >-λk ηk <F (x k ),r μ(x k )>=<x *-x k ,d k >+ηk <r μ(x k ),d k>-λk ηk <F (x k ),r μ(x k )>=<x *-x k ,γk F (z k )>+<x *-x k ,λk F (x k )>+ηk γk <r μ(xk ),F (z k )>ɤ02 收敛分析这一部分,我们考虑算法1㊁算法2的收敛性.当然,如果算法在第k 步停止,则x k 是VI (F ,C )的解.因此,在下面的分析中,我们假设算法1㊁算法2总是产生一个无穷序列.定理1 如果C 是R n 的非空闭凸子集,F 是从R n到自身的连续映射,且满足条件(2),则由算法1产生的序列{x k }收敛于V I (F ,C )的一个解.证 设x *ɪS .定义x (ρ)=ᵑC (x -ρd ) θ(ρ)= x -x * 2- x (ρ)-x * 2(8)将投影不等式x (ρ)-x * 2ɤ x -ρd -x * 2- x -ρd -x (ρ)2= x -x * 2-2ρ<x -x *,d >- x -x (ρ) 2+2ρ<x -x (ρ),d >代入式(8),由式(2),得到θ(ρ)ȡ2ρ<x -x *,d >+ x -x (ρ) 2-2ρ<d ,x -x (ρ)>=2ρ<x -x *,γF (z )+λF (x )>+ x -x (ρ) 2-2ρ<x -x (ρ),d >ȡ2ρηγ<r μ(x ),F (z )>+ x -x (ρ)-ρd 2-ρ2 d 2从而有θ(ρ)ȡ2ηγρ<r μ(x ),F (z )>-ρ2 d 2.62西南师范大学学报(自然科学版) h t t p ://x b b jb .s w u .c n 第38卷Copyright ©博看网. All Rights Reserved.令g (ρ)=2ηγρ<r μ(x ),F (z )>-ρ2 d 2,则g m a x (ρ)=η2γ2<F (z ),r μ(x )>2d 2.由文献[2]的引理2.1和式(3)得 x k +1-x * 2= x k -x * 2-θ(ρk )ɤ x k -x * 2-ηk 2γk 2<F (z k ),r μ(x k )>2d k 2ɤ x k -x * 2-ηk 2γk 2(μ-1-σ)2(α1+α2)2 r μ(x k ) 2即{ x k -x * }是单调递减的收敛数列,从而{x k }有界,且l i m ңk ɕη2k γ2k r μ(x k ) 2=α21l i m ңk ɕη2k r μ(x k ) 4 F (z k )2=0.又因为r μ和F 是连续的,所以序列{ F (z k ) }也是有界的.因此有l i m ңk ɕη2k r μ(xk ) 4=0.即存在{x k }的子列{x k i }和{x k j },使得l i m ңi ɕr μ(x k i ) =0,或l i m ңj ɕηk j=0.如果l i m ңi ɕr μ(x k i ) =0,则存在{x k i}的一个聚点췍x ,使得r μ(췍x )=0,从而췍x 是V I (F ,C )的一个解.用췍x 代替x *,{ x k -췍x }也是单调递减的收敛数列.由于췍x 是{x k i }的一个聚点,所以存在子列{ x k i-췍x }收敛到0,从而整个序列{ x k -췍x }收敛到0,因此l i m ңk ɕx k =췍x .如果l i m ңj ɕηk j =0,由式(3),得到<F (x k j )-F (x k j -ηk j γ-1r μ(x k j )),r μ(x k j )>>σ r μ(x k j) 2.让ңj ɕ,得到l i m ңj ɕr μ(x k j) =0.类似于前面的讨论可得到结论.定理2 如果定理1的条件成立,那么算法2产生一个收敛于V I (F ,C )的解的无穷序列{x k }.证 设x *ɪS .由于x k +1=ᵑC k(x k ),由投影性质,有 x k +1-x *2ɤ x k -x * 2- x k +1-x k 2= x k -x * 2-d i s t 2(x k ,C k )所以{ x k +1-x * 2}单调递减,从而是收敛数列.因此{x k }有界,且l i m ңk ɕd i s t (x k ,C k )=0.由于F 和投影算子是连续的,所以{r μ(xk )}是有界序列,从而存在M >0,使得 d kɤγk F (z k ) +λk F (x k ) =(α1+α2) r μ(xk ) ɤM 显然每个h k 在C 上都是Li p s c h i t z 连续的,且L i p s c h i t z 常数为M >0.由文献[2]的引理2.3和引理1,d i s t (x k ,C k )ȡM -1h k (x k )ȡM -1(μ-1-σ)ηk γk r μ(x k ) 2.因此l i m ңk ɕηk γk r μ(x k ) 2=0.接下来的证明与定理1相同.3 数值实验运用MA T L A B7.0编程,在内存为2.00GM 的笔记本电脑上进行数值实验.将算法1㊁算法2以及文献[2]的算法2.1和文献[1]的算法2.2的运行结果进行比较.在表1㊁表2中,n 表示问题的维数,C P U 表示C P U 运行时间(单位:秒), - 表示C P U 运行时间超过600秒.我们用 r μ(x ) ɤ10-4作为程序结束的标准.在表1㊁表2中,我们选取γ=0.5,σ=4和μ=0.2作为文献[2]中的算法2.1的取值;σ=0.3和γ=0.5作为文献[1]中的算法2.2的取值.这些参数值的选择是由相应参考文献提供的.表1㊁表2中共涉及4个问题,其中问题1为文献[4]的例6.1,问题2为文献[5]中的K o j i m a -S h i n d o 型非线性相补问题N C P (取n =4),问题3为文献[6]中的M a t h i e s e n ,问题4为文献[7]中的N 个公司非合作对策的C o u r n o t -N a s h 型平衡问题.在表1中,问题的初始点为原点.选取σ=4,α1=50,α2=-20,θ=0.5和μ=0.2作为算法1㊁算法2的参数值.表1 各算法在问题1中的实验结果n 算法1迭代数目C P U /秒算法2迭代数目C P U /秒文献[2]的算法2.1迭代数目C P U /秒文献[1]的算法2.2迭代数目C P U /秒10050.10950.405110.577150.59320050.24950.842121.451151.80950051.43555.5531311.0611513.41100057.035533.281374.1617101.42000539.415121.714431.417593.130005109.35585.1----72第8期 郑 莲,等:解变分不等式的两种新的投影算法Copyright ©博看网. All Rights Reserved.表1显示我们的算法1㊁算法2的迭代次数和C P U 运行时间都比文献[2]中的算法2.1以及文献[1]中的算法2.2更少.在表2中,我们取α1=50,σ=30,θ=0.6,α2=-20,和μ=0.002作为算法1和2分别在M a t h i e s e n 1-2和M a t h i e s e n 1中的取值;取α1=50,σ=10,θ=0.6,α2=-20和μ=0.02作为算法2在其他问题中的取值.取x 0=(1,1,1,1)和x 0=(0.3,0.4,0.3)分别为问题2和问题3的初始点.M a t h i e s e n 1和M a t h i e s e n 2分别代表问题2和问题3,H a r n a s h 5和H a r n a s h 10是问题4中分别取n =5和n =10的情况.表2 各算法在问题2-4中的实验结果n 算法1迭代数目C P U /秒算法2迭代数目C P U /秒文献[2]的算法2.1迭代数目C P U/秒文献[1]的算法2.2迭代数目C P U/秒M a t h i e s e n 1150.078120.187370.389280.374M a t h i e s e n 2100.14180.172190.14120.15H a r n a s h 5--60.296120.203220.312H a r n a s h 10--140.312410.312510.468从表2,我们能观察到,算法2在问题2-4等非线性问题中比其他的几种算法更有效;算法1在问题2-3中效果不错,但在问题4中效果不好.参考文献:[1]S O L O D O V M V ,S V A I T E RBF .A N e w P r o j e c t i o n M e t h o d f o rV a r i a t i o n a l I n e q u a l i t y Pr o b l e m s [J ].S I M J JC o n t r o l O p t i m ,1999,37(3):765-776.[2] H E Y i -r a n .A N e w D o u b l eP r o j e c t i o n A l g o r i t h mf o rV a r i a t i o n a l I n e q u a l i t i e s [J ].JC o m p u tA p p lM a t h ,2006,185:166-173.[3] Z E N G Y u ,HUS h a o ,WA N GG u o -d o n g .M o d i f i e dS e l f -A d a p t i v eP r o j e c t i o nM e t h o d f o r S o l v i n g P s e u d o m o n o t o n eV a r i a -t i o n a l I n e q u a l i t i e s [J ].A p p lM a t hC o m p u t ,2011,217:8052-8060.[4] S U N D.A C l a s so f I t e r a t i v e M e t h o d s f o rS o l v i n g N o n l i n e a rP r o j e c t i o nE q u a t i o n s [J ].JO p t i m T h e o r y A p pl ,1996,91(1):123-140.[5] P A N GJS ,G A B R I E LSA.N E /S Q P :AR o b u s tA l g o r i t h mf o r t h eN o n l i n e a r C o m p l e m e n t a r i t y P r o b l e m [J ].M a t hP r o -g r a m ,1993(60):295-337.[6] MA T H I E S E NL .A nA l g o r i t h mB a s e d o n a S e q u e n c e o f L i n e a rC o m p l e m e n t a r i t y P r o b l e m sA p p l i e d t o aW a l r a s i a nE q u i -l i b r i u m M o d e l :A nE x a m p l e [J ].M a t hP r o gr a m ,1987(37):1-18.[7] HA R K E R P T.A c c e l e r a t i n g t h eC o n v e r g e n c eo f t h eD i a g o n a l i z a t i o na n dP r o j e c t i o n A l g o r i t h m s f o rF i n i t e -D i m e n s i o n a l V a r i a t i o n a l I n e q u a l i t i e s [J ].M a t hP r o gr a m ,1988(41):29-59.T w oN e wP r o j e c t i o nA l g o r i t h m s f o r S o l v i n g V a r i a t i o n a l I n e qu a l i t i e s Z H E N G L i a n , G O U Q i n g -m i n g D e p a r t m e n t o fM a t h e m a t i c sa n dC o m p u t e r S c i e n c e ,Y a n g t z eN o r m a l U n i v e r s i t y ,F u l i n g C h o n g q i n g 408100,C h i n a A b s t r a c t :Ac l a s s o f n e wh y p e r p l a n e s a r e o b t a i n e db y a nA r m i j o -t y p e l i n e s e a r c h p r o c e d u r e .B y t h eh y p e r -p l a n e s a n du s i n g d i f f e r e n t p r o j e c t i o n w a y ,ac l a s so fn e w d o u b l e p r o j e c t i o na l g o r i t h m sa n ds e l f -a d a p t i v e o n e s a r e p r o p o s e d .T h e y a r e p r o v e dt ob e g l o b a l l yc o n v e r g e n t t oas o l u t i o no f t h ev a r i a t i o n a l i n e q u a l i t yp r o b l e mu n d e rw e a kc o n d i t i o n .N u m e r i c a l e x p e r i m e n t s p r o v e t h a t n e wa l go r i t h m s a r e v a l i d .K e y w o r d s :v a r i a t i o n a l i n e q u a l i t i e s ;d o u b l e p r o j e c t i o na l g o r i t h m ;s e l f -a d a p t i v e p r o j e c t i o na l g o r i t h m ;c o n -v e r ge n c e 责任编辑 廖 坤82西南师范大学学报(自然科学版) h t t p ://x b b jb .s w u .c n 第38卷Copyright ©博看网. All Rights Reserved.。

具有解耦性能的离散时间线性多变量系统最优跟踪控制富 月 1陈 威1摘 要 在传统线性二次跟踪控制方法的基础上, 针对一类具有强耦合特性的离散时间线性多变量系统, 提出了一种具有解耦性能的最优跟踪控制方法. 首先为实现解耦, 将耦合项作为可测干扰, 基于零和博弈思想提出了一种新的性能指标; 然后针对该性能指标, 利用极小值原理设计最优跟踪控制器, 通过适当加权矩阵的选择, 同步实现解耦和跟踪; 最后进行仿真实验, 仿真结果表明了该方法的有效性以及在最优性能等方面的优越性.关键词 解耦, 跟踪控制, 离散时间线性系统, 多变量系统引用格式 富月, 陈威. 具有解耦性能的离散时间线性多变量系统最优跟踪控制. 自动化学报, 2022, 48(8): 1931−1939DOI 10.16383/j.aas.c190748Optimal Tracking Control Method for Discrete-time Linear MultivariableSystems With Decoupling PerformanceFU Yue 1 CHEN Wei 1Abstract In this paper, for a class of discrete-time multivariable linear systems with strong coupling property,based on the traditional linear quadratic tracking control method, an optimal tracking controller with decoupling performance is proposed. First, in order to achieve decoupling, the coupling term is viewed as the measurable dis-turbance, and then a novel performance index which is inspired by the two-player Zero-Sum game problem is intro-duced. Based on the novel performance index, the optimal tracking controller is derived by using the minimum prin-ciple. Then, it is proved that by choosing appropriate weighting matrices, the proposed method can simultaneously decouple the closed-loop system in dynamic and make the tracking error converge asymptotically. Finally, simula-tions are conducted, whose results demonstrate the effectiveness of the proposed method and its superiority in op-timal performance comparing with the traditional controller.Key words Decoupling, tracking control, discrete-time linear systems, multivariable systemsCitation Fu Yue, Chen Wei. Optimal tracking control method for discrete-time linear multivariable systems with decoupling performance. Acta Automatica Sinica , 2022, 48(8): 1931−1939跟踪和镇定是控制领域的两个典型问题. 一般来说, 相较于镇定问题, 跟踪更为困难. 这是因为镇定只需要在系统的状态或输出受到干扰而偏离原平衡状态时, 施加控制作用, 使得系统状态或输出恢复到原平衡状态即可, 而跟踪控制问题要求系统的状态或输出能够跟随任意参考输入. 跟踪控制不仅是控制理论研究的热点问题, 在工程领域也具有很强的应用背景, 比如机器人运动轨迹跟踪控制[1]、船舶轨迹跟踪控制[2]和飞行器姿态控制[3]等.跟踪控制器的设计方法主要分为两类, 一类是追求跟踪误差渐近收敛的常规跟踪控制方法, 另一类是兼顾跟踪误差和整体性能的最优跟踪控制方法. 常规跟踪控制方法通过反馈实现调节, 利用前馈使得系统状态跟踪参考输入. 由于该方法基于零极点对消原理, 如果系统存在不可对消的不稳定零点, 会导致闭环系统输出产生相移和增益误差[4]. 为解决该问题, 文献[4−5]提出了一种多速率前馈跟踪控制方法, 使得存在不稳定零点的线性系统能够完全跟踪参考输入. 20世纪90年代初, 随着自适应控制的发展以及模糊逻辑系统和神经网络等智能算法的引入, 具有不确定性和非线性特性的复杂系统的跟踪控制问题受到人们的广泛关注. 文献[6]针对一类具有不确定动态的回滞非线性系统, 提出了一种鲁棒自适应反步跟踪控制方法, 该方法将整个非线性系统划分为多个子系统, 对每个子系统进行设计, 直到倒推至系统输入. 随着系统阶数的增加,该方法的推导过程会变得非常复杂, 容易产生复杂收稿日期 2019-10-29 录用日期 2020-03-11Manuscript received October 29, 2019; accepted March 11,2020国家自然科学基金(61991403, 61991400)和辽宁省教育厅创新人才项目(ZX20200070)资助Supported by National Natural Science Foundation of China (61991403, 61991400) and Innovative Talent Project of Liaoning Education Committee (ZX20200070)本文责任编委 张卫东Recommended by Associate Editor ZHANG Wei-Dong1. 东北大学流程工业综合自动化国家重点实验室 沈阳 1100041. State Key Laboratory of Synthetical Automation for Pro-cess Industries, Northeastern University, Shenyang 110004第 48 卷 第 8 期自 动 化 学 报Vol. 48, No. 82022 年 8 月ACTA AUTOMATICA SINICAAugust, 2022度爆炸问题. 文献[7]针对一类模型未知的严反馈的单输入单输出非线性系统, 通过引入动态表面控制技术和最小学习参数方法来解决传统反步法带来的复杂度爆炸的问题, 提出了一种鲁棒自适应跟踪控制方法, 使得系统能够跟踪任意参考输入. 文献[8]针对一类含有外部干扰和建模不确定性的非线性多输入多输出系统, 将模糊控制方法与反步法相结合,设计鲁棒自适应模糊控制器, 保证系统输出信号一致有界并能收敛到参考输入附近. 文献[9]提出一种基于输出跟踪误差的自适应模糊控制方法, 设计带有模糊观测器的模糊控制器, 来减小未知非线性系统的跟踪误差.上述常规跟踪控制方法的目标是找到一个稳定的控制器, 使得系统状态或输出跟踪参考轨迹. 在控制器设计中, 常常要兼顾到系统的跟踪误差和整体性能. 最优跟踪控制方法可以通过最小化二次型性能指标, 一方面使系统跟踪误差渐近收敛, 另一方面使系统获得最优性能. 文献[10]指出线性二次型最优跟踪(Linear quadratic tracking, LQT)控制器由反馈项和前馈项两部分组成, 其中反馈项使闭环系统稳定, 前馈项使闭环系统输出跟踪参考输入. 文献[11]针对连续时间线性多变量系统, 将开环解耦控制与LQT 相结合, 提出了一种近似最优跟踪控制方法, 实现了多变量系统的解耦和跟踪控制. 设计线性最优跟踪控制器的关键在于求解代数黎卡提方程, 由于该方程中包含着系统模型参数信息, 所以对于这种传统的最优跟踪控制方法, 当系统模型参数未知时, 就无法得到有效应用. 为解决这一问题, 文献[12]针对模型参数部分未知的连续时间线性系统, 提出了一种基于策略迭代的自适应动态规划方法, 通过计算代数黎卡提方程的数值解,进而得到近似最优跟踪控制律. 不过这类方法大多要求系统状态完全已知, 为了解决这个问题, 文献[13]针对模型参数部分未知的离散时间线性系统, 仅使用系统输入输出数据, 提出了一种基于值迭代和策略迭代的自适应动态规划方法, 设计近似最优跟踪控制器, 使得系统输出能够跟踪参考输入. 与线性最优跟踪控制器设计方法类似, 设计非线性最优跟踪控制器时需要求解非线性哈密顿−雅可比−贝尔曼方程. 许多专家学者针对这一问题也展开了深入研究. 文献[14]针对模型参数部分未知的连续时间非线性系统, 提出了一种基于多层神经网络的近似最优跟踪控制器设计方法, 先使用神经网络辨识系统模型, 再分别设计反馈神经控制器和前馈神经控制器, 使得系统可以较好的跟踪参考输入, 不过该方法使系统输出和控制输入在初始时刻会产生较大的震荡. 为了抑制这种震荡, 文献[15−16]设计了一种新型性能指标, 并提出了一种启发式动态规划方法, 不仅减小了系统输出和控制输入的波动, 还获得了更好的跟踪性能. 文献[17−19]针对模型参数未知的连续时间非线性系统, 提出了一种数据驱动的自适应动态规划方法, 先利用递归神经网络建立数据驱动模型, 在该模型的基础上设计了基于自适应动态规划的近似最优跟踪控制器, 使得系统状态输出能够渐近跟踪期望轨迹. 毫无疑问, 上述研究工作推动了最优跟踪控制方法的进一步发展与应用,丰富了跟踪控制的研究内容.实际系统往往具有多变量和强耦合特性, 上述跟踪控制方法没有考虑到多变量系统中可能存在的强耦合特性, 无法保证系统的整体性能最优. 本文针对一类具有强耦合特性的离散时间线性多变量系统, 提出了一种具有解耦性能的最优跟踪控制方法.首先将耦合项看作可测干扰, 基于零和博弈思想设计一个由系统跟踪误差、控制输入和耦合干扰补偿构成的性能指标; 然后通过最小化这个新的性能指标, 得到最优跟踪控制律, 并给出了加权矩阵的选择方法, 证明了通过该加权矩阵的选择, 一方面可以动态解耦闭环系统并使其稳定, 另一方面可使闭环系统的状态完全跟踪参考输入; 最后进行了仿真对比实验, 实验结果表明与传统的LQT控制器相比, 该方法无论在跟踪误差还是在系统的整体性能方面都具有一定的优越性.1 问题描述考虑如下离散时间线性多变量系统:x k=[x1(k),x2(k),···,x n(k)]T∈R nu k=[u1(k),u2(k),···,u n(k)]T∈R nA∈R n×n B∈R n×nB式中, 是系统的状态向量,是系统的控制输入向量, 和均为常值矩阵, 并且是可逆的.u∗kx r,k=[x r1(k),x r2(k),···,x rn(k)]T∈R n传统的LQT控制问题是寻找最优跟踪控制律, 使得闭环系统的状态能够跟踪给定参考输入, 并使如下性能指标最小:N x Nx r,N e k= x r,k−x k k P QR式中, 为大于1的正整数, 表示终端时刻, 为终端时刻系统状态, 为终端时刻参考输入,为时刻的跟踪误差, 和为半正定矩阵, 为正定矩阵. 易知, 最优跟踪控制律为[14]:1932自 动 化 学 报48 卷S k V k 式中, 和 分别根据下式反向迭代求解:将式(3)代入式(1), 得到闭环系统方程:P Q Rx r,k x k x ri (k ),i =1,···,n x j (k )(j =1,···,n ;i =j )由式(4) ~ (6)可以看出, 即使加权矩阵 , 和 都为对角矩阵, 也难以保证从 到 的传递函数矩阵是对角的, 也就是说某一个参考输入 的变化会导致其他状态 的变化. 造成这种现象的原因是不同控制回路之间存在耦合. 如果被控对象是线性多变量弱耦合系统, 可以采用分布式控制、模型预测控制等方法, 然而如果被控对象是强耦合的, 上述方法难以获得良好的控制效果.P Λ1Λ2S k V k Q x k x r,k 本文的目的是提出一种具有解耦性能的最优跟踪控制方法, 针对已知的离散时间线性多变量系统(1), 通过预先给定合适的对角半正定矩阵 , 对角正定矩阵 和 , 得到矩阵序列 和 以及对角半正定矩阵 , 设计最优跟踪控制器, 使得闭环系统状态 能够尽可能的跟踪任意参考输入 的变化, 同时尽可能减少不同控制回路之间的耦合影响, 使闭环系统达到最优性能.2 具有解耦性能的最优跟踪控制方法A 1=diag {A ii },B 1=diag {B ii }A 1B 1A B A 2=A −A 1,B 2=B −B 1,A 2B 2为了实现解耦控制, 首先令 , 即 和 均为对角矩阵, 其对角线元素分别等于 和 的主对角元素; 令 即 和 均为主对角元素为零的矩阵, 于是如式(7)所示, 将系统(1)分成2个部分, 第1部分无耦合特性, 第2部分可视为所有耦合干扰:A 2x k +B 2u k 受到二人零和博弈问题的启发, 将式(7)中的耦合干扰 看作可测干扰, 引入如下考虑耦合影响的性能指标:z k =W k x k +X k u k A 2x k +B 2u k P Q k R k M k W k X k k 式中, 作为可测干扰 的补偿项, 为半正定矩阵, 为时变半正定矩阵, 和 为时变对称矩阵, 和 为时变加权矩阵. 为了描述方便, 在不引起混淆的情况下, 后文将上述时变矩阵的下角标 省略.x r,k X M R R −X T MX :=¯R>0定理1. 考虑由式(1)以及参考轨迹 构成的最优跟踪控制问题. 对任意的矩阵 和 ,选择加权对称矩阵 满 足 , 则最小化式(8)的最优跟踪控制律为:S k ∈R n ×n V k ∈R n 式中, 和 分别根据下式反向迭代求解:证明. 根据最小值原理, 定义如下哈密顿函数:λk +1∈R n H k u k 式中, 是拉格朗日乘子向量函数. 根据极值条件, 求 对 的一阶偏导数:∂H k /∂u k =0令 , 得到最优跟踪控制律:∂2H k /∂u 2k =R −X TMX >0由于二阶偏导数 , 因此性能指标式(8)可以通过式(14)实现最小化.根据式(12), 得到状态方程和协态方程分别为:与文献[14]类似, 假设:将式(17)代入式(14), 可得:8 期富月等: 具有解耦性能的离散时间线性多变量系统最优跟踪控制1933u ∗k x k +1由式(18)可知, 依赖未来时刻的状态 , 考虑到物理可实现性, 将式(1)代入式(18), 可得:对式(19)进行移项整理后即得到式(9).将式(1)、式 (14)和式(17)同时代入式(16),得到:利用待定系数法, 对比式(20)与式(17), 得到式(10) ~ (11)反向迭代方程.x 0在初始状态 已知的情况下, 最优跟踪问题的边界条件为:将式(21)与式(17)进行对比,可得式(10) ~ (11)中的边界条件. □Λ1R X M W 推论1. 对任意对角正定矩阵 , 加权对称矩阵 , 以及任意可逆矩阵 , 加权矩阵 和 按照式(22) ~ (23)选择:Λ2则对任意的对角正定矩阵 , 当最优跟踪控制律为:S k ∈R n ×n 式中, 矩阵 满足:V k ∈R n 向量 满足:P Q加权矩阵 为对角半正定矩阵, 加权对角矩阵 满足:不仅能够实现闭环系统的解耦, 而且使跟踪误差渐近收敛到零.证明. 观察式(10), 为了实现解耦控制, 首先令:根据式(28)和式(29), 可得到式(22)和式(23). 将式(22) ~ (23)代入式(10), 得到:Λ2令式(30)等号右边后3项之和等于任意的对角正定矩阵 , 即:R Λ1Λ2Q R Λ1Λ2S k 由于 为自由选择参数矩阵, 因此当给定对角正定矩阵 和 以后, 对任意对角半正定矩阵 ,总可以找到 使上式成立. 将式(31)代入式(30)可得式(25), 因此对任意对角正定矩阵 和 , 都能保证 是对角矩阵. 将式(22) ~ (23)分别代入式(9)和式(11), 可得式(24)和式(26).将式(24)代入式(1)中, 得到闭环系统方程:A 1、Λ1、Λ2、Q S k 由于矩阵 和 都是对角矩阵,从式(25) ~ (26)不难发现闭环系统式(32)已经实现了解耦.Q x r,k x k 将选择对角半正定矩阵 , 使得系统在稳态时,从 到 的传递函数矩阵为单位阵, 实现状态完全跟踪参考输入.z 将式(26)进行 变换后, 通过移项整理可得:z 将式(33)代入式(32)后, 再进行 变换, 移项整理可得:z →1x r,k x k Q 由极值条件可知, 对于阶跃的参考输入, 稳态时 , 因此稳态时要想保证从 到 的传递函数矩阵为单位阵, 那么对角半正定矩阵 需要满足:1934自 动 化 学 报48 卷Q Q 进一步化简整理得到式(27). 由式(27)易知, 加权矩阵 是对角的. 下面证明由式(27)给出的对角矩阵 是半正定矩阵.Q 、Λ1、A 1S k +1Q =diag {Q ii },Λ1=diag {Λii 1},A 1=diag {A ii 1}S k +1=diag {S iik +1}由于式(27)中涉及到的矩阵 和 都是对角矩阵, 令 和.下面针对2种情况进行讨论:A ii 1≤11) 当 时, 由式(27)可知:1−A ii 1≥00<Λii 1/(Λii 1+S iik +1)<1Q ii ≥0由于 , , 因此式(36)等号右边2个括号内的元素都大于等于零, 故 成立.Aii 1>12) 当 时, 由式(27)可知:Q ii Q ii <0式中, 一定大于等于零. 若 , 则有:1+S ii k +1/Λii 1>A ii 11+A ii 1S ii k +1/(Λii1+S ii k +1)<A ii 1.1+A ii 1S ii k +1/(Λii 1+S ii k +1)<A ii11+S ii k +1/Λii 1<A ii 1,Q ii ≥0.a ) 并且 由于 等价于 因此矛盾, 故 1+S ii k +1/Λii 1<A ii 11+A ii 1S ii k +1/(Λii1+S ii k +1)>A ii 1.1+A ii 1S ii k +1/(Λii 1+S ii k +1)>A ii11+S ii k +1/Λii 1>A ii1,Q ii ≥0.b ) 并且 由于 等价于 因此矛盾, 故 Λ1Λ2Q 综上所述, 对于任意的正定对角矩阵 和 ,由式(27)计算得到的加权矩阵 总是对角半正定矩阵. □X M 注1. 当系统本身是解耦的(或耦合性较弱)时,可以选择矩阵 或者 为零矩阵, 此时具有解耦性能的最优跟踪控制器退化为传统的LQT 控制器.P 、Λ1Λ2P 、R Q Λ1Λ2P P Λ1Λ2P Λ2Λ1注2. 本文方法中, 矩阵 和 的选择准则与传统的LQT 方法中 和 的选择准则相同. 也就是说, 当固定 和 时, 越大系统末态跟踪误差越小; 当固定 和 时, 越大系统跟踪误差越小; 当固定 和 时, 越大系统控制能量消耗越小.B 注3.当矩阵 不是方阵时, 若对于离散时间线性多变量系统:CC T CB 当矩阵 和 为可逆矩阵时, 则上述系统可以转化为:此时, 该系统与式(1)具有相同的形式, 采用本文所提方法, 即可实现输入到输出之间的解耦.注4. 本文所研究的对象是确定的, 当系统参数存在匹配和不匹配不确定性时, 一方面可以借鉴补偿控制的思想, 将参数不确定性造成的影响视为一种干扰, 通过干扰观测器, 神经网络或者模糊推理系统等对其进行观测或估计, 并在控制器中加入补偿项予以消除, 详见附录A; 另一方面可以借鉴保性能控制的思想, 设计具有解耦性能的保性能跟踪控制器.算法1. 具有解耦性能的最优跟踪控制算法P Λi (i =1,2)步骤1. 选择加权矩阵 和 ;S k Q 步骤2. 根据式(25)计算得到 , 将结果代入(27)式得到对角加权矩阵 ;V k 步骤3. 根据式(26)计算 ;S k V k P Λi (i =1,2)步骤4.将 和 序列, 加权矩阵 和 代入式(24)和式(32), 得到系统的控制输入和状态.3 仿真实验为了验证本文方法的有效性和优越性, 本节分别采用本文方法和传统LQT 方法进行对比仿真实验, 并对仿真结果进行了比较和分析. 在仿真过程中,采用相同的评估函数来比较2种方法的最优性能,考虑如下两输入−两状态的离散时间线性系统:x k =[x 1(k ),x 2(k )]Tu k =[u 1(k ),u 2(k )]T 式中, 是系统状态向量,是控制输入向量, 对应的系数矩阵和控制矩阵分别为:易知该系统的相对增益矩阵为:根据Bristol-Shinskey 衡量指标, 可以判断出该系统是一个强耦合系统.x r,k =本实验的目的是针对离散时间线性系统(39),设计最优跟踪控制器, 使得最大跟踪误差不超过参考输入幅值的10%, 其中参考输入信号为 8 期富月等: 具有解耦性能的离散时间线性多变量系统最优跟踪控制1935[x r 1(k ),x r 2(k )]T =[2sgn (sin k ),2sgn (cos k )]T .3.1 采用本文所提方法的仿真实验为了实现控制目标, 首先选择加权矩阵:S k Q V k 将上述加权矩阵代入式(25)和式(27), 得到各时刻 和 的值, 然后将结果代入式(26)得到 , 最后将结果代入式(24)和式(32), 得到如图1和图2所示的状态和控制输入曲线. 从图1可以看出, 采用本文所提方法后, 在实现了控制目标的基础上, 不仅消除了不同控制回路之间的耦合影响, 还使得系统在稳态时能完全跟踪参考输入.图 1 本文所提方法系统状态输出Fig. 1 Output curves by using the methodproposed in this paper3.2 采用LQT 方法的仿真实验为了验证本文所提方法的优越性, 采用传统LQT 方法, 选择两组参数对式(39)进行仿真实验.令加权矩阵:R =10−50010−5当加权矩阵 时, 得到如图3和图4所示的状态和控制输入曲线. 结合图1 和图3可以看出, 采用这组参数下的传统LQT 方法, 虽然实现了控制目标, 但是当某一参考输入发生变化时,其他回路状态会受到较大的影响, 而且系统达到稳态后还会存在一定的跟踪误差. 由图2和图4可以看出, 传统LQT 方法与本文所提方法相比, 虽然控制输入变化规律相同, 但是在参考输入发生变化时,明显需要更大的控制输入.R =[10−60010−6]当加权矩阵 时, 得到如图5和图6所示的状态和控制输入曲线. 从图5可以看出,采用这组参数下的传统LQT 方法实现了控制目标,当某一参考输入变化时, 其他回路状态不再受到影响, 但是从图4和图6可以看出, 在这组参数下的传统LQT 控制器的控制输入明显增大.3.3 两种控制方法的整体性能比较为了比较2种不同控制策略的最优性能, 定义如下评估函数:σ=1σ=2式中, 表示本文所提方法的最优性能, 表示传统LQT方法的最优性能, 之后绘制两种方法的评估函数曲线.当采用第1组参数下的传统LQT 方法时, 得到如图7所示的最优性能曲线. 从图7可以看出,本文所提方法的最优性能明显小于传统LQT 方法的最优性能. 由图1 ~ 4 可以看出, 对于传统LQT图 2 本文所提方法控制输入Fig. 2 Input curves by using the methodproposed in this paper−−x 1/x r 1−−x 2/x r 2t /s图 3 传统LQT 方法系统状态输出Fig. 3 Output curves by using the conventionalLQT method1936自 动 化 学 报48 卷方法即使付出了更大的控制输入, 当某一参考输入发生变化时, 其他回路状态还是会受到较大的影响,系统达到稳态时也不能实现完全跟踪; 本文所提方法通过选择合适的加权矩阵, 在较小的控制输入下,不仅消除了系统不同控制回路之间的耦合作用, 还使得系统状态在稳态时总能完全跟踪参考输入, 故具有解耦性能的最优跟踪方法会得到更小的最优性能.图 7 第1组参数下, 2种策略的最优性能比较Fig. 7 Comparison of the performance under thefirst set of parameters当采用第2组参数下的传统LQT 方法时, 得到如图8所示的最优性能曲线. 从图8可以看出,本文方法的最优性能仍然小于传统LQT 方法的最优性能. 由 图1和图5可以看出, 虽然两种控制策略的跟踪效果相同, 但由图2和图6可知, 此时传统LQT 方法需要更大的控制输入, 导致最优性能变得更大.图 8 第2组参数下, 2种策略的最优性能比较Fig. 8 Comparison of the performance under the secondset of parameters4 结束语针对一类具有强耦合特性的离散时间线性多变量系统, 本文提出了一种具有解耦性能的最优跟踪控制方法. 该方法受到二人零和博弈思想的启发,图 4 传统LQT 方法控制输入Fig. 4 Input curves by using the conventionalLQT method图 5 传统LQT 方法系统状态输出Fig. 5 Output curves by using the conventionalLQT method图 6 传统LQT 方法控制输入Fig. 6 Input curves by using the conventionalLQT method8 期富月等: 具有解耦性能的离散时间线性多变量系统最优跟踪控制1937设计了新的性能指标, 并根据极小值原理最小化该性能指标, 得到最优跟踪控制律. 按照本文给出的加权矩阵选择办法, 消除了不同控制回路之间的耦合影响, 使得系统的状态输出可以跟踪任意期望轨迹. 仿真实验表明, 当离散时间线性多变量系统具有强耦合特性时, 该方法可以获得更小的控制输入和更小的最优性能, 并且系统达到稳态时, 系统输出总能完全跟踪参考输入. 在接下来的研究中, 将进一步考虑系统模型部分未知的情况, 将自适应动态规划算法与本文解耦控制方法相结合, 设计近似最优跟踪控制器, 进而实现具有模型不确定性和强耦合特性的线性多变量系统的最优跟踪控制.附录A 基于神经网络补偿的不确定系统最优跟踪控制方法简述:考虑如下具有匹配和不匹配参数不确定性的离散时间非线性系统[20]x k u k A B B d m (x k ,k )∈R n C u (x k ,k )∈R n 式中, 向量 和 以及矩阵 和 同式(1)所示;表示系统中满足匹配条件的不确定性, 表示不满足匹配条件的不确定性.首先, 根据式(A1)的线性标称系统(1)得到具有解耦性能的无干扰最优跟踪控制器, 即式(24), 并假设该控制器能保证与式(A1)组成的闭环系统的输入和状态信号有界. 令:其次, 将式(A1)中匹配不确定性项和不匹配不确定性项统一看做线性标称系统的不确定性项, 即令:则式(A1)简化为:最后, 设计如下基于神经网络补偿的最优跟踪控制器:ˆD(x k ,k )D (x k ,k )ˆD (x k ,k )=NN [ˆWk ,X k ],NN [·]X k ˆWk k W ∗式中, 为 的神经网络估计, 表示神经网络的结构, 为神经网络输入向量, 为 时刻理想权阵 的估计.为验证所提控制器(A7)的有效性, 本文进行了仿真实验. 考虑如下存在匹配和不匹配参数不确定性的离散时间非线性系统:x k u k A B 式中, 向量和 以及矩阵 和 同式(39)所示;K 1K 2X k =[Z 1,Z 2,···,Z 2499],Z i =[x T i ,i ]T ;D k =[E 1,E 2,···,E 2499],E i =x i +1−A x i −B u i ,i =···,首先, 根据式(A2)和式(A3)计算 和 , 得到具有解耦性能的无干扰最优跟踪控制器式(A4), 将其作用到式(A8),从而得到神经网络训练所需的输入数据和导师信号. 本次仿真实验中, 神经网络的输入数据 其中 导师信号 其中 1, 2, 2 499. 然后, 选择分别具有45个和10个隐层节点的双隐层前馈神经网络对不确定项进行估计, 其中节点传递函数为双曲正切函数tansig, 权值更新算法为Polak-Ribiere 修正算法.图A1为采用所提出的基于神经网络补偿的最优跟踪控制方法的状态跟踪曲线, 由图A1可以看出, 该方法不仅消除不同控制回路之间的耦合影响, 而且消除了不确定项对闭环系统的影响, 使得闭环系统的状态能够完全跟踪参考输入的变化.图 A1 基于神经网络补偿的不确定性系统状态跟踪曲线Fig. A1 Tracking curve of uncertain system based onneural network compensationReferencesTien L, Schaffer A. Robust adaptive tracking control based on state feedback controller with integrator terms for elastic joint robots with uncertain parameters. IEEE Transactions on Con-trol Systems Technology , 2018, 26(6): 2259−22671Qiu B, Wang G, Fan Y, Mu D, Sun X. Robust adaptive traject-ory linearization control for tracking control of surface vesselswith modeling uncertainties under input saturation. IEEE Ac-cess , 2018, 7: 5057−50702Chai R, Savvaris A, Tsourdos A, Chai S, Xia Y. Optimal track-ing guidance for aeroassisted spacecraft reconnaissance missionbased on receding horizon control. IEEE Transactions on Aerospace and Electronic Systems , 2018, 54(4): 1575−15883Fujimoto H, Kawamura A. Perfect tracking digital motion con-trol based on two-degree-of-freedom multi-rate feedforward con-trol. In: Proceedings of the International Workshop on Ad-vanced Motion Control. Coimbra, Portugal: IEEE, 1998.322−3274Fujimoto H, Hori Y, Kawamura A. Perfect tracking control based on multi-rate feedforward control with generalized sampling Periods. IEEE Transactions on Industrial Electronics ,51938自 动 化 学 报48 卷。

CWI is the National Research Institute for Mathematics and Computer Science. CWI is part of the Stichting Mathematisch Centrum (SMC), the Dutch foundation for promotion of mathematics and computer science and their applications. SMC is sponsored by the Netherlands Organization for Scientific Research (NWO). CWI is a member of ERCIM, the European Research Consortium for Informatics and Mathematics.
(WODES96), which workshop was held August 19-21, 1996 at Edinburgh, Scotland.
1 Introduction
This paper formulates and solves a problem of existence of communication channels between supervisors in decentralized control of discrete event systems (DES). In decentralized supervisory control of discrete event systems, two or more supervisors with di erent partial observations control a system. Existence of decentralized supervisors for a given speci cation has been studied in 2, 6]. In the design of decentralized control systems, communication channels between supervisors can often be incorporated. An example of such a channel is the common-channel signaling used in communication networks, see 7, Section 12-2]. For a given control task and an observation channel, a question is whether there is su cient information obtained through the channel for a supervisor to synthesize the given control task. The notion of observable languages 3] addresses this question. In the situation where the channel does not provide su cient information but there is another supervisor observing the same system through another channel, the problem might be overcome by communication from the other supervisor. A problem of existence of such a communication channel for resolving the ambiguity due to the insu ciency of the rst channel is formulated. A necessary and su cient condition is presented. As communication always comes at a cost, existence of `minimal' communication channels is also investigated. The paper is organized as follows. Section 2 contains the problem formulation. A necessary and su cient condition is presented in Section 3 and is illustrated by an example 1

discrete signal 控制-回复Discrete Signal Control: Understanding and ApplicationIntroduction:Discrete signal control refers to the process of utilizing discrete signals, which are signals that take on a limited number of values, in various control systems. These signals are characterized by their ability to be quantized and processed. In this article, we will delve into the world of discrete signal control, exploring its principles, techniques, and applications.1. What is a discrete signal?A discrete signal is a signal that is not continuous but rather characterized by distinct and separate values at specific points in time. Unlike continuous signals, which can take on an infinite number of values within a specific range, discrete signals only assume specific discrete values at specific points in time.Discrete signals are typically represented as sequences of numbers, with each number corresponding to a specific point in time. Thesesequences can either be finite or infinite, depending on the length of the signal.2. Why use discrete signals in control systems?Discrete signals offer several advantages in control systems:a. Simplified representation: Quantizing signals into discrete values allows for simpler representation and storage. It reduces the complexity of signal processing and makes it easier to implement control algorithms.b. Time synchronization: Discrete signals enable accurate synchronization between control systems and the signals they receive. With discrete values representing specific points in time, control systems can react precisely and consistently.c. Noise immunity: Discrete signals can tolerate noise better than continuous signals. By quantizing the signal into discrete values, small fluctuations in the signal can be filtered out, leading to improved system performance and stability.3. Techniques for controlling discrete signals:a. Digital control: Digital control is a popular technique for controlling discrete signals. It involves converting the analog signals received by sensors into digital form for processing and manipulation by microprocessors or digital signal processors (DSPs). Digital control allows for precise and flexible control algorithms, making it ideal for complex control systems.b. Sampling and quantization: Sampling is the process of converting continuous signals into discrete signals by periodically measuring the signal at specific points in time. Quantization, on the other hand, involves assigning discrete values to the measured samples. Together, sampling and quantization allow for the representation and analysis of continuous signals using discrete values.c. Discrete-time control systems: Discrete-time control systems use discrete signals to model and control dynamic systems. These systems operate on sampled signals that are processed at fixed intervals. Discrete-time control systems are widely utilized in various fields, including robotics, automation, andtelecommunications.4. Applications of discrete signal control:a. Robotics: Discrete signal control is extensively used in robotics applications. Robots rely on discrete signals to perceive their environment, process information, and execute commands. Using discrete signals, robots can interact with their surroundings and perform tasks with accuracy and precision.b. Process control: Discrete signal control is crucial in process control systems, where precise control over physical variables is essential for maintaining safety and efficiency. Discrete signals enable the monitoring and adjustment of critical process variables such as temperature, pressure, and flow rate.c. Communication systems: Discrete signals play a vital role in communication systems, including digital signal processing, data transmission, and error detection and correction. By converting continuous signals into discrete signals, information can be encoded, transmitted, and decoded accurately and reliably.Conclusion:Discrete signal control is a fundamental aspect of modern control systems. By leveraging the advantages of discrete signals, such as simplified representation, time synchronization, and noise immunity, control engineers can design and implement robust control algorithms. From robotics to process control and communication systems, discrete signal control finds applications in various fields, revolutionizing the way we interact with technology and enhancing the overall performance and efficiency of control systems.。

自动化英语自动化英语专业英语词汇表O-Z 1objective function 目标函数observability index 可观测指数observable canonical form 可观测规范型on-line assistance 在线帮助on-off control 通断控制open loop pole 开环极点operational research model 运筹学模型optic fiber tachometer 光纤式转速表optimal trajectory 最优轨迹optimization technique 最优化技术orbital rendezvous 轨道交会orbit gyrocompass 轨道陀螺罗盘orbit perturbation 轨道摄动order parameter 序参数orientation control 定向控制originator 始发站oscillating period 振荡周期output prediction method 输出预估法oval wheel flowmeter 椭圆齿轮流量计overall design 总体设计overdamping 过阻尼overlapping decomposition 交叠分解2Padeapproximation 帕德近似photoelectric tachometric ransduPareto optimality 帕雷托最优性assive attitude stabilization 被动姿态稳定path repeatability 路径可重复性pattern primitive 模式基元PR (pattern recognition) 模式识别P control 比例控制器peak time 峰值时间penalty function method 罚函数法perceptron 感知器periodic duty 周期工作制perturbation theory 摄动理论pessimistic value 悲观值phase locus 相轨迹phase trajectory 相轨迹phase lead 相位超前cer 光电式转速传感器phrase-structure grammar 短句结构文法process-oriented simulation 面向过程的仿真production budget 生产预算production rule 产生式规则profit forecast 利润预测PERT (program evaluation and review technique) 计划评审技术program set station 程序设定操作器proportional control 比例控制proportional plus derivative controller 比例微分控制器protocol engineering 协议工程prototype 原型pseudo random sequence 伪随机序列pseudo-rate-increment control 伪速率增量控制pulse duration 脉冲持续时间pulse frequency modulation control system 脉冲调频控制系统pulse width modulation control system 脉冲调宽控制系统PWM inverter 脉宽调制逆变器pushdown automaton 下推自动机QC (quality control) 质量管理quadratic performance index 二次型性能指标qualitative physical model 定性物理模型quantized noise 量化噪声quasilinear characteristics 准线性特性queuing theory 排队论resistance thermometer sensor 热电阻resolution principle 归结原理resource allocation 资源分配response curve 响应曲线return difference matrix 回差矩阵reverberation 回响reversible electric drive 可逆电气传动revolute robot 关节型机器人revolution speed transducer 转速传感器rewriting rule 重写规则rigid spacecraft dynamics 刚性航天动力学risk decision 风险分析robotics 机器人学robot programming language 机器人编程语言robust control 鲁棒控制robustness 鲁棒性roll gap measuring instrument 辊缝测量仪root locus 根轨迹roots flowmeter 腰轮流量计rotameter 浮子流量计，转子流量计rotary eccentric plug valve 偏心旋转阀rotary motion valve 角行程阀rotating transformer 旋转变压器Routh approximation method 劳思近似判据routing problem 路径问题sampled-data control system 采样控制系统sampling control system 采样控制系统saturation characteristics 饱和特性scalar Lyapunov function 标量李雅普诺夫函数SCARA (selective compliance assembly robot arm) 平面关节型机器人scenario analysis method 情景分析法scene analysis 物景分析s-domain s 域self-operated controller 自力式控制器self-organizing system 自组织系统self-reproducing system 自繁殖系统self-tuning control 自校正控制semantic network 语义网络semi-physical simulation 半实物仿真sensing element 敏感元件sensitivity analysis 灵敏度分析sensory control 感觉控制sequential decomposition 顺序分解sequential least squares estimation 序贯最小二乘估计servo control 伺服控制，随动控制servomotor 伺服马达settling time 过渡时间sextant 六分仪short term planning 短期计划short time horizon coordination 短时程协调signal detection and estimation 信号检测和估计signal reconstruction 信号重构similarity 相似性simulated interrupt 仿真中断simulation block diagram 仿真框图simulation experiment 仿真实验simulation velocity 仿真速度simulator 仿真器single axle table 单轴转台single degree of freedom gyro 单自由度陀螺single level process 单级过程single value nonlinearity 单值非线性singular attractor 奇异吸引子telemetry 遥测teleological system 目的系统单词解释例句或者词组音标abbrivation 缩写[?,bri:vi`eifn]absolute 绝对absolute output 绝对最大输出[`aebs?lu:t]actuator 执行器against 对比I/O signals against PC CPU allocate 分配allocate the user area in buffer memory [`ael?keit]alter 改变even if the output characteristic is altered by changing offset/gain setting [`o:t?]ambient 环境周围ambient operating temperature [`aembi?nt]analog 模拟analog output [`aen?log]analysis 分析the collection an and analysis of data [?`nael?sis]applicable 可用the applicable CPU for the module assign 分配The teacher has assigned each of us a holiday task. assign I/O number [?`sain]back up battey 备用电池barcode reader/ID 条形码阅读器base unit 主基板baud 波特[bo:d]beforehand 事先binary 二进制12 bit binary [`bain?ri]buffer memory 缓冲存储器bus 总线case 外壳do not remove the module's print board from the case characteristic 特征I/Ocharacterristic [`kaer?kt?`ristik]check 校验the data link status canbe checked child-station 子站common terminal 公共端compatible 兼容compatible with the MODBUS protocol compound 混合compound system communication [`compaund]condensation 结露condition 条件condition setting conductive 导电conductive metal picees configuration 组态system configuration configure 组态confirm 确认how to confirm the operation of the moduleconsumption 消耗current consumption [k?n`s^mp∫n]content 目录control level 控制级convenient 方便more convenient and easy-to-use conventional 传统which conventionaly has been used [k?n,venfen'ael?ti] conversion 转换Analog-Digital conversion module converter 转换器[c?n`v?:t?] conveyor 传送conveyor line [c?n`vei?]corrosive 腐蚀corrosive gas [k?`r?usiv]countermeasure 对策countermeasure for mis-inpute cutoff 切断debug 调试is recommended before debugging dedicated 屏蔽cc-link dedicated cable dedicated 专用dedicated transmission protocoldefault value 缺省值define 解释阐明Offset value and gain value are defined as follow. [di`fain]design 设计design a system device level 现场级diagnosis 诊断diagnosis function [dai?g`n?usis]digital 数字digital inpute DINrail 导轨diverse 不同的各种各样的 a diverse application requirements [dai`v?:s]download 下载duplicate 完全一样[`dju:plik?t]dust 灰尘eliminate 免得[i`limineit]enterprise level 管理级[`ent?prais]erase 清除exceed 超出The number admitted must not exceed 200 [ik`si:d]execute 执行date link is executed using these parameters [`eksikju:t]expand 扩展can be eapanded up to 255networks faulty 故障站field bus 现场总线fix 固定flexibly 灵活的to support a variety systerm flexibly [`fleks?bli]flow 流量format 格式transmission format [`fo:maet]frame fuse 融丝graph 图标坐标图曲线图voltage output characterristic graph [gra:f]guaranteed 担保nomal operration cannot be guaranteed [,gaer?`ti:d] handle 处理hardware manual 硬件手册hint 提示programming hints humidity 湿度ambient operating humdlity individual 独立的inductance 电感inductance load initiate 实施发起can be initiate by a computer [i`nifieit]input 输入input point 输入点数install 安装instruction 指令the FROM instruction insulation 隔离form rubber provides good insulation [,insju`leifn]interface 接口[`int?feis]interlocking 互锁can be used for sequence program interlocking internalexternal 内部internal connection外部interrupt 中断excute an interrupt processinginvalid 无效error invalid station function magnetic 有磁性的magnetic fields [maeg`netik]main circuit 主回路[`s?:kit]malfunction 故障cause system malfunction mandatory 强制[`maed?t?ri]mantenance 维护maintenance costs are reduced [`meit?n?ns]manual 手册User' Manualmechanical 机械michanical life 机械寿命module 模块mount or remove the module [`modju:l]momentary power failure 瞬时断电monitor 监视mount 固定mount or remove the modulemultiple 多样mutiple remote i/o modulesnegative 负observation 观察[obz?`veifn]occupy 占用occupies 1 station [`okju:pai]occur 发生offline 离线offline test offset gain 偏置增益oil mist 油雾optical loop 光缆回路[`optik?l]optimum 最佳的optimum control [`optim?m]output 输出overall 总的overall distance overview 总揽communication overview parameter 参数path 路径transmission path per network perform 进行normal data link cannot be performedperformance specifations 性能规格peripheral 外围When utilizing peripheral device to assign I/Onumber. [p?`rif?ri?r?l]phase 相swith off all phases of the power supply [`feiz] photocouplerpoint 要点port 口Rs232c portpositive 正power line 电源线power on/off 上电断电precaution 注意事项precaution when configuing system print board 印刷电路板do not remove the module's print board from the case procedure 过程follow the procedureprograming interface 编程口protocol 协议protocol communication issues [`pr?ut?col]range 范围rated input voltage 额定输入电压ratio 比率[`reifi?u]recommend 建议is recommended before debuggingreduce 减少the number of steps in operation program can be reducedrefer to 参照refer to Chapter 6register 数据寄存器relay 继电器[`ri:lei]remote I/O 远程网络IO [ri`m?ut]reserved station 预留主站resin 树脂made of resin resistor 电阻resistor load 阻性负载terminating resistor [ri`zist?] resolution 分解，解析nMaximum resolution 最大分辨率[,rez?`lu:fn] restriction 限制no restriction [ri`strikfn]retry 从试scan 扫描link scanscrew 螺丝Teminal- block screwseamless network 无缝网络sequence programme 顺控程序serial communications module 串口模块series 系列Ans Series [`si?ri?s]servo 伺服short 短路signal 信号sink 漏极sink commenslot 槽soures 源极soures commenspecifications 特性input modules specifications stabilizedpower supply 稳压电源[`steib?laiz]standby master station 备用主站start up 起动status 状态data link status step drive 步进storage 存储storage area store 存储switch off 关断swith off all phases of the power supplyswith 开关table 表格transfer 传输transistor 晶体管transmission speed 传输速度transmit 传送data is transmitted in unchanged code triac 双端三相可控硅开关troubleshooting 故障处理unuseble 不可以使用upload 上传utilize 利用When utilizing peripheral device to assign I/O number. [`ju:t?laiz]verify 校验verify the set parameter contentsvoltage 电压high voltage [`v?ultidg]watchdog 看门狗width 范围it will vary in the width of [widθ]wire chips 线头do not let foreign matter such as wire chips ret inside the moduleshift knob 开关按钮press-button 按钮自控专业英语excited by 励磁field coils 励磁线圈air-gap flux distribution 气隙磁通分布direct axis 直轴armature coil 电枢线圈rotating commutator 旋转（整流子）换向器commutator-brush combination 换向器-电刷总线mechanical rectifier 机械式整流器armature m.m.f. wave 电枢磁势波Geometrical position 几何位置magnetic torque 电磁转矩spatial waveform 空间波形sinusoidal –density wave 正弦磁密度external armature circuit 电枢外电路instantaneous electric power 瞬时电功率instantaneous mechanical power 瞬时机械功率effects of saturation 饱和效应reluctance 磁阻power amplifier 功率放大器compound generator 复励发电机rheostat 变阻器self –excitation process 自励过程commutation condition 换向状况cumulatively compounded motor 积复励电动机operating condition 运行状态equivalent T –circuit T型等值电路rotor (stator) winding 转子（定子绕组）winding loss 绕组（铜）损耗prime motor 原动机active component 有功分量reactive component 无功分量electromagnetic torque 电磁转矩retarding torque 制动转矩inductive component 感性（无功）分量abscissa axis 横坐标induction generator 感应发电机synchronous generator 同步发电机automatic station 无人值守电站hydropower station 水电站process of self –excitation 自励过程auxiliary motor 辅助电动机technical specifications 技术条件voltage across the terminals 端电压steady –state condition 瞬态暂态reactive in respect to 相对….呈感性active in respect to 相对….呈阻性synchronous condenser 同步进相（调相）机coincide in phase with 与….同相synchronous reactance 同步电抗algebraic 代数的algorithmic 算法的1--master element主要元件，是指控制开关等元件。

Vol. 41, No. 10
ACTA AUTOMATICA SINICA
October, 2015
A Chebyshev-Gauss Pseudospectral Method for Solving Optimal Control Problems
TANG Xiao-Jun1 WEI Jian-Li2 CHEN Kai2
with the LG points, and are also called Fej´ er-2 or Filippi points[14] . The main contributions of this work are as follows. First, the barycentric Lagrange interpolation is substituted for the classic Lagrange interpolation in the state approximation due to its improved numerical stability and computational efficiency[15] . As a result, the numerical stability associated with the calculation of CG pseudospectral differential matrix is also improved. Second, a simple yet efficient method is presented to alleviate the numerical errors of state differential matrix using the trigonometric identity especially when the number of CG points is large. Third, the costate and constraint multiplier estimates for the proposed method are rigorously derived by comparing the discretized optimality conditions of an optimal control problem with the Karush-Kuhn-Tucker (KKT) conditions of the resulting nonlinear programming problem (NLP) from collocation. The rest of this paper is organized as follows. The scaled continuous-time optimal control problem is stated in Section 1. Section 2 presents the CGPM for solving optimal control problems, and the associated costate and constraint multiplier estimates are derived in detail in Section 3. Section 4 presents the simulation results on two benchmark examples. Finally, some concluding remarks are given in Section 5.

TREE 3: POWER MANAGEMENT 2Supervisors & Voltage Detectors Unique Strengths (So What)Broad Portfolio(It's likely we have your part)Small Packages: SOT-23 and SC-70 (Saves space)Industrial Standard Crosses (Replace high priced and poor delivery suppliers)Battery Management Unique Strengths (So What)Wide variety of charging solutions for Li-Ion batteries(We have the solution for you)Small SOT-23, MSOP, DFN and QFN packages (Saves space)DC-DC Converter (So What)Low-voltage operation (Saves Power)PFM/PWM Auto switch mode (PFM at low loads reduces current, saves power)Small SOT-23 packaging (Saves space)Step-down, Step-up (Efficiently increase or decrease voltage) Charge Pumps (So What)Low-voltage operation (Battery operation)Small SOT-23 packaging (Saves space)Step-down, Step-up (Efficiently increase or decrease voltage)Doubling & Inverting (Meets V OUT needs) Low-Frequency capable (Reduces EMI)Low-Current Operation (Saves power)LDO Unique Strengths (So What)Hundreds of voltages, currents, packages (We have a match for the need)0.5% V OUT accuracy (Fills precision need)Up to 1.5A output current(Able to power high load applications)Op Amp Unique Strengths (So What)Low current versus GBWP (Saves power)TC and MCP6XXX devices RR-I/O (Expands usable voltage range)MCP604X 1.4V operation(Two alkaline cells 90% used =1.8V)MCP644X, 450 nA operation (Use the batteries even longer)Comparators Unique Strengths (So What)Low current versus propagation delay (Saves power)Integrated Features (Saves space)1.8V and 1.4V operation (That stuff about the batteries)Programmable Gain Amplifier Unique Strengths (So What)MUX inputWide bandwidth (2 to 12 MHz) (Reduces demand on MCU I/O)System control of gain(Changes easier through software configurable hardware)TREE 5: LINEARTemperature Sensor Unique Strengths (So What)Wide variety of solutions: logic, voltage and digital output products(Multiple sensor needs met)Small packages (Saves space)Low operating current(Saves power, smaller supply)Field or factory programmable (Low cost vs. flexibility)Programmable hysteresis (Stop system cycling)Multi-drop capability (Great for large systems)Beta compensation (Compatible with processor substrate diodes)Resistance error correction (Compensates for measurement error from long PCB traces)Fan Controllers Unique Strengths (So What)Closed loop fan control (Adjust to meet target speed even on aging fans)Integrated temperature sensing (Consolidate thermal management)Multiple temperature measurements drive one fan (Consolidate thermal management)Built-in ramp rate control and spin up alogorithm (Quick time to market, lower acoustic noise)Ability to detect/predict failure of less expensive 2-wire fans (Saves system cost)Unique solutions for extending fan life and reducing acoustic noise(Less power, nuisance and long fan life)TREE 6: MIXED-SIGNALADC Unique Strengths (So What)Low current at max sampling rate (Saves power, system cost)Small SOT-23 and MSOP packages (Saves space)Up to 24-bit resolution(Ideal for precision sensitive designs)Differential & single ended inputs (Able to cover various design needs)Up to 6 ADC per device(Save board space, system cost)DAC Unique Strengths (So What)Low Supply Current (Saves power)Low DNL & INL (Better accuracy)Extended Temperature Range(Suitable for wide temperature applications)Digital Potentiometers Unique Strengths (So What)64/256 tap (6-bit to 8-bit resolution)(Sufficient resolution for most applications)Non-volatile Memory(Remembers last wiper setting on power up)WiperLock™ Technology(Locks NV memory setting-better than OTP)Small SOT-23 and 2 × 3 DFN packages (Saves space)Low CostMOSFET Drivers (So What)4.5V up to 30V Supply voltages (Fills many application needs)Up to 12A Peak output current(Able to meet demanding design needs)Outstanding robustness and latch-upi mmunity (Ours work when the others burn up)Low-FOM MOSFETs(Support high-efficency applications)TREE 4: POWER MANAGEMENT 3LIN Unique Strengths(So What)Compliant with LIN Bus Specs 1.3, 2.0, 2.1 andSAE J2602 (Allows for reliable interoperability)High EMI Low EME (Meets OEM requirements)On-board V REG available(Saves space, allows for MCU V CC flexibility)CAN Unique Strengths(So What)Simple SPI CAN controller is an easy way toadd CAN Ports (Short design cycles)High speed transceiver meets ISO-11898 (Drop inreplacement for industry standard transceivers)Low-cost, easy-to-use development tools(Tools easy to buy/use, quick design)I/O Expanders Unique Strengths(So What)Configurable inputs (interrupt configuration flexibility)Interrupt on pin change, or change fromregister default (interrupt source flexibility)Can disable automatic address incrementingwhen accessing the device(allows continual access to the port)The 16-bit devices can operate in 8-bit or 16-bitmode (easy to interface to 8-bit or 16-bit MCUs)IrDA Unique Strengths (So What)IrDA protocol handler embedded on chip(Complex design issue solved)Low cost developer's kit available to assistInfrared design-in (Quick design cycle)Small, cost-effective way of replacing serial links(No more wires)Enables system to wirelessly communicatewith PDA (Wireless connectivity solution) TREE 8: INTERFACEAnalog & InterfaceQuestion TreesAnalog & Interface Development ToolsDemonstration Boards, Evaluation Kits and AccessoriesAnalog & Interface LiteratureADM00313EV: MCP73830L 2 × 2 TDFN Evaluation BoardADM00352: MCP16301 High Voltage Buck Converter 600 mA Demonstration BoardADM00360: MCP16301 High Voltage Buck Coverter 300 mA D2PAK Demonstration BoardADM00427: MCP16323 Evaluation Board (Supports MCP16321 and MCP16322)ARD00386: MCP1640 12V/50 mA Two Cells Input Boost Converter Reference DesignMCP1252DM-BKLT: MCP1252 Charge Pump Backlight Demonstration BoardMCP1256/7/8/9EV: MCP1256/7/8/9 Charge Pump Evaluation BoardMCP1630RD-LIC1: MCP1630 Li-Ion Multi-Bay Battery Charger Reference DesignMCP1630DM-NMC1: MCP1630 NiMH Battery Charger Demonstration BoardMCP1640EV-SBC: MCP1640 Sync Boost Converter Evaluation BoardMCP1640RD-4ABC: MCP1640 Single Quad-A Battery Boost Converter Reference DesignMCP1650DM-LED1: MCP165X 3W White LED Demonstration BoardMCP1726EV: MCP1726 LDO Evaluation BoardMCP73831EV: MCP73831 Evaluation KitMCP7383XEV: MCP73837/8 AC/USB Dual Input Battery Charger Evaluation BoardMCP7383XRD-PPM: MCP7383X Li-Ion System Power Path Management Reference DesignMCP7384XEV: MCP7384X Li-Ion Battery Chager Evaluation BoardMCP73871EV: MCP73871 Load Sharing Li-Ion Battery Charger Evaluation BoardTC1016/17EV: TC1016/17 LDO Evaluation BoardVSUPEV: SOT-23-3 Voltage Supervisor Evaluation BoardPowerManagementThermalManagementMCP9700DM-PCTL: MCP9700 Thermal Sensor PICtail Demonstration BoardMCP9800DM-PCTL: MCP9800 Thermal Sensor PICtail Demonstration BoardTC72DM-PICTL: TC72 Digital Temperature Sensor PICtail Demonstration BoardTC74DEMO: TC74 Serial Daughter Thermal Sensor Demonstration BoardTC1047ADM-PCTL: TC1047A Temperature-to-Voltage Converter PICtail™ Demonstration BoardSerial GPIODM-KPLCD: GPIO Expander Keypad and LCD Demonstration BoardMCP23X17: MCP23X17 16-bit GPIO Expander Evaluation BoardInterface MCP2515DM-BM: MCP2515 CAN Bus Monitor Demonstration BoardMCP2515DM-PTPLS: MCP2515 PICtail™ Plus Daughter BoardMCP2515DM-PCTL: MCP2515 CAN Controller PICtail Demonstration BoardMCP215XDM: MCP215X/40 Data Logger Demonstration BoardMCP2140DM-TMPSNS: MCP2140 IrDA® Wireless Temp Demonstration BoardLinear ADM00375: MCP6H04 Evaluation BoardARD00354: MCP6N11 Wheatstone Bridge Reference DesignMCP651EV-VOS: MCP651 Input Offset Evaluation BoardMCP661DM-LD: MCP661 Line Driver Demo BoardMCP6S22DM-PCTL: MCP6S22 PGA PICtail Demonstration BoardMCP6S2XEV: MCP6S2X PGA Evaluation BoardMCP6SX2DM-PCTLPD: MCP6SX2 PGA Photodiode PICtail Demonstration BoardMCP6SX2DM-PCTLTH: MCP6SX2-PGA Thermistor PICtail Demonstration BoardMCP6V01RD-TCPL: MCP6V01 Thermocouple Auto-Zero Ref DesignMCP6XXXDM-FLTR: Active Filter Demo BoardPIC16F690DM-PCTLHS: Humidity Sensor PICtail Demonstration BoardMixed-Signal MCP3221 DM-PCTL: MCP3221 12-bit A/D PICtail Demonstration BoardMCP3421DM-BFG: MCP3421 Battery Fuel Gauge Demonstration BoardMCP3551DM-PCTL: MCP3551 PICtail Demonstration BoardMCP355XDM-TAS: MCP355X Tiny Application Sensor Demonstration BoardMCP355XDV-MS1: MCP3551 Sensor Demonstration BoardMCP402XEV: MCP402X Digital Potentiometer Evaluation BoardMCP4725EV: MCP4725, 12-bit Non-Volatile DAC Evaluation Board (Preferred One)MCP4725DM-PTPLS: MCP4725, 12-bit Non-Volatile DAC PICtail Demonstration BoardADM00398: MCP3911 ADC Evaluation Board for 16-bit MicrocontrollersCorporate Microchip Product Line Card - DS00890Brochures Analog and Interface Product Selector Guide - DS21060Low Cost Development Tools Solutions Guide - DS51560Analog and Interface Guide (Volume 1) - DS00924Analog and Interface Guide (Volume 2) - DS21975Cards Analog Highlights Card - DS21972Microchip Op Amp Discovery Card - DS21947Analog & Interface Question Trees - DS21728Mirochip SAR and Delta-Sigma ACD Discovery Card - DS22101Software Tools MAPS - Microchip Advanced Product SelectorAnalog & Interface Treelink Products PresentationDesign Guides Analog-to-Digital Converter Design Guide - DS21841Digital Potentiometers Design Guide - DS22017Programmable Gain Amplifiers (PGAs), Operational Amplifiersand Comparators Design Guide - DS21861Interface Products Design Guide - DS21883Signal Chain Design Guide - DS21825Power Solutions Design Guide - DS21913Temperature Sensor Design Guide - DS21895Voltage Supervisors Design Guide - DS51548DS21728JPowerManagementLDO & SwitchingRegulatorsCharge PumpDC/DC ConvertersPower MOSFETDriversPWM ControllersSystem SupervisorsVoltage DetectorsVoltage ReferencesLi-Ion/Li-PolymerBattery ChargersUSB Port PowerControllersMixed-SignalA/D ConverterFamiliesDigitalPotentiometersD/A ConvertersV/F and F/VConvertersEnergyMeasurement ICsCurrent/DC PowerMeasurement ICsInterfaceCAN PeripheralsInfraredPeripheralsLIN TransceiversSerial PeripheralsEthernet ControllersUSB PeripheralLinearOp AmpsInstrumentationAmpsProgrammableGain AmplifiersComparatorsSafety & SecurityPhotoelectricSmoke DetectorsIonization SmokeDetectorsIonization SmokeDetector Front EndsPiezoelectricHorn DriversThermalManagementTemperatureSensorsFan Control& HarwareManagementMotor DriveStepper and DC3Ф BrushlessDC Motor DriverTREE 7: MOTOR DRIVE Stepper Unique Strenghts(So What)Industrial standard footprint(Footprint compatible to industrial leaders)Perfect PIC® MCU companion chip(Solid field support)Micro-stepping ready(Enhanced performance)Integration protections(Simplify software development)3-Phase BLDC Unique Strengths(So What)Full-wave sinusoidal(Quiet operation, low mechanical vibration)Sensorless operation (Minimum externalcomponents, no software required)Thin form factor(Fits space concerned applications)Information subject to change. The Microchip name and logo, the Microchip logo, dsPIC, PIC are registered trademarks and MiWi, PICtail and ZENA are trademarks ofMicrochip Technology Incorporated in the U.S.A. and other countries. All other trademarks mentioned herein are property of their respective companies.© 2012, Microchip Technology Incorporated. All Rights Reserved.。

end effect endurance energizing energizing current envelope equal area criterion equal area method equal area stability criterion equipotential surface event logging event record events/fault or disturbance records excessive start time excitation reactance excitation system excitation winding excitation-loss relay exciter existing exit relay external devices external initiation extra high voltage system extremely inverse current relay
I ideal transformer identification IED immunity to eraledciatrtoesdtaetliecctdriosmchaagrngetic energy impedance impedance relay impedance earthed impedance grounded impulse voltage inductance induction motor inductive inductor industrial substations and co-generation infinite bus inhibition time initialize instantaneous instantaneous instantaneous power instantaneous phase overcurrent instantaneous trip instantaneous trip instrument transformer insulated insulating property insulating string insulating transformer insulation insulation level insulator integrate

De nition 1. Let a system be de ned by a quintuple X ; T ; U ; ; A, where X denotes the conguration set, T an ordered time set, U a set of acceptable input symbols possibly depending on the con guration, a set of acceptable input words, and A is a state transition map A : T X ! X . Denote At;! x = At; !; x, with composition by concatenation Ax1 ; a2 ; t1 Ax0 ; a1 ; t0 = AAx0 ; a1 ; t0 ; a2 ; t1 .
1 Work partially supported through grants ASI ARS-99-
170 and MURST RAMSETEow such bounds can be made small at will by re nig quantization su ciently. More recently, some attention has been focused on quantized control systems as speci c models of hierarchically organized systems with interaction between continuous dynamics and logic Wong and Brockett 1999; Elia and Mitter 1999. In these papers, quantization of inputs is regarded as a fundamental characteristic of systems where the resources for implementing the control scheme are limited, such as e.g. when communications between the plant and the controller can only happen through a nite capacity channel. As a consequence of taking such viewpoint, the focal point of research is to understand how to quantize the control system best in some suitable sense, rather than assessing robustness of design with respect to quantization. In their papers, both Wong and Brockett 1999 and Elia and Mitter 1999 focus on the stabilization problem. Authors of the latter paper provide a result on the optimal coarsest quantization for asymptotically stabi-

2-dimensional space3D mapabstractaccess dataAccessibilityaccuracyacquisitionad-hocadjacencyadventaerial photographsAge of dataagglomerationaggregateairborneAlbers Equal-Area Conic projection (ALBER alignalphabeticalphanumericalphanumericalalternativealternativealtitudeameliorateanalogue mapsancillaryANDannotationanomalousapexapproachappropriatearcarc snap tolerancearealAreal coverageARPA abbr.Advanced Research Projects Agen arrangementarrayartificial intelligenceArtificial Neural Networks (ANN) aspatialaspectassembleassociated attributeattributeattribute dataautocorrelationautomated scanningazimuthazimuthalbar chartbiasbinary encodingblock codingBoolean algebrabottombottom leftboundbreak linebufferbuilt-incamouflagecardinalcartesian coordinate system cartographycatchmentcellcensuscentroidcentroid-to-centroidCGI (Common Gateway Interface) chain codingchainscharged couple devices (ccd) children (node)choropleth mapclass librariesclassesclustercodecohesivelycoilcollinearcolumncompactcompasscompass bearingcomplete spatial randomness (CSR) componentcompositecomposite keysconcavityconcentricconceptual modelconceptuallyconduitConformalconformal projectionconic projectionconnectivityconservativeconsortiumcontainmentcontiguitycontinuouscontourcontour layercontrol pointsconventionconvertcorecorrelogramcorrespondencecorridorCostcost density fieldcost-benefit analysis (CBA)cost-effectivecouplingcovariancecoveragecoveragecriteriacriteriacriterioncross-hairscrosshatchcross-sectioncumbersomecustomizationcutcylindrical projectiondangledangle lengthdangling nodedash lineDATdata base management systems (DBMS) data combinationdata conversiondata definition language (DDL)data dictionarydata independencedata integritydata itemdata maintenancedata manipulationData manipulation and query language data miningdata modeldata representationdata tabledata typedatabasedateDBAdebris flowdebugdecadedecibeldecision analysisdecision makingdecomposededicateddeductiveDelaunay criterionDelaunay triangulationdelete(erase)delineatedemarcationdemographicdemonstratedenominatorDensity of observationderivativedetectabledevisediagonaldictatedigital elevation model (DEM)digital terrain model (DTM) digitizedigitizedigitizerdigitizing errorsdigitizing tablediscrepancydiscretediscretedisparitydispersiondisruptiondissecteddisseminatedissolvedistance decay functionDistributed Computingdividedomaindot chartdraftdragdrum scannersdummy nodedynamic modelingeasy-to-useecologyelicitingeliminateellipsoidellipticityelongationencapsulationencloseencodeentity relationship modelingentity tableentryenvisageepsilonequal area projectionequidistant projectionerraticerror detection & correctionError Maperror varianceessenceet al.EuclideanEuclidean 2-spaceexpected frequencies of occurrences explicitexponentialextendexternal and internal boundaries external tablefacetfacilityfacility managementfashionFAT (file allocation table)faultyfeaturefeaturefeedbackfidelityfieldfield investigationfield sports enthusiastfields modelfigurefile structurefillingfinenessfixed zoom infixed zoom outflat-bed scannerflexibilityforefrontframe-by framefreefrom nodefrom scratchfulfillfunction callsfuzzyFuzzy set theorygantrygenericgeocodinggeocomputationgeodesygeographic entitygeographic processgeographic referencegeographic spacegeographic/spatial information geographical featuresgeometricgeometric primitive geoprocessinggeoreferencegeo-relational geosciences geospatialgeo-spatial analysis geo-statisticalGiven that GNOMONIC projection grain tolerance graticulegrey scalegridhand-drawnhand-heldhandicaphandlehand-written header recordheftyheterogeneity heterogeneous heuristichierarchical hierarchicalhill shading homogeneoushosthouseholdshuehumichurdlehydrographyhyper-linkedi.e.Ideal Point Method identicalidentifiable identification identifyilluminateimageimpedanceimpedanceimplementimplementimplicationimplicitin excess of…in respect ofin terms ofin-betweeninbuiltinconsistencyincorporationindigenousinformation integration infrastructureinherentinheritanceinlandinstanceinstantiationintegerintegrateinteractioninteractiveinteractiveinternet protocol suite Internet interoperabilityinterpolateinterpolationinterrogateintersectintersectionIntersectionInterval Estimation Method intuitiveintuitiveinvariantinventoryinvertedirreconcilableirreversibleis adjacent tois completely withinis contained iniso-iso-linesisopleth mapiterativejunctionkeyframekrigingKriginglaglanduse categorylatitudelatitude coordinatelavalayerlayersleaseleast-cost path analysisleftlegendlegendlegendlength-metriclie inlightweightlikewiselimitationLine modelline segmentsLineage (=history)lineamentlinearline-followinglitho-unitlocal and wide area network logarithmiclogicallogicallongitudelongitude coordinatemacro languagemacro-like languagemacrosmainstreammanagerialmanual digitizingmany-to-one relationMap scalemarshalmaskmatricesmatrixmeasured frequencies of occurrences measurementmedialMercatorMercator projectionmergemergemeridiansmetadatameta-datametadatamethodologymetric spaceminimum cost pathmirrormis-representmixed pixelmodelingmodularmonochromaticmonolithicmonopolymorphologicalmosaicmovemoving averagemuiticriteria decision making (MCDM) multispectralmutually exclusivemyopicnadirnatureneatlynecessitatenestednetworknetwork analysisnetwork database structurenetwork modelnodenodenode snap tolerancenon-numerical (character)non-spatialnon-spatial dataNormal formsnorth arrowNOTnovicenumber of significant digit numeric charactersnumericalnumericalobject-based modelobjectiveobject-orientedobject-oriented databaseobstacleomni- a.on the basis ofOnline Analytical Processing (OLAP) on-screen digitizingoperandoperatoroptimization algorithmORorderorganizational schemeoriginorthogonalORTHOGRAPHIC projectionortho-imageout ofoutcomeoutgrowthoutsetovaloverdueoverheadoverlapoverlayoverlay operationovershootovershootspackagepairwisepanpanelparadigmparent (node)patchpath findingpatternpatternpattern recognitionperceptionperspectivepertain phenomenological photogrammetric photogrammetryphysical relationships pie chartpilotpitpixelplanarplanar Euclidean space planar projection platformplotterplotterplottingplug-inpocketpoint entitiespointerpoint-modepointspolar coordinates polishingpolygonpolylinepolymorphism precautionsprecisionpre-designed predeterminepreferences pregeographic space Primary and Foreign keys primary keyprocess-orientedprofileprogramming tools projectionprojectionproprietaryprototypeproximalProximitypseudo nodepseudo-bufferpuckpuckpuckPythagorasquadquadrantquadtreequadtree tessellationqualifyqualitativequantitativequantitativequantizequasi-metricradar imageradii bufferrangelandrank order aggregation method ranking methodrasterRaster data modelraster scannerRaster Spatial Data Modelrating methodrational database structureready-madeready-to-runreal-timerecordrecreationrectangular coordinates rectificationredundantreference gridreflexivereflexive nearest neighbors (RNN) regimeregisterregular patternrelationrelationalrelational algebra operators relational databaseRelational joinsrelational model relevancereliefreliefremarkremote sensingremote sensingremote sensingremotely-sensed repositoryreproducible resemblanceresembleresemplingreshaperesideresizeresolutionresolutionrespondentretrievalretrievalretrievalretrieveridgerightrobustrootRoot Mean Square (RMS) rotateroundaboutroundingrowrow and column number run-length codingrun-length encoded saddle pointsalientsamplesanitarysatellite imagesscalablescalescanscannerscannerscannerscarcescarcityscenarioschemascriptscrubsecurityselectselectionself-descriptiveself-documentedsemanticsemanticsemi-automatedsemi-major axessemi-metricsemi-minor axessemivariancesemi-variogram modelsemi-varogramsensorsequencesetshiftsillsimultaneous equations simultaneouslysinusoidalskeletonslide-show-stylesliverslope angleslope aspectslope convexitysnapsnapsocio-demographic socioeconomicspagettiSpatial Autocorrelation Function spatial correlationspatial dataspatial data model for GIS spatial databaseSpatial Decision Support Systems spatial dependencespatial entityspatial modelspatial relationshipspatial relationshipsspatial statisticsspatial-temporalspecificspectralspherical spacespheroidsplined textsplitstakeholdersstand alonestandard errorstandard operationsstate-of-the-artstaticSTEREOGRAPHIC projection STEREOGRAPHIC projection stereoplotterstorage spacestovepipestratifiedstream-modestrideStructured Query Language(SQL) strung outsubdivisionsubroutinesubtractionsuitesupercedesuperimposesurrogatesurveysurveysurveying field data susceptiblesymbolsymbolsymmetrytaggingtailoredtake into account of … tangencytapetastefullyTelnettentativeterminologyterraceterritorytessellatedtextureThe Equidistant Conic projection (EQUIDIS The Lambert Conic Conformal projection (L thematicthematic mapthemeThiessen mapthird-partythresholdthroughputthrust faulttictiertiletime-consumingto nodetolerancetonetopographic maptopographytopologicaltopological dimensiontopological objectstopological structuretopologically structured data set topologytopologytrade offtrade-offTransaction Processing Systems (TPS) transformationtransposetremendousTriangulated Irregular Network (TIN) trimtrue-direction projectiontupleunbiasednessuncertaintyunchartedundershootsunionunionupupdateupper- mosturban renewaluser-friendlyutilityutility functionvaguevalidityvarianceVariogramvectorvector spatial data model vendorverbalversusvertexvetorizationviablevice versavice versaview of databaseview-onlyvirtualvirtual realityvisibility analysisvisualvisualizationvitalVoronoi Tesselationvrticeswatershedweedweed toleranceweighted summation method whilstwithin a distance ofXORzoom inzoom out三维地图摘要，提取，抽象访问数据可获取性准确，准确度 （与真值的接近程度）获得，获得物，取得特别邻接性出现,到来航片数据年龄聚集聚集，集合空运的, （源自）航空的,空中的艾伯特等面积圆锥投影匹配，调准，校直字母的字母数字的字母数字混合编制的替换方案替代的海拔，高度改善,改良,改进模拟地图，这里指纸质地图辅助的和注解不规则的，异常的顶点方法适合于…弧段弧捕捉容限来自一个地区的、 面状的面状覆盖范围(美国国防部)高级研究计划署排列，布置数组，阵列人工智能人工神经网络非空间的方面， 方向， 方位， 相位，面貌采集，获取关联属性属性属性数据自动扫描方位角，方位，地平经度方位角的条状图偏差二进制编码分块编码布尔代数下左下角给…划界断裂线缓冲区分析内置的伪装主要的，重要的，基本的笛卡儿坐标系制图、制图学流域，集水区像元，单元人口普查质心质心到质心的公共网关接口链式编码链电荷耦合器件子节点地区分布图类库类群编码内聚地线圈在同一直线上的列压缩、压紧罗盘， 圆规， 范围 v.包围方位角完全空间随机性组成部分复合的、混合的复合码凹度，凹陷同心的概念模型概念上地管道,导管,沟渠,泉水,喷泉保形（保角）的等角投影圆锥投影连通性保守的，守旧的社团,协会,联盟包含关系相邻性连续的轮廓,等高线,等值线等高线层控制点习俗，惯例，公约，协定转换核心相关图符合，对应走廊, 通路费用花费密度域，路径权值成本效益分析有成本效益的，划算的结合协方差面层，图层覆盖，覆盖范围标准，要求标准，判据，条件标准，判据，条件十字丝以交叉线作出阴影截面麻烦的用户定制剪切圆柱投影悬挂悬挂长度悬挂的节点点划线数据文件的扩展名数据库管理系统数据合并数据变换数据定义语言数据字典与数据的无关数据的完整性数据项数据维护数据操作数据操作和查询语言数据挖掘数据模型数据表示法数据表数据类型数据库日期数据库管理员泥石流调试十年，十，十年期分贝决策分析决策，判定分解专用的推论的，演绎的狄拉尼准则狄拉尼三角形删除描绘划分人口统计学的说明分母，命名者观测密度引出的，派生的可察觉的发明，想出对角线的，斜的要求数字高程模型数字地形模型数字化数字化数字化仪数字化误差数字化板，数字化桌差异，矛盾不连续的，离散的不连续的，离散的不一致性分散，离差中断，分裂，瓦解，破坏切开的，分割的发散，发布分解距离衰减函数分布式计算分割域点状图草稿，起草拖拽滚筒式扫描仪伪节点动态建模容易使用的生态学导出消除椭球椭圆率伸长包装，封装围绕编码实体关系建模实体表进入,登记想像,设想,正视,面对希腊文的第五个字母ε等积投影等距投影不稳定的误差检查和修正误差图误差离散，误差方差本质，本体，精华以及其他人，等人欧几里得的，欧几里得几何学的欧几里得二维空间期望发生频率明显的指数的延伸内外边界外部表格(多面体的)面工具设备管理样子，方式文件分配表有过失的，不完善的（地理）要素，特征要素反馈诚实，逼真度，重现精度字段现场调查户外运动发烧友场模型外形， 数字，文件结构填充精细度以固定比例放大以固定比例缩小平板式扫描仪弹性，适应性，机动性，挠性最前沿逐帧无…的起始节点从底层完成，实现函数调用模糊的模糊集合论构台,桶架, 跨轨信号架通用的地理编码地理计算大地测量地理实体地理（数据处理）过程地理参考地理空间地理信息，空间信息地理要素几何的，几何学的几何图元地理（数据）处理过程地理坐标参考地理关系的地球科学地理空间的地学空间分析地质统计学的假设心射切面投影颗粒容差地图网格灰度栅格,格网手绘的手持的障碍，难点处置、处理手写的头记录重的,强健的异质性异构的启发式的层次层次的山坡（体）阴影图均匀的、均质的主机家庭色调腐植的困难，阻碍水文地理学超链接的即，换言之，也就是理想点法相同的可识别的、标识识别阐明图像，影像全电阻，阻抗阻抗实现，履行履行,实现牵连,暗示隐含的超过…关于根据…在中间的嵌入的，内藏的不一致性，矛盾性结合，组成公司(或社团)内在的,本土的信息集成基础设施固有的继承，遗传， 遗产内陆的实例，例子实例，个例化整数综合，结合相互作用交互式的交互式的协议组互操作性内插插值询问相交交集、逻辑的乘交区间估值法直觉的直觉的不变量存储，存量反向的，倒转的，倒置的互相对立的不能撤回的，不能取消的相邻完全包含于包含于相等的，相同的线族等值线图迭代的接合,汇接点主帧克里金内插法克里金法标签，标记间隙，迟滞量土地利用类别纬度 （B）纬度坐标熔岩，火山岩图层图层出租，租用最佳路径分析左图例图例图例长度量测在于小型的同样地限制，限度，局限线模型线段谱系，来源容貌，线性构造线性的，长度的，直线的线跟踪的岩性单元局域和广域网对数的逻辑的逻辑的经度 （L）经度坐标宏语言类宏语言宏主流管理人的， 管理的手工数字化多对一的关系地图比例尺排列,集合掩膜matrix 的复数矩阵实测发生频率量测中间的合并墨卡托墨卡托投影法合并合并，融合子午线元数据元数据，也可写为 metadata元数据方法学，方法论度量空间最佳路径镜像错误表示混合像素建模模块化的单色的,单频整体的垄断， 专利权， 专卖形态学镶嵌, 镶嵌体移动移动平均数多准则决策分析多谱线的,多谱段的相互排斥的短视，没有远见的最低点，天底，深渊，最底点本性，性质整洁地成为必要嵌套的、巢状的网络网络分析网状数据库结构网络模型节点节点节点捕捉容限非数值的(字符)非空间的非空间数据范式指北针非新手，初学者有效位数数字字符数值的数值的基于对象的模型客观的，目标的面向对象的模型面向对象的数据库阻碍全能的，全部的以…为基础在线分析处理屏幕数字化运算对象，操作数算子，算符，操作人员优化算法或次，次序组织方案原点，起源，由来直角的，直交的正射投影正射影像缺少结果长出，派出，结果，副产物开头 ，开端卵形的，椭圆形的迟到的管理费用重叠，叠加叠加叠置运算超出过头线软件包成对(双)地，两个两个地平移面,板范例、父节点补钉，碎片，斑点路径搜索图案式样,图案, 模式模式识别感觉，概念，理解力透视图从属， 有关， 适合现象学的，现象的摄影测量的摄影测量物理关系饼图导航洼坑象素平面的平面欧几里得空间平面投影平台绘图仪绘图仪绘图插件便携式，袖珍式，小型的点实体指针点方式点数，分数极坐标抛光多边形多义线，折线多形性，多态现象预防措施精确， 精度（多次测量结果之间的敛散程度） 预定义的，预设计的预定、预先偏好先地理空间主外键主码面向处理的纵剖面、轮廓编程工具投影投影所有权,业主原型，典型最接近的,近侧的接近性假的, 伪的伪节点缓冲区查询（数字化仪）鼠标数字化鼠标鼠标毕达哥拉斯方庭，四方院子象限，四分仪四叉树四叉树方格限定，使合格定性的量的定量的、数量的使量子化准量测雷达影像以固定半径建立缓冲区牧场，放牧地等级次序集合法等级评定法栅格栅格数据模型栅格扫描仪栅格空间数据模型分数评定法关系数据结构现成的随需随运行的实时记录娱乐平面坐标纠正多余的，过剩的， 冗余的参考网格自反的自反最近邻体制，状态，方式配准规则模式关系关系关系代数运算符关系数据库关系连接中肯，关联，适宜，适当地势起伏，减轻地势的起伏评论，谈论，谈到遥感遥感遥感遥感的知识库可再产生的相似，相似性，相貌相似类似，像重取样调整形状居住， 驻扎调整大小分辨率分辨率回答者，提取检索检索检索高压脊右稳健的根部均方根旋转迂回的舍入的、凑整的行行和列的编号游程长度编码行程编码鞍点显著的，突出的，跳跃的，凸出的样品, 标本, 样本卫生状况卫星影像可升级的比例尺扫描扫描仪扫描仪扫描仪缺乏，不足情节模式脚本，过程（文件）灌木安全， 安全性选择选择自定义的自编程的语义的，语义学的语义的，语义学的半自动化长半轴半量测短半轴半方差半变差模型半变差图传感器次序集合、集、组改变， 移动基石,岩床联立方程同时地正弦的骨骼，骨架滑动显示模式裂片坡度坡向坡的凸凹性咬合捕捉社会人口统计学的社会经济学的意大利面条自相关函数空间相互关系空间数据GIS的空间数据模型 空间数据库空间决策支持系统空间依赖性空间实体空间模型空间关系空间关系空间统计时空的具体的，特殊的光谱的球空间球状体，回转椭圆体曲线排列文字分割股票持有者单机标准误差，均方差标准操作最新的静态的极射赤面投影极射赤面投影立体测图仪存储空间火炉的烟囱形成阶层的流方式步幅，进展，进步结构化查询语言被串起的细分，再分子程序相减组， 套件，程序组，代替,取代叠加，叠印代理，代用品，代理人测量测量，测量学野外测量数据免受...... 影响的（地图）符号符号，记号对称性给...... 贴上标签剪裁讲究的考虑…接触，相切胶带、带子风流地，高雅地远程登录试验性的术语台地，露台领域，领地，地区棋盘格的，镶嵌的花样的纹理等距圆锥投影兰伯特保形圆锥射影专题的专题图主题，图层泰森图第三方的阈值生产量，生产能力，吞吐量逆冲断层地理控制点等级,一排,一层,平铺费时间的终止节点允许(误差)、容差、容限、限差色调地形图地形学拓扑的拓扑维数拓扑对象拓扑结构建立了拓扑结构的数据集拓扑关系拓扑交替换位，交替使用，卖掉交换，协定，交易事务处理系统变换，转换转置，颠倒顺序巨大的不规则三角网修整真方向投影元组不偏性不确定性海图上未标明的，未知的欠头线合并并集、逻辑的和上升级最上面的城市改造用户友好的效用， 实用，公用事业效用函数含糊的效力，正确，有效性方差，变差变量(变化记录)图矢量矢量空间数据模型经销商言语的， 动词的对，与…相对顶点 （单数）矢量化可实行的，可行的反之亦然反之亦然数据库的表示只读的虚拟的虚拟现实通视性分析视觉的可视化，使看得见的重大的沃伦网格顶点（复数）分水岭杂草，野草 v.除草，铲除清除容限度加权求和法同时在 ...... 距离内异或放大缩小。

tf
1 2 u (t) dt. 2
(3)
. . .
. .
.
. . . . . . . .
. . . . . . . .
. . . . . . . . .
. .
. .
. .
. .
.
Fei-Yue, Wang (CASIA)
Optimal Control
最优控制介绍
4 / 58
欧拉-拉格朗日方程
∂g d ∂g (x(t), x ˙ (t), t) − [ (x(t), x ˙ (t), t)] = 0. ∂x dt ∂ x ˙ 考察 ∆J = 0 的必要条件：驻值条件 需假定 g 可微 在最优解 x 连续可微时成立
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
(12)
. . . . . . .
Fei-Yue, Wang (CASIA)
Optimal Control
最优控制介绍
9 / 58
HJB 方程和 PMP、经典变分的关系
Optimal Control
最优控制介绍
10 / 58
最优控制问题的数学方法
变分法与庞特里亚金极小值原理：求解常微分方程 动态规划：求解偏微分方程 上述方法主要考察单被控对象的最优控制问题
. . .
. .
.
. . . . . . . .
. . . . . . . .
. . . . . . . . .
Optimal Control
最优控制介绍
8 / 58
Hamilton-Jacobi-Bellman 方程 2/2