
一、函数与几何综合的压轴题
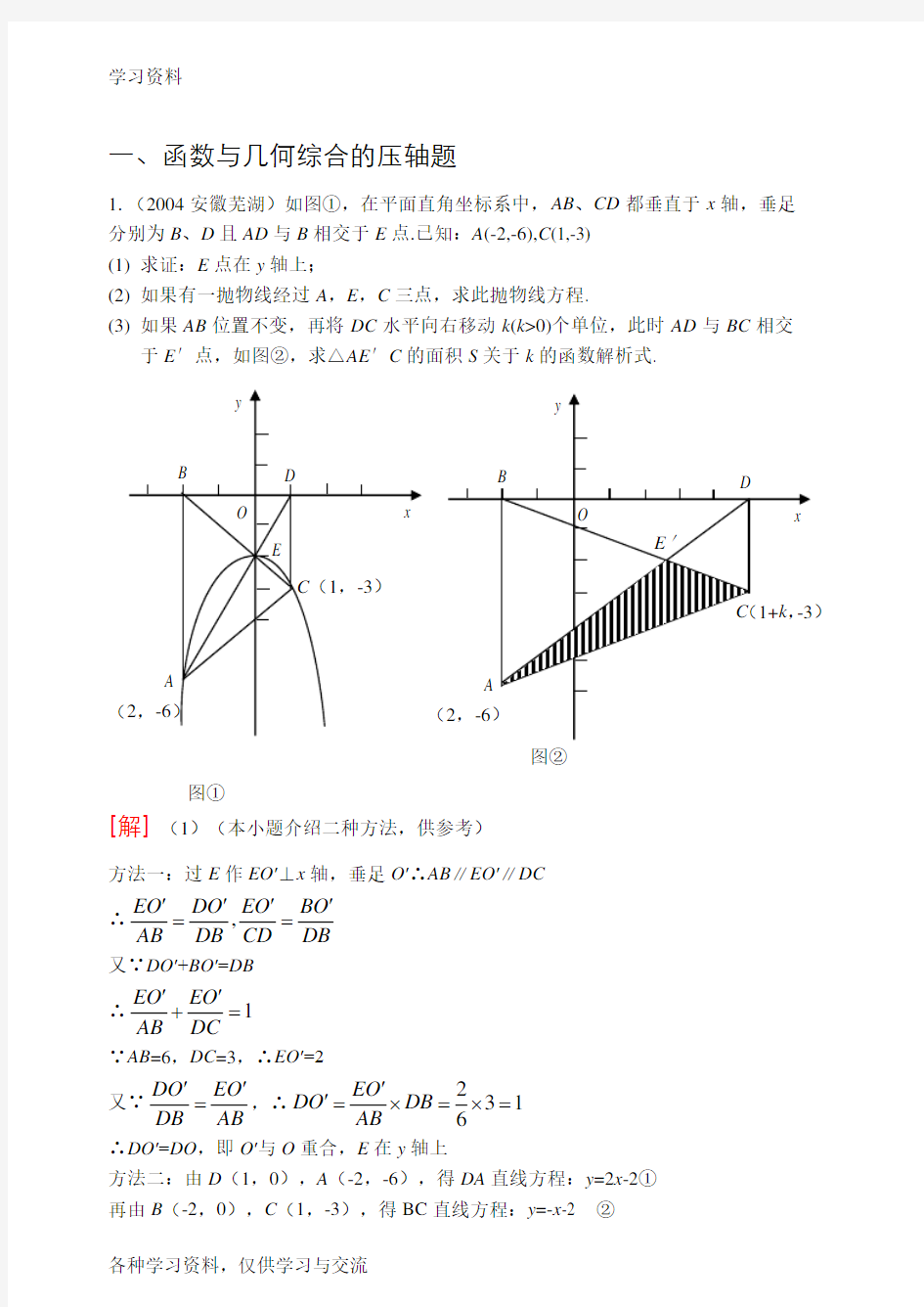
1.(2004安徽芜湖)如图①,在平面直角坐标系中,AB 、CD 都垂直于x 轴,垂足分别为B 、D 且AD 与B 相交于E 点.已知:A (-2,-6),C (1,-3) (1) 求证:E 点在y 轴上;
(2) 如果有一抛物线经过A ,E ,C 三点,求此抛物线方程.
(3) 如果AB 位置不变,再将DC 水平向右移动k (k >0)个单位,此时AD 与BC 相交
于E ′点,如图②,求△AE ′C 的面积S 关于k 的函数解析式.
[解] (1)(本小题介绍二种方法,供参考)
方法一:过E 作EO ′⊥x 轴,垂足O ′∴AB ∥EO ′∥DC ∴
,EO DO EO BO AB DB CD DB ''''
==
又∵DO ′+BO ′=DB ∴
1EO EO AB DC
''
+= ∵AB =6,DC =3,∴EO ′=2 又∵
DO EO DB AB ''=,∴2
316
EO DO DB AB ''=?=?= ∴DO ′=DO ,即O ′与O 重合,E 在y 轴上
方法二:由D (1,0),A (-2,-6),得DA 直线方程:y =2x -2① 再由B (-2,0),C (1,-3),得BC 直线方程:y =-x -2 ② 图①
图②
联立①②得0
2x y =??=-?
∴E 点坐标(0,-2),即E 点在y 轴上
(2)设抛物线的方程y =ax 2+bx +c (a ≠0)过A (-2,-6),C (1,-3)
E (0,-2)三点,得方程组426
32a b c a b c c -+=-??
++=-??=-?
解得a =-1,b =0,c =-2 ∴抛物线方程y =-x 2-2
(3)(本小题给出三种方法,供参考)
由(1)当DC 水平向右平移k 后,过AD 与BC 的交点E ′作E ′F ⊥x 轴垂足为F 。
同(1)可得:1E F E F
AB DC
''+= 得:E ′F =2
方法一:又∵E ′F ∥AB E F DF AB DB '?=
,∴1
3DF DB = S △AE ′C = S △ADC - S △E ′DC =1112
2223
DC DB DC DF DC DB ?-?=?
=1
3
DC DB ?=DB=3+k S=3+k 为所求函数解析式
方法二:∵ BA ∥DC ,∴S △BCA =S △BDA ∴S △AE ′C = S △BDE ′()11
32322
BD E F k k '=
?=+?=+ ∴S =3+k 为所求函数解析式.
证法三:S △DE ′C ∶S △AE ′C =DE ′∶AE ′=DC ∶AB =1∶2
同理:S △DE ′C ∶S △DE ′B =1∶2,又∵S △DE ′C ∶S △ABE ′=DC 2∶AB 2=1∶4 ∴()221
3992
AE C ABCD S S AB CD BD k '?=
=?+?=+梯形 ∴S =3+k 为所求函数解析式.
2. (2004广东茂名)已知:如图,在直线坐标系中,以点M (1,0)为圆心、直径AC 为22的圆与y 轴交于A 、D 两点.
(1)求点A 的坐标;
(2)设过点A 的直线y =x +b 与x 轴交于点B.探究:直线AB 是否⊙M 的切线?并对你的结论加以证明;
(3)连接BC ,记△ABC 的外接圆面积为S 1、⊙M 面积为S 2,若
4
21h
S S =,抛物线 y =ax 2+bx +c 经过B 、M 两点,且它的顶点到x 轴的距离为h .求这条抛物线的解析式.
[解](1)解:由已知AM =2,OM =1,
在Rt △AOM 中,AO =
122=-OM AM ,
∴点A 的坐标为A (0,1)
(2)证:∵直线y =x +b 过点A (0,1)∴1=0+b 即b =1 ∴y =x +1 令y =0则x =-1 ∴B (—1,0), AB =2112
2
2
2
=
+=+AO BO
在△ABM 中,AB =2,AM =2,BM =2
222224)2()2(BM AM AB ==+=+
∴△ABM 是直角三角形,∠BAM =90° ∴直线AB 是⊙M 的切线
(3)解法一:由⑵得∠BAC =90°,AB =2,AC =22, ∴BC =
10)22()2(2222=+=+AC AB
∵∠BAC =90° ∴△ABC 的外接圆的直径为BC ,
∴π
ππ2
5)210()2(221=?=?=BC S
而πππ2)222()2(2
22=?=?=AC S
421h S S =Θ,
5,4225
=∴=h h 即 ππ 设经过点B (—1,0)、M (1,0
y =a (+1)(x -1),(a≠0)即y =ax 2-a ,∴-a =±5,∴a =±5 ∴抛物线的解析式为y =5x 2-5或y =-5x 2+5 解法二:(接上) 求得∴h =5
由已知所求抛物线经过点B (—1,0)、M (1、0),则抛物
线的对称轴是y 轴,由题意得抛物线的顶点坐标为(0,±5)
∴抛物线的解析式为y =a (x -0)2±5
又B (-1,0)、M (1,0)在抛物线上,∴a±5=0, a =±5
∴抛物线的解析式为 y =5x 2-5或y =-5x 2+5 解法三:(接上)求得∴h =5
因为抛物线的方程为y =ax 2+bx +c (a≠0)
由已知得???
??-===?????==?????????
±=-=+-=++5
055c 0b 5544002c b a a a
b a
c c b a c b a 或 =- 解得
∴抛物线的解析式为 y =5x 2-5或y =-5x 2+5.
3.(2004湖北荆门)如图,在直角坐标系中,以点P (1,-1)为圆心,2为半径作圆,交x 轴于A 、B 两点,抛物线)0(2
>++=a c bx ax y 过点A 、B ,且顶点C 在⊙P 上. (1)求⊙P 上劣弧⌒
AB 的长; (2)求抛物线的解析式;
(3)在抛物线上是否存在一点D ,使线段OC 与PD
若不存在,请说明理由.
[解] (1)如图,连结PB ,过P 作PM ⊥x 轴,垂足为
在Rt △PMB 中,PB=2,PM=1, ∴∠MPB
=60°,∴∠APB =120° ⌒
AB 的长=
3
42180120π
π=
???? (2)在Rt △PMB 中,PB=2,PM=1,则MB =MA =3. 又OM=1,∴A (1-3,0),B (1+3,0), 由抛物线及圆的对称性得知点C 在直线PM 上, 则C(1,-3).
点A 、B 、C 在抛物线上,则
???
????++=-+-+-=++++=c b a c b a c b a 3)31()31(0)31()31(02
2 解之得?????-=-==2
21c b a ∴抛物线解析式为222--=x x y
(3)假设存在点D ,使OC 与PD 互相平分,则四边形OPCD 为平行四边形,且PC ∥OD.
又PC ∥y 轴,∴点D 在y 轴上,∴OD =2,即D (0,-2).
又点D (0,-2)在抛物线222
--=x x y 上,故存在点D (0,-2), 使线段OC 与PD 互相平分.
4.(2004湖北襄樊)如图,在平面直角坐标系内,Rt △ABC 的直角顶点C (0
在y 轴的正半轴上,A 、B 是x 轴上是两点,且OA ∶OB =3∶1,以OA 、OB 为直径
的圆分别交AC 于点E ,交BC 于点F .直线EF 交OC 于点Q . (1)求过A 、B 、C 三点的抛物线的解析式;
(2)请猜想:直线EF 与两圆有怎样的位置关系?并证明你的猜想.
(3)在△AOC 中,设点M 是AC 边上的一个动点,过M 作MN ∥AB 交OC 于点N .试问:在x 轴上是否存在点P ,使得△PMN 是一个以MN 为一直角边的等腰直角三角形?若存在,求出P
[解] (1)在Rt △ABC 中,OC ⊥AB ,
∴△AOC ≌△COB .
∴OC 2=OA ·
OB . ∵OA ∶
OB =3∶1,C ∴23.OB OB =g
∴OB =1.∴OA =3. ∴A (-3,0),B (1,0).
设抛物线的解析式为2
.y ax bx c =++
则930,0,a b c a b c c ?-+=?++=??
=?
解之,得a b c ?=?
?
?
=???=??
∴经过A 、B 、C
三点的抛物线的解析式为2y x =- (2)EF 与⊙O 1、⊙O 2都相切.
证明:连结O 1E 、OE 、OF .
∵∠ECF =∠AEO =∠BFO =90°
, ∴四边形EOFC 为矩形. ∴QE =QO . ∴∠1=∠2.
∵∠3=∠4,∠2+∠4=90°, ∴EF 与⊙O 1相切. 同理:EF 理⊙O 2相切.
(3)作MP ⊥OA 于P ,设MN =a ,由题意可得MP =MN =a . ∵MN ∥OA ,
∴△CMN ∽△CAO .
∴
.MN CN
AO CO =
∴3a =
解之,得a =
此时,四边形OPMN 是正方形.
∴3
.2
MN OP ==
∴3
(,0).2
P -
考虑到四边形PMNO 此时为正方形,
∴点P 在原点时仍可满足△PNN 是以MN 为一直角边的等腰直角三角形.
故x 轴上存在点P 使得△PMN 是一个以MN
为一直角边的等腰直角三角形且
3
(,0)2
P -
或(0,0).P 5.(2004湖北宜昌)如图,已知点A(0,1)、C(4,3)、E(415,8
23),P 是以AC 为
对角线的矩形ABCD 内部(不在各边上)的—个动点,点D 在y 轴,抛物线y =ax 2+b x +1以P 为顶点.
(1)说明点A 、C 、E 在一条条直线上;
(2)能否判断抛物线y =ax 2+b x +1的开口方向?请说明理由;
(3)设抛物线y =ax 2+b x +1与x 轴有交点F 、G(F 在G 的左侧),△GAO 与△FAO 的面积差为3,且这条抛物线与线段AE 有两个不同的交点.这时能确定a 、b 的值吗?若能,请求出a 、b 的值;若不能,请确定a 、b 的取值范围. (本题图形仅供分析参考用)
[解] (1)由题意,A(0,1)、C(4,3)确定的解析式为:y=2
1x 将点E 的坐标E(415,823)代入y=21x +1中,左边=8
23,
右边=
21×415+1=8
23
, ∵左边=右边,∴点E 在直线y=2
1
x +1上,即点A 、C 、E 在一条直线上.
(2)解法一:由于动点P 在矩形ABCD 内部,∴点P 的纵坐标大于点A 的纵坐标,而点A 与点P 都在抛物线上,且P 为顶点,∴这条抛物线有最高点,抛物线的开口向下
解法二:∵抛物线
y=ax 2+b x +c
的顶点P 的纵坐标为a
b a 442
—,且P 在矩形ABCD 内
部,∴1<a b a 442—<3,由1<1—a b 42得—a
b 42
>0,∴a <0,∴抛物线的开口向下.
(3)连接GA 、FA ,∵S △GAO —S △FAO =3 ∴
21GO ·AO —2
1
FO ·AO=3 ∵OA=1,∴GO —FO=6. 设F (x 1,0)、G (x 2,0),则x 1、x 2为方程ax 2+b x +c=0的两个根,且x 1<x 2,又∵a <0,∴x 1·x 2=
a
1
<0,∴x 1<0<x 2, ∴GO= x 2,FO= —x 1,∴x 2—(—x 1)=6, 即x 2+x 1=6,∵x 2+x 1= —a b ∴—a
b
=6, ∴b= —6a ,
∴抛物线解析式为:y=ax 2—6ax +1, 其顶点P 的坐标为
由方程组 y=ax 2—6ax +1 y=
2
1
x +1 得:ax 2—(6a +
2
1
)x =0 (3,1—9a ), ∵顶点P 在矩形ABCD 内部, ∴1<1—9a <3, ∴—9
2
<a <0.
∴x =0或x =
a a 21
6
=6+a
21. 当x =0时,即抛物线与线段AE 交于点A ,而这条抛物线与线段AE 有两个不同的交 点,则有:0<6+
a 21≤415,解得:—9
2
≤a <—121 综合得:—
92<a <—121 ∵b= —6a ,∴21<b <3
4
6.(2004湖南长沙)已知两点O(0,0)、B(0,2),⊙A 过点B 且与x 轴分别相交于点O 、C ,⊙A 被y 轴分成段两圆弧,其弧长之比为3∶1,直线l 与⊙A 切于点O ,抛物线的顶点在直线l 上运动. (1)求⊙A 的半径;
(2)若抛物线经过O 、C 两点,求抛物线的解析式;
(3)过l 上一点P 的直线与⊙A 交于C 、E 两点,且PC =CE ,求点E 的坐标; (4)若抛物线与x 轴分别相交于C 、F 两点,其顶点P 的横坐标为m ,求△PEC 的面积关于m 的函数解析式.
[解] (1)由弧长之比为3∶1,可得∠BAO =90o
再由AB =AO =r ,且OB =2,得r = 2 (2)⊙A 的切线l 过原点,可设l 为y =kx
任取l 上一点(b ,kb ),由l 与y 轴夹角为45o可得: b =-kb 或b =kb ,得k =-1或k =1, ∴直线l
的解析式为y =-x 或y =x
又由r ,易得C(2,0)或C(-2,0)
由此可设抛物线解析式为y =ax (x -2)或y =ax (x +2) 再把顶点坐标代入l 的解析式中得a =1 ∴抛物线为y =x 2-2x 或y =x 2+2x
……6分
(3)当l 的解析式为y =-x 时,由P 在l 上,可设P(m ,-m)(m >0) 过P 作PP′⊥x 轴于P′,∴OP′=|m|,PP′=|-m|,∴OP =2m 2,
又由切割线定理可得:OP 2=PC·PE,且PC =CE ,得PC =PE =m =PP′7分
∴C 与P′为同一点,即PE ⊥x 轴于C ,∴m =-2,E(-2,2)…8分 同理,当l 的解析式为y =x 时,m =-2,E(-2,2)
(4)若C(2,0),此时l 为y =-x ,∵P 与点O 、点C 不重合,∴m≠0且m≠2, 当m <0时,FC =2(2-m),高为|y p |即为-m , ∴S =
22(2)()
22
m m m m --=-
同理当0<m <2时,S =-m 2+2m ;当m >2时,S =m 2-2m ;
∴S =22
2(02)2(02)m m m m m m m ?-<>?-+<
2(20)
2(20)
m m m m m m m ?+<->?---<
7.(2006江苏连云港)如图,直线4+=kx y 与函数)0,0(>>=m x x
m
y 的图像交于A 、B 两点,且与x 、y 轴分别交于C 、D 两点.
(1)若COD ?的面积是AOB ?的面积的2倍,求k 与m 之间的函数关系式; (2)在(1)的条件下,是否存在k 和m ,使得以AB 为直径的圆经过点)0,2(P .若存在,求出k 和m 的值;若不存在,请说明理由.
[解](1)设),(11y x A ,),(22y x B (其中2121,y y x x ><),
由AOB COD S S ??=2,得)(2BOD AOD COD S S S ???-= ∴
2
1·OC ·2=OD (21·OD ·-1y 21
·OD ·2y ),
(21y OC =又4=OC ,∴8)
(221=-y y ,即84)(21
221=-+y y y y , 由x
m
y =可得y m x =,代入4+=kx y 可得042=--km y y ①
∴421=+y y ,km y y -=?21,
∴8416=+km ,即m
k 2
-
=. 又方程①的判别式08416>=+=?km ,
∴所求的函数关系式为m
k 2
-
=)0(>m . (2)假设存在k ,m ,使得以AB 为直径的圆经过点)0,2(P
则BP AP ⊥,过A 、B 分别作x 轴的垂线,垂足分别为M ∵MAP ∠与BPN ∠都与APM ∠互余,∴MAP ∠ BPN ∠=. ∴Rt MAP ?∽Rt NPB ?,∴
NB
MP
PN AM =
. ∴212122y x x y -=-,∴0)2)(2(2121=+--y y x x , ∴0)2)(2(212
1=+--y y y m y m , 即0)(4)(222121212=+++-y y y y y y m m ②
由(1)知421=+y y ,221=?y y ,代入②得01282=+-m m ,
∴2=m 或6,又m k 2-=,∴???-==12k m 或??
???-==316k m , ∴存在k ,m ,使得以AB 为直径的圆经过点)0,2(P ,且???-==12k m 或??
??
?-==316k m . 8.(2004江苏镇江)已知抛物线2
(5)5(0)y mx m x m =--->与x 轴交于两点
1(,0)A x 、2(,0)B x 12()x x <,与y 轴交于点C ,且AB =6.
(1)求抛物线和直线BC 的解析式.
(2)在给定的直角坐标系中,画抛物线和直线BC . (3)若P e 过A 、B 、C 三点,求P e 的半径.
(4)抛物线上是否存在点M ,过点M 作MN x ⊥轴于点N ,使MBN ?被直线BC
分成面积比为13:的两部分?若存在,请求出点M 的坐标;若不存在,请说明理由.
[解](1)由题意得:12122155
,, 6.m x x x x x x m m
--+=
?=-= 2
2
1212520
()436,36,m x x x x m m -??+-=+
= ???
解得1251,.7
m m ==-
经检验m =1,∴抛物线的解析式为:2
4y x =+或:由2
(5)50mx m x ---=得,1x =或
5x m
-=
0,m Q >
5
16, 1.m m
-∴-
=∴= ∴抛物线的解析式为24 5.y x x =+-
由2
450x x +-=得125, 1.x x =-=
∴A (-5,0),B (1,0),C (0,-5). 设直线BC 的解析式为,y kx b =+ 则5,5,
0. 5.
b b k b k =-=-??∴?
?
+==?? ∴直线BC 的解析式为5 5.y x =- (2)图象略.
(3)法一:在Rt AOC D 中,5,45.OA OC OAC ==∴∠=?Q
90BPC ∴∠=?.
又BC == ∴P e
的半径PB == 法二:
由题意,圆心P 在AB 的中垂线上,即在抛物线2
45y x x =+-的对称轴直线2
x =-上,设P (-2,-h )(h >0),
连结PB 、PC ,则2
2
2
2
2
2(12),(5)2PB h PC h =++=-+,
由22
PB PC =,即2
2
2
2
(12)(5)2h h ++=-+,解得h =2.
(2,2),P P ∴--∴e 的半径PB ==.
法三:
延长CP 交P e 于点F .
CF Q 为P e 的直径,90.CAF COB ∴∠=∠=? 又,.ABC AFC ACF OCB ∠=∠∴D ~D ,.CF AC AC BC
CF BC OC OC
?∴
=∴=
又AC ==5,CO BC ===∞
5
CF ∴=
=
P ∴e
(4)设MN 交直线BC 于点E ,点M 的坐标为2
(,45),t t t +-则点E 的坐标为
(,55).t t -
若13,MEB ENB S S =D D ::则13.ME EN =::
24
34,45(55).3EN MN t t t ∴=∴+-=-::
解得11t =(不合题意舍去),25,3t =540,.39M ??
∴ ???
若31,MEB ENB S S =D D ::则31.ME EN =::
214,454(55).EN MN t t t ∴=∴+-=-::
解得31t =(不合题意舍去),415,t =()15,280.M ∴
∴存在点M ,点M 的坐标为540,39??
???
或(15,280).
9. 如图,⊙M 与x 轴交于A 、B 两点,其坐标分别为)03(,-A 、)01(,B ,直径CD ⊥x 轴于N ,直线CE 切⊙M 于点C ,直线FG 切⊙M 于点F ,交CE 于G ,已知点G 的横坐标为3.
(1) 若抛物线m x x y +--=22经过A 、B 、D 三点,求m 的值及点D 的坐标. (2) 求直线DF 的解析式.
(3) 是否存在过点G 的直线,使它与(1)中抛物线的两个交点的横坐标之和等于4?若存在,请求出满足条件的直线的解析式;若不存在,请说明理由.
[解] (1) ∵抛物线过A 、B 两点,
∴1
1)3(-=?-m
,m =3.
∴抛物线为322
+--=x x y .
又抛物线过点D ,由圆的对称性知点D 为抛物线的顶点. ∴D 点坐标为)41(,-.
(2) 由题意知:AB =4.
∵CD ⊥x 轴,∴NA =NB =2. ∴ON =1. 由相交弦定理得:NA ·NB =ND ·NC , ∴NC ×4=2×2. ∴NC =1. ∴C 点坐标为)11(--,.
设直线DF 交CE 于P ,连结CF ,则∠CFP =90°. ∴∠2+∠3=∠1+∠4=90°. ∵GC 、GF 是切线, ∴GC =GF . ∴∠3=∠4. ∴∠1=∠2. ∴GF =GP . ∴GC =GP . 可得CP =8.
∴P 点坐标为)17(-,
设直线DF 的解析式为b kx y +=
则???-=+=+-174b k b k 解得???????=
-=8
278
5
b k
∴直线DF 的解析式为:8
27
85+-=x y
(3) 假设存在过点G 的直线为11b x k y +=,
(第9题图)
则1311-=+b k ,∴1311--=k b .
由方程组?
??+--=--=32132
11x x y k x k y 得034)2(112
=--++k x k x 由题意得421=--k ,∴61-=k . 当61-=k 时,040<-=?, ∴方程无实数根,方程组无实数解. ∴满足条件的直线不存在.
10.(2004山西)已知二次函数2
12
y x bx c =
++的图象经过点A (-3,6),并与x 轴交于点B (-1,0)和点C ,顶点为P.
(1)求这个二次函数的解析式,并在下面的坐标系中画出该二次函数的图象; (2)设D 为线段OC 上的一点,满足∠DPC =∠BAC ,求点D 的坐标; (3)在x 轴上是否存在一点M ,使以M 为圆心的圆与AC 、PC 所在的直线及y 轴都相切?如果存在,请求出点M 的坐标;若不存在,请说明理由.
[解] (1)解:∵二次函数21
2
y x bx c =++的图象过点A (-3,6),B (-1,0)
得9
362102
b c b c ?-+=????-+=?? 解得132b c =-???=-??
∴这个二次函数的解析式为:21322
y x x =
-- 由解析式可求P (1,-2),C (3,0) 画出二次函数的图像
(2)解法一:易证:∠ACB =∠PCD =45°
又已知:∠DPC =∠BAC ∴△DPC ∽△BAC ∴
DC PC
BC AC
=
易求4AC PC BC === ∴43DC = ∴45333OD =-= ∴5,03D ??
???
解法二:过A 作AE ⊥x 轴,垂足为E.
设抛物线的对称轴交x 轴于F. 亦可证△AEB ∽△PFD 、 ∴
PE EB PF FD
=. 易求:AE =6,EB =2,PF =2